特殊平行四边形动点问题
北师版九年级数学上册 第1章 特殊平行四边形中的旋转、最值、动点问题 专题训练 (含答案)

6.解:(1)根据图形的对称性,本来DF和BF相等,但是“在正方形AEFG绕点A旋转的过程中,线段DF与BF始终相等”不正确.例如,当点F旋转到AB上时,BF最短(小于AB),而这时DF大于AD,即DF大于BF
(2)如图②,若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段与DG始终相等,并以图为例说明理由.
二、最值问题
7.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.4
∴BD,EG互相平分,∴BO=OD,
∴点O为正方形的角平分线的交点,
∴直线EG必过正方形角平分线的交点
20.解:(1)BG=DE,BG⊥DE,证明如下:
延长BG交DE于点H,
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴△BCG≌△DCE(SAS),
(2)当点E,F的运动时间t为何值时,四边形BEDF为矩形?
24.已知点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为点E,F,点Q为斜边AB的中点.
(1)如图①,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系式是;
(2)如图②,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
平行线动点问题的解题技巧

平行线动点问题的解题技巧平行线动点问题是初中数学中常见的一种几何题型,也是高中数学中的重要考点之一。
这类问题常涉及到平行四边形、三角形等图形,需要运用多种定理和方法进行解题。
本文将从以下几个方面详细介绍平行线动点问题的解题技巧。
一、基本概念在介绍解题技巧之前,我们首先需要了解一些基本概念。
平行线指在同一个平面内不相交的两条直线,它们的斜率相等;动点指随着某种规律不断运动的点。
在平行线动点问题中,我们通常需要确定某个动点在运动过程中所处的位置或满足什么条件时两直线之间的距离最短等。
二、解题思路对于平行线动点问题,我们可以采用以下步骤进行分析和求解:1.画图:根据题目所给条件画出图形,并标出所需求的点或长度。
2.列出已知和未知量:根据图形标注出已知量和未知量,并列出方程或条件式。
3.确定关系式:利用几何定理或代数方法推导出各个量之间的关系式。
4.代入求解:将已知量代入关系式中,求解未知量。
三、常用定理和方法1.平行线的性质:平行线在同一平面内,它们的斜率相等。
2.三角形内角和定理:任何一个三角形的三个内角之和等于180度。
3.全等三角形的性质:两个全等的三角形对应边长相等,对应角度相等。
4.相似三角形的性质:两个相似的三角形对应边长成比例,对应角度相等。
5.勾股定理:直角三角形斜边上的正方形面积等于两腰上各自正方形面积之和。
6.垂线定理:在平面直角坐标系中,点(x,y)到直线Ax+By+C=0的距离为|Ax+By+C|/√(A²+B²)。
7.向量法求解:通过向量法求解可以简化计算过程。
利用向量叉积可判断两条线段是否相交,在一些特殊情况下可以极大地减少计算时间。
四、实例分析下面我们以一个具体例子来说明平行线动点问题的解题技巧:已知ABCD为矩形,P、Q分别在AB、CD上滑动,并且AP=PQ=QB。
若M为AC与QP交点,求证:BM=2AM。
解题思路:1.画图:如图所示,画出矩形ABCD和动点P、Q的运动轨迹。
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
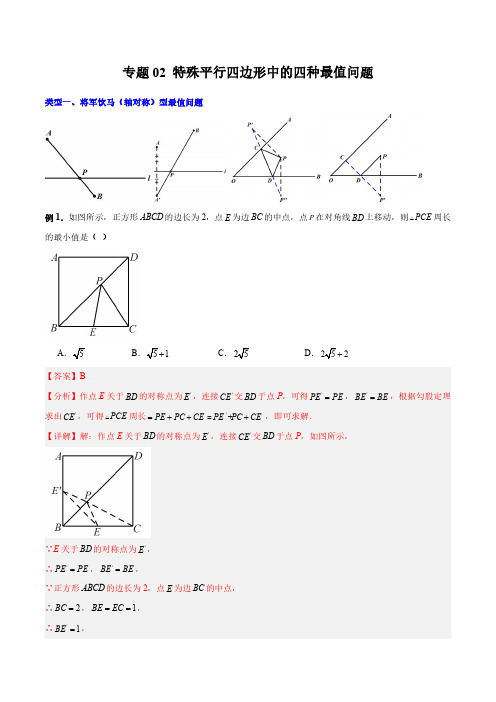
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
初二数学-特殊四边形中的动点问题
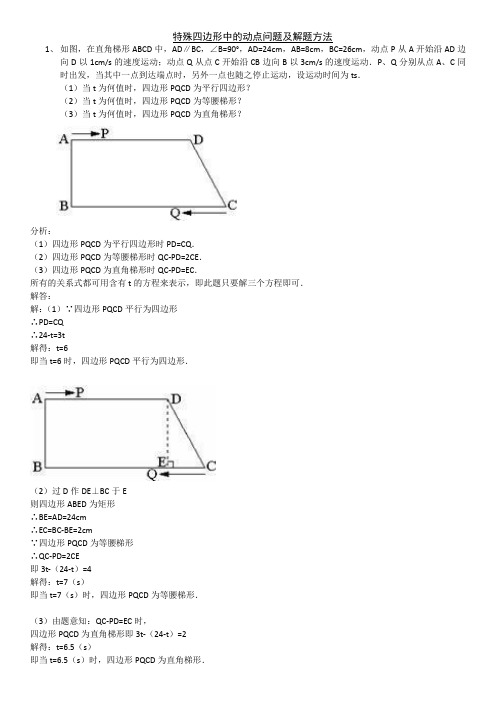
特殊四边形中的动点问题及解题方法1、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?分析:(1)四边形PQCD为平行四边形时PD=CQ.(2)四边形PQCD为等腰梯形时QC-PD=2CE.(3)四边形PQCD为直角梯形时QC-PD=EC.所有的关系式都可用含有t的方程来表示,即此题只要解三个方程即可.解答:解:(1)∵四边形PQCD平行为四边形∴PD=CQ∴24-t=3t解得:t=6即当t=6时,四边形PQCD平行为四边形.(2)过D作DE⊥BC于E则四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即3t-(24-t)=4解得:t=7(s)即当t=7(s)时,四边形PQCD为等腰梯形.(3)由题意知:QC-PD=EC时,四边形PQCD为直角梯形即3t-(24-t)=2解得:t=6.5(s)即当t=6.5(s)时,四边形PQCD为直角梯形.点评:此题主要考查了平行四边形、等腰梯形,直角梯形的判定,难易程度适中.2、如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.分析:(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的性质解答.解答:解:(1)∵CE平分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理,OC=OF,∴OE=OF.(2)当点O运动到AC中点处时,四边形AECF是矩形.如图AO=CO,EO=FO,∴四边形AECF为平行四边形,∵CE平分∠ACB,∴∠ACE= ∠ACB,同理,∠ACF= ∠ACG,∴∠ECF=∠ACE+∠ACF= (∠ACB+∠ACG)= ×180°=90°,∴四边形AECF是矩形.(3)△ABC是直角三角形∵四边形AECF是正方形,∴AC⊥EN,故∠AOM=90°,∵MN∥BC,∴∠BCA=∠AOM,∴∠BCA=90°,∴△ABC是直角三角形.点评:本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.3、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.分析:(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,(2)CB、CN已知,根据勾股定理可求CA=5,即可表示CM;四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;(3)可先根据QN平分△ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t的值.然后根据得出的t的值,求出△MNC的面积,即可判断出△MNC的面积是否为△ABC面积的一半,由此可得出是否存在符合条件的t值.(4)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:①当MP=MC时,那么PC=2NC,据此可求出t的值.②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.综上所述可得出符合条件的t的值.解答:解:(1)∵AQ=3-t∴CN=4-(3-t)=1+t在Rt△ABC中,AC2=AB2+BC2=32+42∴AC=5在Rt△MNC中,cos∠NCM= = ,CM= .(2)由于四边形PCDQ构成平行四边形∴PC=QD,即4-t=t解得t=2.(3)如果射线QN将△ABC的周长平分,则有:MN+NC=AM+BN+AB即:(1+t)+1+t= (3+4+5)解得:t= (5分)而MN= NC= (1+t)∴S△MNC= (1+t)2= (1+t)2当t= 时,S△MNC=(1+t)2= ≠ ×4×3∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分.(4)①当MP=MC时(如图1)则有:NP=NC即PC=2NC∴4-t=2(1+t)解得:t=②当CM=CP时(如图2)则有:(1+t)=4-t解得:t=③当PM=PC时(如图3)则有:在Rt△MNP中,PM2=MN2+PN2而MN= NC= (1+t)PN=NC-PC=(1+t)-(4-t)=2t-3∴[ (1+t)]2+(2t-3)2=(4-t)2解得:t1= ,t2=-1(舍去)∴当t= ,t= ,t= 时,△PMC为等腰三角形点评:此题繁杂,难度中等,考查平行四边形性质及等腰三角形性质.考查学生分类讨论和数形结合的数学思想方法.4、直线y=- 34x+6与坐标轴分别交于A 、B 两点,动点P 、Q 同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿路线O?B?A 运动. (1)直接写出A 、B 两点的坐标; (2)设点Q 的运动时间为t (秒),△OPQ 的面积为S ,求出S 与t 之间的函数关系式;(3)当S= 485时,求出点P 的坐标,并直接写出以点O 、P 、Q 为顶点的平行四边形的第四个顶点M 的坐标.分析:(1)分别令y=0,x=0,即可求出A 、B 的坐标; (2))因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q 由O 到A 的时间是8秒,点P 的速度是2,从而可求出,当P 在线段OB 上运动(或0≤t≤3)时,OQ=t ,OP=2t ,S=t2,当P 在线段BA 上运动(或3<t≤8)时,OQ=t ,AP=6+10-2t=16-2t ,作PD ⊥OA 于点D ,由相似三角形的性质,得 PD=48-6t5,利用S= 12OQ×PD ,即可求出答案;(3)令S= 485,求出t 的值,进而求出OD 、PD ,即可求出P 的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M 的坐标. 解答: 解:(1)y=0,x=0,求得A (8,0)B (0,6), (2)∵OA=8,OB=6,∴AB=10.∵点Q 由O 到A 的时间是 81=8(秒), ∴点P 的速度是 6+108=2(单位长度/秒). 当P 在线段OB 上运动(或O≤t≤3)时, OQ=t ,OP=2t ,S=t2.当P 在线段BA 上运动(或3<t≤8)时, OQ=t ,AP=6+10-2t=16-2t , 如图,做PD ⊥OA 于点D ,由 PDBO=APAB ,得PD= 48-6t5. ∴S= 12OQ?PD=- 35t2+245t .(3)当S= 485时,∵ 485>12×3×6∴点P 在AB 上 当S= 485时,- 35t2+245t= 485 ∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8 AD= 82-(245)2= 325 ∴OD=8- 325= 85 ∴P ( 85, 245) M1( 285, 245),M2(- 125, 245),M3( 125,- 245) 点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象. 5.已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P 从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒.(1)求直线BC 的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的27? (3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围;6.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. ①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等? (2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?四边形中的动点问题课后作业1. 如图,已知AD 与BC 相交于E ,∠1=∠2=∠3,BD =CD ,∠ADB =90°,CH ⊥AB 于H ,CH 交AD 于F.(1)求证:CD ∥AB ;(2)求证:△BDE ≌△ACE ;(3)若O 为AB 中点,求证:OF =12BE.A B D C O P x y AQ CDBP2、如图1―4―2l ,在边长为a 的菱形ABCD 中,∠DAB =60°,E 是异于A 、D 两点的动点,F 是CD 上的动点,满足A E +CF=a ,说明:不论E 、F 怎样移动,三角形BEF 总是正三角形.3、在平行四边形ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F . (1)求证:CF AB =;(2)当BC 与AF 满足什么数量关系时,四边形ABFC 是矩形,并说明理由.4、如图l -4-80,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,过点A 作AG ⊥EB ,垂足为G ,AG 交BD 于F ,则OE=OF . (1)请证明0E=OF(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,AG 交 EB 的延长线于 G ,AG 的延长线交DB 的延长线于点F ,其他条件不变,则仍有OE=OF .问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.5、如图,在梯形ABCD 中,354245AD BC AD DC AB B ====︒∥,,,,∠.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △为等腰三角形.FEDCBAA DCBNE6. 如图所示,有四个动点P 、Q 、E 、F 分别从正方形ABCD 的四个顶点出发,沿着AB 、BC 、CD 、DA 以同样的速度向B 、C 、D 、A 各点移动。
四边形中的动点问题(带答案)
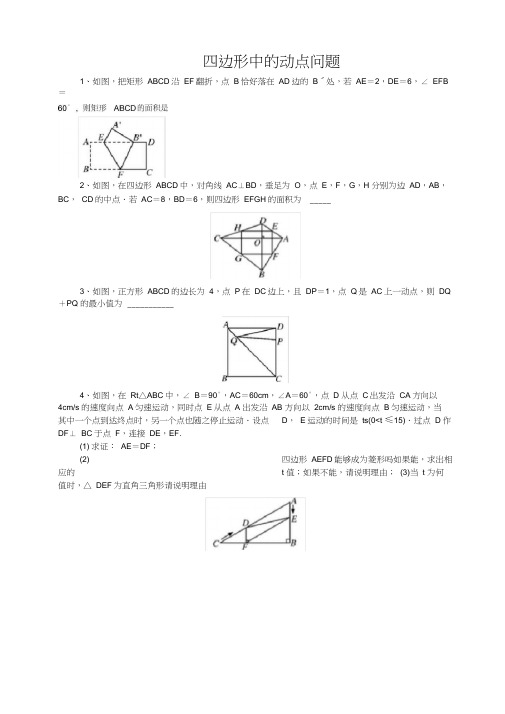
四边形中的动点问题1、如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠ EFB =2、如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H 分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 _____3、如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ +PQ 的最小值为___________4、如图,在Rt△ABC中,∠ B=90°,AC=60cm,∠A=60°,点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动,同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t ≤15).过点 D 作DF⊥ BC于点F,连接DE,EF.(1) 求证:AE=DF;(2) 四边形AEFD能够成为菱形吗如果能,求出相应的t 值;如果不能,请说明理由;(3)当t 为何值时,△ DEF为直角三角形请说明理由5、如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点 A 出发沿射线AG以1cm/s 的速度运动,同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动,设运动时间为t.(1)连接EF,当EF经过AC边的中点 D 时,(1)求证:△ ADE≌△ CDF;:(2)当t 为____ s 时,四边形ACFE是菱形;6、在菱形ABCD中,∠ B=60°,点E在射线BC上运动,∠ EAF=60°,点 F 在射线CD上(1)当点E在线段BC上时(如图1),(1)求证:EC+CF=AB;(2)当点 E 在BC的延长线上时(如图2),线段EC、CF、AB 有怎样的相等关系写出你的猜想,不需证明7、如图,在菱形ABCD中,AB=2,∠ DAB=60°,点E是AD边的中点.点M 是AB边上一动点不与点 A 重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN 是平行四边形;(2)填空:①当AM 的值为____ 时,四边形AMDN 是矩形;②当AM 的值为____ 时,四边形AMDN 是菱形.8、如图,△ ABC中,点O 是边AC上一个动点,过O 作直线MN ∥BC,设MN 交∠ BCA的平分线于点E,交∠ BCA 的外角平分线于点F.(1)探究:线段OE与OF 的数量关系并加以证明;(2)当点O 运动到何处,且△ ABC满足什么条件时,四边形AECF是正方形(3)当点O 在边AC上运动时,四边形BCFE会是菱形吗若是,请证明,若不是,则说明理由.9、如图,已知菱形ABCD中,∠ ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D 重合)分别向直线AB、AD 作垂线,垂足分别为E、F.(1)BD的长是___ ;(2)连接PC,当PE+PF+PC取得最小值时,此时PB 的长是__10、如图,∠ MON=90°,矩形ABCD的顶点A、B分别在边OM,ON 上,当B在边ON 上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O 的最大距离为_____ .11、如图,已知矩形ABCD,AD=4,CD=10,P 是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN 是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN 是菱形;(3)四边形PMEN有可能是矩形吗若有可能,求出AP 的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F 是AC上两动点,分别从A,C两点以相同的速度向C、A 运动,其速度为/s。
2022-2023学年北师大版九年级数学上学期基础知识讲练1-13 特殊平行四边形动点问题

专题1.13 特殊平行四边形动点问题(专项练习)一、单选题类型一、菱形动点问题1.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E,PF⊥AB 于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为()A.4B.245C.6D.4852.如图,在菱形ABCD中,AB=4,点F是CD边上一点,且DF=1,点E是BC边上的一个动点,M、N分别是线段AE、AF的中点,连接EF和MN,当点E在BC边上从点B向点C移动时,线段MN的最小值是()A.1B.1.5C.2D.33.如图,在▱ABCD中,对角线BD⊥AD,AB=16,⊥A=60°,O为BD的中点,E为边AB上一动点,以2cm/s的速度从A点向B点运动,运动时间为ts,连接EO并延长交CD于点F,连接DE、BF,下列结论不成立的是()A.四边形DEBF为平行四边形B.若t=4,则四边形DEBF为菱形C.若t=2,则四边形DEBF为矩形D.若t=6,则四边形DEBF为正方形4.如图,点O为矩形ABCD的对称中心,动点P从点A出发沿AB向点B移动,移动到点B停止,延长PO交CD于点Q,则四边形APCQ形状的变化依次为()A.平行四边形—矩形—平行四边形—矩形B.平行四边形—菱形—平行四边形—矩形C.平行四边形—矩形—菱形—矩形D.平行四边形—菱形—平行四边形类型二、矩形动点问题5.如图,在矩形ABCD中,AB=3,BC=5,点E为CB上一动点(不与点C重合),将⊥CDE沿DE所在直线折叠,点C的对应点C'恰好落在AE上,则CE的长是()A.2B.1C.2D.36.如图,矩形ABCD中,P为AB边上一动点(含端点),E为CD中点,F为CP中点,当点P由B向A运动时,下面对EF变化情况描述正确的是()A.由小变大B.由大变小C.先变大后边小D.先变小后变大7.如图,四边形ABCO是矩形,点D是BC边上的动点(点D与点B、点C不重合),则BAD DOCADO∠+∠∠的值为()A.1B.12C.2D.无法确定8.如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=BN,AD=3AM,E为BC边上一动点,连接DE,将⊥DCE沿DE所在直线折叠得到⊥DC′E,当C′点恰好落在线段MN上时,CE的长为()A.52或2B.52C.32或2D.32类型三、正方形动点问题9.如图,正方形ABCD的面积为225cm,点E为BC边上一动点,点F为CD边上一动点,连接AE、AF,点E和点F在运动的过程中始终保持45EAF∠=︒,则CEF∆的周长()A.10cm B.8cm C.6cm D.4cm10.如图,已知正方形ABCD边长是6,点P是线段BC上一动点,过点D作DE⊥AP 于点E.连接EC,若CE CD=,则⊥CDE的面积是()A.18B.413C.63D.14.411.如图,在边长为6的正方形ABCD中,P是边AD的中点,E是边AB上的一个动点(不与A重合),以线段AE为边在正方形内作等边⊥AEF,M是边EF的中点,连接PM,则在点E运动过程中,PM的最小值是()A.332B.532C.7D.312.如图,在正方形有ABCD中,E是AB上的动点,(不与A、B重合),连结DE,点A关于DE的对称点为F,连结EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG 的延长线于点H ,连接BH ,那么BHAE 的值为( )A .1B .2C .3D .2二、填空题类型一、菱形动点问题13.如图(1)是一张菱形纸片,其中135A ∠=︒,1AB =,点E 为BC 边上一动点.如图(2),将纸片沿AE 翻折,点B 的对应点为B ';如图(3),将纸片再沿AB '折叠,点E 的对应点为E '.当AE '与菱形的边垂直时,BE 的长为______.14.如图,在菱形ABCD 中,⊥ABC =120°,对角线AC 、BD 交于点O ,BD =4,点E 为OD 的中点,点F 为AB 上一点,且AF =3BF ,点P 为AC 上一动点,连接PE 、PF ,则PF ﹣PE 的最大值为 ___.15.如图,已知等边三角形ABC 绕点B 顺时针旋转60︒得到CBD ,E ,F 分别为线段AC 和线段CD 上的动点,且AE CF =,有以下结论:⊥四边形ABDC 为菱形;⊥≅ABE CBF ;⊥BEF 为等边三角形;⊥CFB CGE ∠=∠.其中正确结论有__________.(填序号)16.如图,点E 是菱形ABCD 边AB 的中点,点F 为边AD上一动点,连接EF ,将⊥AEF 沿直线EF 折叠得到⊥A 'EF ,连接A 'D ,A 'C .已知 BC =4,⊥B =120°,当⊥A 'CD 为直角三角形时,线段AF 的长为______.类型二、矩形动点问题17.如图,矩形ABCD 中,AB =3,AD =5.点E 是BC 边上一动点,连接AE .将⊥ABE沿AE 翻折得到⊥AEF ,连接DF .当⊥ADF 的面积为52时,线段BE 的长为______.18.已知矩形ABCD 中,AB =6.点E 为AD 上一个动点,连接CE ,将CDE △沿CE 折叠,点D 落在点F 处,当点F 为线段AB 的三等分点时,AE 的长为______.19.如图,矩形ABCD 中,6AB =,8AD =,动点E 、F 分别从点A 、C 同时出发,以相同的速度分别沿AD 、CB 向终点D 、B 移动,当点E 到达点D 时,运动停止,过点B 作直线EF 的垂线BP ,垂足为点P ,连接CP ,则CP 长的最小值为________.20.如图,矩形ABCD 中,AB =6,BC =8,点E 是CB 上的一个动点,把△DCE 沿DE 折叠,若点C 的对应点C ′刚好落在线段AB 的垂直平分线上,则CE 的长度为_____.类型三、正方形动点问题21.如图,在正方形ABCD 中,点P ,Q 分别是AB ,AD 的中点,点E 是CD 边上一个动点,连接PE ,将四边形PBCE 沿PE 折叠,得到四边形PEFH .(1)若P ,H ,Q 三点在同一条直线上,则BPE ∠的大小为______°;(2)若2AB =,则F ,Q 两点的连线段的最小值为______.22.如图,正方形ABCD 的边长为3,点G 在边AD 上,GD =1,GH ⊥BC 于点H ,点E 是边AB 上一动点(不与点A ,B 重合),EF ⊥CD 于点F ,交GH 于点Q ,点O 、P 分别是EH 和GQ 的中点,连接OP ,则线段OP 的长度为__________.23.如图,在边长为4的正方形ABCD 中,E 、F 分别是边BC 、DC 上的动点,且EF =4,Q 为EF 中点,P 是边AD 上的一个动点,则PQ +PB 的最小值是_____.24.如图,正方形ABCD 中,点E 为BC 边的中点,点P 为边AB上一个动点,连接PE ,以PE 为对称轴折叠PBE △得到PFE △,点B 的对应点为点F ,若2AB =,当射线EF 经过正方形ABCD 边的中点(不包括点E )时,BP 的长为_____________.三、解答题25.如图,将正方形AOBC 放在平面直角坐标系中,点O 是坐标系原点,A 点坐标为(-1,3).(1)求出点B 、C 的坐标:(2)在x 轴上有一动点Q ,过点Q 作PQ ⊥x 轴,交BC 于点P ,连接AP ,将四边形AOBP 沿AP 翻折,当点O 刚好落在y 轴上点E 处时,求点P 、D 的坐标.26.如图,在矩形ABCD 中,6cm AB =,4cm BC =,动点P从点A 出发,以2cm/s 的速度沿AB 向点B 移动,同时,点Q 从点C 出发,以lcm/s 的速度沿CD 向点D 移动(点P 到达点B 停止时,点Q 也随之停止运动),设点P 运动时间为t 秒.(1)试求当t 为何值时四边形APQD 为矩形;(2)P 、Q 两点出发多长时间,线段PQ 的长度为5cm .27.已知矩形ABCD 中,E 是AD边上的一个动点,点F ,G ,H 分别是BC ,BE ,CE 的中点.(1)求证:BGF FHC ≌;(2)当E 是AD 的中点时,四边形EHFG 是什么样的特殊四边形?请证明你的结论.28.如图,在菱形ABCD中,AB=6,⊥DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形;(2)填空:⊥当AM的值为时,四边形AMDN是矩形;⊥当AM的值为时,四边形AMDN是菱形.参考答案1.B【分析】连接BP,通过菱形ABCD的周长为20,求出边长,菱形面积为24,求出SABC的面积,然后利用面积法,SABP+SCBP=SABC,即可求出PE PF的值.解:连接BP,如图,⊥菱形ABCD的周长为20,⊥AB=BC=20÷4=5,又⊥菱形ABCD的面积为24,⊥SABC=24÷2=12,又SABC= SABP+SCBP⊥SABP+SCBP=12,⊥111222AB PF BC PE += , ⊥AB =BC ,⊥()1122AB PE PF += ⊥AB =5,⊥PE +PF =12×25=245. 故选:B .【点拨】本题主要考查菱形的性质,解题关键在于添加辅助线,通过面积法得出等量关系,求出PF +PE 的值.2.B【分析】利用三角形中位线性质求解即可.解:⊥M 、N 分别是线段AE 、AF 的中点,⊥12MN EF =, ⊥点E 在BC 边上从点B 向点C 移动,⊥当点E 运动到点C 的位置时,EF 最小,此时,EF =4-1=3,⊥线段MN 的最小值为1.5.故选:B【点拨】此题考查三角形的中位线的性质,知道当点E 运动到点C 的位置时EF 最小是解答此题的关键.3.D【分析】由▱ABCD ,得EB ∥FD ,再证⊥BOE ⊥△DOF (AAS ),得BE =DF ,即可得出四边形BEDF 是平行四边形,可以判定A ;当t =4时,则AE =2t =8,证⊥ADE 是等边三角形,DE =AE =8,再因四边形DEBF 是平行四边形,所以四边形DEBF 是菱形,可判定B ;当t =2时,则AE =2t =4,同理可得四边形DEBF 是菱形,可判定C ;当t =6时,则AE =2t =12,在AE 上截取AG =AD =8,连接DG ,证⊥BED >120°≠90°,所以四边形DEBF 不可能是正方形,可判定D .解:A 、⊥▱ABCD ,⊥AB ∥CD ,即EB ∥FD ,⊥⊥BEO =⊥DFO ,⊥EBO =⊥FDO ,⊥OB=OD,⊥⊥BOE⊥△DOF(AAS),⊥BE=DF,⊥四边形BEDF是平行四边形,故此选项正确,不符合题意;B、当t=4时,则AE=2t=8,⊥AD⊥BD,⊥⊥ADB=90°,在Rt△ABD中,⊥ADB=90°,⊥A=60°,⊥⊥ABC=30°,⊥AD=12AB=8,⊥AD=AE,⊥⊥ADE是等边三角形,⊥DE=AE=8,⊥四边形DEBF是平行四边形,⊥四边形DEBF是菱形;故此选项正确,不符合题意;C、当t=2时,则AE=2t=4,⊥4182AEAD==,81162ADAB==,AE ADAD AB=,⊥⊥A=⊥A,⊥⊥ADE⊥⊥ABD,⊥⊥AED=⊥ADB=90°,⊥⊥BED=90°,⊥四边形DEBF是平行四边形,⊥四边形DEBF是矩形;故此选项正确,不符合题意;D、当t=6时,则AE=2t=12,在AE上截取AG=AD=8,连接DG,如图,⊥⊥A=60°,⊥⊥ADG是等边三角形,⊥⊥AGD=60°,⊥⊥AED<60°,⊥⊥BED>120°≠90°,⊥四边形DEBF不可能是正方形;故此选错误,符合题意;故选:D.【点拨】本题考查平行四边形的判定与性质,矩形的判定,菱形的判定,正方形的判定,熟练掌握平行四边形的判定,矩形的判定,菱形的判定,正方形的判定是解题的关键.4.B【分析】根据对称中心的定义,矩形的性质,可得四边形APCQ的形状变化情况,这个四边形首先是平行四边形,当对角线互相垂直时,是菱形,然后又是平行四边形,最后点A、B重合时是矩形.解:观察图形可知,四边形APCQ形状的变化一次为:平行四边形—菱形—平行四边形—矩形故选:B.【点拨】本题考查中心对称、矩形的性质、平行四边形的判定与性质、菱形的判定等知识,在重要考点,掌握相关知识是解题关键.5.B【分析】由矩形的性质得出⊥B=⊥C=90°,AD=BC=5,CD=AB=3,由折叠的性质得C'D=CD=3,C'E=CE,由勾股定理得出AC',在Rt△ABE中,由勾股定理得出方程,解方程即可.解:⊥四边形ABCD是矩形,⊥⊥B=⊥C=90°,AD=BC=5,CD=AB=3,由折叠的性质得:C'D=CD=3,C'E=CE,⊥DC'E=⊥C=90°,⊥⊥AC'D=90°,⊥AC,设CE=C'E=x,在Rt△ABE中,BE=5-x,AE=x+4,由勾股定理得:(5-x)2+32=(x+4)2,解得:x=1,故选:B.【点拨】本题考查了翻折变换的性质、矩形的性质、勾股定理等知识;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程是解题的关键.6.B【分析】连接DP,则EF为⊥CDP的中位线,当点P由B向A运动时,DP由大变小,利用中位线的性质即可得到结论.解:连接DP,⊥E为CD中点,F为CP中点,⊥EF为⊥CDP的中位线,DP,⊥EF=12在Rt⊥DAP中,由勾股定理得,DP当点P由B向A运动时,AP的长度逐渐减小,⊥DP减小,⊥EF由大变小,故选:B.【点拨】本题考查了矩形的性质和中位线的性质,解题的关键是连接DP,构造三角形中位线.7.A【分析】过点D 作//DE AB 交AO 于点E ,由平行的性质可知,BAD ADE DOC ODE ∠=∠∠=∠,等量代换可得BAD DOC ADO∠+∠∠的值. 解:如图,过点D 作//DE AB 交AO 于点E ,四边形ABCO 是矩形//AB OC∴//DE AB //,//AB DE DE OC ∴,BAD ADE DOC ODE ∴∠=∠∠=∠1BAD DOC BAD DOC BAD DOC ADO ADE ODE BAD DOC∠+∠∠+∠∠+∠∴===∠∠+∠∠+∠故选:A. 【点拨】本题主要考查了平行线的性质,灵活的添加辅助线是解题的关键.8.B【分析】由矩形的性质得到CD =AB =5,AD =BC =6,⊥A =90°,根据已知条件推出四边形MNCD的矩形,得到⊥DMN =⊥MNC =90°,MN =CD =5,根据折叠的性质得到C ′D =CD =5,C′E=CE ,根据勾股定理得到MC ′3,再由勾股定理即可得到结论.解:设CE =x ,则C ′E =x ,⊥矩形ABCD 中,AB =5,BC =6,⊥CD =AB =5,AD =BC =6,AD ⊥BC ,⊥点M ,N 分别在AD ,BC 上,且3AM =AD ,BN =AM ,⊥DM =CN =4,⊥四边形CDMN 为平行四边形,⊥⊥NCD =90°,⊥四边形MNCD 是矩形,⊥⊥DMN =⊥MNC =90°,MN =CD =5由折叠知,C ′D =CD =5,⊥MC ′3,⊥C ′N =5﹣3=2,⊥EN =CN ﹣CE =4﹣x ,⊥C ′E 2﹣NE 2=C ′N 2,⊥x 2﹣(4﹣x )2=22,解得,x =52,即CE =52. 故选:B .【点拨】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,正确的识别图形是解题的关键.9.A【分析】先根据正方形的性质得AB =AD =5cm ,⊥BAD =⊥B =90°,把⊥ADF 绕点A 顺时针旋转90°可得到⊥ABG ,接着利用“SAS ”证明 EAG EAF ≌,得到EG =EF =BE +DF ,然后利用三角形周长的定义得到△CEF 的周长=CE +CF +BE +DF =CB +CD ,由此即可解决问题.解:⊥四边形ABCD 为正方形,⊥AB =AD ,⊥BAD =⊥B =90°,又正方形ABCD 的面积为225cm ,⊥5cm AB BC CD DA ====⊥把△ADF 绕点A 顺时针旋转90°可得到△ABG ,如图,⊥AG =AF ,BG =DF ,⊥GAF =90°,⊥ABG =⊥B =90°,⊥点G 在CB 的延长线上,⊥⊥EAF =45°,⊥⊥EAG =⊥GAF -⊥EAF =45°,⊥⊥EAG =⊥EAF ,在△EAG 和△EAF 中,AE AE EAG EAF AG AF ⎧⎪∠∠⎨⎪⎩===,⊥ EAG EAF ≌(SAS ),⊥EG =EF ,而EG =BE +BG =BE +DF ,⊥EF =BE +DF ,⊥CEF △的周长=CE +CF +BE +DF =CB +CD =5+5=10cm .故选:A .【点拨】本题考查了全等三角形的判定与性质、正方形的性质等知识,解题的关键是利用旋转添加辅助线构造全等三角形解决问题.10.D【分析】根据正方形的性质和全等三角形的判定可以得到△ADE 和△DCF 全等,然后即可得到CF 和DE 的关系,根据等腰三角形的性质可以得到DF 和DE 的关系,再根据勾股定理可以得到DF 2的值,然后即可计算出△CDE 的面积.解:作CF ⊥ED 于点F ,如图所示,⊥四边形ABCD 是正方形,⊥AD =DC ,⊥CDA =90°,⊥⊥ADE +⊥FDC =90°,⊥CF ⊥DE ,CD =CE ,⊥EF =DF =12DE ,⊥CFD =90°,⊥⊥FDC +⊥DCF =90°,⊥⊥ADE =⊥DCF ,在△ADE 和△DCF 中,AED DFC ADE DCF AD DC ∠=∠⎧⎪∠=∠⎨⎪=⎩ ,⊥⊥ADE⊥⊥DCF(AAS),⊥DE=CF,⊥DF=12CF,⊥⊥CFD=90°,CD=6,⊥DF2+CF2=CD2,即DF2+(2DF)2=62,解得DF2=7.2,⊥S△CDE=2222DE CF DF DF⋅⋅==2DF2=2×7.2=14.4,故选:D.【点拨】本题考查正方形的性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质,解答本题的关键是求出DF2的值.11.A【分析】连接PF,由已知,M在⊥F AE的平分线上,当PM⊥AM时,PM最小,于是得到当P,F,M三点共线时,PM的值最小,连接AM,根据等边三角形的性质得到AM⊥EF,⊥EAM=30°,求得⊥P AM=60°,根据三角函数的定义即可得到结论.解:如图,连接AM,⊥P是边AD的中点,AD=6,⊥AP=3,连接PF,由已知,M在⊥F AE的平分线上,当PM⊥AM时,PM最小⊥此时P,F,M三点共线时连接AM,⊥⊥AEF是等边三角形,M是边EF的中点,⊥AM⊥EF,⊥EAM=30°,⊥⊥P AM=60°,⊥PM AP = 故选 A . 【点拨】本题考查了正方形的性质,等边三角形的性质,解直角三角形,正确的理解题意是解题的关键.12.B【分析】作辅助线,构建全等三角形,证明⊥DAE ⊥⊥ENH ,得AE =HN ,AD =EN ,再说明⊥BNH 是等腰直角三角形,可得结论.解:如图,在线段AD 上截取AM ,使AM =AE ,,⊥AD =AB ,⊥DM =BE ,⊥点A 关于直线DE 的对称点为F ,⊥⊥ADE ⊥⊥FDE ,⊥DA =DF =DC ,⊥DFE =⊥A =90°,⊥1=⊥2,⊥⊥DFG =90°,在Rt ⊥DFG 和Rt ⊥DCG 中,⊥DF DC DG DG=⎧⎨=⎩, ⊥Rt ⊥DFG ⊥Rt ⊥DCG (HL ),⊥⊥3=⊥4,⊥⊥ADC =90°,⊥⊥1+⊥2+⊥3+⊥4=90°,⊥2⊥2+2⊥3=90°,⊥⊥2+⊥3=45°,即⊥EDG =45°,⊥EH ⊥DE ,⊥⊥DEH =90°,⊥DEH 是等腰直角三角形,⊥⊥AED +⊥BEH =⊥AED +⊥1=90°,DE =EH ,⊥⊥1=⊥BEH ,在⊥DME 和⊥EBH 中,⊥1DM BE BEHDE EH =⎧⎪∠=∠⎨⎪=⎩,⊥⊥DME ⊥⊥EBH (SAS ),⊥EM =BH ,Rt ⊥AEM 中,⊥A =90°,AM =AE ,⊥EM =,⊥BH ,即BHAE. 故选:B .【点拨】本题考查了正方形的性质,全等三角形的判定定理和性质定理,等知识,解决本题的关键是作出辅助线,利用正方形的性质得到相等的边和相等的角,证明三角形全等.13【分析】分AE BC '⊥和AE AB '⊥两种情况求解即可.解:⊥当AE BC '⊥时,如图1,⊥四边形ABCD 是菱形,⊥135C BAD ∠=∠=︒,180C B ∠+∠=︒,BC //AD ,⊥45B ∠=︒,90DAF ∠=︒,⊥1359045BAF ∠=︒-︒=︒,⊥45B BAF ∠=∠=︒,⊥AF =BF ,在Rt BAF ∆中,222,1AB AF BF AB =+=,⊥1)AF BF AB ==== 由折叠得,⊥114515,33BAE EAB B AE BAE ''''︒︒=∠=∠=∠=⨯= ⊥⊥151530EAE EAB B AE ︒︒︒''+'=∠+∠==, 又tan ,EF EAF AF∠=⊥tan EF AF EAF =⋅∠=,⊥BE BF EF =-== ⊥当AE AB '⊥时,如图2,即⊥90BAE '︒=,⊥⊥''30B AE B AE BAE ︒∠'=∠==',过点E 作EG AB ⊥于点G ,则,EG BG AG ==,又⊥AB BG AG =+,1EG =,⊥1EG =, ⊥BE ==综上,BE【点拨】本题主要考查了菱形的性质,折叠的性质,用正切值求边长,勾股定理等知识,熟练掌握相关知识是解答本题的关键.14.1【分析】取OB 中点E ',连接PE ',作射线FE '交AC 于点P '.则PE =PE ',当P 与P '重合,P '、E '、F 三点在同一直线上时,PF ﹣PE '有最大值,即为FE '的长.解:如图,取OB 中点E ',连接PE ',作射线FE '交AC 于点P '.则PE =PE ',⊥PF﹣PE=PF﹣PE'≤FE',当P与P'重合,P'、E'、F三点在同一直线上时,PF﹣PE'有最大值,即为FE'的长,⊥在菱形ABCD中,⊥ABC=120°,⊥⊥ABD=60°,⊥DAB=60°,⊥⊥ABD为等边三角形.⊥AB=BD=AD=4.⊥OD=OB=2.⊥点E'为OB的中点,E'B=1,AF=3BF,⊥BF1AB=1,4⊥⊥ABD=60°,⊥⊥BE'F为等边三角形,⊥E'F=FB=1.故PF﹣PE的最大值为1.故答案为:1.【点拨】本题考查了轴对称﹣最大值问题、菱形的性质、等边三角形的判定与性质,熟练运用轴对称的性质和三角形三边关系是解题的关键.15.⊥⊥⊥⊥【分析】⊥由等边三角形旋转的性质可知AB=AC=BD=CD即可判断;⊥利用SAS即可判定△ABE⊥⊥CBF;⊥由全等三角形的性质可知BE=BF,⊥ABE=⊥CBF,再结合⊥ABC=⊥ABE+EBC=60°,即可求出⊥EBF=60°,即证明△BEF为等边三角形;⊥由⊥CFB=⊥CFG+⊥BFG,⊥CGE=⊥CFG+FCG即可判断.解:由等边三角形旋转的性质可知AB=AC=BD=CD,即四边形ABCD为菱形故⊥正确.⊥在△ABE和△CBF中,AB CB BAE BCF AE CF ⎧⎪∠∠⎨⎪⎩===,⊥⊥ABE ⊥⊥CBF (SAS ),故⊥正确;⊥⊥ABE ⊥⊥CBF ,⊥BE =BF ,⊥ABE =⊥CBF ,⊥⊥ABC =⊥ABE +⊥EBC =60°,⊥⊥CBF +⊥EBC =60°,即⊥EBF =60°,⊥⊥BEF 为等边三角形,故⊥正确;⊥⊥CFB =⊥CFG +⊥BFG ,⊥CGE =⊥CFG +FCG ,⊥FCG =⊥BFG =60°,⊥⊥CFB =⊥CGE ,故⊥正确;综上,⊥⊥⊥⊥都正确,故答案为:⊥⊥⊥⊥.【点拨】本题考查了等边三角形的判定与性质,图形旋转的性质,菱形的判定,全等三角形的判定与性质,三角形外角性质,熟练掌握这些知识并利用数形结合的思想解题的关键.16.2或2【分析】分当=90CA D '︒∠时和当=90A DC '︒∠时两种情况讨论求解即可.解:如图1所示,当=90CA D '︒∠时,取CD 中点H ,连接A H ', ⊥1=2A H CD DH '=, ⊥四边形ABCD 是菱形,E 为AB 中点, ⊥1122AE AB CD A H '===,⊥A =180°-⊥B =60°,AB CD , 由折叠的性质可知AE A E '=,AF A F '=,AEF A EF '∠=∠⊥A E A H AB AD ''+==,连接EH ,⊥=AE DH A H '=,AE DH ∥⊥四边形AEHD 是平行四边形,⊥=120AEH B =︒∠∠,AD EH =,⊥由三角形三边的关系可知,当点A '不在线段EH 上时,必有A E A H EH AD ''+>=,这与A H A E CD AD ''+==矛盾,⊥E 、A '、H 三点共线,⊥=60AEF A EF '=︒∠∠,⊥⊥AEF 为等边三角形, ⊥11222AF AE AB BC ====; 如图2所示,当=90A DC '︒∠时,连接BD ,ED ,过点F 作FG ⊥AB 于G ,⊥⊥ABC =120°,四边形ABCD 是菱形,⊥AB =AD ,⊥A =60°,⊥⊥ABD 是等边三角形,⊥E 是AB 中点,⊥DE ⊥AB ,⊥⊥ADE =30°,⊥⊥EDC =90°,⊥此时D A E '、、三点共线,由翻折的性质可得==45AEF A EF '︒∠∠,⊥FG ⊥AE ,⊥A =60°,⊥AEF =45°,⊥⊥AFG =30°,⊥GFE =45°,⊥AF =2AG ,EG =FG ,⊥FG AF ==, ⊥11222AE AG GE AB BC =+===,⊥122AF AF +=,⊥2AF =,故答案为:2或2.【点拨】本题主要考查了菱形的性质,等边三角形的性质与判定,折叠的性质,三角形三边的关系,含30度角的直角三角形的性质,平行四边形的性质与判定,直角三角形斜边上的中线等等,利用分类讨论的思想求解是解题的关键.17.2【分析】过点F作AD的垂线,交AD于M,交BC于N,求出AM长,再根据勾股定理列出方程求解即可.解:过点F作AD的垂线,交AD于M,交BC于N,由翻折可知,AB=AF=3,BE=EF,⊥⊥ADF的面积为52,⊥15 22 AD FM=,⊥AD=5,⊥1FM=,⊥AM==⊥⊥ABN=⊥BAN=⊥AMN=90°,⊥四边形AMNB是矩形,⊥AM BN==⊥BNM=90°,AB=MN=3,⊥FN=MN-FM=2,⊥222)2BE BE=+,解得,BE=【点拨】本题考查了矩形的判定与性质,勾股定理,解题关键是根据面积求出线段长,利用勾股定理列方程.18【分析】 根据题意可求出123BF AB ==,243AF AB ==.再根据折叠的性质和矩形的性质可得出6CF CD AB ===,DE EF =,从而可利用勾股定理求出AD BC ==AE x =,则DE EF x ==.在Rt AEF 中,再次利用勾股定理即可列出关于x 的等式,解出x 即得出答案.解:⊥AB =6,点F 为线段AB 的三等分点, ⊥123BF AB ==,243AF AB ==, 根据折叠和矩形的性质可得出6CF CD AB ===,DE EF =,⊥AD BC ===设AE x =,则DE EF x ==.⊥在Rt AEF 中,222AE AF EF +=,⊥2224)x x +=, 解得:x = ⊥AE =【点拨】本题考查矩形与折叠,勾股定理等知识.利用数形结合的思想是解题关键. 19.4【分析】因为EF 不论如何运动,EF 的中点始终在矩形的对角线的交点上,所以当EF ⊥BC 时,即,E 、F 分别是AD 、BC 的中点时,CP 取得最小值,此时P 与F 重合,即可求解.解:⊥动点E 、F 分别从点A 、C 同时出发,以相同的速度分别沿AD 、CB 向终点D 、B 移动,⊥AE =CF⊥EF 不论如何运动,EF 的中点始终在矩形的对角线的交点上,⊥当EF ⊥BC 时,即,E 、F 分别是AD 、BC 的中点时,CP 取得最小值,此时P 与F 重合,⊥CP =142BC = 故答案为:4【点拨】本题考查了矩形的性质,弄清题意找到P 的位置是解题的关键.20.【分析】利用垂直平分线的性质得出CC '=DC '= DC ,则⊥D C 'C 是等边三角形,进而利用勾股定理得出答案.解:如下图,连接 ,⊥点C '在AB 的垂直平分线上,⊥点C '在DC 的垂直平分线上,⊥CC '=DC '= DC ,则⊥D C 'C 是等边三角形,设CE = x ,易得DE = 2x ,由勾股定理得: (2x )2 -x 2= 62,解得: x =(负值舍去)故答案为:【点拨】本题考查了矩形的性质、翻折变换的性质、勾股定理,等边三角形的性质,解题的关键是证明⊥DC C '是等边三角形.21. 67.5-【分析】(1)易得45APQ ∠=︒,利用翻折的性质得到67.5BPE HPE ∠∠==︒;(2)连接PQ ,PE ,PC ,易证PBC PHF △△≌,得到PF PC ==PQ =P ,Q ,F 在同一条直线上时,FQ 最小,计算可得.解:(1)如图1,易得45APQ ∠=︒,⊥67.5BPE HPE ∠∠==︒,故答案为:67.5;(2)如图2,连接PQ ,PE ,PC ,易证PBC PHF △△≌,⊥PF PC ==PQ =当P ,Q ,F 在同一条直线上时,FQ 最小,--【点拨】此题考查了正方形的性质,全等三角形的判定及性质,勾股定理,正确掌握翻折的性质是解题的关键.22【分析】取QH 的中点M ,连接OM ,由正方形及矩形的性质得出AG =EQ ,GH =CD =3,⊥EQH =90°,求出QE =2,由三角形中位线定理得出OM =12QE =1,OM∥EQ ,求出PM 的长,根据勾股定理可得出答案.解:取QH 的中点M ,连接OM , ⊥四边形ABCD 是正方形,⊥⊥A =⊥B =⊥C =⊥D =90°,⊥EF ⊥CD ,GH ⊥BC ,⊥四边形AEQG ,四边形GHCD 为矩形,⊥AG =EQ ,GH =CD =3,⊥EQH =90°,⊥DG=1,⊥AG=EQ=2,⊥O,M分别为EH,QH的中点,⊥OM=12QE=1,OM∥EQ,⊥⊥OMP=90°,⊥P为GQ的中点,M为QH的中点,⊥PQ=12GQ,QM=12QH,⊥PM=PQ+QM=1113 2222 QG QH GH+==,⊥OP.【点拨】本题主要考查了正方形和矩形的性质,勾股定理的应用,正确作出辅助线是解题得关键.23.2【分析】延长BA到B′,使B′A=AB,PB+PQ=PB′+PQ,当B′,P,Q三点共线时,PB′+PQ的值最小,根据题意,点Q的轨迹是以C为圆心,2为半径的圆弧上,圆外一点B′到圆上一点Q距离的最小值B′Q=B′C﹣2,根据勾股定理即可得到结论.解:如图所示:要,延长BA到B′,使B′A=AB,PB+PQ=PB′+PQ,当B′,P,Q三点共线时,PB′+PQ的值最小,根据题意,点Q的轨迹是以C为圆心,2为半径的圆弧上,圆外一点B′到圆上一点Q距离的最小值B′Q=CB′﹣2,⊥BC=AB=4,⊥BB′=8,⊥B ′C B ′Q =B ′C ﹣2=2,⊥PB ′+PQ 的值最小是2,即PQ +PB 的最小值是2,故答案为:2.【点拨】本题考查了正方形的性质、轴对称-最短路线问题,勾股定理,正确的找到P 点的位置是解题的关键.24.11【分析】分EF 经过正方形ABCD 另三边三种情况求解即可解:⊥EF 经过CD 边中点O 时,⊥四边形ABCD 是正方形,⊥AB=BC=CD=DA ,90C B ∠=∠=︒,⊥点O 是CD 边中点,点E 是BC 边中点, ⊥11,22OC CD EC BC ==. ⊥CE=CO =1,⊥45CEO ∠=︒, 由折叠得11(180)((18045)67.522FEP BEP CEO ∠=∠=︒-∠=︒-︒=︒, ⊥22.5FPE BPE ∠=∠=︒.⊥45FPB FPE BPE ∠=∠+∠=︒,作FG ⊥AB 于G ,作EH ⊥FG 于H ,如图,设FH=x ,则BG=EH=FH=x ,⊥45BPF ∠=︒,⊥PG =FG=x +1,⊥BP =2x +1,由勾股定理得1)PF x =+,由折叠得PB=PF ,⊥211)x x +=+,解得x =.⊥12BP =>,⊥点P 在AB 外,不符合题意;⊥EF 经过AD 边中点O ',如图, 此时,190452FEP BEP ∠=∠=⨯︒=︒, ⊥BP=BE =1;⊥EF 经过AB 中点O '',如图,⊥O ''B=BE ,⊥45EO B ''∠=︒.由折叠得90PFE B ∠=∠=︒,设PF=x ,则,O P PB x ''==,1x +=,⊥1,即1,综上,BP 的长为11,故答案为:11.【点拨】此题考查了正方形的性质,折叠的性质,勾股定理,灵活运用分类讨论思想是解答本题的关键.25.(1)B (3,1)、C (2,4) (2)D (3,5)、P (73,3) 【分析】(1)分别过点A、B做x轴的垂线,垂足为G、H∥证明⊥AGO⊥⊥OHB,根据三角形全等的性质可得出结论;(2)根据对称性和全等的性质可得D(3,5),再求出BC的解析式y=-3x+10,从而可求出点P坐标.解:(1)分别过点A、B做x轴的垂线,垂足为G、H;⊥四边形AOBC是正方形⊥AO= BO,⊥AOB =90°⊥⊥AGO⊥⊥OHB⊥ AG= OH,OG= BH⊥A点坐标为(-1,3)⊥ AG =3,OG=1⊥ OH =3,BH=]⊥B(3,1)同理可得C(2,4)(2)⊥点O与点E关于AP成轴对称⊥AO=AE,AP⊥OE且平分OE⊥E(0,6)根据上面全等可以得到D(3,5)⊥点P的纵坐标是3⊥点P在直线BC上⊥设直线BC为y = kx + b,由条件可得20 30k bk b+=⎧⎨+=⎩,解之得-310k b =⎧⎨=⎩ ⊥y =-3x +10当y =3时,73x =⊥P (73,3) 【点拨】本题主要考查了坐标与图形,一次函数图象上点的坐标特征,正确作出辅助线构造全等三角形是解答本题的关键.26.(1)2;(2)当出发1s 或3s 时,线段PQ 的长度为5cm .【分析】(1)由矩形的性质,得AP DQ =,继而列出关于t 的一元一次方程即可解题; (2)过点P 作PE CD ⊥于点E ,先证明四边形APED 是矩形,再根据矩形的性质解得EQ 的长,最后在Rt PQE △中,根据勾股定理解题即可.解:(1)四边形APQD 为矩形.AP DQ ∴=,26t t ∴=-,36t =,2t ∴=,∴当2t =时四边形APQD 为矩形;(2)过点P 作PE CD ⊥于点E ,90A D DEP ∠∠∠===︒,∴四边形APED 是矩形.2AP DE t ∴==,63EQ CD DE CQ t ∴=--=-,在Rt PQE △中,222PE EQ PQ +=,2(63)9t -=,1t =,3t =,答:当出发1s或3s时,线段PQ的长度为5cm.【点拨】本题考查矩形的判断与性质、勾股定理,涉及解一元一次方程、解一元二次方程等知识,是重要考点,难度较易,掌握相关知识是解题关键.27.(1)详见分析;(2)当E是AD的中点时,四边形EHFG是菱形,证明详见分析【分析】(1)根据三角形中位线定理和全等三角形的判定解答即可;(2)根据菱形的判定解答即可.解:(1)⊥点F,G,H分别是BC,BE,CE的中点,⊥FH⊥BE,12FH BE=,BF=FC,⊥⊥CFH=⊥FBG,FH=BG,⊥⊥BGF⊥⊥FHC;(2)当E是AD的中点时,四边形EHFG是菱形.当E是AD的中点时,AE=ED,⊥四边形ABCD是矩形,⊥AB=CD,⊥A=⊥D=90︒,⊥⊥ABE⊥⊥DCE,⊥BE=CE,⊥BE=2FH,CE=2FG,⊥FH=FG =1122BE CE EG EH===,⊥EH=HF=FG=GE,⊥四边形EGFH是菱形.【点拨】本题考查了菱形的判定,全等三角形的判定和性质,三角形中位线定理,关键是根据全等三角形的判定和菱形的判定解答.28.(1)见分析(2)⊥3;⊥6【分析】(1)利用AAS证△NDE⊥⊥MAE,得出NE=ME,进而得出结论;(2)⊥当四边形AMDN是矩形时⊥AMD=90°,由菱形的性质得AD=6,进而求出AM的值;⊥当四边形AMDN是菱形时,AM=DM,由⊥DAB=60°,得出△AMD为等边三角形,进而求出AM的值.解:(1)证明:⊥四边形ABCD是菱形⊥AB⊥CD⊥⊥DNE=⊥AME,⊥NDE=⊥MAE⊥点E是AD边的中点⊥AE=DE⊥△NDE⊥⊥MAE(AAS)⊥NE=ME⊥四边形AMDN是平行四边形(2)解:⊥当四边形AMDN是矩形时⊥AMD=90°在菱形ABCD中AD=AB=6⊥⊥DAB=60°⊥⊥ADM=30°⊥AM=12AD=3故答案为:3.⊥当四边形AMDN是菱形时,AM=DM⊥⊥DAB=60°⊥⊥AMD为等边三角形⊥AM=AD在菱形ABCD中AD=AB=6⊥AM=6故答案为:6.【点拨】本题考查平行四边形的判定,矩形和菱形的性质,等边三角形的性质,30°的直角三角形的性质,熟练地掌握平行四边的判定方法和矩形菱形的性质是解决问题的关键.。
初二数学《平行四边形中的动点问题》(附练习及答案)

四边形中的动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或直线上运动的一类开放性题目。
解决这类问题关键是动中求静,灵活运用有关数学知识。
数学思想:分类思想、函数思想、方程思想、数形结合思想、转化思想,其注重对几何图形运动变化能力的考查。
这类类问题从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
选择基本的几何图形,让学生经历探索的过程,以能力立意,考查自主探究能力,促进培养学生解决问题的能力。
解决这类问题首先要在动点的运动过程中观察图形的变化情况,需要画出图形在不同位置的情况,才能做好计算推理的过程;其次在变化中找到不变量的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
动点问题题型方法归纳:动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就四边形中的动点问题的常见题型作简单介绍,解题方法、关键给以点拨。
1、如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB =60°,则矩形ABCD的面积是_____________2、如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH 的面积为________(第1题)(第2题)(第3题)3、如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为____________4、如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t s(0 < t ≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由5、如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s 的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s);(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)求当t为何值时,四边形ACFE是菱形;(3)是否存在某一时刻t,使以A、F、C、E为顶点的四边形内角出现直角?若存在,求出t的值;若不存在,请说明理由.6、在菱形ABCD中,∠B=60°,点E在射线BC上运动,∠EAF=60°,点F在射线CD上(1)当点E在线段BC上时(如图1),(1)求证:EC+CF=AB;(2)当点E在BC的延长线上时(如图2),线段EC、CF、AB有怎样的相等关系?写出你的猜想,不需证明7、如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN是平行四边形;(2)填空:①当AM的值为______时,四边形AMDN是矩形;②当AM的值为______时,四边形AMDN是菱形.8、如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)探究:线段OE与OF的数量关系并加以证明;(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?(3)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由.9、如图,已知菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D重合)分别向直线AB、AD作垂线,垂足分别为E、F.(1)BD的长是______;(2)连接PC,当PE+PF+PC取得最小值时,此时PB的长是______(第9题)(第10题)10、如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为______.11、如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD 的中点.(1)求证:四边形PMEN是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN是菱形;(3)四边形PMEN有可能是矩形吗?若有可能,求AP的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F 是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s。
人教版八年级数学下册-难点探究专题(选做):特殊四边形中的综合性问题

难点探究专题(选做):特殊四边形中的综合性问题◆类型一特殊平行四边形的动态探究问题一、动点问题1.(2016·枣庄中考)如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=63,∠BAD=60°,且AB>6 3.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP的最大值和最小值.二、图形的变换问题2.如图①,点O是正方形ABCD两条对角线的交点.分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG,OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.①在旋转过程中,当∠OAG′是直角时,求α的度数;②若正方形ABCD的边长为1,在旋转过程中,求AF′的最大值和此时α的度数,直接写出结果不必说明理由.◆类型二四边形间的综合性问题3.(2016·德州中考)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图②,点P是四边形ABCD内一点,且满足P A=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)参考答案与解析1.解:(1)如图①,过点P 作PG ⊥EF 于点G ,H 为PE 的中点,连接GH ,∴∠PGE=90°,GH =PH =HE =12PE =3.∵PF =PE ,∴∠FPG =∠EPG ,FG =GE =12EF =3 3.在Rt △PGE 中,由勾股定理得PG =PE 2-GE 2=62-(33)2=3.∴PG =GH =PH ,即△GPH 为等边三角形,∴∠GPH =60°,∴∠FPE =∠FPG +∠GPE =2∠GPE =2×60°=120°.(2)如图①,过点P 作PM ⊥AB 于点M ,作PN ⊥AD 于点N ,∴∠ANP =∠AMP =90°.∵AC为菱形ABCD 的对角线,∴∠DAC =∠BAC =12∠DAB =30°,PM =PN .在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF ,∴Rt △PME ≌Rt △PNF ,∴ME =NF .∵∠P AM =30°,AP=10,∴PM =12AP =5.由勾股定理得AM =P A 2-PM 2=5 3.在△ANP 和△AMP 中,⎩⎪⎨⎪⎧∠NAP =∠MAP ,∠ANP =∠AMP =90°,AP =AP ,∴△ANP ≌△AMP ,∴AN =AM =5 3.∴AE +AF =(AM +ME )+(AN -NF )=AM +AN +ME -NF =10 3.(3)如图②,△EFP 的三个顶点分别在AB ,AD ,AC 上运动,点P 在P 1,P 之间运动.P 1O =PO =12PE =3,AE =EF =63,AO =AE 2-EO 2=9.∴AP 的最大值为AO +OP =12,AP 的最小值为AO -OP 1=6.2.(1)证明:如图,延长ED 交AG 于点H .∵四边形ABCD 与OEFG 均为正方形,∴OA =OD ,OG =OE ,∠AOG =∠DOE =90°,∴Rt △AOG ≌Rt △DOE ,∴∠AGO =∠DEO .∵∠AGO +∠GAO =90°,∴∠DEO +∠GAO =90°,∴∠AHE =90°,即DE ⊥AG ;(2)解:①在旋转过程中,∠OAG ′成为直角有以下两种情况:a .α由0°增大到90°过程中,当∠OAG ′为直角时,∵OA =OD =12OG =12OG ′,∴∠AG ′O =30°,∠AOG ′=60°.∵OA ⊥OD ,∴∠DOG ′=90°-∠AOG ′=30°,即α=30°;b .α由90°增大到180°过程中,当∠OAG ′为直角时,同理可求的∠AOG ′=60°,∴α=90°+∠AOG ′=150°.综上,当∠OAG ′为直角时,α=30°或150°;②AF ′长的最大值是2+22,此时α=315°. 3.(1)证明:如图①中,连接BD .∵点E ,H 分别为边AB ,DA 的中点,∴EH ∥BD ,EH =12BD .∵点F ,G 分别为边BC ,CD 的中点,∴FG ∥BD ,FG =12BD ,∴EH ∥FG ,EH =GF ,∴中点四边形EFGH 是平行四边形.(2)解:四边形EFGH 是菱形.理由如下:如图②中,连接AC ,BD .∵∠APB =∠CPD ,∴∠APB +∠APD =∠CPD +∠APD ,即∠APC =∠BPD .在△APC 和△BPD 中,⎩⎪⎨⎪⎧AP =PB ,∠APC =∠BPD ,PC =PD ,∴△APC ≌△BPD ,∴AC =BD .∵点E ,F ,G 分别为边AB ,BC ,CD 的中点,∴EF =12AC ,FG =12BD ,∴EF =FG .∵四边形EFGH 是平行四边形,∴四边形EFGH 是菱形.(3)解:四边形EFGH 是正方形.理由如下:如图②中,设AC 与BD 交于点O .AC 与PD 交于点M ,AC 与EH 交于点N .∵△APC ≌△BPD ,∴∠ACP =∠BDP .∵∠DMO =∠CMP ,∴∠COD =∠CPD =90°.∵EH ∥BD ,AC ∥HG ,∴∠EHG =∠ENO =∠BOC =∠DOC =90°.∵四边形EFGH 是菱形,∴四边形EFGH 是正方形.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.。
特殊平行四边形动点问题

特殊四边形:动点问题题型一:1.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当PA +PD 取最小值时,△APD 中边AP 上的高为A 、17172B 、17174C 、 17178D 、3 2.如图4,在梯形ABCD 中,AD ∥BC ,AD =6,BC =16,E 是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间t = 秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形.3.如图,在梯形ABCD 中,AD ∥BC,E 是BC 的中点,AD=5,BC=12,CD=42,∠C=045,点P 是BC 边上一动点,设PB 长为x.1当x 的值为 时,以点P 、A 、D 、E 为顶点的四边形为直角梯形. 2当x 的值为 时,以点P 、A 、D 、E 为顶点的四边形为平行四边形.3点P 在BC 边上运动的过程中,以点P 、A 、D 、E 为顶点的四边形能否构成菱形试说明理由.4.在一个等腰梯形ABCD 中,AD1.t 为何值时,四边形ABQP 为平行四边形2.四边形ABQP 能为等腰梯形吗如果能,求出t 的值,如果不能,请说明理由;6.梯形ABCD 中,AD ∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P 从点A 开始,沿AD 边,以1厘米/秒的速度向点D 运动;动点Q 从点C 开始,沿CB 边,以3厘米/秒的速度向B 点运动;已知P 、Q 两点分别从A 、C 同时出发,,当其中一点到达端点时,另一点也随之停止运动;假设运动时间为t 秒,问:1t 为何值时,四边形PQCD 是平行四边形2在某个时刻,四边形PQCD 可能是菱形吗为什么3t 为何值时,四边形PQCD 是直角梯形4t 为何值时,四边形PQCD 是等腰梯形5 t 为何值时, APQ 是等腰三角形7.如图,在直角梯形ABCD 中,∠B=90°,AD ‖BC,且AD=4cm,AB=8cm,DC=10cm;若动点P 从点A 出发,以每秒4cm 的速度沿线段AD 、DC 向C 点运动;动点Q 从C 点以每秒5cm 的速度沿CB 向B 点运动;当Q 点到达B 点时,动点P 、Q 同时停止运动;设P 、Q 同时出发,并运动了t 秒; 1直角梯形ABCD 的面积为__________cm 的平方.2当t=________秒时,四边形PQCD 为平行四边形;3当t=________秒时,PQ=DC4是否存在t,使得P 点在线段DC 上,且PQ ⊥DC 如图2所示若存在,列出方程求出此时的t ;若不存在,请说明理由;8.如图,在直角梯形ABCD 中,∠B=90°,AB ‖CD,且AB=4cm,BC=8cm,DC=10cm;若动点P 从点A 出发,以每秒1cm 的速度沿线段AB 、BC 向C 点运动;动点Q 从C 点以每秒1cm 的速度沿CB 向B 点运动;当Q 点到达B 点时,动点P 、Q 同时停止运动;设P 、Q 同时出发,并运动了t 秒; 1直角梯形ABCD 的面积为__________cm 的平方.2当t=________秒时,四边形PBCQ 为平行四边形;3当t=________秒时,PQ=BC.10. 如图,在等腰梯形ABCD 中,AB ∥CD,其中AB=12 cm,CD=6cm ,梯形的高为4,点P 从开始沿AB 边向点B 以每秒3cm 的速度移动,点Q 从开始沿CD 边向点D 以每秒1cm 的速度移动,如果点P 、Q 分别从A 、C 同时出发,当其中一点到达终点时运动停止;设运动时间为t 秒; 1求证:当t 为何值时,四边形APQD 是平行四边形;2PQ 是否可能平分对角线BD 若能,求出当t 为何值时PQ 平分BD ;若不能,请说明理由; 3若△DPQ 是以PQ 为腰的等腰三角形,求t 的值;11.如图,在直角梯形ABCD 中,AB1求CD 的长;2当四边形PBQD 为平行四边形时,求四边形PBQD 的周长;3在点P,点Q 的运动过程中,是否存在某一时刻,使得ΔBPQ 的面积为20cm 2若存在,请求出所有满足条件的t 的值;若不存在,请说明理由;13. 已知,矩形ABCD 中,4AB cm =,8BC cm =,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .1如图10-1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;2如图10-2,动点P 、Q 分别从A 、C 两点同时出发,沿AFB ∆和CDE ∆各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b 单位:cm ,0ab ≠,已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.14.已知:如图,在梯形ABCD 中,AB ∥DC,∠B=90°,BC=8cm,CD=24cm,AB=26Cm,点P 从C 出发,以1cm/s 的速度向D 运动,点Q 从A 出发,以3cm/s 的速度向B 运 动,其中一动点达到端点时,另一动点随之停止运动.从运动开始.1经过多少时间,四边形AQPD 是平行四边形2经过多少时间,四边形AQPD 成为等腰梯形3在运动过程中,P 、Q 、B 、C 四点有可能构成正方形吗为什么A BC D EF 图10-1 O 图10-2 备用图如图,在梯形ABCD 中,AD ∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P 从点B 出发,沿射线BC 的方向以每秒2cm 的速度运动,动点Q 从点A 出发,在线段AD 上以每秒1cm 的速度向点D 运动,点P,Q 分别从点B,A 同时出发,当点Q 运动到点D 时,点P 随之停止运动,设运动的时间为t 秒.①当t 为何值时,四边形PQDC 是平行四边形;②当t 为何值时,以C,D,Q,P 为顶点的梯形面积等于60cm 2 ③是否存在点P,使△PQD 是等腰三角形若存在,请求出所有满足要求的t 的值,若不存在,请说明理由. 15.如图,在梯形ABCD 中,AD ∥BC,AD=6,DC=10,AB=65,∠B=45°.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.16.1求BC 的长.17.2当MN ∥AB 时,求t 的值.18.3△MNC 可能为等腰三角形吗若能,请求出t 的值;若不能,请说明理由.(4)△MNC 可能为直角三角形吗若能,请求出t 的值;若不能,请说明理由.(5)△MNC 为20时,请求出t 的值.如图,直角梯形ABCD 中,AB ∥CD,∠A=90°,AB=34,AD=4,DC=234 ,点P 从点A 出发沿折线段AD-DC-CB 以每秒3个单位长的速度向点B 匀速运动,同时,点Q 从点A 出发沿射线AB 方向以每秒2个单位长的速度匀速运动,当点P 与点B 重合时停止运动,点Q 也随之停止,设点P,Q 的运动时间是t 秒t >0.1当点P 到达终点B 时,求t 的值;2设△APQ 的面积为S,分别求出点P 运动到AD 、CD 上时,S 与t 的函数关系式;3当t 为何值时,能使PQ ∥DB ;4当t 为何值时,能使P 、Q 、D 、B 四点构成的四边形是平行四边形;16.如图,在等腰梯形ABCD 中,AD ∥BC,AB=DC=60,AD=75,BC=135.点P 从点B 出发沿折线段BA-AD-DC 以每秒5个单位长的速度向点C 匀速运动;点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动,过点Q 向上作射线QK ⊥BC,交折线段CD-DA-AB 于点E .点P 、Q 同时开始运动,当点P 与点C 重合时停止运动,点Q 也随之停止.设点P 、Q 运动的时间是t 秒t >0.1当点P 到达终点C 时,求t 的值,并指出此时BQ 的长;2当点P 运动到AD 上时,t 为何值能使PQ ∥DC ;3设射线QK 扫过梯形ABCD 的面积为S,分别求出点E 运动到CD 、DA 上时,S 与t 的函数关系式;不必写出t 的取值范围4△PQE 能否成为直角三角形若能,写出t 的取值范围;若不能,请说明理由.17.如图,直角梯形ABCD 中,AD ∥BC,∠ABC=90°,已知AD=AB=3,BC=33,动点P 从B 点出发,沿线段BC 向点C 作匀速运动;动点Q 从点D 出发,沿线段DA 向点A 作匀速运动.过Q 点垂直于AD 的射线交AC 于点M,交BC 于点N .P 、Q 两点同时出发,速度都为每秒1个单位长度.当Q 点运动到A 点,P 、Q 两点同时停止运动.设点Q 运动的时间为t 秒.1求NC,MC 的长用t 的代数式表示;2当t 为何值时,四边形PCDQ 构成平行四边形3当t 为何值时,射线QN 恰好将△ABC 的面积平分并判断此时△ABC 的周长是否也被射线QN 平分.19.如图,已知直角梯形ABCD 中,AD ∥BC,AB ⊥BC,AD=2,AB=8,CD=10.1求梯形ABCD 的面积S ;2动点P 从点B 出发,以2cm/s 的速度、沿B →A →D →C 方向,向点C 运动;动点Q 从点C 出发,以2cm/s 的速度、沿C →D →A 方向,向点A 运动.若P 、Q 两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t 秒.问:①当点P 在B →A 上运动时,是否存在这样的t,使得直线PQ 将梯形ABCD 的周长平分若存在,请求出t 的值,并判断此时PQ 是否平分梯形ABCD 的面积;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P 、D 、Q 为顶点的三角形恰好是以DQ 为一腰的等腰三角形若存在,请求出所有符合条件的t 的值;若不存在,请说明理由.20.在直角梯形ABCD 中,∠C=90°,高CD=6cm,底BC=10cm 如图1.动点Q 从点B 出发,沿BC 运动到点C 停止,运动的速度都是1cm/s .同时,动点P 也从B 点出发,沿BA →AD 运动到点D 停止,且PQ 始终垂直BC .设P,Q 同时从点B 出发,运动的时间为ts,点P 运动的路程为ycm .分别以t,y 为横、纵坐标建立直角坐标系如图2,已知如图中线段为y 与t 的函数的部分图象.经测量点M 与N 的坐标分别为4,5和2, 25.1求M,N 所在直线的解析式;2求梯形ABCD 中边AB 与AD 的长;3写出点P 在AD 边上运动时,y 与t 的函数关系式注明自变量的取值范围,并在图2中补全整运动中y 关于t 的函数关系的大致图象.22.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3 3,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM 返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒t>0.23.1设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式不必写t的取值范围;24.2当BP=1时,求△EPQ与梯形ABCD重叠部分的面积;已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点,动点P从点A出发,以每秒4个单位的速度,沿折线AOCD 向终点C运动,运动时间是t秒.1D点的坐标为;2当t为何值时,△APD是直角三角形;3如果另有一动点Q,从C点出发,沿折线CBA向终点A以每秒5个单位的速度与P点同时运动,当一点到达终点时,两点均停止运动,问:P、C、Q、A四点围成的四边形的面积能否为28如果可能,求出对应的t;如果不可能,请说明理由.在梯形ABCO中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别是A8,0,B8,10,C0,4.点D4,7为线段BC的中点,动点P从O点出发,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.1求直线BC的解析式;2设△OPD的面积为s,求出s与t的函数关系式,并指出自变量t的取值范围;33当t为何值时,△OPD的面积是梯形OABC的面积的8如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A10,0、C0,8,CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.1求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;2动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;3几秒后线段PD将梯形COAB的面积分成1:3的两部分求出此时点P的坐标已知直角梯形OABC在如图所示的平面直角坐标系中,AB∥OC,AB=10,OC=22,BC=15,动点M从A点出发,以每秒一个单位长度的速度沿AB向点B运动,同时动点N从C点出发,以每秒2个单位长度的速度沿CO向O点运动.当其中一个动点运动到终点时,两个动点都停止运动.1求B点坐标;2设运动时间为t秒;①当t为何值时,四边形OAMN的面积是梯形OABC面积的一半;②当t为何值时,四边形OAMN的面积最小,并求出最小面积;③若另有一动点P,在点M、N运动的同时,也从点A出发沿AO运动.在②的条件下,PM+PN 的长度也刚好最小,求动点P的速度.如图1,以梯形OABC的顶点O为原点,底边OA所在的直线为轴建立直角坐标系.梯形其它三个顶点坐标分别为:A14,0,B11,4,C3,4,点E以每秒2个单位的速度从O点出发沿射线OA 向A点运动,同时点F以每秒3个单位的速度,从O点出发沿折线OCB向B运动,设运动时间为t.1当t=4秒时,判断四边形COEB是什么样的四边形2当t为何值时,四边形COEF是直角梯形3在运动过程中,四边形COEF能否成为一个菱形若能,请求出t的值;若不能,请简要说明理由,并改变E、F两点中任一个点的运动速度,使E、F运动到某时刻时,四边形COEF 是菱形,并写出改变后的速度及t的值如图,在平面直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14,A16,0,C0,2.1如图①,若点P、Q分别从点C、A同时出发,点P以每秒2个单位的速度由C向B运动,点Q以每秒4个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动.设运动时间为t秒0≤t≤4.①求当t为多少时,四边形PQAB为平行四边形②求当t为多少时,直线PQ将梯形OABC分成左右两部分的比为1:2,并求出此时直线PQ 的解析式.2如图②,若点P、Q分别是线段BC、AO上的任意两点不与线段BC、AO的端点重合,且四边形OQPC面积为10,试说明直线PQ一定经过一定点,并求出该定点的坐标.如图,在平面直角坐标系中,直角梯形ABCO的变OC落在x轴的正半轴上,且AB方形ODEF 的两边分别坐落在坐标轴上,且它的面积等于直角梯形ABCO面积,将正方形ODEF沿x轴的正半轴平行移动,设它与直角梯形ABCO的重叠部分面积为S;(1)求正方形ODEF的边长;(2)求OA所在直线的解析式(3)当正方形ODEF移动到顶点O与C重合时,求S的值(4)设正方形ODEF顶点O向右移动的距离为x,当正方形ODEF的边ED与y轴重合时,停止移动,求重叠部分面积S与x的函数关系式;如图,在△ABC中,∠ACB=90°,AC=BC=6cm,等腰RT△DEF中,∠D=90°,EF=在BC所在直线L上,开始时点F与点C重合,让等腰RT△DEF沿直线L向右以每秒1cm的速度做匀速运动,最后点E和点B重合;(1)请直接写出等腰RT△DEF运动6S时与△ABC重叠部分面积(2)设运动时间为xS,运动过程中,等腰RT△DEF与△ABC重叠部分面积为ycm2①在等腰RT△DEF运动6S后至运动停止前这段时间内,求y与x之间的函数关系式②在RT△DEF整个运动过程中,求当x为何值时,y=1/2.题型二:1.如图,正方形ABCD的边长为4cm,两动点P、Q分别同时从D、A出发,以1cm/秒的速度各自沿着DA、AB边向A、B运动;试解答下列各题:1当P出发后多少秒时,三角形PDO为等腰三角形;2当P、Q出发后多少秒,四边形APOQ为正方形;3当P、Q出发后多少秒时,ABCD PQDSS正方形325=∆.2.如图所示,有四个动点P 、Q 、E 、F 分别从正方形ABCD 的四个顶点出发,沿着AB 、BC 、CD 、DA 以同样的速度向B 、C 、D 、A 各点移动;1试判断四边形PQEF 是正方形并证明;2PE 是否总过某一定点,并说明理由;(3)四边形PQEF 的顶点位于何处时,其面积最小,最大各是多少(4)3.已知:如图,边长为a 的菱形ABCD 中,∠DAB=60°,E 是异于A 、D 两点的动点,F 是CD 上的动点;请你判断:无论E 、F 怎样移动,当满足:AE+CF=a 时,△BEF 是什么三角形并说明你的结论;4.如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD 不含B 点上任意一点,将BM 绕点B 逆时针旋转60°得到BN,连接EN 、AM 、CM.⑴ 求证:△AMB ≌△ENB ;⑵ ①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由;⑶ 当AM +BM +CM 的最小值为13 时,求正方形的边长.题型三:1.如图,在直角梯形ABCD 中,AD//BC,∠C =90°,BC =16,DC =12,AD =21;动点P 从点D 出发,沿射线DA 的方向以每秒2两个单位长的速度运动,动点Q 从点C 出发,在线段CB 上以每秒1个单位长的速度向点B 运动,点P,Q 分别从点D,C 同时出发,当点Q 运动到点B 时,点P 随之停止运动;设运动的时间为t 秒;(1)设▲BPQ 的面积为S,求S 与t 之间的函数关系式;(2)当t 为何值时,四边形ABPQ 平行四边形3当t 为何值时,以B 、P 、Q 三点为顶点的三角形是等腰三角形4是否存在时刻t,使得PQ ⊥BD 若存在,求出t 的值;若不存在,请说明理由;E A DB C N M2.如图①,在等腰梯形ABCD中,AD边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N.1如图25-1,当点M在AB边上时,连接BN.△≌△;①求证:ABN ADN②若∠ABC = 60°,AM = 4,∠ABN =α,求点M到AD的距离及tanα的值;2如图25-2,若∠ABC = 90°,记点M运动所经过的路程为x6≤x≤12.试问:x为何值时,△ADN为等腰三角形.4.在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,MF交射线CD于点F,AB=4,BE=x,CF=y1求y关于x的解析式及定义域2当点F在边CD上时,四边形AEFD的周长是否随点E的运动而发生变化请说明理由3当DF=1时,求点A到直线EF的距离;5.如图1,在等腰梯形ABCD中,AD‖BC,E是AB的中点,过点E作EF‖BC交CD于点F;AB=4,BC=6,∠B=60°1求点E到BC的距离;2点P为线段EF上的一个动点,过点P作PM⊥EF交BC于点M,过M作MN‖AB交折线ADC于点N,连接PN,设EP=x.①当点N在线段AD上时,△PMN的形状是否发生改变若不变,求出△PMN的周长,若改变,说明理由.②当点N在线段DC上时,是否存在点P,使△PMN为等腰三角形若存在,请求出所有满足要求的x的值,若不存在,说明理由.6.在平行四边形ABCD中,AD=4cm,∠A=60°,BD⊥AD;一动点P从A出发以每秒1cm的速度沿A-B-C的路线做匀速运动,过点P做直线PM,使PM⊥AD;当点P运动2秒时,另一动点Q也从A 出发沿A-B-C的路线运动,且在AB上以每秒1cm的速度匀速运动,在BC上以每秒2cm的速度匀速运动;过Q做直线QN,使QN∥PM;设点Q的运动时间为t秒0≤t≤10,直线PM与QN截平cm行四边形所得图形的面积为S2①求S关于t的函数关系式;②求S的最大值;7.菱形ABCD中∠A=60°,边长为4CM,动点P从A出发,以1CM/秒的速度沿A-B-C的路线运动,在点P出发1秒后,点Q以同样的速度,沿同样的路径运动,过点P、Q的直线L1、L2互相平行,且都与AB边所在的直线成60°角,设点P运动的时间是X1≤X≤8秒,直线L1、L2在菱形上截出的图形周长为Y厘米1求Y与X的函数关系;2当X取何值时,Y的值最大最大值是多少8.如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G即点F与点G重合时,三个点随之停止移动.设移动开始后第t秒时,△EF G的面积为Scm2.1当t=1秒时,S的值是多少2写出S和t之间的函数解析式,并指出自变量t的取值范围.。
特殊的平行四边形专题(题型详细分类)要点

特殊的平⾏四边形专题(题型详细分类)要点特殊的平⾏四边形讲义知识点归纳矩形,菱形和正⽅形之间的联系如下表所⽰:四边形分类专题汇总专题⼀:特殊四边形的判定矩形菱形正⽅形性质边对边平⾏且相等对边平⾏,四边相等对边平⾏,四边相等⾓四个⾓都是直⾓对⾓相等四个⾓都是直⾓对⾓线互相平分且相等互相垂直平分,且每条对⾓线平分⼀组对⾓互相垂直平分且相等,每条对⾓线平分⼀组对⾓判定 ·有三个⾓是直⾓; ·是平⾏四边形且有⼀个⾓是直⾓; ·是平⾏四边形且两条对⾓线相等. ·四边相等的四边形;·是平⾏四边形且有⼀组邻边相等;·是平⾏四边形且两条对⾓线互相垂直。
·是矩形,且有⼀组邻边相等; ·是菱形,且有⼀个⾓是直⾓。
对称性既是轴对称图形,⼜是中⼼对称图形(1)______________ (2)______________ (3)______________ (4)______________ (5)______________2.矩形的判定⽅法:(1)______________ (2)______________ (3)______________3.菱形的判定⽅法:(1)______________ (2)______________ (3)______________4.正⽅形的判定⽅法:(1)______________ (2)______________ (3)______________5.等腰梯形的判定⽅法:(1)______________ (2)______________ (3)______________【练⼀练】⼀.选择题1.能够判定四边形ABCD是平⾏四边形的题设是().A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠DC.AB=CD,AD=BC D.AB=AD,CB=CD2.具备下列条件的四边形中,不能确定是平⾏四边形的为().A.相邻的⾓互补 B.两组对⾓分别相等C.⼀组对边平⾏,另⼀组对边相等 D.对⾓线交点是两对⾓线中点3.下列条件中,能判定四边形是平⾏四边形的条件是( )A.⼀组对边平⾏,另⼀组对边相等B.⼀组对边平⾏,⼀组对⾓相等C.⼀组对边平⾏,⼀组邻⾓互补D.⼀组对边相等,⼀组邻⾓相等4.如下左图所⽰,四边形ABCD的对⾓线AC和BD相交于点O,下列判断正确的是().A.若AO=OC,则ABCD是平⾏四边形;B.若AC=BD,则ABCD是平⾏四边形;C.若AO=BO,CO=DO,则ABCD是平⾏四边形;D.若AO=OC,BO=OD,则ABCD是平⾏四边形5.不能判定四边形ABCD是平⾏四边形的条件是()A.AB=CD,AD=BC B.AB∥CD,AB=CDC.AB=CD,AD∥BC D.AB∥CD,AD∥BC6.四边形ABCD的对⾓线AC,BD相交于点O,能判断它为矩形的题设是()A.AO=CO,BO=DO B.AO=BO=CO=DOC.AB=BC,AO=CO D.AO=CO,BO=DO,AC⊥BD7.四边形ABCD的对⾓线互相平分,要使它变为矩形,需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD8.在四边形ABCD中,O是对⾓线的交点,下列条件能判定这个四边形是正⽅形的是()A、AC=BD,AB∥CD,AB=CDB、AD∥BC,∠A=∠CC、AO=BO=CO=DO,AC⊥BDD、AC=CO,BO=DO,AB=BC9.在下列命题中,真命题是()A.两条对⾓线相等的四边形是矩形B.两条对⾓线互相垂直的四边形是菱形C.两条对⾓线互相平分的四边形是平⾏四边形D.两条对⾓线互相垂直且相等的四边形是正⽅形10.在下列命题中,正确的是()11.如图,已知四边形ABCD 是平⾏四边形,下列结论中不正确的是() A .当AB=BC 时,它是菱形 B .当AC ⊥BD 时,它是菱形C .当∠ABC=900时,它是矩形D .当AC=BD 时,它是正⽅形12.如图,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是() A .四边形AEDF 是平⾏四边形B .如果90BAC ∠=o ,那么四边形AEDF 是矩形C .如果AD 平分BAC ∠,那么四边形AEDF 是菱形D .如果AD BC ⊥且AB AC =,那么四边形AEDF 是菱形 13.下列条件中不能判定四边形是正⽅形的条件是()。
第十八章平行四边形四边形中的动点问题(教案)人教版八年级数学下册

(五)总结回顾(用时5分钟)
今天的学习,我们了解了平行四边形中动点问题的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对动点问题的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
五、教学反思
在今天的教学中,我发现同学们对平行四边形内动点问题的探究表现得非常积极。他们对于动点的运动规律和性质有了初步的认识,也尝试着将这些知识应用到实际问题中。我觉得这是一个很好的开始,但也发现了一些需要改进的地方。
首先,理论讲授部分,我发现有些同学对动点问题的基本概念掌握不够扎实。可能是我讲解得不够细致,也可能是同学们对这些概念还不够熟悉。在以后的教学中,我需要更加注意这一点,尽量用简单易懂的语言和丰富的例子来帮助他们理解。
3.重点难点解析:在讲授过程中,我会特别强调动点的运动规律和利用平行四边形性质解题这两个重点。对于难点部分,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与动点问题相关的实际问题。
2.实行四边形中的运动规律和性质。
-难点二:在实际问题中,学生可能不知道如何选择合适的定理和性质来解决动点问题。教师应指导学生通过分析问题结构,识别关键信息,进而选择恰当的几何定理进行求解。
-难点三:针对不同动点问题,如路径最短、面积最大等,学生可能不知如何下手。教师应教授学生分类讨论和优化的方法,帮助学生理清思路,找到解题突破口。
4.培养合作意识和团队精神,在小组讨论和探究过程中,学会倾听、交流、表达和协作,共同解决问题。
特殊平行四边形中的三种几何动点问题—2023-2024学年九年级数学上册(北师大版)(解析版)

特殊平行四边形中的三种几何动点问题类型一、面积问题 例.如图,在四边形ABCD 中,AB CD ∥,90BCD ∠=,10cm AB AD ==,=8cm BC .点P 从点A 出发,以每秒3cm 的速度沿折线ABC 方向运动,点Q 从点D 出发,以每秒2cm 的速度沿线段DC 方向向点C 运动.已知动点P ,Q 同时发,当点Q 运动到点C 时,P ,Q 运动停止,设运动时间为t .(1)直接写出CD 的长(cm );(2)当四边形PBQD 为平行四边形时,直接写出四边形PBQD 的周长(cm );(3)在点P 、点Q 的运动过程中,是否存在某一时刻,使得BPQ V 的面积为215cm ?若存在,请求出所有满足条件的t 的值;若不存在,请说明理由.【答案】(1)16(2)(3)存在,满足条件的t 的值为2512秒或5秒【分析】(1)过点A 作AM CD ⊥于M ,根据题意证明四边形ABCD 是平行四边形,然后根据平行四边形的性质以及勾股定理可得结果;(2)当四边形PBQD 是平行四边形,则点P 在AB 上,点Q 在DC 上,则103BP t =−,2DQ t =,根据平行四边形的性质可得1032t t −=,求解得出平行四边形的各边长,求其周长即可;(3)分两种情况进行讨论:①当点P 在线段AB 上时;②当点P 在线段BC 上时;根据三角形面积列方程计算即可.【详解】(1)解:如图1,过点A 作AM CD ⊥于M ,AM CD ⊥,=90BCD ∠︒,∴AM CB ∥,∵AB CD ∥,∴四边形ABCD 是平行四边形,10cm CM AB ∴==,在t R ADM 中,10cm AD =,8cm AM BC ==,根据勾股定理得,6cm DM =,16cm CD DM CM ∴=+=;(2)当四边形PBQD 是平行四边形,则点P 在AB 上,点Q 在DC 上,如图3,由运动知,103BP t =−,2DQ t =,1032t t ∴−=,2t ∴=,此时,4BP DQ ==,12CQ =,根据勾股定理得,BQ =∴四边形PBQD 的周长为()28BP BQ +=+(3)①当点P 在线段AB 上时,即:1003t ≤≤时,如图2,()1110381522BPQ S PB BC t =⋅=−⨯=,2512t ∴=;②当点P 在线段BC 上时,即:1063t <≤时,如图4,310BP t =−,162CQ t =−,()()113101621522BPQ S PB CQ t t ∴=⋅=−−=,5t ∴=或193t =(舍), 即:满足条件的t 的值为2512秒或5秒.【点睛】本题考查了四边形的动点问题,平行四边形的判定与性质,勾股定理,读懂题意,根据相应图形的性质列出方程是解本题的关键.【答案】(1)①12DP t =−;15BQ t =−;②7.5t =(2)()()()220<12=12<151345 15<1844t S t t t t −≤−≤−−≤⎧⎪⎪⎪⎪⎪⎩【分析】(1)①根据路程等于速度乘以时间列代数式即可;②AP BQ =时,四边形APQB 是平行四边形;(2)求出相关线段的长度,利用三角形面积公式,分情况讨论即可.【详解】(1)解:①由题意可知=cm AP t ,cm CQ t =,∴()12cm DP AD AP t =−=−,()15cm BQ BC CQ t =−=−;②当四边形APQB 是平行四边形时,AP BQ =,即15t t =−,解得7.5t =.故答案为:()12cm t −,()15cm t −(2)解:如图,过点D 作DE BC ⊥于点E ,则90A B DEB ∠=∠=∠=︒,∴四边形ABED 是矩形,∴90ADE ∠=︒,()12cm BE AD ==, ∴()15123cm CE BC BE =−=−=,∵120ADC ∠=︒,∴30CDE ADC ADE ∠=∠−∠=︒,∴()26cm DC EC ==,∴)cm DE ===,∴点P 运动到点D 时,需12秒,点P 到点C 时,需18秒;点Q 从点C 到点B 需15秒,从点B 到点A 需15+秒.故分三种情况讨论:①当012t <≤时,如图,11==(1522S BQ AB t ⋅−−)②当1215t <≤时,如图,过点P 作DH BC ⊥于点H ,()18cm PC AD DC t t =+−=−,易知DE PH ∥∴30CPH CDE ∠=∠=︒, ∴()119cm 22CH PC t ==−,∴())cm PH t ==−,∴211(15))22S BQ PH t t =⋅=−−=;③当1518t <≤时,如图,()15cm BQ t BC t =−=−,()111596cm 22BH BC CH t t ⎛⎫=−=−−=+ ⎪⎝⎭, ∴211113(15)(6)4522244S BQ BH t t t t =⋅=−⋅+=−−,综上,))()220<12=12<15134515<1844t S t t t t ≤−≤−−≤⎧⎪⎪⎪⎪⎪⎩.【点睛】本题考查列代数式、三角形面积公式、平行四边形的判定、勾股定理、矩形的判定与性质、含30度角的直角三角形的性质、四边形上的动点问题等,熟练掌握分类讨论思想是解题的关键.【答案】(1)10(2)12(3)S=18(09)6216(918)t t t t <≤⎧⎨−+<≤⎩(4)t= 4或8或12【分析】(1)当t=4时,AP=8,PD=AD -AP=BC -AP=18-8=10;(2)当四边形ABQP为矩形时,AP=BQ,根据不同的时间段AP的关系式求出t值即可;(3)由(2)中不同时间段AP的关系式得出S的分段函数即可;(4)PQ所在的直线将矩形ABCD分成面积比为1:2的两部分时,可能再两个不同的时间段存在12ABQPPDCQss=四边形四边形和12PDCQABQPss=四边形四边形两种可能,根据(3)中面积的函数关系式分段求t值即可.(1)解:当t=4时,AP=2t=8,∴PD=AD-AP=18-8=10,故答案为10(2)解:当四边形ABQP为矩形时,AP=BQ,若0≤t≤9时,AP=2t,则2t=t,解得t=0(不符合题意,舍去);若9<t≤18时,AP=36-2t,则36-2t=t,解得t=12;故答案为12(3)解:当0<t≤9时,S=12(BQ +AP)⋅AB =12(t+2t)×12= 18t;当9<t<18时,S=12(BQ +AP).AB =- 6t + 216.综上所述,S =18(09)6216(918)t tt t<≤⎧⎨−+<≤⎩(4)解:当0≤t≤9时,若12ABQPPDCQss=四边形四边形,则ABQPs四边形=13ABCDS矩形,∴18t=13×12×18,解得t=4;若12PDCQABQPss=四边形四边形,则ABQPs四边形=23ABCDS矩形,∴18t=23×12×18,解得t=8;当9<t≤18时,若12ABQPPDCQss=四边形四边形,则ABQPs四边形=13ABCDS矩形,∴-6t+216=13×12×18,解得t=24(舍);若12PDCQABQPss=四边形四边形,则ABQPs四边形=23ABCDS矩形,∴-6t+216=23×12×18,解得t=12;综上,当t=4或8或12时,PQ所在的直线将矩形ABCD分成面积比为1:2两部分.【点睛】本题主要考查四边形的综合题型,涉及动点问题,矩形的性质,梯形的面积等知识点,会用分类讨论的思想解决问题是解题的关键.如图,在ABD中,几秒钟后,MON的面积为【答案】(1)见解析(2)5米,24平方米;(3)1秒或4秒【分析】(1)根据题意,用“一组对边平行且相等的四边形是平行四边形”先判定平行四边形,再用邻边相等证明菱形;(2)解方程可得OA 、OB 的长,用勾股定理可求AB ,根据“菱形的面积对应对角线积的一半”计算连线面积;(3)根据点M 、N 运动过程中与O 点的位置关系,分三种情况分别讨论.【详解】(1)证明:AO 平分BAD ∠,AB CD ∥,DAC BAC DCA ∠∠∠∴==, ACD ∴是等腰三角形,AD DC =,又AB AD =,AB CD ∴=,∴四边形ABCD 为平行四边形,又AB AD =,∴四边形ABCD 是菱形;(2)解:解方程27120x x −+=,得,14x =,23x = 4OA ∴=,3OB =,利用勾股定理5AB ==,28,26AC OA BD OB ∴====,∴ABCD S =菱形118622AC BD ⨯=⨯⨯24=平方米.(3)解:在第(2)问的条件下,设M 、N 同时出发x 秒钟后,MON 的面积22m ,当点M 在OA 上时,2x <,MON S =12()()4232x x −−=, 解得1214x x ==, (大于2,舍去);当点M 在OC 上且点N 在OB 上时,23x <<,MON S =12()()3242x x −−=,整理得,2580x x −+=,此时,2=541870∆−⨯⨯=−<,∴原方程无解;当点M 在OC 上且点N 在OD 上时,即34x <≤,MON S =12 ()()2432x x −−=,整理得,2540x x −+=,解得1241x x ==, (小于3,舍去).综上所述:M ,N 出发1秒或4秒钟后,△MON 的面积为22m .【点睛】本题考查了菱形的判定方法,菱形的面积计算方法,分类讨论的数学思想.类型二、几何图形存在性问题 Rt ABC 中, (1)求AB AC ,的长;(2)求证:AE DF =;(3)当t 为何值时,DEF 为直角三角形?请说明理由.【答案】(1)AB=5,AC=10;(2)证明见解析(3)当52t =秒或4秒时,DEF 为直角三角形,理由见解析【分析】(1(2)利用已知用未知数表示出DF ,AF 的长,进而得出AE DF =;(3)利用①当90EDF ∠=︒时;②当90DEF ∠=︒时;③当90EFD ∠=︒时,分别分析得出即可.【详解】(1)解:设AB x =,90B ∠=︒,30C ∠=︒,22AC AB x ∴==.由勾股定理得,()(2222x x −=, 解得:5x =, 5AB ∴=,10AC = ;(2)证明:由题意得AE t =,CD=2t ,则102AD t =−,在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴12DF CD t==.又AE t=,AE DF∴=;(3)解:当52t=秒或4秒时,DEF为直角三角形,理由如下:分情况讨论:①∠EDF=∠DFC=90°时,则DE BC∥,∴∠AED=∠B=90°,∠ADE=∠C=30°,∴AD=2AE,∴10-2t=2t,∴52t=;②∠DEF=90°时,∵AB⊥BC,DF⊥BC,∴AE DF.又∵AE=DF,∴四边形AEFD为平行四边形,∴AD EF,∴∠ADE=∠DEF=60°,∴∠AED=30°,∴12AD AE=,∴1 1022t t−=,∴4 t=;③∠EFD=90°时,此种情况不存在. 当52t =秒或4秒时,DEF 为直角三角形.【点睛】本题是四边形综合题目,考查了平行四边形的判定、菱形的判定与性质、勾股定理、直角三角形的性质等知识.理解相关知识是解答关键. (1)连接PD 、PQ 、DQ ,求当t 为何值时,PQD △的面积为(2)当点P 在BC 上运动时,是否存在这样的t 使得△合条件的t 的值;若不存在,请说明理由.【答案】(1)1秒或4秒(2)存在,43t =秒或4)秒【分析】(1)根据正方形的性质和面积公式,利用割补法即可求解;(2)根据勾股定理、等腰三角形的性质得出一元二次方程,分情况讨论以PD 为腰的等腰三角形即可说明.【详解】(1)解:当P 在BC 上时如图:根据题意,得4AB BC CD AD ====AQ t =,4QB t =−,2BP t =,42PC t =−,7PQD ADQ BPQ DPC ABCD S S S S S =−−−=△△△△正方形,1111642(4)4(42)7222t t t t −⨯⨯−⨯−−⨯⨯−=整理,得2210t t −+=,解得121t t ==.当P 在CD 上时,此时24t <≤4(24)82DP t t =−−=− 1(82)472PQD S t ∴=−⨯=△94t ∴=答:当t 为1秒或94秒时,PQD △的面积为27cm .(2)①当PD DQ =时,根据勾股定理,得2216(42)16t t +−=+,解得143t =,24t =(不符合题意,舍去).②当PD PQ =时,根据勾股定理,得22216(42)(4)(2)t t t +−=−+,整理得:28160t t +−=解得14t =,24t =−(不符合题意,舍去).答:存在这样的43t =秒或4)秒,使得PQD △是以PD 为一腰的等腰三角形.【点睛】本题考查了正方形、一元二次方程、等腰三角形的相关知识,解决本题的关键是分类讨论思想的运用.例3.如图,在四边形ABCD 中,AD ∥BC ,∠B =90°,AB =8cm ,AD =12cm ,BC =18cm ,点P 从点A 出发以1cm/s 的速度向点D 运动;点Q 从点C 同时出发,以2cm/s 的速度向点B 运动,当点Q 到达点B 时,点P 也停止运动,设点P ,Q 运动的时间为t s .(1)从运动开始,当t 取何值时,PQ ∥CD ?(2)在整个运动过程中是否存在t 值,使得四边形PQCD 是菱形?若存在,请求出t 值;若不存在,请说明理由;(3)从运动开始,当t 取何值时,四边形PQBA 是矩形?(4)在整个运动过程中是否存在t 值,使得四边形PQBA 是正方形?若存在,请求出t 值;若不存在,请说明理由.【答案】(1)4(2)不存在,理由见解析(3)6(4)不存在,理由见解析【分析】(1(2)利用菱形的判定和性质进行求解即可;(3)利用矩形的判定和性质进行求解即可;(4)利用正方形的判定和性质进行求解即可.(1)解:由运动知,AP =tcm ,CQ =2tcm ,∴DP =AD ﹣AP =(12﹣t )cm ,∵AD BC ∥,要PQ CD ∥,∴四边形CDPQ 为平行四边形,∴DP =CQ ,∴12﹣t =2t ,∴t =4,即t =4时,PQ ∥CD ;(2)不存在,理由:∵四边形PQCD 是菱形,∴CQ =CD ,∴2t =10,∴t =5,此时,DP =AD ﹣AP =12﹣5=7(cm ),而DP≠CD ,∴四边形PQCD 不可能是菱形;(3)如图4,∵∠B =90°,AD ∥BC ,∴当AP =BQ 时,四边形ABQP 是矩形,即t =18﹣2t ,解得:t =6,∴当t =6时,四边形PQBA 是矩形;(4)由当t =6时,四边形PQBA 是矩形,∴AP =6cm ,∵AB =8cm ,∴AP≠AB ,∴矩形PQBA 不能是正方形,即不存在时间t ,使四边形PQBA 是正方形.【点睛】本题考查四边形中的动点问题.解题的关键是熟练掌握平行四边形、菱形、矩形和正方形的判定和性质,确定动点的位置. 例4.如图,在菱形ABCD 中,对角线AC 与BD 交于点O ,且8AC =,6BD =,现有两动点M ,N 分别从A ,C 同时出发,点M 沿线段AB 向终点B 运动,点N 沿折线C D A −−向终点A 运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t (秒).(1)填空:AB = ;菱形ABCD 的面积S = ;菱形的高h = .(2)若点M 的速度为每秒1个单位,点N 的速度为每秒a 个单位(其中52a <),当4t =时在平面内存在点得以A ,M ,N ,E 为顶点的四边形为菱形,请求出所有满足条件的a 的值.【答案】(1)5;24;245(2)1.5或1.94或1.4【分析】(1)先由菱形的性质和勾股定理求得AB ,再跟菱形面积为对角线之积的一半可得S ,最后根据菱形的面积为边长×高,由此可得高h 的长;(2)当4t =,时间固定,AM 的长度也就固定,A 、M 、N 、E 四点要形成菱形,分两大类情况,第一类以AM 为边,这种情况可以画两种菱形;第二类以AM 为对角线,只有一种.因此共三种情况,分别计算.【详解】(1)解:∵四边形ABCD 是菱形,AC 与BD 交于点O ,86AC BD ==,,∴43AO CO BO DO AC BD ====⊥,,,∴AB=5,设菱形的高为h,则菱形ABCD 的面积为186242AB h ⨯⨯=⨯=∴245h =故答案为:5,24,245(2)解:当4t =时,4AM =,①如图2,四边形AMEN 为菱形,4AN AM ∴==,1046ND CD ∴+=−=,46a ∴=,32a =.②如图3,AENM 为菱形,EM 交AN 于点R ,作DP 垂直BC 于P ,菱形面积为24,4.8DP ∴=,75CP ∴=,MAR BCD ∠=∠,AMR PDC ∴∠=∠,AR CP AM CD ∴=,1.12AR ∴=,2.24AN ∴=,()()410 2.244 1.94a ND CD ∴=+÷=−÷=,③如图4,AEMN 为菱形,EN 交AM 于点T ,作BS 垂直CD 于S ,则2AT MT ==,523BT NS ∴==−=,4.8BS =, 1.4CS ∴=,1.43 4.4CN NS CS∴=+=+=,4 4.44 1.1a CN∴=÷=÷=;综上所述,a的取值有1.5或1.94或1.4.【点睛】本题主要考查了菱形的性质、三角函数、勾股定理、面积计算,分类讨论等重要知识点,综合性和技巧性很强,计算量也较大,对学生的能力要求较高,因此综合应用所学知识成为解答本题的关键.类型三、直线位置关系问题(1)直接写出AB的长.(2)当点Q落在AB边上时,用含t的代数式表示【答案】(1)3(2)3523t−或5332t−(3)12、或175(4)920或215【分析】(1)根据勾股定理直接求出AB 的长度;(2)分类讨论Q 在AD 和BD 上的两种情况,DQ AD AQ =−或 DQ AQ AD =−;(3)当平行四边形PQDM 为菱形或矩形时即为轴对称图形,因为PQ AC ⊥,所以当Q 在AB 上时,PQD ∠不可能为直角,平行四边形PQDM 不可能为矩形,只存在菱形的情况,根据PQ DQ =建立等量解出t 值;当Q 在BC 上时,表示出DQ 的长度较为复杂,所以可以表示出2DQ ,利用22PQ DQ =建立方程解出t 值;当Q 点在BC 中点时,平行四边形PQDM 为矩形,可直接求得t 值;(4)因为平行四边形PQDM 的四个顶点顺序已经确定,所以Q 在过点D 的AC 平行线的下方,分类讨论Q 在AD 上和在CN (见详解图)上的两种况下QM 平行于不同边时的情况,注意,根据平行线的定义,当Q 在AB 上时,QM 不可能平行于AB ,当Q 在BC 上时,QM 不可能平行于BC .【详解】(1)解:在Rt ABC 中,222AB AC BC =−,∴3=AB ;(2)解:P 从点A 出发以每秒个单位的速度沿AC 向终点C 运动,∴AP t =,PQ AC ⊥,∴APQ ABC △△∽,::3:4:5AB BC AC =,∴::3:4:5AP QP AQ =, ∴5533AP t AQ ==,点D 是边AB 的中点,∴32AD BD ==, ∴ 3523DQ t =−或5332t −;(3)解:当平行四边形PQDM 为菱形或矩形时即为轴对称图形, ∴ PQ DQ =或平行四边形PQDM 某一内角为90︒,①当Q 在AB 上时,990510t t ⎛⎫≤≤≠ ⎪⎝⎭,由(1)得43PQ t =,3523DQ t =−或5332t −, ∴354233t t −=或534323t t −=, 解得12t =或92, 990510t t ⎛⎫≤≤≠ ⎪⎝⎭,∴12t =;Q 在AB 上时,PQD ∠不可能为90︒,故不存在矩形的情况;②如图,当Q 在BC 上时,955t ≤≤,CPQ CBA △△∽,∴::4:3:5CP QP CQ =,AP t =,∴5CP t =−, ∴()354PQ t =−,()554CQ t =−, ∴()55945444BQ t t =−−=−, ∴222222359254511724416816DQ BD BQ t t t ⎛⎫⎛⎫=+=+−=−+ ⎪ ⎪⎝⎭⎝⎭, 当22PQ DQ =时,平行四边形PQDM 为菱形, ∴()22254511735168164t t t ⎡⎤−+=−⎢⎥⎣⎦,解得t =,955t ≤≤,∴t =;当Q 点在BC 中点时,平行四边形PQDM 为矩形, 此时485255t −=⨯=, 解得175t =;综上所述:当平行四边形PQDM 为轴对称图形时,t 的值为12、或175;(4)解:平行四边形PQDM ,∴Q 在过点D 的AC 平行线的下方, ①如图,Q 在AD 上,9010t ≤<,QM AC ∥时,易得DQM QAP △△∽,平行四边形PQDM ,∴43DM QP t ==, 由(1)得3523DQ t =−, ∴35523443t DQ DM t −==, 解得920t =;②如图,Q 在AD 上,9010t ≤<,QM BC ∥时, 易得DQM QPA △△∽,∴35423453tDQDM t−==,解得8245t=(舍);③过点D的平行线交BC于点N,点Q在CN上移动才可能会出现平行四边形PQDM的对角线QM平行于直角三角形的边,此时1755t≤≤,如图,当QM AC∥时,延长DM交AC于点H,平行四边形PQDM,∴()354DM PQ t==−且DH AC⊥,QM AC∥,∴四边形MQPH为矩形,∴()354MH PQ DM t===−,∴()365245t DH−⨯==,解得215t=;不存在QM AB∥的情况;综上所述:当QM与Rt ABC△的某条边平行时,t的值为920或215.【点睛】本题考查了几何动点问题,涉及到相似、平行线的性质、平行四边形以及特殊的平行四边形的性质和判定,还会用到分类讨论的思想,难度较大,解决本题的关键是能准确找到不同的情况并对问题进行分类讨论.【答案】(1)BD =,9BE cm =(2)PQ AD ⊥,理由见详解(3)存在,t 的值为125或4(4)或【分析】(1)可求出30ADB ∠=︒,根据含30︒的直角三角形的性质可得212AD AB cm ==,BD =,根据平行四边形的性质可得AD BC ∥,则30DBC ∠=︒,即可得12DE BD =,BE =,即可求解; (2)先证四边形DEQP 是平行四边形,可得四边形DEQP 是矩形,即可得出结论;(3)分两种情况讨论,由平行四边形的性质可得AP BQ =,列出方程可求解;(4)分两种情况讨论,由轴对称的性质和等边三角形的性质以及勾股定理可求解.【详解】(1)四边形ABCD 是平行四边形,90ABD Ð=°,60A ∠=︒,6AB cm =,30ADB ∴∠=︒,AD BC ∥,212AD AB cm ∴==,BD ==,30DBC ADB ∠=∠=︒,DE BC ⊥,12DE BD ∴==,BE =,9BE cm ∴==;(2)PQ AD ⊥,理由如下:如图1,动点P 从点D 出发沿DA 以1/s cm 的速度向终点A 运动,同时点Q 从点B 出发,以4/cm s 的速度沿射线BC 运动,∴当95t =时,95PD =,365BQ =, 369955QE BE BQ PD ∴=−=−==, AD BC ,∴四边形DEQP 是平行四边形,DE BC ⊥,∴四边形DEQP 是矩形,PQ AD ∴⊥;(3)存在,当CD 为边时,四边形PQCD 是平行四边形,PD CQ ∴=,124t t ∴=−,125t ∴=;当CD 为对角线时,四边形PCQD 是平行四边形,PD CQ ∴=,412t t ∴=−,4t ∴=,综上所述:t 的值为125或4;(4)如图,当点P 的对称点在线段CD 上时,60ADQ QDC ∴∠=∠=︒,60QDC BCD ∴∠=∠=︒,CDQ ∴是等边三角形,CD CQ ∴=,6124t ∴=−,32t ∴=,过点P 作PH BC ⊥于H ,则PH DE ==,32EH PD cm ==, 60BCD ∠=︒,6CD AB cm ==,DE BC ⊥,13cm 2CE CD ∴==,32QH CQ EH CE cm ∴=−−=,在Rt PQH 中,PQ =; 如图,当点P 的对称点在线段CD 的延长线上时,120CDA ∠=︒,60PDP '∴∠=︒,点P 的对称点在线段CD 的延长线上,1302CDQ PDP '∴∠=∠=︒,BCD CDQ CQD ∠=∠+∠, 30CDQ CQD ∴∠=∠=︒,6CD CQ ∴==,12618BQ ∴=+=,418t ∴=,92t ∴=,过点P 作PH BC ⊥于H ,则PH DE ==,92EH PD cm ==,60BCD ∠=︒,6CD AB cm ==,DE BC ⊥,132CE CD cm ∴==,272QH CQ EH CE cm ∴=++=,在Rt PQH 中,PQ ==;综上所述:点P ,Q 之间的距离为或.【点睛】本题是四边形综合题,考查了平行四边形的性质,直角三角形的性质,等边三角形的判定和性质等知识,利用分类讨论思想解决问题是解题的关键.课后训练1.如图,在四边形ABCD 中,AB CD ∥,90A ∠=︒,24cm DC =,26cm AB =,动点P 从D 开始沿DC 边向C 点以1cm /s 的速度运动,动点Q 从点B 开始沿BA 向A 点以3cm /s 的速度运动,P ,Q 分别从点D ,B 同时出发,当其中一点到达终点时,另一点也随之停止运动,运动的时间为t 秒.(1)t 为何值时,四边形DPQA 为矩形?(2)t 为何值时,四边形PQBC 为平行四边形?【答案】(1)当132t =秒时,四边形DPQA 为矩形(2)当6t =秒时,四边形PQBC 为平行四边形【分析】(1)根据AB CD ∥,矩形的判定和性质,得AQ DP =,求出t ,即可;(2)根据平行四边形的判定和性质,得PC QB =,求出t ,即可.【详解】(1)∵AB CD ∥,∴AQ DP ∥,当AQ DP =时,四边形DPQA 为平行四边形,∵90A ∠=︒,∴平行四边形DPQA 为矩形,∵动点P 从D 开始沿DC 边向C 点以1cm /s 的速度运动,动点Q 从点B 开始沿BA 向A 点以3cm /s 的速度运动, ∴cm DP t =,3cm BQ t =,∴263AQ AB BQ t =−=−,∴263t t =−,解得:261342t ==, ∴当132t =秒时,四边形DPQA 为矩形.(2)∵AB CD ∥,∴QB PC ∥,当PC QB =时,四边形PQBC 为平行四边形,∴24PC t =−,∴243t t −=,解得:6t =,∴当6t =秒时,四边形PQBC 为平行四边形.【点睛】本题考查动点与几何的综合,矩形和平行四边形的知识,解题的关键是掌握矩形和平行四边形的判定和性质. 在ABC 中, 发现:(1)在点O 的运动过程中,OE 与OF 的关系是(2)当=2t 时,=EF ______cm .【答案】(1)OE OF =,详见解析(2)8cm ,探究:3,拓展:=AB 10cm【分析】()1根据角平分线的定义、平行线的性质分别得到OEC ACE ∠=∠,ACF OFC ∠=∠,根据等腰三角形的判定定理得到OE OC =,OF OC =,等量代换证明结论;()2根据直角三角形斜边上的中线的性质解答;探究:根据矩形的判定定理得到=OA OC 时,四边形AECF 是矩形,进而求出OA ,求出t ;拓展:根据正方形的对角线平分一组对角得到45ACE ∠=︒,进而得到90ACB ∠=︒,根据勾股定理计算,得到答案.【详解】(1)解:OE OF =,理由如下:CE 平分ACB ∠,BCE ACE ∴∠=∠,EF BC ∥,BCE OEC ∴∠=∠,OEC ACE ∴∠=∠,OE OC ∴=,同理可得,ACF OFC ∠=∠,OF OC ∴=,OE OF ∴=,故答案为:OE OF =;(2)由题意得,当=2t 时,2cm OA =,则4cm OC AC OA =−=,BCE ACE ∠=∠,GCF ACF ∠=∠,90ECF ∴∠=︒,OE OF =,()28cm EF OC ∴==,故答案为:8; 探究:当=3t 时,四边形AECF 是矩形,理由如下:90ECF ∠=︒,OE OF =,∴当=OA OC 时,四边形AECF 是矩形,此时,3cm OA OC ==,3t ∴=时,四边形AECF 是矩形,故答案为:3;拓展:当四边形AECF 是正方形时,45ACE ∠=︒,CE 平分ACB ∠,290ACB ACE ∴∠=∠=︒,()10cm AB ∴=.【点睛】本题考查的是正方形的性质、矩形的判定、平行线的性质以及直角三角形斜边上的中线的性质,掌握矩形的判定定理、正方形的性质是解题的关键. 3.已知正方形ABCD 中,8AB BC CD DA ====,90A B C D ∠=∠=∠=∠=︒.动点P 以每秒2个单位速度从点B 出发沿线段BC 方向运动,动点Q 同时以每秒8个单位速度从B 点出发沿正方形的边BA AD DC CB −−−方向顺时针作折线运动,当点P 与点Q 相遇时停止运动,设点P 的运动时间为t .(1)当运动时间为 秒时,点P 与点Q 相遇;(2)当BQ PD ∥时,求线段DQ 的长度;(3)连接PA ,当PAB 和QAD 全等时,求t 的值.【答案】(1)3.2(2)3.2(3)t 为0.8或83【分析】(1)先判断出点P ,Q 相遇时,必在正方形的边BC 上,利用运动路程之和为正方形的正常建立方程即可;(2)先判断出四边形BQDP 是平行四边形,得出BP DQ =,进而表示出BP ,DQ ,用BP DQ =建立方程求解即可;(3)分点Q 在正方形的边AB ,AD ,CD ,BC 上,建立方程求解即可得出结论;【详解】(1)解:点P 的运动速度为2,8BC =,∴点P 运动到点C 的时间为4,点Q 的运动速度为8,∴点Q 从点B 出发沿BA AD DC CB −−−方向顺时针作折线运动到点C 的时间为(888)83++÷=,∴点P ,Q 相遇时在边BC 上,284832t t ∴+=⨯=,3.2t ∴=,故答案为3.2;(2)解:如图1,//BQ PD ,∴点Q 只能在边AD 上,四边形ABCD 是正方形,//AD BC ∴,∴四边形BQDP 是平行四边形,BP DQ ∴=,2288t t ∴=⨯−,1.6t ∴=,288 3.2DQ t ∴=⨯−=;(3)解:①当点Q 在边AB 上时,如图2,AB AD =,ABP DAQ ∠=∠,要使PAB ∆和ΔQAD 全等,只能是PAB QDA ≅,BP AQ ∴=,88AQ t =−,2BP t =,882t t ∴−=,0.8t ∴=,②当点Q 在边AD 时,不能构成QAD ,③当点Q 在边CD 上时,如图3,同①的方法得,要使PAB 和QAD 全等,只能是PAB QAD ≅,BP DQ ∴=,2816t t ∴=−,83t ∴=,④当点Q 在边BC 时,QAD 不是直角三角形,而PAB 是直角三角形,所以,不能全等;即:当PAB 和QAD 全等时,t 的值为0.8或83;【点睛】本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会分类讨论. 4.如图,在ABCD Y 中,9034BAC CD AC ∠=︒==,,.动点P 从点A 出发沿AD 以1cm /s 速度向终点D 运动,同时点Q 从点C 出发,以4cm /s 速度沿射线CB 运动,当点P 到达终点时,点Q 也随之停止运动,设点P 运动的时间为t 秒()0t >.(1)CB 的长为______.(2)用含t 的代数式表示线段QB 的长.(3)连接PQ ,①是否存在t 的值,使得PQ 与AC 互相平分?若存在,求出t 的值;若不存在,请说明理由;②是否存在t 的值,使得PQ 与AB 互相平分?若存在,求出t 的值;若不存在,请说明理由.(4)若点P 关于直线AQ 对称的点恰好落在直线AB 上,请直接写出t 的值.【答案】(1)5(2)55404QB t t ⎛⎫=−<≤ ⎪⎝⎭或5454QB t t ⎛⎫=−> ⎪⎝⎭(3)①不存在,理由见解析;②存在,t 的值为53(4)t 的值为12或2【分析】(1)根据平行四边形的性质得3AB DC ==,再根据勾股定理即可求解;(2)根据题意可得4CQ t =,先求出当点Q 与点B 重合时,所花费的时间,再根据题意分两种情况讨论即可:当点Q 在线段BC 上时和当点Q 在线段CB 的延长线上时;(3)①连接PC AQ ,,假设PQ 与AC 互相平分,则可得四边形APCQ 是平行四边形,进而可得AP CQ =,解得即可到答案;②连接PB AQ ,,假设PQ 与AB 互相平分,则可得四边形APBQ 是平行四边形,进而可得AP BQ =,解得即可到答案;(4)根据题意分两种情况讨论即可:当点P 关于直线AQ 对称的点落在点A 下方时和当点P 关于直线AQ 对称的点落在点A 上方时.【详解】(1)∵四边形ABCD 是平行四边形,∴3AB DC ==,∵90BAC ∠=︒,∴5BC =,故答案为:5;(2)在ABCD Y 中,AD BC =,AD BC ∥,由题意得,4CQ t =,当点Q 与点B 重合时,45t =, ∴5s 4t =, 当点Q 在线段BC 上时,54QB BC CQ t =−=−,当点Q 在线段CB 的延长线上时,45QB CQ BC t =−=−, 综上所述,55404QB t t ⎛⎫=−<≤ ⎪⎝⎭或5454QB t t ⎛⎫=−> ⎪⎝⎭;(3)①不存在,理由如下:如图,连接PC AQ ,,若PQ 与AC 互相平分,则四边形APCQ 是平行四边形,∴AP CQ =,∵4AP t CQ t ==,,∴4t t =,解得0=t (不合题意),∴不存在t 的值,使得PQ 与AC 互相平分;②存在,如图,连接PB AQ ,,若PQ 与AB 互相平分,则四边形APBQ 是平行四边形,∴AP BQ =,∴45t t =−, ∴5s 3t =, ∴当5s 3t =时,PQ 与AB 互相平分; (4)当点P 关于直线AQ 对称的点落在点A 下方时,如图,由对称得,PAQ P AQ '∠=∠,∵AD BC ∥,∴PAQ AQB ∠=∠,∴P AQ AQB '∠=∠,即BAQ AQB ∠=∠,∴3BQ AB ==,∴2CQ BC BQ =−=,∴42t =,解得12t =;当点P 关于直线AQ 对称的点落在点A 上方时,如图,由对称得,12∠=∠,∵AD BC ∥,∴13∠=∠,∵24∠∠=∴3=4∠∠,∴3BQ AB ==,∴8CQ BC BQ =+=,∴48t =,解得2t =,综上所述,t 的值为12或2.【点睛】本题考查了平行四边形的判定和性质、勾股定理的应用和动点问题,灵活运用所学知识求解是解决本题的关键. 5.如图,矩形ABCD 中,4CD =,30CBD ∠=︒.一动点P 从B 点出发沿对角线BD 方向以每秒2个单位长度的速度向点D 匀速运动,同时另一动点Q 从D 点出发沿DC 方向以每秒1个单位长度的速度向点C 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P 、Q 运动的时间为t 秒()0t >.过点P 作PE BC ⊥于点E ,连接EQ ,PQ .(1)求证:PE DQ =;(2)四边形PEQD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.(3)当t 为何值时,PQE V 为直角三角形?请说明理由.【答案】(1)见解析(2)能,83t =(3)当2t =或165,见解析【分析】(1)由垂直得90BEP ∠=︒,在Rt BEP 中,2BP t =,由30CBD ∠=︒,可得PE t =,即可证明结果;(2)先证明四边形PEQD 是平行四边形,82PD t =−,DQ t =,当PD DQ =时,四边形PEQD 为菱形,即可求解;(3)分类讨论:①当90EPQ ∠=︒,②当90PQE ∠=︒,③当90PEQ ∠=︒即可.【详解】(1)证明:∵PE BC ⊥,∴90BEP ∠=︒,在Rt BEP 中,2BP t =,∵30CBD ∠=︒,∴PE t =,又∵DQ t =,∴PE DQ =;(2)解:能,理由如下:∵四边形ABCD 为矩形,PE BC ⊥,90BEP C ︒∠==∠,∴PE DQ ∥,由(1)知,PE DQ =,∴四边形PEQD 为平行四边形,在Rt CBD 中,4CD =,30CBD ∠=︒,∴28BD CD ==,∵2BP t =,∴82PD BD BP t =−=−,若使平行四边形PEQD 为菱形,则需PD DQ =,即82t t −=, ∴83t =, 即当83t =时,四边形PEQD 为菱形; (3)解:①当90EPQ ∠=︒时,四边形EPQC 为矩形,∴PE QC =,∵PE t =,4QC t =−,∴4t t =−,即2t =;②当90PQE ∠=︒时,90DPQ PQE ∠=∠=︒,在Rt DPQ 中,906030PQD ∠=︒−︒=︒,∴2DQ DP =,∵DQ t =,82DP t =−∴()282t t =−,即165t =.③当90PEQ ∠=︒时,此种情况不存在,综上所述,当2t =或165时,PQE V 为直角三角形.【点睛】本题考查动点问题、菱形的判定与性质及矩形的性质,找到动点运动的规律和路线、速度、以及是否停止和有无取值范围是解题的关键.(1)=a ______cm ,b =______cm ;(2)t 为何值时,EP 把四边形BCDE 的周长平分?(3)另有一点Q 从点E 出发,按照E D C →→的路径运动,且速度为1cm /s ,若P 、Q 两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t 为何值时,BPQ V 的面积等于26cm .【答案】(1)3,3(2)2s =t(3)3s 2或11s 3或5s【分析】(1)由非负性可求a ,b 的值;(2)先求出18cm BCDE C =四边形,可得9cm BE BP +=,可求4cm BP =,即可求解;(3)分三种情况讨论,由三角形的面积公式可求解.【详解】(1)∵()230a −=,∴30,290a a b −=+−=,∴3,3a b ==;故答案为:3,3;(2)∵3cm,3cm AE DE ==,∴6cm AD BC ==,∴18cm BCDE C BC CD DE EB =+++=四边形,∵EP 把四边形BCDE 的周长平分,∴9cm BE BP +=,∴4cm BP =,点P 在BC 上,∴42s 2t ==;(3)①点P在BC上(03)t<≤,∵12462BPQtS=⨯⨯=V,∴3.2t=;②相遇前,点P在CD上13 (3)3t<≤,∵[]1(4(3)(26)662BPQS t t=⨯−−−−⨯=,∴113t=;③相遇后,点P在CD上13(5)3t<≤,∵[]1(3)(26)4662BPQS t t=⨯−+−−⨯=,∴.5t=;∴综上所述,当3s2t=或11s3或5s时,BPQV的面积等于26cm.【点睛】本题考查了矩形的性质,非负数的性质,一元一次方程的应用等知识,利用分类讨论思想是解本题的关键.角形与DCQ全等.【答案】(1)1(2)54t=或4或232(3) 3.5t=,5.5或10【分析】(1)根据题中条件求出AP 的长即可求解;(2)分三种情况讨论:①当点P 在AB 上时,②当点P 在BC 上时,③当点P 在AD 上时;(3)连接CQ ,要使一个三角形与DCQ 全等,则另一条直角边必须等于DQ ,分类讨论即可.【详解】(1)解:动点P 的速度是2cm/s ,∴当2t =时,224AP =⨯=,∵5cm AB =,∴BP =1cm ;(2)解:①当点P 在AB 上时,CDP △是等腰三角形,∴PD CP =,在长方形ABCD 中,,90AD BC A B =∠=∠=︒,∴()HL DAP CBP ≌,∴AP BP =, ∴1522AP AB ==,∵动点P 的速度是2cm/s , ∴54t =;②当点P 在BC 上时,CDP △是等腰三角形,如图所示,∵90C ∠=︒,∴5CD CP ==,∴3BP CB CD =−=, ∴53422AB BP t ++===;③当点P 在AD 上时,CDP △是等腰三角形.如图所示,∵90D Ð=°,∴5DP CD ==, ∴585523222AB CB CD DP t ++++++===, 综上所述,54t =或4或232时,CDP △是等腰三角形; (3)解:根据题意,如图,连接CQ ,∵5,90,6AB CD A B C D DQ ==∠=∠=∠=∠=︒=,∴要使一个三角形与DCQ 全等,则另一条直角边必须等于DQ .①当点P 运动到1P 时,16CP DQ ==,此时1DCQ CDP △≌△, ∴点P 的路程为:1527AB BP +=+=, ∴72 3.5t =÷=;②当点P 运动到2P 时,26BP DQ ==,此时2CDQ ABP △≌△, ∴点P 的路程为:25611AB BP +=+=,∴112 5.5t =÷=③当点P 运动到3P 时,35AP DQ ==,此时3CDQ BAP △≌△, ∴点P 的路程为:3585220AB BC CD DP +++=+++=, ∴20210t =÷=,④当点P 运动到4P 时,即P 与Q 重合时,46DP DQ ==,此时4CDQ CDP △≌△, ∴点P 的路程为:4585624AB BC CD DP +++=+++=∴24212t =÷=,此结果舍去,不符合题意,综上所述,t 的值可以是: 3.5t =,5.5或10.【点睛】本题考查了动点问题,灵活运用分类讨论思想是解题关键.。
人教版初二数学8年级下册 第18章(平行四边形)动点问题专项训练(含答案)

人教版数学八年级下期第十八章平行四边形动点问题训练1.如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在的直线对着得到△BQN,延长QN交BA的延长线于点M.(1)求证:AP⊥BQ;(2)当P在BC何处时,点N是MQ的中点.(3)若AB=3,P是BC的三等分点,求QM的长;2.如图,四边形ABCD是正方形,点E是边BC的动点,连接AE,以AE为边在AE的右上侧作Rt△AEF,使得∠AEF=90°,AE=EF,再过点F作FG⊥BC,交BC的延长于点G.(1)求证:∠BAE=∠GEF;(2)求证:CG=FG;(3)填空:若正方形ABCD的边长是2,当点E从点B运动到点C的过程中,点F也随之运动,则点F运动的痕迹的长是______.3.如图,点P是正方形ABCD(在小学,同学们学习过:正方形四边相等,四个角都是直角)对角线AC上一动点,点E在射线BC上,且PB=PE,连结PD,O为AC 中点.(1)如图①,当点P在线段AO上时,猜想PE与PD的关系,并说明理由;(2)如图②,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由.4.如图,已知菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD上两个动点,若AE=DF,连接BF与DE相交于点G,连接CG,(1)求∠BGE的大小;(2)求证:GC平分∠BGD.5.如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB.(1)如图1所示,当∠DPA'=10°时,∠A'PB=______度;(2)如图2所示,当PA'⊥BC时,求线段PA的长度;(3)当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF 沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.6.如图,边长为8的正方形ABCD的対角线AC,BD交于点O,M是AB边上一动点,ME⊥AO,MF⊥BO.(1)求证:四边形OEMF为矩形;(2)连接EF,求EF的最小值.7.如图,在正方形ABCD中,点E是AD边上的一个动点,连接BE,以BE为斜边在正方形ABCD内部构造等腰直角三角形BEF,连接CF.(1)求证:∠DEF+∠CBF=90°;,求△BEF的面积;(2)若AB=3,△BCF的面积为32(3)求证:DE=2CF.8.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.(1)求证:△NDE≌△MAE;(2)求证:四边形AMDN是平行四边形;(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.9.如图,已知四边形ABCD为正方形,AB=42,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFC,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.10.如图,已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.(1)求证:△BGF≅△FHC;(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.11.如图,已知矩形ABCD中,AB=5,AD=2+13.菱形EFGH的顶点H在边AD上,且AH=2,顶点G、E分别是边DC、AB上的动点,连结CF.(1)当四边形EFGH为正方形时,直接写出DG的长;(2)若△FCG的面积等于3,求DG的长;(3)试探究点G运动至什么位置时,△FCG的面积取得最小值.12.如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E,F,已知AD=4,试说明AE2+CF2的值是一个常数.13.如图,在△ABC中,CA=CB,∠ACB=90°,AB=5,点D是边AB上的一个动点,连接CD,过C点在上方作CE⊥CD,且CE=CD,点P是DE的中点.(1)如图①,连接AP,判断线段AP与线段DE的数量关系并说明理由;(2)如图②,连接CP并延长交AB边所在直线于点Q,若AQ=2,求BD的长.14.如图,D、E分别是△ABC的边AB、AC的中点,O是△ABC内一动点,F、G分别是OB、OC的中点.判断四边形DEGF的形状,并说明理由.15.在正方形ABCD中,如图1,点E是AB边上的一个动点(点E与点A、B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE.(2)如图2,当点E运动到AB中点时,连接DG,若AB=2,求DG的长.16.如图,在矩形ABCD中,BC=4,AB=10,E为CD边上的一点,DE=7,动点P从点A出发,以每秒1个单位的速度沿着边AB向终点B运动,连接PE.设每秒运动的时间为t秒.(1)求BE的长;(2)当t为多少秒时,△BPE是直角三角形.参考答案1.(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C=90°,AB=BC,在△ABP和△BCQ中,AB=BC∠ABC=∠CBP=CQ,∴△ABP≌△BCQ(SAS),∴∠BAP=∠CBQ,∵∠BAP+∠APB=90°,∴∠CBQ+∠APB=90°,∴∠BEP=90°,∴AP⊥BQ;(2)解:由折叠的性质得:NQ=CQ,∠BNQ=∠C=90°,∠NBQ=∠CBQ,∴∠BNM=90°,∵点N是MQ的中点,∴NQ=MN,由(1)得:MQ=MB,∴MN=12MB,∴∠MBN=30°,∴∠CBN=60°,∴∠NBQ=∠CBQ=30°,∴CQ=33BC,∴BP=CQ=33BC,即BP=33BC时,点N是MQ的中点.(3)解:∵四边形ABCD是正方形,AB=3,P是BC的三等分点,∴BP=2CP,或CP=2BP,①当BP=2CP时,BP=2,由折叠的性质得:NQ=CQ=BP=2,BN=BC=3,∵∠NQB=∠CQB=∠ABQ,∴MQ=MB,设MQ=MB=x,则MN=x-2,在Rt△MBN中,MB2=BN2+MN2,即x 2=32+(x -2)2,解得:x =134,即MQ =134;②当CP =2BP 时,BP =1,由折叠的性质得:NQ =CQ =BP =1,BN =BC =3,∵∠NQB =∠CQB =∠ABQ ,∴MQ =MB ,设MQ =MB =x ,则MN =x -1,在Rt △MBN 中,MB 2=BN 2+MN 2,即x 2=32+(x -1)2,解得:x =5,即MQ =5;综上所述,若AB =3,P 是BC 的三等分点,QM 的长为134或5.2.解:(1)∵∠AEF =90°,∴∠AEB +∠FEG =90°,∵四边形ABCD 是正方形,∴∠B =90°,∴∠AEB +∠BAE =90°,∴∠BAE =∠GEF ,(2)在△ABE 和△EGF 中,∠ABE =∠EGF ∠BAE =∠GEF AE =EF,∴△ABE ≌△EGF (AAS ),∴BE =GF ,AB =EG ,∴BE =CG ,∴CG =FG ;(3)223.解:(1)当点P在线段AO上时PE=PD且PE⊥PD.理由:当点P在线段AO上时,在△ABP和△ADP中AB=AD∠BAP=∠DAP=45∘AP=AP∴△ABP≌△ADP,∴BP=DP,∵PB=PE,∴PE=PD,如图,过点P作PM⊥CD于点M,作PN⊥BC于点N,∵AC平分∠BCD,∴PM=PN,在Rt△PNE与Rt△PMD中,∵PD=PE,PM=PN∴Rt△PNE≌Rt△PMD,∴∠DPM=∠EP N,易得∠MPN=90∘,∴∠DPE=90∘,故PE⊥PD,PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;(2)当点P在线段OC上时,(1)中的猜想成立;如图2,当点P在线段OC上时,∵四边形ABCD是正方形,AC为对角线,∴BA=DA,∠BAP=∠DAP=45°,又PA=PA,∴△BAP≌△DAP(SAS),∴PB=PD,又∵PB=PE,∴PE=PD,①当点E与点C重合时,PE⊥PD;②当点E在BC的延长线上时,如图2所示,∵△BAP≌△DAP,∴∠ABP=∠ADP,∠CDP=∠CBP,∵PB=PE,∴∠CBP=∠PEC,故∠PEC=∠PDC,∵∠1=∠2,∴∠DPE=∠DCE=90°,∴PE⊥PD,综上所述:PE⊥PD,当点P在线段OC上时,(1)中的猜想成立;4.解:(1)∵四边形ABCD是菱形∴AD=AB,∠BAD=60°∴△ADB是等边三角形∴AD=AB=BD,∠DAB=∠ADB=∠ABD∵AE=DF,∠DAB=∠ADB=60°,AD=BD∴△ADE≌△DBF(SAS)∴∠ADE=∠DBF又∠BGE=∠BDE+∠DBF=∠BDE+∠ADE=∠ADB∴∠BGE=∠ADB=60°(2)如图,过点C作CN⊥BF于点N,过点C作CM⊥ED于点M,由(1)得∠ADE=∠DBF∴∠CBF=60°+∠DBF=60°+∠ADE=∠DEB又∠DEB=∠MDC∴∠CBF=∠CDM∵BC=CD,∠CBF=∠CDM,∠CMD=∠CNG=90°∴Rt△CBN≌Rt△CDM(AAS)∴CN=CM,且CN⊥BF,CM⊥ED∴点C在∠BGD的平分线上即GC平分∠BGD5.856.(1)证明:∵ME⊥AO,MF⊥BO,∴∠MEO=90°,∠MFO=90°,∵正方形ABCD的対角线AC,BD交于点O,∴∠EOF=90°,∴四边形OEMF为矩形;(2)解:∵边长为8的正方形ABCD的対角线AC,BD交于点O,∴利用勾股定理可以得到OA=OB=42,当M在AB的中点时,EF有最小值,最小值=OE2+OF2=(22)2+(22)2=4.7.证明:(1)过点F作MN⊥AD于点M,交BC于点N,∴∠MEF+∠EFM=90°,∵∠EFB=90°,∴∠BFN +∠EFM =90°,∴∠MEF =∠BFN ,在正方形ABCD 中,AD ∥BC .∴MN ⊥BC ,∴∠FBN +∠BFN =90°,∴∠FBN +∠MEF =90°,即∠DEF +∠CBF =90°;证法二:在正方形ABCD 中,AD ∥BC ,∴∠DEB +∠CBE =180°,即∠DEF +∠BEF +∠EBF +∠CBF =180°,∵∠EFB =90°,∴∠BEF +∠EBF =90°,∴∠DEF +∠CBF =90°;(2)由(1)得MN ⊥AD ,∴正方形ABCD 的性质得四边形MNCD 是矩形,∴MN =CD =AB =3,在△BFN 与△FEM 中,由(1)得∠MEF =∠BFN ,∠EMF =∠FNB =90°,∵△BEF 为等腰直角三角形,∴BF =EF ,在△BFN 与△FEM 中,∠EMF =∠FNB ∠MEF =∠BFN BF =EF,∴△BFN ≌△FEM (AAS ),∵BC =AB =3,∴S △BCF =12BC ⋅FN =32FN =32,∴FN =1.∴BN =FM =MN -FN =2,在Rt △BFN 中,EF =BN 2+FN 2=12+22=5,∴S △BEF =12BF 2=12×(5)2=52;(3)在△BFN与△FEM中由(2)△BFN≌△FEM,MD=NC,∴BN=FM,EM=FN,∵MN=AB=BC,∴FM+FN=BN+NC,∴FN=NC=MD=EM,∴∠FCN=45°,DE=2MD=2CN,CF,在Rt△FNC中,CN=22∴DE=2×2CF=2CF.28.(1)证明:∵四边形ABCD是菱形,∴ND∥AM,∴∠NDE=∠MAE,∵点E是AD中点,∴DE=AE,在△NDE和△MAE中,∠NDE=∠MAEDE=AE,∠DEN=∠AEM∴△NDE≌△MAE(ASA);(2)∵△NDE≌△MAE,∴ND=MA,∴四边形AMDN是平行四边形;(3)解:当AM=1时,四边形AMDN是矩形.理由如下:∵四边形ABCD是菱形,∴AD=AB=2,∵四边形AMDN是矩形,∴DM⊥AB,即∠DMA=90°,∵∠DAB=60°,∴∠ADM=30°,∴AM=12AD=1.9.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,∵正方形ABCD,∴∠BCD=90°,∠ECN=45°,∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,∴四边形EMCN为正方形,∵四边形DEFG是矩形,∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,∴∠DEN=∠MEF,又∠DNE=∠FME=90°,在△DEN和△FEM中,∠DNE=∠FME EN=EM∠DEN=∠FEM,∴△DEN≌△FEM(ASA),∴ED=EF,∴矩形DEFG为正方形,(2)CE+CG的值为定值,理由如下:∵矩形DEFG为正方形,∴DE=DG,∠EDC+∠CDG=90°,∵四边形ABCD是正方形,∵AD=DC,∠ADE+∠EDC=90°,∴∠ADE=∠CDG,在△ADE和△CDG中,AD=CD∠ADE=∠CDG DE=DG,∴△ADE≌△CDG(SAS),∴AE=CG,∴AC=AE+CE=2AB=2×42=8,∴CE+CG=8是定值.10. (1)∵点F,H分别是BC,CE的中点,∴FH //BE ,FH =12BE ,∴∠CFH =∠CBG .又∵点G 是BE 的中点,∴FH =BG .又∵BF =FC ,∴△BGF ≅△FHC .(2)连接EF ,GH .当四边形EGFH 是正方形时,可知EF ⊥GH且EF =GH .∵在△BEC 中,点G ,H 分别是BE ,EC 的中点,∴GH =12BC =12AD =12a ,且GH //BC ,∴EF ⊥BC .又∵AD //BC ,AB ⊥BC ,∴AB =EF =GH =12a ,∴S 矩形ABCD =AB ⋅AD =12a ⋅a =12a 211.解:(1)∵四边形EFGH 为正方形,∴HG =HE ,∠ADG =∠HAE =90°,∵∠DHG +∠AHE =90°,∠DHG +∠DGH =90°,∴∠DGH =∠AHE ,∴△DGH ≌△AHE (AAS ),∴DG =AH =2;(2)如图,作FM⊥DC,M为垂足,连结GE.∵AB∥CD,∴∠AEG=∠MGE,∵HE∥GF,∴∠HEG=∠FGE,∴∠AEG-∠HEG=∠MGE-∠FGE,即∠AEH=∠MGF,又∠A=∠M=90°,HE=FG,∴△AHE≌△MFG,∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离恒等于2,∴S▵FCG=1×2⋅GC=3,2解得GC=3,∴DG=2;(3)设DG=x,则CG=5-x,由(2)可知,S△FCG=5-x.要使△FCG的面积最小,须使x最大,∵在Rt△DHG中,DH=13,∴当GH取得最大时,x最大当点E与点B重合时,HE最大,此时,HE=22+52=29,则GH=HE=29,在Rt△DHG中,x=(29)2−(13)2=4,∴当DG=4时,△FCG的面积取得最小值.12.解:∵四边形ABCD是正方形,∴∠AEB=∠BFC=90°,AB=BC,又∵∠ABE+∠FBC=∠BCF+∠FBC,∴∠ABE=∠BCF,在△ABE和△BCF中,AB=BC∠ABE=∠BCF∴△ABE≌△BCF(AAS),∠AEB=∠BFC∴AE=BF,∴AE2+CF2=BF2+CF2=BC2=AD2=16为常数.13.解:(1)AP=1DE,理由如下:2连接AE.∵CE⊥CD,∴∠ACE+∠ACD=90°,∵∠ACB=90°,∴∠BCD+∠ACD=90°,∴∠ACE=∠BCD,在△BCD和△ACE中,CE=CD∠ACE=∠BCD,AC=BC∴△BCD≌△ACE(SAS),∴∠EAC=∠B=45°,∴∠EAD=90°,∵P为DE中点,DE.∴AP=12(2)①当Q在边AB上时,连接AE,EQ.∵P 为DE 中点,CE =CD ,∴PC 垂直平分DE ,∴DQ =QD ,∵AB =5,AQ =2,∴BD =3,设BD =AE =x ,则QD =EQ =3-x ,在Rt △AEQ 中,AE 2+AQ 2=QE 2,即x 2+22=(3-x )2解得x =56;当Q 在BA 延长线上时,连接AE ,EQ ,如图,设BD =AE =x ,同理可得AE 2+AQ 2=QE 2,即x 2+22=(7-x )2解得x =4514.综上可得BD =56或4514.14.解析 四边形DEGF 是平行四边形.理由:∵D 、E 分别是△ABC 的边AB 、AC 的中点,∴DE =12BC ,DE //BC ,∵F、G分别是OB、OC的中点,BC,FG//BC,∴FG=12∴DE=FG,DE//FG,∴四边形DEGF是平行四边形15.(1)证明:∵BF⊥CE,∴∠CGB=90°,∴∠GCB+∠GBC=90°,又∵四边形ABCD为正方形,∴∠GBA+∠GBC=90°,∴∠GCB=∠FBA,又∵BC=AB,∠FAB=∠EBC=90°,在△ABF与△BCE中,∠GCB=∠FBABC=AB,∠EBC=∠FAB∴△ABF≌△BCE(SAS);(2)解:过点D作DH⊥CE于点H,∵E为AB中点,∴EB=1,∵AB=2,∴BC=2,∴CE=BC2+EB2=22+12=5,在Rt △CEB 中,由CE •BG =EB •BC 得BG =EB ⋅BC CE =1×25=255,∴CG =455,∵∠DCE +∠BCE =∠BCE +∠CBF =90°,∴∠DCE =∠CBF ,又∵DC =BC =2,∠CHD =∠CGB =90°,在△CHD 与△BGC 中,∠CHD =∠CGB =90°∠DCE =∠CBF DC =BC,∴△CHD ≌△BGC (AAS )∴CH =BG =255,∴GH =CG -CH =255=CH ,∵DH =DH ,∠CHD =∠GHD =90°,在△DGH 与△DCH 中,GH =CH ∠GHD =∠CHD DH =DH,∴△DGH ≌△DCH (SAS ),∴DG =DC =2.16.解:(1)在矩形ABCD 中,∠C =∠B =90°,CD =AB =10,在Rt △BCE 中,CE =CD -ED =10-7=3,根据勾股定理得,BE =BC 2+CE 2=42+32=5,(2)①当以P 为直角顶点时,即∠BPE =90°,则∠C =∠B =∠BPE =90°,∴四边形CBPE 是矩形,∴BP =CE =3,即10-t =3,∴t =7,②当以E 为直角顶点时,即∠BEP =90°,由勾股定理得,BE 2+PE 2=BP 2,过点P 作PF ⊥CD 于F ,则PF=AD=4,DF=AP,设AP=t,则EF=7-t,BP=10-t,PE2=42+(7-t)2,∴52+42+(7-t)2=(10-t)2,,解得,t=53∴当t=7或5秒时,△BPE是直角三角形.3。
浙教版八年级数学下册第5章专题十二 特殊四边形中的动点问题

专题
∴△ADE≌△CDG. ∴AE=CG. ∴AC=AE+CE=CG+CE. ∵AC= 2AB, ∴CE+CG= 2AB.
专题
∵EM⊥BC,EN⊥CD,∴∠EMC=∠ENC=90°, ∴∠NEC=45°,∴NE=NC, ∴四边形EMCN是正方形. ∴EM=EN,∠NEM=90°. ∴∠MEF+∠FEN=90°. ∵四边形DEFG是矩形,∴∠DEF=90°. ∴∠DEN+∠NEF=90°,∴∠DEN=∠MEF.
专题
在△DEN 和△FEM 中, ∠ END=NEEM=,∠FME, ∠DEN=∠FEM, ∴△DEN≌△FEM. ∴ED=EF, ∴矩形 DEFG 是正方形.
专题
又∵EF⊥AC, ∴四边形AFCE为菱形. ∴AF=CF. 设AF=CF=x cm,则BF=(8-x)cm. 在Rt△ABF中,由勾股定理,得AB2+BF2 =AF2,即42+(8-x)2=x2,解得x=5. ∴AF=5 cm.
专题
(2)动点P,Q分别从A,C两点同时出发 ,沿△AFB和 △CDE各边匀速运动一周,即点P自A→F→B→A停止, 点Q自C→D→E→C停止.在运动过程中,已知点P的 速度为5 cm/s,点Q的速度为4 cm/s,运动时间为t s, 当以A,C,P,Q四点为顶点的四边形是平行四边形 时,求t的值.
专题
若以A,C,P,Q四点为顶点的四边形是平行四边形, 则PC=QA. ∵四边形ABCD为矩形, ∴AB=CD=4 cm,AD=BC=8 cm. ∵AF=CF=5 cm,点P的速度为5 cm/s,点Q的速度 为4 cm/s,运动时间为t s,
专题
∴PC=PF+FC=PF+FA=5t cm,QA =(AD+CD)-(QD+CD)=(12-4t)cm. ∴5t=12-4t,解得 t=43. 故当以 A,C,P,Q 四点为顶点的四边 形是平行四边形时,t 的值为43.
中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)

中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)学校:___________班级:___________姓名:___________考号:___________1.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,ab ≠0),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.2.(1)如图1,点P 为矩形ABCD 对角线BD 上一点,过点P 作//EF BC ,分别交AB 、CD 于点E 、F .若2BE =,PF=6,AEP △的面积为1S ,CFP 的面积为2S ,则12S S +=________;(2)如图2,点P 为ABCD 内一点(点P 不在BD 上),点E 、F 、G 、H 分别为各边的中点.设四边形AEPH 的面积为1S ,四边形PFCG 的面积为2S (其中21S S >),求PBD △的面积(用含1S 、S的代数式表示);2(3)如图3,点P为ABCD内一点(点P不在BD上)过点P作//EF AD,HG//AB与各边分别相交于点E、F、G、H设四边形AEPH的面积为1S,四边形PGCF的面积为2S(其中21),S S求PBD△的面积(用含1S、2S的代数式表示);(4)如图4 点A B C D把O四等分.请你在圆内选一点P(点P不在AC BD 上)设PB PC BC围成的封闭图形的面积为1S PA PD AD围成的封闭图形的面积为2S PBD△的面积为3S PAC△的面积为4S.根据你选的点P的位置直接写出一个含有1S2S3S4S的等式(写出一种情况即可).3.已知直线y=x+4与x轴y轴分别交于A B两点∠ABC=60°BC与x轴交于点C.(1)试确定直线BC的解析式.(2)若动点P从A点出发沿AC向点C运动(不与A C重合)同时动点Q从C点出发沿CBA向点A运动(不与C A重合) 动点P的运动速度是每秒1个单位长度动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S P点的运动时间为t秒求S与t的函数关系式并写出自变量的取值范围.(3)在(2)的条件下当△APQ的面积最大时y轴上有一点M 平面内是否存在一点N 使以A Q M N为顶点的四边形为菱形?若存在请直接写出N点的坐标;若不存在请说明理由.4.如图在等腰梯形ABCD中AB∥DC AB=8cm CD=2cm AD=6cm.点P 从点A出发以2cm/s的速度沿AB向终点B运动;点Q从点C出发以1cm/s的速度沿CD DA向终点A运动(P Q两点中有一个点运动到终点时所有运动即终止).设P Q同时出发并运动了t秒.(1)当PQ将梯形ABCD分成两个直角梯形时求t的值;(2)试问是否存在这样的t 使四边形PBCQ的面积是梯形ABCD面积的一半?若存在求出这样的t的值若不存在请说明理由.5.如图在平面直角坐标系中以坐标原点O为圆心2为半径画⊙O P是⊙O上一动点且P在第一象限内过点P作⊙O的切线与轴相交于点A与轴相交于点B.(1)点P在运动时线段AB的长度也在发生变化请写出线段AB长度的最小值并说明理由;(2)在⊙O上是否存在一点Q使得以Q O A P为顶点的四边形时平行四边形?若存在请求出Q点的坐标;若不存在请说明理由.6.如图已知长方形ABCD中AD=6cm AB=4cm 点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动同时点Q在线段BC上由点B向点C运动.(1)若点Q的运动速度与点P的运动速度相等经过1秒后△AEP与△BPQ是否全等请说明理由并判断此时线段PE和线段PQ的位置关系;(2)若点Q的运动速度与点P的运动速度相等运动时间为t秒设△PEQ的面积为Scm2请用t的代数式表示S;(3)若点Q的运动速度与点P的运动速度不相等当点Q的运动速度为多少时能够使△AEP与△BPQ全等?7.如图长方形ABCD中5cm,8cm==现有一动点P从A出发以2cm/s的速度沿AB BC----返回到点A停止设点P运动的时间为t秒.长方形的边A B C D At=时BP=___________cm;(1)当2(2)当t为何值时连接,,△是等腰三角形;CP DP CDP(3)Q为AD边上的点且6DQ=P与Q不重合当t为何值时以长方形的两个顶点及点P为顶点的三角形与DCQ全等.8.如图平行四边形ABCD中6cmB∠︒G是CD的中点E是BC==60AB=8cm边AD上的动点EG的延长线与BC的延长线交于点F连接CE DF.(1)求证:四边形CEDF是平行四边形;(2)①AE=______时四边形CEDF是矩形;②AE=______时四边形CEDF是菱形.9.在平面直角坐标系中点A在第一象限AB⊥x轴于点B AC⊥y轴于点C已知点B(b0)C(0 c)其中b c满足|b﹣8|6+-=0.c(1)直接写出点A坐标.(2)如图2 点D从点O出发以每秒1个单位的速度沿y轴正方向运动同时点E从点A出发以每秒2个单位的速度沿射线BA运动过点E作GE⊥y轴于点G设运动时间为t 秒当S四边形AEGC<S△DEG时求t的取值范围.(3)如图3 将线段BC平移使点B的对应点M恰好落在y轴负半轴上点C的对应点为N连接BN交y轴于点P当OM=4OP时求点M的坐标.10.如图在平面直角坐标系中点A B的坐标分别是(﹣4 0)(0 8)动点P从点O出发沿x轴正方向以每秒1个单位的速度运动同时动点C从点B出发沿12.在四边形ABCD中//,90,10cm,8cm∠=︒===点P从点A出发沿折线AB CD BCD AB AD BCABCD方向以3cm/s的速度匀速运动;点Q从点D出发沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发当一个点到达终点时另一点也停止运动设运动时间为()s t.(1)求CD的长;(2)当四边形PBQD为平行四边形时求四边形PBQD的周长;(3)在点P Q的运动过程中是否存在某一时刻使得BPQ的面积为220cm若存在请求出所有满足条件的t的值;若不存在请说明理由.13.在平面直角坐标系中矩形OABC的边OA任x轴上OC在y轴上B(4 3)点M从点A开始以每秒1个单位长度的速度沿AB→BC→CO运动设△AOM的面积为S 点M运动的时间为t.(1)当0<t<3时AM=当7<t<10时OM=;(用t的代数式表示)(2)当△AOM为等腰三角形时t=;(3)当7<t<10时求S关于t的函数关系式;(4)当S=4时求t的值.14.如图1 在平面直角坐标系中正方形OABC的边长为6 点A C分别在x y 正半轴上点B在第一象限.点P是x正半轴上的一动点且OP=t连结PC将线段PC绕点P顺时针旋转90度至PQ连结CQ取CQ中点M.(1)当t=2时求Q与M的坐标;(2)如图2 连结AM以AM AP为邻边构造平行四边形APNM.记平行四边形APNM 的面积为S.①用含t的代数式表示S(0<t<6).②当N落在△CPQ的直角边上时求∠CPA的度数;(3)在(2)的条件下连结AQ记△AMQ的面积为S'若S=S'则t=(直接写出答案).15.如图平面直角坐标系中矩形OABC的顶点B的坐标为(7 5)顶点A C 分别在x轴y轴上点D的坐标为(0 1)过点D的直线与矩形OABC的边BC交于点G 且点G不与点C重合以DG为一边作菱形DEFG 点E在矩形OABC的边OA 上设直线DG的函数表达式为y=kx+b(1)当CG=OD时求直线DG的函数表达式;(2)当点E的坐标为(5 0)时求直线DG的函数表达式;(3)连接BF 设△FBG的面积为S CG的长为a 请直接写出S与a的函数表达式及自变量a 的取值范围.16.如图 在四边形ABCD 中 //AD BC 3AD = 5DC = 42AB = 45B ∠=︒ 动点M 从点B 出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从点C 出发沿线段CD 以每秒1个单位长度的速度向终点D 运动 设运动的时间为s t .(1)求BC 的长.(2)当//MN AB 时 求t 的值(3)试探究:t 为何值时 MNC ∆为等腰三角形?参考答案:1.(1)证明:∵四边形ABCD 是矩形∴AD ∥BC∴∠CAD =∠ACB ∠AEF =∠CFE∵EF 垂直平分AC 垂足为O∴OA =OC∴△AOE ≌△COF∴OE =OF∴四边形AFCE 为平行四边形又∵EF ⊥AC∴四边形AFCE 为菱形设菱形的边长AF =CF =x cm 则BF =(8﹣x )cm在Rt △ABF 中 AB =4cm由勾股定理得42+(8﹣x )2=x 2解得x =5iii )如图3 当P 点在AB 上 Q 点在CD 上时 AP =CQ 即12﹣a =b 得a +b =12. 综上所述 a 与b 满足的数量关系式是a +b =12(ab ≠0).2.(1)过P 点作AB∥MN∵S 矩形AEPM +S 矩形DFPM =S 矩形CFPN +S 矩形DFPM =S 矩形ABCD -S 矩形BEPN又∵11,,22AEP CFP AEPM CFPN SS S S ==矩形矩形 ∴1==26=62AEP CFP S S ⨯⨯, ∴1212.S S +=(2)如图 连接PA PC在APB △中 因为点E 是AB 中点可设APE BPE S S a ==同理 ,,BPF CPF CPG DFG DPH APH S S b S S c S S d ======所以APE APH CPF AEPH PFCG CPG S S SS a b d S S c =+++=++++四边形四边形 BPE BPF DPH DPH EDFP HPGD S S S S S S a b c d +=+++=+++四边形四边形.所以12EBFP HPGD AEPH PFCG S S S S S S +++=+四边形四边形四边形四边形所以1212ABD ABCD SS S S ==+ 所以1DPH APH S S S a ==-. ()()()1121121PBD ABD BPE PDH S S S S S S S S a S a S S =-++=+-++-=-.(3)易证四边形EBGP 四边形HPFD 是平行四边形.EBP SHPD S .()()121211122222ABD ABCD EBF HPD EBP HPD SS S S S S S S S S ==+++=+++ ()()12112FBD ABD EBP HPD S S S S S S S =-++=-. (4)试题解析:(1)由已知得A 点坐标(﹣4﹐0) B 点坐标(0﹐43﹚ ∵OB=3OA ∴∠BAO=60° ∵∠ABC=60° ∴△ABC 是等边三角形 ∵O C=OA=4 ∴C 点坐标﹙4 0﹚ 设直线BC 解析式为y kx b =+∴ ∴直线BC 的解析式为343y x =-+; ﹙2﹚当P 点在AO 之间运动时 作QH⊥x 轴 ∵QH CQ OB CB= ∴2843QH t = ∴QH=3t ∴S △APQ =AP•QH=132t t ⋅=232t ﹙0<t≤4﹚ 同理可得S △APQ =t·﹙833t -﹚=23432t t -+﹙4≤t<8﹚∴223(04)2{343?(48)2t t S t t t <≤=-+≤<; (3)存在 如图当Q 与B 重合时 四边形AMNQ 为菱形 此时N 坐标为(4 0) 其它类似还有(﹣4 8)或(﹣4 ﹣8)或(﹣4 ).4.(1)53(2)存在 使四边形PBCQ 的面积是梯形ABCD 面积的一半.(1)过D 作DE⊥AB 于E 过C 作CF⊥AB 于F 通过Rt ADE Rt BCF ∆≅∆ 得AE BF = 若四边形APQD 是直角梯形 则四边形DEPQ 为矩形 通过AP AE EP =+ 代入t 值 即可求解(2)假设当时 通过点Q 在CD 上或在AD 上 两种情况进行讨论求解5.(1)线段AB 长度的最小值为4理由如下:连接OP如图② 设四边形APQO 为平行四边形因为OQ PA ∥ 90APO ︒∠=所以90POQ ︒∠= 又因为OP OQ =所以45PQO ︒∠= 因为PQ OA ∥所以PQ y ⊥轴.设PQ y ⊥轴于点H在Rt △OHQ 中 根据2,45OQ HQO ︒=∠= 得Q 点坐标为(2,2-)所以符合条件的点Q 的坐标为(2,2-)或(2,2-).6.(1)∵长方形ABCD∴∠A =∠B =90°∵点E 为AD 的中点 AD =6cm∴AE =3cm又∵P 和Q 的速度相等可得出AP =BQ =1cm BP =3 ∴AE =BP在△AEP 和△BQP 中∴y=xy 3=4-y⎧⎨⎩ 解得:x=1y=1⎧⎨⎩ (舍去). 综上所述,点Q 的运动速度为32cm /s 时能使两三角形全等.7.(1)1(2)54t =或4或232 (3) 3.5t = 5.5或10(1)解:动点P 的速度是2cm/s∴当2t =时 224AP =⨯=∵5cm AB =∴BP =1cm ;(2)解:①当点P 在AB 上时 CDP △是等腰三角形∴PD CP =在长方形ABCD 中 ,90AD BC A B =∠=∠=︒∴()HL DAP CBP ≌∴AP BP =∴1522AP AB ==∵动点P 的速度是2cm/s∵90D5DP CD == 2AB CB CD t ++=∴要使一个三角形与DCQ 全等①当点P运动到1P时16△≌△DCQ CDPCP DQ==此时1∴点P的路程为:1527AB BP+=+=∴72 3.5t=÷=;②当点P运动到2P时26△≌△CDQ ABPBP DQ==此时2∴点P的路程为:25611+=+=AB BP∴112 5.5t=÷=③当点P运动到3P时35△≌△CDQ BAP==此时3AP DQ∴点P的路程为:3585220AB BC CD DP+++=+++=∴20210t=÷=④当点P运动到4P时即P与Q重合时46△≌△CDQ CDPDP DQ==此时4∴点P的路程为:4585624+++=+++=AB BC CD DPt=÷=此结果舍去不符合题意∴24212综上所述t的值可以是: 3.5t= 5.5或10.8.(1)四边形ABCD是平行四边形∥∴BC AD∴∠=∠FCG EDGG是CD的中点∴=CG DG△中在CFG△和DEGCFG∴≅(ASA)DEGFG EG∴=又CG DG=∴四边形CEDF是平行四边形.2)①当5AE=如图过60B∠=12BM∴=5AE=DE AD∴=在MBA△BM DEB=⎧⎪∠=∠⎨⎪(SAS)MBA EDC∴≅CED AMB∴∠=∠四边形CEDF是平行四边形∴平行四边形CEDF②当2AE cm =时 四边形CEDF 是菱形 理由如下:四边形ABCD 是平行四边形8AD ∴= 6CD AB == 60CDE B ∠=∠=︒2AE =6DE AD AE ∴=-=DE CD ∴=CDE ∴∆是等边三角形CE DE ∴=四边形CEDF 是平行四边形∴平行四边形CEDF 是菱形故答案为:2;9.(1)解:∵|b ﹣8|6c +-=0∴b -8=0 c -6=0∴b =8 c =6∵B (b 0) C (0 c )∴B (8 0) C (0 6)又∵AB ⊥x 轴 AC ⊥y 轴∴A (8 6);(2)∵AB ⊥x 轴 AC ⊥y 轴 GE ⊥y 轴∴四边形AEGC 是矩形设运动时间为t 秒∴OD =t AE =2t DG =6+2t-t =6+t∴S 四边形AEGC =8×2t =16t S △DEG =12×(6+t )×8=4t +242∵OM=4OP∴-m=-4×62m解得m=-12综上所述m的值为-4或-12.10.(1)∵点A B的坐标分别是(﹣4 0)(0 8)∴OA=4 OB=8∵点C运动到线段OB的中点∴OC=BC=12OB=4∵动点C从点B出发沿射线BO方向以每秒2个单位的速度运动∴2t=4解之:t=2;∵PE=OA=4 动点P从点O出发沿x轴正方向以每秒1个单位的速度运动∴OE=OP+PE=t+4=2+4=6∴点E(6 0)(2)证明:∵四边形PCOD是平行四边形∴OC=PD OC∥PD当点C在y轴的负半轴上时③如果点M在DE上时24163(3)22t tt--=++解得423t=+④当N在CE上时28(3)8214tt tt-⋅++-=-+解得12t=综上分析可得满足条件的t的值为:t1=28﹣16 3t2=2 t3=4+2 3t4=12.11.(1) ()30D,,()1,3E;(2)933022933222572222t tS t tt t⎧⎛⎫-+≤≤⎪⎪⎝⎭⎪⎪⎛⎫=-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-≤⎪ ⎪⎝⎭⎩<(3)198s解:(1)3922y x=-+当y=0时39=022x-+则x=3 即点()30D,当y=3时39=322x-+则x=1 故点()1,3E故:()30D,,()1,3E;(2)如图1 ①当点P在OD段时此时0≤t<32119()2223233S PD OC t t=⨯⨯=⨯-⨯=-+;②当点P在点D时此时t=32此时三角形不存在0S=;''6ADP BEP S S -=-30232t t ⎛⎫≤≤ ⎪⎝⎭⎫<≤⎪;即当点P 在边AB 上运动 且PD PE +的值最小时 运动时间t 为198s . 12.(1)16cm ;(2)(8813)cm +;(3)53t =秒或395秒 解:(1)如图1过A 作AM DC ⊥于M在四边形ABCD 中 //AB CD 90BCD ∠=︒//AM BC ∴∴四边形AMCB 是矩形10AB AD cm == 8BC cm =8AM BC cm ∴== 10CM AB cm ==在Rt AMD ∆中 由勾股定理得:6DM cm =10616CD DM CM cm cm cm =+=+=;(2)如图2当四边形PBQD 是平行四边形时 PB DQ =即1032t t -=解得2t =此时4DQ = 12CQ = 22413BQ BC CQ =+=所以()28813PBQD C BQ DQ =+=+;1003t 14(102BPQ BP BC ==解得53t =;P 在BC 上时 63t1(32BP CQ t =此方程没有实数解;CD 上时:在点Q 的右侧54(34PQ BC =6< 不合题意若P 在Q 的左侧 如图6 即3485t <14(534)202BPQ S PQ BC t ∆==-= 解得395t =; 综上所述 当53t =秒或395秒时 BPQ ∆的面积为220cm . 13.(1)t 10-t ;(2)5;(3)S =20-2t ;(4)2或8. 解:(1)当0<t <3时 点M 在线段AB 上 即AM =t 当7<t <10时 点M 在线段OC 上 OM =10-t故填:t 10-t ;(2)∵四边形ABCO 是矩形 B (4 3)∴OA =BC =4 AB =OC =3∵△AOM 为等腰三角形∴只有当MA =MO 此时点M 在线段BC 上 CM =BM =2 ∴t =3+2=5故填:5;(3)∵当7<t <10时 点M 在线段OC 上∴114(10)20222S OA OM t t =⋅⋅=⨯⨯-=-;(4)①当点M 在线段AB 上时 4=12×4t 解得t =2;②当点M 在线段BC 上时 S =6 不符合题意;当点M 在线段OC 上时 4=20-2t 解得t =8.∴OD =OP +PD =8∴Q (8 2)∵M 是CQ 的中点 C (0 6)∴M (4 4);(2)①∵△COP ≌△PDQ∴OP =OQ =t OC =PD =6∴OD =t +6∴Q (t +6 t )∵C (0 6)∴M (62t + 62t +) 当0<t <6时 S =AP ×y M =(6﹣t )×62t +=2362t -; ②分两种情况:a 当N 在PC 上时 连接OB PM 如图2﹣1所示:∵点M 的横 纵坐标相等∴点M 在对角线BD 上∵四边形OABC 是正方形∴OC =OA ∠COM =∠AOM∴∠MPA =12(180°﹣45°)=67.5° ∴∠CPA =67.5﹣45=22.5°;综上所述 当点N 在△CPQ 的直角边上时 ∠CPA 的度数为112.5°或22.5°;(3)过点M 作MH ⊥x 轴于点H 过点Q 作QG ⊥x 轴于点G∵AMQ AHM AGQ MHGQ S S S S =--△△△梯形∴S '=12(62t ++t )•62t +﹣12(6﹣62t +)•62t +﹣12t •t =3t ①当0<t <6时 即点AP 在点A 左侧时 如图3所示:∵S =S '∴2362t -=3t 解得:t =﹣3+35 或t =﹣3﹣35(舍去);②当t >6时 即点P 在点A 右侧时 如图4所示:S =AP ×y M =(t ﹣6)×62t +=2362t - ∵S =S '将D (0 1)G (10 5)代入y=kx+b 得:1105b k b =⎧⎪⎨+=⎪⎩解得:21051k b ⎧=⎪⎨⎪=⎩∴当CG=OD 时 直线DG 的函数表达式为y=2105x+1.(3)设DG 交x 轴于点P 过点F 作FM⊥x 轴于点M 延长MF 交BC 于点N 如图所示.∵DG∥EF∴∠FEM=∠GPO.∵BC∥OA∴∠DGC=∠GPO=∠FEM.在△DCG 和△FME 中90DCG FME DGC FEMDG FE⎧∠=∠=⎪∠=∠⎨⎪=⎩ ∴△DCG≌△FME(AAS )∴FM=DC=4.∵MN⊥x 轴∴四边形OMNC 为矩形在Rt△CDH 中 由勾股定理可得: HC=22543-=∴BC=BK+KH+HC=4+3+3=10;(2)如图② 过D 作DG∥AB 交BC 于G 点 则四边形ADGB 为平行四边形 ∴BG=AD=3∴GC=BC−BC=10−3=7由题意得 当M N 运动t 秒后 CN=t CM=10−2t∵AB∥DG MN∥AB∴DG∥MN∴∠NMC=∠DGC又∵∠C=∠C∴△MNC ~△GDC∴CN CM CD CG=, ∴10257tt -=解得t=5017; (3)第一种情况:当NC=MC 时 如图③22∵∠C=∠C∠MFC=∠DHC=90°∴△MFC~△DHC∴FC MCHC DC=即:1 102253tt-=解得:t=6017;综上所述当t=103t=258或t=6017时△MNC为等腰三角形.。
最新北师大版九年级数学上册《特殊的平行四边形》全章热门考点整合及答案

全章热门考点整合应用名师点金:本章内容是中考的必考内容,主要考查与特殊平行四边形中菱形、矩形、正方形有关的计算和证明等问题.近几年又出现了许多与特殊平行四边形有关的开放探索题、操作题以及与全等、相似、函数知识相结合的综合题.其主要考点可概括为:一个定理、三个图形、三个判定与性质、四个技巧、两种思想.一个定理——直角三角形斜边上的中线定理1.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.求证:(1)四边形ADEF是平行四边形;(2)∠DHF=∠DEF.(第1题)三个图形图形1菱形2.如图,在△ABC中,D,E分别是AB,AC的中点,过点E作EF∥AB,交BC于点F.(1)求证:四边形DBFE是平行四边形.(2)当△ABC满足什么条件时,四边形DBFE是菱形?并说明理由.(第2题)图形2矩形3.如图,在▱ABCD中,点O是AC与BD的交点,过点O的直线与BA的延长线,DC的延长线分别交于点E,F.(1)求证:△AOE≌△COF.(2)连接EC,AF,则EF与AC满足什么数量关系时,四边形AECF是矩形?请说明理由.(第3题)图形3正方形4.如图,在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后得△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.(1)判断线段DE,FG的位置关系,并说明理由;(2)连接CG,求证:四边形CBEG是正方形.(第4题)三个判定与性质判定与性质1菱形5.如图,在△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC 交AD于点F.求证:四边形CDEF是菱形.(第5题)判定与性质2矩形6.【2015·湘西州】如图,在▱ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:(1)△ADE≌△CBF;(2)四边形DEBF为矩形.(第6题)判定与性质3正方形7.如图,E为正方形ABCD的边AB的延长线上一点,DE交AC于点F,交BC于点G,H 为GE的中点.求证:FB⊥BH.(第7题)四个技巧技巧1解与四边形有关的折叠问题的技巧(轴对称变换法】8.如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD 沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,求阴影部分图形的周长.(第8题)技巧2解与四边形有关的旋转问题的技巧(特殊位置法】9.如图,正方形ABCD的对角线相交于点O,点O也是正方形A′B′C′O的一个顶点,如果两个正方形的边长都等于1,那么正方形A′B′C′O绕顶点O转动,两个正方形重叠部分的面积大小有什么规律?请说明理由.(第9题)技巧3解与四边形有关的动点问题的技巧(固定位置法】10.如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)求对角线AC的长及菱形ABCD的面积.(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.技巧4解中点四边形的技巧11.如图,在△ABC中,AB=AC,点O在△ABC的内部,∠BOC=90°,OB=OC,D,E,F,G分别是AB,OB,OC,AC的中点.(1)求证:四边形DEFG是矩形;(2)若DE=2,EF=3,求△ABC的面积.(第11题)思想1转化思想12.如图,在四边形ABCD中,∠C=90°,∠ABD=∠CBD,AB=CB,P是BD上一点,PE ⊥BC ,PF ⊥CD ,垂足分别为点E ,F.求证:PA =EF.(第12题)思想2 数形结合思想 13.[阅读]在平面直角坐标系中,以任意两点P(x 1,y 1),Q(x 2,y 2)为端点的线段的中点坐标为⎝⎛⎭⎪⎫x 1+x 22,y 1+y 22. [运用](1)如图,矩形ONEF 的对角线相交于点M ,ON ,OF 分别在x 轴和y 轴上,O 为坐标原点,点E 的坐标为(4,3),则点M 的坐标为________.(2)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D 与点A ,B ,C 构成平行四边形的顶点,求点D 的坐标.(第13题)答案1.证明:(1)∵点D ,E 分别是AB ,BC 的中点, ∴DE ∥AC.同理可得EF ∥AB. ∴四边形ADEF 是平行四边形. (2)由(1)知四边形ADEF 是平行四边形, ∴∠DAF =∠DEF.在Rt △AHB 中,∵D 是AB 的中点, ∴DH =12AB =AD.∴∠DAH =∠DHA. 同理可得HF =12AC =AF ,∴∠FAH =∠FHA.∴∠DAH +∠FAH =∠DHA +∠FHA. ∴∠DAF =∠DHF. ∴∠DHF =∠DEF.2.(1)证明:∵D ,E 分别是AB ,AC 的中点, ∴DE 是△ABC 的中位线. ∴DE ∥BC. 又∵EF ∥AB ,∴四边形DBFE 是平行四边形. (2)解:答案不唯一,下列解法供参考. 当AB =BC 时,四边形DBFE 是菱形. 理由:∵D 是AB 的中点, ∴BD =12AB.∵DE 是△ABC 的中位线, ∴DE =12BC.又∵AB =BC ,∴BD =DE. 又∵四边形DBFE 是平行四边形, ∴四边形DBFE 是菱形.3.(1)证明:∵四边形ABCD 是平行四边形, ∴OA =OC ,AB ∥CD. ∴∠AEO =∠CFO. 又∵∠AOE =∠COF , ∴△AOE ≌△COF(AAS).(2)解:当AC =EF 时,四边形AECF 是矩形.理由如下:由(1)知△AOE≌△COF,∴OE=OF.又∵AO=CO,∴四边形AECF是平行四边形.又∵AC=EF,∴四边形AECF是矩形.4.(1)解:DE⊥FG.理由如下:由题意,得∠A=∠BDE=∠GFE,∠ABC=∠DBE=90°,∴∠BDE+∠BED=90°.∴∠GFE+∠BED=90°.∴∠FHE=90°,即DE⊥FG.(2)证明:∵△ABC沿射线AB平移至△FEG,∴CB∥GE,CB=GE.∴四边形CBEG是平行四边形.∵∠GEF=∠ABC=90°,∴四边形CBEG是矩形.∵BC=BE,∴四边形CBEG是正方形.(第5题)5.证明:如图,连接CE,交AD于点O.∵AC=AE,∴△ACE为等腰三角形.∵AO平分∠CAE,∴AO⊥CE,且OC=OE.∵EF∥CD,∴∠2=∠1.又∵∠DOC=∠FOE,∴△DOC≌△FOE(ASA).∴OD=OF.即CE与DF互相垂直且平分.∴四边形CDEF是菱形.6.证明:(1)∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB.又∵DE⊥AB,BF⊥CD,∴∠DEA=∠BFC=90°.∴△ADE≌△CBF.(2)∵△ADE≌△CBF,∴AE=CF.∵CD=AB,∴DF=BE.又∵CD∥AB,∴四边形DEBF为平行四边形.又∵∠DEB=90°,∴四边形DEBF为矩形.7.证明:∵四边形ABCD是正方形,∴CD=CB,∠DCF=∠BCF=45°,DC∥AE,∠CBE=90°,∴∠CDF=∠E.又∵CF=CF,∴△DCF≌△BCF.∴∠CDF=∠CBF.∴∠CBF=∠E.∵H为GE的中点,∴HB=HG=12GE.∴∠HGB=∠HBG.∵∠CDG+∠CGD=90°,∠CGD=∠HGB=∠HBG,∴∠FBG+∠HBG=90°.即∠FBH=90°,∴FB⊥BH.8.解:∵在矩形ABCD中,AB=10,BC=5,∴CD=AB=10,AD=BC=5.又∵将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,∴根据轴对称的性质可得A1E=AE,A1D1=AD,D1F=DF.设线段D1F与线段AB交于点M,则阴影部分的周长为(A1E+EM+MD1+A1D1)+(MB+MF+FC+CB)=AE+EM+MD1+AD+MB+MF+FC+CB=(AE+EM+MB)+(MD1+MF+FC)+AD+CB=AB+(FD1+FC)+10=AB+(FD+FC)+10=10+10+10=30.9.解:两个正方形重叠部分的面积保持不变,始终是1 4 .理由如下:∵四边形ABCD是正方形,∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°. ∵四边形A′B′C′O是正方形,∴∠EOF=90°.∴∠EOF=∠BOC.∴∠EOF-∠BOF=∠BOC-∠BOF.即∠BOE =∠COF.∴△BOE ≌△COF.∴S △BOE =S △COF .∴两个正方形重叠部分的面积等于S △BOC .∵S 正方形ABCD =1×1=1,∴S △BOC =14S 正方形ABCD =14. ∴两个正方形重叠部分的面积保持不变,始终是14. 10.解:(1)在菱形ABCD 中,AG =CG ,AC ⊥BD ,BG =12BD =12×16=8, 由勾股定理得AG =AB 2-BG 2=102-82=6,所以AC =2AG =2×6=12.所以菱形ABCD 的面积=12AC ·BD =12×12×16=96. (2)不发生变化.理由如下:如图①,连接AO ,则S △ABD =S △ABO +S △AOD ,所以12BD ·AG =12AB ·OE +12AD ·OF. 即12×16×6=12×10·OE +12×10·OF. 解得OE +OF =9.6,是定值,不变.(3)发生变化.如图②,连接AO ,则S △ABD =S △ABO -S △AOD ,所以12BD ·AG =12AB ·OE -12AD ·OF. 即12×16×6=12×10·OE -12×10·OF. 解得OE -OF =9.6,是定值,不变.所以OE +OF 的值发生变化,OE ,OF 之间的数量关系为OE -OF =9.6.(第10题)11.(1)证明:如图,连接AO 并延长交BC 于H ,∵AB =AC ,OB =OC ,∴AH 是BC 的中垂线,即AH ⊥BC 于H.∵D ,E ,F ,G 分别是AB ,OB ,OC ,AC 的中点,(第11题)∴DG ∥EF ∥BC ,DE ∥AH ∥GF.∴四边形DEFG 是平行四边形.∵EF ∥BC ,AH ⊥BC ,∴AH ⊥EF.又∵DE ∥AH ,∴EF ⊥DE ,∴四边形DEFG 是矩形.(2)解:∵D ,E ,F 分别是AB ,OB ,OC 的中点.∴AO =2DE =4,BC =2EF =6.∵△BOC 是等腰直角三角形,∴OH =12BC =3. ∴AH =OA +OH =4+3=7.∴S △ABC =12×6×7=21.(第12题)12.证明:如图,连接PC.∵PE ⊥BC ,PF ⊥CD ,∠ECF =90°.∴∠PEC =∠PFC =∠ECF =90°.∴四边形PECF 是矩形.∴PC =EF.在△ABP 和△CBP 中,⎩⎪⎨⎪⎧AB =CB ,∠ABP =∠CBP ,BP =BP ,∴△ABP ≌△CBP(SAS).∴PA =PC.∴PA =EF.点拨:本题运用了转化思想将四边形中的边转化到三角形中,通过用等式的传递性证明两条线段相等.13.解:(1)(2,1.5)(2)设点D 的坐标为(x ,y).若以点A ,B ,C ,D 为顶点构成的四边形是平行四边形,①当AB 为对角线时,∵A(-1,2),B(3,1),C(1,4),∴-1+32=1+x 2,2+12=4+y 2. ∴x =1,y =-1.∴点D 的坐标为(1,-1).②当BC 为对角线时,∵A(-1,2),B(3,1),C(1,4),∴3+12=-1+x 2,1+42=2+y 2. ∴x =5,y =3.∴点D 的坐标为(5,3).③当AC 为对角线时,∵A(-1,2),B(3,1),C(1,4),∴-1+12=3+x 2,2+42=1+y 2. ∴x =-3,y =5.∴点D 的坐标为(-3,5).综上所述,点D 的坐标为(1,-1)或(5,3)或(-3,5).。
八年级数学下册动点问题构成平行四边形解题技巧(一)

八年级数学下册动点问题构成平行四边形解题技巧(一)八年级数学下册动点问题构成平行四边形解题技巧什么是动点问题?动点问题是数学中经常遇到的一类问题,它通常涉及到平行四边形的性质和特点。
解决动点问题需要一定的技巧和方法。
动点问题解题技巧以下是一些解决八年级数学下册动点问题的技巧:•确定动点的位置和性质在解决动点问题时,首先要确定动点的位置和性质。
根据问题所给条件,我们可以确定动点在平行四边形内部、边界上还是延长线上。
这些信息有助于我们确定动点的坐标。
•确定平行四边形的特点平行四边形有一些独特的性质,利用这些性质可以解决动点问题。
例如,平行四边形的对角线相互平分,对角线长相等等。
通过确定平行四边形的特点,我们可以推断出关于动点的一些性质。
•运用向量法或坐标法求解在解决动点问题时,我们可以运用向量法或坐标法来求解。
向量法常用于证明或推导问题,而坐标法常用于具体计算。
具体选择使用哪种方法要根据问题的特点和要求来决定。
•画图辅助解题绘制图形是解决动点问题的重要步骤。
通过画图,我们可以更好地理解问题,并帮助我们找到解题的思路。
画图时,注意要准确绘制出平行四边形的形状和各个元素的位置关系。
•通过推理和运算得出答案在完成前面步骤后,我们可以通过推理和运算来得出最终的答案。
根据题目所要求的内容,进行逻辑推理和数学运算,得出问题的解答。
总结解决八年级数学下册动点问题需要我们熟悉平行四边形的性质和特点,并掌握相应的解题技巧。
通过确定动点的位置和性质、确定平行四边形的特点、运用向量法或坐标法、画图辅助解题以及通过推理和运算得出答案,我们可以有效地解决动点问题。
希望以上技巧能帮助到你解决八年级数学下册动点问题,在数学学习中取得更好的成绩!对于八年级数学下册动点问题构成平行四边形解题,下面给出了更具体的步骤和实例来帮助你更好地理解和应用这些技巧。
1.确定动点的位置和性质首先,从题目中找出关于动点的相关信息,然后根据这些信息来确定动点的位置和性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊四边形:动点问题题型一:1.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当PA +PD 取最小值时,△APD 中边AP 上的高为( )A 、17172B 、17174 C 、 17178D 、3 2.如图4,在梯形ABCD 中,AD ∥BC ,AD =6,BC =16,E 是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间t = 秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形. 3.如图,在梯形ABCD 中,AD ∥BC,E 是BC 的中点,AD=5,BC=12,CD=42,∠C=045,点P 是BC 边上一动点,设PB 长为x.(1)当x 的值为 时,以点P 、A 、D 、E 为顶点的四边形为直角梯形.(2)当x 的值为 时,以点P 、A 、D 、E 为顶点的四边形为平行四边形.(3)点P 在BC 边上运动的过程中,以点P 、A 、D 、E 为顶点的四边形能否构成菱形试说明理由.4.在一个等腰梯形ABCD 中,AD//BC ,AB=CD ,AD=10cm ,BC=30cm ,动点P 从点A 开始沿AD 边向点D 以每秒1cm 的速度运动,同时动点Q 从点C 开始沿CB 边向点B 以每秒3cm 的速度运动,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t s.(1).t 为何值时,四边形ABQP 为平行四边形(2).四边形ABQP 能为等腰梯形吗如果能,求出t 的值,如果不能,请说明理由。
6.梯形ABCD 中,AD ∥BC ,∠B=90°,AD=24cm ,AB=8cm ,BC=26cm ,动点P 从点A 开始,沿AD 边,以1厘米/秒的速度向点D 运动;动点Q 从点C 开始,沿CB 边,以3厘米/秒的速度向B 点运动。
已知P 、Q 两点分别从A 、C 同时出发,,当其中一点到达端点时,另一点也随之停止运动。
假设运动时间为t 秒,问:7.(1)t 为何值时,四边形PQCD 是平行四边形8.(2)在某个时刻,四边形PQCD 可能是菱形吗为什么9.(3)t 为何值时,四边形PQCD 是直角梯形10.(4)t 为何值时,四边形PQCD 是等腰梯形(5) t 为何值时, APQ 是等腰三角形7.如图,在直角梯形ABCD 中,∠B=90°,AD ‖BC ,且AD=4cm ,AB=8cm ,DC=10cm 。
若动点P 从点A 出发,以每秒4cm 的速度沿线段AD 、DC 向C 点运动;动点Q 从C 点以每秒5cm 的速度沿CB 向B 点运动。
当Q 点到达B 点时,动点P 、Q 同时停止运动。
设P 、Q 同时出发,并运动了t 秒。
(1)直角梯形ABCD的面积为__________cm的平方.(2)当t=________秒时,四边形PQCD为平行四边形。
(3)当t=________秒时,PQ=DC(4)是否存在t,使得P点在线段DC上,且PQ⊥DC(如图2所示)若存在,列出方程求出此时的t;若不存在,请说明理由。
8.如图,在直角梯形ABCD中,∠B=90°,AB‖CD,且AB=4cm,BC=8cm,DC=10cm。
若动点P从点A出发,以每秒1cm的速度沿线段AB、BC向C点运动;动点Q从C点以每秒1cm的速度沿CB向B点运动。
当Q点到达B点时,动点P、Q同时停止运动。
设P、Q同时出发,并运动了t秒。
(1)直角梯形ABCD的面积为__________cm的平方.(2)当t=________秒时,四边形PBCQ为平行四边形。
(3)当t=________秒时,PQ=BC.10. 如图,在等腰梯形ABCD中,AB∥CD,其中AB=12 cm,CD=6cm ,梯形的高为4,点P从开始沿AB边向点B以每秒3cm的速度移动,点Q从开始沿CD边向点D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时运动停止。
设运动时间为t秒。
(1)求证:当t为何值时,四边形APQD是平行四边形;(2)PQ是否可能平分对角线BD若能,求出当t为何值时PQ平分BD;若不能,请说明理由;(3)若△DPQ是以PQ为腰的等腰三角形,求t的值。
11.如图,在直角梯形ABCD中,AB//CD,∠C=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿线段AB方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动。
已知动点P、Q同时出发,当点Q运动到点C时,P、Q运动停止,设运动时间为t(s).(1)求CD的长。
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P,点Q的运动过程中,是否存在某一时刻,使得ΔBPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由。
13. 已知,矩形ABCD中,4=,AC的垂直平分线EF分别交AD、BC于BC cm=,8AB cm点E、F,垂足为O.(1)如图10-1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;(2)如图10-2,动点P、Q分别从A、C两点同时出发,沿AFB∆和CDE∆各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q 四点为顶点的四边形是平行四边形时,求t的值.②若点P、Q的运动路程分别为a、b(单位:cm,0ab≠),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.14.已知:如图,在梯形ABCD 中,AB ∥DC ,∠B=90°,BC=8cm ,CD=24cm ,AB=26Cm ,点P 从C 出发,以1cm/s 的速度向D 运动,点Q 从A 出发,以3cm/s 的速度向B 运 动,其中一动点达到端点时,另一动点随之停止运动.从运动开始.(1)经过多少时间,四边形AQPD 是平行四边形(2)经过多少时间,四边形AQPD 成为等腰梯形(3)在运动过程中,P 、Q 、B 、C 四点有可能构成正方形吗为什么如图,在梯形ABCD 中,AD ∥BC ,∠B=90°,AD=16cm ,AB=12cm ,BC=21cm ,动点P 从点B 出发,沿射线BC 的方向以每秒2cm 的速度运动,动点Q 从点A 出发,在线段AD 上以每秒1cm 的速度向点D 运动,点P ,Q 分别从点B ,A 同时出发,当点Q 运动到点D 时,点P 随之停止运动,设运动的时间为t (秒).①当t 为何值时,四边形PQDC 是平行四边形;②当t 为何值时,以C ,D ,Q ,P 为顶点的梯形面积等于60cm 2③是否存在点P ,使△PQD 是等腰三角形若存在,请求出所有满足要求的t 的值,若不存在,请说明理由.15.如图,在梯形ABCD 中,AD ∥BC ,AD=6,DC=10,AB=65,∠B=45°.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.16.(1)求BC 的长.17.(2)当MN ∥AB 时,求t 的值.18.(3)△MNC 可能为等腰三角形吗若能,请求出t 的值;若不能,请说明理由.(4)△MNC 可能为直角三角形吗若能,请求出t 的值;若不能,请说明理由.(5)△MNC 为20时,请求出t 的值.如图,直角梯形ABCD 中,AB ∥CD ,∠A=90°,AB=34,AD=4,DC=234 ,点P 从点A 出发沿折线段AD-DC-CB 以每秒3个单位长的速度向点B 匀速运动,同时,点Q 从点A 出发沿射线AB 方向以每秒2个单位长的速度匀速运动,当点P 与点B 重合时停止运动,点Q 也随之停止,设点P ,Q 的运动时间是t 秒(t >0).(1)当点P 到达终点B 时,求t 的值;(2)设△APQ 的面积为S ,分别求出点P 运动到AD 、CD 上时,S 与t 的函数关系式;(3)当t 为何值时,能使PQ ∥DB ;(4)当t为何值时,能使P 、Q 、D 、B 四点构成的四边形是平行四边形。
A BC D E F 图10-1 O 图10-2 备用图16.如图,在等腰梯形ABCD中,AD∥BC,AB=DC=60,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当点P到达终点C时,求t的值,并指出此时BQ的长;(2)当点P运动到AD上时,t为何值能使PQ∥DC;(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的函数关系式;(不必写出t的取值范围)(4)△PQE能否成为直角三角形若能,写出t的取值范围;若不能,请说明理由.3,动点P从B 17.如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=3点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形(3)当t为何值时,射线QN恰好将△ABC的面积平分并判断此时△ABC的周长是否也被射线QN平分.19.如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以2cm/s的速度、沿B→A→D→C方向,向点C运动;动点Q从点C出发,以2cm/s的速度、沿C→D→A方向,向点A运动.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分若存在,请求出t的值,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形若存在,请求出所有符合条件的t的值;若不存在,请说明理由.20.在直角梯形ABCD 中,∠C=90°,高CD=6cm ,底BC=10cm (如图1).动点Q 从点B 出发,沿BC 运动到点C 停止,运动的速度都是1cm/s .同时,动点P 也从B 点出发,沿BA →AD 运动到点D 停止,且PQ 始终垂直BC .设P ,Q 同时从点B 出发,运动的时间为t (s ),点P 运动的路程为y (cm ).分别以t ,y 为横、纵坐标建立直角坐标系(如图2),已知如图中线段为y 与t 的函数的部分图象.经测量点M 与N 的坐标分别为(4,5)和(2, 25).(1)求M ,N 所在直线的解析式;(2)求梯形ABCD 中边AB 与AD 的长;(3)写出点P 在AD 边上运动时,y 与t 的函数关系式(注明自变量的取值范围),并在图2中补全整运动中y 关于t 的函数关系的大致图象.22.如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,AD=6,BC=8,AB=3 3M 是BC 的中点.点P 从点M 出发沿MB 以每秒1个单位长的速度向点B 匀速运动,到达点B 后立刻以原速度沿BM 返回;点Q 从点M 出发以每秒1个单位长的速度在射线MC 上匀速运动.在点P ,Q 的运动过程中,以PQ 为边作等边三角形EPQ ,使它与梯形ABCD 在射线BC 的同侧.点P ,Q 同时出发,当点P 返回到点M 时停止运动,点Q 也随之停止.设点P ,Q 运动的时间是t 秒(t >0).23.(1)设PQ 的长为y ,在点P 从点M 向点B 运动的过程中,写出y 与t 之间的函数关系式(不必写t 的取值范围);24.(2)当BP=1时,求△EPQ 与梯形ABCD 重叠部分的面积;25.已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点,动点P从点A出发,以每秒4个单位的速度,沿折线AOCD向终点C运动,运动时间是t秒.(1)D点的坐标为;(2)当t为何值时,△APD是直角三角形;(3)如果另有一动点Q,从C点出发,沿折线CBA向终点A以每秒5个单位的速度与P点同时运动,当一点到达终点时,两点均停止运动,问:P、C、Q、A四点围成的四边形的面积能否为28如果可能,求出对应的t;如果不可能,请说明理由.在梯形ABCO中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别是A (8,0),B(8,10),C(0,4).点D(4,7)为线段BC的中点,动点P从O点出发,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.(1)求直线BC的解析式;(2)设△OPD的面积为s,求出s与t的函数关系式,并指出自变量t的取值范围;3(3)当t为何值时,△OPD的面积是梯形OABC的面积的8如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分求出此时点P的坐标已知直角梯形OABC在如图所示的平面直角坐标系中,AB∥OC,AB=10,OC=22,BC=15,动点M从A点出发,以每秒一个单位长度的速度沿AB向点B运动,同时动点N从C点出发,以每秒2个单位长度的速度沿CO向O点运动.当其中一个动点运动到终点时,两个动点都停止运动.(1)求B点坐标;(2)设运动时间为t秒;①当t为何值时,四边形OAMN的面积是梯形OABC面积的一半;②当t为何值时,四边形OAMN的面积最小,并求出最小面积;③若另有一动点P,在点M、N运动的同时,也从点A出发沿AO运动.在②的条件下,PM+PN 的长度也刚好最小,求动点P的速度.如图(1),以梯形OABC的顶点O为原点,底边OA所在的直线为轴建立直角坐标系.梯形其它三个顶点坐标分别为:A(14,0),B(11,4),C(3,4),点E以每秒2个单位的速度从O点出发沿射线OA向A点运动,同时点F以每秒3个单位的速度,从O点出发沿折线OCB 向B运动,设运动时间为t.(1)当t=4秒时,判断四边形COEB是什么样的四边形(2)当t为何值时,四边形COEF是直角梯形(3)在运动过程中,四边形COEF能否成为一个菱形若能,请求出t的值;若不能,请简要说明理由,并改变E、F两点中任一个点的运动速度,使E、F运动到某时刻时,四边形COEF 是菱形,并写出改变后的速度及t的值如图,在平面直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14,A(16,0),C(0,2).(1)如图①,若点P、Q分别从点C、A同时出发,点P以每秒2个单位的速度由C向B 运动,点Q以每秒4个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动.设运动时间为t秒(0≤t≤4).①求当t为多少时,四边形PQAB为平行四边形②求当t为多少时,直线PQ将梯形OABC分成左右两部分的比为1:2,并求出此时直线PQ的解析式.(2)如图②,若点P、Q分别是线段BC、AO上的任意两点(不与线段BC、AO的端点重合),且四边形OQPC面积为10,试说明直线PQ一定经过一定点,并求出该定点的坐标.如图,在平面直角坐标系中,直角梯形ABCO的变OC落在x轴的正半轴上,且AB//OC,BC⊥OC,AB=4,BC=7,OC=10.正方形ODEF的两边分别坐落在坐标轴上,且它的面积等于直角梯形ABCO面积,将正方形ODEF沿x轴的正半轴平行移动,设它与直角梯形ABCO 的重叠部分面积为S。
