构造中位线的方法

合集下载

1初中数学《几何辅助线秘籍》中点模型地构造1(倍长中线法;构造中位线法)

实用标准文案开场:1 •行礼；2•晨读；3•检查作业；4•填写表格5•如图所示,已知在-ABC中，AD是BC边上的中线f F是AD上的一点，连接BE并延长交AC于点F , AE二EF ,求证：AC = BF.6•如图所示.在二ABC中，分别以AB、AC为直角边向夕卜做等腰直角三角形^ABD和SCE , F为BC边上中点，FA的延长线交DE于点G ,求证：①DE二2AF ;②FG丄DE .7•如图所示，在R2ABC中，ZBAC二90。

，点D为BC的中点，点巳F分别为AB、AC上的点，且EDJLFD.以线段BE、EF、FC为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形，或者是钝角三角形？8•四边形ABCD是矩形岸是BC边上的中点，MBE沿看直线AE翻折，点B落在点F处. 直线AF与直线CD交于点G,请探究线段AB、AG、GC之间的关系.2•已知r如图,四边形ABCD中,AC. BD相交于点6 且AC = BD Z E x F分别是AD. BC 的中点，EF分别交AC、BD于点M. N・求证：0M二ON.CA p B3.BD、CE分别是的-ABC外角平分线，过A作AF丄BD , AG丄CE ,垂足分别是F、G ,易证FG=|( AB+BC+AC](1)若BD、CE分别是-ABC的内角平分线，FG与△ ABC三边有怎样的数量关系？画出图形实用标准文案3 •如图川ABC 中，AB 二BC,zABC 二90J 点E、F 分别在AB. AC 上.且AE 二EF,点QCE;(2)0BW0M.M分别为AF、CE的中点.求证：(1)OM詁实用标准文案4•如图r zDBC = zBCE 二90°, M 为DE 的中点.求证:MB 二MC.教学后记学生签名：家长签名:。

北师大版八年级数学下册6.4《三角形的中位线》知识点精讲

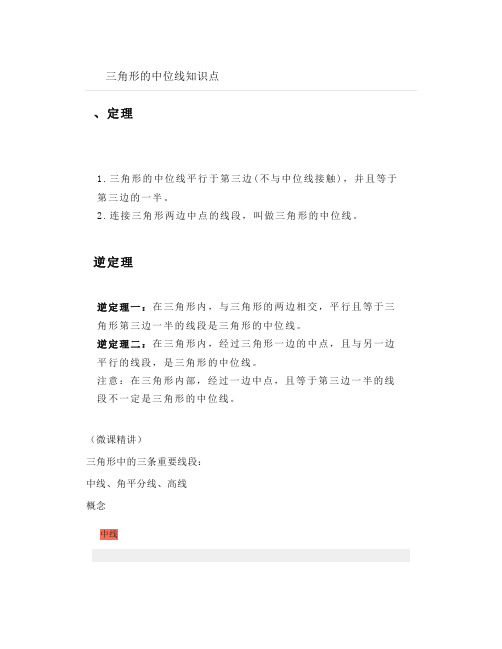
、定理1.三角形的中位线平行于第三边(不与中位线接触)，并且等于第三边的一半。

2.连接三角形两边中点的线段，叫做三角形的中位线。

逆定理逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。

逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。

注意：在三角形内部，经过一边中点，且等于第三边一半的线段不一定是三角形的中位线。

（微课精讲）三角形中的三条重要线段：中线、角平分线、高线概念中线在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形的中线（median）。

三角形的三条中线交于一点，这点称为三角形的重心。

如图，AD是边BC上的中线，BE是边AC上的中线，CF是边AB上的中线三条中线交于点O，点O称为△A BC的重心角平分线在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线。

如图，AD平分∠BAC，BE平分∠ABC，CF平分∠ACB，三角形三条角平分线交于点O点O称为△ABC的内心高线从三角形的一个顶点向它的对边所在直线作垂线，定点和垂足之间的线段叫做三角形的高线，简称三角形的高。

如图，AD⊥BC，BE⊥AC，CF⊥AB三角形三条高线交于点O点O称为△ABC的垂心以上是我们在初一时所学的三角形三条重要线段，今天，我们将学习三角形中第四条重要的线段——中位线（知识点精讲)中位线概念：连接三角形两边中点的线段叫做三角形的中位线性质：三角形的中位线平行于第三边，且等于第三边的一半。

如图，E、F分别是三角形AB、AC边上的中点，所以，EF是三角形BC 边所对的中位线，则EF∥BC且EF=1/2BC三角形的中位线衍生出很多重要的图形，其中最重要的就是中点四边形（微课堂精讲）中点四边形任意画一个四边形，以四边形的中点为顶点组成一个新四边形，这个新四边形称为——中点四边形中点四边形一定是平行四边形证明：连接AC因为E、F分别为AB、BC的中点，所以EF平行且等于AC的一半同理，GH平行且等于AC的一半因此，EF∥HG，EF=HG所以，四边形EFGH是平行四边形思考：四边形ABCD满足什么条件时，四边形EFGH是菱形？矩形？正方形？三角形中位线的解题策略三角形的中位线定理，既有线段的位置关系，又有线段的数量关系，它是一个在三角形中遇到中点，必须联想到的重要定理之一。

典中点平行四边形专训5 构造中位线解题的五种常用方法

典中点平行四边形专训5 构造中位线解题的五种常用方法◐名师点金◑三角形的中位线具有两方面的性质：一是位置上的平行关系,二是数量上的倍分关系.因此,当题目中给出三角形两边的中点时,可以直接连出中位线;当题目中给出一边的中点时,往往需要找另一边的中点,作出三角形的中位线。

典例剖析：如图,在△ABC 中,BD,CE 分别平分∠ABC,∠ACB,AM ⊥CE 于点M,AN ⊥BD 于点N.求证:MN=21(AB+AC-BC)解题秘方:图中不存在中点,但结论与三角形中位线定理很类似,因此应设法寻找中点,再构造三角形的中位线.要证明MN=21(AB+AC-BC),可找以MN 为中位线的三角形,故延长AM 交BC 于点F,延长AN 交BC 于点G,易证明2MN=FG,而FG=BC+FC-BC.又易证明BG=AB,FC=AC,故问题得解。

方法1：连接两点构造三角形的中位线1.如图,点B 为AC 上一点,分别以AB,BC 为边在AC 同侧作等边△ABD 和等边△BCE,点P,M,N 分别为AC,AD,CE 的中点。

(1)求证PM=PN ；(2)求∠MPN 的度数。

方法2：已知角平分线及垂直构造中位线2.如图,在△ABC 中,点M 为BC 的中点,AD 为△ABC 的外角平分线,且AD ⊥BD.若AB=12,AC=18,求DM 的长。

3.如图,在△ABC 中,已知AB=6,AC=10,AD 平分∠BAC,BD ⊥AD 于点D,点E 为BC 的中点，求DE 的长。

方法3：倍长法构造三角形的中位线4.如图,在△ABC 中,∠ABC=90°,BA=BC ，△BEF 为等腰直角三角形,∠BEF=90°,M 为AF 的中点，求证ME=21CF方法4：已知两边中点,取第三边中点构造三角形的中位线5. 如图,在△ABC 中,∠C=90°,CA=CB,E,F 分别为CA,CB 上一点,CE=CF,M,N 分别为AF 、BE 的中点，求证AE=2MN方法5：已知一边中点推理得出另一边中点再取第三边中点构造三角形的中位线6.如图,在△ABC 中,AB=AC,AD ⊥BC 于点D,点P 是AD 的中点,连接BP 并延长交AC 于点N ，求证AN=31AC。

梯形中位线的三种证明方法

梯形中位线的三种证明方法对于初学者来说，学习几何知识可能是一件让人望而生畏的事情。

但是，梯形中位线的三种证明方法是一个很好的开始，这是因为这些证明方法相对简单而且既有趣味性又有启发性。

梯形中位线是指梯形的两条非平行边中的中心线段。

也就是说，梯形中位线从一个梯形的顶点开始，到位于这个梯形另一端的中心点，这两个中心点将这个梯形的一条侧面平分。

因此，我们可以将梯形中位线简单地定义为连接梯形的两条非平行边的中心点的线段。

下面我们来看看有哪些证明方法：第一种证明方法：重心法这是一种最简单的证明方法之一。

它利用梯形的重心的概念，以及梯形中位线与重心之间的几何关系。

梯形的重心是指梯形部分的所有质心的平均值。

这个点总是在梯形中位线上。

将梯形划分成两个三角形，它们的重心到它们所在的梯形中位线的距离相等。

通过简单的计算可以证明这一点。

第二种证明方法：向量法这是一种基于向量概念的证明方法。

通过向量和向量的和，我们可以证明梯形中位线的两个端点与中位线的中心点组成一个三角形。

当然，这个三角形是等腰的，因为向量的大小相等。

我们可以使用如下的向量算法：- 声明梯形的四个顶点坐标（A、B、C和D）。

- 计算相邻顶点之间的向量（AB、BC、CD和DA）。

- 计算梯形的对角线向量（AC和BD）。

- 计算梯形中位线向量（M1和M2）。

- 判断中位线向量是否相等。

第三种证明方法：相似三角形法这是一种利用相似三角形的证明方法，在初学者中非常流行。

我们考虑用两种方法构造相似三角形。

第一种方法：从较小的梯形构建相似三角形。

假设我们有一个梯形ABCD，其中AB || DC，BC ⊥ CD，AC ⊥ BD，M是连接梯形的两条非平行边的中心点。

我们考虑将这个梯形从M处分成两个三角形。

然后我们可以构建一个新的中位线MP，将三角形AMP与三角形DMP进行比较。

因为AM = MD，所以MP是DMP的中位线。

此外，我们可以证明三角形AMP与三角形DMP是相似的。

2021年中考复习第07讲—中点五大模型

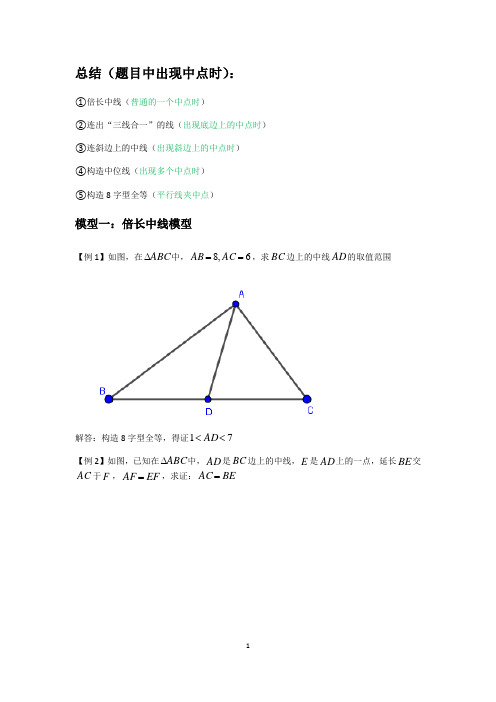
总结（题目中出现中点时）：①倍长中线（普通的一个中点时）②连出“三线合一”的线（出现底边上的中点时） ③连斜边上的中线（出现斜边上的中点时） ④构造中位线（出现多个中点时） ⑤构造8字型全等（平行线夹中点）模型一：倍长中线模型【例1】如图，在ABC ∆中，6,8==AC AB ，求BC 边上的中线AD 的取值范围解答：构造8字型全等，得证71<<AD【例2】如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上的一点，延长BE 交AC 于F ，EF AF =，求证：BE AC =解答：①方法一：倍长中线【DG AD =构造8字型全等+集散思想】 ②方法二：类倍长中线【DE DG =构造8字型全等+集散思想】可证【例3】如图，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，AD EF //交CA 的延长线于点F ，交AB 于点G ，若CF BG =，求证：AD 为ABC ∆的角平分线解答：类倍长中线+集散思想，可证模型二：平行线夹中点模型【例1】如图，在菱形ABCD 中，110=∠A ，F E ,分别是边AB 和BC 的中点，CD EP ⊥于点P ，则=∠FPC （）A.35 B.45 C.50 D.55解答：构造8字型全等【延长EF 和DC 交于点G 】，得证D【例2】如图，在平行四边形ABCD 中，AD BE AD CD ⊥=,2于点F E ,为DC 的中点，连接BF EF ,，下列结论 ①ABF ABC ∠=∠2 ②BF EF =③EFB DEBC S S ∆=2四边形 ④DEF CFE ∠=∠3 其中正确结论有（）A.1个B.2个C.3个D.4个解答：双平模型+平行线夹中点模型，得证D【例3】如图，在菱形ABCD 和正三角形BGF 中，60=∠ABC ，点F 在AB 的延长线上，点P 是DF 的中点，连接PC PG ,，求证：PC PG 3=解答：①方法一：延长CP 交AB 于点E ，连接EG CG ,②方法二：延长GP 交AD 于点E ，连接CG CE , 可证模型三：三线合一模型【例1】如图，在等腰三角形ABC 中，BC AC =，D 是BC 的中点，过C 作CE DE ⊥，CF DF ⊥，且CE CF =，求证：EDA FDB ∠=∠解答：可证【例2】如图，在ABC ∆中，5,6AB AC BC ===，M 为BC 中点，MN AC ⊥于点N ，则MN 的长度（） A.165 B.125 C.95 D.65解答：得证B【例3】如图，在ABC ∆中，,,,AB AC BAD CAD BD BE AM BM >∠=∠==，E 为AD 延长线上一点，N 在DE 上，//MN AC ，求证：ND NE =解答：双平模型+三线合一，可证【例4】如图所示，在ABC ∆中，AB AC =，90BAC ∠=，D 是AC 的中点，AF BD ⊥于点E ，交BC 于点F ，连接DF ，求证：ADB CDF ∠=∠解答：①方法一：三线合一模型 ②方法二：十字型三垂直模型可证模型四：斜边中线模型【例1】如图，在ABC ∆中，BD 和CE 是高，M 为BC 的中点，P 为DE 的中点，求证：PM DE ⊥解答：可证【例2】如图，在ABC ∆中，2B C ∠=∠，AD BC ⊥于点D ，M 是BC 中点，10AB =，求DM 的长度解答：可证【例3】已知，ABD ∆和ACE ∆都是直角三角形，且90ABD ACE ∠=∠=，如图甲，连接DE ，设M 为DE 的中点（1）说明：MB MC =（2）设BAD CAE ∠=∠，固定ABD ∆，让Rt ACE ∆绕顶点A 在平面内旋转到图乙位置，试问：MB MC =是否还能成立？并证明其结论解答：（1）①方法一：斜边中线模型【方程思想用字母表示角】 ②方法二：平行夹中点模型③方法三：相似【作MF BC ⊥交BC 于点M 1DM BFEM CF==得证】（2）成立，同理可证【例4】已知Rt ABC ∆中，AC BC =，90C ∠=，D 为AB 边的中点，90EDF ∠=，EDF ∠绕D 点旋转，它的两边分别交,AC CB （或它们的延长线）与,E F（1）当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEF CEF ABC S S S ∆∆∆+=（2）当EDF ∠绕D 点旋转到和DE AC 不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明，若不成立,,DEF CEF ABC S S S ∆∆∆又有怎样的数量关系？请写出你的猜想，不需证明解答：（1）可证（2）图2成立，同理可证；图3不成立12DEF CEF ABC S S S ∆∆∆-=模型五：中位线模型【例1】已知四边形ABCD 是梯形，//AD BC ，如图，,E F 是,BD AC 中点，试写出EF 与,AD BC 之间的关系解答：①方法一：中位线+三点共线，得证1()2EF BC AD =- ②方法二：平行线夹中点模型，构造8字型全等，得证1()2EF BC AD =- 【例2】如图，在四边形ABCD 中，CD AB =，F E ,分别是AD BC ,的中点，连结EF 并延长，分别与CD BA ,的延长线交于点N M ,，证明：CNE BME ∠=∠解答：【等对边四边形（方法连接对角线）】可证【例3】在ABC ∆中，AB AC >，D 点在AC 上，CD AB =，F E ,分别是AD BC ,的中点，连结EF 并延长，与BA 的延长线交于点G ，若60=∠EFC ，连结GD ，判断AGD ∆的形状并证明解答：【类等对边四边形（方法连接对角线）】可证【例4】如图，在四边形ABCD 中，AC 与BD 相交于点O ，BD AC =，F E ,分别是CD AB ,的中点，连结EF ，分别交BD AC ,于点N M ,，判断OMN ∆的形状解答：【中点四边形（方法连接对角线）】可证。

中位线的构造

八下数学思维解法技巧培优小专题【典例丄】（2019-赤壁市模拟）如图，在四边形肋CD 中，点分别是边AB 、AD 的中点，若BC=15, CD=9, EF=6, ZAFE=55° ,则ZQC= 145 °・【点拨】连接BD •根据三角形中位线定理得到肋=2£F=12, £F 〃肋，根据勾股定理的逆定理得到ZBDC=9Q° ,结合图形计算即可.【解析】解：连接BD ，T 点F 分别是边AB. AD 的中点，:.BD=2EF=12, EF//BD.:• ZADB= ZAFE=55° ,BD 2+CD 2=225, 卅=225,:.BD 2+CD 2=BC 19:.ZBDC=90° ,••• ZADC= ZADB+ZBDC= 145° ,故答案为:145. 连接两点构造中位线中佞线的构31A・100°B. 120° C. 140°D・160°【典例2】（2019・宁波期末）如图，在0BC中D E分别是.IB, AC的中点，点F, G在BC上,且BC=4BF=4CG, £F 与DG 相交于点O,若ZDFE=40° , ZZ）GE=80°,那么ZDOE的度数是（）A【点拨】连接皿利用中位线的性质，可得DE=；BC,由BC=4BF=4CG可得FG= *BC,易得DE //FGRDE=FG,易得四边形DEFG为平行四边形，可得DF//EG,利用平行线的性质可得ZDGE= Z FDG,由外角的性质可得结果.【解析】解：连接DE,TD, E分别是.IB, AC的中点，:.DE//BC且9：BC=4BF=4CG,:.FG=^BC,.•・四边形DEFG为平行四边形，:.DF//EG.:• ZDGE= ZFDG=W ,V ZP/T=40°,I CDCZD利用"••• ZDOE=80° +40° =120° ,【典例3】（2019・钦州期末）如图，MBC中，M是EC中点…Q平分ZBAC. ED丄“10于D,若AB=12, JC=16,则MD等于2・【点拨】延长他交zlC于H 根据等腰三角形的性质得到BD=DH.根据三角形中位线定理计算即可.【解析】解：延长交JC于H,T.1D 平分ABAC. BDW:・BD=DH、AH=4B=\2,:.HC=AC-AH=4.TM 是EC 中点，BD=DH,:.MD=字CH=2,故答案为：2.AB【典例4】（2019・南开区期中）如图，HABC中一3是中线,AE是角平分线，CF丄于F」B=5,AC=2.则DF的长为（）A. 3B. 2.5 C・ 1.5 D・1【点拨】延长CF交肋于证明MFCs/XAFH可得CF=FH, AH=4C,然后求岀EH,再根据三角形的中位线平行于第三边并且等于第三边的一半可得詁丹.【解析】解：如图，延长CF交肋于H,•••一匹是角平分线，A ZCAF= ZHAF.TCF 丄A ZJFC=Z.4FH=90° ,在△JFC和厶1?7/中.Z.CAF =乙HAFT AF =AF ,LAFC=乙AFH•••△zLFCPZUFH （如），:・CF=FH・ AH=AC,:.BH=AB - .1H=AB - AC=5・2 = 3,又•••.ID是中线，•••DF是的中位线, :.DF=^BH=^x3 = 1.5. 故选：C.区中点构造中位线【典例5】（2019-成都期末）已知：如图一Q、恥分别是厶拐C的中线和角平分线—3丄BE, AD=BE3^5-2 —【点拨】过D点作DF//BE，则DF=^BE=\. F为EC中点.在RtZ^WF中求岀的长度，根据已知条件易知G为3中点，因此E为廿中点，贝ij AC= |jF.【解析】解：过刀点作DF//BE.•••・!□是AABC的中线,AD丄BE,：・F为EC中点,AD丄DF,【典例6]（2019-福田如图，已知在3=24,点E是BC上一点,BE=10,连接DE、\\1D=BE=2,则DF=X V22 + 12 =屈「BE是AABC的角平分线，.10丄PE•••△dEG 幻△DEG,•••G为中点,•••E为M中点,:・AE=EF=CF,故答案为：芋【点拨】连接取加的中点F,连接MF、NF,证明NF、分别是△PDE、肋的中位线，由三角形中位线定理得出NF〃恥，MF//AD、NF= ^BE=5. MF=^AD= 12.证出AF丄MF,在Rt/\MNF中，由勾股龙理即可得出答案・CB【解析】解：连接取肋的中点F,连接MF、NF、如图所示：TM、N、F分别是DE、BD的中点，:・NF、妙分别是△$£）£、厶血的中位线，:.NF//BE. MF//AD, NF=；BE=5,临=訓=\2.V ZJCB=90° ,•••JD 丄BC、\9MF//AD.•••MF 丄BC.•:NFUBE、•••NF 丄MF.在Rt^MNF中，由勾股宦理得：MN= \NF2 + MF2=^52 + 122 =13；故答案为:13.【典例刀（2019-成都校级月考）如图，41BC中，ZJ5C=90° , BA=BC.△BEF为等腰直角三角形, ZBEF=9L , M为2F的中点，求证:ME=^CF・E【点拨】延长EF到D, DE=EF,连接JD、BD,判断岀是等腰直角三角形，根据等峻血角三角形的性质可得加=BF,再求出ZCBF= ZABD,然后利用“边角边”证明&BD和ZkCBF全等，根据全等三角形对应边相等可得.3=CF,再根据三角形的中位线平行于第三边并且等于第三边的一半可得ME=i W,从而得到ME= i-CF・【解析】证明：如图，延长EF到D，l-li DE=EF,连接肋、BD,••仏BEF为等腰直角三角形，ZBEF=9L ,•••ZBFE=45° , BE丄DF,•••恥垂直平分DF,A ZBDE=45° ,:・、BDF是等腰直角三角形，:・BD=BF. ZDBF=90° ,V ZCBF+Z.1BF= Z ABC= 90° ,ZABLH ZABF= ZDBF= 90c,:.ZCBF=Z.1BD.在HABD和ZkCBF 中,AB = BC乙CBF = J LABD^BD = BF:.AABD^ACBF (SAS).:・AD=CF.•・・M为.IF的中点，DE=EF,:.ME是ZUDF的中位线，：.ME=【典例8】（2019-成都校级月考）如图，点P为'ABC的边EC的中点，分别以AC为斜边作RtZD 和RtAJC£> 且ZB3=Za(E,求证：PD=PE.【点拨】如图，分别取肿、JC的中点M M连接DM、PM、PN、NE,构建三角形中位线，利用三角形中位线左理和直角三角形斜边的中线等于斜边的一半证得3DP沁NPE (SJS),则该全等三角形的对应边相等：PD=PE・【解析】证明：如图，分别取肿、2C的中点M、N,连接DM、PM、PN、NE.•・•点P为HABC的边BC的中点，.・.PM为/\ABC的中位线，:.PM=扣C・又TWE为直角斜边上的中线，:・NE=AN=扣C.:・MP=NE・同理DM=RV・TD忆=桃AZ1 = Z3,・・・Z5=2Z1 (三角形外角定理).同理，Z6=2Z2.又Z1 = Z2,AZ5=Z6.又PM//AC, PN//AB,AZ7=Z9, Z8=Z9,AZ7=Z &•••Z5+Z7=Z6〒Z8,即ZDMP= ZPNE,DM = PM:.在\MDP与ANPE中，乙DMP =厶PNE,MP = NE:.HMDPS HNPE（SAS）,:・PD=PE・1.（2019・武汉）如图，在△.ISC中，ZJCB=60°C=l, D是边，毎的中点，E是边BC上一点.若^平分△磁的周长，则DE的长是_亨_.【点拨】延长BC至使CM=CA,连接MM,作CN丄于M 根据题意得到ME=£P,很据三角形中位线宦理得到根据等腰三角形的性质求岀厶1CN,根据正弦的概念求岀汁算即可.【解析】解：延长BC至M,使CM=CA.连接凡皿作CN丄凡“于N,•••DE平分ZU5C的周长，:.ME=EB.又AD=DB,B. 20C. 12 D ・10:.DE= jjM, DE//AM.V ZJCB=60° ,A ZJCM= 120° ,VCM=G4,A ZJCV=60°、AN=MN 、：..4N=AC^mZACN=学\/3t• nr — J3• • DE — •故答案为：■-—・22・（2019・宽城区期末）如图，D 是ZUBC 内一点，BD 丄CD, E 、F 、G 、H 分别是边AB 、BD 、CD. AC 的中点.若-W=10, BD=J CD=6,则四边形EFGH 的周长是（）【点拨】利用勾股定理列式求出BC 的长,再根据三角形的中位线平行于第滋并且等于第三边的一半A. 24求出EH=FG= ^BC. EF=GH=*1D,然后代入数据进行讣算即可得解.【解析】解：•:BD1CD,肋=8, 3=6,:・BC= \BD2 +CD2 = V 82+ 62=10,•:E、F、G、H分别是AB. AC. CD、的中点，:・EH=FG=专BC, EF=GH=4D,•••四边形EFGH的周长=EH+GH+FG+EF=AD-BC,又mo,•••四边形EFGH的周长=10+10=20,故选：B.3・(2019・英徳市期末)如图，在中，BF平分ZABC, AG丄BF,垂足为点交BC于点G, E为/C的中点，连结DE, DE=2.5cm, AB=4cm,则BC的长为9 期・【点拨】由条件“BF平分AG丄肿•'可判怎三角形肋G是等腰三角形(AB=GB).再由条件临为HC的中点”，可判怎a是三角形的中位线，由此可得GC=2DE 进而可求出BC的长.【解析】解：TEF 平分ZABC. AG丄BF.:./\ABG是等腰三角形,A. 3 D ・4AB ~ GB =4d ♦•:BF 平分 ZABC.：..4D=DG.YE 为dC 的中点，.・.D£是ZUGE 的中位线,:.DE= *CG,:.CG=2DE=5cm.:.BC=BG+CG=4+5 = 9m ,故答案为：94. （2019-通川区期末）如图，/\ABC 中，D 、E 分别是BC 、AC 的中点，平分ZABC,交DE 于点、F, 若BC=6、则DF 的长是（）【点拨】利用中位线怎理，得到DE 〃肋，根据T •行线的性质，可得ZEDC=ZABC 、再利用角平分线的性质和三角形内角外角的关系，得到进而求出DF 的长.【解析】解：在△肋C 中，D 、E 分别是BC 、AC 的中点,:.DE//AB,:.ZEDC= ZABC. 2•：BF平分ZABC.:.ZEDC=2ZFBD・在△BDF 中，ZEDC= ZFBD+ZBFD.:.ZDBF=ZDFB・:.FD=BD= ；BC= | x6 = 3・故选：2.5.（2019-松北区一模）如图，和BE分别为三角形MC的中线和角平分线，.Q丄BE,若AD=BE=4,则FC的长」【点拨】过D点作〃恥，则F为EC中点,在RtAADF中求出2F的长度，根据已知条件易知6为3中点，因此E为廿中点，则AC=【解析】解：过D点作DF〃EE,如图所示：•••JD是ZUBC的中线,AD丄BE,；・F为EC中点，AD丄DF,\\1D=BE=4.则DF=2, AF= \!AD2 + DF2 =2>/5,•:BE是HABC的角平分线…ID丄:.HABG 竺4DBG,:.AC= |jF=3 洛.故答案为：3尽6.（2019-垦利区期末）如图，在四边形ABDC中，E、F、G、H分别为」B、BC、CD、的中点，并且E、F、G、H四点不共线.当AC=6, BD=*时，四边形EFGF的周长是一14 .【点拨】根据三角形中位线宦理得到FG〃EH, FG=£H根据平行四边形的判左龙理和周长解答即可.【解析】解：TF，G分别为BC, CD的中点，:.FG= FG//BD.VE, H分别为AB, D」的中点，•••EH=$BD=4, EH//BD.:.FG//EH. FG=EH,•••四边形EFGH为平行四边形,:.EF=GH=^1C=3.•••四边形EFGH的周长=3+3+4+4 =14,故答案为：147.(2019・怀化)已知：如图，在HABC中，DE、DF是/XABC的中位线，连接EF. AD,其交点为O・求证：(1)HCDE9HDBF；(2)O4 = OD・【点拨】(1〉根据三角形中位线，可得DF打CE的关系，DB 口 DC的关系，根据SAS.可得答案;(2)根据三角形的中位线，可得DF与AE的关系，根据平行四边形的判定与性质，可得答案.【解析】证明：(1)•:DE、DF是ZL3C的中位线，:.DF=CE. DF//CE. DB=DC・•: DF"CE、:•乙C=ZBDF ・DC = BD住HCDE和△DBF中厶C=乙BDF.CE = DF:.△ CDE9 /XDBF(SJS)：(2) •:DE、DF是WBC的中位线,:.DF=AE, DF//AE,•••四边形DE.1F是平行四边形,•：EF 口.10 交于O 点，:.AO=OD8・（2019-尚志市期中）如图在直角HABC中，ZBAC=9Q Q,点D是BC中点,连接,3,点E为.Q的中点，过点/作AF//BC 交线段恥的延长线于点F,连接CF.（1）求iiE： -1F=DC；（2）在不添加任何辅助线的情况下，请直接写出所有而积等于ZUEF而枳2倍的三角形.【点拨】（1）由“MS”町证HAFE皿DBE；（2）根据等髙模型即可解决问题.【解析】证明：（1）•:AF〃BC、:.ZAFE= ZDBE•••△4BC是宜角三角形，.3是BC边上的中线，E是的中点,：..1E=DE. BD=CD在和△DBE中，LAFE =乙DBELAEF =乙BED，AE = DE:.^AFE^ADBE (zUS)：(2)解：•:AE=DE・•: S ABD=2S「.BDE=2S• AEF・•:DB=DC、BD=AF, ：..1F=CD9/.四边形ADCF是平行四边形,S； ADC=s； dCF=s(ABF；•••而积等于而枳2倍的三角形有：0CD, £\ABD、ZUCF. “AFB.。

中考数学精讲篇考点系统复习第四章三角形方法技巧突破(二) “中点”之六大模型

3．如图，在△ABC 中，D 是 AB 上一点，AD＝AC，AE⊥CD，垂足为 E，EF ∥BD，交 BC 于点 F，若 BD＝10，则 EF 的长为__5__.
模型四：遇到三角形一边上的中点(中线或与中点有关的线段)，考虑倍长中线法构造全等三角形【模型展示】
【模型归纳】题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
2．如图，在△ABC 中，∠ABC＝90°，∠C＝52°，BE 为 AC 边
上的中线，AD 平分∠BAC，交 BC 边于点 D，过点 B 作 BF⊥AD，
垂足为 F，则∠EBF 的度数为
( B)
A．19° B．33° C．34° D．43°
模型三：等腰三角形中遇到底边上的中点，常联想“三线合一”的性质【模型展示】
6．★(2020·武汉)如图，在半径为 3 的⊙O 中，AB 是直径，AC 是弦，D
是A︵C的中点，AC 与 BD 交于点 E.若 E 是 BD 的中点，则 AC 的长是( D )
A.52 3
B．3 3
C．3 2
D．4 2
7．(2020·衢州)如图，△ABC 内接于⊙O，AB 为⊙O 的直径，AB＝10，AC ＝6，连接 OC，弦 AD 分别交 OC，BC 于点 E，F，E 是 AD 的中点． (1)求证：∠CAD＝∠CBA； (2)求 OE 的长．
如图，∠ABC＝∠ADC＝90°.M，N 分别是 AC，BD 的中点，AC＝10，
BD＝8，则 MN 为
( A)
A．3
B．4
C．5
D．6
【思路点拨】连接 MB，MD，利用直角三角形斜边上的中线等于斜边的一半可证 MB＝MD，再由 NB＝ND，根据等腰三角形“三线合一”性质，得 MN⊥BD，在 Rt△BMN 中，利用勾股定理即可求解．

1初中数学《几何辅助线秘籍》中点模型的构造1(倍长中线法;构造中位线法).pptx

D
G E
A
B
F
C
2
ቤተ መጻሕፍቲ ባይዱ
奉爱树教育个性化辅导
7.如图所示，在 Rt△ABC 中，∠BAC＝90°，点 D 为 BC 的中点，点 E、F 分别为 AB、AC 上的点，且 ED⊥FD.以线段 BE、EF、FC 为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形，或者是钝角三角形？
A
E F
B
D
A
B
D
E
C
F
3
奉爱树教育个性化辅导
做辅助线思路二：构造中位线法
经典例题 2：梯形 ABCD 中，AD∥BC，AD＝12，BC＝16，中位线 EF 与对角线分别相交于 H 和
G，则 GH 的长是
.
【课堂训练】 1.已知，如图，四边形 ABCD 中，AB＝CD，E、F 分别是 AD、BC 的中点，BA、FE 的延长线相交于点M，CD、FE 的延长线相交于点N.求证：∠AME＝∠DNE.
1 别为 AF、CE 的中点.求证：（1）OM＝ CE；（2）OB＝ 2 OM.
2
4.如图，∠DBC＝∠BCE＝90°，M 为 DE 的中点，求证：MB＝MC.
教
学
后
记
学生签名：
家长签名：
8
2.如图，在△ABC 中，BD⊥AC 于 D，CE⊥AB 于 E，点 M、N 分别是 BC、DE 的中点， 1 求证：MN⊥DE；
MN
2 连结 ME、MD，若∠A＝60°，求的值.
DE
7
奉爱树教育个性化辅导
3.如图，△ABC 中，AB＝BC，∠ABC＝90°，点 E、F 分别在 AB、AC 上，且 AE＝EF，点 O、M 分

专训常用构造中位线的五种方法

4．四周一片（），听不到一点声响。 5．越是在紧张时刻，越要保持头脑的（）。
八、句子工厂。
1．世界上有多少人能亲睹她的风采呢？（陈述句）
_________________________________ ______ ______ ______ ______ ______ ______ ______ 2．达·芬奇的“蒙娜丽莎”是全人类文化宝库中一颗璀璨的明珠。（缩写句子） ___________________________________ ______ ______ ______ ______ ______ ______ ____ 3．我在她面前只停留了短短的几分钟。她已经成了我灵魂的一部分。（用关联词连成一句话） __________________________________ ______ ______ ______ ______ ______ ______ _____
证明：如图，延长FE至N，使EN＝EF，连接BN，AN.
易得ME＝
1 2
AN.∵EF＝EN，∠BEF＝90°，
∴BE垂直平分FN.∴BF＝BN.∴∠BNF＝∠BFN.
∵△BEF为等腰直角三角形，∠BEF＝90°，
∴∠BFN＝45°.∴∠BNF＝45°，
∴∠FBN＝90°，即∠FBA＋∠ABN＝90°.
3、别想一下造出大海，必须先由小河川开始。 4、自信是所有成功人士必备的素质之一，要想成功，首先必须建立起自信心，而你若想在自己内心建立信心，即应像洒扫街道一般，首先将相当于街道上最阴湿黑暗之角落的自卑感清除干净，然后再种植信心，并加以巩固。信心建立之后，新的机会才会随之而来。

微专题中点问题六大方法

第3题图
方法四遇到三角形一边垂线过这边中点时，利用垂直平分线的性质例 4 如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝4，点D是AB的中点，过点
7 D作DE⊥AB交BC的延长线于点E，则CE 的长为____6____．【思考】点D是AB的中点且DE⊥AB，你想到了哪些学过的知识：D__E_是__线__段__A_B__的__垂__直__ _平__分__线__，__线__段__垂__直__平__分__线__上__的__点__到__线__段__两__端__点__的__距__离__相__等__．_
W
点击链接至综合提升
针对训练
5. 如图，AB是⊙O的直径，C是⊙O上的一点，OD⊥BC于点D，AC＝6，则OD的长为
(B)
A
第5题图
6. 如图，AB是半圆O的直径，△ABC的两边AC，BC分别交半圆于D，E，且E为BC的中点，已知∠BAC＝50°，则∠C＝____6_5_°__．
例5题图
方法总结如图，(1)圆心O是直径的中点，常与已知中点连接，或过点O作一边的平行线或垂直构造中位线解题； (2)圆中遇到弦的中点，联想“垂径定理”，出现“四中点一垂直”解决相应问题； (3)圆中遇到弧的中点，利用“一等四等”、“垂径定理”解决相应问题．
点E是弦AB的中点
点C是 »AB 的中点
∵D是BC的中点，∴BD＝CD，
∵∠BDG＝∠CDA，AD＝GD，
∴△ADC≌△GDB(SAS)．
∴AC＝GB，∠G＝∠EAF. 又∵AF＝EF，
∴∠EAF＝∠AEF.
∵∠AEF＝∠BED，
∴∠G＝∠BED.
例6题解图①
∴BE＝BG.
∴BE＝AC.
【思考】聪明的你还能想到哪些作辅助线的方法，至少再写出一种并解答．

三角形中位线中的常见辅助线

三角形中位线中的常见辅助线知识梳理知识点一中点一、与中点有关的概念三角形中线的定义：三角形顶点和对边中点的连线等腰三角形底边的中线三线合一底边的中线、顶角的角平分线、底边的高重合三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边．直角三角形斜边中线：直角三角形斜边中线等于斜边一半斜边中线判定：若三角性一边上的中线等于该边的一半,则这个三角形是直角三角形二、与中点有关的辅助线方法一：倍长中线解读：凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的可以旋转等长度的线段,从而达到将条件进行转化的目的;方法二：构造中位线解读：凡是出现中点,或多个中点,都可以考虑取另一边中点,或延长三角形一边,从而达到构造三角形中位线的目的;方法三：构造三线合一解读：只要出现等腰三角形,或共顶点等线段,就需要考虑构造三线合一,从而找到突破口其他位置的也要能看出方法四：构造斜边中线解读：只要出现直角三角形,或直角,则考虑连接斜边中线段,第一可以出现三条等线段,第二可以出现两个等腰三角形,从而转化线段关系;其他位置的也要能看出常见考点构造三角形中位线考点说明：①凡是出现中点,或多个中点,都可以考虑取四边形对角线中点、等腰三角形底边中点、直角三角形斜边中点或其他线段中点;②延长三角形一边,从而达到构造三角形中位线的目的;“题中有中点,莫忘中位线”．与此很相近的几何思想是“题中有中线,莫忘加倍延”,这两个是常用几何思想,但注意倍长中线的主要目的是通过构造三角形全等将分散的条件集中起来．平移也有类似作用．典型例题【例1】已知：AD 是ABC △的中线,AE 是ABD △的中线,且AB BD =,求证：2AC AE =．举一反三1. 如右下图,在ABC ∆中,若2B C ∠=∠,AD BC ⊥,E 为BC 边的中点．求证：2AB DE =．2. 在ABC ∆中,90ACB ∠=︒,12AC BC =,以BC 为底作等腰直角BCD ∆,E 是CD 的中点,求证：AE EB ⊥且AE BE =．【例2】已知四边形ABCD 的对角线AC BD =,E 、F 分别是AD 、BC 的中点,连结EF 分别交AC 、BD 于M 、N ,求证：AMN BNM =∠∠．举一反三1. 已知四边形ABCD 中,AC BD <,E F 、分别是AD BC 、的中点,EF 交AC 于M ；EF 交BD 于N ,AC 和BD 交于G 点．求证：GMN GNM ∠>∠．2. 已知：在ABC ∆中,BC AC >,动点D 绕ABC ∆的顶点A 逆时针旋转,且AD BC =,连结DC ．过AB 、DC 的中点E 、F 作直线,直线EF 与直线AD 、BC 分别相交于点M 、N ． 1如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连结HE 、HF ,求证： AMF BNE ∠=∠2当点D 旋转到图2中的位置时,AMF ∠与BNE ∠有何数量关系请证明．【例3】如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点．求证：BF EF =．举一反三1.如图所示,在三角形ABC 中,D 为AB 的中点,分别延长CA 、CB 到点E 、F,使DE=DF ．过E 、 F 分别作直线CA 、CB 的垂线,相交于点P,设线段PA 、PB 的中点分别为M 、N ．求证： 1DEM FDN ∆∆≌；2PAE PBF ∠=∠．3. 已知：在ABC ∆中,分别以AB 、AC 为斜边作等腰直角三角形ABM ,和CAN ,P 是边BC 的中点．求证：PM PN =4. 如图所示,已知ABD ∆和ACE ∆都是直角三角形,且90ABD ACE ∠=∠=︒,连接DE ,设M 为DE 的中点．1求证MB MC =．2设BAD CAE ∠=∠,固定Rt ABD ∆,让Rt ACE ∆移至图示位置,此时MB MC =是否成立请证明你的结论．5. 在△ABC 中,AB=AC,分别以AB 和AC 为斜边,向△ABC 的外侧作等腰直角三角形,M 是BC 边中点中点,连接MD 和ME1如图1所示,若AB=AC,则MD 和ME 的数量关系是EDDBC2如图2所示,若AB≠AC 其他条件不变,则MD 和ME 具有怎样的数量和位置关系请给出证明过程；3在任意△ABC 中,仍分别以AB 和AC 为斜边,向△ABC 的内侧作等腰直角三角形,M 是BC 的中点,连接MD 和ME,请在图3中补全图形,并直接判断△MED 的形状．图1 图2 图3【例4】以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,90BAD CAE ∠=∠=︒.连接DE ,M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系．1如图① 当ABC ∆为直角三角形时,AM 与DE 的位置关系是________；线段AM 与DE 的数量关系是________；2将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转θ︒090θ<<后,如图②所示,1问中得到的两个结论是否发生改变并说明理由．举一反三1. 1如图1,BD 、CE 分别是ABC △的外角平分线,过点A 作AD BD AE CE ⊥⊥、,垂足分别为D E 、,连接DE ．求证：()12DE BC DE AB BC AC =++，∥2如图2,BD CE 、分别是ABC △的内角平分线,其他条件不变； 3如图3,BD 为ABC △的内角平分线,CE 为ABC △的外角平分线,其他条件不变;则在图2、图3两种情况下,DE BC 、还平行吗它与ABC △三边又有怎样的数量关系请你写出猜测,并给与证明．2. 已知ABC ∆中,90ACB ∠=︒,AB 边上的高线CH 与ABC ∆的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F ．求证：EF AB ∥．【例5】等腰梯形ABCD 中,AB CD ∥,AC BD =,AC 与BD 交于点O ,60AOB ∠=︒,P 、Q 、R分别是OA 、BC 、OD 的中点,求证：PQR ∆是正三角形．举一反三1. AD 是ABC ∆的中线,F 是AD 的中点,BF 的延长线交AC 于E ．求证：13AE AC =．【例6】如左下图,在梯形ABCD 中,AB CD ∥,E 、F 分别是AC 、BD 中点．求证：EF AB ∥,且()12EF AB CD =-．举一反三2. 在课外小组活动时,小慧拿来一道题原问题和小东,小明交流原问题：如图1,已知ABC ∆,90ACB ∠=︒,45ABC ∠=︒,分别以AB BC ，为边向外作ABD ∆和BCE ∆,且DA DB =,EB EC =,90ADB BEC ∠=∠=︒,连接DE 交AB 于点F ,探究线段DF 与EF 的数量关系;小慧同学的思路是：过点D 作DG AB ⊥于G ,构造全等三角形,通过推理使问题得解小东同学说：我做过一道类似的题目,不同的是,30ABC ∠=︒,60ADB BEC ∠=∠=︒图1F E D CB A小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况;请你参考小慧同学的思路,探究并解决这三位同学提出的问题：1写出原问题中DF 与EF 的数量关系2如图2,若30ABC ∠=︒,60ADB BED ∠=∠=︒,原问题中的其他条件不变,你在1中得到的结论是否发生变化请写出你的猜想并加以证明；3如图3,若2,ADB BEC ABC ∠=∠=∠原问题中的其他条件不变,你在1中得到的结论是否发生变化请写出你的猜想并加以证明;真题演练1. 已知：AOB △中,2AB OB ==,COD △中,3CD OC ==,ABO DCO =∠∠. 连接AD BC 、、,点M 、 N 、P 分别为AO 、DO 、BC 的中点.1如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则PMN △的形状是________________,此时AD BC=________； 2如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN △∽BAO △,并计算ADBC 的值用含α的式子表示；3在图2中,固定AOB △,将COD △绕点O 旋转,直接写出PM 的最大值.图1 图22.如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形,M、N分别是CE、CF 的中点.1求证：△DMN是等边三角形；2连接EF,Q是EF中点,CP⊥EF于点P. 求证：DP＝DQ.同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考：小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线；小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.3.在△ABC中,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP．过点P作PE ⊥AB于点E,PF⊥AC于点F．1如图1,当AB=AC时,判断的DE与DF的数量关系,直接写出你的结论；2如图2,当AB AC,其它条件不变时,1中的结论是否发生改变请说明理由．图1 图24.探究问题：已知AD、BE分别为△ABC的边BC、AC上的中线,且AD、BE交于点O.1△ABC为等边三角形,如图1,则AO︰OD=__________；2当小明做完1问后继续探究发现,若△ABC 为一般三角形如图2,⑴中的结论仍成立,请你给予证明.3运用上述探究的结果,解决下列问题：如图3,在△ABC 中,点E 是边AC 的中点,AD 平分∠BAC , AD ⊥BE 于点F ,若AD =BE =4. 求：△ABC 的周长.图1 图2 图3 5. 如图1,在四边形ABCD 中,AB CD =,E F 、分别是BC AD 、的中点,连结EF 并延长,分别与 BA CD 、的延长线交于点M N 、,则BME CNE ∠=∠不需证明．温馨提示：在图1中,连结BD ,取BD 的中点H ,连结HE HF 、,根据三角形中位线定理,证明HE HF =,从而12∠=∠,再利用平行线性质,可证得BME CNE ∠=∠．问题一：如图2,在四边形ADBC 中,AB 与CD 相交于点O ,AB CD =,E F 、分别是BC AD 、的中点,连结EF ,分别交DC AB 、于点M N 、,判断OMN △的形状,请直接写出结论．问题二：如图3,在ABC △中,AC AB >,D 点在AC 上,AB CD =,E F 、分别是BC AD 、的中点,连结EF 并延长,与BA 的延长线交于点G ,若60EFC ∠=°,连结GD ,判断AGD △的形状并证明．图1 图2 图330ABO DCO ∠=∠=︒6. 我们知道三角形三条中线的交点叫做三角形的重心．经过证明我们可得三角形重心具备下面的性质：重心到顶点的距离与重心到该顶点对边中点的距离之比为2:1．请你用此性质解决下面的问题.已知：如图,点O 为等腰直角三角形ABC 的重心,90CAB ∠=︒,直线m 过点O ,过A B C 、、三点分别作直线m 的垂线,垂足分别为点D E F 、、.1当直线m 与BC 平行时如图1,请你猜想线段BE CF 、和AD 三者之间的数量关系并证明； 2当直线m 绕点O 旋转到与BC 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立若成立,请给予证明；若不成立,线段AD BE CF 、、三者之间又有怎样的数量关系请写出你的结论,不需证明．7. 以平面上一点O 为直角顶点,分别画出两个直角三角形,记作AOB 和COD ,其中1点E 、F 、M 分别是AC 、CD 、DB 的中点,连接FM 、EM ．2 ①如图1,当点D 、C 分别在AO 、BO 的延长线上时,FM EM =_______； ②如图2,将图1中的AOB 绕点O 沿顺时针方向旋转α角060α<<,其他条件不变,判断FM EM 的值是否发生变化,并对你的结论进行证明；3如图3,若BO = ,点N 在线段OD 上,且2NO = ．点P 是线段AB 上的一个动点,在将AOB 绕点O 旋转的过程中,线段PN 长度的最小值为_______,最大值为_______．。

三角形中的“中点模型”方法总结（重点知识）

三角形中的“中点模型”方法总结（重点知识）三角形是初中数学必考的重要知识点，学好三角形是学好初中几何的关键。

而在三角形相关题目中出现最多的就是中点和角平分线，今天我们来总结一下，遇到中点都有那些处理方法。

掌握了这几种方法，应对三角形相关题目时，同学们将得心应手！类型一倍长中线或类中线类型二遇等腰三角形，构造“三线合一”类型三遇RT三角形斜边的中点，构造斜边的中线类型四遇多个中点，构造中位线例题分析：1、遇到中点，常想倍长中线法例题分析：如图，在△ABC中，AB=10，AC=6，那么BC边上的中线AD的取值范围是。

解:延长AD到E,使DE=AD,连接BE.∵ BD=CD AD=DE ∠CDA=∠BDE∴ △ADC≌△EDB (两边及其夹角对应相等的两个三角形全等)∴ AC=BE (全等三角形的对应边相等)∵ AC=BE AC=6∴ BE=6∵ BE=6 AB=10 AB-BE＜AE∴ 4＜AE∵ BE=6 AB=10 AE＜AB+BE∴ AE＜16∵ 4＜AE AE＜16∴ 4＜AE＜16∵ 4＜AE＜16 AD=12×AE∴ 2＜AD＜82、遇等腰三角形，构造“三线合一”如图，△ABC是等腰直角三角形，AB=AC，D是斜边BC的中点，E. F分别是AB、AC边上的点，且DE⊥DF.请说明：DE=DF；证明：连接AD,∵等腰直角三角形ABC，∴∠C=∠B=45°，∵D为BC的中点，∴AD⊥BC，AD=BD=DC，AD平分∠BAC，∴∠DAC=∠B AD=45∘=∠B,∠ADC=90°，∵DE⊥DF，∴∠EDF=90°，∴∠ADF+∠FDC=90°,∠FDC+∠BDE=90°，∴∠BDE=∠ADF，在△BDE和△ADF中∠B=∠DAFBD=AD∠BDE=∠ADF，∴△BDE≌△ADF，∴DE=DF.3、遇多个中点，构造中位线如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )A. 3B. 2.5C. 2D. 1.5解：如图,连接BD,取BD的中点G,连接MG、NG,∵点M，N分别是AD、BC的中点，∴MG是△ABD的中位线，NG是△BCD的中位线，∴AB=2MG，DC=2NG，∴AB+DC=2(MG+NG)，由三角形的三边关系，MG+NG>MN，∴AB+DC>2MN，∴MN<>∴MN<>故选：A.。

人教版初中数学八年级下册期末提分题习题课件第2课时方法训练构造三角形中位线的五种常用方法

4．如图，在四边形 ABCD 中，AB 与 CD 不平行，M，N 分别是 AD，BC 的中点．若 AB＝10，CD＝8，求 MN 长度的取值范围．
解：如图，取 BD 的中点 P，连接 PM，PN. ∵M 是 AD 的中点，P 是 BD 的中点， ∴PM 是△ABD 的中位线，
∴PM＝12AB＝5. 同理得 PN＝21CD＝4. 在△PMN 中，∵PM－PN<MN<PM＋PN， ∴1<MN<9.
2．如图，在△ABC 中，已知 AB＝6，AC＝10，AD 平分∠BAC， BD⊥AD 于点 D，点 E 为 BC 的中点．求 DE 的长．
解：如图，延长 BD 交 AC 于点 F. ∵AD 平分∠BAC， ∴∠BAD＝∠CAD. ∵BD⊥AD， ∴∠ADB＝∠ADF.
又 AD＝AD，∴△ADB≌△ADF(ASA)．ቤተ መጻሕፍቲ ባይዱ∴AF＝AB＝6，BD＝FD. ∵AC＝10， ∴CF＝AC－AF＝10－6＝4. ∵E 为 BC 的中点，BD＝FD， ∴DE 是△BCF 的中位线． ∴DE＝21CF＝12×4＝2.
∵△ABD 和△BCE 是等边三角形， ∴AB＝DB，BE＝BC，∠ABD＝∠CBE＝60°. ∴∠ABE＝∠DBC. ∴△ABE≌△DBC. ∴AE＝DC. ∴PM＝PN.
(2)求∠MPN 的度数．解：如图，设 PM 交 AE 于 F，PN 交 CD 于 G， AE 交 CD 于 H. 由(1)知△ABE≌△DBC，∴∠BAE＝∠BDC. ∴∠AHD＝∠ABD＝60°，∴∠FHG＝120°. 由三角形中位线定理可得 PM∥CD，PN∥AE， ∴四边形 PFHG 为平行四边形．∴∠MPN＝∠FHG＝120°.
5．如图，在△ABC 中，AB＝AC，AD⊥BC 于点 D，点 P 是 AD 的中点，延长 BP 交 AC 于点 N.求证 AN＝13AC.

三角形中位线的证明方法

三角形中位线的证明方法嘿，咱今儿个就来聊聊三角形中位线的证明方法。

你说这三角形中位线啊，那可真是个神奇的玩意儿！咱先得知道啥是三角形中位线吧。

就是连接三角形两边中点的线段，就这么一条线，却有着大用处呢！那怎么证明它的性质呢？咱可以用倍长中线法呀！就好比是给这条中位线找个“双胞胎兄弟”，把它延长一倍，嘿，你猜怎么着，就能构造出全等三角形啦！这就像是搭积木，一块一块地拼起来，最后就拼成了我们想要的样子。

或者还可以用平行四边形法来证明。

想象一下，中位线和第三边平行，就好像是两条平行线永不相交一样。

然后呢，再利用平行四边形的性质，就能顺顺利利地证明出来啦！这就像是走迷宫，找到了正确的路，一下子就走通了。

还有啊，我们可以通过相似三角形来证明呢！中位线把三角形分成了几个小三角形，它们之间有着相似的关系，就像是一个大家庭里的兄弟姐妹，有着相似的地方。

通过这些相似关系，就能把中位线的性质给弄清楚啦！你说这三角形中位线的证明方法是不是很有趣？就像是在玩一个智力游戏，不断地探索，不断地发现。

而且啊，这在实际生活中也有用处呢！比如建房子的时候，工程师们就得用到这些知识，来保证房子的结构稳定。

你想想看，如果没有这些证明方法，我们怎么能知道中位线的那些奇妙性质呢？那很多建筑可能就盖不起来啦，很多设计也没法实现了。

所以说啊，别小看这小小的三角形中位线和它的证明方法，它们可是有着大能量呢！我们可得好好掌握它们，就像掌握一门神奇的武功秘籍一样，在数学的世界里畅游无阻。

怎么样，现在是不是对三角形中位线的证明方法有了更清楚的认识啦？是不是觉得数学也没那么难啦？嘿嘿，那就对啦！让我们继续在数学的海洋里遨游吧！。

谈中位线的构造方法

谈中位线的构造方法
方海国
【期刊名称】《理科考试研究（初中版）》
【年(卷),期】2017(024)002
【摘要】中位线定理在解题中具有广泛的应用,是平面几何中的一个重要定理.在同一个题设下,包含两个结论.分别是两线段所在直线的位置关系(平行)、两线段的数量关系(倍半).同时,需要根据具体情况按需选用这一定理,不一定同时需要两个结论,有时需要平行关系,有时需要有倍分关系.本文根据题设的若干情况举例说明了中位线的构造方法.
【总页数】3页(P6-8)
【作者】方海国
【作者单位】甘肃省高台县第二中学 734300
【正文语种】中文
【相关文献】
1.以"三角形的中位线"为例,r谈翻转课堂模式下初中数学的教学设计
2.以“三角形的中位线”为例,谈翻转课堂模式下初中数学的教学设计
3.不同的课题与学生,需要不同的教法——谈"三角形中位线定理"一课的不同教法
4.不同的课题与学生,需要不同的教法——谈“三角形中位线定理”一课的不同教法
5.三角形中位线构造方法的探究与建议
因版权原因，仅展示原文概要，查看原文内容请购买。

中位线的构造(原卷版)

C. 140°D. 160°八下数学思维解法技巧培优小专题专题11 中佞线的构建【典例1】（2019・赤壁市模拟）如图，在四边形ABCD ,点民F 分别是边AB 、AD 的中点，若BC= 15,【点拨】连接血根据三角形中位线定理得到BD=2EF=、2, EF//BD,根据勾股定理的逆定理得到ZBDC =90° ,结合图形计算即可.【典例2】（2019・宁波期末）如图，在ZXJPC 中刀，E 分别是.45, AC 的中点，点F, G 在EC 上，且BC=4BF=4CG, £F 与DG 相交于点O,若ZDFE=40° , ZDG£=80° ,那么乙DOE 的度数是（【点拨】连接利用中位线的性质，可得DE=；BC,由BC=4BF=4CG 可得FG=；BC,易得DE//FG 且DE=FG,易得四边形财Z?为平行四边形，可得DF//EG,利用平行线的性质可得乙DGE=ZFDG,由外角的性质可得结果.连接两点构造中位线120°吕利用"角平分线+垂直"构造中位线【典例3】（2019・钦州期末）如图，/\ABC中，M是EC中点,AD平分ABAC, BDLAD于D 若AB=12, JC=16,则⑷等于____________ ・【点拨】延长少交加于"，根据等腰三角形的性质得到AH=AB=\2,根据三角形中位线定理计算即可.A. 3 D・1【典例4】（2019・南开区期中）如图，HABC中一Q是中线,AE是角平分线，CF丄2E于K AB=5,【点拨】延长CF交朋于〃，证明厶AFC^HAFH可得CF=FH、AH=AC,然后求出8",再根扌居三角形的中位线平行于第三边并且等于第三边的一半可得DF= ^BH.区中点构造中位线【典例5】（2019・成都期末）已知：如图，恥分别是41BC的中线和角平分线，-3丄BE, AD=BE=2,则的长等于【点拨】过。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

已知一边中点，取另一边中点构造中位线
5、如图，在⊿ABC中，∠C=90o，CA=BC， E、F分别为CA，CB上一点，CE=CF，M、N分别为AF、 BE中点，求证：AE= 2 MN。
已知两边中点，取第三边中点构造中位线
6、如图，在⊿ABC中，AB=AC，AD⊥BC于点D，点P是AD的中点，延长BP交AC于点N，求证： AC=3AN。
大垸镇中学八年级数学备课组
连接两点构造三角形的中位线
1、如图，点B为AC上一点，分别以AB，BC为边在 AC同侧作等边三角形ABD和等边三角形BCE，点 P,M,N分别为AC，AD，CE的中点。（1）求证：PM=PN；（2）求∠MPN的度数。
已知角平分ห้องสมุดไป่ตู้和垂直构造中位线
2、如图，在⊿ABC中，点M为BC的中点，AD为 ⊿ABC的外角平分线，且AD⊥BD，若AB=12， AC=18，求DM的长。
已知角平分线和垂直构造中位线【练习】
3、如图，在⊿ABC中，已知AB=6，AC=10，AD平分∠BAC，BD⊥AD于点D，点E为BC的中点，求DE 的长。
倍长法构造中位线
4、如图，在⊿ABC中，∠ABC=90o，BA=BC， ⊿BEF为等腰直角三角形，∠BEF=90o，M为AF的中点，求证：CF=2ME。