自适应陷波器课程设计

合集下载

基于lms的自适应陷波器的设计与实现

基于lms的自适应陷波器的设计与实现下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!基于LMS的自适应陷波器的设计与实现1. 引言自适应信号处理技术在滤波器设计中具有重要应用，特别是在抑制干扰信号方面表现出色。

级联自适应陷波器设计及不同步脉冲计数补偿

级联自适应陷波器设计及不同步脉冲计数补偿刘桂雄;万勇;黄坚;潘云飞【摘要】为减小计数误差及实现多路不同步异频脉冲信号的高精度测量,设计了一款可实时估计周期脉冲信号相位的级联自适应陷波器(CANF).首先在前端固定一自适应因子为0的Liu型自适应陷波器(LANF),然后将LANF的输出作为Mojiri型自适应陷波器(MANF)的输入,再利用MANF的估计频率实时调整LANF,最后在流量计标准装置中实现CANF的相位实时估计,并对两路不同步脉冲信号进行精度补偿.仿真实验结果表明CANF的计数误差小于±0.047个脉冲,工程应用实验结果表明CANF的计数误差小于±0.045个脉冲,说明了文中通过实时计算信号相位进行计数补偿的方法能有效提高脉冲计数检定精度和多路并行检定的实用性.【期刊名称】《华南理工大学学报（自然科学版）》【年(卷),期】2016(044)005【总页数】6页(P84-89)【关键词】陷波器;级联;自适应算法;不同步脉冲;误差补偿【作者】刘桂雄;万勇;黄坚;潘云飞【作者单位】华南理工大学机械与汽车工程学院,广东广州510640;广州能源检测研究院,广东广州510170;华南理工大学机械与汽车工程学院,广东广州510640;广州能源检测研究院,广东广州510170【正文语种】中文【中图分类】TH-3将测量量转化为计数脉冲是工业生产、实时监测、自动化控制等领域广泛使用的技术手段,但一次检定多个频率、相位不一致的脉冲信号时,难以应用同步计数法来消除计数误差.文献[1- 2]针对异频不同步信号提出了一种相位补偿方法,但只适合测量两路不同步信号的计数值,并且需要使用高频信号发生器HP8664A产生辅助测量信号.使用时间数字转换器(TDC)也是提高脉冲计数精度的有效方法,但脉冲计数测量对象通常是低频脉冲信号,对时间精度要求不高(微秒级)[3- 6];TDC应用于微秒级时间间隔测量时存在电路规模大、动态范围有限及易受干扰脉冲影响等问题.由于周期脉冲信号可通过傅里叶级数分解为不同频率正弦信号的线性叠加,滤除周期信号3次谐波及以上分量,就可以在获取同频基波信号的同时滤除随机干扰.笔者在前期研究的流量标准装置中嵌入基于陷波滤波器的脉冲补偿算法,计数精度提高了0.06个[7],而自适应陷波滤波器(ANF)[8]可自动使其陷波频率跟随输入信号频率变化、抑制噪声,并提取信号幅值、频率、相位.为减小计数误差,有效提高计数精度,文中在通用数据采集卡基础上,应用ANF技术,设计了一款可实时估计周期脉冲信号相位的级联自适应陷波器(CANF),并提出了一种多路不同步脉冲计数补偿方法.Regalia[9]在局部平均方法、自适应律基础上设计了第一类型ANF,但其受正弦信号幅值、频率耦合的影响,频率估计暂态响应速度受幅值大小的影响明显.Liu等[10]根据缓慢积分流形原理设计了一种收敛速度几乎不受幅值影响的全局收敛归一化ANF(LANF),但LANF仅能处理单正弦输入信号,不适合测试计量领域的周期脉冲信号.Mojiri等[11- 12]采用局部平均方法、Lasalle不变集理论设计了一种固定自适应增益为γ的ANF(MANF);MANF能很好地处理受谐波干扰的正弦输入信号,近年来获得了广泛的工程应用[13- 16],但均未讨论输入为周期方波的情况.为探讨MANF处理周期脉冲信号的性能,设周期脉冲幅值为A、初相位为φ、角频率为ω,则根据傅里叶级数展开式可得到信号在任意t时刻的测量值f:令二阶系统状态变量分别为x1、x2,其微分分别为2,阻尼比为ξ,自适应增益为γ,角频率ω的瞬态估计值为θ,其微分为,则将式(1)作为输入而设计的MANF为[8]对于周期输入信号,动态系统(2)、(3)具有唯一的周期轨道Γ1:Γ1=(x1,x2,θ)=设基波信号幅值为k=2A/,则周期脉冲基波信号为y=ksin(ωt+φ).同理,设状态变量为x3、x4,自适应增益为γ,则设计的LANF为[7]根据LANF原理,状态变量x3、x4的稳态周期轨道为.由Γ2可以看出,x4与输入基波信号同频、同相.按缓慢积分流形原理设置γ=0,则LANF为将CANF应用于多路不同步脉冲计数补偿,则可以根据稳态周期轨道Γ2求得第i路脉冲在任一稳态时刻的相位:令第i路脉冲信号在计数起始时刻t0的相位为φsi,计数停止时刻t1的相位为φei,上升沿检测法脉冲计数值为Ni,则补偿计数值,图2为脉冲计数补偿原理示意图. 2.1 仿真实验对MANF和CANF分别输入相同的脉冲信号:幅值A=10 V、频率f=10 Hz、初相φ0=0 rad,设置ξ=0.7,γ=1,角频率预估初值θ0=100 rad/s,则MANF和CANF状态变量x1、x2的稳态响应曲线、角频率估计曲线分别如图3、4所示.2.2 计数补偿效果实验在研华工控机610L上配置转换精度为16位、最高采样频率为250 kHz的阿尔泰PCI8602型数据采集卡.采用AFG2021-SC信号发生器产生4路相位随机的标准信号(幅值为5 V,频率分别为80、160、200、2 Hz),并利用上升沿检测手段对第4路信号进行整周期截取产生标准时间信号,以减小Windows计时误差对测量结果的影响.上位机对输入脉冲信号振幅做±1处理,并乘以/4后输入CANF,即输入信号基波为y=sin(ωt+φ).在CANF算法开始运行前对前3路信号进行测周处理,并据此预设CANF角频率估计初值θ0.CANF相关参数为:阻尼比ξ=0.15,自适应因子γ=0.1.表1为对3路输入脉冲信号进行计数补偿的实验数据,测量时长分别为1.0、2.5、5.0 s.可以看出,上升沿检测法计算所得脉冲个数在很多情况下均存在±1的计数误差,但经过CANF实时估计相位进行计数补偿后,计数误差小于±0.047个脉冲.图5为CANF状态变量x3、x4的80 Hz脉冲响应曲线,由于单通道实际采样频率仅为2.5 kHz,80 Hz输入信号造成了状态变量的正弦度较差,但实验曲线的幅值、频率及相位均符合其稳态周期轨道Γ2,故根据x3、x4计算的补偿脉冲计数值具有较高的精度.2.3 工程应用实验文中根据缓慢积分流形原理设计了一款级联自适应陷波器,并将其应用于多路不同步脉冲计数补偿.仿真与实验结果表明:①该级联自适应陷波器的谐波干扰抑制能力好,可限制无限次奇次谐波叠加引起的干扰,很好地解决了LANF仅能处理单正弦输入信号、MANF不能处理周期脉冲信号的问题;②该级联陷波器的频率、相位估计准确性在3组不同步计数补偿实验中的计数误差小于±0.047个脉冲;③在双台位流量计标准装置上实现的工程应用实验中的计数误差小于±0.045个脉冲.这种通过实时计算信号相位进行计数补偿的方法能有效地提高脉冲计数检定精度和多路并行检定的实用性.。

陷波器设计

数字信号处理课程设计报告书题目陷波器设计课程设计任务书课题题目摘要随着数字技术的发展，数字滤波器在许多领域得到广泛的应用。

它是通信、语言、图像、自动控制、雷达、航空航天、生物医学信号处理等领域中的一种基本处理部件，具有稳定性好、精度高、灵活性大等突出优点。

在信号采集时，往往受到50Hz电源频率干扰，尤其是在供电系统不稳定、外界环境适应性差时严重影响要采集信号的正确判断。

本设计研究一种在MATLAB语言环境下分别用IIR和FIR滤波器设计方法设计实现一个数字陷波器，并将设计的滤波器应用到混合的正弦信号，通过仿真测试，用两种方法设计的滤波器可以很好的消除50Hz的工频干扰，并分析比较了各种方法所设计的陷波器性能。

在设计IIR数字陷波器过程中,是用椭圆数字陷波滤波器的设计方法，而FIR数字陷波器的设计主要用窗函数法、频率采样法及等波纹逼近法。

FIR滤波器可以得到严格的线性相位，但它的传递函数的极点固定在原点，只能通过改变零点位置来改变性能，为了达到高的选择性，必须用较高的阶数，对于同样的滤波器设计指标，FIR滤波器要求的阶数可能比IIR 滤波器高5～10倍。

IIR滤波器的设计可以利用模拟滤波器的许多现成的设计公式、数据和表格，计算的工作量较小。

关键词数字陷波器；50Hz工频干扰；IIR和FIR滤波器目录课程设计任务书 (I)摘要 (II)1设计概述 (1)1.1设计背景 (1)1.2设计目的 (1)1.3设计内容及要求 (1)2设计方案及实现 (2)2.1总体方案设计 (2)2.2设计原理 (2)2.2.1数字陷波器原理 (2)2.2.2IIR数字陷波器原理 (3)2.2.3FIR数字陷波器原理 (3)3设计结果分析 (8)3.1IIR数字陷波器设计 (8)3.2FIR数字陷波器设计 (10)3.2.1用窗函数法设计陷波器 (10)3.2.2频率采样法设计陷波器 (12)3.2.3基于切比雪夫等波纹逼近法 (13)4总结 (16)1 设计概述1.1 设计背景在我国采用的是50Hz 频率的交流电，所以在平时需要对信号进行采集处理和分析时，常会存在50Hz 的工频干扰，对我们的信号处理造成很大干扰，因此50Hz 陷波器在日常成产生活中被广泛应用，其技术已基本成熟。

(完整word版)自适应滤波器课程设计

目录引言 01 自适应滤波器简介 (2)2 自适应滤波原理 (2)3 自适应滤波算法 (4)4 自适应滤波算法的理论仿真与DSP实现 (6)4.1 MATLAB仿真 (6)4.2 DSP的理论基础 (9)4.3自适应滤波算法的DSP实现 (10)5 结语 (13)参考文献 (14)附录自适应滤波子程序 (15)引言滤波是电子信息处理领域的一种最基本而又极其重要的技术。

在有用信号的传输过程中，通常会受到噪声或干扰的污染。

利用滤波技术可以从复杂的信号中提取所需要的信号，同时抑制噪声或干扰信号，以便更有效地利用原始信号。

滤波器实际上是一种选频系统，它对某些频率的信号予以很小的衰减，让该部分信号顺利通过；而对其他不需要的频率信号则予以很大的衰减，尽可能阻止这些信号通过。

在电子系统中滤波器是一种基本的单元电路，使用很多，技术也较为复杂，有时滤波器的优劣直接决定产品的性能，所以很多国家非常重视滤波器的理论研究和产品开发。

近年来，尤其数字滤波技术使用广泛，数字滤波理论的研究及其产品的开发一直受到很多国家的重视。

从总的来说滤波可分为经典滤波和现代滤波。

经典滤波要求已知信号和噪声的统计特性，如维纳滤波和卡尔曼滤波。

现代滤波则不要求己知信号和噪声的统计特性，如自适应滤波。

自适应滤波的原理就是利用前一时刻己获得的滤波参数等结果，自动地调节现时刻的滤波参数，从而达到最优化滤波。

自适应滤波具有很强的自学习、自跟踪能力，适用于平稳和非平稳随机信号的检测和估计。

自适应滤波一般包括3个模块：滤波结构、性能判据和自适应算法。

其中，自适应滤波算法一直是人们的研究热点，包括线性自适应算法和非线性自适应算法，非线性自适应算法具有更强的信号处理能力，但计算比较复杂，实际应用最多的仍然是线性自适应滤波算法。

线性自适应滤波算法的种类很多，有LMS自适应滤波算法、R路自适应滤波算法、变换域自适应滤波算法、仿射投影算法、共扼梯度算法等[1]。

1 自适应滤波器简介自适应滤波器属于现代滤波器的范畴，自适应滤波器是相对固定滤波器而言的，固定滤波器属于经典滤波器，它滤波的频率是固定的，自适应滤波器滤波的频率则是自动适应输入信号而变化的，所以其适用范围更广。

6-8自适应陷波滤波器

§6-8自适应陷波滤波器自适应消噪器可以作自适应陷波器用。

主要解决那些原始输入信号是由有用信号和一个多余的正弦干扰叠加组成的。

消除这种干扰的传统方法是利用陷波滤波器。

6.8.1陷波滤波器(Adaptive Notch Filter) 在线性滤波器中，常常需要从以下信号中消除单正弦分量t A t s t x 0sin )()(ω+=这个正弦分量，相当于仪器中的50Hz 交流电干扰，应排除其对信号s(t)的干扰，但在滤除过程，又要求基本上不改变接受信号中的其他频率分量，因此，要求其频率特性为)1696(,0,1)(00-⎩⎨⎧=≠=∆ ωωωωωt j e H 如果陷波滤波器的频率特性是周期变化的，则如图：6.8.2自适应陷波滤波器自适应陷波滤波器的频率特性的陷井中心频率除等于外加的正弦或余弦频率外，还随它的改变而自动的修改滤波参数来对准，即自适应的跟踪。

其优点是很容易控制带宽，消噪声的能力没有限制，能够准确跟踪干扰频率。

图6-27所示为两个自动加权的、单频的自适应陷波滤波器，他的原始输入可以是任一种信号：随机的或确定的，周期的或瞬时的。

假设参考输入是一个纯余弦波)cos(0ϕω+kT C ，原始输入与参考输入均以采样频率f T s =1同步采样，考虑x 1(k) 与x 2(k)间存在90’相移，即：)(sin )()cos()(0201ϕωϕω+=+=kT s C k x kT C k x它们通过相关抵消回路以最小均方算法去控制w1(k)与w2(k)加权，而由两个加权输出相加，成为自适应陷波滤波器的输出。

根据LMS 算法，由式（6-114）则：)1706(2,1),()(2)()1(-=+=+ i k x k e k w k w i i i μμ为收敛因子。

为确定自适应陷波滤波器的传递函数，根据上面讨论，可以画出LMS 算法工作原理的流程图。

如图：先求c 点至f点传输支路的输出响应，令c 点加上一个单位采样序列δ()k m -，有⎩⎨⎧≠==-=m k m k m k k e ,0,1)()(δ d 点的响应是：⎩⎨⎧≠=+=-+=m k m k kT C m k kT C k e k x ,0),cos()()cos()()(001ϕωδϕω它在幅度上按 k=m 时刻的x 1(k)瞬时值采样。

自适应滤波器课程设计

自适应滤波器课程设计一、课程目标知识目标：1. 理解自适应滤波器的基本概念，掌握其工作原理和应用领域；2. 学会推导自适应滤波器的算法，并能运用相关理论知识分析滤波性能；3. 了解自适应滤波器在信号处理、通信等领域的实际应用。

技能目标：1. 能够运用所学知识设计简单的自适应滤波器，完成特定信号的处理任务；2. 掌握使用编程软件（如MATLAB）进行自适应滤波器仿真实验，提高实际操作能力；3. 培养独立分析问题、解决问题的能力，提高团队协作和沟通表达能力。

情感态度价值观目标：1. 培养学生对信号处理领域的兴趣，激发学生主动探索科学问题的热情；2. 培养学生严谨、认真的学习态度，养成勤奋刻苦的学习习惯；3. 增强学生的国家使命感和社会责任感，使其认识到自适应滤波器在我国科技发展中的重要作用。

本课程针对高年级本科生，结合课程性质、学生特点和教学要求，将课程目标分解为具体的学习成果。

在教学过程中，注重理论与实践相结合，提高学生的实际操作能力，培养学生解决实际问题的能力。

通过本课程的学习，使学生能够掌握自适应滤波器的核心知识，为未来从事相关领域的研究和工作打下坚实基础。

二、教学内容1. 自适应滤波器基本概念：滤波器分类、自适应滤波器的定义及其与传统滤波器的区别；2. 自适应滤波器原理：线性最小均方（LMS）算法、递推最小均方（RLS）算法、归一化算法等；3. 自适应滤波器的应用：信号处理、通信、语音识别等领域；4. 自适应滤波器设计：基于MATLAB工具箱的滤波器设计流程及参数配置；5. 自适应滤波器性能分析：收敛性分析、计算复杂度分析、数值稳定性分析；6. 实践教学：设计并实现一个简单的自适应滤波器，完成特定信号处理任务。

教学内容按照以下进度安排：1. 第1周：自适应滤波器基本概念，教材第1章；2. 第2周：自适应滤波器原理，教材第2章；3. 第3周：自适应滤波器的应用，教材第3章；4. 第4周：自适应滤波器设计，教材第4章；5. 第5周：自适应滤波器性能分析，教材第5章；6. 第6周：实践教学，结合教材第4章和第5章内容进行。

自适应陷波器课程设计

一．课程设计的主要内容与基本要求：
1.1 主要内容
在通信系统和电子系统中，经常会受到诸如 50Hz 工作频率等单频或窄带干扰的影响。这种干扰的存在，严重影响了信号接收或检测的可靠性和正确性，需要采用自适应信号陷波器消除此干扰。当自适应噪声抵消系统的参考输入为单一频率正弦信号时，则系统可以构成自适应信号陷波器。本设计主要内容是在掌握自适应滤波器原理的基础上，设计一个陷波器，从宽带滤去单一音频信号干扰。方案的选择：
主要参考资料：
1. 胡广书. 现代信号处理教程. 清华大学出版社. 2005.06 2. 高西全. 数字信号处理. 西安电子科技大学出版社. 2009.01 3. matlab 信号处理相关书籍 4. 相关网络资源 685 5. /bookfiles/734/10073422620.shtml
其中 x(k)是带有特定频率干扰的信号，也即输入的原始信号，可见它是从自适应滤波器的期望信号端输入的；而 sin(2π f0/fs k)和 cos(2π f0/fs k)，是我们已知的频率为 f0 的干扰信号（其中 fs 是采样率），将它们分别乘以 W1 和 W2 进行适当的线性组合，就可以使其输出 y(k)接近实际的干扰，最后输出的误差 e(k)就是我们感兴趣的信号。如何进行 W1 和 W2 的选择这其实是自适应算法需要完成的工作，具体来说就是采用某种准则来构建一个关于误差 e(k)的函数，通过是误差 e(k)最小化来求得 W1 和 W2，最常用的准则就是使误差的均方和最小。
当我们知道原始信号里的干扰信号频率是多少时例如最常见的50hz工频干扰这时我们只需要知道这个干扰信号的相位和幅度然后就可以完全的再现这个干扰信号然后我们就可以直接的从原始信号中将其减去从而就得到了我们想要的信号成分

Matlab课程设计自适应陷波器

Matlab课程设计自适应陷波器一、教学目标本节课的教学目标是使学生掌握自适应陷波器的设计原理和MATLAB实现方法。

通过本节课的学习，学生应能够理解自适应陷波器的基本概念，掌握自适应陷波器的设计步骤，并能够利用MATLAB进行自适应陷波器的仿真和实现。

具体来说，知识目标包括：1.掌握自适应陷波器的基本原理和设计方法。

2.理解自适应陷波器在信号处理中的应用。

3.熟悉MATLAB中自适应陷波器的实现方法。

技能目标包括：1.能够使用MATLAB设计自适应陷波器。

2.能够进行自适应陷波器的仿真和实验。

情感态度价值观目标包括：1.培养学生的创新意识和实践能力。

2.增强学生对信号处理和自适应陷波器应用的兴趣。

二、教学内容本节课的教学内容主要包括自适应陷波器的设计原理、MATLAB实现方法和应用案例。

具体包括以下几个部分：1.自适应陷波器的基本原理：介绍自适应陷波器的工作原理、特点和应用场景。

2.自适应陷波器的设计方法：讲解自适应陷波器的设计步骤和方法，包括滤波器设计、自适应算法选择等。

3.MATLAB实现方法：介绍如何在MATLAB中实现自适应陷波器，包括MATLAB函数和编程方法。

4.应用案例：通过实际案例分析，使学生了解自适应陷波器在信号处理中的应用，并能够进行仿真和实验。

三、教学方法为了达到本节课的教学目标，将采用以下几种教学方法：1.讲授法：通过讲解自适应陷波器的设计原理和MATLAB实现方法，使学生掌握基本概念和理论。

2.案例分析法：通过分析实际应用案例，使学生了解自适应陷波器的应用场景和效果。

3.实验法：让学生动手进行自适应陷波器的仿真和实验，提高学生的实践能力和创新意识。

四、教学资源为了支持本节课的教学内容和教学方法的实施，将准备以下教学资源：1.教材：提供相关章节的自适应陷波器设计原理和MATLAB实现方法的教材。

2.多媒体资料：制作PPT和视频等多媒体资料，帮助学生更好地理解和掌握自适应陷波器的设计和实现。

50hz陷波器课程设计

50hz陷波器课程设计一、课程目标知识目标：1. 学生能理解50Hz陷波器的基本原理，掌握其电路构成及工作原理。

2. 学生能掌握陷波器的设计方法，包括电路参数的计算和元件的选择。

3. 学生了解50Hz陷波器在实际应用中的功能，如消除电力线干扰等。

技能目标：1. 学生能运用所学知识，设计并搭建一个简单的50Hz陷波器电路。

2. 学生能够运用示波器、信号发生器等仪器，测试陷波器的性能，并分析测试结果。

3. 学生能够通过团队合作，解决在设计过程中遇到的问题，提高实际操作能力。

情感态度价值观目标：1. 学生培养对电子技术的兴趣，增强学习动力，培养创新意识。

2. 学生在学习过程中，养成积极思考、主动探究的良好习惯。

3. 学生通过合作学习，培养团队精神，提高沟通与协作能力。

本课程针对高中电子技术课程，结合学生已有知识基础和认知特点，注重理论与实践相结合，培养学生实际操作能力和团队协作精神。

通过本课程的学习，学生能够掌握50Hz陷波器的设计与应用，为后续电子技术课程打下坚实基础。

二、教学内容本章节教学内容主要包括以下几部分：1. 50Hz陷波器的基本原理：介绍陷波器的作用、原理，以及其在电子技术中的应用。

2. 陷波器电路构成及工作原理：详细讲解陷波器的电路构成，包括电阻、电容、运算放大器等元件的作用，以及陷波器的工作原理。

3. 电路参数计算与元件选择：教授如何根据实际需求计算陷波器的电路参数，并指导学生进行元件的选择。

4. 50Hz陷波器设计方法：分析不同类型的陷波器设计方法，以实例形式讲解具体设计步骤。

5. 陷波器性能测试与评估：介绍测试陷波器性能的仪器及方法，如示波器、信号发生器等，并教授如何分析测试结果。

6. 实际应用案例分析：通过分析陷波器在实际应用中的案例，使学生更好地理解其功能。

教学内容安排和进度：1. 第1课时：50Hz陷波器基本原理及作用。

2. 第2课时：陷波器电路构成及工作原理。

3. 第3课时：电路参数计算与元件选择。

(完整word版)50HZ自适应陷波器

一课题意义的及要求陷波器也叫带阻滤波器，能保证在其他频率信号不损失的情况下，有效地抑制输入信号中某一频率的干扰。

由于我国采用的是50Hz 的交流电，所以在平时需要对信号进行采集处理和分析时，经常会存在50Hz 工频干扰，对于信号的处理造成很大的干扰，于是，很有必要设计50Hz 的陷波器。

采用自适应滤波组成的陷波器，与一般硬件组成的固定网络的陷波器比较，它既能自适应地准确跟踪干扰频率又容易控制带宽。

在本次设计中，应用自适应滤波器滤除输入随机信号中的50Hz 工频干扰，并分析比较了不同算法在此设计中的优缺点，及在何种参数下效果最优和那一种机构更适合此设计。

二自适应陷波器原理自适应陷波器原理图其原始输入为任意信号s(t)与t 0cos ω单频干扰的叠加，经采样后送入k d 端，k d =k d +)cos(0kt ω。

参考输入分两路，其中一路经︒90向移，两路都经过采样后加到1x 及2x 端，它门分别是)c o s (0,1φω+=kt c x k)sin(0,2φω+=kt c x k所以，采用两个权可以使组合后的正弦波的振幅和相位都能加以调整，而两个权也意味着有两个自由度待调整。

经过k k x w ,1,1与k k x w ,2,2相加得到k y ，其相位和振幅得到相应调整后可与原输入中的干扰分量相一致，使输出k e 中的0 频率的干扰得以抵消，达到陷波的目的。

三结构及方法的选择自适应滤波器的结构有横向滤波器和格型结构，用自适应横向滤波器实现陷波，比较简单且易于实现，而格型滤波器的计算复杂，不易于实际运用。

故本设计中选择横向滤波器结构。

在算法选择方面，分别对LMS 算法，RLS 算法，进行了仿真实验。

比较了其优劣。

四 LMS 算法不同参数的实验结果分析3.1带有50Hz 工频干扰的随机信号及其功率谱图3.2不同步长对输出结果的影响下图依次是u =0.003，u =0.03 u =0. 3时的输出功率谱图观察得出当u比较小，取0.003时，对干扰信号的削弱比较小，对干扰信号临近频率的信号削弱也很小，随着u的不断增大，对50Hz干扰信号的削弱越来越强，但同时对临近信号的影响也越大。

学位论文-—设计一个简单的陷波器

本科生毕业论文（设计）题目：设计一个简单的陷波器前言.....................................................1.滤波器基本内容介绍......................................1.1滤波器的概念...........................................1.2滤波器的分类...........................................1.3陷波器与滤波器的关系...................................2.陷波器的设计............................................2.1陷波器的特性...........................................2.2陷波器设计原理.........................................2.3陷波器设计的实例......................................2.5陷波器设计程序........................................3.陷波器的仿真及性能分析................................. 结束语参考文献致谢本文介绍了滤波器的基本概念，滤波器的种类，分析了各种常见滤波器的功能用途。

并且指明了陷波器是一种特殊功用的带阻滤波器。

另外，还分析了现有的几种常见的设计方案。

选择借助Z变换和零极点设计数字陷波器。

陷波器的设计，实质上是数学逼近理论的应用．通过计算让物理可实现的实际陷波器频率特性逼近理想的或给定的频率特性，以达到去除干扰提取有用信号的目的．借助z变换和零极点来设计陷波器就是利用离散时间系统z变换和对该系统中零点和极点的分析来进行设计陷波器。

基于LMS的自适应陷波器的设计与实现

The Design and Implementation of Adaptive Notch Filter Based on LMS Algorithm
作者：陈颉
作者机构：安康学院电子与信息工程学院,陕西安康725000
出版物刊名：安康学院学报
页码： 113-116页
年卷期： 2016年第5期
主题词：一般陷波器自适应陷波器 LMS算法自适应干扰对消
摘要：自适应陷波器是一种特殊的滤波器,它能够通过不断地自我学习和调整使系统始终工
作在最佳状态。

本文针对一般陷波器的缺陷,在LMS算法的基础上,设计了自适应陷波器,并通过Matlab编程实现了抑制单频干扰和双频干扰的自适应陷波器。

系统测试结果表明,合理选择收
敛因子值,可以使自适应滤波器具有优良的滤波特性。

该研究为微弱信号检测以及消除各种通信系统中的窄带干扰提供了参考价值。

自适应谱线增强器和陷波器的设计

自适应谱线增强器和陷波器的设计1 引言自适应谱线增强器最早是Widrow 等人与1975年在研究自适应噪声相消时提出来的，目的是将正弦波与宽带噪声分离出来，并提取正弦波信号。

相反，如果正弦波信号是希望抑制的噪声或干扰，实现这一任务的的自适应滤波器称为陷波器。

现在，自适应谱线增强器和陷波器已广泛的应用于瞬时频率估计，谱分析，窄带检测，语音编码，窄带干扰抑制，干扰检测，数字式数据接收机的自适应载体恢复的领域。

自适应陷波器是用来恢复淹没在背景噪声中的未知频率的正弦信号以及估计正弦信号的频率。

在自适应陷波器的设计中，我们总是希望得到足够的尖截止特性，为了达到这个目的，自适应FIR 滤波器通常需要很高的阶数，从而导致计算量很大，但是自适应IIR 滤波器只用二阶就能得到最佳的近似。

一个IIR 陷波器是指在单位圆上，它的幅度响应在某一个特定值处为零，此值我们称为陷波频率，而它的幅度在单位圆上的其他点时几乎是连续不变的。

我们利用陷波器的输入减去输出，便可以得到具有尖截至特性的带通滤波器，从而在有效减小背景干扰噪声的同时，恢复输入信号中的正弦信号。

考虑下面的观测信号)()sin()()()(1n v n w A n v n s n x i pi i i +Θ+=+=∑= （1）式中Ai ，wi ，oi 分别是第i 个正弦波信号的幅值，频率和初始相位：v(n)为加性的宽带噪声，可以是有色的。

希望设计的滤波器，让含噪声的信号x(n)通过该滤波器后，输出中只含有P 个正弦波信号s(n)，而没有其他任何信号或噪声。

由于P 个正弦波信号的功率谱为P 条离散的谱线，所以这种只抽取正弦波信号的滤波器称为谱线增强器。

令H(w)是谱线增强器的传递函数，为了抽取P 个正弦波，并拒绝所有其他信号和噪声，传递函数H(w)必须满足以下条件：p w w w H .....,0,1)(0其他若〈= （2）反之，若陷波器的传递函数p w w w H .....1,0)(0其他若〈= （3）则滤波器将抑制掉P 个正弦波信号，并让v(n)完全通过，这种滤波器的作用相当一个正弦波的陷阱，故称为陷波器。

低通50Hz陷波器课程设计报告

中南民族大学电子技术课程设计报告题目学院专业年级姓名学号指导教师年月日指导教师评语：总分：指导教师签名：电子技术课程设计任务书设计题目：（选题题目）学生姓名：学号：专业班级：一、设计条件1．可选元件（1）选题规定的“可选、限选元件”（2）电阻、电容、电感、电位器等，按需使用（3）自备元件2．可用仪器万用表，示波器，交流毫伏表，信号发生器，直流稳压电源二、设计任务及要求1．设计任务根据技术要求和已知条件，完成选题电路的设计、装配与调试。

2．设计要求（1）选题规定的“设计内容和要求”；（2）选择电路方案，完成对确定方案电路的设计。

包括：计算电路元件参数、选择元件、画出总体电路原理图；（3）用软件仿真整体或部分核心实验电路，得出适当结果；（4）装配、调试作品，按规定格式写出课程设计报告书。

三、时间安排1．第12周前：布置设计任务，讲解设计要求、实施计划、设计报告等要求。

2．第14周前：理解课题要求，准备元器件。

3．第15～16周：资料查阅，方案设计，模拟仿真，实际制作。

4．第17～18周：完成设计与制作，答辩，提交设计报告。

指导教师签名：年月日一、实验名称低通50Hz 陷波器二、实验要求设计一个低通50Hz 陷波电路，要求直流稳压电源供电，多级有源滤波： ① 3dB 低通截止频率：100Hz （可选：扩展到1dB ） ② 3dB 带阻中心频率：50Hz （可选：扩展到1dB ） ③ 总电压增益：≥10（可选：扩展到100）三、实验目的1、掌握有源滤波电路的设计方法2、掌握二阶有源带阻滤波器电路的设计方法3、了解有源滤波电路的性能特点4、了解二阶有源带阻滤波器的性能特点5、掌握有源滤波电路的安装与调试方法6、掌握二阶有源带阻滤波器的安装与调试方法7、掌握滤波器有关参数的测量、计算方法8、理论应用于实践，增强动手能力四、相关概念①、有源滤波电路：若滤波电路含有有源元件（双极型管、单极型管、集成运放）组成，成为有源滤波电路。

陷波器的设计和仿真

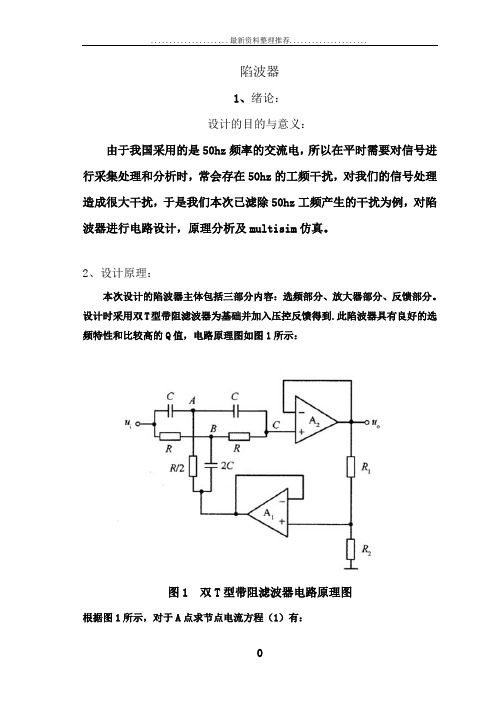
陷波器1、绪论：设计的目的与意义：由于我国采用的是50hz频率的交流电，所以在平时需要对信号进行采集处理和分析时，常会存在50hz的工频干扰，对我们的信号处理造成很大干扰，于是我们本次已滤除50hz工频产生的干扰为例，对陷波器进行电路设计，原理分析及multisim仿真。

2、设计原理：本次设计的陷波器主体包括三部分内容：选频部分、放大器部分、反馈部分。

设计时采用双T型带阻滤波器为基础并加入压控反馈得到.此陷波器具有良好的选频特性和比较高的Q值，电路原理图如图1所示：图1 双T型带阻滤波器电路原理图根据图1所示，对于A点求节点电流方程（1）有：()()()0200=-+-+-n U mU sC U U sC U U A A A i（1）同样，对于B 点求节点电流方程（2）有： ()()()000=-+-+-sC U mU n U U n U U B B B i（2）同样，对于C 点有节点电流方程（3）： ()()00B 0A =-+-n U U sC U U(3) 式中212R R R m +=，R n 1=。

由上述的（1）、（2）、（3）式可以得到此电路的传输函数为()()C n s m s C n s snC m C s n C s n U U s G i -+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=-+++==14C n 14)(22222222220 此时令ωj =s 得ωωωωωωω0202202)1(4)(G m j j ----=其中RC 10=ω。

当0ωω=时）（ωj G =0，此时能滤除RCf π210=的频率，而对于其他频率，）（ωj G 约为1，能很好的使其他频率的信号通过。

令）（ωj G =0.707得到两个截止频率为： ()⎥⎦⎤⎢⎣⎡-+-+=)1(214120m m f f H ()⎥⎦⎤⎢⎣⎡---+=)1(214120L m m f f 此时可以得到陷波器的带宽BW 和其Q 值0)1(4BW f m f f L H -=-=)1(410m f f f Q L H -=-= 则只要我们取m 值接近1时，就能得到窄带滤波效果和高Q 值，使陷波器的性能达到最佳。

实验五、陷波器

12．根据系统设计要求和步骤，调整电路RC值，得出实验要求的电路幅频曲线，并记录电路元器件参数；
四、实验步骤
（二）硬件电路实践 1. 首先将直流稳压电源接成正负电源形式，并调整电压旋钮将输出电压调至±12v，关闭电源； 2. 实验板如图：将电源插在J9电源插座上，注意实验板上的正负电源线的颜色，把对应的电源插头插到直流稳压电源上，检查无误后，打开电源，实验板上两个指示灯亮，说明连接正确，否则连接有误，请检查电源连接； 3. 调零：用示波器检查J6(Vout)电位，并调整RV1，使J6电位为0V；
1# 增益控制 2# 阻抗变换 3# 陷波 4# 阻抗变换
调零
实验电路板
信号输出
调零
陷波器
信号输入
电源
安全隔离
二、基本原理
由节点导纳方程可以得到电路的传递函数为：
A( s) ቤተ መጻሕፍቲ ባይዱ Vo( s) = Vi ( s) Avf [1 + ( 1 + 2(2 − Avf ) s
ωn
s
)2 ] +( s
ωn
陷波器仿真、实验五陷波器仿真、制作与调试
http://218.199.94.50
张日欣 2009.4
一、实验目的
1．熟悉陷波器的类型与特性以及在ECG放大器中的作用； 2．学习双T陷波器的设计方法，掌握陷波器的相关指标； 3．掌握陷波器的调试方法，调试陷波器电路，使调试后的陷波器达到以下主要指标：
（1）在仿真信号源[simulation sources]工具箱中选择正弦波1K信号源，并放入设计图合适位置，并连入电路中；（2）设置信号源参数：信号源标识；[attribute]->[part]为100hz；

气动伺服弹性系统的自适应陷波器算法设计

航空科学技术
Aeronautical Science & Technology
Mar. 25 2020 Vol. 31 No.03 73-78
气动伺服弹性系统的自适应陷波器算法设计
王雨 1，崔茅 1，张公平 2，3，唐炜 1，*
1. 西北工业大学，陕西西安 710129 2. 中国空空导弹研究院，河南洛阳 471009 3. 航空制导武器航空科技重点实验室，河南洛阳 471009
本文利用最小均方（least Mean Square, LMS）算法对测量反馈信号进行迭代运算，实时估计弹性振动频率，并将此
收稿日期：2019-09-05；退修日期：2019-10-21；录用日期：2019-12-25 基金项目：航空科学基金（20170153002）；国家自然科学基金（61573289）；陕西省自然科学基础研究计划（2019JM-042） *通信作者：Tel.：029-88431365 E-mail：tangwei@ 引用格式：Wang Yu，Cui Mao，Zhang Gongping，et al. Adaptive notch filter design approach for aeroservoelastic system［J］. Aeronautical
针对这一问题，George[4]将导弹的弹性模态看作一种未建模不确定性来设计鲁棒控制器，实现对弹性信号抗扰动的姿态控制。然而鲁棒控制器设计过程较为复杂，控制器阶次一般较高，且控制性能对模型具有一定的依赖性。朱
敬举等[5]的研究表明，使用二阶固定极点式陷波器可以有效消除导弹固定频率的弹性振动信号对控制回路的影响。然而，我们知道在导弹的飞行过程中，随着其所携带的燃料的不断燃烧，弹体的整体质量和刚度分布将不断降低，造成弹性振动频率不断下降，传统的固定极点式陷波滤波器无法满足在导弹的整个飞行过程中对弹性振动信号进行滤除。因此，迫切需要设计一种陷波中心频率能够随振动频率实时改变的自适应陷波器，对飞行中导弹的振动信号进行滤除，以保证控制系统的准确性和稳定性。 Choongseok[6]基于 Guass-Newton 算法对运载火箭的多阶弹性模态进行估计，取得了理想的效果，但这种方法只适用于模态频率变化缓慢的情况。陈光山等[7]利用消除记忆最小二乘法在线辨识弹性模态频率，实现了对弹性振动信号的自适应滤波，但该方法对弹性振动频率的辨识精度不高，不利于陷波器的设计。

一种基于LMS算法自适应陷波器的设计

一种基于LMS算法自适应陷波器的设计
陈智
【期刊名称】《郧阳师范高等专科学校学报》
【年(卷),期】2015(0)6
【摘要】通信和电子系统工作过程中经常会受到单频或窄带干扰信号的影响,一种基于LMS算法的陷波器结构及其算法仿真,能对单频干扰的原始正弦信号进行恢复.【总页数】2页(P5-6)
【作者】陈智
【作者单位】郧阳师范高等专科学校汽车与电子工程系,湖北十堰 442000
【正文语种】中文
【中图分类】TN713
【相关文献】
1.一种基于改进LMS算法的自适应消噪滤波器 [J], 朱慧敏
2.一种基于改进LMS算法的自适应消噪滤波器 [J], 朱慧敏
3.一种基于FIR的自适应滤波器LMS算法设计与实现 [J], 周飚;汪烈军
4.一种基于时分复用的复系数自适应IIR陷波器的FPGA设计与实现 [J], 齐亮;田红心;朱艳艳
5.一种新变步长LMS算法在二阶自适应陷波器中的应用 [J], 雷振宇;胡光锐;孙丽萍
因版权原因，仅展示原文概要，查看原文内容请购买。