第32届中国数学奥林匹克
第32届中国数学奥林匹克获奖名单
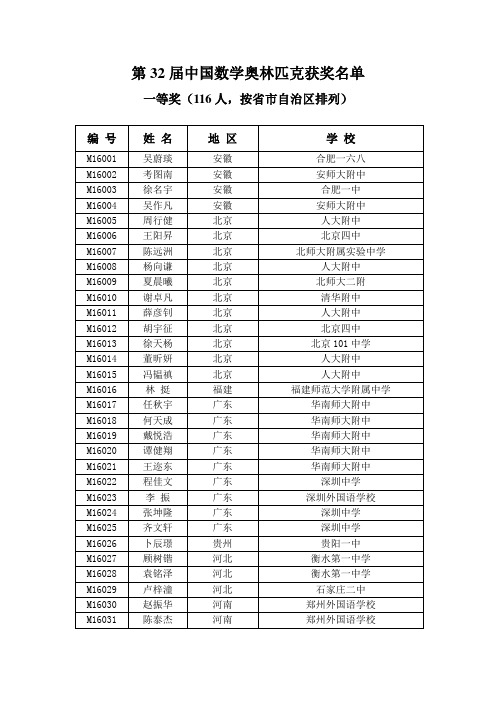
第32届中国数学奥林匹克获奖名单一等奖(116人,按省市自治区排列)编号姓名地区学校M16001 吴蔚琰安徽合肥一六八M16002 考图南安徽安师大附中M16003 徐名宇安徽合肥一中M16004 吴作凡安徽安师大附中M16005 周行健北京人大附中M16006 王阳昇北京北京四中M16007 陈远洲北京北师大附属实验中学M16008 杨向谦北京人大附中M16009 夏晨曦北京北师大二附M16010 谢卓凡北京清华附中M16011 薛彦钊北京人大附中M16012 胡宇征北京北京四中M16013 徐天杨北京北京101中学M16014 董昕妍北京人大附中M16015 冯韫禛北京人大附中M16016 林挺福建福建师范大学附属中学M16017 任秋宇广东华南师大附中M16018 何天成广东华南师大附中M16019 戴悦浩广东华南师大附中M16020 谭健翔广东华南师大附中M16021 王迩东广东华南师大附中M16022 程佳文广东深圳中学M16023 李振广东深圳外国语学校M16024 张坤隆广东深圳中学M16025 齐文轩广东深圳中学M16026 卜辰璟贵州贵阳一中M16027 顾树锴河北衡水第一中学M16028 袁铭泽河北衡水第一中学M16029 卢梓潼河北石家庄二中M16030 赵振华河南郑州外国语学校M16031 陈泰杰河南郑州外国语学校M16032 迟舒乘黑龙江哈尔滨市第三中学M16033 黄桢黑龙江哈尔滨市第三中学M16034 姚睿湖北华中师范大学第一附属中学M16035 魏昕湖北武汉二中M16036 黄楚昊湖北武钢三中M16037 刘鹏飞湖北武汉二中M16038 赵子源湖北华中师范大学第一附属中学M16039 徐行知湖北武钢三中M16040 吴金泽湖北武汉二中M16041 李弘梓湖北武汉二中M16042 施奕成湖北华中师范大学第一附属中学M16043 袁睦苏湖北武汉二中M16044 王子迎湖北武汉二中M16045 袁昕湖北华中师范大学第一附属中学M16046 陈子瞻湖北湖北省黄冈中学M16047 詹立宸湖北华中师范大学第一附属中学M16048 严子恒湖北武钢三中M16049 陈贵显湖北华中师范大学第一附属中学M16050 张騄湖南长沙市长郡中学M16051 刘哲成湖南长沙市雅礼中学M16052 仝方舟湖南长沙市长郡中学M16053 谢添乐湖南长沙市雅礼中学M16054 尹龙晖湖南长沙市雅礼中学M16055 黄磊湖南长沙市雅礼中学M16056 肖煜湖南长沙市长郡中学M16057 吴雨澄湖南湖南师范大学附属中学M16058 方浩湖南长沙市第一中学M16059 郭鹏吉林东北师大附中M16060 丁力煌江苏南京外国语学校M16061 朱心一江苏南京外国语学校M16062 高轶寒江苏南京外国语学校M16063 彭展翔江西高安二中M16064 刘鸿骏江西江西省吉安市第一中学M16065 孔繁淏辽宁大连二十四中M16066 孔繁浩辽宁东北育才学校M16067 孟响辽宁大连24中M16068 毕梦达辽宁辽宁省实验中学M16069 韩序舜辽宁大连育明高级中学M16070 姜霁恒辽宁东北育才学校M16071 辛正则山东山东省胜利第一中学M16072 王浩然山东山东日照一中M16073 吕青峰山东烟台一中M16074 张子洲山西山西大学附属中学M16075 张入文山西山西大学附属中学M16076 祁晴山西山西大学附属中学M16077 张文龙山西康杰中学M16078 王亦茁陕西西安高新第一中学M16079 李纪琛陕西西安高新第一中学M16080 蒋诗琪上海上海市上海中学M16081 李亚臻上海上海市华东师大二附中M16082 侯喆文上海上海市华东师大二附中M16083 庄子杰上海上海市上海中学M16084 范峻昊上海上海市上海中学M16085 张之奕上海上海市上海中学M16086 李羽航上海复旦大学附属中学M16087 鲁一逍上海上海市上海中学M16088 贺炅炀上海上海市上海中学M16089 马健翔上海上海市华东师大二附中M16090 马致远上海上海市华东师大二附中M16091 朱昦曈上海上海市华东师大二附中M16092 彭淏四川成都七中M16093 叶添四川成都七中嘉祥外国语学校M16094 蒋佳轩四川成都七中M16095 李为远四川成都七中M16096 方一杰四川成都七中嘉祥外国语学校M16097 郭子棋四川成都七中M16098 石元峰四川成都七中M16099 程思睿四川成都七中M16100 赵川喆天津天津市第一中学M16101 肖逸南浙江杭州二中M16102 叶奇浙江乐成寄宿中学M16103 连家睿浙江乐成寄宿中学M16104 滕丁维浙江乐成寄宿中学M16105 葛佳迪浙江乐成寄宿中学M16106 陈柯润浙江乐成寄宿中学M16107 江元旸浙江宁波市鄞州中学M16108 吴雨航浙江镇海中学M16109 贺宇昕浙江镇海中学M16110 金士雯浙江乐成寄宿中学M16111 柴劲航浙江蛟川书院M16112 俞博仁浙江乐成寄宿中学M16113 李纯浙江镇海中学M16114 俞志远浙江镇海中学M16115 冯信钦重庆重庆八中M16116 赵兰昕重庆重庆八中二等奖(141人,按省市自治区排列)编号姓名地区学校M16117 王踞秋安徽合肥一中M16118 李世欣安徽安师大附中M16119 胡杨安徽合肥一中M16120 冯梓轩北京人大附中M16121 欧阳铭晖北京人大附中M16122 魏宇辰北京清华附中M16123 刘鑫焱北京首师大附中M16124 孔鼎问北京人大附中M16125 丘铱可北京清华附中M16126 魏澜北京人大附中M16127 王昕阳北京北师大附属实验中学M16128 高国荃北京北京五中M16129 郑书恒福建厦门双十中学M16130 吴炜宏福建厦门一中M16131 王星瀚甘肃西北师大附中M16132 林立聪广东华南师大附中M16133 刘润声广东华南师大附中M16134 吴天昊广东深圳中学M16135 文豪广东广东省中山市中山纪念中学M16136 郑含之广东深圳中学M16137 唐山茖广东华南师大附中M16138 王浩翔广东深圳中学M16139 邓海航广东深圳市高级中学M16140 刘文博广东深圳中学M16141 叶展宏广西柳州高中M16142 冯双全贵州贵阳一中M16143 牛钰涵海南海南中学M16144 王征翊海南海南中学M16145 闫顺兴河北衡水第一中学M16146 杨帅河北唐山一中M16147 曹烁河北石家庄二中M16148 闫乙铭河北石家庄二中M16149 李泽乾河北石家庄二中南校M16150 郑媛洁河北石家庄二中M16151 郭彦婷河北邯郸市一中M16152 王泽昊河南郑州一中M16153 张斐然河南郑州一中M16154 潘晓凡河南郑州一中M16155 喻君钊河南郑州外国语学校M16156 兰倬铭黑龙江哈尔滨市第三中学M16157 王哲威黑龙江哈师大附中M16158 李俊博黑龙江哈尔滨市第三中学M16159 刘泓黑龙江哈尔滨市第三中学M16160 杨柳霏湖北武汉二中M16161 周沐风湖北武汉二中M16162 周达明湖北武钢三中M16163 梅峻豪湖北湖北夷陵中学M16164 李师铨湖南长沙市雅礼中学M16165 刘麒轩湖南长沙市雅礼中学M16166 段剑儒湖南长沙市雅礼中学M16167 肖尧湖南长沙市雅礼中学M16168 刘予培湖南长沙市长郡中学M16169 肖澍旸湖南长沙市雅礼中学M16170 邱添湖南长沙市雅礼中学M16171 刘恺睿湖南长沙市雅礼中学M16172 罗文林湖南湖南师范大学附属中学M16173 谢茗远湖南长沙市长郡中学M16174 江林铮湖南湖南师范大学附属中学M16175 胡宗庆湖南长沙市第一中学M16176 初炜康吉林吉大附中M16177 徐洋吉林东北师大附中M16178 李濛初吉林吉大附中M16179 于卓吉林东北师大附中M16180 刘泽楠吉林东北师大附中M16181 王佳泓吉林东北师大附中M16182 吴清玉吉林东北师大附中M16183 王艺纯吉林吉大附中M16184 张洗月江苏江苏省天一中学M16185 王卓然江苏南师附中M16186 邹汉文江苏南师附中M16187 乌家宁江苏南京外国语学校M16188 俞然枫江苏南京树人学校M16189 高诚江苏无锡市第一中学M16190 吴逸飞江苏泰州中学M16191 何家亮江苏苏州中学M16192 张天越江苏江苏省启东中学M16193 付伟中江西江西省樟树中学M16194 张继霖江西江西师大附中M16195 陈自元江西景德镇二中M16196 谢宇辉江西鹰潭一中M16197 符文鑫江西江西师大附中M16198 肖海尧江西江西省吉安市第一中学M16199 黄柏贺辽宁东北育才学校M16200 鲍思辰辽宁东北育才学校M16201 任一诺辽宁大连二十四中学M16202 康书瑞辽宁大连育明高中M16203 李昶霖山东烟台一中M16204 王志伟山东山东省胜利第一中学M16205 乔羽山东莱芜一中M16206 李颜山东齐河县第一中学M16207 王庆恺山东莱芜一中M16208 郭若一山西山西大学附属中学M16209 侯雨廷山西山西大学附属中学M16210 李震之山西山西省太原市第五中学M16211 王泽宇陕西西工大附中M16212 赵沁涵陕西西安高新第一中学M16213 刘洪禹陕西西工大附中M16214 陈煜陕西西安交大附中M16215 张可儿陕西西安高新第一中学M16216 乔丹上海上海市上海中学M16217 陆致远上海上海市上海中学M16218 蒋天泽上海上海市市北初级中学M16219 金及凯上海上海市市北初级中学M16220 李肇基上海上海市上海中学M16221 胡灏远上海上海市华东师大二附中M16222 张若桐上海上海市七宝中学M16223 马啸阳上海上海市上海中学M16224 韩笑上海上海市上海中学M16225 万丰诚上海上海市上海中学M16226 卢睿四川成都七中M16227 宣涵潇四川成都七中M16228 彭云剑四川成都七中M16229 姚舜天四川成都七中M16230 陈博洋四川成都七中嘉祥外国语学校M16231 黄轶之四川成都七中M16232 吕昊珉四川绵阳中学M16233 罗涵雨四川成都七中M16234 吴重霖天津耀华中学M16235 尹嘉晖天津耀华中学M16236 刘梓辰天津天津市南开中学M16237 杨溢诚天津天津市第一中学M16238 韩晓峥天津耀华中学M16239 王首樵天津耀华中学M16240 王天祺天津天津市南开中学M16241 李明远天津天津市南开中学M16242 解尧平天津天津实验中学M16243 陈正杰新疆乌鲁木齐市第一中学M16244 陈致远云南云南师范大学附属中学M16245 高敏博云南云南师范大学附属中学M16246 李保罗浙江乐成寄宿中学M16247 聂涵韬浙江镇海中学M16248 应铖阳浙江蛟川书院M16249 华奕轩浙江杭州二中M16250 何旭峥浙江衢州二中M16251 张诚彪浙江杭州二中M16252 赵艺涵重庆重庆巴蜀中学M16253 宋铭源重庆重庆巴蜀中学M16254 叶安宁重庆重庆巴蜀中学M16255 聂扬重庆重庆巴蜀中学M16256 杨埔重庆重庆南开中学M16257 李函阳重庆重庆南开中学三等奖(106人,按省市自治区排列)编号姓名地区学校M16258 钱伟康安徽安师大附中M16259 承君阳安徽安师大附中M16260 王凡安徽芜湖一中M16261 初佳慧北京北师大附属实验中学M16262 王匡云福建福州一中M16263 俞宸福建福建省莆田第一中学M16264 王腾勇福建厦门双十中学M16265 柯志发福建厦门大学附属实验中学M16266 陈昶侃福建福建省莆田第一中学M16267 顾炜东福建福建省泉州市第七中学M16268 詹俊宁福建福建省莆田第一中学M16269 肖智文甘肃甘肃省兰州第一中学M16270 袁梓萌甘肃西北师大附中M16271 刘瑾哲甘肃甘肃省兰州第一中学M16272 蒋博文甘肃甘肃省兰州第一中学M16273 蒋博文广西广西师范大学附属外国语学校M16274 陈俊麒广西南宁三中M16275 田路广西广西师范大学附属外国语学校M16276 丁佩雪贵州贵阳一中M16277 申月洋贵州贵阳一中M16278 傅东东海南海口中学M16279 王兴铃海南海南华侨中学M16280 郭凌月河北邯郸市一中M16281 李淳一河北石家庄二中M16282 刘泽霖河南郑州外国语学校M16283 唐博睿河南郑州一中M16284 王泽植河南郑州外国语学校M16285 郑煜衡河南郑州一中M16286 王健铭黑龙江哈师大附中M16287 苏博黑龙江哈尔滨市第三中学M16288 王鼎黑龙江哈师大附中M16289 张睿桐湖北武汉外国语学校M16290 周家梁湖北武钢三中M16291 陈芷芮湖北武汉二中M16292 孙鸿儒湖北华中师范大学第一附属中学M16293 王逸泽湖南长沙市雅礼中学M16294 曹一凡湖南湖南师范大学附属中学M16295 胡东健湖南长沙市雅礼中学M16296 夏添湖南长沙市雅礼中学M16297 孙汉存吉林东北师大附中M16298 徐靖博吉林吉林一中M16299 刘坤瓒吉林东北师大附中M16300 董勃言吉林吉林一中M16301 谭诚吉林东北师大附中M16302 朱俊泽吉林吉大附中M16303 陈天睿江苏江苏省盐城中学M16304 施彧江苏江苏省天一中学M16305 杨元江苏江苏省扬州中学M16306 陆苏扬江苏南京外国语学校M16307 胡亚建江西鹰潭一中M16308 黄沛铖江西江西省余江一中M16309 钟涵江西江西省吉安市第一中学M16310 赵昀昇江西南昌大学附属中学M16311 寇一雯辽宁东北育才学校M16312 张听海辽宁东北育才学校M16313 郭苑珩辽宁葫芦岛市第一高级中学M16314 赵一阳辽宁东北育才学校M16315 韩炎均辽宁东北育才学校M16316 王渤辽宁大连24中M16317 郑清源内蒙古呼和浩特市第二中M16318 李怡德内蒙古鄂尔多斯市一中M16319 陈亚鑫内蒙古鄂尔多斯市一中M16320 张羽内蒙古赤峰市二中M16321 郎一凡宁夏银川一中M16322 刘晰鸣宁夏银川一中M16323 杨舜尧宁夏吴忠中学M16324 冯捷宁夏银川一中M16325 王智旸青海师大附中M16326 刘路平山东山东省胜利第一中学M16327 刘雨佳陕西西安铁一中学M16328 高旖泽陕西西工大附中M16329 申文旭陕西西安铁一中学M16330 张淼陕西西安铁一中学M16331 祁皓琛陕西西工大附中M16332 周博文上海上海市上海中学M16333 陈绪高四川成都七中M16334 李圆直四川成都七中M16335 周川四川遂宁市安居育才中学M16336 冉本立四川绵阳东辰学校M16337 张乐四川成都七中M16338 陈琦元四川绵阳中学M16339 张轩恺四川成都七中M16340 刘旭铠四川绵阳东辰学校M16341 李翼龙天津耀华中学M16342 蔡雨雷西藏拉萨市北京中学M16343 周鑫西藏林芝市第一中学M16344 陈祺云西藏拉萨中学M16345 李壮壮西藏林芝市第一中学M16346 杨继钊西藏西藏民族大学附属中学M16347 杨浩然新疆乌鲁木齐市第七十中学M16348 王子健新疆乌鲁木齐市第一中学M16349 蒋晓雅新疆乌鲁木齐市第一中学M16350 姚瑞凌新疆新疆兵团第二中学M16351 李筱航云南云南师范大学附属中学M16352 梁翥云南云南师范大学附属中学M16353 汪宇晨浙江衢州二中M16354 金慕晗浙江蛟川书院M16355 方彦哲浙江镇海中学M16356 周杭琪浙江杭州二中M16357 王思迦重庆重庆八中M16358 李卓勋重庆重庆南开中学M16359 谢飞扬重庆重庆南开中学M16360 杨芯重庆重庆南开中学M16361 周振宇重庆重庆巴蜀中学M16362 陈金海重庆重庆巴蜀中学M16363 崔郝好重庆重庆巴蜀中学。
2022-2023学年广东省河源市龙川县宏图学校八年级(下)开学数学试卷(含解析)

2022-2023学年广东省河源市龙川县宏图学校八年级(下)开学数学试卷一、单选题:本大题共10小题,每小题3分,共30分。
1.下列运算正确的是()A.a6÷a=a6B.(xy2)3=xy6C.()﹣1=﹣2D.20160=12.数学中的对称之美无处不在,下列是小明看到的他所在小区的垃圾桶上的四幅垃圾分类标志图案,如果不考虑图案下面的文字说明,那么这四幅图案既是轴对称图形又是中心对称图形的是()A.B.C.D.3.下列计算正确的是()A.a2•a3=a6B.3a2+2a3=5a5C.a3÷a2=a D.(a﹣b)2=a2﹣b24.若点P(2,﹣3)与点Q(x,y)关于x轴对称,则x,y的值分别是()A.﹣2,3B.2,3C.﹣2,﹣3D.2,﹣35.在第32届夏季奥林匹克运动会(即2020年东京奥运会)上,中国健儿勇于挑战,超越自我,生动诠释了奥林匹克精神和中华体育精神,共获得38金32银18铜的骄人战绩.在下列的运动标识中,是轴对称图形的是()A.B.C.D.6.下列算式中,结果等于a6的是()A.a4+a2B.(a2)2•a2C.a2•a3D.a2+a2+a27.如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E.若AB=12,BC=20,则线段EF的长为()A.2B.3C.4D.58.顶角为36°的等腰三角形我们把这种三角形称为“黄金三角形”,它的底与腰的比值为黄金比.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为()A.B.C.D.9.如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E,F,设AD=a,BC=b,则四边形AEFD的周长是()A.3a+b B.2(a+b)C.2b+a D.4a+b10.如图,在锐角△ABC中,AB=AC,D,E是△ABC内的两点,AD平分∠BAC,∠EBC =∠E=60°,若BE=6cm,DE=2cm,则BC的长度是()A.6 cm B.6.5 cm C.7 cm D.8 cm二、填空题:本大题共7小题,每小题4分,共28分。
奥数简介

奥数简介“奥数”是奥林匹克数学竞赛的简称。
1934年—1935年,前苏联开始在列宁格勒和莫斯科举办中学数学竞赛,并冠以数学奥林匹克竞赛的名称,1959年在布加勒斯特举办第一届国际数学奥林匹克竞赛。
国际数学奥林匹克作为一项国际性赛事,由国际数学教育专家命题,出题范围超出了所有国家的义务教育水平,难度大大超过大学入学考试。
有关专家认为,只有5%的智力超常儿童适合学奥林匹克数学,而能一路过关斩将冲到国际数学奥林匹克顶峰的人更是凤毛麟角。
1934年和1935年苏联开始在列宁格勒和莫斯科举办中学数学竞赛,并冠以数学奥林匹克的名称。
1959年罗马尼亚数学物理学会邀请东欧国家中学生参加,在布加勒斯特举办了第一届国际数学奥林匹克竞赛,从此每年举办一次,至今已举办了43届。
近年来中国代表在数学奥林匹克上的成绩就像中国健儿在奥运会的成绩一样,突飞猛进,从40届到第43届,中国代表队连续四年总分第一。
奥数分类为:浓度问题、分数比大小问题、行程问题、分数巧算、逻辑推理、工程问题、牛顿问题、数字的巧算问题。
奥数与一般数学有一定的区别:奥数相对比较深.小学数学奥林匹克活动的蓬勃发展,极大地激发了广大少年儿童学习数学的兴趣,成为引导少年积极向上,主动探索,健康成长的一项有益活动.国际奥林匹克数学竞赛奖项名称: 国际奥林匹克数学竞赛其他名称: International Mathematics Olympiad创办时间: 1959年主办单位: 由参赛国轮流主办奖项介绍:国际奥林匹克数学竞赛是国际中学生数学大赛,在世界上影响非常之大。
国际奥林匹克竞赛的目的是:发现鼓励世界上具有数学天份的青少年,为各国进行科学教育交流创造条件,增进各国师生间的友好关系。
这一竞赛1959年由东欧国家发起,得到联合国教科文组织的资助。
第一届竞赛由罗马尼亚主办,1959年7月22日至30日在布加勒斯特举行,保加利亚、捷克斯洛伐克、匈牙利、波兰、罗马尼亚和苏联共7个国家参加竞赛。
广东省东莞市2023-2024学年三年级上学期期末综合练习数学试卷(含答案)

广东省东莞市2023-2024学年三年级上学期期末综合练习数学试卷一、填空题。
1.(2分)①8000米= 千米,②180秒= 分,③4厘米= 毫米,④3吨= 千克。
2.(2分)填上合适的单位名称。
①身高130 。
②厚9 。
③可载货4 。
④每天睡觉9 。
3.(2分)用分数表示如图的涂色部分。
4.(2分)在横线上填上“>”“<”或“=”。
①70毫米 7厘米,②30秒 5分,③197+604 800,④602×5 3000。
5.(2分)把平均分给了6个小朋友,每个小朋友分得,每个小朋友 颗,5个小朋友分得,5个小朋友分得 颗。
6.(2分)一件上衣324元,一条裤子298元,妈妈想买一套这样的衣服,大约应准备 元,收银员应收 元。
7.(2分)最大的三位数与最大的一位数的和是 ,差是 ,积是 。
8.(2分)填一填。
9.(2分)把一根铁丝围成一个长5分米、宽3分米的长方形,围成的长方形的周长是 分米,如果把这根铁丝围成一个正方形,正方形的边长是 分米。
10.(2分)刘阿姨的水果商店昨天进苹果、梨、枣、香蕉、葡萄、樱桃、石榴这几种水果,今天进了桃子、草莓、枣、石榴、香蕉、火龙果这几种水果,两天都进的水果有 ,两天一共进了 种水果。
二、选择题。
请将正确答案的字母填写在题中括号内。
11.(2分)第32届夏季奥林匹克运动会男子100米半决赛,中国运动员苏炳添跑100米的时间不到10( ),他打破了亚洲纪录,成为中国“飞人”、亚洲的骄傲。
A.时B.分C.秒D.无法确定12.(2分)学校上午8:10上课,小明8:45到校,他迟到了( )A.10分钟B.35分钟C.30分钟D.25分钟13.(2分)在笔算428﹣154时,如图中框格计算的“12﹣5”表示( )A.12个一减5个一得7个一B.12个十减5个十得7个十C.12个百减5个百得7个百D.12个百减5个十得7个十14.(2分)如图中,涂色部分表示的是( )A.B.C.D.15.(2分)下列估测中,最接近实际的是( )A.一辆汽车每小时行85千米B.一张作业纸厚大约8毫米C.成年人平均每秒走20米D.一头大象约重5千克16.(2分)妹妹今年4岁,哥哥今年12岁,今年哥哥的年龄是妹妹的( )倍。
湖北省武汉市部分重点中学2024-2025学年高三上学期第一次联考数学试卷(含答案)

湖北省部分重点中学2025届高三第一次联考高三数学试卷考试时间:2024年11月11日下午14:00-16:00试卷满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.1.已知集合,,则( )A. B. C. D.2.已知为虚数单位,若,则( )A. B. C. D.3.已知向量,满足,,则向量在向量方向上的投影向量为( )A. B. C. D.4.已知角,满足,,则( )A.B. C.D.5.已知函数在区间上有极值,则实数的取值范围是( )A. B. C. D.6.将正奇数按照如图排列,我们将3,7,13,21,31……,都称为“拐角数”,则下面是拐角数的为()A.55B.77C.91D.1137.已知等腰梯形的上底长为1,腰长为1,若以等腰梯形的上底所在直线为轴,旋转一周形成一个几何体,则该几何体表面积的最大值为( )A. B. C. D.8.已知函数,的定义域均为,是奇函数,且,201x A xx -⎧⎫=≤⎨⎬+⎩⎭{}220Bx Nx x =∈+-≤∣AB = (]1,1-{}0,1,2{}0,1{}1,0,1-i ()()1122z i i ++=-+z =1i-+1i --1i +1i-a b ()3,4a = ()2,1b =- b a68,2525⎛⎫⎪⎝⎭(6,8)68,55⎛⎫⎪⎝⎭(4,2)αβtan 2α=()sin 2cos sin βαβα=-tan β=2323-4343-()26ln 1f x x x ax =++-(1,2)a 8,⎡--⎣(8,--7,⎡--⎣(8,7)--(2π+(1π+(3π+()f x ()g x R ()1f x +()()114f x g x -++=,则下列结论正确的是( )A.为奇函数B.为奇函数C.D.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,有选错的得0分.9.已知正实数,满足,则的可能取值为( )A.8B.9C.10D.1110.已知双曲线的左、右焦点分别为,.过的直线与双曲线的右支交于,两点.的内心为,的内心为,则下列说法正确的有( )A.双曲线的离心率为2B.直线的斜率的取值范围为C.的取值范围为D.11.在正三棱锥中,,三棱锥的内切球球心为,顶点在底面的射影为,且中点为,则下列说法正确的是( )A.三棱锥的体积为3B.二面角C.球的表面积为D.若在此三棱锥中再放入一个球,使其与三个侧面及内切球均相切,则球三、填空题:本题共3小题,每小题5分,共15分.12.已知点在抛物线上,为抛物线的焦点,直线与准线相交于点,则线段的长度为_____.()()24f x g x +-=()f x ()g x ()()9136k f k g k =⎡⎤-=⎣⎦∑()()9136k f k g k =⎡⎤+=⎣⎦∑x y 2x y +=2291x y x y+++22:13y C x -=1F 2F 2F l C A B 12AF F △1I 12BF F △2I AB (),-∞+∞12I I ⎡⎢⎣2112tan3tan22AF F AF F ∠∠=P ABC -AB =PA =P ABC -O P ABC Q PQ M P ABC -M AB P --O 43π1O O 1O (),4A a 24y x =F AF B FB13.已知直线与曲线相切,则实数的值为_____.14.某人有两把雨伞用于上下班,如果一天上班时他在家而且天下雨,只要有雨伞可取,他将拿一把去办公室,如果一天下班时他在办公室而且天下雨,只要有雨伞可取,他将拿一把回家.如果天不下雨,那么他不带雨伞.假设每天上班和下班时下雨的概率均为,不下雨的概率均为,且与过去情况相互独立.现在两把雨伞均在家里,那么连续上班两天,他至少有一天淋雨的概率为_____.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知数列为等比数列,数列满足,且.(1)求数列的通项公式;(2)数列满足,记数列的前项和为,求.16.(15分)如图,在中,角,,所对的边分别为,,,已知.(1)求;(2)若,,将沿折成直二面角,求直线与平面所成角的正弦值.17.(15分)为倡导节能环保,实现废旧资源再利用,小明与小亮两位小朋友打算将自己家中的闲置玩具进行交换,其中小明家有2台不同的玩具车和2个不同的玩偶,小亮家也有与小明家不同的2台玩具车和2个玩偶,他们每次等可能的各取一件玩具进行交换.(1)两人进行一次交换后,求小明仍有2台玩具车和2个玩偶的概率;(2)两人进行两次交换后,记为“小明手中玩偶的个数”,求随机变量的分布列和数学期望.18.(17分)已知椭圆,不过原点的直线与椭圆相交于不同的,两点,与直线交于点,且,y ax=()x ef xx=a1323{}na{}n b()()*21nnnb n N=+-∈()1,0n n na b b Rλλλ+=-∈>{}na{}nc2n nc n a={}n c n n T9TABC△A B C a b csin sin sin sinA B B Cc a b++=-A3,0BC BD AB AD=⋅=2AD=ABC△AD B AD C'--AB'B CD'X X()2222:10x yC a ba b+=>>()2,1P O l C A B OP Q2AB QB=直线与轴,轴分别交于点,.(1)求椭圆的标准方程;(2)当的面积取最大值时,求的面积.19.(17分)2022年7月,在重庆巴蜀中学读高一的瞿霄宇,夺得第63届国际数学奥林匹克(IMO )满分金牌.同年9月26日,入选2022年阿里巴巴全球数学竞赛获奖名单,同时成为了本届获奖者中年龄最小的选手.次年9月16日,他再接再厉,在2023阿里巴巴全球数学竞赛中获金奖.他的事迹激励着广大数学爱好者勇攀数学高峰,挖掘数学新质生产力.翔宇中学高二学生小刚结合自己“强基计划”的升学规划,自学了高等数学的罗尔中值定理:如果上的函数满足条件:①在闭区间上连续;②在开区间可导;③.则至少存在一个,使得.据此定理,请你尝试解决以下问题:(1)证明方程:在内至少有一个实根,其中,,,;(2)已知函数在区间内有零点,求的取值范围.l x y M N C APB △MON △R ()f x [],a b (,)a b ()()f a f b =(),c a b ∈()0f c '=()43254320ax bx cx dx a b c d +++-+++=(0,1)a b c d R ∈()()()2222222xf x emx e m x m R =-----∈(0,1)m湖北省部分重点中学2025届高三第一次联考数学试卷参考答案及评分标准选择题:1234567891011CAADBCADCDABDACD填空题:12. 13. 14.解答题:15.(13分)解:(1)因为为等比数列,所以,即,化简得.因为,得.因此,易知为等比数列;(2)由(1)知,.,16.(15分)解:(1),,化简得.由余弦定理得,,故;(2)设,,在中,由得,解得.①在中,.②由①、②得.,,从而.二面角为直二面角,,平面平面,平面,10324e 2881{}n a 2213a a a =()()()2755177λλλ-=--()()210λλ-+=0λ>2λ=()()()11122122131n n nn n n n n a b b +++⎡⎤=-=+--+-=--⎣⎦{}n a ()231nn c n=--22222291293123489135T c c c ⎡⎤=++⋯+=-⨯-+-+-+-=⎣⎦ sin sin sin sin A B B C c a b ++=-a b b c c a b++∴=-222b c a bc +-=-2221cos 22b c a A bc +-==-23A π=BD x =2CD x =ACD △sin sin CD AD DAC C ∠=22sin30sin x C=1sin 2C x=ABD △2sin sin 3AD B C BD x π⎛⎫===- ⎪⎝⎭sin B x ==BD ∴=CD =AB = B AD C '--AB AD '⊥AB D ' ACD AD =AB '⊂AB D '平面建立如图所示的空间直角坐标系,易知,,,,,,.设平面的法向量,则有,即令,解得.故直线与平面.17.(15分)解:(1)若两人交换的是玩具车,则概率为,若两人交换的是玩偶,则概率也为,故两人进行一次交换后,小明仍有2台玩具车和2个玩偶的概率为.(5分)(2)可取的值为0、1、2、3、4,一次交换后,小明有1个玩偶和3台玩具车的概率为,有3个玩偶和1台玩具车的概率也为,经过两次交换后,,AB ∴'⊥ACD()0,0,0A ()D ()C (B '(AB ∴='(B C =' (B D '=B CD '(),,n x y z = 00n BC n BD ⎧⋅=⎪⎨⋅=⎪'⎩'x ⎧-=⎪⎨-=⎪⎩1y =()4n =cos ,n AB n AB n AB ⋅∴=''='AB 'B CD '111224⨯=111224⨯=111442+=X 111224⨯=111224⨯=()1111044464P X ==⨯⨯=()1131331117144444422232P X ==⨯⨯+⨯⨯+⨯⨯=()13313311111117244444422222232P X ==⨯⨯+⨯⨯+⨯⨯+⨯⨯=()1131311117344444422232P X ==⨯⨯+⨯⨯+⨯⨯=,故随机变量的分布列为:01234.18.(17分)解:(1)设椭圆左顶点为,则坐标为.由,解得.因为椭圆的离心率为,得.所以椭圆的标准方程为:;(2)设坐标为,坐标为,由于和为椭圆上两点,两式相减,得,整理得.(*)设坐标为,由得为线段的中点,,.由在线段所在直线上,且坐标为,则有,即.由(*)得,故.设直线方程为,联立直线与椭圆的方程,得,整理得.()1111444464P X ==⨯⨯=X X P1647321732732164()1717710123426432323264E X ∴=⨯+⨯+⨯+⨯+⨯=C D D (,0)a -PD ==2a =C c e a ==c =1b =C 2214x y +=A (),A A x y B (),B B x y A B C 22221414A AB Bx y x y ⎧+=⎪⎪∴⎨⎪+=⎪⎩()222204A B A B x x y y -+-=222214A B A B y y x x -=--Q (),Q Q x y 2AB QB =Q AB 2A B Q x x x +∴=2A BQ y y y +=Q OP P (2,1)12OQ OP k k ==12Q A B OQ QA B y y y k x x x +===+222214A B A B A B A B A B A B y y y y y y x x x x x x -+-=⨯=--+-12A B AB A B y y k x x -==--l 1,02y x m m =-+≠l C 221412x y y x m ⎧+=⎪⎪⎨⎪=-+⎪⎩()222210x mx m -+-=由,得且.因为直线与椭圆相交于和两点,所以,.点到直线的距离为且.记,.由,及得即当时,取最大值.此时直线方程为,与坐标轴交点为,19.(17分)证明:(1)设,,则,在上连续,在上可导.又,由罗尔中值定理知:至少存在一个,使得成立,.故方程在内至少有一个实根.(2),在区间内有零点,不妨设该零点为,则,.0>△m <<0m ≠l C A B 2A B x x m +=()221A B x x m =-B AB x ∴=-==P l d 122APB S AB d ∴==-=△m <<0m ≠()()()2222f m mm =--()()()2421f m m m m =---'()0f m '=m <<0m ≠m =m =APB S △l 12y x =-()1M -N ⎛ ⎝12MON S OM ON ∴== △()()5432F x ax bx cx dx a b c d x =+++-+++[]0,1x ∈()()4325432F x ax bx cx dx a b c d '=+++-+++()F x ∴[]0,1(0,1)()()010F F ==()00,1x ∈()00F x '=()432000054320ax bx cx dx a b c d ∴+++-+++=()43254320ax bx cx dx a b c d +++-+++=(0,1)()()2222222xf x emx e m x =----- m R ∈(0,1)1x ()10f x =()10,1x ∈由于,易知在和上连续,且在和上可导.又,由罗尔中值定理可得,至少存在一个,使;至少存在一个,使得.方程在上至少有两个不等实根和.设,,则.,.当,即时,,故在上单调递增;方程在上至多有一个实根,不符合题意,舍去当,即时,,故在上单调递减.方程在上至多有一个实根,不符合题意,舍去当时,由得,时,有单调递减;时,有单调递增.在上的最小值.注意到,则有.方程在上至少有两个不等实根,,解得.结合,且,,()()224222xf x e mx e m '=----()f x '[]10,x []1,1x ()10,x ()1,1x ()()()1010f f x f ===()210,x x ∈()20f x '=()31,1x x ∈()30f x '=∴()()2242220x f x e mx e m '=----=(0,1)2x 3x ()()()224222xg x f x emx e m ==--'--()0,1x ∈()282x g x e m =-'()0,1x ∈ ()2288,8x e e ∴∈1 28m ≤4m ≤()()0820g x g m >=-'≥'()g x (0,1)()0g x =(0,1)2 228m e ≥24m e ≥()()21820g x g e m <=-'≤'()g x (0,1)()0g x =(0,1)3 244m e <<()0g x '=()1ln 0,124mx =∈10,ln 24m x ⎛⎫∴∈ ⎪⎝⎭()()0,g x g x '<1ln ,124m x ⎛⎫∈ ⎪⎝⎭()()0,g x g x '>()g x ∴(0,1)()min 1ln 24m g x g ⎛⎫= ⎪⎝⎭()221422525202g e e e e e e ⎛⎫=+-<-=-<⎪⎝⎭()min 11ln 0242m g x g g ⎛⎫⎛⎫=≤< ⎪ ⎪⎝⎭⎝⎭()0g x =(0,1)()()2206201220g m e g e m ⎧=+->⎪∴⎨=-+>⎪⎩222622e m e -<<+244m e <<22262 2.564e ->⨯->222222224e e e e +<+=故的取值范围为.m ()2226,22e e -+。
历年中国参加国际数学奥林匹克竞赛选手详细去向第26届IMO

历年中国参加国际数学奥林匹克竞赛选手详细去向第26届IMO(1985年,芬兰赫尔辛基)吴思皓(男)上海向明中学确规定铜牌上海交通大学王锋(男)北京大学(根据yongcheng先生提供的信息修订)目前作企业软件第27届IMO(1986年,波兰华沙)李平立(男)天津南开中学金牌北京大学方为民(男)河南实验中学金牌北京大学张浩(男)上海大同中学金牌复旦大学荆秦(女)陕西西安八十五中银牌北京大学,现在美国哈佛大学任教林强(男)湖北黄冈中学铜牌中国科技大学第28届IMO(1987年,古巴哈瓦那)刘雄(男)湖南湘阴中学金牌南开大学滕峻(女)北京大学附中金牌北京大学林强(男)湖北黄冈中学银牌中国科技大学潘于刚(男)上海向明中学银牌北京大学何建勋(男)广东华南师范大学附中铜牌中国科技大学高峡(男)北京大学附中铜牌北京大学,现在北大任教第29届IMO(1988年,澳大利亚堪培拉)团体总分第二陈晞(男)上海复旦大学附中金牌复旦大学,美国密苏里大学,美国哈佛大学,现在加拿大Alberta大学数学系任教授韦国恒(男)湖北武汉武钢三中银牌北京大学查宇涵(男)南京十中银牌北京大学,在中科院数学所任副研究员邹钢(男)江苏镇江中学银牌北京大学王健梅(女)天津南开中学银牌北京大学何宏宇(男)以满分成绩获第29届国际数学奥林匹金牌,1993年破格列入美国数学家协会会员,1994年获博士学位,现任亚特兰大乔治大学教授、博士生导师,从事现代数学研究前沿的《李群》《微分几何》等方向的研究,在《李群》的研究上已有重大突破。
第30届IMO(1989年,原德意志联邦共和国布伦瑞克)团体总分第一罗华章(男)重庆水川中学金牌北京大学俞扬(男)吉林东北师范大学附中金牌吉林大学霍晓明(男)江西景德镇景光中学金牌中国科技大学唐若曦(男)四川成都九中银牌中国科技大学颜华菲(女)北京中国人民大学附中银牌北京大学本科,1997年获美国麻省理工博士,现任Texax A&M Uneversity 数学系教授,美国数学会常务理事会成员,Mathematical Reviews评论员。
2024年第22届中国女子奥林匹克竞赛数学试卷

2024年第22届中国女子奥林匹克竞赛数学试卷1、求所有的三元正整数组(aa,bb,cc),满足aa2aa=bb2bb+cc2cc.2、如图,用144根完全相同的长度为1的细棒摆成边长为8的正方形网格状图形.问:至少需要取走多少根细棒,才能使得剩余图形中不含矩形?请证明你的结论.3、设aa,bb,cc,dd都是不超过1的非负实数.证明:11+aa+bb+11+bb+cc+11+cc+dd+11+dd+aa⩽41+2√aabbccdd4.4、如图,四边形AAAAAAAA内接于圆Γ,对角线AAAA,AAAA互相垂直,交点为EE.设FF是边AAAA上一点,射线FFEE交Γ于点PP,线段PPEE上一点QQ满足PPQQ⋅PPFF=PPEE2,过点QQ且垂直于AAAA的直线交AAAA于点RR.证明:RRPP=RRQQ.5、如图,在锐角△AAAAAA 中,AAAA <AAAA ,AAAA 是高,GG 是重心,PP 、QQ 分别是内切圆与边AAAA 、AAAA 的切点,MM 、NN 分别是线段AAPP 、AAQQ 的中点.设AA 、EE 是△AAAAAA 内切圆上两点,满足:∠AAAAAA +∠AAAAAA =180°,∠AAEEAA +∠AAAAAA =180°.证明:直线MMAA ,NNEE ,GGAA 三线共点.6、设实数xx 1,xx 2,⋯,xx 22满足对任意1⩽ii ⩽22,有2ii−1⩽xx ii ⩽2ii .求(xx 1+xx 2+⋯+xx 22)�1xx 1+1xx 2+⋯+1xx 22� 7、给定奇素数pp 和正整数aa 、bb 、mm 、rr ,其中pp ∤aabb ,且aabb >mm 2.证明:至多只有一对正整数(xx ,yy )满足xx 与yy 互素,且aaxx 2+bbyy 2=mmpp rr .8、对于平面直角坐标系中任意两点AA (xx 1,yy 1)、AA (xx 2,yy 2),定义dd (AA ,AA )=|xx 1−xx 2|+|yy 1−yy 2|,设PP 1,PP 2,⋯,PP 2023是该坐标系中2023个两两不同的点.记λλ=mmaaxx 1⩽ii <jj⩽2023dd�PP ii ,PP jj �mmii mm 1⩽ii <jj⩽2023dd�PP ii ,PP jj �.(1) 证明:λλ⩾44.(2) 给出一组PP 1,PP 2,⋯,PP 2023,使得λλ=44.1 、【答案】(1,4,4),(2,4,4),(4,5,6),(4,6,5);【解析】设xx mm=mm2nn,则当nn⩾2时,xx mm−xx mm+1=mm−12nn+1>0,故12=xx1=xx2>xx3>xx4>⋯,不妨设bb⩽cc,由条件等式得aa<bb⩽cc,(1)若bb=cc,则aa2aa=bb2bb−1,故bb aa=2bb−aa−1∈ZZ,设bb=aaaa(aa>1),则aa=2aaaa−aa−1⩾aaaa−aa,即(aa−1)(aa−1)⩽1,由aa⩾2知aa=1或2,均有bb=2bb−2,得bb=4,(2)若bb<cc,则aa2aa⩽aa+12aa+1+aa+22aa+2=3aa+42aa+2①⇒aa⩽4,注意到,xx1=xx2=12,xx3=38,xx4=14,xx5=532,xx6=332<18,若aa=1或2,则xx bb+xx cc=12⇒xx bb>14⇒bb=3,此时cc无解.若aa=3,则xx bb+xx cc=38⇒xx bb>316⇒bb=4,此时cc无解;若aa=4,则式①等号成立,即bb=5,cc=6,经检验,满足要求,综上,所求(aa,bb,cc)为(1,4,4),(2,4,4),(4,5,6),(4,6,5).【标注】 ( 数论模块 )2 、【答案】43;【解析】首先证明至少需要移除43根细棒,假设图形中不含矩形,则每个有界连通区域至少由3个单位正方形组成,即面积至少为3,记[xx]表示不超过实数xx的最大整数,这样至多有�643�=21个有界连通区域,每取走一根细棒至多使得有界连通区域的个数减少1(将两个有界连通区域合并为一个有界连通区域,或者将一个有界连通区域与无界连通区域合并),最初时有64个有界连通区域,故至少取走64−21=43根细棒,下图给出了取走43根细棒的例子,其中每个有界连通区域的面积均是3,且图中不含矩形.【标注】 ( 数论模块 )3 、【答案】证明见解析;【解析】注意到,当√aacc⩽xx时,1xx+aa+1xx+cc−2xx+√aacc=(√aa−√cc)2(√aacc−xx)(xx+aa)(xx+cc)(xx+√aacc)⩽0,①由条件可知√aacc⩽1⩽1+bb,√aacc⩽1+dd,在式①中取xx=1+bb和xx=1+dd,分别得11+aa+bb+11+bb+cc⩽21+bb+√aacc,11+cc+dd+11+dd+aa⩽21+dd+√aacc,可见以√aacc代替aa和cc时,不等式左边不减,而右边不变,故不妨设aa=cc,类似地,不妨设bb=dd,这样,原不等式变为证明11+aa+bb⩽11+2√aabb,由均值不等式aa+bb⩾2√aabb可知上式成立.【标注】 ( 不等式 )4 、【答案】证明见解析;【解析】如图,作EEEE//AAFF,交AAPP于点EE,交AAPP于点YY,延长EEQQ、YYQQ,分别交AAAA于点SS、TT,联结AAPP,记⊙AAAAAA表示过AA,AA,AA三点的圆,由PPPP PPPP=PPPP PPPP=PPPP PPPP⇒EEQQ//AAEE,类似地,YYQQ//AAEE,由∠EEEESS=∠AAEEEE=∠AAAAAA=∠EEAASS⇒EE,EE,SS,AA四点共圆,由∠PPEEEE=∠PPAAAA=∠PPAAEE⇒EE,EE、PP,AA四点共圆,故EE,EE,SS,PP,AA五点共圆,类似地,YY,EE、TT,PP,AA五点共圆,由∠PPQQTT=∠PPEEAA=∠PPSSTT⇒PP,SS、QQ,TT四点共圆,由SSQQ//AAEE,TTQQ//AAEE,AAEE⊥AAEE⇒SSQQ⊥TTQQ,由∠RRQQSS=90°−∠QQEEYY=90°−∠QQTTSS=∠RRSSQQ,可知RR是⊙PPSSQQTT的圆心.从而,RRPP=RRQQ.【标注】 ( 平面几何 )5 、【答案】证明见解析;【解析】在△AAAAAA的外接圆上取点FF,使得AAAAAAFF是等腰梯形.直线FFAA与⊙AAAAAA的另一个交点为LL,与中线AAAA交于点GG′.如图,由AAFF=2AAAA⇒PPGG′GG′KK=PPPP HHKK=2⇒GG′是△AAAAAA的重心⇒点GG′与GG重合,故∠AALLAA=∠AALLFF=12AAFF⌢∘=12AAAA⌢∘=∠AAAAAA,结合条件∠AAAAAA+∠AAAAAA=180°得∠AAAAAA+∠AALLAA=180°⇒AA,LL,AA,AA四点共圆,类似可证∠AALLAA=∠AAAAAA,且AA,LL,AA、EE四点共圆,由于∠AALLAA=∠AAAAAA,PPAA与⊙AALLAAAA切于点AA,记△AAAAAA的内切圆为Γ,PPAA是Γ与⊙AALLAAAA的外公切线,由MMPP =MMAA 可知MM 是Γ与⊙AALLAAAA 的等幂点,从而,直线MMAA 是Γ与⊙AALLAAAA 的根轴,类似可证直线NNEE 是Γ与⊙AALLAAEE 的根轴,又直线GGAA 是⊙AALLAAAA 与⊙AALLAAEE 的根轴,故直线MMAA 、NNEE 、GGAA 要么三线共点,要么两两平行.若MMAA 、NNEE ,AAAA 两两平行,则⊙AALLAAAA 的圆心OO 1,⊙AALLAAEE 的圆心OO 2、Γ的圆心II 三点共线, 由于∠AAAAAA 与∠AAEEAA 都是钝角,于是,点OO 1,OO 2在AAAA 下方,显然点II 在AAAA 上方,设OO 1、OO 2、II 在AAAA 上的投影分别为EE 、YY 、ZZ ,则EE ,YY 分别是AAAA 、AAAA 的中点,由AAAA <AAAA 知点YY 、ZZ 在AAAA 同侧,且AAZZ =PPAA+BBAA−PPBB 2>BBAA 2>AAHH 2=AAYY , 故点ZZ 在线段EEYY 上.因此,OO 1、OO 2、II 不可能共线,矛盾, 从而,MMAA 、NNEE 、GGAA 三线共点.【标注】 ( 平面几何 )6 、【答案】 �212−1−1211�2 ;【解析】 设yy ii =xx ii 211(ii =1,2,⋯,22) , 注意到, ff (tt )=tt +1tt在区间(0,1]上递减,在区间[1,+∞)上递增,对1⩽ii ⩽11,有1212−ii ⩽yy ii ⩽1211−ii ⇒yy ii +1yy ii ⩽212−ii +1212−ii ; 对12⩽ii ⩽22,有 2ii−12⩽yy ii ⩽2ii−11⇒yy ii +1yy ii ⩽2ii−11+12ii −11, 则 �∑22ii=1xx ii ��∑22ii=11xx ii �=�∑22ii=1yy ii ��∑22ii=11yy ii� ⩽14���yy ii +1yy ii �mm ii=1�2⩽14���212−ii +1212−ii �11ii=1+��2ii−11+12ii −11�22ii=12�2=�21+22+⋯+211+121+122+⋯+1211�2 =�212−1−1211�2, 当xx ii =�2ii−1,1⩽ii ⩽112ii ,12⩽ii ⩽22 时,上式等号成立, 故所求最大值是 是�212−1−1211�2. 【标注】 ( 不等式 )7 、【答案】 证明见解析;【解析】 反证法.假设有两对不同的正整数解 (xx 1,yy 1)、(xx 2,yy 2),由于xx 1与yy 1互素,于是,pp ∤xx 1yy 1, 类似地,pp ∤xx 2yy 2,由 aaxx 12≡−bbyy 12(mod pp rr )aaxx 22≡−bbyy 22(mod pp rr ),可知 aabbxx 12yy 22≡aabbxx 22yy 12(mod pp rr ) 又pp ∤aabb ,故pp rr |(xx 12yy 22−xx 22yy 12), 注意到,xx 1yy 2−xx 2yy 1与xx 1yy 2+xx 2yy 1不能都被pp 整除,否则,pp |2xx 1yy 2,这与pp 是奇素数且pp ∤xx 1yy 1xx 2yy 2矛盾, 故pp rr |(xx 1yy 2−xx 2yy 1)或pp rr |(xx 1yy 2+xx 2yy 1), 若xx 1yy 2−xx 2yy 1=0,则 xx 1xx 2=yy1yy 2, 结合aaxx 12+bbyy 12=aaxx 22+bbyy 22,可知xx 1=xx 2,yy 1=yy 2,这与(xx 1,yy 1)≠(xx 2,yy 2)矛盾, 因而,xx 1yy 2−xx 2yy 1≠0, 若pp rr |(xx 1yy 2+xx 2yy 1),则xx 1yy 2+xx 2yy 1⩾pp rr ,若pp rr |(xx 1yy 2−xx 2yy 1),则xx 1yy 2+xx 2yy 1⩾|xx 1yy 2−xx 2yy 1|⩾pp rr ,因此总有xx 1yy 2+xx 2yy 1⩾pp rr ,利用条件aabb>mm2和上式有mm2pp2rr=(aaxx12+bbyy12)(aaxx22+bbyy22)=(aaxx1xx2−bbyy1yy2)2+aabb(xx1yy2+xx2yy1)2⩾aabb(xx1yy2+xx2yy1)>mm2pp2rr,矛盾.故假设不成立,原命题成立.【标注】 ( 数论模块 )8 、【答案】 (1) 证明见解析;(2) 见解析;【解析】 (1) 对aa=1,2,⋯,2023,设PP aa(xx aa,yy aa),记uu aa=xx aa+yy aa,vv aa=xx aa−yy aa,记AA=mmaaxx1⩽ii⩽jj⩽2023dd�PP ii,PP jj�,则对于任意1⩽ii、jj⩽2023,有|uu ii−uu jj|=|�xx ii−xx jj�+�yy1−yy jj�|⩽|xx ii−xx jj|+|yy ii−yy jj|=dd�PP ii,PP jj�⩽AA,因此,uu1,uu2,⋯,uu2023中的最大数与最小数之差不超过AA,即全在某个区间[aa,aa+AA]中,类似地,vv1,vv2,⋯,vv mm全在某个区间[bb,bb+AA]中,对aa、ll=1,2,⋯,44,考虑区域AA aa,ll=��uu+vv2,uu−vv2�|aa+aa−144AA⩽uu⩽aa+aa44AA,bb+ll−144AA⩽vv⩽bb+ll44AA�,点PP ii,PP2,⋯,PP2023落在这442=1936个区域中,由抽屉原理知存在两点在同一区域,假设PP1、PP jj∈AA aa,ll,记UU=uu ii−uu jj,VV=vv ii−vv jj,则−DD44⩽UU、VV⩽DD44,dd�PP ii,PP jj�=|xx ii−xx jj|+|+|yy ii−yy jj|=�uu ii+vv ii−uu jj+vv jj�+�uu ii−vv ii−uu jj−vv jj�=�UU+VV 2�+�UU−VV 2� ∈�±UU+VV 2±UU−VV 2�={UU ,−UU ,VV ,−VV },由于每种情况都有 dd�PP ii ,PP jj �⩽mmaaxx {|UU |,|VV |}⩽DD 44, 故 mmii nn 1⩽ii<jj⩽2023dd�PP ii ,PP jj �⩽dd�PP ii ,PP jj �⩽DD 44⇒λλ⩾44. (2) 关于构造,取点集MM ={(xx ,yy )∈ZZ 2|xx ,yy 同奇偶,|xx +yy |⩽44,|xx −yy |⩽44} =��uu+vv 2,uu−vv 2�|uu =0,±2,±4,⋯,±44;vv =0,±2,±4,⋯,±44�, 集合MM 中共有452=2025个点,从中任选2023个点作为PP 1,PP 2,⋯,PP 2023,则 dd�PP ii ,PP jj �=|xx ii −xx jj |+|yy ii −yy jj |是偶数且大于0,即dd�PP ii ,PP jj �⩾2, 另一方面,dd�PP ii ,PP jj �=|xx ii −xx jj |+|yy ii −yy jj |⩽mmaaxx�|(xx ii +yy ii )−�xx jj +yy jj �|,|(ii yy ii )−�xx jj −yy jj �|�⩽88, 故此时λλ=mmaaxx 1⩽ii <jj⩽2023dd�PP ii ,PP jj �mmii mm 1⩽ii <jj⩽2023dd�PP ii ,PP jj �⩽882,由(1)知此时λλ=44, 图1是nn =25个点满足λλ=4的例子,图2是16个区域划分,可以用来证明nn =17个点时λλ⩾4.第11页, 共11页【标注】。
2019年自主招生初审通过名单公示
东北育才学校 郑州外国语学校 朝阳市第一高级中学 吉林市第一中学校 大连市第一中学 大连市育明高级中学 衡水志臻中学 大连市第二十四中学 大连市第二十四中学 郑州外国语学校 大连市育明高级中学 福建省安溪第一中学 鞍山市第一中学 东北育才学校科学高中部 河南省实验中学 大连市育明高级中学 鄂尔多斯市第一中学
191014101000110 江首航 男
辽宁省
191014101000117 毕启智 男
河南省
191014101000136 邓轶斌 男
辽宁省
191014101000142 战东阳 女
吉林省
191014101000144 冯玉泽 男
辽宁省
191014101000148 牛铎霖 男
辽宁省
191014101000157 王志广 男
河北省
191014101000162 陈虹冰 男
辽宁省
191014101000172 任彦安 男
辽宁省
191014101000175 张啸宇 男
河南省
191014101000202 周塬峻 男
辽宁省
191014101000207 易梓豪 男
福Байду номын сангаас省
191014101000232 毛鸣阳 男
辽宁省
191014101000235 姜泓宇 男
第32届中国化学奥林匹克(初赛)一等奖 2018年全国中学生生物学联赛(省级赛区)一等奖 2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖 2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖
第27届全国中学生生物学竞赛三等奖 2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖
