复合材料力学讲义
复合材料力学-各向异性弹性力学基础

复合材料的弹性模量取决于增强相和基体相的弹性模量以及它们之 间的界面结合强度。
强度和韧性
复合材料的强度和韧性取决于增强相的分布、数量和尺寸,以及它 们与基体相之间的界面结合强度。
04
复合材料的各向异性弹性力学分析
复合材料的弹性常数
弹性常数是复合材料在受到外力作用时表现出的刚 度特性,描述了复合材料的应力与应变之间的关系 。
与单一材料的应力-应变关系不 同,复合材料的应力-应变关系 通常是非线性的,因为它们由 多种材料组成,且各组分材料 的性质和排列方式可能不同。
复合材料的应力-应变关系需要 通过实验测定,因为它们的数 值取决于复合材料的微观结构 和组成。
复合材料的本构方程
本构方程是描述复合材料在受到外力作用时如何响应的数学模型,即描述 了复合材料在不同外力作用下的应力和应变的变化关系。
各向异性材料的分类
按来源分类
天然各向异性材料(如木材、 骨骼等)、人造各向异性材料 (如复合材料、玻璃纤维增强 塑料等)。
按结构分类
晶体各向异性材料、纤维增强 各向异性材料、织物增强各向 异性材料等。
按对称性分类
单轴各向异性材料、正交各向 异性材料、各项同性材料等。
各向异性弹性力学的基本方程
01
汽车零部件
复合材料还用于制造汽车中的各种 零部件,如刹车片、气瓶和油箱等, 以提高其耐久性和安全性。
汽车轻量化
复合材料的轻质特性使其成为汽车 轻量化的理想选择,有助于提高车 辆的燃油效率和动力性能。
建筑领域的应用
建筑结构加固
复合材料可以用于加固建 筑结构,提高其承载能力 和耐久性,如桥梁、大坝 和高层建筑等。
未来研究方向
进一步深入研究复合材料的各向异性性质,探索 其在不同环境和载荷条件下的行为和性能。
复合材料力学讲义第二版
• 已知单层的性质,主要关注沿厚度方向的应力和 应变的变化
Center for Composite Materials, Harbin Institute of Technology
单层板的应力-应变关系
1 Q 11 2 Q 21 0 12 Q 12 Q 22 0 0 1 0 2 Q 66 12
Center for Composite Materials, Harbin Institute of Technology
复合材料两个典型特征
Center for Composite Materials, Harbin Institute of Technology
引言
Center for Composite Materials, Harbin Institute of Technology
复合材料的尺度
Center for Composite Materials, Harbin Institute of Technology
引言
Center for Composite Materials, Harbin Institute of Technology
Strain-Stress Relations
• 直法线不变假设
• 在上述假设基础上建立的层合板理论称为经典层 合板理论
Center for Composite Materials, Harbin Institute of Technology
经典层合理论
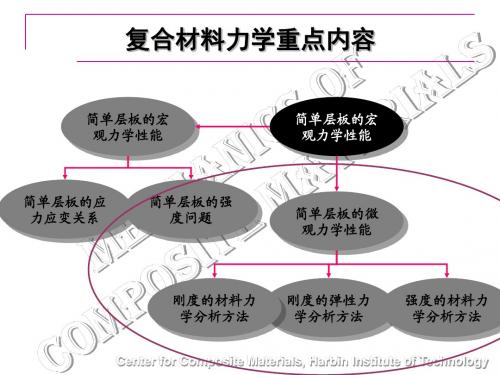
复合材料力学重点内容
简单层板的宏 观力学性能 简单层板的宏 观力学性能
简单层板的应 力应变关系
简单层板的强 度问题
复合材料力学Lecture-4

s
s
方形
s
d
d
三角形
s
第四章、单层板弹性理论 复合材料力学
对方形排列,总面积A=s2,纤维面积
Af
=π d2 4
纤维的体积含量为:
Vf
=
Af
/
A
=
π
⎛ ⎜
d
2
⎞ ⎟
4⎝s⎠
最大值在s=d时出现: V f max = π / 4 = 0.785 (4.5)
类似,三角形排列的纤维体积含量为:
Vf
=
由前一章可知,单向复合材料是横观各向同性的, 共有5个独立的弹性常数,称为等效弹性常数,如果 将它们都一一确定,单层板的弹性问题也就完全解 决。
第四章、单层板弹性理论 复合材料力学
解决的方法分为宏观力学(Macromechanics)与细 观力学(Micromechanics)两类 。
宏观力学的方法是分别针对不同的单向复合材料, 直接进行实验测定材料的5个等效弹性常数。
+ Vmε
m yy
=
V
f
(
σ
f yy
Ef
)
+
Vm
σ (
E
m yy
m
)
=
⎜⎛ ⎜⎝
Vf Ef
+
Vm Em
⎟⎟⎠⎞σ
yy
即,
1 E yy
= Vf Ef
+
Vm Em
(4.9)
4.3.3 面内剪应力
根据加载条件和基本假设,有:
σ xx
=
σ
f xx
=
σ
m xx
=0
σ
yy
复合材料力学培训讲座(ppt 32页)

20.01.2020
30
NUDT 12.6
第一章 引言
Chap.01
1.4 本课程的主要任务
复合材料的性能特性 结构分析基础 典型构件受力和变形分析
1.5 处理方法
复合材料力学、 结构分析基础 建立各种材料体系的本构关系及控制方程
20.01.2020
31
全复合材料汽车——汽油之后的变革
高性能体育器械-网球、棒球、高尔夫球、赛车、滑雪、 鱼杆
人造器官
输油管道、储罐、压力容器等
20.01.2020
13
NUDT 12.6
六、复合材料的制备
Chap.01
传统意义上的复合材料的制造,目前使用最广、 效果最好的是纤维增强:
采用熔铸、浸渍、层压等方法,把玻璃纤维、 有机纤维、碳纤维及其织物嵌入树脂基体中;
20.01.2020
2
NUDT 12.6
Chap.01
课程简介 目的 内容 内容: 考核 复合材料力学:包括细观力学和层合板理论,以 参考书 及静力、动力和稳定分析及结构优化设计(典型
结构设计)。
20.01.2020
3
NUDT 12.6
Chap.01
课程简介 内容:
目的
第一章 引言
20.01.2020
12
NUDT 12.6
Chap.01
五、复合材料的特点及应用
复合材料具有高比强度、高比刚度、材料轻、耐腐蚀、抗 疲劳性能、减振性能和高温性能好意即可设计等特点
它最早应用于国防、航空、航天等尖端科学技术领域,近 年来,汽车、造船、建筑、化工石油、体育用品、生物、 医疗、娱乐等部门也推广使用复合材料
先进复合材料 树脂基复合材料 金属基复合材料 陶瓷基复合材料 碳/碳复合材料
复合材料力学讲义
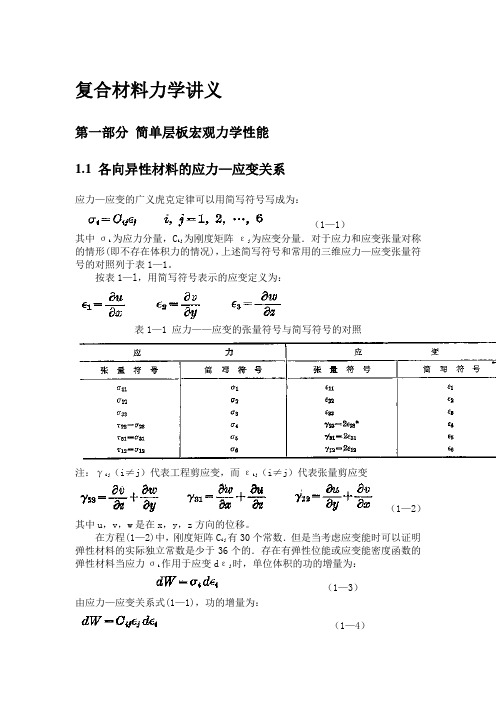
复合材料力学讲义第一部分简单层板宏观力学性能1.1各向异性材料的应力—应变关系应力—应变的广义虎克定律可以用简写符号写成为:(1—1)其中σi 为应力分量,Cij为刚度矩阵εj为应变分量.对于应力和应变张量对称的情形(即不存在体积力的情况),上述简写符号和常用的三维应力—应变张量符号的对照列于表1—1。
按表1—l,用简写符号表示的应变定义为:表1—1 应力——应变的张量符号与简写符号的对照注:γij (i≠j)代表工程剪应变,而εij(i≠j)代表张量剪应变(1—2)其中u,v,w是在x,y,z方向的位移。
在方程(1—2)中,刚度矩阵Cij有30个常数.但是当考虑应变能时可以证明弹性材料的实际独立常数是少于36个的.存在有弹性位能或应变能密度函数的弹性材料当应力σi 作用于应变dεj时,单位体积的功的增量为:(1—3)由应力—应变关系式(1—1),功的增量为:(1—4)沿整个应变积分,单位体积的功为:(1—5)虎克定律关系式(1—1)可由方程(1—5)导出:(1—6)于是(1—7)同样(1—8)因W的微分与次序无,所以:(1—9)这样刚度矩阵是对称的且只有21个常数是独立的。
用同样的方法我们可以证明:(1—10)其中S是柔度矩阵,可由反演应力—变关系式来确定应变应力关系式为ij(1—11)同理(1—12)即柔度矩阵是对称的,也只有21个独立常数.刚度和柔度分量可认为是弹性常数。
在线性弹性范围内,应力—应变关系的一般表达式为:(1—13)实际上,关系式(1—13)是表征各向异性材料的,因为材料性能没有对称平面.这种各向异性材料的别名是全不对称材料.比各向异性材料有更多的性能对称性的材料将在下面几段中叙述.各种材料性能对称的应力—应变关系式的证明由蔡(Tais)等给出。
如果材料有一个性能对称平面应力—应变关系式可简化为(1—14)对称平是z=0.这种材料称为单对称材料.单对称材料有13个独立的弹性常数。
第七章复合材料力学性能的复合规律ppt课件

u m
(常见情况)
①当 Vf 较低时
单层板中纤维断裂(图7.11(d))而附加到基体 上的额外载荷不足以使基体开裂,而可以全部承受, 此时复合材料的强度为:
1u
muVm
u m
1Vf
②当 Vf 较高时 纤维断裂时,转移载荷大。
u 1
m
u f
m
Vf
1.0 0
u 1
uf Vf
m (1Vf )
1 Vm V f
或
E2 Em E f
E2
EmV f
EmE f E f (1 V f )
⑶单向板的主泊松比ν12
复合材料的主泊松比——是指在轴向外加应力时横 向应变与纵向应变的比值。
横向收缩,纵向伸长
主泊松比
12
2 1
1 —纵向应变
2 —横向应变
横向变形增量 W为:
W W f Wm
W
12
W
1
W f
f
VfW
1
Wm
m
VmW
1
121W V f f 1W Vm m1W
12 V f f Vm m
⑷单层板的面内剪切模量G12
假定纤维和基体所承受的剪切应力相等,并假 定复合材料的剪切特性是线性的,总剪切变量为D。
试样的剪切特性: f m
若试样宽度为W,则有剪切应变:
u 主要依赖于
1
u m
在纤维断裂前先发生
基体断裂,于是所有载荷转移到纤维上。
树脂破坏时(和破坏后): m 0
刚破坏时: f f
纯树脂破坏时:
u 1
u m
纯纤维破坏时: u 1
u f
当V f 很小时,纤维不能承受这些载荷而破坏,故有:
复合材料力学(全套课件240P)

第一章、引言
复合材料力学
随直径减小,玻璃纤维拉伸强度趋 向于原子间的内聚强度11,000MPa
随直径减小,玻璃纤维拉伸强度 趋向于玻璃板材的强度170MPa
这是因为细小的纤维直径直接导致以下结果: 1) 更少、更小的微观裂纹;
2) 聚合物链延展并取向;
3) 结晶更少并且晶体间的断层密度更低;等等。
第一章、引言
复合材料力学
宏观力学(Macromechanical or phenomenological) 理论: 根据沿某些特定方向测试得到的复合材料的 宏观力学性能预报其受其它任意载荷的力学特性。 细观力学(Micromechanical)理论: 仅仅根据组成 材料的力学性能预报复合材料受任意载荷作用的 力学特性。 细观理论与宏观理论相比的优点: • 只需一次性确定组成材料的性能参数, 大大节省时间与金钱; • 可以事先由组成材料设计复合材料的性能。
第一章、引言
1.3 组成材料
1.3.1 增强体
复合材料力学
典型增强纤维
1) 玻璃纤维(Glass fiber) 分为E型、 S型、A型和C型,主要成份为SiO2, 另 含有些其它氧化物。 E (electrical insulator)型玻璃纤维应用最广, 1938 年实现商业化生产。现代复合材料诞生于1940年。 S型玻璃纤维比E型纤维的模量、强度及韧性都高, 但价格更高,最初主要是军用。
复合材料是由两种或两种以上性能各异的单一材 料,经过物理或者化学的方法组合而成的一种新 型材料。
复合材料分为天然与人工合成两大类。天然复合 材料种类繁多,包括一些动、植物组织如人的骨 格。我们只讨论人工合成复合材料 。 大多数人工合成的复合材料都是由两相构成:一个 是增强相,为非连续体;另一个是基体(matrix)相, 为连续体。
复合材料力学讲义(第二版)2精品PPT课件

Center for Composite Materials, Harbin Institute of Technology
CMCs: Increased toughness
Center for Composite Materials, Harbin Institute of Technology
CMCs: Increased toughness
• (A) Crack Deflection (偏转) – A crack meeting the reinforcement is deflected along the interface where energy is used to effect separation
– The properties of the fibre
– The properties of the resin
– The ratio of fibre to resin in the composite (Fibre Volume Fraction)
– The geometry and orientation of the fibres in the composite
TERMINOLOGY / CLASSIFICATION
• Composites
– Multiphase material w/significant proportions of ea. Phase
• Matrix — The continuous phase
– Purpose is to transfer stress to other pБайду номын сангаасases, protect phases from environment
复合材料力学ppt

yx
y
yz
zx zy z
变形分析
物质坐标和空间坐标 应变张量的定义 微小应变张量的几何解释 主应变和应变主轴 应变协调方程
几何方程
x
u , x
yz
y
v , y
zx
z
w z
,
xy
w y
v z
;
u z
w ; x
v x
u y
.
x
yx
zx
xy y zy
x z
– 美国国防部委托国家科学研究院发表的面向21世纪国 防需求的材料研究报告指出
• 复合材料包括三要素:
• 基体材料 • 增强相 • 复合方式界面结合形式
• 复合材料的分类
– 按增强剂形状不同;可分为颗粒 连续纤维 短纤维 弥散晶须 层状 骨架或网状 编织体增强复合材料 等
– 按照基体材料的不同;复合材料包括聚合物基复合 材料 金属基复合材料 陶瓷基复合材料 碳/碳复合 材料等
y z
z
变形协调方程
2 x y 2
2 y x 2
2 xy xy
2 y z 2
2 z y 2
2 yz yz
2 z x 2
2 x z 2
2 xz zx
x
xz y
xy z
yz x
2 2x yz
y
xy z
yz x
zx y
2 2y zx
z
yz x
zx y
xy z
2 2z xy
物理方程— 本构关系 Hooke 定理
on S :
s
u u*
v v*
w w*
• 第三类基本问题
– 在弹性体的一部分表面上都给定了外力;在 其余的表面上给定了位移;要求确定弹性体 内部及表面任意一点的应力和位移
复合材料力学讲义

第32页/共132页
圆形截面纤维增强复合材料对E2的影响
上述分析基于纤维的横截面为方形或矩形时导出实际为圆形,对模型进行修正欧克尔采用了折算半径的概念,令R=df/sdf为圆截面纤维的直径,s为纤维的间距
折算半径实际上反映了纤维含量体积比Vf的影响
第33页/共132页
圆形截面纤维增强复合材料对E2的影响
Ec = (0.4)(6.9x103 MPa) + (0.6)(72.4x103 MPa) = 46.2 x 103 MPa
第21页/共132页
刚度的材料力学分析方法
串联模型
与试验值相比,较小,由于纤维随机排列,兼有串联和并联的成分
(iso-stress)
表观弹性模量E2的确定:
第22页/共132页
引 言
第2页/共132页
引 言
用实验方法系统测定各种复合材料的宏观弹性特性和微观力学性能的关系涉及参数太多,费用巨大复合材料性能不稳定和试验误差,使试验结果较为分散单用试验手段很难获得全面的、系统的和有良好规律的结果,需要有理论配合微观力学研究改进复合材料宏观特性减少试验工作量反向推算复合材料中纤维和基体的平均特性
In Borsic fiber-reinforced aluminum, the fibers are composed of a thick layer of boron deposited on a small – diameter tungsten filament.
第7页/共132页
引 言
第15页/共132页
引 言
简单层板假设宏观均匀线弹性宏观地正交各向异性无初应力纤维假设均匀性线弹性各向同性规则地排列完全成一直线
复合材料力学-ppt课件
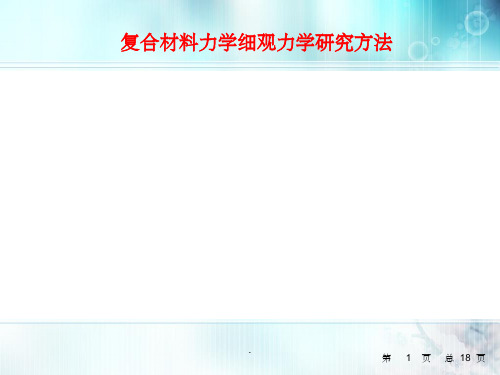
研究方法
如何将多夹杂问题转化为单夹杂问题进行求解是细观 力学的核心问题。对这个问题求解作不同的假设形成了许 多细观力学的近似方法。
成熟的细观力学方法
1、稀疏方法; 2、Mori-Tanaka法(背应力法); 3、自洽法(自相似理论); 4、广义自洽法; 5、Eshelby等效夹杂理论; 6、微分法; 7、Hashin变分原理求解上下限方法
. 第 18 页 总 18 页
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
. 第 5 页 总 18 页
一、稀疏解法
. 第 6 页 总 18 页
二、自洽法
. 第 7 页 总 18 页
三、广义自洽法
. 第 8 页 总 18 页
四、Mori-Tannka方法
. 第 9 页 总 18 页
五、 Eshelby等效夹杂理论
. 第 10 页 总 18 页
. 第 11 页 总 18 页
复合材料力学细观力学研究方法
. 第 1 页 总 18 页
. 第 2 页 总 18 页
. 第 3 页 总 18 页
引言
建立复合材料的宏观性质与相材料微结构参数的关系是实现复合材 料设计乃至进一步优化的关键。细观力学的重要任务就是根据复合材料 的组成与内部细观结构预测复合材料的宏观性能。近年米,由于计算机 性能的快速提高。可以方便地进行高性能计算,满足细观力学精细网格 和大量运算的要求。应用细观尺度的有限元网格模拟宏观材料微结构组 成,为建立细观力学和宏观材料之间的联系提供了一条途径。
六、微分法
. 第 12 页 总 18 页
. 第 13 页 总 18 页
七、 Hashin变分原理求解上下限方法
复合材料力学Lecture-3
本课程中,更多采用柔度矩阵[Sij]。若需要刚度矩阵, 只需对柔度矩阵求逆。各向同性材料的柔度矩阵是:
S
ij
S ij 0
S ij 0
(3.5)
其中,[Sij]和[Sij]分别是与正应力和剪应力相关的 分块柔度矩阵:
第三章、弹塑性力学基础
正交各向异性材料的分块柔度矩阵与(3.5)相同, 但两个分块子矩阵分别是:
1 12 13 E11 E11 E11 23 1 [ S ij ] E 22 E 22 1 sym m etric E 33
第三章、弹塑性力学基础
3.1 应力-应变关系
3.1.1. 符号记法
复合材料力学
右手螺旋法则下的直角坐标系通常用(x, y, z)和(x1, x2, x3)表示:
z
x2 x3 x1
y
x
如果他们表示同一个坐标系,通常总是有x=x1, y=x2, z=x3。
第三章、弹塑性力学基础
i 代表该应力作用平面的外法线 沿xi方向; j 代表该应力指向xj方向。 一点的应力张量(矩阵)总 是对称的,即ji=ij 这样,就只有6个应力分量 是独立的,可以缩减成一个 应力矢量{i} :
(1 2 )(1 2 )
K66 C33 0
3.2 坐标变换
由于复合材料本征上是各相异性体,其分析往往 需要借助不同的坐标系,因此,必须考虑它们之 间的坐标变换。
第三章、弹塑性力学基础
复合材料力学
如前所述,材料主轴(或局部)坐标系(x1, x2, x3)总是 这样选取,使得x1总是沿单向复合材料的轴线方向。 为确定从局部坐标系(x1, x2, x3)到总体坐标系(x, y, z)变 换关系,定义方向余弦:
复合材料力学Lecture-5

(4.22)
再假定该复合材料只受横向力作用。根据横向应变方 程,类似有:
f m f m σ 22 σ 22 σ 22 ⎛ V f / E22 + Vm a / E ⎞ ⎟σ 22 ε 22 = = V f f + Vm m = ⎜ ⎜ ⎟ E22 E22 E V f + Vm a ⎝ ⎠
(4.23)
第四章、单层板弹性理论
复合材料力学
因此,a11、a22、a21、a33可以看作为多变量(即材料 参数和几何参数)的函数,因而可以相对材料参数作 幂级数展开。 由于当两种组成材料(纤维和基体)的性能变的完 全相同时,桥联矩阵必须要能够退化为单位矩阵, 据此写出一般的展开式为:
f a11 = 1 + λ11 (1 − E m / E11 ) + ...
m f f m f m ( S11 − S11 + S 22 − S 22 )a12 = ( S12 − S12 )(a 22 − a11 )
(4.21)
现在,假定纤维和基体分别是各向同性材料如玻璃 纤维与环氧树脂。此时,上式的左边恒为0,右边 a22≠a11。因此,上述等式成立的必要条件是 :
第四章、单层板弹性理论
f a11 = E m / E11
(4.25) (4.26) 0<β <1 (4.27)
a21=0
Em a 22 = β + (1 − β ) f E 22
第四章、单层板弹性理论
Gm a33 = α + (1 − α ) f G12
复合材料力学
(4.28)
0<α <1
将(4.26)代入(4.20),得到非0因变量a12为: (4.26)代入(4.20),得到非
《复合材料力学》课件

本课程将介绍《复合材料力学》的基本概念和原理,帮助您加深对复合材料 的理解。让我们一起探索这个引人入胜的领域!
课程介绍
本节课将介绍复合材料的定义和用途,以及复合材料的发展历程和重要性。
复合材料概述
碳纤维复合材料
探索碳纤维复合材料的独特性质 和广泛应用领域。
纤维增强复合材料
复合材料破坏
深入了解复合材料的破坏模式和失效预测方法。
层间剪切破坏
了解复合材料的层间剪切破坏机制源自阻尼性能。拉伸应力研究复合材料在拉伸载荷下的应力应变关系和断 裂性能。
剪切应力
了解复合材料在剪切加载下的应力传递和破坏行 为。
压缩应力
了解复合材料在压缩状态下的应力传递和稳定性。
应变分析
线性应变
研究复合材料的线弹性行为,理 解应变的定义和计算方法。
蠕变应变
深入了解复合材料的蠕变行为和 长期稳定性。
疲劳应变
探索复合材料在循环加载下的应 变累积和损伤机制。
了解纤维增强材料的制备方法和 优越性能。
复合材料的结构
深入了解复合材料的组成和层次 结构。
力学基础
1
静力学
了解复合材料在静态负载下的行为和力
动力学
2
学原理。
探索复合材料在动态负载下的响应和振
动特性。
3
固体力学
学习固体力学的基本概念和数学模型, 以理解复合材料的变形和应力分析。
应力分析
弯曲应力
探索复合材料受弯曲载荷时的应力分布和失效机 制。
弹性力学
1
胶合弹性性能
研究复合材料胶合界面的弹性行为和界
多层复合材料
2
面破坏机制。
了解多层复合材料的弹性性能和层间剪
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复合材料力学讲义第一部分简单层板宏观力学性能1.1各向异性材料的应力—应变关系应力—应变的广义虎克定律可以用简写符号写成为:(1—1)其中σi为应力分量,C ij为刚度矩阵εj为应变分量.对于应力和应变张量对称的情形(即不存在体积力的情况),上述简写符号和常用的三维应力—应变张量符号的对照列于表1—1。
按表1—l,用简写符号表示的应变定义为:表1—1 应力——应变的张量符号与简写符号的对照注:γij(i≠j)代表工程剪应变,而εij(i≠j)代表张量剪应变(1—2)其中u,v,w是在x,y,z方向的位移。
在方程(1—2)中,刚度矩阵C ij有30个常数.但是当考虑应变能时可以证明弹性材料的实际独立常数是少于36个的.存在有弹性位能或应变能密度函数的弹性材料当应力σi作用于应变dεj时,单位体积的功的增量为:(1—3)由应力—应变关系式(1—1),功的增量为:(1—4)沿整个应变积分,单位体积的功为:(1—5)虎克定律关系式(1—1)可由方程(1—5)导出:(1—6)于是(1—7)同样(1—8)因W的微分与次序无,所以:(1—9)这样刚度矩阵是对称的且只有21个常数是独立的。
用同样的方法我们可以证明:(1—10)其中S ij是柔度矩阵,可由反演应力—变关系式来确定应变应力关系式为(1—11)同理(1—12)即柔度矩阵是对称的,也只有21个独立常数.刚度和柔度分量可认为是弹性常数。
在线性弹性范围内,应力—应变关系的一般表达式为:(1—13)实际上,关系式(1—13)是表征各向异性材料的,因为材料性能没有对称平面.这种各向异性材料的别名是全不对称材料.比各向异性材料有更多的性能对称性的材料将在下面几段中叙述.各种材料性能对称的应力—应变关系式的证明由蔡(Tais)等给出。
如果材料有一个性能对称平面应力—应变关系式可简化为(1—14)对称平是z=0.这种材料称为单对称材料.单对称材料有13个独立的弹性常数。
如果材料有两个正交的材料性能对称平面则对于和这两个平面相垂直的第三个平面亦具有对称性。
在沿材料主方向的坐标系中的应力—应变关系式是:(1—15)该材料称为正交各向异性材料。
注意到正应力σ1 σ2 σ3和剪应变ε23 ε31 ε13之间没有像各向异性材料中存在的(例如由C14的存在)相互作用。
同样,剪应力和正应变之间没有相互作用,不同平面内的剪应力和剪应变之间也没有相互作用。
还注意到在刚度矩阵中现在只剩下9个独立常数。
如果材料的每一点有一个各个方向的力学性能都相同的平面,那末该材料称为横观各向异性材料.例如,假定1—2平面是该特殊的各向同性平面,那末刚度中的下标l和2是可以互换的.这样应力—应变关系式中只有5个独立常数且可写成(1—16)如果材料有无穷多个性能对称平面那么上述关系式就简化为各向同性材料的情形,此时刚度炬阵中只有2个独立常数。
(1—17)五种最常用的材料性能对称情形的应变—应力关系式见方程(1—18),(1—19),(1—20),(1—21)和(1—22)。
各向异性材料(21个独立常数)(1—18)单对称材料(13个独立常数)(对于z=0的平面对称)(1—19)正交各向异性材料(9个独立常数)(1-20)横观各向同性材料(5个独立常数)(1-2平面是各向同性平而)(1—21)各向同性材料(2个独立常数)(1—22)1.2正交各向异性材料的工程常数工程常数(也称技术常数)是广义的弹性模量、泊松比和剪切模量以及其它性能常数.这些常数可用简单试验如轴向拉伸和疲劳试验来确定.因而具有明显的物理解释.这些常数比上一节中使用的比较抽象的柔度和刚度矩阵更为直观。
最简单的试验是在已知载荷或应力下测量相应的位移或应变.这样柔度矩阵比刚S ij比刚度矩阵C ij能更直接确定.对正交各向异性材料用工程常数表示的柔度矩阵为(1—23)其中E1 E2 E3——分别为1,2,3方向上的弹性模量υij——为应力在i方向作用时j方向的横向应变的泊松比即(1—24)此处σi=0,其它应力全为零G23 G31 G12——依次为2—3,3—1,1—2平面的剪切模量。
对于正交各向异性材料,只有9个独立常量,因为(1—25)这是由于柔度矩阵是方程(1—9)证明的对称刚度矩阵(C ij)的逆阵,当用工程常数代入方程(1—25)时,可得(1—26)这样正交各向异性材料必须满足这三个互等关系。
只有υ12 υ13和υ23需要进一步研究,因为υ12 υ13和υ23能用前三个泊松比和弹性模量来表达.后三个泊松比亦不应忽视,因为在某些试验中它们可以测到.在正交各向异性材料中υ12和υ21的区别可用图1—1来说明,该图表示了两种在单向应力作用下的正方形单元。
第—种情况应力作用在图1—1的1方向。
由方程(1—20)和(1—23)得到应变为(1—27)所以变形为图1-1 υ12和υ21的区别(1—28)其中裁荷方向由上标表示.第二种情况是,伺样的应力值作用在图2—1中2方向,可得应变为(1—29)而变形为(1—30)显然,如果E1〉E2,则1Δ1〈2Δ2。
但是,由互等关系,不管E1和E2关系如何,1Δ2=2Δ1这是用贝蒂(Betti)定理来处理各向异性材料的一个推广。
即当应力作用在2方向引起的横向变形(或横向应变)和应力作用在1方向引起的相同。
由于刚度矩阵和柔度矩阵是互为逆阵,由矩阵代数可得正交各向异性材料的矩阵之间的关系为(1—32)其中(1—33)在方程(1—32)中,符号S和C在每一处都可互换以得到逆转关系式.用工程常数表示正交各向异性材料的刚度矩阵C ij可由方程(1—23)表示的柔度矩阵S ij的求逆得到,或者把S ij代入方程(1—32)和(1—33)得到.方程(1—15)中的非零刚度是(1—34)其中(1—35)特别指出,假如要明确一种材料是否是正交各向异性的,可以从各种角度进行力学性能试验,看它是否存在剪力耦合影响的方向,由此确定材料是否是正交各向异性的、各向同性的、或是其它的。
确定材料主方向的最简单方法是直观法.但是,应用直观法材料的特性必须能很容易地用肉眼看出。
例如在用硼/环氧带制成的纤维增强简单层板中(图1—9),容易看出纵向就是l—方向.同样,2—方向在带平面中垂直于纵向的方向.而3—方向则由垂直于带平面定出。
1.3 弹性常数的限制1.3.1 各向同性材料对各向同性材料,弹性常数必须满足某些关系式.如剪切模量可由弹性模量贝E 和泊松比,确定(1—36)为了使E和G总是正值,即正的正应力或剪应力乘上对应的正应变或剪应变产生正功,于是(1—37)同样,如果各向同性体承受着静压力P的作用,体积应变(即三个正应变或拉伸应变之和)定义为(1—38)于是体积模量(1—39)是正值.只要E是正值,则(1—40)因为如果体积模量是负值,则静压力将引起各向同性材料体积膨胀.因此对各向同性材料,泊松比的范围是(1—41)1.3.2 正交各向异性材料正交各向异性材料弹性常数间的关系较为复杂.为了避免陷入基于各向同性材料工作基础上的错觉,那些关系式应认真研究,首先,应力分量和对应的应变分量的乘积表示应力所做的功,所有应力分量所做的功必须是正值,以免产生能量.该条件提供了弹性常数数值上的热力学限制.事实上对前面各向同性材料所做的就是这个限制的结果.该限制由伦普里尔(lempriere)推广到正交各向异性材料。
他要求联系应力—应变的矩阵在形式上是正定的,即有正的主值或不变量.于是,刚度和柔度矩阵两者都是正定的.这个数学条件可由下述物理论证来代替,如每次只有一个正应力作用,对应的应变由柔度矩阵对角线元素决定.于是,这些元素必须是正的,即(1—42)或用工程常数表示(1—43).同样,在适当的限制下,可能只有一个拉伸应变的变形.再则,功只是由相应应力产生的.这样,由于所作的功是由刚度矩阵的对角线元素决定的,这些元素必须是正的,即(1—44)由方程(1—34)(1—45)同时,因为正定矩阵的行列式必须是正的,得(1—46)由方程(1—32),根据刚度矩阵是正值导出(1—47)利用柔度矩阵的对称性方程(1—12),得(1—48)于是方程(1—45)可以写为(1—49)如果S ij用工程常数表示,方程(1—49)也可以从方程(1—47)得到.同样,方程(1—46)可以表示为(1—50)亦可改写为(1—51)为了得到用另外二个泊松比υ32和υ13来表达一个泊松比υ21界限,方程(1—51)可进一步化为(1—52) 对υ32和υ13可得相似的表达式。
前述对正交各向异性材料工程常数的限制,可以用来检验实验数据,看它们在数学弹性模型的范围内是否与实际相一致.在硼/环氧复合材料的试验中,迪克森(Dickerson)和戴马蒂诺(DiMartino)报道说,在1方向加载荷引起2方向应变的泊松比(υ12)高达1.97,两个方向的弹性模量是E1=11.86*106磅/英寸2,E2=1.33*106磅/英寸2,于是(1—53) 和条件(1—54) 是满足的。
因此,即使我们按照各向同性材料的直觉知识不能接受这么大的数值,但υ12=1.97却是一个合理的数据。
文献没有报道充分的资料以证明行列式条件(2—46),这个条件可能是比较严格的。
文献报道了另一个泊松比υ21为0.22,这个值满足对称条件或互等关系(1—48)。
只有测定的材料性能满足限制条件,我们才有信心着手用这种材料设计结构物。
否则,我们就有理由怀疑材料模型或实验数据,或者二者都怀疑。
1.4 正交各向异性简单层板的强度1.4.1 强度概念在描述层合板时,正交各向异性简单层板的强度特性如同刚度特性一样是一个重要的基础。
因为要得到简单层板所有可能方向的强度特性事实上是不可能的,必须确定一个方法,以得到用材料主方向的特性表示任意方向上的特性。
在此,众所周知的主应力和主应变的概念是无价值的。
这里的中心点是主应力和主应变是与材料方向无关的最大值;应力和应变的方向对各向同性材料毫无意义。
因为正交各向异性材料的主应力轴和主应变轴不一定是一致的。
还有,在一个方向的强度比另一个方向低,所以最大应力不一定是控制设计的应力,必须合理比较实际的应力场和许用的应力场。
前面几节中在刚度关系方面已完成的工作可用作计算实际应力场的基础,尚待确定的是许用应力场。
建立在材料主方向的许用应力或强度,是研究正交各向异性简单层板强度的基础。
对于应力作用在其自身平面内的简单层板,如果简单层板的拉伸强度和压缩强度是相等的,它具有三个基本强度:X——轴向或纵向强度Y——横向强度S——剪切强度(单位:力/面积,即许用应力)。
这些强度的方向表示在图1—2中;显然,这些强度是应力σ1、σ2、τ12。
单独作用的结果图1—2 单向增强简单层板基本强度的确定X=50000磅/英寸2Y=1000磅/英寸2S=2000磅/英寸2根据纤维的方向,像强度一样刚度在l—方向高而在2—方向低。
