复合材料力学大作业
复合材料力学实验(第一组)

复合材料力学与结构设计实验报告专业:复合材料组队:第一组姓名:郑勇斌学号:4203090107中南大学航空航天学院实验一 单层复合材料拉伸强度测定1. 目的掌握单层复合材料拉伸强度的测定方法并了解其各向异性强度特性。
2. 内容、方法要求试件两端用金属片或玻璃片加固,加强片厚度1~2mm ,采用粘接剂粘接,要求在实验过程中加强片不脱落。
试件尺寸规定见表1。
不同纤维方向的时间尺寸是不同的,试件形状如图1所示。
表1 拉伸试件尺寸(单位mm )符号 名称 尺寸L 总长 250 L 1 端部加强片间距 150± 5 L 2 端部加强片长度 50 b 中间平行段宽度25±0.5 t厚度2~10LbtL 1L 2图1 拉伸试件形状示意图用0o 试件,尺寸按照表1,采用材料试验机加载,由试验机画出载荷-夹头位移曲线,用引伸计或电阻应变片测量ε1,ε2,并求出破坏时最大载荷。
由下列公式计算强度E 1,X t ,v 21。
用引伸计或电阻应变片测量ε1,ε2。
测定E 1,X t ,v 21的计算公式如下:12112111,,L t P P E X bt btενεε==-= 式中,b 为试件的宽度,t 为试件的厚度,P 1为1方向的载荷,P L1为1方向极限载荷,1ε,2ε分别为1,2方向的应变。
0o 拉伸试验分别如图2所示。
图2 拉伸试验曲线3. 报告要求(1) 说明实验方法和步骤、试件材料。
答:实验方法:实验步骤:1、准备阶段. 画夹持线25mm-30mm ;用丙酮处理应变片;多次,不同部位量取工作区的长度,厚度,宽度,取平均值;将应变片贴在式样的中部,并使其不留下气泡;焊锡处理端片,将应变片角线焊在端片上;将导线与角线相连,剪除多余的角线。
2.实验阶段。
将试样夹在检测仪器上;将做好的另一只板连接到应变器上作为补偿;将导线与应变器相连;电脑检测连接情况;清零;开始。
记录阶段:记录实验数据,讨论。
复合材料作业1

复合材料作业、作业1.证明横观各向同性材料泊松比的限制条件:2112(')'E E νν-<<式中,E ν为各向同性面(1O2面)的弹性模量和泊松比,31323==',E =E'ννν 。
解:已知应变能密度表达式:1111W {}{}={}[S]{}{}[C]{}2222T T T i i σεσεσσεε===由于热力学的限制,应力做功的总和必为正值,因此[C][S]和是正定矩阵。
因此,[S]的对角元素须是正值,即 112233445566S ,S ,S ,S ,S ,S >0, 由各向异性材料的弹性常数与柔度系数关系:131********111213222212223313233331323344235566311210001000000000100000000000100000000001000000100E E E S S S E E E S S S E E E S S S S G S S G G νννννν--⎛⎫ ⎪ ⎪ ⎪-- ⎪⎛⎫ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭可以得到: 123233112E ,E ,E ,G ,G ,G >0, 因正定矩阵行列式必须为正,得到12211331233212233112312=0E E E ννννννννν----∆>由于123E ,E ,E 0>,只需122113312332122331120ννννννννν----> (1) 由横观各向同性性质: 1122121211==S S E E E E E =⇒=⇒ 3'E E =由[S]的对称性质:122111221122121122==ES S E E E νννννν--=⇒=⇒= 1331113311331133=''E E S S E E E E ννννν--=⇒=⇒= 2332223322332233=''E ES S E E E E ννννν--=⇒=⇒= 将上述性质代入(1)式,得到222222242222221(')(')2(')()0'''[+(')]12(')(')()0'''[+(')](1('))0''112(')'E E E E E E E E EE E E E EE E EE νννννννννννννν---->⇒-+-+>⇒-+->⇒-<<-设 22(')'Ex E ν= 可看出0x > 由不等式1x 2(x 0)x +≥> 可知1111x x x -≤-< 即 22112(')'2(')'E E E E νν-<ν 的范围为2112(')'E E νν-<<证毕。
复合材料大作业

先进复合材料制造技术复合材料表面的金属化姓名丁志兵班级05021104学号2011301263复合材料表面的金属化材料作为社会进步的物质基础和先导,在人类历史发展的过程中一直都是人类进步的里程碑。
每一种新材料的发现和利用都会为社会生产力的提高以及人类生活品质的提升带来巨大的变化。
同时,材料制造的水平也是衡量一个国家科学技术和经济发展的重要因素之一。
复合材料是由两种或两种以上不同性质的材料,通过物理或化学的方法,在宏观上组成具有新性能的材料。
各种材料在性能上互相取长补短,产生协同效应,使复合材料的综合性能优于原组成材料而满足各种不同的要求。
复合材料的发展具有悠久的历史,自20 世界40 年代因航空工业发展的需要而发展出的玻璃纤维增强复合材料(也称玻璃钢),复合材料这一新材料的名称因此而进入人们的视线。
复合材料的出现,使得材料科学的内容产生了极大的丰富,并且因其自身的广泛而优异的性能而得到快速的发展,人们将复合材料的出现视为人类进步发展的里程碑。
科学家预言:“复合材料在21 世纪中将支撑着科学技术的进步和挑起经济实力的脊梁”,“21 世纪将是复合材料的时代”,“先进复合材料在21世纪中将在航空航天技术领域中发挥越来越重要的作用”。
随着时代的进步和科技的发展,复合材料结构已经广泛应用于航空航天、船舶、车辆、建筑工程等多个领域,的确,21 世纪将是复合材料的时代,复合材料必将肩负着重要的责任。
树脂基复合材料以其质轻、高比强度、高比模量、热膨胀系数小、性能可设计性等一系列优点,已经成为国内外航天器结构部件的首选材料,广泛应用于各类卫星天线、相机结构组件、裕架、太阳能电池板等。
在航天器中,用复合材料代替金属材料,在保持原有力学性能,甚至更高的同时,可有效减轻航天器的重量,节约发射成本。
但是,由于特殊的空间使用环境和航天技术新的发展需求,树脂基复合材料面临以下的问题,严重影响了该类材料的进一步应用。
1)空间防护能力不足,制约航天器向长寿命方向发展。
复合材料力学设计作业1

1、为什么结构复合材料中增强材料的形态主要为纤维?2、简述树脂基复合材料的优点和缺点?3、为什么新一代客机中复合材料用量会大幅提高?其复合材料零部件主要用到复合材料的哪些优点?4、为什么卫星中采用了较多的复合材料?答:1、利用复合材料的各种良好的力学性能用于制造结构的材料,称为结构复合材料,它主要有基体材料和增强材料两种组分组成。
其中增强材料承受主要载荷,提供复合材料的刚度和强度,基本控制其力学性能;基体材料固定和保护增强纤维,传递纤维间剪力和防止纤维屈曲,并改善复合材料的某些性能。
用以加强制品力学性能或其他性能的材料,在橡胶工业中又称补强剂。
分纤维状和粒状材料两种。
增强材料的增强效应取决于与被增强材料的相容性,为增进相容能力,有些增强材料在使用前需要进行表面处理。
对粒状增强材料,尚需考虑其表面积(决定于粒径、形状和孔隙度)。
据报道,平均粒径在0.2μm以下的增强材料,随粒径的减小,制品的模量、抗张强度、屈服强度和伸长率均有所增加。
平均粒径较大的增强材料,由于粒径分布的不同其结果不一致。
所以,结构力学复合材料力学性能难以控制。
增强材料就象树木中的纤维,混凝土中的钢筋一样,是复合材料的重要组成部分,并起到非常重要的作用。
例如在纤维增强复合材料中,纤维是承受载荷的组元,纤维的力学性能决定了复合材料的性能。
所以说结构复合材料中增强材料的形态主要为纤维。
2、树脂基复合材料的优点:1)比强度高、比模量大2)耐疲劳性能好3)阻尼减震性能好4)破损安全性好5)耐化学腐蚀性好6)树脂基复合材料是一种优良的电气绝缘材料,电性能好7)树脂基复合材料热导率低、线膨胀系数小,优良的绝热材料,热性能良好。
树脂基复合材料的缺点:1)树脂基复合材料的耐热性较低2)材料的性能分散性大。
3、用复合材料设计的飞机结构,可以推进隐身和智能结构设计的发展,有效地减少了机体结构重量,提高了飞机运载能力,降低了发动机油耗,减少了污染排放,提高了经济效益;复合材料优异的抗疲劳和耐介质腐蚀性能,提高了飞机结构的使用寿命和安全性,减少了飞机的维修成本,从而提高了飞机结构的全寿命期(是指结构从论证立项开始,有设计研制、生产研制、销售服务、使用运行、维护修理,一直到报废处理的整个寿命期)经济性;复合材料结构有利于整个设计与整体制造技术的应用,可以减少结构零部件的数量,提高结构的效率与可靠性,降低制造和运营成本,并可明显改善飞机气动弹性特性,提高飞机性能。
复合材料力学试题

复合材料力学试题答案判断题(正确的在括弧内划√,错误的在括弧内划×)。
1.“宏观力学”是在研究复合材料力学性能时,假定材料是均质的。
(√)2.单层是层合板的基本单元,在复合材料结构设计中又叫做三次结构。
(×)3.层合板由若干具体不同纤维方向的单层叠合而成,在复合材料机构设计中又叫二次结构。
(√)4.复合材料力学中,1为纵向,2为横向,应力规定拉为负,压为正。
(×)5.在单层板(正交各向异性)材料中,τ12不仅形成剪切变形,还存在剪拉耦合效应。
(×)6.在单层正交各向异性板中,11)1(11σεE =。
(√) 7.在单层正交各向异性板中,11122)1(2)2(221συσεεεE E -=+=。
(√) 8.单层板的工程弹性常数有5个,且相互独立。
(×)9.柔量矩阵{S}是对称矩阵,而模量举证{Q}不是对称矩阵。
(×)10.在正交单层板中,Q16=Q26=0,Q61=Q62,但其值不为零。
(×)11.在复合材料力学中,对于工程弹性常数存在如下关系:2121υυ=E E 。
(√) 12.在单层板偏轴刚度中,应力转换和应变转换关系式中,m=sin θ,n=cos θ。
(×)13. 在单层板偏轴刚度中,应力转换和应变转换关系式中存在如下关系:[][][]T T T 1-=σε。
(√)14.在ij Q 中,11Q 、22Q 是θ的偶函数,16Q 、26Q 也是θ的偶函数。
(×) 15.玻璃钢复合材料在拉伸时发生变形,所以是一种塑性材料。
(×)16.利用复合材料的强度准则,可以判断复合材料设计过程的安全性,同时可以计算极限载荷。
(×)17.利用最大应力准则判断材料安全性时,如果判断式大于1,说明材料的机构是安全的。
(×)18.在复合材料中,利用强度比可以计算复合材料的极限载荷。
(√)20.在对称层合板中,)()(z z --=θθ。
复合材料刚度习题(力学)

复合材料的刚度——练习一
确定E1ν1和E2ν2等厚度双金属(如习题二)的简支梁,梁中 截面C受集中力P作用
求:梁中截面应力。
A
C
B
t
h
t
l
l
2
2
b
复合材料的刚度——练习二
硼/环氧B4/5505正交对称层合板[902/02]S,单层厚度为 t=0.1mm,Nx 100N/m 其它内力分量均为零 。 求:各铺层应力。
(4)层合板铺层变形
2.19 0.2 0T
k
0
zk
0.73 0.067
0.73 0.067
0T 0T
10-3
2.19 0.2 0T
zk
zk
zk 1 2
复合材料的刚度——习题五
练习三中的层合板,Nx N y Nxy M y M xy 0, M x 50N.m/m 计算该层合板的铺层应变和应力。
复合材料的刚度——习题四
硼/环氧B4/5505规则斜交反对称层合板[45/-45]T,单层厚 度为t=0.4mm,求该层合板的刚度。 已知:E1 208GPa, E2 18.9GPa, G12 5.7GPa, v21 0.23
解:(1)正轴刚度
209 4.4 0
Q
4.4
19
0
GPa
0 0 5.7
2
1
Q2
E2
1
2 2
2
0
2 1
0
0
0
1
2
2
(2)等厚度双层
ht
x
t
N
A Qktk Q1t Q2t A1 A2 k 1
B
N
Qk
k 1
复合材料原理作业及解答

b、证明偶联剂在玻璃纤维/树脂界面上的偶联效果一定有着更为 本质的因素在起作用。
12、解释化学键理论与优先吸附理论,并指出其成功之处与不足之处。
(P40-41) (1) 化学键理论 认为:基体树脂表面的活性官能团与增强体表面的官能团能起化学反应。 因此树脂基体与增强体之间形成化学键的结合,界面的结合力是主价键 力的作用。偶联剂正是实现这种化学键结合的架桥剂。
11 、解释润湿理论所包含的内容,并指出其成功之处与不足之处。
(P39) 润湿理论:
指出:要使树脂对增强体紧密接触,就必须使树脂对增强体表面很 好地浸润。 前提条件:液态树脂的表面张力必须低于增强体的临界表面张力。 结合方式:属于机械结合与润湿吸附。
优点:解释了增强体表面粗化、表面积增加有利于提高与基体树脂 界面结合力的事实。 不足:a、不能解释施用偶联剂后使树脂基复合材料界面粘结强度 提高的现象。
成功之处:在偶联剂应用于玻璃纤维复合材料中得到很好应用,也被界 面研究的实验所证实。 偶联剂在界面所起的作用:用Br2破坏偶联剂双键,制品强度下降。 局限性: a、聚合物不具备活性基团;b、不具备与树脂反应的基团。 (2) 优先吸附理论
提出背景:解释化学键不能解释的现象。 当玻璃纤维被偶联剂覆盖后,偶联剂对树脂中的某些组分“优先吸附”, 这样,改变了树脂对玻璃表面的浸润性。 认为:界面上可能发生增强体表面优先吸附树脂中的某些组分,这些组
《复合材料力学》试题

《复合材料力学》考试题1.已知玻璃/环氧单向复合材料,玻璃纤维E f =7.5×104MPa,环氧E m =3.5×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =60GPa,E2 =20GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
1.已知玻璃/环氧单向复合材料,玻璃纤维E f =7.0×104MPa,环氧E m =3.0×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =55GPa,E2 =17.5GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
1.已知玻璃/环氧单向复合材料,玻璃纤维E f =8.0×104MPa,环氧E m =4.0×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =65GPa,E2 =22GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
14-15第一学期复合材料力学卷A
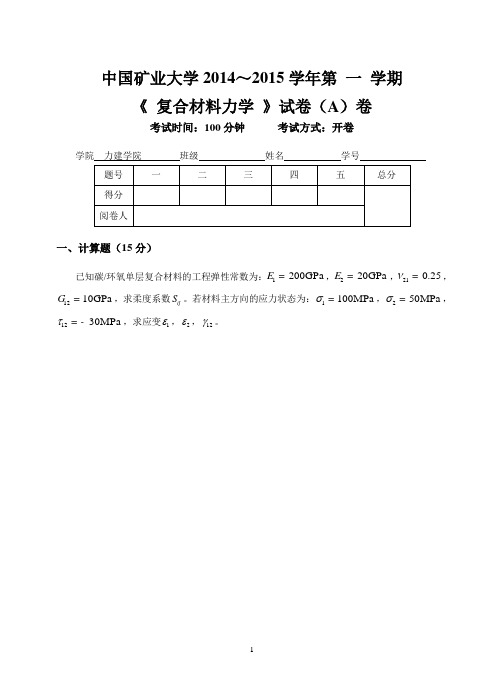
中国矿业大学2014~2015学年第 一 学期《 复合材料力学 》试卷(A )卷考试时间:100分钟 考试方式:开卷学院 力建学院 班级 姓名 学号一、计算题(15分)已知碳/环氧单层复合材料的工程弹性常数为:1200GPa E =,220GPa E =,210.25ν=,1210GPa G =,求柔度系数ij S 。
若材料主方向的应力状态为:1100MPa σ=,250MPa σ=,1230MPa τ=-,求应变1ε,2ε,12γ。
某复合材料单层板受力后发生面内变形,0.3%x ε=,0.2%y ε=,0.1%xy γ=,纤维与x 轴的夹角45θ=?。
其工程弹性常数为:160GPa E =,210GPa E =,210.30ν=,128GPa G =,求该材料在主方向的应力1σ,2σ,12τ。
如图所示,复合材料单层板承受偏轴向压缩,纤维与x 轴的夹角60θ=?,80MPa y σ=-。
强度参数为:t 1200MPa X =,c 1200MPa X =,t 50MPa Y =,c 200MPa Y =,70MPa S =。
试用最大应力理论和Hill-蔡强度理论校核其是否安全。
已知玻璃/环氧单向复合材料,玻璃纤维的f 80GPa E =,f 0.25ν=,环氧树脂的m 0.35ν=,纤维体积含量f 60%c =。
该复合材料的纵向弹性模量150GPa E =,试用串联和并联模型计算2E 、21ν和12ν。
五、计算题(25分)如图,正交铺设对称层合板()s 0/90鞍,单层厚度1mm k t =,已知:单层的正轴刚度矩阵[]120404200GPa 0010Q 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫。
求:(1)层合板的拉伸和弯曲刚度矩阵;(2) 层合板沿y 方向受拉伸,100N/mm =y N ,求90˚铺层主方向的应力1σ,2σ,12τ。
复合材料结构力学作业

一. 对材料AS4/3501-6进行设计已知61.1,134.0,3.0,86.6,65.9,2.147======ρυmm t GPa G MPa E MPa E T L MPa S MPa Y MPa Y MPa X MPa X C T c T 105,186,4.49,1468,2356=-==-==最大正应力准则为pi pi Tpi Tpi CpiTSY Y X X R 1222221111,,minσσσσσ=12STEP I Special Stacking Sequence (SSS)(一) 在Task I 载荷作用下已知Longitudinal Load =100 kN ,Transverse Load =-5 kN , Shear Load =30kN外加载荷可等效为{}{}m kN N N N N TT/600502000122211-==对[]0n S 度铺设层合板,{}MPa T447837314925}{-=σ,带入最大正应力准则得N=max{,,}=,所以[]0n S 所需的最小层数为层,且12σ先破坏 对[]90n S 度铺设层合板{}{}MPa T447814925373--=σN=max{,,}=,所以[]90n S 所需的最小层数为层,且22σ先破坏 对[](45)n S ±度铺设层合板45度 {}{}MPa T 3.19125.1801.5496-=σ, N=max{,,}=-45度 {}{}MPa T3.19127.3808.1218=σ, N=max{, ,}=所以对[](45)n S ±度铺设层合板,共需要*4=层,且12σ先破坏对[](0/60)n S ±度铺设层合板0度 {}{}MPa T7.2272.65.6366-=σ, N=max{,,}=+60度{}{}MPa T8.4507.1852267-=σ, N=max{,,}=-60度{}{}MPa 2237.3815.1918T-=σ, N=max{,,}=所以对[](0/60)n S ±度铺设层合板,共需要*6=层,且22σ先破坏 绘制在表格中,如下所示:从上表中可以看到,[]0n s 所需的层数最少,即质量最轻对])45/45/(90/0[z y x-铺层,设+45度和-45度的层数相同(1) 当0度铺层占10%,90度铺层占0%时, 则45度和-45度各占45%时 0度 {}MPa T43987030809}{-=σ, N=+45度 {}MPa T 6.24899.1484.9050}{-=σ, N=-45度 {}MPa T6.24891.5855.268}{-=σ, N=代入最大正应力准则进行校核,经比较得,N=,所以共需要*2=层(2) 当0度铺层占10%,90度铺层占10%时, 则45度和-45度各占40%时 0度,{}MPa T48243327954}{-=σ, N=max{,,}=90度, {}MPa T 482155514524}{-=σ, N=max{,,}=45度, {}MPa T200232211831}{=σ, N=max{,,}=-45度, {}MPa T6.20017.8005.1598}{=σ, N=max{,,}=代入最大正应力准则进行校核,经比较得,N=,所以共需要*2=层(3) 当0度铺层占10%,90度铺层占20%时, 则45度和-45度各占35%时90度 {}MPa T534158310498}{--=σ, N=+45度 {}MPa T 177943414048}{-=σ, N=-45度 {}MPa T17785.9652.2702}{=σ, N=经比较得,N=,所以共需*2=层(4) 当0度铺层占10%,90度铺层占25%时, 45度和-45度各占% 0度,{}MPa T5659027327}{-=σ, N=90度, {}MPa T3.5655.16149092}{--=σ, N=45度, {}MPa T171648115117}{=σ, N=-45度,{}MPa T.1.17169.10427.3118}{=σ, N=经比较得,N=,所以共需要*2=层(5)当0度铺层占10%,90度铺层占30%时, 则45度和-45度各占30%时 0度 {}MPa T606927618}{-=σ, N=90度 {}MPa T8.59916557933}{-=σ, N=+45度 {}MPa T 167552516207}{-=σ, N=-45度 {}MPa T16756.11202.3477}{=σ, N=经比较得,N=,所以共需要*2=层(6)当0度铺层占10%,90度铺层占40%时, 则45度和-45度各占25%时 0度 {}MPa T68313028732}{=σ, N=90度 {}MPa T 6839.17608.6107}{-=σ, N=+45度 {}MPa T164260618561}{-=σ, N= -45度 {}MPa T164212854062}{=σ, N=经比较得,N=,所以共需要*2=层(7)当0度铺层占10%,90度铺层占50%时, 45度和-45度各占20% 0度,{}MPa T79325530507}{=σ, N=90度,{}MPa T5.7936.19028.4691}{--=σ, N=-45度,{}MPa T6.16589.14724888}{=σ, N=经比较得,N=,所以共需要*2=77层(8)当0度铺层占10%,90度铺层占60%时, 则45度和-45度各占15%时 0度 {}MPa T94637832990}{=σ, N=1490度 {}MPa T2.9463.20863607}{--=σ, N= +45度 {}MPa T172076224781}{-=σ, N=-45度 {}MPa T172017024701}{=σ, N=经比较得,N=,所以共需要*2=层(9)当0度铺层占10%,90度铺层占75%时, 则45度和-45度各占%时 0度 {}MPa T145062239942}{=σ, N=90度 {}MPa T8.144925721729.6-}{-=σ, N=+45度 {}MPa T196487734490}{-=σ, N=-45度 {}MPa T5.196323173722}{=σ, N=经比较得,N=,所以共需要*2=层(10)当0度铺层占25%,90度铺层占0%时, 则45度和-45度各占%时 0度 {}MPa T50756820231}{-=σ, N=+45度 {}MPa T16329.1-8284.7}{-=σ, N= -45度 {}MPa T9.16326.4949.2475}{-=σ, N=经比较得,N=,所以共需要*2=层(11)当0度铺层占25%,90度铺层占10%时, 则45度和-45度各占%时0度 {}MPa T56526519118}{-=σ, N=90度 {}MPa T5.5635.10725.9458}{--=σ, N=+45度 {}MPa T134712610829}{-=σ, N=-45度 {}MPa T5.13465.6844.1169}{-=σ, N=经比较得,N=,所以共需要*2=层(12) 当0度铺层占25%,90度铺层占25%时, 则45度和-45度各占25%时0度,{}MPa T6831819099}{-=σ, N=90度,{}MPa T2.68314117.5669}{--=σ, N=45度,{}MPa T116722213964}{-=σ, N=max{,,}=-45度,{}MPa T1.11676.9006.534}{-=σ, N=max{,,}=经比较得,N=,所以共需要*2=层(13)当0度铺层占25%,90度铺层占50%时, 则45度和-45度各占%时 0度 {}MPa T104722721050}{=σ, N=90度 {}MPa T 10473.13271.2452}{--=σ, N=+45度 {}MPa T110725720408}{-=σ, N= -45度 {}MPa T110712978.1809}{-=σ, N=经比较得,N=,所以共需要*2=层(14)当0度铺层占50%,90度铺层占0%时, 则45度和-45度各占25%时0度 {}MPa T68335712870}{-=σ, N=90度 {}MPa T2.6837.4718.9106}{--=σ, N= +45度 {}MPa T6.10351.1823.9131}{--=σ, N=-45度 {}MPa T6.10356.4967.5367}{-=σ, N=经比较得,N=,所以共需要*2=层(15)当0度铺层占50%,90度铺层占10%时, 则45度和-45度各占20%时0度 {}MPa T79312712568}{-=σ, N=90度 {}MPa T793.5-4.7185492.7-}{=σ, N= +45度 {}MPa T 8519811957}{--=σ, N=-45度 {}MPa T8518.6894882}{-=σ, N=经比较得,N=,所以共需要*2=层(16)当0度铺层占50%,90度铺层占25%时, 则45度和-45度各占%时0度 {}MPa T10475212812}{=σ, N=90度 {}MPa T10474.7839.2819}{--=σ, N=+45度 {}MPa T73710216105}{--=σ, N=-45度 {}MPa T6.7366.9379.6112}{-=σ, N=经比较得,N=,所以共需要*2=层在图表中表示如下:的层数最少,为22层,此时的重量最轻。
复合材料力学作业

复合材料力学课程设计一、 层合板失效载荷计算1、 问题描述:已知:九层层合板,正交铺设,铺设比为0.2m =。
受载荷x N N =,其余载荷均为零。
每个单层厚度为0.2t mm =。
玻璃/环氧单层板性能:41 5.4010E Mpa =⨯,42 1.8010E Mpa =⨯,120.25ν=,3128.8010G Mpa =⨯,31.0510t c X X Mpa ==⨯,2.810t Y Mpa =⨯,14.010c Y Mpa =⨯, 4.210S Mpa =⨯。
求解:1、计算各铺层应力?2、最先一层失效的载荷?2、 使用mat lab 编程求解:将输入文件“input.txt ”经由程序“strain.m ”运行,得到输出文件“output.txt ”。
求解程序见附录一。
3、计算结果:(其中R 是强度比)求单层刚度Q1:18382.97872 4595.74468 0.00000 4595.74468 55148.93617 0.00000 0.00000 0.00000 8800.00000 Q2:55148.93617 4595.74468 0.00000 4595.74468 18382.97872 0.00000 0.00000 0.00000 8800.00000 Q3:18382.97872 4595.74468 0.00000 4595.74468 55148.93617 0.000000.00000 0.00000 8800.00000 Q4:55148.93617 4595.74468 0.00000 4595.74468 18382.97872 0.000000.00000 0.00000 8800.00000 Q5:18382.97872 4595.74468 0.00000 4595.74468 55148.93617 0.000000.00000 0.00000 8800.00000 Q6:55148.93617 4595.74468 0.00000 4595.74468 18382.97872 0.000000.00000 0.00000 8800.00000 Q7:18382.97872 4595.74468 0.00000 4595.74468 55148.93617 0.000000.00000 0.00000 8800.00000 Q8:55148.93617 4595.74468 0.00000 4595.74468 18382.97872 0.000000.00000 0.00000 8800.00000 Q9:18382.97872 4595.74468 0.00000 4595.74468 55148.93617 0.000000.00000 0.00000 8800.00000求中面应变Ez:0.0306235*R-0.00290497*R0.00477273*R 求各层应力 CC1:-19.4684*R549.6*R-42.0*RC2:1675.5*R87.3356*R42.0*RC3:-19.4684*R549.6*R-42.0*RC4:1675.5*R87.3356*R42.0*RC5:-19.4684*R549.6*R-42.0*RC6:1675.5*R87.3356*R42.0*RC7:-19.4684*R549.6*R-42.0*RC8:1675.5*R87.3356*R42.0*RC9:-19.4684*R549.6*R-42.0*R最先一层失效载荷:Nx/t)1: 0.05088(Nx/t)2: 0.27584(Nx/t)3: 0.05088(Nx/t)4: 0.27584(Nx/t)5: 0.05088(Nx/t)6: 0.27584(Nx/t)7: 0.05088(Nx/t)8: 0.27584(Nx/t)9: 0.05088 则最先一层失效载荷为(Nx/t)1:0.05088即90ο铺层最先失效。
工程力学 第17章 复合材料的力学行为 习题及解析

工程力学(静力学与材料力学)习题解答第17章 复合材料的力学行为17-1 图示结构中,两种材料的弹性模量分别为E a 和E b ,且已知E a >E b ,二杆的横截面面积均为bh ,长度为l ,两轮之间的间距为a ,试求: 1.二杆横截面上的正应力;2.杆的总伸长量及复合弹性模量;3.各轮所受的力。
知识点:静不定问题,复合弹性模量 难度:很难 解答:解:1.P Nb Na F F F =+ (1) b a l l ∆=∆ (2) bhE lF l a Na a =∆ (3) bhE lF l b b Nb =∆ (4)将(3)、(4)代入(2),得bNba Na E F E F =(5)(1)、(5)联立解得P b a a Na F E E E F +=,P b a bNb F E E E F +=bh F E E E bh F P b a a Na a +==σ,bh F E E E bh F Pb a b Nb b +==σ2.由(3)式 bhE E lF bh E l F l )(b a P a Na a +==∆ 设复合弹性模量E c)2(c P bh E lF l =∆,由于a l l ∆=∆,比较两式得2ba c E E E +=3.由于F Na >F Nb ,所以,轮C 、轮G 脱离接触面,所以受力为零。
0)(=∑F k M ,022R Nb Na =--a F hF h F H∴ b a b a P R 2E E E E a h F F H +-=,ba ba P R R 2E E E E a h F F F H D +-==17-2 玻璃纤维/环氧树脂单层复合材料由2.5kg 纤维与5kg 树脂组成。
已知玻璃纤维的弹性模量E f =85GPa ,密度f ρ= 2500kg/m 3,环氧树脂的弹性模量E m = 5GPa ,密度m ρ= 1200kg/m 3。
试求垂直于纤维方向和平行于纤维方向的弹性模量E y 和E x 。
复合材料结构力学作业

一. 对材料AS4/3501-6进行设计已知61.1,134.0,3.0,86.6,65.9,2.147======ρυmm t GPa G MPa E MPa E T LMPa S MPa Y MPa Y MPa X MPa X C T c T 105,186,4.49,1468,2356=-==-==最大正应力准则为pi pi Tpi Tpi CpiTSY Y X X R 1222221111,,minσσσσσ=12STEP I Special Stacking Sequence (SSS)(一) 在Task I 载荷作用下已知Longitudinal Load =100 kN ,Transverse Load =-5 kN , Shear Load =30 kN 外加载荷可等效为{}{}m kN N N N N TT/600502000122211-== 对[]0n S 度铺设层合板,{}MPa T447837314925}{-=σ,带入最大正应力准则得 N=max{6.3349,2.0054,42.6476}=42.6476,所以[]0n S 所需的最小层数为42.6层,且12σ先破坏对[]90n S 度铺设层合板{}{}MPa T447814925373--=σ N=max{0.2541,302.1255,42.6476}=302.1255,所以[]90n S 所需的最小层数为302.1255层,且22σ先破坏对[](45)n S ±度铺设层合板 45度 {}{}M P aT3.19125.1801.5496-=σ, N=max{2.3328,3.6538,18.2124}=18.2124 -45度{}{}M P a T3.19127.3808.1218=σ, N=max{0.51732,7.7065 ,18.2124}=18.2124所以对[](45)n S ±度铺设层合板,共需要18.21*4=72.84层,且12σ先破坏 对[](0/60)n S ±度铺设层合板 0度{}{}MPa T7.2272.65.6366-=σ, N=max{2.7022,0.0333,2.1686}=2.7022+60度{}{}MPa T8.4507.1852267-=σ, N=max{0.9622,3.7591,4.2933}=4.2933-60度{}{}MPa 2237.3815.1918T-=σ, N=max{1.3069,7.7267,2.1248}=7.37267 所以对[](0/60)n S ±度铺设层合板,共需要7.37*6=44.22层,且22σ先破坏从上表中可以看到,[]0n s 所需的层数最少,即质量最轻对])45/45/(90/0[z y x-铺层,设+45度和-45度的层数相同(1) 当0度铺层占10%,90度铺层占0%时, 则45度和-45度各占45%时 0度 {}M P a T43987030809}{-=σ, N=13.08 +45度 {}MPa T 6.24899.1484.9050}{-=σ, N=23.71-45度 {}MPa T6.24891.5855.268}{-=σ, N=23.71代入最大正应力准则进行校核,经比较得,N=23.71,所以共需要23.71*2=47.42层 (2) 当0度铺层占10%,90度铺层占10%时, 则45度和-45度各占40%时 0度,{}MPa T48243327954}{-=σ, N=max{11.865,2.328,4.5905}=11.86590度, {}MPa T482155514524}{-=σ, N=max{9.8937,31.48,4.5905}=31.4845度, {}MPa T200232211831}{=σ, N=max{5.0216,6.5182,19.07}=19.07 -45度, {}MPa T6.20017.8005.1598}{=σ, N=max{0.6783,16.2085,19.0629}=19.0629代入最大正应力准则进行校核,经比较得,N=31.48,所以共需要31.48*2=62.96层 (3) 当0度铺层占10%,90度铺层占20%时, 则45度和-45度各占35%时 0度 {}M P aT53518327248}{-=σ, N=11.57 90度 {}MPa T534158310498}{--=σ, N=32.04+45度 {}MPa T177943414048}{-=σ, N=16.94 -45度 {}MPa T17785.9652.2702}{=σ, N=19.53 经比较得,N=32.04,所以共需32.04*2=64.08层(4) 当0度铺层占10%,90度铺层占25%时, 45度和-45度各占32.5% 0度,{}MPa T5659027327}{-=σ, N= 11.690度, {}MPa T3.5655.16149092}{--=σ, N= 32.682245度, {}MPa T171648115117}{=σ, N= 16.3429 -45度,{}MPa T.1.17169.10427.3118}{=σ, N= 21.1113经比较得,N=32.68,所以共需要32.68*2=65.36层(5)当0度铺层占10%,90度铺层占30%时, 则45度和-45度各占30%时 0度 {}M P a T606927618}{-=σ, N=11.72 90度 {}MPa T8.59916557933}{-=σ, N=15.95 +45度 {}MPa T167552516207}{-=σ, N=22.67 -45度 {}MPa T16756.11202.3477}{=σ, N=33.49 经比较得,N=33.49,所以共需要33.49*2=66.98层(6)当0度铺层占10%,90度铺层占40%时, 则45度和-45度各占25%时 0度 {}M P aT68313028732}{=σ, N=12.2 90度 {}MPa T6839.17608.6107}{-=σ, N=15.64 +45度 {}MPa T164260618561}{-=σ, N=26.0 -45度 {}MPa T164212854062}{=σ, N=35.65经比较得,N=35.65,所以共需要35.65*2=71.3层(7)当0度铺层占10%,90度铺层占50%时, 45度和-45度各占20% 0度,{}MPa T79325530507}{=σ, N= 12.9590度,{}MPa T5.7936.19028.4691}{--=σ, N= 38.545度,{}MPa T165968521327}{-=σ, N= 15.8 -45度,{}MPa T6.16589.14724888}{=σ, N=14.3经比较得,N=38.5,所以共需要38.5*2=77层(8)当0度铺层占10%,90度铺层占60%时, 则45度和-45度各占15%时 0度 {}M P a T94637832990}{=σ, N=14 90度 {}MPa T2.9463.20863607}{--=σ, N=42.2+45度 {}MPa T172076224781}{-=σ, N=16.3-45度 {}MPa T172017024701}{=σ, N=34.46经比较得,N=42.2,所以共需要42.2*2=84.4层(9)当0度铺层占10%,90度铺层占75%时, 则45度和-45度各占6.25%时 0度 {}M P aT145062239942}{=σ, N=16.95 90度 {}MPa T8.144925721729.6-}{-=σ, N=52.07+45度 {}MPa T196487734490}{-=σ, N=18.7 -45度 {}MPa T5.196323173722}{=σ, N=46.9经比较得,N=52.07,所以共需要52.07*2=104.14层(10)当0度铺层占25%,90度铺层占0%时, 则45度和-45度各占37.5%时 0度 {}M P aT50756820231}{-=σ, N=8.5883 +45度 {}MPa T16329.1-8284.7}{-=σ, N=15.55 -45度 {}MPa T9.16326.4949.2475}{-=σ, N=10.01经比较得,N=15.55,所以共需要15.55*2=31.10层(11)当0度铺层占25%,90度铺层占10%时, 则45度和-45度各占32.5%时 0度 {}M P a T56526519118}{-=σ, N=8.11 90度 {}MPa T5.5635.10725.9458}{--=σ, N=21.71+45度 {}MPa T134712610829}{-=σ, N=13.85 -45度 {}MPa T5.13465.6844.1169}{-=σ, N=12.83经比较得,N=21.71,所以共需要21.71*2=43.42层(12) 当0度铺层占25%,90度铺层占25%时, 则45度和-45度各占25%时 0度,{}MPa T6831819099}{-=σ, N= 8.1 90度,{}MPa T2.68314117.5669}{--=σ, N=23.0945度,{}MPa T116722213964}{-=σ, N=max{5.93,4.5,11.1}=11.1 -45度,{}MPa T1.11676.9006.534}{-=σ, N=max{0.36,18.23,11.1}=18.23经比较得,N=23.09,所以共需要23.09*2=46.18层(13)当0度铺层占25%,90度铺层占50%时, 则45度和-45度各占12.5%时 0度 {}M P aT104722721050}{=σ, N=9.97 90度 {}MPa T10473.13271.2452}{--=σ, N=26.8 +45度 {}MPa T110725720408}{-=σ, N=10.54-45度 {}MPa T110712978.1809}{-=σ, N=26.21 经比较得,N=26.8,所以共需要26.8*2=53.6层(14)当0度铺层占50%,90度铺层占0%时, 则45度和-45度各占25%时 0度 {}M P aT68335712870}{-=σ, N=6.5 90度 {}MPa T 2.6837.4718.9106}{--=σ, N=9.55+45度 {}MPa T6.10351.1823.9131}{--=σ, N=9.86 -45度 {}MPa T6.10356.4967.5367}{-=σ, N=11.05经比较得,N=11.05,所以共需要11.05*2=22.1层(15)当0度铺层占50%,90度铺层占10%时, 则45度和-45度各占20%时 0度 {}M P a T79312712568}{-=σ, N=7.55 90度 {}MPa T793.5-4.7185492.7-}{=σ, N=14.54 +45度 {}MPa T8519811957}{--=σ, N=8.1 -45度 {}MPa T8518.6894882}{-=σ, N=13.96 经比较得,N=14.54,所以共需要14.54*2=29.08层(16)当0度铺层占50%,90度铺层占25%时, 则45度和-45度各占12.5%时 0度 {}M P a T10475212812}{=σ, N=9.9790度 {}MPa T 10474.7839.2819}{--=σ, N=15.85 +45度 {}MPa T73710216105}{--=σ, N=7.01 -45度 {}MPa T6.7366.9379.6112}{-=σ, N=18.97经比较得,N=18.97,所以共需要18.97*2=37.94层需的层数最少,为22层,此时的重量最轻。
复合材料力学计算题

复合材料力学计算题
非常抱歉,我无法给予实时运算的帮助。
但是,我可以为您提供一些复合材料力学计算的基本步骤和原则,以便您自己进行计算。
复合材料力学计算通常涉及以下几个主要方面:
1. 复合材料的弹性力学性能:包括弹性模量、剪切模量和泊松比等。
这些参数可通过试验测定获得,或通过理论模型进行估算。
2. 复合材料的层合板弯曲理论:层合板的弯曲行为可通过柯西方程和空间弯曲理论进行计算。
3. 复合材料的断裂力学:包括拉伸强度、压缩强度、剪切强度等。
这些参数可通过试验测定获得,或通过理论模型进行估算。
4. 复合材料的疲劳行为:复合材料的疲劳寿命可通过疲劳试验和应力分析估算。
常用的疲劳寿命模型有S-N曲线和Crack growth模型等。
5. 复合材料的失效分析:通过强度分析,确定复合材料在给定载荷下是否会发生破坏。
常用的失效分析方法有损伤力学、层内剪切破坏和层间剪切破坏等。
在进行复合材料力学计算时,需要先确定要研究的问题,然后采用合适的理论模型进行计算。
常见的理论模型有经典层合板理论、离散层板理论、三维弹性理论等。
另外,复合材料的力学行为受到其纤维和基体的影响。
常见的纤维包括碳纤维、玻璃纤维和有机纤维等,常见的基体材料包括树脂、金属和陶瓷等。
这些材料的力学性质可以通过试验获
得,或通过已有的数据进行估算。
最后,进行复合材料力学计算时,需要注意选择合适的计算软件或编程语言,如MATLAB、ANSYS、ABAQUS等,以便进行数值计算和模拟。
希望以上信息对您有所帮助!如果您有任何更具体的问题或需要进一步的帮助,请随时提问。
复合材料力学课后答案

复合材料力学课后答案1. 引言。
复合材料是由两种或两种以上的不同材料组合而成的材料,具有优良的综合性能,被广泛应用于航空航天、汽车、建筑等领域。
复合材料力学是研究复合材料在受力作用下的力学性能和行为的学科,对于了解复合材料的性能和设计工程结构具有重要意义。
本文将针对复合材料力学课后习题进行解答,帮助学生加深对复合材料力学的理解。
2. 课后答案。
2.1. 什么是复合材料?复合材料是由两种或两种以上的不同材料组合而成的材料,通过各种方式相互作用形成一种新的材料。
复合材料通常由增强相和基体相组成,增强相起到增强和刚度作用,基体相起到传递载荷和保护增强相的作用。
2.2. 复合材料的分类有哪些?根据增强相的形式,复合材料可以分为颗粒增强复合材料、纤维增强复合材料和层合板复合材料;根据基体相的形式,复合材料可以分为金属基复合材料、塑料基复合材料和陶瓷基复合材料。
2.3. 复合材料的力学性能有哪些?复合材料的力学性能包括强度、刚度、韧性、疲劳性能等。
其中,强度是指材料抵抗外部力量破坏的能力;刚度是指材料抵抗形变的能力;韧性是指材料抵抗断裂的能力;疲劳性能是指材料在循环载荷下的耐久性能。
2.4. 复合材料的力学行为受哪些因素影响?复合材料的力学行为受到多种因素的影响,包括增强相的类型、含量和排布方式,基体相的类型和性能,界面的结合情况,制备工艺等因素都会对复合材料的力学行为产生影响。
2.5. 复合材料的应用领域有哪些?复合材料由于其优良的性能,在航空航天、汽车、建筑、体育器材等领域得到了广泛的应用。
例如,航空航天领域的飞机机身、汽车领域的碳纤维车身、建筑领域的钢-混凝土复合梁等都是复合材料的典型应用。
3. 结论。
通过对复合材料力学课后习题的解答,可以加深学生对复合材料力学的理解,帮助他们更好地掌握复合材料的基本概念、分类、力学性能、影响因素和应用领域。
同时,也可以引导学生将理论知识应用到实际工程中,为未来的工程实践打下坚实的基础。
复合材料力学上机作业

《复合材料力学》课程上机指导书(力学121-2)河北工业大学机械学院力学系2015年9月目录作业1 单向板刚度及柔度的计算 (1)作业2 单向板的应力、应变计算 (2)作业3 绘制表观工程常数随 的变化规律 (3)作业4 绘制强度准则的理论曲线(包络线) (4)作业5 层合板的刚度计算 (5)作业6 层合板的强度计算 (6)附录作业提交说明……………………………………………. . 7作业1 单向板刚度及柔度的计算一、要 求(1)选用FORTRAN 、VB 、MAPLE 或MATLAB 编程计算下列各题;(2)上机报告内容:源程序、题目内容及计算结果;(3)材料工程常数的数值参考教材自己选择;(4)上机学时:2学时。
二、题 目1、已知单层板材料工程常数1E ,2E ,12G ,计算柔度矩阵[S ]和刚度矩阵[Q ]。
(玻璃/环氧树脂单层板材料的M Pa 1090.341⨯=E ,M Pa 1030.142⨯=E ,M Pa 1042.0412⨯=G ,25.021=μ)2、已知单层板材料工程常数1E ,2E ,12G ,21μ及θ,计算柔度矩阵][S 和刚度矩阵][Q 。
(M Pa 1090.341⨯=E ,M Pa 1030.142⨯=E ,M Pa 1042.0412⨯=G ,25.021=μ,︒=30θ)作业2 单向板的应力、应变计算一、要 求1、选用FORTRAN 、VB 、MAPLE 或MATLAB 编程计算下列各题;2、上机报告内容:源程序、题目内容及计算结果;3、材料工程常数的数值请参考教材, 自己选择;4、上机学时:2学时。
二、题 目1、已知单层板的应力x σ、y σ、xy τ,工程常数1E ,2E ,12G ,21μ及θ,求x ε、y ε、xy γ;1σ、2σ、12τ;1ε、2ε、12γ。
(知︒=30θ,应力M Pa 160=x σ,M Pa 60=y σ,M Pa 20=xy τ,工程常数M Pa 1090.341⨯=E ,M Pa 1030.142⨯=E ,M Pa 1042.0412⨯=G ,25.021=μ,︒=30θ)2、已知1σ、2σ、12τ,工程常数1E ,2E ,12G ,21μ及θ,求1ε、2ε、12γ;x ε、y ε、xy γ;x σ、y σ、xy τ。
复合材料力学行为研究实验(有试件图)

复合材料力学行为研究实验一般材料力学研究的是均匀分布、各向同性的材料,但是现在又出现了并且在工程上越来越广泛使用的一种材料叫复合材料。
它是一种各向异性材料。
复合材料是两种或两种以上不同性能的材料用物理或化学方法制成的具有新性能的材料,一般复合材料的性能优于其组分材料的性能。
复合材料在力学行为上有什么特点,各向异性表现在哪些方面?各向异性材料如何测量它的弹性常数,不同纤维铺层方向和不同加载方向的力学性能有何差别,什么是沿轴性态和离轴性态?… 为了便于学生研究探讨这些问题,我们专门加工了一种增强材料沿单向铺层的复合材料板(如图1所示)。
由于是单向增强,所以回避了许多复合材料研究上的复杂问题。
图1 单层复合材料构造形式 图2 坐标定义本试验主要研究的具体材料是玻璃纤维单向增强复合材料。
玻璃纤维的弹性模量约为80~85GPa, 基体是环氧树脂,其弹性模量约为3~5Gpa 。
其纤维与环氧树脂的体积比约为1:1。
同时还提供了双向增强复合材料(正交增强),其两个方向纤维的比例为18:14和部分金属材料。
一.实验原理和试验方法材料的弹性常数是描述材料力学性能的一项基本参数。
作为衡量材料的刚度和弹性变形行为的特征值,它是理论计算和工程设计中一项非常重要的指标。
我们熟知的材料,比如金属材料都是各向同性材料,独立的弹性常数是两个,即扬氏弹性模量E 和泊松比υ(或剪切弹性模量G)。
而复合材料,由于其突出的各向异性的性质,独立的弹性常数增加了。
为了测定复合材料的弹性常数, 将被测材料加工为纤维与加载方向成0°、45°和90°的三种试件。
每种试件的三个方向的应变即纵向应变、横向应变和45゜方向的应变均采用粘贴电阻片的方法测量。
应变片信号按一定的组桥方式接到测量电桥上,可利用数字静态应变仪直接定点读取应变信号或利用数据采集系统自动纪录载荷、应变数据。
对实验数据进行线性回归的处理,按下列公式计算出复合材料的弹性常数:0°试件:111εσ=E 1212εε-=μX σX XY 2390°试件: 222εσ=E 2112εε-=μ45°试件: )(24512Y X G ε-εσ= 坐标的定义如图2表示。
复合材料力学大作业

二零一六年——二零一七年第一学期复合材料力学实验报告实验名称:层合板的强度分析班级:工程力学13-2班姓名:刘志强学号: 02130857指导教师:董纪伟层合板的强度分析问题:有三层对称正交铺设层合板,总厚度为t ,外层厚12t ,内层厚t 65,材料为硼/环氧,受轴向拉力x N 作用,MPa E 51100.2⨯=,MPa E 42100.2⨯=,30.021=v ,MPa G 312106⨯=,MPa X t 3100.1⨯=,MPa X c 3100.2⨯=,MPa Y t 2100.6⨯=,MPa Y c 200=,MPa S 60=,试求层合板极限载荷)/(t N x 。
解:1,开始破坏时的“屈服”强度值:(1)计算ij ij Q A 和: 由:)(t)(1051.71,3341'得MPa A A A ⨯==-(2)求000,,xyy x γεε (3)求各层应力(4)用Hill-蔡强度理论求第一个屈服载荷强度理论表达式:将上述数据代入解得:显然第一、三层先破坏,即N x /t=252.3MPa 为第一屈服载荷,此时:各层应力为:2、进行第二次计算:(1)求削弱后的复合板刚度: 其中第一、三层板材料第一主方向破坏后,[]MPaQ 43,11000002.01810000⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=不能抗剪,故Q=0,继续计算复合板刚度A:66(2)、求应变和应力:(3)、由Hill-蔡强度理论得:/t=500.5代入第二层求得应力:将Nx即第二层第二主方向破坏,因此层合板在N方向全部破坏,层合板不能继续承x受载荷。
三层对称正交铺设层合板轴向拉伸ANSYS模拟1,定义单元类型:进入前处理,选择添加shell linear layer 99单元,如图:图1:定义shell99单元2,设置单元属性:关闭Labrary of Element Types窗口,打开options设置单元属性:在k8的下拉窗口选择All layers,如图:图2:设置单元属性3,添加单元实常数:关闭添加单元窗口,打开添加实常数窗口,给shell99添加厚度、层合信息。
14-15第一学期复合材料力学卷A

中国矿业大学2014~2015学年第 一 学期《 复合材料力学 》试卷(A )卷考试时间:100分钟 考试方式:开卷学院 力建学院 班级 姓名 学号一、计算题(15分)已知碳/环氧单层复合材料的工程弹性常数为:1200GPa E =,220GPa E =,210.25ν=,1210GPa G =,求柔度系数ij S 。
若材料主方向的应力状态为:1100MPa σ=,250MPa σ=,1230MPa τ=-,求应变1ε,2ε,12γ。
某复合材料单层板受力后发生面内变形,0.3%x ε=,0.2%y ε=,0.1%xy γ=,纤维与x 轴的夹角45θ=?。
其工程弹性常数为:160GPa E =,210GPa E =,210.30ν=,128GPa G =,求该材料在主方向的应力1σ,2σ,12τ。
如图所示,复合材料单层板承受偏轴向压缩,纤维与x 轴的夹角60θ=?,80MPa y σ=-。
强度参数为:t 1200MPa X =,c 1200MPa X =,t 50MPa Y =,c 200MPa Y =,70MPa S =。
试用最大应力理论和Hill-蔡强度理论校核其是否安全。
已知玻璃/环氧单向复合材料,玻璃纤维的f 80GPa E =,f 0.25ν=,环氧树脂的m 0.35ν=,纤维体积含量f 60%c =。
该复合材料的纵向弹性模量150GPa E =,试用串联和并联模型计算2E 、21ν和12ν。
五、计算题(25分)如图,正交铺设对称层合板()s 0/90鞍,单层厚度1mm k t =,已知:单层的正轴刚度矩阵[]120404200GPa 0010Q 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫。
求:(1)层合板的拉伸和弯曲刚度矩阵;(2) 层合板沿y 方向受拉伸,100N/mm =y N ,求90˚铺层主方向的应力1σ,2σ,12τ。
复合材料力学试题

复合材料力学试题答案判断题(正确的在括弧内划√,错误的在括弧内划×)。
1.“宏观力学”是在研究复合材料力学性能时,假定材料是均质的。
(√)2.单层是层合板的基本单元,在复合材料结构设计中又叫做三次结构。
(×)3.层合板由若干具体不同纤维方向的单层叠合而成,在复合材料机构设计中又叫二次结构。
(√)4.复合材料力学中,1为纵向,2为横向,应力规定拉为负,压为正。
(×)5.在单层板(正交各向异性)材料中,τ12不仅形成剪切变形,还存在剪拉耦合效应。
(×)6.在单层正交各向异性板中,11)1(11σεE =。
(√) 7.在单层正交各向异性板中,11122)1(2)2(221συσεεεE E -=+=。
(√) 8.单层板的工程弹性常数有5个,且相互独立。
(×)9.柔量矩阵{S}是对称矩阵,而模量举证{Q}不是对称矩阵。
(×)10.在正交单层板中,Q16=Q26=0,Q61=Q62,但其值不为零。
(×)11.在复合材料力学中,对于工程弹性常数存在如下关系:2121υυ=E E 。
(√) 12.在单层板偏轴刚度中,应力转换和应变转换关系式中,m=sin θ,n=cos θ。
(×)13. 在单层板偏轴刚度中,应力转换和应变转换关系式中存在如下关系:[][][]T T T 1-=σε。
(√)14.在ij Q 中,11Q 、22Q 是θ的偶函数,16Q 、26Q 也是θ的偶函数。
(×) 15.玻璃钢复合材料在拉伸时发生变形,所以是一种塑性材料。
(×)16.利用复合材料的强度准则,可以判断复合材料设计过程的安全性,同时可以计算极限载荷。
(×)17.利用最大应力准则判断材料安全性时,如果判断式大于1,说明材料的机构是安全的。
(×)18.在复合材料中,利用强度比可以计算复合材料的极限载荷。
(√)20.在对称层合板中,)()(z z --=θθ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复合材料力学上机作业(2013年秋季)班级力学C102学生姓名赵玉鹰学号105634成绩河北工业大学机械学院2013年12月30日作业1 单向板刚度及柔度的计算一、要 求(1)选用FORTRAN 、VB 、MAPLE 或MATLAB 编程计算下列各题;(2)上机报告内容:源程序、题目内容及计算结果;(3)材料工程常数的数值参考教材自己选择;(4)上机学时:2学时。
二、题 目1、已知单层板材料工程常数1E ,2E ,12G ,计算柔度矩阵[S ]和刚度矩阵[Q ]。
(玻璃/环氧树脂单层板材料的MPa 1090.341⨯=E ,MPa 1030.142⨯=E ,MPa 1042.0412⨯=G ,25.021=μ,MPa 1001=σ,MPa 302-=σ,MPa 1012=τ) ●Maple 程序> restart:> with(linalg):> E[1]:=3.9e10:> E[2]:=1.3e10:> G[12]:=0.42e10:> mu[21]:=0.25:> mu[12]:=E[1]*mu[21]/E[2]:> Q[11]:=E[1]/(1-mu[12]*mu[21]):> Q[12]:=mu[12]*E[2]/(1-mu[12]*mu[21]):> Q[13]:=0:> Q[21]:=Q[12]:> Q[22]:=E[2]/(1-mu[12]*mu[21]):> Q[23]:=0:> Q[31]:=Q[13]:> Q[32]:=Q[23]:> Q[33]:=G[12]:>Q:=evalf(matrix(3,3,[[Q[11],Q[12],Q[13]],[Q[21],Q[22],Q[23]],[Q[31],Q[32],Q[33]]]),4);:= Q ⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.48001011.120010110..12001011.160010110.0.0..421010> S[11]:=1/E[1]:> S[12]:=-mu[21]/E[2]:> S[13]:=0:> S[23]:=0:> S[21]:=-mu[12]/E[1]:> S[22]:=1/E[2]:> S[33]:=1/G[12]:> S[32]:=S[23]:> S[31]:=S[13]:>S:=evalf(matrix(3,3,[[S[11],S[12],S[13]],[S[21],S[22],S[23]],[S[31],S[32],S[33]]]),4);:= S ⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.256410-10-.192310-100.-.192310-10.769210-10-0.0.-0..238110-9答:刚度矩阵:= Q ⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.48001011.120010110..12001011.160010110.0.0..421010, 柔度矩阵:= S ⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.256410-10-.192310-100.-.192310-10.769210-10-0.0.-0..238110-9。
2、已知单层板材料工程常数1E ,2E ,12G ,21μ及θ,计算柔度矩阵][S 和刚度矩阵][Q 。
(M P a 1090.341⨯=E ,MPa 1030.142⨯=E ,MPa 1042.0412⨯=G ,25.021=μ,︒=30θ)●Maple 程序> restart:> With(linalg):> E[1]:=3.9e10:> E[2]:=1.3e10:> G[12]:=0.42e10:> mu[21]:=0.25:> theta:=Pi/6:> mu[12]:=E[1]*mu[21]/E[2]:> Q[11]:=E[1]/(1-mu[12]*mu[21]):> Q[12]:=mu[12]*E[2]/(1-mu[12]*mu[21]):> Q[16]:=0:> Q[21]:=Q[12]:> Q[22]:=E[2]/(1-mu[12]*mu[21]):> Q[26]:=0:> Q[61]:=Q[16]:> Q[62]:=Q[26]:> Q[66]:=G[12]:>Q:=matrix(3,3,[[Q[11],Q[12],Q[16]],[Q[21],Q[22],Q[26]], [Q[61],Q[62],Q[66]]]):> S:=inverse(Q):> T[sigma11]:=(cos(theta))^2:> T[sigma12]:=(sin(theta))^2:> T[sigma16]:=-2*sin(theta)*cos(theta):> T[sigma21]:=(sin(theta))^2:> T[sigma22]:=(cos(theta))^2:> T[sigma26]:=2*sin(theta)*cos(theta):> T[sigma61]:=sin(theta)*cos(theta):> T[sigma62]:=-sin(theta)*cos(theta):> T[sigma66]:=(cos(theta))^2-(sin(theta))^2:>T[sigma]:=matrix(3,3,[[T[sigma11],T[sigma12],T[sigma16]],[T[sigma21],T[sigma22],T[sigma26]],[T[sigma61],T[sigma62],T[sigma66]]]):> T[sigma1]:=inverse(T[sigma]):> T[epsilon11]:=(cos(theta))^2:> T[epsilon12]:=(sin(theta))^2:> T[epsilon16]:=sin(theta)*cos(theta):> T[epsilon21]:=(sin(theta))^2:> T[epsilon22]:=(cos(theta))^2:> T[epsilon26]:=-sin(theta)*cos(theta):> T[epsilon61]:=-2*sin(theta)*cos(theta):> T[epsilon62]:=2*sin(theta)*cos(theta):> T[epsilon66]:=(cos(theta))^2-(sin(theta))^2:>T[epsilon]:=matrix(3,3,[[T[epsilon11],T[epsilon12],T[epsilon16]],[T[epsilon21],T[epsilon22],T[epsilon26]],[T[epsilon61],T[epsilon62],T[epsilon66]]]):> Q1:=evalf(evalm(T[sigma1]&*Q&*T[epsilon]),4);:= Q1⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.60211011.39711011.25011011.39731011.23921011.64081010-.25031011-.64081010-.11921011 > S1:=evalf(inverse(Q1),4);:= S1⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥-.384110-10.492710-10-.541010-10.493010-10-.144310-10.956710-10.541610-10-.957210-10-.217210-10 答:柔度矩阵][S : := S1⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥-.384110-10.492710-10-.541010-10.493010-10-.144310-10.956710-10.541610-10-.957210-10-.217210-10 刚度矩阵][Q : := Q1⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.60211011.39711011.25011011.39731011.23921011.64081010-.25031011-.64081010-.11921011作业2 单向板的应力、应变计算一、要 求1、选用FORTRAN 、VB 、MAPLE 或MATLAB 编程计算下列各题;2、上机报告内容:源程序、题目内容及计算结果;3、材料工程常数的数值参考教材自己选择;4、上机学时:2学时。
二、题 目1、已知单向板的应力x σ、y σ、xy τ,工程常数1E ,2E ,12G ,21μ及θ,求x ε、y ε、xy γ;1σ、2σ、12τ;1ε、2ε、12γ。
(知︒=30θ,应力MPa 160=x σ,MPa 60=y σ,MPa 20=xy τ,工程常数MPa 1090.341⨯=E ,MPa 1030.142⨯=E ,MPa 1042.0412⨯=G ,25.021=μ,︒=30θ)●Maple 程序> restart:> With(linalg):> E[1]:=3.9e10:> E[2]:=1.3e10:> G[12]:=0.42e10:> mu[21]:=0.25:> theta:=Pi/6:> mu[12]:=E[1]*mu[21]/E[2]:> Q[11]:=E[1]/(1-mu[12]*mu[21]):> Q[12]:=mu[12]*E[2]/(1-mu[12]*mu[21]):> Q[13]:=0:> Q[21]:=Q[12]:> Q[22]:=E[2]/(1-mu[12]*mu[21]):> Q[23]:=0:> Q[31]:=Q[13]:> Q[32]:=Q[23]:> Q[33]:=G[12]:>Q:=matrix(3,3,[[Q[11],Q[12],Q[13]],[Q[21],Q[22],Q[23]],[Q[31],Q[32],Q[33]]]):> T[sigma11]:=(cos(theta))^2:> T[sigma12]:=(sin(theta))^2:> T[sigma13]:=-2*sin(theta)*cos(theta):> T[sigma21]:=(sin(theta))^2:> T[sigma22]:=(cos(theta))^2:> T[sigma23]:=2*sin(theta)*cos(theta):> T[sigma31]:=sin(theta)*cos(theta):> T[sigma32]:=-sin(theta)*cos(theta):> T[sigma33]:=(cos(theta))^2-(sin(theta))^2:>T[sigma]:=matrix(3,3,[[T[sigma11],T[sigma12],T[sigma13]],[T[sigma21],T[sigma22],T[sigma23]],[T[sigma31],T[sigma32],T[sigma33]]]):> T[epsilon11]:=(cos(theta))^2:> T[epsilon12]:=(sin(theta))^2:> T[epsilon13]:=sin(theta)*cos(theta):> T[epsilon21]:=(sin(theta))^2:> T[epsilon22]:=(cos(theta))^2:> T[epsilon23]:=-sin(theta)*cos(theta):> T[epsilon31]:=-2*sin(theta)*cos(theta):> T[epsilon32]:=2*sin(theta)*cos(theta):> T[epsilon33]:=(cos(theta))^2-(sin(theta))^2:>T[epsilon]:=matrix(3,3,[[T[epsilon11],T[epsilon12],T[epsilon13]],[T[epsilon21],T[epsilon22],T[epsilon23]],[T[epsilon31],T[epsilon32],T[epsilon33]]]):> sigma[x]:=160:> sigma[y]:=60:> tau[xy]:=20:> sigma[a]:=matrix(3,1,[sigma[x],sigma[y],tau[xy]]): > sigma[zhu]:=evalf(evalm(T[sigma]&*sigma[a]),4);:= σzhu ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥117.7102.353.30 > Qni:=inverse(Q):> epsilon[zhu]:=evalf(evalm(Qni&*sigma[zhu]),4);>:= εzhu ⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥.105110-8.560610-8.126910-7 > Tni[epsilon]:=inverse(T[epsilon]):> epsilon[a]:=evalf(evalm(Tni[epsilon]&*epsilon[zhu]),4);:= εa ⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥-.330410-8.996110-8.240010-8 答:=m,=Pa ,=。
