Lingo的基本用法
LINGO应用教程
第十章 LINGOLingo 软件是求解线性规划、非线性规划的数学软件,也可用于一些线性和非线性方程组的求解等。
Lingo 实际上也是最优化问题的一种建模语言,包括许多常用的数学函数供使用者建立优化模型时调用,并可以接受与其他数据文件交换数据。
第一节 LINGO 软件的基本使用方法1.1 LINGO 使用入门在windows 操作系统下启动LINGO 后,将进入LINGO 集成环境,包括主框架窗口和模型窗口两部分。
主框架窗口集成了菜单和命令按钮,模型窗口用于输入模型。
例1 求解数学模型12121212max 23..4310351200x x s t x x x x x x ++≤+≤≥≥解:在模型窗口输入LINGO 求解模型如下:输入模型后选择菜单LINGO|Solve 或者按工具栏的,LINGO开始编译模型,如有语法错误将返回一个错误的消息并指明错误出现的位置;如果通过编译,LINGO将激活Solver运算器寻求模型的最优解,首先出现Solver Status状态窗口显示模型求解的运算状态信息:状态窗口显示的信息含义如下:“Global optimal solution found”表示得到全局最优解。
“Objective value: 7.454545”表示最优目标值为7.454545。
“Total solver iterations:2” 表示迭代2次得到结果。
“V alue”给出最优解中各变量的值:x1=1.272727,x2=1.636364。
Reduced Cost 值列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时,目标函数的变化率。
其中基变量的reduced cost值应为0,对于非基变量xj,相应的reduced cost值表示当某个变量xj 增加一个单位时目标函数减少的量( max型问题)。
本例中此值均为0。
SLACK OR SURPLUS值给出约束条件的松驰变量或剩余变量的值。
Lingo基本用法总结
Lingo基本用法总结(除集函数部分)LINGO是用来求解线性和非线性优化问题的简易工具。
Lingo免费版可以支持30个未知数,lingo破解版可以支持几万个未知数、几万个约束条件。
当你在windows下开始运行LINGO系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO中求解如下的LP问题:在模型窗口中输入如下代码:min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击工具条上的按钮即可。
得到如下结果:所以当x1为250,x2为100时目标函数得到最大值。
算术运算符Lingo 中变量不区分大小写,以字母开头不超过32个字符算术运算符是针对数值进行操作的。
LINGO 提供了5种二元运算符: ^ 乘方 ﹡ 乘 / 除 ﹢ 加 ﹣ 减 LINGO 唯一的一元算术运算符是取反函数“﹣”。
这些运算符的优先级由高到底为:高 ﹣(取反) ^ ﹡/ 低 ﹢﹣运算符的运算次序为从左到右按优先级高低来执行。
运算的次序可以用圆括号“()”来改变。
例:在x1+x2>=350,x1>=100,2*x1+x2<=600的条件下求2*x1+3*x2的最小值 在代码窗口中编写 min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后单击上面菜单lingo 菜单下solve 键即可。
数学函数标准数学函数:@abs(x) 返回x 的绝对值@sin(x) 返回x 的正弦值,x 采用弧度制 @cos(x) 返回x 的余弦值 @tan(x) 返回x 的正切值 @exp(x) 返回常数e 的x 次方 @log(x) 返回x 的自然对数@lgm(x) 返回x 的gamma 函数的自然对数 @sign(x) 如果x<0返回-1;否则,返回1@floor(x) 返回x 的整数部分。
Lingo的基本用法

例2:基金的优化使用(2001年建模竞赛C题)
假设某校基金会得到了一笔数额为M万元的基金, 打算将其存入银行,校基金会计划在n年用部分本 息奖励优秀师生,要求每年的奖金额相同,且在n 年仍保留原基金数额.银行存款税后年利率表如下:
银行存款税后利率表 存期 税后年利率% 1年 1.8 2年 2.16 3年 2.592 5年 2.88
解:设两种产品的生产量分别为 x1 和 x2 , 则该问题的数学模型为: 目标函数:max z = 200 x1 + 300 x2
x1 ≤ 100 x ≤ 120 2 约束条件: x1 + 2 x2 ≤ 160 xi ≥ 0, i = 1, 2
在Model窗口内输入如下模型: max=200*x1+300*x2; x1<=100; x2<=120; x1+2*x2<=160; 注:Lingo默认所有的决策变量都非负,因 而变量非负条件可以不必输入.
Lingo的主要功能特色:
既能求解线性规划问题,也有较强的求解非线性规 划问题的能力; 输入模型简练直观; 运行速度快,计算能力强; 内置建模语言,提供几十个内部函数,从而能以较 少语句,较直观的方式描述较大的优化模型; 将集合的概念引入编程语言,很容易将实际问题转 化为lingo模型; 能方便的与Excel,数据库等其他软件交换数据.
Lingo的语法规定:
求目标函数的最大值或最小值分别用"max="或"min= "来 表示; 每个语句必须以分号";"结束,每行可以有多个语句,语 句可以跨行; 每个语句必须以字母开头,由字母,数字和下划线所组成, 长度不超过32个字符,不区分大小写; 可以给语句加上标号,例如[OBJ] max=200*x1+300*x2; 以!开头,以;结束的语句是注释语句; 如果对变量的取值范围没有作特殊说明,则默认所有决策变 量都非负; Lingo模型以语句"Model:"开头,以"End"结束,对于 比较简单的模型,这两个语句可以省略.
第3讲LINGO基本使用方法

新余学院 建模组
目前为止找到的可行 解的最佳目标函数值
有效步数
目标函数值的界
特殊求解程序当前运行步数: 分枝数(对B-and-B程序); 子问题数(对Global程序); 初始点数(对Multistart程序)
上一页
下一页
Xinyu University MCM
优优优化化化建建建模模模
(2) min z 3x1 2x2 x3
s.t. 2x1 x2 x3 5, 4x1 3x2 x3 3 x1 x2 x3 2 x1, x2 , x3 0
2020/1/15
新余学院 建模组
上一页
下一页
Xinyu University MCM
二、在LINGO中使用集合
注意:用“[]”表示该部分内容可选。下同,不再赘述。
2020/1/15
新余学院 建模组
上一页
下一页
Xinyu University MCM
优优优化化化建建建模模模
例语1法可:以定se义tn一a个m名e[为/mstuedmenbts的er原_l始is集t/,][它:a具tt有ri成bu员tJeo_hlni、stJ]i;ll、Rose和Mike
MonthM..MonthN Jill 0 Oc1t4..Ja按n 列赋值 Oct,Nov,Dec,Jan
Rose 0 17 MonthYearM..MonthYeMariNkeOc1t201031.;.Jan2002
Oct2001,Nov2001,Dec2001 ,Jan2002
enddata
③ 集成员不放在集定义中,而在随后的数据部分来定义。
2020/1/15
新余学院 建模组
lingo基本用法

lingo基本用法以下是 9 条关于“lingo 基本用法”的内容:1. 嘿,你知道吗,lingo 里的变量定义可简单啦!就像给东西起个名字一样自然。
比如说,咱要算一堆苹果的数量,那就可以设个变量叫apple_num 呀,这不就清楚明白啦!2. 哇塞,lingo 的约束条件就像是给问题加上规矩。
就好比说,规定一个房间最多能进 10 个人,这就是个约束呀。
比如限制某种资源不能超过多少,lingo 就能很好地处理呢!3. 哎呀呀,lingo 的目标函数那可重要了!这就好比是你要去追求的目标。
比如你想让利润最大化,那目标函数就是让利润相关的表达式达到最大呀!像算怎么卖东西能赚最多钱,lingo 就能帮你找到答案哟!4. 嘿,lingo 的表达式书写也不难呢!就像写个数学式子一样。
比如 2x +3y 这么简单明了。
要计算一些关系,用它来写表达式再合适不过了!5. 哇哦,lingo 里的集合定义多有意思啊!像是把一群相关的东西归到一起。
比如把不同类型的商品归成一个集合,然后对它们进行统一的处理呀,是不是很方便呀?6. 哎呀,lingo 的求解命令一敲,就等着答案出来啦!就像你按下按钮,机器就开始工作一样。
你看,多神奇啊,一下子就知道结果了呢!7. 嘿,lingo 还能处理复杂的数据呢!就像一个聪明的小助手,不管多乱的数据它都能理清楚。
比如算一大堆乱七八糟数字的关系,lingo 绝对能应付得来呀!8. 哇,lingo 的模型建立虽然要动点脑筋,但一旦建好了,那可太好用啦!就跟盖房子一样,辛苦一点,盖好了住着就舒服啦。
你想想,自己建的模型能用起来,多有成就感呀!9. 哎呀呀,掌握了 lingo 的基本用法,那真的是能解决好多问题呢!不管是算数量还是优化方案,都不在话下。
所以呀,还不赶紧去学学,让它为你服。
Lingo的基本应用
第十五章Lingo的基本应用1、LINDO和LINGO软件能求解的模型:2、Lingo初级语法:语句分行书写,顺序与数学模型一致;每一条语句都要以“;”结尾;语句不区分大小写,书写方式与代数函数相近;目标函数以“min=”或者“max=”表示;注释语句用“!”开头;“>”和“>=”以及“<”和“<=”没有区别;如果不写明决策变量的取值范围,则默认为非负实数。
3、线性规划案例:生产计划每天:50桶牛奶时间480小时至多加工100公斤A1 要求:制订生产计划,使每天获利最大1)奶制品生产的Lingo模型2)Lingo求解2)Lingo求解报告//结果报告(Solution Report)4)开启灵敏度分析(Range)功能5)查看灵敏度分析(Range)必须先求解才能得到灵敏度分析报告//目标函数系数范围分析当目标函数中x1的系数(产品A1的收益)增加不超过8个单位或者减少不超过2.66667个单位时(x2系数维持不变),不需改变生产计划。
//约束条件右边值灵敏度分析如果牛奶资源的数量增加不超过10桶或者减少不超过6.666667桶(其他模型参数不变),则它将仍然作为紧缺资源;如果A1生产资源减少超过40个单位(其他模型参数不变),则它将转化为紧缺资源。
4、城市垃圾处理问题(最小吨*公里)小区供水问题(最大供水收益)代数式线性规划模型(垃圾运输)代数式线性规划模型(小区供水)5、如何表示具有下标的变量:1)从C语言的类比来理解:2)具有下标的变量可以看作某种数组变量中的元素;3)除去下标后的符号可以看作是数组变量的名称;4)下标可以看作是在数组中的索引值;5)单下标变量对应于一个一维数组,称为“简单集合”;6)多下标变量对应于一个多维数组,而多维数组可以看作是多个一维数组的笛卡尔积,称为“派生集合”。
6、Lingo中如何定义具有下标的变量?1)在Lingo中使用“集合变量”的形式表达规划模型中具有下标的变量2)定义集合变量需要三个基本要素:集合的名称集合的形式(简单集合还是派生集合?集合的元素个数是多少?)集合变量的名称7、定义简单集合的语法:集合名称/下标范围/: 变量列表;(变量之间用“,”分隔)例:brand/1..6/: a, b;(集合的名称是brand,/1..6/表示这种集合包含6个元素,下标的范围是从1到6,并且定义了两个这种集合形式的变量分别用a、b表示,该语句相当于定义了a1~a6以及b1~b6两组变量)例:type/1..4/;(也可以只定义集合形式不定义集合变量)8、定义派生集合的语法:集合名称(分量集合列表): 变量列表;1)分量集合列表分别对应于派生集合的每一个维度,定义了每一个维度分别属于哪一种简单集合2)例:product(brand, type): p, x;(集合的名称是product,该集合的第一个维度与brand集合的类型相同,第二个维度与type 集合的类型相同,并且定义了两个集合变量p和x。
LINGO基本用法与运算函数

例如,目标函数中有求和表达式ΣCijXij(i从1 到10,j从1到20),若用直接输入的方式,将有 200个系数与200个变量相乘再相加,需要输入 长长一大串,既不便于输入,又不便于修改, 别人看不懂,可读性较差.
LINGO提供了建模语言,能够用较少语 句描述目标函数和约束条件,为建立大规 模数学规划模型提供了方便.我们以一个 运输规划模型为例说明其用法。
办法是用现成软件求解.LINGO是专门
用来求解各种规划问题的软件包,其功
能十分强大,是解决最优化问题的最佳
选择。
LINGO的基本用法和运算 函数
§1.1 LINGO 入门
LINGO的基本用法和运算 函数
一、概况
LINGO 是 美 国 LINDO 系 统 公 司 ( Lindo SystemInc)开发的求解数学规划系列软件中的一 个(其它软件为LINDO,GINO,What’s Best等 等),的主要功能是求解大型线性、非线性和整数 规 划 , 目 前 的 版 本 是 11.0 . 可 以 从 Internet 网 址 http://下载该软件的安装文件lingo11.exe,执行该 文件即可在计算机内安装LINGO 软件系统,首次 运行该软件时,要求用户输入密码,如果输入了正 确的密码,则该软件就成了正式版,如果密码不对 或不输入密码,则该软件就成为演示版.
1.目标函数(求某个数学表达式的最大值或最 小值);
2. 决策变量,即目标函数值取决于哪些变量;
3. 约束条件,即对变量附加一些条件限制(等 式或不等式).
LINGO的基本用法和运算 函数
例1:某工厂有两条生产线,分别用来生产 M和P两种型号的产品,利润分别为200元/个 和300元/个,生产线的最大生产能力分别为 每日100和120,生产线每生产一个M产品需 要1个劳动日进行调试、检测等工作,而每个 P产品需要2个劳动日,该厂每天只有160个 劳动日可用,假如原材料等其它条件不受限 制,问应如何安排生产计划,使获得的利润 最大?
LINGO简易用法

LINGO 是用来求解线性和非线性运筹学优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LING 高效的求解器可快速求解并分析结果。
1、LINGO快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1 的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例 1.1 如何在LINGO 中求解如下的LP 问题:在模型窗口中输入如下代码:然后点击工具条上的按钮a134 即可。
例 1.2使用LINGO软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如下表。
使用LINGO 软件,编制程序如下:然后点击工具条上的按钮a134 即可。
2、LINGO中的集对实际问题建模的时候,总会遇到一群或多群相联系的对象,比如工厂、消费者群体、交通工具和雇工等等。
LINGO 允许把这些相联系的对象聚合成集(sets)。
一旦把对象聚合成集,就可以利用集来最大限度的发挥LINGO建模语言的优势。
现在我们将深入介绍如何创建集,并用数据初始化集的属性。
学完本节后,你对基于建模技术的集如何引入模型会有一个基本的理解。
2.1 为什么使用集集是LINGO建模语言的基础,是程序设计最强有力的基本构件。
借助于集,能够用一个单一的、长的、简明的复合公式表示一系列相似的约束,从而可以快速方便地表达规模较大的模型。
2.2 什么是集集是一群相联系的对象,这些对象也称为集的成员。
一个集可能是一系列产品、卡车或雇员。
每个集成员可能有一个或多个与之有关联的特征,我们把这些特征称为属性。
属性值可以预先给定,也可以是未知的,有待于LINGO求解。
LINGO 有两种类型的集:原始集(primitive set)和派生集(derived set)。
LINGO用法
域名
含义
可能的显示
Model Class
当前模型的类 型
LP,QP,ILP,IQP,PILP, PIQP,NLP, INLP,PINLP (以I开头表示IP,以PI开 头表示PIP)
"Global Optimum", "Local Optimum",
State
"Feasible", "Infeasible"(不可行), 当前解的状态 "Unbounded"(无界),
"Interrupted"(中断),
"Undetermined"(未确定)
Objective
当前解的目标 函数值
实数
当前约束不满 Infeasibility足是的不总满量足(的不约
束的个数)
实数(即使该值=0,当前解也可能不可 行,因为这个量中没有考虑用上下界形式 给出的约束)
Iterations
目前为止的迭 代次数
例1.1 如何在LINGO中求解如下的LP问题: 在模型窗口中输入如下代码: min=2*x1+3*x2; x1+x2>=350; x1>=100;
2*x1+x2<=600;
然后点击工具条上的按钮 即可。 >=和<=可写成>和< 一个表达式可写成多行,如 min=2*x1 +3*x2; LINGO WINDOWS命令
变量框(Variables)
Total显示当前模型的全部变量数,Nonlinear显示其中的非线性变
量数,Integers显示其中的整数变量数。非线性变量是指它至少处于某
LINGO使用说明

LINGO使用说明一、LINGO的基本特性1.建模语言:LINGO使用一种直观的建模语言,被称为LINGO语言,它使用简洁的语法和自然语言类似的表达方式,使用户能够轻松地描述问题。
2.线性优化:LINGO支持线性规划(LP)和整数线性规划(ILP),它的线性优化功能包括线性约束、线性目标函数和变量定义,可以解决诸如生产优化、资源分配等问题。
3.非线性优化:LINGO还支持非线性规划(NLP)和全局优化(GLO),可以解决包括非线性约束和非线性目标函数的问题。
它提供了多种求解方法和算法,如牛顿法、逐次线性规划等。
4.约束和限制:LINGO能够处理各种类型的约束和限制,包括等式约束、不等式约束、逻辑约束等。
用户可以根据具体问题定义约束,LINGO会自动处理约束的完整性和一致性。
5.求解器:LINGO内置了一系列高效的求解器,如线性规划求解器、非线性规划求解器、整数规划求解器等。
用户可以根据问题的复杂程度选择最适合的求解器。
6.结果分析:LINGO可以生成详细的结果报告,包括优化解、约束条件、目标函数值等。
用户可以通过结果报告来分析问题的解决方案,做出决策。
二、LINGO的使用方法2.创建模型:在LINGO中,用户需要先创建一个模型文件,来描述问题。
可以通过鼠标点击“新建模型”按钮或选择文件菜单中的“新建”选项来创建一个新的模型文件。
3.定义变量:在模型文件中,用户可以定义变量。
变量可以是整数、二进制或连续的,并为每个变量分配一个名称、类型和取值范围。
4.定义目标函数:在模型文件中,用户可以定义一个目标函数。
目标函数可以是线性的或非线性的,并定义在变量上。
5.定义约束:在模型文件中,用户可以定义约束。
约束可以是线性的或非线性的,并定义在变量上。
用户需要通过约束来限制变量的取值范围。
6.设置求解器:在模型文件中,用户可以选择合适的求解器来解决问题。
LINGO提供了多种求解器,用户可以根据问题的复杂程度选择最适合的求解器。
lingo用法

Lingo 是一种专门用于线性规划和整数规划的建模和求解语言。
它提供了一种简洁的方式来描述数学模型,并使用线性规划算法求解这些模型。
下面是Lingo 的一些基本用法示例:
1. 变量定义:
- 定义实数变量:`X = 0.5;`
- 定义整数变量:`INT_VAR Y;`
2. 目标函数定义:
- 最小化目标函数:`MIN = 2*X + 3*Y;`
- 最大化目标函数:`MAX = -X + 4*Y;`
3. 约束条件定义:
- 等式约束:`EQUATION C1: X + Y = 10;`
- 不等式约束:`INEQUATION C2: X >= 5;`
- 范围约束:`5 <= Y <= 20;`
4. 求解模型:
- 使用默认求解器求解:`SOLVE;`
- 指定求解器和参数:`SOLVE WITH LP_METHOD=3;` 以上是Lingo 的一些基本用法示例,实际上,Lingo 还提供了更多的功能和语法,用于描述更复杂的数学模型和问题。
它可以处理
线性规划、整数规划、混合整数规划等多种类型的问题,并提供了丰富的优化算法和工具来求解这些问题。
LINGO的基本用法

试确定各货栈到各客户处的货物调运数量, 使总的运输费用 最小
返回X的整数部分(向最靠近0的方向取整)
@LGM(X)
返回X的gamma函数的自然对数值
@MOD(X,Y)
运算对象是两个数
#GT# #GE#
左边大于右边时为真,否则为假 左边大于或等于右边时为真,否则为假
#LT#
左边小于右边时为真,否则为假
#LE#
左边小于或等于右边时为真,否则为假
预算对象是逻辑值 或逻辑表达式
#NOT# #AND# #OR#
单目运算符,表示对运算对象取反(即真变假,假变真) 两个运算对象都真时为真,否则为假 两个运算对象都假时为假,否则为真
◆生成图形
由模型生成图形,以矩阵形式显示 模型的系数.
◆调试
调试结果,找到充分行(Sufficient Rows)和必要行 (Necessary Rows). ◆模型统计资料
◆查看(以为本方式显示模型内容)
13
LINGO 教 程
◆命令行窗口
主要是为用户交互地测试命令脚本 而设计.(通常不用)
◆状态窗口
@FOR(VD(J): @SUM(WH(I): X(I, J)) =DJ(J));
21
§1.4 LINGO的运算符和函数
一、 LINGO的常用运算符. 1. 算术运算符.
LINGO 教 程
^* / + -
lingo的语法规则

lingo的语法规则Lingo是一种优化建模语言,它遵循一定的语法规则。
以下是一些Lingo的语法规则:1. 变量声明: 在Lingo中,变量需要在使用之前声明。
变量可以是连续的实数、整数或者集合。
2. 目标函数: 目标函数是Lingo模型的核心部分,用于表示需要优化的目标。
目标函数可以使用MAX或MIN关键字来指定最大化或最小化目标。
3. 约束条件: 约束条件是限制问题解的约束,通常由等式或不等式表示。
约束条件可以包括等式约束、不等式约束和逻辑约束。
4. 集合: Lingo允许使用集合来表示一组变量或一组约束。
集合可以用于定义变量、参数、约束等。
5. 参数: 参数是用于定义模型的数据,可以是数值型或字符型。
参数可以在模型中直接使用,也可以通过集合引用。
6. 运算符: Lingo支持多种运算符,包括算术运算符、逻辑运算符和关系运算符。
运算符的优先级遵循常规的数学规则。
7. 语句格式: Lingo语句通常以分号结尾,每行可以包含多个语句。
语句可以跨行,以提高可读性。
8. 注释: Lingo允许使用注释来解释模型或添加额外信息。
注释以“!”开头,可以出现在模型的任何位置。
9. 标号: Lingo允许给语句添加标号,以便在模型中引用或识别特定语句。
标号以方括号开头和结尾,例如[OBJ]。
10. 模型结构: Lingo模型以“MODEL:”开头,以“END”结束。
在模型中,可以包含多个目标函数、约束条件、参数等。
以上是Lingo的一些基本语法规则,使用这些规则可以帮助你构建有效的优化模型并解决实际问题。
LINGO的基本用法2
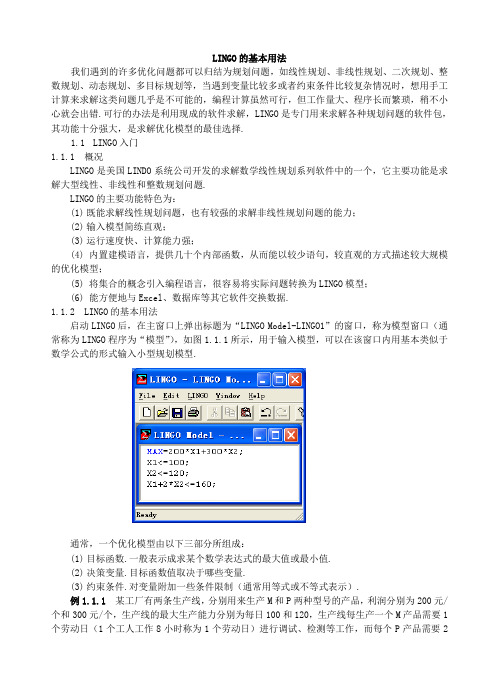
LINGO的基本用法我们遇到的许多优化问题都可以归结为规划问题,如线性规划、非线性规划、二次规划、整数规划、动态规划、多目标规划等,当遇到变量比较多或者约束条件比较复杂情况时,想用手工计算来求解这类问题几乎是不可能的,编程计算虽然可行,但工作量大、程序长而繁琐,稍不小心就会出错.可行的办法是利用现成的软件求解,LINGO是专门用来求解各种规划问题的软件包,其功能十分强大,是求解优化模型的最佳选择.1.1LINGO入门1.1.1 概况LINGO是美国LINDO系统公司开发的求解数学线性规划系列软件中的一个,它主要功能是求解大型线性、非线性和整数规划问题.LINGO的主要功能特色为:(1)既能求解线性规划问题,也有较强的求解非线性规划问题的能力;(2)输入模型简练直观;(3)运行速度快、计算能力强;(4)内置建模语言,提供几十个内部函数,从而能以较少语句,较直观的方式描述较大规模的优化模型;(5)将集合的概念引入编程语言,很容易将实际问题转换为LINGO模型;(6)能方便地与Excel、数据库等其它软件交换数据.1.1.2 LINGO的基本用法启动LINGO后,在主窗口上弹出标题为“LINGO Model-LINGO1”的窗口,称为模型窗口(通常称为LINGO程序为“模型”),如图1.1.1所示,用于输入模型,可以在该窗口内用基本类似于数学公式的形式输入小型规划模型.通常,一个优化模型由以下三部分所组成:(1)目标函数.一般表示成求某个数学表达式的最大值或最小值.(2)决策变量.目标函数值取决于哪些变量.(3)约束条件.对变量附加一些条件限制(通常用等式或不等式表示).例1.1.1某工厂有两条生产线,分别用来生产M和P两种型号的产品,利润分别为200元/个和300元/个,生产线的最大生产能力分别为每日100和120,生产线每生产一个M产品需要1个劳动日(1个工人工作8小时称为1个劳动日)进行调试、检测等工作,而每个P产品需要2个劳动日,该厂工人每天共计能提供160劳动日,假如原材料等其它条件不受限制,问应如何安排生产计划,才能使获得的利润最大?解 设两种产品的生产量分别为12,x x ,则该问题的数学模型为 目标函数 12max z 200300x x =+.约束条件 1212100,120,2160,0,1,2.j x x x x x j ≤⎧⎪≤⎪⎨+≤⎪⎪≥=⎩(1.1.1)在Model 窗口输入如下模型: MAX =200*X1+300*X2; X1<=100; X2<=120;X1+2*X2<=160;注 LINGO 默认所有决策变量都是非负,因而变量非负条件可以不必输入. 选菜单File|Save As (或按F5)将模型存盘,默认文件格式的扩展名为.lg4. 选菜单File|Print (或按F7)可以在打印机上输出该模型. LINGO 的语法规定:(1) 求目标函数的最大值或最小值分别用MAX=…或MIN=…来表示;(2) 每个语句必须以分号“;”结束,每行可以有多个语句,语句可以跨行;(3) 变量名称必须以字母(A ~Z )开头,由字母、数字和下划线所组成,长度不超过32个字符,不区分大小写;(4) 可以给语句加上标号,例如[OBJ] MAX =200*X1+300*X2; (5) 以!开头,以“;”号结束的语句是注释语句;(6) 如果对变量的取值范围没有作特殊说明,则默认所有决策变量都非负;(7) LINGO 模型以语句“MODEL:”开头,以“END ”结束,对于比较简单的模型,这两个语句可以心省略.选菜单LINGO|Solve (或按Ctrl+S ),或用鼠标点击“求解”按钮,如果模型有语法错误,则弹出一个标题为“LINGO Error Message ”(错误信息)的窗口,指出在哪一行,有怎样的错误,每种错误都有一个编号.如果语法通过,LINGO 用内部所带的求解程序求出模型的解,然后弹出一个标题为“LINGO Solver Status ”(求解状态)的窗口,其内容为变量个数、约束条件个数、优化状态、非零变量个数、耗费内存、所花时间等信息,点击Close 关闭该窗口,屏幕上出现标题为“Solution Report ”(解的报告)的信息窗口,显示优化计算的步数、优化后的目标函数值、列出各变量的计算结果,本例的具体内容如下: Global optimal solution found.Objective value: 29000.00 Total solver iterations: 0Variable Value Reduced CostX1 100.0000 0.000000 X2 30.00000 0.000000Row Slack or Surplus Dual Price 1 29000.00 1.000000 2 0.000000 50.00000 3 90.00000 0.0000004 0.000000 150.0000该报告说明:目标函数值为29000,变量值分别为X1=100,X2=30.“Reduced Cost ”的含义是缩减成本系数(最优解中变量的Reduced Cost 值自动取零),“Row ”是输入模型中的行号,“Slack or Surplus ”的意思为松弛或剩余,即约束条件左边与右边的差值,对于“<=”不等式,右边减左边的差值称为Slack(松弛),对于“>=”不等式,左边减右边的差值称为Surplus (剩余),当约束条件的左右两边相等时,松弛或剩余的值为零,如果约束条件无法满足,即没有可行解,则松弛或剩余的值为负.“Dual Price ”的意思是影子价格,上面报告中Row 2的松弛值为0,意思是说第二行的约束条件,即第一条生产线最大生产能力已达到饱和状态(100个),影子价格为50,含义是:如果该生产线最大生产能力增加1,能使目标函数值,即利润增加50;报告中Row 3的松弛值为90,表示按照最优解安排生产(X2=30),则第三行的约束条件,即第二条生产线的最大生产能力120剩余了90,因此增加该生产线的最大生产能力对目标函数的最优值不起作用,故影子价格为0;以上结果可以保存到文件中(扩展名为.lgr ).例1.1.2 基金的优化使用(2001年建模数学竟赛C 题).假设某校基金会得到了一笔数额为M 万元的基金,打算将其存入银行,校基金会计划在n 年内每年用部分本息奖励优秀师生,要求每年的奖金额相同,且在n 年仍保留原基金数额.银行存款税后年利率见表1.1.2.表1.1.2 银行存款税后利率表存期 1年 2年 3年 5年 税后年利率%1.82.162.5922.88校基金会获得最佳的基金使用计划,以提高每年的奖金额,请在5000M =万元、5n =年的情况下设计具体存款方案.1.2 用LINGO 编程语言建立模型1.1节介绍了LINGO 的基本用法,其优点是输入模型较直观,一般的数学表达式无须作大的变换即可直接输入.对于规模较少的规划模型,用直接输入方式是有利的,但是,如果模型的变量和约束条件个数都比较多,若仍然用直接输入方式,虽然也能求解并得出结果,但是这种做法有明显不足之处:模型的编幅很长,不便于分析修改和扩展,例如,目标函数中有求和表达式102011ij iji j c x==∑∑,若直接输入的方式,将有200个ij c 和200个ij x 相乘再相加.1.2.1 LINGO 模型的基本组成LINGO 建模语言引入了集合的概念,为建立大规模数学规划模型提供了方便.用LINGO 语言编写程序来表达一个实际优化问题,称为LINGO 模型.例1.2.1 某公司有6个供货栈(仓库),现有8个客户各要一批货,各供货栈到8个客户处的单位货物运输价见表1.2.1.解 引入决策变量ij x ,表示从第i 个货栈到第j 个客户的货物运量.用符号ij c 表示从第i 个货栈到第j 个客户的单位货物运价,i a 表示第i 个货栈的最大供货量,j d 表示第j 个客户的需求量.则本问题的数学模型为:6811min ij ij i j z c x ===∑∑,8161,1,2,,6..,1,2,,80,1,2,,6,1,2,,8ij i j ij j i ij x a i s t x d j x i j ==⎧≤=⎪⎪⎪==⎨⎪⎪≥==⎪⎩∑∑ (1.2.1)1.集合定义部分LINGO 将集合(SET)的概念引入建模语言,集合是一组相关对象构成的组合,代表模型中的实际事物,并与数学变量及常量联系起来,是实际问题到数学的抽象.例1.2.1中的6个仓库可以看成是一个集合,8个客户可以看成另一个集合.每个集合在使用之前需要预先给出定义,定义集合时要明确三方面内容:集合的名称、集合内的成员(组成集合的个体,也称元素)、集合的属性(可以看成是与该集合有关的变量或常量,相关于数组).定义仓库集合:WH/w1..w6/:AI;其中WH 是集合的名称,w1..w6是集合内成员,“..”是特定的省略号(如果不用该省略号,也可以把成员一一列举出来,成员之间用逗号或空格分开),表明该集合有6个成员,分别对应6个货栈,AI 是集合的属性,它可以看成一个一维数组,有6个分量,分别表示各货栈现有货物的总数.集合、成员、属性的命名规则与变量相同,可按自己的意愿,用有一定意义的字母数字串来表示,式中“/”和“/:”是规定的语法规则.定义客户集合:VD/v1..v8/:DJ;该集合有8个成员,DJ 是集合的属性(有8个分量)表示各客户的需求量. 定义表示运输关系(路线)的集合:LINKS(WH,VD):C,X;该集合以初始集合WH 和DJ 为基础,称为衍生集合(或称派生集合),C 和X 是该衍生集合的两个属性.衍生集合的定义语句有如下要素组成:(1) 集合的名称; (2) 对应的初始集合;(3) 集合的成员(可以省略不写明); (4) 集合的属性(可以没有).定义衍生集合时可以用罗列的方式将衍生集合的成员一一列举出来,如果省略不写,则默认衍生集合的成员取它的所对应初始集合的所有可能的组合,上述衍生集合LINKS 的定义中没有指明成员,而它对应的初始集合WH 有6个成员,VD 有8个成员,因此LINKS 成员取WH 和VD 的所有可能组合,即集合LINKS 有48个成员,48个成员可以排列成一个矩阵,其行数与集合WH 的成员个数相等,列数与集合VD 的成员个数相等.相应地,集合LINKS 的属性C 和X 都相当于二维数组,各有48个分量,C 表示货栈i w 到客户j v 的单位货物运价,X 表示货栈i w 到客户j v 的货物运量.本模型完整的集合定义为:SETS :WH/W1..W6/:AI; VD/V1..V8/:DJ; LINKS(WH,VD):C:X; ENDSETS注 集合定义部分以语句SETS :开始,以语句ENDSETS 结束,这两个语句必须单独成一行. ENDSETS 后面不加标点符号.2.数据初始化(数据段)LINGO 建模语言通过对数据初始化部分来实现对已知属性赋以初始值,格式为: DATA :AI=60,55,51,43,41,52;DJ=35,37,22,32,41,32,43,38; C=6,2,6,7,4,2,5,9 4,9,5,3,8,5,8,2 5,2,1,9,7,4,3,3 7,6,7,3,9,2,7,1 2,3,9,5,7,2,6,5 5,5,2,2,8,1,4,3;ENDDATA3.目标函数和约束条件目标函数表达式 6811min ij iji j z c x===∑∑用LINGO 语句表示为:MIN =@SUM (LINKS(I,J):C(I,J)*X(I,J));式中,@SUM 是LINGO 提供的内部函数,其作用是对某个集合的所有成员,求指定表达式的和,该函数需要两个参数,第一个参数是集合名称,指定对该集合所有成员求和,如果此集合是一个初始集合,它有m 个成员,则求和运算对这m 个成员进行,相当于求1mi =∑,第二参数是一个表达式,表示求和运算对该表达式进行.此处@SUM 的第一个参数是LINKS(I,J),表示求和运算对衍生集合LINKS 进行,该集合的维数是2,共有48个成员,运算规则是:选对48个成员分别求表达式C(I,J)*X(I,J)的值,然后求和,相当于求6811ij iji j c x==∑∑,表达式中的C 和X 是集合LINKS 的两个属性,它们各有48个分量.注 如果表达式中参与运算的属性属于同一个集合,则@SUM 语句中索引(相当于矩阵或数组的下标)可以省略,假如表达式中参与运算的属性属于不同的集合,则不能省略属性的索引.本例的目标函数可以表示成:MIN =@SUM (LINKS:C*X);约束条件81,1,2,,6iji j xa i =≤=∑实际上表示了6个不等式,用LINGO 语言表示该约束条件,语句为:@FOR (WH(I):@SUM (VD(J):X(I,J))<=AI(I));语句中的@FOR 是LINGO 提供的内部函数,它的作用是对某个集合的所有成员分别生成一个约束表达式,它有两个参数,第一个参数是集合名称,表示对该集合的所有成员生成对应的约束表达式,上述@FOR 的第一个参数是WH ,它表示货栈,共6个成员,故应生成6个约束表达式,@FOR 的第二个参数是约束表达式的具体内容,此处再调用@SUM 函数,表示约束表达式的左边是求和,是对集合VD 的8个成员,并且对表达式X(I,J)中的第二维J 求和,即81ijj x=∑,约束表达式的右边是集合WH 的属性AI ,它有6个分量,与6个约束表达式一一对应.本语句中的属性分别属于不同的集合,所以不能省略索引I ,J.注 @SUM 和@FOR 函数可以嵌套使用.同样地,约束条件61,1,2,,8ijj i cd j ===∑用LINGO 语句表示为:@FOR (VD(J):@SUM (WH(I):X(I,J))=DJ(J)); 目标函数及约束条件的模型为:MIN =@SUM (LINKS(I,J):C(I,J)*X(I,J)); @FOR (WH(I):@SUM (VD(J):X(I,J))<=AI(I));@FOR(VD(J):@SUM(WH(I):X(I,J))=DJ(J));4.完整的模型MODEL:SETS:WH/W1..W6/:AI;VD/V1..V8/:DJ;LINKS(WH,VD):C,X;ENDSETSDATA:AI=60,55,51,43,41,52;DJ=35,37,22,32,41,32,43,38;C=6,2,6,7,4,2,5,94,9,5,3,8,5,8,25,2,1,9,7,4,3,37,6,7,3,9,2,7,12,3,9,5,7,2,6,55,5,2,2,8,1,4,3;ENDDATAMIN=@SUM(LINKS(I,J):C(I,J)*X(I,J));@FOR(WH(I):@SUM(VD(J):X(I,J))<=AI(I));@FOR(VD(J):@SUM(WH(I):X(I,J))=DJ(J));END注 LINGO模型以语句MODEL:开始,以语句END结束,这两个语句单独成一行.完整的模型由集合定义、数据段、目标函数和约束条件等部分组成,这几个部分的先后次序无关紧要,!开头语句是注释语句(可有可无).选择菜单LINGO|Solve(或按Ctrl+S),或用鼠标点击“求解”按钮,在“Solution Report”信息窗口中,看到具体求解结果.最优运输方案1.3 LINGO的运算符和函数1.3.1 LINGO的常用运算符1.算术运算符^乘方﹡乘/除﹢加﹣减LINGO唯一的一元算术运算符是取反函数“﹣”.算术运算术的优先级别为:单目“-”最高,其余依次为^,*和/,+和-,同级自左至右,加括号可改变运算次序.2.逻辑运算符在LINGO中,逻辑运算符主要用于集循环函数的条件表达式中,来控制在函数中哪些集成员被包含,哪些被排斥.在创建稀疏集时用在成员资格过滤器中.LINGO具有9种逻辑运算符:3.关系运算符关系运算符通常用在约束条件表达式中,用来指定约束条件表达式左边与右边必须满足的关系,有以下三种:= <= >= LINGO中没有单独的“<”和“>”关系.1.3.2 LINGO函数在默认情况下,LINGO规定变量是非负的,也就是说下界为0,上界为+∞。
LINGO软件的基本使用方法

模(即编程)语言,系统推荐的是采用LINGO。安装后
可通过“LINGO|Options|File Format”命令修改缺省
的建模(即编程)语言。
第一次运行时提示输入授权密码,如图:
LINGO软件的主要特色
两种命令模式 Windows模式: 通过下拉式菜单命令驱动LINGO运
行(多数菜单命令有快捷键,常用的菜单命令有快捷
输出结果备注: LINGO是将它作为PINLP(纯整数非线性规划)来求解, 因此找到的是局部最优解。
通过菜单 “WINDOW| Status Window”看到状态窗 口,可看到最佳目标值 “Best Obj”与问题的上界 “Obj Bound”已经是一样的, 当前解的最大利润与这两个 值非常接近,是计算误差引 起的。如果采用全局最优求 解程序(后面介绍),可以验 证它就是全局最优解。
1 2 3 4
输入窗口如下:
程序语句输入的备注:
•LINGO总是根据“MAX=”或“MIN=”寻找目标函数, 而除注释语句和TITLE语句外的其他语句都是约束条 件,因此语句的顺序并不重要 。 •限定变量取整数值的语句为“@GIN(X1)”和 “@GIN(X2)”,不可以写成“@GIN(2)”,否则 LINGO将把这个模型看成没有整数变量。
按钮),图形界面,使用方便;
(这里主要介绍这种模式)
命令行 模式:仅在命令窗口(Command Window)下操 作,通过输入行命令驱动LINGO运行 。
LINGO的文件类型 •.LG4:LINGO格式的模型文件,保存了模型窗口中所 能够看到的所有文本和其他对象及其格式信息;
•.LNG:文本格式的模型文件,不保存模型中的格式信 息(如字体、颜色、嵌入对象等); •.LDT:LINGO数据文件;
lingo基础用法

lingo基础用法Lingo是一种计算机编程语言,它的基础用法包括以下几个方面:1. 变量声明和赋值:可以使用Lingo语言声明变量,并给变量赋值。
例如:```global myVariable -- 声明一个全局变量put 5 into myVariable -- 将值5赋给变量myVariable```2. 条件语句:可以使用条件语句来根据条件执行不同的代码块。
例如:```if myVariable = 5 thenput "It's five!" into messageanswer messageend if```3. 循环语句:可以使用循环语句来反复执行特定的代码块。
例如:```repeat with i = 1 to 10put i into messageanswer messageend repeat```4. 函数和命令:Lingo提供了许多内置的函数和命令,可以执行特定的操作。
例如:```put the date into currentDate -- 获取当前日期get the long name of sprite 1 -- 获取精灵1的长名称```5. 脚本和行为:可以使用Lingo编写脚本和行为,控制多媒体项目的行为。
例如:```on mouseUpgo to the next frameend```上述是Lingo语言的基础用法,只是其中的一小部分。
Lingo 还提供了丰富的功能和特性,包括面向对象编程、多媒体处理等。
要更深入地学习和使用Lingo,建议参考Lingo的官方文档或相关教程。
LINGO的基本用法

cij xij ;
i1 j 1
用LINGO语句表示为:
MIN = @SUM(LINKS(I, J): C(I, J)*X(I, J));
注: ① @SUM是LINGO提供的内部函数,其作用是对某个
集合的所有成员,求指定表达式的和.
安
@SUM有两个参数:集合名称和表达式
阳
师 范
② 如果表达式中参与运算的属性属于同一个集合,则
与 统
◆模型统计资料
计 学
◆查看(以为本方式显示模型内容)
院
运
筹
◆命令行窗口
学
实
主要是为用户交互地测试命令脚本
验
而设计.(通常不用)
◆状态窗口
[求解器状态]
[变量]
安
阳
师 范
[扩展求解器状态]
学
院
数
学
与
统
计
学
院
[约束] [非零系数]
[内存使用量] [已运行时间]
运 筹
§1.3 用LINGO编程语言建立模型
W1
6
2
6
7
4
2
5
9
安 阳
W2
4
9
5
3
8
5
8
2
师
W3
5
2
1
9
7
4
3
3
范 学
W4
7
6
7
3
9
2
7
1
院 数
W5
2
3
9
5
7
2
6
5
学
W6
5
5
2
2
8
lingo知识点总结

lingo知识点总结Lingo 是一个用于多媒体和跨平台软件开发的高级编程语言。
它以其简单易用,高效快速的特点,广泛应用于多媒体制作、交互式应用程序开发等领域。
Lingo 语言自身也有许多重要的知识点,包括基本语法、面向对象编程、多媒体处理等内容。
在本文中,将对Lingo 的知识点进行总结和介绍,希望能够帮助大家更好地理解和使用 Lingo 语言。
一、基本语法1. 变量和常量:在 Lingo 语言中,可以通过变量和常量来存储和表示数据。
变量是可以改变数值的,而常量是一旦定义就不可改变的数值。
变量和常量的使用可以帮助我们更好地处理数据和逻辑关系。
2. 数据类型:Lingo 语言支持多种数据类型,包括整型、浮点型、布尔型、字符串等。
不同的数据类型有不同的操作方法和适用范围,熟练掌握数据类型可以帮助我们更好地处理数据。
3. 运算符:Lingo 语言支持多种运算符,包括算术运算符、比较运算符、逻辑运算符等。
运算符的使用可以帮助我们进行数值计算和逻辑判断。
4. 控制语句:Lingo 语言支持多种控制语句,包括条件语句、循环语句、跳转语句等。
控制语句的使用可以帮助我们控制程序的流程和逻辑。
5. 函数和方法:在 Lingo 语言中,可以通过函数和方法来封装和重用代码。
函数和方法的使用可以帮助我们更好地组织和管理代码。
6. 事件处理:Lingo 语言支持事件处理,可以方便地处理用户输入或系统事件。
事件处理的使用可以帮助我们开发交互式应用程序。
二、面向对象编程1. 类和对象:在Lingo 语言中,可以通过类和对象来进行面向对象编程。
类是对象的模板,对象是类的实例。
类和对象的使用可以帮助我们更好地组织和管理代码。
2. 继承和多态:Lingo 语言支持继承和多态,可以方便地重用代码和扩展功能。
继承和多态的使用可以帮助我们更好地设计和组织代码。
3. 封装和抽象:Lingo 语言支持封装和抽象,可以方便地隐藏代码细节和实现复杂功能。
LINGO教程(基本语法)(1)

LINGO 教 程
问题的模型(可以看出是LP模型 ) 目标函数是所有费用的和 约束条件主要有两个: 1)能力限制: RP ( I ) 40, I 1,2,3,4 2)产品数量的平衡方程:
•.LNG:文本格式的模型文件,不保存模型中的格式信 息(如字体、颜色、嵌入对象等); •.LDT:LINGO数据文件;
•.LTF:LINGO命令脚本文件; •.LGR:LINGO报告文件; •.LTX: LINDO格式的模型文件;
9
除“LG4”文件外, 另外几种格式的文件 都是普通的文本文件, 可以用任何文本编辑 器打开和编辑。
4. LINGO的主要菜单命令
5. LINGO命令窗口
3
LINGO 教 程
LINGO软件的安装
安装过程: 与LINDO for Windows类似. 安装文件20M多一点,需要接受安装协议、选择安装 目录(缺省C:\LINGO9)。 安装完成前,在出现的对话框(如图)中选择缺省的建
模(即编程)语言,系统推荐的是采用LINGO。安装后
按钮),图形界面,使用方便;
(这里主要介绍这种模式)
命令行 模式:仅在命令窗口(Command Window)下操 作,通过输入行命令驱动LINGO运行 。
6
LINGO 教 程
从LINDO 到 LINGO LINGO 9.0功能增强,性能稳定,解答结果可靠。与
LINDO相比,LINGO 软件主要具有两大优点:
lingo入门教程

lingo入门教程Lingo是一种广泛应用于计算机编程和计算机科学领域的编程语言。
它是用于Adobe Director(一种多媒体应用程序)中的脚本语言,用于控制多媒体元素和动画。
Lingo的语法比较简单易懂,有助于创建交互式和多媒体项目。
下面是一些Lingo的基本概念和用法。
1. 变量(Variables): 在Lingo中,变量用于存储数据值。
变量可以是数字、文本或其他数据类型。
要创建变量,可以使用关键字`global`或`local`,后跟变量名和初始值(可选)。
例如:```global myVariable = 10local myText = "Hello World"```2. 条件语句(Conditional statements): 条件语句用于根据条件执行特定的代码块。
常用的条件语句有`if-then`和`if-then-else`。
例如:```if myVariable > 5 thenalert "Value is greater than 5"elsealert "Value is less than or equal to 5"end if```3. 循环(Loops): 循环用于重复执行一段代码块,直到满足指定条件为止。
Lingo提供了`repeat`和`repeat while`循环语句。
例如:```repeat with i = 1 to 5put iend repeat```4. 函数(Functions): 函数是一组预定义的代码,用于执行特定的任务。
Lingo提供了许多内置函数,如`alert`、`put`等。
您还可以创建自己的函数。
例如:```on multiplyNumbers(a, b)return a * bend multiplyNumbersput multiplyNumbers(2, 4) -- 输出8```这些只是Lingo的一些基本概念和用法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LINGO的基本用法一.集合的基本用法集合(set)及其属性(attribute)的概念基本集合与派生集合集合名[/元素列表/][:属性列表];集合名(父集合列表)[/元素列表/][:属性列表];稠密集合与稀疏集合元素过滤法基本集合的隐式列举法:数字型 1..n字符数字型Car101..Car208日期型MON..FRI月份型OCT..JAN年月型OCT2007..JAN2008二.模型结构(1)集合段从“sets:”到“endsets”(2)数据输入段从“data:”到“enddata”属性=常数列表(3)目标和约束段MIN=表达式(4)计算段从“calc:”到“endcalc”,对原始数据的计算处理(5)初始段从“init:”到“endinit”,定义迭代初值用属性=常数列表(6)注释从感叹号到分号三.函数基本数学函数@ABS(X) @COS(X) @EXP(X) @FLOOR(X)@LGM(X) @LOG(X) @MOD(X,Y) @POW(X,Y)@SIGN(X) @SIN(X) @SMAX(list) @SMIN(list)@SQR(X) @SQRT(X) @TAN(X)其中@LGM(X) =ln(X-1)!集合循环函数@FOR @MIX @MIN @PROD@SUM用法:集合函数名(集合名(集合索引列表)|条件:表达式组)集合操作函数@IN @IN(集合名,集合元素名,…集合元素名)@INDEX @INDEX(集合名,集合元素名)@WRAP @WRAP(i,N),循环计数@SIZE @SIZE(集合名)变量定界函数@BND(L,X,U) @BIN(X) @FREE(X) @GIN(X) 分别对变量取值限制:上下界,0-1值,取消非负限制,整数概率分布函数@PNS(X) 标准正态分布@PSL(X) 正态线性损失@PBN(P,N,X) 二项分布@PHG 超几何分布@PTD(N,X) t分布@PFD(N,D,X) F分布@PPS(A,X) 泊松分布@PPL(A,X) 泊松线性损失@PCX(N,X) X平方分布@RAND(seed) 随机数服务系统函数@PEL(A,X) @PFS(A,X,C) @PEB(A,X)文件输入输出函数@FILE(fn) @TEXT(…fn‟) @OLE结果报告函数@ITERS() 返回迭代次数@NEWLINE(n) 输出n个新行@STRLEN(string) 返回字符串的长度@NAME(reference) 返回变量名或行名@WRITE 用于数据段,输出变量,字符串或换行@WRITEFOR 是@WRITE在循环情况下的推广@FORMAT 以格式描述符方式输出数值@DUAL(varname) 返回解答中变量的判别数或结束行的影子价格@STATUS() 返回求解后的最后状态其他函数@IF @IF(条件,true结果,false结果)@WARN @WARN(‘text’,条件)@USER @USER(用户编写的函数dll或obj文件)四.文件传输通过文本文件传输数据@FILE和@TEXT通过Excel文件传输数据@OLE例题! 背包问题 Knapsack Problem! max z=sum(i=1~n)ci xi! st. sum ai xi <=b, xi=0/1;model:title背包问题;sets:wp/w1..w8/:a,c,x;endsetsdata:a=1 3 4 3 3 1 5 10; c=2 9 3 8 10 6 4 10; enddatamax=@sum(wp:c*x);@for(wp:@bin(x));@sum(wp:a*x)<=15;end!装箱问题!=======;model:title装箱问题;sets:wp/w1..w30/:w; xz/v1..v30/:y; links(wp,xz):x; endsetsdata:w=0.51,0.51,0.51,0.51,0.51,0.51,0.27,0.27,0.27,0.27,0.27,0.27,0.26,0.26,0.26,0.26,0.26,0.26,0.23,0.23,0.23,0.23,0.23,0.23,0.23,0.23,0.23,0.23,0.23,0.23;enddatamin=@sum(xz(i):y(i));C=1;@for(links:@bin(x));@for(xz:@bin(y));@for(wp(i):@sum(xz(j):x(i,j))=1);@for(xz(j):@sum(wp(i):w(i)*x(i,j))<=C*y(j)); end@for(o(j):cun(2,j)= cun(1,j)+x(2,j)-he(2,j) ;z2= @sum(o(j): cun(2,j));@for(o(j):cun(3,j)= cun(2,j)+x(3,j)-he(3,j) ;z3= @sum(o(j): cun(3,j));@for(o(j):cun(4,j)= cun(3,j)+x(4,j)-he(4,j) ;z4= @sum(o(j): cun(4,j));@for(o(j):cun(5,j)= cun(4,j)+x(5,j)-he(5,j) ;z5= @sum(o(j): cun(5,j));@for(o(j):cun(6,j)= cun(5,j)+x(6,j)-he(6,j) ;z6= @sum(o(j): cun(6,j));食品加工一项食品加工业,对几种粗油精炼,然后加以混合成为成品食用油。
原料油有两大类,共5种。
两种植物油,V1和V2,三种非植物油,O1、O2和O3。
各种原料油均从市场采购,未来半年中原料油的市场价格(元/吨)如下成品油售价1500元/吨。
植物油和非植物油要在不同的生产线精炼,每个月最多可炼植物油200吨,非植物油250吨。
精练过程中没有重量损失,精炼费用可以忽略。
每种原料油最多可存储1000吨备用。
存储费为每吨每月50元。
成品油和经过精炼的原料油不能存储。
对成品油限定其硬度在3至6单位之间。
各种原料油的硬度如下假设硬度是线性地混合的。
为使公司获得最大利润,应采取什么样的采购和加工方案。
现存有5种原料油每种500吨,要求在6月底仍然有这样多存货。
@for(month(i) : @sum(o(j): y(j)*he(i,j))/@sum(o(j):he(i,j)) >3 ) ;z2= z1+@sum(o(i):x(2)(i) - @sum(o(i):he(2)(i) ;z3= z2+@sum(o(i):x(3)(i) - @sum(o(i):he(3)(i) ;z4= z3+@sum(o(i):x(4)(i) - @sum(o(i):he(4)(i) ;z5= z4+@sum(o(i):x(5)(i) - @sum(o(i):he(5)(i) ;研究总利润和采购与加工方案适应不同的未来市场价格应如何变化。
考虑如下的价格变化方式:2月份植物油价上升x%,非植物油上升2x%;3月份植物油价上升2x%,非植物油上升4x%;其余月份保持这种线性的上升势头。
对不同的值x(直到20),就方案的必要的变化及对利润的影响,作出全面计划。
@for(o(j):cun(1,j)= 500+x(1,i)-he(1,j) ;@for(o(j):cun(2,j)= cun(1,j)+x(2,j)-he(2,j) ;@for(o(j):cun(3,j)= cun(2,j)+x(3,j)-he(3,j) ;@for(o(j):cun(4,j)= cun(3,j)+x(4,j)-he(4,j) ;@for(o(j):cun(5,j)= cun(4,j)+x(5,j)-he(5,j) ;@for(o(j):cun(6,j)= cun(5,j)+x(6,j)-he(6,j) ;@for(month(i):he(i,1) +he(i,2)<200);@for(month(i):he(i,3) +he(i,4)+he(i,5)<250);@for(links(i,j): cun(i,j) <1000 ) ;@for(o(j):cun(6,j)=500 );@for(month(i) : @sum(o(j): y(j)*he(i,j)) <6 *@sum(o(j):he(i,j)) ) ;@for(month(i) : @sum(o(j): y(j)*he(i,j)) >3*@sum(o(j):he(i,j)) );飞行管理问题在约一万米高空边长160公里的长方形区域内有若干架飞机(最多6架)在水平飞行。
当一架飞机新进入该区域,地面调度中心根据记录的数据(各架飞机的位置和速度向量),要立即计算并判断是否会发生飞机相撞。
如果会相撞,则应计算如何调整各架飞机飞行的方向角,以避免相撞。
不相撞的标准为飞机间的距离大于8公里,所有飞机的航速均为800公里/小时,新进入的飞机与其它飞机的距离都在60公里以上。
试建立一个避免碰撞的数学模型,要求方向调整角的幅度尽量小,且不超过30度,计算误差不超过0.01度。
设飞行区域的四个顶点的坐标为(0, 0)、(160, 0)、(160, 160)和(0, 160)。
当前飞行记录为(6号为新进入的飞机)! 飞行管理;model:sets:feiji/p3 .. p6/:zt,zt0,dzt,zt1,xi0,yi0;juli/l1 .. l3001/:L;endsetsdata:xi0=150,145,130,0;yi0=155,50,150,0;zt=220.5,159,230,52;enddata@for(juli(i):L(i)=90+(i-1)/100);@for(feiji:@bnd(-0.08,dzt,0.08));@for(feiji:zt0=zt*3.14159265359/180);@for(feiji:zt1=zt0+dzt);@for(juli(i):@for(feiji(j)|j#lt#4:@for(feiji(k)|k#gt#j:(xi0(j)-xi0(k) +L(i)*(@cos(zt1(j))-@cos(zt1(k))))^2+(yi0(j)-yi0(k)+L(i)*(@cos(zt1(j) )-@cos(zt1(k))))^2>=64)));min=@sum(feiji:@abs(dzt));end。
