微观模型与分子动理论
大学物理-气体分子动理论
v
v１ v２ v３ … …
Ｎ ΔＮ１ ΔＮ２ ΔＮ３ … …
速率为 vi 的概率为：
Pi
Ni N
长时间“观测”理想气体分子的速率 v ：
v
0 ~ +∞ 连续分布
速率为 v → v + dv 的概率为：
Pv~vdv
dNv N
0
???
速率分布函数
Pv~vdv
dNv N
f (v)dv
f (v) dNv Ndv
刚性双原子分子的动能
分子动能
平动动能
t x
t y
t z
转动动能
r
r
t x
t y
t z
r
r
1 kT 2
t x
t y
t z
r
r
5 kT 2
温度较高时，双原子气体分子不能看作刚性分子，分子
平均能量更大，因为振动能量也参与能量均分
理想气体分子的平均能量
分子模型 刚性单原子分子 刚性双原子分子 刚性多原子分子
每个分子频繁地发生碰撞，速度也因此不断变化；
二、压强形成的微观解释
单个分子与器壁碰撞 冲力作用瞬间完成，大小、位置具有 偶然性；
大量分子（整个气体系统）与器壁碰撞 气体作用在器壁上是一个持续的、不 变的压力；
压强是气体分子给容器壁冲量的 统计平均量
三、理想气体的压强公式
建立三维直角坐标系 Oxyz
vz i N
气体处于平衡态时，气体分子沿各个方向运动的机会均等。
vx vy vz
气体分子速率平方的平均值
v v1 v2 v3 … …
Ｎ ΔＮ１ ΔＮ２ ΔＮ３ … …
v
新高考物理考试易错题易错点30分子动理论内能附答案
易错点30 分子动理论 内能易错总结1．与阿伏加德罗常数相关的物理量宏观量：摩尔质量M 、摩尔体积V mol 、物质的质量m 、物质的体积V 、物质的密度ρ； 微观量：单个分子的质量m 0、单个分子的体积V 0其中密度ρ＝m V ＝M V mol ，但是切记ρ＝m 0V 0是没有物理意义的．2．微观量与宏观量的关系 (1)分子质量：m 0＝M N A ＝ρV molN A.(2)分子体积：V 0＝V mol N A ＝MρN A (适用于固体和液体)．(对于气体，V 0表示每个气体分子所占空间的体积) (3)物质所含的分子数：N ＝nN A ＝m M N A ＝VV mol N A .3．两种分子模型 （1）球体模型固体和液体可看作一个一个紧挨着的球形分子排列而成，忽略分子间空隙，如图甲所示．d ＝36V 0π＝36V molπN A (V 0为分子体积)． （1）立方体模型气体分子间的空隙很大，把气体分成若干个小立方体，气体分子位于每个小立方体的中心，每个小立方体是每个气体分子平均占有的活动空间，忽略气体分子的大小，如图乙所示．d ＝3V 0＝3V molN A (V 0为每个气体分子所占据空间的体积)． 4．扩散现象(1)扩散现象是由物质分子的无规则运动产生的．(2)气体物质的扩散现象最显著；常温下物质处于固态时扩散现象不明显．(3)扩散现象发生的显著程度与物质的温度有关，温度越高，扩散现象越显著，这表明温度越高，分子运动得越剧烈． (4)分子运动的特点 ①永不停息；②无规则．5．布朗运动(1)微粒的大小：做布朗运动的微粒是由许多分子组成的固体颗粒而不是单个分子．其大小直接用人眼观察不到，但在光学显微镜下可以看到(其大小在10－6 m的数量级)．(2)布朗运动产生的原因：液体分子不停地做无规则运动，不断地撞击微粒．如图，悬浮的微粒足够小时，来自各个方向的液体分子撞击作用力不平衡，在某一瞬间，微粒在某个方向受到的撞击作用较强，在下一瞬间，微粒受到另一方向的撞击作用较强，这样，就引起了微粒的无规则运动．(3)实质及意义：布朗运动实质是由液体分子与悬浮微粒间相互作用引起的，反映了液体分子的无规则运动．(4)影响因素①悬浮的微粒越小，布朗运动越明显．②温度越高，布朗运动越激烈．6．热运动(1)分子的“无规则运动”，是指由于分子之间的相互碰撞，每个分子的运动速度无论是方向还是大小都在不断地变化．(2)热运动是对于大量分子的整体而言的，对个别分子无意义．(3)分子热运动的剧烈程度虽然受到温度影响，温度高分子热运动快，温度低分子热运动慢，但分子热运动永远不会停息．7．气体压强的产生单个分子碰撞器壁的冲力是短暂的，但是大量分子频繁地碰撞器壁，就会对器壁产生持续、均匀的压力．所以从分子动理论的观点来看，气体的压强等于大量气体分子作用在器壁单位面积上的平均作用力．8．决定气体压强大小的因素(1)微观因素①与气体分子的数密度有关：气体分子数密度(即单位体积内气体分子的数目)越大，在单位时间内，与单位面积器壁碰撞的分子数就越多，气体压强就越大．②与气体分子的平均速率有关：气体的温度越高，气体分子的平均速率就越大，每个气体分子与器壁碰撞时(可视为弹性碰撞)给器壁的冲力就越大；从另一方面讲，分子的平均速率越大，在单位时间内器壁受气体分子撞击的次数就越多，累计冲力就越大，气体压强就越大．(2)宏观因素①与温度有关：体积一定时，温度越高，气体的压强越大．②与体积有关：温度一定时，体积越小，气体的压强越大．9．气体压强与大气压强的区别与联系气体压强大气压强区别①因密闭容器内的气体分子的数密度一般很小，由气体自身重力产生的压强极小，可忽略不计，故气体压强由气体分子碰撞器壁产生②大小由气体分子的数密度和温度决定，与地球的引力无关③气体对上下左右器壁的压强大小都是相等的①由于空气受到重力作用紧紧包围地球而对浸在它里面的物体产生的压强．如果没有地球引力作用，地球表面就没有大气，从而也不会有大气压强②地面大气压强的值与地球表面积的乘积，近似等于地球大气层所受的重力值③大气压强最终也是通过分子碰撞实现对放入其中的物体产生压强联系两种压强最终都是通过气体分子碰撞器壁或碰撞放入其中的物体而产生的10．分子力、分子势能与分子间距离的关系(如图所示)分子间距离r r＝r0r>r0r<r0分子力F 等于零表现为引力表现为斥力分子力做功W 分子间距增大时，分子力做负功分子间距减小时，分子力做负功分子势能E p最小随分子间距的增大而增大随分子间距的减小而增大由分子间的相对位置决定，随分子间距离的变化而变化．分子势能是标量，正、负表示的是大小，具体的值与零势能点的选取有关．12．分子势能的影响因素(1)宏观上：分子势能跟物体的体积有关．(2)微观上：分子势能跟分子间距离r有关，分子势能与r的关系不是单调变化的．13．内能的决定因素(1)宏观因素：物体内能的大小由物质的量、温度和体积三个因素决定，同时也受物态变化的影响．(2)微观因素：物体内能的大小由物体所含的分子总数、分子热运动的平均动能和分子间的距离三个因素决定．14．温度、内能和热量的比较(1)温度宏观上表示物体的冷热程度，是分子平均动能的标志．(2)内能是物体中所有分子的热运动动能与分子势能的总和．(3)热量指在热传递过程中，物体吸收或放出热的多少．15．内能和机械能的区别与联系易错类型：对物理概念理解不透彻1．（2021·全国高三课时练习）以下所述现象中，属于通过热传递改变了物体内能的是（）A．将一段铁丝反复弯折，弯折处会发热B．放在空气中的一杯热水会冷却C．在转动的砂轮上磨车刀，车刀发热D．电流通过电阻丝【答案】B【详解】弯折铁丝是用力对物体做功，在转动的砂轮上磨车刀是摩擦力做功，电流通过电阻丝做功，三者都是通过做功改变物体的内能，热水放在空气中，通过热辐射等方式向外传递了热量，自身的内能减少，温度下降，是通过热传递方式改变的内能。
分子动理论的基本内容
分子动理论的基本内容
分子动理论是研究物质微观结构和宏观性质之间关系的理论，它是热力学和统计物理学的基础，对于理解物质的热力学性质和运动规律具有重要意义。
分子动理论的基本内容包括分子的运动状态、分子间的相互作用以及与宏观性质的关联等方面。
首先，我们来看分子的运动状态。
根据分子动理论，分子具有三种基本的运动状态，即平动、转动和振动。
平动是指分子沿各个方向做直线运动，转动是指分子围绕自身中心进行旋转运动，振动是指分子内部原子相对位置的周期性变化。
这些运动状态决定了物质的宏观性质，如固体、液体和气体的状态。
其次，分子间的相互作用也是分子动理论的重要内容。
分子之间存在各种相互作用力，包括范德华力、静电力、共价键和离子键等。
这些相互作用力决定了物质的热力学性质，如融化点、沸点、热容等。
此外，分子间的相互作用还决定了物质的化学性质，如溶解度、反应活性等。
最后，分子动理论还涉及到分子与宏观性质之间的关联。
根据分子动理论，宏观性质可以通过分子的平均运动状态来描述，如温度可以看作是分子平均动能的度量，压强可以看作是分子对容器壁的撞击力。
因此，分子动理论为我们提供了一种从微观角度理解宏观性质的方法，为热力学和统计物理学的发展提供了重要的理论基础。
总之，分子动理论是研究物质微观结构和宏观性质之间关系的重要理论，它涉及到分子的运动状态、分子间的相互作用以及与宏观性质的关联。
通过深入理解分子动理论的基本内容，我们可以更好地理解物质的性质和行为，为科学研究和工程实践提供理论指导。
分子动力学的理论及应用
分子动力学的理论及应用分子动力学是一种重要的计算化学方法，用来模拟复杂分子体系的动力学行为。
它从微观角度描述了分子系统的运动和相互作用，可应用于化学、材料学、生物学等多个领域。
本文将介绍分子动力学的基本理论和应用。
一、分子动力学的理论分子动力学核心在于牛顿第二定律，即F=ma。
该定律强调了物体所受到的力和它所产生的加速度之间的关系。
在分子动力学中，分子作为物体，其受力情况和加速度可通过势能函数来描述。
分子系统的能量可通过哈密顿量求得，其中包括分子所受到的所有势能和动能。
为了求解分子的动力学行为，需要进行时间演化。
具体地，需要在短时间内求解分子所受到的力，在此基础上根据分子的质量和加速度来更新分子的位置和速度。
这一过程类似于在离散时间点上计算微分方程。
在分子动力学中，最关键的参数是分子势能函数。
势能函数的形式多种多样，包括经验关系式、量子化学方法和经验分子力场等。
其中，经验分子力场最为常见，其包含了许多常见分子的实验数据，并将这些数据拟合到一个函数形式上。
二、分子动力学的应用分子动力学应用范围极广，常用于计算化学、材料学和生物学等领域。
以下是三个领域的典型应用：1. 计算化学多数化学反应的步骤很难通过实验分析。
分子动力学为计算化学提供了一种可靠的方法，可模拟和计算反应的中间态和过渡态。
这种方法可以为了解化学反应的机理提供深入的视角。
2. 材料学分子动力学也可用于研究材料的物理特性。
例如，可通过模拟来研究硅材料的分子运动、固态异质性等。
这种方法对于材料表面和表面处理技术的研究相当重要。
3. 生物学生物体系是极其复杂的，分子动力学可用于揭示生物分子之间的相互作用和运动。
例如，分子动力学模拟可以被用来研究蛋白质的折叠过程、膜生物学等。
特别是在新药开发中，分子动力学可为药物分子的设计和优化提供有价值的信息。
三、结论综上所述，分子动力学是一种强大的计算化学方法，用于预测分子系统和化学反应的医学性能。
分子动力学理论和技术的不断发展，使其在化学、材料学和生物学等多个领域具有重要的应用。
大学物理第16章气体动理论
pA
lim N
NA N
1 2
抛硬币的 统计规律
2020/1/15
DUT 余 虹
4
16.1 理想气体的压强
一、分子的作用力与压强
总数N 个，分子质量m ，摩尔质量，
体积V，温度T。
F
气体分子频繁碰撞 容器壁——给容器
壁冲量。大量分子在t 时间内给予I
的冲量，宏观上表现为对器壁的平均
vf
v
d
v
0
f
vd v
0
vf
v d
v
麦克斯韦分布律
v 1.60 RT
2020/1/15
DUT 余 虹
21
（3）方均根速率 v 2
一段速率区间v1~v2的方均速率
f v
v122
v2 v 2 d N N v v2 2 f v d v
v1 v2 d N
作用力
F I t
气体对容器壁的压强
P F I S S t
2020/1/15
DUT 余 虹
5
二、P 与微观量 的关系
分子按速度区 间分组
第i 组: 速度 近vi 似~ 认vi 为 都dv是i v i
分子数N
i ，分子数密度
ni
Ni V
考察这组分子给面元A的冲量
一 碰壁前速度 vix viy viz
一、速率分布函数
处于平衡态的气体，每个分子 朝各个方向运动的概率均等。
可是大量分子速度分 量的方均值相等。
一个分子，某一时刻速度
v
通常 v xv y v z
v
分子动理论知识点总结
分子动理论知识点总结分子动理论知识点总结11.分子动理论(1)物质是由大量分子组成的分子直径的数量级一般是10-10m。
(2)分子永不停息地做无规章热运动。
①扩散现象：不同的物质相互接触时，可以彼此进入对方中去。
温度越高，扩散越快。
②布朗运动：在显微镜下看到的悬浮在液体(或气体)中微小颗粒的无规章运动，是液体分子对微小颗粒撞击作用的不平衡造成的，是液体分子永不停息地无规章运动的宏观反映。
颗粒越小，布朗运动越明显;温度越高，布朗运动越明显。
(3)分子间存在着相互作用力分子间同时存在着引力和斥力，引力和斥力都随分子间距离增大而减小，但斥力的改变比引力的改变快，实际表现出来的是引力和斥力的合力。
2.物体的内能(1)分子动能：做热运动的分子具有动能，在热现象的讨论中，单个分子的动能是无讨论意义的，重要的是分子热运动的平均动能。
温度是物体分子热运动的平均动能的标识。
(2)分子势能：分子间具有由它们的相对位置决断的势能，叫做分子势能。
分子势能随着物体的体积改变而改变。
分子间的作用表现为引力时，分子势能随着分子间的距离增大而增大。
分子间的作用表现为斥力时，分子势能随着分子间距离增大而减小。
对实际气体来说，体积增大，分子势能增加;体积缩小，分子势能减小。
(3)物体的内能：物体里全部的分子的动能和势能的总和叫做物体的内能。
任何物体都有内能，物体的内能跟物体的温度和体积有关。
(4)物体的内能和机械能有着本质的区分。
物体具有内能的`同时可以具有机械能，也可以不具有机械能。
3.转变内能的两种方式(1)做功：其本质是其他形式的能和内能之间的相互转化。
(2)热传递：其本质是物体间内能的转移。
(3)做功和热传递在转变物体的内能上是等效的，但有本质的区分。
4.★能量转化和守恒定律5★.热力学第肯定律(1)内容：物体内能的增量(U)等于外界对物体做的功(W)和物体汲取的热量(Q)的总和。
(2)表达式：W+Q=U(3)符号法那么：外界对物体做功，W取正值，物体对外界做功，W取负值;物体汲取热量，Q取正值，物体放出热量，Q取负值;物体内能增加，U取正值，物体内能减削，U取负值。
气体分子运动论
第一章 气体动理论§1 理想气体的压强和温度 一．理想气体的微观模型1．忽略分子大小（看作质点）分子线度分子间平均距离2．忽略分子间的作用力（分子与分子或器壁碰撞时除外） 3．碰撞为完全弹性4．分子服从经典力学规律二．平衡态理想气体分子的统计假设 1．按位置的均匀分布分子在各处出现的概率相同（重力不计）。
容器内各处分子数密度相同：n = dN/dV = N/V2．速度按方向的分布均匀由于碰撞,分子往各方向运动的概率相同2222310vv v v v v v z y x z y x ======其中⎺v 2x = (v 21x + v 22x + … + v 2N x )/N⎺v 2 = ⎺v 2x +⎺v 2y +⎺v 2z三．理想气体压强公式：分子平均平动动能：分子质量：分子数密度其中22213231v n n v n P t tμεμεμ===v i推导： 速度分组：数密度的数密度：∑=+→ii i i i n n v d v v n ρρρ一个分子碰壁一次对壁的冲量ix v μ2面光滑在y,z 方向冲量＝0 全部分子在dt 时间内对dA 的冲量()()∑=∑=∑=>iixi ixall ix i ix ix ix i ix v n dtdA v dtdA v n v v dtdA v n v I d 222μμμ压强2222223131v n p v n v n n v n n v n dtdA I d P x iixi iixi μμμμμ===∑∑=＝＝ 压强与平均平动动能的关系tt n P v εμε32212==压强是大量分子碰撞器壁单位面积作用力的统计平均值 四．温度的微观含义1．温度和平均平动动能的关系kTnkTP n P t t2332===εε 2．温度的统计意义标志分子无规运动的剧烈程度 只能用于大量分子的集体 3．方均根速率-分子速率的一种描述MRT kT v kTv t 33232122====μμε§2 能量均分定理,理想气体的内能 一．自由度● 决定物体空间位置所需独立坐标的数目 ● 自由质点：平动自由度t = 3 ● 刚体绕通过质心轴的转动：转动自由度 r= 3二． 能量按自由度的均分定理1.定理（用经典统计可证明）在温度为T 的热平衡态下，物质（气体，液体和固体）分子的每个自由度都具有相同的平均动能 kT 21.● 平均平动动能xyz θφψθ, φ ：轴方向ψ ：自转角度()kTkT v v v v v v t kT kT t z y x z y x z y x t 21212121213,232222222===========εεεμμμε ● 平均转动动能kT r r 2=ε● 平均振动能（动能＋势能）：假定是简谐振动：平均动能＝平均势能kT S kT S kT S v 2222=+=ε● 总自由度s r t i 2++=其中t —平动自由度r —转动自由度 s —振动自由度● 总能量:kT i 2=ε2．重要情况● 单原子分子（He ，Ar ）：kTkT i t i 2323====ε ● 刚性双原子分子（H 2，O 2）：绕对称轴的转动无意义不计ψ自由度kTr t i 255232r ==+=+==ε● 刚性多原子分子（H 2O ）：kTr t i 3633==+=+=ε ● 晶格点阵上的离子：kTs i 36322==⨯==ε 二．理想气体的内能1．内能:分子动能，分子中原子间的势能和分子间势能的总和 2．理想气体内能分子间势能为零内能只包括分子的平动，转动，振动动能和振动势能.内能只与T 有关。
专题04 分子动理论与微观粒子(解析版)
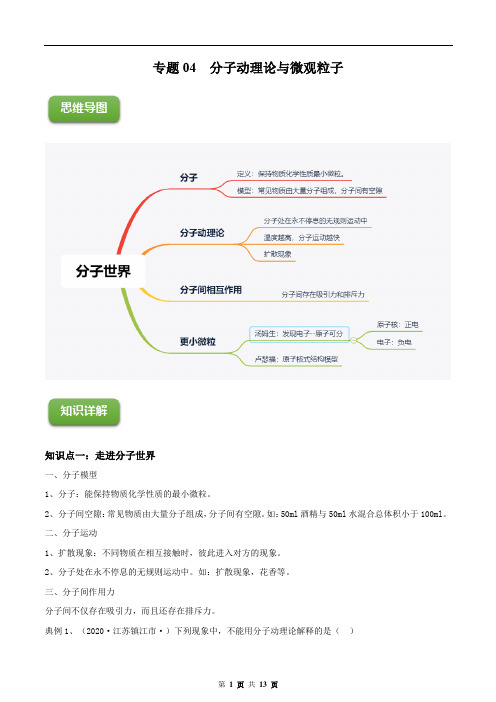
专题04 分子动理论与微观粒子思维导图知识详解知识点一：走进分子世界一、分子模型1、分子：能保持物质化学性质的最小微粒。
2、分子间空隙：常见物质由大量分子组成，分子间有空隙。
如：50ml酒精与50ml水混合总体积小于100ml。
二、分子运动1、扩散现象：不同物质在相互接触时，彼此进入对方的现象。
2、分子处在永不停息的无规则运动中。
如：扩散现象，花香等。
三、分子间作用力分子间不仅存在吸引力，而且还存在排斥力。
典例1、（2020·江苏镇江市·）下列现象中，不能用分子动理论解释的是（）A．海绵很容易被压缩B．湿衣服在阳光下逐渐晒干C．春天，校园里花香扑鼻D．高压下，油罐里的油能从罐壁渗出【答案】A【解析】A．海绵很容易被压缩，是海绵受力时形状发生改变，是宏观物体的运动，与分子动理论没有关系，故A 符合题意；B．湿衣服在阳光下晾晒时，由于温度较高，衣服上的水分子运动速度加快，所以衣服逐渐变干，与分子动理论有关，故B不符合题意；C．校园里花香扑鼻，是花香分子扩散到空气中的结果，与分子动理论有关，故C不符合题意；D．分子之间存在间隙，所以在高压下，油罐里的油从罐的分子间渗出，与分子动理论有关，故D不符合题意。
故选A。
典例2、（2020·江苏徐州市·九年级其他模拟）新冠肺炎疫情期间戴口罩能有效预防飞沫传播，要勤洗手，做好消毒工作，下列说法正确的是（）A．新冠病毒随飞沫传播是一种分子运动B．口罩有效是因为制作材料分子间没有空隙C．闻到酒精消毒液的气味是因为分子运动D．内层吸水层能够有效吸收呼出的水蒸气，说明分子之间存在斥力【答案】C【解析】A．分子很小，直接用肉眼看不到，飞沫是肉眼可以看到的；所以新冠病毒随飞沫传播是机械运动，不是分子的运动，故A错误；B．由分子热运动可知分子之间存在间隙，所以口罩材料分子之间也有空隙，故B错误；C．可以闻到酒精味，是由于酒精分子在不停地做无规则运动，故C正确；D．内层吸水层能够有效吸收呼出的水蒸气分子，吸收作用体现的是分子间存在引力，而不是斥力，故D 错误。
《分子动理论》微观粒子,宏观现象解
《分子动理论》微观粒子，宏观现象解在我们日常生活的这个世界里，存在着无数令人惊叹的现象，从香气四溢的花朵到热气腾腾的茶水，从坚固无比的金属到柔软细腻的丝绸。
而在这看似纷繁复杂的表象背后，隐藏着一个神秘而又迷人的微观世界。
这个微观世界的规律和行为，正是由分子动理论所揭示的。
分子动理论，它就像是一把神奇的钥匙，能够帮助我们打开理解宏观世界种种现象的大门。
那什么是分子动理论呢？简单来说，它是研究物质内部分子运动规律及其与宏观物理性质之间关系的理论。
让我们先来了解一下分子动理论的几个重要观点。
首先，物质是由大量分子组成的。
这些分子极其微小，肉眼无法直接看见，但它们却是构成物质的基本单元。
比如，一滴水里面就包含了难以计数的水分子。
其次，分子在不停地做无规则运动。
想象一下，在一个封闭的房间里，喷了一点香水，很快整个房间都能闻到香味。
这就是因为香水分子在空气中不断地运动、扩散。
这种无规则运动的快慢与温度有关，温度越高，分子运动就越剧烈。
再者，分子之间存在着相互作用力。
分子间既存在引力，又存在斥力。
当分子间距离较小时，斥力起主要作用；当分子间距离较大时，引力起主要作用。
那么，分子动理论是如何解释宏观现象的呢？我们先来看固体的特性。
固体具有一定的形状和体积，这是因为固体分子之间的距离较小，分子间作用力较大，使得分子只能在平衡位置附近振动，从而保持了固体的形状和体积。
液体呢，它没有固定的形状，但有一定的体积。
这是因为液体分子之间的距离比固体稍大，分子间作用力相对较小，分子能够在一定范围内自由移动，所以液体可以流动，但分子间的引力又使得液体保持一定的体积。
气体则与固体和液体有很大的不同。
气体既没有固定的形状，也没有固定的体积。
这是因为气体分子之间的距离很大，分子间作用力极其微弱，分子可以自由地运动，充满整个容器。
再来说说热传递现象。
当我们把一杯热水和一杯冷水混合在一起，最终会达到一个共同的温度。
这是因为热水中的分子运动速度快，冷水分子运动速度慢，通过分子间的碰撞和相互作用，能量从高温处传递到低温处，直到温度均匀。
《分子动理论》微观视角,宏观现象
《分子动理论》微观视角，宏观现象在我们日常生活的世界中，存在着各种各样奇妙的现象，从热气腾腾的开水逐渐冷却，到香气四溢的花朵散发芬芳，从金属的热胀冷缩，到气球中的气体可以被压缩。
这些看似平凡的现象背后，其实隐藏着微观世界的奥秘。
而分子动理论，就为我们揭示了这一微观世界的规律，帮助我们理解宏观现象的本质。
要理解分子动理论，首先得知道物质是由大量分子组成的。
这些分子非常小，小到我们用肉眼根本无法直接看到。
但可别因为它们小就忽视了它们的存在和作用。
就拿一滴水来说，看似微不足道，但这一滴水中所含的水分子数量，那可是一个极其庞大的数字。
分子在不停地做无规则运动，这是分子动理论的一个重要观点。
想象一下，在一个封闭的房间里，打开一瓶香水，不一会儿，整个房间都能闻到香水的味道。
这就是因为香水中的分子在不断地运动，从瓶子里扩散到房间的各个角落。
再比如，我们把墨水滴到清水中，过一段时间，整杯水都会变黑，这也是墨水分子无规则运动的结果。
这种分子的无规则运动，温度越高就越剧烈。
所以，煮开水的时候，随着水温升高，水的蒸发速度会加快，因为水分子运动得更活跃了，更容易从液态变成气态跑到空气中。
分子之间存在着相互作用力，既有引力，也有斥力。
当分子间的距离比较小时，斥力起主要作用；而当分子间的距离比较大时，引力起主要作用。
比如，固体很难被压缩，就是因为分子间的距离较近，斥力很大；而液体又很难被拉伸，是因为分子间存在引力，不让它们轻易分开。
气体的性质可以很好地用分子动理论来解释。
气体分子之间的距离很大，它们能够自由地运动，并且充满整个容器。
这就是为什么给气球充气时，气体能均匀地分布在气球内部。
而且，气体的压强与分子的运动和碰撞有关。
当气体分子运动得越剧烈，碰撞容器壁的频率和力度越大，气体的压强就越大。
比如，给自行车打气时，越打越费劲，就是因为车胎内气体分子增多，运动加剧，压强增大。
液体的表面张力现象也能从分子动理论的角度来理解。
由于液体表面的分子受到的内部分子的引力大于外部气体分子的引力，所以液体表面的分子有一种向内收缩的趋势，从而形成了表面张力。
1.1分子动理论-2020-2021学年高二物理同步课堂(新教材人教版选择性必修第三册)
第一章分子动理论第1节分子动理论的基本内容（一）、物体是由大量分子组成的一、分子的大小除一些有机物质的大分子外，多数分子大小的数量级为10－10m.二、分子的两种模型与阿伏加德罗常数的应用1．分子的两种模型(1)球体模型对固体和液体，分子间距比较小，可以认为分子是一个一个紧挨着的球．设分子的体积为V，由V＝43π⎝⎛⎭⎫d23，可得分子直径d＝36Vπ.(2)立方体模型由于气体分子间距比较大，是分子直径的10倍以上，此时常把分子占据的空间视为立方体，认为分子处于立方体的中心(如图2所示)，从而计算出气体分子间的平均距离为a＝3 V.三、阿伏加德罗常数1．定义：1 mol的任何物质都含有相同的粒子数，这个数量用阿伏加德罗常数表示，值为6.02×1023_mol－1，在粗略计算中可取6.0×1023mol－1.2．阿伏加德罗常数的应用(1)N A的桥梁和纽带作用阿伏加德罗常数是宏观世界和微观世界之间的一座桥梁．它把摩尔质量M mol、摩尔体积V mol、物体的质量m、物体的体积V、物体的密度ρ等宏观量，跟单个分子的质量m0、单个分子的体积V0等微观量联系起来，如图所示．其中密度ρ＝m V ＝M mol V mol ，但要切记对单个分子ρ＝m 0V 0是没有物理意义的．(2)常用的重要关系式 ①分子的质量：m 0＝M molN A.②分子的体积：V 0＝V mol N A ＝M mol ρN A (适用于固体和液体)．注意：对于气体分子V molN A 只表示每个分子所占据的空间．③质量为m 的物体中所含有的分子数：n ＝mN AM mol .④体积为V 的物体中所含有的分子数：n ＝VN AV mol .（二）、分子在做永不停息的无规则运动 一、扩散现象1．定义：不同物质能够彼此进入对方的现象．2．产生原因：扩散现象不是外界作用引起的，而是分子无规则运动的直接结果，是分子永不停息做无规则热运动的实验证据． 3．发生扩散的条件任何情况下都可以发生，与外界因素无关． 4．影响扩散的因素(1)浓度差：总是从浓度大向浓度小处扩散，两边浓度相同时，保持动态平衡； (2)物态：气态扩散最显著，液态次之，固态最慢；(3)温度：在两种物质一定的前提下，温度越高，扩散现象越显著． 5．扩散运动的两个特点：(1)永不停息；(2)无规则性．6．应用举例：在高温条件下通过分子的扩散，在纯净半导体材料中掺入其他元素． 7．扩散现象的实质：扩散现象是物质分子永不停息地做无规则运动的证明． 二、布朗运动1．定义：悬浮在液体(或气体)中的固体微粒的不停的无规则运动．它首先是由英国植物学家布朗在1827年用显微镜观察悬浮在水中的花粉微粒时发现的．2．产生的原因：大量液体或气体分子对固体小微粒撞击的不平衡造成的． 3．影响因素：(1)固体颗粒越小，布朗运动越显著； (2)温度越高，布朗运动越剧烈．4．特点：(1)布朗运动是永不停息的，说明液体(或气体)分子的运动是永不停息的． (2)布朗运动是无规则的，说明液体(或气体)分子的运动是无规则的． (3)温度越高，布朗运动越激烈，说明分子运动的剧烈程度与温度有关．5．研究对象：悬浮在液体或气体中的固体小颗粒，不是固体颗粒中的单个分子，也不是液体分子． 6．悬浮微粒的无规则运动不是分子的运动，但是它间接地反映了液体或气体分子的无规则运动． 特别提醒：①布朗运动是固体微粒的运动，热运动是分子的运动．②布朗运动间接反映了分子永不停息的无规则的热运动．三、热运动1．定义：分子永不停息的无规则运动．2．宏观表现：布朗运动和扩散现象．3．特点(1)永不停息；(2)运动无规则；(3)温度越高，分子的热运动越激烈．（三）、分子之间存在着引力和斥力．一、分子间的作用力1．分子间有空隙(1)气体很容易被压缩，表明气体分子间有很大的空隙．(2)水和酒精混合后总体积会变小，说明液体分子间有空隙．(3)压在一起的金片和铅片，各自的分子能彼此进入到对方的内部说明固体分子间也存在着空隙．2．分子间的作用力(1)分子间总是同时存在引力和斥力，实际表现出来的是它们的合力．(2)当两个分子间的距离为r0时，分子所受的引力与斥力大小相等，此时分子所受的合力为零．当分子间的距离小于r0时，作用力的合力表现为斥力；当分子间的距离大于r0时，作用力的合力表现为引力．(3)分子间作用力随分子间距离而变化，引力和斥力都随分子间距离的增大而减小，但斥力的变化比引力的变化要快．(如图1所示)当r＝r0时，F引＝F斥，F＝0.当r<r0时，F引和F斥都随分子间距离的减小而增大，但F斥增大得更快，分子力表现为斥力．当r>r0时，F引和F斥都随分子间距离的增大而减小，但F斥减小得更快，分子力表现为引力．当r≥10r0(10－9m)时，F引和F斥都十分微弱，可认为分子间无相互作用力(F＝0)．(4)分子力F随距离变化的图象如图所示，当r<r0时，合力随距离的增大而减小；当r>r0时，合力随距离的增大先增大后减小．二、分子动理论1．内容：物体是由大量分子组成的，分子在做永不停息的无规则运动，分子之间存在着引力和斥力．2．统计规律(1)微观方面：各个分子的运动都是无规则的，带有偶然性．(2)宏观方面：大量分子的运动有一定的规律，叫做统计规律．大量分子的运动受统计规律的支配．【例题1】已知水银的摩尔质量为M,密度为ρ,阿伏加德罗常数为N A,则水银分子的直径是()A. B.C. D.【答案】A【解析】1 mol水银的体积V=,1个水银分子的体积V0=,若把水银分子看成球体,则V0=πd3,所以d=。
《分子动理论》微观粒子,宏观桥梁
《分子动理论》微观粒子，宏观桥梁在我们生活的这个世界里，从微小的尘埃到浩瀚的星辰，从一滴水到一片海洋，从一个细胞到整个生物界，一切物质都有着内在的规律和联系。
而分子动理论，就像是一把神奇的钥匙，帮助我们打开了理解物质世界的大门，让我们能够从微观粒子的角度去探索宏观世界的奥秘，成为了连接微观与宏观的一座坚实桥梁。
让我们先从微观粒子说起。
在肉眼无法直接观测的微观世界里，存在着无数的粒子，如分子、原子和离子等。
这些微观粒子时刻都在不停地运动着，它们的运动并非像我们在宏观世界中看到的物体那样有规律和可预测。
想象一下，在一个封闭的容器中，充满了气体分子。
这些分子就像一群顽皮的孩子，以极高的速度四处奔跑、碰撞。
它们没有特定的方向，也没有固定的轨迹，有的只是混乱而又充满活力的运动。
而且，分子之间存在着一定的间隔。
这就意味着，即使是看起来紧密排列的物质，在微观层面上，分子之间依然存在着空隙。
分子之间还存在着相互的作用力。
当分子相互靠近时，它们会产生斥力，试图将彼此推开；而当分子相互远离时，又会产生引力，试图将彼此拉近。
这种相互作用的力量，使得分子在一定的范围内保持相对的稳定。
那么，这些微观粒子的运动和相互作用与宏观世界又有什么关系呢？这就要提到分子动理论的几个重要概念和规律了。
首先是温度。
在宏观世界中，我们用温度来衡量物体的冷热程度。
而在微观世界里，温度的本质是分子热运动的剧烈程度。
温度越高，分子的运动就越剧烈；温度越低，分子的运动就相对缓慢。
比如，在炎热的夏天，我们能感受到热气腾腾，这是因为空气中的分子运动剧烈，撞击我们的皮肤，让我们觉得燥热。
而在寒冷的冬天，分子运动减缓，传递给我们的能量减少，我们就会感到寒冷。
再来说说压强。
当我们给一个封闭的气体容器施加压力时，从微观角度看，实际上是增加了单位体积内分子撞击容器壁的次数和力量。
反之，如果减小压力，分子撞击容器壁的次数和力量就会减少。
这就是为什么打气筒能够将气体压缩进轮胎，而轮胎内的高压气体又能支撑起车辆的重量。
高二物理：分子动理论的微观量与宏观量
(3)阿伏加德罗常数NA＝6.02×1023mol－1，是联系宏观世界和微观世界的桥梁．
2．分子的两种模型
3 (1)球体模型直径为 d＝
6πV0.(常用于固体和液体)
(2)立方体模型边长为 d＝3 V0.(常用于气体，d 是两相邻气体分子间的平均
距离,并非气体分子的大小。)
3．利用阿伏加德罗常数进行微观量的估算
个气体分子占有的空间)． (4)物质所含的分子数：N＝MMmolNA＝VVmolNA＝MρmVolNA.
2.典例剖析
1．[固体、液体微观 量与宏观量] (2016·长江调研)(多 选)钻石是首饰和高
A．a
克拉钻石
所含有 的分
子数为
0
.2a M
NA
B．a
克拉钻石所 含有的
分子数
为
aNA M
强度钻头、刻刀等工 具中的主要材料，设 钻石的密度为ρ(单位 为kg/m3)，摩尔质量
d＝ 3 VNmA(立方体模型)．
4.备选训练
【备选训练】(多选)若以 μ 表示
水的摩尔质量，V 表示在标准状
态下水蒸气的摩尔体积，ρ 表示
在标准状态下水蒸气的密度，NA 表 示 阿 伏 加 德 罗 常 数 ， m0 、 V0 分别表示每个水分子的质量和
体积，下面关系正确的有( )
A．NA＝ρmV0 C．ρ<NAμV0
E 符合题意。 答案 BDE
解析显隐
3.规律方法 阿伏加德罗常数是联系宏观量和微观量的桥梁
常见微观量的求解表达式 (1)一摩尔物质的体积：Vm＝Mρ . (2)单位质量中所含分子数：n＝NMA. (3)单位体积中所含分子数：n′＝ρMNA. (4)分子间的距离：
d＝ 3 6πVNmA(球体模型)，
分子动理论物质微观粒子的运动
分子动理论物质微观粒子的运动分子动理论：物质微观粒子的运动物质的微观结构和性质一直是科学探索的焦点之一。
分子动理论是一种解释物质内部微观粒子（如分子、原子、离子等）运动特性的理论。
本文将从分子动理论的基本概念、运动规律、应用以及局限性等方面进行阐述。
一、基本概念分子动理论是通过运用统计学和热力学的方法，解释物质微观粒子在宏观尺度上表现出的性质。
它认为物质是由大量微观粒子组成的，而这些微观粒子在不断地运动着。
根据分子动理论，物质的宏观性质是由微观粒子的运动状态所决定的。
二、运动规律1. 分子运动的无规则性：根据分子动理论，微观粒子的运动是具有无规则性的。
它们的速度、方向、碰撞等都是随机发生的，符合统计规律。
这种无规则性造成了物质在宏观尺度上表现出的熵增现象。
2. 粒子间的相互作用：微观粒子之间存在着各种相互作用力，例如分子之间的万有引力、电磁力等。
这些相互作用力影响着微观粒子的运动状态，决定了物质的宏观性质。
3. 分子的碰撞与能量转移：分子之间的碰撞是微观粒子运动的重要表现形式。
在碰撞过程中，能量可以通过传递和转移的方式在粒子之间传导。
这种能量传递与转移是宏观热学现象的重要原因之一。
三、应用分子动理论的应用广泛涉及到物质的各个领域，如化学、物理、生物等。
以下是一些具体的应用示例：1. 温度和热量：分子动理论解释了温度和热量之间的关系。
温度是物质微观粒子平均动能的度量，而热量则是能量的传递和转移。
分子动理论解释了加热和散热的机制，以及它们对物质性质的影响。
2. 物态变化：分子动理论能够解释物质在不同温度下的物态变化。
例如，当物质受热时，微观粒子的动能增加，分子之间的相互吸引力减小，从而引起物质的熔化、汽化等现象。
3. 扩散和溶解：分子动理论对扩散和溶解现象也有解释。
扩散是指物质微观粒子由高浓度区域向低浓度区域的运动，而溶解是指溶质的粒子离散分布于溶剂中。
分子动理论提供了解释这些现象的基础。
四、局限性尽管分子动理论在解释物质微观粒子运动方面具有重要意义，但它仍然存在一定的局限性。
3-2-理想气体分子动理论
分子在每一个自由度上具有相等的平均平动动 能，其大小等于 1 kT。 2 上述结论可推广到振动和转动，得到：
c、气体分子之间和气体分子与器壁分子 之间的碰撞都是完全弹性的。
第二节 理想气体分子动理论
理想气体微观模型统计性假设：
1.同种气体分子的大小和质量完全相同; 2.气体分子所受的重力可忽略； 3.平衡态时，分子的位置分布是均匀的； 分子速度按方向的分布是均匀的； 4.遵循力学规律。
第二节 理想气体分子动理论
v
2 x
v
i 1
N
2 ix
P mn v
2 x
N
第二节 理想气体分子动理论
P
2 nmv x
应用统计规律
2 v2 v2 vx y z 2 vx
1 2 P nmv 3
2 vy
2 vz
1 3
v2
2 P n 3
气体分子的平均平动动能
1 2 mv 2
第二节 理想气体分子动理论
He ( x, y, z)
O
x
y
x、y、z ：平动自由度 t =3
单原子分子自由度为： i= t =3
第二节 理想气体分子动理论
b、双原子分子
H2、O2、N2、Cl2、HCl、CO
双原子分子中的两个原子是由化学键 连接起来的。
刚性双原子分子
两个原子之间的距离固定不变的分子。 非刚性双原子分子(不讨论)
P
T1 T2 T3
P1
0
T1 T2
T3
等温线
V1
V
第二节 理想气体分子动理论
二、理想气体微观模型
理想气体是气体的一种理想化的模型，这是 为了突出气体的主要因素，忽略次要因素。 共性： 在通常的压强和温度下，一般气体都遵从 气体的三条实验定律，亦即它们在P、V、 T的变化关系上都具有共性。 个性： 不同的气体遵从三条实验定律的准确程度不同。 目的： 揭示气体所遵循的共同规律性，为研究真实气 体的规律奠定基础。
分子动理论的主要内容是什么
分子动理论的主要内容是什么
分子动理论是描述气体、液体和固体微观结构和性质的理论框架，其主要内容包括以下几点：
1. 分子模型：分子动理论假设物质是由大量微观粒子（如分子、原子等）组成的。
这些微观粒子在空间中不断运动，并且彼此之间存在相互作用。
2. 分子运动：分子动理论认为，物质的宏观性质（如压强、温度等）是由微观粒子的运动状态决定的。
分子在空间中做各种随机运动，包括平动、转动和振动等。
3. 碰撞：分子之间存在相互作用力，它们会不断地发生碰撞。
碰撞导致分子的能量转移和动量变化，从而影响物质的宏观性质。
4. 理想气体模型：分子动理论假设理想气体中的分子是无限小的、质量可以忽略不计的硬球，它们之间不存在相互作用力。
根据这些假设，可以推导出理想气体的状态方程和热力学性质。
5. 宏观性质的解释：分子动理论可以解释许多宏观性质，如气体的压强、体积、温度等，以及相变过程中的能量转移和吸放热等现象。
6. 热力学规律：分子动理论与热力学定律相一致，如玻意耳定律、查理定律、阿伏伽德罗定律等。
总的来说，分子动理论是描述物质微观结构和性质的重要理论框架，它通过研究微观粒子的运动状态和相互作用来解释物质的宏观性质和行为。
分子动理论
一些人获得更多的成就，
主要是由于他们对放在他
们面前的问题比起一般人
能够更加专注和坚持，而 不是由于他的天赋比别人 高多少。 ______道尔顿
道尔顿 1766年9月6日出生在英国的昆布兰地区， 父亲是个农村工匠，收入低微，养不起道尔顿兄弟姐 妹 6 人。使得道尔顿的小妹妹和小弟弟冻饿而死。这 件事在道尔顿的心灵中，留下了一个永久的伤痕。
道尔顿还研究过颜色，首先发现了人类的色盲现 象，他在1794年，出版了《关于各种颜色显现程度的 反常视例》一书，介绍了人类的色盲情况。他通过实 验发现，有相当多的人都有色盲症，他的兄弟姐妹， 几乎都有这种病，他自己也有轻微的色盲症。由于道 尔顿发现了色盲症，并且他本人也有轻微的这种病， 所以欧洲人当时把色盲症叫“道尔顿病”，至今有些 地方还在这样叫。
理想单原子气体：质心位臵 3个坐标（x,y,z) （自由度数是3）
11 1 1 1 1 2 2 2 2 mv x mv y mv z mv kT 32 2 2 2 2
3 kT 2
理想气体分子，每一个自由度的平均平动能都是
1 kT 2
刚性分子：
单原子分子自由度 3 双原子分子自由度 5 多原子分子自由度 6
0
v 2 Nf ( v)dv N
3kT v m
vrms v
2
3kT m
3RT
2kT RT vp 1.41 m
v 1.60 8kT RT 1.60 m
分布 碰撞次数 平均动能
vrms
f (v )
3kT RT 1.73 m
vp v v
授课教师： 吴 艳 茹
实验结论：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3 3 m 28.9 10 1% 0.289 10 kg Ar质量 3
m3 0.289 0.007 摩尔数 v3 M mol 3 40
1mol空气在标准状态下的内能
i3 i1 i2 E v1 RT v2 RT v3 RT 2 2 2 1 (i1v1 i2 v2 i3v3 ) RT 2
理想气体系统由氧气组成，压强P =1 atm，温度T = 27℃。求（1）单位体积内的分子数；（2）分子 的平均平动动能和平均转动动能；（3）单位体积 中的内能。
解（1） 根据
p nkT
p 1.013105 25 3 n 2 . 45 10 m kT 1.3810 23 300
n dN N dV V
平衡态分子速度取向各方向等概率
vx v y vz
2 2 1 v2 vx v2 v y z 3
分子数目很大，满足大概率事件
三、理想气体压强公式
器 壁
气体分子
总的效果是一个持续的平均作用力
研究对象：一定质量处于平衡态的理想气体 宏观：大量分子频繁撞击容器壁的结果 微观：容器壁单位时间、单位面积所受的平均冲力
度的转动能量相等，而且均等于 kT 2
在温度为T 的平衡态下，气体分子的每一个自
由度都平均地具有 kT/2 的动能。
3. 理想气体的内能
动能 • 热力学系统的内能
相互作用势能
化学能、核能
•理想气体内能-----分子平动动能与转动＝ kT N A RT 2 2
二、 研究分子运动规律的方法
研究对象：热力学系统（宏观系统） 包含大量分子、 原子构成的系统 分为孤立系统、封闭系统和开放系统 热 力 学 研究方法：
分子动理论
宏观量 ( Macroscopic quantity ) 表征系统整体的物理量，可直接测量 如气体质量、体积、压强、温度等 广延量（可加性） 强度量（无可加性） 微观量 （Microscopic quantity） 描述微观粒子个体的物理量，一般不易直接测量 如分子质量、直径 、速度 、动量 、能量等
摩尔理想气体的内能
i E＝ RT 2
理想气体内能仅是温度的函数
在一个具有活塞的容器中盛有一定的气体。如果压 缩气体并对它加热，使它的温度从27℃升到177 ℃ ，体积减少一半，求：
（1）气体压强变化多少？ （2）这时气体分子的平均平动动能变化多少？
解：
(1)
p1V1 p2V2 T1 T2 由已知 : V1 2V2 , T1 273 27 300 K , T2 273 177 450 K
一、 理想气体状态方程 1. 平衡态（Equilibrium
state ）
热力学系统------大量微观粒子（分子、原子等） 组成的宏观物体 热平衡态-----在不受外界影响的条件下，系统宏观
性质不随时间改变的状态
平衡条件： (1)系统与外界宏观上无能量和物质交换
(2)系统宏观性质不随时间改变
条件：气体质量不变
R 8.31J mol1 K -1
m pV RT vRT M
23 1
R 23 -1 玻尔兹曼常数 k 1.3810 J K NA m N 假设N为体积为V 内的气体分子数总数 v
N A 6.02310 mol
M
NA
p nkT
n 单位体积中的分子数
i tr3
双原子分子 平动自由度 t =3 转动自由度 r =2
y
x z
C ( x, y, z )
y
i tr5
三原子分子
平动自由度 t=3 转动自由度 r=3
z
C ( x, y, z )
x
平动 t 转动 r 0 2 3
i tr6
单原子分子：He… 双原子分子：O2… 多原子分子：NH3 … 3 3 3
1 分子的平均平动动能 t m0 v 2 2
说明：
统计关系式
宏观可测量量
2 p n t 3
微观量的统计平均值
1）物理意义： 揭示了压强的统计意义
表明了压强的两个影响因素
2）适应范围： 含有大量分子的热力学系统 3）动态影响： T不变，V↓→p↑ V不变，T↑→p↑
2. 温度的统计解释
2. 状态参量
(State Quantity )
在热学、热力学系统中，表示物体宏观性质 的物理量------状态参量
p 气体对单位面积容器壁的正压力 (Pa)
(力学参量)
V
气体所能达到的空间 (几何参量)
宏观上表示物体的冷热程度 微观上反映分子运动的剧烈程度 (热力学参量)
(m )
3
T
(K)
3. 理想气体状态方程 p1V1 p2V2 T1 T2 一般形式
混合气体总压强等于组成该混合气体各成分气 体的分压强之和。
解：容器内不同气体的温度相同，分子的平均平动动能也相同。
t1 t 2
分子数密度满足
ti
tn
n ni
2 2 2 P n tk ni ti ni ti Pi 3 3 3
1 3 3kT 3RT m0 v2 kT v2 2 2 m0 M
四、能量均分定理与理想气体内能 1. 自由度 i 确定一个物体的空间位置所需要的独立坐标数目。
单原子分子
双原子分子
多原子分子
以刚性分子（分子内原子间距离保持不变）为例
单原子分子
平动自由度 t =3
z
C ( x, y, z )
1 (5 0.789 5 0.208 3 0.007) 8.31 273 2 3 5.68 10 J
本次课小结
1.理想气体的状态方程
m pV RT vRT M
p nkT
2.压强、温度与平均平动动能的关系
2 p n 3
1 t m0 v 2 2
二、理想气体微观模型
1.理想气体分子模型（力学性质假设）
质点 (线度<<间距)，服从牛顿定律 除碰撞瞬间，分子间、分子与器壁无相互作用
分子间、分子与器壁间的碰撞为完全弹性碰撞
弹性 自由运动 质点 模型
在压力不太大、温度不太低时，与实际附合很好
2.理想气体分子性质（分子集体统计性假设）
同种气体分子大小、性质相同 无外场时，平衡态分子按位置均匀分布
2 mol 水 2 mol 氢气 1 mol 氧气
UH2O 6RT UH2 5RT
U O2 5 RT 2
U
H2
U O 2 U H 2O U H 2O
7.5 6 25% 6
就质量而言，空气是由76%的N2，23%的O2和1%的Ar 三种气体组成，它们的分子量分别为28、32、40。空气 的摩尔质量为28.910-3kg，试计算1mol空气在标准状态 下的内能。
热运动(thermal motion)
3. 分子间存在着吸引力与排斥力
C1 C2 表 达 式： F m n r r ( m n)
C1 rm
平衡位置： r0 1010 m 吸引力
r r0
C2 rn
分子间作用力曲线
排斥力 r r0
分子力是短程力，有效作用距离： 102d
Chap.5 Kinetic Theory of Molecular
理想气体状态方程
理想气体压强公式
能量均分定理 理想气体内能 重点：气态方程、压强与温度的微观本质 难点：统计概念与方法
第一节 物质的微观模型
一、气体动理论的基本观点 1. 物质是由大量的原子或分子组成，分子间存在间隙 2. 分子或原子都在做永不停息的无规则运动 特点：小、多、快、乱
研究方法：
单个分子 对容器壁 的平均作 用力 所有分子 对容器壁 的平均作 用力 利用压强 定义与统 计求平均
利用等概
率原理
理想气体 压强
1.理想气体压强公式 考察单个分子i 对A2面的作用力
N个同类气体分子，每个分子质量均为m
考虑第 i 个分子，其速度 vi vixi viy j viz k y
N
N
2 v ix
利用统计平均概念 平均值
v v v v ＝ N N
2 x 2 1x 2 2x 2 Nx
p nm0 v
2 x
等概率原理：分子沿各个方向运动的机会均相等
vx v y vz
2 2 2
2
2
2
1 2 vx v y vz v 3
2 1 2 1 2 2 p nm0 v n ( m0 v ) n t 3 3 3 2
V1T2 2V2 450 p2 p1 3 p1 V2T1 V2 300
(2) 3 kT 2
3 t 2 t1 k (T2 T1 ) 2 3 1.38 1023 (450 300) 3.111021 J 2
利用理想气体的压强公式推到Dalton 分压定律。
宏观量总是微观量的统计平均值
分子热运动的无序性及统计规律性
•单个分子的运动具有无序性 •大量分子的运动具有规律性 统计规律是指大量偶然事 件整体所遵循的规律。方 法——求统计平均值 统计规律特点: （1）只对大量偶然的事件才有意义 （2）它是不同于个体规律的整体规律 （3）总是伴随着涨落
第二节 理想气体分子动理论
2
单位时间单个分子施于器壁A2的平均作用力
I i m0 v ix Fix t l1
所有分子对A2面的平均作用力