华中科技大学土木工程与力学学院
985 211 土木专业学校

985大学北京大学山东大学土建与水利学院大连理工大学上海交通大学土木工程系华中科技大学土木工程与力学学院东北大学资源与土木工程学院天津大学建筑工程学院土木系东北大学土木工程研究所同济大学土木工程学院浙江大学城市学院厦门大学土木工程系清华大学土木工程学会浙江大学土木系清华大学土木工程系中南大学土木建筑学院211大学北京工业大学建工学院石河子大学水建学院长安大学南京理工大学土木工程系大连海事大学四川大学建筑与环境学院土木系东北林业大学土木工程学院太原理工大学建筑与土木工程学院东南大学土木建筑学院武汉理工大学土木工程与建筑学院福州大学土木工程学院西南交通大学土木工程学院广西大学土木建筑工程学院新疆大学河海大学土木与交通学院新疆大学建筑工程学院湖南大学土木工程学院云南大学城市建设与管理学院土木工程系华南理工大学土木与交通学院郑州大学江南大学环境与土木工程学院中国矿业大学(北京)力学与建筑工程学院内蒙古大学交通学院上海大学土木工程系南昌大学建筑工程学院北京交通大学土木建筑学院重庆大学土木工程学院北京林业大学土木系普通大学安徽工业大学上海师范大学安徽建筑工业学院石家庄铁道大学安徽理工大学土木学院绍兴文理学院深圳大学土木工程学院沈阳建筑大学土木工程学院沈阳大学建筑工程学院沈阳建筑大学地铁研究所北京建筑工程学院土木与交通工程学院沈阳建筑大学北京建筑工程学院苏州科技学院土木学院北京耐恒检测科技发展有限公司台州学院建筑工程长江大学城市建设学院山东科技大学土木建筑学院长沙理工大学土建学院天津城市建设学院土木工程系长沙理工大学交通运输工程学院铜陵学院长沙大学土木工程系皖西学院常州大学皖西学院建筑与土木工程系常州工学院潍坊学院建筑工程学院重庆交通大学土木建筑学院科技处温州大学建筑与土木工程学院成都大学城乡建设学院温州大学建工学院大连大学建筑工程学院五邑大学土木建筑学院大连大学土木教研室武汉工程大学大连海洋大学土木工程学院武汉工程大学环境与城市建设学院大连民族学院土木建筑工程学院武汉工业学院土建学院武汉科技大学武汉理工大学出版社东北电力大学建筑工程学院西安建筑科技大学东北石油大学土木建筑工程学院西安建筑科技大学土木工程学院福建工程学院土木工程系西安科技大学福建农林大学交通学院西安理工大学土木系福建三明学院西北工业大学力学与土木建筑学院广东工业大学土木与交通工程学院西北农林科技大学水利与建筑工程学院广东石油化工学院建筑工程学院西华大学建筑与土木工程学院广西工学院土木建筑工程系西南科技大学土木工程与建筑学院广西工学院鹿山学院西南林业大学交通与土木工程学院广州大学土木工程学院厦门理工学院土木工程与建筑学院贵州大学土木建筑工程学院湘潭大学土木工程与力学学院贵州民族学院建筑工程学院湘潭大学贵州师范大学材料与建筑工程学院孝感学院哈尔滨工业大学孝感学院城市建设学院桂林理工大学应用技术学院烟台大学土木学院哈尔滨工业大学土木工程学院盐城工学院哈尔滨学院工学院盐城工学院土木工程学院杭州邦威机电控制工程有限公司燕山大学合肥工业大学土木与水利工程学院扬州大学建筑科技与工程学院合肥学院建筑工程系云南农业大学建筑工程学院河北大学建筑工程学院浙江工业大学河北工程大学土木工程学院浙江工业大学建筑工程学院河北科技大学建筑工程学院浙江海洋学院船舶与建筑工程学院河北科技师范学院城市建设学院浙江科技学院建筑工程学院河北农业大学城建学院浙江树人大学城建学院河南城建学院土木与材料工程系郑州大学出版社河南大学土木建筑学院中国电力大学出版社河南工业大学土木工程系中国计划出版社河南信阳师范学院土木工程学院中国建筑工业出版社黑龙江科技学院建筑工程学院中国建筑工业出版社教材中心湖北工业大学中国矿业大学(江苏) 建筑工程学院力学湖南城市学院土木工程学院中国土木工程学会湖南工业大学土木工程学院中南林业科技大学湖南工学院建筑系重庆科技学院建工学院土木系湖南科技大学土木工程学院青海大学土木工程学院湖南科技学院土木工程与建设管理系清华大学建设管理系湖南理工学院土木建筑工程学院人民交通出版社湖南文理学院人民交通出版社土木中心华北科技学院土木工程系三峡大学土木与建筑学院华北水利水电学院山东科技大学土木建筑学院华东交通大学土木建筑学院山东理工大学建筑工程学院华南农业大学土木与水利工程学院陕西理工学院华侨大学土木工程学院宁波大学建筑工程与环境学院华中科技大学武昌分校城市建设学院宁波工程学院建工学院化学工业出版社攀枝花学院土木工程学院淮海工学院土木工程学院青岛理工大学土木工程学院淮阴工学院建筑工程学院青岛农业大学建筑工程学院机械工业出版社内蒙古农业大学水利与土木建筑工程学院吉林北华大学交通建筑工程学院南通大学吉林北华大学南京工业大学交通学院吉林建筑工程学院交通科技与工程学院南京工程学院建工学院吉林建筑工程城建学院南京工程学院建筑工程学院吉林建筑工程学院土木工程学院南京工业大学土木工程学院济南大学南京工业大学交通学院佳木斯大学建筑工程学院南京航天航空大学土木系佳木斯职教集团建筑工程系南京理工大学泰州科技学院嘉兴学院建筑工程学院南京林业大学土木工程学院江苏科技大学土木学院南阳理工学院土木系江苏科技大学(张家港校区)土木学院兰州理工大学土木工程学院江西科技师范学院建筑工程学院辽宁工程技术大学土木与交通学院科技出版社鲁东大学土木工程学院昆明理工大学土木系内蒙古工业大学土木工程学院昆明理工大学建筑工程学院内蒙古科技大学昆明学院城乡建设与工程管理系兰州交通大学土木工程学院学院力学。
土木类国家教学名师
张亚英,王强,甄进平,韩宇峰,赵春荣
111
国家“十五”规划教材《水工建筑物》(教材)
天津大学,大连理工大学,西安理工大学
林继镛,张社荣,林皋,练继建,苗隆德,彭新民,杨敏,迟世春
240
开放•交叉•融合—以设计创新为核心的建筑学专业本科教学新体系
东南大学
王建国,钱强,龚恺,韩冬青,陈薇
国家级教学成果奖获得者名单(2014年):
一等奖:
序号
成果名称
完成单位
完成人
24
20年磨一剑——与国际实质等效的中国土木工程专业评估制度的创立与实践
同济大学、高等教育土木工程专业评估委员会、东南大学、苏州科技学院、南京工业大学、哈尔滨工业大学
李国强、沈祖炎、赵琦、邱洪兴、何若全、陈以一、孙伟民、何志方、何敏娟、赵宪忠、邹超英
哈尔滨工业大学
梅洪元、孙澄、周立军、邵郁、徐洪澎、李玲玲、邢凯、陆诗亮、史立刚
186
建筑学科创新型人才培养教育体系的探索与实践
华南理工大学
孙一民、肖毅强、冯江、庄少庞、苏平
214
面向转型期我国城乡建设需求的城乡规划专业人才培养体系改革与实践
西安建筑科技大学
刘克成、陈晓键、段德罡、周庆华、李昊、任云英、惠劼、白宁、王侠、李小龙
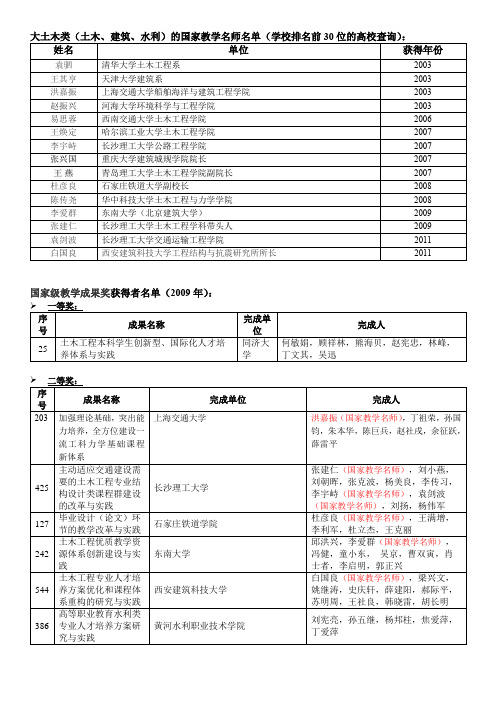
大土木类(土木、建筑、水利)的国家教学名师名单(学校排名前30位的高校查询):
姓名
单位
获得年份
袁驷
清华大学土木工程系
2003
王其亨
天津大学建筑系
2003
洪嘉振
上海交通大学船舶海洋与建筑工程学院
2003
赵振兴
河海大学环境科学与工程学院
2003
易思蓉
不满学校职称评审状告教育部 武汉一大学讲师败诉

不满学校职称评审状告教育部武汉一大学讲师败诉千龙网讯武汉一名大学讲师因不满学校职称评审向法院起诉,状告教育部行政不作为,6月10日,北京市第一中级人民法院对该案进行了一审宣判,讲师败诉。
据法院介绍,今年49岁的华中科技大学土木工程与力学学院讲师王晓华,因其在学校举行的高级专业技术职务资格评审中未通过副教授的资格评审,认为学校在资格评审工作中存在弄虚作假的问题,而教育部又对其提出的行政复议作出了不予受理决定,因而向法院起诉。
2002年,华中科技大学进行了高级专业技术职务的评聘工作。
评聘委员会认定王晓华在学校没有主持或参加过一项科学研究项目,不符合《华中科技大学申报专业技术职务的条件》中副教授任职资格。
王晓华认为其符合副教授的任职资格,该校在职称评定问题上存在弄虚作假问题,故多次向湖北省教育厅及教育部等部门反映、检举。
2002年12月,湖北省教育厅作出了“对王晓华职称问题申诉的复函”,经调查,认为王晓华反映的问题是不属实的,并希望其进一步努力,为评聘高一级教师职务创造条件。
2003年1月,王晓华向教育部递交了“行政复议及检举信”。
而教育部作出行政复议不予受理决定,理由为华中科技大学是经过国家批准具有评定副教授职务资格的高等学校,该校具有制定具体的评聘条件和程序,并组织相应的教师职务评审委员会的法定权力,教师职务评审委员会的评审行为不属于具体行政行为,王晓华因不符合条件而未能通过教师职务评审,属于学校内部的正常管理活动。
法院认为,根据高等教育法第37条的规定,评聘教师及其他专业技术人员职务是高等学校的自主权。
华中科技大学专业技术职务评聘委员会有权在教育部核定的专业技术职务岗位的职数范围内对副教授的任职资格进行审定,教育部据此对王晓华提出的行政复议申请不予受理是正确的。
宣判当天,王晓华表示将继续提起上诉。
出庭的教育部委托代理人认为,这个案件看似告的是教育部,其实是高校人事制度改革与旧的人事制度的冲突。
现在高校中有很多教师年龄大、资格老,但是学术水平相对年轻一些的教师来说有一定差距。
桥梁检测与加固实验报告

桥梁检测与加固实验报告学生姓名:施宏侣学生学号: U201215572所在班级:道桥1202班华中科技大学土木工程与力学学院2016年01月目录实验一混凝土块无损实验实验二悬索桥缩尺模型实验实验三钢筋混凝土梁正截面受弯性能实验实验四连续梁荷载横向分布实验实验五、钢框架动载试验实验一、混凝土块无损实验【实验时间】2015年12月18日上午【实验说明】一、无损实验包括混凝土完整性、裂缝深度、钢筋保护层厚度和钢筋分布实验。
试验模型试验仪器如图,在混凝土块的右侧划线交点处作为节点来通过超声波测时间来检测混凝土块中是否有损伤。
裂缝深度是通过将仪器对准一条侧线测超声波的速度来反映是否有裂缝,如有裂缝则速度会发生改变。
【实验数据】混凝土完整性实验数据图一图二混凝土裂缝深度实验数据图三钢筋保护层厚度和钢筋分布实验由于实验仪器故障,故未做。
a b c d e f g h i101112a b c d e34561501251007550507510012515093.290.893.2141.6149.21.0731.6522.1461.7662.011无裂缝15012510075505075100125150102.01132.48098121.20.9801.1332.52.5512475有裂缝T/μs T/μs V/km/sV/km/s【实验分析】根据图一完整性实验数据分析,我们知道速度均在4.2km/s和3.9km/s 附近变化,说明其混凝土块还是有损伤的,不然在同样距离的情况下,超声波传播的速度应该是一样的,有图可知,b方向应该是完整性较好,其他线都或有损伤。
图二为另一方向的完整性测试,速度在4.0km/s和3.6km/s附近变化,也发现其有损伤。
有无裂缝对超声波传播的速度也是有影响的,在无裂缝情况下,超声波会沿着最短的路径传播,而如果有裂缝的话那超声波的传播速度就会变化,图三就反映了这种变化。
实验二、悬索桥缩尺模型实验【实验时间】2015年12月18日下午【实验说明】(一)静载试验1、贴应变片;2、安装位移计;3、预加载:预加载一级荷载(在主跨L/2、L/4、3L/4,边跨L/2上同时加载),每加载点15kN,每级停歇5分钟后读取数据。
-结构动力学试卷及答案
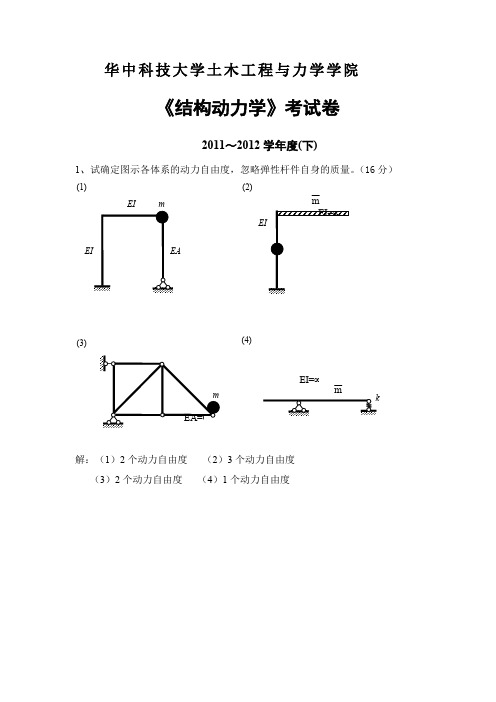
华中科技大学土木工程与力学学院《结构动力学》考试卷2011~2012学年度(下)1、试确定图示各体系的动力自由度,忽略弹性杆件自身的质量。
(16分)m(1)(2)EIm(3)(4)mEI=∞解:(1)2个动力自由度 (2)3个动力自由度 (3)2个动力自由度 (4)1个动力自由度2、试求图示结构的自振频率(15分)ωAB解:图示结构为单自由度体系,以横梁转角为自由度。
ϕ由 有:0A M =∑ 2220lm x dx ml kl ϕϕϕ⋅⋅⋅⋅++=⎰化简得:()303klm m ϕϕ⋅⋅+=+ 自振频率∴ω=3、如图所示体系,各杆长为l ,EI=常数,1处有集中质量m ,2处受动力偶;,试建立体系的微分方程,并作出动弯矩幅值图。
()M t =M sint θθ(14分)lsin M tθ解:结构体系的、如下图所示:1M p Ml1MpM sin M tθ3111122=2EI 233l l l l EIδ⎛⎫∴⨯⨯⨯⨯=⎪⎝⎭ 21111sin sin 236MMl l l M t t EI EI θθ⎛⎫∆=⨯⨯⨯= ⎪⎝⎭ 体系微分方程为:∴()321112sin 36M t l Ml y m y m y tEI EI δθ⋅⋅⋅⋅⎛⎫⎛⎫=-+∆=-⋅+⋅ ⎪ ⎪⎝⎭⎝⎭33sin 24EI My y t ml mlθ⋅⋅⇒+⋅=⋅2max23331133344622M M Ml y EI EI EI ml ml EIml ml ml θ∴=⋅=⋅=---惯性力幅值∴22max3362EI Ml MI m y m ml EI lθ==⋅⋅=4、图示(a )所示梁的跨中有一台电动机,实测得此梁自由振动时跨中点位移时程曲线如图所示(b ),周期T=0.06s ,若忽略梁的分布质量。
(20分)(a)()y t (b)试求:(1)阻尼比;(2)共振时的动力系数;(3)共振时电动机每分钟ξβ的转数 n ;(4)若电动机转数为600r/min ,由于其离心力引起梁中点稳态的振幅为2mm ,求共振时的振幅A 。
华中科技大学土木工程与力学学院学院 2010~2011学年度第二学期课表

周 次 1 2 3 4 5 6 上 7 课 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
考 试
教学进程
课程名称 学时数 学 分上课考 试理论力学(一) 80+8(实验)/5.5 郑慧明(副教授) 大学物理(一)56/3.5 喻力华(副教授) 微积分(一)下88/5.5 贺云峰(讲师) 中国语文32/2 骆琳(副教授) C++语言程序设计36+20(上机)/3.5 张建国(讲师) 思政课社会实践32/2 肖会平(讲师)
1
2
3
4
5
6 上
7 8 课
9
10 11 12 13 14 15 16 17 18 19 20 21 22 考 试 考 试 上 课
任课教师姓名职称
专业班 星期 节次
工程力学0801-0802班 55人 工程力学0801-0802班(55人) 0801 复合材料力学 10-12、14-18 振动力学 1-10 西十二N406 西十二N405
院(系)主管教学负责人签字: 主管教学负责人签字:
李黎
制表人: 制表人:程建国
联系电话: 联系电话:87543238
17——2
2010~2011学年度第二学期课表 华中科技大学土木工程与力学学院学院 2010~2011学年度第二学期课表
周 次 教学进程
课程名称 学时数 学 分 实验力学48+32(实验)/5 匡健(副教授) 疲劳与断裂40/2.5 杨新华(教授) 复合材料力学32+8(上机)/2.5 陈建桥(教授) 形势与政策3 刘家俊(教授) 振动力学40+8(实验)/3 何锃(教授) 实验流体力学24+8(实验)/2 李万平(教授) 工程材料力学性能测试24(实验)/1.5 李建兵(讲师) 毕业实习3W/3 胡洪平(副教授)、张雄(讲师)
理论力学06——08试题

五、 半径为 r 的均质圆盘 B 由均质连杆 AB 和曲柄 OA 带动,在半径为 5r 的固定 得分
圆上运动,圆盘 B 与固定圆之间光滑无摩擦。AB=4r,OA=2r. B 为圆盘 B 的质心。 OA 的质量为 m/2, 圆盘 B 和连杆 AB 的质量均为 m..在图示位置 OA 以匀角速度 转动,求此瞬时固定圆对圆盘 B 的约束力。 (限用动静法求解,其它方法不
华中科技大学土木工程与力学学院 《理论力学》考试卷(A 卷,闭卷) (机械大类专业用) 2008~2009 学年度第一学期
学号 题号 得分 一、判断题(每小题 2 分,共 10 分) (正确的在括号内画√,错误的画×) 1. 如图圆轮在力偶距为 M 的力偶和力 F 的共同作用下平衡, 这说明一个力 偶可用一个合适的力与之平衡。 ( ) 一 专业 二 三 班级 四 五 六 姓名 七 总分
华中科技大学土木与力学学院 《理论力学》考试卷(A 卷,闭卷)
(限机类大平台 60 学时学生使用) 2006~2007 学年度第一学期 成绩 学号
题号 得分 得分 一、画受力图及基本计算题( 6分 6 36分 ) 一
专业
二 三
班级
四
学生姓名
五 六 总分
1 在图示结构中,各构件的自重及各处摩擦力忽略不计,在 BC 上作用一力偶矩为 M 的力偶。
画出整体和部件 DAC 和 BC 的受力图(要求受力图中力的个数最少) 。
2 水平圆盘的半径为r , 外缘C处作用已知力F。力F位于圆盘C处的切平面内,且 与C处圆盘的切线夹角为60 o ,其他尺寸如图所示。求力F对z轴之矩。
第 1页 / 共8页
3 均质箱体 ABCD的宽度 b 1 m, 高 h 2 m, 重 P 200 kN, 放在倾角为30 o的 斜面上。箱体与斜面之间的摩擦因数 f s 0.2。今在箱体的 C点上作用一个 恒力 F,其方向如图。求使箱体处于平衡状态的最小 F。
华中科技大学土木工程及力学学院

华中科技大学土木工程与力学学院2012年统招硕士研究生复试工作安排(不含力学专业)根据研究生院的总体部署,我院2012年硕士研究生入学考试的复试工作(工程管理硕士除外)将于3月26日开始,报考专业学位工程管理硕士(代码125600)复试工作于4月4日开始。
为了有序地、稳妥地完成此项工作,现将全院复试工作安排如下:学院不再以邮寄等其它方式发2012年统招硕士研究生复试工作安排(力学专业)根据研究生院的总体部署,我系2012年硕士研究生入学考试的复试工作将于3月31日开始。
为完成好此项工作,现将力学系复试工作安排如下:2012年土木工程与力学学院研究生入学考试复试线力学专业可接收部分院内外优质调剂生,申请调剂的考生须满足以下条件:1、符合学校调剂要求,总分在340分以上;2、本科阶段学习过2门(含)以上力学专业核心课程且成绩优良;3、服从专业分配(力学有三个专业:流体力学、固体力学、工程力学);4、调剂申请截止日期为:3月26日17:00;5、复试名单将于3月27日17:00上网公布。
华中科技大学土木工程与力学学院2012年硕士研究生复试及录取工作细则2012年硕士研究生入学考试的复试工作即将开始,按照学校统一部署, 本着“公正、公平、公开”的原则,特制定以下复试及录取细则:1.学院成立研究生招生工作领导小组,对整个复试工作和录取进行统一领导。
2.根据学校和学院校划定的分数线,参加复试的生源比例一般按120%掌握(含调剂生)。
3.对以同等学力报考的考生,加强对本科专业课程和实验技能的考核,加试两门专业基础课程。
4.复试由专业课笔试、外语听力口试和综合面试三部分组成。
5.复试成绩总分为100分,由各分项成绩加权组成,即复试成绩=笔试成绩×40%+综合口试成绩×40%+听力及口试成绩×20%。
6.考生的总成绩由初试成绩和复试成绩加权组成,即总成绩=0.6×初试成绩/5+0.4×复试成绩。
振动与冲击 JOURNAL OF VIBRATION AND SHOCK

第26卷第4期Vol. 26 No. 4 2007振动与冲击 JOURNAL OFVIBRATION AND SHOCK运用小波分析方法进行结构模态参数识别朱宏平,翁顺(1.华中科技大学土木工程与力学学院,武汉430074)摘要结构的模态参数反映了结构自身特性,是基于动态特性的结构损伤识别和健康评估的重要因子。
本文首 先介绍了环境激励下基于小波分析的模态参数识别方法,针对土木工程结构的前几阶自振频率处于低频区域以及环境激 励下结构响应信号信噪比很低的特点,着重论述了采用小波方法抑制原始测量信号中的高频成分(即噪音),从而突出结 构低频特性的降噪处理方法的基本原理。
通过比较传统傅里叶变换、短时傅里叶变换和小波变换三种方法对一实际高层 建筑结构现场测试信号的处理结果以及有限元分析结果,认为小波分析方法可以更精确、更有效地识别工程结构的模态 参数。
关键词:傅里叶变换,短时傅里叶变换,小波变换,降噪,模态参数中图分类号:TN911.6; TU311.4 文献标识码:A在高层建筑抗震、抗风、健康监测及损伤诊断等研 究中,结构模态参数是非常重要的设计参数之一,基于 环境激励的模态参数识别方法越来越受到人们的重 视[1]。
目前国内外在结构模态参数识别方面的研究方 法有很多,主要可以分为:①频域方法:它是建立在频 响函数的理论基础上的,频域法的最大优点是利用频 域平均技术,最大限度地抑制了噪声影响,使模态定阶 问题容易解决,但也存在着如功率泄露、频率混叠、离 线分析等问题)②时域方法:是直接利用响应的时域信 号进行模态参数识别。
与频域法相比,时域法对于分 离密集模态有更好的效果;③小波分析法[2(:比短时傅 里叶变换具有更好的时频窗口特性,克服了傅里叶变 换中时-频分辨率恒定的弱点,因此它能在具有足够 时间分辨率的前提下分析信号中的短时高频成分,又 能在很好的频率分辨率下估计信号中的低频。
④基于 H HT 变换的非平稳信号的处理方法:它以瞬时频率 为基本量,以固有模态信号为基本信号,用于非平稳 信号处理;⑤基于模拟进化的模态参数识别的方法:该方法实现了基于达尔文进化理论的整体优化算法 用于识别线性振动结构的模态参数。
华中科技大学土木工程与力学学院2015~2016学年度第一学期课表

9—11 形势与政策 15周 西五楼417(与电气、力学合班)
备注
说明
1、《交通安全实验》教师自行安排实验时间与地点。(与交运合班) 2、《交通工程实验》教师自行安排实验时间与地点。 考试时间安排:(本学期课程考试时间如下,具体通知以届时考试安排为准。) 1、《交通心里与安全》第10周周1(2015年11月2日)上午; 2、《管理学与企业管理》第 3、《运输与物流设备》第12周周1(2015年11月16日)下午; 4、《交通工程》第20周周1 5、《专业英语》第20周周3(2016年1月13日)下午; 6、《工程力学(二)》第2 7、《仓储与配送管理》第21周周1(2016年1月18日)下午; 8、《电子商务与物流设备》
华中科技大学土木工程与力学学院2015~2016学年度
周 次 1 2 3 4 5 6 7 8 9 上
形势与政策3(上课)(吕良洪/副教授)
10 11 12 13 课
教学进程
课程名称
专业英语32/2(陈星/讲师) 交通心里与安全32/2(张席洲/副教授) 电子商务与物流信息系统32/2(叶艳兵/讲师) 运输与物流设备32/2(张席洲/副教授)
管理学与企业管理 1-8周 东五楼114 电子商务与物流信息系统 11-18周 东五楼114 交通工程 1-10周 东五楼114 仓储与配送管理 11-18周 东五楼114 交通心里与安全 1-8周 (与交工合班) 西十二楼N411 路面管理与管理系统 9-14周 东五楼114 专业英语 11-18周 东五楼114 东五楼114 东五楼114 管理学与企业管理 1-8周 东五楼114 电子商务与物流信息系统 11-18周 东五楼114
工程力学(二) 1-15周 运输与物流设备 1-8周
实验报告

《结构试验》教学实验指导书及实验报告熊世树编写学生姓名:***学生学号:U*********所在班级:道桥1101班华中科技大学土木工程与力学学院2014年05月目录实验一钢筋混凝土梁正截面受弯性能实验钢筋混凝土梁正截面受弯性能实验报告实验二悬索桥缩尺模型实验悬索桥缩尺模型实验报告实验三混凝土强度、缺陷及保护层厚度无损检测混凝土强度、缺陷及保护层厚度的检测报告实验四钢框架动载实验钢框架动载实验报告实验一钢筋混凝土梁正截面受弯性能实验一、实验目的1、通过梁的试验设计,掌握试验设计的主要内容;2、通过对钢筋混凝土梁正截面的承载力、刚度及抗裂度的实验测定,进一步熟悉钢筋混凝土受弯构件实验的一般过程。
3、进一步熟悉结构实验的常用仪表的选择和使用方法。
4、加深对钢筋混凝土梁正截面受弯性能的认识。
二、试件1、试件:试件为普通钢筋混凝土简支梁,截面尺寸及配筋图2-1所示。
混凝土:实验2测试,钢筋:主筋Ⅱ级,其它Ⅰ级图2-1 试件尺寸及配筋三、仪器设备1、加载设备:手动千斤顶和分配梁2、应变仪YE-25383、应变计4、百分表5、裂缝测试仪6、荷载传感器四、实验方案设计根据上述试验梁,完成实验设计(加载设计和观测设计)。
主要确定实验加载装置、加载制度;进行测点布置和仪器选择。
1、加载系统设计2、加载程序根据开裂荷载、标准荷载和破坏荷载进行加载制度设计,采用分级加载,在标志荷载时细分2-4级,并给出加载程序表。
(1)开裂荷载确定为准确测定开裂荷载值,实验过程中应注意观察第一条裂缝的出现。
在此之前应把荷载级取为标准荷载的5%。
(2)破坏荷载确定当试件进行到破坏时,注意观察试件的破坏特征并确定其破坏荷载值。
当发现下列情况之一时,即认为该构件已经达到破坏,并以此时的荷载作为试件的破坏荷载值。
●正截面强度破坏:①受压混凝土破坏;②纵向受拉钢筋被拉断;③纵向受拉钢筋达到或超过屈服强度后致使构件挠度达到跨度的1/50;或构件纵向受拉钢筋处的最大裂缝宽度达到1.5毫米。
梯形钢屋架课程设计任务书

《钢结构设计原理》课程设计任务书与指导书华中科技大学土木工程与力学学院建工系钢结构教研室二0一四年元月任务书一、题目:厂房××m钢屋架设计二、目的通过钢结构课程设计,进一步了解钢结构的结构型式、结构布置和受力特点,掌握钢结构的计算简图、荷载组合和内力分析,掌握钢结构的构造要求等。
综合应用钢结构的材料、连接和基本构件的基本理论、基本知识,进行整体钢结构设计计算,并绘制钢结构施工图。
三、设计资料某车间跨度为24(21,27,30)m,厂房总长度102m,柱距6m,车间内设有两台50/10t中级工作制软钩桥式吊车,地区计算温度高于-20℃,无侵蚀性介质,地震设防烈度为6度,屋架下弦标高为18m;采用1.5×6 m预应力钢筋混凝土大型屋面板,Ⅱ级防水,卷材屋面,桁架采用梯形钢桁架,两端铰支在钢筋混凝土柱上,上柱截面尺寸为450×450mm,混凝土强度等级为C25,屋架采用的钢材及焊条为:学号(编号)为单号的同学用Q235B钢,焊条为E43型;学号(编号)为双号的同学用Q345钢,焊条为E50型。
屋架形式四、设计任务及要求1.完成设计计算书一份内容:(1)设计资料、设计依据(2)选择钢屋架的材料,并明确提出对保证项目的要求;(3)确定屋架形式及几何尺寸,屋盖及支撑布置;(4)进行荷载汇集、杆件内力计算、内力组合,选择各杆件截面;(5)节点设计:设计下弦节点、上弦节点、再分式腹杆节点、支座节点、屋脊节点及下弦中央节点等。
(6)填板设计(7)材料统计要求:(1)书写工整(不能用圆珠笔或铅笔),表示要清楚,计算步骤明确,计算公式和数据来源应有依据;(2)图表应用得当(应附有与设计有关的插图和说明),各种图形应按比例并用仪器绘制。
2.绘制钢屋架施工图(A1一张)(1)屋架几何尺寸和内力简图(1:100);(2)构件详图:屋架正立面图(轴线图比例1:20,节点及杆件比例1:10),上、下弦平面图,端部侧面图、跨中及中间部位剖面图;(3)零件或节点大样图(1:5);(4)材料表;(5)设计说明。
2019华中科技大学土木工程与力学学院硕士复试(MEM)工程管理专业复试结果公示

土木工程与力学学院 2000120374 工程管理 工程管理 178.00 35.60 76.60 30.64 66.24 非全日制 专硕待录取
备注:1、公示期5个工作日。公示期间接受社会监督和考生申诉。 2、待录取考生4月1日15:00在西六楼309室领取双向选择意向表与导师双向选择,学院留存联交回西六楼309室。 3、所有考生(含免试推荐生)暂不签录取协议,等学校统一安排。
8 许梦 104879000148010 工程管理 工程管理 193.00 38.60 79.60 31.84 70.44 非全日制 专硕待录取
9 何文青 104879000120889 工程管理 工程管理 178.00 35.60 85.80 34.32 69.92 非全日制 专硕待录取
10 贾吉祥 104879000148066 工程管理 工程管理 185.00 37.00 81.60 32.64 69.64 非全日制 专硕待录取
初试复试6040马超104879000121654工程管理工程管理210004200856034247624非全日制专硕待录取104879000121151工程管理工程管理219004380810032407620非全日制专硕待录取柳海东104879000121224工程管理工程管理213004260812032487508非全日制专硕待录取赵国梁104879000148389工程管理工程管理211004220814032567476非全日制专硕待录取104879000120942工程管理工程管理207004140816032647404非全日制专硕待录取104879000121414工程管理工程管理186003720858034327152非全日制专硕待录取熊文静104879000121223工程管理工程管理186003720844033767096非全日制专硕待录取104879000148010工程管理工程管理193003860796031847044非全日制专硕待录取104879000120889工程管理工程管理178003560858034326992非全日制专硕待录取10贾吉祥104879000148066工程管理工程管理185003700816032646964非全日制专硕待录取11叶子怡104879000148566工程管理工程管理182003640812032486888非全日制专硕待录取12104879000120518工程管理工程管理173003460836033446804非全日制专硕待录取13104879000121381工程管理工程管理174003480818032726752非全日制专硕待录取14104879000120374工程管理工程管理178003560766030646624非全日制专硕待录取2019年土木工程与力学学院硕士复试mem工程管理专业复试结果公示序号姓名考生编号原报专业复试专业初试总分3所有考生含免试推荐生暂不签录取协议等学校统一安排
工程项目管理研究生学校

一、国内知名院校1. 华中科技大学华中科技大学土木工程与力学学院开设工程管理专业硕士(专硕),招生人数较多,推免生比例较高。
学校拥有雄厚的师资力量,注重理论与实践相结合,为学生提供丰富的实习和实践机会。
2. 厦门大学厦门大学管理学院承办的项目管理硕士(MSPM)非全日制研究生,依托管理学院的学科优势与师资力量,强化学生专业化的项目管理技能和企业管理知识,培养具备国际视野与战略思维的高级复合型人才。
3. 南京农业大学南京农业大学经管院企业管理专业项目管理方向,由王树进导师领衔,其在业内具有较高影响力。
学校注重培养学生的实践能力,为学生提供丰富的实习和实践机会。
4. 华南理工大学华南理工大学在职研究生工程项目管理方向,由研究生院统一管理,工商管理学院负责培养。
课程设置及师资配备严格按研究生培养方案进行,为学生提供全面掌握专业知识和技能的机会。
二、国外知名院校1. 麻省理工学院(MIT)MIT的工程管理专业在国际上享有盛誉,其课程设置注重理论与实践相结合,培养学生的创新能力和解决问题的能力。
2. 斯坦福大学斯坦福大学的工程管理专业在全球范围内具有较高的知名度,学校注重培养学生的领导力、沟通能力和团队合作精神。
3. 加州大学伯克利校区加州大学伯克利校区工程管理专业在国内外享有较高声誉,学校注重培养学生的实践能力和创新精神。
4. 利兹大学利兹大学的工程项目管理工学硕士项目,旨在培养学生掌握项目管理流程、项目生命周期金融、规划和管理等技能,为学生提供丰富的实习和实践机会。
总结:工程项目管理研究生专业在国内外的知名院校都有较为成熟的培养体系。
学生在选择院校时,可以根据自身兴趣、职业规划和院校特点进行综合考虑。
同时,注重理论与实践相结合,积极参加实习和实践,将有助于提高自身的综合素质和就业竞争力。
结构力学课程作业-超静定梁影响线(详解)

结构力学课程作业——连续梁的影响线、最不利荷载布置及内力包络图班级学号姓名华中科技大学土木工程与力学学院二0一三年十月结构力学课程作业一、题目EI=C K123x 1l 2l 3l二、要求1、用力法计算求得支点弯矩1M 、2M 的影响线;2、用挠度法计算求得支点弯矩1M 、2M 的影响线;3、求第二跨内截面K 的弯矩,剪力影响线及支座1反力影响线;4、在求影响线的基础上,进行均布移动荷载的最不利布置;5、连续梁承受均布活荷载18p KN m =及恒载12q KN m =时,绘出弯矩、剪力包络图。
三、计算由此可以求得2312211122122()()=,,363l l l l lEI EI EI δδδδ++===25 151212X=0.25L 3已知 115l m=212l m=312l m=30.250.25123x l m==⨯=111X l α≤≤≤≤当 0 ,即 0时()()11111112211230PP l PP l l ds M M l EI EI ds M M EIαδααδ-==⨯-⨯==⎰⎰得力法方程:2122111212321121()()()(1)(1)0366()()()063l l l l M X M X EI EI EIl l l M X M X EI EI ααα+++-+=++=解之得112175()(1)(1)1775()(1)(1)68M X M X αααααα=--+=-+大致弯矩图如下:由图可求出:1121121111211211111123()()825()(1)(1)4272()()125()(1)(1)272()()()205()=(1)(1)+272K QK R M X M X M X M X M X F X l M X M X M X F X l l ααααααααααα+==--+-==-+-=-++-+221X l α≤≤≤≤当 0 ,即 0时()()2211221123PP l l ds M M l EI EI αδαα-==⨯-⨯⎰()()2222211123P Pl l ds M M l EI EI αδαα+==⨯-⨯⎰得力法方程:212221222223221222()()()(1)(2)0366()()()(1)(1)0636l l l l M X M X EI EI EIl l l l M X M X EI EI EI αααααα+++--=+++-+=解之得1212()(1)(75)17M X ααα=--- 226()(1)(511)17M X ααα=--+大致弯矩图如下:由图可求出:21222222122212221212123,0.253()()(1)(57141)()99434()()(1)(921)()34()()()(1)(101145)()(1)(1)170K QK R X M X M X M X M X M X F X l M X M X M X F X l l αααααααααααααααα≤≤≤≤+--=+=+---=-=----=-++-=+-当 0即 0时大致弯矩图如下:由图可求出:212222221222122212121212,13()()(1)(57141)()3(1)3(1)434()()(1)(921)()(1)(1)34()()()(1)(101145)()(1)(1)170K QK R X M X M X M X M X M X F X l M X M X M X F X l l αααααααααααααααα≤≤≤≤+--=+-=+----=+-=+----=-++-=+-当 3即 0.25时331X l α≤≤≤≤当 0 ,即 0时3110PP l dsM M EIδ==⎰ ()()3322321123PP l l ds M M l EI EI αδαα-==⨯-⨯⎰得力法方程1221323223321323()()()036()()()(1)(2)0636l l lM X M X EI EIl l l l M X M X EI EI EI ααα++=+++--=解之得132312()(1)(2)1754()(1)(2)17M X M X αααααα=--=---大致弯矩图如下:由图可知:3132332313321323131312123()()9()(1)(2)434()()11()(1)(2)34()()()63()(1)(2)170K QK R X M X M X M X M X M X F X l M X M X M X F X l l αααααααααα≤≤≤≤+==----==----=-+=---当 0,即 01时下面用挠度法计算M 1(X),M 2(X)211122122313121111111111111212111213()(1)(1)6()(1)(75)24()(1)(2)248.52(20.25)66()75()(1)(1)17()12()(1)(75)17(()l y X EI l y X EI l y X EIl l EI EI EI y X M X y X M X y X M X αααααααααδδδαααδαααδ=-+=--=---'''=+=⨯+-==-=--+=-=---=-11)12(1)(2)17αααδ=-- 同理求得212122222222222322()(1)(1)68()6()(1)(511)17()54()(1)(2)17M X y X M X y X M X αααδαααδαααδ=-=-+=-=--+=-=---与力法求得值相同画出M1,M2 影响线1()()()K QK R M X F X F X 根据力法中求得的、、总长度/m置Mk(X) F Q k(X) F R1(X)第一跨0 0.0000 0.0000 0.00001.5 0.1 -0.3003 0.0455 0.17463 0.2 -0.5824 0.0882 0.34474.5 0.3 -0.8280 0.1255 0.50586 0.4 -1.0191 0.1544 0.65327.5 0.5 -1.1374 0.1723 0.78269 0.6 -1.1647 0.1765 0.889410.5 0.7 -1.0828 0.1641 0.969112 0.8 -0.8735 0.1324 1.017113.5 0.9 -0.5187 0.0786 1.0289 15 1 0.0000 0.0000 1.000016.2第二跨0.1 0.5419 -0.0817 0.945817.4 0.2 1.1901 -0.1774 0.867818 0.25 1.5510 -0.2293 0.8214 18 0.25 1.5510 0.7707 0.821418.6 0.3 1.3347 0.7167 0.771019.8 0.4 0.9656 0.6042 0.660721 0.5 0.6728 0.4890 0.541922.2 0.6 0.4461 0.3746 0.419823.4 0.7 0.2756 0.2648 0.299424.6 0.8 0.1511 0.1633 0.185925.8 0.9 0.0626 0.0738 0.0844 27 1 0.0000 0.0000 0.000028.2第三跨0.1 -0.0453 -0.0553 -0.063429.4 0.2 -0.0762 -0.0932 -0.106730.6 0.3 -0.0945 -0.1155 -0.132331.8 0.4 -0.1016 -0.1242 -0.142333 0.5 -0.0993 -0.1213 -0.139034.2 0.6 -0.0889 -0.1087 -0.124535.4 0.7 -0.0723 -0.0883 -0.101236.6 0.8 -0.0508 -0.0621 -0.071237.8 0.9 -0.0262 -0.0320 -0.036739 1 0.0000 0.0000 0.0000 求出Mk的影响线求出F Qk的影响线求出F R1的影响线我们知道,求某一截面的Mmax,Mmin,F Q max,F Q min,要先求出这一截面的M恒,F恒,这种情况下全梁布满荷载q,如下图所示然后根据此截面的弯矩、剪力影响线布置荷载,若其M影响线为Mmax的荷载布置Mmin的荷载布置F Qmax 的荷载布置F Q min 的荷载布置则M 恒=q*(S1+S2+S3+S4)Mmax=M 恒+P*(S2+S4) Mmin=M 恒+P*(S1+S3) FQ 同理求出(S 表示曲线与横轴所包围的面积,上为“+”,下为“—”,也就是对应包络图函数对坐标轴的积分)显然仅仅单跨满载组合无法计算出绝对的Mmax 、Mmin 、F Q max 、F Q min ,现在考虑每跨仅有部分布置荷载的情况!!! 现在求某一点(K 点)的弯矩、剪力影响线的函数表达式一、集中力在第一跨时112175()(1)(1)1775()(1)(1)68M X M X αααααα=--+=-+1111111111111111175()()+(1-)(1)(1)15(1-)17()5()(1)(1)17175()()+(1)(1)(1)+15(1)17()5()(1)17K K QK K QK X l M X M X l M X F X l M X M X l M X F X l λαλλλαλαααλααααααλαλλαλαααλαα=≤≤==--++=-=--+-≤≤=-=--+-=+-=-当 K 点在第一跨时,设,则当 0时,当 时,(1)(1)(1)αααα-++-21112121111275()(1)()()(54)(1)(1)68()()125()(1)(1)272K K QK X l M X M X M X M X M X F X l λλλλαααααα==-+=--+-==-+当 K 点在第二跨时,设,则3121211375()(1)()(1)(1)(1)68()25()(1)(1)272K K QK X l M X M X M X F X l λλλαααααα==-=--+=-=--+当 K 点在第三跨时,设 ,则二、集中力在第二跨时1212()(1)(75)17M X ααα=--- 226()(1)(511)17M X ααα=--+ 1212122112()()(1)(75)17()4()(1)(75)85K K QK X l M X M X M X F X l λλλαααααα===---==---当 K 点在第一跨时,设,则22122222212220126()(1)()()+(1)(1)(1)(75)(1)(511)1717+12(1)()()(1)(921)()34K K QK X l M X M X M X l M X M X F X l λαλλλλαλαααλαααλαααααα=≤≤=-+-=------+----=-=-当 K 点在第二跨时,设,当时2122222212221126()(1)()()+(1)(1)(1)(75)(1)(511)171712(1)()()(1)(921)()(1)(1)34K QK M X M X M X l M X M X F X l λαλλλαλαααλαααλαααααα≤≤=-+-=------++----=+-=+-当时322222236()(1)()(1)(1)(511)17()1()(1)(511)34K K QK X l M X M X M X F X l λλλαααααα==-=---+=-=-+当 K 点在第三跨时,设,则三、集中力在第三跨时132312()(1)(2)1754()(1)(2)17M X M X αααααα=--=--- 1313133112()()(1)(2)17()4()(1)(2)85K K QK X l M X M X M X F X l λλλαααααα===--==--当 K 点在第一跨时,设,则23132323133201254()(1)()()(1)(1)(2)(1)(2)1717()()11()(1)(2)34K K QK X l M X M X M X M X M X F X l λαλλλλαααλαααααα=≤≤=-+=-------==---当 K 点在第二跨时,设,当时33233233312332154()(1)()+(1-)(1)(1)(2)12(1-)17()9()(1)(2)34154()(1)()+(1)(1)(1)(2)12(1)17()K K QK K QK X l M X M X l M X F X l M X M X l M F X λαλλλαλαααλααααααλαλλαλαααλα=≤≤=-=----+=--=---≤≤=--=----+-=-当 K 点在第三跨时,设,则当 0时,当 时,33()9(1)(1)(2)(1)34X l ααααα+-=--+- 现在对这些函数进行积分3221022210122211222112012013037515()(2)(1)68251()(2)6827515()(1)(1)68251()(1)(1)6829()=173()853()17()K QK K QK K Q K K Q K K M X d F X d M X d F X d M X d F X d M X d F X λλλλαλλλλαλλλαλλλλαλλαλααλ=--+-=---=--+-=--+--=-=⎰⎰⎰⎰⎰⎰⎰当点在第一跨时10185d α=⎰1101105432220432220154322275()=(54)272125()10886212525()(7)6(1)1742212191()(10)3442236212525()(6)(7)6(1)3417422(K Q K K QK K QK K M X d F X d M X d F X d M X d F λλλαλααλλλλλλαλλλλαλλλλλλλ-==--+-++-=-+-=-++-+-++-⎰⎰⎰⎰⎰当点在第二跨时143222130130112191)(10)(1)13634422633()3411()136K Q K X d M X d F X d λαλλλλααα=--++--==-⎰⎰⎰110110120120432220432220143275()=(1)27225()108821()(1)347()136541()(1)()6(1)174911()()34425411()(1)(1744K Q K K Q K K QK K K M X d F X d M X d F X d M X d F X d M X d λλλαλααλααλλλλλλαλλλλαλλλλ-=-=--==---++-=-+-=----+⎰⎰⎰⎰⎰⎰⎰当点在第三跨时22143222)6(1)9111()()(1)34442QK F X d λλλαλλλλ⎡⎤+-⎢⎥⎣⎦⎡⎤=--++-⎢⎥⎣⎦⎰根据计算所需,计算下列积分K 点在第一跨时λ10()K M X d λα⎰10()QK F X d λα⎰11()K M X d λα⎰11()QK F X d λα⎰120()K M X d α⎰120()QK F X d α⎰130()K M X d α⎰0.0 0.0000 0.0000 0.0000 0.4265 0.0000 -0.0353 0.0000 0.1 0.0653 -0.0065 0.4994 0.3329 -0.0529 -0.0353 0.0176 0.2 0.2227 -0.0258 0.7567 0.2522 -0.1059 -0.0353 0.0353 0.3 0.4156 -0.0576 0.8285 0.1841 -0.1588 -0.0353 0.0529 0.4 0.5901 -0.1016 0.7687 0.1281 -0.2118 -0.0353 0.0706 0.5 0.6962 -0.1572 0.6273 0.0836 -0.2647 -0.0353 0.0882 0.6 0.6893 -0.2234 0.4489 0.0499 -0.3176 -0.0353 0.1059 0.7 0.5313 -0.2994 0.2717 0.0259 -0.3706 -0.0353 0.1235 0.8 0.1920 -0.3840 0.1256 0.0105 -0.4235 -0.0353 0.1412 0.9 -0.3493 -0.4759 0.0317 0.0023 -0.4765 -0.0353 0.1588 1.0-1.1029 -0.5735 0.0000 0.0000 -0.5294 -0.0353 0.1765K 点在第二跨时λ11()KM X d α⎰ 110()QKFX d α⎰ 2()KM X d λα⎰20()QK F X d λα⎰12()K M X d λα⎰12()QKFX d λα⎰13()KM X d α⎰13()QK F X d λα⎰0.0 -1.1029 0.1149 0.0000 0.0000 -0.5294 0.5074 0.1765 -0.0809 0.1 -0.9651 0.1149 0.0333 -0.0040 -0.0315 0.4113 0.0794 -0.0809 0.2 -0.8272 0.1149 0.1220 -0.0168 0.2909 0.3242 -0.0176 -0.0809 0.3 -0.68930.11490.2435-0.03980.46060.2471 -0.1147-0.08090.4 -0.5515 0.1149 0.3691 -0.0737 0.5062 0.1810 -0.2118 -0.0809 0.5 -0.4136 0.1149 0.4660 -0.1190 0.4605 0.1264 -0.3088 -0.0809 0.6 -0.2757 0.1149 0.4998 -0.1759 0.3578 0.0832 -0.4059 -0.0809 0.7 -0.1379 0.1149 0.4368 -0.2440 0.2320 0.0513 -0.5029 -0.0809 0.8 0.0000 0.1149 0.2458 -0.3226 0.1142 0.0300 -0.6000 -0.0809 0.9 0.1379 0.1149 -0.0994 -0.4109 0.0306 0.0182 -0.6971 -0.0809 1.0 0.27570.1149-0.6176-0.50740.00000.0147 -0.7941-0.0809K 点在第三跨时λ11()KM X d α⎰110()QKFX d α⎰120()KMX d α⎰120()QKFX d α⎰3()KM X d λα⎰30()QKFX d λα⎰13()KMX d λα⎰13()QKFX d λα⎰0 0.2757 -0.0230 -0.6176 0.0515 0.0000 0.0000 -0.7941 0.5662 0.1 0.2482 -0.0230 -0.5559 0.0515 0.0282 -0.0026 -0.2029 0.4688 0.2 0.2206 -0.0230 -0.4941 0.0515 0.1097 -0.0114 0.2150 0.3776 0.3 0.1930 -0.0230 -0.4324 0.0515 0.2334 -0.0278 0.4707 0.2940 0.4 0.1654 -0.0230 -0.3706 0.0515 0.3808 -0.0529 0.5827 0.2191 0.5 0.1379 -0.0230 -0.3088 0.0515 0.5267 -0.0878 0.5763 0.1540 0.6 0.1103 -0.0230 -0.2471 0.0515 0.6399 -0.1333 0.4825 0.0995 0.7 0.0827 -0.0230 -0.1853 0.0515 0.6847 -0.1902 0.3370 0.0564 0.8 0.0551 -0.0230 -0.1235 0.0515 0.6216 -0.2590 0.1795 0.0252 0.9 0.0276 -0.0230 -0.0618 0.0515 0.4082 -0.3401 0.0524 0.0063 10.0000 -0.0230 0.0000 0.0515 0.0000 -0.4338 0.0000 0.000011112301111230=(()()())(()()())K K K QK QK QK QK M q M X d M X d M X d F q F X d F X d F X d αααααα++=++⎰⎰⎰⎰⎰⎰恒恒根据影响线方程,当K 点在第一跨:集中力在第一跨的时候,画出Mk 的影响线,集中力在其他跨的时候不出现零点(影响线与坐标轴横轴相交)(结点除外);F Q 影响线图不出现零点(结点除外)。
土力学实验报告-土木工程解析

土力学实验报告专业班级实验小组姓名学号华中科技大学土木工程与力学学院2015年11 月前言土力学是一门有关土——一种特殊建筑材料的学科。
厂房、铁路、公路、港口码头等工业建筑以及城市中各种民用建筑都是以土作为地基介质的。
而土的形成过程又是一个极其复杂的地质过程。
土的性质不仅与天然形成环境有关,且与其地质历史中的变化有关。
土工实验就是通过对土进行物理及其力学性质的实验分析,了解土的组成、物理性质与力学性质,为工程设计提供土工计算的参数与指标。
所以土工实验中将其实验项目按其性质与方法分为物理性质实验与力学性质实验。
物理性质实验是对土的组成、物理及水理特征进行分析评价。
实验项目包括粒度测定,含水量测定、容重测定、液限塑限测定等。
力学性质实验是对土在各种状态下的力学性质进行测定,实验项目包括压缩性实验、直剪实验、无侧限抗压实验以及三轴实验等。
土作为一种特殊的材料,特点就在于其三相组成和复杂的地质形成过程。
因此,对于土工实验的要求不仅在于了解土体性质,更重要地在于对土这种材料在工程活动中其性质变化过程的模拟。
土工实验作为土力学的实践课,它要求学生首先重视土力学基本原理理论的学习,进而了解土工实验原理并掌握实验方法以及实验数据的分析整理与指标的选择。
2015年11月目录实验一土的密度实验 (4)实验二土的含水量(率)实验 (6)实验三黏性土的液限、塑限的测定 (8)实验四土的侧限压缩实验(固结实验) (12)实验五土的直剪实验 (14)实验一土的密度实验一、实验目的二、基本原理三、仪器设备四、操作步骤五、记录格式密度实验(环刀法)六、思考题1. 什么是土的重度、天然重度、水下重度、干重度?2. 开土样时怎样准确测定环刀内土的体积?削土刀是否能用力反复刮平土面?3. 简述天平的使用规则。
实验二土的含水量(率)实验一、实验目的二、基本原理三、仪器设备四、操作步骤五、记录格式含水率实验六、思考题1. 土的含水量的测定方法有几种?各自适用条件是什么?2. 如何使用烘箱和干燥器?该实验的温度应控制在多少度?3 土样盒为什么要上下都编号?4. 土样烘干后能否立即称重?为什么?实验三黏性土的液限、塑限的测定3.1搓条法及平衡锥法一、实验目的二、基本原理三、仪器设备四、操作步骤五、记录格式液塑限实验班级姓名土样编号实验日期六、思考题1. 什么是土的界限含水量?土有几种界限含水量?其物理意义是什么?2. 用平衡锥法测定土的液限时,如何将土调拌均匀?试样杯中土样的装入过程有什么要求?3. 用搓条法测定土的塑限时,为什么不能无压滚动?4. 能否用电吹风的热风将土中含水率降低?5. 该实验为什么要取两个以上的平行样?3.2 液限塑限联合测定法一、仪器设备二、操作步骤三、记录格式液塑限联合测定实验班级姓名土样编号实验日期四、数据处理1. 根据实验数据在双对数坐标上绘制h~w的关系曲线。
土力学试验报告 华中科技大学

土质学与土力学实验报告专业___________班级___________实验小组__________姓名___________学号___________华中科技大学土木工程与力学学院2010年10 月前言土质学与土力学是一门有关土——一种特殊建筑材料的学科。
厂房、铁路、公路、港口码头等工业建筑以及城市中各种民用建筑都是以土作为地基介质的。
而土的形成过程又是一个极其复杂的地质过程。
土的性质不仅与天然形成环境有关,且与其地质历史中的变化有关。
土工试验就是通过对土进行物理及其力学性质的试验分析,了解土的组成、物理性质与力学性质,为工程设计提供土工计算的参数与指标。
所以土工试验中将其试验项目按其性质与方法分为物理性质试验与力学性质试验。
物理性质试验是对土的组成、物理及水理特征进行分析评价。
试验项目包括粒度测定,含水量测定、容重测定、液限塑限测定等。
力学性质试验是对土在各种状态下的力学性质进行测定,试验项目包括压缩性试验、直剪试验、无侧限抗压试验以及三轴试验等。
土作为一种特殊的材料,特点就在于其三相组成和复杂的地质形成过程。
因此,对于土工试验的要求不仅在于了解土体性质,更重要地在于对土这种材料在工程活动中其性质变化过程的模拟。
土工试验作为土力学的实践课,它要求学生首先重视土力学基本原理理论的学习,进而了解土工试验原理并掌握试验方法以及试验数据的分析整理与指标的选择。
2010年10月目录土工试验开样记录 (4)试验一土的粒度成分测定 (5)试验二土的密度试验 (9)试验三土的含水量(率)试验 (12)试验四土的比重试验 (14)试验五粘性土的液限、塑限的测定 (16)试验六渗透定律试验* (19)试验七土的侧限压缩试验(固结试验) (23)试验八土的直剪试验 (26)试验九土的三轴试验 (32)试验十土的击实试验 (35)试验十一无侧限抗压强度试验 (38)土工试验开样记录工程名称________________ 钻孔号__________ 实验日期______________ 天气情况__________试验一土的粒度成分测定一、实验目的二、基本原理三、仪器设备四、操作步骤五、记录格式(二)密度计法(比重计法)六、误差分析七、思考题1. 什么是颗粒分析?颗分有什么意义?2. 实验室进行颗粒分析的方法有几种?各适用条件是什么?3. 如何做累积百分曲线?曲线的陡缓程度说明什么问题?4. 用筛析法进行颗分时,如何保证实验精度?试验二土的密度试验一、实验目的二、基本原理三、仪器设备四、操作步骤五、记录格式(一)密度试验记录表(蜡封法)工程名称钻孔编号土样说明试验日期试验者计算者校核者(二)密度试验(环刀法)六、思考题1. 什么是土的重度、天然重度、水下重度、干重度?2. 开土样时怎样准确测定环刀内土的体积?削土刀是否能用力反复刮平土面?3. 简述天平的使用规则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
土木工程与力学学院
土木工程与力学学院共有教职工180余人,其中:中国工程院院士2人(双聘),国家杰出青年基金获得者1人,国家教学名师1人,长江学者讲座教授1人,教育部新世纪人才4人,博士生导师30人,教授36人,副教授57余人。
学院下设力学系、建筑工程系、道路与桥梁工程系、工程管理系以及交通工程系等5个系。
拥有“控制结构湖北省重点实验室”和“工程结构分析与安全评定湖北省重点实验室”,拥有建设部批准的“建筑工程隔震减震产品检测中心” 、湖北省建设厅批准的“土木工程质量检测中心”(一级资质),建设部批准的“全国监理工程师培训中心”,以及学校重点研究平台“工程计算与仿真中心”、“工程管理研究中心”等。
承办了《固体力学学报》中英文版,其中《固体力学学报》英文版由国际著名出版商Elsevier发行,是我国最早受SCI检索的学术刊物之一;还承办了《华中科技大学学报(城市科学版)》,该学报于2005年被国家新闻出版署评为我国权威期刊。
学院跨越力学、土木工程、交通工程及管理科学与工程4个一级学科。
力学和土木工程为湖北省一级学科重点学科,桥梁与隧道工程为建设部重点学科。
本院设立有“力学”和“土木工程”两个博士后流动站。
拥有“力学”和“土木工程”两个一级学科博士和硕士学位授予权,以及“工程管理”博士学位授予权,且在“道路与铁道工程”、“交通运输规划与管理”两个二级学科点可以授予硕士学位(即共有11个二级学科可以授予博士学位,13个二级学科可以授予硕士学位);同时,还培养建筑与土木工程,项目管理、和交通运输工程3个领域的工程硕士。
目前,在读全日制硕、博士研究生达500名。
在科学研究与社会服务方面,土木工程与力学学院形成了自己的特色,主要研究方向有:工程结构隔震、消能减振及主动控制;微尺度力学与跨尺度关联;智能材料与结构;流固耦合动力学;工程计算与仿真计算;数字化施工集成关键技术及其应用;工程结构的损伤智能检测与寿命评估;地基处理技术;基础应力波检测技术;大跨度桥梁结构理论与实践;土木工程中的数值计算方法与虚拟仿真技术等。
在“建筑物隔震成套技术”、“轨道交通集成关键技术”、“工程结构损伤检测集成系统”、“拱桥结构分析与设计”等方面取得了一批高水平的科研成果。
2001年以来获国家自然科学奖1项,国家科技进步二等奖4项,省部级科技奖16项、省部级教学奖4项。
年平均发表学术论文300余篇,每年有100余篇论文被三大索引收录,其中每年被SCI收录的论文有30余篇。
近几年,学院承担了国家自然科学基金、博士点基金、省基金、国际合作项目等纵向课题项目50余项;作为首席单位,承担了国家“十一五”支撑计划项目1项;同时,还承担沪蓉高速公路、武汉地铁等大型工程科研
项目多项,年科研经费近3000万。
建筑工程系具有结构工程、防灾减灾与防护工程两个博士学位和硕士学位授予权。
师资力量雄厚,学术梯队合理,有国家杰出青年基金获得者1名和一批年富力强的知名学者和学术带头人。
本学科的科学研究紧跟国际学术前沿,工程研究立足国家重大项目,科研成果直接服务实践,人才培养顺应社会需求。
该学科在“工程结构隔震减震”和“工程结构的损伤集成检测”等方面具有明显优势,总体学术水平跻身于国内前列。
道路与桥梁工程系具有桥梁与隧道工程、岩土工程博士学位授予权,还可以授予道路与铁道工程硕士学位。
我院桥梁学科在国内设置较早,该系毕业的研究生绝大多数已成为所在单位的技术骨干,部分毕业生已走上了领导岗位。
近年来,该系参与完成了一批有重要影响的科研项目,获得了国家级和省部级奖多项。
岩土工程学科近年来发展迅速,在国内已具一定的影响力;桥梁学科理论联系实际,参与了一批大中型桥梁的设计和施工监测;道路工程学科紧密结合工程实际,在路网规划和管理方面具有特色。
该系培养的人才具有较扎实的理论基础和实践能力,毕业生深受社会欢迎。
交通运输工程系具有交通运输规划与管理硕士学位授予权,是全国最早开设交通运输工程专业的单位之一。
近年来,该系面向国家需求,立足重大工程,注重学科基础,培养和引进了一批学术骨干,师资队伍建设取得明显成效。
在城市交通管理、城市连续交通等重点领域主持或参与了一批国家及省部级研究项目,取得了一批有重要影响的科研成果。
该系十分注重国际交流与合作,同德国PTV公司一直保持着良好的合作关系,为研究生的科研提供了良好的实际操作平台。
工程管理系具有“工程管理”博士学位授予权,以及“管理科学与工程”和“工程管理”硕士学位授予权。
工程管理系学科覆盖面广,顺应国民经济发展和人才市场的需求,紧密跟踪最新研究前沿,积极主持和参加国家、省部级科研项目和重大工程建设项目。
近年来,在“轨道交通集成关键技术”等方面取得了一批有重要影响的科研成果,不仅推动了学科的理论发展,而且直接为生产实践服务。
该系以大型工程项目管理的理论和实践为依托,着力培养学生的创新能力、实践能力、工程管理能力。
毕业生以其扎实的理论水平和良好的综合素质赢得了社会的赞誉。
一直以来,学院十分注重国际学术交流和合作,为研究生成才创造了浓厚的学术氛围和广阔的发展空间。
学院先后与美国的加州大学伯克利分校、密西根大学、佛罗里达州立大学,日本的东京大学、京都大学、名古屋大学、九州大学及德国、英国、澳大利亚、新加坡、香港等国家和地区的著名大学建立了教师和学生交流关系;与美国土木工程协会、德国、日本
等国的大公司建立了国际科研合作关系。
多次主办/承办国内外高水平学术会议,每年邀请国内外著名学者和企业家来我院讲学超过30人次。
2010年我院各学科(不含力学学科)共计招收科学硕士研究生112人,专业硕士23人,其中接收推荐免试科学硕士31人、专业硕士10人,直博生1人。
2011年拟接受各类推免生的比例与往年大体持平。
拟招收的学术型研究生中,推免生占学术型研究生招生总人数的35%左右;拟招收的专业学位研究生中,推免生占专业学位研究生招生总人数的15%左右。
根据学校文件精神,我院专业学位研究生的资助包含学业助学金、单项奖学金和国家助学贷款三部分,其中:
1、学业助学金用于资助研究生生活费。
专业学位研究生的学业助学金按学校下拨到学院的专项经费额度进行发放,一般每半年集中发放一次。
2、单项奖学金用于奖励在科技成果、学术论文、学习成绩、社会活动等方面取得突出成绩的研究生。
专业学位研究生可以参评单项奖学金,奖金额度一般分为2000元、1000元和500元三个等级。
/GradAdmission/Show.asp?id=615。
