2016第十六届中环杯三年级决赛详解
15届中环杯三年级决赛试题

第十五届“中环杯”小学生思维能力训练活动
三年级决赛
得分:
三尧动手动脑题:(每题10分,共20分)
13.5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米。
求:单个长方形的面积。
14.D 老师将分别写有1、2、……、13这13个数字的13张牌按从小到大的顺序顺时针放在一个圆周上,开始的时候所有牌都是牌面朝上,每次翻动可以将一张牌翻成牌面朝下(一旦变成牌面朝下,这张牌就不能再翻动了)。
D 老师翻牌的规则为:若一张牌面朝上的牌上数字为A ,并且与这张牌相隔2张的牌也是牌面朝上的,那么D 老师就可以翻动写有数字A 的这张牌。
比如:只要写有数字9或者2的牌是牌面朝上,那么D 老师就可以翻动写有数字12的牌(当然,前提是写有数字12的牌还是牌面朝上的)。
最后,只要D 老师将12张牌翻成牌面朝下,那么就算D 老师成功了。
为了获得成功,D 老师有多少种不同的翻牌顺序
?
三年级第3页三年级第4
页答案详解,敬请关注唯课数学公众号vclassedu。
三年级中环杯知识点提纲复习

三年级中环杯知识点提纲复习三年级初赛考纲:一、代数类:1. 整数巧算★二、应用类:1. 盈亏问题初步★2. 植树问题3. 方阵问题4. 平均数问题★5. 周期问题★6. 用列表法解应用题7. 火柴棒搭出的数学问题8. 找规律填数★9. 填运算符号解题★三、几何类:1. 长方形和正方形周长与面积★2. 巧求多边形的周长★四、数论类:3. 带余除法★4. 加减法数字迷★5. 数阵图★五、组合类:1. 一笔画2. 几何计数★3. 较简单的容斥原理★4. 较简单的逻辑推理★5. 枚举★三年级决赛考纲(除了初赛考纲中的内容,新增):一、代数类1. 定义新运算2. 等差数列与等比数列★3. 小数初步(不要求小数的四则运算,但是需要了解a = 0.4b代表什么含义)二、应用类1. 行程问题★2. 和差倍问题★3. 年龄问题★4. 鸡兔同笼问题★5. 还原问题6. 归一问题7. 会利用一次方程或方程组解应用题★三、几何类1. 巧求多边形的面积★2. 三角形的初步认识★3. 平行四边形、梯形的面积公式★4. 立体几何初步★(不要求表面积、体积之类的,主要以数图形为主)四、数论类1. 位值原理★2. 熟练掌握被2,3,4,5,7,8,9,11,13,25,125 整除的数的规律,并且具备自己推导别的数整出规律的能力(比如自己可以推导出除以37 的数的规律)★3. 乘除法数字迷★4. 数表★5. 数阵图的最值问题★五、组合类1. 标数法解决最短路径问题★2. 最不利原则★3. 简单的加乘原理★4. 简单的最值问题★。
2016年第十六届四年级中环杯决赛试题详解

2016年第十六届四年级中环杯决赛试题(详解)1、 计算:0.2×63+1.9×126+196×9=【解析】(计算:积不变原则;提取公因数;)原式=0.2×7×9+1.9×9×14+14×14×9=1.4×9+14×9×1.9+14×9×14=1.4×9+1.4×9×19+1.4×9×140=1.4×9×(1+19+140)=1.4×9×160=14×9×16=20162、 一个质数a 比一个完全平方数b 小10,则a 的最小值是 。
(说明:完全平⽅数是指能表示为⼀个整数的平⽅的数,比如4=22,9=32,所以4、9都是完全平⽅数)【解析】(数论:质数和完全平方数的基本性质)因为质数a 与完全平方数b 相差10,所以a 和b 的末尾相同完全平方数的末尾只能是0、1、4、5、6、9除了2、5以外其余质数的末尾只能是1、3、7、9当a=5时,b=15,15不是完全平方数。
所以a 的末尾一定是1或者9当b 的末尾是1时,符合的完全平方数有81、121、441、……对应的a 就是71、120、431、……这时最小的a 是71当b 的末尾是9时,符合的完全平方数有49、169、289、……对应的a 就是39、159、279、……综上,质数a 的最小值就是713、 如图,C 、E 、B 三点共线,CB ⊥AB ,AE ∥DC ,AB=8,CE=5,则△AED 的面积是 .【解析】(几何:平行线间的等积变形和三角形面积计算公式)联结AC ,因为AE ∥DC ,所以△AED 的面积等于△ACE 的面积,△ACE 的面积等于5×8÷2=20,所以△AED 的面积也是204、 三支蜡烛分别能燃烧30、40、50分钟(但是不是同时点燃的),已知这三支蜡烛同时处于燃烧状态的时间有10分钟,只有一只蜡烛处于燃烧状态的时间有20分钟,那么正好有两只蜡烛同时处于燃烧状态的时间有 分钟。
2016第十六届中环杯三年级决赛详解

第16届中环杯三年级决赛一、填空题A(本大题共8小题,每题6分,共48分):1.计算:45211763⨯+⨯=______。
【答案】20162.一个三位数abc满足a b c⨯⨯仍然是一个三位数。
满足条件的最小abc为______。
【答案】2693.D老师手里有60颗红色玻璃珠和50颗黑色玻璃珠。
一个神奇的机器被使用一次后会将4颗红色玻璃珠变成1颗黑色玻璃珠,或者将5颗黑色玻璃珠变成2颗红色玻璃珠。
D老师使用了30次这个机器后,红色玻璃珠就全没有了。
这时,黑色玻璃珠有________颗。
【答案】204.下图是一个乘法数字谜,最后的乘积为______。
【答案】565005.一个五位数abcde,从五个数码中任意取出两个数码,构成一个两位数(保持数码在原先五位数中的前后顺序),这样的两位数有10个:33、37、37、37、38、73、77、78、83、87,则abcde=________。
【答案】378376.有四头奶牛,每头奶牛要么是正常的,要么是变异的。
一头正常的奶牛有4条腿,并且永远说假话;一头变异的奶牛要么有3条腿、要么有5条腿,并且永远说真话。
主人问四头奶牛:“你们一共有多少条腿?”四头奶牛的回答分别为:13、14、15、16。
那么,这四头只奶牛一共有________条腿【答案】157.我们用()P n 表示正整数n 的所有非零数码之积,比如:()1231236P =⨯⨯=,()2062612P =⨯=。
则()()()12999P P P +++= ________。
【答案】973358.如图,长方形ABCD 中,R P Q M 、、、分别为AD 、BC 、CD 、RQ 的中点。
若长方形ABCD 的面积为32,则三角形AMP 的面积为________.【答案】10二、填空题B (本大题共4小题,每题8分,共32分):9.下图中有_____个三角形【答案】7610.若N 是84的倍数,并且N 只有6、7这两种数码,则满足要求的N 最小为_______.【答案】7677611.一共有6个人,每两人之间要么互为朋友,要么没有关系。
三年级上册数学试题-第十四届中环杯三年级决赛全国通用 PDF 含答案

【分析】几何,割补法; 第一次走了 2 秒,那么 P、Q 在 CD,BC 的中点,那么 SABCD = 100 × 8 = 800(cm2 ) ; 第二次走了 5 秒,如图割补,可以得 S重 = 800 ÷(16 × 2)× 23 = 575(cm2 ) 。
14.数字 1,2,3,4,5 放在一个圆圈上,我们将符合下面描述的放置方法称为一种“中环”放置方 法:对于 1~15 中的某一个数字 n,无法取圆圈上的若干个相邻数字,使得它们的和为 n,如 果两种放置方法通过旋转或者翻折后相同,我们视其为同一种放置方法。所有“中环”位置 方法一共有多少种? (说明:如果下图这样放置,则 1-5 可以取单独的一个数,6=5+1,7=3+4,8=5+1+2, 9=2+3+4,10=1+2+3+4,11=5+1+2+3,12=4+5+1+2,13=3+4+5+1,,14=2+3+4+5,15=1+2+3+4+5 , 所以 1~15 中的所有数字都取到了,这不是一种“中环放置方法。)
或者竖直放置,并且任意两艘船不会相邻(如果一艘船中的某一格与另一艘船相邻,就认
为这两艘船相邻)。表中右边和下面的数字表示这行、这列中小船占据的方格数量,有波浪
线的地方表示这里不能放置船。图中已经给出了两个方格(方块与船中的方块对应,图与
船中的图对应)。请你画出最后的结果(注意:圆、方块、半圆要画清楚)。
【分析】计数,标数法 经过标数求得 P = 130 , Q = 65 。
P − 2Q + 2014 = 130 + 65 × 2 + 2014 = 2014 。 7.甲、乙、丙三人做游戏,甲心里想一个两位数,然后将这个两位数乘以 100,乙心里想一 个数,然后将这个一位数乘以 10,丙心里想一个一位数,然后将这个数乘以 7。最后,将 三个人的乘积全部加起来,得到的结果是 2024。那么,甲、乙、丙原先心里所想的数之和 为( )。 【分析】数论,位值原理 23 ab ×100 + 10c + 7d = 2024 , 展开1000a + 100b + 10c + 7d = 2024 , 不定方程,从系数大的开始定, a = 2 或 a = 1 20 + 1 + 2 = 23 , 20 + 1 + 2 = 23 ; 杯 = 1,发现无解。
第十届中环杯决赛题+解析

题型一、填空题二、动手动脑题共计得分第十届“中环杯”小学生思维能力训练活动三年级决赛一、填空题:(每题5分,共50分。
)1.计算:2401-2009+199+1209=()。
2.一堆糖一共15颗,老师拿走一些后,8个学生正好平分了剩下的糖,那么老师拿走了()颗糖。
3.M 是两位数,如果M÷11=A ……B ,当A+B 的和最大时,M=穴雪。
4.20个孩子排成一排,从第1个孩子开始报数,要求每相邻4个孩子报出来的数字和为28。
已知第2个孩子报出的数字为6,第7个孩子报出的数字为8,第12个孩子报出的数字为4,则第5个孩子报出的数字为()。
5.小王和小明出去吃午饭。
小王带了50元,小明带了30元,他们各自买了一份相同的快餐。
已知小王剩下的钱是小明剩下的钱的3倍,则他们午饭一共花了()元。
6.一辆小轿车上还有一只备用轮胎,一次长途旅行中,司机适当地调换轮胎,使每只轮胎的行程相同。
小轿车共行了600千米,那么每只轮胎平均行()千米。
7.小林与小胖比赛爬楼梯,小林跑到第6楼时,小胖恰好跑到第5楼。
以这样的速度,小林跑到第31楼时,小胖跑到第()楼。
8.31个同学要坐船过河,渡口处只有一条能载6人的小船穴无船工雪。
他们要全部渡过河去,至少要使用这条小船渡河()次。
9.有A 、B 、C 三人,一位是导演,一位是编辑,一位是司机。
已知A 的年龄比编辑大,司机的年龄比导演大,编辑的年龄比C 大。
那么,这三人中,导演是(),编辑是(),司机是()。
10.仓库存有一批钢材,由两个汽车队负责运往工地。
已知甲队单独运要29天,乙队每天可运30吨。
现在由甲、乙两队同时运输,运了8天之后,甲队的汽车坏了一辆,每天少运5吨,结果又运了4天才全部运完。
那么这批钢材共有()吨。
二、动手动脑题:(每题10分,共50分。
)1.如图,将两个任意大小的三角形部分重叠,它们的公共部分是由3条线段组成的。
那么经过你的摆放后,它们的公共部分的边数最大可能是多少?请画出示意图。
2016年中环杯初赛模拟卷及答案

(新舟教育吴忠良供题) 【答案】 3.75 4. 从自然数 1 ~ 20 中选出 4 个数(不重复),把所有的可能性按顺序排列如 下(每种可能性中 4 个数都是从小到大的):(1,2,3,4)、(1, 2,3,5)、(1,2,3,6)、……、(1,2,3,20)、(1,2,4, 5)、(1,2,4,6)、……、(1,2,4,20)、……、(16,18,
4 5
4 4
2 5
2016 年第 16 届中环杯七年级初赛模拟试卷 填空题(共 10 题,前 5 题每题 4 分,后 5 题每题 6 分) 1. 计算: 23 2 22 2 2 1 33 2 32 2 3 1 243 2 242 2 24 1 ________.
1
x y z 20
3
y3 z3 _____. xyz
2 y 3
3
______.
5. 若 p, q 都是素数,关于 x 的方程 x4 px3 q 0 有整数根,满足要求的有序数 对 p, q 有_____对 6. 现有 20 个正整数,它们依次为 12 5 、 22 5 、 、 202 5 ,计算其中任意相 邻两数的最大公约数,请写出所有可能出现的最大公约数: _______________. (四季教育供题) 7. 若多项式 f x 满足:对任意 x ,均有 f x 4 f x 7 x 3 ,并且 f 0 5 ,则
7. 如果一个等差数列的每一项都是整数,其中某相邻四项之和为 30,某相 邻五项之和也是 30。前面所提的“相邻四项”与“相邻五项”中相同的 数字最少有_____个 8. 一条直线上有两个钉子,相距 20 厘米,一根弹性均匀的白色绳子两头系 在两个钉子上,甲要将这根绳子涂成红色,他每次最多可以将 2 厘米涂 成红色,但乙在旁边捣乱,甲每涂 1 次,乙都将一个钉子沿直线向外移 动 1 厘米,即绳子均匀的拉长 1 厘米,问甲要将绳子全部涂成红色至少要 涂 次 (四季教育供题) 9.
第十六届“华杯赛”小学组决赛试题A答案
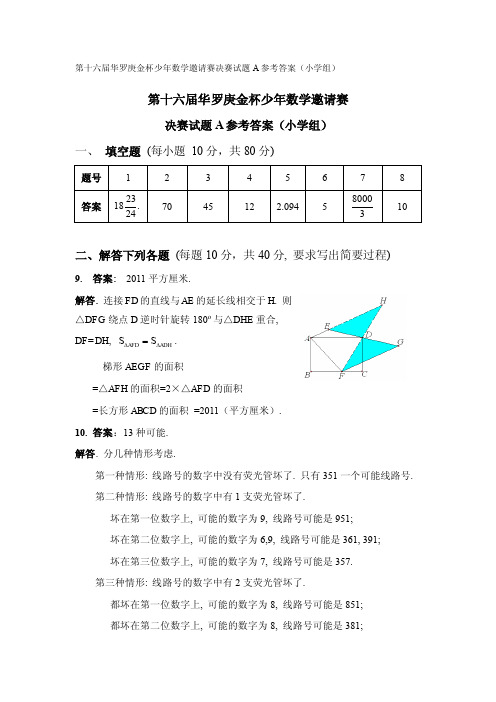
第十六届华罗庚金杯少年数学邀请赛决赛试题A 参考答案(小学组)一、 填空题 (每小题 10分,共80分)二、解答下列各题 (每题10分,共40分, 要求写出简要过程)9. 答案: 2011平方厘米.解答. 连接FD 的直线与AE 的延长线相交于H . 则△DFG 绕点D 逆时针旋转180o 与△DHE 重合,DF=DH , ADH AFD S S ∆∆=.梯形AEGF 的面积=△AFH 的面积=2×△AFD 的面积=长方形ABCD 的面积 =2011(平方厘米).10. 答案:13种可能.解答. 分几种情形考虑.第一种情形: 线路号的数字中没有荧光管坏了. 只有351一个可能线路号. 第二种情形: 线路号的数字中有1支荧光管坏了.坏在第一位数字上, 可能的数字为9, 线路号可能是951;坏在第二位数字上, 可能的数字为6,9, 线路号可能是361, 391;坏在第三位数字上, 可能的数字为7, 线路号可能是357.第三种情形: 线路号的数字中有2支荧光管坏了.都坏在第一位数字上, 可能的数字为8, 线路号可能是851;都坏在第二位数字上, 可能的数字为8, 线路号可能是381;都坏在第三位数字上, 可能的数字为4, 线路号可能是354;坏在第一、二位数字上, 第一位数字可能的数字为9,第二位数字可能的数字为6,9, 线路号可能是961, 991;坏在第一、三位数字上, 第一位数字可能的数字为9,第三位数字可能的数字为7, 线路号可能是957;坏在第二、三位数字上,第二位数字可能的数字为6,9, 第三位数字可能的数字为7,线路号可能是367, 397.所以可能的线路号有13个:351,354,357,361,367,381,391,397,851,951,957,961,991.11. 答案: 3, 5.解答. 设这个月的第一个星期日是a 日(71≤≤a ), 则这个月内星期日的日期是a k +7, k 是自然数, 317≤+a k . 要求有三个奇数.当a =1时, 要使7k +1是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时,177+=+k a k 分别为1, 15, 29, 这时20号是星期五.当a =2时, 要使7k +2是奇数, k 为奇数, 即k 可取1, 3两个值, 7k +2不可能有三个奇数.当a =3时, 要使7k +3是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时377+=+k a k 分别为3, 17, 31, 这时20号是星期三.当74≤≤a 时, a k +7不可能有三个奇数.12. 答案: 253.解:令k m 15=, k 是自然数, 首先考虑满足下式的最大的m ,.201115151153152151≤⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡m m 于是.2011213152)1(1515)1(152151150151511531521512≤-=+-=+⨯-++⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡k k k k k kk m m 因此.402213152≤-k k 又40224114171317152>=⨯-⨯, 40223632161316152<=⨯-⨯,得知k 最大可以取16. 当16=k 时, m =240. 注意到这时312161952363220112131520112+⨯==-=--k k . 注意到20112024131618161513151615121516152151615115161515161511516152151>=⨯+=⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡-⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ 而201120081216181615121516153152151<=⨯+=⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ .所以253 是满足题目要求的n的最小值.三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.答案: 312解答. 由于2+0+1+1=4 且0+1+2+3+4+6+7+8+9=40, 4≡40(mod 9), 所以, 九个不同的汉字代表的数字:0, 1, 2, 3, 4, 6, 7, 8, 9.易知:40-4=36, 36÷9=4(次), 说明此算式共发生四次进位.“4=2+2=1+1+2=1+2+1”显然:①华=1, “4=2+2”无解②华=1, “4=1+1+2”有解A:28+937+1046=2011, 可组成算式36种(6×6×1=36)B:69+738+1204=2011, 可组成算式48种(6×4×2=48)C:79+628+1304=2011, 可组成算式48种(6×4×2=48)③华=1, “4=1+2+1”有解A:46+872+1093=2011, 可组成算式36种(6×6×1=36)B:98+673+1240=2011, 可组成算式72种(6×6×2=72)C:97+684+1230=2011, 可组成算式72种(6×6×2=72)总计:72×3+96=216+96=312(种).14.解答. 如左下图, 设M, N, P分别为棱GC, GF, GH的中点, 'M, 'N, 'P 分别为棱AE, AD, AB的中点, O为正方体的中心(长方形BDHF的中心).(1)第一只蜘蛛甲可以把爬虫控制在右上图所示的范围内.首先蜘蛛甲做与爬虫关于点O的对称方向的移动, 不妨设爬虫由G沿棱GC 向点M移动, 蜘蛛甲由A沿棱AE向点'M移动, 爬虫被限制在GM上. 当爬虫到达点M时, 蜘蛛甲也同时到达点'M. 然后蜘蛛甲改变策略, 做与爬虫关于平面BDHF对称的方向移动.a) 当爬虫到达点B, D, F, H时, 蜘蛛甲捉住爬虫.b) 当爬虫未到达点B, D, F, H时, 爬虫被控制在左上图所示的范围内.(2) 蜘蛛乙先移动到点G, 由于右上图无环路, 蜘蛛乙可以跟在爬虫后面, 总可以捉住爬虫.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第16届中环杯三年级决赛
一、填空题A(本大题共8小题,每题6分,共48分):
1.计算:45211763
⨯+⨯=______。
【答案】2016
2.一个三位数abc满足a b c
⨯⨯仍然是一个三位数。
满足条件的最小abc为______。
【答案】269
3.D老师手里有60颗红色玻璃珠和50颗黑色玻璃珠。
一个神奇的机器被使用一次后会
将4颗红色玻璃珠变成1颗黑色玻璃珠,或者将5颗黑色玻璃珠变成2颗红色玻璃珠。
D老师使用了30次这个机器后,红色玻璃珠就全没有了。
这时,黑色玻璃珠有
________颗。
【答案】20
4.下图是一个乘法数字谜,最后的乘积为______。
【答案】56500
5.一个五位数abcde,从五个数码中任意取出两个数码,构成一个两位数(保持数码在
原先五位数中的前后顺序),这样的两位数有10个:33、37、37、37、38、73、77、
78、83、87,则abcde=________。
【答案】37837
6.有四头奶牛,每头奶牛要么是正常的,要么是变异的。
一头正常的奶牛有4条腿,并
且永远说假话;一头变异的奶牛要么有3条腿、要么有5条腿,并且永远说真话。
主人问四头奶牛:“你们一共有多少条腿?”
四头奶牛的回答分别为:13、14、15、16。
那么,这四头只奶牛一共有________条腿
【答案】15
7.我们用()P n 表示正整数n 的所有非零数码之积,比如:()1231236P =⨯⨯=,
()2062612P =⨯=。
则()()()12999P P P +++= ________。
【答案】97335
8.如图,长方形ABCD 中,R P Q M 、、、分别为AD 、BC 、CD 、RQ 的中点。
若长方形
ABCD 的面积为32,则三角形AMP 的面积为________.
【答案】10
二、填空题B (本大题共4小题,每题8分,共32分):
9.下图中有_____
个三角形
【答案】76
10.若N 是84的倍数,并且N 只有6、7这两种数码,则满足要求的N 最小为_______.
【答案】76776
11.一共有6个人,每两人之间要么互为朋友,要么没有关系。
如图,每个人都画了一幅
图描述另外五个人之间的朋友关系(如果某两人是朋友关系,代表这两人的点之间用线段相连)。
如果小明画的是第一幅图(左上的这幅图),那么小明有________个朋友
【答案】4
12.现在有()12N N +÷张多米诺骨牌,每张骨牌上都写有两个数字,这两个数字都是1~N
中的数(这两个数可以相同),任意两张骨牌上的两组数字不能相同。
现在,将这些多米诺骨牌排成若干列“火车”,每列“火车”中间的任意两张相邻骨牌上的相邻数字相同。
下图给出了3N =时的一列“火车”。
1
33332222111当2016N =时,至少需要______列“火车”才能将()2016201612⨯+÷张骨牌全部用完。
【答案】1008
三、动手动脑题(本大题共2小题,每题10分,共20分):
13.我们用A B C D E
、、、、分别表示甲、乙、丙、丁、戊这五个同学手中的金币数量,这些金币总和我们用n表示,也就是说n A B C D E
=++++。
已知
(1)A B C D E
、、、、均大于等于1;
(2)A B C D E
<<<<;
(3)五个同学都知道n的值以及他自己手中的金币数量;
对于某个n来说,若存在一种金币分配(金币总和定下来以后,可以根据上面的要
求分配每人手中的金币数量),使得任意一个同学都无法猜到所有人手中的金币数
量,则n就称为“中环数”。
求:最小的“中环数”。
【答案】19
14.如图,从左下角A走到右上角B,每次只能向右或者向上走一格,要求行走路径正好
穿过AB一次(下图的路径穿过AB三次,仅仅接触到AB上的点不算穿过),不同的
行走路径有多少种?
【答案】330
积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,积极参与数学,。
