(完整版)一元二次方程整数根问题的十二种思维

合集下载

求一元二次方程的整数根的方法

2.关于x的方程x2 mx m 1 0的两个根都是正整数，
求m的值.
解：设方程的两个正整数根分别为x1, x2 则x1 x2 m，于是m必为正整数设＝m2－4m－4 k 2(k为非负整数)
则(m＋k－2)(m－k－2)＝8,
m＋k－2 m－k－2, m＋k－2与m－k－2
同奇偶，则
＝－
2
2 m＋1
所以m＋1＝1， 2，
所以m＝－3，－2，0，1
关于因式分解法的总结整理
• 当一元二次方程整数根具有这样的特征：几个因式的积=整数常数，此时方可使用因式分解法。
•二、求根公式法
1.设关于x的方程x2－（m－2）x＋m2－m－2＝0有正整数根，求正整数m的值.
解：＝(m - 2)2 4(m2 m 2) 3m2 12 0, 所以m2 4. 所以－2 m 2，所以m＝1或2；当m＝1时，x＝1或－2；当m＝2时，x1＝x2＝0. 所以m＝1【. 可否用因式分解法？】
一、因式分解法
1.设关于x的方程2x2 -mx-m2 -2＝0只有整数根，
求m的值.
解：设方程的两个整数根分别为x1, x2
则x1
x2
m ，于是m必为偶数. 2
原方程可化为（x－m）（2x m) 2因x，m均为整数
Байду номын сангаасx－m 1 2x m＝2
或
2x－x mm＝21或
2x－x mm＝－－1 2或
• 3、已知方程(x-a)(x-8)-1=0有两个整根，求a的值.(展开、移项、讨论)
• 4、
解：由韦达定理得 :
x1
x2
10 m m
,
x1x2
2m m
6

含参数的一元二次方程的整数根问题.

含参数的一元二次方程的整数根问题本帖隐藏的内容需要回复才可以浏览例1 m是什么整数时，方程(m2-1)x2-6(3m-1)x＋72＝0有两个不相等的正整数根．解法1首先，m2-1≠0，m≠±1．Δ=36(m-3)2＞0，所以m≠3．用求根公式可得由于x1，x2是正整数，所以m-1=1，2，3，6，m+1=1，2，3，4，6，12，解得m=2．这时x1=6，x2=4．解法2首先，m2-1≠0，m≠±1．设两个不相等的正整数根为x1，x2，则由根与系数的关系知所以m2-1=2，3，4，6，8，9，12，18，24，36，72，即m2＝3，4，5，7，9，10，13，19，25，37，73，只有m2=4，9，25才有可能，即m=±2，±3，±5．经检验，只有m=2时方程才有两个不同的正整数根．说明一般来说，可以先把方程的根求出来(如果比较容易求的话)，然后利用整数的性质以及整除性理论，就比较容易求解问题，解法1就是这样做的．有时候也可以利用韦达定理，得到两个整数，再利用整除性质求解，解法2就是如此，这些都是最自然的做法．例2 已知关于x的方程a2x2-(3a2-8a)x＋2a2-13a＋15=0(其中a是非负整数)至少有一个整数根，求a的值．分析“至少有一个整数根”应分两种情况：一是两个都是整数根，另一种是一个是整数根，一个不是整数根．我们也可以像上题一样，把它的两个根解出来．解因为a≠0，所以所以所以只要a是3或5的约数即可，即a=1，3，5．例3设m是不为零的整数，关于x的二次方程mx2-(m-1)x＋1＝0有有理根，求m的值．解一个整系数的一元二次方程有有理根，那么它的判别式一定是完全平方数．令Δ=(m-1)2-4m＝n2，其中n是非负整数，于是m2-6m+1=n2，所以 (m-3)2-n2=8，(m-3＋n)(m-3-n)＝8．由于m-3＋n≥ｍ-3-n，并且(m-3＋n)+(m-3-n)=2(m-3)是偶数，所以m-3＋n与m-3-n同奇偶，所以说明一个整系数的一元二次方程如果有整数根或有理根，那么它的判别式一定是完全平方数，然后利用平方数的性质、解不定方程等手段可以将问题解决．例4 关于x的方程ax2+2(a-3)x+(a-2)=0至少有一个整数解，且a是整数，求a的值．解当a=0时，原方程变成-6x-2=0，无整数解．当a≠０时，方程是一元二次方程，它至少有一个整数根，说明判别式Δ＝4(a-3)2-4a(a-2)＝4(9-4a)为完全平方数，从而9-4a是完全平方数．令9-4a=n2，则n是正奇数，要使x1为整数，而n为正奇数，只能n=1，从而a=2．要使x2为整数，即n-3｜4，n可取1，5，7，从而a=2，-4，-10．综上所述，a的值为2，-4，-10．说明本题是前面两种方法的“综合”．既要用判别式是平方数，又要用直接求根．有时候，往往是几种方法一同使用．例5 已知关于x的方程x2＋(a-6)x＋a=0的两根都是整数，求a的值．解设两个根为x1≥ｘ2，由韦达定理得从上面两式中消去a得x1x2+x1+x2＝6，所以 (x1＋1)(x2+1)=7，所以a=x1x2=0或16．说明利用韦达定理，然后把参数消去，得到的是关于x1，x2的不定方程，而求解这个对称的不定方程往往是容易入手的．例6求所有有理数r，使得方程rx2+(r+1)x＋(r-1)=0的所有根是整数．分析首先对r=0和r≠０进行讨论．r=0时，是关于x的一次方程；r≠０时，是关于x的二次方程，由于r是有理数，处理起来有些困难，这时用直接求根或用判别式来做，均不能奏效．可用韦达定理，先把这个有理数r消去．解当r=0时，原方程为x-1=0，所以x=1．当r≠０时，原方程是关于x的一元二次方程，设它的两个整数根为x1，x2，且x1≥ｘ2，则消去r得x1x2-x1-x2＝2，所以(x1-1)(x2-1)=3．例7已知a是正整数，且使得关于x的一元二次方程ax2＋2(2a-1)x＋4(a-3)=0至少有一个整数根，求a的值．解将原方程变形为(x＋2)2a= 2(x＋6)．显然x＋2≠0，于是由于a是正整数，所以a≥1，即所以 x2+2x-8≤0，(x＋4)(x-2)≤0，所以-4≤x≤2(x≠-2)．当x=-4，-3，-1，0，1，2时，得a的值为1，6，10，3，说明从解题过程中知，当a=1时，有两个整数根-4，2；当a=3，6，10时，方程只有一个整数根．有时候，在关于x的一元二次方程中，如果参数是一次的，可以先对这个参数来求解．例8 已知方程x2+bx+c=0与x2+cx＋b=0各有两个整数根x1，x2(2)求证：b-1≤c≤b＋1；(3)求b，c的所有可能的值．解 (1)由x1x2＞0知，x1与x2同号．若x1＞0，则x2＞0，(2)由(1)知，x1＜0，x2＜0，所以x1≤-1，x2≤-1．由韦达定理c-(b-1)=x1x2＋x1＋x2＋1=(x1＋1)(x2+1)≥0，所以c≥ｂ-1．同理有所以c≤b+1，所以 b-1≤c≤b+1．(3)由(2)可知，b与c的关系有如下三种情况：(i)c=b＋1．由韦达定理知x1x2=-(x1＋x2)＋1，所以 (x1＋1)(x2＋1)=2，解得x1＋x2=-5，x1x2=6，所以b=5，c=6．(ii)c=b．由韦达定理知x1x2=-(x1＋x2)，所以 (x1+1)(x2＋1)=1，所以x1=x2=-2，从而b=4，c=4．(iii)c=b-1．由韦达定理知所以综上所述，共有三组解：(b，c)=(5，6)，(4，4)，(6，5)．练习二十六1．填空：(1)方程x2+px+1997=0恰有两个正整数根x1，x2，(2)已知k为整数，且关于x的方程(k2-1)x2-3(3k-1)x＋18=0有两个不相同的正整数根，则k=____．(3)两个质数a，b恰好是关于x的方程x2-21x＋t=0的两个根，(4)方程x2+px＋q=0的两个根都是正整数，并且p+q=1992，则方程较大根与较小根的比等于____．(5)已知方程(a2-1)x2-2(5a+1)x＋24=0有两个不相等的负整数根，则整数a的值是____．2．设m为整数，且4＜m＜40，又方程(x2-2(2m-3)x+4m2-14m+8＝0有两个整数根，求m的值及方程的根．3．已知关于x的一元二次方程x2+(m-17)x+m-2=0的两个根都是正整数，求整数m的值．4．求使关于x的方程a2x2＋ax＋1-7a2=0的两根都是整数的所有正数a．5．求所有的整数a，使得关于x的二次方程ax2＋2ax＋a-9＝0至少有一个整数根．。

一元二次方程整数根问题的解法技巧

7 7
时,
1 2
7 ( 舍去). 故所有正数 a 的和是: 1 +
①
+
2 (x + 6) ≥ 1, 解得 - 4 ≤ x ≤ 2. 取 x 的整数 (x + 2) 2 值为 x = - 4, - 3, - 1, 0, 1, 2, 分别代入 ①, 得 a 的整
26;
= [ a (a + 2) ] 2 是完全平方式, 则原方程可用十字相乘
当 2m + 1 = 49 时, m = 24, 方程两根分别为 38,
52.
法因式分解为: [ ax -
《数学教学通讯》 2005 年 9 月 ( 下半月) ( 总第 238 期) ③ 令 ∃ = p t + q = n 2 ( 或 ( 2n + 1) 2 ) , 由此求出 t 后代入原方程, 先求出两根, 再求参数. 例 5 ( 1991 年南昌市初中数学竞赛题) 已知 a 为整数, 方程 x + ( 2a + 1) x + a = 0 有整数根 x 1、 x 2,
6 (k + 1) = 1.
解得 k = 8, 或 k = 46. 分别代入
41 130 ,2或 , - 17. 9 9
原方程可解得方程的有理根为 -
∴ x 1 = - n2, x 2 = ∴
4 4
(n + 1) 2 ,
4
x2 1
-
x2 2
=
4
(- n2) 2
-
三、利用一元二次方程根与系数的关系求解
= k (k + 2) ,
2
k- 1 = 1k
1
k
( 因 k 为实数, 此时不能推出 k = 1, - 1) ・・ ② - ① 消去参数 k , 得 x 1 x 2 - x 1 - x 2 = 2,

一元二次方程的整数根问题--数不清

设(5p－132)2－17 404＝n2(n＞0，n为自然数).移项分解可得
(5p－132＋n)(5p－132－n)
＝22×19×229. 又(5p－132＋n)，(5p－132－n)同奇偶，所以，
解得p＝76.
注：从表面上看，此题中的p是一切实数，但由韦达定理判断它实际上是自然数，故可采用前法求得.
各位博友，请留下您的足迹，让我不断学习、成长！数不清谢谢您！
听课+开课+反思=成长!
态度决定一切！
一元二次方程的整数根问题
数不清
[ 2011-3-5 22:15:00 | By: 数不清 ]
一元二次方程的整数根问题
1
推荐迄今为止，尚未找到使得整系数一元二次方程有整数根的充分条件，通常的方法都是通过讨论其判别式，利用根与系数的关系进行分析和归纳，即使用必要条件解题，然后通过检验确定答案.下面举例说明常用的几种方法，并指出每种方法适合的范围.
例4
设m为整数，且4＜m＜40，又方程x2－2(2m－3)x＋4m2－14m＋8
＝0有两个整数根.求m的值及方程的根.
(1993,天津市初中数学竞赛)
分析：考察判别式△＝4(2m＋1)，因是关于m的一次式，故例1，例2的方法均不可用 .
广 Re:期末宣誓词 Re:《牵一只蜗牛去散步》 Re:《牵一只蜗牛去散步》 Re:我心目中的好老师(29号的家长 Re:真情献给党 Re:我心目中的好老师(29号的家长 Re:真情献给党 Re:信封?关爱?感悟
有理根问题本质上也是整数根的问题，要求方程的根的判别式必须为一个整数或有理数的完全平方.考察判别式
△ ＝232＋36(n2＋2n＋2)
＝36(n＋1)2＋565.

一元二次方程整数根问题的几种思维策略

一元二次方程整数根问题的几种思维策略一、利用判别式例1. 当m 是什么整数时，关于x 的一元二次方程2440mx x -+=与2244450x mx m m -+--=的根都是整数。

解：∵方程2440mx x -+=有整数根，∴⊿=16-16m ≥0，得m ≤1又∵方程2244450x mx m m -+--=有整数根∴⊿=16m 2－4(4m 2－4m －5) ≥0 得54m ≥-. 综上所述，54-≤m≤1 ∴x 可取的整数值是－1，0，1 当m=－1时，方程为－x 2-4x+4=0 没有整数解，舍去。

而m≠0 ∴ m=123.（东城）已知关于x 的一元二次方程2220x ax b ++=，0,0>>b a .（1）若方程有实数根，试确定a ，b 之间的大小关系；（2）若a ∶b 1222x x -=，求a ，b 的值；（3）在（2）的条件下，二次函数222y x ax b =++的图象与x 轴的交点为A 、C （点A 在点C 的左侧），与y 轴的交点为B ，顶点为D .若点P （x ，y ）是四边形ABCD 边上的点，试求3x －y 的最大值.解：(1) ∵ 关于x 的一元二次方程2220x ax b ++=有实数根,∴ Δ=,04)2(22≥-b a 有a 2－b 2≥0，（a+b ）（a-b ）≥0. ∵ 0,0>>b a ,∴ a+b ＞0,a －b ≥0.∴ b a ≥. …………………………2分（2） ∵ a ∶b，∴ 设2,a k b ==(k ＞0).解关于x 的一元二次方程22430x kx k ++=，得 -3x k k =-或.当12,= -3x k x k =-时，由1222x x -=得2k =.当123,= -x k x k =-时，由1222x x -=得25k =-（不合题意，舍去）.∴ 4,a b ==. …………………………5分（3）当4,a b ==2812y x x =++与x 轴的交点为、C 的交点坐标分别为A （－6，0）、（－2，0），与y 轴交点坐标为（0，12），顶点坐标D 为（－4，－4）.设z ＝3x －y ，则3y x z =-.画出函数2812y x x =++和3y x =的图象，若直线3y x =平行移动时，可以发现当直线经过点C 时符合题意，此时最大z 的值等于－6 ……………7分二、利用求根公式例2．设关于x 的二次方程2222(68)(264)4k k x k k x k -++--+=的两根都是整数，求满足条件的所有实数k 的值。

一元二次方程结题12种思路

初三数学一元二次方程整数根问题的十二种思维策略一. 利用判别式例1.（黑龙江中考题）当m 是什么整数时，关于x 的一元二次方程2440mx x -+=与2244450x mx m m -+--=的根都是整数。

解：∵方程2440mx x -+=有整数根，∴⊿=16-16m ≥0，得m ≤1又∵方程2244450x mx m m -+--=有整数根∴22164(445)0m m m =---≥V 得54m ≥-综上所述，－45≤m ≤1 ∴x 可取的整数值是-1，0，1当m=-1时，方程为－x 2-4x+4=0 没有整数解，舍去。

而m ≠0 ∴ m=1例2．（四川竞赛题）已知方程210x mx m +-+= 有两个不相等的正整数根，求m 的值。

解：设原方程的两个正整数根为x 1，x 2，则m =－(x 1+x 2)为负整数.∴244m m =+-V 一定是完全平方数设2244m m k +-=（k 为正整数）∴22(2)8m k +-=即：(2)(2)8m k m k +++-=∵m+2+k ≥m+2-k,且奇偶性相同∴2422m k m k ++=⎧⎨+-=⎩或2224m k m k ++=-⎧⎨+-=-⎩ 解得m=1＞0（舍去）或m=－5。

当m=－5时，原方程为x 2-5x+6=0，两根分别为x 1=2，x 2=3。

二. 利用求根公式例3．（全国联赛题）设关于x 的二次方程2222(68)(264)4k k x k k x k -++--+=的两根都是整数，求满足条件的所有实数k 的值。

解：22222(264)4(4)(68)4(6)k k k k k k =-----+=-V 由求根公式得222642(6)2(68)k k k x k k -++±-=-+ 即 12241,142x x k k =--=---- 由于x ≠-1，则有12244,211k k x x -=--=-++ 两式相减，得1224211x x -=++ 即 12(3)2x x +=-由于x 1，x 2是整数，故可求得122,4x x ==-或122,2x x =-=-或121,5x x ==-分别代入，易得k=310，6，3。

一元二次方程整数根问题的十二种思维策略

一元二次方程整数根问题的十二种思维策略邹振兴　(江苏省兴化市城西中学　225700) 含有字母系数的一元二次方程整数根问题,一般要求待定字母值或整数根.这类问题涉及的知识面广,其解法灵活多样,技巧性强,需要有较强的综合分析问题的能力,是近几年各地数学竞赛及中考的热门问题.本文试图在已有常用解法的基础上,再作新的探索,并归纳出这类问题的思考策略.1　利用判别式例1　当m是什么整数时,关于x的一元二次方程m x2-4x+4=0与x2-4m x+ 4m2-4m-5=0的根都是整数.(2000年黑龙江省中考试题)解　∵方程m x2-4x+4=0有整数根,∴∃=16-16m≥0,得m≤1.∵方程x2-4m x+4m2-4m-5=0有整数根,∴∃=16m2-4(4m2-4m-5)≥0,得m ≥-54.综上有-54≤m≤1.∴m可取的整数值为-1,0,1.将此三个数分别代入原方程,可知:当m =1时,已知的两方程的根都是整数.例2　已知方程x2+m x-m+1=0有两个不相等的正整数根,求m的值.(1996年四川省初中数学竞赛题)解　设原方程的两个正整数根为x1, x2,则m=-(x1+x2)为负整数.∴原方程为整系数一元二次方程,它有整数根,从而判别式∃=m2+4m-4一定是完全平方数.设m2+4m-4=k2(k为正整数),∴(m+2)2-k2=8,即(m+2+k)(m+2-k)=8.注意到m+2+k>m+2-k,且这两式同奇偶性,可得m+2+k=4,m+2-k=2或m+2+k=-2,m+2-k=-4.解得m=1>0(舍去)或m=-5.当m=-5时,原方程为x2-5x+6=0,两根分别为x1=2,x2=3.2　利用求根公式例3　设关于x的二次方程(k2-6k+ 8)x2+(2k2-6k-4)x+k2=4的两根都是整数,求满足条件的所有实数k的值.(2000年全国初中数学联赛试题)解　∃=(2k2-6k-4)2-4(k2-4)(k2-6k+8)=4(k-6)2,由求根公式可得x=-2k2+6k+4±2(k-6)2(k2-6k+8).即x1=-1-2k-4,x2=-1-4k-2.由于x≠-1,则有k-4=-2x1+1　①,k-2=-4x2+1　②.②-①得:2x1+1-4x2+1=2.即x1(x2+3)=-2.由于x1,x2是整数,故可求得x1=2,x2 =-4;或x1=-2,x2=-2;或x1=1,x2= -5.分别代入①,②并检验可得k=103,6,3. 3　利用方程根的定义例4　b为何值时,方程x2-bx-2=0和x2-2x-b(b-1)=0有相同的整数根?并且求出它们的整数根.(1992年四川省初中数学竞赛试题)解　设相同的整数根为Α,由根的定义,它们适合于两方程,有Α2-bΑ-2=Α2-2Α-b(b-1),整理得(2-b)Α=(2-b)(1+b).当b≠2时,Α=1+b,代入第一个方程得(1+b)2-b(1+b)-2=0,解得b=1,Α=2;・43・中学数学月刊 2001年第12期当b=2时,两方程无整数根.∴b=1,相同的整数根为2.4　利用因式分解例5　已知关于x的方程(a-1)x2+2x -a-1=0的根都是整数,那么符合条件的整数a有个.(2000年全国初中数学竞赛试题)解　当a=1时,x=1.当a≠1时,原方程左边因式分解得(x-1)[(a-1)x+(a+1)]=0,即得x1=1,x2=-1+21-a.∵x是整数,∴1-a=±1,±2,∴a=-1,0,2,3.由上可知符合条件的整数a有5个.例6　当m是什么整数时,关于x的方程x2-(m-1)x+m+1=0的两根都是整数?(1994年福州市初中数学竞赛试题)解　设方程的两整数根分别是x1,x2,由韦达定理得x1+x2=m-1　①,x1x2=m +1　②,②-①消去m,可得x1x2-x1-x2 =2.∴(x1-1)(x2-1)=3=1×3=(-1)×(-3).则有x1-1=1,x2-1=3,即x1=2,x2=4;或x1-1=-1,x2-1=-3,即x1=0,x2=-2.由此x1・x2=8或0,分别代入②得:m=7或m=-1.∴当m=7或-1时,原方程两根都是整数. 5　利用根与系数的关系例7　求所有正实数a,使得方程x2-ax +4a=0仅有整数根.(1998年全国初中数学联赛试题)解　设方程两整数根为x1,x2,且x1≤x2,由根与系数关系得x1+x2=a>0　①,x1x2=4a>0　②.由①得　a2≤x2≤a　③.将③代入②得4a=x1x2≤x1a;4a=x1x2≥x1・a2,∴4≤x1≤8.显然x1≠4,故x1可取5,6,7,8,依次代入原方程可得a1=x21x1-4=25,x2=20;a2=x21x1-4=18,x2=12;a3=x21x1-4=493不是整数;a4=x21x1-4=16,x2=8.∴a取25或18或16.6　构造新方程例8　方程(x-a)(x-8)-1=0有两个整数根,求a的值.(1996年全国初中数学联赛试题)解　原方程变为(x-8)2+(8-a)(x-8)-1=0.设y=x-8,则得新方程为y2+(8-a)y-1=0.设它的两根为y1,y2,则y1+y2=a-8,y1y2=-1.∵x是整数,∴y1,y2也是整数,则y1,y2只能分别为1,-1或-1,1,即y1+y2=0,∴a=8.7　构造等式例9　求所有的正整数a,b,c,使得关于x的方程x2-3ax+2b=0,x2-3bx+2c=0,x2-3cx+2a=0的所有的根都是正整数.(2000年全国初中数学联赛试题C卷)解　设三个方程的正整数解分别为x1与x2,x3与x4,x5与x6,则有x2-3ax+2b=(x-x1)(x-x2);x2-3bx+2c=(x-x3)(x-x4);x2-3cx+2a=(x-x5)(x-x6).令x=1并将三式相加,注意到x i≥1(i=1,2,…,6),有3-(a+b+c)=(1-x1)(1-x2)+(1-x3)(1-x4)+(1-x5)(1-x6)・53・2001年第12期中学数学月刊 ≥0+0+0=0,但a≥1,b≥1,c≥1,又有3-(a+b+c)≤0,∴3-(a+b+c)=0.故a=b=c=1.8　分析等式例10　n为正整数,方程x2-(3+ 1)x+3n-6=0有一个整数根,则n=.(1993年安徽省初中数学竞赛试题)解　不妨设已知方程的整数根为Α,则Α2-(3+1)Α+3n-6=0,整理得Α2-Α-6=3(Α-n).因为Α为整数,所以Α2-Α-6为整数, 3(Α-n)也一定为整数,要使3(Α-n)为整数,必有Α=n,由此得Α2-Α-6=0,即n2-n-6=0.解得n=3或-2(舍去).∴n=3.9　反客为主例11　求出所有正整数a,使方程ax2+ 2(2a-1)x+4(a-3)=0至少有一个整数解.(第三届《祖冲之杯》初中数学竞赛试题)解　由原方程知x≠2,不妨反客为主,将原方程整理成关于a的一元一次方程(x2+4x+4)a=2x+12,得a=2x+12(x+2)2≥1(因a是正整数).则得(x+4)(x-2)≤0,解得-4≤x≤2.因此,x只能取-4,-3,-1,0,1,2.将这六个值分别代入a的表达式得x=-4, a=1;　x=-3,a=6;x=-1, a=10;　x=0,a=3;x=1,a=149;x=2,a=1.故所求a的正整数值是1,3,6,10.10　利用配方法例12　已知方程(a2-1)x2-2(5a+1)x+24=0有两个不等的负整数根,则整数a 的值是.(第四届《祖冲之杯》初中数学竞赛试题)解　原方程可变为a2x2-10ax-x2-2x+24=0,即a2x2-10ax+25=x2+2x+1,亦即(ax-5)2=(x+1)2.∴ax-5=±(x+1),得x1=6a-1,x2=4a+1　(a≠±1).当a-1=-1,-2,-3,-6,即a=0, -1,-2,-5时,x1为负整数.但a=0时,x2>0;a=-5时,x1=x2=-1,又a≠-1,∴a=-2.11　利用奇偶分析例13　已知方程x2-1999x+a=0有两个质数根,则常数a=.(1999年江苏省第十四届初中数学竞赛试题)解　设方程的两个质数根为x1,x2(x1< x2).由根与系数关系得:x1+x2=1999,故x1,x2不可能均为奇数,其中必有一个偶数,而2是唯一的偶质数,于是x1=2,x2=1997 (也是质数),所以a=p q=2×1997=3994. 12　利用反证法例14　不解方程,证明方程x2-1997x +1997=0无整数根.证明　假设方程有两个整数根Α,Β,则Α+Β=1997,ΑΒ=1997,由第二式知Α,Β均为奇数,于是Α+Β为偶数,但这与第一式相矛盾,所以Α,Β不可能都是整数.假设方程只有一个整数根,则Α+Β不可能是整数,也与第一式矛盾,所以方程不可能只有一个整数根.综上可知,原方程无整数根.・63・中学数学月刊 2001年第12期。

一元二次方程整数根问题

一元二次方程整数根问题的十二种思维策略班级__________ 姓名________________1•利用判别式例1.( 2000年黑龙江中考题) 当m是什么整数时，关于x的一元二次方程2 2 2mx 4x 4 0与x 4mx 4m 4m 5 0的根都是整数。

解：丁方程mx 4x 4 0有整数根，=16-16m>0,得 m K 1又T方程x 2 4 mx 4 m 2 4 m 5 0有整数根二V 16 m24(4 m24m 5) 0 得m545综上所述，—K n K 14/• x可取的整数值是-1 , 0, 1当m=-1时，方程为—x 2-4x+4=0没有整数解，舍去。

而 0 /• m=1例2. (1996年四川竞赛题)已知方程x2mx m 1 0有两个不相等的正整数根，求m的值。

解：设原方程的两个正整数根为x1，x2，则m=- (x1+x2)为负整数.2-V m 4m 4 一定是完全平方数设m2 4 m 4 k 2 ( k为正整数)二(m 2) 2k 28即: (m 2 k)(m 2 k) 8■/ m+2+k> m+2-k,且奇偶性相同m 2 k 4 或m2k 2 m 2 k 2 m 2 k 4 解得m=1> 0 (舍去)或 m=- 5。

2当m=—5时，原方程为x -5x+6=0，两根分别为x1 =2，x2=3。

2.利用求根公式例 3. ( 2000 年全国联赛)设关于 x 的二次方程根都是整数，那么符合条件的整数 a 有 ______________解:当a=1时,x=1当a z 1时，原方程左边因式分解，得(x-1)[(a-1)x+(a+1)]=0 即得X 1 1,X 21 21 a•/ X 是整数/. 1-a= ± 1, ± 2, /• a=-1,0,2,3 由上可知符合条件的整数有 5个.例6.(1994年福州竞赛题)当m 是什么整数时,关于x 的方程(k 2 6k 8)X 2 (2k 2 6k 4)X k 24的两根都是整数，求满足条件的所有实数k 的值。

一元二次方程整数根问题的十二种思维

一元二次方程整数根问题的十二种思维策略一. 利用判别式例1. （2000年黑龙江中考题）当 m是什么整数时，关于 x的一元二次方程mx2 4x 4 0与x2 4mx 4m2 4m 5 0的根都是整数。

解：•••方程mx2 4x 4 0有整数根，• • •/ =16-16m》0，得 im^ 1又•••方程x2 4mx 4m2 4m 5 0有整数根2 2 5•- V 16m 4（4m 4m 5） 0 得m —45综上所述，—一 w m^ 14• x可取的整数值是-1 , 0, 1当m=-1时，方程为—x 2-4x+4=0没有整数解，舍去。

而 0 •m=1例2. （1996年四川竞赛题）已知方程x2 mx m 1 0有两个不相等的正整数根，求m的值。

解：设原方程的两个正整数根为x1 , x 2，则m=—（x^x?）为负整数.2• V m 4m 4一定是完全平方数2 2设m 4m 4 k ( k为正整数)• (m 2)2 k28即：(m 2 k)(m 2 k) 8■/ m+2+k> m+2-k,且奇偶性相同m 2 k 4或m2 m 2 k 2"m 2 k 2 k 4解得m-1> 0 （舍去）或m-— 5。

当m=- 5时，原方程为x2-5x+6-0 两根分别为x1 -2, X2-3。

利用求根公式例3. （2000年全国联赛）设关于 x的二次方程（k2 6k 8）x2（2k2 6k 4）x k2 4 的两根都是整数，求满足条件的所有实数k的值。

2 2 2 24) 4( k 4)(k 6k 8) 4(k 6)10 易得 k= 一 , 6, 3。

3利用方程根的定义并且求出它们的整数根？解：两式相减，整理得 (2-b)x=(2-b)(1+b)解得 b=1,x=2当b=2时，两方程无整数根.••• b=1,相同的整数根是2四•利用因式分解那么符合条件的整数 a 有.解：当a=1时,x=1当1时,原方程左边因式分解得(x-1)[(a-1)x+(a+1)]=02即得 x 1 1,x 2 1 -1 a•/ X 是整数 ••• 1-a= ± 1, ± 2,的两根都是整数？由求根公式得xX i 由于XH -1 , 两式相减，即 x 1 (x 2 由于X 1, 2 k 2 6k 4 2(k 6)2(k 2 6k 8)2 22则有k 2 x , 1 3) 2x 2是整数, X i 4x 2 1故可求得 X 1 2,X 2 4x 2 14 或 X 1 2,X 22或为 1,x 2 5 例4.b 为何值时，方程 x 2 bx 2 2X b(b 1)0有相同的整数根? 解：设方程的两整数根分别是 x 1 , x 2，由韦达定理得 2 解：V (2k 6k 分别代入, 当2时,x=1+b,代入第一个方程，得(1 b)2 b(1 b)例5. (2000年全国竞赛题)已知关于 x 的方程(a 1)x 2 2xa 1 0的根都是整数, 由上可知符合条件的整数有 --a=-1,0,2,3例6.(1994年福州竞赛题)当 m 是什么整数时，关于x 的方程x 2(m 1)x m 1 0由②①消去m ,可得x1x2x2x 2(X1 1)(X2 1) 3 1 3 1 ( 3)则有x 1 1 x1 1 1或x 1 3 x21 3解得: % 2 x10或X2 4 x2 2由此X1 X2 8或0，分别代入②，得m 7或m 1五•利用根与系数的关系例7.(1998年全国竞赛题)求所有正实数a使得方程x2 ax 4a 0仅有整数根解：设方程的两整数根分别是x,，x2，且为x2由根与系数的关系得x| x2a 0L ①x, x24a 0L ②由①得a x2a③2将③代入②得4 a x/2 x,a/ a4a X i x2x2二4 x18显然x1丰4,故x1可取5, 6, 7, &从而易得a=25, 18, 16。

一元二次方程的公共根与整数根（讲义）

一元二次方程的公共根与整数根一、公共根问题二次方程的公共根问题的一般解法：二次方程的公共根问题的一般解法：设公共根，设公共根，代入原方程(两个或以上)，然后通过恒等变形求出参数的值和公共根．二、整数根问题对于一元二次方程20ax bx c ++=(0)a ¹的实根情况，可以用判别式24b ac D =-来判别，但是对于一个含参数的一元二次方程来说，要判断它是否有整数根或有理根，那么就没有统一的方法了，只能具体问题具体分析求解，当然，经常要用到一些整除性的性质．方程有整数根的条件：如果一元二次方程20ax bx c ++=(0)a ¹有整数根，那么必然同时满足以下条件： ⑴24b ac D =-为完全平方数；⑵ 242b b ac ak -+-=或242b b ac ak ---=，其中k 为整数．以上两个条件必须同时满足，缺一不可．另外，如果只满足判别式为完全平方数，则只能保证方程有有理根(其中a 、b 、c 均为有理数) 三、方程根的取值范围问题先使用因式分解法或求根公式法求出两根，然后根据题中根的取值范围来确定参数的范围．一、一元二次方程的公共根【例1】求k 的值，使得一元二次方程210x kx +-=，2(2)0x x k ++-=有相同的根，并求两个方程的根．【例2】设,,a b c 为ABC D 的三边，且二次三项式222x ax b ++与222x cx b +-有一次公因式，证明：ABC D 一定是直角三角形．一定是直角三角形．【例3】三个二次方程20ax bx c ++=，20bx cx a ++=，20cx ax b ++=有公共根．有公共根．⑴ 求证：0a b c ++=； ⑵ 求333a b c abc++的值．的值．【例4】试求满足方程270x kx --=与26(1)0x x k --+=有公共根的所有的k 值及所有公共根和所有相异根．异根．【例5】二次项系数不相等的两个二次方程222(1)(2)(2)0a x a x a a --+++=和知识点睛例题精讲222(1)(2)(2)0b x b x b b --+++=(其中a ，b 为正整数)有一个公共根，求b abaa b a b --++的值．的值．二、一元二次方程的整数根【例6】 k 为什么实数时，关于x 的方程2(6)(9)(11715)540k k x k x ----+=的解都是整数？的解都是整数？【例7】若关于x 的方程()()()26911715540k k x k x ----+=的解都是整数，则符合条件的整数k 的值有_______个．个．【例8】已知a 是正整数，如果关于x 的方程32(17)(38)560x a x a x +++--=的根都是整数，求a 的值及方程的整数根．方程的整数根．【例9】若k 为正整数，且关于k 的方程22(1)6(31)720k x k x ---+=有两个相异正整数根，求k 的值．的值．【例10】关于x 的二次方程2222(68)(264)4k k x k k x k -++--+=的两根都是整数．求满足条件的所有实数k 的值．的值．【例11】当m 为何整数时，方程222525x mx m -+=有整数解．有整数解．【例12】已知关于x 的方程24832x nx n --=和22(3)220x n x n -+-+=，是否存在这样的n 值，使第一个方程的两个实数根的差的平方等于第二个方程的一整数根？若存在，请求出这样的n 值；若不存在，请说明理由．在，请说明理由．【例13】求所有有理数r ，使得方程2(1)(1)0rx r x r +++-=的所有根是整数．的所有根是整数．【例14】已知关于x 的方程2(6)0x a x a +-+=的两根都是整数，求a 的值．的值．【例15】已知k 为常数，关于x 的一元二次方程22(2)(46)80k k x k x -+-+=的解都是整数，求k 的值．的值．【例16】已知p 为质数，二次方程222510x px p p -+--=的两根都是整数，请求出p 的所有可能的值．的所有可能的值．【例17】已知1240m <<，且关于x 的二次方程222(1)0x m x m -++=有两个整数根，求整数m ．【例18】若一直角三角形两直角边的长，a 、b ()a b ¹均为整数，且满足24a b m ab m +=+ìí=î．试求这个直角三角形的三边长．角形的三边长．【例19】关于x 的方程22(3)(2)0ax a x a +-+-=至少有一个整数解，且a 是整数，求a 的值．的值．【例20】已知方程()22238213150ax a a x a a --+-+=(a 是非负整数)至少有一个整数根，那么a = ．【例21】当m 是什么整数时，关于x 的一元二次方程2440mx x -+=与2244450x mx m m -+--=的根都是整数．是整数．【例22】设m 为整数，且440m <<，方程()2222341480x m x m m --+-+=有两个整数根，求m 的值及方程的根．方程的根．【例23】当m 为何整数时，方程222525x mx m -+=有整数解．有整数解．【例24】已知方程()22238213150ax a a x a a --+-+=(a 是非负整数)至少有一个整数根，那么a = ．【例25】若关于x 的方程()()()26911715540k k x k x ----+=的解都是整数，则符合条件的整数k 的值有_______个．个．【例26】设方程2(2)(3)0mx m x m --+-=有整数解，试确定整数m 的值，并求出这时方程所有的整数解．【例27】已知a 是正整数，且使得关于x 的一元二次方程22(21)4(3)0ax a x a +-+-=至少有一个整数根，求a 的值．的值．【例28】已知关于x 的方程2222(38)213150a x a a x a a --+-+= (其中a 是非负整数)至少有一个整数根，求a 的值．的值．【例29】已知b ，c 为整数，方程250x bx c ++=的两根都大于1-且小于0，求b 和c 的值．的值．【例30】已知a ，b 都是正整数，试问关于x 的方程21()02x abx a b -++=是否有两个整数解？如果有，请求出来；如果没有，请给出证明．求出来；如果没有，请给出证明．【例31】已知方程20x b x c ++=及20x cx b ++=分别各有个两个整整数根12,x x 及12,x x ¢¢，且120x x >，120x x ¢¢>．⑴ 求证：10x <，20x <，10x ¢<，20x ¢<； ⑵ 求证：11b c b -+≤≤； ⑶ 求,b c 所有可能的值．所有可能的值．【例32】设p q 、是两个奇整数，试证方程2220x px q ++=不可能有有理根．不可能有有理根．【例48】求所有的正整数a ，b ，c 使得关于x 的方程的方程222320,320,320x ax b x bx c x cx a -+=-+=-+=的所有的根都是正整数．的所有的根都是正整数．【例49】 n 为正整数，方程2(31)360x x n -++-=有一个整数根，则n =__________．【例50】求出所有正整数a ，使方程22(21)4(3)0ax a x a +-+-=至少有一个整数根．至少有一个整数根．【例51】已知方程22(1)2(51)240a x a x --++=有两个不等的负整数根，则整数a 的值是的值是______________________________．．【例52】不解方程，证明方程2199719970x x -+=无整数根无整数根【例53】已知方程219990x x a -+=有两个质数根，则常数a =________．【例54】已知方程210x mx m +-+=有两个不相等的正整数根，求m 的值．的值．【例55】当m 是什么整数时，关于x 的方程2(1)10x m x m --++=的两根都是整数？的两根都是整数？【例56】设方程2(2)(3)0mx m x m --+-=有整数解，试确定整数m 的值，并求出这时方程所有的整数解．【例57】已知a 是正整数，如果关于x 的方程()()321738560x a x a x +++--=的根都是整数，求a 的值及方程的整数根．方程的整数根．【例58】若k 为正整数，且关于k 的方程()()221631720k x k x ---+=有两个相异正整数根，求k 的值．的值．【例59】设a 为质数，b c ，为正整数，且满足为正整数，且满足 ()()2922509410225112a b c a b c b c ì+-=+-ïí-=ïî求()a b c +的值．的值．。

初中数学-一元二次方程的整数根

一元二次方程的整数根阅读与思考解一元二次方程问题时，我们不但需熟练地解方程，准确判断根的个数、符号特征、存在范围，而且要能深入地探讨根的其他性质，这便是大量出现于各级数学竞赛中的一元二次方程的整数根问题。

这类问题因涵盖了整数的性质、一元二次方程的相关理论，融合了丰富的数学思想方法而备受命题者的青睐..解整系数（即系数为整数）一元二次方程的整数根问题的基本方法有：1．直接求解若根可用有理式表示，则求出根，结合整除性求解.2．利用判别式在二次方程有根的前提下，通过判别式确定字母或根的范围，运用枚举讨论、不等分析求解3．运用根与系数的关系由根与系数的关系得到待定字母表示的两根和、积式，从中消去待定字母，再通过因式分解和整数性质求解.4．巧选主元若运用相关方法直接求解困难，可选取字母为主元，结合整除知识求解.例题与求解【例1】已知关于x 的方程032)1280()8)(4(2=+----x k x k k 的解都是整数，求整数k 的值. 解题思路：用因式分解法可得到根的表达式，因方程类型未指明，故须按一次方程、二次方程两种情形讨论，这样确定k 的值才能全面而准确.【例2】 q p ,为质数且是方程0132=+-m x x 的根，那么q p p q +的值是（）A ．22121 B ．22123 C ．22125 D ．22127 解题思路：设法求出q p ,的值，由题设条件自然想到根与系数的关系【例3】关于y x ,的方程29222=++y xy x 的整数解),(y x 的组数为（）A ．2组B ．3组C ．4组D ．无穷多组解题思路：把29222=++y xy x 看作关于x 的二次方程，由x 为整数得出关于x 的二次方程的根的判别式是完全平方数，从而确定y 的取值范围，进而求出x 的值.【例4】试确定一切有理数r ，使得关于x 的方程01)2(2=-+++r x r rx 有根且只有整数根.解题思路：因方程的类型未确定，故应分类讨论. 当0≠r 时，由根与系数的关系得到关于r 的两个不等式，消去r ，先求出两个整数根.【例5】试求出这样的四位数，它的前两位数字与后两位数字分别组成的两位数之和的平方，恰好等于这个四位数.解题思路：设前后两个两位数分别为y x ,，99,10≤≥y x ，则y x y x +=+100)(2，即0)()50(222=-+-+y y x y x ，于是将问题转化为求一元二次方程有理根、整数根的问题.【例6】试求出所有这样的正整数解a ，使得二次方程0)3(4)12(22=-+-+a x a ax 至少有一个整数根.解题思路：本题有两种解法. 由于a 的次数较低，可考虑“反客为主”，以a 为元，以x 为已知数整理成一个关于a 的一元一次方程来解答；或考虑因方程根为整数，故其判别式为平方式.能力训练A 级1．已知方程019992=+-a x x 有两个质数根，则._______=a2．已知一元二次方程012=+-+m mx x （m 是整数）有两个不相等的整数根，则._________=m3．若关于x 的一元二次方程0442=+-x mx 和0544422=--+-m m mx x 的根都是整数，则整数m 的值为__________4．若k 正整数，且一元二次方程0)1(2=+--k px x k 的两个根都是正整数，则)(k p pk k p k+的值等于______________.5．两个质数b a ,恰是x 的整系数方程0212=+-t x x 的两个根，则ba ab +等于（） A ．2213 B ．2158 C ．492402 D ．38365 6．若062=-+mx x 的两个根都是整数，则m 可取值的个数是（）A ．2个B ．4个C ．6个D ．以上结论都不对7．方程019972=++px x 恰有两个整数根21,x x ，则)1)(1(21++x x p 的值是（） A ．1 B ．1- C ．21-D ．21 8．若b a ,都是整数，方程020082=-+bx ax 的相异两根都是质数，则b a +3的值为（） A ．100 B ．400 C ．700 D ．10009．求所有的实数k ，使得方程0)1()1(2=-+++k x k kx 的根都是整数.10．已知关于x 的方程23842=--n nx x 和022)3(22=+-+-n x n x ，是否存在这样的n 值，使第一个方程的两个实数根的差的平方等于第二个方程的一整数根？若存在，求出这样的n 值；若不存在，请说明理由.11．若关于x 的方程0)2()3(22=-+-+a x a ax 至少有一个整数根，求整数a 的值.。

一元二次方程思维导图脑图

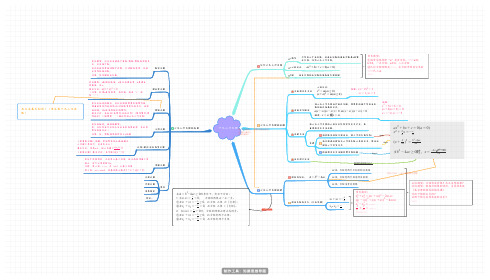
一元二次方程认识一元二次方程概念只含有一个未知数，并且未知数的最高次数是2的整式方程，叫作一元二次方程。

一般形式ax +2bx +c =0(a = 0)解满足方程的未知数的值就是方程的解常见题型：①通常需要判断“a”是否为零。

——a=0，b≠0，一次方程；a≠0，二次方程②已知方程的解是……，求方程中的其它参数——代入法……一元二次方程的求解①直接开平方法一般形式：x =2m (m ≥0)(x +n )=2m (m ≥0)例题： (x −2)=21x =11,x =23②因式分解法将一元二次方程进行因式分解，使其变成两个含有未知数的因式相乘的形式。

或解得，a (x −x )(x −1x )=20(x −x )(x −1x )=20x =x 或x =1x 2例题：x +25x +6=0(x +2)(x +3)=0x =1−2,x =2−3③配方法将一元二次方程的一般形式化为完全平方公式，再直接用开平方法求解。

步骤把常数项移到方程右边，把二次项系数化为1将方程两边都加上一次项系数一半的平方，使左边配成一个完全平方用直接开平方法解出原方程的解④求根公式法一元二次方程的根根的判别式： Δ=b −24acΔ>0，方程有两个不相等的实数根Δ=0，方程有两个相等的实数根Δ<0，方程没有实数根根与系数的关系（韦达定理）x +1x =2−ab x ⋅x =12ac常见推论：…………x +12x =22(x +1x )−222x x 12(x −1x )=22(x +1x )−224x x 12x −13x =23……±x 11=x 21……正向题型：方程有没有根？怎么求整数根？逆向题型：根据方程根的情况，求其他参数（某字母的值或取值范围）讨论下根的正负性？证明下根与其他参数的关系？……一元二次方程的应用数字问题常见题型：①已知连续两个奇数/偶数/整数的积是多少，求这两个数。

②已知给出某两位数个位数、十位数的条件，求满足条件的两位数。

初中数学一元二次方程整数根问题

一元二次方程整数根问题形如02=++c bx ax 的一元二次方程的整数根是一元二次方程的性质中较为复杂的问题，它不仅涉及到二次方程的相关知识，而且还经常用到因式分解、整除和不定方程的解法等有着知识，具有较强的综合性和技巧性。

因此成为近年来各种自招考试的热点。

下面就以试题为例，谈谈这类题的几种解题常用方法。

一、根与系数之间的关系设一元二次方程20(0)ax bx c a ++=≠的两根为12,x x ，则1212,,b c x x x x a a+=-=反之，若两数12,x x 满足1212,b cx x x x a a+=-=，则这两数是方程20ax bx c ++=的两根。

利用根与系数的关系（韦达定理），可以不直接求方程20(0)ax bx c a ++=≠而知其根的正负性质：一元二次方程20(0)ax bx c a ++=≠在240b ac ∆=-≥的条件下：(1)0ca <时，方程的两根必然一正一负； (2)0ba -≥时，方程的正根不小于负根的绝对值；(3)0ba -<时，方程的正根小于负根的绝对值；(4)0ca>时，方程的两根同正或同负.1、当含有某个参数k 的一元二次方程的左边比较容易分解成两个一次因式的积时，我们可以先利用因式分解直接求方程的解，通常它们是关于k 的分式形式的解。

然后利用其根是整数的要求来解不定方程。

2、一元二次方程02=++c bx ax 在042≥-=∆ac b 时有实数根ab x 2∆±-=，所以要使整系数的一元二次方程有整数根，必须ac b 42-=∆为完全平方数，并且∆±-b 为a 2的整数倍。

故处理此类问题，常可用判别式来解决，又可细分为两类：（1）先求参数范围。

可由不等式0≥∆求出参数的范围，再求解。

（2）再设参数法，即设2k =∆（k 是整数）。

当2k =∆为关于原参数的一次式时，用代入法来解；当2k =∆为关于原参数的二次式时，用分解因式法来解。

一元二次方程的整数根问题讲解

一元二次方程的整数根问题讲解资料编号:202209071101对于含参一元二次方程,我们经常会遇到整数根的问题.这类问题的解决,往往要借助公式法或因式分解法,用参数表示出方程的两个实数根（或表示出其中一个实数根）,然后对结果进行变形处理,并作出讨论.得出参数的值之后,需要进行检验,看参数的值是否符合题意.例1. 已知关于x 的一元二次方程()0222=++-x m mx .（1）证明:不论m 为何值,方程总有实数根;（2）m 为何整数时,方程有两个不相等的正整数根?分析:（1）要证明一元二次方程总有实数根,只需证明总有△≥0即可,注意△≥0是要证明的结论,不是证明的条件;（2）利用公式法或因式分解法,用参数表示出方程的根,然后对结果进行变形或作出讨论.得出参数的值后需要进行检验.（1）证明:()[]m m 822-+-=∆()22244-=+-=m m m ∵()22-m ≥0∴△≥0∴不论m 为何值,方程总有实数根;（2）解:()0222=++-x m mx ()m m m m m m x 2222222-±+=-±+=∴mm m m x m m m m m x 2222,12222221=+-+===-++= ∵m 为整数,21,x x 为正整数∴1=m 或2=m由题意可知:12≠m,∴2≠m ∴1=m .点评（1）也可利用因式分解的方法求解方程,如下:由题意可知:0≠m()0222=++-x m mx()()()()02101210222=--=---=+--mx x x x mx x mx mx∴01=-x 或02=-mx ∴mx x 2,121==. （2）若把题目改为“已知关于x 的方程()0222=++-x m mx .”结果又将如何? 例2. 已知关于x 的一元二次方程05242=+--m x x 有两个不相等的实数根.（1）求实数m 的取值范围;（2）若该方程的两个根都是符号相同的整数,求整数m 的值.分析:（1）根据方程有两个不相等的实数根,即0>∆,建立关于参数m 的不等式求解;（2）这里对参数m 的要求比较苛刻,有三点:①m 的值是整数;②保证方程的两个根符号相同;③保证方程的两个根都是整数.注意,最后要对求出的m 的值进行检验.解:（1）由题意可得:()()025442>---=∆m 解之得:21>m ; （2）由题意可得:⎪⎩⎪⎨⎧>->02521m m 解之得:2521<<m ∵m 为整数∴1=m 或2=m .当1=m 时,0342=+-x x ,解之得:3,121==x x ,符合题意;当2=m 时,0142=+-x x ,解之得:32,3221-=+=x x ,不符合题意,舍去. 综上所述,整数m 的值为1.例3. 已知关于x 的一元二次方程()01222=+++-k k x k x .（1）求证:无论k 取何值,方程都有两个不相等的实数根;（2）如果方程的两个实数根为21,x x ,且k 与21x x 都为整数,求k 所有可能的值. 分析:（1）只需证明无论k 取何值,都有0>∆即可;（2）由求根公式或因式分解的方法,求出方程的两个实数根,分别作为21,x x ,共有两种表示结果,分两种情况讨论.（1）证明:()[]()k k k +-+-=∆22412 ()01441222>=--+=k k k ∴无论k 取何值,方程都有两个不相等的实数根;（2）解:()01222=+++-k k x k x21122112±+=±+=k k x ∴k k x k k x =-+=+=++=2112,1211221或1,21+==k x k x 当k x k x =+=21,1时,k k k x x 11121+=+= ∵k 与21x x 都为整数 ∴1-=k 或1=k ;当1,21+==k x k x 时,111111121+-=+-+=+=k k k k k x x ∵k 与21x x 都为整数 ∴0=k 或2-=k .综上所述,1-=k 或1=k 或0=k 或2-=k . 例4. 关于x 的一元二次方程()01212=++--m mx x m .（1）求出方程的根;（2）m 为何整数时,此方程的两个根都为正整数? 解:（1）由题意可知:01≠-m ,1≠m . ()()()()()11122212114222-±=-±=--+--±=m m m m m m m m m x ∴111,1121=--=-+=m m x m m x ; （2）∵m 为整数,21,x x 为正整数121121111-+=-+-=-+=m m m m m x ∴11=-m 或21=-m∴2=m 或3=m .。

一元二次方程整数根问题

一元二次方程整数根问题的十二种思维策略班级__________ 姓名__________1.利用判别式例1.（2000年黑龙江中考题）当m 是什么整数时，关于x 的一元二次方程2440mx x -+=与2244450x mx m m -+--=的根都是整数。

解：∵方程2440mx x -+=有整数根，∴⊿=16-16m ≥0，得m ≤1又∵方程2244450x mx m m -+--=有整数根∴22164(445)0m m m =---≥ 得54m ≥-综上所述，－45≤m ≤1∴x 可取的整数值是-1，0，1当m=-1时，方程为－x 2-4x+4=0 没有整数解，舍去。

而m ≠0 ∴ m=1 例2．（1996年四川竞赛题）已知方程210x mx m +-+= 有两个不相等的正整数根，求m 的值。

解：设原方程的两个正整数根为x 1，x 2，则m=－(x 1+x 2)为负整数.∴244m m =+-一定是完全平方数设2244m m k +-=（k 为正整数）∴22(2)8m k +-=即：(2)(2)8m k m k +++-=∵m+2+k ≥m+2-k,且奇偶性相同∴2422m k m k ++=⎧⎨+-=⎩或2224m k m k ++=-⎧⎨+-=-⎩ 解得m=1＞0（舍去）或m=－5。

当m=－5时，原方程为x 2-5x+6=0，两根分别为x 1=2，x 2=3。

2.利用求根公式例3.（2000年全国联赛）设关于x 的二次方程2222(68)(264)4k k x k k x k -++--+=的两根都是整数，求满足条件的所有实数k 的值。

解：22222(264)4(4)(68)4(6)k k k k k k =-----+=-由求根公式得222642(6)2(68)k k k x k k -++±-=-+即 12241,142x x k k =--=---- 由于x ≠-1，则有12244,211k k x x -=--=-++ 两式相减，得1224211x x -=++ 即 12(3)2x x +=-由于x 1，x 2是整数，故可求得122,4x x ==-或122,2x x =-=-或121,5x x ==-分别代入，易得k=310，6，3。

一元二次方程的整数根问题的解题策略分析

一元二次方程的整数根问题的解题策略分析摘要：一元二次方程的整数根问题是初中数学竞赛常见的题型，由于这类问题涵盖了整数的性质，一元二次方程的相关知识，并且融合了许多数学思想方法而备受命题者的青睐，然而笔者发现，许多学生在解答这类问题时，仍然没有系统的思考方法，还要走很多的弯路，有时对题目甚至无从下手。

本文将常见的一元二次方程整数根问题的解法进行了整理，现分类讲解如下。

关键词：一元二次方程整数根整除根与系数关系一、利用一元二次方程两根的因式分解形式求解例1、当m是什么整数时，关于x的一元二次方程x2-mx-2m2-4=0的根为整数。

分析与解：由原方程得：x2-mx-2m2-4=4，分解因式，得(x+m)(x-2m)=4由于x、m均为整数，所以x+m、x-2m也为整数，故它们的取值有如下可能：解得，当m=0时，x=±2；当m=1时，x1=3,x2=-2；当m=-1时，x1=-3,x2=2；综上所述：当m=0、-1、1时，原方程的根为整数。

说明：当一元二次方程的根与参数都为整数时，可以利用因式分解将一元二次方程ax2+bx+c=zh整数（a≠0）化为a（x-x1）(x-x2)=整数（a≠0）的形式后再利用整除的性质求解。

二、利用一元二次方程根的判别式求解例2、m是何整数时，关于x的一元二次方程(m2-1)x2-6(3m-1)x+72=0有两个不相等的正整数根。

分析与解：由题意可知，m2-1≠0，即m≠±1，△=36（m-3）2，发现△是一个完全平方式，即方程的两根是可以表示为两个有理式：再利用整除性，要使得x1,x2都是正整数，则m-1=1、6、2、3；m+1=1、12、2、6、3、4，即可解得m=2、3，又考虑到方程是两个不相等的实数根，所以m≠3，综上所述：m=2。

说明：当判别式△是一个完全平方式或完全平方数时，即一元二次方程的根可以用有理式表示，则可直接求出方程的两根，再结合整除的性质进行求解；例3、当m是何整数时，关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0的根都是整数。

论文：浅谈一元二次方程的整数根问题

此文发表在《中学数学杂志》2012年第6期（总第272期、教研版）上浅谈一元二次方程的整数根问题在各级各类的初中数学竞赛中,一元二次方程的整数根问题备受命题者的青睐,本文介绍几种求一元二次方程的整数根的方法以及与此有关的问题的解法.1、整系数一元二次方程整数根的求法：➊利用判别式：整系数一元二次方程有整数解时，判别式是完全平方数，利用这条性质可以确定整参数的值，但需验证这些值是否使方程的根为整数。

例1、设m 是整数，4<m<40,方程x 2-2(2m-3)x+4m 2-14m+8=0有两个整数根，求m 的值。

解：已知方程的判别式⊿=4(2m+1),它是一个完全平方数，所以2m+1也是一个完全平方数。

又∵4<m<40，∴9<2m+1<81,从而2m+1=25或49, ∴m=12或者24。

代入已知方程，得：x=16,26或x=38,52.综上所述，所求m 的值为12，24。

➋利用韦达定理：利用韦达定理处理二次方程有两整数根，其思路是由x 1+x 2=-b a ,x 1x 2=ca 消去其中的参数，得整数根x 1,x 2的一个不定方程，解这个不定方程可求得其整数根，从而可确定方程中参数的值，最后需验证所求的参数值满足⊿≣0。

例2、求一切实数k,使得关于x 的方程:5x 2-5kx+66k-1=0的两根均为正整数。

解：设x 1,x 2是方程的正整数解，则⎩⎨⎧x 1+x 2=kx 1x 2=66k-15消去k,得：5x 1x 2=66(x 1+x 2)-1 ∴(5x 1-66)(5x 2-66)=4351=19×229不妨设x 1≢x 2,则 ⎩⎨⎧5x 1-66=195x 2-66=229∴x 1=17, x 2=59. ∴k=x 1+x 2=76又⊿=25k 2-20(66k-1)=25×762-20×(66×76-1)=2102>0 ∴k=76为所求。

一元二次方程整数根问题

一元二次方程整数根问题整数根问题是指求解方程中的根为整数的问题。

对于一元二次方程，其解可以通过求根公式得到，即：x = (-b ± √(b^2 - 4ac)) / (2a)要使方程的解为整数，那么√(b^2 - 4ac) 必须是一个整数，并且分子(-b ± √(b^2 - 4ac))能够被2a整除。

现在我们来讨论一元二次方程整数根问题的求解方法。

首先，我们需要判断方程是否有整数解。

根据韦达定理，一元二次方程ax^2 + bx + c = 0的两个根x1和x2的和等于-b/a，两个根的乘积等于c/a。

因此，如果b^2 - 4ac是一个完全平方数，并且b也能够被2a整除，那么方程就存在整数解。

接下来，我们需要找出满足上述条件的完全平方数以及能够整除b的2a的因子。

对于完全平方数的判断，一种常见的方法是通过试除法，即从1开始逐个尝试将数字平方，并与b^2 - 4ac进行比较。

如果找到一个平方数等于b^2 - 4ac，则方程存在整数解；否则，方程不存在整数解。

对于能够整除b的2a的因子的查找，我们可以通过因式分解的方式来获取对应的因子。

具体步骤如下：1.判断方程是否有整数解：- 计算判别式D = b^2 - 4ac；-判断D是否为完全平方数：（此处省略使用试除法判断完全平方数的具体步骤）；-判断b是否能够被2a整除；2.若方程有整数解，则寻找满足条件的解：-进行因式分解：将2a进行因式分解，找出所有的因子；-判断每个因子能否整除b；-若能整除b，则代入一元二次方程并计算解；通过上述步骤，我们可以找到一元二次方程的整数根。

需要注意的是，在实际求解过程中，可能会遇到以下情况：-判别式D不是一个完全平方数；-方程的系数a和b的范围较大；-存在复数解或实数解而非整数解；对于D不是完全平方数的情况，方程不存在整数解。

此时，我们可以考虑使用其他方法，如试除法、辗转相除法等寻找方程的实数或复数解。

一元二次方程的整数根的四种思维方法-

一元二次方程的整数解形如02=++c bx ax 的一元二次方程的整数根是一元二次方程的性质中较为复杂的问题，它不仅涉及到二次方程的相关知识，而且还经常用到因式分解、整除和不定方程的解法等有着知识，具有较强的综合性和技巧性。

一、利用因式分解构造不定方程解题当c bx ax ++2能够直接分解因式时，可以将原方程化为0))((2211=++n x m n x m 的形式，求出两根，消去两根中表示已知量的字母，得到关于两根的不定方程，通过解不定方程求解。

例1 设关于x 的二次方程-++-2222()86(k x k k 4)462=+-k x k 的两个根都是整数，求满足条件的所有实数k 的值。

练习：m 是什么整数时，方程(m 2-1)x 2-6(3m -1)x ＋72＝0有两个不相等的正整数根．通过上例可以看出，解这类题的思维方法是：第一步，若二次项系数是含字母的代数式时，要分它为0和不为0的两种情况讨论，当它不为0时，将方程化为0))((2211=++n x m n x m 的形式；第二步，求出方程的两根；第三步，消去表示已知量的字母，构造关于两根的不定方程；第四步，解不定方程，并检验。

二、利用“若两根为整数，则其和、积必为整数”解题当形如02=++c bx ax 的方程中，所含的表示已知量的字母是整数时，先利用韦达定理求出两根之和与积，然后利用“若两根为整数，则其和、积必为整数”，以及整除的有关知识解题。

例2 求使关于x 的方程062)1()1(322=-++-+a x a x a 的根均为整数的所有整数a .练习：试确定一切有理数r ，使得关于x 的方程01)2(2=-+++r x r rx 有根且只有整数根．通过上例可以看出，解这类题的思维方法是：第一步，讨论二次项系数的情况，若二次项系数不为0时，由韦达定理求出两根的和与积；第二步，将两根之和与积的代数式写成一个整式与一个分式的和的形式，并且分式的分子一定为整数；第三步，根据整除的性质，可知分式的分母一定是分子的约数，从而求出字母的可能取值；第四步，将字母的可能值分别代入原方程检验确定结果。