计量经济学第五章.
计量经济学第五章协整与误差修正模型
根据需要对数据进行变换，如对数变换、差 分变换等，以满足模型对数据的要求。
模型参数估计方法选择
01
最小二乘法（OLS ）
适用于满足经典假设的线性回归 模型，通过最小化残差平方和来 估计模型参数。
02
广义最小二乘法（ GLS）
适用于存在异方差性的模型，通 过加权最小二乘法进行参数估计 ，以消除异方差性的影响。
误差修正模型定义
误差修正模型（Error Correction Model，简称ECM）是一种具有特定形式的计 量经济学模型，用于描述变量之间的长期均衡关系和短期动态调整过程。
该模型通过引入误差修正项，将变量的短期波动和长期均衡关系结合起来，从而 更准确地刻画经济现象。
误差修正项解释
误差修正项（Error Correction Term，简称ECT）是误差修正模型中的核 心部分，表示变量之间的长期均衡误差。
长期均衡
协整关系反映了时间序列之间的长期均衡，即使短期内有所偏离，长期内也会恢复到均 衡状态。
线性组合平稳
协整序列的线性组合可以消除非平稳性，得到平稳序列。
协整检验方法
EG两步法
首先通过OLS回归得到残差序列，然 后对残差序列进行单位根检验（如 ADF检验），判断其是否平稳。
Johansen检验
适用于多变量协整关系的检验，通过 构建似然比统计量来判断协整向量的 个数。
计量经济学第五章协 整与误差修正模型
汇报人：XX
目 录
• 协整理论概述 • 误差修正模型介绍 • 协整与误差修正模型关系 • 协整检验方法及应用举例 • 误差修正模型建立与评估 • 案例研究：金融市场波动性分析
01
协整理论概述
协整定义及性质
计量经济学第五章
∴ β 2的显著水平为α的置信区间为
ˆ ˆ ˆ ˆ [ β 2 − t α se( β 2 )，β 2 + t α se( β 2 )]
2 2
同理，β1的显著水平为α的置信区间为
ˆ ˆ ˆ ˆ [ β1 − t α se( β1 )，β1 + t α se( β1 )]
2 2
9
置信区间的宽度与估计量的标准差成 正比，因此，估计量的标准差常被喻 为估计量的精度(precision)
4
置信区间的图形表示
ˆ ˆ Pr( β 2 -δ ≤ β 2 ≤ β 2 + δ ) = 1 - α
置信区间
β2
样本估计值
ˆ β 2 -δ
ˆ β2
真实值存在、未知
置信下限
ˆ β2 + δ
置信上限
区间估计的理解： （1）随机区间包含 β 2 的概率为 1 − α （2）置信区间是一个随机的区间，它随样本的不 同而改变 5 （3）它的概率描述是在平均意义上而言的
步骤 2：给定显著性水平 α 和自由度 n − 2， 查表得到临界值 t α
0.3落在区间外， 所以拒绝H0假设
0.4268
0.5914
17
2、单侧检验 、
有些时候我们可能对要检验的结果具有某些先 验的信息, 例如， 知道 β > 0.3而不会β < 0.3。在 这种情况下，应该做单侧检验： H1 : β > 0.3 H0 : β ≤ 0.3
显著性检验法
显著性检验时利用样本结果，来证实一个零假设 的真伪的一种检验程序。 显著性检验的基本思想：在虚拟假设下，根据 基本思想： 基本思想 样本构造检验统计量（作为估计量）的抽样分布 （置信区间），以此决定是否接受零假设。
计量经济学第五章
1. 用有约束模型(R)求出残差(resid); 2. 以残差(resid)为因变量,所有的说明自变量做 自变量进行回归分析; 3. 原假设: 新加说明变量的系数为零,计算统计 量LM=nR² ~X² (J, a) • n 为表示样本数, R² 表示以残差为因变量进 行回归分析得到的R² 值。
12
用Eviews的多重共线性检验1
相关系数法 首先同时选择所有的自变量; 然后双击-出现选择栏时点击 Open Group/View/Correlations; 观察各自变量之间的大小。
13
用Eviews的多重共线性检验2
VIF(Variance Inflation Factor)法 方差扩大因子法—VIF>10时严重。 如果完全共线性时，出现“Near Singular Matix） • 计算自变量的VIF。(存方程时不妨命名为eqxx)。它 是xx为因变量,其余变量为自变量的方程。 • 主窗口命令行输入scalar vifxx=1/(1-eqxx.@R² )发 现新标量vifxx /同时主窗口的左下角出现“vifxx successfully created”/双击vifxx时,主窗口的左下角 出现VIF值。
第五章
回归分析中常见的 问题及对策
本章学习的主要内容
•误设定(misspecification or specification) •多重共线性(multicollinearity) •异方差性(heteroskedasticity) •自相关(autocorrelation)
2
一、误设定模型的检验
14
用Eviews的多重共线性对策
Quick/Estimate Equation的对话框中 对数法： 直接输入log(Y) c log(X1) log(X2)… 或 差分法： 输入Y-Y(-1) C X1-X1(-1) X2-X2(-1)… 但差分常常会丢失一些信息,运用时应慎重。
《计量经济学》第五章习题及参考答案.doc
第五章经典单方程计量经济学模型：专门问题一、内容提要本章主要讨论了经典单方程回归模型的几个专门题。
第一个专题是虚拟解释变量问题。
虚拟变量将经济现象中的一些定性因素引入到可以进行定量分析的回归模型，拓展了回归模型的功能。
本专题的重点是如何引入不同类型的虚拟变量来解决相关的定性因素影响的分析问题，主要介绍了引入虚拟变量的加法方式、乘法方式以及二者的组合方式。
在引入虚拟变量时有两点需要注意，一是明确虚拟变量的对比基准，二是避免出现“虚拟变量陷阱”。
第二个专题是滞后变量问题。
滞后变量包括滞后解释变量与滞后被解释变量，根据模型中所包含滞后变量的类别又可将模型划分为自回归分布滞后模型与分布滞后模型、自回归模型等三类。
本专题重点阐述了产生滞后效应的原因、分布滞后模型估计时遇到的主要困难、分布滞后模型的修正估计方法以及自回归模型的估计方法。
如对分布滞后模型可采用经验加权法、Almon多项式法、Koyck方法来减少滞项的数目以使估计变得更为可行。
而对自回归模型，则根据作为解释变量的滞后被解释变量与模型随机扰动项的相关性的不同，采用工具变量法或OLS 法进行估计。
由于滞后变量的引入，回归模型可将静态分析动态化，因此，可通过模型参数来分析解释变量对被解释变量影响的短期乘数和长期乘数。
第三个专题是模型设定偏误问题。
主要讨论当放宽“模型的设定是正确的”这一基本假定后所产生的问题及如何解决这些问题。
模型设定偏误的类型包括解释变量选取偏误与模型函数形式选取取偏误两种类型，前者又可分为漏选相关变量与多选无关变量两种情况。
在漏选相关变量的情况下，OLS估计量在小样本下有偏，在大样本下非一致；当多选了无关变量时，OLS估计量是无偏且一致的，但却是无效的；而当函数形式选取有问题时，OLS估计量的偏误是全方位的，不仅有偏、非一致、无效率，而且参数的经济含义也发生了改变。
在模型设定的检验方面，检验是否含有无关变量，可用传统的t检验与F检验进行；检验是否遗漏了相关变量或函数模型选取有错误，则通常用一般性设定偏误检验（RESET检验）进行。
计量经济学 第五章习题答案
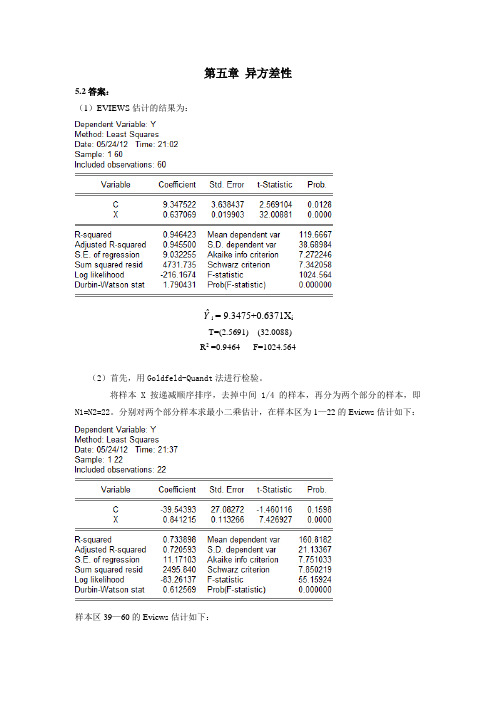
第五章异方差性5.2答案：（1）EVIEWS估计的结果为：Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564（2）首先，用Goldfeld-Quandt法进行检验。
将样本X按递减顺序排序，去掉中间1/4的样本，再分为两个部分的样本，即N1=N2=22。
分别对两个部分样本求最小二乘估计，在样本区为1—22的Eviews估计如下：样本区39—60的Eviews估计如下：得到两个部分各自的残差平方和，即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为： F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05，查F 分布表，得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值，有F =4.1390>F 0.05=(20,20)=2.12，说明该模型的随机误差项存在异方差。
其次，用White 法进行检验结果如下：给定α=0.05，在自由度为2下查卡方分布表，得χ2=5.9915。
比较临界值与卡方统计量值，即nR2=10.8640>χ2=5.9915，同样说明模型中的随机误差项存在异方差。
（2）用权数W1=1/X，作加权最小二乘估计，得如下结果用White法进行检验得如下结果：F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。
比较临界值与卡方统计量值，即nR2=5.9519<χ2=5.9915，说明加权后的模型中的随机误差项不存在异方差。
其估计的结果为：Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案：（1）EVIEWS估计结果：Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 （2）利用White方法检验异方差，则White检验结果见下表：由上述结果可知，该模型存在异方差。
计量经济学第五章 异方差
X 20000
5.3异方差的侦查
利用残差图——绘制残差平方与X散点图
（一般把异方差看成是由于解释变量的变化而引起的）
5.1异方差的概念
三、异方差产生的原因 模型设定误差：省略了重要的解释变量
例：真实模型 Yi 1 2 X 2i 3 X 3i i 采用模型 Yi 1 2 X 2i i
如果X3随着X2的不同而对Y产生不同的影响，则 该影响体现在扰动项中。
测量误差： 一方面，测量误差常常在一定时间内逐渐增加，如X 越大，测量误差就会趋于增大 另一方面，测量误差随时间变化趋于减少，如抽样技 术的改进使得测量误差减少。
)
2 i
5.1异方差的概念
6 Y
4
300 Y
200
2
100
0 0
X
0
X
10
20
30
0
5000
10000
15000
20000
250
Y
二、常见的异方差类型： 200
递增型异方差：
150
100
递减型异方差：
50
条件异方差（略）：
0 0
X
10
20
30
时间序列数据和截面数据中都有可能存在异方差。
经济时间序列中的异方差常为递增型异方差。
ˆ 2 ei2 (Yi ˆX i )2 (( ˆ) X i i )2
n 1
n 1
n 1
5.2异方差的后果
E (vaˆr(ˆ ))
E(
ˆ 2
X
2 i
)
E(
(( ˆ)X
(n 1)
《计量经济学》第五章最新完整知识
《计量经济学》第五章最新完整知识第五章多元线性回归模型在第四章中，我们讨论只有一个解释变量影响被解释变量的情况，但在实际生活中，往往是多个解释变量同时影响着被解释变量。
需要我们建立多元线性回归模型。
一、多元线性模型及其假定多元线性回归模型的一般形式是i iK K i i i x x x y εβββ++++= 2211令列向量x 是变量x k ，k =1，2，的n 个观测值，并用这些数据组成一个n ×K 数据矩阵X ，在多数情况下，X 的第一列假定为一列1，则β1就是模型中的常数项。
最后，令y 是n 个观测值y 1, y 2, …, y n 组成的列向量，现在可将模型写为：εββ++=K K x x y 11构成多元线性回归模型的一组基本假设为假定1. εβ+=X y我们主要兴趣在于对参数向量β进行估计和推断。
假定2. ,0][][][][21=?=n E E E E εεεε 假定3. n I E 2][σεε='假定4. 0]|[=X E ε我们假定X 中不包含ε的任何信息，由于)],|(,[],[X E X Cov X Cov εε= （1）所以假定4暗示着0],[=εX Cov 。
（1）式成立是因为，对于任何的双变量X ，Y ，有E(XY)=E(XE(Y|X))，而且])')|()([(])')((),(EY X Y E EX X E EY Y EX X E Y X Cov --=--=))|(,(X Y E X Cov =这也暗示βX X y E =]|[假定5 X 是秩为K 的n ×K 随机矩阵这意味着X 列满秩，X 的各列是线性无关的。
在需要作假设检验和统计推断时，我们总是假定：假定6 ],0[~2I N σε 二、最小二乘回归 1、最小二乘向量系数采用最小二乘法寻找未知参数β的估计量β，它要求β的估计β?满足下面的条件 22min ?)?(ββββX y X y S -=-? （2）其中()()∑∑==-'-=-?-nj Kj j ij i X y X y x y X y 1212ββββ，min 是对所有的m 维向量β取极小值。
计量经济学课件第5章
回归分析是通过样本所估计的参数来代替总体的 真实参数，或者说是用样本回归线代替总体回归线。
尽管从统计性质上已知，如果有足够多的重复抽 样，参数的估计值的期望（均值）就等于其总体的 参数真值，但在一次抽样中，估计值不一定就等于 该真值。
那么，在一次抽样中，参数的估计值与真值的差 异有多大，是否显著，这就需要进一步进行统计检 验。
单侧检验与双侧检验：P67。
5
只有将非预期结果作为原假设，才能控制拒绝原 假设事实上为真但偶然被拒绝的概率，即控制拒绝 原假设犯错误的概率。但反之不真，即在原假设为 假时，无法确切地知道将其错误地接受为真的概率。
即拒绝原假设，我们知道犯错误的概率，但接受 原假设，不知道犯错误的概率，所以最好说不拒绝 而不是接受。
由样本推断总体，可能会犯错误, 第一类错误：原假设H0符合实际情况，检验结果 将它否定了，称为弃真错误。 第二类错误：原假设H0不符合实际情况，检验结果 无法否定它。称为取伪错误。 例：P68，图5-1，图5-2。
8
5.1.3 假设检验的判定规则
判定规则:在检验一个假设时,首先计算样本统计量, 将样本统计值与预先选定的临界值比较,根据比较 结果决定是否拒绝原假设.即临界值将估计值的取 值范围分为两个区域,接受域和拒绝域,来决定是否 拒绝还是接受.
产生不正确推断时所面对的两类错误。
4
5.1.1 古典原假设和备选假设
原假设或者零假设（null hypothesis）,待检验的 假设，用符号H0表示, 代表研究者的非预期取值. 例如,你预期参数是正值,则建立虚拟假设为:
H0： <=0 备选假设，对研究者预期取值的表述，用符号HA表示，
接上例，备选假设为： HA ： >0
计量经济学第五章(新)
利用Eviews得回归方程为：
ˆ ln y 1.6524 0.3397 ln x1 0.9460 ln x2
t = (-2.73) p= (0.0144*) R2=0.995 (1.83) (0.085) (9.06) (0.000**)
对回归方程解释如下：斜率系数0.3397表示 产出对劳动投入的弹性，即表明在资本投入保持 不变的条件下，劳动投入每增加一个百分点，平 均产出将增加0.3397个百分点。同样地，在劳动 投入保持不变的条件下，资本投入每增加一个百 分点，产出将平均增加0.8640个百分点。两个弹 性系数相加为规模报酬参数，其数值等于1.1857 ，表明墨西哥经济的特征是规模报酬递增的（如 果数值等于1，属于规模报酬不变；小于1，则属 于规模报酬递减）。
20.5879 z 1 20.5879 x (4.6794 ) (4.3996 ** )
3、半对数模型和双对数模型
形式为：
ln y 0 1 x u y 0 1 ln x u
的模型称为半对数模型。 把形式为:
ln y 0 1 ln x u
即可利用多元线性回归分析的方法处理了。
例如，描述税收与税率关系的拉弗曲线：抛物线 t = a + b r + c r2 c<0
t：税收；
r：税率
设 z1 = r， z 2 = r2， 则原方程变换为 s = a + b z1 + c z 2 c<0
例 某生产企业在1981-1995年间每年的产量和总成本如下 表，试用回归分析法确定其成本函数。
表5-1 墨西哥的实际GDP、就业人数和实际固定资本
年份 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 GDP 114043 120410 129187 134705 139960 150511 157897 165286 178491 199457 212323 226977 241194 260881 277498 296530 306712 329030 354057 374977 就业人数 8310 8529 8738 8952 9171 9569 9527 9662 10334 10981 11746 11521 11540 12066 12297 12955 13338 13738 15924 14154 固定资产 182113 193749 205192 215130 225021 237026 248897 260661 275466 295378 315715 337642 363599 391847 422382 455049 484677 520533 561531 609825
计量经济学课件-第五章
假定系数服从以下多项式分布
bj a0 a1 j ar jr j 1, 2, p
• 则：
b0 a0 b1 a0 a1
ar
b p
a0 a1 p
ar p r
• 如果 r 2
b0 a0 b1 a0 a1 a2
b0 b1 b2
b0
b0
b0
2
对原模型做Koyck变换
Yt b0 X t b0 X t 1 b0 2 X t 2
Ut
1
Yt 1 b0 X t 1 b0 X t 2 b0 2 X t 3
U t 1 2
Yt 1 b0 X t 1 b0 2 X t 2 b0 3 X t 3 U t 1
p
i 1
bt
i
称为长期（long-run）或均衡乘数（total
distributed-lag multiplier），表示X变动一个单位，由于
滞后效应而形成的对Y均值总影响的大小。
• （2）自回归分布滞后模型（autoregressive distributed-lag model）
模型中的解释变量仅包含X的当期值与被解释 变量Y的一个或多个滞后值
Yt a b0 X t b1Yt1 b2Yt2 bqYtq Ut
• 3、分布滞后模型的OLS估计 （1）估计中存在的问题： 无限分布滞后：样本有限，无法估计； 有限分布滞后： 没有先验准则确定滞后长度； 滞后期过长导致丧失过多自由度； 容易出现多重共线；
• （2）一般处理
各种方法的基本思想大致相同：都是通过对各滞后变 量加权，组成新变量从而有目的地减少滞后变量的数 目，以缓解多重共线性，保证自由度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图6－1 两变量线性回归模型的异方差
Y
0
Xi
Xj
X
5
图6.1中对应线性回归模型误差项的方差 随着 X i 或i 的增大而增大，这种异方差称 为“递增异方差”，是异方差最常见的 类型。 但也有方差变化趋势与上述相反的“递 减异方差”，或者先增后减或先减后增 的其他复杂类型的异方差。
6
异方差的本质特征是误差项波动幅度的变化。 一般来说，随着经济变量数值的增大，波动幅 度往往也会相应的增大。 这一方面是因为随机因素的作用有随着经济变 量数值的增大而增大的可能，另一方面也可能 是随机性因素本身的变化规律作用的结果，此 外也可能是观测和统计误差随着经济变量数值 的增大而放大的结果。这些因素最终都可能导 致线性回归模型误差项异方差问题。
7
由于数据和随机误差项性质的差异，一 般来说异方差问题在截面数据的线性回 归分析中更加常见，在时间序列数据中 则相对要少一些。 值得注意的是，当线性回归模型存在解 释变量缺落、函数形式不准和参数改变 等模型定式误差问题时也会表现出与异 方差相似的特征，容易与由误差项变动 幅度变化引起的真正异方差混淆。
(c)
e
i
X k
(d)
e
i
X k
17
图6.2 异方差的发现和识别
(e)
e
i
X k
(f)
e
i
X k
18
残差序列图分析虽然直观简便，但有时 无法作出明确的判断，特别是残差分布 形态不很典型时很难得出结论。 为此提出了一些更严密的判断方法，戈 德菲尔德-夸特（Goldfeld-Quandt）检验 和戈里瑟（Glejser）检验是其中比较常 见的两种。
2 i
2
9
2 若记 A X i 0 0 1 X i 1X i ，则
Var( i) E i A X i 2 A2 X i
2
因此Var( i) 是 X i的函数，即模型表现出 异方差性。 这种异方差本质上与误差项波动变化的 异方差是不同的，是模型误差项均值非 零的系统偏差导致的，我们称这种异方 差为“假性的”。
2 e K 1 i2 2 F i2 nc 2 ei1 K 1 2 i1 2 e i2 2 e i1 i1 i2
11
最小二乘估计量方差确定的困难，则会 对以参数估计量的统计性质和分布特征 为基础的统计推断等分析，以及区间估 计和区间预测等造成严重影响，使这些 统计推断失去基础。
12
第二节 异方差的发现和判断
一、 残差序列图分析
二、 戈德菲尔德-夸特检验 三、 戈里瑟检验
13
一、残差序列分析
利用模型回归残差序列的分布形态进行分析， 是发现和判断异方差问题的基本方法。 以i 或 X k 为横轴，残差e为纵轴，作残差序列的 分布图形，那么模型不存在异方差问题时，回 归残差应该均匀地分布在横轴上下的一定范围 内，如图6.2（a）。 如果残差序列的分布形态如图6.2（b），ei的 分布有随着 X k 的增大而越分散的趋势，那么应 该怀疑存在异方差性，而且是递增异方差。
14
图6.2 异方差的发现和识别
(a) e
i
X k
(b) e
i
X k
15
如果残差序列分布形态如图6.2（c）或 （d），应该考虑递减异方差或复杂异方 差的可能性。 如果残差序列分布形态如图6.2（e）或 （f），应该考虑假性异方差，也就是参 数变化或函数设定偏差的可能性等。
16
图6.2 异方差的发现和识别
19
二、戈德菲尔德-夸特检验
这种方法适合检验样本容量较大的线性 回归模型的递增或递减型异方差性。 我们以递增异方差为例说明戈-夸检验的 思路和方法。 模型存在递增异方差时会在回归残差序 列的分布中反映出来，表现为其发散程 度随某个解释变量的增大而不断增大。
20
如果将样本按 X i 排序，那么对应较小 X i 的回归残差，平均将明显小于对应较大 的 X i 的回归残差。 把按 X i 排序的观测样本分成数目相同的 两部分，并为了加强显著性起见，去掉 中间占样本总数大约1/4到1/3的部分样 本，同时注意使剩余样本数为偶数。来自第五章异方差1
本章结构
第一节 异方差及其影响 第二节 异方差的发现和判断
第三节 异方差的克服和处理
2
第一节 异方差及其影响
一、异方差及其分类 二、异方差的危害
3
一、异方差及其分类
两变量和多元线性回归模型第三条假设 都要求误差项是同方差的，就是误差项 的方差是常数，即Var( ) 2不随i 变化。 i 如果这条假设不满足，这时候称线性回 归模型存在“异方差”或“异方差性” 。 异方差可以用图6.1中对应解释变量不同 观测值 X i 和 X j 的误差项，分布密度函数 形状不同加以反映。
8
2 Y X 例如两个变量有真实关系 0 1 其中误差项满足线性回归模型的所有假 设。 但如果误以为Y 和X 之间的关系是：
并认为 E( i) 0 ，那么
2
1X Y 0
1 X 1X i Var ( i) E ( i ) E i 0 0
10
二、异方差的危害
异方差对以最小二乘估计为核心的线性 回归分析的作用和价值有严重影响。 异方差虽然不会影响最小二乘估计的无 偏性，但最小二乘估计量方差的估计和 最小方差性，都是以模型误差项同方差 假设为基础的。 当线性回归模型的误差项存在异方差问 题时，普通最小二乘估计不再是方差最 小的估计，某种形式的加权最小二乘估 计才是最小方差的有效估计。
21
对两个子样本分别进行回归，并计算这 两组样本各自的回归残差平方和，若这 两个残差平方和有明显差异或者它们之 比明显异于1，就表明存在递增异方差问 题。 可以利用F 检验确定上述残差平方和之 比是否异于1。
22
最小二乘估计的回归残差平方和服从卡 方分布，因此用上述两个残差平方和可 以构造统计量 n c