【最新】一章渗流理论基础
地下水动力学(第一章 渗流理论基础-2-专)

∂2H ∂2ψ ∂2H ∂2ψ −K = ; −K =− 2 ∂x∂y ∂y2 ∂y∂x ∂x
二、流网及其性质
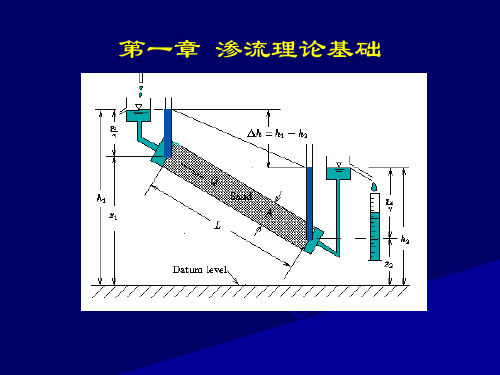
流网:在渗流场内,取一组流线和一组等势线 组成的网格。 流网的性质: 流网的性质: 1. 在各向同性介质中,流线与等势线处处垂直, 故流网为正交网格。 证明:等水头线和流线的梯度为:
gradH = ∇H = ∂H ∂H i+ j ∂x ∂y
一般地下水流都为Darcy流。 思考题
§1—3 岩层透水特征分类和渗透系数张量 一、岩层透水特征分类 据岩层透水性随空间坐标的变化情况,将岩层 分为均质的和非均质的两类。 均质岩层:在渗流场中,所有点都具有相同的 渗透系数。 非均质岩层:在渗流场中,不同点具有不同的 渗透系数。 非均质岩层有两种类型:一类透水性是渐变的, 另一类透水性是突变的。 均质、非均质:指 与空间坐标的关系 与空间坐标的关系, 均质、非均质 指K与空间坐标的关系,即不同位 是否相同; 置K是否相同; 是否相同
K1M1 + K2M2 M1 + M2 Kp − Kv = − M1 M2 M1 + M2 + K1 K2 M1M2 = >0 (K1M1 + K2M2 )(M1 + M2 )
(K1 − K2 )
2
地下水动力学习题及答案(1)

《地下水动力学》习题集第一章渗流理论基础一、解释术语1. 渗透速度2. 实际速度3. 水力坡度4. 贮水系数5. 贮水率6. 渗透系数7. 渗透率8. 尺度效应9. 导水系数二、填空题1.地下水动力学是研究地下水在孔隙岩石、裂隙岩石和岩溶岩石中运动规律的科学。
通常把具有连通性的孔隙岩石称为多孔介质,而其中的岩石颗粒称为骨架。
多孔介质的特点是多相性、孔隙性、连通性和压缩性。
2.地下水在多孔介质中存在的主要形式有吸着水、薄膜水、毛管水和重力水,而地下水动力学主要研究 重力水的运动规律。
3.在多孔介质中,不连通的或一端封闭的孔隙对地下水运动来说是无效的,但对贮水来说却是 有效的。
4. 地下水过水断面包括_空隙_和_固体颗粒_所占据的面积.渗透流速是_过水断面_上的平均速度,而实际速度是_空隙面积上的平均速度。
在渗流中,水头一般是指 测压管水头 ,不同数值的等水头面(线)永远 不会相交。
5. 在渗流场中,把大小等于_水头梯度值_,方向沿着_等水头面_的法线,并指向水头_降低_方向的矢量,称为水力坡度。
水力坡度在空间直角坐标系中的三个分量分别为H x ∂-∂、H y ∂-∂_和Hz ∂-∂。
6. 渗流运动要素包括_流量、_渗流速度、_压强和_水头等等。
7. 根据地下水渗透速度_矢量方向_与_空间坐标轴的关系,将地下水运动分为一维、二维和三维运动。
8. 达西定律反映了渗流场中的_能量守恒与转换_定律。
9. 渗透率只取决于多孔介质的性质,而与液体的性质无关,渗透率的单位为2或。
10. 渗透率是表征岩石渗透性能的参数,而渗透系数是表征岩层透水能力的参数,影响渗透系数大小的主要是岩层颗粒大小以及水的物理性质,随着地下水温度的升高,渗透系数增大。
11. 导水系数是描述含水层出水能力的参数,它是定义在平面一、二维流中的水文地质参数。
12. 均质与非均质岩层是根据_岩石透水性与空间坐标_的关系划分的,各向同性和各向异性岩层是根据岩石透水性与水流方向关系划分的。
1渗流基本理论

§1 渗流的基本概念
3、多孔介质中地下水的运动 比较复杂(源于多孔介质的广义性),包括两大类, 运动特点各不相同。 (1)第一类为地下水在孔隙、细小裂隙或发育微弱、 分布均匀的溶隙中运动,具有统一的流场,运动方 向基本一致,符合达西定律,称为达西流。 (2)第二类为地下水沿较大裂隙和溶隙的运动,仍 具有统一的流场,运动方向基本一致,但已不符合 达西定律,流态仍为层流。
§1 渗流的基本概念
根据岩石空隙的性质及其成因,含水介质可划分为: ①孔隙介质:含有孔隙的岩石松散沉积物(黄土:特 殊的孔隙—裂隙介质)。 ②裂隙介质:含有裂隙的坚硬岩石(碎屑岩、火成 岩)。 ③溶隙(岩溶)介质:含有溶隙(穴)的可溶性岩石 (石灰岩、白云岩)。
§1 渗流的基本概念
(3)多孔介质 狭义:孔隙介质 广义:包括孔隙介质、裂隙介质(细小裂隙)和某些 岩溶不十分发育(溶隙分布较均匀)的由石灰岩和 白云岩组成的岩溶介质,都称为多孔介质。 2、多孔介质的特征 (1)空(孔)隙性 ①有效孔隙(Effective pores) 多孔介质中相互连通的,不为结合水所占据的 那部分孔隙。 有效孔隙中存在的是重力水和少量毛细水。
§1 渗流的基本概念 一、地下水在多孔介质中的运动
1、什么是多孔介质? (1)介质 一种物质存在于另一种物质的内部时,后者就 是前者的介质。 《辞海》中的解释:“物体系统在其间存在或物理 过程(力、能量的传递)在其间进行的物质”。 (2)含水介质 地下水存在并运动于岩土空隙中,具有空隙的 岩土称之为含水介质。
§1 渗流的基本概念
4、一点异议 还有一种运动形式:地下水沿大裂隙和发育良好的 岩溶管道的运动,方向没有规律,分属不同的地下 水流动系统,流态为紊流。 属于非多孔介质中地下 水的运动。 地下水在多孔介质和非多孔介质中地下水的运动形 式不同—流态不同(根据雷诺数Re可判断流态)。 @教材上一直将多孔介质中的运动分为: (1)在孔隙和裂隙中运动 (2)大裂隙和管道(岩溶发育好)中运动 我个人认为不妥:多孔介质而非含水介质。
第一章 渗流的基本概念和基本定律

PZ1 PZ2 PZ
Q KA Z L
要求记忆
对于水平地层,则有: Q KA P
L
第一节 线性渗流规律
二.达西定律的讨论
v w ①渗流速度 与真实速度
v Q A
w Q A
渗流流量 渗流面积
孔隙度
v w
第一节 线性渗流规律
② 达西定律的适用条件
ⅰ:流体为牛顿流体.
ⅱ:渗流速度必须在适当的范围内(即流体为层流流动).
纯溶洞结构 裂缝孔隙结构 双重介质 溶洞孔隙结构 裂缝溶洞结构 三重介质 溶洞--裂缝--孔隙结构
二 储集层外部形状及简化
① 根据储集层的厚度:层状油藏,块状油藏 (球形流)
② 根据边界条件:定压边界,封闭边界 ③ 根据平面延伸系数:
长轴 <3 圆形地层 短轴 >3 条带形地层
三 储集层的特点
① 储集性 a e m
第三节 油藏能量及驱动方式
三.油藏驱动方式
驱动方式:在油藏开采过程中主要依靠哪种能量来驱 动,就称为何种驱动方式.
①刚性水压驱动:边水或注入水动:边水供应不足,油藏压力变小,水区 和油区的流体及岩石弹性膨胀.
第三节 油藏能量及驱动方式
③弹性驱动:岩石及流体的弹性能为主要 的驱油动力.(封闭边界,无 气顶,无注入水)
第二节 渗流的基本概念
④ 真实速度:
Q V A
A ---真实渗流面积
A A
V V
—透明度 在数值上与孔隙度相等
第二节 渗流的基本概念
三.油藏中压力的概念
① 原始地层压力Pi 油田未开发前的地层中流体承受的压力. 对于同一水动力学系统其压力梯度曲线
(即P~H曲线)应该为一直线. 一个油藏若处于多个水动力学系统,其
第一章 弹性多孔介质渗流理论1讲解

1.1.1 多孔介质的孔隙性
反映多孔介质的孔隙性,采用孔隙率或孔隙比。用以下的 方法定义多孔介质在一点 x (xl, x2 , x3 )的“孔隙率”n(x)
量或参数,例如水头、浓度、孔隙率、渗透系数等也相应成为空 间中的连续甚至可微的函数,从而避免了弄清多孔介质微观结构 的困难。基于这一尺度研究多孔介质中发生的现象称为宏观水平 上的方法。
为简单起见,我们来考虑饱和流体,此时多孔介质的孔隙空间 全部为所考虑的流体所充满。设a是对孔隙空间中流体所定义的 一种微观水平上的量(数量或向量),在表征体元[U0(x)]的孔隙空 间[U0,v(x)]上量a的积分平均值为
基本上保持为常数,因而可以把它确定为点 x 处的孔隙率。另一 方面, [U0(x)]又是足够小,以致和整个渗流区域相比可近似看 作一个点。这样定义的多孔介质质点也称为多孔介质的表征体元;
让渗流区域中的每个数学点都联系着一个多孔介质质点,则 本来是由固体颗粒和孔隙所构成的多孔介质,就可以近似看成是 由完全充满空间的多孔介质质点所构成的连续介质,各种有关的
设V为位于点x的流体质点速度
V ( x ) ? u( x)i ? v( x ) j ? w( x)k
(1-14)
若用Va表示组分a的速度,则整个流体体系,可以定义以下两个 平均速度,即质量平均速度
和体积平均速度
N
? V ? ? aV a a?1
N
? V ?? vaVa a ?1
(1-15) (1-16)
下面考虑处于静止状态下,承压含水层的受力情况 (见图11)。为简化讨论,假设含水砂层的颗粒之间没有粘聚力。在含水 层中切一水平的横截面,面积为A。若设A=1,按Terzaghi 一维 固结理论,作用在该平面上的上冠荷载分别由颗粒 (固体骨架)和 水承担,即
【免费下载】渗流力学基本理论

目录第一章渗流理论基础 (1)1.1渗流的基本概念 (1)1.2渗流基本定律 (7)1.3岩层透水特征及水流折射定律 (11)1.4流网及其应用 (14)1.5渗流连续方程 (19)1.6渗流基本微分方程 (24)1.7数学模型的建立及求解 (32)第一章渗流理论基础1.1 渗流的基本概念1.1.1 多孔介质及其特性1.1.1.1多孔介质的概念多孔介质(Porous medium):地下水动力学中具有空隙的岩石。
广义上包括孔隙介质、裂隙介质和岩溶不十分发育的由石灰岩和白云岩组成的介质,统称为多孔介质。
孔隙介质:含有孔隙的岩层,砂层、疏松砂岩等;裂隙介质:含有裂隙的岩层,裂隙发育的花岗岩、石灰岩等。
1.1.1.2 多孔介质的性质(1) 孔隙性:有效孔隙和死端孔隙。
孔隙度(Porosity)是多孔介质中孔隙体积与多孔介质总体积之比(符号为n),可表示为小数或百分数,n=Vv/V。
有效孔隙(Effective pores)是多孔介质中相互连通的、不为结合水所占据的那一部分孔隙。
有效孔隙度(Effective Porosity)是多孔介质中有效孔隙体积与多孔介质总体积之比(符号为n e),可表示为小数或百分数,n e=V e/V。
死端孔隙(Dead-end pores )是多孔介质中一端与其它孔隙连通、另一端是封闭的孔隙。
(2) 连通性:封闭和畅通,有效和无效。
(3) 压缩性:固体颗粒和孔隙的压缩系数推导。
(4) 多相性:固、液、气三相可共存。
其中固相的成为骨架,气相主要分布在非饱和带中,液相的地下水可以吸着水、薄膜水、毛管水和重力水等形式存在。
固相—骨架matrix气相—空气,非饱和带中液相—水:吸着水Hygroscopic water薄膜水pellicular water毛管水capillary water重力水gravitational water1.1.1.3多孔介质中的地下水运动比较复杂,包括两大类,运动特点各不相同,分别满足于孔隙水和裂隙岩溶水的特点。
第一章渗流理论基础

地下水动力学:是研究地下水在孔隙岩石、裂隙岩石和岩溶岩石中运动规律的科学。
它是模拟地下水流基本状态和地下水中溶质运移过程,对地下水从数量上和质量上进 行定量评价和合理开发利用,以及兴利防害的理论基础。
第一章渗流理论基础§—1渗流的基本概念、地下水在含水岩石中的运动1多孔介质:具有孔隙的岩石。
含水介质一般分为三类: 孔隙介质:含有孔隙水的岩层。
裂隙介质:含裂隙水的岩层。
岩溶(Karst )介质:含岩溶水的岩层。
、地下水和多孔介质的性质1地下水的状态方程地下水的状态方程:实际上是地下水的体积和密度随压力变化的方程。
:_ 1dVV dp等温条件下,水的压缩系数为: 设初始压强p o 时,水的体积为V o ,当压强变到p 时,体积变为V ,由上式得: V 二V o V =V 0e 七p T )用Taylor 级数展开,舍去高次项,得到如下的状态方程:V = V o [1- 3 ( P-P 0)] p = po [1- 3 ( p-p o )] 2多孔介质的某些性质 (1) 多孔介质的孔隙性孔隙度:指孔隙体积和多孔介质总体积之比。
有效孔隙:互相连通的、不为结合水所占据的那一部分孔隙。
有效孔隙度:指有效孔隙体积和多孔介质总体积之比。
死端孔隙:一端与其它孔隙连通,另一端是封闭的,其中的地下水是相对停滞的。
(2) 多孔介质的压缩性天然条件下,一定深度处的多孔介质,要受到上覆岩层荷重的压力。
荷重增加,将引起 多孔介质的压缩。
多孔介质的压缩系数:VdV V 。
V1 dV b dV 』W 觀厂 dd d 乂 趙忆d VunV L多孔介质的压缩包括固体 上式令V b d V b d 、上式变为:a = (1-n )固体骨架的压缩性比孔隙的压缩性小的多,上式变为:a =n a p三、贮水率和贮水系数1.水位变化对含水层厚度的影响有效应力 地下水位下降,水压力减小,有效应力增大,多孔介质被压缩。
多孔介质的压缩包括固体颗粒的压缩和孔隙的压缩。
第一章 渗流的基本概念和基本定律

KA
P1
P2
L
三.渗流力学常用单位制
① 工程单位制 (公斤.米.秒) ② 物理单位制 (克.厘米.秒) ③ 混合单位制 (达西单位制) ④ 国际单位制
第二节.非线性渗流定律
非线性渗流:渗流速度 v 与压力梯度不成线 性关系的渗流.分高速和低速两 种。
dP dL
0
第二节.非线性渗流定律
一.产生非线性渗流的原因
Q A H1 H2 A H Z1 Z2 L
Q KiA L
Q
KiA
L
K i--比例常数,渗流系数
第一节 线性渗流规律
进一步实验表明:
岩石绝对 渗透率
Ki
流体重率
Ki K
Q KA L
v Q K A L
v ~ v ~ 呈 线性 关 系
第一节 线性渗流规律
根据力的平衡关系有:
A(P1 P2 ) Ag(Z1 Z2 ) AvL
Q vA A[(P1 gZ1) (P2 gZ2 )] L
令K 得:
Q K A PZ1 PZ2 KA [ P1 P2 gSin]
L
L
该公式即为倾斜地层考虑重力影响的达西公式.
若为水平地层,则有: Q
纯溶洞结构 裂缝孔隙结构 双重介质 溶洞孔隙结构 裂缝溶洞结构 三重介质 溶洞--裂缝--孔隙结构
二 储集层外部形状及简化
① 根据储集层的厚度:层状油藏,块状油藏 (球形流)
② 根据边界条件:定压边界,封闭边界 ③ 根据平面延伸系数:
长轴 <3 圆形地层 短轴 >3 条带形地层
三 储集层的特点
① 储集性 a e m
压力梯度曲线则为一条折线.
第二节 渗流的基本概念
第一章 渗流理论基础

第一章渗流理论基础一、名词解释1. 渗透速度:表示水流在过水断面上的平均流速,不能代表任何真实水流的速度。
2. 实际速度:表示地下水在孔隙中的真实速度。
3. 水力坡度:把大小等于梯度值,方向沿着等水头面的法线,指向水头降低方向的矢量称为水力坡度。
4. 贮水系数:当水头变化1m时,从单位水平面积,高度为承压含水层厚度的柱体中释放或贮存的水量。
5. 贮水率:当水头下降1m时,单位体积承压含水层释放出来的水量。
6. 渗透系数:也称水力传导系数,当水力坡度J=1时,渗透系数在数值上等于渗透速度。
7. 渗透率:表示多孔介质能使气体或液体通过介质本身的能力,只与岩石性质有关,与液体性质无关。
8. 导水系数:T=KM,是一个水文地质参数,即水力坡度J=1时,通过整个含水层厚度上的单宽流量。
二、填空题1.地下水动力学是研究地下水在、、和中运动规律的科学。
(孔隙岩石、裂隙岩石、岩溶岩石)2.通常把具有连通性的孔隙岩石称为多孔介质,而其中的岩石颗粒称为。
(骨架)3.地下水在多孔介质中存在的主要形式有、薄膜水、毛管水和重力水,而地下水动力学主要研究的运动规律。
(吸着水、重力水)4.在多孔介质中,不连通的或一端封闭的孔隙对地下水运动来说是,但对贮水来说却是。
(无效、有效)5.地下水的过水断面包括空隙和固体颗粒所占据的面积,渗透流速是上的平均速度,而实际速度是的平均速度。
(过水断面、空隙面积)6.在渗流场中,把大小等于,方向沿着的法线,并指向水头降低方向的矢量,称为水力坡度。
(梯度值、等水头面)7.渗流运动要素包括流量Q、、压强p和等。
(渗流速度v、水头H)8.根据地下水与的关系,将地下水运动分为一维、二维和三维运动。
(运动方向、空间坐标轴)9.渗透率是表征的参数,而渗透系数是表征岩层的参数。
(岩层渗透性能、透水能力)10.影响渗透系数大小的主要因素是以及。
(岩石性质、渗透液体的物理性质)11.导水系数是描述含水层的参数,它是定义维流中的水文地质参数。
第1章渗流理论基础
25
1.1 渗流的基本概念
1.1.5 渗流速度
渗流是充满整个岩石截面的假想水流。在垂直于 渗流方向取的一个岩石截面,称为过水断面。 地下水的过水断面是整个岩石截面,既包括空隙 面积也包括固体颗粒所占据的面积。
当渗流平行流动时,过水断面为平面,弯曲流动
时则为曲面(图1-6 )。
26
1.1 渗流的基本概念
22
1.1 渗流的基本概念
实际的地下水流仅存在于空隙空间。为了便于研
究,用一种假想水流来代替真实的地下水流。这 种假想水流的性质(如密度、粘滞性等)和真实 地下水相同;但它充满了既包括含水层空隙的空 间,也包括岩石颗粒所占据的空间。
23
1.1 渗流的基本概念
假想水流运动时,满足以下条件:
3
1.1 渗流的基本概念
1.1.1 地下水在含水岩石中的运动
在地下水动力学中,把具有孔隙的岩石称为多孔介质。 含有孔隙水的岩层,如砂层或疏松砂岩等称为孔隙介质, 也称多孔介质。 含裂隙水的岩石,如裂隙发育的石英岩、花岗岩等称为裂 隙介质。 广义地说,可以把孔隙介质、裂隙介质和某些岩溶不十分 发育的由石灰岩和白云岩组成的介质都称为多孔介质。
渗透速度,比流量)为:
Q A
渗流速度代表渗流在过水断面上的平均流速。它不代表任 何真实水流的速度,只是一种假想速度。假设整个过水断
面都被水充满时,地下水就以这种速度流动。
28
1.1 渗流的基本概念
实际上,地下水仅仅在空隙中流动。在空隙中的不
同地点,地下水运动的方向和速度都可能不同,平 均速度 称为实际平均流速。速度v 和地下水的实际
1)地下水的状态方程 在等温条件下,水的压缩系数为:
康-第一章 渗流基本理论

大区域的水均衡计算经常用于区域的水资源评价
以微分单元体做水均衡可以推导渗流连续性方程。
2.2.2、渗流定律
(一)达西定律—线性渗透定律
H.Darcy—
法国水力学家,1856年(以实验为 基础研究时期)通过大量的室内 实验得出的
实验条件:
1)等径圆筒装入均匀砂样,断面为ω
2)上(下各)置一个稳定的溢水装 置——保持稳定水流
发生渗流的区域称为渗流场。 渗流场由固体骨架和岩石空隙中的水两部分组成。 渗流只发生在岩石空隙中。
(理想)渗流模型
z 理想渗流的概念:地下水充满整个含水层或含水系统 (包括空隙和固体骨架),渗流充满整个渗流场。
理想渗流等效简化原则: z 理想渗流通过某断面的流量应等于通过该断面内孔隙
面积的实际流量:质量等效。 z 理想渗流通过某岩层所受到的阻力与实际水流所受到
针对复杂的地下水渗透运动 ,提出两种研究方法: 一种是以研究微观运动为主,采用统计平均的方法来确
定地下水运动的宏观规律性 ; 另一种是从宏观角度出发,采用试验及数学分析方法,
对大量微观运动进行宏观研究,得出各种运动条件下地下水 运动的基本规律。
根据第二种研究方法对实际的地下水流动进行概化研 究,给出渗流模型:即假象的地下水在岩石空隙中的运动模 型。
z
y
x
图1-2-8a 一维流
图1-2-8b1 平面二维流
图1-2-8b2 剖面二维流
三维流图示
图1-2-8c 三维流
承压水的一维流动
渠道向河流渗漏的地下水二维流动 (a)平面图 (b)剖面图
均质各向同性含水层中潜水井抽水 时的地下水运动
(a)平面图 (b)剖面图
河弯处潜水的三维流动 (a)平面图 (b)剖面图
第一章_渗流理论基础

u
渗流速度=n 实际平均流速
Q An
(1-1a)
若确定渗流场中任一点的渗流速度,可以按以下方法进行 讨论: 设以P点为中心的REV的平均渗流速度矢量为v,令REV 的体积为 V0,其中空隙体积为n V0,在空隙中的不同 地点,流速u不同,将u 在全部空隙体积n V0中求积分, 再除以REV体积 V0,即为渗流速度,表示为:
2 v
H Hn Z
P
Z
P g
(1-7)
意义:渗流场中任意一点的水头实际上反映该点单位质量液 体具有的总机械能,地下水在运动过程中不断克服阻力,消 耗总机械能,因此沿地下水流程,水头线是一条降落曲线。
• Head, Total — The sum of the Elevation Head (distance of a point above datum), the Pressure Head (the height of a column of liquid that can be supported by static pressure only at the point), and the velocity Head (the height to which the liquid can be raised by its own kinetic energy. Also see Hydraulic Head. • Hydraulic Head — (1) The height of the free surface of a body of water above a given point beneath the surface. (2) The height of the water level at the headworks or an upstream point of a waterway, and the water surface at a given point downstream. (3) The height of a hydraulic grade line above the center line of a pressure pipe, at a given point. • Piezometric Head — Synonymous with Hydraulic Head, which is now commonly used.
渗流理论基础.
体,是渗流场中其物理量的平均值能够近似代替整个渗流 场的特征值的代表性单元体积。 REV具备两个性质:
(1) 其体积和面积,大于个别空隙而小于渗流场,其中的渗流可以从 一点连续运动到另一点; (2) 通过单元体的运动要素(流量Q、水头h、压力p、实际水头受到 的阻力R)与真实水流相等,运动要素是连续变化的。
因Vs=constant,故
故
只在垂直方向上有压缩,
(1-62) (1-63)
上两式表示垂直厚度变化、孔隙度变化与水的压强变化的关 系。 • 水头降低时含水层释出水的特征,取面积为1m2、厚度为l m (即体积为l m3)的含水层,考察当水头下降1m时释放的 水量。此时,有效应力增加了H=g×1=g。 • 介质压缩体积减少所释放出的水量(dVb)为 • 与水体积膨胀所释放出的水量(dV)之和
REV的作用:
(1) 把物理性质看作是坐标的函数,孔隙度n、导水系数T、给水度 和渗透系数均连续。 (2) 渗流的要素可以微分、积分,可以用微分方程来描述渗流要素。
10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
dL 1 2 3 4 5 6 7 8 9 10
2) 多孔介质的性质
Porosity —the property of containing openings or interstices. In rock or soil, it is the ratio of the volume of openings in the material to the bulk volume of the material. Porosity, Effective — The amount of interconnected pore space in a material available for fluid transmission; expressed as a percentage of the total volume occupied by the interconnecting interstices. Porosity may be primary, formed during deposition or cementation of the material, or secondary, formed after deposition or cementation, such as fractures.
第1章 渗流的基础知识和基本定律

纯溶洞结构简化模型
16
第一节 油气储集层
二、外部几何形状及其简化
以背斜构造为例,对其外部几何形状进行简化。对实际油藏进行水平投影,如 下图所示。 油水分界面(油水接触面)->油水边界(内含油边界、外含油边界) 油气分界面(油气接触面)->油气边界 如果有露头->供给边界(有水源供应) 封闭边界(边界是封闭的)
油藏外部形状及其简化示意图
17
第一节 油气储集层
三、油气储集层的特点
1.储容性 油气储集层具有储存和容纳流体的能力,即储容性。 绝对孔隙度:岩石内总的孔隙体积占岩石体积的百分数。 公式:φt=Vt/V×100% 用途:计算油气藏的绝对储量。 有效孔隙度:岩石中有效孔隙体积占岩石体积的百分数。 公式:φ=Ve/V×100% 用途:计算油气藏的可采储量。
20
第一章 渗流的基础知识和基本定律
第一节 油气储集层 第二节 渗流的基本概念 第三节 力学分析及油藏驱动方式 第四节 线性渗流与非线性渗流
21
第二节 渗流的基本概念
一、渗流的三种基本几何形式 1.平面单向流 流体质点沿同一方向运动。 特点:流线相互平行,垂直于流动方向的截面上各点 的渗流速度相等;如果流动是稳定渗流,那么流动方 向上任一点的压力只是沿程位移x的线性函数。
折算压力计算示意图
30
第一章 渗流的基础知识和基本定律
第一节 油气储集层 第二节 渗流的基本概念 第三节 力学分析及油藏驱动方式 第四节 线性渗流与非线性渗流
31
第三节 渗流过程中的力学分析及油藏的驱动方 式
一、力学分析
油气水在岩石孔道中流动,受到各种力的作用。 1.流体的重力 地球对流体的吸引力称为流体的重力。 重力有时是动力,有时是阻力。
第一章 渗流理论基础

由水的压缩性得: dV V dp n g ng
二者之和表示面积为1个单位、厚度为1个单位的含水层,当 水 头降低1个单位时所释出的水量,用符号 s 表示,即:
s dVb dV g ng g n
称为贮水率或释水率。其量纲为(L-1)。
东北大学资土学院孙宝亮11渗流的基本概念孔隙多孔隙少砂颗粒具规则形状的砂岩具不规则形状的砂岩且分选差粉砂颗粒粘土很小数量的粘土和粉沙颗粒间孔隙空间小数量的裂隙孔隙空间破裂的页岩没破裂的页岩不渗透的岩石没胶结的砂岩胶结的砂岩胶结物孔隙空间孔隙度和渗透性多孔的并可渗透的孔隙度和渗透性降低多孔的并不可渗透的砂颗粒孔隙空间多孔的砂岩胶结的砂岩细粒砂岩有不规则形状的砂岩破裂的页岩没破裂的页岩很小数量的粘土和粉砂颗粒间孔隙空间粉砂颗粒不渗透的岩石胶结物小数量的裂隙孔隙空间孔隙度孔隙度原生孔隙原生孔隙次生孔隙次生孔隙沉积物或沉积岩岩浆岩和变质岩孔隙颗粒花岗岩破裂破裂可渗透的砂岩断裂的花不同的土和岩石供水渗透的孔隙大小是不同的
次生孔隙
岩浆岩和变质岩
好井
差井
井
可渗透的 砂岩
干井
好井
好井
断裂的花 岗岩
不同的土和岩石供水渗透的孔隙大小是不同的。水在大的孔隙 运动更容易。砾石的孔隙大,水渗透的快;粘土的孔隙太小, 水几乎不能渗透。 一些岩层太坚固,能隔水。其它易碎有很多裂隙,如果裂隙连 通,水就可通过。
§1.1 渗流的基本概念
'
σ′ 为作用于多孔介质表面的应力 Vb 为多孔介质的体积 α 为多孔介质的压缩系数
Vb=Vs+Vv,Vs为固体骨架体积,而Vv为其中的孔隙体积。 n=VV/Vb
1 dVb 1 dVs 1 dVV ' ' Vb d Vb d Vb d '
渗流1---渗流的基本概念和基本规律

渗流力学:专门研究渗流的运动形态和运动规律的科学。
渗流力学
张凯
2
第一章 绪 论
二、渗流的分类
地下渗流:存在于地层中,如:油、气、水、地热等在地 层中的流动。 层中的流动
工程渗流:存在于化工、冶金、机械、环保中,如渗碳、 超精细过滤。
生物渗流:存在于动、植物中,如水、矿物质、血液在生 物中的流动。渗流ຫໍສະໝຸດ 学 张凯 7
第一章 绪 论
五、参考书
葛家理 .《油气层渗流力学》北京:石油工业出版社 1982年 刘尉宁.《渗流力学基础》北京:石油工业出版社 1985 年 葛家理.《现代油藏渗流力学原理》北京:石油工业出 版社 2001年 郎兆新.《油气地下渗流力学》东营:石油大学出版社 《油气地下渗流力学》东营 石油大学出版社 2001年
特点:含油气丰富,常形成 大油气藏 大油气藏。
渗流力学 张凯 15
第一章 绪 论
2、地层油气藏
(3)不整合覆盖油气藏 存在于储集层上倾部分 被剥蚀,然后又被不渗透岩 层不整合遮挡形成的圈闭中。 层不整合遮挡形成的圈闭中 特点:闭合面积大,含油气 丰富。 丰富 美国普鲁德霍湾油田东西长64公 里,南北宽32公里,面积约 2000平方公里,为一向西南倾 伏的鼻状构造,北部被断层所切, 东部被一不整合所削蚀,其上被 下白垩系海相页岩不整合封闭 下白垩系海相页岩不整合封闭。
14
第一章 绪 论
2、地层油气藏
(2)生物礁油气藏
礁型油田的一个著名实例, 是墨西哥黄金港环礁带和扎波 里卡礁型油气田。 里卡礁型油气田 黄金巷环礁带位于墨西哥 城东北的坦皮科湾沿岸到墨西 哥湾海上,包括:(1)老黄金 巷带;(2)新黄金巷带;(3) 海上黄金巷带 整个环礁带呈 海上黄金巷带。整个环礁带呈 椭圆形,长轴为北西-南东向, 长约150km。
地下水动力学习题

《地下水动力学》习题集第1章 渗流理论基础习题1-1 渗流的基本概念一、填空题1. 地下水动力学是研究地下水在 、 和 中运动规律的科学。
通常把 称为多孔介质,而其中的岩石颗粒称为 。
多孔介质的特点是 、 、 和 。
2. 地下水在多孔介质中存在的主要形式有 、 、 、 和 ,而地下水动力学主要研究 的运动规律。
3. 在多孔介质中,不连通的或一端封闭的孔隙对地下水运动来说是 ,但对贮水来说却是 。
4. 假想水流的 、 、 以及 都与真实水流相同,假想水流充满 。
5. 地下水过水断面包括 和 所占据的面积。
渗流速度是 上的平均速度,而实际速度是 的平均速度。
6. 在渗流中,水头一般是指 ,不同数值的等水头面(线)永远 。
7. 在渗流场中,把大小等于 ,方向沿着 的法线,并指向水头 方向的矢量,称为水力坡度。
水力坡度在空间直角坐标系中的3个分量分别为 、 和 。
8. 渗流运动要素包括 、 、 和 等。
9. 根据地下水渗透速度 与 关系,将地下水运动分为一维、一维和三维运动。
二、判断及选择题10. 地下水在多孔介质中运动,因此可以说多孔介质就是含水层。
( )11. 地下水运动时的有效孔隙度等于排水(贮水)时的有效孔隙度。
( )12. 对含水层来说其压缩性主要表现在空隙和水的压缩上。
( )13. 贮水率)(βαρμn g s +=也适用于潜水含水层。
( )14. 贮水率只适用于三维流微分方程。
( )15. 贮水系数既适用于承压含水层,也适用于潜水含水层。
( )16. 在一定条件下,含水层的给水度可以是时间的函数,也可以是一个常数。
( )17. 潜水含水层的给水度就是贮水系数。
( )18. 在其他条件相同而只是岩性不同的两个潜水含水层中,在补给期时,给水度μ大,水位上升大;μ小,水位上升小。
在蒸发期时,μ大,水位下降大;μ小,水位下降小。
()19. 决定地下水流向的是()。
(1)压力的大小;(2)位置的高低;(3)水头的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)各向同性与各向异性
根据岩层透水性与渗流方向的关系划分,若渗流 场中,某一点的K与渗流方向无关,则该岩层是各向 同性的,反之则为各向异性。
各向同性岩层(isotropic strata /aquifer):渗流 场中某一点的渗透系数不取决于方向,即不管渗流方 向如何都具有相同渗透系数的岩层。
K
Kxx Kyx
Kxy Kyy
(1-24b)
即有
v =K·J
(1-25)
渗透系数是对称张量,即Kxy=Kyx,Kxz=Kzx,Kyz=Kzy。 在各向异性介质中,水力坡度与渗流方向不一致,但在三个
方向上两者是平行的,而且这三个方向称为主方向。
主渗透系数(主值)是指沿主方向测得的渗透系数,用
K1、K2、K3表示,有Kxx=K1,Kyy=K2,Kzz=K3,此时:
Confined aquifer
Land surface
water table Equipotential lines
Flow line
99m
Head above the datum plane
98m
97m
96m
95m
94m 93m 92m
Bedrock
图1-16水流折射
• Heterogeneity — Characteristic of a medium in which material properties vary from point to point. Contrast with Homogeneity.
• If hydraulic conductivity is consistent throughout a formation, regardless of position, the formation is homogeneous. If hydraulic conductivity within a formation is dependent on location, the formation is heterogeneous.
K1 K2
H1
x H2
x
因为 H1 H2
,
x x
则得到水流折射定律:
tg1 K 1 tg2 K2
y
பைடு நூலகம்
(1-32)
y
介质Ⅱ
2r
介质Ⅰ
2 2n
1n 1
1r
界面 x
渗流折射时必须满足介质 的Ⅱ方程(2r 1-32)。
法线
根据水流折射原理和达西定律,2 可以
介质Ⅰ
帮助分析流场的水动力条件2n 的变化。界 x 面
(1)水流平行层面
特点:水流为稳定流,岩 层水平分布,各段流量之和 等于各部分流量之和,且各 段具有统一的水头,各段具 有相同的水力坡度。
1
2
H 1
M 1 M 2 M 3
K 1 K 2 K 3
H 2
M n
K n
l
图1-14 层状岩层中平行于层面的渗流
根据达西定律有:
n
n
H
q qi KiMi
i1
(1-29)
(2)水流垂直层面
特点:水流垂直层面运动,每段水流具有相同的单宽
流量,且每段水力坡度不同。
由 ,由此推导出, qi Kib M H 1,q2K2b M H 2
H1b qM K11,H2bM K22
H H 1 H 2 .. . H nb qi n 1M K ii
依次类推,有
H1
n
Mi
x
K xx
H x
K xy
H y
K xz
H z
y
K yx
H x
K yy
H y
K yz
H z
z
K zx
H x
K zy
H y
K zz
H z
(1-23)
(1-23)
(1-24a)
即可写成:
K KKxyxx
Kxy Kyy
Kxz Kyz
Kzx Kzy Kzz
(1-24a)
图1-13
在二维空间中,
各向异性岩层(anisotropic strata /aquifer):渗 流场中某一点的渗透系数取决于方向,渗透系数随渗 流方向不同而不同的岩层。
• Isotropy — That condition in which a medium has the same properties in all directions.
界面
1n
介质Ⅱ
1
介质Ⅰ
1r
渗流折射现象
讨论水流折射定律, 可以的出以下结论:
(1)若K1=K2,则,1=2, 表明在均质介质中水流不发生折
射。
(2)若K1≠K2,而且K1,K2均不为0时, 1=0,则 2=0,表
明水流垂直通过界面时水流不发生折射。
(3)若K1≠K2,且K1,K2均不为0, 若1=900,则 2=900,表
K1 0 0
K
0
K2
0
0 0 K3
(1-26)
Homogeneous Heterogeneous
Isotropic ; ;
; ;
Anisotropic ; ;
; ;
1.3.3 层状岩层的等效渗透系数
在自然界中很常见的非均质岩层多是由许多透水性各不 相同的薄层相互交替组成的层状岩层。当每一分层的渗透系 数Ki和厚度面Mi已知时,可求出平行于层面的渗透系数Kp和 垂直于层面的渗透系数Kv。
i1
L
若把其视为整体时,有
H qKpM L
故
KpML Hi n1KiMi L H
水平岩层的等效渗透系数为:
等效导水系数为
n
Mi Ki
K p i1 M
n
n
Tp Ti MiKi
i1
i1
(1-27) (1-28)
垂直方向岩性渐变时,有
1M
K p M 0 K(z)dz
M
Tp 0 K(z)dz
均质岩层(Homogeneous strata/aquifer):渗流场中所 有点都具有相同参数的岩层。
非均质岩层(inhomogeneous /heterogeneous strata /aquifer):渗流场中所有点不都具有相同参数的岩层,渗 透系数K=K(x,y,z),为坐标的函数。
非均质分为两类,即渐变的和突变的。
• Anisotropy —
• (1) The condition of having different properties in different directions.
• (2) The condition under which one or more of the hydraulic properties of an aquifer vary according to the direction of the flow.
明水流平行于界面时水流不发生折射。
(4)当水流斜向通过界面时,水流发生折射,介质的渗透系 数越大,θ值也越大,流线也越靠近界面。介质相差越大,两 角的差值也越大。
Land surface
water table Unconfined aquifer
Confining bed
Flaw line
Bedrock
第一章 渗流理论基础
肖长来 吉林大学环境与资源学院
2009-9
§1.3 岩层透水特征及水流折射定律
1.3.1 岩层透水特征分类 (1)均质与非均质
根据岩层透水性随空间坐标的变化情况划分,若渗流场 中,任意点都具有相同的渗透系数,或渗透系数不随空间 坐标的变化而变化,则该岩层是均质的,反之则为非均质。 岩石的非均质分两类,一类是渐变的,另一类是突变的。
如图所示:水流由K1介质进入 K2介质中,二者交界面 上某一点的渗流速度和水头在两介质中的值依次为V1、V2 和H1、H2。对于界面上的任一点应满足以下条件:
H H 2 V1n V 2 n
由下图中几何条件有:
(1-31)
tg1
v1 v2n
,tg2
v2 v2n
则有
tg 1 tg2
v1 v2
1.3.2 渗透系数张量 岩石的透水性是用渗透系数来衡量的。渗透系
数实际上是个张量。 (1)对于各向同性介质,其中任一点的渗透系
数值与渗流方向无关,是一个标量,水力坡度与 渗流方向是一致的。
此时,可以表示为如下表达式:
x K H x, y K H y, z K H z
(2)对于各向异性介质,K与渗流方向有关,K不再是标 量,水力坡度与渗流方向一般是不一致的。此时,可以表 示为如下表达式:
H2 H Hn
Kv
i1
n M i
i1 K i
(1-30)
H0
Q
K1 K2
Hn
Kn
b
可见,取决于Ki最小的分层(阻 力最大),Ki=0,则 Kv =0。 另外,总是有 Kp Kv 。
M1 M2
Mn
M
图1-15 层状岩层中垂直于层面的渗流
1.3.4 突变界面的水流折射定律
根据水流连续性条件,当水流斜向由一种介质进入另一 种介质时,会发生折射。
• Homogeneity — Characteristic of a medium in which material properties are identical throughout. A material is homogeneous if its hydrologic properties are everywhere identical.
