13二端口网络参数和方程
演示文稿二端口网络参数和方程

二端口网络参数和方程
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念
1. 一端口网络
I
+
U
Z
-
(Y)
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。
i1 +
u1
i1
–
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
i2 +
u2 – i2
4. 二端口与四端网络的区别:
二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
i1
i2
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
i1
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
线性RLCM 受控源
四端网络
例1
R
C
C
滤波器 n:1
变压器
三极管 传输线
3. 二端口(two-port)
如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
整理可得
I1 = (Y1 Y2 )U1 - Y2U2 I2 = -Y2U1 (Y2 Y3 )U2
二端口网络的参数

元素为阻抗,
单位是 。
与Y参数方程相同, Z11、Z12、Z21、Z22取决于电路结
构及参数。根据Z参数方程及I1 、I2,可求得 U1 、U 2 。
确定Z参数:
UU12
ZZ1211II11ZZ1222II22
在1-1' 端输入I1 ,将2-2'端开路,即 I2 0 代入上式 有
U1
Z11I1
有
A
U1 U 2
I2 0
称为输出端开路时传输电压比
C
I1 U 2
I2 0
称为输出端开路时转移导纳(S)
UI11CAUU22DB
( (
II22))
2、在输出端短路,即U 2 0 时
有
B
U1 I2
U2 0
称为输出端短路时转移阻抗()
对于图所示的一端口网络来说
Z
U I
或者
Y
I U
U Z I (以电流 I 为已知量)
或者 I YU (以电压U 为已知量)
一、Y 参数及方程(短路导纳参数)
已知 U1、U 2 ,求 I1 、I2 。 由替代定理可将 U1 、U 2 所在支路用理想电压源代替。
•
1 I1
•
I2 2
•
U1
N
•
U2
1′
确定Y参数:
II12 YY1211UU11YY1222UU24
在1-1' 端加 U1,将2-2' 端短路,即 U 2 0 代入上式
I1 Y11U1
Y11
I1 U1
U 2 0
称为输出端短路时的输入导纳(S)
I2 Y21U1
Y21
I2 U1
U 2 0
【推荐】电路原理基础:第二章 二端口网络的方程和参数
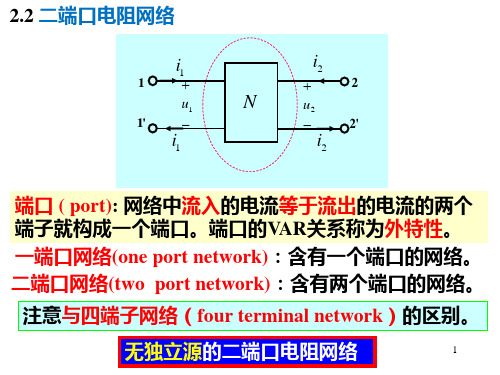
D
i1 i2
u2 0, 10
四、H参数方程: 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程,则可求得其他参数,
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性(reciprocal)
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源,则网络参数就具有如下性质:
(1) R12 R21 (3) T AD - BC 1
注意与四端子网络(four terminal network)的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关,用端口电压、电流(共四个量)间的关 系反映,共六种情况。
2
一、R参数方程:
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
双口网络的方程和参数

1.1双口网络的阻抗矩阵
若已知端口电流İ1和İ2,可以应用替代定理将两个端口电流 都看作是外施的电流源,这样就可以根据叠加定理,1和2 分别为各个电流源单独作用时所产生的电压之和,即
V1 Z11I1 Z12I2 V2 Z21I1 Z22I2
(13.1)
式中Z11、Z12、Z21、Z22称为双口网络的Z参数,由于这些 参数表明了电流对电压的关系,具有阻抗特性,因此又称 为阻抗参数。这些参数可以实际测量获得,也可按照下面 式子计算得到
2006-1-1
!
2
端口2开路时,端口1的驱动阻抗:
Z11
V1 I1
端口2开路时,端口1对端口2的转移阻抗:Z
I2 0
21
V2 I1
I2 0
端口1开路时,端口2对端口1的转移阻抗:Z12
V1 I2
I1 0
端口1开路时,端口2的驱动阻抗: Z22 VI22 I10
2006-1-1
!
3
• 可以看出,这些参数都是由一个端口开路时测得 的,因此又称为开路阻抗参数。根据式(13.1)所示, 可进一步得到其矩阵形式
7
解 假设正弦激励的角频率为ω,作出相量模型图,同时将受控电流
源转化为受控电压源如图13.8(b)所示。若假想左右两端加上电压
分别为1和2的电压源,并以网孔为回路,应用回路法,列写回路
方程为
V1
(R
j
1
C
)I1
RI2
j C
I
V2 RI1 2RI2
再根据主控量与回路电流的关系有İ = İ1 + İ2,则整理上述方程为
所以得到
0.1 j0.2 0.1
Y
二端口网络参数和方程和等效电路相关知识讲解培训

(1) H 参数
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
矩阵形式:
UI21
H11
H
21
H12 H 22
UI12
(2) H 参数的计算与测定
H11
U 1 I1
U 2 0
H21
I2 I1
U 2 0
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
Y21
I2 U 1
U 2 0 Yb Y12
Ya Yb Y11 即:Yb Y12 Y21
Yb Yc Y22
解之得
Ya Y11 Y12 Yb Y12 Yc Y22 Y12
注意: (1) 等效只对两个端口的电压,电流关系成立。对端 口间电压则不一定成立。
(2) 适用于互易网络。
I2
Y12U1 Y22U 2
Y21 Y12
U 1
I2
其中
I1 I'2
Y11U 1 Y12U 1
Y12U 2 Y22U 2
相当于一互易二端口,
可求出其等效电路(型):
(计算见前例)
•
I1
+
•
U1
Yb
Ya
Yc
I2
+
•
U2
而I2 I2 Y21 Y12 U1相 当 于 在 端 口2并 入 一 受 控 源.
C
I1 U 2
I2 0
D
I1 I2
U 2 0
U1 AU 2 BI2
I1
CU 2
DI2
(3) 互易二端口 Y12 Y21
T 参数满足: AD BC 1
二端口网络的网络参数-文档资料

阻抗参数[Z]
u1
U1 Z e1
, i1
I1
Z e1
u2
U2 Ze2
, i2
I2
Ze2
代入整理可得 [u] [z][i]
其中,
z
z11 / ze1
z12 / ze1ze2
z21 / ze1ze2 z22 / பைடு நூலகம்e2
1、2 导纳参数[Y]
在上述双端口网络中, 以U1、U2为自变量, I1、I2 为因变量, 则可得另一组方程:
U 2
I
2
其中,[A]称为转移矩阵,方阵中各参数的物理意义 如下:
A11
U1 U2
|I2 0
A12
U1 I2
|U2 0
表示T2开路时电压的转移参数 表示T2短路时转移阻抗
转移参数[A]
A21
I1 U2
|I2 0
表示T2
A22
I1 I2
|U2 0
表示T2短路时电流的转移参数
若将网络各端口电压、电流对自身特性阻抗归一
对于如下图所示的两个网络的级联:
U1
I1
A1
U2
I
2
U2
I
2
A2
U3
I3
转移参数[A]
+ I1
I2
I3 +
+
U1
[A1]
U2
[A2]
U3
-
-
-
双端口网络的级联
转移参数[A]
则有
U1
I1
A1
A2
U3
I3
令 A A1A2
则对于n个双端口网络级联 A A1A2 An
散射参数[S]
电路原理13.1.4二端口网络及其参数方程 - 二端口网络及其参数方程2
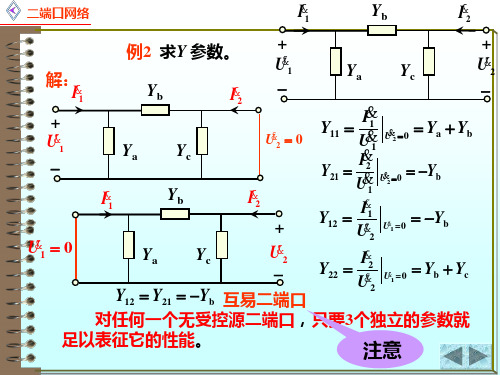
II&&12
Y
UU&&12
Y 1
II&&12
UU&&12
对称二端口 Z11 Z22 (Z12 Z21 )
Z11
Z
21
Z12 Z22
Y11 Y21
Y12 1
Y22
1 ΔY
Y22 Y21
Y12
Y11
若矩阵 Z 与 Y 非奇异
Y Z 1 Z Y 1
二端口网络
+ U1
解一: I1 1
+ U1
2 I2
+
2
U2
2
+ 2 U2
UI11
T11 T21
T12
T22
U2 I2
I1 1
+ U1
2 I2 2
T11
U1 U2
1 2 I2 0 2 1.5
T21
I1 U2
I2 =0 0.5S
T12
U1 I2
U2 =0
I1[1 + (2//2)] 4Ω 0.5I1
Yb
Y22
I&2 U&2
U&1 =0 Yb Yc
对任何一个无受控源二端口,只要3个独立的参数就
足以表征它的性能。
注意
二端口网络
Y
Y11 Y21
Y12
Y22
若Y12 Y21,称为互易二端口。 进一步,若Y11 Y22 ,则称为对称二端口。
I&1
Yb
I&2
+ U&1
Ya
Yc
+ U&2
二端口网络的传输参数、混合参数方程

放大小信号时的交流微变等效电路
U1 H11I1 H12U2 rbeI1
I2
H 21I1
H 22U 2
I1
1 rce
U2
忽 略
H
H11 H 21
H12 H 22
rbe
0
1
rce
P66 [例7-7]
解:求 H参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
P66 [例7-7]续 解:再求 T 参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
U1 2U 2
,
I1
I2 2
I1
I1
U1 3
即
I1
I2 2
2U 2 3
先列出 T 参数方程的结构,再具体化
U1 AU2 B( I2) 2U2 2U2 0
I1
CU2
D(
I
)=
2
U1 3
I1
2 3
电流 放大倍数
转移电导
转移电阻
二 端 口 网 络 参 数 方 程 小 结
二端口网络参数方程小结
互易二端口网络不含受控源,从互易网络应满足的 条件可知,四个参数中只有三个是独立的。
第7章 二端口网络的概念
7.1 二端口网络的端口条件及导纳参数、阻 抗参数方程
7.2 二端口网络的传输参数、混合参数方程 7.3 互易二端口网络的等效电路与级联
二端口网络的导纳参数、阻抗参数是基本参数, 而传输参数、混合参数是工程中的应用参数。
7.2.1 二端口网络的传输参数方程
U1
AU 2
B(
I
)
2
A
C、D的定义为:
电路分析基础课件第13章 二端口网络

•
I
•
2I
2
+
NN
•
U2
••
I 1I 1
•+
U1
••
II2 2
++
NN
••
UU2 2
Y12
I1 U 2
U1 0
Y22
I2 U 2
U1 0
转移导纳 输入导纳
Y → 短路导纳参数
例2-1 求图示二端口的Y 参数。
解
•
I I I •
•
1 11
Yb YbYb
•
I I I •
•
2
2
2
++
•
••
UU1
1U01
第13章 二端口网络
13-1 13-2 13-3 13-4 13-5 13-6
二端口网络 二端口的方程和参数 二端口的等效电路 二端口的转移函数 二端口的连接 回转器和负阻抗转换器
重点
1. 二端口的参数和方程 2. 二端口的等效电路 3. 二端口的转移函数
13-1 二端口网络
在工程实际中,研究信号及能量的传输和 信号变换时,经常碰到如下二端口电路。
•
I1
例2-8 求二端口T 参数。 +
•
U1
解
n 0
T
0
1
n
1
2
•
I2
+
2
•
U2
A U1 U2
I2 0 1.5
B
U1 I2
U2 0
4Ω
C I1 U2
I2 0 0.5 S
D I1 I2
U2 0
2
二端口网络的网络参数

测量原理:利用频谱分析仪的频率扫描功能,对二端口网络的传输函数进行测量。
测量步骤:将二端口网络接入频谱分析仪,设置合适的频率范围和分辨率,进行频率扫描, 记录传输函数的幅度和相位信息。
测量精度:频谱分析仪的频率精度和幅度分辨率决定了测量精度,高精度的频谱分析仪可以 提高测量准确性。
参数计算的意义:通过计算电压反射 系数,可以了解网络对不同频率和幅 值的入射电压的响应特性,从而优化 网络设计。
定义:电流反射系数是描述二端口 网络输入端口对入射波和反射波的 幅度和相位变化的参数
物理意义:电流反射系数反映了网 络对入射波的反射能力,其值范围 在-1到1之间
添加标题
添加标题
添加标题
影响因素:网络阻抗与源阻抗的差异越大,电压反射系数越大
意义:电压反射系数是二端口网络的重要参数,用于分析网络的性能和稳定性
定义:电流反射系数是指入射波 与反射波的幅度之比
意义:电流反射系数反映了网络 对入射波的反射能力,是二端口 网络的重要参数之一
计算公式:反射系数 = (Z_2 Z_1) / (Z_2 + Z_1),其中 Z_2为输出阻抗,Z_1为输入 阻抗
调整网络分析仪的 参数设置
记录测量结果并进 行数据处理
验证测量结果的准 确性和可靠性
测量步骤:将信号发生器连接到二端口网络的输入端,将示波器连接到输出端,调整信号发生器输出信号的幅度 和频率,观察示波器上的输出波形
注意事项:确保信号发生器和示波器的性能良好,连接正确,避免外界干扰对测量结果的影响
测量结果:通过示波器观察到的输出波形可以计算出二端口网络的参数,如电压放大倍数、输入阻抗等
添加标题
二端口网络参数和方程

二端口网络参数和方程
(一)二端口网络参数
1.信道容量:信道容量是指一个无线信道最多能够传输的数据量,在
二端口网络中,信道容量是由调制的方式,比特率或带宽等决定的。
2.频带广度:频带广度是指一个无线信道的带宽,它是每秒传输的信
息量的测量,以千赫兹(kHZ)或兆赫兹(MHz)为单位,在二端口网络中,频带广度决定着信号传输的稳定性和传输速率。
3.功率:功率是指一个无线信号发射时所消耗的能量,在二端口网络中,功率决定着信号的范围大小,通常以毫瓦(mW)为单位。
4.幅度:幅度是指一个信号的大小,它用来描述一个信号的有效值,
在二端口网络中,幅度表示了发射信号的强度,通常以分贝(dB)为单位。
5.噪声:噪声是指除信号外的其他所有的电磁波,噪声会影响信号的
传输效果,在二端口网络中,噪声是由环境因素造成的,例如电磁干扰和
不完全的编码,通常以分贝(dB)为单位。
(二)二端口网络方程
1.传输率:传输率是指一个信号在无线信道中传输的速率,它由发射
信号的功率和接收信号的功率决定,可以用下面的方程来计算:传输率= 10* log[(发射功率-接收功率)/接收功率]
2.信噪比:信噪比是指信号。
电路原理13.2.1二端口网络的等效电路 - 二端口网络及其参数方程3二端口网络的等效电路1

Y
Z
T
H
互易 Y12Y21 Z12Z21 detT1 H12 -H21 对称 Y11Y22 Z11Z22 T11T22 detH1
4. 含有受控源的二端口有四个独立参数。
二端口网络
§13.2 二端口的等效电路
目的:将复杂抽象的二端口网络用简单直观的等效电路代替。 原则:等效前后网络的端口电压、电流关系相同。即二端口
I&1 Z1
Z1 Z11 - Z12 Z2 Z12 Z21
U&1
Z2
-
Z3 Z22 - Z21
Z3 I&2
+ U&2 -
二端口网络
互易网络
Z12 Z21
I&1 Z11-Z12
+
U&1
Z12
-
Z22-Z12 I&2
+ U&2 -
Z参数对称(Z11 Z22),则等效电路也对称。
二端口网络
二端口网络
例9 求H参数。 I&1
+
U&1
R1
-
I&1
I&2
+ R2 U&2
-
UI21
H11I1 H 21I1
H12U2 H 22U2
解: U&1 R1I&1 R1I&1 0 U&2
I&2
I&1
1 R2
U&2
H
R1
0
1/R2
二端口网络
小结 1.六套参数,还有逆传输参数和逆混合参数。
2.采用6种参数描述同一二端口的原因: (1)为描述电路方便,测量方便。 (2)有些电路只存在某几种参数。
一、二端口网络的Y方程和Y参数
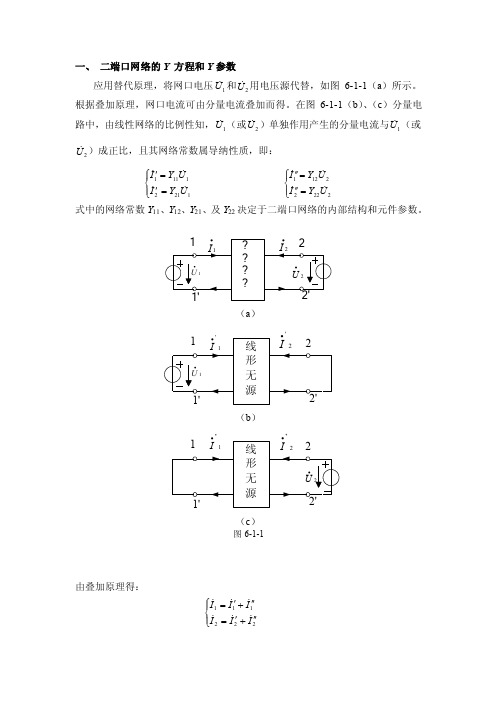
一、 二端口网络的Y 方程和Y 参数应用替代原理,将网口电压1U 和2U 用电压源代替,如图6-1-1(a )所示。
根据叠加原理,网口电流可由分量电流叠加而得。
在图6-1-1(b )、(c )分量电路中,由线性网络的比例性知,1U (或2U )单独作用产生的分量电流与1U (或2U )成正比,且其网络常数属导纳性质,即: ⎪⎩⎪⎨⎧='='12121111U Y I U Y I⎪⎩⎪⎨⎧=''=''22222121U Y I U Y I 式中的网络常数Y 11、Y 12、Y 21、及Y 22决定于二端口网络的内部结构和元件参数。
(a )(b )(c )图6-1-1由叠加原理得:⎪⎩⎪⎨⎧''+'=''+'=222111I I I I I I即22212122121111UY U Y I U Y U Y I +=+=其矩阵形式为..111112..212222Y Y U I Y Y U I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦此方程称为Y 参数方程。
〔Y 〕称为Y 参数,其元素定义为: .111.1.20|U I Y U ==.221.1.20|U I YU ==.112.2.10|U I Y U ==.222.2.10|U I YU ==式中:Y 11-为二端口短路时,一端口的入端导纳; Y 22-为一端口短路时,二端口的入端导纳;Y 12-为一端口短路时,一端口对二端口的转移导纳; Y 21-为二端口短路时,二端口对一端口的转移导纳。
【例】求图中所示 二端口网络的Y 参数,其中R 1=5Ω,R 2=5Ω,R 3=5Ω。
5Ω121'2'1I ∙∙方法一:根据定义求解 (1)Y 参数方程为:22212122121111UY U Y I U Y U Y I +=+=(2)根据Y 参数的定义:.111.1.20|U I Y U ==.221.1.20|U I YU ==根据替代定理,在端口1-1’上外施电压1U ,而把端口2-2’短路,即令02=U ,如图所示:1U ∙2U ∙1∙2∙=Y 11表示端口2-2’短路时,端口1-1’处的输入导纳或驱动导纳;Y 21表示端口2-2’短路时,端口2-2’与端口1-1’之间的转移导纳。
二端口网络的H方程和H参数

二端口网络的H方程和H参数
H方程是一组以二端口网络的电流İ1和电压表征电压
和电流İ2的方程,即以İ1和另一端口的电压为独立变量,和另一端口电流İ2作为待求量,
方程的结构为:
上式称为二端口网络的H参数方程。
系数 H11、H12、H21、H22称为二端口网络的H参数,其中H12、H21无量纲;H11具有阻抗性质,量纲为欧姆;H22具有导纳的性质,量纲为西门子。
由于H参数的量纲不完全相同,物理量具有混合之意,故也称为混合参数方程。
H参数其矩阵形式为:
H参数可以通过二端口网络的出口短路和入口开路来分析计算或测量来确定。
H11是输出端短路时,输入端的入端阻抗。
在晶体管电路中称为晶体管的输入电阻;
H12是输入端开路时,输入与输出端的电压之比。
在晶体管电路中称为晶体管的内部电压反馈系数或反向电压传输比;
H21是输出端短路时,输出端与输入端电流之比。
在晶体管电路中称为晶体管的电流放大倍数或电流增益。
H22输入端开路时,输出端的入端导纳。
在晶体管电路中称为晶体管的输出电导。
二端口网络的网络参数

5
阻抗参数[Z]
u1
U1 Z e1
, i1
I1
Z e1
u2
U2 Ze2
, i2
I2
Ze2
代入整理可得 [u] [z][i]
其中,
z
z11 / ze1
z12 / ze1ze2
z21 / ze1ze2 z22 / ze2
6
1、2 导纳参数[Y]
在上述双端口网络中, 以U1、U2为自变量, I1、I2为 因变量, 则可得另一组方程:
对于同一端口网络阻抗矩阵与导纳矩阵有以下关系
ZY I Y Z 1
其中,I 为单位矩阵
10
1、3 转移参数[A]
转移矩阵也称为[A]矩阵, 它在研究网络级联 特性时特别方便。在上述双端口网络中,若用端
口“2”的电压U2、电流-I2作为自变量, 而端口“1”
的电压U1和电流I1作为因变量, 则可得如下线性方
转移参数[A]
Zin
U1 I1
A11U 2 A21U 2
A12 (I2 ) A22 (I2 )
A11Zl A21Zl
二端口网络的网络参数 二端口网络是微波系统中最基本的型式,在描述 网络的参数中,阻抗参数、导纳参数、转移参数和 散射参数是最常用的网络参数。 其中,阻抗参数[Z]和导纳参数[Y]最易直观地和 集中参数电路相联系,转移参数[A]便于级联运算, 散射参数[S]便于与微波测量直接联系。
1
1、1 阻抗参数[Z]
U1
+ -
双口 网络
+ -
U2
Ze2
T1
T2
双端口网络
3
阻抗参数[Z]
写成矩阵形式:
U1 U2
三、二端口网络的T方程和T参数(精)

三、 二端口网络的T 方程和T 参数在上述内容中我们已经介绍了Y 参数和Z 参数的求法,Y 参数和Z 参数都可用来描述一个二端口网络的端口外特性。
但在许多工程实际问题中,往往还要求知道一个端口的电流、电压与另一个端口的电流、电压之间的直接关系。
若把Y 参数方程:22212122121111U Y U Y I U Y U Y I +=+=的第二式化为2212212211I Y U Y Y U +-= 代入Y 参数方程第一式中,整理可得:221112212211121)(I Y Y U Y Y Y Y I +-= 把以上两式写成下列形式⎪⎩⎪⎨⎧-=-=221221I D U C I I B U A U式中 ⎪⎪⎩⎪⎪⎨⎧-=-=-=-=2111212211212121221Y Y D Y YY Y C Y B Y Y A A 、B 、C 、D 称为二端口网络的一般参数、传输参数、T 参数或A 参数。
它们的具体含义可用下式说明:221==I U UA A 是输出端开路时,输入电压与输出电压的比值; 0221=-=I I UB B 是输出端短路时,输入端对输出端的转移阻抗; 0221==I U IC C 是输出端开路时,输入端对输出端的转移导纳; 0221==U I I D D 是输出端短路时,输入电流与输出电流的比值。
可见,A 是一个量纲为一的量纲;B 的量纲为Ω;C 的量纲为s ;D 也是量纲为一的量。
对于无源线性二端口网络A 、B 、C 、D 只有3个是独立的,因为Y 11=Y 22,故A =D 。
所以T 参数方程为:其中 ⎥⎦⎤⎢⎣⎡=D C B A T ,称为T 参数矩阵。
AD BC 可逆时,-=1AD BC A D =对称时满足:-=1,【例】 求例1中电路的T 参数【解】:方法一:根据定义求解(略)方法二:根据KCL 直接列方程求解(略)方法三:根据T 参数与Y 参数或Z 参数的转换公式(可在表6-1中查到)求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆---=2111212121221Y Y Y Y Y Y Y T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆=1222212121111Z Z Z Z Z Z Z T 其中 2112221122211211Y Y Y Y Y Y Y Y Y -==∆2112221122211211Z Z Z Z Z Z Z Z Z -==∆因为已知例1的 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 12.004.016.0=-=∆Y所以 ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=26.0522.04.02.012.02.012.04.0T⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2211D I U C B A I U【例 】:已知...1111122...2211222(1)(2)U Z I Z I U Z I Z I =+=+ ,求T 参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二端口网络
其矩阵形式为
Z11 U 1 = U 2 Z 21
Z11 Z= Z 21 Z12 Z 22
Z12 I 1 Z 22 I2
称为Z 参数矩阵
Z 参数的实验测定
U Z11 = 1 I 1 U Z 21 = 2 I
2 2 1 3 2
2
整理可得
= (Y Y )U -Y U I 1 1 2 1 2 2 = -Y U (Y Y )U I
2 2 1 2 3
2
二端口网络
I 1
U 1
+
I 2
线性 网络 2
-
1
+ U 2 -
如果线性网络内部不含独立源,且有 l 个独立回路, 则可列写l个回路电流方程:
Z12 = Z 21 Z11 = Z 22 ( Z12 = Z 21 )
若矩阵 Z 与 Y 非奇异
Y = Z -1
Z = Y -1
二端口网络
即
Z11 Z12 1 Y22 -Y12 Z Z = ΔY -Y Y 21 22 21 11
I 1
+ U Za Zb Zc -
I 2
2 4 2
+ U 1 -
+ U 2 -
互易二端口
Y12 = Y12
等效电路
16 Z1-1 U = 0 = 2 (5 // 10) = 2 3 16 Z 2- 2 U = 0 = 10 //[10 (5 // 2)] = 1 3
故
1 3 Y11 = = S Z1-1 16 1 3 Y22 = = S Z 2-2 16
I 2
I 1
I 2
=0 U 1
I Y11 = 1 U = 0 = Ya Yb 2 U 1 =0 U 2 I Y21 = 2 U = 0 = -Yb U1 2 I Y12 = 1 U = 0 = - Yb + U 1
2
U 2 -
I Y22 = 2 U 2
- Yb Yb
非互易二端口网络(网络内部有受控源)有四个独立参数。
二端口网络
三、Z参数和方程 + U 1 -
I 1
线性 无源
I 2
U 2 -
=Y U I 1 11 1 Y12U 2 由Y 参数方程 I 2 = Y21U 1 Y22U 2
i1
i2
i1 二端口 i2 i1
i2
i1
i2
i1
i2
i3 i4 四端网络
具有公共端的二端口
二端口网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。 u1 1 i1 3 3
i
i1
R i2
4 4
i2
2
1
i1
i2
2
u2 -
1-1’ 2-2’是二端口
3-3’ 4-4’不是二端口,是四端网络
R
I 2
U 1 U 2来自整理得- = j ( L L 2 M ) I j ( L M ) I = j8 I j4 I U 1 1 2 1 2 2 1 2 = j ( L M ) I ( j L R) I = j4 I (3 j3) I U 2 2 1 2 2 1 2
若网络内部无受控源(满足互易定理),则导纳矩阵Y对称
12 = 21 Y12 = Y21
互易二端口网络四个参数中只有三个是独立的。 Yb I I 1 2 例2 求Y 参数。 + + U U 1 2 Ya Yc -
二端口网络
解:
+ U 1 -
I 1
Ya
Yb Yc Yb Ya Yc
-
=Y U I 1 a 1 Yb (U1 - U 2 )
= Y (U -U ) - gU I 2 b 2 1 1
则
= (Y Y )U -Y U I 1 a b 1 b 2
= (- g - Y )U Y U I 2 b 1 b 2
注意
Ya Yb Y= - g - Yb
对称二端口只有2个参数是独立的。 对称二端口是指两个端口电气特性上对称。电路结构 左右对称的,端口电气特性对称;电路结构不对称的二端 口,其电气特性也可能是对称的。这样的二端口也是对称 二端口。
二端口网络
例3 I1 2 + U 1 5
10 10
I 2
2 I 1
+ U 2 -
I 1
+ U1 线性 无源
I 2
I Y12 = 1 U 2 I Y22 = 2 U
=0 1 U 2
转移导纳
=0 U 1
I 1
线性 无源
I 2
自导纳
=0 2 U 1
+ U 2 -
Y参数是在一个端口短路情况下通过计算或测试求得的, 所以又称为短路导纳参数。
Z I Z11 I 1 12 2 Z1 l I l = U 1 Z I Z I =U Z 21 I 1 22 2 2l l 2 Z I Z I = 0 解得 Z I
31 1 32 2 3l l
Z I Zl1 I 1 l 2 2 Z ll I1 = 0
rI 1
例5
+
I 2
+ U
-
1
2
-
=Z I Z (I I ) = ( Z Z )I Z I U 1 a 1 b 1 2 a b 1 b 2
= rI +Z I U 2 1 c 2 + Zb ( I1 + I 2 ) = (r + Zb ) I1 + ( Zb + Zc )I 2
= 11 U 21 U I 1 1 2 = 12 U 22 U I 2 1 2
二端口网络
分别用Y11、Y12、 Y21、 Y22表示这些系数,上式可写为:
=Y U I 1 11 1 Y12U 2 =Y U I 2 21 1 Y22U 2
= j L I U 1 1 1 j M ( I1 I 2 ) j L2 ( I1 I 2 ) j MI1 =RI j L ( I I ) j MI U 2 2 2 1 2 1
二端口网络
I 1
L1 M L2
开路输入阻抗
=0 I 2
开路转移阻抗
=0 1 I 2
二端口网络
U Z12 = 1 I 2 U Z 22 = 2 I
开路转移阻抗
=0 I 1
开路输入阻抗
=0 2 I 1
Z参数是在一个端口开路情况下通过计算或测试求得
的,所以Z参数又称开路阻抗参数。 互易二端口 对称二端口
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。 端口的概念: 端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
+ u1 –
i1 i1
二端口网络
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
=0 U 2
= -Yb - g
I 1
=0 U 1
Ya
I 2
+ U 2 -
gU 1
I Y12 = 1 U2 I Y22 = 2 U2
=0 U 1
= -Yb
= Yb
=0 U 1
二端口网络
解二 + U 1 -
I 1
Ya
Yb
I 2
gU 1
+
U 2
,U . 可解出U 1 2
即:
Y22 - Y12 U1 = I1 Δ Δ U = - Y21 I Y11 2 1 Δ Δ
=Z I I 2 11 1 Z 12 I 2 =Z I I 2 21 1 Z 22 I 2
其中 =Y11Y22 –Y12Y21
线性RLCM 受控源
四端网络
二端口网络
例1 R C 滤波器 n:1
C
三极管
变压器
传输线
二端口网络
3. 二端口(two-port) 如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。 i1 线性RLCM 受控源 i1 i2 i2
+ u1 –
+ u2 –
二端口网络
4. 二端口与四端网络的区别: 二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
和I 可视为 端口电流 I 1 2 和U 共同作用产生。 U 1 2
二端口网络
Y 参数的实验测定 I Y11 = 1 自导纳 U 1 U2 =0 I Y21 = 2 转移导纳 U
=Y U Y U I 1 11 1 12 2 I 2 = Y21U1 Y22U 2
二端口网络
第13章 二端口网络
13-1 二端口网络及其参数方程
13-2 二端口网络的等效电路
13-3 二端口网络的网络函数 13-4 二端口网络的连接 13-5 二端口网络的实例
二端口网络
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念 1. 一端口网络 I + U Z (Y)
