固体物理(黄昆)第一章习题

合集下载

固体物理习题与答案

《固体物理学》习题解答黄昆原著韩汝琦改编（志远解答，仅供参考）第一章晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= （4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

固体物理考题第一章晶体的结构

第一章晶体的结构简单回答下面的问题：1 a原胞与单胞有什么不同？何谓布拉菲格子？何谓倒格子？以一结点为顶点，以三个不同方向的周期为边长的平行六面体可作为晶格的一个重复单元．体积最小的重复单元，称为原胞或固体物理学原胞.它能反映晶格的周期性．原胞的选取不是惟一的，但它们的体积都相等．为了同时反映晶体对称的特征，结晶学上所取的重复单元，体积不一定最小，结点不仅在顶角上，还可以是体心或面心．这种重复单元称作晶胞、惯用晶胞或布喇菲原胞．晶体内部结构可以看成是由一些相同的点子在空间作规则的周期性无限分布，这些点子的总体称为布喇菲点阵。

布拉菲格子：由基元代表点（格点）在空间中的周期性排列所形成的晶格。

倒格子*（Reciprocal Lattice，Reciprocal有相互转换的含意）已知有正格子基矢，定义倒格矢基矢为:；； .其中为正格子原胞体积。

由平移操作所产生的格点叫倒格点：为倒格矢;倒格点的总体叫倒格子，叫一组倒格基矢。

由与所决定的点阵为互为倒格子b晶体的宏观对称性可以概括为多少点群？晶体中有几种基本对称素？多少个晶系？这些晶系分别包括哪些布拉菲格子？晶体学中共有32种点群八种基本对称素C1 (1)、C2 (2)、C3 (3)、C4 (4)、C6 (6)、Ci (i)、CS (m)和 S4七大晶系十四种布拉菲格子c什么是晶体、准晶体和非晶体？晶体:组成固体的原子（或离子）在微观上的排列具有长程周期性非晶体：组成固体的粒子只有短程序（在近邻或次近邻原子间的键合：如配位数、键长和键角等具有一定的规律性），无长程周期性准晶:有长程的取向序，沿取向序的对称轴方向有准周期性，但无长程周期性2试推导面心和体心立方点阵的x射线衍射的系统消光规律3多晶体与单晶体的x射线衍射图有什么区别？多晶（衍射环对应一个晶面）；单晶（衍射点对应一个晶面）4a）何谓晶体、准晶体及非晶体？它们的x光或电子衍射有何区别？黄昆第45页晶体：衍射图样是一组组清晰的斑点非晶体：由于原子排列是长程无序的，衍射图样呈现为弥散的环，没有表征晶态的斑点准晶体：衍射图样具有五重对称的斑点分布，斑点的明锐程度不亚于晶体的情况(b)何谓布拉菲格子、晶体学点群、晶系和晶体学空间群？C1 (1)、C2 (2)、C3 (3)、C4 (4)、C6 (6)及S1，S2，S3，S4，S5这十种对称素组成32个不同的点群结晶学中把a, b, c满足同一类要求的一种或数种布喇菲格子称为一个晶系。

固体物理黄昆答案第一章

将上式代入 ε = Az T ε Az 得
⎛ ⎜ 0 ⎞ ⎜ ⎜ ε 23 ⎟ = ⎟ ⎜− ⎜ ε 33 ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ 1 3 ε11 + ε 22 4 4 3 3 ε11 + ε 22 4 4 3 − ε 32 2 − 3 3 ε11 + ε 22 4 4 3 1 ε11 + ε 22 4 4 1 − ε 32 2 − 3 ⎞ ε 23 ⎟ 2 ⎟ ⎟ 1 − ε 23 ⎟ 2 ⎟ ⎟ ε 33 ⎟ ⎟ ⎠
a 2
r
r
r r
a r 2
r
r r
a r 2
r
r
课后答案网
同理：可见由为基矢构成的格子为面心立方格子。
面心立方格子原胞基矢: 面心立方格子原胞体积：倒格子基矢：同理可见由
* vc =
ww
晶面系.
r r r r 1.5证明：倒格子矢量 G = h1b1 + h2b2 + h3b3 垂直于密勒指数为 (h1 , h2 , h3 ) 的
倒格子基矢 b1 =
v
kh da w. co m
案网
1 h k l ( )2 + ( )2 + ( )2 a b c
并说明面指数简单的晶面，其面密度比较大，容易解理解：简单正交系
课后答案网
sc
bcc
fcc 第 n 近距离 1
n
1 2 3 4 5 6
第 n 近邻第 n 近距离数 6 1 12 8 6
操作构成群 C4 ， C4 = ( C1 , C2 , C3 , C4 ) 群中任意两个元素的乘积仍然是群中的元素（具体过程乘积在此省略，请验证）。
答

(参考资料)固体物理习题带答案

D E ( ) ，其中，表示沿 x ， y ， z 轴的分量，我们选取 x ， y ， z
沿立方晶体的三个立方轴的方向。
显然，一般地讲，如果把电场 E 和晶体同时转动， D 也将做相同转动，我们将以 D' 表示转
动后的矢量。
设 E 沿 y 轴，这时，上面一般表达式将归结为：Dx xyE, Dy yyE, Dz zy E 。现在
偏转一个角度 tg 。（2）当晶体发生体膨胀时，反射线将偏转角度
tg ，为体胀系数
3
解：（1）、布拉格衍射公式为 2d sin ，既然波长改变，则两边同时求导，有
2d cos ，将两式组合，则可得 tg 。
（2）、当晶体发生膨胀时，则为 d 改变，将布拉格衍射公式 2d sin 左右两边同时对 d
考虑把晶体和电场同时绕 y 轴转动 / 2 ，使 z 轴转到 x 轴， x 轴转到 z 轴， D 将做相同
转动，因此
D'x Dz zy E
D'y Dy yyE
D'z Dx xy E 但是，转动是以 E 方向为轴的，所以，实际上电场并未改变，同时，上述转动时立方晶体
的一个对称操作，所以转动前后晶体应没有任何差别，所以电位移矢量实际上应当不变，即
第一章：晶体结构 1．证明：立方晶体中，晶向[hkl]垂直于晶面(hkl)。
证明：晶向 [hkl] 为 h1 k2 l3 ，其倒格子为
b1
2
a1
a2
a3
(a2 a3 )
b2
2
a1
a3 a1 (a2 a3)
b3
2
a1
a1
a2
(a2 a3)
。可以知道其倒格子矢量

黄昆版固体物理学课后答案解析答案 (2)

《固体物理学》习题解答黄昆原着韩汝琦改编（陈志远解答，仅供参考）第一章晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π=（2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。

黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆原着韩汝琦改编（陈志远解答，仅供参考）第一章晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 31.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…1.3、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩由倒格子基矢的定义：1232()b a a π=⨯Ω31230,,22(),0,224,,022a aa a a a a a a a Ω=⋅⨯==，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++ 同理可得：232()2()b i j k ab i j k aππ=-+=+-即面心立方的倒格子基矢与体心立方的正格基矢相同。

固体物理习题答案

第一章思考题
5、试画出体心立方和面心立方(100)、(110)、(111)面上格点的分布图。 (100) (110) (111)
体心立方
面心立方
第一章思考题
6、怎样判断一个体系对称性的高低？讨论对称性有何物理意义。答：一个物理体系对称性用其具有的对称操作集合来描述。一个体系具有的对称操作越多，其对称性就越高。在数学上，基本操作的集合构成 “群”，每个基本操作称为群的一个元素。由于晶格周期性限制，描述晶体宏观对称性的“点群” 只有32种。描述晶体微观对称性的“空间群”只有230种。一个物理体系，如知道其几何对称性，就可在一定程度上确定它的某些物理性质。例如，若原子结构具有中心反演对称性，则原子无固定偶极矩；若一个体系具有轴对称性，偶极矩必在对称轴上；若有对称面，偶极矩必在对称面上。由此可见，不必讨论体系结构细节，仅从体系的对称性，就可对其物理性质作出某些判断。对称理论已成为定性和半定量研究物理问题的重要方法。
第一章习题
1.1 何谓布拉菲格子？画出NaCl晶格所构成的布拉菲格子，说明基元代表点构成的格子是面心立方晶体，每个原胞中含几个格点？解：由基元代表点-格点-形成的晶格称为布拉菲格子或布拉菲点阵。它的特征是每个格点周围的情况(包括周围的格点数目和格点配置的几何方位等)完全相同。基元由相邻的一个Na+和一个Cl−构成，基元代表点 (如： Na+ 位置) 构成面心立方晶格。每个原胞中含一个格点。
a3
a 2
a 2
( i j)
a
2
A
k j i
a3 h3
aB
a h
( i j)
k
2
2
( i j) a i

固体物理-第一章习题解答参考ppt课件

d 2 r
a
G h h 1 h 2 h 3 2 h 1 h 2 h 3 2 h 1 h 2 h 3 2
上式中等效晶面指数{1,0,0}晶面族、（1,1,1)、(-1,-1,-1)晶面对应的面间距最大，面间距，
d a 3
格点体密度，
1 4
a3
最大面密度，
d.a 43
a 3
4 3a2
1/2属于该等边三角形
2a
(111)
a
2a
(111)
1/6属于该等边三角形
等边三角形面积，
S12a2asin600 3a2
2
2格点面密度，2 4S 3a.21.5 求立方晶系晶面族 h的k l面间距；
cb
a
晶胞基矢 a a i ,b a j,c a k
倒格子基矢 a r2 ir,b r2 r j,c r2 k r
界面方程：
kx
ky
2 a
kx
ky
2 a
2 kx ky a
kx
ky
2 a
与第1布里渊区界面围成的区域为第2布里渊区
.
第3布里渊区：
离原点再次远有４个倒格点 (h12,h20)(,h12,h20), (h10,h22)(,h10,h22)
界面方程：
kx
2
a
,kx
2
a
,
ky
2
a
,ky
2
a
与第1、2布里渊区界面围成区域为第3布里渊区
b
1 2
(b3
b1 )
c
1 2
(b1
b2)
与晶面族(hlk垂)直的倒格矢：
G hkl
h a

黄昆版固体物理学课后答案解析答案 (3)

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r 同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。

《固体物理学(黄昆)》课后习题解答

v0
证
� 倒格子基矢 b1
=
2π
�� a2�× a3� a1 ⋅ a2 × a3
� b2
=
2π
�� a3�× a1� a1 ⋅ a2 × a3
� b3
=
2π
�� a1�× a2� a1 ⋅ a2 × a3
�� 倒格子体积 v0* = b1 ⋅ (b2 × b3 )
v0*
=
(2π )3 v03
《固体物理》习题解答
第一章习题
1.1 如果将等体积球分别排列下列结构，设x表示刚球所占体积与总体积之比，证明
结构简单立方(书P2, 图1-2) 体心立方(书P3, 图1-3)
面心立方(书P3, 图1-7)
六方密排(书P4, 图1-6)
金刚石(书P5, 图1-8)
x
π / 6 ≈ 0.52 3π / 8 ≈ 0.68
2π / 6 ≈ 0.74
2π / 6 ≈ 0.74 3π /16 ≈ 0.34
解设n为一个晶胞中的刚性原子数，r表示刚性原子球半径，V表示晶胞体积，则致
4π nr3
密度为: ρ =
（设立方晶格的边长为a） r取原子球相切是的半径于是
3V
结构
r
n
V
简单立方
a/2
1
a3
体心立方
a/2
1
a3
ρ π / 6 ≈ 0.52
� b3
=
2π
�� a1�× a2� a1 ⋅ a2 × a3
� a � � � � a� � � � a� � �
体心立方格子原胞基矢 a1 =
(−i 2
+
j + k ),

《固体物理学(黄昆)》课后习题答案(1)

证
倒格子基矢 b1 = 2π � 2�
�
� � a × a3 � a1 ⋅ a2 × a3
� � � a3 × a1 b2 = 2π � � � a1 ⋅ a2 × a3 � � � a1 × a2 b3 = 2π � � � a1 ⋅ a2 × a3
倒格子体积 v0 = b1 ⋅ (b2 × b3 )
感谢大家对木虫和物理版的支持！ 2
《固体物理》习题解答
� � �� a � a a3 a3 1 2 CA = − , CB = − h1 h3 h2 h3 �� Gh1h2h3 ⋅ CA = 0 容易证明 � �� Gh1h2h3 ⋅ CB = 0 � � � � G = h1b1 + h2b2 + h3b3 与晶面系 (h1h2 h3 ) 正交。
r a/2 a/2 n 1 1 2 4 2 V a3 a3 a3 a3
ρ
π / 6 ≈ 0.52
3π / 8 ≈ 0.68 2π / 6 ≈ 0.74 2π / 6 ≈ 0.74 3π /16 ≈ 0.34
1/ 2
3a / 4
2a / 4
a/2
2a 3 ≈ 1.633
1/ 2
c ⎛3⎞ 1.2 证明理想的六角密堆积结构（hcp）的轴比 = ⎜ ⎟ 2 ⎝8⎠
0 ⎞ ⎟ 0 ⎟ 选择相应的坐标变换 ε 33 ⎟ ⎠
⎛ ε1 0 ⎜ 可得到 ε = ⎜ 0 ε 2 ⎜0 0 ⎝
同理 b2 = 2π � 3�
可见由 b1 , b2 , b3 为基矢构成的格子为面心立方格子面心立方格子原胞基矢
� � �
� � � a1 = a( j + k ) / 2 � � � a2 = a(k + i ) / 2 � � � a3 = a(i + j ) / 2 � � � a × a3 � a1 ⋅ a2 × a3 � 2π � � � b1 = (−i + j + k ) a

黄昆固体物理解答

0 ⎜ ⎜ 0 ε 22 ⎜ 0 ε 32 ⎝
由上式可得 ε 23 = 0, ε 32 = 0, ε11 = 0
0 ⎞ ⎛ ε11 0 ⎜ 可得六角晶系的介电常数为 ε = ⎜ 0 ε 22 0 ⎟ ⎟ ⎜ 0 ⎟ 0 ε 33 ⎠ ⎝ ⎛ ε1 0 0 ⎞ ⎟ 选择相应的坐标变换即可得到 ε = ⎜ ⎜ 0 ε 2 0 ⎟ ，原命题得证。 ⎜0 0 ε ⎟ 2⎠ ⎝
(2) 体心立方（书P3，图1-3）
r 取原子球相切时的半径（体对角线的 1/4 ）， r= 3a / 4 ,n=2, V ＝ a 3 所以
ρ=
n 4π r 3 3 = 3π / 8 V
(3) 面心立方（书P4，图1-7）
r 取原子球相切时的半径（面对角线的 1/4 ） r= 2a / 4 ,n=4, V ＝ a 3 ，所以
r
r
0 ⎞ ⎛ ε11 0 ⎜ ε = ⎜ 0 ε 22 ε 23 ⎟ ⎟ ⎜ 0 ε ε 33 ⎟ 32 ⎝ ⎠
将上式代入 ε = Az T ε Az 得
⎛ ⎜ 0 ⎞ ⎜ ⎜ ε 23 ⎟ = ⎟ ⎜− ⎜ ε 33 ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ 1 3 ε11 + ε 22 4 4 3 3 ε11 + ε 22 4 4 3 − ε 32 2 − 3 3 ε11 + ε 22 4 4 3 1 ε11 + ε 22 4 4 1 − ε 32 2 − 3 ⎞ ε 23 ⎟ 2 ⎟ ⎟ 1 − ε 23 ⎟ 2 ⎟ ⎟ ε 33 ⎟ ⎟ ⎠
A
D
C
设想一个由正负两种离子相间排列的无限长的离子键取任一负离子作参考离子这样马德隆常数中的正负号可以这样取即遇正离子取正号遇负离子取负号用表示相邻离子间的距离于是有前边的因子2是因为存在着两个相等距离的离子一个在参考离子左面一个在其右面故对一边求和后要乘2马德隆常数为22讨论使离子电荷加倍所引起的对nacl晶格常数及结合能的影响排斥势看作不变ncdr于是当e变为2e23若一晶体两个离子之间的相互作用能可以表示为平衡间距r0解答初稿作者固体物理习题解答1003的计算晶体内能dudr为常数n为原胞数目固体物理习题解答1003109510191024经过sp杂化后形成的共价的方向求共价键之间的夹sp轨道杂键其方向沿着立方体的四条对角线化过程形成的共体结构容价键如右图所示

黄昆固体物理习题

β N −m Nα m r0 (α − )= (1 − )r0− m nβ n 2 2 mα m Nα m nβ − n − = (1 − )( ) m 2 n mα
则平均单个原子的结合能为
m 1 m nβ − n − α (1 − )( ) m 2 n mα
（3）体变模量为
K = (V
以及其中 Z 为一个与结构有关的常数。有
= aj ， a3 = ak ，可以马上求出：
b1 = 2π 2π 2π i ， b2 = j ， b3 = k a a a
因为倒格子基矢互相正交，因此其大小为
h k l 2π Ghkl = (hb1 ) 2 + (kb2 ) 2 + (lb3 ) 2 = 2π ( ) 2 + ( ) 2 + ( ) 2 = a a a a
U = N [−
但是现在
A′ B + ] r rn
A′ =
同样在平衡位置满足
α q ′2 ，而 q′ = 2q 。 4πε 0
∂U =0 ∂r
则求得晶格常数为
B 1 n −1 = r0′ A′ n
所以
B n1 r0′ = ( n) −1 A′
与原来的晶体相比，为
B n −1 1 r0′ ( A′ n) A n1 1− n −1 ( ) 4 = = = 1 r0 A′ B ( n) n −1 A
第一章、晶体结构 1.1 如果将等体积球分别排列成下列结构，设 x 表示钢球所占体积与总体积之比，证明 x 结构简单立方体心立方面心立方六方密排金刚石
π / 6 ≈ 0.52
3π / 8 ≈ 0.68
2π / 6 ≈ 0.74 2π / 6 ≈ 0.74

固体物理习题及答案

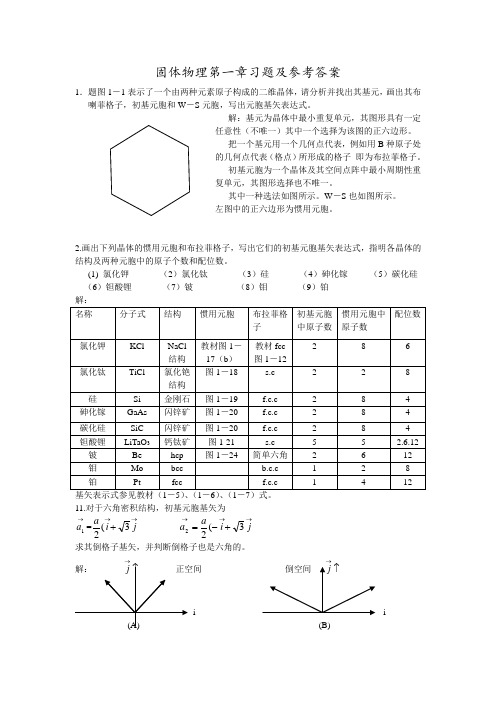
固体物理第一章习题及参考答案1．题图1－1表示了一个由两种元素原子构成的二维晶体，请分析并找出其基元，画出其布喇菲格子，初基元胞和W －S 元胞，写出元胞基矢表达式。

解：基元为晶体中最小重复单元，其图形具有一定任意性（不唯一）其中一个选择为该图的正六边形。

把一个基元用一个几何点代表，例如用B 种原子处的几何点代表（格点）所形成的格子即为布拉菲格子。

初基元胞为一个晶体及其空间点阵中最小周期性重复单元，其图形选择也不唯一。

其中一种选法如图所示。

W －S 也如图所示。

左图中的正六边形为惯用元胞。

2.画出下列晶体的惯用元胞和布拉菲格子，写出它们的初基元胞基矢表达式，指明各晶体的结构及两种元胞中的原子个数和配位数。

(1) 氯化钾（2）氯化钛（3）硅（4）砷化镓（5）碳化硅（6）钽酸锂（7）铍（8）钼（9）铂解：基矢表示式参见教材（1－5）、（1－6）、（1－7）式。

11.对于六角密积结构，初基元胞基矢为→1a =→→+j i a 3(2 →→→+-=j i a a 3(22求其倒格子基矢，并判断倒格子也是六角的。

倒空间 ↑→ji i (B)由倒格基失的定义，可计算得Ω⨯=→→→3212a a b π=a π2)31(→→+j i →→→→→+-=Ω⨯=j i a a a b 31(22132ππ→→→→=Ω⨯=k ca ab ππ22213正空间二维元胞（初基）如图（A ）所示，倒空间初基元胞如图（B ）所示（1）由→→21b b 、组成的倒初基元胞构成倒空间点阵，具有C 6操作对称性，而C 6对称性是六角晶系的特征。

（2）由→→21a a 、构成的二维正初基元胞，与由→→21b b 、构成的倒初基元胞为相似平行四边形，故正空间为六角结构，倒空间也必为六角结构。

12．用倒格矢的性质证明，立方晶格的（hcl ）晶向与晶面垂直。

证：由倒格矢的性质，倒格矢→→→→++=321b l b k b h G hkl 垂直于晶面（h 、k 、l ）。

固体物理学(黄昆_高教版)_答案

《固体物理学》习题解答黄昆原著韩汝琦改编第一章晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnV x =（1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r8r34ar 34x 3333=π=π=π=（2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒=n=2, Vc=a 3∴68.083)r 334(r 342ar342x 3333≈π=π⨯=π⨯=（3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r344ar344x 3333≈π=π⨯=π⨯=（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯n=32126112+⨯+⨯=6个74.062r224r 346x 33≈π=π⨯=（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r338r 348ar348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(a c2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

黄昆固体物理习题解答-完整版

⎜⎝ε31 ε32 ε33 ⎟⎠ ⎜⎝ − ε31 ε32 ε33 ⎟⎠
⎜⎝ 0 ε32 ε33 ⎟⎠
⎜⎛ ε11 + 3ε 22
− 3ε11 + 3ε 22 − 3ε 23 ⎟⎞
得
⎜⎛ ε11 ⎜0 ⎜⎝ 0
0 ε 22 ε 32
0 ⎟⎞
⎜ ⎜
ε 23 ⎟ = ⎜ −
ε33 ⎟⎠
⎜ ⎜
⎜⎝
44
3ε11 + 3ε 22
《固体物理》习题解答
第一章习题
1.1 如果将等体积球分别排列下列结构，设x表示刚球所占体积与总体积之比，证明
结构简单立方(书P2, 图1-2) 体心立方(书P3, 图1-3)
面心立方(书P3, 图1-7)
六方密排(书P4, 图1-6)
金刚石(书P5, 图1-8)
x
π / 6 ≈ 0.52 3π / 8 ≈ 0.68
最后，感谢各位虫友一直以来对小木虫物理版的支持！同时也希望，今后能后更多的虫友来加入物理版，把这里建成大家交流的乐园！
zt978031 2010 年 4 月 7 日
目录
第一章习题··························· 1 第二章习题··························· 6 第三章习题···························10 第五章习题···························31 第六章习题···························36 第七章习题···························42
倒格子基矢 b1
=
2π
a2 × a3 a1 ⋅ a2 × a3

《固体物理》第一章作业题

（2）AC
=
OC
−
OA
=
→c +
1 2
→
a+
→
b
−
→
(a+
→
b)
=
−
1 2
→
a+
→
b−
2
→
c
可见
→
AC
与晶列
→
a+
→
b−
2
→
c
平行，因此AC晶列的
晶列指数为 112。
由《固体物理教程》（1.3）式可得面心立方结构晶胞基矢与原胞基矢的关系
→
→→→
a = − a1+ a2 + a3
→ →→→
b = a1− a2 + a3
第二章习题
2.3
若一晶体的相互作用能可以表示为 u(r)
=
−
rm
+
rn
,
求 1）平衡间距 r0 2）结合能 W（单个原子的）
3）体弹性模量
4）若取
m = 2, n = 10, r0 = 0.3 nm, W = 4 eV ，计算 , 值.
解
1）晶体内能U (r)
=
N 2
(−
rm
+
rn
置的原子球与处在8个角顶位置的原子球相切，因此晶胞空间对角线的长度为 3a = 4r,V = a3,一个晶胞内含有2个原子，所以
x = n 4 r3 = 2 4 ( 3 a)3 = 3 0.68
V3
a3 3 4
8
（3）面心立方对面心立方晶体，任一个原子有12个最近邻，如图（c）所示。中

东南大学固体物理习题解答-完整版

黄昆《固体物理》习题解答目录第一章习题 (1)第二章习题 (6)第三章习题 (10)第五章习题 (31)第六章习题 (36)第七章习题 (42)ρ ⨯ • ⨯ ⨯ • ⨯ ⨯ • ⨯ • ⨯ b 2 b 3 第一章习题1.1 如果将等体积球分别排列下列结构，设x 表示刚球所占体积与总体积之比，证明结构x简单立方(书P2, 图1-2) π / 6 ≈ 0.52体心立方(书P3, 图1-3) 3π / 8 ≈ 0.68 面心立方(书P3, 图1-7) 2π / 6 ≈ 0.74 六方密排(书P4, 图1-6) 2π / 6 ≈ 0.74 金刚石(书P5, 图1-8)3π /16 ≈ 0.34解设n 为一个晶胞中的刚性原子数，r 表示刚性原子球半径，V 表示晶胞体积，则致4π nr 3密度为: = （设立方晶格的边长为a ） r 取原子球相切是的半径于是3V结构 r n V ρ 简单立方 a/2 1 a 3 π / 6 ≈ 0.52体心立方 a/2 1 a 3 3π / 8 ≈ 0.68 面心立方 3a / 4 2 a 3 2π / 6 ≈ 0.74 六方密排 2a / 44 a 32π / 6 ≈ 0.74 金刚石a/222a 33π /16 ≈ 0.34c 3 1/ 21.2 证明理想的六角密堆积结构（hcp ）的轴比 = ≈ 1.6332 8c c 3 1/ 2解由1.1题，六角密排中h = a = 2 r - ，故 = ≈ 1.633 2 2 81.3 证明：体心立方晶格的倒格子是面心立方；面心立方晶格的倒格子是体心立方¸ 解由倒格子定义b 1 = 2π ¸ ¸ a 2 a 3 ¸ ¸ ¸a 1 a 2 a 3 ¸ = 2π ¸ ¸ a 3 a 1 ¸ ¸ ¸ a 1 a 2 a 3 ¸ = 2π ¸ ¸ a 1 a 2¸ ¸ ¸ a 1a 2 a 3 ¸ a ¸ ¸ ¸ ¸ a ¸ ¸ ¸ ¸ a ¸ ¸ ¸体心立方格子原胞基矢a 1 = 2 (-i + j + k ), a 2 = 2 (i - j + k ), a 3 = 2(i - j + k )¸ ¸ ⨯ ¸ π ¸ ¸ ¸ ¸ ¸ ¸ 倒格子基矢b = 2π a 2 a 3 =2 ⋅ a (i - j + k ) ⨯ a (i + j - k )1¸ ¸ ¸ a 1a 2 a 3 v 0 2 2 2 3 2 3•⨯⨯⨯•⨯•⨯⨯•⨯⨯⋅⨯⨯⨯b3=2π⋅a2¸ ¸ ¸-+⨯¸ ¸ ¸+- =2π ¸+¸v4(i j k ) (i j k ) ( j k )a¸ ¸ ⨯¸π¸ ¸¸ π¸ ¸同理b = 2π a3 a1=2(i +k ) b =2(i +j )2. . . 3a1⋅a2⨯a3a a¸ ¸ ¸可见由b1, b2 , b3 为基矢构成的格子为面心立方格子面心立方格子原胞基矢¸ ¸ ¸a1=a( j +k ) / 2¸ ¸ ¸a2=a(k +i ) / 2¸ ¸ ¸a3=a(i +j ) / 2¸ ¸ ⨯¸¸ π¸ ¸ ¸倒格子基矢b= 2π a2 a3 b =2(-i +j +k )1¸ 2π¸ ¸ ¸ 1a1a2a3¸ ¸ ¸a¸ 2π¸ ¸ ¸同理b2 = (i -j +k )ab3= (i -j +k )a¸ ¸ ¸可见由b1, b2 , b3 为基矢构成的格子为体心立方格子(2π)31.4证明倒格子原胞的体积为v，其中v0 为正格子原胞体积¸证倒格子基矢b1¸b2= 2π= 2π¸ ¸a2a3¸ ¸ ¸a1a2a3¸ ¸a3a1¸ ¸ ¸a1a2a3¸= 2π¸ ¸a1a2¸ ¸ ¸a1a2a3¸ ¸ ¸倒格子体积v*=b ⋅(b ⨯b )v*=(2π)330 1 2 3¸ ¸ ¸ ¸ ¸ ¸(a2a3) (a3a1) (a1a2) v*=(2π)3v¸ ¸ ¸ ¸1.5证明：倒格子矢量G =h1b1 +h2b2 +h3b3 垂直于密勒指数为(h1h2h3 ) 的晶面系。

黄昆版固体物理学课后答案解析答案 (1)

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

固体物理(黄昆)

PART ONE 填空问题Q01_01_001 原胞中有p 个原子。

那么在晶体中有3支声学波和33p −支光学波？Q01_01_002 按结构划分，晶体可分为7大晶系, 共14布喇菲格子?Q01_01_004 面心立方原胞的体积为314a Ω=；其第一布里渊区的体积为334(2)*a πΩ= Q01_01_005 体心立方原胞的体积为32a Ω=；第一布里渊区的体积为332(2)*a πΩ= Q01_01_006 对于立方晶系，有简单立方、体心立方和面心立方三种布喇菲格子。

Q01_01_007 金刚石晶体是复式格子，由两个面心立方结构的子晶格沿空间对角线位移 1／4 的长度套构而成，晶胞中有8个碳原子。

Q01_01_008 原胞是最小的晶格重复单元。

对于布喇菲格子，原胞只包含1个原子；Q01_01_009 晶面有规则、对称配置的固体，具有长程有序特点的固体称为晶体；在凝结过程中不经过结晶（即有序化）的阶段，原子的排列为长程无序的固体称为非晶体。

由晶粒组成的固体，称为多晶。

Q01_01_010 由完全相同的一种原子构成的格子，格子中只有一个原子，称为布喇菲格子。

满足ij j i b a πδ2=⋅G G ⎩⎨⎧≠===)(0)(2j i j i π 关系的1b G ,2b G ,3b G 为基矢，由322211b h b h b h G h K K K K ++=构成的格子，称作倒格子。

由若干个布喇菲格子相套而成的格子，叫做复式格子。

其原胞中有两个以上的原子。

Q01_03_001 由N 个原胞构成的晶体，原胞中有l 个原子，晶体共有3lN 个独立振动的正则频率。

Q01_03_002 声子的角频率为ω，声子的能量和动量表示为ω=和q K =。

Q01_03_003 光学波声子又可以分为纵光学波声子和横光学波声子，它们分别被称为极化声子和电磁声子Q01_03_004 一维复式原子链振动中，在布里渊区中心和边界，声学波的频率为 ⎪⎩⎪⎨⎧→±==0,02,)2(211q a q M πβω；光学波的频率⎪⎪⎩⎪⎪⎨⎧±=→=a q m q 2)2(0)2(21212πβµβωQ01_04_001 金属的线度为L ，一维运动的自由电子波函数ikx e Lx 1)(=ψ；能量m k E 222==；波矢的取值Ln k π2= Q01_04_002 电子在三维周期性晶格中波函数方程的解具有()()ik r kr e u r k ψ⋅=K K K K K K 形式？式中()k u r K K 在晶格平移下保持不变。

固体物理(黄昆)第一章习题

固体物理习题与答案

固体物理考题第一章晶体的结构

固体物理 黄昆答案 第一章

(参考资料)固体物理习题带答案

黄昆版固体物理学课后答案解析答案 (2)

黄昆版固体物理学课后答案解析答案

固体物理习题答案

固体物理-第一章习题解答参考ppt课件

黄昆版固体物理学课后答案解析答案 (3)

《固体物理学(黄昆)》课后习题解答

《固体物理学(黄昆)》课后习题答案(1)

黄昆固体物理解答

黄昆固体物理习题

固体物理习题及答案

固体物理学(黄昆_高教版)_答案

黄昆固体物理习题解答-完整版

《固体物理》第一章作业题

东南大学固体物理习题解答-完整版

黄昆版固体物理学课后答案解析答案 (1)

固体物理(黄昆)

固体物理黄昆答案第一章