Arena仿真概述课案
仿真系统与软件-Arena基础

9/36
(2)Advanced Process
10/36
(3)Advanced Transfer
11/36
(4)Reports panel
12/36
(5)Navigate panel
13/36
4. Arena流程窗口:Flowchart window
Describe dynamic processes
– – –
Resource animation Two plots Some (passive) labels, artwork
17/36
18/36
(1) Create Flowchart Module
“Birth” node for entities Gave this instance of the Create-type module the Name Part Arrives to System
–
– –
Can edit via dialog – double-click in leftmost column Double-click where indicated to add new row Right-click on row, column to do different things
–
Queues, Resources, Entity types, Variables … others
Arena keeps internal lists of different kinds of names
– –
Presents existing lists to you where appropriate Helps you remember names, protects you from typos
Arena概述与仿真建模基本操作

第5章Arena建模基本操作5.1 Arena建模概述5.1.1Arena功能与特点Arena是一种支持用于离散事件仿真可视化交互式仿真软件(VIS)。
应用Arena,用户可以交互地建立模型,创建系统的动画,运行仿真器,收集仿真输出的数据,创建查看需要的统计报告。
Arena还包括输入分析器,它是一个输入数据分析的工具。
用流程图将系统表示成实体相关活动的逻辑网络。
Arena通过完整层次化结构(hierarchical)保持了建模的灵活性。
Arena支持分层建模,即一些模型元素可以代表一个下层模型;下层模型可以包含更深一层的模型。
分层建模可以将复杂的模型分解成更小更容易理解的模型单元。
5.1 Arena建模概述5.1.1Arena功能与特点提供了13个(Arena10.0)建模模板(Template),每个模板中提供了许多用于图形仿真建模与分析的模块(Module),将这些模块组合起来就能构建出各种不同的仿真模型(Model)。
为了便于组织和显示,各模块按类型组合在一个面板(Panel)中构成模板。
通过面板间的切换,可以很方便地找到所有的仿真建模构件集。
不同模板的面板中的模块可以在同一个模型中混合使用。
Arena是与微软Office兼容的产品,它的工具栏和菜单栏与Office是类似的。
同时Arena使用网络化多媒体动画技术(OLE 动画)和VBA视窗技术与桌面应用程序的整合。
嵌入在流程导航工具Visio里的接口使得用Visio画的流程图可以自动导入Arena中。
5.1 Arena建模概述5.1.1Arena功能与特点Arena应用领域✓物流领域,Arena的应用涉及从供应商到客户的整个供应链,包括供应商管理、库存管理、制造过程、分销物流、配送中心选址规划/商务过程以及客户服务等。
✓制造过程仿真:①生产过程中的工艺过程计划、设备布置等;②生产管理中的生产计划、库存管理;③制造过程的经济性、风险性分析,辅助企业投资决策;④各种先进制造模式如虚拟组织及敏捷供应链管理的可视化仿真等。
arena仿真详细教程

Arena仿真中文教程目录第一章:Arena3.0基础知识本节介绍Arena3.0安装到硬盘上以后如何创建Arena的工作环境。
1.1 Arena3.0的安装和调试Arena3.0的安装同一般的软件类似,打开disk1文件夹,双击应用文件Setup.exe运行安装程序,设置好安装路径后开始安装,安装结束后点击Finish完成安装。
如果是在Windows98操作系统下安装Arena3.0需要在安装前预装Visual Basic 6.0,否则,Arena3.0不能运行。
1.2 Arena3.0的面板、菜单和工具栏1.2.1 Arena3.0的启动在Arena安装完成后,Arena会在桌面上自动生成快捷方式的图标,双击图标即可进入Arena界面;同时,也可以在硬盘上的Arena\目录下双击Arena.exe文件进入。
在进入Arena后点击工具栏上的新建图标,打开Arena3.0的操作桌面(Desktop),如图1-1:图1-11.2.2 Desktop操作桌面简介1.操作桌面的结构Arena提供了十分方便的操作桌面以保证用户能够快速、简洁的建立仿真模型。
Arena的操作桌面主要由工具栏(Toolbars)、菜单栏、状态栏(Status bar)、建模界面组成。
下文对这几部分的主要功能将一一介绍。
2、工具栏:工具栏集中了我们建立仿真模型所要用到的主要工具,它由Standard(标准工具栏)、(视图工具栏)等组成,下面将注意介绍:●Standard:这个工具栏提供了新建、保存和打印等功能,如图1-2:图1-2●View:提供了视图功能,用户对建模区进行视图操作如图1-3:图1-3其中经常用到的功能有:Zoom in:放大Zoom out:缩小View All:建模区全部视图,即,以建立模型的全部视图。
View Previous:当前视图的前一视图。
View Region:选择视图区域。
●Arrange:Arena3.0为了用户能够创建生动、形象的动画,提供了功能齐全的绘图工具,Arrange工具栏(图1-4)就是为Arena的绘图提供支持的。
Arena Simulation 模拟仿真案例

TABLE OF CONTENTSTitle Page No.Abstract (2)Introduction (2)Research (3)Description of the Arena simulation model (4)Information (4)Steps of the system (6)Model overview (6)Step 1: Arrival stage (7)Step 2: Registration stage (8)Step 3: Doctoring stage (10)Step 4: Exit stage (14)The result (14)The number of statistical and curve diagrams (14)Report (15)Analyze the result (17)Conclusion (20)References (21)AbstractThe medical effectiveness and efficiency is an important index to measure the merits and demeritsof a hospital, which means that a good medical institution should not only have superior professional skill, but also have efficient and high-quality services. But in many smaller and older hospital or clinics, the long queue and outdated equipments are common issues. This model using Arena software is designed to improve these problems. First, a model is established to simulate a certain clinic that only have tradition artificial registration ways and some outdated equipment, and then the self-service equipment registration and the online registration are added into initial model, and more advanced medical devices also are added to assist in diagnosing patients for some complex diseases, which can reduce the diagnosis time of patients and the pressure of doctors. In addition, we will discuss the results, through comparing the original operational data (without self-service registration) with new system (including the self-service registration), we can further analyze the feasibility of the application and draw a conclusion.Key words: hospital, self-service, simulation system, Arena.IntroductionWith the growth of population and the development of science and technology, the health care industry has also improved greatly. Many of the most advanced medical devices have been applied to treatment and testing, which improves the efficiency and accuracy of doctors, and Internet technology is also used in many programs, some new, large-scale hospitals or clinics not only have an advantage in medical effects, but also give people a better experience in terms of service quality, medical environment and other details. Although they are more expensive, they still attract a lot of patients with a variety of advantages. But some of the smaller or older hospitals or clinics are facing many problems about capital, resource, efficiency and so on. For example, insufficient resources cannot meet the growing number of patients, a small number of outdated devices that can't meet the current physical therapy level. In order to solve these problems, there are two common ways, one is to expand the hospital directly with a large amount of money, but most of these hospitals cannot afford it, the other is to improve their medical facilities on the existing conditions, thereby matching the current needs, and the second method is the better way more medical institutions choose.ResearchAccording some researches, many of medical institutions’ work hours are from 8 a.m. to 5 p.m., and the busy hours is between 9.00 and 11.00 a.m. and 13.00 and 15.00 p.m., and the lunch time is between 11 a.m. and 1p.m..For the online registry and self-service by equipments, because they have some shortcomings, they do not have the face-to-face counseling and have more complex procedures, so these forms of service cannot completely replace artificial registration. However, some people who are familiar with the medical procedure or feel it is too long of queues of the artificial registration will be willing choose these forms of registration.About medical equipments, in recent years, advanced medical devices have been designed to be more efficient and smaller, shorter applications and high automation, which make it very practical, convenient, accurate and so on. So superior hospitals usually use advanced equipment to assist doctors, which also makes hospitals more competitive.In addition, a patient who goes to the doctor usually needs several times such as initial diagnosis, rediagnosis, buying medicine and so on. Therefore, the patient will choose the next process in a certain proportion after the diagnosis.This table summarizing above informationDescription of the Arena simulation modelThis model simulates the working mode of a small clinic base on some research data and hypothesis parameters. The workflow of the model: Arrival – Registration – Waiting doctor – diagnosis –Payment – Lab – Medicine – Exit.InformationArrival distributionInter-arrival rate: Random Exponential distribution with a mean of 5 minutesArrival during busy hours (9.00-11.00 a.m.): constant with 1 person/2 minutesArrival during busy hours (13.00-15.00 p.m.): constant with 1 person/2 minute Resources:According to some factors like lunch time, the resource value and resource types are set by different condition in the model.Schedule:Setting the schedule depend on allocation of resources. Take the doctor 1 for example. The time from 11.00 a.m. to 12.00 noon is the lunch hour, so the value is set to be 0 during this time.Queue:Because some patients need a repeat queue, so some assignments are used to set priority queue levels for some entities and processes apply the corresponding rules in a particular queue.Assignment:Some principles are assigned at some points in order to ensure the system to meet actual situations.Steps of the system Model overviewLayout a clinicStep 1: Arrival stageThe first stage is mainly used to set the entity arrival form and the time limit. The parameter settings are shown in the picture below.Step 2: Registration stageStep2.1This stage is to set the registration method selection. According to the parameter settings in the below picture, the patient selects the registration method. When the number of the queue of an artificial registration is more than 2, the patient needs to choose the self-service ways.Step 2.2This stage shows registering processes, there are two original artificial registration processes and new extra two registration methods, self-service equipments and online registration. The parameter settings are shown in the picture below.Step 3: Doctoring stageStep 3.1When the second stage is completed, people need to go to the waiting area first, which is the area in which queues are generated due to the limited resources of doctors. When there is no waiting queue in the waiting area, the patient goes directly to the doctor's offices, but if there is a queue in this process, the patient needs to join the queue for waiting resources to be released. The values are shown in the picture below.Step 3.2In this station, the number of waiting each doctor is limited to 2. If there are no spaces in the queues, patients need to go to the waiting area.Step 3.3This stage is the main stage of diagnosis, and the parameter settings of the three branches are same. The branch of doctor 1 will be described as a representative.Step 3.4This is the final stage of doctoring including four parts payment, lab, taking medicine, leaving directly, and the special part is the doing my lab , when this process is over, the patient needs to go back to the previous doctor's office, so it is needed to set the patient's waiting priority as high.Step 4: Exit stageThis is the final stage, people will leave and the simulation system finish.The resultThe number of statistical and curve diagramsReportWIP (the mean number of entities in the system)Queue of processes in the systemResources used in the systemAnalyze the resultDuring the nine hours of the system was running, 214 patients arrive, and 62 patients register by the self-services and 54 patients do a lab, which indicate that the self-service play an important role. By canceling the self-service registration methods to change the model to original registration ways, different data will be got. Comparing this data with improving system’s date, we can find that when there is not self-service, the waiting time of queues of artificial registrations is relatively long, 24.93 and 17.53 minutes, while the system add the self-service, the time becomes short, 2.98 and 1.06 minutes. When the clinic does not add the self-service registration ways, and under presumably same average process time (14.53 and 14.38 minutes), the average waiting time of each entity in the clinic is 38.39 minutes and the average total time is 61.92 minute, but in the adding self-service registration system, they are 12.9 and 36.09 minutes respectively. So it can be determined that adding the self-service registration system can reduce the waiting time of patients, and make the process of medical care shorter.ConclusionBased on above analysis, when the simulation model of a clinic adds the self-service registration, under the same average time of process, the waiting time becomes shorter. Although the utilization rate of two employees working at the registration desk has been reduced, the waiting time is considered to be an important issue impacting the service quality of the clinic. And the investment is very less than adding more employees.In this model, the result does not directly respond the effect of adding new medical devices used to assist in doctors, but because of these devices, when the improving model was established, the value of the process of doctor was set to be shorter. In other words, more advanced medical equipments mean less time spend on diagnosis and more patients coming. In fact, the self-service and advanced equipments have a lot of benefits for both internal and external aspects of a hospital or clinic. For the internal aspect, it not only can improve work efficiency and accuracy, but also reduce the pressure of employees, and for the external aspect, it can raise the reputation of a medical institution, and attract more people, which will bring more profits.Sum up, the simulation model provide a good way to help some hospitals or clinics to analyze and perfect their service quality.Lab exam Spring 2020 References[1]. Chinese Journal of Modern Medicine, Mar 2018.[2].Google research - Google map – Clinics in Dubai[3].Book: Kelton, W.D., Sadowski, R.P., and Sturrock, D.T: Simulation with Arena, Fourth Edition, 2007, McGraw Hill (with limited student edition of Arena on CD-Rom).[4].In a computer where Arena installed, use the following path: Start/Programs/Rockwell Software/Arena/Online Books Very useful examples are available when you opened Arena in a computer and use the help. You can use Arena help and Arena SMART files from the help menuModeling of Engineering Management Systems Page 21。
arena系统仿真课程设计

arena系统仿真课程设计一、课程目标知识目标:1. 学生能理解arena系统仿真的基本概念,掌握仿真模型构建的基本步骤。
2. 学生能描述仿真软件Arena的操作流程,运用Arena软件进行简单的仿真实验。
3. 学生了解仿真技术在项目管理、生产流程等领域的应用。
技能目标:1. 学生能够运用Arena软件构建简单的仿真模型,进行数据分析和参数优化。
2. 学生能够通过实际案例,分析问题、设计解决方案,运用仿真技术验证方案的有效性。
3. 学生能够运用Arena软件进行实验设计,独立完成仿真实验,并撰写实验报告。
情感态度价值观目标:1. 学生对系统仿真产生兴趣,认识到其在解决实际问题中的价值。
2. 学生在团队协作中培养沟通、合作能力,养成积极探索、主动学习的习惯。
3. 学生能够通过仿真实验,培养严谨的科学态度和问题分析能力。
课程性质:本课程为实践性较强的课程,旨在通过实际操作,让学生掌握Arena系统仿真的基本技能。
学生特点:学生为高年级本科生,具备一定的理论基础和实际操作能力,对新技术有较高的接受度。
教学要求:结合学生特点,注重理论与实践相结合,鼓励学生动手实践,培养实际应用能力。
通过课程学习,使学生在实际操作中掌握仿真技术,提高解决实际问题的能力。
教学过程中,注重培养学生的团队协作、沟通表达和问题分析能力。
二、教学内容1. Arena系统仿真基本概念:仿真模型、仿真引擎、事件调度等。
2. Arena软件操作流程:软件界面介绍、基本操作、模型构建与运行。
3. 常用仿真元素及其应用:实体、资源、队列、处理器、决策点等。
4. 仿真模型构建方法:识别系统元素、建立逻辑关系、设置参数、运行与调试。
5. 实际案例分析:项目管理系统、生产流程优化、物流配送等。
6. 数据分析与参数优化:输出分析、敏感度分析、优化算法应用。
7. 实验设计与实验报告撰写:设计实验方案、实施实验、分析结果、撰写报告。
教学大纲安排:第一周:Arena系统仿真基本概念介绍,软件安装与界面熟悉。
Arena仿真软件系统.pptx

•电子部件封装的具体建模思路 -两种不同的实体到达模型,每一种都有自己的时间分 布, 要分别两个Create模块来产生到达的部件。 -不同类型的部件的处理时间也不相同,使用两个 assign 模 块来定义其属性,分别賦予其封装处理时间。部件在 封 装操作中,使用包含在封装时间属性里的时间变量。 -两个准备区和封装操作使用各自的P rocess 模块来仿真。 -封装结束后,要对部件进行检查,结果部件将会根据一 定的概率去不同的地点。用Decide模块的两个选择支决 定部件的去向。 -使用Process和Decide模块对重新加工区进行仿真。 -用三个独立的Record和Dispose模块组仿真部件离开系 统 (运走,返修后运走,破碎),并通过这些模块获得相 应的循 环时间统计量。
>家庭抵押(home mortgage)流程分析 (1)绘制流程图
-产生抵押申请实体 -评判申请 -决定申请是否被接受 -消除申请实体中 止仿真程序 (2)什么是模块? 在Arena中,模块是流程图的组成部分以 及数据的载体,仿真所需要的信息都储 存 在模块中。
1
>基本程序模板 • Create:它是流程的开始,实体从该模块进入仿 真过 程。 • Dispose:它是流程的结尾,实体从该模块退出仿 真 过程。 • Process:处理一项活动,通常需要一个或更多的 资 源,并且需要消耗一些时间来完成 • Decide:是程序的分支部分,实体只可以选择一 个 分支。 • Batch:在继续运行流程之前,收集一些实体 • Separate:在并行的程序中复制实体,或是将先 前 所建立的一组实体分散成其他组。 • Assign:改变一些参数的值(在仿真过程中), 例如实体的类型或仿真变量。 • Record:拥有统计功能,统计实体的数量和时间 周 期。
arena仿真教程第4章

Arena中国
原书 P107
输入界面 4-4 确定产品 B 的封装时间和到达时间
创建了两种产品到达模块并给封装时间赋值之后,接下来可以利用先前放置的两个 Process 模块来建立两个预处理区域的模型了。Prep A Process 区域的完成对话框如输入界面 4-5 所示。 Process 模块有四个可能的活动类型选项:Delay,Seize Delay,Seize Delay Release 以及 Delay Release。Delay 会产生一个经历指定时间延迟的活动,这个活动不需要占用资源。由 于预处理区域需要占用机器或资源, 因此需要一个活动来实现排队等待, 直到获得预处理区 的资源,然后延迟至操作时间完成为止。Seize Delay 活动提供了等待和延迟功能,但它在 操作完成后并不释放资源给下一实体使用, 使用这个活动的前提是, 资源必须在下游的某一 个模块中能得到释放。Seize Delay Release 选项提供了准确建立预处理区域的各种活动的组 合。Delay Release 活动假设实体先前占用了一种资源,在此处经历一段延迟后,释放了这种 资源。
原书 P106 图 4-2 建立模块的视图
我们给这个模块命名,并指定实体类型为 Part A。设置到达间隔时间为均值 5 的随机数 (即服从指数分布) ,单位设置为分钟(Minutes) ,其余项采用默认值,完成后点击 OK 键 接受模块设定。
3
Arena中国
2
Arena中国
相应的值。当产品接受封装操作时,就可以使用与 Sealer Time 属性关联的时间值,而不像 模型 3-1 中那样在操作时刻才生成这个时间值。 与模型 3-1 类似,两个预处理区域和封装操作都有各自的 Process 模块。封装操作完成 后要实施检查,通过“投币”选择来决定产品下一步进入哪个区域。这里使用一个基于投币 原理的“决策” (Decide)模块,因此返工区域拥有 Process 和 Decide 两个模块,以及“通 过”和“未通过”等选项。模型中使用三个单独的“记录” (Record)和“处理”模块(装 运、返工合格、废料处理) ,这样就可以按照装运、返工合格以及废品处理等几部分进行分 类统计。所有这些模块都包含在“基本操作”面板中。
arena仿真教程第3章

3.2 Arena 的窗口组成
在这一部分,我们将打开一个现成的模型,看看Arena的各种窗口,以便读者熟悉,同 时介绍一些Arena的基本术语。
3.2.1 打开模型文件
已有的模型可以通过 File>Open 菜单命令打开 (或者单击 弹出 “打开文件” 对话框) ,
文件名称会出现在滚动框内,当然你也可以直接搜索其它文件夹或磁盘。找到名为 Model 03-01.doe 的文件(Arena 文件的默认扩展名为.doe1)。当使用典型安装时,该模型文件保存 在 Arena 7.0 文件夹下的 Book Examples 文件夹内。单击文件名选中该文件,并点击 Open 按钮即可(或者双击该文件名)。
Arena中国
等同于 File >Template Panel >Attach。这些模板文件(扩展名为.tpo)保存在 Arena 7.0 文件夹下的 Template 文件夹中。 模板断开 (当你不再需要相应的建模元素出现在活动面板里时) , 等同于 File >Template Panel >Detach。 关联帮助按钮,提供关于菜单或者工具栏命令的帮助。单击它鼠标箭头上会增加一个 问号,用带有问号的箭头单击想要得到帮助的工具栏按钮或者菜单命令即可得到相应 的帮助信息,关闭帮助窗口后鼠标指针就会返回原来的单箭头。 工具提示(Tooltips)可以提供另外一种更加快速和简洁的关于工具栏按钮的帮助。将 鼠标停留在某个按钮上面保持一两秒种不动, 就会出现一个小方框显示该按钮的名称。 如果 你想知道那个按钮更多的信息,可以使用 ,也可以在帮助系统中查阅相关信息(因为你
Arena中国
操作窗口,如移动、调整大小、最大化、最小化和关闭。 对菜单的操作。书中使用如下符号“M > C> S > T”,表示打开菜单M,从中选择C, 然后从子菜单中选择S(如果有的话)t键的使用。“Ctrl+任意键”意味着同时按下Ctrl键和任意键(这一 点同样适用于“Alt+任意键”和“Shift+任意键”)。如果“任意键”是键盘键,则不区分 大小写。“任意键”也可以是鼠标点击,例如“Ctrl+单击”可以拓展某个选择使其包括增 列项目。 对文本和其它项目的剪切 Cut(或者菜单命令 Edit>Cut,或者组合快捷键 Ctrl+X), 复制 Copy(或 Edit>Copy,或 Ctrl+C)和粘贴 Paste(或 Edit>Paste,或 Ctrl+V)。 填写对话框,包括输入和编辑文本条目、按下按钮、选定和清除(即取消选定)选 项框、 从一列选择按钮 (单选按钮) 中单击选中其中一个按钮、 以及从下拉菜单中选择项目。 如果读者对以上提到的操作不熟悉,在阅读下面的内容前最好先要复习一下Windows 操作指南。 下面来到电脑旁,电脑中已按随书附带的说明书安装了 Arena 系统(可以参阅附录 E 来了解如何安装 Arena 教学版,安装程序在随书附带的光盘内),找到 Arena 图标或快捷方 式并双击它(或者启动 Windows,单击开始按钮,在程序菜单中找到 Rockwell Software,进 而找到 Arena 7.0 子菜单,最后在其中找出 Arena 7.01 的图标并单击来启动 Arena),很快 Arena 版权窗口就会出现,如果你运行的是教学版(本书光盘提供的即为该版本)或评估版 的 Arena,你将会看到一个相应的信息框,阅读后请点击确定(OK)(由于 OK 按钮是默认 选项,也可以在键盘上之间点击回车键)。 此时在Arena窗口左上方会出现文件 (File) 、 视图 (View) 、 工具 (Tools) 和帮助 (Help) 菜单(如果一个空的模型文件在Arena启动后被自动打开,则还可以看到其它几个菜单)。 你还可以看到含有不同按钮的工具栏, 不过在打开模型文件之前, 只有如下几个工具栏可用 (处于激活状态): 创建一个新的空模型文件,这个按钮等同于菜单命令 File >New 和键盘操作 Ctrl+N。 显示一个对话框用以打开一个以前保存过的模型,等同于 File >Open 和 Ctrl+O。你 可能需要在其它文件夹或磁盘中去寻找所要打开的模型文件。 模板添加(系统提供了若干模板(Template),每个模板中包含了相应的建模元素),
系统建模与仿真实验指导书ⅠARENA二维仿真建模实验

系统建模与仿真实验指导书ⅠARENA二维仿真建模实验一、实验目的:1简单流水线建模实验掌握ARENA二维仿真软件的基本操作,掌握ARRIVE、DEPART、SEVER、INSPECT、SIMULATION等模块的应用与连接,学会采用该软件建立一条简单的生产流水线,并进行逻辑模块的参数设置和物理模块的界面设计,建成的仿真系统能运行并返回需要的统计数据。
2生产制造过程仿真建模实验借助工业工程综合实验——装配线设计实验的成果——装配线的结构与布局以及各主要工位的操作数据,通过ARENA软件进行仿真建模,比较系统运行的结果,对综合实验的设计方案进行验证实验,调整参数,寻求优化方案,进行优化设计实验。
二、实验步骤主要解决的四个问题:1)模型的建立,确定该系统需要的模块类型和数量:输入(Arrive),输出(Depart),加工操作(Sever),检验操作(Inspect)以及他们的先后顺序和连接关系2)参数设置:包括模块内参数设置和系统参数设置3)统计分析功能的建立:成品及废品平均流程时间、成品率、废品率以及其方差设置和实现,并能对此进行分析和评价,重新调整参数以实现系统优化;4)界面优化,利用系统工具或者画图工具,对仿真运行界面进行优化,体现更清晰的运动状态和物流路径,模拟加工过程的实现附:上机操作指导软件工具介绍一、Arena 软件工具的特点Arena是一个Microsoft Windows下的工具,所以它的基本界面你应该早已熟悉,但是由于Arena仿真软件是属于专业软件,并不常见,国内对该软件的操作方面的资料甚少,而且还都是外文版,所以有必要对Arena的操作界面以及相关的仿真建模操作和模块进行介绍。
(一)、操作界面图 3-1 Arena的界面1 File 菜单在这个菜单里,你可以新建Arena模型文件,打开现有模型,关闭窗口,存储模型或创建一个只许观看的模型,你也可以引进CAD图形,将AUTOCAD作为Arena 的支持工具,而在一些情况下,活动元素将允许你使用现有的详尽的机器设备的图形。
仿真学Arena详解 Chapter 02 Slides.ppt

Part Number
Arrival Time
Interarrival Time
Service Time
1
0.00
1.73
2.90
2
1.73
1.35
1.76
3
3.08
0.71
3.39
4
3.79
0.62
4.52
5
4.41
14.28
4.46
6
18.69
0.70
4.36
7
19.39
15.52
2.07
8
34.91
– System has a chance of operating in a stable way in the long run, i.e., might not “explode”
– If all interarrivals and service times were exactly at their mean, there would never be a queue
Decompose the problem Terminology Simulation by hand Some basic statistical issues
• Spreadsheet simulation
Simple static, dynamic models
• Overview of a simulation study
parts (a.k.a. cycle time):
P
TSi
i 1 , P
max TSi
i 1,...,P
TSi = time in system of part i
arena仿真中文教程
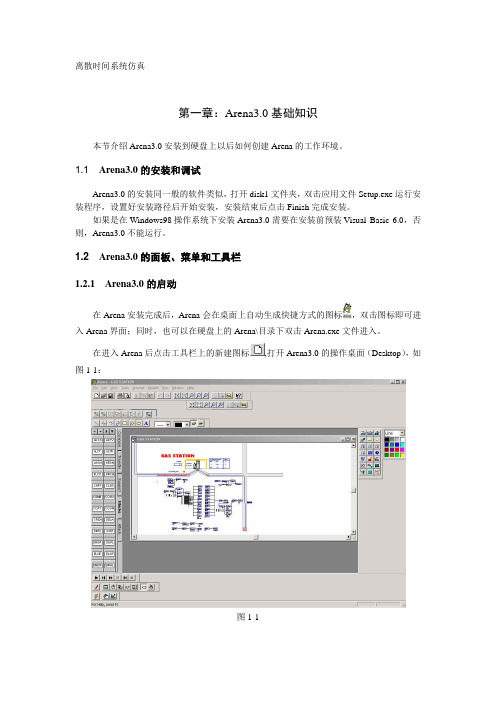
离散时间系统仿真第一章:Arena3.0基础知识本节介绍Arena3.0安装到硬盘上以后如何创建Arena的工作环境。
1.1 Arena3.0的安装和调试Arena3.0的安装同一般的软件类似,打开disk1文件夹,双击应用文件Setup.exe运行安装程序,设置好安装路径后开始安装,安装结束后点击Finish完成安装。
如果是在Windows98操作系统下安装Arena3.0需要在安装前预装Visual Basic 6.0,否则,Arena3.0不能运行。
1.2 Arena3.0的面板、菜单和工具栏1.2.1 Arena3.0的启动在Arena安装完成后,Arena会在桌面上自动生成快捷方式的图标,双击图标即可进入Arena界面;同时,也可以在硬盘上的Arena\目录下双击Arena.exe文件进入。
在进入Arena后点击工具栏上的新建图标,打开Arena3.0的操作桌面(Desktop),如图1-1:图1-11.2.2 Desktop操作桌面简介1.操作桌面的结构Arena提供了十分方便的操作桌面以保证用户能够快速、简洁的建立仿真模型。
Arena的操作桌面主要由工具栏(Toolbars)、菜单栏、状态栏(Status bar)、建模界面组成。
下文对这几部分的主要功能将一一介绍。
2、工具栏:工具栏集中了我们建立仿真模型所要用到的主要工具,它由Standard(标准工具栏)、(视图工具栏)等组成,下面将注意介绍:●Standard:这个工具栏提供了新建、保存和打印等功能,如图1-2:图1-2●View:提供了视图功能,用户对建模区进行视图操作如图1-3:图1-3其中经常用到的功能有:Zoom in:放大Zoom out:缩小View All:建模区全部视图,即,以建立模型的全部视图。
View Previous:当前视图的前一视图。
View Region:选择视图区域。
●Arrange:Arena3.0为了用户能够创建生动、形象的动画,提供了功能齐全的绘图工具,Arrange工具栏(图1-4)就是为Arena的绘图提供支持的。
Arena-仿真概述解析

◦ 也可以构造出“假”实体,只是用于建模的方便
◦ 例如,Breakdown demon, break angel
◦ 一个系统中可以同时具有多个不同类型的实体
2020/10/18
14
模拟中需考虑的对象 (continued...)
Attributes属性
◦ 同一类型实体的特征,用来描述和区分实体 ◦ 同一类实体都具有相同的属性,但属性值不同,例如:
义 ◦ 在模拟结束时,可以使用这些累加器来计算最终输出
性能指标
2020/10/18
20
模拟中需考虑的对象 (continued...)
对于本例中,统计累加器可以有
◦ 当前所生产的零件数 ◦ 当前所有排队时间 ◦ 已经通过队列的零件个数 ◦ 当前最大排队时间 ◦ 总周转时间 ◦ 当前最大周转时间
◦ 队列长度曲线Q(t)下的区域大小=排队时间×排队长度 ◦ 最大Q(t)=最大队长 ◦ 服务台忙的时间B(t)
◦ 传统制造行业 ◦ 服务业 ◦ 医疗健康业 ◦ “商业流程”
◦ 仍然是大多数是在大企业中得到应用 ◦ 通常只是一种辅助工具
2020/10/18
28
计算机仿真技术的沿革 (continued…)
目前
◦ 逐渐在小型企业中得到推广 ◦ 成为了一种标准工具 ◦ 通常会在设计过程的前期进行应用 ◦ 可以进行实时控制
◦ 到达时间 ◦ 停留日期 ◦ 优先级 ◦ 颜色
◦ 对于特定实体,必须绑定属性值 ◦ 属性可以视为(实体的)“局部”变量 ◦ 在ARENA中有些属性是自动生成的,有些则需要进行定义
2020/10/18
15
模拟中需考虑的对象 (continued...)
仿真软件Arena中文版培训手册

Arena仿真软件培训手册(中文版)1仿真概述1.1仿真的定义、特点和用途仿真是以系统理论、形式化理论随机过程理论、统计理论以及优化理论为基础,借助计算机和仿真软件对实际系统行为进行动态实验研究的方法。
通俗而言,仿真是基于一定的知识或假设,对实际系统进行模拟,从而更加深入地了解整个系统,并且对系统做出科学的调整、改善和优化,为辅助决策提供依据。
对于包含多种随机因素的复杂系统,通常难于用数学模型或解析方法精确地描述和求解时,可以根据系统内部的逻辑关系和数学关系,面向系统的实际过程和行为来构造仿真模型,在很少假设或不作假设的前提下建立包括系统主要因素和具体细节的模型框架,并通过仿真实验运行,得到复杂系统的解。
仿真的优越性:①它可以将研制过程、运行过程和实施过程放在实验室中进行,具有良好的可控制性、无破坏性、可复现性和经济性等特点;②系统仿真在理论上体现了实验思考的方法论,用它可以探索高技术领域和复杂系统深层次的运动机理和规律性,给出人们直观逻辑推理不能预见的系统动态特征,具有科学的先验性;③系统仿真建模具有面向过程的特点,仿真模型与所研究系统的运行过程在形式上和逻辑上存在对应性,避免了建立抽象数学模型的困难,显著简化了建模过程,具有很好的直观性。
仿真与线性规划和网络技术一起被称为运筹学在应用领域中的三大支柱。
在工业生产、交通运输、能源供应、医疗卫生、航空航天、军事作战、制造过程以及社会服务等领域发挥了重要作用,展现出了美好的前景。
仿真的实际用途体现在两大方面:事前分析认证和事后分析改善。
最终目的是要辅助决策,降低成本,提高效益。
①国防军事领域。
新装备研制过程仿真、作战仿真等等;②生产制造领域。
生产线布局、设施规划、厂址选择、瓶颈分析、资源分配等等;③供应链管理领域。
物流规划、库存决策、运输规划等等;④社会服务领域。
系统性能分析、业务流程分析、投资决策分析(决策方案比较)等等。
仿真应用的具体表现:提高设备利用率、减少排队等待、有效分配资源、减小缺货损失、减小资源故障带来的影响、确定最优批量问题、确定最优加工顺序问题、解决物料搬运问题、日常运作决策、实时监控、方案筛选,……。
Arena仿真概述详解

2018/10/12
10
分析过程 (continued…)
排队论
? 需要额外对模型的假设 ? 最为通用的模型: M/M/1 queue
? 到达间隔时间 ~ exponential ? 服务时间 ~ exponential, independent of interarrivals ? 且一般具有 E(service) < E(interarrival) ? 最终为稳态 (long-run, forever) ? 确定的解析分析结果:如,队列中的平均等待时间为
时间单位:分钟
到达时间:
? 间隔到达时间:
服务时间:
模拟到20(模拟)分钟时终止仿真 ,如恰好在第 20分钟时结束 ,届 时在系统中仍有零件(正在加工或在队列中等待),那它们 也只能完不成加工了。
2018/10/12
4
表2-1 零件的到达、间隔和服务时间(单位:分钟)
零件编号 1 2 3 4 5 6 7 8 9 10 11
N>1
6
队列中所有零件的 最大排队时间:
max Di
i ?1,? ,N
仿真过程中开始在钻床接受服务的零件的最大排 队等待时间(maximum waiting time in queue)。这 是用来度量最坏情况的,对于确定对顾客的服务水平 保证应该会有所帮助。这个量越小越好。
2018/10/12
7
件到达的速度要快(在平均意义下) ? 只考虑平均值的话,是对模型的过度简化,彻底忽略了随机性。
按照以上平均值来考虑,这个模型就等价于一个均匀到达,均匀 服务的模型,可以直接应用初中数学进行解决,也就无所谓队列 问题了! ? 我们的目标——介于完全随机和完全稳定之间的合理模型 ? 这种简单估测方法具有非常大的局限性
arena仿真详细教程

Arena仿真中文教程目录第一章:基础知识本节介绍安装到硬盘上以后如何创建Arena的工作环境。
的安装和调试的安装同一般的软件类似,打开disk1文件夹,双击应用文件运行安装程序,设置好安装路径后开始安装,安装结束后点击Finish完成安装。
如果是在Windows98操作系统下安装需要在安装前预装Visual Basic ,否则,不能运行。
的面板、菜单和工具栏1.2.1 A的启动在Arena安装完成后,Arena会在桌面上自动生成快捷方式的图标,双击图标即可进入Arena界面;同时,也可以在硬盘上的Arena\目录下双击文件进入。
在进入Arena后点击工具栏上的新建图标,打开的操作桌面(Desktop),如图1-1:图1-11.2.2 Desktop操作桌面简介1.操作桌面的结构Arena提供了十分方便的操作桌面以保证用户能够快速、简洁的建立仿真模型。
Arena的操作桌面主要由工具栏(Toolbars)、菜单栏、状态栏(Status bar)、建模界面组成。
下文对这几部分的主要功能将一一介绍。
2、工具栏:工具栏集中了我们建立仿真模型所要用到的主要工具,它由Standard(标准工具栏)、(视图工具栏)等组成,下面将注意介绍:Standard:这个工具栏提供了新建、保存和打印等功能,如图1-2:图 1-2View:提供了视图功能,用户对建模区进行视图操作如图1-3:图 1-3其中经常用到的功能有:Zoom in:放大Zoom out:缩小View All:建模区全部视图,即,以建立模型的全部视图。
View Previous:当前视图的前一视图。
View Region:选择视图区域。
Arrange:为了用户能够创建生动、形象的动画,提供了功能齐全的绘图工具,Arrange工具栏(图1-4)就是为Arena的绘图提供支持的。
图1-4它主要的功能有:Bring to front:移到最上Send to back:移到最下Group:合并Ungroup:取消合并Vertical Flip:垂直对齐Horizontal Flip:水平对齐Rotate:旋转Connect:连接Draw:这个工具栏(图1-5)提供了简单的绘图工具,用户可以利用这些工具在模型中绘制简单的图形。
Arena仿真概述详解

服务时间: 模拟到20(模拟)分钟时终止仿真,如恰好在第20分钟时结束,届 时在系统中仍有零件(正在加工或在队列中等待),那它们 也只能完不成加工了。
2018/10/12
4
表2-1 零件的到达、间隔和服务时间(单位:分钟) 零件编号 1 2 3 4 5 6 7 到达时间 0.00 1.73 3.08 3.79 4.41 18.69 19.39 到达间隔 1.73 1.35 0.71 0.62 14.28 0.70 15.52 服务时间 2.90 1.76 3.39 4.52 4.46 4.36 2.07
对系统状态进行初始化
2018/10/12
24
简单处理系统的特色 仿真时钟(ARENA中内置)
仿真过程中的当前时间值记在一个特殊变量中, 称为仿真时钟(simulation clock)。与实际时间不同, 仿真时钟并不是连续推进、均匀取值的,而是从当 前事件的发生时间跳跃到下一个事件的发生时间。 因为相继两个事件之间系统没有发生变化,所有也 就没有必要浪费时间来考虑这两个事件之间的过程。
2018/10/12
21
简单处理系统中的事件
新零件到达系统(Arrivial)
到达:新零件进入系统。 ◦ 安排下一个新零件的适时到达,也即将其到达事件 记录插入未来事件表; ◦ 更新随时间离散变化的各统计量(从上一事件发生 到现在); ◦ 把到达零件的到达时间(即仿真时钟的当前值)保 存在一个属性中,用以在后面计算该零件的系统逗留 时间和排队时间; ◦ 如果钻床空闲,则到达零件立即开始加工(其排队 时间为零),将钻床状态置为“忙”,并安排该零件 的离开事件,统计该零件的排队时间; ◦ 否则,如果钻床正在加工其它零件,则将到达零件 置于队列末尾,队长变量加1。
Arena课程设计

Arena课程设计一、课程目标知识目标:1. 学生能理解并掌握Arena课程中关于某一学科的核心理念及关键知识点,如数学的分数概念、物理的能量守恒等。
2. 学生能运用所学知识解决实际问题,例如通过数学模型进行问题分析,运用物理知识解释现象等。
技能目标:1. 学生掌握科学的研究方法,具备收集、整理、分析信息的能力,能够运用所学知识进行实际操作。
2. 学生能够运用Arena课程提供的工具和资源,开展自主探究和合作学习,提高解决问题的能力。
情感态度价值观目标:1. 学生培养对学科的兴趣和热情,树立积极向上的学习态度,形成自主学习的习惯。
2. 学生在团队协作中学会尊重他人、沟通协作,培养集体荣誉感和责任感。
3. 学生能够认识到所学知识在实际生活中的应用和价值,激发对科学探究的热情。
课程性质分析:本课程为学科拓展课程,旨在帮助学生深入理解学科知识,提高解决实际问题的能力。
学生特点分析:学生处于某一特定年级,具备一定的学科基础和认知能力,但需要在实践中提高运用知识的能力。
教学要求:1. 教学内容与课本紧密联系,注重知识点的拓展和延伸。
2. 教学过程中注重培养学生的实践能力和创新精神,提高学生的学科素养。
3. 教学评价关注学生的过程表现和实际成果,以促进学生全面发展。
二、教学内容本课程依据课程目标,结合学科特点和学生的认知水平,选择以下教学内容:1. 知识点讲解:依据课本章节,系统讲解学科核心概念、原理及其应用,如数学中的分数运算、物理中的力学原理等。
2. 实践操作:结合知识点,设计实践活动,让学生在实际操作中掌握知识,如数学分数的实践活动、物理实验等。
3. 案例分析:选取与知识点相关的实际案例,引导学生运用所学知识分析问题、解决问题。
4. 合作探究:组织学生进行小组讨论,针对特定问题进行合作探究,培养学生的团队协作能力和创新思维。
教学内容安排及进度:第一课时:知识点讲解,介绍学科核心概念、原理,让学生对课程内容有整体的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◦ 也可以构造出“假”实体,只是用于建模的方便
◦ 例如,Breakdown demon, break angel
◦ 一个系统中可以同时具有多个不同类型的实体
2018/10/20
14
模拟中需考虑的对象 (continued...)
Attributes属性
◦ 同一类型实体的特征,用来描述和区分实体 ◦ 同一类实体都具有相同的属性,但属性值不同,例如:
队列中的最大队长:
0t 20
max Q (t )
间,或成为周转时间)
P i 1Fi P ,
2018/10/20
零件的平均和最大停留时间 (在系统中停留的时
i 1,,P
max Fi
Fi = flowtime of ith part
8
20
B(t )dt
0
20
机器设备的使用率 (忙率)
◦ ◦ ◦ ◦ 到达时间 停留日期 优先级 颜色
◦ 对于特定实体,必须绑定属性值 ◦ 属性可以视为(实体的)“局部”变量 ◦ 在ARENA中有些属性是自动生成的,有些则需要进行定义
2018/10/20
15
模拟中需考虑的对象 (continued...)
(全局) Variables变量
◦ ◦ ◦ ◦ 反映了系统的特征,而与实体无关 名称和取值对于整个系统来说是唯一的 不与实体绑定 实体可以对变量进行访问,并改变变量取值,例如:
8 9 10 11
2018/10/20
34.91 38.06 39.82 40.82
3.15 1.76 1.00 .
3.36 2.37 5.38 .
5
研究目标:输出性能指标
整个模拟时间内的总生产量 (P) 在20分钟加工过程中的的总产量(total production;在钻床完 成服务并离开的零件数)。其值应越大越好。
队列中零件的平均排队时间:
i 1
Di
N
N
N = no. of parts completing queue wait Di = waiting time in queue of ith part Know: D1 = 0 N>1
6
2018/10/20
队列中所有零件的最大排队时间:
i 1,,N
Arena 概貌
仿真基本术语和概念
2018/10/20
2
系统:简单处理系统
一般目标:
◦ 估计总零件生产量 ◦ 排队时间,排队长度,机器忙率
时间单位设定:可任意,但是 …
◦ 必须一致 ◦ 时间设定必须合理,可以在有限的实际时间内运行结束
2018/10/20
3
模型特征
初始时间为0,且初始状态为空闲 时间单位:分钟 到达时间:
研究目标:输出性能指标(continued...)
◦ 即钻床处于忙态的时间占仿真总时间的比例。这是另一个随时间离散变 化的统计量,其随时间变化的函数为如下“忙态”函数
B (t ) d t 其它需要的指标
◦ information overload? 20 ◦ 并不是指标越多越好
0
Байду номын сангаас
20
1 B(t ) 0
◦ 间隔到达时间:
服务时间: 模拟到20(模拟)分钟时终止仿真,如恰好在第20分钟时结束,届 时在系统中仍有零件(正在加工或在队列中等待),那它们 也只能完不成加工了。
2018/10/20
4
表2-1 零件的到达、间隔和服务时间(单位:分钟) 零件编号 1 2 3 4 5 6 7 到达时间 0.00 1.73 3.08 3.79 4.41 18.69 19.39 到达间隔 1.73 1.35 0.71 0.62 14.28 0.70 15.52 服务时间 2.90 1.76 3.39 4.52 4.46 4.36 2.07
2 S A S
S E ( Service Time) A E (Interarrival Time)
◦ 存在的问题:有效性,估计均值,长期有效,但是未必对于某个问题有 效。 ◦ 通常用于对平均性能进行考虑时应用
2018/10/20
11
模拟的机制
单个操作(到达,服务时间)按照实际过程进行处理 对系统变化,事件都按照实际“时间”,实际顺序进行 处理
对不同对象之间的交互作用进行逐个模拟
默认安置“观测者”来对输出性能指标进行收集 具体的,穷举式的分析方法 在过程中任何事物都是具体和清晰的
◦ 然后就需要考虑大量细节,存放大量的过程参数和变量 ◦ 幸好有模拟软件来进行跟踪和帮助
2018/10/20
13
模拟中需考虑的对象
Entity 实体
◦ 系统的“参与者”,在系统的移动,状态发生变化, 可以影响其它实体或者被其它实体影响 ◦ 动态对象 — 需要进行创建,进行移动,以及离开系统 (根据需要) ◦ 通常表示“实际”的事物
max Di
仿真过程中开始在钻床接受服务的零件的最大排 队等待时间(maximum waiting time in queue)。这 是用来度量最坏情况的,对于确定对顾客的服务水平 保证应该会有所帮助。这个量越小越好。
2018/10/20
7
研究目标:输出性能指标 (continued...)
队列的平均队长:
如果钻床在t时刻忙 如果钻床在t时刻闲
2018/10/20
9
分析过程
常规估测分析方法
◦ 平均间隔到达时间= 4.987 minutes ◦ 平均服务时间 = 3.351 minutes ◦ 从以上的分析来看,还是比较有希望的,因为完成服务的速度比零 件到达的速度要快(在平均意义下) ◦ 只考虑平均值的话,是对模型的过度简化,彻底忽略了随机性。 按照以上平均值来考虑,这个模型就等价于一个均匀到达,均匀 服务的模型,可以直接应用初中数学进行解决,也就无所谓队列 问题了! ◦ 我们的目标——介于完全随机和完全稳定之间的合理模型 ◦ 这种简单估测方法具有非常大的局限性
2018/10/20
10
分析过程 (continued…)
排队论
◦ 需要额外对模型的假设 ◦ 最为通用的模型: M/M/1 queue
◦ ◦ ◦ ◦ ◦ 到达间隔时间 ~ exponential 服务时间 ~ exponential, independent of interarrivals 且一般具有E(service) < E(interarrival) 最终为稳态 (long-run, forever) 确定的解析分析结果:如,队列中的平均等待时间为
