2008年中考试题压轴题精选讲座一-几何与函数问题
数学f1初中数学2008年数学各地中考压轴题汇编
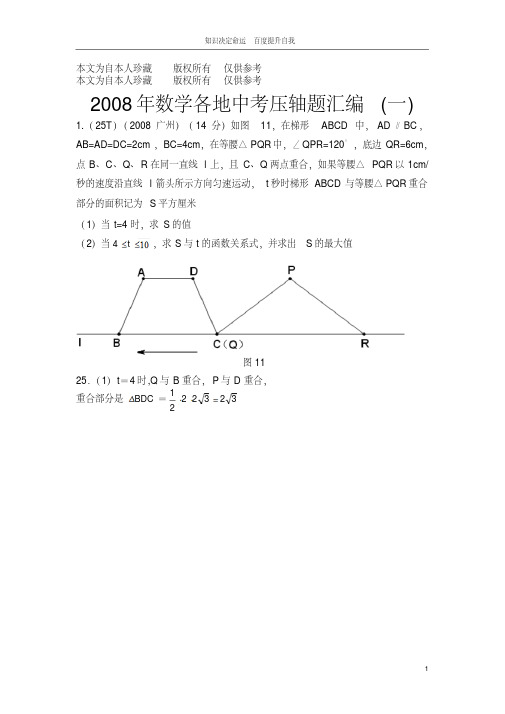
本文为自本人珍藏版权所有仅供参考本文为自本人珍藏版权所有仅供参考2008年数学各地中考压轴题汇编(一)1.(25T )(2008广州)(14分)如图11,在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2cm ,BC=4cm ,在等腰△PQR 中,∠QPR=120°,底边QR=6cm ,点B 、C 、Q 、R 在同一直线l 上,且C 、Q 两点重合,如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米(1)当t=4时,求S 的值(2)当4t,求S 与t 的函数关系式,并求出S 的最大值25.(1)t =4时,Q 与B 重合,P 与D 重合,重合部分是BDC =3232221图112.(28T)(佳木斯市)(本小题满分10分)如图,在平面直角坐标系中,点(30)C ,,点A B ,分别在x 轴,y 轴的正半轴上,且满足2310OBOA .(1)求点A ,点B 的坐标.(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP .设ABP △的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,是否存在点P ,使以点A B P ,,为顶点的三角形与AOB △相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.28.解:(1)2310OB OA 230OB,10OA ·························································(1分)yxAOC B3OB ,1OA点A ,点B 分别在x 轴,y 轴的正半轴上(10)(03)A B ,,,····································································(2分)(2)求得90ABC······················································································(3分)23(023)23(23)t t S tt≤(每个解析式各1分,两个取值范围共1分)·············································(6分)(3)1(30)P ,;22133P ,;34133P ,;4(323)P ,(每个1分,计4分)···························································································································(10分)注:本卷中所有题目,若由其它方法得出正确结论,酌情给分.3.(19T)(湖北黄岗罗田.本小题14分)如图,已知ABC 中,AB =a ,点D 在AB 边上移动(点D 不与A 、B 重合),DE//BC ,交AC 于E ,连结CD .设S S S S ABC DEC ,1.(1)当D 为AB 中点时,求S S 1:的值;(2)若ADx S Sy ,1,求y 关于x 的函数关系式及自变量x 的取值范围;(3)是否存在点D ,使得S S 114成立?若存在,求出D 点位置;若不存在,请说明理由.19、解:(1)DE BC D AB //,为的中点,21AC AEABADABC ADE ,∽.S S AD AB ADE ()214S S AE ECADE11,∴411SS .(2)∵AD =x ,y SS =1,∴xx a ADDB AE EC S S ADE===△1.又∵222ax ABAD SS ADE==△,∴S △ADE =22ax ·S∴S 1=x xa 22ax S ∴221aaxxSS ,即y =-x a21+xa 1自变量x 的取值范围是:0<x <a .(3)不存在点D ,使得S S 114成立.理由:假设存在点D ,使得S S 114成立,那么S Sy11414,即.∴-21ax 2+a1x >41,∴(a1x -21)2<0 ∵(a1x -21)2≥∴x 不存在,即不存在点D ,使得S S 114成立.4.(27T)(江苏省宿迁市.本题满分12分)如图,⊙O 的半径为1,正方形ABCD 顶点B 坐标为)0,5(,顶点D 在⊙O 上运动.(1)当点D 运动到与点A 、O 在同一条直线上时,试证明直线CD 与⊙O 相切;(2)当直线CD 与⊙O 相切时,求CD 所在直线对应的函数关系式;(3)设点D 的横坐标为x ,正方形ABCD 的面积为S ,求S 与x 之间的函数关系式,并求出S 的最大值与最小值.5.(25T)(大连市14分)如图25-1,正方形ABCD 和正方形QMNP ,∠M =∠B ,M是正方形ABCD 的对称中心,MN 交AB 于F ,QM 交AD 于E .⑴求证:ME = MF .⑵如图25-2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME 与线段MF 的关系,并加以证明.⑶如图25-3,若将原题中的“正方形”改为“矩形”,且AB = mBC ,其他条件不变,探索线段ME 与线段MF 的关系,并说明理由.⑷根据前面的探索和图25-4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由.图25 - 4图25 - 3图25 - 2图25 -1APQQPQPABCDFM NABCE MNBCDEMNFDPQD AFN ME CB6.(26T)(辽宁省十二市)(本题14分)如图16,在平面直角坐标系中,直线33yx与x 轴交于点A ,与y 轴交于点C ,抛物线51D CB AOxy第27题223(0)3y axx c a经过A B C ,,三点.(1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由;(3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.八、(本题14分)26.解:(1)直线33yx与x 轴交于点A ,与y 轴交于点C .(10)A ,,(03)C ,······························································································1分点A C ,都在抛物线上,23033a cc333a c 抛物线的解析式为2323333yx x ··························································3分顶点4313F ,··································································································4分(2)存在···················································································································5分1(03)P ,·················································································································7分2(23)P ,··················································································································9分(3)存在·················································································································10分理由:解法一:延长BC 到点B ,使B C BC ,连接B F 交直线AC 于点M ,则点M 就是所求的点.·····················································································11分过点B 作B HAB 于点H .yA O xyBFC图16B 点在抛物线2323333yxx 上,(30)B ,在Rt BOC △中,3tan3OBC,30OBC,23BC,在Rt BB H △中,1232B H BB ,36BHB H,3OH,(323)B ,····················································12分设直线B F 的解析式为ykxb 233433k bkb 解得36332k b33362y x·····································································································13分3333362y x yx解得371037x y,310377M,在直线AC 上存在点M ,使得MBF △的周长最小,此时310377M ,.14分解法二:过点F 作AC 的垂线交y 轴于点H ,则点H 为点F 关于直线AC 的对称点.连接BH 交AC 于点M ,则点M 即为所求.·····················11分过点F 作FGy 轴于点G ,则OB FG ∥,BC FH ∥.90BOC FGH ,BCOFHGHFGCBO同方法一可求得(30)B ,.在Rt BOC △中,3tan 3OBC,30OBC,可求得33GHGC,A OxyBF C 图10H M GGF 为线段CH 的垂直平分线,可证得CFH △为等边三角形,AC 垂直平分FH .即点H 为点F 关于AC 的对称点.5303H ,·············································12分设直线BH 的解析式为y kx b ,由题意得03533k b b解得539533k b553393y ·····································································································13分55339333y x yx解得371037x y310377M,在直线AC 上存在点M ,使得MBF △的周长最小,此时310377M ,.14分7.(28T)(南通市28题14分)已知双曲线k yx与直线14yx 相交于A 、B 两点.第一象限上的点M (m ,n )(在A 点左侧)是双曲线k yx上的动点.过点B 作BD ∥y 轴交x 轴于点D .过N (0,-n )作NC ∥x 轴交双曲线k y x于点E ,交BD 于点C .(1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值.(2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.(3)设直线AM 、BM 分别与y 轴相交于P 、Q 两点,且MA=pMP ,MB=qMQ ,求p -q 的值.(第28题)yO·AD xB CEN M ·28.解:(1)∵D (-8,0),∴B 点的横坐标为-8,代入14y x 中,得y=-2.∴B 点坐标为(-8,-2).而A 、B 两点关于原点对称,∴A (8,2).从而8k.,,,,,,,,,,,,,,,,,,,,,,,,,,3分(2)∵N (0,-n ),B 是CD 的中点,A 、B 、M 、E 四点均在双曲线上,∴mn k ,B (-2m ,-2n ),C (-2m ,-n ),E (-m ,-n ).,,,,,4分S矩形DCNO22mn k,S △DBO =1122mnk,S △OEN=1122mnk ,,,,,,,7分∴S四边形OBCE =S 矩形DCNO-S △DBO -S △OEN =k .∴4k .,,,,,,,,,,8分由直线14yx及双曲线4yx,得A (4,1),B (-4,-1),∴C(-4,-2),M(2,2).,,,,,,,,,,,,,,,,,,,,,9分设直线CM 的解析式是y ax b ,由C 、M 两点在这条直线上,得42,2 2.a b a b解得23a b.∴直线CM 的解析式是2233yx.,,,,,,,,,,,,,,,,,,11分(3)如图,分别作AA 1⊥x 轴,MM 1⊥x 轴,垂足分别为A 1、M 1.设A 点的横坐标为a ,则B 点的横坐标为-a .于是111A M MA a mpMPM Om .同理MB m aqMQ m ,,,,,,,,,,,,13分∴2a mmap qm m.,,,,,,,,14分8.(29T)(庆阳市.2分)一条抛物线2yxmx n 经过点03,与43,.(1)求这条抛物线的解析式,并写出它的顶点坐标;(2)现有一半径为1、圆心P 在抛物线上运动的动圆,当P 与坐标轴相切时,求圆心P 的坐标;(3)P 能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线2yxmx n 使P 与两坐标轴都相切(要说明平移方法).29.本小题满分12分(1)∵抛物线过04,3,,3两点,∴23443n m n ,.···················································································1分解得43m n,.························································································2分∴抛物线的解析式是243yxx ,顶点坐标为21,. ···················3分(第28题)y O · A xBM ·QA 1P M 1O xy图15(2)设点P 的坐标为00()x y ,,当P 与y 轴相切时,有0||1x ,∴01x . ·····································5分由01x ,得201430y ;由01x ,得2(1)4(1)38y .此时,点P 的坐标为121018P P ,,,.·····································6分当P 与x 轴相切时,有0||1y ,∴01y . ······························7分由01y ,得200431xx ,解得022x ;由01y ,得20431xx ,解得02x .此时,点P 的坐标为34(221)(221)P P ,,,,5(21)P ,-.··············9分综上所述,圆心P 的坐标为:121018P P ,,,,34(221)(221)P P ,,,,5(21)P ,-.注:不写最后一步不扣分.(3)由(2)知,不能.································································10分设抛物线243y xx 上下平移后的解析式为2(2)1yx h ,若P 能与两坐标轴都相切,则0||x 0||1y ,即x 0=y 0=1;或x 0=y 0=-1;或x 0=1,y 0=-1;或x 0=-1,y 0=1.·······11分取x 0=y 0=1,代入2(2)1y x h ,得h=1.∴只需将243yxx 向上平移1个单位,就可使P 与两坐标轴都相切.···············································································································12分说明:对于以上各解答题学生试卷中出现的不同解法,请参考本标准给分.9.(25T)(上海市.题满分14分,第(1)题满分3分,第(2)题满分7分,第(3)题满分4分)正方形ABCD 的边长为2,E 是射线CD 上的动点(不与点D 重合),直线AE 交直线BC于点G ,∠BAE 的平分线交射线BC 于点O .(1)如图8,当CE =32时,求线段BG 的长;(2)当点O 在线段BC 上时,设x EDCE ,BO =y ,求y 关于x 的函数解析式;(3)当CE =2ED 时,求线段BO 的长.A DBG EC图8O 备用图A BCD25.解:(1)在边长为2的正方形ABCD中,32CE,得34DE,又∵//AD BC ,即//AD CG ,∴12CG CE ADDE,得1CG --(2分)∵2BC ,∴3BG --(1分)(2)当点O 在线段BC 上时,过点O 作AG OF,垂足为点F ,∵AO 为BAE 的角平分线,90ABO,∴y BO OF--(1分)在正方形ABCD中,BCAD //,∴CG CEx ADED.∵2AD ,∴x CG2--(1分)又∵CEx ED,2CEED,得xx CE12--(1分)∵在Rt △ABG 中,2AB ,22BGx ,90B,∴2222AG xx.∵2AF AB,∴22222FGAGAF x x--(1分)∵OF AB FGBG,即AB yFG BG,得122222x x x y,)0(x ;(2分)(1分) (3)当ED CE 2时,①当点O 在线段BC 上时,即2x,由(2)得32102yOB;--(1分)②当点O 在线段BC 延长线上时,4CE,2DC ED,在Rt △ADE 中,22AE .设AO 交线段DC 于点H ,∵AO 是BAE 的平分线,即HAEBAH ,又∵CD AB //,∴AHE BAH .∴AHE HAE .∴22AEEH .∴224CH--(1分)∵CDAB//,∴BOCO ABCH ,即BOBO 22224,得222BO .(2分)10.(25T)(烟台市.题满分14分)如图,抛物线21:23L y xx 交x 轴于A 、B 两点,交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ,2L 交x 轴于C 、D 两点. (1)求抛物线2L 对应的函数表达式;(2)抛物线1L 或2L 在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形.若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线1L 上的一个动点(P 不与点A 、B 重合),那么点P 关于原点的对称点Q 是否在抛物线2L 上,请说明理由.11.(14T)(荷泽市.题满分12分)在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.(1)用含x的代数式表示△MNP的面积S;(2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?24.(本题满分12分)解:(1)∵MN ∥BC ,∴∠AMN=∠B ,∠AN M =∠C .∴△AMN ∽△ABC .∴AMANABAC ,即43x AN .∴AN =43x .,,,,,2分∴S =2133248MNPAMNSSx xx.(0<x <4)………………3分(2)如图2,设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN .在Rt △ABC 中,BC =22ABAC =5.由(1)知△AMN ∽△ABC .∴AM MNABBC ,即45x MN .∴54MN x,∴58ODx .…………………5分过M 点作MQ ⊥BC 于Q ,则58MQ ODx.在Rt △BM Q 与Rt △BCA 中,∠B 是公共角,∴△BMQ ∽△BCA .∴BM QMBCAC .∴55258324x BMx ,25424AB BM MAx x .∴x =4996.∴当x =4996时,⊙O 与直线BC 相切.,,,,,,,,,,,,,,,,7分ABCMND 图2OABCMNP图1OABCMNP 图3O(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.∵MN∥BC,∴∠AMN=∠B,∠AOM=∠APC.∴△AMO ∽△ABP.∴12AM AOAB AP.AM=MB=2.故以下分两种情况讨论:①当0<x≤2时,2Δ83xSy PMN.∴当x=2时,2332.82y最大…………………………………………8分②当2<x<4时,设PM,PN分别交BC于E,F.∵四边形AMPN是矩形,∴PN∥AM,PN=AM=x.又∵MN∥BC,∴四边形MBFN是平行四边形.∴F N=BM=4-x.∴424 PF x x x.又△PEF ∽△ACB.∴2PEFABCSPFAB S.∴2322PEFS x.……………………………………………………… 9分MNP PEFy S S=222339266828x x x x.,,,,,,,,10分当2<x<4时,29668y x x298283x.∴当83x时,满足2<x<4,2y最大.综上所述,当83x时,y值最大,最大值是2.,,,,,,,,,,,12分。
2008年全国中考数学压轴题精选1含答

2008年全国中考数学压轴题精选(一)1(08福建莆田26题)(14分)如图:抛物线经过A (-3,0)、B (0,4)、C (4,0)三点.(1) 求抛物线的解析式.(2)已知AD = AB (D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值;(3)在(2)的情况下,抛物线的对称轴上是否存在一点M ,使MQ+MC 的值最小?若存在,请求出点M 的坐标;若不存在,请说明理由。
(注:抛物线2y ax bx c =++的对称轴为2bx a=-) (08福建莆田26题解析)(1)解法一:设抛物线的解析式为y = a (x +3 )(x - 4) 因为B (0,4)在抛物线上,所以4 = a ( 0 + 3 ) ( 0 - 4 )解得a= -1/3 所以抛物线解析式为2111(3)(4)4333y x x x x =-+-=-++解法二:设抛物线的解析式为2(0)y ax bx c a =++≠,依题意得:c=4且934016440a b a b -+=⎧⎨++=⎩ 解得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩所以 所求的抛物线的解析式为211433y x x =-++(2)连接DQ ,在Rt △AOB 中,2222345AB AO BO =+=+= 所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD =?7 – 5 = 2 因为BD 垂直平分PQ ,所以PD=QD ,PQ ⊥BD ,所以∠PDB=∠QDB 因为AD=AB ,所以∠ABD=∠ADB ,∠ABD=∠QDB ,所以DQ ∥AB 所以∠CQD=∠CBA 。
∠CDQ=∠CAB ,所以△CDQ ∽ △CABDQ CD AB CA = 即210,577DQ DQ ==所以AP=AD – DP = AD – DQ=5 –107=257 ,2525177t =÷= 所以t 的值是257(3)答对称轴上存在一点M ,使MQ+MC 的值最小 理由:因为抛物线的对称轴为122b x a =-= 所以A (- 3,0),C (4,0)两点关于直线12x =对称 连接AQ 交直线12x =于点M ,则MQ+MC 的值最小 过点Q 作QE ⊥x 轴,于E ,所以∠QED=∠BOA=900 DQ ∥AB ,∠ BAO=∠QDE , △DQE ∽△ABOQE DQDE BO ABAO == 即 107453QE DE== 所以QE=87,DE=67,所以OE = OD + DE=2+67=207,所以Q (207,87)设直线AQ 的解析式为(0)y kx m k =+≠则2087730k m k m ⎧+=⎪⎨⎪-+=⎩ 由此得 8412441k m ⎧=⎪⎪⎨⎪=⎪⎩ 所以直线AQ 的解析式为8244141y x =+ 联立128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩由此得128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 所以M 128(,)241则:在对称轴上存在点M 128(,)241,使MQ+MC 的值最小。
2008年全国中考数学压轴题精选精析(一)

2008年全国中考数学压轴题精选精析(一)1.(08广东中山22题)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB 重合,直角边不重合,已知AB=8,BC=AD=4,AC 与BD 相交于点E ,连结CD .(1)填空:如图9,AC= ,BD= ;四边形ABCD 是 梯形. (2)请写出图9中所有的相似三角形(不含全等三角形). (3)如图10,若以AB 所在直线为x 轴,过点A 垂直于AB 的直线为y 轴建立如图10的平面直角坐标系,保持ΔABD 不动,将ΔABC 向x 轴的正方向平移到ΔFGH 的位置,FH 与BD 相交于点P ,设AF=t ,ΔFBP 面积为S ,求S 与t 之间的函数关系式,并写出t 的取值值范围.(08广东中山22题解析)解:(1)1分等腰;…………………………2分(2)共有9对相似三角形.(写对3-5对得1分,写对6-8对得2分,写对9对得3分)①△DCE 、△ABE 与△ACD 或△BDC 两两相似,分别是:△DCE ∽△ABE ,△DCE ∽△ACD ,△DCE ∽△BDC ,△ABE ∽△ACD ,△ABE ∽△BDC ;(有5对)②△ABD ∽△EAD ,△ABD ∽△EBC ;(有2对) ③△BAC ∽△EAD ,△BAC ∽△EBC ;(有2对)所以,一共有9对相似三角形.…………………………………………5分(3)由题意知,FP ∥AE , ∴ ∠1=∠PFB , 又∵ ∠1=∠2=30°, ∴ ∠PFB =∠2=30°,∴ FP =BP (6)过点P 作PK ⊥FB 于点K ,则F K B K =∵ AF =t ,AB =8, ∴ FB =8-t ,1(8)2B K t =-.在Rt △BPK 中,1tan 2(8)tan 30)26PK BK t t =⋅∠=-︒=-. ……………………7分∴ △FBP 的面积11(8)(8)226S FB PK t t =⋅⋅=⋅-⋅-,∴ S 与t 之间的函数关系式为:DCBE图9图1028)12S t =-,或24123S t =-+…………………………………8分t 的取值范围为:08t ≤<. …………………………………………………………9分2.(08湖北十堰25题)已知抛物线b ax ax y ++-=22与x 轴的一个交点为A(-1,0),与y 轴的正半轴交于点C .⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标;⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.(08湖北十堰25题解析)解:⑴对称轴是直线:1=x ,点B 的坐标是(3,0). ……2分说明:每写对1个给1分,“直线”两字没写不扣分.⑵如图,连接PC ,∵点A 、B 的坐标分别是A(-1,0)、B (3,0), ∴AB =4.∴.AB PC 242121=⨯==在Rt △POC 中,∵OP =PA -OA =2-1=1, ∴.POPCOC 3122222=-=-=∴b =.3 ………………………………3分 当01=-=,y x 时,,a a 032=+--∴.a 33= ………………………………4分∴.x x y 3332332++-= ………………5分⑶存在.……………………………6分理由:如图,连接AC 、BC .设点M 的坐标为),(y x M .①当以AC 或BC 为对角线时,点M 在x 轴上方,此时CM ∥AB ,且CM =AB .由⑵知,AB =4,∴|x|=4,3==OC y .∴x =±4.∴点M 的坐标为)3,4()3,4(-或M .…9分说明:少求一个点的坐标扣1分.②当以AB 为对角线时,点M 在x 轴下方. 过M 作MN ⊥AB 于N ,则∠MNB =∠AOC =90°. ∵四边形AMBC 是平行四边形,∴AC =MB ,且AC ∥MB .∴∠CAO =∠MBN .∴△AOC ≌△BNM .∴BN =AO =1,MN =CO . ∵OB =3,∴0N =3-1=2.∴点M 的坐标为(2,M . ……………………………12分说明:求点M 的坐标时,用解直角三角形的方法或用先求直线解析式,然后求交点M 的坐标的方法均可,请参照给分.综上所述,坐标平面内存在点M ,使得以点A 、B 、C 、M 为顶点的四边形是平行四边形.其坐标为123((2,M M M -.说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分。
2008年数学中考试题分类汇编(压轴题)

2008年数学中考试题分类汇编压轴题(2008年芜湖市)如图,已知 (4,0)A ,(0,4)B ,现以A 点为位似中心,相似比为9:4,将OB 向右侧放大,B 点的对应点为C . (1) 求C 点坐标及直线BC 的解析式;(2) 一抛物线经过B 、C 两点,且顶点落在x 轴正半轴上,求该抛物线的解析式并画出函数图象;(3) 现将直线BC 绕B 点旋转与抛物线相交与另一点P ,请找出抛物线上所有满足到直线AB距离为P .河北 周建杰 分类(2008年泰州市)29.已知二次函数y 1=ax 2+bx +c (a ≠0)的图像经过三点(1,0),(-3,0),(0,-23). (1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分) (2)若反比例函数y 2=x2(x >0)的图像与二次函数y 1=ax 2+bx +c (a ≠0)的图像在第一象限内交于点A (x 0,y 0),x 0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;(4分) (3)若反比例函数y 2=xk(x >0,k >0)的图像与二次函数y 1=ax 2+bx +c (a ≠0)的图像在第一象限内的交点A ,点A 的横坐标x 0满足2<x 0<3,试求实数k 的取值范围.(5分)(2008年南京市)28.(10分)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为(h)x ,两车之间的距离.......为(km)y ,图中的折线表示y 与x 之间的函数关系.根据图象进行以下探究: 信息读取(1)甲、乙两地之间的距离为 km ; (2)请解释图中点B 的实际意义; 图象理解(3)求慢车和快车的速度;(4)求线段BC 所表示的y 与x 之间的函数关系式,并写出自变量x 的取值范围; 问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?(2008年巴中市)已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E .(1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?第29题图(第28题)y(2008年自贡市)抛物线)0(2≠++=a c bx ax y 的顶点为M ,与x 轴的交点为A 、B (点B 在点A 的右侧),△ABM 的三个内角∠M 、∠A 、∠B 所对的边分别为m 、a 、b 。
08年全国中考数学压轴题精选(3)(含答案)

2008年全国中考数学压轴题精选精析(三)25.(08江西南昌)24.如图,抛物线2212191128y ax ax P y ax ax ⎛⎫=--+-=-- ⎪⎝⎭经过点且与抛物线,,相交于A B ,两点. (1)求a 值;(2)设211y ax ax =--+与x 轴分别交于M N ,两点(点M 在点N 的左边),221y ax ax =--与x 轴分别交于E F ,两点(点E 在点F 的左边),观察M N E F ,,,四点的坐标,写出一条正确的结论,并通过计算说明;(3)设A B ,两点的横坐标分别记为A B x x ,,若在x 轴上有一动点(0)Q x ,,且A B x x x ≤≤,过Q 作一条垂直于x 轴的直线,与两条抛物线分别交于C ,D 两点,试问当x 为何值时,线段CD 有最大值?其最大值为多少?(08江西南昌24题解析)24.解:(1)点1928P ⎛⎫- ⎪⎝⎭,在抛物线211y ax ax =--+上,1191428a a ∴-++=, ·············································································· 2分 解得12a =. ··························································································· 3分(2)由(1)知12a =,∴抛物线2111122y x x =--+,2211122y x x =--. ····· 5分当2111022x x --+=时,解得12x =-,21x =. 点M 在点N 的左边,2M x ∴=-,1N x =. ·········· 6分 当2111022x x --=时,解得31x =-,42x =. 点E 在点F 的左边,1E x ∴=-,2F x =. ················································ 7分0M F x x +=,0N E x x +=,∴点M 与点F 对称,点N 与点E 对称. ······················································ 8分(3)102a =>. ∴抛物线1y 开口向下,抛物线2y 开口向上. ·············· 9分根据题意,得12CD y y =-22211111122222x x x x x ⎛⎫⎛⎫=--+---=-+ ⎪ ⎪⎝⎭⎝⎭. ········································· 11分A B x x x ≤≤,∴当0x =时,CD 有最大值2. ········································ 12分说明:第(2)问中,结论写成“M N ,,E F ,四点横坐标的代数和为0”或“MN EF =”均得1分.26.(08江西南昌)25.如图1,正方形ABCD 和正三角形EFG 的边长都为1,点E F ,分别在线段AB AD ,上滑动,设点G 到CD 的距离为x ,到BC 的距离为y ,记HEF ∠为α(当点E F ,分别与B A ,重合时,记0α=). (1)当0α=时(如图2所示),求x y ,的值(结果保留根号);(2)当α为何值时,点G 落在对角形AC 上?请说出你的理由,并求出此时x y ,的值(结果保留根号);(3)请你补充完成下表(精确到0.01):154560750.03 0 0.290.290.130.03(4)若将“点E F ,分别在线段AB AD ,上滑动”改为“点E F ,分别在正方形ABCD 边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点G 运动所形成的大致图形.62621.732sin150.259sin 750.96644-+==,≈,≈.)A (F DH DA(08江西南昌25题解析)25.解:(1)过G 作MN AB ⊥于M 交CD 于N ,GK BC ⊥于K .60ABG ∠=,1BG =,2MG ∴=,12BM =. ········································································· 2分12x ∴=-,12y =. ············································································ 3分 (2)当45α=时,点G 在对角线AC 上,其理由是: ··································· 4分 过G 作IQ BC ∥交AB CD ,于I Q ,, 过G 作JP AB ∥交AD BC ,于J P ,.AC 平分BCD ∠,GP GQ ∴=,GI GJ ∴=.GE GF =,Rt Rt GEI GFJ ∴△≌△,GEI GFJ ∴∠=∠.60GEF GFE ∠=∠=,AEF AFE ∴∠=∠. 90EAF ∠=,45AEF AFE ∴∠=∠=.即45α=时,点G 落在对角线AC 上. ······················································· 6分 (以下给出两种求x y ,的解法) 方法一:4560105AEG ∠=+=,75GEI ∴∠=.在Rt GEI △中,6sin 754GI GE +==,14GQ IQ GI ∴=-=-. ······························································· 7分1x y ∴== ··········································································· 8分方法二:当点G 在对角线AC 上时,有122+=, ·············································································· 7分 B (EA (FDQ解得6214x +=-6214x y +∴==-. ··········································································· 8分 (3)α153045607590x0.130.030 0.030.130.29 0.50 y0.50 0.29 0.13 0.03 00.03 0.13······················································· 10分 (4)由点G 所得到的大致图形如图所示: ·············································································· 12分说明:1.第(2)问回答正确的得1分,证明正确的得2分,求出x y ,的值各得1分;2.第(3)问表格数据,每填对其中4空得1分;3.第(4)问图形画得大致正确的得2分,只画出图形一部分的得1分. 27.(08山东滨州)23、(1)探究新知:如图1,已知△ABC 与△ABD 的面积相等,试判断AB 与CD 的位置关系,并说明理由.BDCA(2)结论应用:①如图2,点M 、N 在反比例函数y=)0(>k xk的图象上,过点M 作ME ⊥y 轴,过点N 作NF ⊥x 轴,垂足分别为E ,F. 试应用(1)中得到的结论证明:MN ∥EF.H AC DBy xONMF E②若①中的其他条件不变,只改变点M ,N 的位置如图3所示,请判断MN 与E 是否平行.(08山东滨州23题解析)23.(1)证明:分别过点C 、D 作.CG AB DH AB ⊥⊥、 垂足为G 、H ,则090.CGA DHB ∠=∠=CG DHABC ABD ∴∴∴∴与的面积相等CG=DH四边形CGHD 为平行四边形AB CD.(2)①证明:连结MF ,NE设点M 的坐标为11(,)x y ,点N 的坐标为22(,)x y , ∵点M ,N 在反比例函数()0ky k x=的图象上,∴11x y k =,22x y k =2,ME y NF x OF x ⊥⊥∴=1轴,轴OE=y112211221122EFM EFN EFM EFN Sx y k S x y k S S ∴====∴=由(1)中的结论可知:MN ∥EF 。
2008年全国各地中考试题压轴题精选讲座四

2008年全国各地中考试题压轴题精选讲座四抛物线与几何问题【知识纵横】抛物线的解析式有下列三种形式:1、一般式:2y ax bx c =++(a ≠0);2、顶点式:y =a(x—h) 2-+k ;3、交点式:y=a(x —x 1)(x —x 2 ) ,这里x 1、x 2 是方程ax 2 +bx+c=0的两个实根。
解函数与几何的综合题,善于求点的坐标,进而求出函数解析式是解题的基础;而充分发挥形的因素,数形互动,把证明与计算相结合是解题的关键。
【典型例题】【例1】 (浙江杭州) 在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b )。
平移二 次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B ,C 两点(∣OB ∣<∣OC ∣),连结A ,B 。
(1)是否存在这样的抛物线F ,OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO=23,求抛物线F 对应的二次函数的解析式。
【思路点拨】(1)由关系式OC OB OA ⋅=2来构建关于t 、b 的方程;(2)讨论t 的取值范围,来求抛物线F 对应的二次函数的解析式。
【例2】(江苏常州)如图,抛物线24y x x =+与x 轴分别相交于点B 、O,它的顶点为A,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l,设P 是直线l 上一动点.(1)求点A 的坐标;(2)以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3)设以点A 、B 、O 、P 为顶点的四边形的面积为S, 点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.【思路点拨】(3)可求得直线l 的函数关系式是y=-2x ,所以应讨论①当点P 在第二象限时,x<0、 ②当点P 在第四象限是,x>0这二种情况。
2008年全国各地中考试题压轴题精选讲座四抛物线与几何问题-1

抛物线与几何问题的参考答案【典型例题】【例1】 (浙江杭州)(1)∵ 平移2tx y -=的图象得到的抛物线F 的顶点为Q , ∴ 抛物线F 对应的解析式为:b t x t y +--=2)(. ∵ 抛物线与x 轴有两个交点,∴0>b t .令0=y , 得-=t OB t b,+=t OC tb , ∴ -=⋅t OC OB (|||||tb)( +t t b )|-=2|t 22|OA t tb == , 即22tt t b ±=-, 所以当32t b =时, 存在抛物线F 使得||||||2OC OB OA ⋅=.-- 2分 (2) ∵BC AQ //, ∴ b t =, 得F : t t x t y +--=2)(,解得1,121+=-=t x t x . 在∆Rt AOB 中,1) 当0>t 时,由 ||||OC OB <, 得)0,1(-t B , 当01>-t 时, 由=∠ABO tan 23=||||OB OA =1-t t , 解得3=t , 此时, 二次函数解析式为241832-+-=x x y ; 当01<-t 时, 由=∠ABO tan 23=||||OB OA =1+-t t , 解得=t 53, 此时,二次函数解析式为-=y 532x +2518x +12548. 2) 当0<t 时, 由 ||||OC OB <, 将t -代t , 可得=t 53-, 3-=t ,(也可由x -代x ,y -代y 得到) 所以二次函数解析式为 =y 532x +2518x –12548或241832++=x x y . 【例2】(江苏常州) (1)∵4)2(422-+=+=x x x y ∴A(-2,-4)(2)四边形ABP 1O 为菱形时,P 1(-2,4)四边形ABOP 2为等腰梯形时,P 1(5452-,) 四边形ABP 3O 为直角梯形时,P 1(5854,-)四边形ABOP 4为直角梯形时,P 1(51256-,)(3)由已知条件可求得AB 所在直线的函数关系式是y=-2x-8,所以直线l 的函数关系式是y=-2x ①当点P 在第二象限时,x<0, △POB 的面积x x S POB 4)2(421-=-⨯⨯=∆ ∵△AOB 的面积84421=⨯⨯=∆AOBS , ∴)0(84<+-=+=∆∆x x S S S PO B AO B ∵286264+≤≤+S ,∴⎪⎩⎪⎨⎧+≤+≥286264S S 即⎪⎩⎪⎨⎧+≤+-+≥+-2868426484x x ∴⎪⎪⎩⎪⎪⎨⎧-≤-≥22412232S x∴x 的取值范围是22322241-≤≤-x ②当点P 在第四象限是,x>0,过点A 、P 分别作x 轴的垂线,垂足为A ′、P ′ 则四边形POA ′A 的面积44)2(21)2(224+=⋅⋅-+⋅+=-='∆'''x x x x x S S S O P P A A P 梯形P A A PO ∵△AA ′B 的面积42421=⨯⨯='∆B A A S∴)0(84>+=+='∆'x x S S S B A A A A PO ∵286264+≤≤+S ,∴⎪⎩⎪⎨⎧+≤+≥286264S S 即⎪⎩⎪⎨⎧+≤++≥+2868426484x x ∴⎪⎪⎩⎪⎪⎨⎧-≤-≥21242223S x ∴x 的取值范围是21242223-≤≤-x【例3】(浙江丽水)(1)设O A 所在直线的函数解析式为kx y =,∵A (2,4), ∴42=k , 2=∴k ,∴O A 所在直线的函数解析式为2y x =(2)①∵顶点M 的横坐标为m ,且在线段O A 上移动,∴2y m =(0≤m ≤2).∴顶点M 的坐标为(m ,2m ).∴抛物线函数解析式为2()2y x m m=-+. ∴当2=x 时,2(2)2y m m=-+224m m =-+(0≤m ≤2). ∴点P 的坐标是(2,224m m -+). ② ∵PB =224m m -+=2(1)3m -+, 又∵0≤m ≤2, ∴当1m =时,PB 最短(3)当线段PB 最短时,此时抛物线的解析式为()212+-=x y .假设在抛物线上存在点Q ,使Q M A P M AS S =. 设点Q 的坐标为(x ,223x x -+). ①当点Q 落在直线O A 的下方时,过P 作直线PC //AO ,交y 轴于点C , ∵3P B =,4AB =,(第24题)∴1A P =,∴1O C =,∴C 点的坐标是(0,1-).∵点P 的坐标是(2,3),∴直线PC 的函数解析式为2=x y ∵Q M A P M A S S =,∴点Q 落在直线12-=x y 上. ∴223x x -+=21x -. 解得122,2x x ==,即点Q (2,3). ∴点Q 与点P 重合.∴此时抛物线上不存在点Q ,使△QMA 与△A P M 的面积相等.②当点Q 落在直线O A 的上方时,作点P 关于点A 的对称称点D ,过D 作直线DE //AO ,交y 轴于点E ,∵1A P =,∴1E OD A ==,∴E 、D 的坐标分别是(0,1),(2,5), ∴直线DE 函数解析式为12+=x y . ∵Q M A P M AS S =,∴点Q 落在直线12+=x y 上. ∴223x x -+=21x +. 解得:122x =+222x =-. 代入12+=x y ,得1522y =+,2522y =- ∴此时抛物线上存在点(12Q ,()225,222--Q 使△QMA 与△P M A 的面积相等.综上所述,抛物线上存在点(12Q ,()225,222--Q 使△QMA 与△P M A 的面积相等.【例4】(广东省深圳市)(1)方法一:由已知得:C (0,-3),A (-1,0)将A 、B 、C 三点的坐标代入得⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a解得:⎪⎩⎪⎨⎧-=-==321c b a所以这个二次函数的表达式为:322--=x x y (2)存在,F 点的坐标为(2,-3)易得D (1,-4),所以直线CD 的解析式为:3--=x y∴E 点的坐标为(-3,0) ∵以A 、C 、E 、F 为顶点的四边形为平行四边形∴F 点的坐标为(2,-3)或(―2,―3)或(-4,3) 代入抛物线的表达式检验,只有(2,-3)符合∴存在点F ,坐标为(2,-3)(3)如图,①当直线MN 在x 轴上方时,设圆的半径为R (R>0),则N (R+1,R ), 代入抛物线的表达式,解得2171+=R ②当直线MN 在x 轴下方时,设圆的半径为r (r>0), 则N (r+1,-r ),代入抛物线的表达式,解得2171+-=r∴圆的半径为2171+或2171+-. (4)过点P 作y 轴的平行线与AG 交于点Q , 易得G (2,-3),直线AG 为1--=x y .设P (x ,322--x x ),则Q (x ,-x -1),PQ 22++-=x x .3)2(212⨯++-=+=∆∆∆x x S S S GPQ APQ APG 当21=x 时,△APG 的面积最大 此时P 点的坐标为⎪⎭⎫⎝⎛-415,21,827的最大值为APG S ∆.【例5】(山东济南)(1)设抛物线的解析式为2(1)3y a x =-- 将A (-1,0)代入: 20(11)3a =--- ∴ 34a =∴ 抛物线的解析式为23(1)34y x =--,即:2339424y x x =--(2)是定值,1PM PNBE AD+= ∵ AB 为直径,∴ ∠AEB =90°,∵ PM ⊥AE ,∴ PM ∥BE∴ △APM ∽△ABE ,∴ PM APBE AB =① 同理:PN PB AD AB = ② ① + ②:1PM PN AP PBBE AD AB AB+=+=(3)∵ 直线EC 为抛物线对称轴,∴ EC 垂直平分AB ∴ EA =EB ∵ ∠AEB =90°∴ △AEB 为等腰直角三角形. ∴ ∠EAB =∠EBA =45° ....................... 7分如图,过点P 作PH ⊥BE 于H ,由已知及作法可知,四边形PHEM 是矩形, ∴PH =ME 且PH ∥ME 在△APM 和△PBH 中 ∵∠AMP =∠PHB =90°, ∠EAB =∠BPH =45° ∴ PH =BH且△APM ∽△PBH∴ PA PM PB BH=∴PA PM PMPB PH ME==① 在△MEP 和△EGF 中,∵ PE ⊥FG , ∴ ∠FGE +∠SEG =90° ∵∠MEP +∠SEG =90° ∴ ∠FGE =∠MEP ∵ ∠PME =∠FEG =90° ∴△MEP ∽△EGF ∴PM EF ME EG = ② 由①、②知:PA EFPB EG=【学力训练】 1、(广东梅州)(1) DC ∥AB ,AD =DC =CB ,∴ ∠CDB =∠CBD =∠DBA ,∠DAB =∠CBA , ∴∠DAB =2∠DBA ,∠DAB +∠DBA =90, ∴∠DAB =60, ∠DBA =30, AB =4, ∴DC =AD =2, R t ∆AOD ,OA =1,OD =3,∴A (-1,0),D (0, 3),C (2, 3).(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A (-1,0),B (3,0), 故可设所求为 y =a (x +1)( x -3) 将点D (0,3)的坐标代入上式得, a =33-. 所求抛物线的解析式为 y =).3)(1(33-+-x x 其对称轴L 为直线x =1. (3) ∆PDB 为等腰三角形,有以下三种情况:①因直线L 与DB 不平行,DB 的垂直平分线与L 仅有一个交点P 1,P 1D =P 1B , ∆P 1DB 为等腰三角形; ②因为以D 为圆心,DB 为半径的圆与直线L 有两个交点P 2、P 3,DB =DP 2,DB =DP 3, ∆P 2DB , ∆P 3DB 为等腰三角形;③与②同理,L 上也有两个点P 4、P 5,使得 BD =BP 4,BD =BP 5.由于以上各点互不重合,所以在直线L 上,使∆PDB 为等腰三角形的点P 有5个. 2、(广东肇庆)(1)由5x x 122+=0,(1分)得01=x ,5122-=x .∴抛物线与x 轴的交点坐标为(0,0)、(512-,0).(3分) (2)当a =1时,得A (1,17)、B (2,44)、C (3,81), 分别过点A 、B 、C 作x 轴的垂线,垂足分别为D 、E 、F ,则有ABC S ∆=S ADFC 梯形 -ADEB S 梯形 -BEFC S 梯形=22)8117(⨯+-21)4417(⨯+-21)8144(⨯+=5(个单位面积)(3)如:)(3123y y y -=.事实上,)3(12)3(523a a y ⨯+⨯= =45a 2+36a . 3(12y y -)=3[5×(2a )2+12×2a -(5a 2+12a )] =45a 2+36a . ∴)(3123y y y -=. 3、(青海西宁)(1)圆心1O 的坐标为(20),,1O 半径为1,(10)A ∴,,(30)B ,……1分 二次函数2y x bx c =-++的图象经过点A B ,,∴可得方程组10930b c b c -++=⎧⎨-++=⎩解得:43b c =⎧⎨=-⎩∴二次函数解析式为243y x x =-+-(2)过点M 作MF x ⊥轴,垂足为F . OM 是1O 的切线,M 为切点,1O M OM ∴⊥(圆的切线垂直于经过切点的半径).在1Rt OO M △中,1111sin 2O M O OM OO ∠== 1O OM ∠为锐角,130OOM ∴∠=1cos302OM OO ∴===在Rt MOF △中,3cos3032OF OM ===. 13sin 3032MF OM ===. ∴点M 坐标为332⎛ ⎝⎭,设切线OM 的函数解析式为(0)y kx k =≠,332k =,3k ∴=∴切线OM 的函数解析式为y x =(3)存在.①过点A 作1AP x ⊥轴,与OM 交于点1P .可得11Rt Rt APO MOO △∽△(两角对应相等两三角形相似)113tan tan 303P A OA AOP =∠==,113P ⎛∴ ⎝⎭, ②过点A 作2AP OM ⊥,垂足为2P ,过2P 点作2P H OA ⊥,垂足为H . 可得21Rt Rt APO O MO △∽△(两角对应相等两三角开相似) 在2Rt OP A △中,1OA =,23cos302OP OA ∴==,在2Rt OPH △中,223cos 4OH OPAOP =∠==,2221sin 224P H OP AOP =∠==,234P ⎛∴ ⎝⎭∴符合条件的P 点坐标有13⎛⎝⎭,,344⎛ ⎝⎭, 4、(辽宁12市) 解:(1)直线y =x 轴交于点A ,与y 轴交于点C .(10)A ∴-,,(0C点A C ,都在抛物线上,0a c c⎧=++⎪∴⎨⎪=⎩a c ⎧=⎪∴⎨⎪=⎩ ∴抛物线的解析式为23y x x =顶点1F ⎛ ⎝⎭ (2)存在1(03)P 2(23)P (3)存在理由: 解法一:延长BC 到点B ',使B C BC '=,连接B F '交直线AC 于 点M ,则点M 就是所求的点.过点B '作B H AB '⊥于点H .B点在抛物线2y x x =(30)B ∴,在Rt BOC △中,tan OBC ∠=, 30OBC ∴∠=,BC =在Rt BB H '△中,12B H BB ''==6BH H '=,3OH ∴=,(3B '∴--,设直线B F '的解析式为y kx b =+A OxyBF CHBM33k b k b ⎧-=-+⎪∴⎨-=+⎪⎩解得2k b ⎧=⎪⎪⎨⎪=-⎪⎩62y x ∴=-y y x ⎧=⎪∴⎨=⎪⎩解得37x y ⎧=⎪⎪⎨⎪=⎪⎩37M ⎛∴ ⎝⎭, ∴在直线AC 上存在点M ,使得MBF △的周长最小,此时377M ⎛- ⎝⎭,.5、(四川资阳) (1) ∵以AB 为直径作⊙O′,交y 轴的负半轴于点C , ∴∠OCA+∠OCB=90°, 又∵∠OCB+∠OBC=90°, ∴∠OCA=∠OBC ,又∵∠AOC= ∠COB=90°, ∴ΔAOC ∽ ΔCOB , ∴OA OC OC OB=. 又∵A(–1,0),B(9,0),∴19OC OC =,解得OC=3(负值舍去). ∴C(0,–3),设抛物线解析式为y=a(x+1)(x –9),∴–3=a(0+1)(0–9),解得a=13,∴二次函数的解析式为y=13(x+1)(x –9),即y=13x 2–83x –3.(2) ∵AB 为O′的直径,且A(–1,0),B(9,0), ∴OO′=4,O′(4,0),∵点E 是AC 延长线上一点,∠BCE 的平分线CD 交⊙O′于点D ,∴∠BCD=12∠BCE=12×90°=45°,连结O′D 交BC 于点M ,则∠BO′D =2∠BCD=2×45°=90°,OO′=4,O′D=12AB=5. ∴D(4,–5).∴设直线BD 的解析式为y=kx+b (k≠0) ∴90,4 5.k b k b +=⎧⎨+=-⎩解得1,9.k b =⎧⎨=-⎩∴直线BD 的解析式为y=x –9.(3) 假设在抛物线上存在点P ,使得∠PDB=∠CBD ,图10设射线DP交⊙O′于点Q,则BQ CD=.分两种情况(如答案图1所示):①∵O′(4,0),D(4,–5),B(9,0),C(0,–3).∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,因此,点Q1(7,–4)符合BQ CD=,∵D(4,–5),Q1(7,–4),∴用待定系数法可求出直线DQ1解析式为y=13x–193.解方程组211933183.33y xy x x⎧=-⎪⎪⎨⎪=--⎪⎩,得11xy⎧=⎪⎪⎨⎪=⎪⎩22xy⎧⎪⎪⎨⎪⎪⎩∴点P1坐标为),[坐标为)不符合题意,舍去].②∵Q1(7,–4),∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合BQ CD=.∵D(4,–5),Q2(7,4).∴用待定系数法可求出直线DQ2解析式为y=3x–17.解方程组2317183.33y xy x x=-⎧⎪⎨=--⎪⎩,得1138xy=⎧⎨=-⎩,;221425.xy=⎧⎨=⎩,∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].∴符合条件的点P有两个:P1941+2941-+,P2(14,25).6、(辽宁沈阳)(1)点E在y轴上理由如下:连接AO,如图所示,在Rt ABO△中,1AB =,BO=,2AO∴=1sin2AOB∴∠=,30AOB∴∠=由题意可知:60AOE∠=306090BOE AOB AOE∴∠=∠+∠=+=点B在x轴上,∴点E在y轴上.(2)过点D作DM x⊥轴于点M1OD =,30DOM∠=∴在Rt DOM△中,12DM=,2OM=点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭,由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),点A的坐标为(抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A,122D ⎛⎫⎪ ⎪⎝⎭,代入22y ax bx =++中得321331242a a ⎧-+=⎪⎨++=⎪⎩ 解得89539a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为:285329y x x =-+(3)存在符合条件的点P ,点Q .10分 理由如下:矩形ABOC 的面积3AB BO ==∴以O B P Q ,,,为顶点的平行四边形面积为23由题意可知OB 为此平行四边形一边, 又3OB =OB ∴边上的高为2依题意设点P 的坐标为(2)m ,点P在抛物线2829y x =-+上28229m ∴-+=解得,10m =,28m =-1(02)P ∴,,228P ⎛⎫- ⎪ ⎪⎝⎭以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,PQ OB == ∴当点1P 的坐标为(02),时, 点Q的坐标分别为1(Q,2Q ;当点2P的坐标为28⎛⎫- ⎪ ⎪⎝⎭时,点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭,42Q ⎫⎪⎪⎝⎭.7、(苏州市) (1)OH =1;k =33,b =332;(2)设存在实数a ,是抛物线y =a(x +1)(x -5)上有一点E ,满足以D 、N 、E 为顶点的三角形与等腰直角△AOB 相似∴以D 、N 、E 为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以DN 为直角边的等腰直角三角形,另一类是以DN 为斜边的等腰直角三角形. ①若DN 为等腰直角三角形的直角边,则ED ⊥DN . 由抛物线y =a(x +1)(x -5)得:M(-1,0),N(5,0) ∴D(2,0),∴ED =DN =3,∴E 的坐标是(2,3). 把E(2,3)代入抛物线解析式,得a =31- ∴抛物线解析式为y =31-(x +1)(x -5) 即y =31-x 2+34x +35②若DN 为等腰直角三角形的斜边,则DE ⊥EN ,DE =EN . ∴E 的坐标为(3.5,1.5)把E(3.5,1.5)代入抛物线解析式,得a =92-.∴抛物线解析式为y =92-(x +1)(x -5),即y =92-x 2+98x +910当a =31-时,在抛物线y =31-x 2+34x +35上存在一点E(2,3)满足条件,如果此抛物线上还有满足条件的E 点,不妨设为E ’点,那么只有可能△DE ’N 是以DN 为斜边的等腰直角三角形,由此得E ’(3.5,1.5).显然E ’不在抛物线y =31-x 2+34x +35上,因此抛物线y =31-x 2+34x +35上没有符合条件的其他的E 点.当a =92-时,同理可得抛物线y =92-x 2+98x +910上没有符合条件的其他的E 点.当E 的坐标为(2,3),对应的抛物线解析式为y =31-x 2+34x +35时.∵△EDN 和△ABO 都是等腰直角三角形,∴∠GNP =∠PBO =45°. 又∵∠NPG =∠BPO ,∴△NPG ∽△BPO . ∴PBPN POPG=,∴PB ·PG =PO ·PN =2×7=14,∴总满足PB ·PG <210.当E 的坐标为(3.5,1.5),对应的抛物线解析式为y =92-x 2+98x +910时,同理可证得:PB ·PG =PO ·PN =2×7=14,∴总满足PB ·PG <210.。
2008年全国各地中考试题压轴题精选讲座三几何问题

函数及图像与几何问题的参考答案【典型例题】【例1】(山西太原)(1)在1y x =+中,当0y =时,10x +=,1x ∴=-,点B 的坐标为(10)-,.在334y x =-+中,当0y =时,33044x x -+=∴=,,点C 的坐标为(4,0).由题意,得1334y x y x =+⎧⎪⎨=-+⎪⎩,.解得87157x y ⎧=⎪⎪⎨⎪=⎪⎩,. ∴点A 的坐标为81577⎛⎫⎪⎝⎭,.(2)当CBD △为等腰三角形时,有以下三种情况,如图(1).设动点D 的坐标为()x y ,.由(1),得(10)(40)B C -,,,,5BC ∴=. ①当11BD D C =时,过点1D 作11D M x ⊥轴,垂足为点1M ,则1112BM M C BC ==. 11553312222BM OM x ∴==-==,,.33153428y ∴=-⨯+=,点1D 的坐标为31528⎛⎫⎪⎝⎭,.②当2BC BD =时,过点2D 作22D M x ⊥轴,垂足为点2M ,则2222222D M M B D B +=.21M B x =--,2223354D M x D B =-+=,,2223(1)354x x ⎛⎫∴--+-+= ⎪⎝⎭.解,得121245x x =-=,(舍去).此时,312243455y ⎛⎫=-⨯-+= ⎪⎝⎭. A yx y xD 2图(1)图(2) D1 CD 4D 3 M 2 M 1 O B B OCA D 1D 2E 1E 2M 4∴点2D 的坐标为122455⎛⎫- ⎪⎝⎭,.③当3CD BC =,或4C D B C =时,同理可得34(03)(83)D D -,,,.由此可得点D 的坐标分别为12343151224(03)(83)2855D D D D ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,,,,,,. (3)存在.以点E D O A ,,,为顶点的四边形是平行四边形有以下三种情形,如图(2). ①当四边形11AE OD为平行四边形时,1120BE CD =②当四边形21AD E O为平行四边形时,1210BE CD =③当四边形12AOD E为平行四边形时,2120BE CD =. 【例2】(浙江湖州)(1)证明:设11()E x y ,,22()F x y ,,AOE △与FOB △的面积分别为1S ,2S ,由题意得11ky x =,22k y x =.1111122S x y k ∴==,2221122S x y k ==. 12S S ∴=,即AOE △与FOB △的面积相等.(2)由题意知:E F ,两点坐标分别为33k E ⎛⎫⎪⎝⎭,,44k F ⎛⎫ ⎪⎝⎭,,1111432234ECF S EC CF k k ⎛⎫⎛⎫∴==-- ⎪⎪⎝⎭⎝⎭△, 11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S ∴=---=---=--△△△△△△矩形11112212243234OEF ECF ECF S S S k S k k k ⎛⎫⎛⎫∴=-=--=--⨯-- ⎪⎪⎝⎭⎝⎭△△△2112S k k ∴=-+. 当161212k =-=⎛⎫⨯- ⎪⎝⎭时,S 有最大值.131412S -==⎛⎫⨯- ⎪⎝⎭最大值.(3)解:设存在这样的点F ,将CEF △沿EF 对折后,C 点恰好落在OB 边上的M 点,过点E 作EN OB ⊥,垂足为N .由题意得:3EN AO ==,143EM EC k ==-,134MF CF k ==-, 90EMN FMB FMB MFB ∠+∠=∠+∠=,EMN MFB ∴∠=∠.又90ENM MBF ∠=∠=,ENM MBF ∴△∽△.EN EM MB MF ∴=,11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭∴==⎛⎫-- ⎪⎝⎭, 94MB ∴=. 222MB BF MF +=,222913444k k ⎛⎫⎛⎫⎛⎫∴+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得218k =.21432k BF ∴==. ∴存在符合条件的点F ,它的坐标为21432⎛⎫⎪⎝⎭,.【例3】(浙江嘉兴)(1)(20)A ,,2OA ∴=.作BG OA ⊥于G ,OAB △为正三角形,1OG ∴=,3BG .3)B ∴,.连AC ,90AOC ∠=,60ACO ABO ∠=∠=,2tan 303OC OA∴==. 03C ⎛⎫∴ ⎪ ⎪⎝⎭,.(2)90AOC ∠=,AC ∴是圆的直径,又CD 是圆的切线,CD AC ∴⊥.30OCD ∴∠=,2tan 303OD OC ==.203D ⎛⎫∴- ⎪⎝⎭,. 设直线CD 的函数解析式为(0)y kx b k =+≠,(第24题)则3203b k b⎧=⎪⎪⎨⎪=-+⎪⎩,解得k b ⎧=⎪⎨=⎪⎩∴直线CD的函数解析式为3y =+. (3)2AB OA ==,23OD =,423CD OD ==,BC OC ==, ∴四边形ABCD的周长6. 设AE t =,AEF △的面积为S ,则33AF t =+-,13sin 6032S AF AE t ⎛⎫==- ⎪ ⎪⎝⎭. 2333937333S t t t ⎛⎫⎛+=-=-++ ⎪ ⎪ ⎢⎥⎝⎭⎝⎭⎣⎦. ∴当t =时,max 7338S =.点E F ,分别在线段AB AD ,上,02320323tt ⎧⎪∴⎨-+⎪⎩≤≤≤≤132t +≤. 9t +=2t ≤≤, AEF ∴△38. 【例4】(杭州市)(1)设动点出发t 秒后,点P 到达点A 且点Q 正好到达点C 时,BC BA t ==,则1630,102BPQ S t t ∆=⨯⨯=∴=(秒)则()()10,2BA cm AD cm ==; (2)可得坐标为()()10,30,12,30M N (3)当点P 在BA 上时,()213sin 010210y t t B t t =⨯⨯⨯=≤<;当点P 在DC 上时,()()1101859012182y t t t =⨯⨯-=-+<≤ 图象略.【学力训练】1. (07台州市)(1)OCD △与ADE △相似. 理由如下:由折叠知,90CDE B ∠=∠=°,1290∠+∠=∴°,13902 3.∠+∠=∴∠=∠,又90COD DAE ∠=∠=∵°, OCD ADE ∴△∽△. (2)3tan 4AE EDA AD ∠==∵,∴设3AE t =, 则4AD t =.由勾股定理得5DE t =.358OC AB AE EB AE DE t t t ==+=+=+=∴.由(1)OCD ADE △∽△,得OC CDAD DE=, 845t CD t t =∴, 10CD t =∴.在DCE △中,222CD DE CE +=∵,222(10)(5)(55)t t +=∴,解得1t =.83OC AE ==∴,,点C 的坐标为(08),,点E 的坐标为(103),, 设直线CE 的解析式为y kx b =+,1038k b b +=⎧⎨=⎩,∴,解得128k b ⎧=-⎪⎨⎪=⎩,,182y x =-+∴,则点P 的坐标为(160),.(3)满足条件的直线l 有2条:212y x =-+,212y x =-. 画出两条直线(图略).2、(浙江衢州)(1) ∵A ,B 两点的坐标分别是A(10,0)和B(8,32),∴381032OAB tan =-=∠,∴︒=∠60OAB当点A ´在线段AB 上时,∵︒=∠60OAB ,TA=TA ´, ∴△A ´TA 是等边三角形,且A T TP '⊥, ∴)t 10(2360sin )t 10(T P -=︒-=,)t 10(21AT 21AP P A -===',∴2TPA )t 10(83T P P A 21S S -=⋅'=='∆, 当A ´与B 重合时,AT=AB=460sin 32=︒,所以此时10t 6<≤。
2008年全国中考数学压轴题精选(5)(含答案)

2008年全国中考数学压轴题精选精析(五)1.(08云南双柏)25.(本小题(1)~(3)问共12分;第(4)、(5)问为附加题10分,每小题5分已知:抛物线y =ax 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,其中点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB 、OC 的长(OB <OC )是方程x 2-10x +16=0的两个根,且抛物线的对称轴是直线x =-2.(1)求A 、B 、C 三点的坐标; (2)求此抛物线的表达式; (3)求△ABC 的面积;(4)若点E 是线段AB 上的一个动点(与点A 、点B 不重合),过点E 作EF ∥AC 交BC 于点F ,连接CE ,设AE 的长为m ,△CEF 的面积为S ,求S 与m 之间的函数关系式,并写出自变量m 的取值范围;(5)在(4)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由.2. (08浙江湖州)24.(本小题12分)已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B C,重合),过F点的反比例函数(0)ky k x=>的图象与AC 边交于点E . (1)求证:AOE △与BOF △的面积相等; (2)记OEF ECF SS S =-△△,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将CEF △沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.3.(08浙江嘉兴)24.如图,直角坐标系中,已知两点(00)(20)O A ,,,,点B 在第一象限且OAB △为正三角形,OAB △的外接圆交y 轴的正半轴于点C ,过点C 的圆的切线交x 轴于点D .(1)求B C ,两点的坐标; (2)求直线CD 的函数解析式; (3)设E F ,分别是线段AB AD ,上的两个动点,且EF 平分四边形ABCD 的周长.试探究:AEF △的最大面积?4.(08浙江丽水)24.如图,在平面直角坐标系中,已知点A 坐标为(2,4),直线2=x与x 轴相交于点B ,连结OA ,抛物线2x y =从点O 沿OA 方向平移,与直线2=x交于点P ,顶点M到A 点时停止移动. (1)求线段OA所在直线的函数解析式; (2)设抛物线顶点M 的横坐标为m , ①用m 的代数式表示点P 的坐标; ②当m 为何值时,线段PB 最短;(3)当线段PB 最短时,相应的抛物线上是否存在点Q ,使△QMA 的面积与△PMA 的面积相等,若存在,请求出点Q 的坐标;若 不存在,请说明理由.5.(08浙江衢州)24、(本题14分)已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,32),C(0,32),点T 在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点A ′),折痕经过点T ,折痕TP 与射线AB 交于点P ,设点T 的横坐标为t ,折叠后纸片重叠部分(图中的阴影部分)的面积为S ; (1)求∠OAB 的度数,并求当点A ′在线段AB 上时,S 关于t 的函数关系式; (2)当纸片重叠部分的图形是四边形时,求t 的取值范围;(3)S 存在最大值吗?若存在,求出这个最大值,并求此时t 的值;若不存在,请说明理由。
中考数学压轴题讲解分析:一次函数与几何综合问题.doc

中考数学压轴题讲解分析:一次函数与几何综合问题下面我们先来看一道典型例题。
中考数学,一次函数与几何相关综合题,典型例题分析1:如图,已知一次函数y=-x+7与正比例函数y=4x/3的图象交于点A,且与x轴交于点B.(1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O﹣C﹣A 的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA 或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.考点分析:一次函数综合题.题干分析:(1)根据图象与坐标轴交点求法直接得出即可,再利用直线交点坐标求法将两直线解析式联立即可得出交点坐标;(2)①利用S梯形ACOB-S△ACP-S△POR-S△ARB =8,表示出各部分的边长,整理出一元二次方程,求出即可;②根据一次函数与坐标轴的交点得出,∠OBN=∠ONB =45°,进而利用勾股定理以及等腰三角形的性质和直角三角形的判定求出即可。
解题反思:此题主要考查了一次函数与坐标轴交点求法以及三角形面积求法和等腰直角三角形的性质等知识,此题综合性较强,利用函数图象表示出各部分长度,再利用勾股定理求出是解决问题的关键。
动态综合问题一直是中考数学压轴题非常喜欢考查的内容,解决此类问题需要考生根据变量之间的关系,对动态几何中的“变量”进行分类讨论,如运动的点、运动的线等等。
考生要想正确解决此类问题,关键在于要抓住点与线的运动和变化,数量之间的关系也随之发生着变化,再把这些“变化”的几何问题就转化为函数问题。
中考数学,一次函数与几何相关综合题,典型例题分析2:如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B 不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.(1)用含t的式子表示点E的坐标为_______;(2)当t为何值时,∠OCD=180°?(3)当点C与点F不重合时,设△OCF的面积为S,求S与t之间的函数解析式.考点分析:一次函数综合题;相似三角形的判定与性质.题干分析:(1)由点B坐标为(0,8),可知OB=8,根据线段垂直平分线的定义可知:AE=4,从而求得:BE=t+4,故此点E 的坐标为(t+4,8);(2)过点D作DH⊥OF,垂足为H.先证明△OBA∽△AEC,由相似三角形的性质可知,EC/AB=AE/OB可求得EC=t/2,从而得到点C的坐标为(t+4,8﹣t/2),因为∠OCD=180°,CF∥DH,可知,OF/OH=FC/DH即从(t+4)/(t+8)=(8﹣t/2)/8而可解得t的值;(3)三角形OCF的面积=OF•FC/2从而可得S与t的函数关系式.解题反思:本题主要考查的是相似三角形的性质和判定,用含字母t 的式子表示点C的坐标是解题的关键。
2008年全国各地中考试题压轴题精选讲座四抛物线与几何问题

新世纪教育网 精品资料 版权所有@新世纪教育网2008年全国各地中考试题压轴题精选讲座四抛物线与几何问题【知识纵横】抛物线的解析式有下列三种形式:1、一般式:2y ax bx c =++(a ≠0);2、顶点式:y =a(x —h) 2-+k ;3、交点式:y=a(x —x 1)(x —x 2 ) ,这里x 1、x 2 是方程ax 2 +bx+c=0的两个实根。
解函数与几何的综合题,善于求点的坐标,进而求出函数解析式是解题的基础;而充分发挥形的因素,数形互动,把证明与计算相结合是解题的关键。
【典型例题】【例1】 (浙江杭州) 在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b )。
平移二 次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B ,C 两点(∣OB ∣<∣OC ∣),连结A ,B 。
(1)是否存在这样的抛物线F ,OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO=23,求抛物线F 对应的二次函数的解析式。
【思路点拨】(1)由关系式OC OB OA ⋅=2来构建关于t 、b 的方程;(2)讨论t 的取值范围,来求抛物线F 对应的二次函数的解析式。
【例2】(江苏常州)如图,抛物线24y x x =+与x 轴分别相交于点B 、O,它的顶点为A,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l,设P 是直线l 上一动点.(1)求点A 的坐标;(2)以点A 、B 、O 、P 为顶点的四边形中,有菱形、等 腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3)设以点A 、B 、O 、P 为顶点的四边形的面积为S, 点P 的横坐标为x,当46S +≤+,求x 的取值范围.【思路点拨】(3)可求得直线l 的函数关系式是y=-2x ,所以应讨论①当点P 在第二象限时,x<0、 ②当点P 在第四象限是,x>0这二种情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年中考试题压轴题精选讲座一-几何与函数问题“他山之石可以攻玉”【编者的话】新课改后的中考数学压轴题已从传统的考察知识点多、难度大、复杂程度高的综合题型,逐步转向数形结合、动态几何、动手操作、实验探究等方向发展。
这些压轴题题型繁多、题意创新,目的是考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等。
从数学思想的层面上讲:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想;(5)转化思想等。
但纵观全国各省、市的中考数学试题,它的压轴题均是借鉴于上年各地的中考试题演变而来。
所以,研究上年各地的中考试题,就能找到今年中考数学试题的热点的形成和命题的动向,它有利于我们教师在教学中研究对策,把握方向。
只的这样,学生能力得以的培养,解题方法、技巧得以掌握,学生才能顺利地解答未来中考的压轴题。
2008年全国各地中考试题压轴题精选讲座一几何与函数问题【知识纵横】- 2 -- 3 -客观世界中事物总是相互关联、相互制约的。
几何与函数问题就是从量和形的侧面去描述客观世界的运动变化、相互联系和相互制约性。
函数与几何的综合题,对考查学生的双基和探索能力有一定的代表性,通过几何图形的两个变量之间的关系建立函数关系式,进一步研究几何的性质,沟通函数与几何的有机联系,可以培养学生的数形结合的思想方法。
【典型例题】【例1】(上海市)已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域;(2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求 线段BE 的长.【思路点拨】(1)取AB 中点H ,联结MH ;(2)先求出 DE; (3)分二种情况讨论。
【例2】(山东青岛)已知:如图(1),在Rt ACB△中,90C ∠=,4cm AC =,3cm BC =,点P 由B 出发沿BA 方向向点A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设B A D M EC BAD C 备用图- 4 -- 5 -并求x 为何值时,y 的值最大,最大值是多少? 图(1) 图(2)图(3)【思路点拨】(1)证△AMN ∽ △ABC ;(2)设直线BC 与⊙O 相切于点D ,连结AO ,OD ,先求出OD (用x 的代数式表示),再过M 点作MQ ⊥BC 于Q ,证△BMQ ∽△BCA ;(3)先找到图形娈化的分界点,x =2。
然后 分两种情况讨论求y 的最大值: ① 当0<x ≤2时, ② 当2<x <4时。
【学力训练】1、(山东威海) 如图,在梯形ABCD 中,AB∥CD,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC 上运动,并保持MN∥AB ,ME⊥AB ,NF⊥AB ,垂足分别为E ,F .(1)求梯形ABCD 的面积; (2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能, 求出正方形MEFN 的面积;若不能,请说明理由.2、(浙江温州市)如图,在Rt ABC △中,90A ∠=,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作AB M N DOA B M N PO A B MN O CD A BEF NM A BC D ER P- 6 -QR BA∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使PQR △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.3、(湖南郴州)如图,平行四边形ABCD 中,AB =5,BC =10,BC 边上的高AM =4,E 为 BC 边上的一个动点(不与B 、C 重合).过E 作直线AB 的垂线,垂足为F . FE 与DC 的延长线相交于点G ,连结DE ,DF ..(1) 求证:ΔBEF ∽ΔCEG . (2) 当点E 在线段BC 上运动时,△BEF 和 △CEG 的周长之间有什么关系?并说明你的理由.(3)设BE =x ,△DEF 的面积为 y ,请你求出y 和x 之间的函数关系式,并求出当x 为何 值时,y 有最大值,最大值是多少?4、(浙江台州)如图,在矩形ABCD 中,9AB =,33AD =P 是边BC 上的动点(点P 不与点B ,点C 重合),过点P 作直线PQ BD ∥,交CD 边于Q 点,再把PQC △沿着动直线PQ 对折,点C 的对应点是R 点,设CP 的长度为x ,PQR △与矩形ABCD 重叠部分的面积为y .(1)求CQP ∠的度数;(2)当x 取何值时,点R 落在矩形ABCD 的AB 边上?(3)①求y 与x 之间的函数关系式;②当x 取何值时,重叠部分的面积等于矩形面积的727?MB DC E FG x A- 7 -参考答案【典型例题】【例1】(上海市)(1)取AB 中点H ,联结MH ,M为DE 的中点,MH BE ∴∥,1()2MH BE AD =+. 又AB BE⊥,MH AB ∴⊥. 12ABM S AB MH ∴=△,得12(0)2y x x =+>; (2)由已知得22(4)2DE x =-+以线段AB 为直径的圆与以线段DE 为直径的圆外切,1122MH AB DE ∴=+,即2211(4)2(4)222x x ⎡+=+-+⎣.解得43x =,即线段BE 的长为43; (3)由已知,以A N D ,,为顶点的三角形与BME △相似,D Q C B P R AB A DC (备 BA D C (备- 8 -又易证得DAM EBM ∠=∠.由此可知,另一对对应角相等有两种情况:①ADN BEM∠=∠;②ADB BME ∠=∠.①当ADN BEM∠=∠时,AD BE∥,ADN DBE∴∠=∠.DBE BEM ∴∠=∠. DB DE∴=,易得2BE AD =.得8BE =;②当ADB BME ∠=∠时,AD BE∥,ADB DBE ∴∠=∠.DBE BME∴∠=∠.又BED MEB ∠=∠,BED MEB ∴△∽△.DE BEBE EM∴=,即2BE EM DE=,得.解得12x=,210x=-(舍去).即线段BE 的长为2.综上所述,所求线段BE 的长为8或2.【例2】(山东青岛)(1)在Rt△ABC 中,522=+=AC BC AB ,由题意知:AP = 5-t ,AQ = 2t , 若PQ ∥BC ,则△APQ ∽△ABC ,∴=AC AQ AB AP ,∴5542t t -=,∴710=t . (2)过点P 作PH ⊥AC 于H . ∵△APH ∽△ABC ,∴=BC PH AB AP ,∴=3PH 55t -,∴t PH 533-=, ∴tt t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=.(3)若PQ 把△ABC 周长平分,则图 B A PH- 9 -AP+AQ=BP+BC+CQ .∴)24(32)5(t t t t -++=+-, 解得:1=t .若PQ 把△ABC 面积平分,则ABCAPQS S ∆∆=21, 即-253t +3t =3.∵ t =1代入上面方程不成立, ∴不存在这一时刻t ,使线段PQ 把Rt△ACB 的周长和面积同时平分.(4)过点P 作PM ⊥AC 于M,PN ⊥BC 于N ,若四边形PQP ′ C 是菱形,那么PQ =PC . ∵PM ⊥AC 于M ,∴QM=CM .∵PN ⊥BC 于N ,易知△PBN ∽△ABC .∴AB BPAC PN =, ∴54t PN =, ∴54t PN =, ∴54t CM QM ==,∴425454=++t t t ,解得:910=t . ∴当910=t 时,四边形PQP ′ C 是菱形. 此时37533=-=t PM , 84==t CM , 在Rt△PMC 中,9505816494922=+=+=CM PM PC ,∴菱形PQP ′ C 边长为9505.【例3】(山东德州)(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C .PB A Q P 图M N- 10 -∴ △AMN ∽ △ABC .∴ AM AN AB AC=,即43x AN =. ∴ AN =43x . ∴ S =2133248MNPAMN SS x x x ∆∆==⋅⋅=.(0<x <4)(2)如图(2),设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN . 在Rt△ABC 中,BC 22AB AC +=5. 由(1)知 △AMN ∽ △ABC .∴ AM MN AB BC=,即45x MN =. ∴ 54MN x =, ∴58OD x=.过M 点作MQ ⊥BC 于Q ,则58MQ OD x ==. 在Rt△BMQ 与Rt△BCA 中,∠B 是公共角, ∴ △BMQ ∽△BCA .∴ BM QM BC AC=. ∴55258324xBM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ABMND图( 2)O AMN P图 (1)O∴当x =4996时,⊙O 与直线BC 相切. (3)随点M 的运动,当P 点落在直线BC 上时,连结AP ,则O 点为AP 的中点.∵ MN ∥BC ,∴ ∠AMN =∠B ,∠AOM =∠APC . ∴ △AMO ∽ △ABP .∴ 12AM AO AB AP ==. AM =MB =2. 故以下分两种情况讨论: ① 当0<x ≤2时,2Δ83x S y PMN==.∴ 当x =2时,2332.82y=⨯=最大② 当2<x <4时,设PM ,PN 分别交BC 于E ,F . ∵ 四边形AMPN 是矩形,∴ PN ∥AM ,PN =AM =x . 又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形. ∴ FN =BM =4-x . ∴ ()424PF x x x =--=-. 又△PEF ∽ △ACB . ∴2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭.∴ ()2322PEFSx ∆=-.BMN图 ( 4)OE FA CMNP图 (3)OMNP PEFy SS ∆∆=-=()222339266828xx x x --=-+-.当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭.∴ 当83x =时,满足2<x <4,2y=最大.综上所述,当83x =时,y 值最大,最大值是2. 【例3】(山东德州)(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C . ∴ △AMN ∽ △ABC . ∴AM ANAB AC=,即43x AN=. ∴ AN =43x . ∴ S =2133248MNPAMN SS x x x ∆∆==⋅⋅=.(0<x <4)(2)如图(2),设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN . 在Rt △ABC 中,BC 22AB AC +=5. 由(1)知 △AMN ∴ AM MNAB BC=,即45x MN=. ∴54MN x =,ABMND图( 2)O∴58OD x=.过M 点作MQ ⊥BC 于Q,则58MQ OD x==.在Rt △BMQ 与Rt △BCA 中,∠B 是公共角, ∴ △BMQ ∽△BCA . ∴ BM QMBC AC=.∴55258324xBM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ∴ 当x =4996时,⊙O 与直线BC 相切. (3)随点M 的运动,当P 点落在直线BC 上时,连结AP ,则O 点为AP 的中点. ∵ MN ∥BC ,∴ ∠AMN =∠B ,∠AOM =∠APC .∴ △AMO ∽ △ABP .∴12AM AO AB AP ==. AM =MB =2.故以下分两种情况讨论:① 当0<x ≤2时,2Δ83x S y PMN==.∴ 当x =2时,2332.82y=⨯=最大② 当2<x <4时,设PM ,PN 分别交BC 于E ,AMNP图 (3)OBMNP图 (1)OF .∵ 四边形AMPN 是矩形, ∴ PN ∥AM ,PN =AM =x . 又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形. ∴ FN =BM =4-x . ∴()424PF x x x =--=-.又△PEF ∽ △ACB . ∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭.∴()2322PEF S x ∆=-.MNP PEFy S S ∆∆=-=()222339266828xx x x --=-+-.当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭.∴ 当83x =时,满足2<x <4,2y =最大.综上所述,当83x =时,y 值最大,最大值是2. 【学力训练】1、(山东威海)(1)分别过D ,C 两点作DG ⊥AB 于点G ,CH ⊥AB 于点H . ∵ AB ∥CD ,∴ DG =CH ,DG ∥CH .C D NM∴ 四边形DGHC 为矩形,GH =CD =1. ∵ DG =CH ,AD =BC ,∠AGD =∠BHC =90°, ∴ △AGD ≌△BHC (HL ).∴ AG =BH =2172-=-GH AB =3. ∵ 在Rt △AGD 中,AG =3,AD =5, ∴ DG =4. ∴()174162ABCD S +⨯==梯形.(2)∵ MN ∥AB ,ME ⊥,NF ⊥AB ,∴ ME =NF ,ME ∥NF .∴ 四边形MEFN 为矩形.∵ AB ∥CD ,AD =BC , ∴ ∠A =∠B .∵ ME =NF ,∠MEA =∠NFB =90°, ∴ △MEA ≌△NFB (AAS ). ∴ AE =BF . 设AE =x ,则EF =7-2x .∵ ∠A =∠A ,∠MEA =∠DGA =90°, ∴ △MEA ∽△DGA .∴ DG ME AG AE =.∴ ME =x 34. C D A BE FNMG H∴6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形.当x =47时,ME =37<4,∴四边形MEFN 面积的最大值为649. (3)能.由(2)可知,设AE =x ,则EF =7-2x ,ME =x 34. 若四边形MEFN 为正方形,则ME =EF . 即=34x7-2x .解,得1021=x .∴ EF =21147272105x -=-⨯=<4. ∴ 四边形MEFN 能为正方形,其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形. 00000000………….2、(浙江温州市)(1)Rt A ∠=∠,6AB =,8AC =,10BC ∴=.点D 为AB 中点,132BD AB ∴==. 90DHB A ∠=∠=,B B ∠=∠.BHD BAC∴△∽△,DH BDAC BC ∴=,3128105BD DH AC BC ∴==⨯=. (2)QR AB∥,90QRC A ∴∠=∠=.C C ∠=∠,RQC ABC ∴△∽△,RQ QC AB BC∴=,10610y x -∴=, 即y 关于x 的函数关系式为:365y x =-+.(3)存在,分三种情况:①当PQ PR =时,过点P 作PM QR ⊥于M ,则QM RM =.1290∠+∠=,290C ∠+∠=,1C∴∠=∠.84cos 1cos 105C ∴∠===,45QM QP ∴=, 1364251255x ⎛⎫-+ ⎪⎝⎭∴=,185x ∴=. ②当PQ RQ =时,312655x -+=, 6x ∴=.③当PR QR =时,则R 为PQ 中垂线上的点, 于是点R 为EC 的中点,11224CR CE AC ∴===.A B C D ER P H QM 2 1 A B D E R P H Q AB CDE RP H Qtan QR BAC CR CA==,366528x -+∴=,152x ∴=. 综上所述,当x 为185或6或152时,PQR △为等腰三角形.3、(湖南郴州)(1) 因为四边形ABCD 是平行四边形, 所以AB DG所以,B GCE G BFE∠=∠∠=∠所以BEF CEG △∽△(2)BEF CEG △与△的周长之和为定值.理由一: 过点C 作FG 的平行线交直线AB 于H , 因为GF ⊥AB ,所以四边形FHCG 为矩形.所以 FH =CG ,FG =CH因此,BEF CEG △与△的周长之和等于BC +CH +BH 由 BC =10,AB =5,AM =4,可得CH =8,BH =6,所以BC +CH +BH =24 理由二:由AB =5,AM =4,可知 在Rt△BEF 与Rt△GCE 中,有:A M xH GF EDCB4343,,,5555EF BE BF BE GE EC GC CE ====,所以,△BEF 的周长是125BE , △ECG 的周长是125CE 又BE +CE =10,因此BEF CEG与的周长之和是24.(3)设BE =x ,则43,(10)55EF x GC x ==-所以21143622[(10)5]2255255y EF DG x x x x ==-+=--配方得:2655121()2566y x =--+.所以,当556x =时,y 有最大值.最大值为1216. 4、(浙江台州)(1)如图,四边形ABCD 是矩形,AB CD AD BC∴==,.又9AB =,33AD =,90C ∠=,9CD ∴=,33BC =3tan 3BC CDB CD ∴∠==30CDB ∴∠=.PQ BD∥,30CQP CDB ∴∠=∠=.(2)如图(1),由轴对称的性质可知,RPQ CPQ△≌△,RPQ CPQ∴∠=∠,RP CP =.由(1)知30CQP ∠=,60RPQ CPQ ∴∠=∠=,D QCB PA60RPB ∴∠=,2RP BP ∴=.CP x=,PR x ∴=,33PB x=.在RPB △中,根据题意得:2(33)x x=,解这个方程得:23x =(3)①当点R 在矩形ABCD 的内部或AB 边上时,023x <≤21133222CPQSCP CQ x x x =⨯⨯==△,RPQ CPQ△≌△,∴当023x <≤232y x =当R 在矩形ABCD 的外部时(如图(2)),2333x <<在Rt PFB △中,60RPB ∠=,22(33)PF BP x ∴==,又RP CP x==,363RF RP PF x ∴=-=- 在Rt ERF △中,30EFR PFB ∠=∠=,36ER x ∴=-. 21331818322ERF S ER FR x x ∴=⨯=-+△,RPQ ERF y S S =-△△, ∴当2333x <2318183y x x =+-.综上所述,y 与x 之间的函数解析式是:223(023)318183(2333)x x y x x x <=⎨⎪+-<⎩≤.D QCBP R A 图(2)F E- 21 - ②矩形面积933273=⨯=,当023x <≤时,函数23y x =随自变量的增大而增大,所以y 的最大值是3727的值72737327=⨯=, 而7363>,所以,当03x <<y 的值不可能是矩形面积的727; 当2333x << 231818373x x +-=332x =为33233> 所以332x = 所以332x = 综上所述,当332x =PQR △与矩形ABCD 重叠部分的面积等于矩形面积的727.。
