统计学基础第四章
统计学基础 第四章 综合指标

统计学基础第四章综合指标【教学目的】1.掌握总量指标的概念及其种类2.掌握相对指标的概念及其计算方法3.掌握平均指标的概念、特点及其计算方法4.掌握变异指标的概念及其计算方法【教学重点】1.总量指标的概念及其种类2.相对指标的概念及其计算方法3.平均指标的概念、特点及其计算方法4.变异指标的概念及其计算方法【教学难点】1.总量指标的分类辨析2.各种相对指标的区别及其计算方法3.平均指标的概念、特点的理解,计算方法的运用4.变异指标的概念的理解,计算方法的运用【教学时数】教学学时为14课时【教学内容参考】第一节总量指标一、总量指标的意义总量指标是反映总体的规模、水平的指标,是最基本的指标,又称绝对数。
【案例】例如,2008年全国社会消费零售总额达到108488亿元;全国固定资产投资总额为172291亿元;全国粮食总产量达到52850万吨。
这些指标都属于总量指标。
通过上述总量指标数值的大小,就可以对我国社会消费品零售总额、固定资产投资额、粮食总产量等情况有一个直观的认识。
总量指标数值的大小随总体范围的大小而增加或减少,总体范围大,指标数值就大;总体范围小,指标数值就小。
有时总量指标也表现为同一总体在不同的时间、空间条件下的差数。
【案例】2007年我国粮食总产量为50160.3万吨,2008年我国粮食总产量比2007年增加了2689.7万吨,这一增加量也是总量指标。
总量指标作为增加量时,其数值表现为正值;作为减少量时,其数值表现为负值。
总量指标是我们认识社会经济现象的起点。
了解现象的基本情况一般先从总量开始。
【案例】要了解2008年辽宁省文化事业基本情况,通过明晰下列总量指标即可:年末全省共有艺术表演团体65个,文化馆、艺术馆123个,公共图书馆128个,博物馆37个,档案馆153个。
全年出版报纸123种,出版量19.1亿份;出版杂志324种,出版量0.8亿册;出版图书8884种,出版量1.7亿册。
年末有广播电台15座,电视台16座,有线电视用户680.8万户,比上年增加86.2万户,其中,数字电视用户166.5万户,比上年增加62.1万户。
第四章统计学基础课后习题答案

第四章综合指标一、单选题1.B 2.D 3.D 4.D 5.B二、多选题1.BDE 2.BCE 3.AC三、简答题1.总量指标是反映现象总体在一定时间、地点条件下的总规模和总水平的指标。
总量指标的作用:(1)反映社会经济现象总体的基本状况和基本实力;(2)计算相对指标和平均指标的基础。
2.结构相对指标将总体分为性质不同的部分,用各部分和总体数值对比;比例相对指标是同一总体两个不同部分之间的数值对比;比较相对指标是用两个不同总体的同类指标数值对比。
3.强度相对指标是对两个性质不同而又有密切联系的指标进行对比,反映现象强度、密度、或普及程度的相对指标。
在表现形式上同平均指标类似,单平均指标是总体标志总量处以总体单位个数,强度相对指标是两个不同性质单密切联系的总体指标之比。
4.时点指标和时期指标的区别:(1)时期指标具有可加性,不同时期的指标数值相加表明较长时期的总量。
时点指标不具有可加性;(2)时期指标的数值大小和时间长短有关,时点指标则无关;(3)时期指标的数值可以连续计数,时点指标的数值只能间断计数。
5.权数可理解为对计算结果的影响因素,在数据未分组时可用简单算术平均,对分组数据适用加权算术平均。
在各数据的权数都为1时两者相等。
6.联系:两者都是平均指标的一种,调和平均数作为算术平均数的变形使用区别:(1)变量不同:算术平均数是x,调和平均数是1/x 。
(2)权数不同:算术平均数是f或n,代表次数(单位数),调和平均数是xf 或M,代表标志总量。
四、计算题1.(1)结构指标:男性人口(女性人口)/人口总数×100%(2)比例指标:男性人口/女性人口×100%、女性人口/男性人口×100%(3)动态指标:1990年人口总数/1982年人口总数×100%-1等2.3.单位成本的计划数=520×(1-5%)=494 元单位成本的实际数=520×(1-6%)=488.8元降低成本计划完成程度=(1-6%)/(1-5%)×100%=98.95%超额完成了1.05%。
统计学基础第四章

4.2.4 比较相对指标
(一)概念 (二)计算公式
(一)概念
比较相对指标是将不同空间条件下同类 指标数值进行对比,反映同类事物在同 一时期不同空间条件下数量对比关系, 一般用百分数表示。也可以用倍数。
(二)计算公式
比较相对指标=某地区某一指标数值另一地区 同类指标数值×100%
随着研究目的的改变,比较指标的分子和分母 的数值可以对换。在经济管理工作中,将各单 位的技术经济指标与同类的先进水平对比,或 与规定的标准水平对比,便可找出差距。比较 相对指标的特点有:对比的分子与分母必须是 同质现象;分子、分母可互换。
2.时点指标(又称存量指标) 是反映现象处于某一时点上(某一时刻或某一瞬间)的数量水平。
例如,人口数、学校数、企业数、商店数、物资库存数量、银行 储蓄余额、牲畜存栏数等。时点指标有以下特点: (1)时点指标不能累计相加。因为,这种累计总量的重复计算没有 实际意义。例如,某班有学生45人。第一天统计实有45人,第二 天统计实有45人,但不能把两天实有人数加在一起说该班实有人 数为90人。 (2)时点指标数值的大小与时点的间隔长短没有直接关系。虽然时 点指标数值也会随着时间的变化而出现增减变动,但它与相邻时 点的间隔长短无关。例如,某种原材料的库存量多少只与原材料 的购进、拨出、消费等有关而与时间间隔无直接关系。 (3)时点指标是通过专门组织的一次性的全面调查所取得的标准时 点上的数值。
4.2 相对分析
4.2.1 相对指标 4.2.2 结构相对指标 4.2.3 比例相对指标 4.2.4 比较相对指标 4.2.5 强度相对指标 4.2.6 动态相对指标 4.2.7 计划完成相对指标
4.2.1 相对指标
(一)概念 (二)表现形式
(一)概念
统计学第4章综合指标

直接观察数据中出现次数最多的数。
平均指标在统计分析中应用
描述统计
用平均指标描述数据的集中 趋势和一般水平,如用算术 平均数描述班级学生的平均 成绩。
比较分析
通过比较不同组数据的平均 指标,揭示它们之间的差异 和联系,如比较不同班级的 平均成绩以评估教学效果。
推断统计
在总体分布未知的情况下, 利用样本平均指标对总体进 行推断,如通过样本均值推 断总体均值。
总量指标的作用
作为计算相对指标和平均指标的基础
描述社会经济现象的总规模和总水平
总量指标种类与计算方法
总量指标的种类
01
时点指标:反映现象在某一时刻上的总量 ,如年末人口数、股票价格等。
03
02
时期指标:反映现象在一段时期内的总量, 如国内生产总值、人口数等。
04
总量指标的计算方法
直接计数法:对总体单位进行逐一计数, 然后汇总得到总量指标。
相对指标种类与计算方法
结构相对指标
部分与总体之比,反映总
总体中不同部分数量之比,反映各部分之间的 比例关系。
比较相对指标
同一现象在不同空间条件下的数量对比,反映现象在不同地区的差异程度。
相对指标种类与计算方法
强度相对指标
两个性质不同但有一定联系的总量指标之比,反映现象的强度、密度和普遍程度。
平均指标种类与计算方法
算术平均数
$bar{x} = frac{sum x}{n}$,其中$sum x$为所有数值之和,$n$为 数值个数。
几何平均数
$G = sqrt[n]{prod x_i}$,其中$prod x_i$为所有数值之积,$n$为 数值个数。
中位数
将数据从小到大排列,若数据量为奇数则取中间数,若数据量为偶数 则取中间两数的平均值。
统计学第四章重点知识点

第四章 差异量教学目的:1.理解全距、四分位距、百分位距、平均差、方差、标准差和差异系数等概念;2.掌握各种差异量指标的计算方法。
数据的分布特征不仅有集中趋势,还有离中趋势。
以动态的眼光,从不同的角度看,数据是向中间变动的,也是向两端变动的。
两组数据可能平均水平相同,但两组数据的分布特征并不完全相同。
【如】:比较以下两组数据 A 组:88、82、73、76、81 B 组:92、86、70、72、80两组平均数,80==B A X X 但R A =88-73=15,R B=92-70=22。
即A 组较集中,B 组较分散。
因此,我们描述一组数据的分布特征,既要描述其集中趋势,也要描述其离中趋势。
差异量:表示一组数据的离中趋势或变异程度的量称为差异量。
常用的差异量指标有全距、四分位距、百分位距、平均差、方差、标准差和差异系数。
第一节全距、四分位距、百分位距一、全距全距:是一组数距中最大值与最小值之差。
优点:意义明确,计算方便。
缺点:反响不灵敏,易受极端值影响。
二、四分位距〔一〕四分位距的的概念四分位距:是指一组按大小顺序排列的数据中间部位50%个频数距离的一半。
QD :表示四分位距; Q 3:表示第三四分位数; Q 1:表示第一四分位数。
所以:四分位距的公式又为: 〔二〕四分位数的计算方法 1、原始数据计算法〔1〕将数据由小到大进行排列;〔2〕分别求出三位四分位数〔点〕;〔3〕代入公式计算。
【例如】:有以下16个数据25、22、29、12、40、15、14、39、37、31、33、19、17、20、35、30,其中四分位距的计算方法如下:〔1〕先将原始数据从小到大排列好;12、14、15、17、*19、20、22、25、*29、30、31、33、*35、37、39、40Q1=18 Md=27 Q3=34〔2〕求出Q1、Md、Q3;〔3〕将Q1、Md、Q3的得数代入公式〔4.1〕。
2、频数分布表计算法利用频数分布表计算公式为:关键是分别计算P75和P25,百分位数计算方法掌握了,这里的计算就不会有什么问题。
统计学基础综合指标

统计学——第四章综合指标
比较相对指标:用两个不同总体的同类指标数值对比,以反映某一现 象在同一时间内不同空间条件下发展的均衡程度。
比较相对指标= 某一总体的某类指标数值 另一总体的同类指标数值
例1:2005年美国的GDP为124550.7亿美元,人均GDP为43740美元, 而同年中国的GDP为22289.0亿美元,人均GDP为1740美元。则
statistics
统计学——第四章综合指标
第二节 相对指标
statistics
统计学——第四章综合指标 相对指标的概念
相对指标(相对数):是通过两个有联系的指标进行对比, 以反映现象总体的数量结构、变化程度或现象之间的数量 关系。(男生占全班人数的百分比)
相对指标=对比数 基数
statistics
第三节 平均指标
statistics
统计学——第四章综合指标 平均指标
平均指标的概念(统计平均数):是反映统计数据(总体单位 标志)一般水平的统计指标。
平均指标的特点:将各统计数据的差异抽象化,代表了全部 统计数据的一般水平,反映了现象总体的综合数量特征。
statistics
统计学——第四章综合指标 平均指标的作用
全期计划数
statistics
统计学——第四章综合指标
2.计划指标是相对数
实际完成百分比
计划完成情况相对数 ?
? 100%
计划百分比
①当计划指标是增长率时
计划完成情况相对数
?
1 1
? ?
实际增长率 计划增长率
? 100%
②当计划指标是降低率时
计划完成情况相对数
?
1 ? 实际降低率 1 ? 计划降低率
统计学(第4章)

连续变动结果的总量指标,时期指标是
一个流量。
时间维度上
时期指标的三个特点 具有可加性
时期指标可以累计
时期指标数值大小与时期长短有直接关系
时期指标的数值一般为连续登记
2019/6/15
第四章 描述统计
5
统计学
2、时点指标
时点指标又叫存量指标,是指反映社 会经济现象在某一时点上的总量指标,
四 季度
1 500
计划完成百分数=
1400+1420+1470+1500 5000
=115.8%
注:2010年第一季度前的四个季度的累计量已达5000,说明五年计 划提前三个季度完成。
2019/6/15
第四章 描述统计
33
统计学
(2)累计法
如何确定提前 完成时间?
计算公式:
计划完成相对指标 长期计划期间实际累计完成数 长期计划规定的累计数
时点指标是一个存量。
时间维度上
时点指标的三个特点
不具可加性
不同时点指标数值是不能累加
时点指标数值大小与时点间隔长短无直 接关系
时点指标一般为间断统计
2019/6/15
第四章 描述统计
6
统计学
三、总量指标的计量单位
1、实物量单位(包括度量衡单位) 2、价值量单位 3、劳动量单位(工时和工日)
5 000 1 250 1 340 1 280
102.4
52.4
4 000 1 000 1 030 1 215
121.5
56.1
2 000 500 600 400
80.0
50.0
11 000 2 750 2 970 2 895 105.33
统计学基础(第4章总量指标与相对指标)

2020/7/3
.
12
(二)货币单位
用货币单位来作为计量事物数量的统计指标称为 价值指标。如国内生产总值、进出口贸易额、工 业增加值、工资总额、销售收入、利润等。
(三)劳动单位是用劳动消耗时间来表示的计量单 位,如工时、工日等。
2020/7/3
.
13
四、计算和使用总量指标应注意的问题 (一)要注意现象的同类性 (二)要有明确的统计含义和统计方法 (三)要统一计量单位
第四章 总量指标 与相对指标
Fundamentals of Statistics
2020/7/3
.
1
教学目的与要求:
本章主要介绍统计指标的意义、种 类及其计算和应用。通过学习要求 掌握: 1.总量指标的概念、作用及种类; 2.相对指标的概念、作用及常见相对 指标的特点及计算方法.
2020/7/3
.
2、度量衡单位,如t(吨),kg(千克)m(米),立 方米,平方米等。
3、双重或多重计量单位,如台/kw,台/t等。
2020/7/3
.
11
4、复合单位,是将两种计量单位结合在一起以乘 积表示某事物数量的计量单位,如发电量用kw·h, 货物周转量用t·km表示。
5、标准实物单位,是按照一定的折算标准来度量 被研究对象数量的一种计量单位。例如,各种氮肥 以含氮量100%、为标准单位进行折算等。
2020/7/3
.
10
三、总量指标的计量单位
总量指标表现一定社会经济现象的具体数值,有 一定的计量单位,一般分为实物单位、劳动单位 和价值单位。 (一)实物单位,是根据事物的属性和特点而规定 的计量单位。它一般有五种:
1、自然单位是根据事物的自然表现形态来度量其 数量的单位。如人口按人,汽车按辆等。
统计学基础课件 第四章 总量指标和相对指标

❖ 作用
1. 反映总体内在的结构特征;
2. 用于不同对象的比较评价;
3. 反映事物发展变化的过程和趋势。
❖ 计量形式
1.有名数
2.无名数
第四章 总量指标和相对指标
二、相对指标的种类及计算方法
❖ 值
结构相对数
100%
总体全部数值
第四章 总量指标和相对指标
引例:
男性人口的 比重为50.8﹪
女性人口的 比重为49.2﹪
比1980年末的 9.9亿人增加
了28﹪
1999年末我国共有 总人口12.6亿人,其 中男性人口为6.4亿, 女性人口为6.2亿。
人口性别比 为1.03:1
人口出生率 为15.23‰
人口密度为 130人/平方公里
51.52﹪
特 ⒈为无名数,可用百分数或一比几或几比几表示; 点 ⒉分子分母可以互换;
3.用来反映组与组之间的联系程度或比例关系。
第四章 总量指标和相对指标
二、相对指标的种类及计算方法
3.比较相对指标 :比较相对数 某一总体的某指标数值
另一总体的该指标数值
例:某年某地区甲、乙两个公司商品销售额 分别为5.4亿元和3.6亿元。则
第四章 总量指标和相对指标
三、总量指标的计量单位 按计量单位分
实物量单位
价值量单位
劳动量单位
第四章 总量指标和相对指标
实物量单位
❖ 实物单位是根据事物的属性和特点而采用的计量单位,有 自然单位、度量衡单位和标准实物单位等。
1.自然单位 2.度量衡单位 3.复合计量单位 4.多重计量单位 3.标准实物单位
❖ 特点:
▪ 表现形式为绝对数 ▪ 总量指标反映了总体的规模信息 ▪ 只有有限总体才能准确计算总量指标
统计基础知识第四章综合指标习题及答案(1)

第四章综合指标一、单项选择题1.按反映的时间状况不同,总量指标可分为( B )(2012年1月)A.时间指标和时点指标B.时点指标和时期指标C.时期指标和时间指标D.实物指标和价值指标2.计算相对数的平均数时,如果掌握了分子资料而没有掌握分母资料,则应采用( C )(2012年1月)A.算术平均数B.几何平均数C.调和平均数D.算术平均和调和平均都可以3.某企业今年计划劳动生产率比去年提高10%,而实际却提高了5%,则劳动生产率的计划完成程度为( D )(2011年10月)A.5% B.50%C.-5%4.某企业计划2008年产值达到5000万元,但实际产值完成了5500万元,则该企业产值计划完成相对指标为( D ) (2011年1月)A.10%C.100%D.110%5.强度相对指标表现出的两种形式是指( B ) (2011年1月)A.复名数和无名数B.有名数和无名数C.复名数和单名数D.重名数和单名数6.第一批产品不合格率为1.5%,第二批不合格率为2%,第三批不合格率为4%,第一批产品占总数的40%,第二批占20%,则这三批产品的平均不合格率为( B ) (2011年1月)A.1.5%7.平均差与标准差的主要区别是( C ) (2010年10)A.意义有本质的不同B.适用条件不同C.对离差的数学处理方法不同D.反映了变异程度的不同8.某企业计划2008年产值达到5500万元,但实际产值完成了5000万元,则该企业产值计划完成相对指标为( B )(2010年1)A.10%C.100%D.110%9.第一批产品不合格率为1%,第二批不合格率为1.5%,第三批不合格率为2%,第一批产品占总数的35%,第二批占40%,则这三批产品的平均不合格率为( B )(2010年1)10.如果所有标志值的频数都减少为原来的1/5,而标志值仍然不变,那么算术平均数( A ) (2010年1)A.不变B.扩大到5倍C.减少为原来的1/5D.不能预测其变化11.某企业10月份计划要求销售收入比上月增长8%,实际增长12%,其超计划完成程度为( D )B.50%C.150%12.在下列两两组合的平均指标中,哪一组的两个平均数不受极端数值的影响?( D )(2009年1月)A.算术平均数和调和平均数B.几何平均数和众数C.调和平均数和众数D.众数和中位数13.比较相对指标是( B )(2008年10月)A.现象在时间上数值的对比B.现象在空间上数值的对比C.现象的部分数值与总体数值的对比D.现象内部的部分与部分的对比二、多项选择题1.下列指标中的结构相对指标是( ACD )(2012年1月)A.集体所有制企业职工占职工总数的比重B.某年人均消费额C.某年积累额占国民收入的比重D.大学生占全部学生的比重E.某工业产品产量比上年增长的百分比2.下列指标中属于动态相对指标的有( ABD )(2011年10月)A.2000年到2007年某地区人口增长了6.48%B.2007年某地区GDP为2000年的196.3%C.2007年某地区生产总值中,第一、二、三产业分别占28.4%、44.3%、27.3%D.2007年某地区国民收入为1952年的2364.2%E.2007年某地区国民收入使用额中积累和消费分别占34.1%和65.9%3.无名数的具体表现形式有( ABCDE ) (2011年1月)A.系数B.倍数C.成数D.百分数E.千分数4.众数的特点包括( CD ) (2011年1月)A.便于代数运算B.稳健性高C.不受极端值影响D.可适用于品质标志E.代表性高5.与标志值同计量单位的标志变异指标有( ABC ) (2010年10)A.极差B.平均差C.标准差D.方差E.平均差系数和标准差系数6.总量指标的计算必须遵从下列哪些原则?( ACE )(2010年1)A.同类性B.非同类性C.明确总量指标的统计含义D.计算人员必须相同E.计量单位必须一致7.平均指标的特点主要包括( ACE )(2010年1)A.具体差异抽样化B.可以就不同类事物计算C.只能就同类事物计算D.反映了变量值的分布状况E.反映了变量值的集中趋势8.经调查得知某地区2007年人口自然增长率为7‰;这一指标属于( BE )(2009年10)A.总量指标B.相对指标C.质量指标D.数量指标E.强度相对指标9.分子分母有可能互换计算的相对指标有( CE )(2009年1月)A.计划完成相对指标B.结构相对指标C.比较相对指标D.动态相对指标E.强度相对指标10.下列指标中属于时期指标有( ACE )(2008年10月)A.工业增加值B.职工人数C.出生的人口数D.商品库存量E.国民生产总额三、判断题1.在相对指标中,有名数主要用于表现比较相对指标的数值。
统计学基础-第四章--综合指标

统计学基础-第四章--综合指标统计学基础第四章综合指标【教学⽬的】1.掌握总量指标的概念及其种类2.掌握相对指标的概念及其计算⽅法3.掌握平均指标的概念、特点及其计算⽅法4.掌握变异指标的概念及其计算⽅法【教学重点】1.总量指标的概念及其种类2.相对指标的概念及其计算⽅法3.平均指标的概念、特点及其计算⽅法4.变异指标的概念及其计算⽅法【教学难点】1.总量指标的分类辨析2.各种相对指标的区别及其计算⽅法3.平均指标的概念、特点的理解,计算⽅法的运⽤4.变异指标的概念的理解,计算⽅法的运⽤【教学时数】教学学时为14课时【教学内容参考】第⼀节总量指标⼀、总量指标的意义总量指标是反映总体的规模、⽔平的指标,是最基本的指标,⼜称绝对数。
【案例】例如,2008年全国社会消费零售总额达到108488亿元;全国固定资产投资总额为172291亿元;全国粮⾷总产量达到52850万吨。
这些指标都属于总量指标。
通过上述总量指标数值的⼤⼩,就可以对我国社会消费品零售总额、固定资产投资额、粮⾷总产量等情况有⼀个直观的认识。
总量指标数值的⼤⼩随总体范围的⼤⼩⽽增加或减少,总体范围⼤,指标数值就⼤;总体范围⼩,指标数值就⼩。
有时总量指标也表现为同⼀总体在不同的时间、空间条件下的差数。
【案例】2007年我国粮⾷总产量为50160.3万吨,2008年我国粮⾷总产量⽐2007年增加了2689.7万吨,这⼀增加量也是总量指标。
总量指标作为增加量时,其数值表现为正值;作为减少量时,其数值表现为负值。
总量指标是我们认识社会经济现象的起点。
了解现象的基本情况⼀般先从总量开始。
【案例】要了解2008年辽宁省⽂化事业基本情况,通过明晰下列总量指标即可:年末全省共有艺术表演团体65个,⽂化馆、艺术馆123个,公共图书馆128个,博物馆37个,档案馆153个。
全年出版报纸123种,出版量19.1亿份;出版杂志324种,出版量0.8亿册;出版图书8884种,出版量1.7亿册。
统计学第4章 参数估计

无偏性
(unbiasedness)
无偏性:估计量抽样分布的数学期望等于被
估计的总体参数
抽样分布
中,样本 P(ˆ)
均值、比 率、方差
无偏
有偏
分别是总
A
B
体均值、
比率、方
差的无偏
估4计- 2量3
ˆ
统计学
STATISTICS
有效性
(efficiency)
有效性:对同一总体参数的两个无偏点估计
置信水平(1-α)表达了区间估计的可靠性。 它是区间估计的可靠概率。
显著性水平α表达了区间估计的不可靠的概 率。
4 - 20
统计学§4.2 点估计的评价标准
STATISTICS
对于同一个未知参数,不同的方法得到的估 计量可能不同,于是提出问题
应该选用哪一种估计量? 用何标准来评价一个估计量的好坏?
常用 标准
4 - 21
(1) 无偏性 (2) 有效性 (3) 一致性
统计学 定义 STATISTICS
无偏性
(unbiasedness)
若 E(ˆ)
则称 ˆ是 的无偏估计量.
定义的合理性
我们不可能要求每一次由样本得到的
估计值与真值都相等,但可以要求这些估 计值的期望与真值相等.
4 - 22
统计学
量,有更小标准差的估计量更有效
P(ˆ)
ˆ1 的抽样分布
B
无偏估计量还 必须与总体参 数的离散程度
比较小
4 - 24
A
ˆ2 的抽样分布
ˆ
统计学
有效性
STATISTICS
定义 设 ˆ1 1(X1, X 2, , X n )
统计学第四章_平均指标和变异指标

=
f
=
A
x
nA
=
x
n
简单算均数是加权 算均数的一个特例
cyz
14
※关于加权算术平均数的几点说明
⑶权数作用的实质,不在于各组次数多少,
而在于各组次数占总次数的比重即权重系数 的大小。因此,加权算术平均数可采用权重 系数作权数。 x f x f xn f n x1 f1 x2 f 2 xn f n 公式: x = 1 1 2 2 = n
x = x n
cyz
=
20+21+22+24+25 5
= 22.4(件)
9
3.加权算术平均数(资料已分组)!
每人日产零件 数(件)X 16 17 工人数(人) f 12 20 权重系数 f/∑f 0.12 0.20
18 19
20
30 23
15
0.30 0.23
0.15
合计
cyz
100
1.00
21
代表水平,反映数据分布的集中趋势。
一是根据各项数据来计算的平均指标,它能够概括反映所
有各项数据的平均水平,这种平均指标称为数值平均数。 二是把总体中处于特殊位置上的数据看做平均数,这种平 均值称为位置平均数。 数值平均数:算术平均数、调和平均数、几何平均数 位置平均数:众数、中位数
cyz
5
二.平均数的种类及计算
志总量,可用基本公式。
cyz 8
2.简单算术平均数(资料未分组)
若所给资料是总体各单位的标志值,则先将
各标志值简单相加得出标志总量,再除以标 志值的个数,求得平均数。 x1 x2 ... xn x 公式: x= = n n
《统计学》第四章

•各个变量值与算术平均数的离差平方总和为最小 证 明 : 值。 设 x 为 不 等 于 x 的 任 意 值 , c = x − x
0 0
Σ ( x − x )2 = 最 小 值
x 0 = x − c , 则 以 x 0为 中 心 的 离 差 总 和 为 : Σ ( x − x0 )2 = Σ
[x − ( x − c ) ]
3、调和算术平均数:调和平均数是常 用的另一种平均指标,它是根据标志 值的倒数计算的,又称为倒数平均数。
m1 + m2 + ⋅⋅⋅ + mn H = m1 m2 = mn x1 + x2 + ⋅⋅⋅ + xn
∑m ∑
i =1 i =1 n mi xi
n
i
例、假定有A 例、假定有A、B两家公司员工的月工资资 料如下表所示:要求计算平均工资。
60 70 20 150
50 40 25 115
工资总额 平均工资 = ,但职工人数(分母)未知。 职工人数 各组工资总额 m 各组职工人数 = ,f = 各组工资水平 x H A公司 =
∑m ∑
i =1 i =1 3 mi xi
3
i
48000 + 70000 + 32000 = 48000 + 70000 + 32000 800 1000 1600
250
3.13
42 50 × 5 + 150 × 42 + 52.50 16 + 150 × 13 250 × 350 = + 200—300 16 5 + 42 + 16 + 132504 20.00 16900 = 300—400 13 16.25 350 80 =400以上 (百吨) 211 . 26 4 5.00 450 合计 80 100.00 —
统计学 第四章 参数估计

由样本数量特征得到关于总体的数量特征 统计推断(statistical 的过程就叫做统计推断 的过程就叫做统计推断 inference)。 统计推断主要包括两方面的内容一个是参 统计推断主要包括两方面的内容一个是参 数估计(parameter estimation),另一个 数估计 另一个 假设检验 。 是假设检验(hypothesis testing)。
ˆ P(θ )
无偏 有偏
A
B
θ
ˆ θ
估计量的无偏性直观意义
θ =µ
•
•
•
• •
• • • •
•
2、有效性(efficiency)
有效性:对同一总体参数的两个无偏点估计 有效性: 量,有更小标准差的估计量更有效 。
ˆ P(θ )
ˆ θ1 的抽样分布
B A
ˆ θ2 的抽样分布
θ
ˆ θ
பைடு நூலகம்
3、一致性(consistency)
置信区间与置信度
1. 用一个具体的样本 所构造的区间是一 个特定的区间, 个特定的区间,我 们无法知道这个样 本所产生的区间是 否包含总体参数的 真值 2. 我们只能是希望这 个区间是大量包含 总体参数真值的区 间中的一个, 间中的一个,但它 也可能是少数几个 不包含参数真值的 区间中的一个
均值的抽样分布
总体均值的区间估计(例题分析)
25, 95% 解 : 已 知 X ~N(µ , 102) , n=25, 1-α = 95% , zα/2=1.96。根据样本数据计算得: x =105.36 96。 总体均值µ在1-α置信水平下的置信区间为 σ 10 x ± zα 2 = 105.36 ±1.96× n 25 = 105.36 ± 3.92
统计学第四章统计分析指标
计划完成相对指标
产值计划完成程度若大于100%,说明超额完 成计划;若小于100%,说明没有完成计划, 为正指标。 单位成本计划完成程度若大于100%,说明成 本比计划高,没有完成计划;若小于100%, 说明超额完成计划,为逆指标。 计划完成相对数的分子分母不能互换,在指 标含义、计算范围、核算方法等方面要一致。
计划完成相对指标
长期(通常是五年)计划完成情况—水平法和累计法
总体的一部分单位 总体另一部分单位 比例相对数
人口性别比例 积累与消费比例 农轻重比例
…
…
比例相对指标
人口出生性别比正常值一般在103到107之间。但 我国人口的出生性别比自20世纪80年代中期以来 迅速攀升。 1995年,0岁~4岁人口性别比:118.38 2000年,0岁~4岁人口性别比:120.17 2003年,0岁~4岁人口性6
(1)计划数为绝对数
计划完成相对数=(实际完成数÷同期计划数)×100%
适用于研究分析社会经济现象的规模或水平的计划完成 程度。
计划完成相对指标
〔例〕 某公司2010年计划销售某种产品30万件, 实际销售32万件,则该公司2010年销售计划完成相对 指标是多少?超额完成计划多少?
销售计划完成相对指标 = (32/30)*100% = 106.7% 超额完成计划 = 106.7% - 100% = 6.7%
t1时段
t2时段
t3时段
时期指标的特点: 1. 不同时期的时期指标数值具有可加性; 2. 时期指标的数值大小与时期长短有直接关系; 3. 时期指标数值是连续登记、累计的结果。
时点指标的特点: 1. 不同时期的时点指标数值不具有可加性。 2. 时点指标的数值大小与时间间隔长短无关。 3. 时点指标的数值是间断计数的。
统计基础知识第四章综合指标习题及答案

统计基础知识第四章综合指标习题及答案第四章综合指标一、单项选择题1.按充分反映的时间状况相同,总量指标可以分成(b)(2021年1月)a.时间指标和时点指标c.时期指标和时间指标b.时点指标和时期指标d.实物指标和价值指标2.排序相对数的平均数时,如果掌控了分子资料而没掌控分母资料,则应当使用(c)(2021年1月)a.算术平均数c.调和平均数顺利完成程度为(d)(2021年10月)a.5%c.-5%b.50%d.95.45%b.几何平均数d.算术平均和调和平均值都可以3.某企业今年计划劳动生产率比去年提高10%,而实际却提高了5%,则劳动生产率的计划4.某企业计划2021年产值达至5000万元,但实际产值顺利完成了5500万元,则该企业产值计划顺利完成相对指标为(d)(2021年1月)a.10%c.100%a.复名数和无名数c.复名数和单名数b.90.9%d.110%b.有名数和无名数d.重名数和单名数5.强度相对指标整体表现出来的两种形式就是指(b)(2021年1月)6.第一批产品不合格率为1.5%,第二批不合格率为2%,第三批不合格率为4%,第一批产品占总数的40%,第二批占20%,则这三批产品的平均不合格率为(b)(2021年1月)a.1.5%c.4.5%a.意义存有本质的相同c.对Matches的数学处置方法相同划完成相对指标为(b)(2021年1)a.10%c.100%b.90.9%d.110%b.2.6%d.5.1%b.适用于条件相同d.充分反映了变异程度的相同7.平均差与标准差的主要区别是(c)(2021年10)8.某企业计划2021年产值达至5500万元,但实际产值顺利完成了5000万元,则该企业产值计9.第一批产品不合格率为1%,第二批不合格率为1.5%,第三批不合格率为2%,第一批产品占总数的35%,第二批占40%,则这三批产品的平均不合格率为(b)(2021年1)a.1.5%c.4.5%b.1.45%d.5.1%10.如果所有标志值的频数都减少为原来的1/5,而标志值仍然不变,那么算术平均数(a)(2021年1)a.不变c.增加为原来的1/5b.不断扩大至5倍d.无法预测其变化11.某企业10月份计划要求销售收入比上月增长8%,实际增长12%,其超计划完成程度为(d)a.103.7%b.50%c.150%d.3.7%12.在以下两两女团的平均指标中,哪一组的两个平均数不受到极端数值的影响?((2021年1月)a.算术平均数和调和平均数b.几何平均数和众数c.调和平均数和众数d.众数和中位数13.比较相对指标就是(b)(2021年10月)a.现象在时间上数值的对比b.现象在空间上数值的对比c.现象的部分数值与总体数值的对比d.现象内部的部分与部分的对比二、多项选择题1.下列指标中的结构相对指标是(acd)(2021年1月)a.集体所有制企业职工占职工总数的比重b.某年人均消费额c.某年积累额占国民收入的比重d.大学生占全部学生的比重e.某工业产品产量比上年快速增长的百分比2.下列指标中属于动态相对指标的有(abd)(2021年10月)a.2000年到2021年某地区人口增长了6.48%b.2021年某地区gdp为2000年的196.3%c.2021年某地区生产总值中,第一、二、三产业分别占到28.4%、44.3%、27.3%d.2021年某地区国民收入为1952年的2364.2%e.2021年某地区国民收入使用额中积累和消费分别占34.1%和65.9%3.无名数的具体表现形式有(abcde)(2021年1月)a.系数b.倍数c.成数d.百分数e.千分数4.众数的特点包括(cd)(2021年1月)a.便于代数运算b.稳健性高c.不受极端值影响d.可适用于品质标志e.代表性低5.与标志值同计量单位的标志变异指标有(abc)(2021年10)a.极差b.平均差c.标准差d.方差e.平均差系数和标准差系数)d6.总量指标的排序必须遵守以下哪些原则?(ace)(2021年1)a.同类性c.明确总量指标的统计含义e.计量单位必须一致7.平均指标的特点主要包含(ace)(2021年1)a.具体内容差异样本化c.就可以就同类事物排序e.充分反映了变量值的分散趋势8.经调查得知某地区2021年人口自然增长率为7‰;这一指标属于(be)(2021b.可以就不同类事物计算d.反映了变量值的分布状况b.非同类性d.计算人员必须相同年10)a.总量指标c.质量指标e.强度相对指标9.分子分母有可能交换排序的相对指标存有(ce)(2021年1月)a.计划顺利完成相对指标c.比较相对指标e.强度相对指标10.下列指标中属于时期指标有(ace)(2021年10月)a.工业增加值c.出生的人口数e.国民生产总额三、判断题1.在相对指标中,出名数主要用作整体表现比较相对指标的数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
任务二
相对指标的计算及运用
(二)相对指标的作用
(1)相对指标通过数量之间的对比,可以表明事物相关程度、发 展程度,它可以弥补总量指标的不足,使人们清楚了解现象的相 对水平和普遍程度。例如,某企业去年实现利润50万元,今年实 现55万元,则今年利润增长了10%,这是总量指标不能说明的。
(2)把现象的绝对差异抽象化,使原来无法直接对比的指标变为 可比。不同的企业由于生产规模条件不同,直接用总产值、利润 比较评价意义不大,但如果采用一些相对指标,如资金利润率、 资金产值率等进行比较,便可对企业生产经营成果做出合理评价。
4
ห้องสมุดไป่ตู้
任务一
总量指标的计算及运用
时点指标是反映社会经济现象在某一时刻或某一时点上的状况的 总量,如商品库存量、资产占用额、人口数、企业数等等。 时点指标具有如下特点: (1)不具有可加性。不同时点上的两个时点指标数值相加不具有 实际意义。
(2)数值大小与登记时间的间隔长短无直接关系。时点指标仅仅 反映社会经济现象在一瞬间上的数量,每隔多长时间登记一次对 它没有直接影响。 (3)指标数值是间断计数的。时点指标没有必要进行连续登记, 有的也是不可能连续进行登记的,如:一国的总人口数。
1.理解总量指标的概念、种类和运用;
2.理解相对指标的概念、种类,掌握相对指标的计算方法及运用; 3.理解平均指标的概念、种类,掌握平均指标的计算方法及运用; 4.理解标志变异指标的概念、种类,掌握标志变异指标的计算方法 及运用; 5.会用Excel描述统计工具计算各种综合指标。
统计学基础
项目四
综合指标的计算及运用
[项目概述]经过统计整理,我们得到了条理化的统计数据。接下来, 该进行的工作是统计分析。统计分析的方法有综合指标分析法、动态 分析法、指数分析法、抽样推断法、相关分析与回归分析法等。我们 将首先学习综合指标分析法。综合指标法主要运用总量指标、相对指 标、平均指标、标志变异指标来反映出现象在具体时间、地点、条件 下的总体规模、相对水平、平均水平和差异程度,概括地描述总体的 综合数量特征及其变动趋势。 [学习目标]
任务一
总量指标的计算及运用
一、总量指标的概念 总量指标是用来反映社会经济现象在一定条件下的总规模、 总水平或工作总量的统计指标。总量指标用绝对数表示,也 就是用一个绝对数来反映特定现象在一定时间上的总量状况, 它是一种最基本的统计指标。 二、总量指标的种类 (一)按其说明总体的内容不同分为总体单位总量和总体标 志总量 总体单位总量是用来反映统计总体内包含总体单位个数多少 的总量指标。 总体标志总量是统计总体各单位某一方面数量标志值的总和。
7
任务二
相对指标的计算及运用
一、相对指标的概念和作用
(一)相对指标的概念 相对指标又称相对数,是通过两个有联系的指标进行对比,以反 映现象总体的数量结构、变化程度或现象之间的数量关系。例如, 男女比例、经济增长速度、公路密度等等,都属于相对指标的概 念范畴。 相对指标有两种表现形式:无名数和有名数。无名数是一种抽象 化的数值,多以系数、倍数、成数、百分数或千分数表示。有名 数有计量单位,多采用复合单位形式。如,人均粮食产量用“千 克/人”表示,人口密度用“人/平方公里”表示等。
5
任务一
总量指标的计算及运用
(三)按总量指标所采用计量单位不同来划分为实物指标、价值 指标和劳动量指标
1.实物指标
实物指标是用实物单位计量的总量指标。实物单位是根据事物的 属性和特点而采用的计量单位,主要有自然单位、度量衡单位和 标准实物单位。 2.价值指标 价值指标是用贷币单位计量的总量指标。如国内生产总值、社会 商品零售额、产品成本等,都是货币为单位来计量的。 3.劳动量指标 劳动量指标是以劳动时间作为计量单位的总量指标。如“工日”、 “工时”等都属于劳动单位。
6
任务一
总量指标的计算及运用
四、总量指标的计算和运用
正确计算总量指标必须注意以下几点: 1.明确界定总量指标的涵义、范围 例如,要正确计算工资总额,必须先明确工资的实质和构成要计 算第三产业增加值,就应事先明确第三产业增加值的涵义和所包 括的范围。 2.注意现象的同类性 即不同种类的实物总量指标的数值不能加总,只有同类现象才能 计算出总量。例如,不能把钢、煤、棉、粮进行简单的加总。
10
(一)计划完成程度相对指标
计划完成程度相对指标是社会经济现象在某时期内 实际完成数值与计划任务数值对比的结果,一般用 百分数来表示。基本计算公式为:
实际完成数 计划完成程度相对指标 = 100 % 计划任务数
11
(一)计划完成程度相对指标
1.计划数为绝对数和平均数时 使用绝对数和平均数计算计划完成程度相对指标时,可直接 用上述计算公式。 【例4-1】某企业2010年产品计划产量1000件,实际完 成1120件,则产量计划完成程度为: 计划完成程度相对指标=
3
任务一
总量指标的计算及运用
(二)按其反映总体的时间状况不同分为时期指标与时点指标 时期指标是反映社会经济现象在一定时期内发展的总量,如国民收 入,国内生产总值、工资总额、人口出生数、人口死亡数等。 时期指标具有如下特点: (1)具有可加性。时间上相邻的时期指标相加能够得到另—更长 时期的总量指标。 (2)指标数值的大小与所属时期的长短直接相关。—般来讲,时 期越长,指标数值就越大。 (3)必须连续登记而得。时期指标数值的大小取决于整个时期内 所有时间上的发展状况,只有连续登记得到的时期指标才会准确。
9
任务二
相对指标的计算及运用
(3)说明总体内在的结构特征,为深入分析事物的性质提供依据。 例如计算一个地区不同经济类型的结构,可以说明该地区经济的 性质。又如计算一个地区的第一、二、三产业的比例,可以说明 该地区社会经济现代化程度等。
二、相对指标的种类、计算及运用
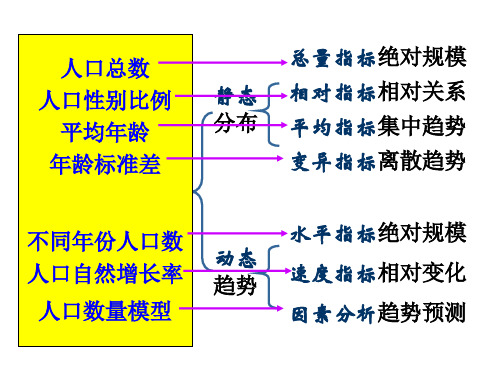
根据研究的目的的不同及对比基础不同,相对指标一般可分为计 划完成程度相对指标、结构相对指标、比例相对指标、比较相对 指标、强度相对指标和动态相对指标。
