全等三角形经典编辑题型50题(含规范标准答案)
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE (AAS )∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=E G ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题带问题详解

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB从D 做辅助线3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含问题详解)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形经典题型50题(含答案),推荐文档
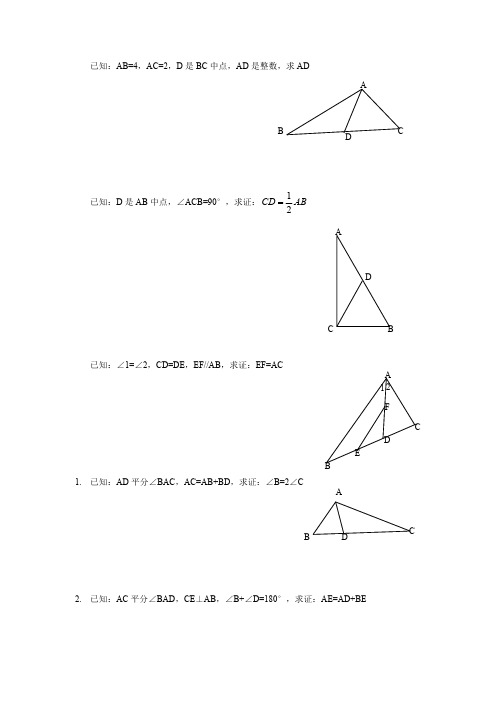
E
∵∠ABD+∠ADB=90°,∠ACF+∠CDE=90°
又∵∠ADB=∠CDE
D
∴∠ABD=∠ACF 在△ABD 和△ACF 中 ∠ABD=∠ACF, AB=AC,
∠BAD=∠CAF=90° ∴△ABD≌△ACF(ASA) ∴BD=CF ∴BD=2CE
B
C
25、(10 分)如图:DF=CE,AD=BC,∠D=∠C。求证:△AED≌△
BFC。
D
EF
C
A
26、(10 分)如图:AE、BC 交于点 M,F 点在 AM 上, BE∥CF,BE=CF。 求证:AM 是△ABC 的中线。 证明: ∵BE‖CF ∴∠E=∠CFM,∠EBM=∠FCM ∵BE=CF
B
ቤተ መጻሕፍቲ ባይዱB A
F
M
C
E
∴△BEM≌△CFM
∴BM=CM ∴AM 是△ABC 的中线.
C
B
D
2. 已知:AC 平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
6. 如图,四边形 ABCD 中,AB∥DC,BE、CE 分别平分∠ABC、∠BCD,且点 E 在 AD 上。求证:BC=AB+DC。
.
7.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠C
D
AC 是公共边,所以 AAS==>三角形 ADC 全等于三角形
ABC. 所以 BC 等于 DC,角 3 等于角 4,EC=EC 三角形
A
1 2
5 E6
3 4
C
DEC 全等于三角形 BEC 所以∠5=∠6
13.已知:如图,DC∥AB,且 DC=AE,E 为 AB 的中点,
全等三角形证明经典50题(含答案)

1. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
2. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDB ACDF21EEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC3.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE4. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC∴∠EAD =∠CAD∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )∴∠E =∠C∵AC =AB+BD∴AE =AB+BD∵AE =AB+BE∴BD =BE∴∠BDE =∠E∵∠ABC =∠E+∠BDE∴∠ABC =2∠E∴∠ABC =2∠C5. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFECD B A∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC又∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
全等三角形经典题型50题(有答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E ,使DE=AD ,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB —BE<AE 〈AB+BE 即:10—2〈2AD<10+2 4<AD 〈6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED ,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF ,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF.所以 ∠EBF=∠BEF.又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2).ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS)∴EG=AC ∵EF//AB ∴∠DF E=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案解析)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)
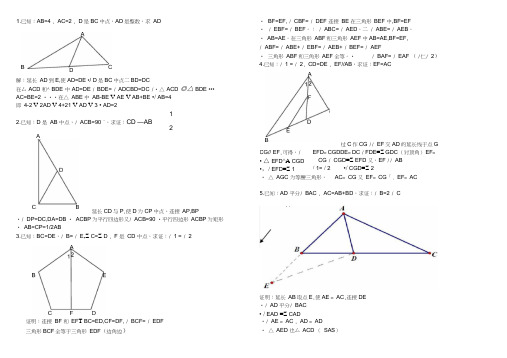
证明:连接 BF 和 EF T BC=ED,CF=DF, / BCF= / EDF 三角形BCF 全等于三角形 EDF (边角边)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 ADD • BF=EF, / CBF= / DEF 连接 BE 在三角形 BEF 中,BF=EF • / EBF= / BEF 。
: / ABC= / AED 。
二 / ABE= / AEB 。
• AB=AE 。
在三角形 ABF 和三角形 AEF 中AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF • 三角形 ABF 和三角形 AEF 全等。
•/ BAF= / EAF ( /仁/ 2)4.已知:/ 1 = / 2, CD=DE , EF//AB ,求证:EF=AC解:延长 AD 到E,使AD=DE •/ D 是BC 中点二BD=DC 在厶 ACD 和^ BDE 中 AD=DE / BDE= / ADCBD=DC /•△ ACD ◎△ BDE ••• AC=BE=2 •••在△ ABE 中 AB-BE V AE V AB+BE •/ AB=4 即 4-2 V 2AD V 4+21 V AD V 3 • AD=21 2.已知:D 是 AB 中点,/ ACB=90 °,求证:CD —AB 2A CG// EF ,可得,/• △ EFD ^A CGD•,/ EFD =Z 1过C 作CG // EF 交AD 的延长线于点GEFD = CGDDE = DC / FDE =Z GDC (对顶角) EF = CG / CGD =Z EFD 又,EF // AB / 1= / 2 •/ CGD =Z 2 • △ AGC 为等腰三角形, AC = CG 又 EF = CG 「. EF = AC 延长CD 与P ,使D 为CP 中点。
连接 AP,BP •/ DP=DC,DA=DB • ACBP 为平行四边形又/ ACB=90 •平行四边形 ACBP 为矩形 • AB=CP=1/2AB 3.已知:BC=DE ,/ B= / E ,Z C=Z D , F 是 CD 中点,求证:/ 1 = / 2 5.已知:AD 平分/ BAC , AC=AB+BD ,求证:/ B=2 / C证明:延长 AB 取点E ,使AE = AC ,连接DE •/ AD 平分/ BAC• / EAD =Z CAD•/ AE = AC , AD = AD • △ AED 也厶 ACD ( SAS )•••/ E = Z C•/ AC = AB+BD •AE = AB+BD•/ AE = AB+BE •BD = BE •••/ BDE =Z E •••/ ABC =Z E+ / BDE •••/ ABC = 2 / E •••/ ABC = 2 / C ••• AE = AF + FE = AD + BE12.如图,四边形ABCD中,AB 在AD上。
(完整版)全等三角形证明经典50题(含答案)
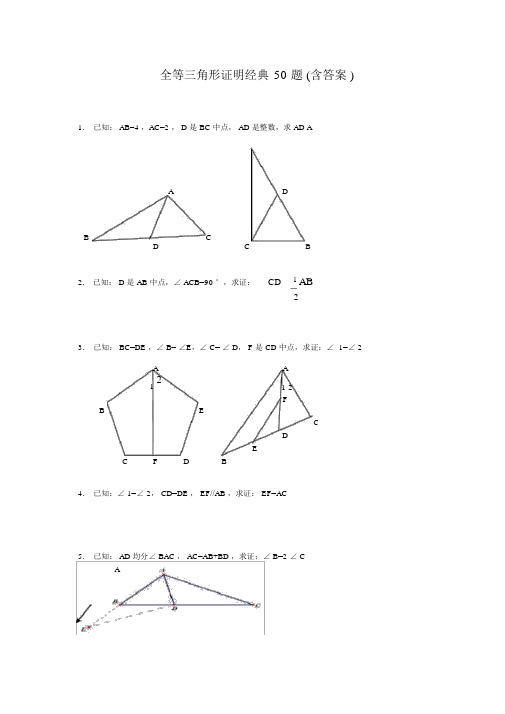
全等三角形证明经典50 题 (含答案 )1.已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求 AD AA DB CD C B2. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB23.已知: BC=DE ,∠ B= ∠E,∠ C= ∠ D, F 是 CD 中点,求证:∠ 1=∠ 2A A1 21 2BFECDEC FD B4.已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=AC5.已知: AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CA6.已知: AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、 CE 分别均分∠ ABC 、∠ BCD ,且点 E 在 AD上。
求证: BC=AB+DC 。
E DCFA B13.已知: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F=∠ C14.P 是∠ BAC 均分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB CAP DB15. 已知∠ ABC=3 ∠ C,∠ 1=∠2, BE⊥ AE ,求证: AC-AB=2BE16.已知, E 是 AB 中点, AF=BD , BD=5 , AC=7 ,求 DCDF A CE B18.如图,在△ABC 中, BD =DC ,∠ 1=∠ 2,求证: AD⊥BC .19.如图, OM 均分∠ POQ ,MA ⊥ OP,MB⊥ OQ , A、 B 为垂足, AB 交 OM 于点 N.求证:∠ OAB=∠OBA20.( 5 分)如图,已知 AD ∥BC,∠ PAB 的均分线与∠ CBA 的均分线订交于 E, CE 的连线交AP 于 D .求证: AD +BC =AB.PACEDCD BA B21.如图,△ ABC 中, AD 是∠ CAB 的均分线,且AB=AC+CD,求证:∠ C=2∠ B22.( 6 分)如图①, E、F 分别为线段AC 上的两个动点,且DE ⊥AC 于 E, BF⊥AC 于 F ,若 AB=CD , AF=CE, BD 交 AC 于点 M.(1)求证: MB=MD , ME =MF(2)当 E、F 两点挪动到如图②的地点时,其他条件不变,上述结论可否建立?若建立请赐予证明;若不建立请说明原因.23.已知:如图,DC∥ AB,且 DC =AE, E 为 AB 的中点,( 1)求证:△ AED≌△ EBC.( 2)观看图前,在不添协助线的状况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):AE ODB C24.( 7 分)如图,△ ABC 中,∠ BAC=90 线垂直于过 C 点的直线于 E,直线 CE 交求证: BD =2CE.度, AB=AC, BD 是∠ ABC 的均分线, BD 的延伸BA 的延伸线于 F.FAED证明:B C25、如图: DF=CE, AD=BC,∠ D=∠ C。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF 连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) BA CDF2 1EADBC∴△EFD≌△CGD EF=CG∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C 证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE7.已知:AB=4,AC=2,D是BC中点,AD是整数,求ADADB CA解:延长AD到E,使AD=DE ∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:1CD AB∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=29.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点, AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:1CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD B CBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:1CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD已知:D 是AB 中点,∠ACB=90°,求证:12CD AB已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC1. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C2. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BECDB ADBCAB A CDF2 1 E6. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
.7.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠C8已知:AB=CD,∠A=∠D,求证:∠B=∠CDCBAFEAB CD9.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE10.如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.12.如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.13.已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):FAEDCBOEDCBA24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE . 证明:延长BA 、CE ,两线相交于点F ∵BE ⊥CE ∴∠BEF=∠BEC=90° 在△BEF 和△BEC 中 ∠FBE=∠CBE, BE=BE, ∠BEF=∠BEC∴△BEF ≌△BEC(ASA) ∴EF=EC ∴CF=2CE∵∠ABD+∠ADB=90°,∠ACF+∠CDE=90° 又∵∠ADB=∠CDE∴∠ABD=∠ACF 在△ABD 和△ACF 中 ∠ABD=∠ACF, AB=AC, ∠BAD=∠CAF=90° ∴△ABD ≌△ACF(ASA) ∴BD=CF ∴BD=2CE 25、(10分)如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
证明:∵BE‖CF ∴∠E=∠CFM ,∠EBM=∠FCM ∵BE=CF∴△BEM ≌△CFMFE DCBA MFECBAFE DCBA∴BM=CM ∴AM 是△ABC 的中线.27、(10分)如图:在△ABC 中,BA=BC ,D 是AC 的中点。
求证:BD ⊥AC 。
三角形ABD 和三角形BCD 的三条边都相等,它们全等,所以角ADB 和角CDB 相等,它们的和是180度,所以都是90度,BD 垂直AC28、(10分)AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF 证明:在△ABD 与△ACD 中AB=ACBD=DCAD=AD ∴△ABD ≌△ACD ∴∠ADB=∠ADC ∴∠BDF=∠FDC 在△BDF 与△FDC 中BD=DC ∠BDF=∠FDCDF=DF ∴△FBD ≌△FCD ∴BF=F C29、(12分)如图:AB=CD ,AE=DF ,CE=FB 。
求证:AF=DE 。
因为AB=DCAE=DF,CE=FB CE+EF=EF+FB 所以三角形ABE=三角形CDF 因为 角DCB=角ABFAB=DC BF=CE 三角形ABF=三角形CDE 所以AF=DE30.公园里有一条“Z ”字形道路ABCD ,如图所示,其中AB∥CD ,在AB ,CD ,BC 三段路旁各有一只小石凳E ,F ,M ,且BE =CF ,M 在BC 的中点,试说明三只石凳E ,F ,M 恰好在一条直线上.证:∵AB 平行CD (已知)∴∠B=∠C (两直线平行,内错角相等)∵M 在BC 的中点(已知)∴EM=FM (中点定义)在△BME 和△CMF 中 BE=CF (已知) ∠B=∠C (已证) EM=FM (已证)∴△BME 全等与△CMF (SAS )∴∠EMB=∠FMC (全等三角形的对应角相等) ∴∠EMF=∠EMB+∠BMF=∠FMC+∠BMF=∠BMC=180°(等式的性质) ∴E ,M ,F 在同一直线上31.已知:点A 、F 、E 、C 在同一条直线上, AF =CE ,BE ∥DF ,BE =DF .求证:△ABE ≌△CDF . 证明:∵AF=CE ∴AF+EF=CE+EF ∴AE=CF ∵BE//DF ∴∠BEA=∠DFC 又∵BE=DF ∴⊿ABE ≌⊿CDF (SAS )32.已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。
DCBA FDCBAFE D C BADAFE连结BD ,得到等腰三角形ABD 和等腰三角形BDC ,由等腰△两底角相等得:角ABC=角ADC 在结合已知条件证得:△ADE ≌△ABF 得AE=AF33.如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.因为角1=角2∠3=∠4所以角ADC=角ABC.又因为AC 是公共边,所以AAS==>三角形ADC 全等于三角形ABC.所以BC 等于DC ,角3等于角4,EC=EC 三角形DEC 全等于三角形BEC 所以∠5=∠634.已知AB ∥DE ,BC ∥EF ,D ,C 在AF 上,且AD =CF ,求证:△ABC ≌△DEF .因为D,C 在AF 上且AD=CF 所以AC=DF 又因为AB 平行DE ,BC 平行EF 所以角A+角EDF ,角BCA=角F (两直线平行,内错角相等)然后SSA (角角边)三角形全等35.已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F ,求证:BE =CD .证明:因为 AB=AC , 所以 ∠EBC=∠DCB 因为 BD ⊥AC ,CE ⊥AB 所以 ∠BEC=∠CDB BC=CB (公共边) 则有 三角形EBC 全等于三角形DCB 所以 BE =CD36、如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F 。
求证:DE =DF . AAS 证△ADE≌△ADF37.已知:如图, AC ⊥BC 于C , DE ⊥AC 于E , AD ⊥AB 于A , BC =AE .若AB = 5 ,求AD 的长?654321E DCBAAC B DEF AEB FDCBAE角C=角E=90度角B=角EAD=90度-角BAC BC=AE △ABC ≌△DAE AD=AB=538.如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MC 证明∵AB=AC∴△ABC 是等腰三角形∴∠B=∠C又∵ME=MF ,△BEM 和△CEM 是直角三角形 ∴△BEM 全等于△CEM ∴MB=MC39.如图,给出五个等量关系:①AD BC = ②AC BD = ③CE DE = ④D C ∠=∠ ⑤DAB CBA ∠=∠.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明. 已知: 求证: 证明:已知1,2求证4因为AD=BC AC=BD ,在四边形ADBC 中,连AB 所以△ADB 全等于△BCA 所以角D=角C以4,5为条件,1为结论。
即:在四边形ABCD 中,∠D=∠C ,∠A=∠B ,求证:AD=BC因为 ∠A+∠B+∠C+∠D=360∠D=∠C ,∠A=∠B ,所以 2(∠A+∠D)=360°, ∠A+∠D=180°,所以 AB//DC40.在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.CMF E BC D E(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,而AD ⊥MN 于D ,BE ⊥MN 于E ,∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE .在Rt △ADC 和Rt △CEB 中,{∠ADC=∠CEB ∠ACD=∠CBE AC=CB ,∴Rt △ADC ≌Rt △CEB (AAS ),∴AD=CE ,DC=BE ,∴DE=DC+CE=BE+AD ;(2)不成立,证明:在△ADC 和△CEB 中,{∠ADC=∠CEB=90°∠ACD=∠CBE AC=CB ,∴△ADC ≌△CEB (AAS ),∴AD=CE ,DC=BE ,∴DE=CE-CD=AD-BE ; 41.如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。
求证:(1)EC=BF ;(2)EC ⊥BF (1)证明;因为AE 垂直AB 所以角EAB=角EAC+角CAB=90度因为AF 垂直AC 所以角CAF=角CAB+角BAF=90度所以角EAC=角BAF 因为AE=AB AF=AC 所以三角形EAC 和三角形FAB 全等所以EC=BF 角ECA=角F (2)(2)延长FB 与EC 的延长线交于点G 因为角ECA=角F(已证)所以角G=角CAF 因为角CAF=90度所以EC 垂直BF42.如图:BE ⊥AC ,CF ⊥AB ,BM=AC ,CN=AB 。
求证:(1)AM=AN ;(2)AM ⊥AN 。
证明:(1)∵BE ⊥AC ,CF ⊥AB ∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°∴∠ABM=∠ACN ∵BM=AC ,CN=AB ∴△ABM ≌△NAC ∴AM=AN(2)∵△ABM ≌△NAC ∴∠BAM=∠N ∵∠N+∠BAN=90°∴∠BAM+∠BAN=90°即∠MAN=90°∴AM ⊥AN43.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.求证:BC ∥EF 连接BF 、CE ,证明△ABF 全等于△DEC (SAS ),然后通过四边形BCEF 对边相等的证得平行四边形BCEF 从而求得BC 平行于EF 44.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等吗?请说明理由在AB 上取点N ,使得AN=AC ∠CAE=∠EAN ,AE 为公共边,所以三角形CAE 全等三角形EAN 所以∠ANE=∠ACE 又AC 平行BD所以∠ACE+∠BDE=180而∠ANE+∠ENB=180 所以∠ENB=∠BDE ∠NBE=∠EBNBE 为公共边, 所以三角形EBN 全等三角形EBD所以BD=BN 所以AB=AN+BN=AC+BDF C A M NE 1234 A E B M C F45、(10分) 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .证明:∵AD 是中线∴BD=CD ∵DF=DE ,∠BDE=∠CDF ∴△BDE ≌△CDF ∴∠BED=∠CFD ∴BE‖CF46、(10分)已知:如图,AB =CD ,DE ⊥AC ,BF ⊥AC ,E ,F 是垂足,DE BF . 求证:AB CD ∥.证明:∵DE ⊥AC ,BF ⊥AC ,∴∠DEC=∠AFB=90°,在Rt △DEC 和Rt △BFA 中,DE=BF ,AB=CD ,∴Rt △DEC ≌Rt △BFA ,∴∠C=∠A ,∴AB ∥CD .47、(10分)如图,已知∠1=∠2,∠3=∠4,求证:AB=CD【待定】48、 (10分)如图,已知AC ⊥AB ,DB ⊥AB ,AC =BE ,AE =BD ,试猜想线段CE 与DE 的大小与位置关系,并证明你的结论.结论:CE>DE 。
