立体图形的计算公式
什么是体积和容量的计算公式

什么是体积和容量的计算公式?体积和容量是数学中与三维图形和物体相关的概念,它们表示了物体所占据的空间大小。
下面将介绍几种常见图形和物体的体积和容量计算公式。
一、长方体的体积和容量计算公式:长方体是一个具有长、宽和高的立体图形,其体积和容量计算公式如下:1. 体积:长方体的体积等于其长、宽和高的乘积。
体积= 长× 宽× 高2. 容量:长方体的容量等于其体积。
容量= 体积二、正方体的体积和容量计算公式:正方体是一个具有相等边长的长方体,其体积和容量计算公式如下:1. 体积:正方体的体积等于边长的立方。
体积= 边长× 边长× 边长2. 容量:正方体的容量等于其体积。
容量= 体积三、圆柱体的体积和容量计算公式:圆柱体是一个具有圆底和等高侧面的立体图形,其体积和容量计算公式如下:1. 体积:圆柱体的体积等于底面积乘以高度。
体积= 底面积× 高度底面积= π × 半径²2. 容量:圆柱体的容量等于其体积。
容量= 体积需要注意的是,圆柱体的底面可以是圆或其他形状,但最常见的是圆底圆柱体。
四、球体的体积和容量计算公式:球体是一个具有球面的立体图形,其体积和容量计算公式如下:1. 体积:球体的体积等于四分之三乘以半径的立方。
体积= (4/3) × π × 半径³2. 容量:球体的容量等于其体积。
容量= 体积需要注意的是,球体的体积和容量计算公式是基于球的半径。
通过了解图形和物体的体积和容量的计算公式,你可以计算不同形状和物体的体积和容量,并进一步应用于解决实际问题,如计算容器的容量、物体的体积等。
体积和容量计算是几何学中的基础知识,也是学习更高级数学和应用数学的基础。
平面图形和立体图形的计算公式知识讲解

平面图形和立体图形的计算公式平面图形和立体图形的计算公式1、正方形(C:周长 S:面积 a:边长)周长=边长×4 C=4a 面积=边长×边长 S=a×a=2a2、正方体(V:体积 a:棱长)表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长 V=a×a×a=3a3、长方形( C:周长 S:面积 a:边长)周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体(V:体积 s:面积 a:长 b: 宽 h:高)(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh5、三角形(s:面积 a:底 h:高)面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形(s:面积 a:底 h:高)面积=底×高 s=ah7、梯形(s:面积 a:上底 b:下底 h:高)面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形(S:面积 C:周长л d=直径 r=半径)(1)周长=直径×л=2×л×半径 C=лd=2лr(2)面积=半径×半径×л=π2r9、圆柱体(v:体积 h:高 s:底面积 r:底面半径 c:底面周长)(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2 (3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体(v:体积 h:高 s:底面积 r:底面半径)体积=底面积×高÷3。
平面图形和立体图形的计算公式

平面图形和立体图形的计算公式1、正方形(C:周长 S:面积 a:边长)周长=边长×4 C=4a 面积=边长×边长 S=a×a=2a2、正方体(V:体积 a:棱长)表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长 V=a×a×a=3a3、长方形( C:周长 S:面积 a:边长)周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体(V:体积 s:面积 a:长 b: 宽 h:高)(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh5、三角形(s:面积 a:底 h:高)面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形(s:面积 a:底 h:高)面积=底×高 s=ah7、梯形(s:面积 a:上底 b:下底 h:高)面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形(S:面积 C:周长л d=直径 r=半径)(1)周长=直径×л=2×л×半径 C=лd=2лr(2)面积=半径×半径×л=π2r9、圆柱体(v:体积 h:高 s:底面积 r:底面半径 c:底面周长)(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2 (3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体(v:体积 h:高 s:底面积 r:底面半径)体积=底面积×高÷3。
人教版六年级数学下册《立体图形特征及计算公式》整理复习

立体图形的计算公式
名称
计算公式
长方体
棱长总和=(长+宽+高)×4 表面积=(长×宽+长×高+宽×高)×2
体积=长×宽×高 或 体积=底面积×高
棱长总和=棱长×12
正方体 表面积=棱长×棱长×6
体积=棱长3 或 体积=底面积×高
立体图形整理复习
立体图形的特征
图形
图形的特征
面:6个,一般是长方形(特殊时会有两相等。 顶点:8个,相交于同一个顶点的3条棱分别叫做长、宽、高。
面:6个,完全相同的正方形。 棱:12条,长度都相等。 顶点:8个。
面:3个,上下两个完全相同的圆形,侧面沿高展开后是个长方形或正方形。 高:无数条,上下底面之间的距离叫做高。
圆柱 侧面积=底面周长×高
体积=底面积×高
底面积=π×半径2
1
圆锥 体积=底面积×高×3
表面积=侧面积+底面积×2
常用立体图形体积公式

常用的立体图形体积公式:
长方体:V=abc(长方体体积=长×宽×高)
正方体:V=a³(正方体体积=棱长×棱长×棱长)
圆柱(正圆):V=πr²×h【圆柱(正圆)体积=圆周率×底半径×底半径×高】圆锥(正圆):V=πr²×h÷3【圆锥(正圆)体积=圆周率×底半径×底半径×高÷3】
角锥:V=rS×h÷3【角锥体积=底面积×高÷3】
柱体:V=sh(柱体体积=底面积×高)
表面积的公式
1、柱体
(1)棱柱
每个面的面积相加
)特殊长方体、正方体(
长方体:S=2(ab+ah+bh)
正方体:S=6a^2
(2)圆柱
S=2πr^2+2πrh
2、锥体
(1)棱锥
每个面的面积相加
(2)圆锥
S=πr^2+πrl
3、台体
(1)棱台
每个面的面积相加
(2)圆台
S=πr^2+πr′ ^2+πrl+πr′ l
4、球
S=4πr^2
提问人的追问2010-03-07 08:00 请问台体是什么呀??
回答人的补充2010-03-07 09:49。
4.立体图形的体积、表面积、侧面积几何重心与转动惯量计算公式
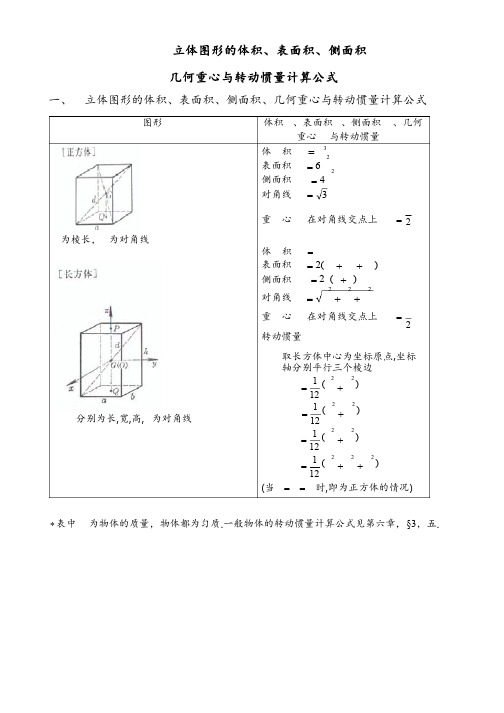
立体图形的体积、表面积、侧面积几何重心与转动惯量计算公式一、 立体图形的体积、表面积、侧面积、几何重心与转动惯量计算公式图形 体积、表面积、侧面积、几何重心与转动惯量为棱长,为对角线分别为长,宽,高,为对角线体 积 3=表面积26=侧面积24=对角线 3=重 心 在对角线交点上2=体 积 =表面积 )(2++=侧面积 )(2+=对角线222++=重 心 在对角线交点上2= 转动惯量取长方体中心为坐标原点,坐标轴分别平行三个棱边)(12122+=)(12122+=)(12122+=)(121222++= (当==时,即为正方体的情况)*表中为物体的质量,物体都为匀质.一般物体的转动惯量计算公式见第六章,§3,五.图形 体积、表面积、侧面积、几何重心与转动惯量为边长,为高为底边长,为高,为对角线为棱数,为底边长,为高,为斜高 体 积 =表面积 +=2侧面积 )(++=式中为底面积重 心2=(、分别为上下底重心)转动惯量对于正三棱柱()取为坐标原点,轴与棱平行1248324==体 积 225981.2233»=表面积61962.563322+»+= 侧面积 6=对角线224+=重 心2=(、分别为上下底重心)转动惯量取为坐标原点,轴与棱平行12583524==体 积 31=表面积 +=侧面积2'==式中为底面积,'为一侧三角形面重 心4h GQ = (Q 为底面的重心)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Ja,b,c,p,q,r 为棱长h 为高体积 011111010101028812222222222222c b ac p qb p r a q r V = 重心PQ GQ 41= (P 为顶点,Q 为底面的重心)体积)''(3FF F F h V ++=式中F F ,'分别为上下底面积重心 '''3'24FF F F F FF F PQ GQ ++++=(P ,Q 分别为上下底重心)分别为上下底边长,为棱数,为高,为斜高体 积÷÷øöççèæ÷øöçèæ++=2''13表面积 ++='侧面积 )'(2+=式中,'分别为上下底面积重 心2222'''3'24++++= (、分别为上下底重心)图形 体积、表面积、侧面积、几何重心与转动惯量两底为矩形,分别为上下底边长,为高,1为截头棱长体积]'')')('([6++++= '''1--=重心''2''2''3''2++++++= (分别为上下底重心)底为矩形,a,b为其边长,h为高,a’为上棱长r为半径 重心'2'2aaaaPQGQ++=(P为上棱中点,Q为下底面重心)体 积33352360.0634ddrV»==pp 表面积24rS p=重 心 G与球心O重合转动惯量取球心O为坐标原点mrJJJzyx252===mrJo253=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[半球体]r为半径,O为球心r为球半径,a为弓形底圆半径,h为拱高,a为锥角(弧度)r为球半径,a为拱底圆半径,h为拱高 体 积 331232drVpp==表面积23rS p=侧面积22rM p=重 心 rGO83=转动惯量取球心O为坐标原点,z轴与GO重合 mrJJJzyx252===mrJo253=体 积 hrhrV220944.232»=p表面积 )2(ahrS+=p侧面积 (锥面部分) rM pa=重 心 )2(83hrGO-=转动惯量z轴与GO重合úûùêëé-÷øöçèæ-=2sin2cos2cos1215225aaap rJz÷øöçèæ+-=2cos2cos32533aahmr体 积)3(3)3(6222hrhhahV-=+=pp表面积 )2()2(222aharhS+=+=pp 侧面积(球面部分))(222harhM+==pp重 心)3()2(432hrhrGO--=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[球台]r为球半径,a¢,a分别为上下底圆的半径,h为高R为中心半径,D为中心直径,r为圆截面半径,d为圆截面直径体 积 )'33(6222haahV++=p表面积 )'2(22aarhS++=p侧面积 rhM p2=2222222'÷÷øöççèæ--+=hhaaar重 心22244'33'23haaaahGO++-=222222'33'422haahaahGQ++++=(Q为下底圆心)体 积 222242DdRrVpp==表面积 DdRrS224pp==重 心 G在圆环的中心上转动惯量取圆环的中心为坐标原点,z轴垂直于圆环所在平面mRrJJyx÷÷øöççèæ+==28522mRrJz÷øöçèæ+=2243图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J [圆柱体]r 为底面半径,h 为高R 为外半径,r 为内半径,h 为高r 为底圆半径,h,H 分别为最小,最大高度,a 为截角,D 为截头椭圆轴体 积h r V 2p = 表面积)(2h r r S +=p 侧面积rh M p 2= 重 心 2hGQ =(P ,Q 分别为上下底圆心) 转动惯量 取重心G 为坐标原点,z 轴垂直底面m h r J J y x ÷øöçèæ+==34122m r J z 22=体 积th R r R h V p p 2)(22=-= 表面积 )(222r R M S -+=p侧面积 R h r R h M p p 4)(2=+= 式中t 为管壁厚,R 为平均半径重 心2h GQ = 转动惯量 取z 轴与GQ 重合 m r R J z 2)(22+=体 积 )(22h H r V +=p 表面积 ÷øöçèæ++=a p cos 112r M S ÷øöçèæ+++=2D h H r r p 侧面积 )(h H r M +=p 截头椭圆轴22)(4h H r D -+= 重 心tan 22r h H +a)(2tan 2h H r GK +=a (GQ 为重心到底面距离,GK 为重心到轴线O O ¢的距离)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Jh 为截段最大高度,b 为底面拱高,2a 为底面弦长,r 为底面半径,a 2为弧所对圆心角(弧度)体 积])(3)3([3222a r b r a r a bh V -+-=÷øöçèæ--=a a a cos sin 31sin 33a b hr侧面积(柱面部分)])[(2a r b b rhM +-=a体 积abc abc V 1888.434»=p 重 心G 在椭球中心O 上 转动惯量 取椭球中心为坐标原点,z 轴与c 轴重合m c b J x )(5122+=m a c J y)(5122+= m b a J z)(122+=a,b,c 为半轴图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J体 积h r V 23p= 表面积 )(l r r S +=p 侧面积 rl M p = 母 线 22h r l +=重 心4h GQ = (Q 为底圆中心,O 为圆锥顶r为底圆半径,h为高,l为母线r,R分别为上,下底圆半径,h为高,l为母线上下底平行,F¢,F分别为上,下底面积,F为中截面面积,h为高取圆锥顶点为坐标原点,z轴与GQ 重合mhrJJyx÷÷øöççèæ+==22453mrJz2103=体 积 )(322RrrRhV++=p表面积 )(22rRMS++=p侧面积 )(rRlM+=p母 线22)(hrRl+-=圆锥高(母线交点到底圆的距离)rRhrhH-+=重 心2222324rRrRrRrRhGQ++++=(P,Q分别为上下底圆心)体 积 )4'(60FFFhV++»[注] 棱台、圆台、球台、圆锥、棱柱、圆柱等都是拟棱台的特例图形 体积V、表面积S、侧面积M、几何重心G与转动惯量Jd 为上,下底圆直径,D 为中截面直径,h 为高母线为圆弧时: 体积)2(26180.0)2(122222d D h d D hhV +»+=p2)2(08727.0d D h +»母线为抛物线时: 体积 ÷øöçèæ++=2243215d Dd D h V p )348(05236.022d Dd D h ++» 重心2h GQ = (P ,Q 分别为上下底圆心)二、 多面体[正四面体] [正八面体] [正十二面体] [正二十面体]图形面数f4 8 12 20 棱数k 6 12 30 30 顶点数e 462012体积V 31179.0a34714.0a36631.7a31817.2a表面积S27321.1a24641.3a26457.20a26603.8a表中a 为棱长.[欧拉公式] 一个多面体的面数为f ,棱数为k ,顶点数为e ,它们之间满足 2=+-f k e。
立体图形的基本知识与计算方法

立体图形的基本知识与计算方法一、立体图形的概念与分类1.立体图形的定义:立体图形是具有三维空间的图形,它包括长度、宽度和高度三个维度。
2.立体图形的分类:a)几何体:根据面的形状和结构,几何体可以分为以下几种类型:•单体几何体:如球体、立方体、圆柱体、圆锥体等;•复合几何体:如长方体、棱柱、棱锥等;•旋转体:如圆环、圆台等。
b)非几何体:如圆柱面、圆锥面、球面等。
二、立体图形的计算方法1.体积的计算:a)单体几何体的体积计算公式:•球体:V = (4/3)πr³;•立方体:V = a³;•圆柱体:V = πr²h;•圆锥体:V = (1/3)πr²h。
b)复合几何体的体积计算公式:•长方体:V = lwh;•棱柱:V = Bh;•棱锥:V = (1/3)Bh。
c)旋转体的体积计算公式:•圆柱面:V = πR²h;•圆锥面:V = (1/3)πR²h;•球面:V = (4/3)πR³。
2.表面积的计算:a)单体几何体的表面积计算公式:•球体:S = 4πr²;•立方体:S = 6a²;•圆柱体:S = 2πrh + 2πr²;•圆锥体:S = πrl + πr²。
b)复合几何体的表面积计算公式:•长方体:S = 2(lw + lh + wh);•棱柱:S = 2(B + Ph);•棱锥:S = 2(B + P)。
c)旋转体的表面积计算公式:•圆柱面:S = 2πRh + 2πR²;•圆锥面:S = πrl + πR²;•球面:S = 4πR²。
三、立体图形的性质与特点1.立方体:立方体有六个面,均为正方形,对角线相等,体积和表面积的计算公式如上所述。
2.球体:球体是一种对称的立体图形,体积和表面积的计算公式如上所述。
3.圆柱体:圆柱体由两个平行的圆形底面和一个侧面组成,体积和表面积的计算公式如上所述。
图形公式大全表

图形公式大全表所有图形的公式一、平面图形公式:1、正方形 s=a²或对角线×对角线÷2 c=4a2、平行四边形 s=ah3、三角形s=ah÷24、梯形s=(a b)×h÷25、圆形s=πr2 c=πd6、椭圆s=πr7、扇形 s=lr/2二、立体图形公式:1、长方体的表面积=2×(长×宽长×高宽×高) 用符号表示是:s=2(ab bc ca)2、长方体的体积 =长×宽×高用符号表示是:v=abh 或底面积×高用符号表示是:v=sh3、正方体的表面积=棱长×棱长×6 用符号表示是:s=a²×64、正方体的体积=棱长×棱长×棱长用符号表示是:v=a³5、圆柱的侧面积=底面周长×高用符号表示是:s侧=πd×h6、圆柱的表面积=2×底面积侧面积用符号表示是:s=πr²×2 dπh7、圆柱的体积=底面积×高用符号表示是:v=πr²×h8、圆锥的体积=底面积×高÷3 用符号表示是:v=πr²×h÷39、圆锥侧面积=1/2*母线长*底面周长10、圆台体积=[s s′ √(ss′)]h÷311、球体体积=(1/3*s*h)*(4*pi*r²)/s=4/3*pi*r²三、立体几何图形:1、柱体:包括圆柱和棱柱。
棱柱又可分为直棱柱和斜棱柱,按底面边数的多少又可分为三棱柱、四棱柱、n棱柱;棱柱体积都等于底面面积乘以高,即v=sh;2、锥体:包括圆锥体和棱锥体,棱锥分为三棱锥、四棱锥及n棱锥;棱锥体积为v=sh/3 ;3、旋转体:包括圆柱、圆台、圆锥、球、球冠、弓环、圆环、堤环、扇环、枣核形等。
平面图形和立体图形的计算公式

平面图形和立体图形的计算公式1、正方形(C:周长S:面积a:边长)周长=边长×4 C=4a 面积=边长×边长 S=a×a=2a2、正方体(V:体积a:棱长)表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长 V=a×a×a=3a3、长方形(C:周长S:面积a:边长)周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体(V:体积s:面积a:长b: 宽h:高)(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh5、三角形(s:面积a:底h:高)面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形(s:面积a:底h:高)面积=底×高 s=ah7、梯形(s:面积a:上底b:下底h:高)面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形(S:面积C:周长лd=直径r=半径)(1)周长=直径×л=2×л×半径 C=лd=2лr(2)面积=半径×半径×л=π2r9、圆柱体(v:体积h:高s:底面积r:底面半径c:底面周长)(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2 (3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体(v:体积h:高s:底面积r:底面半径)体积=底面积×高÷3。
立体图形计算公式

立体图形计算公式立体图形长方体的表面积= (长×宽+长×高,宽×高)×2 用符号表示是:(a×b+a×h+b×h)×2长方体的体积 =长×宽×高用符号表示是:a×b×h正方体的表面积=棱长×棱长×6 用符号表示是:a×a×6正方体的体积=棱长×棱长×棱长用符号表示是:a^3圆柱的侧面积=底面圆的周长×高用符号表示是:πd×h圆柱的表面积=2×底面积+侧面积用符号表示是:πr^2×2+dπh圆柱的体积=底面积×高用符号表示是:πr^2×h圆锥的体积=底面积×高?3 用符号表示是: πr^2×h?3圆锥侧面积=1/2*母线长*底面周长长方体(正方体、圆柱体)的体积=底面积×高用符号表示是:长方形:a×b×h 正方形:a3 圆柱形:πr^2×h圆台体积=[S+S′+?(SS′)]h?3立体图形长方体的表面积= (长×宽+长×高,宽×高)×2 用符号表示是:(a×b+a×h+b×h)×2长方体的体积 =长×宽×高用符号表示是:a×b×h正方体的表面积=棱长×棱长×6 用符号表示是:a×a×6正方体的体积=棱长×棱长×棱长用符号表示是:a^3圆柱的侧面积=底面圆的周长×高用符号表示是:πd×h圆柱的表面积=2×底面积+侧面积用符号表示是:πr^2×2+dπh圆柱的体积=底面积×高用符号表示是:πr^2×h圆锥的体积=底面积×高?3 用符号表示是: πr^2×h?3圆锥侧面积=1/2*母线长*底面周长长方体(正方体、圆柱体)的体积=底面积×高用符号表示是:长方形:a×b×h 正方形:a3 圆柱形:πr^2×h圆台体积=[S+S′+?(SS′)]h?3立体图形长方体的表面积= (长×宽+长×高,宽×高)×2 用符号表示是:(a×b+a×h+b×h)×2长方体的体积 =长×宽×高用符号表示是:a×b×h正方体的表面积=棱长×棱长×6 用符号表示是:a×a×6正方体的体积=棱长×棱长×棱长用符号表示是:a^3圆柱的侧面积=底面圆的周长×高用符号表示是:πd×h圆柱的表面积=2×底面积+侧面积用符号表示是:πr^2×2+dπh圆柱的体积=底面积×高用符号表示是:πr^2×h圆锥的体积=底面积×高?3 用符号表示是: πr^2×h?3圆锥侧面积=1/2*母线长*底面周长长方体(正方体、圆柱体)的体积=底面积×高用符号表示是:长方形:a×b×h 正方形:a3 圆柱形:πr^2×h圆台体积=[S+S′+?(SS′)]h?3。
小学数学立体图形知识汇总

小学数学立体图形知识汇总(一)长方体1、特征六个面都是长方形(有时有两个相对的面是正方形)。
相对的面面积相等,12条棱相对的4条棱长度相等。
有8个顶点。
相交于一个顶点的三条棱的长度分别叫做长、宽、高。
两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
把长方体放在桌面上,最多只能看到三个面。
长方体或者正方体6个面的总面积,叫做它的表面积。
2、计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1、特征六个面都是正方形六个面的面积相等12条棱,棱长都相等有8个顶点正方体可以看作特殊的长方体S表=6a²v=a3(三)圆柱1、圆柱的认识圆柱的上下两个面叫做底面。
圆柱有一个曲面叫做侧面。
圆柱两个底面之间的距离叫做高。
进一法:实际中,使用的材料都要比计算的结果多一些,因此,要保留数的时候,省略的位上的是4或者比4小,都要向前一位进1。
这种取近似值的方法叫做进一法。
2、计算公式s侧=chs表=s侧+s底×2v=sh/3(四)圆锥1、圆锥的认识圆锥的底面是个圆,圆锥的侧面是个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
测量圆锥的高:先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面之间的距离。
把圆锥的侧面展开得到一个扇形。
v=sh/3(五)球1、认识球的表面是一个曲面,这个曲面叫做球面。
球和圆类似,也有一个球心,用O表示。
从球心到球面上任意一点的线段叫做球的半径,用r表示,每条半径都相等。
通过球心并且两端都在球面上的线段,叫做球的直径,用d表示,每条直径都相等,直径的长度等于半径的2倍,即d=2r。
2、计算公式d=2r。
4. 立体图形的体积、表面积、侧面积 几何重心与转动惯量计算公式

r,R分别为上,下底圆半径,h为高,l为母线
上下底平行, , 分别为上,下底面积, 为中截面面积,h为高
体积
表面积
侧面积
母线
重心
(Q为底圆中心,O为圆锥顶点)
转动惯量
取圆锥顶点为坐标原点,z轴与GQ重合
体积距离)
重心
(P,Q分别为上下底圆心)
两底为矩形,a’,b’,a,b分别为上下底边长,h为高, 为截头棱长
底为矩形,a,b为其边长,h为高,a’为上棱长
r为半径
体积
重心
(P,Q分别为上下底重心)
体积
重心
(P为上棱中点,Q为下底面重心)
体积
表面积
重心G与球心O重合
转动惯量
取球心O为坐标原点
图形
体积V、表面积S、侧面积M、几何重心G与转动惯量J
R为外半径,r为内半径,h为高
r为底圆半径,h,H分别为最小,最大高度, 为截角,D为截头椭圆轴
体积
表面积
侧面积
重心
(P,Q分别为上下底圆心)
转动惯量
取重心G为坐标原点,z轴垂直底面
体积
表面积
侧面积
式中t为管壁厚, 为平均半径
重心
转动惯量
取z轴与GQ重合
体积
表面积
侧面积
截头椭圆轴
重心
(GQ为重心到底面距离,GK
8
12
20
棱数k
6
12
30
30
顶点数e
4
6
20
12
体积V
表面积S
表中a为棱长.
[欧拉公式]一个多面体的面数为f,棱数为k,顶点数为e,它们之间满足
平面图形和立体图形的计算公式

平面图形和立体图形的计算公式
1、正方形(C:周长S:面积a:边长)
周长=边长x 4 C=4a 面积=边长x边长S=a x a=a2
2、正方体(V:体积a:棱长)
表面积=棱长x棱长x 6 S 表=a x a x6
体积=棱长x棱长x棱长V=a x a x a=a3
3、长方形(C :周长S :面积a :边长)
周长=(长+ 宽)x 2 C=2(a+b)
面积=长乂宽S=ab
4、长方体(V: 体积s: 面积a: 长b: 宽h: 高)
(1)表面积(长x宽+长x高+宽x高)x 2 S=2(ab+ah+bh)
⑵体积=长乂宽x高V=abh
5、三角形(s :面积a :底h :高)
面积=底乂咼* 2 s=ah 宁2
三角形高= 面积x 2宁底三角形底=面积x 2宁高
6、平行四边形(s :面积a :底h:高)
面积=底乂高s=ah
7、梯形(s :面积a:上底 b :下底h:高)
面积=(上底+下底)x高* 2 s=(a+b)x h宁2
8、圆形(S :面积C :周长JI d=直径r=半径)
(1)周长=直径x J =2x J x 半径C= J d=2 J r
⑵面积二半径x半径x J = n r2
9、圆柱体(v:体积h:高s:底面积r:底面半径c:底面周长)(1)侧面积=底面周长x高=ch(2 J r或J d)(2)表面积= 侧面积+底面积
x 2
(3)体积=底面积x高(4)体积=侧面积* 2x半径。
平面图形和立体图形的计算公式

----WORD格式--可编辑--------平面图形和立体图形的计算公式1、正方形(C:周长S :面积a:边长)周长=边长× 4 C=4a面积 =边长×边长 S=a ×a=a22、正方体(V: 体积 a:棱长)表面积 =棱长×棱长× 6S 表 =a×a×6体积 =棱长×棱长×棱长V=a × a× a=a33、长方形( C:周长S :面积a:边长)周长 =( 长 +宽 ) × 2C=2(a+b)面积 =长×宽S=ab4、长方体(V:体积s:面积a:长b:宽h:高)(1)表面积 ( 长×宽 +长×高 +宽×高 ) ×2 S=2(ab+ah+bh)(2)体积 =长×宽×高 V=abh5、三角形(s:面积 a :底h:高)面积 =底×高÷ 2s=ah÷2三角形高 =面积×2÷底三角形底 =面积× 2÷高6、平行四边形(s:面积 a:底h :高)面积 =底×高 s=ah7、梯形(s:面积 a :上底b:下底 h:高)面积 =( 上底 +下底 ) ×高÷ 2s=(a+b) × h ÷ 28、圆形(S:面积 C :周长л d= 直径r= 半径)(1)周长 =直径×л=2×л×半径 C= лd=2л r(2)面积 =半径×半径×л =πr29、圆柱体(v:体积h:高s:底面积r:底面半径c:底面周长)(1)侧面积 =底面周长×高 =ch(2 лr 或лd) (2) 表面积 =侧面积 +底面积× 2 (3) 体积 =底面积×高( 4)体积=侧面积÷2×半径10、圆锥体(v:体积h:高s:底面积r:底面半径)体积 =底面积×高÷3。
立体图形概念及公式

一、常用空间图形公式:1、正方体(V:体积a:棱长L:棱长总和)正方体表面积=棱长×棱长×6 S表=a×a×6正方体棱长总和=棱长×12 L=a×12正方体体积=棱长×棱长×棱长=底面积×高V=a×a×a2、长方体(V:体积s:面积a:长b: 宽h:高)san长方体表面积=(长×宽+长×高+宽×高)×2 S=(ab+ah+bh)×2 长方体棱长总和×=(长+宽+高)×4=长×4+宽×4+高× 4长方体体积=长×宽×高V=abh(长方体、正方体)都适用:体积=底面积×高=横截面积×长高=体积÷底面积3、正方形(L:周长S:面积a:边长)正方形周长=边长×4 L=4a正方形面积=边长×边长S=a×a4、长方形(L:周长S:面积a:边长)长方形周长=(长+宽)×2 L=2(a+b)长方形面积=长×宽S=ab5、三角形(s:面a:底h:高)三角形面积=底×高÷2 s=ah÷2三角形的高=面积×2÷底三角形的底=面积×2÷高6、平行四边形(s:面积a:底h:高)平行四边形面积=底×高s=ah7、梯形(s:面积a:上底b:下底h:高)梯形面积=(上底+下底)×高÷2 s=(a+b)× h÷2表面积和体积只可能数值一样,但不能比较大小,因为它们所表示的意义不一样。
二、常用单位换算1、长度单位换算(10):1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米2、面积单位换算(100):1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米3、体(容)积单位换算(1000):1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升三、概念:1、体积:物体所占的空间大小。
立体几何面积和体积公式

立体几何面积和体积公式立体几何面积和体积公式立体几何是三维空间中物体的形状和大小的研究,可以从表面面积和体积两方面进行探究。
在数学中,计算几何就是研究空间中的几何图形及其性质的一门学科,而立体几何是计算几何的一个重要分支。
本文将简要介绍立体几何的面积和体积公式。
一、立体几何面积公式立体图形表面的面积是指该物体上外表面积的总和。
立体几何面积公式的推导是通过三维几何公式及微积分基本定理进行特定面积的求导推导的。
至于常见图形的具体推导将在下面讨论。
1.长方体表面积公式长方体一共有6个面,每个面的面积都是$l \times w$。
根据此,长方体的表面积公式可以表示为$ S=2lw+2lh+2wh$。
2.球体表面积公式球体的表面积为球的表面面积,即 $S=4\pi r^2 $,其中,$\pi$是圆周率,$r$是球体的半径。
3.圆锥表面积公式圆锥的表面积是锥和底面的总和。
锥的表面积为$S_a=\pi rl$,其中 $l$ 为斜高,$r$ 为底面半径。
底面的面积为$S_b=\pi r^2$。
根据此,圆锥表面积公式可以表示为$S_a+S_b=\pi r^2+\pi rl$。
4.圆柱表面积公式圆柱的表面积是上下两个圆面积和侧面积之和。
上下圆面积为 $\pi r^2$,侧面积为$l \times 2 \pi r$。
根据此,圆柱表面积公式可以表示为$ S=2 \pi r^2 +2\pi rl$。
5.正四面体表面积公式正四面体相对简单,它的表面积是所有面积的总和,即 $S=a^2\sqrt{3}$,其中,$a$是正四面体的边长。
6.棱锥表面积公式棱锥的表面积是锥和底面的总面积。
锥体积为$S_a=\sqrt{h^2+b^2}$,其中,$h$ 为棱锥高,$b$ 为底部边长。
底面积为 $S_b=\frac{1}{2}(bl)$,其中,$l$ 为底部棱长。
根据此,棱锥表面积公式可以表示为$S=S_a+S_b=\frac{1}{2}bh+\frac{1}{2}bl+\sqrt{h^2+b^ 2}$。
立体图形的认识与计算

计算方法:根据立体图形的形状和结构,计算其顶点数
立体图形的边数是指构成立体图形的面的数量。
边数是立体图形分类的一种重要依据。
边数相同的立体图形可能具有相似的几何特性。
不同边数的立体图形具有不同的几何特性。
定义:立体图形中面的数量
01
02
性质:立体几何中的图形具有三维空间特性,包括形状、大小、位置等。
空间关系:立体几何研究图形之间的空间关系,如平行、相交、垂直等。
03
04
定理和公理:立体几何有一系列定理和公理,用于推导和证明空间图形的性质和关系。
定义:空间向量是有大小和方向的量,表示为矢量或向量
空间向量的模:表示空间向量的长度或大小
土木工程:立体图形在土木工程中用于描述建筑物的结构和外观
机械设计:立体图形在机械设计中用于描述零件的形状和尺寸
立体几何模型:用于描述三维空间中的形状和物体
计算几何模型:用于计算几何形状的面积、体积等
数学建模竞赛:立体图形的应用是数学建模竞赛中常见的主题之一
物理学建模:用于描述物理现象和物体运动规律的模型
医学影像:医学影像的呈现需要使用立体图形进行三维重建和可视化
电子科技:电路板、芯片等的设计需要使用立体图形进行建模和仿真
机械制造:机械零件的设计和制造需要使用立体图形进行建模和模拟
建筑行业:建筑设计、施工、装修等环节需要使用立体图形进行空间分析和设计
定义:立体几何是研究空间图形和空间关系的科学,包括点、线、面、体等基本元素。
计算方法:通过顶点和边数计算
特性:不同立体图形的面数不同,与立体图形的形状有关
分类:平面图形和立体图形
