5求图示桁架指定杆的内力
理论力学4.4第4-4章平面简单桁架的内力计算

x y
0, F2 20 0 0, F1 0
解得: F1 0 F2 20kN
20kN
C
FAx F3 F4 FAy
10kN 10kN 10kN 10kN
F1
A
FBy
F2
FAx
解:(1) 取整体为研究对象
FAy
F1
(3) 取节点A为研究对象
F 0 , F F F cos 45 0 x Ax 4 3 F 0 , F F F sin 45 0 y Ay 1 3
F 0, F F 0, F M 0,
再以截面m-n左面部分为研究对象 MC 0
F3 A C FA F2 F4 F1
Fa F1b FA 2a 0 F1 4a F b
F
F
b
FB
例 题 4
C
求:桁架1、2杆的力。 解:(1) 取整体为研究对象
D a
M
解得:
a
B
0, P.2a FAy 3a 0
FAy 2P 3
α A E F FAC α α C α α
O α B C F G D FBC FGy FGx M
2M CG 2l cos 30 FBC 3l 参考受力图(b), 选x轴与FOB垂直。 ' O O F 0 , F . COS 30 F . COS 60 0 x BC AB
Fi Fix i Fiy j FR
i 1 i 1 i 1
n
n
n
理论力学作业解答2013

学号 姓名11-5 力F 沿正六面体的对顶线AB 作用,F =100N ,求F 在ON 上的投影。
解:2220.330N 0.410.30.40.4x F F =-=-++ 2220.440N 0.410.30.40.4y F F ==++ 2220.440N 0.410.30.40.4z F F ==++ ON 方向单位矢量0.40.20.20.2ON j k =+ 400.4400.2N+N 83.8N 0.410.20.410.2ON F F ON =⋅==1-8 试求附图所示的力F对A点的矩,已知 1r =0.2m,2r =0.5m,F =300N 。
解:力F 作用点B o o121(sin 60,cos 60)r r r -o cos 60x F F =,o sin60y F F =o o 121()sin60(cos60)15kN m A y x M F r F r r F =⋅--⋅=-⋅1-9 试求附图所示绳子张力F T 对A 点及对B 点的矩。
已知F T =10kN ,l =2m ,R =0.5m,α=30°。
解:()100.55kN m A T T M F F R =⋅=⨯=⋅o o ()(sin 60)10(2sin 600.5) 5103=-12.3kN mB T T M F F l R =-⋅-=-⨯-=-⋅1-11 钢缆AB 的张力 F T =10kN 。
写出该张力F T 对x 、y 、z 轴的矩及该力对O 点的矩(大小和方向)。
解:(1)kN 36.2231104111222=⋅=++⋅=T Tx F FkN 36.2231104111222-=⋅-=++⋅-=T Ty F FkN 43.9234104114222-=⋅-=++⋅-=T Tz F F(2)对轴的矩(位置矢量k j r OA42+==)m kN 43.9234042)(⋅-=-=⋅-⋅=Ty Tz T x F F F MB2m kN 43.923404)(⋅==⋅=Tx T y F F M ,20()2 4.72kN m 32z T Tx M F F =-⋅=-=-⋅ (3)对点的矩()9.439.43 4.72(kN m)O T T x y z M F r F i j k M i M j M k =⨯=-+-=++⋅1-13 工人启闭闸门时,为了省力,常常用一根杆子插入手轮中,并在杆的一端C 施力,以转动手轮。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
工程力学32 静定平面桁架结构的内力计算

定
12kN
12kN
结 构
3m 3
6kN D
F
J
6kN
L
的 内 力
FxA
AC E G
IK
B
4m 6
FyA
FyB
计 算 1.求支座反力
FxA 0 FyA 36kN FyB 36kN
2020/10/4
重庆工程职业技术学院
11
静定桁架
结 构
12kN 12kN
12kN H 12kN
12kN
力 学
3m 3
静 定
3、注意:
结
(1)一般结点上的未知力不能多余两个。
构 的
(2)可利用比例关系求解各轴力的铅直、水平分量。
内
力
计
算
2020/10/4
重庆工程职业技术学院
10
静定桁架
结 三、静定平面桁架的内力计算
构 (一)结点法
力
以一个结点为隔离体,用汇交力系的平衡方程求解
学
各杆的内力的方法。
静
12kN
12kN H 12kN
结 构 力 学
静 定 结 构 的 内 力 计 算
结 一、概述 构 力 学
静定桁架
静
定
结
构
的
主桁架
内
力
计
算
2020/10/4
重庆工程职业技术学院
2
结 一、概述 构
力 学
静定桁架
静 理想桁架的三点假设:
定
结
(1)所有的结点都是无摩擦的理想铰结点;
构
(2)各杆的轴线都是直线,并通过铰的中心;
的
(3)荷载和支座反力都作用在结点上。
南京航空航天大学 结构力学 课后习题答案 第6章

6-1 题6-1图所示平面桁架,各杆Ef 相同,求在载荷P 作用下桁架各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除1-2杆的约束, 代之以约束力X 1,如图6-1a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>> 下的内力N 1,内力分别如图6-1b,6-1c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1PEfdEf l N i i )223(2111+===∑ δ EfPdEf l N N i i P P 2111-===∆∑(4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:PP d EfEf Pd X P 172.0)223()223(22/1111≈-=+=∆-=δ(5)用叠加原理11X N N N P +=求出各杆的内力PN N P N N P N N P N )12(;)222(;)22(;)223(45342414251312-==-==-==-=6-2 题6-2图所示平面桁架,杆长AD=DC=BC=1m,AC 杆和BD 杆的截面积A AC =A BD =200mm 2,A AD =A DC =A BC =150mm 2, 各杆材料均相同,E =200KN/mm 2,当C 点受垂直载荷P =100KN 作用时,求该结构各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除CD 杆的约束, 代之以约束力X 1,如图6-2a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>>下的内力N 1,内力分别如图6-2b,6-2c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1P1150.0803342111≈+===∑ i i Ef l N δ4316.048093411-≈-===∆∑P Ef l N N i i P P (4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:755.3663437233480480934/1111≈--=+⨯--=∆-=P P X P δ(5)用叠加原理求出各杆的内力: 11X N N N P +=KN N C B 480.88=-KN N D B 252.3-=-748.46=-C A NKN N D A 877.1=-KN N D C 755.3=-如图6-2d 所示。
结构力学第2章习题及参考答案
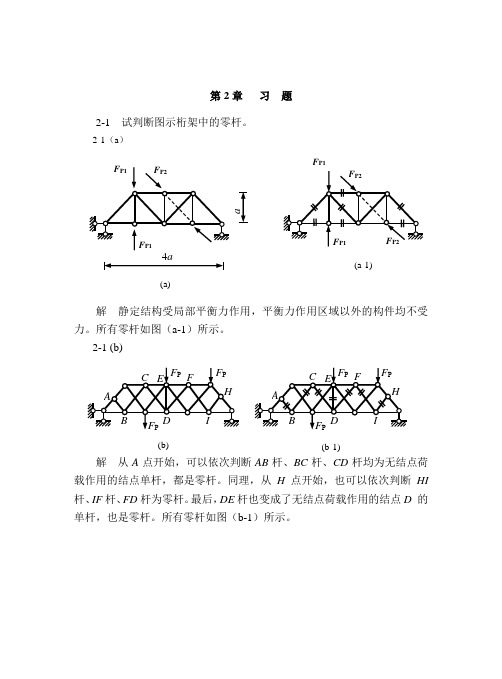
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
土木工程力学形成性考核册(带答案)

土木工程力学(本)形成性考核册作业一一、选择题(每小题2分,共20分)1.三刚片组成几何不变体系的规则是(B)A 三链杆相联,不平行也不相交于一点B 三铰两两相联,三铰不在一直线上C 三铰三链杆相联,杆不通过铰D 一铰一链杆相联,杆不过铰2.在无多余约束的几何不变体系上增加二元体后构成(C)A 可变体系B 瞬变体系C 无多余约束的几何不变体系D 有多余约束的几何不变体系3.瞬变体系在一般荷载作用下,(C)A产生很小的内力 B不产生内力C产生很大的内力 D不存在静力解答4.已知某体系的计算自由度W=-3,则体系的( D )A自由度为3 B自由度等于0C 多余约束数等于3D 多余约束数大于等于35.不能作为建筑结构使用的是(D)A无多余约束的几何不变体系B有多余约束的几何不变体系C 几何不变体系 D几何可变体系7.下图所示结构的弯矩图形状应为(A)A 折线B 圆弧C 双曲线D 抛物线二、判断题(每小题2分,共20分)1.多余约束是体系中不需要的约束。
(⨯)2.如果体系的计算自由度大于零,那么体系一定是几何可变体系。
(∨)3.两根链杆的约束作用相当于一个单铰。
(⨯)4.一个体系是有n个自由度的几何可变体系,那么加入n个约束后就成为无多余约束的几何不变体系。
(⨯)题2-7图原结构是一个无多余约束的几何不变体系。
2.解:由二元体分析法原结构是一个无多余约束的几何不变体系。
3.解:显然,体系是具有两个多余约束的几何不变体系。
4.解:由三刚片规则,可知体系是无多余约束的几何不变体系。
四、绘制下图所示各结构的弯矩图。
(每小题10分,共30分)⨯ ⨯1.作弯矩图如下:2.解: 作弯矩图如下:3.D M解: 作弯矩图如下:五、计算图示桁架中指定杆件的内力。
解:求支座反力 由AM=0∑B P P F 4a F 2a F 3a 0--= PB 5F F ()4=↑ 由yF=0∑A P P P 5F F F F 04+--= P A 3FF ()4=↑用Ⅰ-Ⅰ截面将桁架截开,保留右边部分,受力如图: 由yF=0∑N1P P 5F sin 45F F4︒+-=N1P F F 4=-(压) 由CM=0∑M 图(kN •m )F F F P F 4ⅠP N3N15F a F a F cos 45a 04--︒= N3P 3F F 2=(拉)取结点C 为研究对象,作受力图如下: 显然:N2P F F =-(压)作业二一、选择题(每小题2分,共10分)1.用力法计算超静定结构时,其基本未知量为(D )A 杆端弯矩B 结点角位移C 结点线位移D 多余未知力2.力法方程中的系数ij δ代表基本体系在1=j X 作用下产生的(C )A i XB j XC i X 方向的位移D j X 方向的位移 3.在力法方程的系数和自由项中( B )A ij δ恒大于零B ii δ恒大于零C ji δ恒大于零D iP ∆恒大于零4.下列哪一条不是图乘法求位移的适用条件?( D ) A 直杆 B EI 为常数C P M 、M 至少有一个为直线形D P M 、M 都必须是直线形 5.下图所示同一结构在两种不同荷载作用下,它们之间的关系是(D ) A A 点的水平位移相同 B C 点的水平位移相同 C C 点的水平位移相同 D BC 杆变形相同F F N4二.判断题(每小题2分,共10分)1.静定结构由于支座移动引起的位移与刚度无关。
结构力学 第五章 作业参考答案

结构力学 第五章习题 参考答案2005级 TANG Gui-he (整理)5-1 试用结点法计算图示桁架各杆的内力。
5-2 试用结点法计算图示桁架各杆的内力。
解:由整体平衡条件可解得支座反力 F A =1.5F F B =1.5F 取结点A 为隔离体,如图,用数解法可解得 F A C =-2.12F F A B =1.5F 同理,依次取结点B 、C 、 D 、E 为隔离体,并由对称性可得各杆的内力如图。
4 * 8m60k N60k N6M 2MA B C D E FG H 解:由 M H =0 可得支座F a y=75kN.由 F Y=0 得 F h y=45kN 取 A 结点为隔离体,利用数解法可得 F N AB=-100kN. F NAC=125kN. 再取 C 点为隔离体,利用投影法和力平衡 可得 F N BC=-50,F NCE=103.1kN.同理依次取 B , D , E , G , F 可得各杆内力(如图所标)AC-60k N -90k N -100k N 45k N75k N125k N 75k N 42.4k N61.8k N 103.1k N -60k N -50k N -30k N55-4试判断图示桁架中的零杆。
解:图中红色的杆件为零杆在杆中标有 为零杆其中用到K 型和T 型结构判断原理5-5试用截面法计算图示桁架中指定杆件的内力。
2解:(1)求出支座竖向反力为2.5F (↑),(2)作截面I -I ,由∑M A=0得: 2.5F ×15-10F -5F +6F N 1=0 → F N 1=-3.75F (3)由∑M B=0得: 2.5F ×10-F ×5-F N 2×6=0 → F N 2=3.33F (4)利用勾股定理求出A B 杆长7.8F N 4x =5F N 4/3.84 由∑M C=0得: 2.5F ×10-5F +F N 1×6+6×5F N 4/7.8=0 → F N 4=0.65F (5)取结点B 为分析对象,由∑F Y=0得: F N 4×6/7.8+F N 3=0 → F N 3=-0.5F5-6试用截面法计算图示桁架中指定杆件的内力。
《结构力学》习题解答(内含解答图)

解:将固定铰支座换为单铰,如图(b),由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结BF为刚片Ⅱ,铰结△CDE为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支撑杆F相连,虚铰在无穷远处,刚片Ⅰ与刚片Ⅲ是由杆AC和支撑杆E相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是由杆BC和杆FD相连,虚铰在两杆的延长线的交点处。此时,三铰不共线,该体系为几何不变体,且无多余约束。
所以,体系是几何不变得,且无多余约束。
习题2-2试对图示体系进行几何组成分析。
解:从图2-15(b)可知,杆件CD和链杆3及铰D构成二元体,可以去掉;取杆件CB为刚片Ⅰ,基础作为刚片Ⅱ,根据规则一,两刚片是通过杆AB、链杆1、2组成几何不变体。所以,整个体系为几何不变体系,且无多余约束。
习题2-2图习题2-2解答图
习题2-10试对图示体系进行几何组成分析。
习题2-10图习题2-10解答图
解:由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结△ABF为刚片Ⅱ,铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆EA和支撑杆F相连,虚铰在两杆的延长线的交点处,刚片Ⅰ与刚片Ⅲ是由杆EC和支撑杆D相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是铰B相连。此时,三铰不共线,该体系为几何不变体,且无多余约束。
习题2-26图习题2-26解答图
解:将链杆截断,截断一处,去掉一个约束,共去掉四个约束;再将刚性联结杆截断,截断一处,去掉三个约束,共去掉十二个约束,如图(b)。此时,体系变成与基础独立相连的三个单一杆件,见图(b)。所以,该体系具有十六个多余约束的几何不变体。
2.3.2提高题
提高题2-1 试对图示体系作几何组成分析。
所以,由规则一知,体系是几何不变体,且无多余约束。
工程力学_复习题

工程力学(理、材)_复习题(总16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2《工程力学》本科复习题一、 单项选择题:解题要求:根据工程力学的基本概念和理论,从每小题的四个备选答案中选出一个正确的答案,并将正确答案的字母填写在相应的括号内。
1.若( B )中各分力对任意点之矩的矢量和为零,则该力系一定为平衡力系。
(A )汇交力系; (B )力偶系; (C ) 平面一般力系; (D )空间一般力系。
2. 应力是指( B )。
(A )受力物体截面上内力的分力, (B )受力物体截面上内力的分布集度, (C )受力物体截面上每一点的内力, (D )受力物体内部对外力的响应力。
(A )比例极限P σ; (B )弹性极限e σ; (C )屈服极限s σ; (D )强度极限b σ。
3. 用公式[]nuσσ=确定材料的许用应力值时,通常脆性材料是以其( D )作为极限应力(式中的u σ)。
(A )比例极限P σ; (B )弹性极限e σ; (C )屈服极限s σ; (D )强度极限b σ。
4. 杆件内力矢量沿其轴线的分量,称为( A )。
(A )轴力, (B )剪力, (C )扭矩, (D )弯矩。
5.关于扭弯组合:①公式WT M 22+≤[]σ是用( ①C )强度理论,为扭弯组合下的圆轴所建立的强度条件计算式。
② 公式WT M 2275.0+≤[]σ是用( D )强度理论,为扭弯组合下的圆轴所建立的强度条件计算式。
(A )第一 ; (B )第二; (C )第三; (D )第四6. 题图所示四个力系中,各力大小均为F ,分别以不同方式作用在边长为a 的正方形的四个顶点,其中一个力系的最简结果是一个力偶之矩M =Fa 且逆时针转动的合力偶,该力系是( D )。
(A )(B )(C )(D )一、6题 图7. 如图(a )所示,重为G 的均质圆柱在夹板AB 与墙壁AC 之间,夹板A 端有固定铰链支座与墙壁连接,B 端用绳索CB 拉住,CB 垂直于墙壁,若不计夹板AB 的自重和各接触处的摩擦。
结构力学 06静定桁架和组合结构--习题.

N
3
3 5
75
50
0
即
N2
N3
125 3
N2 20.8kN(压) N3 20.8kN(拉)
-4 -4 2m -4 -4
结构力学电子教程
6 静定桁架和组合结构
6.4 作图示组合结构的内力图。
(a)
A
q=1kN/m I
F
C
G
I-I截面右部分: q=1kN/m
B
C
B
4kN
G
4kN D +4
2m 2m
解: 反力如图。
E
I
2m
+4 4
4kN
2m
2
2
4k
Q (kN)
4
M (kNm)
+4
N (kN)
结构力学电子教程
6 静定桁架和组合结构
建筑力学(第二版)
张曦 主编
结构力学电子教程
6 静定桁架和组合结构
习题14-10 试用结点法求图示桁架各杆的轴力。
(a)
A
C
60kN
30kN
M C
0:
N1 4 303
0
N1 22.5kN(拉)
M D
0 : N2 4 306 0
N2
45kN(压)
(3)II-II截面右部分
X
3 0 : 22.5 45 N3 5 0
N3
37.5kN(拉)
结构力学电子教程
30 20kN
D
NDC
NDE
30 5kN
结构力学(2.1.2)--静定结构内力分析习题及参考答案

Fp
Fp
4×d
(d)
3-7 试求图示抛物线( y 4 fx(l x) / l 2 ) 三铰拱距左支座 5m 的截面内力。
4m 4m 3d
4m
5 kNF P 1
d
10 kN 1 F3(Pf×)d F2P
2
NN N
习题 3-6 图
2
d
N
15 kN
1
d2/02kN/md d/2
40 kN·m
y
A
B 20 kN
8×1 m
习题 3-5 图
杆件的内力。
80 kN
1 N
2 N
4m 2m
4m
2m
(a)
2m 2m 2×d
20 kN
3.6 试 用 较 简单的 方法求 图示桁 架指定
4
3
1
N 2
NN
Fp
Fp
Fp Fp 8×d
Fp
Fp N
Fp N
(b)
3×2 m d
60 kN
1
N
2
N
4×2 m (c)
Fp 1
2m
6m
6m
2m
(b)
习题 3-16 图
l
3m
4m 4m
3-17 试作图示组合结构的弯矩图和轴力图。
20 kN/m
B
C
A 4m 4m 4m 4m
(a)
习题 3-17 图
20 kNA 20 kN/m
BCD源自4m4m4m(b)
3-1 略
参考答案
3-2 (a) FNAB 25kN (b) FNAB 2.5FP
A
3m
(a) C
桁架内力计算

第3章静定结构的内力计算
例题3
A C
18kN 3
试求图示桁架1、2、3、4杆内力
B
1 2
3kN 6kN 6kN 6kN 3kN
D
n m
H F
4
G
2×2=4m
解: 1、求支反力 A、B支反力分别为18kN、6kN 2、求内力 截面法求联系杆内力 m-m截面
E
n 2×8=16m m
B
1
6kN
3kN 6kN 6kN 6kN
对称 K形 结点
FNCD FNCE
FNCD FNCE
FN FNx FNy l lx ly
A FP FP
FNCD FNCE 0
D E B FP C FP
反对称 同一 杆件
FNDE FNED
FNDE FNED
FNDE FNED 0
结构力学
第3章静定结构的内力计算
2kN
x
FNA1 A FR Ax FR Ay
FN52
FN41
1
FN12 FN15
FN21
FN23
FNA4
FN4A
4
8 kN
FN46
FN1A FN14
FN25
FN51
FN53
FN63
FN54
5
FN56
FN65
6
FN6B
结构力学
1 4 2
第3章静定结构的内力计算
4 3
3m
6 2
A FR Ax FR Ay
FN21
FN23
FNA4
FN4A
4
8 kN
FN46
FN1A
FNB3
力学计算题部分

1、作如图所示多跨梁各段的受力图。
本题考核的知识点是物体的受力分析方法。
解:作AB段的受力图如图(a),作BC段的受力图如图(b)取梁BC为研究对象。
受主动力1F 作用。
C处是可动铰支座,它的反力是垂直于支承面的C F ,指向假设垂直支承面向上;B处为铰链约束,它的约束力可用两个互相垂直的分力Bx F 、By F 表示,指向假设如图。
取梁AB为研究对象。
A处是固定铰支座,它的反力可用Ax F 、Ay F 表示,指向假设如图;D处是可动铰支座,它的反力是垂直于支承面的D F ,指向假设向上;B处为铰链约束,它的约束力是BxF '、By F ',与作用在梁BC上的Bx F 、By F 是作用力与反作用力的关系,其指向不能再任意假定。
2、桥墩所受的力如图所示,求力系向O点简化的结果,并求合力作用点的位置。
已知kN F P 2740=,kN G 5280=,kN F Q 140=,kN F T 193=,m kN m ⋅=5125。
本题考核的知识点是平面一般力系的平衡方程和解题方法。
本题是一个平面一般力系向向O点简化的问题。
解:坐标系如图kN R X 333)140(193-=-+-=' kN R Y8020)2740(5280-=-+-=' 主矢kN R R R YX 9.802622='+'=' 方向1.243338020tan =--=''=XYR R α 主矩m kN M O ⋅=+⨯+⨯=106765125211937.10140注意:①主矢R '由力系中各力的矢量和确定,所以,主矢与简化中心的位置无关。
对于给定的力系,选取不同的简化中心,所得主矢相同。
②主矩由力系中各力对简化中心的矩的代数和确定,简化中心的位置不同,各点对其的矩不同,所以,主矩一般与简化中心的位置有关。
3、如图所示,简支梁中点受力P F 作用,已知kN F P 20=,求支座A和B的反力。
5 平面桁架结构力学

FP FP
FP FP FP
a
6a
计算顺序:按与“几何组成顺序相反”的原则进行计算,逐次建 立各结点的平衡方程,保证每个节点上的未知力都不能超过两个时, 方能将所有内力解出;避免在结点间解联立方程。
运用结点法分析时的注意事项:
1、避免使用三角函数 N
l ly
N lx
NY X
N=X =Y
l
lx
ly
2、轴力的正负号规定:拉力为正
➢ 高层建筑中,通过斜撑,加强结构的抗风能力。同 时也起到了跨间支撑作用。
z
x
y
计算组合结构时应注意:
① 注意区分链杆(只受轴力)和梁式杆(受轴力、剪 力和弯矩);
② 前面关于桁架结点的一些特性对有梁式杆的结点不 在适用;
③ 一般先计算支座反力、链杆的轴力,然后计算梁式 杆的内力;
④ 取隔离体时,尽量不截断梁式杆。
1 2 Nb
1.5P
P
VB 1.5P
Y 0 N a P V A 0 .5 P M 2 0 N b3 4d 1 .5 P 2 d0
Nb 2.25P
1‘ 2‘ 3‘ 4‘ e
a
cd
b
A 1 2 3 4 5
P PP 6d
4d d3
B
(2) N c
VA 1.5P
Yc1.5PP0.5P Nc 54Yc 0.62P 5
空间桁架(三维)
——组成桁架的杆件不都 在同一平面内。
(2)按外型分类 平行弦桁架
三角形桁架 抛物线桁架 梯形桁架
(3)按几何组成分类 简单桁架 联合桁架 复杂桁架
(4)按受力特点分类: 梁式桁架 拱式桁架
§5 - 2 结 点 法
结构力学作业

一、判断1.(5分)图(a)对称结构可简化为图(b)结构来计算。
()••纠错得分:5知识点:结构力学展开解析答案正确解析2.(5分)图示对称刚架,在反对称荷载作用下,半边结构图(c)所示。
()••纠错得分:5知识点:结构力学展开解析答案错误解析3.(5分)图示简支斜梁,在荷载P作用下,若改变B支座链杆方向,则梁的内力将是M、N不变,Q改变。
()••纠错得分:5知识点:3.2 多跨静定梁的内力分析展开解析答案错误解析4.(5分)计算图示桁架中指定杆件内力,各杆EA=常数,N2=−P/2。
()••纠错得分:5知识点:结构力学展开解析答案正确解析5.(5分)图(a)所示桁架结构可选用图(b)所示的体系作为力法基本体系。
()••纠错得分:5知识点:结构力学展开解析答案正确解析6.(5分)图示对称结构,EI=常数;较简便的力法基本结构如图所示。
()••纠错得分:5知识点:结构力学展开解析答案正确解析7.(5分)图示结构中杆AC由于加热伸长了Δ,则杆AB的变形是0。
()••纠错得分:5知识点:结构力学,3.3 静定平面刚架的内力分析展开解析答案正确解析8.(5分)图示结构EI=常数,求K点的竖向位移时,由图乘法得:ΔK=(1/EI)×y1ω1。
()••纠错得分:5知识点:结构力学展开解析答案错误解析9.(5分)图示体系的几何组成为几何不变,无多余联系。
()••纠错得分:5知识点:结构力学展开解析答案正确解析10.(5分)图示为一刚架的力法基本体系,E=常数。
其δ12为EI/8。
()••纠错得分:5知识点:结构力学展开解析答案错误解析11.(5分)图示刚架,EI=常数,B点的竖向位移(↓)为Pl3/(6EI)。
()••纠错得分:5知识点:结构力学,3.3 静定平面刚架的内力分析展开解析答案错误解析12.(5分)下图能用力矩分配法计算。
()••纠错得分:5知识点:结构力学展开解析答案错误解析13.(5分)图示结构EI=常数,在给定荷载作用下,固定端的反力矩为,逆时针旋转。
第6章内力和内力图(桁架内力计算)

工程力学教程电子教案
内力和内力图
13
例题 6-1
解:先取整体为研究对象,受力如图所示。由平衡方 先取整体为研究对象 受力如图所示。 受力如图所示 程 ∑Fx = 0,FAx + FE = 0
∑Fy = 0, FB + FAy − FC = 0 ∑MA(F) = 0,
联立求解得 FAx= -2 kN, FB = 2 kN
工程力学教程电子教案
内力和内力图
32
内力的大小及指向只有将物体假想地截开后才 能确定。 能确定。
拉压杆横截面上的内力,由任一横截面 拉压杆横截面上的内力,由任一横截面(m-m) 一边分离体的平衡条件可知, 一边分离体的平衡条件可知,是与横截面垂直的 分布力,此分布内力的合力称为轴力。 分布力,此分布内力的合力称为轴力。用符号 FN 表示。 表示。
工程力学教程电子教案
内力和内力图
20
例题 6-2
由平衡方程
先取整体为研究对象, 作受力图。 解:先取整体为研究对象 作受力图。
∑Fx = 0,FAx + FE = 0 ∑Fy = 0, FB + FAy − FC = 0 ∑MA(F) = 0,
− FC × a − FE × a + FB × 3a = 0
工程力学教程电子教案
内力和内力图
12
6.1.3 平面简单桁架的内力计算 1. 节点法 取节点为研究对象来求解桁架杆件的内力。 取节点为研究对象来求解桁架杆件的内力。
例题 6-1
如图平面简单桁架,已知铅垂力 如图平面简单桁架,已知铅垂力FC= 4 kN,水 , 平力F 平力 E =2 kN。求各杆内力。 。求各杆内力。
− FC × a − FE × a + FB × 3a = 0
工程力学与建筑结构作业(答案)

工程力学与建筑结构作业一、选择题1。
作用在同一刚体上的两个力大小相等、方向相反、且沿着同一条作用线,这两个力是:()A。
作用力与反作用力 B.平衡力 C。
力偶2.既能限制物体转动,又能限制物体移动的约束是:()A.柔体约束B.固定端约束 C。
活动铰链约束3.三种不同的截面形状(圆形、正方形、空心圆)的等截面直杆,承受相同的轴向拉力P,比较材料用量,则。
( )A.正方形截面最省料 B。
圆形截面最省料C。
空心圆截面最省料 D。
三者用料相同4.. ( )A.轴力最大 B. 面积最小 D. 不能确定5。
杆件内任何截面的工作应力应小于等于( )。
A。
危险应力 B。
最小应力 C.允许应力 D.最大应力6、梁的内力主要有 .A.弯矩和剪力 B。
轴力和扭矩 C。
弯矩和扭矩 D. 轴力和剪力7、若梁的截面是T形截面,则截面上的最大拉应力和最大压应力的数值。
A.不同 B。
相同 C。
不一定()8.截面大小相等的两根细长压杆,形状一为圆形,另一为圆环形,其它条件相同,为形的临界力大。
A。
圆形的柔度大 B. 圆形的回转半径大C。
圆形的临界力大 D. 圆形的临界应力大9.两端支承情况和截面形状沿两个方向不同的压杆,总是沿着值大的方向失稳。
A.强度 B。
刚度 C。
柔度 D。
惯性矩10. 下列说法正确的是:。
A. 荷载标准值要大于荷载设计值B。
荷载标准值要小于荷载设计值C。
强度标准值要小于强度设计值D。
强度标准值要大于强度设计值11. 混凝土保护层厚度是指。
A.箍筋的外皮至混凝土外边缘的距离B。
钢筋的外皮至混凝土外边缘的距离C。
纵向受力钢筋截面形心至混凝土外边缘的距离D。
箍筋的截面形心至混凝土外边缘的距离二.填空题1。
平面汇交力系的合力对平面内任一点之矩,等于各个分力对同一点的力矩的代数和.这就是合力矩定理。
2。
平面一般力系平衡的充分和必要条件是:∑Fx=0,∑Fy=0,∑m=0。
3.设计构件需满足强度、刚度、稳定性三个方面的要求。
