财政收入预测matlab
matlab的predict函数

MATLAB中的predict函数是一个非常有用的工具,它可以用来预测未来的数据值。
这个函数可以用于各种不同的应用,例如金融预测、天气预测、股票预测等。
在本文中,我们将介绍predict函数的基本用法和一些实际的示例。
一、predict函数的基本用法predict函数的语法如下:Ypred = predict(Mdl,Xnew)其中,Mdl是一个训练好的模型,Xnew是一个新的输入数据。
predict函数会根据训练好的模型Mdl,预测出Xnew对应的输出值Ypred。
下面是一个简单的例子,用于演示predict函数的基本用法:% 生成一些随机数据X = randn(100,3);Y = X(:,1) + 2*X(:,2) - 0.5*X(:,3) + randn(100,1);% 训练一个线性回归模型Mdl = fitlm(X,Y);% 生成一些新的输入数据Xnew = randn(10,3);% 预测新的输出值Ypred = predict(Mdl,Xnew);在这个例子中,我们首先生成了一些随机的输入数据X和对应的输出数据Y。
然后,我们使用fitlm函数训练了一个线性回归模型Mdl。
接着,我们生成了一些新的输入数据Xnew,并使用predict函数预测了它们对应的输出值Ypred。
二、predict函数的实际应用除了上面的例子之外,predict函数还可以用于各种不同的应用。
下面是一些实际的示例。
1. 金融预测在金融领域,predict函数可以用于预测股票价格、汇率等。
下面是一个简单的例子,用于演示如何使用predict函数预测股票价格:% 读取股票数据data = readtable('AAPL.csv');% 提取收盘价数据Y = data.Close;% 提取其他特征数据X = data(:,{'Open','High','Low','Volume'});% 分割训练集和测试集trainSize = round(size(X,1)*0.8);Xtrain = X(1:trainSize,:);Ytrain = Y(1:trainSize);Xtest = X(trainSize+1:end,:);Ytest = Y(trainSize+1:end);% 训练一个线性回归模型Mdl = fitlm(Xtrain,Ytrain);% 预测测试集的输出值Ypred = predict(Mdl,Xtest);在这个例子中,我们首先读取了一个股票数据文件。
财政收入预测问题1要点
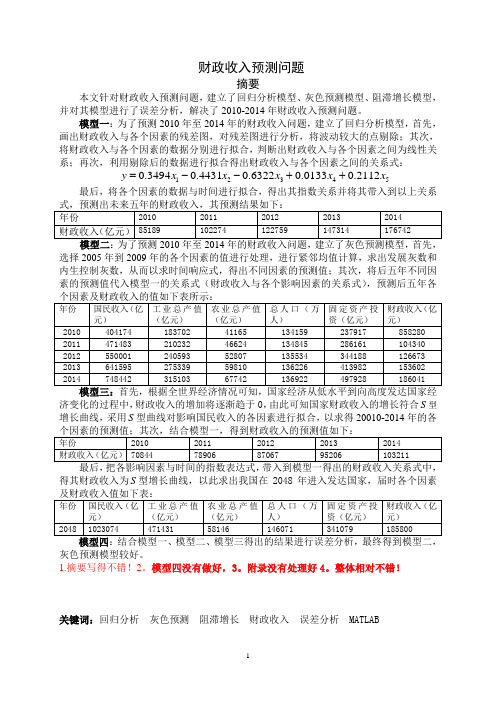
财政收入预测问题摘要本文针对财政收入预测问题,建立了回归分析模型、灰色预测模型、阻滞增长模型,并对其模型进行了误差分析,解决了2010-2014年财政收入预测问题。
模型一:为了预测2010年至2014年的财政收入问题,建立了回归分析模型,首先, 画出财政收入与各个因素的残差图,对残差图进行分析,将波动较大的点剔除;其次,将财政收入与各个因素的数据分别进行拟合,判断出财政收入与各个因素之间为线性关系;再次,利用剔除后的数据进行拟合得出财政收入与各个因素之间的关系式:123450.34940.44310.63220.01330.2112y x x x x x =--++ 最后,将各个因素的数据与时间进行拟合,得出其指数关系并将其带入到以上关系式,预测出未来五年的财政收入,其预测结果如下:年份2010 2011 2012 2013 2014 财政收入(亿元) 85189102274 122759 147314 176742 模型二:为了预测2010年至2014年的财政收入问题,建立了灰色预测模型,首先,选择2005年到2009年的各个因素的值进行处理,进行紧邻均值计算,求出发展灰数和内生控制灰数,从而以求时间响应式,得出不同因素的预测值;其次,将后五年不同因素的预测值代入模型一的关系式(财政收入与各个影响因素的关系式),预测后五年各个因素及财政收入的值如下表所示:年份 国民收入(亿元)工业总产值(亿元) 农业总产值(亿元)总人口(万人)固定资产投资(亿元) 财政收入(亿元)2010 404174 183702 41165 134159 237917 858280 2011 471483 210232 46624 134845 286161 104340 2012 550001 240593 52807 135534 344188 126673 2013 641595 275339 59810 136226 413982 153602 201474844231510367742136922497928186041模型三:首先,根据全世界经济情况可知,国家经济从低水平到向高度发达国家经济变化的过程中,财政收入的增加将逐渐趋于0,由此可知国家财政收入的增长符合S 型增长曲线,采用S 型曲线对影响国民收入的各因素进行拟合,以求得20010-2014年的各个因素的预测值;其次,结合模型一,得到财政收入的预测值如下:年份 2010 20112012 2013 2014 财政收入(亿元) 70844789068706795206103211最后,把各影响因素与时间的指数表达式,带入到模型一得出的财政收入关系式中,得其财政收入为S 型增长曲线,以此求出我国在2048年进入发达国家,届时各个因素及财政收入值如下表:年份 国民收入(亿元)工业总产值(亿元) 农业总产值(亿元) 总人口(万人) 固定资产投资(亿元) 财政收入(亿元) 2048 102307447143158146146071341079185800模型四:结合模型一、模型二、模型三得出的结果进行误差分析,最终得到模型二, 灰色预测模型较好。
使用MATLAB进行数据预测和预测

使用MATLAB进行数据预测和预测引言:数据预测和预测在许多领域中都具有重要的应用价值。
它们可以帮助我们预测未来的发展趋势,做出合理的决策,并在经营和决策中提供有力的支持。
在这一过程中,MATLAB作为一种功能强大的编程语言和数据分析工具,为我们提供了一个强大的工具箱,可以进行数据预测和预测。
数据预处理:在开始数据预测和预测之前,我们首先需要对数据进行预处理。
预处理包括数据清洗、数据归一化、特征选择等步骤。
通过这些步骤,我们可以提高数据的质量,减少噪声的影响,并使数据更适合于预测模型的建立。
数据清洗是指删除或修复数据中的错误值、缺失值和异常值。
在MATLAB中,我们可以使用一些函数和工具箱来处理这些问题。
例如,我们可以使用`isnan`函数来检测缺失值,并使用`fillmissing`函数来填充缺失值。
对于异常值,我们可以使用一些统计方法,如3σ原则或箱线图来识别和处理。
数据归一化是将不同尺度的数据映射到统一的尺度上。
这是因为不同尺度的数据可能对预测模型的训练和预测产生不利影响。
在MATLAB中,有许多方法可以实现数据归一化,如MinMax归一化、Z-score归一化等。
我们可以使用`mapminmax`函数来实现MinMax归一化,并使用`zscore`函数来实现Z-score归一化。
特征选择是从原始数据中选择最相关的特征,以降低数据维度并提高预测模型的准确性。
在MATLAB中,我们可以使用一些算法和函数来实现特征选择。
例如,我们可以使用`fsrnca`函数(基于相关系数的特征选择)或`sequentialfs`函数(基于逐步搜索的特征选择)来选择最佳特征子集。
在完成数据预处理后,我们可以使用各种算法和方法进行数据预测。
在MATLAB中,有许多经典的预测算法和函数可供选择。
以下是几个常用的预测方法。
1. 线性回归:线性回归是一种基本的预测方法,它使用线性模型来建立输入变量和输出变量之间的关系。
财政收入预测问题

财政收入预测问题 Prepared on 22 November 2020财政收入预测问题摘要财政收入是衡量一个地区和国家经济实力的重要标准,控制着国民经济的命脉, 对财政收入进行定量分析并对其做出比较准确的预测可以为相关部门或者企业制定发展规则,实施相关措施提供可靠的理论预测参考。
科学、合理地预测财政收入,对于克服年度预算收支确定的随意性和盲目性,正确处理财政与经济的相互关系具有十分重要的意义。
本文为预测未来五年的财政收入,运用灰色预测法,建立了相应的预测模型。
首先,根据已知信息可知,财政收入与国民收入、工业总产值、农业总产值、总人口、固定资产投资等五种因素有关,结合附表中给出的数据,对财政收入有关的因素进行回归拟合,并结合残差图进行分析,得出财政收入与国民收入、工业总产值、农业总产值、固定资产投资等四种因素的线性相关关系较为显着,表明这四种因素对财政收入的影响较大,而总人口对其影响相对较小一些。
其次,对回归分析的得到的方程进行整合,得出财政收入与五种因素的一个关系式:然后,运用灰色预测法,通过Matlab 软件对数据处理分析,确立了其预测模型方程,即:关键词:Matlab 软件 财政收入 回归分析 灰色预测法 线性相关1 问题重述国家的财政收入与国民收入、工业总产值、农业总产值、总人口、固定资产投资等因素有关,根据附表中所给出的19782009-年的原始数据,对其进行处理分析,构造预测模型,并利用该模型对2010年至2014年的财政收入作出预测。
2 问题假设与符号说明问题假设1 财政收入只与本文给出的五种因素有关,其它因素不考虑;2 未来五年内无经济危机及重大自然灾害发生;3 本文收集的数据均真实、可靠。
符号说明x :年份时间 0β:回归参数1β:财政收入与各因素的参数 2r :判定系数 i y :预测值(1~5i =); a :发展灰数 b :内生控制灰数 B :数据矩阵Y :常数矩阵 (0)()X k :原始数据列(1)()X k :累加生成列 (0)ˆ()Xk :相应的模拟误差序列 (1)ˆ()Xk :相应的累减生成序列 1S :(0)()X k 序列的均方差 2S :残差的均方差 0S :小残差概率s :残差平方和 k e :各种因素残差概率(0)∆:绝对误差 φ:相对误差序列 )(k η:关联系数 i r :关联度p :分辨率 ∆:平均模拟相对误差 k ∆:k 点相当对误差 C :方差比3 问题分析首先,由本文给出的关系可知,财政收入与国民收入、工业总产值、农业总产值、总人口、固定资产投资等五种因素有关。
【数学建模】国家财政收入的影响因素的评价及预期收入的预测

国家财政收入的影响因素的评价及预期收入的预测【摘要】国家的财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
首先,我们根据所给数据,对数据进行描述性分析。
之后,我们对数据进行了回归分析,构造了预测模型,并获得了模型的回归系数估计值及其置信区间。
然后,考虑到每个回归系数置信区间包含零点与否的情况,我们对模型进行了改进,并得到了其交互式画面。
考虑到数据的时间序列属性,我们对模型进行了自相关性诊断,作出残差散点图,初步判定其大部分点落在1,3象限,随机误差表现出正自相关趋势。
但在之后的D-W检验中,我们计算出了DW值,自相关系数估计值 ˆ,依照样本容量和回归变量数目,查阅了D-W分布表,得到检验的临界值d L和d U。
在分析DW所在区间时,我们发现模型的自相关状态不能确定。
之后,我们代入所给数据1952年-1980年的各项经济指标,得出的预测值与实际值相当吻合。
最后,我们根据网络上查到的数据,利用该模型对1990年和2000年的财政收入作出预测,并对结果进行了分析。
关键词:MATLAB 财政收入回归模型自相关性诊断自相关系数 D-W检验一、问题重述国家的财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关,根据所给数据,对数据进行分析,构造预测模型,并利用该模型对1990年和2000年的财政收入作出预测。
二、问题假设1.财政收入只与问题重述中提到的6个因素有关;2.所给数据真实准确,无录入错误。
三、符号说明y:财政收入;x1:国民收入;x2:工业总产值;x3:农业总产值;x4:总人口;x5:就业人口;x6:固定资产投资;β0,β1,β2,β3,β4,β5,β6:回归系数;ε:随机误差。
四、问题分析、模型的建立与求解1.问题的分析首先对数据作初步分析。
分别作出财政收入与6个因素的散点图,并用Excel自带的回归分析求出了各自自变量对y的R2(决定系数,越接近1则拟合程度越好):图1 x1-y散点图图2 x2-y散点图图3 x3-y散点图图4 x4-y散点图图5 x5-y散点图由该图可以明显看出,最右边有一个异常点:1981年就业人口攀升为73280,较之前有大幅度增长,但财政收入明显地低于预测值,为使个别数据不致影响整个模型,我们将该异常数据去掉。
[毕业设计论文]财政收入预测与分析MATLAB
![[毕业设计论文]财政收入预测与分析MATLAB](https://img.taocdn.com/s3/m/6467b52d0b4c2e3f57276396.png)
一、根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型和Logistic 模型中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。
表1 美国人口统计数据提示:指数增长模型:r te x t x 0)(=解:设)(t x 为第t 年美国人口数,记时刻(t=0)的人口为0x 。
假设人口增长率为常数r,则有t t rx t x t t x ∆=-∆+)()()( 令0→∆t ,有关于)(t x 的微分方程0)0(,x x rx dtdx==,故可解出得到热口指数增长模型:rt e x t x 0)(=,(1)将(1)式去对数,可得0ln ,ln ,x a x y a rt y ==+=用MATLAB 软件计算可得r=0.214/10年,0x =-36.6198,预测估计美国2010年的人口数为x(2010)= 598.4,拟合图17801800182018401860188019001920194019601980050100150200250300350用MA TLAB 解题具体步骤如下: 程序:t=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 106.5 123.2 131.7 150.7 179.3 204 226.5]v=log(y);p=polyfit(t,v,1) %得到指数模型参数值r 和a 结果:y =Columns 1 through 93.9000 5.3000 7.2000 9.6000 12.9000 17.1000 23.2000 31.4000 38.6000Columns 10 through 1850.2000 62.9000 76.0000 92.0000 106.5000 123.2000 131.7000 150.7000 179.3000Columns 19 through 20204.0000 226.5000 p =0.0214 -36.6198 程序:ti=1790:2:1980; vi=polyval(p,ti); yi=exp(vi)plot(t,y,'*',ti,yi,'r')legend('数据点(x,y)','拟合曲线y=f(x)'))x(2010)=exp(0.0214*2010-36.6198) %估计2010年美国人口 Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭首先我们可用微积分将连续的微分方程离散化,不妨设x(t)表示第t 次所得人口数,r 为人口固有增长率,根据logistic 模型()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭,m x ,为人口容量,以下用k 代替m x ,可得:())())(1()()1(t x kt x r t x t x -=-+))(1()()()1(kt x r t x t x t x -=-+这里可以假设)()()1(t x t x t x y -+=,)(t x x =,则krs sx r y =-=,现在我们可以用线性拟合,借助matlab 来进行运算得到r,ky=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5]; t=1:20; for k=1:19x(k)=(y(k+1)-y(k))/y(k); endA=polyfit(y(1:19),x,1) %求出参数r 与s A =-0.0014 0.3368这里求出r=0.3368,k=0.3368/0.0014=240.57143(下面的b0就是这里求出) function y=lin(b,t);f(x)=b(1)./[1+(b(1)./3.9-1).*exp(-b(2).*t)];t=1:20;y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5]; b0=[240.57143,0.3368]; b=nlinfit(t,y,'lin',b0) b0 =240.5714 0.3368 b =312.6056 0.2615这里就求出了函数的值r=0.2615,m x =312.6065,0x =3.9(最初的值,1790年的) 则可求出()te t x 2615.0155282.8016065.312-+=t=1790:10:1980;y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5];x1=1:20;F=312.6056./[1+80.155282.*exp(-0.2615.*x1)]; plot(t,y,'r*');hold on plot(x1,F,'b-');hold off ,legend('数据点(xi,yi)','拟合曲线y=f(x)') xlabel('t'),ylabel('x(t)') 下面是图形预测2010年,当t=23时,求出美国2010年的人口为261.4142结论:从以上两个图形可以看出,logistic 拟合的更好,误差更少,预测用logistic 模型更加准确。
R语言课程设计--BP神经网络预测财政收入

摘要随着社会的不断发展,经济制度在不断建立与完善,财政工作不仅面临着机遇,而且也面临着重大的挑战。
这主要体现在:一方面国家宏观经济调控需要财政职能的履行,另一方面,当下经济发展迅速,目前的一些财政工作已经难以再满足其发展需求。
因此,政府更加期望通过财政工作的预见性来辅助相关财政政策的制定实施,因此,财政收入预测是当前社会一个迫切需要的研究课题。
本文选取了1999年到2013年的财政数据,包括财政收入表和四种税收表,数据主要来源于广州市统计局的统计年鉴与泰迪智能科技有限公司。
本文旨在分析财政收入的影响因素及预测情况。
在研究财政收入影响因素之前,首先分析了四种税收的主要影响因素,因为税收在财政收入中所占比重很大,并且税收与地方财政收入政策的制定息息相关,因此本文细化了税收因素的分析,主要运用SAS软件,通过典型相关分析模型分别找到了影响四种税收的主要因素,另外也分别找出了影响全市税收的主要区域。
税收的细分研究,看似与文章脱节,实际上为广州市制定相应税收的政策都提供了一定的理论依据。
接着进行了本文的研究重点,即关于财政收入的预测,首先运用SAS软件通过主成分分析,成功将财政收入的17个指标降维,筛选出10个主要影响财政收入的指标。
最后,运用MATLAB 软件,通过BP神经网络[5]进行了预测,得到了2014与2015年的财政收入的预测值,并且与真实值对比,发现预测结果与真实值并不是相差很大。
本文成功的建立了财政收入的预测模型,为广州市制定相应的财政政策都提供了一定的理论依据。
关键词:财政预测典型相关主成分分析 BP神经网络AbstractWith the continuous development of the society, the economic system is constantly established and perfected, and financial work is not only faced with opportunities, but also faces major challenges. This is mainly reflected in: on the one hand, the national macroeconomic control needs the financial function of the implementation, on the other hand, the current rapid economic development, some of the current financial work has been difficult to meet their development needs. Therefore, the government is more hope that through the financial work of the foresight to assist the formulation and implementation of the relevant fiscal policy, therefore, the fiscal revenue forecast is an urgent need for the current research topic.This paper chooses the fiscal data from 1999 to 2013, including the fiscal revenue statement and four tax forms. The data mainly come from the Statistical Yearbook of Guangzhou Municipal Bureau of Statistics and Teddy Intelligent Technology Co., Ltd. This paper aims to analyze the influencing factors and forecasting of fiscal revenue. Before studying the influencing factors of fiscal revenue, the paper first analyzes the main influencing factors of the four kinds of taxes, because the tax revenue is very large in the fiscal revenue, and the tax is closely related to the formulation of the local fiscal revenue policy. Therefore, this paper elaborates the tax factor Analysis, the main use of SAS software, through the typical correlation analysis model were found to affect the four main factors of taxation, respectively, also found the main areas of the city's tax revenue. Tax segmentation research, seemingly out of line with the article, in fact, for the development of the corresponding tax policy in Guangzhou City have provided a certain theoretical basis. Then we focus on the research of this paper, that is, the forecast of fiscal revenue, the first use of SAS software through the principal component analysis, the success of the 17 indicators of fiscal revenue dimensionality, screening out 10 major factors affecting the main revenue. Finally, using MATLAB software, BP neural network is used to predict, and the forecast value of fiscal revenue in 2014 and 2015 is obtained. Compared with the real value, it is found that the predicted result is not very different from the real value. This paper has successfully established the forecasting model of fiscal revenue, which provides a theoretical basis for the formulation of the corresponding fiscal policy in Guangzhou.Key words: financial forecasting typical correlation principal component analysis BP neural network目录摘要 (I)Abstract (II)目录 (1)§1绪论 (2)1.1研究背景及意义 (2)1.2研究问题概述 (3)1.3研究思路和行文框架 (3)§2税收的相关分析 (5)2.1数据的准备 (5)2.2数据预处理 (5)2.4税收相关关系的求解与结果分析 (10)2.5本章总结 (17)§3财政收入的主要因素分析 (18)3.1数据准备 (18)3.2主成分分析模型的建立 (18)3.3财政收入主要因素的求解与结果分析 (19)3.3本章总结 (22)§4 BP神经网络预测财政收入 (23)4.1数据准备 (23)4.2 BP神经网络模型建立 (23)4.3财政收入预测的求解与结果分析 (26)4.4本章总结 (29)§5研究结论 (30)参考文献 (31)致谢 (32)§1绪论1.1研究背景及意义财政收入体现了一个国家财力及经济发展状况。
数学建模作业——中国1978-1997年的财政收入与国内生产总值

数学建模财政收入与国内生产总值的关系问题(关于中国1978-1997年的财政收入与国内生产总值)摘要本文研究的是财政收入与国内生产总值的关系问题,根据1978-1997年财政收入和国内生产总值的相关数据,建立了简单线性回归模型。
同时,运用MATLAB 软件对模型进行求解,得出较为科学合理的结果。
首先,我们建立1978—1997年的财政收入与国内生产总值的线性回归方程,根据1978年-1997年的数据,运用MATLAB 求解出相关参数。
因此,在此模型下,财政收入与国内生产总值的线性回归方程为∧∧+=t t X Y 100036.08375.857。
然后,由参照系数9916.02=r 可知,总离差平方和的99%被样本回归直线解释,即仅有不到1%未被解释。
因此,样本回归直线对样本点的拟合优度是很高的。
当然,财政收入除了与国内生产总值有关外,还与其他一些外部因素相关,如税收政策、税收的利率等。
因此,可以通过搜集更多的实际数据,建立多元线性回归方程优化我们的模型。
关键词:财政收入国内生产总值线性回归MATLAB一、问题重述根据中国1978年-1997年的财政收入Y和国内生产总值X的数据(表一),完成以下两个问题:1.建立财政收入对国内生产总值的简单线性回归模型,并解释斜率系数的经济意义;2.对此模型进行评价。
中国1978-1997年的财政收入与国内生产总值(单位:亿元)数据来源:《中国统计年鉴》二、问题分析在中国1978年-1997年的财政收入和国内生产总值的关系问题中,我们首先考虑到以下几个问题:①建立怎样的线性回归模型;②我们该如何对建立的模型进行评价;③当财政收入和国内生产总值的数据发生变化时,模型应该做出怎样的修改;④当考虑与财政收入相关的其他因素,如税收政策、税收的利率时,我们的模型又该如何优化。
因此,建立怎样的线性回归模型,对中国1978年-1997年财政收入与国内生产总值的数据进行处理,是我们首先要解决的问题。
基于MATLAB的回归分析模型在经济预测分析中的应用

一、灰色预测模型的原理
一、灰色预测模型的原理
灰色预测模型通过将原始数据序列进行累加生成具有指数规律的新数据序列, 然后建立GM(1,1)模型进行预测。该模型使用一阶微分方程来描述数据的生成过 程,并利用最小二乘法估计参数。通过预测得到的新数据序列可以还原为原始数 据的预测值。
二、MATLAB实现灰色预测模型
五、结论
五、结论
回归分析模型在经济预测分析中具有重要的应用价值,而基于MATLAB的回归 分析工具箱为其提供了强大的支持。通过使用MATLAB回归分析工具箱,经济学家 可以更加准确地建立回归模型、评估模型性能并进行预测。这些功能和应用场景 使得基于MATLAB的回归
五、结论
分析模型成为经济学领域中一种非常有价值的分析工具。
二、MATLAB回归分析工具箱
二、MATLAB回归分析工具箱
MATLAB是一款广泛应用于科学计算、工程学、数学等领域的数据分析软件。 其中,MATLAB回归分析工具箱是一款强大的数据分析工具,用于进行回归分析模 型的建立、评估和预测。通过MATLAB回归分析工具箱,用户可以轻松地处理数据、 选择合适的回归模型、进行模型评估和预测等任务。
五、结论
未来研究方向包括进一步优化回归分析模型算法以提高预测精度、研究更加 复杂的模型类型以适应更多元化的数据关系、以及将回归分析模型应用于更多领 域的经济预测和分析中。此外,如何有效地将人工经验与机器学习相结合,也是 未来研究的一个重要方向。
参考内容
内容摘要
灰色预测模型(Grey Model, GM)是一种广泛使用的预测方法,特别是在处 理具有不完全信息和不确定因素的数据时。它利用生成数据序列来建立预测模型, 进而预测未来发展趋势。本篇文章将探讨如何使用MATLAB实现灰色预测模型,并 展示其在经济分析中的应用。
财政收入预测数学模型

财政收入预测数学模型财政收入预测问题摘要财政收入是国民经济发展的重要指标.准确地预测财政收入对合理安排国民经济各部门的比例关系,促进国民经济有计划,按比例、稳步地向前发展,搞好财政收支平衡有重要意义。
要做好财政收入的预算,对财政收入进行较好的预测是非常必要的。
财政收入是政府宏观调控的重要手段,受众多因素的影响。
建立财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投之间的线性回归模型,用逐步回归法建立合适的回归模型,并利用MATLAB软件求解关键词线性回归财政收入 MATLAB1(问题的重述财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
下表列出了1952-1981年的原始数据。
问题(1)建立财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投之间的线性回归模型,分析模型的可靠性; 问题(2)当变量之间存在较严重的多重共线性性时,传统的线性回归方法不再可靠,试建立变量之间多重相关性的评价指标,并将其用于评价工业总产值、农业总产值、总人口、就业人口、固定资产投之间的多重共线性,给出具体的评价说明;问题(3)采用逐步回归法建立合适的回归模型,并给出评价; 问题(4)利用(广义)差分变换建立新的回归模型,将其与线性回归模型、逐步回归模型等进行对比,给出您的评价。
问题(5)将以上问题整理成一篇数学建模论文提交。
2.模型的假设先假设自变量,假设设国民收入为x1、工业总产值为x2、农业总产值为x3、总人口为x4、就业人口为x5、固定资产投资为x6,财政收入为y3.模型的建立与分析1)模型初步认为是线性回归模型,则模型为:y=b0+b1x1+b2x2+b3x3+b4x4+b5x5+b6x6 matlab编程使用线性回归模型求解得到结果:b =159.1440 bint =-118.6528 436.94070.4585 0.1781 0.7389-0.0112 -0.0601 0.03761-0.5125 -0.9115 -0.11360.0008 -0.0035 0.0051-0.0028 -0.0058 0.00030.3165 -0.0746 0.7076stats =0.9835 228.2925 0F=228.2925远大于F检验临界值, p=0.0000。
MatLab应用范例之财政收入预测问题数学模型
MatLab应用范例之财政收入预测问题数学模型赵崇新本文的唯一授权方为百度文库,为保证您使用的版本为正版,请到百度文库购买。
请支持原创,您的支持是我前进的动力!摘要:本文给出财政收入及其相关因素的样本数据,分别建立线性回归模型,逐步回归模型和广义差分模型对其进行分析,最后得出逐步回归模型为其最佳预测模型。
关键词:线性回归模型;逐步回归模型;广义差分模型;统计回归模型财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定下面分别建立线性回归模型,逐步回归模型和广义差分模型,对样本数据进行分析。
1.线性回归模型[1] ⑴模型假设设第t 年的国民收入为t x 1、工业总产值t x 2、农业总产值t x 3、总人口t x 4、就业人口t x 5、固定资产投资t x 6,财政收入为t y .为了大致地分析t y 与nt x (6~1 n )的关系,分别画出它们的散点图.先在Matlab 中创建样本数据的M 文件,命名为“data1”,再在命令窗口输入: M=dlmread('data1.m'); y=M(:,8); x1=M(:,2);[p,s]=polyfit(x1,y,1); y1=polyval(p,x1);plot(x1,y,'o',x1,y1,'r-') xlabel('x1t'),ylabel('yt')可得t y 对t x 1的散点图,其他如此类推.图1.1 t y 对t x 1的散点图 图1.2 t y 对t x 2的散点图图1.3 t y 对t x 3的散点图 图1.4 t y 对t x 4的散点图图1.5 t y 对t x 5的散点图 图1.6 t y 对t x 6的散点图⑵模型建立可见,t y 与nt x 基本呈线性关系,建立线性回归模型:t t t t t t t t x b x b x b x b x b x b b y ε+++++++=6655443322110式中,6543210,,,,,,b b b b b b b 为回归系数,t ε为随机误差, )1,0(~N t ε.⑶模型求解在Matlab 的命令窗口输入: M=dlmread('data1.m'); y1=M(:,8); n=size(M,1);X1=[ones(n,1) M(:,2:7)];[b1 bint1 r1 rint1 s1]=regress(y1,X1)得到:t t t t t t t t x x x x x x y ε++++=6543210.3165.00280-0008.05125.0-0.012-5854.059.14401⑷结果分析因为15983.021≈=R ,42.2)03,6(5292.22850.01=>=F F ,50.001<=p ,所以从整体来看,模型基本可用.检查6543210,,,,,,b b b b b b b 的估计值及其置信区间,发现0b 的置信区间包含零点,这表明模型并不可靠.因为01=p ,所以可能存在变量之间的多重共线性.下面用判定系数检验法判断是否存在多重共线性.在Matlab 的命令窗口输入: M=dlmread('data1.m'); n=size(M,1);X1=[ones(n,1) M(:,2:7)]; R=corrcoef(X1)可得nt x 的自相关系数,如下表:表1.4 n x 的自相关系数可见,nt x 的自相关系数大部分都超过0.85,所以变量之间存在多重共线性.为了消除变量之间的多重共线性,可用逐步回归法消除.2.逐步回归模型[1] ⑴模型建立在Matlab 的命令窗口输入: M=dlmread('data1.m'); y1=M(:,8); n=size(M,1);X1=[ones(n,1) M(:,2:7)]; stepwise(X1,y1)[b2,bint2,r2,rint2,s2]=regress(y1,[ones(n,1) X1(:,[1])])弹出Stepwise Regression 对话框,按下All Steps 键后,显示如下:图2.1 逐步回归模型的计算结果得到逐步回归模型:t t t t t x x x y ε++=6420.0041-0.7501-0.60776.768427⑵结果分析虽然5983.09813.02122=<=R R ,但5292.22855.337412=>=F F ,且按下Export 键,确保勾上Coefficients 项与Confidence Intervals 项,在Workspace 可查得:变量之间的多重共线性虽然已经消除,但是同一变量可能存在序列相关性,可用广义差分法消除.3.广义差分模型[1] ⑴模型建立设ρ为残差的自相关系数,由⎩⎨⎧++++=++++=1-1)-6(61)-(441)-(2201-6644220t t t t t tt t t t x b x b x b b y x b x b x b b y ρερρρρρε两式相减得:)-()-()-()-()-1(-1-1)-(6661)-(4441)-(22201-t t t t t t t t t t x x b x x b x x b b y y ρεερρρρρ++++=作广义差分变换,令1-*-t t t y y y ρ=,1)-(*-t i it t x x x =,1--t t t u ρεε=则t t t t t u x b x b x b b y ++++=*66*44*220*用Matlab 的命令窗口输入:M=dlmread('data1.m'); y1=M(:,8); n=size(M,1);X1=[ones(n,1) M(:,2:7)];[b2,bint2,r2,rint2,s2]=regress(y1,[ones(n,1) X1(:,[2,4,6])]);DW=sum(diff(r2).^2)/sum(r2(2:n).^2) rho=1-DW/2y3=y1(2:n,:)-rho*M(1:n-1,8);X3=M(2:n,[2,4,6])-rho*M(1:n-1,[2,4,6]);[b3 bint3 r3 rint3 s3]=regress(y3,[ones(n-1,1) X3])得到:t t t t t u x x x y ++=*6*4*2*0.0040-0.7437-0.6027265.8733⑵结果分析因为 1.9187=DW ,查Durbin-Watson Significance Tables 得,0.998=L d ,1.931=U d ,所以U L d DW d <<,逐步回归模型的自相关性不能确定,广义差分模型并不可取。
基于MATLAB的回归分析模型在经济预测分析中的应用

基于MATLAB的回归分析模型在经济预测分析中的应用[摘要]经济预测是企业决策的前提与基础, MATLAB 具有强大的数据处理和分析功能,可以方便、快捷、准确、直观地进行回归数学建模和预测分析。
本文通过案例分析, 运用MATLAB统计工具箱中提供的命令regress建立回归分析数学模型, 并进行回归预测分析,取得很好的效果。
[关键词]MATLAB;经济预测;回归分析一、引言现代企业经营管理离不开决策,决策的正确与否关系到企业的生存与发展。
而正确的决策要依据正确的预测,预测分析是决策的前提与基础。
预测分析的方法种类繁多,随分析对象和预测期限不同而有差异,但基本方法可分为定量预测分析法和定性预测分析法。
定量预测分析法是指运用数学模型预测未来的方法。
回归分析法是根据事物的因果关系对变量的预测方法,它是定量预测方法的一种。
因果关系普遍存在,比如,产量对生产成本的影响预测、销量的预测、资金需要量的预测和财政收入的预测等,都可以运用回归分析法建立数学模型,进行预测分析。
但在实际工作中,由于数据量大、涉及的因素多以及计算的复杂性,给手工建立数学模型和进行预测分析造成了很大的困难,有的根本无法进行。
MATLAB,即“矩阵实验室”,是美国MathWorks公司自20世纪80年代中期推出的数学软件,用于线性代数、自动控制理论、概率论及数理统计、数字信号处理、时间序列分析、动态系统仿真等高级课程的基本教学工具,可解决工程、科学计算和数学学科中许多问题。
在MATLAB统计工具箱中提供了命令regress,可以实现多元线性回归,具体用法是:C = regress(Y,X)或[C,bint,r,rint,stats]= regress(Y,X,α)。
其中Y是因变量数据向量,X是自变量数据矩阵,α为显著性水平(缺省时设定为0.05)。
输出向量C,bint为回归系数估计值及其置信区间;r,rint为残差(向量)及其置信区间;stats是用于检验回归模型的统计量,有3个数值,第一个是R2,R是相关系数,第二个是F统计量值,第三个是与统计量F对应的概率p,当p Y =[4 600,5 500,5 850 ,5 350 ,6 400]′;> X =[20,75,60,45,100]′;> X =[ones(5,1)X];>[C,bint,r,rint,stats]= regress(y,x,0.05);计算出:回归系数C=[4 319.452 054 794 52;20.342 465 753 424 7];相关系数R=0.927 180 192 204 934;统计量F对应的概率p=0.023 329 564 442 655。
投资额与GDP和财政收入的回归分析及预测_翟世杰

投资额与GDP和财政收入的回归分析及预测翟世杰杜启花(青岛大学经济学院2007级硕士研究生山东青岛266071)摘要:文章首先运用MATLAB工具对1991-2008年我国GDP、财政收入与投资额等数据进行回归分析,得出固定资产投资与GDP及财政收入的回归模型。
其次,分别建立年份对GDP与财政收入的拟合曲线,预测出2009———2010年的GDP 与财政收入值,进而推出未来两年的投资额预测值。
Abstract:The article first using the MATLAB tool to1991-2008year data and so on our country GDP,financial revenue and investment cost carries on the regression analysis,obtains the investment in the fixed assets and GDP and the financial revenue regression model.Next,establishes the year separately to GDP and the financial revenue fitted curve,forecasts2009———2010GDP and the financial revenue value,will then promote in the future two year investment cost predicted value.关键词:投资GDP财政收入预测key words:Investment GDP Financial revenue Forecast作者简介:翟世杰,(1984-10,女,山东聊城人,青岛大学经济学院研究生,研究方向:经济统计理论与方法;杜启花(1983-10,女,山东日照人,青岛大学经济学院研究生,研究方向:西方经济学)【中图分类号】F810【文献标识码】A【文章编号】1004-7069(2009)-11-0133-02一、引言一国财政收入主要来源于劳动者新创造的国民收入,因此,一国财政收入规模决定于该国国民收入的规模,决定于该国经济发展的水平和状况。
财政收入预测数学模型

财政收入预测数学模型财政收入预测问题摘要财政收入是国民经济发展的重要指标.准确地预测财政收入对合理安排国民经济各部门的比例关系,促进国民经济有计划,按比例、稳步地向前发展,搞好财政收支平衡有重要意义。
要做好财政收入的预算,对财政收入进行较好的预测是非常必要的。
财政收入是政府宏观调控的重要手段,受众多因素的影响。
建立财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投之间的线性回归模型,用逐步回归法建立合适的回归模型,并利用MATLAB软件求解关键词线性回归财政收入 MATLAB1(问题的重述财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
下表列出了1952-1981年的原始数据。
问题(1)建立财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投之间的线性回归模型,分析模型的可靠性; 问题(2)当变量之间存在较严重的多重共线性性时,传统的线性回归方法不再可靠,试建立变量之间多重相关性的评价指标,并将其用于评价工业总产值、农业总产值、总人口、就业人口、固定资产投之间的多重共线性,给出具体的评价说明;问题(3)采用逐步回归法建立合适的回归模型,并给出评价; 问题(4)利用(广义)差分变换建立新的回归模型,将其与线性回归模型、逐步回归模型等进行对比,给出您的评价。
问题(5)将以上问题整理成一篇数学建模论文提交。
2.模型的假设先假设自变量,假设设国民收入为x1、工业总产值为x2、农业总产值为x3、总人口为x4、就业人口为x5、固定资产投资为x6,财政收入为y3.模型的建立与分析1)模型初步认为是线性回归模型,则模型为:y=b0+b1x1+b2x2+b3x3+b4x4+b5x5+b6x6 matlab编程使用线性回归模型求解得到结果:b =159.1440 bint =-118.6528 436.94070.4585 0.1781 0.7389-0.0112 -0.0601 0.03761-0.5125 -0.9115 -0.11360.0008 -0.0035 0.0051-0.0028 -0.0058 0.00030.3165 -0.0746 0.7076stats =0.9835 228.2925 0F=228.2925远大于F检验临界值, p=0.0000。
【数学建模】国家财政收入的影响因素的评价及预期收入的预测

国家财政收入的影响因素的评价及预期收入的预测【摘要】国家的财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
首先,我们根据所给数据,对数据进行描述性分析。
之后,我们对数据进行了回归分析,构造了预测模型,并获得了模型的回归系数估计值及其置信区间。
然后,考虑到每个回归系数置信区间包含零点与否的情况,我们对模型进行了改进,并得到了其交互式画面。
考虑到数据的时间序列属性,我们对模型进行了自相关性诊断,作出残差散点图,初步判定其大部分点落在1,3象限,随机误差表现出正自相关趋势。
但在之后的D-W检验中,我们计算出了DW值,自相关系数估计值 ˆ,依照样本容量和回归变量数目,查阅了D-W分布表,得到检验的临界值d L和d U。
在分析DW所在区间时,我们发现模型的自相关状态不能确定。
之后,我们代入所给数据1952年-1980年的各项经济指标,得出的预测值与实际值相当吻合。
最后,我们根据网络上查到的数据,利用该模型对1990年和2000年的财政收入作出预测,并对结果进行了分析。
关键词:MATLAB 财政收入回归模型自相关性诊断自相关系数D-W检验一、问题重述国家的财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关,根据所给数据,对数据进行分析,构造预测模型,并利用该模型对1990年和2000年的财政收入作出预测。
二、问题假设1.财政收入只与问题重述中提到的6个因素有关;2.所给数据真实准确,无录入错误。
三、符号说明y:财政收入;x1:国民收入;x2:工业总产值;x3:农业总产值;x4:总人口;x5:就业人口;x6:固定资产投资;β0,β1,β2,β3,β4,β5,β6:回归系数;ε:随机误差。
四、问题分析、模型的建立与求解1.问题的分析首先对数据作初步分析。
分别作出财政收入与6个因素的散点图,并用Excel自带的回归分析求出了各自自变量对y的R2(决定系数,越接近1则拟合程度越好):图1 x1-y散点图图2 x2-y散点图图3 x3-y散点图图4 x4-y散点图图5 x5-y散点图由该图可以明显看出,最右边有一个异常点:1981年就业人口攀升为73280,较之前有大幅度增长,但财政收入明显地低于预测值,为使个别数据不致影响整个模型,我们将该异常数据去掉。
财政收入预测matlab
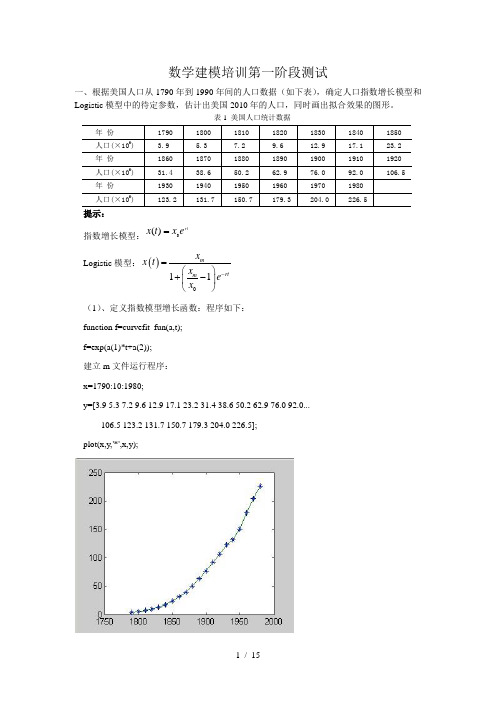
数学建模培训第一阶段测试一、根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型和Logistic 模型中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。
表1 美国人口统计数据年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 1930 1940 1950 1960 1970 1980 人口(×106)123.2131.7150.7179.3204.0226.5提示:指数增长模型:rte x t x 0)(=Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭(1)、定义指数模型增长函数:程序如下: function f=curvefit_fun(a,t); f=exp(a(1)*t+a(2)); 建立m 文件运行程序: x=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0... 106.5 123.2 131.7 150.7 179.3 204.0 226.5]; plot(x,y,'*',x,y);x=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0... 106.5 123.2 131.7 150.7 179.3 204.0 226.5];plot(x,y,'*',x,y);a0=[0.001,1];a=lsqcurvefit('curvefit_fun',a0,x,y);a1=num2str(a)disp(a1);xi=1790:2:2020;yi=curvefit_fun(a,xi);hold on;plot(xi,yi,'r')x1=2010;y1=curvefit_fun(a,x1)hold off(2)、二、f(x)的定义如下:2226,04()56,010,231,x x x x f x x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且其它1、写一个函数文件f(x)实现该函数,要求参数x 可以是向量; (1)建立函数文件: function y=f(x); x=-10:0.1:10 y1=zeros(size(x)); y2=zeros(size(x)); y3=zeros(size(x)); n=length(x); for k=1:nif x(k)<0&x(k)~=-4; y1(k)=x(k).^2+x(k)-6;elseif x(k)>=0&x(k)<10&x(k)~2&x(k)~=3; y2(k)= x(k).^2-5*x(k)+6; else y3(k)=x(k).^2-x(k)-1; end end y=y1+y2+y32、作出该函数的图形;(2)、先建立函数文件,再运行程序 function y=f(x); x=-10:0.1:10 y1=zeros(size(x));y2=zeros(size(x));y3=zeros(size(x));n=length(x);for k=1:nif x(k)<0&x(k)~=-4;y1(k)=x(k).^2+x(k)-6;elseif x(k)>=0&x(k)<10&x(k)~2&x(k)~=3; y2(k)= x(k).^2-5*x(k)+6;else y3(k)=x(k).^2-x(k)-1;endendy=y1+y2+y3plot(x,y)3、求出f(x)的零点与最值。
数学模型——财政预测问题
4925
971
94974
39377
454
723
1978
2475
5590
1058
96259
39856
550
922
1979
2702
6065
1150
97542
40581
564
890
1980
2791
6592
1194
98705
41896
568
826
1981
2927
6862
1273
100072
73280
496
810
解:
一、问题假设:
财政收入只与题目中提到的Biblioteka 个因素相关。二、符号说明:
财政收入:y;
国民收入:x1;
工业总产值:x2;
农业总产值:x3;
总人口:x4;
就业人口:x5;
固定资产投资:x6;
回归系数:β0、β1、β2、β3、β4、β5、β6;
随即误差:ε。
三、问题分析、模型建立:
1、由表格中的数据关系得出y与6因素具有以下关系:y=β0+β1x1+β2x2+β3x3+β4x4+β5x5+β6x6+ε.
461
67295
25110
66
230
1963
779
1046
514
69172
26640
85
266
1964
943
1250
584
70499
27736
129
323
1965
1152
1581
财政收入预测1

财政收入预测摘要本文就财政收入预测问题,建立了四个数学模型,并解决了后五年的财政预测,和到达经济发达水平的年份。
模型一:回归分析预测模型首先,画出各项因素和财政收入的散点图,经计算并确定其都为线性关系。
其次,假设出它们之间总的线性方程式,利用回归拟合,求得总的方程式。
最后,分别画出各因素与年份之间的散点图,并拟合出都为指数关系,预测出后五年的各项数值,代入财政收入的方程式,从而预测出后五年的财政收入。
模型二:灰色预测模型首先,取2005到2009五年中各因素的数据,分别将各因素的数据进行累加,再将累加的数据分别求得邻近均值B=[143773,267434,422510,605993];将原来的数据和邻近均值代入公式利用最小二乘法求出发展灰数a=-0.185和内生控制灰数u=87117.然后,再把a和u代入时间响应方程式中可以预测出每年各因素的值.(以国民收入为例)模型三:S形曲线预测模型首先采用S型曲线的一般公式并对其线性化,然后分别从各因素中取等距的三个点代入公式确定公式中的未知数,,a b k的值,其次预算出1978--2009各个影响因素的预测值,最后将求得的各因素的预测值以及后五年的预测值带入到模型一财政收入的预测模型中对财政收入进行预测。
表3利用S形曲线预测出后五年的财政收入图形趋于平稳,因次2049年国家经济达到发达水平。
表4 2049年各项数值模型四:误差分析对以上三个模型所求得结果进行误差分析,并判断出模型二的预测方法误差最小,因此模型二的更具合理性关键词:1.1相关信息(1)财政收入与国民收入、工业总产值、农业总产值、总人口、固定资产投资等因素有关.(2)根据全世界的经济情况可以得知,当一个国家的经济水平较低时,财政收入增长较快.当国家经济从一个低水平向经济高度发达国家变化的过程中,财政收入的增加逐渐趋于平稳,增速也逐步趋于0.1.2 问题提出问题一:用回归分析法(最小二乘法)构造出财政收入的预测模型并对其值进行预测.问题二:对于像中国这样的发展中国家而言,财政收入的增长是非常快的,用灰色预测法预测出后五年各因素的预测值,并代入到问题一财政收入的预测模型中进行对财政收入预测.问题三:我国的经济正处于快速发展的阶段,用阻滞增长的方法预测出后五年各因素的预测值后,代入到问题一财政收入预测模型中进行对财政收入的预测;并估计我国将在哪年进入经济发达国家,届时我国的各项因素值与财政收入的值将达到多少.问题四:将上述问题用相对误差与绝对误差相结合的办法进行误差分析,分别将上诉问题财政收入的预测结果进行比较,说明哪个结果更具有合理性.2 模型假设与符号说明2.1模型假设2.2符号说明符号说明x:国民收入;1x:工业总产值;2x:农业总产值3x:总人口4x:固定资产投资;5t:年份;y:财政收入;a:表示发展灰数;u:表示内生控制灰数;k:要预测值的年数;x:原始数据;1x:累加数据;3.1 问题一的分析首先,利用回归分析进行预测,画出各类别因素与财政收入的散点图,对散点图进行分析,看其符合六种基本方程中的何种方程,假设出方程;在所假设方程的基础上,对其进行回归拟合,求出其方程,并拟合出相关系数,判断相关系数是否接近于1。
经济预测方法与MATLAB编程第6章 趋势外推预测法

x1 8 4 11 9 7 12 5 3 5 24 2 15 x2 27 32 64 42 67 70 89 34 82 56 60 88 x3 10 16 12 11 10 17 26 28 27 18 30 32 x4 54 60 25 50 39 32 20 56 38 32 42 28 y 82 80 106 90 96 108 105 80 97 116 90 115
t检验是对回归系数是否显著性的一种假设检验。
n
ˆ1
(xi x )2
T
i 1
Q /(n 2)
当 | T | t1 (n 2) ,拒绝原假设H0 : 1 0,接受备选假设 H1 : 1 0 2
即 1 与0有显著性区别,所对应的变量x对y的影响不容忽视 即x作为y的解释变量,其线性关系是显著的;
jk xj xk
1 jkn
完全型
y 0 1x1 2x2 L mxm
jk xj xk
1 j,kn
(2)多元二项式回归命令 格式: rstool(X,Y,’model’, alpha) 说明: X:n×m矩阵,Y:n列向量。 Model:表多元二项式模型的形式,有“linear ”、 “Pure Quadratic ”、“interactions”、“Full Quadratic”
2
M
m
则线性回归方程为
y 0 1x1 L k xk
(2)多元线性回归法的命令
b=regress( Y,X )
% 确定回归系数的点估计值
[b, bint,r,rint,stats]=regress(Y,X,alpha) % 求回归系数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模培训第一阶段测试一、根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型和Logistic 模型中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。
表1 美国人口统计数据年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 1930 1940 1950 1960 1970 1980 人口(×106)123.2131.7150.7179.3204.0226.5提示: 指数增长模型:rt e x t x 0)(=Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭(1)、定义指数模型增长函数:程序如下: function f=curvefit_fun(a,t); f=exp(a(1)*t+a(2)); 建立m 文件运行程序: x=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0... 106.5 123.2 131.7 150.7 179.3 204.0 226.5]; plot(x,y,'*',x,y);x=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0... 106.5 123.2 131.7 150.7 179.3 204.0 226.5];plot(x,y,'*',x,y);a0=[0.001,1];a=lsqcurvefit('curvefit_fun',a0,x,y);a1=num2str(a)disp(a1);xi=1790:2:2020;yi=curvefit_fun(a,xi);hold on;plot(xi,yi,'r')x1=2010;y1=curvefit_fun(a,x1)hold off(2)、二、f(x)的定义如下:2226,04()56,010,231,x x x x f x x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且其它1、写一个函数文件f(x)实现该函数,要求参数x 可以是向量; (1)建立函数文件: function y=f(x); x=-10:0.1:10 y1=zeros(size(x)); y2=zeros(size(x)); y3=zeros(size(x)); n=length(x); for k=1:nif x(k)<0&x(k)~=-4; y1(k)=x(k).^2+x(k)-6;elseif x(k)>=0&x(k)<10&x(k)~2&x(k)~=3; y2(k)= x(k).^2-5*x(k)+6; else y3(k)=x(k).^2-x(k)-1; end end y=y1+y2+y32、作出该函数的图形;(2)、先建立函数文件,再运行程序 function y=f(x); x=-10:0.1:10y1=zeros(size(x));y2=zeros(size(x));y3=zeros(size(x));n=length(x);for k=1:nif x(k)<0&x(k)~=-4;y1(k)=x(k).^2+x(k)-6;elseif x(k)>=0&x(k)<10&x(k)~2&x(k)~=3; y2(k)= x(k).^2-5*x(k)+6;else y3(k)=x(k).^2-x(k)-1;endendy=y1+y2+y3plot(x,y)3、求出f(x)的零点与最值。
(3)、零点:Y1=[1 1 -6];x1=roots(Y1);if x1<0&x1~=-4;disp(x1);else disp([]);endY2=[1 -5 6];x2=roots(Y2);if x2>=0&x2<10&x2~=2&x2~=3; disp(x2);else disp([]);endY3=[1 -1 -1];x3=roots(Y3);if x3>=10|x3==-4|x3==2|x3==3; disp(x3);else disp([]);endx1x2x3运行程序:三、财政收入预测问题:财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
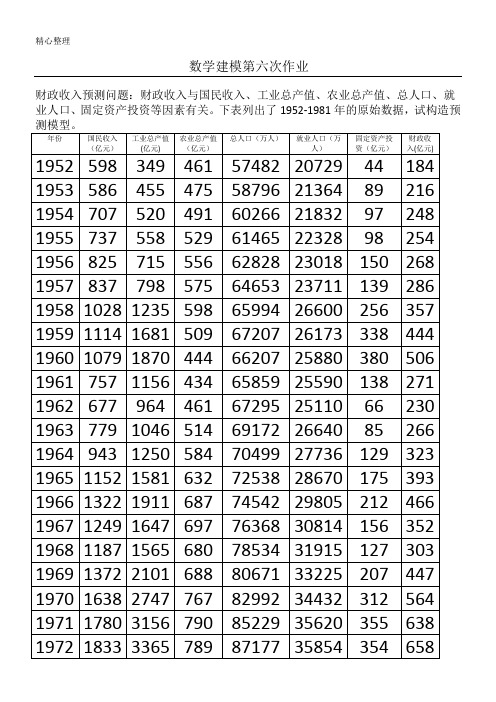
下表列出了1952-1981年的原始数据。
1、编程将数据读入MATLAB,对数据进行探索性分析;2、请你分析表中是否存在不合理数据,如果存在,找出不合理数据;3.、构造预测模型;4、将以上分析组织成一篇数学建模论文。
表3 1952-1981数据分析财政收入的影响因素以及预测财政收入摘要:财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
根据所给出的数据,对数据进行分析。
一开始我们可以看出,财政收入与各因素都是随着时间的增加而增加的。
首先,根据影响因素数据,用MATLAB中的绘图功能绘画出财政收入与各因素之间的散点图,从图中可以知道,财政收入与各因素成正的线性关系。
然后,根据所画的图形,对数据进行了回归分析,并构造预测模型y=ax1+bx2+cx3+dx4+ex5+fx6而后运用回归思想获得模型的回归系数。
接着对模型进行分析,分析残差的数值,以及利用模型比较预测值与残差值之间的差距。
关键词:matlab 回归分析残差(一)问题重述。
财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。
根据这些因素,预测财政收入问题。
(二)问题假设。
1、财政收入只与所给的6个因素有关;2、所给的数据准确无误。
(三)、符号说明。
y:财政收入;x1:国民收入;x2:工业总产值;x3:农业总产值;x4:总人口;x5:就业人口;x6:固定资产投资;r:残差;(四)、问题分析,模型建立和求解。
1、对数据进行初步分析。
作出y对各因素的散点图。
如下:其中,y-x5的图中,有一点特别地偏离,就业人口不断增长的时候,财政收入却减少,这是不合理的现象。
为了减少干扰,我们把这个不合理的数据去掉。
2、模型的建立。
根据对散点图的分析,我们可以假设y=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6对回归模型建立M文件model.m如下:function yy=model(beta0,X)a=beta0(1);b=beta0(2);c=beta0(3);d=beta0(4);e=beta0(5);f=beta0(6);x1=X(:,1);x2=X(:,2);x3=X(:,3);x4=X(:,4);x5=X(:,5);x6=X(:,6);yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;主程序p5.m如下:X=[598 349 461 57482 20729 44;586 455 475 58796 21364 89;707 520 491 60266 21832 97;737 558 529 61465 22328 98;825 715 556 62828 23018 150;837 798 575 64653 23711 139;1028 1235 598 65994 26600 256;1114 1681 509 67207 26173 338;1079 1870 444 66207 25880 380;757 1156 434 65859 25590 138;677 964 461 67295 25110 66;779 1046 514 69172 26640 85;943 1250 584 70499 27736 129;1152 1581 632 72538 28670 175;1322 1911 687 74542 29805 212;1249 1647 697 76368 30814 156;1187 1565 680 78534 31915 127;1372 2101 688 80671 33225 207;1638 2747 767 82992 34432 312;1780 3156 790 85229 35620 355;1833 3365 789 87177 35854 354;1978 3684 855 89211 36652 374;1993 3696 891 90859 37369 393;2121 4254 932 92421 38168 462;2052 4309 955 93717 38834 443;2189 4925 971 94974 39377 454;2475 5590 1058 96259 39856 550;2702 6065 1150 97542 40581 564;2791 6592 1194 98705 41896 568;2927 6862 1273 100072 73280 496];y=[184.00 216.00 248.00 254.00 268.00 286.00 357.00 444.00 506.00 ...271.00 230.00 266.00 323.00 393.00 466.00 352.00 303.00 447.00 ...564.00 638.00 658.00 691.00 655.00 692.00 657.00 723.00 922.00 ...890.00 826.00 810.0]';beta0=[0.50 -0.03 -0.60 0.01 -0.02 0.35];betafit = nlinfit(X,y,'model',beta0)结果为:betafit =0.3459 -0.0180 -0.3700 0.0030 -0.0020 0.4728即y=0.3459x1-0.0180x2-0.3700x3+0.0030x4-0.0020x5+0.4728x63、结果分析:上图是nlintool交互式拟合曲线。
