平行线培优练习题与中考真题

合集下载

平行线的性质与判定解答题培优专练(原卷)

平行线的性质与判定解答题培优专练1．（2022春·浙江温州·七年级校考期中）如图1，直线AB∥CD，△ABE的顶点E在AB与CD 之间.(1)若∠ABE=150°，∠BAE=20°．△当△CDE=2△EDM时，求△BED的度数.△如图2，作出△CDE的角平分线DF，当DF平行于△ABE中的一边时，求△BED的度数.(2)如图3，△CDE的角平分线DF交EB的延长线于点H，连结BF，当△ABH=2△HBF，1 2∠BED+13∠F=40°时，求△CDE的度数.2．（2022春·浙江金华·七年级校联考期中）如图，直线PQ∥MN，一副直角三角板△ABC、△DEF 中，△ACB=△EDF=90°，△ABC=△BAC=45°，△DFE=30°，△DEF=60°．(1)若△DEF如图1摆放，当ED平分△PEF时，则△DFM=．(2)若图2中△ABC固定，将△DEF沿着AC方向平移，边DF与直线PQ相交于点G，作△FGQ 和△GF A的角平分线GH、FH相交于点H（如图3），求△GHF的度数．(3)若图2中△DEF固定，（如图4）将△ABC绕点A顺时针旋转，1分钟转半圈，旋转至AC 与直线AN首次重合的过程中，当线段BC与△DEF的一条边平行时，请直接写出旋转的时间．（单位必须化成秒）3．（2022春·浙江金华·七年级校联考阶段练习）如图1，已知MN∥PQ,，B在MN上，C在PQ上，A在B的左侧，D在C的右侧，DE平分△ADC，BE平分△ABC，直线DE，BE交于点E，△CBN＝120°．(1)若△ADQ＝100°，求△BED的度数；(2)在图1中过点D作△ADQ的角平分线与直线BE相交于点F，如图2，试探究△DEB与△DFE 的关系；(3)若改变线段AD的位置，使得点D在点C的左侧，其他条件不变，若△ADQ＝n°，过点D 作△PDA的角平分线与直线BE相交于点G，求△BED+△DGE的和是多少度？（用含n的代数式表示）4．（2022春·浙江湖州·七年级统考期末）长江汛期即将来临，为了便于夜间查看江水及两岸河堤的情况，防汛指挥部在一危险地带两岸各安置了一探照灯（如图1），假定这一带长江两岸河堤是平行的，即PQ∥MN，连结AB，且∠ABN=45°．灯A射线自AQ顺时针旋转至AP便立即回转，灯B射线自BM顺时针旋转至BN便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是1度/秒，灯B转动的速度是3度/秒．(1)若两灯同时转动，在灯B射线第一次转到BN之前，两灯射出的光线交于点C．△如图1，当两灯光线同时转动50秒时，求∠ABC的度数．△如图2，过C作CD⊥BC交PQ于点D，则在转动过程中，求∠ABC与∠ACD的比值，并说明理由．(2)若灯A射线先转动30秒，灯B射线才开始转动，在灯A射线第一次转到AP之前，B灯转动几秒，两灯的光线互相平行？5．（2021春·浙江衢州·七年级校考期中）如图1，将一副直角三角板放在同一条直线AB上，它们的一边分别与直线AB重合，其中△ONM=30°，△OCD=45°，将图1中的三角板OMN 绕点O按每秒15°的速度沿逆时针方向旋转α°．（0°＜α°＜180°）．(1)当△AOM＝105°时，求旋转角的度数．(2)当两块三角板中至少有一组边互相平行时，求旋转的时间．(3)将图1中的三角板OMN绕点O按逆时针方向旋转得到图2，MN与CD相交于点E，若△CEN=β°时，试探究α与β的数量关系，并直接写出结论．6．（2022春·浙江金华·七年级统考期末）如图，已知AB∥CD，直线MN交AB于点M，交CD于点N．点E是线段MN上一点，P，Q分别在射线MA，NC上，连接PE，QE，PF平分△MPE，QF平分△CQE．（1）如图1，若PE△QE，△EQN＝64°，则△MPE＝°，△PFQ＝°．（2）如图2，求△PEQ与△PFQ之间的数量关系，并说明理由．（3）如图3，当PE△QE时，若△APE＝150°，△MND＝110°，过点P作PH△QF交QF的延长线于点H．将直线MN绕点N顺时针旋转，速度为每秒5°，直线MN旋转后的对应直线为M′N，同时△FPH绕点P逆时针旋转，速度为每秒10°，△FPH旋转后的对应三角形为△F′PH′，当直线MN首次落到CD上时，整个运动停止．在此运动过程中，经过t秒后，直线M′N恰好平行于△F′PH′的一条边，请直接写出所有满足条件的t的值．7．（2022春·浙江嘉兴·七年级校考期中）如图1，点O为直线AB上一点，过点O作射线OC，使△AOC＝60°．将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方，其中△OMN＝30°．(1)将图1中的三角尺绕点O顺时针旋转至图2，使一边OM在△BOC的内部，且恰好平分△BOC，求△CON的度数；(2)将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周，OC也以每秒1°的速度绕点O顺时针方向旋转，当三角尺停止运动时，OC也停止运动．△在旋转的过程中，问运动几秒时，边MN恰好与射线OC平行；△将图1中的三角尺绕点O顺时针旋转至图3，使ON在△AOC的内部，请探究△AOM与△NOC 之间的数量关系（直接写出结果）．8．（2022春·浙江台州·七年级校联考阶段练习）如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分△AEF交CD于点M，且△FEM＝△FME．(1)判断直线AB与直线CD是否平行，并说明理由；(2)如图2，点G是射线MD上一动点（不与点M，F重合），EH平分△FEG交CD于点H，过点H作HN△EM于点N，设△EHN＝α，△EGF＝β．△当点G在点F的右侧时，若β＝56°，求α的度数；△当点G在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．9．（2021春·浙江绍兴·七年级校考阶段练习）已知直线l1∥l2，直线l3，l4分别与l1，l2交于点B，F和A，E，点P是直线l3上一动点（不与点B，F重合），设△BAP＝△1，△PEF＝△2，△APE＝△3．(1)如上图，当点P在B，F两点之间运动时，试确定△1，△2，△3之间的关系，并给出证明；(2)当点P在B，F两点外侧运动时，试探究△1，△2，△3之间的关系，画出图形，给出结论，不必证明．10．（2022春·浙江衢州·七年级统考期末）已知△ABC与△ADE共顶点A，∠BAC=∠DAE=90∘，顶点B和C在直线l1上（点B在点C的左侧），顶点D和E在直线l2上（点D在点E的左侧），且直线l1∥l2．(1)如图1，顶点A在l1与l2之间，判断△BAD与∠ABC+∠ADE是否相等，并说明理由．(2)如图2，顶点A在l1与l2之间，△ABC的外角平分线与△AED的角平分线交于点F，若∠BAD=70∘，求△BFE的度数．(3)若顶点A在直线l2的下方，且顶点B、A、D不在一条直线上，△ABC的外角平分线与△AED 的角平分线交于点F，记∠BAD=α，∠BFE=β，请探究α与β的数量关系，并直接写出结论．11．（2022春·浙江金华·七年级统考期末）如图，AB、CD被AC所截，AB∥CD，△CAB＝108°，点P为直线AB上一动点（不与点A重合），连CP，作△ACP和△DCP的平分线分别交直线AB于点E、F．(1)当点P在点A的右侧时△若△ACP＝36°，则此时CP是否平分△ECF，请说明理由．△求△ECF的度数．(2)在点P运动过程中，直接写出△APC与△AFC之间的数量关系．12．（2022春·浙江湖州·七年级统考期末）如图1，已知直线AB∥CD，∠CMN=60∘，射线ME 从MD出发，绕点M以每秒a度的速度按逆时针方向旋转，到达MC后立即以相同的速度返回，到达MD后继续改变方向，继续按上述方式旋转；射线NF从NA出发，绕点N以每秒b度的速度按逆时针方向旋转，到达NB后停止运动，此时ME也同时停止运动．其中a，b满足方程组{4a+b=173a−2b=10．(1)求a，b的值；(2)若NF先运动30秒，然后ME一起运动，设ME运动的时间为t，当运动过程中ME∥NF时，求t的值；(3)如图2，若ME与NF同时开始转动，在ME第一次到达MC之前，ME与NF交于点P，过点P 作PQ⊥ME于点P，交直线AB于点Q，则在运动过程中，若设∠NME的度数为m，请求出∠NPQ 的度数（结果用含m的代数式表示）．13．（2022春·浙江绍兴·七年级统考期末）已知AB△CD，(1)如图1，若△ABE＝160°，△CDE＝120°，求△BED的度数；(2)如图2，若BF平分△ABE，DF平分△CDE，则△BFD与△BED有怎样的数量关系，并说明理由；(3)如图3，若BF平分△ABE，DF平分△CDE，则△BFD与△BED有怎样的数量关系，并说明理由．14．（2022春·浙江宁波·七年级校考期中）如图，直线PQ∥MN，一副三角尺（∠ABC=∠CDE= 90°，∠ACB=30°，∠BAC=60°，∠DCE=∠DEC=45°）按如图△放置，其中点E在直线PQ 上，点B，C均在直线MN上，且CE平分∠ACN．(1)求∠DEQ的度数．(2)如图△，若将三角形ABC绕点B以每秒2度的速度按逆时针方向旋转（A，C的对应点分别为F，G），设旋转时间为t(s)(0≤t≤90)．△在旋转过程中，当BG∥CD时，求t的值．△若在三角形ABC绕点B旋转的同时，三角形CDE绕点E以每秒1度的速度按顺时针方向旋转（C，D的对应点为H，K），请直接写出当BG∥HK时t的值．15．（2022春·浙江金华·七年级校考期中）（1）如图1，点E在BC上，△A＝△D，△ACB＝△CED．请说明AB∥CD的理由．（2）如图2，AB∥CD，BG平分△ABE，与△EDF的平分线交于H点，若△DEB比△DHB大60°．求△DEB的度数．（3）保持（2）中所求的△DEB的度数不变，如图3，AB∥CD，BM平分△EBK，DN平分△CDE，作BP∥DN，则△PBM的度数是否改变？若不变，请直接写出△PBM的度数；若改变，请说明理由．16．（2022春·浙江湖州·七年级校联考阶段练习）（1）【问题】如图1，若AB∥CD，∠BEP=25°，∠PFC=150°，求∠EPF的度数；（提示：过点P作PQ∥AB）（2）【问题迁移】如图2，AB∥CD，点P在AB的上方，∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；（3）【联想拓展】如图3所示，在（2）的条件下，已知∠EPF=α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．17．（2022春·浙江宁波·七年级校联考期末）如图△，AB，BC被直线AC所截，点D是线段AC 上的点，过点D作DE∥AB，连接AE，∠B=∠E=60°.(1)请说明AE∥BC；(2)将线段AE沿着直线．．AC平移得到线段PQ，连接DQ．△.如图△，当DE⊥DQ时，则∠Q的度数=_____________；△.在整个运动中，当∠Q=2∠EDQ时，∠Q=_____________．18．（2022春·浙江宁波·七年级校考期中）如图，直线CD//EF，点A、B分别在直线CD、EF上（自左向右分别为点C、A、D和点E、B、F），△ABF=60°，射线AM自射线AB的位置开始，绕点A以每秒1°的速度沿逆时针方向旋转，同时，射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转，当射线BN旋转到BF的位置时，两者均停止运动，设旋转时间为x秒．(1)如图1，直接写出下列答案：△△BAD的度数是；△当旋转时间x= 秒时，射线BN过点A．(2)如图2，若AM∥BN，求此时对应的旋转时间x的值．(3)若两条射线AM和BN所在直线交于点P，△如图3，若点P在CD与EF之间，且△APB=126°，求旋转时间x的值；△若旋转时间x<24，求△APB的度数（用含x的代数式表示）．19．（山西省忻州市代县2021-2022学年七年级下学期期末数学试题）如图1，AB∥CD，点E 为直线AB，CD外一点．(1)若AE⊥AB，∠C=65°，求出△E的度数．(2)如图2，点F在BA的延长线上，连接BE，EF，若CE⊥CD，EF平分∠AEC，∠B=∠AEB，求∠BEF的度数：(3)如图3，在（2）的条件下，过点F作∠BFG=∠BFE，交EC的延长线于点G，延长EF 交CD于点H，过点F作FI∥BE交CD于点I．当FH平分∠IFG时，请直接写出∠CHF的度数．20．（山东省日照市岚山区2021-2022学年七年级下学期期末考试数学试题）（1）阅读下面材料：已知：如图1，AB∥CD，E为AB，CD之间一点，连接AE，CE，得到∠AEC．求证：∠AEC+∠A+∠C=360°．解答过程如下，并请你在括号内填写推理的依据：过点E作EF∥AB，则有∠AEF+∠A=180°（______）．△AB∥CD，△EF∥CD（______）．△∠FEC+∠C=180°（______）．△∠AEF+∠A+∠FEC+∠C=360°,又△∠AEC=∠AEF+∠FEC△∠AEC+∠A+∠C=360°．假若将具有图1特征的图形称为“平行凸折线”，“平行凸折线”的性质可以表述如下：若AB∥CD，E为AB，CD之间一点，则有∠AEC+∠A+∠C=360°（2）已知：直线m∥n，点A，B在直线m上，点C，D在直线n上，连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．△如图2，当点D在点C的左侧时，若∠ADC=80°，∠BED=160°，请你结合（1）中“平行凸折线”的性质，求∠ABC的度数；△如图3，当点D在点C的右侧时，设∠ABC=α，∠ADC=β，请直接写出∠BED的度数（用含有α，β的式子表示）．21．（江苏省江阴市周庄中学2021-2022学年七年级下学期3月限时作业数学试题）（1）光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学知识有△1=△2，△3=△4，请判断光线a与光线b是否平行，并说明理由．（2）光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，如图2有一口井，已知入射光线a与水平线OC的夹角为42°，问如何放置平面镜MN，可使反射光线b正好垂直照射到井底？（即求MN与水平线的夹角）（3）如图3，直线EF上有两点A、C，分别引两条射线AB、CD．△BAF=110°，△DCF=60°，射线AB、CD分别绕A点，C点以1度/秒和3度/秒的速度同时顺时针转动，设时间为t，在射线CD转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．22．（2021春·浙江·七年级阶段练习）如图1，已知AB△CD，△B＝30°，△D＝120°；(1)若△E＝60°，则△F＝；(2)请探索△E与△F之间满足的数量关系？说明理由；(3)如图2，已知EP平分△BEF，FG平分△EFD，反向延长FG交EP于点P，求△P的度数．23．（2022春·浙江台州·七年级台州市书生中学校考期中）“一带一路”让中国和世界更紧密，“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯，便于夜间查看道路安全情况，如图，灯A射线AM′自AM顺时针旋转至AN便立即回转，灯B射线BQ′自BQ顺时针旋转至BP便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足√5−a+|b−a+3|=0，假定主道路的两边是平行的，即PQ△MN．(1)求a、b的值；(2)若灯B的射线BQ′先转动30秒，灯A的射线AM′才开始转动，在射线BO′到达BP之前，射线AM′转动几秒，两灯的光束互相平行？(3)若灯A、B的射线AM′，BQ′同时转动t秒，在射线BQ′到达BP之前，记射线AM′与BQ′交于点H，若两束光束垂直，求t的值．24．（2021春·浙江·七年级专题练习）问题情境在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG （△EFG＝90°，△EGF＝60°）”为主题开展数学活动．操作发现(1)如图（1），小明把三角尺的60°角的顶点G放在CD上，若△2＝2△1，求△1的度数；(2)如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明△AEF与△FGC之间的数量关系；结论应用(3)如图（3），小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG=α，则△CFG等于______（用含α的式子表示）．25．（2021春·浙江衢州·七年级浙江省衢州市衢江区实验中学校考开学考试）将一副三角板中的两个直角顶点C叠放在一起（如图△），其中△A＝30°，△B＝60°，△D＝△E＝45°．(1)猜想△BCD与△ACE的数量关系，并说明理由；(2)若△BCD＝4△ACE，求△BCD的度数；(3)若按住三角板ABC不动，绕顶点C转动三角DCE，试探究△BCD等于多少度时CE△AB，并简要说明理由．26．（2022春·浙江金华·七年级义乌市绣湖中学教育集团校联考阶段练习）如图，直线MN//PQ，将一副三角板中的两块直角三角板如图1放置，△ACB＝△EDF＝90°，△ABC＝△BAC＝45°，△DFE＝30°，△DEF＝60°，此时点A与点E重合．(1)对于图1，固定△ABC的位置不变，将△DEF绕点E按顺时针方向进行旋转，旋转至DE与BC首次平行，如图2所示，求此时△F AC的度数．(2)对于图1，固定△ABC的位置不变，将△DEF沿AC方向平移至点F正好落在直线MN上，再将△DEF绕点F按顺时针方向进行旋转，如图3所示．△若边EF与边BC交于点G，试判断△BGF﹣△EFN的值是否为定值，若是定值，则求出该定值，若不是定值，请说明理由；△对于图3，固定△ABC的位置不变，将△DEF绕点F顺时针方向以每秒10°的速度进行旋转，当EF与直线MN首次重合时停止运动当经过t秒时，线段DE与△ABC的一条边平行，求满足条件的t的值．27．（2020春·浙江杭州·七年级统考期末）问题情境：如图1，已知AB△CD，∠APC=108°．求∠PAB+∠PCD的度数．经过思考，小敏的思路是：如图2，过P作PE△AB，根据平行线有关性质，可得∠PAB+∠PCD=360°−∠APC=252°．问题迁移：如图3，AD△BC，点P在射线OM上运动，∠ADP=∠α，∠BCP=∠β．(1)当点P在A、B两点之间运动时，∠CPD、∠α、∠β之间有何数量关系？请说明理由．(2)如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β之间的数量关系．(3)问题拓展：如图4，MA1△NA n，A1−B1−A2−⋯−B n−1−A n是一条折线段，依据此图所含信息，把你所发现的结论，用简洁的数学式子表达为．28．（2020春·浙江宁波·七年级统考期中）已知AM∥CN，点B为平面内一点，AB⊥BC于B．(1)如图，直接写出∠A和∠C之间的数量关系．(2)如图，过点B作BD⊥AM于点D，求证：∠ABD=∠C．(3)如图，在（2）问的条件下，点E，F在DM上，连接BE，BF，CF，BF那平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．29．（2021春·浙江金华·七年级统考期末）如图1，在△ABC中，△B＝65°，△BAC＝75°，D 为AC边上一点，分别过点A、D作BC、AB的平行线交于点E．（1）求△E的度数．（2）点P为直线AC上的一个动点，过点P作PF△AE，且PF＝AE，连DF．△如图2，当点P在点C的右侧，且△PFD＝25°时，判断DE与DF的位置关系，并说明理由．△在整个运动中，是否存在点P，使得△PFD＝2△EDF？若存在，请求出△PFD的度数，若不存在，请说明理由．30．（2021春·浙江宁波·七年级统考期末）如图，直线CD//EF，点A，B分别在直线CD，EF上（自左向右分别为点C，A，D和点E，B，F），∠ABF=60°．射线AM自射线AB的位置开始，绕点A以每秒1°的速度沿逆时针方向旋转，同时，射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转，当射线BN旋转到BF的位置时，两者均停止运动，设旋转时间为x秒．（1）如图1，直接写出下列答案：△∠BAD的度数是______．△当旋转时间x=______秒时，射线BN过点A．（2）如图2，若AM//BN，求此时对应的旋转时间x的值．（3）若两条射线AM和BN所在直线交于点P．△如图3，若点P在CD与EF之间，且∠APB=126°，求旋转时间x的值．△若旋转时间x<24，求∠APB的度数（直接写出用含x的代数式表示的结果）．。

中考数学数学第五章相交线与平行线的专项培优练习题(及答案

中考数学数学第五章相交线与平行线的专项培优练习题(及答案一、选择题1．下列说法中，正确的有（）①等腰三角形的两腰相等；②等腰三角形底边上的中线与底边上的高相等；③等腰三角形的两底角相等；④等腰三角形两底角的平分线相等．A．1个B．2个C．3个D．4个2．如图所示，下列说法不正确的是（）A．∠1和∠2是同旁内角B．∠1和∠3是对顶角C．∠3和∠4是同位角D．∠1和∠4是内错角3．如图，AB∥CD，∠1=120°，则∠2＝（）A．50°B．70°C．120°D．130°4．如图，直线a∥b，直线l与a，b分别交于A，B两点，过点B作BC⊥AB交直线a于点C，若∠1＝65°，则∠2的度数为（）A．115°B．65°C．35°D．25°5．如图所示，若∠1＝∠2＝45°，∠3＝70°，则∠4等于（）A ．70°B ．45°C ．110°D ．135°6．如图，//AB CD ，PF CD ⊥于F ，40AEP ∠=︒，则EPF ∠的度数是（）A ．120︒B ．130︒C ．140︒D ．150︒7．如图，∠1=70°，直线a 平移后得到直线b ，则∠2-∠3（）A ．70°B ．180°C ．110°D ．80°8．两条平行线被第三条直线所截，则下列说法错误的是（）A ．一对邻补角的平分线互相垂直B ．一对同位角的平分线互相平行C ．一对内错角的平分线互相平行D ．一对同旁内角的平分线互相平行9．下列定理中，没有逆定题的是（）①内错角相等，两直线平行②等腰三角形两底角相等③对顶角相等④直角三角形的两个锐角互余．A ．1个B ．2个C ．3个D ．4个10．如图，直线a 和直线b 被直线c 所载，且a//b ，∠2=110°,则∠3=70°，下面推理过程错误的是（）A ．因为a//b ，所以∠2=∠6=110°，又∠3+∠6=180°(邻补角定义）所以∠3=180︒-∠6=180︒-110︒=70︒B ．//,13,12180a b ︒∴∠=∠∠+∠=1180218011070︒︒︒︒∴∠=-∠=-=所以370︒∠=C ．因为a//b 所以25∠=∠又∠3+∠5=180°(邻补角定义），3180518011070︒︒︒︒∴∠=-∠=-=D ．//,42110a b ︒∴∠=∠=，43180︒∠+∠=，∴∠3=180°−∠4=180°−110°=70°所以3180418011070︒︒︒︒∠=-∠=-=二、填空题11．如图，已知AB 、CD 相交于点O,OE ⊥AB 于O ，∠EOC=28°，则∠AOD=_____度；12．如图，AB ∥CD ，∠1=64°，FG 平分∠EFD ，则∠EGF=__________________°．13．如图，已知A 1B //A n C ，则∠A 1＋∠A 2＋…＋∠A n 等于__________(用含n 的式子表示)．14．如图，∠AEM ＝∠DFN ＝a ，∠EMN ＝∠MNF ＝b ，∠PEM ＝12∠AEM ，∠MNP ＝12∠FNP ，∠BEP ，∠NFD 的角平分线交于点I ，若∠I ＝∠P ，则a 和b 的数量关系为_____（用含a 的式子表示b ）．15．已知：如图放置的长方形ABCD 和等腰直角三角形EFG 中，∠F=90°，FE=FG=4cm ，AB=2cm ，AD=4cm ，且点F ，G ，D ，C 在同一直线上，点G 和点D 重合．现将△EFG 沿射线FC 向右平移，当点F 和点C 重合时停止移动．若△EFG 与长方形重叠部分的面积是4cm 2，则△EFG 向右平移了____cm ．16．α∠与β∠的两边互相垂直，且o 50α∠=，则β∠的度数为_________.17．如图，已知AB ∥CD,∠EAF =14∠EAB,∠ECF=14∠ECD ,则∠AFC 与∠AEC 之间的数量关系是_____________________________18．如图，直线AB 、CD 相交于点O ，OE 平分∠AOC ，OF ⊥OE 于点O ，若∠AOD ＝70°，则∠AOF ＝______度．19．一副直角三角尺叠放如图 1 所示，现将 45°的三角尺ADE 固定不动，将含 30°的三角尺 ABC 绕顶点 A 顺时针转动（旋转角不超过 180 度），使两块三角尺至少有一组边互相平行．如图 2：当∠BAD=15°时，BC ∥DE ．则∠BAD （0°＜∠BAD ＜180°）其它所有可能符合条件的度数为________．20．将一张长方形纸片折叠成如图所示的形状，则∠ABC=_________．三、解答题21．对于平面内的∠M 和∠N ，若存在一个常数k ＞0，使得∠M ＋k ∠N ＝360°，则称∠N 为∠M 的k 系补周角．如若∠M ＝90°，∠N ＝45°，则∠N 为∠M 的6系补周角．（1）若∠H ＝120°，则∠H 的4系补周角的度数为；（2）在平面内AB ∥CD ，点E 是平面内一点，连接BE ，DE ．①如图1，∠D ＝60°，若∠B 是∠E 的3系补周角，求∠B 的度数；②如图2，∠ABE 和∠CDE 均为钝角，点F 在点E 的右侧，且满足∠ABF =n ∠ABE ，∠CDF =n ∠CDE （其中n 为常数且n ＞1），点P 是∠ABE 角平分线BG 上的一个动点，在P 点运动过程中，请你确定一个点P 的位置，使得∠BPD 是∠F 的k 系补周角，并直接写出此时的k 值（用含n 的式子表示）．22．为了探究n 条直线能把平面最多分成几部分,我们从最简单的情形入手:①一条直线把平面分成2部分;②两条直线可把平面最多分成4部分;③三条直线可把平面最多分成7部分;④四条直线可把平面最多分成11部分;……把上述探究的结果进行整理,列表分析:直线条数把平面最多分成的部分数写成和的形式 12 1+1 24 1+1+2 37 1+1+2+3 411 1+1+2+3+4 … … …(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;(2)当直线条数为10时,把平面最多分成____部分;(3)当直线条数为n 时,把平面最多分成多少部分?23．(1)如图1，已知任意ABC ∆，过点C 作//DE AB ，求证：180A B ACB ∠+∠+∠=︒；(2)如图2，求证：∠AGF=∠AEF+∠F ；(3)如图3，//,119,AB CD CDE GF ∠=︒交DEB ∠的角平分线EF 于点,150F AGF ∠=︒，求F ∠的度数．24．如图1，//,AB CD 直线MN 分别交AB CD 、于点,E F BEF ∠、与EFD ∠的角平分线交于点P EP ，与CD 交于点G GH EG ⊥,交MN 于H ．（1）求证：// ;PF GH （2）如图2，连接PH K ,为GH 上一动点，PHK HPK PO ∠=∠,平分EPK ∠交MN 于,Q 则HPQ ∠的大小是否发生变化？若不变，求出其值；若改变，请说明理由．25．如图，AB ∥CD ．（1）如图1，∠A 、∠E 、∠C 的数量关系为．（2）如图2，若∠A ＝50°，∠F ＝115°，求∠C ﹣∠E 的度数；（3）如图3，∠E ＝90°，AG ，FG 分别平分∠BAE ，∠CFE ，若GD ∥FC ，试探究∠AGF 与∠GDC 的数量关系，并说明理由．26． [问题解决]：如图1，已知AB ∥CD ，E 是直线AB ，CD 内部一点，连接BE ，DE ，若∠ABE=40°，∠CDE=60°，求∠BED 的度数．嘉琪想到了如图2所示的方法，但是没有解答完，下面是嘉淇未完成的解答过程：解：过点E 作EF ∥AB ，∴∠ABE=∠BEF=40°∵AB ∥CD ，∴EF ∥CD ，…请你补充完成嘉淇的解答过程：[问题迁移]：请你参考嘉琪的解题思路，完成下面的问题：如图3，AB ∥CD ，射线OM 与直线AB ，CD 分别交于点A ，C ，射线ON 与直线AB ，CD 分别交于点B ，D ，点P 在射线ON 上运动，设∠BAP=α，∠DCP=β．（1）当点P在B，D两点之间运动时(P不与B，D重合)，求α，β和∠APC之间满足的数量关系．（2）当点P在B，D两点外侧运动时(P不与点O重合)，直接写出α，β和∠APC之间满足的数量关系．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【解析】分析：等腰三角形中顶角平分线，底边中线及高互相重合，即三线合一，两腰上的角平分线、中线及高都相等．详解：①等腰三角形的两腰相等；正确；②等腰三角形底边上的中线与底边上的高相等；正确；③等腰三角形的两底角相等；正确；④等腰三角形两底角的平分线相等．正确．故选D．点睛：本题主要考查了等腰三角形的性质以及命题与定理的概念，能够熟练掌握．2．A解析：A【分析】根据对顶角、邻补角、同位角、内错角定义判断即可．【详解】A. ∠1和∠2是邻补角，故此选项错误；B. ∠1和∠3是对顶角，此选项正确；C. ∠3和∠4是同位角，此选项正确；D. ∠1和∠4是内错角，此选项正确；故选A.【点睛】此题考查对顶角，邻补角，同位角，内错角，同旁内角，解题关键在于掌握各性质定义. 3．C解析：C【分析】由平行线性质和对顶角相等可以得到解答．【详解】解：如图，由对顶角相等可以得到∠3＝∠1=120°又AB∥CD，∴∠2＝∠3=120°．故选C．【点睛】本题考查平行线和对顶角的综合应用，由题意发现角的相等关系是解题关键．4．D解析：D【解析】解：∵直线a∥b，∴∠1+∠ABC+∠2=180°．又∵BC⊥AB，∠1=65°，∴∠2=180°﹣90°﹣65°=25°．故选D．5．C解析：C【分析】根据对顶角的性质可得∠1＝∠5，再由等量代换得∠2＝∠5，即可得到到a∥b，利用两直线平行同旁内角互补可得∠3＋∠4=180°，最后根据∠3的度数即可求出∠4的度数．【详解】解：∵∠1与∠5是对顶角，∴∠1＝∠2＝∠5＝45°，∴a∥b，∴∠3+∠6＝180°，∵∠3＝70°，∴∠4=∠6＝110°．故答案为C．【点睛】本题考查了对顶角的性质、平行线的性质及判定，其中掌握平行线的性质和判定是解答本题的关键．6．B解析：B【分析】过点P作MN∥AB，结合垂直的定义和平行线的性质求∠EPF的度数．【详解】解：如图，过点P作MN∥AB，∵∠AEP=40°，∴∠EPN=∠AEP=40°∵AB∥CD,PF⊥CD于F，∴PF⊥MN，∴∠NPF=90∴∠EPF=∠EPN+∠NPF=40°+90°=130°故答案为B【点睛】本题考查了平行线的判定定理和性质，作出辅助线构造平行线是解答本题的关键．7．C解析：C【解析】【分析】作AB∥a,先证AB∥a∥b，由平行线性质得∠2=180°-∠1+∠3，变形可得结果.【详解】作AB∥a,由直线a平移后得到直线b，所以，AB∥a∥b所以，∠2=180°-∠1+∠3，所以，∠2-∠3=180°-∠1=180°-70°=110°.故选：C【点睛】本题考核知识点：平行线性质.解题关键点：熟记平行线性质.8．D解析：D【解析】试题分析：A 、两条平行线被第三条直线所截，一对邻补角的平分线互相垂直，故本选项正确；B 、两条平行线被第三条直线所截，同位角的平分线互相平行，故本选项正确；C 、两条平行线被第三条直线所截，内错角的平分线互相平行，故本选项正确；D 、两条平行线被第三条直线所截，同旁内角的平分线互相垂直，故本选项错误；故选：D ．9．A解析：A【解析】试题分析：根据题意可知：①的逆命题是两直线平行，内错角相等，是真命题，是逆定理；②的逆命题是有两个角相等的三角形是等腰三角形，是真命题，是逆定理；③的逆命题是相等的两个角是对顶角，是假命题，不是逆定理；④的逆命题是有两个锐角互余的三角形是直角三角形，是真命题，是逆定理.只有一个不是逆定理.故选：A10．D解析：D【分析】根据平行线的性质结合邻补角的性质对各选项逐一进行分析判断即可得．【详解】A ．因为a//b ，所以∠2=∠6=110°，又∠3+∠6=180°(邻补角定义）所以∠3=180︒-∠6=180︒-110︒=70︒，正确，不符合题意；B ． //,13,12180a b ︒∴∠=∠∠+∠=，1180218011070︒︒︒︒∴∠=-∠=-=，所以370︒∠=，正确，不符合题意；C ．因为a//b ，所以25∠=∠，又∠3+∠5=180°(邻补角定义），3180518011070︒︒︒︒∴∠=-∠=-=，正确，不符合题意；D ． //,42180a b ︒∴∠+∠=，∴∠4=180°-∠2=180°-110°=70°，43∠=∠，∴∠3=70°，故D 选项错误，故选D ．【点睛】本题考查了平行线的性质，熟练掌握“两直线平行，同位角相等”、“两直线平行，内错角相等”、“两直线平行，同旁内角互补”是解题的关键．二、填空题11．62【详解】∵，，∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.解析：62【详解】∵OE AB ⊥，28EOC ∠=，∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.12．【分析】根据两直线平行，同位角相等求出∠EFD ，再根据角平分线的定义求出∠GFD ，然后根据两直线平行，内错角相等解答．【详解】解：∵AB ∥CD ，∠1=64°，∴∠EFD=∠1=64°，∵解析：【分析】根据两直线平行，同位角相等求出∠EFD ，再根据角平分线的定义求出∠GFD ，然后根据两直线平行，内错角相等解答．【详解】解：∵AB ∥CD ，∠1=64°，∴∠EFD=∠1=64°，∵FG 平分∠EFD ，∴∠GFD=12∠EFD=12×64°=32°， ∵AB ∥CD ，∴∠EGF=∠GFD=32°．故答案为：32．考点：平行线的性质．13．【分析】过点向右作，过点向右作，得到，根据两直线平行同旁内角互补即可得出答案．【详解】解：如图，过点向右作，过点向右作,故答案为：．【点睛】本题考查了平行线的性质定理,根据题解析：()1180n -⋅︒【分析】过点2A 向右作21//A D A B ，过点3A 向右作31//A E A B ，得到321////...////n A E A D A B A C ，根据两直线平行同旁内角互补即可得出答案．【详解】解：如图，过点2A 向右作21//A D A B ，过点3A 向右作31//A E A B1//n A B A C321////...////n A E A D A B A C ∴112180A A A D ∴∠+∠=︒,2323180DA A A A E ∠+∠=︒...()11231...1180n n A A A A A A C n -∴∠+∠++∠=-⋅︒故答案为：()1180n -⋅︒．【点睛】本题考查了平行线的性质定理,根据题意作合适的辅助线是解题的关键．14．．【分析】分别过点P 、I 作ME∥PH，AB∥GI，设∠AME=2x，∠PNF=2y，知∠PEM=x，∠MNP=y，由PH∥ME 知∠EPH=x，由EM∥FN 知PH∥FN，据此得∠HPN=2y，∠E 解析：81209a b =-︒．【分析】分别过点P 、I 作ME ∥PH ，AB ∥GI ，设∠AME=2x ，∠PNF=2y ，知∠PEM=x ，∠MNP=y ，由PH ∥ME 知∠EPH=x ，由EM ∥FN 知PH ∥FN ，据此得∠HPN=2y ，∠EPN=x+2y ，同理知3902EIF x x ∠︒-+＝，根据∠EPN=∠EIF 可得答案．【详解】分别过点P 、I 作ME ∥PH ，AB ∥GI ，设∠AME ＝2x ，∠PNF ＝2y ，则∠PEM ＝x ，∠MNP ＝y ，∴∠DFN ＝2x ，∵PH ∥ME ，∴∠EPH ＝x ，∵EM ∥FN ，∴PH ∥FN ，∴∠HPN ＝2y ，∠EPN ＝x +2y ，同理，3902EIF x x ∠︒-+＝， ∵∠EPN ＝∠EIF ，∴3902x x ︒-+＝x +2y ， ∴339042b ︒-a ＝， ∴91358b a =︒-， ∴81209b -︒a ＝，故答案为：81209b-︒a＝．【点睛】本题主要考查平行线的判定与性质，解题的关键是熟练掌握平行线的判定与性质．15．3或2+【解析】分析：分三种情况讨论：①如图1，由平移的性质得到△HDG是等腰直角三角形，重合部分为△HDG，则重合面积=DG2=4，解得DG=，而DC＜，故这种情况不成立；②如图解析：3或2+22【解析】分析：分三种情况讨论：①如图1，由平移的性质得到△HDG是等腰直角三角形，重合部分为△HDG，则重合面积=12DG2=4，解得DG=22，而DC＜22，故这种情况不成立；②如图2，由平移的性质得到△HDG、△CGI是等腰直角三角形，重合部分为梯形HDCI，则重合面积=S△HDG－S△CGI，把各部分面积表示出来，解方程即可；③如图3，由平移的性质得到△CGI是等腰直角三角形，重合部分为梯形EFCI，则重合面积=S△EFG－S△CGI，把各部分面积表示出来，解方程即可．详解：分三种情况讨论：①如图1．∵△EFG是等腰直角三角形，∴△HDG是等腰直角三角形，重合部分为△HDG，则重合面积=12DG2=4，解得：DG=22，而DC=2＜22，故这种情况不成立；②如图2．∵△EFG是等腰直角三角形，∴△HDG、△CGI是等腰直角三角形，重合部分为梯形HDCI，则重合面积=S△HDG－S△CGI =12DG2－12CG2=4，即：12DG2－12（DG-2）2=4，解得：DG=3；③如图3．∵△EFG是等腰直角三角形，∴△CGI是等腰直角三角形，重合部分为梯形EFCI，则重合面积=S△EFG－S△CGI =12EF2－12CG2=4，即：12×42－12（DG-2）2=4，解得：DG=222+或222-（舍去）．故答案为：3或222．点睛：本题主要考查了平移的性质以及等腰三角形的知识，解题的关键是分三种情况作出图形，并表示出重合部分的面积．16．130°或50°【解析】【分析】作图分析，若两个角的边互相垂直，那么这两个角必相等或互补，可据此解答．【详解】如图∵β的两边与α的两边分别垂直，∴α+β=180°故β=130°，在上述情解析：130°或50°【解析】【分析】作图分析，若两个角的边互相垂直，那么这两个角必相等或互补，可据此解答．【详解】如图∵β的两边与α的两边分别垂直，∴α+β=180°故β=130°，在上述情况下，若反向延长∠β的一边，那么∠β的补角的两边也与∠α的两边互相垂直，故此时∠β=50；综上可知：∠β=50°或130°，故正确答案为：【点睛】本题考核知识点：四边形内角和. 解题关键点：根据题意画出图形，分析边垂直的2种可能情况.17．4∠AFC=3∠AEC【解析】【分析】连接AC，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，根据平行线性质得出∠BAC+∠ACD=180°，求出∠CAE+∠ACE=18解析：4∠AFC=3∠AEC【解析】【分析】连接AC，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，根据平行线性质得出∠BAC+∠ACD=180°，求出∠CAE+∠ACE=180°-（4x°+4y°），求出∠AEC=4（x°+y°），∠AFC ═3（x°+y°），即可得出答案．【详解】连接AC ，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，∵AB ∥CD ，∴∠BAC+∠ACD=180°，∴∠CAE+4x°+∠ACE+4y°=180°，∴∠CAE+∠ACE=180°-（4x°+4y°），∠FAC+∠FCA=180°-（3x°+3y°），∴∠AEC=180°-（∠CAE+∠ACE ）=180°-[180°-（4x°+4y°）]=4x°+4y°=4（x°+y°），∠AFC=180°-（∠FAC+∠FCA ）=180°-[180°-（3x°+3y°）]=3x°+3y°=3（x°+y°），∴∠AFC=34∠AEC ，即：4∠AFC=3∠AEC ，故正确答案为：4∠AFC=3∠AEC.【点睛】本题考查了平行线性质和三角形内角和定理的应用，注意：两直线平行，同旁内角互补．18．145【分析】由已知、角平分线和垂直的定义可以得到∠AOE 和∠EOF 的大小，从而得到∠AOF 的值．【详解】解：∵,∵OE 平分∠AOC，∴,∵OF⊥OE 于点O ，∴∠EOF＝90°，∴∠A解析：145【分析】由已知、角平分线和垂直的定义可以得到∠AOE 和∠EOF 的大小，从而得到∠AOF 的值．【详解】解：∵70180110AOD AOC AOD ∠=︒∴∠=︒-∠=︒，,∵OE 平分∠AOC ，∴1552AOE AOC ∠=∠=︒, ∵OF ⊥OE 于点O ，∴∠EOF ＝90°，∴∠AOF ＝∠AOE+∠EOF ＝55°+90°=145°，故答案为145．【点睛】本题考查邻补角、角平分线和垂直以及角度的运算等知识，根据有关性质和定义灵活计算是解题关键．19．45°，60°，105°，135°．【解析】分析：根据题意画出图形，再由平行线的判定定理即可得出结论．详解：如图，当AC ∥DE 时,∠BAD=∠DAE=45°；当BC ∥AD 时,∠DAE=∠解析：45°，60°，105°，135°．【解析】分析：根据题意画出图形，再由平行线的判定定理即可得出结论．详解：如图，当AC ∥DE 时,∠BAD =∠DAE =45°；当BC ∥AD 时,∠DAE =∠B =60°；当BC ∥AE 时,∵∠EAB =∠B =60°,∴∠BAD =∠DAE +∠EAB =45°+60°=105°；当AB ∥DE 时,∵∠E =∠EAB =90°,∴∠BAD =∠DAE +∠EAB =45°+90°=135°.故答案为45°,60°,105°,135°.点睛：本题考查了平行线的判定与性质.要证明两直线平行，需使其所构成的同位角、内错角相等（或同旁内角是否互补）.20．73°【解析】试题解析：∵∠CBD=34°，∴∠CBE=180°-∠CBD=146°，∴∠ABC=∠ABE=∠CBE=73°．解析：73°【解析】试题解析：∵∠CBD=34°，∴∠CBE=180°-∠CBD=146°，∴∠ABC=∠ABE=12∠CBE=73°．三、解答题21．（1）60°；（2）①75°，②当BG上的动点P为∠CDG的角平分线与BG的交点时，满足∠BPD是∠F的k系补周角，此时k=2n，推导见解析.【分析】（1）直接利用k系补周角的定义列方程求解即可．（2）①依据k系补周角的定义及平行线的性质，建立∠B ED、∠B、∠D的关系式求解即可.②结合本题的构图特点，利用平行线的性质得到：∠ABF+∠CDF+∠F=360°,结合∠ABF=n∠ABE，∠CDF=n∠CDE（其中n为常数且n＞1），又由于点P是∠ABE角平分线BG上的一个动点，通过构造相同特殊条件猜想出一个满足条件的P点，再通过推理论证得到k的值（含n的表达式），即说明点P即为所求.【详解】解：（1）设∠H的4系补周角的度数为x，则有120°+4x=360°，解得：x=60°∴∠H的4系补周角的度数为60°；（2）①如图，过点E作EF//AB，∵AB//EF,∴EF//CD，∴∠B=∠1,∠D=∠2，∴∠1+∠2=∠B+∠D ，即∠B ED=∠B+∠D ，∵∠BED+3∠B=360°，∠D ＝60，∴360360B B ︒-∠=∠+︒，解得：∠B=75°，∴∠B=75°；②预备知识，基本构图：如图，AB//CD//EF,则∠ABE+∠BEG=180°，∠DCE+∠GEC=180°，∴∠ABE+∠BEG+∠DCE+∠GEC=360°，即∠ABE+∠DCG+∠BEC=360°如图：当BG 上的动点P 为∠CDG 的角平分线与BG 的交点时，满足∠BPD 是∠F 的k 系补周角，此时k=2n.理由如下：若∠BPD 是∠F 的k 系补周角，则∠F+k ∠BPD=360°，∴k ∠BPD=360°-∠F又由基本构图知：∠ABF+∠CDF=360°-∠F ， ∴k ∠BPD=∠ABF+∠CDF ，又∵∠ABF =n ∠ABE ，∠CDF =n ∠CDE ，∴k ∠BPD= n ∠ABE+ n ∠CDE ，∵∠BPD=∠PHD+∠PDH,∵AB//CD ，PG 平分∠ABE ，PD 平分∠CDE ，∴∠PHD=∠ABH=12ABE ∠ ,∠PDH=12CDE ∠， ∴2k (ABE ∠+CDE ∠)=n(∠ABE+∠CDE)， ∴k=2n.【点睛】本题主要考查平行线的基本性质及基本构图的应用.题型较新颖，发散性较强，理解题意，熟练掌握平行线的性质及其基本构图是解题的关键.22．(1) 16； (2) 56； (3)(1)12n n +⎡⎤+⎢⎥⎣⎦部分【分析】（1）根据已知探究的结果可以算出当直线条数为5时，把平面最多分成16部分；（2）通过已知探究结果，写出一般规律，当直线为n 条时，把平面最多分成1+1+2+3+…+n ，求和即可．【详解】（1）16;1+1+2+3+4+5.（2）56.根据表中规律知,当直线条数为10时,把平面最多分成56部分,即1+1+2+3+…+10=56.（3）当直线条数为n 时,把平面最多分成1+1+2+3+…+n=(1)12n n +⎡⎤+⎢⎥⎣⎦部分. 【点睛】本题考查了图形的变化，通过直线分平面探究其中的隐含规律，运用了从特殊到一般的数学思想，解决此题关键是写出和的形式．23．（1）见详解；（2）见详解；（3）29.5°．【分析】（1）根据平行线的性即可A ACD ∠=∠，B BCE ∠=∠，再根据平角的定义进行等量代换即可证明；（2）因为根据平角的定义和三角形的内角和定理即可得到结论；（3）根据平行线的性质得到119DEB ∠=︒，61AED ∠=︒，由角平分线的性质得到59.5DEF ∠=︒，根据三角形的外角的性质即可得到结论．【详解】（1）如图1所示，在ABC ∆中，//DE AB ，A ACD ∴∠=∠，B BCE ∠=∠．180ACD BCA BCE ∠+∠+∠=︒，180A B ACB ∴∠+∠+∠=︒．即三角形的内角和为180︒；（2）180AGF FGE ∠+∠=︒，由（1）知，180GEF F FGE ∠+∠+∠=︒，AGF AEF F ∴∠=∠+∠；（3）//AB CD ，119CDE ∠=︒，119DEB CDE ∴∠=∠=︒，18061AED CDE ∠=︒-∠=︒，∵EF 平分DEB ∠，59.5DEF ∴∠=︒，120.5AEF AED FED ∴∠=∠+∠=︒，150AGF ∠=︒，AGF AEF F ∠=∠+∠，150120.529.5F ∴∠=︒-︒=︒．【点睛】本题考查了平行线的性质，三角形的内角和定理的证明与应用，三角形外角定理证明与应用，熟练掌握平行线的性质定理是解题的关键，此类题目每一步都为后续解题提供了解题条件或方法．24．（1）详见解析；（2）HPQ ∠的大小不发生变化，一直是45︒．【分析】（1）利用平行线的性质推知180BEF EFD ∠+∠=︒；然后根据角平分线的性质、三角形内角和定理证得90EPF ∠=︒，即EG PF ⊥，故结合已知条件GH EG ⊥，易证//PF GH ；（2）利用三角形外角定理、三角形内角和定理求得49039022∠=︒-∠=︒-∠；然后由邻补角的定义、角平分线的定义推知14522QPK EPK ∠=∠=︒+∠；最后根据图形中的角与角间的和差关系求得HPQ ∠的大小不变，是定值45︒．【详解】解：（1）证明：如图1，//AB CD ，180BEF EFD ∴∠+∠=︒．又BEF ∠与EFD ∠的角平分线交于点P ，1()902FEP EFP BEF EFD ∴∠+∠=∠+∠=︒， 90EPF ∴∠=︒，即EG PF ⊥．GH EG ⊥，//PF GH ∴；（2）HPQ ∠的大小不发生变化，理由如下：如图2，12∠=∠， 322∠=∠∴．又GH EG ⊥，49039022∠=︒-∠=︒-∠∴．18049022EPK ∠=︒-∠=︒+∠∴．PQ ∵平分EPK ∠，14522QPK EPK ∴∠=∠=︒+∠． ∴245HPQ QPK ∠=∠-∠=︒，∴HPQ ∠的大小不发生变化，一直是45︒．【点睛】本题主要考查平行线的性质和判定，掌握平行线的性质和判定是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④//a b ，////b c a c ⇒．25．（1）∠AEC ＝∠C +∠A ；（2）∠C ﹣∠E ＝15°；（3）2∠AGF +∠GDC ＝90°．理由见解析．【分析】（1）过点E 作EF ∥AB ，知AB ∥CD ∥EF ，据此得∠A=∠AEF ，∠C=∠CEF ，根据∠AEC=∠AEF+∠CEF 可得答案；（2）分别过点E 、F 作FM ∥AB ，EN ∥AB ，设∠NEF=x=∠EFM ，知∠AEF=x+50°，∠MFC=115°-x ，据此得∠C=180°-（115°-x ）=x+65°，进一步计算可得答案；（3）分别过点E 、F 、G 作FM ∥AB ，EN ∥AB ，GH ∥AB ，设∠GAE=x=∠GAB ，∠GFM=y ，∠MPC=z ，知∠GPE=y+z ，从而得2x+2y+z=90°，∠C=180°-z ，根据GD ∥FC 得∠D=z ，由GH ∥AB ，AB ∥CD 知∠AGF=x+y ，继而代入可得答案．【详解】（1）∠AEC ＝∠C +∠A ，如图1，过点E 作EF ∥AB ，∵AB∥CD，∴AB∥CD∥EF，∴∠A＝∠AEF，∠C＝∠CEF，则∠AEC＝∠AEF+∠CEF＝∠A+∠C，故答案为：∠AEC＝∠C+∠A；（2）如图2，分别过点E、F作FM∥AB，EN∥AB，设∠NEF＝x＝∠EFM，则∠AEF＝x+50°，∠MFC＝115°﹣x，∴∠C＝180°﹣（115°﹣x）＝x+65°，∴∠C﹣∠E＝x+65°﹣（x+50°）＝15°；（3）如图3，分别过点E、F、G作FM∥AB，EN∥AB，GH∥AB，设∠GAE＝x＝∠GAB，∠GFM＝y，∠MPC＝z，则∠GPE＝y+z，∴2x+2y+z＝90°，∠C＝180°﹣z，∵GD∥FC，∴∠D＝z，∵GH∥AB，AB∥CD，∴∠AGF＝x+y，∴2∠AGF+∠GDC＝90°．【点睛】本题主要考查平行线的性质，解题的关键是掌握两直线平行内错角相等的性质．26．[问题解决]见解析；[问题迁移]（1）∠APC=α+β；（2）当点P在BN上时，∠APC=β-α；当点P在OD上时，∠APC=α-β．【分析】问题解决：过点E作EF∥AB，依据平行线的性质，即可得到∠BED的度数；问题迁移：（1）过P作PQ∥AB，依据平行线的性质，即可得出α，β和∠APC之间满足的数量关系．（2）分两种情况讨论：过P作PQ∥AB，易得当点P在BN上时，∠APC=β-α；当点P在OD上时，∠APC=α-β．【详解】问题解决：如图2，过点E作EF∥AB，∴∠ABE=∠BEF=40°∵AB∥CD，∴EF∥CD，∴∠B=∠BEF，∠D=∠DEF，∴∠BED=∠B+∠D=40°+60°=100°；问题迁移：（1）如图3，过P作PQ∥AB，∵AB∥CD，∴PQ∥CD，∴∠BAP=∠APQ，∠DCP=∠CPQ，∴∠APC=∠BAP+∠DCP，即∠APC=α+β；（2）如图4，当点P在BN上时，∠APC=β-α；如图5，当点P在OD上时，∠APC=α-β．【点睛】本题主要考查了平行线的性质与判定的运用，解决问题的关键是掌握：两直线平行，内错角相等，并利用角的和差关系进行推算．。

平行线培优练习题及中考真题

相交线与平行线一、选择题1. （2011山东德州4,3分）如图，直线l 1∥l 2， ∠1=40°，∠2=75°，则∠3等于（A ）55° （B ） 60° （C ）65° （D ） 70°【答案】C2. （2011山东日照，3，3分）如图，已知直线AB CD ∥，125C ∠=°，45A ∠=°，那么E ∠的大小为（）（A ）70° （B ）80° （C ）90° （D ）100°【答案】B3. （2011山东泰安，8 ，3分）如图，l ∥m ，等腰直角三角形ABC 的直角顶点C 在直线m 上，若∠β=200，则∠α的度数为（）A.250B.300C.200D.350 【答案】A4. （2011四川南充市，3，3分）如图，直线DE 经过点A,DE ∥BC,,∠B=60°,下列结论成立的是（）（A ）∠C=60° （B ）∠DAB=60° （C ）∠EAC=60° （D ）∠BAC=60°EDCBAl 1l 2123【答案】B5. （2011山东枣庄，2，3分）如图，直线AB ∥CD ，∠A ＝70︒，∠C ＝40︒，则∠E 等于（）A ．30° Ｂ．40° C ．60° Ｄ．70° 【答案】A6. （2010湖北孝感，3，3分）如图，直线AB 、CD 相交于点O ，OT ⊥AB 于O ，CE ∥AB 交CD 于点C ，若∠ECO=30°，则∠DOT=（） A.30° B.45° C. 60° D. 120°【答案】C7. （2011河北，2，2分）如图1∠1+∠2=（）1图1A ．60°B ．90°C ．110°D ．180° 【答案】B8. （2011宁波市，8，3分）如图所示，AB ∥CD ，∠E ＝37°， ∠C ＝20°， ∠EAB 的度数为 A ． 57° B ． 60° C ． 63° D． 123°【答案】A9. （2011浙江衢州，12,4分）如图，直尺一边AB 与量角器的零刻度线CD 平行，若量角器的一条刻度线OF 的读书为70°，OF 与AB 交于点E ,那么AEF ∠= 度.A CB D E【答案】7010．（2011浙江绍兴，3，4分）如图，已知//,,34AB CD BC ABE C BED ∠∠=︒∠平分，则的度数是( )A.17︒B. 34︒C. 56︒D. 68︒AD【答案】D11. （2011浙江义乌，8，3分）如图，已知AB ∥CD ，∠A =60°，∠C =25°，则∠E 等于A. 60°B. 25°C. 35°D. 45° 【答案】C12. （2011四川重庆，4，4分）如图，AB ∥CD ，∠C ＝80°，∠CAD ＝60°，则∠BAD 的度数等于( )A ．60°B ．50°C ． 45°D ． 40° 【答案】D13. （2011浙江丽水，5，3分）如图，有一块含有45°角的直角三角板的两个顶点放在直尺ABCDE60°的对边上.如果∠1＝20°，那么∠2的度数是（）A ．30°B .25°C .20°D .15° 【答案】B14. （2011台湾台北，8）图(二)中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角。

浙教版2022-2023学年七下数学第一章平行线培优测试卷(解析版)

浙教版2022-2023学年七下数学第一章平行线培优测试卷（解析版）一、选择题（本大题有10小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的.1．如图，在长为xm，宽为ym的长方形草地ABCD中有两条小路l1和l2、l1为W状，l2为平行四边形状，每祭小路的右边线都是由小路左边线右移1m得到的两条小路l1、l2的占地面积的情况是（）A．l1占地面积大B．l2占地面积大C．l2和l1占地面积一样大D．无法确定【答案】C【解析】小路l2可看作高为y，底为2的平行四边形，由平行四边形面积公式S=ah，则面积为：S2=2y；小路l1可看作四个小的平行四边形组成，小平行四边形的底可看作2，所有小平行四边形的高之和为y，由平行四边形面积公式S=ah，则面积为：S1=2y；则S1=S2，故答案为：C.2．下列说法中：①在同一平面内，不相交的两条线段一定平行；②两条直线被第三条直线所截，同位角相等；③相等的角是对顶角；④等角的补角相等，不正确的有（）A．1个B．2个C．3个D．4个【答案】C【解析】①在同一平面内，不相交的两条线段一定平行，判断错误；②两条直线被第三条直线所截，同位角相等，判断错误；③相等的角是对顶角，判断错误；④等角的补角相等，判断正确.故答案为：C.3．如图，直线a，b被直线c所截，下列说法不正确的是（）A．∠1与∠2是内错角B．∠3与∠4是同旁内角C．∠2与∠5是同位角D．∠2与∠4是内错角【答案】A【解析】∵∠1和∠2是对顶角，不是内错角，∴A选项不正确，符合题意.故答案为：A.4．图，点A，B，E共线，下列条件中不能判断AD∥BC的是（）A．∠1=∠2B．∠A=∠5C．∠3=∠4D．∠A+∠ABC=180°【解析】A 、∠1＝∠2可利用内错角相等，两直线平行判定AD∠BC ，故此选项不符合题意； B 、∠A ＝∠5可利用同位角相等，两直线平行判定AD∠BC ，故此选项不符合题意； C 、∠3＝∠4，可根据内错角相等，两直线平行判定CD∠BA ，不能判定AD∠BC ，故此选项符合题意； D 、∠A ＋∠ABC ＝180°可利用同旁内角互补，两直线平行判定AD∠BC ，故此选项不符合题意；故答案为：C ．5．如图.已知AB//CD .直线EF 分别交AB ，CD 于点E ，F ，EG 平分∠BEF .若∠1=50°.则∠2的度数为（）A ．50°B ．65°C ．60°D ．70° 【答案】B【解析】∵AB∠CD ，∴∠1+∠BEF=180°，∠2=∠BEG ， ∴∠BEF=180°-50°=130°，又∵EG 平分∠BEF ， ∴∠BEG=12∠BEF=65°，∴∠2=65°. 故答案为：B.6．如图，将一块三角板的直角顶点放在直尺的一边上，当∠2=38°时，∠1=（）A ．52°B ．38°C ．42°D ．60°【答案】A 【解析】【解答】如图：∠3=∠2=38°（两直线平行同位角相等）， ∴∠1=90°﹣∠3=52°，故选A ．7．如图，直线c 与直线a 相交于点A ，与直线b 相交于点B ， ∠1=130∘ ， ∠2=60∘ ，若要使直线 a ∥b ，则将直线a 绕点A 按如图所示的方向至少旋转（）A ．10∘B ．20∘C ．60∘D ．130∘【答案】A【解析】∵∠2＝60°，∴若要使直线a∠b ，则∠3应该为60°，又∵∠1＝130°，∴直线a绕点A按顺时针方向至少旋转：60°−50°＝10°，故答案为：A.8．如图，直线AB//CD，将含有45°角的三角板EFP的直角顶点F放在直线CD上.顶点E放在直线AB上，若∠1=28°，则∠2的度数为（）A．45°B．17°C．25°D．30°【答案】B【解析】过点P作PM∠AB，∵AB∠CD，∴AB∠PM∠CD，∴∠3=∠1=28∘,∵∠EPF=45∘,∴∠2=∠4=∠EPF−∠3=45∘−28∘=17∘.故答案为：B.9．如图，ΔABC是直角三角形，它的直角边AB=6，BC=8，将ΔABC沿边BC的方向平移到ΔDEF的位置，DE交AC于点G，BE=2，ΔCEG的面积为13.5，下列结论：①ΔABC平移的距离是4：②DG=1.5；③AD∥CF；④四边形ADFC的面积为6．其中正确的结论是（）A．①②B．②③C．③④D．②④【答案】B【解析】∵直角三角形ABC的直角边AB＝6，BC＝8，将直角三角形ABC沿边BC的方向平移到三角形DEF的位置，①∵BE=2，∴三角形ABC平移的距离是2，故①不符合题意，②∵ΔABC沿边BC的方向平移到ΔDEF的位置，BC=8，BE=2，∴BE=BC−BE=6，DE=AB=6，∵ΔCEG的面积为13.5，且ΔCEG是直角三角形，∴GE=4.5，∴DG=DE−GE=1.5，故②符合题意，③∵ΔABC沿边BC的方向平移到ΔDEF的位置，ΔABC是直角三角形，∴∠ B=∠ DEC=90°， ∴AD∠CF ，故③符合题意，④四边形ADFC 的面积＝2×6＝12．故④不符合题意，故答案为：B ．10．如图1，当光线从空气斜入射到某种透明的液体时发生了折射，满足入射角∠1与折射角∠2的度数比为3∠2．如图2，在同一平面上，两条光线同时从空气斜射入这种液体中，两条入射光线与水平液面夹角分别为α，β，在液体中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（）A ．23 （α＋β）＝γB ．23 （α＋β）＝120°－γC ．α＋β＝γD ．α＋β＋γ＝180° 【答案】B【解析】如图2，分别作出两条入射关系的法线并延长，与折线的夹角分别为∠1和∠2，再过γ角的顶点作法线的平行线，夹角分别为∠3和∠4，∴∠1=∠3，∠2=∠4， ∴γ=∠1+∠2①，又∵入射角与折射角的度数比为3：2， ∴∠1=23（90°-α），∠2=23（90°-β），∴γ=23（90°-α）+23（90°-β）=23（180°-α-β），∴γ=120°-23（α+β），即23（α+β）=120°-γ.故答案为：B.二、填空题（本大题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案.11．在同一平面内，三条互不重合的直线 a 、 b 、 c ，若 a ∠ b ， a ∠ c ，则 . 【答案】b ∠ c【解析】∵a∠b ，a∠c ∴b∠c12．如图所示，能与∠1构成同位角的角有个．【答案】3【解析】由同位角的定义知，能与∠1构成同位角的角有∠2、∠3、∠4，共3个．13．如图，在直线AB外取一点C，经过点C作AB的平行线，这种画法的依据是．【答案】同位角相等，两直线平行【解析】如图，由图形痕迹可得∠BDE=∠CEF，则根据同位角相等，两直线平行可判断经过点C的直线与AB平行．故答案为：同位角相等，两直线平行．14．如图，在三角形ABC中，AB=2BC=4cm．把三角形ABC沿AB方向平移1cm，得到三角形A1B1C1，连接CC1，则四边形BB1C1C的周长为cm．【答案】6【解析】根据平移的性质可：BC=B′C′，CC′=BB′，∵平移的距离为1cm，∴CC′=BB′=1cm，∵2BC=4cm，∴BC=2cm，∴BC=B′C′=2cm，∴四边形BB′C′C的周长为：BC+B′C′+CC′+BB′=2+2+1+1=6cm，故答案为：6．15．如图，已知直线a∥b，c∥d，若∠1、∠2是图中的两个角，且这两个角的两边分别平行，∠1=（2x−3）°，∠2=（3x−17）°，则x值为．【答案】14或40【解析】如图，∵c ∥d ，∴∠1+∠2=180°，∴（2x -3）°+（3x -17）°=180°，解得：x =40，如图，∵a ∥b ，c ∥d ，∴∠2+∠3=180°，∠1+∠3=180°， ∴∠1=∠2，∴（2x -3）°=（3x -17）° 解得：x=14综上：x 的值为：14或40 故答案为：14或40 16．如图，AD //BC ，点P 是射线BC 上一动点，且不与点B 重合．AM 、AN 分别平分∠BAP 、∠DAP ，∠B =α，∠BAM =β，在点P 运动的过程中，当∠BAN =∠BMA 时，12α+2β= ．【答案】90°【解析】∵AD//BC∴∠BMA=∠DAM ，∠B+∠BAD=180° ∵AM 平分∠BAP ，∴∠BAM=∠MAP=12∠BAP ，∵AN 平分∠DAP ，∴∠DAN=∠NAP=12∠DAP ，∵∠BAN=∠BMA∴∠DAM=∠BAN∵∠BAM=∠BAN−∠MAN，∠DAN=∠DAM−∠MAN ∴∠BAM=∠DAN∴∠BAM=14∠BAD∵∠B=α，∠BAM=β∴∠BAM=14∠BAD=β∴∠BAD=4β∴α+4β=180°∴12α+2β=90°故答案为：90°．三、解答题（本题有8小题，第17～20题每题7分，第21题8分，第22～24题每题10分，共66分）解答应写出文字说明，证明过程或推演步骤.17．如图，AD⊥BC于点D，EF⊥BC于点F，且∠1+∠3=180°.（1）试判断DG与AC的位置关系，并说明理由.（2）若∠3=3∠2，求∠C的度数.【答案】（1）解：如图，DG//AC理由：∵AD⊥BC，EF⊥BC∴AD//EF∴∠4+∠3=180°∵∠1+∠3=180°∴∠1=∠4∴DG//AC（2）解：∵AD⊥BC∴∠1+∠2=90°∵∠3=3∠2∴∠1+∠3=∠1+3∠2=180°∴∠2=45°由(1)得DG//AC∴∠C=∠2=45°18．如图，在∠ABC中，D，E，F分别是三边上的点，且DE平分∠ADF，∠ADF=2∠DFB.（1）判断DE与BC的位置关系，并说明理由.（2）若EF∠AB，∠DFE=3∠CFE，求∠ADE的度数.【答案】（1）证明：DE与BC的位置关系为：DE∠BC.理由：∵DE平分∠ADF，∴∠ADF=2∠EDF，∵∠ADF=2∠DFB，∴∠EDF=∠DFB，∴DE∠BC.（2）解：∵EF∠AB，∴∠CFE=∠B，设∠CFE=∠B=x，∵DE∠BC，DE平分∠ADF，∴∠DFB＝∠EDF＝∠ADE＝x，∵∠DFB＋∠DFE＋∠CFE＝180°，∴x+3x+x=180°，解之：x=36°，∴∠ADE的度数36º.19．如图，由若干个小正方形构成的网格中有一个△ABC，△ABC的三个顶点都在格点上，按要求进行下列作图：（只借助于网格，需写出结论）∠过点B画出AC的平行线BD；∠画出先将△ABC向右平移2格，再向上平移3格后的△A ′B ′C ′.【答案】解：（1）BD就是所求作的图形（2）∠A'B'C'即为所求作图形.20．如图，∠ABC和∠BCD的平分线交于点P，延长CP交AB于点Q，且∠PBC+∠PCB=90°（1）求证：AB//CD.（2）探究∠PBC与∠PQB的数量关系.【答案】（1）证明：∵BP平分∠ABC，∴∠ABC=2∠PBC.∵CP平分∠BCD，∴∠BCD=2∠PCB，∴∠ABC+∠BCD=2∠PBC+2∠PCB又∵∠PBC+∠PCB=90∘∴∠ABC+∠BCD=180∘∴AB//CD.（2）解：∵CP平分∠DCB，∴∠PCD=∠PCB.∵AB//CD，∴∠PCD=∠PQB，∴∠PCB=∠PQB.又∵∠PBC+∠PCB=90∘∴∠PBC+∠PQB=90°21．如图，MN∠BC，BD∠DC，∠1=∠2=60°，DC是∠NDE的平分线．（1）AB与DE平行吗？请说明理由；（2）试说明：∠ABC=∠C；（3）求∠ABD的度数．【答案】（1）解：AB∠DE，理由如下：∵MN∠BC，∠1= 60°，∴∠ABC=∠1=60°，又∵∠1=∠2，∴∠ABC=∠2，∴AB∠DE（2）解：∵MN∠BC，∴∠NDE+∠2= 180°，∴∠NDE=180°-∠2= 180°-60°=120°，∵DC是∠NDE的角平分线，∴∠EDC=∠NDC=12∠NDE=60°，∵MN∠BC，∴∠C=∠NDC=60°，∴∠ABC=∠C（3）解：∵∠ADC+∠NDC=180°，∠NDC= 60°，∴∠ADC=180°-∠NDC=180°-60°=120°，∵BD∠DC，∴∠BDC= 90°，∴∠ADB=∠ADC-∠BDC=120°-90°=30°，∵MN∠BC，∴∠DBC=∠ADB=30°，∵∠ABC=∠C=60°，∴∠ABD=30°22．已知，∠AOB=90°，点C在射线OA上，CD//OE.（1）如图1，若∠OCD=120°，求∠BOE的度数；（2）把“ ∠AOB=90°°”改为“ ∠AOB=120°”，射线OE沿射线OB平移，得到O′E，其它条件不变（如图2所示），探究∠OCD,∠BO′E的数量关系；（3）在（2）的条件下，作PO′⊥OB，垂足为O′，与∠OCD的角平分线CP交于点P，若∠BO′E=α，用含α的式子表示∠CPO′（直接写出答案）.【答案】（1）解：∵CD//OE，∴∠AOE=∠OCD=120°，∴∠BOE=360°-90°-120°=150°（2）解：如图2，过O点作OF//CD，∴CD//OE，∴OF∠OE，∴∠AOF=180°-∠OCD，∠BOF=∠EO'O=180°-∠BO'E，∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO'E=360°-（∠OCD+∠BO'E）=120°，∴∠OCD+∠BO'E=240°（3）30°+ 1 2α【解析】（3）如图，∵CP是∠OCD的平分线，∴∠OCP= 12∠OCD，∴∠CPO'=360°-90°-120°-∠OCP=150°-12∠OCD=150°-12（240°-∠BO'E）=30°+ 12α23．已知AB//CD，（1）如图1，若∠ABE=160°，∠CDE=120°，求∠BED的度数；（2）如图2，若BF平分∠ABE，DF平分∠CDE，则∠BFD与∠BED有怎样的数量关系，并说明理由；（3）如图3，若BF平分∠ABE，DF平分∠CDE，则∠BFD与∠BED有怎样的数量关系，并说明理由．【答案】（1）解：延长AB交DE于点F．∵∠ABE+∠EBF=180°，∴∠EBF=20°．∵AB//CD，∴∠CDE=∠BFE=120°．∵∠EBF+∠BED+∠BFE=180°，∴∠BED=180°−20°−120°=40°．（2）解：∠BED=2∠BFD．理由：延长AB交FD于点N，交DE于点M．∵BF平分∠ABE，DF平分∠CDE，∴∠ABF=12∠ABE，∠CDF=12∠CDE．∵AB//CD，∴∠CDF=∠ANF，∠AME=∠CDE．∵∠E=180°−∠BME−∠EBM=180°−∠CDE−(180°−∠ABE)=∠ABE −∠CDE ，又∵∠F =∠ABF −∠ANF=∠ABF −∠CDF=12∠ABE −12∠CDE =12(∠ABE −∠CDE)，∴∠E =2∠F ．即∠BED =2∠BFD ．（3）解：∠BED +2∠BFD =360°理由：过点F 作FM//AB ，过点E 作EN//CD ．∵BF 平分∠ABE ，DF 平分∠CDE ∴∠ABF =∠FBM =12∠ABE ，∠CDF =∠FDE =12∠CDE ．∵FM//AB ，EN//CD ，AB//CD ，∴AB//FM//EN//CD ， ∴∠BFM =∠ABE ，∠MFD =∠CDF ，∴∠BFD =12(∠ABE +∠CDE) ∵∠BFD +∠FBE +∠FDE +∠BED =360°， ∴∠BED +∠BFD +12(∠ABE +∠CDE)=360°， ∴∠BED +2∠BFD =360°．24．已知，直线AB//DC ，点P 为平面内一点，连接AP 与CP .（1）如图1，点P 在直线AB 、CD 之间，若∠BAP =50°，∠DCP =20°，求∠APC 的度数. （2）如图2，点P 在直线AB 、CD 之间，∠BAP 与∠DCP 的角平分线相交于点K ，写出∠AKC 与∠APC 之间的数量关系，并说明理由.（3）如图3，点P 在直线AB 、CD 下方，∠BAP 与∠DCP 的角平分线相交于点K ，直接写出∠AKC 与∠APC 之间的数量关系.【答案】（1）解：如图1，过P 作PE//AB ，∵AB//CD ，∴PE//AB//CD ，∴∠APE =∠BAP ，∠CPE =∠DCP ，∴∠APC =∠APE +∠CPE =∠BAP +∠DCP =50°+20°=70°；（2）解：∠AKC=12∠APC.理由：如图2，过K作KE//AB，∵AB//CD，∴KE//AB//CD，∴∠AKE=∠BAK，∠CKE=∠DCK，∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK，过P作PF//AB，同理可得，∠APC=∠BAP+∠DCP，∵∠BAP与∠DCP的角平分线相交于点K，∴∠BAK+∠DCK=12∠BAP+12∠DCP=12(∠BAP+∠DCP)=12∠APC，∴∠AKC=12∠APC；（3）解：∠AKC=12∠APC.理由：如图3，过K作KE∠AB，∵AB∠CD，∴KE∠AB∠CD.∴∠BAK=∠AKE，∠DCK=∠CKE.∴∠AKC=∠AKE−∠CKE=∠BAK−DCK.过P作PF∠AB，同理可得，∠APC=∠BAP−∠DCP.∵∠BAP与∠DCP的平分线交于点K，∴∠BAK−∠DCK=12∠BAP−12∠DCP=12(∠BAP−∠DCP)=12∠APC，∴∠AKC=12∠APC.。

九年级数学下册2023年中考专题培优训练平行线与相交线【含答案】

九年级数学下册2023年中考专题培优训练平行线与相交线一、单选题（每题3分，共30分）(共10题；共30分)a∥b AC⊥b 1．（3分）（2022·兰州）如图，直线，直线c与直线a，b分别相交于点A，B，，垂∠1=52°∠2=足为C．若，则（）A．52°B．45°C．38°D．26°2．（3分）（2022·青海）数学课上老师用双手形象的表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）.从左至右依次表示（）A．同旁内角、同位角、内错角B．同位角、内错角、对顶角C．对顶角、同位角、同旁内角D．同位角、内错角、同旁内角AB∠13．（3分）（2022·贵阳）如图，将菱形纸片沿着线段剪成两个全等的图形，则的度数是（）A．40°B．60°C．80°D．100°∥4．（3分）（2022·鄂州）如图，直线l1l2，点C、A分别在l1、l2上，以点C为圆心，CA长为半径画弧，交l1于点B，连接AB.若∠BCA＝150°，则∠1的度数为（）A．10°B．15°C．20°D．30°AB∥CD，AE∥CF，∠BAE=75°∠DCF5．（3分）（2022·长沙）如图，，则的度数为（）65°70°75°105°A．B．C．D．a∥b c a，b A，C B b AB⊥AC 6．（3分）（2022·泸州）如图，直线，直线分别交于点，点在直线上，，若∠1=130°∠2，则的度数是（）30°40°50°70°A．B．C．D．Rt△ABC∠C=90°，∠BAC=30°7．（3分）（2022·山西）如图，是一块直角三角板，其中．直尺的一DE∥CB∠DAB边DE经过顶点A，若，则的度数为（）A．100°B．120°C．135°D．150°∠ABC∠DEF8．（3分）（2022·盐城）小明将一块直角三角板摆放在直尺上，如图所示，则与的关系是（）A．互余B．互补C．同位角D．同旁内角9．（3分）（2022·朝阳）将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上，∠EFG＝90°，∠EGF＝60°，∠AEF＝50°，则∠EGC的度数为（）A．100°B．80°C．70°D．60°AB CD10．（3分）（2022·潍坊）如图是小亮绘制的潜望镜原理示意图，两个平面镜的镜面与平行，入AB∠1=40°10′∠6射光线l与出射光线m平行．若入射光线l与镜面的夹角，则的度数为（）100°40′99°80′99°40′99°20′A．B．C．D．二、填空题（每空3分，共18分）(共6题；共18分)a∥b∠1=110°∠211．（3分）（2022·眉山）如图，已知，，则的度数为 .∥∥12．（3分）（2022·济宁）如图，直线l1，l2，l3被直线l4所截，若l1l2，l2l3，∠1＝126°32'，则∠2的度数是．13．（3分）（2022·绵阳）两个三角形如图摆放，其中∠BAC＝90°，∠EDF＝100°，∠B＝60°，∠F＝40°，BC∥EFDE与AC交于M，若，则∠DMC的大小为．14．（3分）（2022·湘西）1.如图，直线a∥b，点C、A分别在直线a、b上，AC⊥BC，若∠1＝50°，则∠2的度数为．15．（3分）（2021·泰州）如图，木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住，∠EGB＝100°，∠EHD＝80°，将木棒AB绕点G逆时针旋转到与木棒CD平行的位置，则至少要旋转 °.AB CD16．（3分）（2021·湘西）如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为、CD//BE∠1=20°，若，的度数是 .三、解答题（共8题，共72分）(共8题；共72分)17．（6分）（2022·陕西）如图，在△ABC中，点D在边BC上，CD=AB，DE∥AB，∠DCE=∠A.求证：DE=BC.18．（8分）（2022·金华）图1是光伏发电场景，其示意图如图2，EF为吸热塔，在地平线EG上的点B，B'处各安装定日镜(介绍见图3).绕各中心点(A，A')旋转镜面，使过中心点的太阳光线经镜面反射3后到达吸热器点F处.已知AB=A'B'=1m，EB=8m，EB'=8 m，在点A观测点F的仰角为45º（1）（4分）点F的高度EF为 m.（2）（4分）设∠DAB=α，∠D'A'B'=β，则α与β的数量关系是 .19．（8分）（2021·泰州）如图（1）（4分）如图①，O为的中点，直线l1、l2分别经过点O、B，且l1∥l2，以点O为圆心，OA长为半径画弧交直线l2于点C，连接AC.求证：直线l1垂直平分AC；（2）（4分）如图②，平面内直线l1∥l2∥l3∥l4，且相邻两直线间距离相等，点P、Q分别在直线l1、l4上，连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D，使线段PD最短.（两种工具分别只限使用一次，并保留作图痕迹）AB//DE，AB=DE，BF=CE 20．（8分）（2021·常州）如图，B、F、C、E是直线l上的四点， .△ABC≌△DEF（1）（4分）求证：；△ABC△A′BC（2）（4分）将沿直线l翻折得到 .△A′BC①用直尺和圆规在图中作出（保留作图痕迹，不要求写作法）；②连接，则直线与l 的位置关系是▲ .A ′D A ′D 21．（10分）（2021·绵阳）如图，点是的边上的动点，，连接，并将M ∠ABC BA BC =6MC 线段绕点逆时针旋转得到线段 .MC M 90°MN（1）（5分）如图1，作，垂足在线段上，当时，判断点是MH ⊥BC H BC ∠CMH =∠B N 否在直线上，并说明理由；AB （2）（5分）如图2，若，，求以、为邻边的正方形的面积 .∠ABC =30°NC//AB MC MN S 22．（10分）（2022·宁波模拟）有一组对边平行，一个内角是它对角的两倍的四边形叫做倍角梯形.（1）（3分）已知四边形ABCD 是倍角梯形，AD ∥BC ，∠A ＝100°，请直接写出所有满足条件的∠D 的度数；（2）（3分）如图1，在四边形ABCD 中，∠BAD+∠B ＝180°，BC ＝AD+CD.求证：四边形ABCD 是倍角梯形；（3）（4分）如图2，在（2）的条件下，连结AC ，当AB ＝AC ＝AD ＝2时，求BC 的长.23．（12分）（2022·鹿城会考）在Rt △ABC 中，AB=，BC=，过点C 作CG AB ，CF 平分3545∥∠ACD 交射线BA 于点F ，D 是射线CG 上的一个动点，连接AD 交CF 于点E.（1）（4分）求CF 的长.（2）（4分）当△ACE 是等腰三角形时，求CD 的长.（3）（4分）当B 关于AD 的对称点B'落在CF 上时，求的值.DEAE 24．（10分）（2022·宁波模拟）如图（1）（3分）【基础巩固】ABCD AD//BC，∠ACD=∠B△ABC∼△DCA 如图①，在四边形中，，求证：；（2）（3分）【尝试应用】ABCD E BC∠AED∠C BE=2，EC=4如图②，在平行四边形中，点在上，与互补，AE，求的长；（3）（4分）【拓展提高】ABCD E∠AED∠C F CD 如图③，在菱形中，为其内部一点，与互补，点在上，EF//AD AD=2EF AE=3，CF=1DE，且，，求的长.答案解析部分1．【答案】C2．【答案】D3．【答案】C4．【答案】B5．【答案】C6．【答案】B7．【答案】B8．【答案】A9．【答案】B10．【答案】C11．【答案】110º12．【答案】53°28′13．【答案】110°14．【答案】40°15．【答案】2016．【答案】40°17．【答案】证明：∵DE∥AB，∴∠EDC=∠B.又∵CD=AB，∠DCE=∠A，∴△CDE≌△ABC(ASA).∴DE=BC.18．【答案】（1）9（2）α-β=7.5°19．【答案】（1）证明：如图①，连接OC，∵OB=OA，l1∥l2，∴直线l1平分AC，由作图可知：OB=OA=OC，∴∠ACB=90°，∴l2垂直AC，∵l1∥l2，∴l1垂直AC，即直线l1垂直平分AC（2）解：如图②，以l2与PQ的交点O为圆心，OP长为半径画弧交直线l3于点C，连接PC并延长交直线l4于点D，此时线段PD最短，点D即为所求.BF=CE20．【答案】（1）证明：∵，∴BC=EF，AB//DE∵，∴∠ABC=∠DEF，AB=DE又∵，∴△ABC≌△DEF△A′BC（2）解：①如图所示，即为所求；；②平行N AB21．【答案】（1）解：结论：点在直线上；∠CMH=∠B∠CMH+∠C=90°∵，，∠B+∠C=90°∴，∠BMC=90°CM⊥AB∴，即 .CM90°BA N AB∴线段逆时针旋转落在直线上，即点在直线上.CD⊥AB D（2）解：作于，MC=MN∠CMN=90°∵，，∠MCN=45°∴，NC//AB∵，∠BMC=45°∴，BC=6∠B=30°∵，，CD=3MC=2CD=32∴，，S=MC2=18MC MN S=18∴，即以、为邻边的正方形面积 . 22．【答案】（1）满足条件的∠D的度数为160°或130°DE∥AB（2）证明：过点D作，交BC于点E，∠BAD+∠B=180°∵，AD∥BC∴，DE∥AB∵，∴四边形ABED为平行四边形，∴ ，，AD =BE ∠B =∠DEC =∠ADE ∵ ，BC =BE +CE ∴ ，BC =AD +CE 又∵ ，BC =AD +CD ∴ ，，CE =CD BC >AD ∴ ，∠CDE =∠DEC ∴ ，∠ADC =∠ADE +∠CDE =2∠B ∴四边形ABCD 是倍角梯形；（3）解：如图所示：过点A 作交BC 于点E ，AE ∥DC∵ ，AB =AC ∴ ，∠B =∠ACB ∵ ，AD =AC ∴ ，∠ACD =∠D ∵ ，，AD ∥BC AE ∥DC ∴四边形AECD ∴ ，，∠ACB =∠DAC ∠AEC =∠D =2∠B 设，则，∠B =α∠D =∠ACD =2α∵ ，∠DAC +∠D +∠ACD =180°∴ ，α+2α+2α=180°∴ ，α=36°∴ ，∠B =∠ACB =36°∴ ，∠BAC =∠AEB =108°∵ ，∠B =∠B ∴ ，△ABE ∽△CBA ∴，AB BC =BE AB 设，AE =BE =CD =x 则，BC =2+x∴ ，22+x =x 2∴ ，22=x(x +2)∴ 或（舍去），x =5−1x =−5−1∴ .CD =5−1∴ .BC =AD +CD =2+5−1=5+123．【答案】（1）解：∵Rt △ABC ，AB=，BC=，3545∴AC=AB 2+BC 2=55∵CG ∥AB ，∴∠GCF=∠AFC ，∵CF 平分∠ACD ，∴∠GCF=∠ACF ，∴∠ACF=∠AFC ，∴AF=AC=，55∴BF=，55+35=85∴在Rt △BCF ，CF=；BC 2+BF 2=(45)2+(85)2=20（2）解：①如图，当CE=AE 时，可得∠ACF=∠CAE ，∴∠CAE=∠CFA ，∵∠ACE=∠FCA ，∴△ACE ∽△FCA∴CE AC =AC CF ∴CE 55=5520∴CE =254∴CF =554∵CD ∥AB∴△CDE ∽△FAE∴CD AF =CE EF 即CD 55=2555∴CD =25511②如图，当AC=CE 时CE =AC =55∴EF =20−55∵CD AF =CE EF ∴CD 55=5520−55∴-CD =100+255综上所述，CD=25511（3）解：如图，过点B’作B’M ⊥AB 于M ，DN ⊥BF 于N ，交BB'于点H ，连接AB’由（1）可知tan ∠F=12设B’M=x ，则FM=2x∴AM =55−2x在Rt △AB’M 中，AB '2=AM 2+B 'M2∴(35)2=(55−2x )2+x2解得：x 1=25+2(舍去)，x 2=25−2∴BM=45+4∴tan∠B'BM=25−245+4由垂直可得∠BNH=∠DNA，∵∠BHN=∠DHB'，∴∠ADN=∠B’BM∴tan∠ADN=tan∠B'BM=25−245+4∴ANDN=25−245+4∴AN=35−5∴CD=5由①DEAE=CDAF=555=524．【答案】（1）证明：∵AD// BC，∴∠ACB=∠CAD，又∵∠ACD=∠B，∴△ABC∽△DCA.（2）解：∵四边形ABCD为平行四边形，∴AD//BC，AB// DC，∴∠DAE=∠AEB，∠C+∠B=180°又∵∠AED+∠C=180°，∴∠AED=∠B，∴△ABE∽△DEA∴BEAE=AEAD∵BE=2，EC=4，∴AD=BC=6，∴AE2=BE⋅AD=12，∴AE=23（3）解：如图，延长FE交AB于点G，∵EF//AD，∴∠DFE=∠C，∵AG// DF，∴四边形AGFD为平行四边形，∴AG=DF，AD=GF，由(2)可知﹐△AGE∽△DEA，∴AEGE=ADAE=DEAG∵AD=2EF∴AE2=GE⋅AD=AD22即，AD=2AE∴CD=AD=2AE=32∴AG=DF=32−1∴DE=2AG=2DF=6−2。

专题训练平行线培优习题

A. 7பைடு நூலகம்° B. 60°
C. 45° D. 30°
5、如图8所示，AB∥CD，AD与BC交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=度。
6、如图，l∥m，等边△ABC的顶点A在直线m上，则∠α=_________．
7、（2015•绵阳）如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F=．
14
（
（
15、如图5，ABCD是正方形，点G是BC上的任意一点，于E，，交AG于F．
求证：．
16．如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则∠A2013=度。
专题训练平行线培优习题
一、基础过关
1、（2011四川泸州）如图，∠1与∠2互补，∠3=135°，则∠4 的度数是（）
A.4 5°B.55°C.65°D.75°
2、如图，直线l1∥l2，∠1=55°，∠2=65°则∠3 = _______________.
3、下列四个图形中大于的是（）
4、将一副三角板按图中的方式叠放，则∠ 等于
17、如图，在等腰梯形ABCD中，AD∥BC，AB=CD=AD，∠B=60°，DE⊥AC于点E，已知该梯形的高为 .(1)求证: ∠ACD=30°；(2)DE的长度.
18、如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．求证：BC∥EF．
（C）若∠MON＝90°，则MN与⊙O相切
（D）l1和l2的距离为2

人教版七年级数学下册平行线培优试卷

EN M DA （第9题图）D AEB O C七年级数学（下）假期培优试卷(1)班级姓名一、选择题（每小题3分，共36分）1、青藏高原是世界上海拔最高的高原，它的面积约为 2 500 000平方千米.将 2 500 000用科学记数法表示为（）Ａ．70.2510⨯ Ｂ．72.510⨯ Ｃ．62.510⨯Ｄ．52510⨯2、已知代数式3y 2－2y+6的值是8，那么32y 2－y+1的值是 ( ) A ．1 B ．2 C ．3 D ．43、2、在│-2│，-│0│，（-2）5，-│-2│，-（-2）这5个数中负数共有 ( )A ．1 个B ． 2个C ． 3个D ． 4个 4．在解方程5113--=x x 时，去分母后正确的是（） A ．5x ＝15－3(x －1) B ．x ＝1－(3 x －1)C ．5x ＝1－3(x －1)D ．5 x ＝3－3(x －1)5．如果x y 3=，)1(2-=y z ，那么x －y ＋z 等于（）A ．4x －1B ．4x －2C ．5x －1D ．5x －2 6、下列说法中错误．．的个数是（）（1）过一点有且只有一条直线与已知直线平行。

（2）过一点有且只有一条直线与已知直线垂直。

（3）在同一平面内，两条直线的位置关系只有相交、平行两种。

（4）不相交的两条直线叫做平行线。

（5）有公共顶点且有一条公共边的两个角互为邻补角。

A. 1个B. 2个C. 3个D. 4个7、某品牌手机的进价为1200元，按原价的八折出售可获利14%，则该手机的原售价为（）A ．1800元 B ．1700元 C ．1710元 D ．1750元 8、某中学学生军训，沿着与笔直的铁路并列的公路匀速前进，每小时走4500米。

一列火车以每小时120千米的速度迎开来，测得火车头与队首学生相遇，到车尾与队末学生相遇，共经过60秒。

如果队伍长500米，那么火车长（）A ．1500米B ．1575米C ．2000米D ．2075米9．如图，点C 、O 、B 在同一条直线上，∠AOB=90°，∠AOE=∠DOB ，则下列结论：①∠EOD=90°；②∠COE=∠AOD ； ③∠COE=∠DOB ；④∠COE+∠BOD=90°.其中正确的个数是（） A ．1 B ．2 C ．3 D ．410．如图，把一张长方形的纸片沿着EF 折叠，点C 、D 分别落在M 、N 的位置，且∠MFB=21∠MFE. 则∠MFB=（）A ．30°B ．36°C ．45°D ．72° 11、如右图所示，点E 在AC 的延长线上，下列条件中能判断．．．CD AB //（）A. ∠3= ∠4B. ∠1 =∠2C. ∠D= ∠DCED. ∠D ＋∠DCE=180° 12、一学员练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（）A. 第一次向左拐 30，第二次向右拐 30B. 第一次向右拐 50，第二次向左拐130 C. 第一次向右拐50，第二次向右拐130 D. 第一次向左拐50，第二次向左拐130 二、填空题（每小题3分，共18分）13．用吸管吸易拉罐内的饮料时，如图①∠1=100°，则∠2= （易拉罐的上下底面互相平行）14．有一个与地面成30°角的斜坡，如图②，现要在斜坡上竖一电线杆，当电线杆与斜坡成的∠1= °时，电线杆与地面垂直。

中考数学总复习《相交线与平行线》专项测试卷-附参考答案

中考数学总复习《相交线与平行线》专项测试卷-附参考答案（测试时间60分钟满分100分）学校:___________姓名：___________班级：___________考号：___________一、选择题（共8题，共40分）1.如图，直线a与直线b被直线c所截，b⊥c，垂足为A，∠1=69∘若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转( )A．69∘B．49∘C．31∘D．21∘2.下列四个命题中，它的逆命题成立的是( )A．如果x=y，那么x2=y2B．直角都相等C．全等三角形对应角相等D．等边三角形的每个角都等于60∘3.如图，直线AB，CD相交于点O，OE，OF，OG分别是∠AOC，∠BOD，∠BOC的平分线，以下说法不正确的是( )A．∠DOF与∠COG互为余角B．∠COG与∠AOG互为补角C．射线OE，OF不一定在同一条直线上D．射线OE，OG互相垂直4.如图，直线a∥b，将三角尺的直角顶点放在直线b上，若∠1=35∘，则∠2等于( )A．45∘B．55∘C．35∘D．65∘5.如图，下列几组角的位置关系是内错角的是( )A．∠1和∠2B．∠3和∠4C．∠2和∠3D．∠1和∠46.如图，ED，CM与AO交于点C，OB，ON与AO交于O点，那么下列说法正确的是( )① ∠2和∠4是同位角；② ∠1和∠3是同位角；③ ∠ACD和∠AOB是内错角；④ ∠1和∠4是同旁内角；⑤ ∠ECO和∠AOB是内错角；⑥ ∠OCD和∠4是同旁内角．A．②③⑤B．①③⑤C．②③④D．①⑤⑥7.如图，两条直线被第三条直线所截，在所标注的角中，下列说法不正确的是( )A．∠1与∠5是同旁内角B．∠1与∠2是邻补角C．∠3与∠5是内错角D．∠2与∠4是对顶角8.如图，点O在直线AB上，OC⊥OD若∠AOC=120∘，则∠BOD的度数为( )A．30∘B．40∘C．50∘D．60∘二、填空题（共5题，共15分）9.已知∠AOB和∠BOC互为邻补角，且∠BOC:∠AOB=4:1，射线OD平分∠AOB，射线OE⊥OD，则∠BOE=．10.如图，若∠ADE=∠ABC，则DE∥BC，理由是．11.如图，已知∠B=∠D，要使BE∥DF，还需补充一个条件，你认为这个条件应该是．（填一个即可）12.如图，已知∠1=60∘，∠2=60∘，∠3=120∘，则直线a，b，c之间的位置关系为．13.如图，如果∠2=100∘，那么∠1的同位角的度数为．三、解答题（共3题，共45分）14.如图EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=116∘，∠ACF=20∘求∠FEC的度数．15.如图，已知两条直线DM∥CN，线段AB的两个端点．A，B分别在直线OM，CN上∠C=∠BAD，点E在线段BC上，且DB平分∠ADE．(1) 求证：AB∥CD．(2) 若沿着NC方向平移线段AB，那么∠CBD与∠CED度数之间的关系是否随着AB 位置的变化而变化？若变化，请找出变化规律；若不变化，请确定它们之间的数量关系．16.如图，已知DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2求证：CD⊥AB．参考答案1. 【答案】D2. 【答案】D3. 【答案】C4. 【答案】B5. 【答案】B6. 【答案】D7. 【答案】C8. 【答案】A9. 【答案】72∘或108∘10. 【答案】同位角相等，两直线平行11. 【答案】∠B=∠COE（答案不唯一）12. 【答案】a∥b∥c13. 【答案】80∘14. 【答案】∵EF∥AD，AD∥BC∴EF∥BC．∵AD∥BC∴∠ACB+∠DAC=180∘．∵∠DAC=116∘∴∠ACB=64∘．∵∠ACF=20∘∴∠FCB=∠ACB−∠ACF=44∘．∵CE平分∠BCF∴∠BCE=22∘．∵EF∥BC∴∠FEC=∠ECB．∴∠FEC=22∘．15. 【答案】(1) ∵DM∥CN∴∠BAD=∠NBA∵∠C=∠BAD∴∠C=∠NBA∴AB∥CD．(2) ∵DB平分∠ADE∴∠ADB=∠EDB∵DM∥CN∴∠ADB=∠CBD∴∠CBD=∠EDB∵DM∥CN∴∠CED=∠EDA∵∠EDA=2∠EDB∠CED．∴∠CDB=1216. 【答案】∵DG⊥BC，AC⊥BC（已知）∴∠DGB=∠ACB=90∘（垂直定义）∴DG∥AC（同位角相等，两直线平行）∴∠2=∠ACD（两直线平行，内错角相等）∵∠1=∠2（已知）∴∠1=∠ACD（等量代换）∴EF∥CD（同位角相等，两直线平行）∴∠AEF=∠ADC（两直线平行，同位角相等）∵EF⊥AB（已知）∴∠AEF=90∘（垂直的定义）∴∠ADC=90∘（等量代换）∴CD⊥AB（垂直的定义）．。

平行线练习题及答案

平行线练习题及答案一、选择题1. 在平面内，如果两条直线不相交，那么这两条直线被称为：A. 相交线B. 垂直线C. 平行线D. 异面直线答案：C2. 根据平行线的性质，下列哪项是错误的？A. 平行线之间的距离处处相等B. 平行线永远不会相交C. 如果一条直线与两条平行线中的一条相交，则与另一条也相交D. 平行线可以确定一个平面答案：C3. 如果直线AB与直线CD平行，且点E在直线AB上，点F在直线CD 上，那么直线EF与AB的关系是：A. 平行B. 垂直C. 相交D. 无法确定答案：D二、填空题4. 如果直线l1与直线l2平行，且直线l1上的点P到直线l2的距离为d，那么直线l1上任意一点到直线l2的距离都是________。

答案：d5. 平行线的性质之一是，如果一条直线与两条平行线中的一条相交，则与另一条________。

答案：不相交三、判断题6. 平行线在任何情况下都不会相交。

（）答案：正确7. 如果两条直线相交，它们就不可能平行。

（）答案：正确8. 平行线之间的夹角总是90度。

（）答案：错误四、简答题9. 解释什么是平行线，并给出平行线的基本性质。

答案：平行线是两条直线在同一个平面内，且不论延伸多远都不相交的直线。

基本性质包括：平行线之间的距离处处相等，平行线永远不会相交，如果一条直线与两条平行线中的一条平行，则与另一条也平行。

10. 描述如何使用直尺和三角板来检验两条直线是否平行。

答案：首先，使用直尺画出两条直线。

然后，用三角板的一边与直线之一对齐，确保没有间隙。

接着，将三角板沿着直线滑动，检查三角板的另一边是否始终与另一条直线平行。

如果始终平行，则两条直线平行。

五、计算题11. 在平面直角坐标系中，已知直线l1的方程为y=2x+3，直线l2的方程为y=2x+5。

请判断这两条直线是否平行，并给出理由。

答案：这两条直线是平行的。

因为它们的斜率相同，都是2，而截距不同，分别是3和5。

根据平行线的性质，当两条直线的斜率相同时，它们是平行的。

人教版七年级数学下册 5.2.1 平行线培优训练(含答案)

人教版七年级数学下册5.2.1《平行线》培优训练一、选择题（共10小题，3*10=30）1．在同一平面内，下列说法中，错误的是()A．过两点有且只有一条直线B．过一点有无数条直线与已知直线平行C．过直线外一点有且只有一条直线与已知直线平行D．过一点有且只有一条直线与已知直线垂直2．若直线a∥b，b∥c，则a∥c的依据是()A．平行公理B．等量代换C．等式的性质D．平行于同一条直线的两条直线互相平行3.下列生活实例中；①交通道口的斑马线；②天上的彩虹；③体操的纵队；④百米跑道线；⑤火车的平直铁轨线．其中属于平行线的有()A．1个B．2个C．3个D．4个4．在同一平面内，不重合的两条直线的位置关系可能是( )A．平行B．垂直或平行C．相交或平行D．相交或垂直5．下列说法正确的是( )A．同一平面内没有公共点的两条线段平行B．两条不相交的直线是平行线C．同一平面内没有公共点的两条直线平行D．同一平面内没有公共点的两条射线平行6.平面上有P、Q、R三点，以下说法正确的是()A．经过这三点，必有一条直线C．一定可以画三条直线，使它们两两相交于这三点D．经过这三点，至多能画两条平行直线7．过一点画已知直线的平行线，则( )A．有且只有一条B．可能有两条C．不存在D．不存在或只有一条8．若直线a∥b，b∥c，则a∥c的依据是( )A．平行线的基本事实B．等量代换C．等式的性质D．平行于同一条直线的两条直线平行9．己知直线AB及AB外一点P，若过点P作一直线与AB平行，那么这样的直线()A．有且只有一条B．有两条C．不存在D．无数条10．如图，AB∥CD，EF∥AB，AE∥MN，BF∥MN，由图中字母标出的互相平行的直线共有() A．4组B．5组C．6组D．7组二．填空题（共8小题，3*8=24）11．下列生活实例：①交通路口的斑马线；②天上的彩虹；③百米跑道线；④一段平直的火车铁轨线．其中属于平行线的有____________．12．在同一平面内，_______的两条直线叫做平行线．如图，AB平行于CD，可表示为_________．13．在同一平面内，直线a与b满足下列条件，写出其对应的位置关系：(1)a与b没有公共点，则a与b______；(2)a与b有且只有一个公共点，则a与b______；(3)a与b有两个公共点，则a与b______．14．如图，PC∥AB，QC∥AB，则点P，C，Q在一条直线上．理由是___________________________．15．如图，经过直线a外一点O的4条直线中，OB∥a，则与直线a相交的直线有( ) 条16．如图，若AB∥CD，经过点E可画EF∥AB，则EF与CD的位置关系是___，其理由是________________________________________________________．17. 如图所示，直线AB，CD是一条河的两岸，并且AB∥CD，点E为直线AB，CD外一点，现想过点E作河岸CD的平行线，只需过点E作________的平行线即可，其理由是________________________________．18．已知点P是直线AB外一点，CD、EF分别是过点P的两条直线，若AB∥CD，那么AB与EF 的关系是_______，理论依据是____________________________________________________________. 三．解答题（共6小题，46分）19．(6分) 如图，完成下列各题：(1)用直尺在网格中完成：①画出直线AB的一条平行线，②经过点C画直线垂直于CD；(2)用符号表示上面①，②中的平行、垂直关系．20．(6分) 如图，P，Q分别是直线EF外两点，画图并回答问题：(1)过点P画直线AB∥EF，过点Q画直线CD∥EF；(2)AB与CD有怎样的位置关系？为什么？21．(6分)观察如图所示的正方体，用符号表示下列两棱的位置关系：(1)AA1____AB；BB1____DD1；(2)A1C1____AC；AD1____BC1；(3)CC1____A1C1；B1C1____C1D1.22．(6分) 如图，直线AB，CD是一条河的两岸，并且AB∥CD，点E为直线AB，CD外一点，若要过点E作河岸CD的平行线，则只需过点E作河岸AB的平行线即可，其理由是什么？这样的直线能作多少条？为什么？23．(6分) 如图，将一张长方形硬纸片对折，MN是折痕，把面ABNM平放在桌面上，另一个面CDMN 任意改变位置，试探索AB与CD的位置关系，并说明理由．24．(8分) 如图，在∠AOB的内部有一点P，∠AOB＝60°.(1)过点P作PC∥OA，PD∥OB；(2)量出∠CPD的度数，说出它与∠AOB的关系．25．(8分)在同一平面内，三条直线有多少个交点？甲：在同一平面内，三条直线有0个交点，因为a∥b∥c，如图①；乙：在同一平面内，三条直线只有1个交点，因为a，b，c交于同一点，如图②. 以上说法谁对谁错？为什么？参考答案1-5BDDCC 6-10 ADDAC11. ①③④12. 不相交，AB∥CD13. 平行，相交，重合14. 经过直线外一点，有且只有一条直线与这条直线平行15. 316. 平行，如果两条直线都与第三条直线平行，那么这两条直线也互相平行17. AB，平行于同一条直线的两条直线平行18. 相交，同一平面内，一条直线与两条平行线中的一条相交，则必与另一条直线也相交19. 解：(1)如图所示，(2)AB∥EF，GC⊥CD.20. 解：(1)如图所示，(2)AB∥CD.理由：因为AB∥EF，CD∥EF，所以AB∥CD(如果两条直线都与第三条直线平行，那么这两条直线也互相平行)21. 解：(1)⊥，∥(2)∥，∥(3)⊥，⊥22. 解：其理由是：如果两条直线都与第三条直线平行，那么这两条直线也互相平行；这样的直线只能作1条，因为经过直线外一点，有且只有一条直线与这条直线平行23. 解：因为MN为长方形纸片对折折痕，所以MN∥AB，MN∥CD，所以AB∥CD，理由：如果两条直线都与第三条直线平行，那么这两条直线也互相平行(2)∠CPD＝60°或120°，它与∠AOB相等或互补25. 解：都不对，因为除了甲、乙两种说法外，在同一平面内，三条直线交点的个数还有两种情况，即有2个交点或3个交点，如图：，所以在同一平面内，三条直线有0个或1个或2个或3个交点。

2024年中考数学总复习考点培优训练第四章第一节线段、角、相交线与平行线

B. 50°
C. 55°
D. 60°
第16题图
C. 55° D. 60°
第2题图
第一节线段、角、相交线与平行线
3. 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，
已知线段PA＝6，则线段PB的长度为( C )
A. 3
B. 4
C. 6
D. 7
4. (2023北京)如图，∠AOC＝∠BOD＝90°，∠AOD＝126°，
则∠BOC的大小为( C )
第一节
线段、角、相交线与平行线
第一节线段、角、相交线与平行线
基础过关
1. (2022柳州)如图，从学校A到书店B有①、②、③、④四条路
线，其中最短的路线是( Leabharlann )A. ①B. ②
C. ③
D. ④
第1题图
2. (2023兰州)如图，直线AB与CD相交于点O，则∠BOD＝( B
)
A. 40° B. 50°
10. (2022桂林)如图，点C是线段AB的中点，若AC＝2 cm，则AB ＝__4____cm. 11. (2022株洲)如图所示，点O在一块直角三角板ABC上(其中 ∠ABC＝30°)，OM⊥AB于点M，ON⊥BC于点N，若OM＝ON，则∠ABO＝__1_5__度．
第10题图
第11题图
第一节线段、角、相交线与平行线
第一节线段、角、相交线与平行线
7. (2023河南)如图，直线AB，CD相交于点O，若∠1＝80°，
∠2＝30°，则∠AOE的度数为( B ) A. 30° B. 50°
C. 60° D. 80°
第7题图
8. (2023金华)如图，已知∠1＝∠2＝∠3＝50°，则∠4的度数是

七年级数学培优试卷有答案(第29讲：平行线问题) (浙教版)

七年级数学培优试卷有答案（第29讲：平行线问题）（浙教版）七年级数学培优试卷有答案（第29讲：平行线问题）-（浙教版）七年级数学优秀试卷（第29讲：平行线问题）中有答案（浙江教育版）第29讲期中复习专题――平行线问题一、基础训练1．如图，由ab∥cd，得∠1等于()a．∠2b．∠3c．∠4d．∠52．如图所示，下列条件中，不能判定ab∥cd的是()a、ab∥ef，cd∥efb。

∠5＝∠交流。

∠abc＋∠bcd＝1800d。

∠2＝∠3a1e三ba1d3542e51243l1l2c245d是第1题图C图2e图33．如图所示，在下列条件中，不能判断l1∥l2的是()a．∠1＝∠3b．∠2＝∠3c．∠4＋∠5＝1800d．∠2＋∠4＝18004.如图所示，将直尺和三角尺堆叠在一起。

在图中标记的角度中，与之互补的角度数∠ 1是（）a．2个b．3个c．4个d．5个5．如图，ab∥cd，直线ef分别交ab，cd于e、f，eg平分∠bef，若∠1＝500，则∠2＝()a、公元前500年600年650年750年a645321e1bc2egd图4第5题图6.已知：a（-2,4），ab‖X轴，ab=5，则B点的坐标为_________7．如图，已知∠abc＝∠adc，∠1＝∠2，则图中有哪些平行的线段？并说明理由．ad二1bc8.如图所示，AC二分法∠ 令人不快的∠ 1 = ∠ 2.验证：CD‖ab第1页共5页d2c1a3b9.如图所示，在四边形ABCD、ab‖CD、BC‖ad中，它们之间的尺寸关系是什么∠ A 和∠ C∠ B和∠ D请解释你的理由ab10.如图所示，被平分∠ 阿卜杜勒，德平分∠ BDC，∠ 1 ＋∠ 2=900，则直线AB和CD的位置关系如下：何？说明你的理由．ab1e2cd∥ 光盘∠, 电子束∠ d=1300，如图EB所示cod12.如图所示，直线ad在两点a和D处与AB和CD相交，EC和BF在e、C、B和F处与AB和CD相交，如果∠ 1.＝∠2，∠b＝∠c，说明∠a＝∠d．eab1hg2cde13．如图，已知∠1＋∠2＝l800，∠3＝∠b，试判断∠aed与∠acb的大小关系，并对结论进行证明．ade3421cb第2页共5页E14。

第一章平行线培优训练试题(含解析)

第一章平行线培优训练试题答案一．选择题：1.答案：C解析：∵b a //，∴0180231=∠+∠+∠， ∵0501=∠，32∠=∠，05018022-=∠∴，0652=∠∴，故选择C2.答案：B解析：∵c a //,c b //,∴b a //,故①正确； ∵c a ⊥,c b ⊥，∴b a //，故②正确； ∵ c a ⊥,c b //，∴b a ⊥，故③错误；∵ c 截b a ,所得的内错角的邻补角相等，∴b a //，故④正确；故选择B3.答案：C解析：∵△ABE 向右平移2cm 得到△DCF ， ∴EF=AD=2cm ，AE=DF ， ∵△ABE 的周长为16cm ， ∴AB+BE+AE=16cm ，∴四边形ABFD 的周长=AB+BE+EF+DF+AD =AB+BE+AE+EF+AD =16cm+2cm+2cm =20cm ．故选C ．4.答案：B解析：过B 作l DB //，∵m l //，∴m DB //， ∴0201=∠=∠DBC ，∴ABD ∠=∠2，∵045=∠ABC ，∴0002520452=-=∠=∠ABD ，故选择B5.答案：A解析：∵∠BEF 是△AEF 的外角，∠1=20°，∠F=30°， ∴∠BEF=∠1+∠F=50°， ∵AB ∥CD ，∴∠2=∠BEF=50°，故选A6.答案：C解析：∵AB ∥CD ，∠A=50°， ∴∠ADC=∠A=50°，∵∠AEC 是△CDE 的外角，∠C=30°， ∴∠AEC=∠C+∠D=30°+50°=80°，故选：C ．7.答案：C解析：当AD//BC 时，BCA DAC ∠=∠，CBD ADB ∠=∠，故②④能使AD//BC 满足，故选择C8.答案：B解析：∵∠1＝80°，∠2＝100°，∴01801008021=+=∠+∠， ∴b a //，∴08543=∠=∠，故选择B9.答案：C解析：∵CD AB //，∴0180=∠+∠AOD ODC ， ∵050=∠ODC ，∴0130=∠AOD ，∵OE 平分AOD ∠，∴065=∠=∠DOE AOE ，故①正确；∵OF OE ⊥，∴090=∠EOF ，∵065=∠EOD ，∴025=∠DOF ， ∵CD AB //，∴050=∠=∠BOD CDO ，∴025=∠=∠DOF BOF ， ∴OF 平分BOD ∠，故②正确；∵CD OG ⊥，∴090=∠OGD ，∵050=∠GDO ，∴040=∠GOD ， ∵065=∠EOD ，∴025=∠=∠DOF GOE ，故③正确； ∵040,65=∠=∠GOD AOE ，∴GOD AOE ∠≠∠，故④错误，故选择C10.答案；B解析：如图，∵EG ∥DB ， ∴∠1=∠2，∠1=∠3， ∵AB ∥EF ∥DC ，∴∠2=∠4，∠3=∠5=∠6，∴与∠1相等的角有∠2、∠3、∠4、∠5、∠6共5个．故选：B ．二．填空题：11.答案：12解析：∵周长为10的△ABC 沿BC 方向平移1个单位得到△DEF ， ∴CF AD DF AC ==,，∴四边形ABFD 的周长为1212.答案：504解析：宽向道路总长为20米，长向道路总长为30米，道路宽2米，故道路面积为：9622230220=⨯-⨯+⨯，长方形面积为6003020=⨯，草地面积为：50496600=-13.答案：0270 解析：如图，∵a ∥b ，∴∠2+∠3=180°，则∠3=180°﹣∠2， ∵b ∥c ，∴∠1+∠4=180°，则∠4=180°﹣∠1，∵∠BAC=90°， ∴∠3+∠4=90°，∴180°﹣∠2+180°﹣∠1=90°， ∴∠1+∠2=270°．14.答案：03021⎪⎭⎫⎝⎛+n解析：根据题意得：∵BE=2AE=2A ′E ，∠A=∠A ′=90°， ∴△ABE 、△A ′BE 都为30°、60°、90° 的三角形， ∴∠1=∠AEB=60°，∴∠AED ′=180°﹣∠1﹣∠AEB=180°﹣60°﹣60°=60°， ∴∠DED ′=∠AED+∠AED ′=n °+60°=（n+60）°， ∴∠2=21∠DED ′=（21n+30）°， ∵A ′D ′∥BC ， ∴∠BCE=∠2=（21n+30）°．故答案为：（21n+30）．15.答案：078解析：如图，分别过K 、H 作AB 的平行线MN 和RS ， ∵AB ∥CD ，∴AB ∥CD ∥RS ∥MN ，∴∠RHB=∠ABE=21∠ABK ，∠SHC=∠DCF=21∠DCK ，∠NKB+∠ABK=∠MKC+∠DCK=180°， ∴∠BHC=180°﹣∠RHB ﹣∠SHC=180°﹣21（∠ABK+∠DCK ），∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣（180°﹣∠ABK）﹣（180°﹣∠DCK）=∠ABK+∠DCK﹣180°，∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC，又∠BKC﹣∠BHC=27°，∴∠BHC=∠BKC﹣27°，∴∠BKC=180°﹣2（∠BKC﹣27°），∴∠BKC=78°，故答案为：78°．16.答案：70°或110°解析：如图：分为三种情况：第一种情况：如图①，∵∠B+∠C=110°，∴∠A=180°﹣（∠B+∠C）=70°，∵DE∥AB，DF∥AC，∴∠A=∠DFB，∠FDE=∠DFB，∴∠FDE=∠A=70°；第二种情况：如图②，∵∠B+∠ACB=110°，∴∠BAC=180°﹣（∠B+∠ACB）=70°，∵DE∥AB，DF∥AC，∴∠BAC=∠E=70°，∠FDE+∠E=180°，∴∠FDE=110°；第三种情况：如图③，∵∠ABC+∠C=110°，∴∠BAC=180°﹣（∠ABC+∠C）=70°，∵DE∥AB，DF∥AC，∴∠BAC=∠E=70°，∠FDE+∠E=180°，∴∠FDE=110°；故答案为：70°或110°．三．解答题：17.解析：CD AB // ，∴0180=∠+∠D BAD ， ∵AFD ∠=∠4，018042=∠+∠+∠∴D ， ∵018031=∠+∠+∠B ，∵43,21∠=∠∠=∠ ∴D B ∠=∠，∴0180=∠+∠B BAD ，∴BE AD //18.解析：∵AE ⊥BC ，FG ⊥BC ，∴AE ∥FG ， ∴∠2＝∠CFG .∵∠1＝∠2，∴∠CFG ＝∠1，∴AB ∥CD19. 证明：∵∠1＋∠2＝180°（已知）， ∠1＋∠4＝180°（一平角）， ∴∠2＝∠4.∴BD ∥FE （内错角相等两直线平行）. ∴∠3＝∠ADE （两直线平行内错角相等）. ∵∠3＝∠B （已知），∴∠B ＝∠ADE.∴DE ∥BC （同位角相等两直线平行）.∴∠AED ＝∠ACB （两直线平行同位角相等）.20.解析：（1）∵DE 平分∠ADC ，∠ADC=70°，∴∠EDC =21∠ADC=21×70°=35°；（2）过点E 作EF ∥AB ，∵AB ∥CD ， ∴AB ∥CD ∥EF ， ∴∠ABE=∠BEF ，∠CDE=∠DEF ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC=n °，∠ADC=70°， ∴∠ABE=21∠ABC=21n °，∠CDE=21∠ADC=35°，∴∠BED=∠BEF+∠DEF=21n °+35°；（3）过点E 作EF ∥AB∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC=n °，∠ADC=70° ∴∠ABE=21∠ABC=21n °，∠CDE=21∠ADC=35° ∵AB ∥CD ，∴AB ∥CD ∥EF ，∴∠BEF=180°-∠ABE=180°-21n °，∠CDE=∠DEF=35°， ∴∠BED=∠BEF+∠DEF=180°-21n °+35°=215°-21n °. 故∠BED 的度数发生了改为，改变为（215－21n ）°.21.解析：（1）证明：∵∠EAB=180°﹣∠BAC ﹣∠FAC ，∠BAC=90°，∠FAC=30°，∴∠EAB=60°，又∵∠ABC=60°，∴∠EAB=∠ABC ，∴EF ∥GH ；（2）解：不发生变化，理由是：经过点A 作AM ∥GH ，又∵EF ∥GH ，∴AM ∥EF ∥GH ，∴∠FCA+∠CAM=180°，∠MAB+∠ABH=180°，∠CBH=∠ECB ，又∵∠CAM+∠MAB=∠BAC=90°， ∴∠FCA+∠ABH=270°，又∵BC 平分∠ABH ，CD 平分∠FCA ， ∴∠FCD+∠CBH=135°，又∵∠CBH=∠ECB ，即∠FCD+∠ECB=135°， ∴∠BCD=180°﹣（∠FCD+∠ECB ）=45°．22．解析：（1）如图1，过点E 作l ∥AB ， ∵AB ∥CD ，∴l ∥AB ∥CD ， ∴∠1=∠BME ，∠2=∠DNE ， ∵∠MEN=∠1+∠2， ∴∠E=∠BME+∠END ，故答案为：∠E=∠BME+∠END ；（2）如图2，∵EF 平分∠MEN ，NP 平分∠END ，∴MEN NEF ∠=∠∴21，END ENP ∠=∠21， ∵EQ ∥NP ，∴END ENP QEN ∠=∠=∠21，∵∠MEN=∠BME+∠END ， ∴∠MEN ﹣∠END=∠BME=m °， ∴∠FEQ=∠NEF ﹣∠NEQ()021212121n END MEN END MEN =∠-∠=-∠=，（3）n ∠GEH=∠GEK ﹣∠BMN ．如图3，∵∠BMN=n •∠EMN ，∠GEK=n •∠GEM ，∴GEK nGEM BMN n EMN ∠=∠∠=∠∠1,1， ∵EH ∥MN ，∴BMN nEMN HEM ∠=∠=∠1，∵∠GEH=∠GEM ﹣∠HEM ，BMN nGEK n ∠-∠=11， ∴n ∠GEH=∠GEK ﹣∠BMN ．23.解析：（1）∵OM ⊥ON ，∴∠MON=90°，在四边形OBCD 中，∠C=∠BOD=90°， ∴∠OBC+∠ODC=360°﹣90°﹣90°=180°；故答案为180°；（2）证明：延长DE 交BF 于H ，如图1， ∵∠OBC+∠ODC=180°，而∠OBC+∠CBM=180°，∴∠ODC=∠CBM ，∵DE 平分∠ODC ，BF 平分∠CBM ，∴∠CDE=∠FBE ，而∠DEC=∠BEH ，∴∠BHE=∠C=90°，∴DE ⊥BF ；（3）解：DG ∥BF ．理由如下：作CQ ∥BF ，如图2，∵∠OBC+∠ODC=180°，∴∠CBM+∠NDC=180°， ∵BF 、DG 分别平分∠OBC 、∠ODC 的外角， ∴∠GDC+∠FBC=90°， ∵CQ ∥BF ，∴∠FBC=∠BCQ ，而∠BCQ+∠DCQ=90°，∴∠DCQ=∠GDC ，∴CQ ∥GD ，∴BF ∥DG ．。

第五章相交线与平行线(过关测试)【培优卷】(解析版)

第五章相交线与平行线（培优卷）考试时间:120分钟满分：120分一、单选题（每小题3分，共18分）1．已知三角形ABC ，过AC 的中点D 作AB 的平行线，根据语句作图正确的是（）A ．B ．C ．D ．【答案】B 【分析】根据中点的定义，平行线的定义判断即可．【详解】解：过AC 的中点D 作AB 的平行线，正确的图形是选项B ，故选：B ．【点睛】本题考查作图——复杂作图，平行线的定义，中点的定义等知识，解题关键是理解题意，灵活运用所学知识解决问题．2．如图，直线1l ，2l 被3l 所截得的同旁内角为a ，b ，要使12l l ∥，只要使（）A ．90a b +=°B ．a b=C ．116033a b +=°D ．090a °<£°，90180b °£<°【答案】C【分析】由同旁内角互补两直线平行即可判定出12l l ∥，变形后即可得到正确的选项．【详解】解：当180°a b +=，即116033a b +=°时，12l l ∥，故C 正确．故选：C ．【点睛】本题主要考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．3．在同一平面内，两条直线的位置关系可能是（）A ．相交或垂直B ．垂直或平行C ．平行或相交D ．相交或垂直或平行【答案】C 【分析】根据两条直线有一个交点的直线是相交线，没有交点的直线是平行线，可得答案．【详解】在同一平面内，两条直线有一个交点，两条直线相交；在同一平面内，两条直线没有交点，两条直线平行，故C 正确；故选：C ．【点睛】本题主要考查了同一平面内，两条直线的位置关系，注意垂直是相交的一种特殊情况，不能单独作为一类．4．（2021·安徽·统考中考真题）设a ，b ，c 为互不相等的实数，且4155b a c =+，则下列结论正确的是（）A ．a b c>>B ．c b a >>C ．4()a b b c -=-D ．5()a c a b -=-【答案】D【分析】举反例可判断A 和B ，将式子整理可判断C 和D ．【详解】解：A ．当5a =，10c =，41655b a c =+=时，c b a >>，故A 错误；B ．当10a =，5c =，41955b a c =+=时，a b c >>，故B 错误；C ．4()a b b c -=-整理可得1455b a c =-，故C 错误；D ．5()a c a b -=-整理可得4155b a c =+，故D 正确；故选：D ．【点睛】本题考查等式的性质，掌握等式的性质是解题的关键．5．已知直线a 、b 、c 在同一平面内，则下列说法错误的是( )A ．如果a ∥b ，b ∥c ，那么a ∥cB ．a ⊥b ，c ⊥b ，那么a ∥cC ．如果a 与b 相交，b 与c 相交，那么a 与c 一定相交D ．如果a 与b 相交，b 与c 不相交，那么a 与c 一定相交【答案】C【分析】根据如果两条直线都与第三条直线平行，那么这两条直线也互相平行，同一平面内，垂直于同一条直线的两直线平行进行分析即可．【详解】A．如果a∥b，b∥c，那么a∥c，说法正确；B．a⊥b，c⊥b，那么a∥c，说法正确；C．如果a与b相交，b与c相交，那么a与c一定相交，说法错误；D．如果a与b相交，b与c不相交，那么a与c一定相交，说法正确．故选C．【点睛】此题主要考查了平行公理及推论，关键是熟练掌握所学定理．6．一副直角三角尺叠放如图所示，现将30°的三角尺ABC固定不动，将45°的三角尺BDE绕顶点B逆时Ð所有符合条件的针转动，点E始终在直线AB的上方，当两块三角尺至少有一组边互相平行时，则ABE度数为（）A．45°，75°，120°，165°B．45°，60°，105°，135°C．15°，60°，105°，135°D．30°，60°，90°，120°【答案】A【分析】分DE∥AB，DE∥AC，BE∥AC，AC∥BD，分别画出图形，根据平行线的性质和三角板的特点求解．【详解】解：如图，①DE∥AB，∴∠D+∠ABD=180°∴∠ABD=90°∴∠ABE=45°；②DE∥AC，∵∠D=∠C=90°，∴B ，C ，D 共线，∴∠ABE=∠CBE+∠ABC=180°-45°+30°=165°；③BE ∥AC ，∴∠C=∠CBE=90°，∴∠ABE=∠ABC+∠CBE=120°；④AC ∥BD ，∴∠ABD=180°-∠A=120°，∴∠ABE=∠ABD-∠DBE=75°，综上：∠ABE 的度数为：45°或75°或120°或165°．【点睛】本题考查了三角板中的角度计算，平行线的性质，解题的关键是注意分类讨论，做到不重不漏．二、填空题（每小题3分，共18分）7．“若0ab ＞，则0a ＞，0b ＞”_____命题（选填“是”或“不是”）．【答案】是【分析】根据命题的定义判断即可．【详解】若0ab ＞，则0a ＞，0b ＞是一个命题.故答案为：是．【点睛】本题主要考查了命题的判断，掌握定义是解题的关键．即是表示判断一件事情的句子是命题. 8．有一个密码箱，密码由三个数字组成，甲、乙、丙三个人都开过，但都记不清了．甲记得：这三个数字分别是7，2，1，但第一个数字不是7；乙记得：1和2的位置相邻；丙记得：中间的数字不是1．根据以上信息，可以确定密码是__．【答案】127【分析】先根据第一个数字不是7，得出第一个数字是1或2，再根据1和2相邻，进而得出第三个是7，即可得出结论．【详解】解：∵三个数字分别是7，2，1，但第一个数字不是7，∴第一个数为1或2，∵1和2的位置相邻，∴前两个数字是1，2或2，1，第三位是数字7，∵中间的数字不是1，∴第一个数字只能是1，第二个数字为2，即密码为127，故答案为：127【点睛】此题主要考查了推理与论证，判断出第三个数是7是解本题的关键．9．（2022秋·黑龙江佳木斯·七年级校考期中）将直角梯形ABCD平移得梯形EFGH，若===，则图中阴影部分的面积为_________平方单位．10,2,4HG MC MG【答案】36【分析】根据图形可知图中阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积，恰好等于梯形EFGH的面积减去梯形EFMD的面积．【详解】根据平移的性质得S梯形ABCD =S梯形EFGH，Q DC = HG = 10，MC= 2，MG = 4，\DM = DC - MC = 10 - 2 = 8，\S阴影= S梯形ABCD-S梯形EFMD=S梯形EFGH-S梯形EFMD =S梯形HGMD=()12DM HG MG+g=12×(8+10)×4= 36．故答案为：36．【点睛】主要考查了梯形的性质和平移的性质，要注意平移前后图形的形状和大小不变，本题的关键是能得到：图中阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积，恰好等于梯形EFGH的面积减去梯形EFMD的面积．10．把命题“等角的余角相等”改写成“如果……那么……”的形式:__________________________. 是______命题(填“真”或“假”)【答案】如果两个角是两个相等角的余角，那么这两个角相等. 真【分析】根据命题由题设和结论组成,把条件“两个角是同角的余角”写在如果的后面,把结论“这两个角相等"写在那么的后面即可【详解】命题“同角的余角相等”改写成“如果..,那么."的形式是“如果两个角是同角的余角,那么这两个角相等”如果两个角是同角的余角,那么这两个角相等是真命题【点睛】此题考查命题与定理，掌握三角形的性质是解题关键11．如图所示，在△ABC中，∠C＝90°，AC＝BC＝5，现将△ABC沿着CB的方向平移到△A′B′C′的位置．若平移的距离为2，则图中阴影部分的面积为________．【答案】8【分析】图中阴影部分的面积等于大三角形的面积减小三角形的面积，根据面积公式计算即可．【详解】解：∵∠C=90°，AC=BC=5，平移的距离为2，∴BC′=DC′=3∴阴影面积=5×5÷2-3×3÷2=8．故答案为8．【点睛】本题考查平移的性质，比较简单，解答此题的关键是利用平移的性质得出小三角形的底和高．12．（2022秋·重庆·七年级重庆市綦江中学校考阶段练习）如图，直线MN∥PQ，点A在直线MN与PQ之间，点B在直线MN上，连接AB．∠ABM的平分线BC交PQ于点C，连接AC，过点A作AD⊥PQ交PQ于点D，作AF⊥AB交PQ于点F，AE平分∠DAF交PQ于点E，若∠CAE=45°，∠ACB=52∠DAE，则∠ACD的度数是_____．【答案】27°##27度【分析】延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°，然后结合图形，利用各角之间的关系求解即可．【详解】解：延长FA与直线MN交于点K，由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD)=45°-12∠FAD=45°-12(90°-∠AFD)=12∠AFD，∵MN∥PQ，∴∠AFD=∠BKA=90°-∠KBA=90°-(180°-∠ABM)=∠ABM-90°，∴∠ACD=12∠AFD=12(∠ABM-90°)=∠BCD-45°，即∠BCD-∠ACD=∠BCA=45°，∴∠ACD=90°-(45°+∠EAD)=45°-∠EAD=45°-25∠BCA=45°-18°=27°，故∠ACD的度数是27°，故答案为：27°．【点睛】本题利用平行线、垂直、角平分线综合考查角度的计算，理解题意，综合运用这些知识点是解题关键．三、解答题（每小题6分，共30分）13．（2022秋·福建福州·七年级统考期末）如图，已知AGF ABC Ð=Ð，12180Ð+Ð=°．（1）试判断BF 与DE 的位置关系，并说明理由；（2）若BF AC ^，2140Ð=°，求AFG Ð的度数．【答案】（1）//BF DE ，理由见解析；（2）50°【分析】（1）根据已知条件，先证明 FG//BC ，继而得 ∠1=∠3 ，根据 ∠1+∠2=180° 等量代换得 ∠3+∠2=180° ，从而得证；（2）由（1）的结论，求得 ∠1 ，再根据 BF ⊥AC ，求得 ∠1 的余角即可．【详解】解：()1//BF DE ，理由如下：AGF ABC Ð=ÐQ ，//GF BC \，13\Ð=Ð，12180Ð+Ð=°Q ，32180\Ð+Ð=°，//BF DE \；()2//BF DE Q ，BF AC ^，DE AC \^，12180Ð+Ð=°Q ，2140Ð=°，140\Ð=°，904050AFG \Ð=°-°=°．【点睛】本题考查了平行线的性质与判定，求一个角的余角，熟练平行线的性质与判定是解题的关键．14．学习了两条直线平行的判定方法1后，谢老师接着问：“由同位角相等，可以判断两条直线平行，那么能否利用内错角相等来判定两条直线平行呢？”如图，直线AB 和CD 被直线EF 所截，∠2＝∠3，AB ∥CD 吗？说明理由．现请你补充完下面的说理过程：答：AB ∥CD理由如下：∵∠2＝∠3（已知）且（）∴∠1＝∠2∴AB ∥CD （）【答案】∠1＝∠3；对顶角相等；同位角相等，两直线平行【分析】根据已知条件及对顶角相等得出∠1＝∠2，由同位角相等，两直线平行即可证明．【详解】解：AB ∥CD理由如下：∵∠2＝∠3（已知）且∠1＝∠3（对顶角相等）∴∠1＝∠2∴AB ∥CD （同位角相等，两直线平行），故答案为：∠1＝∠3；对顶角相等；同位角相等，两直线平行．【点睛】题目主要考查对顶角相等及平行线的判定，理解题意，熟练掌握平行线的判定是解题关键．15．如图，己知点P 、Q 分别在AOB Ð的边OA OB 、上，按下列要求画图：(1)画射线PQ；(2)过点P画垂直于射线OB的线段PC，垂足为点C；(3)过点Q画直线QM平行于射线OA．【答案】(1)见解析(2)见解析(3)见解析【分析】根据题意过用直尺作图，分别P画垂直于射线OB的射线PC，垂足为点C；过点Q画直线QM平行于射线OA．【详解】（1）如图，射线PQ为所求；（2）如图，线段PC为所求；（3）如图，直线QM为所求【点睛】此题主要考查了基本作图，正确把握相关定义是解题关键．16．指出下列命题的题设和结论，并判断它们是真命题还是假命题，如果是假命题，举出一个反例．（1）两个角的和等于平角时，这两个角互为补角；（2）内错角相等；（3）两条平行线被第三条直线所截，内错角相等．【答案】（1）题设：如果两个角的和等于平角时，结论：那么这两个角互为补角；是真命题；（2）题设：如果两个角是内错角，那么这两个角相等；是假命题，反例见解析；（3）题设：如果两条平行线被第三条直线所截，结论：那么内错角相等．是真命题．【分析】（1）根据将命题写成“如果…，那么…”的形式，“如果”后面写题设，“那么”后面写结论可得题设和结论，根据平角的定义可得该命题是真命题；（2）根据将命题写成“如果…，那么…”的形式，“如果”后面写题设，“那么”后面写结论可得题设和结论，根据平行线的性质可得该命题是假命题；利用相交直线被第三条直线所截，内错角不相等可举反例；（3）根据将命题写成“如果…，那么…”的形式，“如果”后面写题设，“那么”后面写结论可得题设和结论，根据平行线的性质可得该命题是真命题；．【详解】（1）题设：如果两个角的和等于平角，结论：那么这两个角互为补角；是真命题；（2）题设：如果两个角是内错角，那么这两个角相等；是假命题，如图∠1与∠2是内错角，∠2＞∠1；（3）题设：如果两条平行线被第三条直线所截，结论：那么内错角相等．是真命题．【点睛】本题考查了命题与定理的相关知识．将命题写成“如果…，那么…”的形式，就是要明确命题的题设和结论，“如果”后面写题设，“那么”后面写结论．关键是明确命题与定理的组成部分，会判断命题的题设与结论．17．如图，AE⊥BC，FG⊥BC，∠1＝∠2，求证：AB∥CD．【答案】见解析【分析】首先由AE⊥BC，FG⊥BC可得AE∥FG，根据两直线平行，同位角相等及等量代换可推出∠A=∠2，利用内错角相等，两直线平行可得AB∥CD．【详解】证明：如图，设BC与AE、GF分别交于点M、N.∵AE⊥BC，FG⊥BC，∴∠AMB=∠GNB=90°，∴AE∥FG，∴∠A=∠1；又∵∠2=∠1，∴∠A=∠2，∴AB∥CD．【点睛】本题考查了平行线的性质及判定，熟记定理是正确解题的关键．四、解答题（每小题8分，共24分）18．如图，点O是直线AB上一点，OD平分∠AOC，∠BOE=3∠COE,∠DOE=81°，求∠BOE，∠AOD的度数.【答案】∠BOE=27°，∠AOD=72°．【分析】设∠COE=x ，则∠AOD=81°-x ，则∠BOE=3x ，∠AOC=2 ∠AOD ，由∠AOC+∠BOC=180° ，列方程2()81x °-+4x=180°，解方程求解即可．【详解】解：设∠COE=x ，∵∠BOE=3∠COE ，OD 平分∠AOC ，∠DOE DOC COE=Ð+Ð81ADO DOC DOE COE x\Ð=Ð=Ð-Ð=°-Q ∠BOE=3∠COE ，则∠BOE=3x ，∠AOC=2()81x °-，∵O 是直线AB 上一点，∴ ∠AOC+∠BOC=180° ，∴2()81x °-+4x=180°，解得9x =°∠AOD=81°-972°=°∴∠BOE=27°，∠AOD= 72°．【点睛】本题考查的是角平分线的定义，角的和差运算，邻补角的含义，解本题的关键是运用方程的思想解决几何问题．19．如图，直线AB ，CD 相交于点O ，OB 平分∠EOD ．(1)若∠BOE ：∠EOC ＝1：4，求∠AOC 的度数；(2)在（1）的条件下，画OF ⊥CD ，请直接写出∠EOF 的度数．【答案】(1)30°(2)30°或150°【分析】（1）设BOE x Ð=，则4EOC x Ð=，先根据角平分线的定义可得BOD BOE x Ð=Ð=，22EOD BOE x Ð=Ð=，再根据邻补角的定义求出x 的值，从而可得BOD Ð的度数，然后根据对顶角相等即可得；（2）先求出60,90EOD FOD Ð=°Ð=°，再分①点F 在AB 的上方和②点F 在AB 的下方两种情况，根据角的和差即可得．【详解】（1）解：由题意，设BOE x Ð=，则4EOC x Ð=，OB Q 平分EOD Ð，22EOD BOE x \Ð=Ð=，BOD BOE x Ð=Ð=，180EOD EOC Ð+Ð=°Q ，24180x x \+=°，解得30x =°，30BOD \Ð=°，由对顶角相等得：30AOC BOD Ð=Ð=°．（2）解：由（1）可知，23060EOD Ð=´°=°，OF CD ^Q ，90FOD \Ð=°，由题意，分以下两种情况：①如图，当点F 在AB 的上方时，则150EOF EOD FOD Ð=Ð+Ð=°；②如图，当点F 在AB 的下方时，则30EOF FOD EOD Ð=Ð-Ð=°；综上，EOF Ð的度数为30°或150°．【点睛】本题考查了与角平分线有关的计算、对顶角相等、一元一次方程的应用，较难的是题（2），正确分两种情况讨论是解题关键．20．如图，已知直线,,AB CD AC 上的点M ，N ，E 满足ME NE ^，90,AME CNE ACD Ð+Ð=Ð°的平分线CG 交MN 于G ，作射线GF AB ∥．(1)直线AB 与CD 平行吗？为什么？(2)若66CAB Ð=°，求CGF Ð的度数．【答案】(1)平行，理由见解析(2)123°【分析】（1）利用已知条件和三角形内角和定理，通过等量代换可得180A ACD Ð+Ð=°，由同旁内角互补，两直线平行，可得//AB CD ；（2）利用,66AB CD CAB Ð=°∥，求出ACD Ð，再利用角平分线的定义求出GCD Ð，再证GF CD ∥，利用两直线平行，同旁内角互补，即可求出CGF Ð．（1）解：//AB CD ．理由如下：∵ME NE ^，∴90MEN Ð=°，∴90AEM CEN Ð+Ð=°，∵180A AEM AME Ð+Ð+Ð=°，180ACD CEN CNE Ð+Ð+Ð=°，∴360A ACD AEM CEN AME CNE Ð+Ð+Ð+Ð+Ð+Ð=°，∵90AME CNE Ð+Ð=°，90AEM CEN Ð+Ð=°，∴180A ACD Ð+Ð=°，∴//AB CD ；（2）解：∵66AB CD CAB ∥，Ð=°，∴180114ACD CAB Ð=°-Ð=°，∵CG 平分ACD Ð，∴1572GCD ACD Ð=Ð=°，∵AB CD GF AB ∥，∥，∴GF CD ∥．∴180CGF GCD Ð+Ð=°，∴18057123CGF Ð=°-°=°．【点睛】本题考查平行线的判定与性质，角平分线的定义，三角形内角和定理，垂直的定义等，熟练掌握平行线的判定定理和性质定理是解题的关键．五、解答题（每小题9分，共18分）21．如图，//AC BD ，BC 平分ABD Ð，设ACB Ð为a ，点E 是射线BC 上的一个动点．（1）若30a =°时，且BAE CAE Ð=Ð，求CAE Ð的度数；（2）若点E 运动到1l 上方，且满足100BAE Ð=°，:5:1BAE CAE ÐÐ=，求a 的值；（3）若:()1BAE CAE n n ÐÐ=>，求CAE Ð的度数（用含n 和a 的代数式表示）．【答案】（1）60°；（2）50°；（3）18021n a °--或18021n a°-+【分析】（1）根据平行线的性质可得CBD Ð的度数，再根据角平分线的性质可得ABE 的度数，应用三角形内角和计算BAC Ð的度数，由已知条件BAE CAE Ð=Ð，可计算出CAE Ð的度数；（2）根据题意画出图形，先根据:5:1BAE CAE ÐÐ=可计算出CAE Ð的度数，由100BAE Ð=°可计算出BAC Ð的度数，再根据平行线的性质和角平分线的性质，计算出CBD Ð的度数，即可得出结论；（3）根据题意可分两种情况，①若点E 运动到1l 上方，根据平行线的性质由a 可计算出CBD Ð的度数，再根据角平分线的性质和平行线的性质，计算出BAC Ð的度数，再:BAE CAE n ÐÐ=，BAE BAC CAE Ð=Ð+Ð，列出等量关系求解即可等处结论；②若点E 运动到1l 下方，根据平行线的性质由a 可计算出CBD Ð的度数，再根据角平分线的性质和平行线的性质，计算出BAC Ð的度数，再:BAE CAE n ÐÐ=，BAE BAC CAE Ð=Ð-Ð列出等量关系求解即可等处结论．【详解】解：（1）30a =°Q ，//AC BD ，30CBD \Ð=°，BC Q 平分ABD Ð，30ABE CBD \Ð=Ð=°，1801803030120BAC ABE a \Ð=°-Ð-=°-°-°=°，又BAE CAE Ð=ÐQ ，111206022CAE BAC \Ð=Ð=´°=°；（2）根据题意画图，如图1所示，100BAE Ð=°Q ，:5:1BAE CAE ÐÐ=，20CAE \Ð=°，1002080BAC BAE CAE \Ð=Ð-Ð=°-°=°，//AC BD Q ，180100ABD BAC \Ð=°-Ð=°，又BC Q 平分ABD Ð，111005022CBD ABD \Ð=Ð=´°=°，50CBD a \=Ð=°；（3）①如图2所示，//AC BD Q ，CBD ACB a \Ð=Ð=，BC Q 平分ABD Ð，22ABD CBD a \Ð=Ð=，1801802BAC ABD a \Ð=°-Ð=°-，又:BAE CAE n ÐÐ=Q ，():BAC CAE CAE n \Ð+ÐÐ=，(1802):CAE CAE n a °-+ÐÐ=，解得18021CAE n a°-Ð=-；②如图3所示，//AC BD Q ，CBD ACB a \Ð=Ð=，BC Q 平分ABD Ð，22ABD CBD a \Ð=Ð=，1801802BAC ABD a \Ð=°-Ð=°-，又:BAE CAE n ÐÐ=Q ，():BAC CAE CAE n \Ð-ÐÐ=，(1802):CAE CAE n a °--ÐÐ=，解得18021CAE n a°-Ð=+．综上CAE Ð的度数为18021n a °--或18021n a°-+．【点睛】本题主要考查平行线的性质和角平分线的性质，两直线平行，同位角相等．两直线平行，同旁内角互补．两直线平行，内错角相等．合理应用平行线的性质是解决本题的关键．22．如图，//AB CD ，C 在D 的右侧，BE 平分ABC Ð，DE 平分ADC Ð，,BE DE 所在直线交于点E ，80ADC Ð=°．（1）若50ABC Ð=°，求BED Ð的度数；（2）将线段BC 沿DC 方向平移，使得点B 在点A 的右侧，其他条件不变，若120ABC Ð=°，求BED Ð的度数．【答案】（1）65°；（2）20°或160°【分析】1）作//EF AB ，如图1，利用角平分线的定义得到25ABE Ð=°，40EDC Ð=°，利用平行线的性质得到25BEF ABE Ð=Ð=°，40FED EDC Ð=Ð=°，从而得到BED Ð的度数；（2）作//EF AB ，如图2，利用角平分线的定义得到60ABE Ð=°，40EDC Ð=°，利用平行线的性质得到120BEF Ð=°，40FED EDC Ð=Ð=°，从而得到BED Ð的度数；如图3，利用//AB CD 得到240Ð=°，然后根据三角形外角性质可计算出BED Ð．【详解】解：（1）作//EF AB ，如图1，BE Q 平分ABC Ð，DE 平分ADC Ð，1252ABE ABC \Ð=Ð=°，1402EDC ADC Ð=Ð=°，//AB CD Q ，//EF CD \，25BEF ABE Ð=Ð=°Q ，40FED EDC Ð=Ð=°，254065BED \Ð=°+°=°；（2）作//EF AB ，如图2，BE Q 平分ABC Ð，DE 平分ADC Ð，1602ABE ABC \Ð=Ð=°，1402EDC ADC Ð=Ð=°，//AB CD Q ，//EF CD \，180120BEF ABE Ð=°-Ð=°Q ，40FED EDC Ð=Ð=°，12040160BED \Ð=°+°=°．如图3，BE Q 平分ABC Ð，DE 平分ADC Ð，11602ABC \Ð=Ð=°，1402EDC ADC Ð=Ð=°，//AB CD Q ，240\Ð=°，12BED Ð=Ð+ÐQ ，604020BED \Ð=°-°=°．如图4，BE Q 平分ABC Ð，DE 平分ADC Ð，1602ABE ABC \Ð=Ð=°，12402ADC Ð=Ð=°，//AB CD Q ，160ABE \Ð=Ð=°，3240Ð=Ð=°Q ，而12BED Ð=Ð+Ð，604020BED \Ð=°-°=°．综上所述，BED Ð的度数为20°或160°．【点睛】本题考查了平移的性质：解题的关键是把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．也考查了平行线的性质．六、解答题（本大题共12分）23．（2022秋·贵州黔西·七年级校考阶段练习）已知：直线EF 分别与直线AB ，CD 相交于点G ，H ，并且∠AGE+∠DHE ＝180°．（1）如图1，求证：AB ∥CD ；（2）如图2，点M 在直线AB ，CD 之间，连接GM ，HM ，求证：∠M ＝∠AGM+∠CHM ；（3）如图3，在（2）的条件下，射线GH 是∠BGM 的平分线，在MH 的延长线上取点N ，连接GN ，若∠N＝∠AGM ，∠M ＝∠N+12∠FGN ，求∠MHG 的度数．【答案】（1）见解析；（2）见解析；（3）60°【分析】（1）根据已知条件和对顶角相等即可证明；（2）如图2，过点M 作MR ∥AB ，可得AB ∥CD ∥MR ．进而可以证明；（3）如图3，令∠AGM ＝2α，∠CHM ＝β，则∠N ＝2α，∠M ＝2α+β，过点H 作HT ∥GN ，可得∠MHT ＝∠N ＝2α，∠GHT ＝∠FGN ＝2β，进而可得结论．【详解】（1）证明：如图1，∵∠AGE+∠DHE ＝180°，∠AGE ＝∠BGF ．∴∠BGF+∠DHE ＝180°，∴AB ∥CD ；（2）证明：如图2，过点M 作MR ∥AB ，又∵AB ∥CD ，∴AB ∥CD ∥MR ．∴∠GMR ＝∠AGM ，∠HMR ＝∠CHM ．∴∠GMH ＝∠GMR+∠RMH ＝∠AGM+∠CHM ．（3）解：如图3，令∠AGM ＝2α，∠CHM ＝β，则∠N ＝2α，∠M ＝2α+β，∵射线GH 是∠BGM 的平分线，∴()111809022FGM BGM AGM a Ð=Ð=°-Ð=°-，∴∠AGH ＝∠AGM+∠FGM ＝2α+90°﹣α＝90°+α，∵12M N FGN Ð=Ð+Ð，∴1222FGN a b a +=+Ð，∴∠FGN ＝2β，过点H 作HT ∥GN ，则∠MHT ＝∠N ＝2α，∠GHT ＝∠FGN ＝2β，∴∠GHM＝∠MHT+∠GHT＝2α+2β，∠CHG＝∠CHM+∠MHT+∠GHT＝β+2α+2β＝2α+3β，∵AB∥CD，∴∠AGH+∠CHG＝180°，∴90°+α+2α+3β＝180°，∴α+β＝30°，∴∠GHM＝2（α+β）＝60°．【点睛】本题考查了平行线的判定与性质，对顶角的性质，角平分线的性质，解决本题的关键是掌握平行线的判定与性质．。

10平行线综合练习培优篇

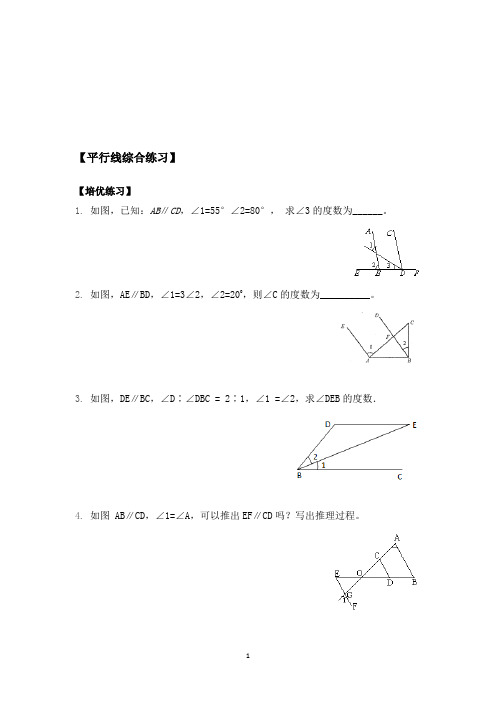
【平行线综合练习】【培优练习】1.如图，已知：AB∥CD，∠1=55°∠2=80°，求∠3的度数为______。

2.如图，AE∥BD，∠1=3∠2，∠2=200，则∠C的度数为__________。

3.如图，DE∥BC，∠D∶∠DBC = 2∶1，∠1 =∠2，求∠DEB的度数．4.如图 AB∥CD，∠1=∠A，可以推出EF∥CD吗？写出推理过程。

5. ∠CAB 、∠C 1A 1B 1都是锐角，AC ∥A 1C 1，AB ∥A 1B 1。

求证∠CAB ＝C 1A 1B 1。

6. 如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。

求证：AD ∥BE 。

7. 如图，已知，于D ，为上一点，于F ，交CA 于G .求证.8. 如图，已知AB ∥CD ，∠1=∠2，则∠E 与∠F 的大小关系；9. 如图，已知： AB ∥CD ，BE ∥CF ．求证：∠1=∠4．ABC ∆AD BC ⊥E AB EF BC ⊥//DG BA 12∠=∠F10.如图，已知AB∥CD，试再添上一个条件，使∠1 =∠2成立．（要求给出两个以上答案，并选择其中一个加以证明）11.如图，AB∥CD，直线EF分别交AB、CD于E、F两点，∠BEF的平分线交CD于G，若∠EFG=72°，则∠EGF等于（）A．36° B．54° C．72° D．108°12.如图，AB∥CD，∠BED=∠DEF，∠EFD=400，则∠EDF =__________。

13.如图，将一张长方形纸条折叠，如果∠1=1000，则∠2=__________。

14.已知AE平分∠CAD，AE∥BC。

求证∠B＝∠C。

15.AB∥CD，HP平分∠DHF，若∠AGH=80°，求∠DHP的度数.16.如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数.17.如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数.18.已知，如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD求证：∠EGF=90°19.已知DB∥FG∥EC，A是FG上一点，∠ABD＝60°，∠ACE＝36°，AP平分∠BAC，求：⑴∠BAC的大小；⑵∠PAG的大小.20.如图，AB ∥DE ，试问∠B 、∠E 、∠BCE 有什么关系．21.如图，已知AB ∥CD ，求证：∠ABE ＋∠BED ＋∠EDC ＝3600。

中考数学总复习《相交线与平行线》专项提升练习题-附答案

中考数学总复习《相交线与平行线》专项提升练习题-附答案学校：___________班级：___________姓名：___________考号：___________一、单选题1．已知∠α的两边分别与∠β的两边垂直，且∠α=20°，则∠β的度数为（）A．20°B．160°C．20°或160°D．70°2．如图，直线a∥b，AC丄AB，AC交直线b于点C，∠1=65°，则∠2的度数是（）A．65°B．50°C．35°D．25°3．如图，下列条件中，能判定AB∥CD的是（）A．∠1=∠4B．∠4=∠6C．∠2+∠5=180°D．∠1+∠3=180°4．若将一副三角板按如图所示的方式放置，则下列结论不正确的是（）A．∠1=∠3 B．如果∠2=30°，则有AC∥DEC．如果∠2=30°，则有BC∥AD D．如果∠2=30°，必有∠4=∠C5．如图，已知AB∥CD，∠2=135°，则∠1的度数是（）A．35°B．45°C．55°D．65°6．如图，AB∥CD∥EF，AF∥CG，则图中与∠F（不包括∠F）相等的角有（）A．1个B．2个C．3个D．4个7．如图，将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG，若DE∥CG，FG∥CD根据所标数据，则∠A的度数为（）A．54°B．64°C．66°D．72°8．把三角板ABC按如图所示的位置放置，已知∠CAB=30°，∠C=90°过三角板的顶点A、B分别作直线AD、BE，且AD//BE，∠DAE=120° .给出以下结论：（1）∠1+∠2=90°；（2）∠2=∠EAB；（3）CA平分∠DAB .其中正确结论有（）A．0个B．1个C．2个D．3个二、填空题9．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=48°，则∠AED为°．10．如图，AB∥CD，∠1=40°，MN平分∠EMB，则∠2的度数是．11．如图AB∥CD，∠CED=90°，∠AEC=37°，则∠D的度数为．12．如图，已知直线c与直线a，b分别交于点A，B，且∠2=65°，若直线a//b，则∠3的度数为．13．将一副直角三角板如图放置（其中∠A=60°，∠F=45°）点E在AC上ED//BC，则∠AEF的度数是．三、解答题14．如图所示，∠1=65°，∠2=65°，∠3=115°，试说明DE // BC，DF // AB．15．已知直线AB和CD相交于点O，射线OE⊥AB于O，射线OF⊥CD于O，且∠AOF=25°，求∠BOC与∠EOF 的度数．16．如图所示，已知AB//DC，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E试说明AD//BC .17．如图，网格中所有小正方形的边长都为1，A，B，C都在格点上．利用格点画图（不写作法）：①过点C画直线AB的平行线CM；②过点A画直线BC的垂线，垂足为G；③过点A画直线AB的垂线，交BC于点H．18．如图，已知点E在直线DC上，射线EF平分∠AED，过E点作EB⊥EF，G为射线EC上一点，连结BG，且∠EBG+∠BEG=90°．（1）求证：∠DEF=∠EBG；（2）若∠EBG=∠A，试判断AB与EF的位置关系，并说明理由．答案1．C2．D3．B4．C5．B6．D7．B8．C9．11410．110°11．53°或53度12．115°13．165°14．解：∵∠1=65°，∠2=65°∴∠1=∠2∴DE∥BC∵∠1=∠4=65°，∠3=115°∴∠3+∠4=65°+115°=180°∴DF∥AB．15．解：∵OF⊥CD∴∠FOD=90°．∴∠AOD=∠AOF+∠FOD=25°+90°=115°．∴∠BOC=115°．∵OE⊥AB∴∠AOE=90°．∴∠EOF=90°﹣25°=65°．16．解：∵AB//CD∴∠BAE=∠CFE∵AE平分∠BAD∴∠BAE=∠DAF∴∠CFE=∠DAF∵∠CFE=∠E∴∠DAF=∠E∴AD//BC .17．解：①直线CD为所作；②线段AG为所作；③线段HA为所作；18．（1）证明：∵EB⊥EF∴∠FEB=90°∴∠DEF+∠BEG=180°-90°=90°，又∠EBG+∠BEG=90°∴∠DEF=∠EBG（2）解：AB∥EF，理由如下：∵EF平分∠AED∠AED∴∠AEF=∠DEF= 12∵∠EBG=∠A，∠DEF=∠EBG∴∠A=∠AEF∴AB∥EF。

平行线培优训练题

A A 1 A 2A 3B 1 B 2B 图1平行线与相交线培优题型1 已知：如图1，∠B 1＋∠B 2=∠A 1＋∠A 2＋∠A 3（即向左凸出的角的和等于向右凸出的角的和），求证：AA 1∥BA 3（想一想：如果把例1的折线变成几条，且∠B ＋∠B 1＋∠B 2＋…＋∠B n =∠A 1＋∠A 2＋…＋∠A n ，那么AA 1∥BA n 成立吗？若成立，试加以证明；若不成立，请说明理由。

）2, 如图2，已知AB ∥CD ，∠AFE=α，∠ECB=β，求证：∠E=α＋β－180°。

3, 已知，如图3，AB ∥CD ，BC ∥DE ，BF 平分∠ABC ，DG 平分∠EDC ，求证：DG ⊥BF 。

4, 如图5，正方形ABCD 对角线AC 分成几段，以每一段为对角线作正方形，设这几个小正方形的周长之和为P ，正方形ABCD 的周长为L ，求证：P=L 。

A FB E D α βC 图2 A BF G CDE 图3A C D5, 如图6，AB ∥ED ，α=∠A ＋∠E ，β=∠B ＋∠C ＋∠D ，求证：β=2α。

6,平面上有10条直线，且无任何三条交于一点，欲使它们出现31个交点，试问：怎样安排才能办到？7,如图8，已知AB ∥CD ，被直线EF 所截交AB 、CD 于M 、N ，MP 平分∠EMB ，NQ 平分∠MND ，求证：MP ∥NQ 。

8,如图9，已知∠AB E ＋∠DEB=180°，∠1=∠2。

求证：∠F=∠G 。

9,如图10，已知∠ADE=∠B ，∠1=∠2，GF ⊥AB ，求证：CD ⊥AB 。

图621A B CF G D E 图9 F B 图1010,如图11，∠1=∠2，∠C=∠D ，求证：∠A=∠F 。

11.如图12,已知∠ABC=∠ADC ，BF 和DE 分别平分∠ABC 和∠ADC ，且∠1=∠2，求证：DF ∥EB 。

12.如图13，点B 、E 、C 、F 在一条直线上，并且AB ∥DE ，∠A=∠D ，AC ⊥BF ，求证：DF ⊥BF 。

初中数学相交线和平行线提高题与常考题型和培优题

订交线与平行线提升题与常考题和培优题(含分析)一．选择题（共12 小题）1．如图， AB∥CD，CD⊥EF，若∠ 1=124°，则∠ 2=（）A．56°B．66°C．24°D．34°2．如图是婴儿车的平面表示图，此中AB∥ CD，∠ 1=120°，∠ 3=40°，那么∠ 2的度数为（）A．80°B．90°C．100°D．102°3．如图，直线 a∥b，若∠ 2=55°，∠ 3=100°，则∠ 1 的度数为（）A．35°B．45°C．50°D．55°4．如图，△ ABC的面积为 2，将△ ABC沿 AC方向平移至△ DFE，且 AC=CD，则四边形 AEFB的面积为（）A．6B．8C．10D．125．如图，点 D、 E、 F 分别在 AB， BC，AC上，且 EF∥AB，要使 DF∥BC，只要再有条件（）A．∠ 1=∠2 B．∠ 1=∠DFE C．∠ 1=∠AFD D．∠2=∠AFD 6．如图，与∠ 1 是同旁内角的是（）A．∠ 2 B．∠3 C．∠ 4 D．∠5）7．如图，在以下条件中，不可以判断直线 a 与 b 平行的是（A．∠ 1=∠2 B．∠ 2=∠3 C．∠ 3=∠5 D．∠ 3+∠4=180°8．如图，直线a、b 被直线c 所截，以下条件能使a∥b 的是（）A．∠ 1=∠6 B．∠ 2=∠6 C．∠ 1=∠3 D．∠ 5=∠79．如图，将一副三角板叠放在一同，使直角的极点重合于点O，AB∥OC， DC与OB交于点 E，则∠ DEO的度数为（）A．85°B．70°C．75°D．60°10．如图， AB∥CD，AE均分∠ CAB交 CD于点 E，若∠ C=50°，则∠ AED=（）A．65° B．115° C．125° 11．如图， AB∥CD，DA⊥ AC，垂足为D．130°A，若∠ ADC=35°，则∠ 1 的度数为（）A．65°B．55°C．45°D．35°12．如图，直线 a∥ b，∠ 1=85°，∠ 2=35°，则∠3=（）A．85°B．60°C．50°D．35°二．填空题（共12 小题）13．如图，已知 BD∥AC，∠ 1=65°，∠ A=40°，则∠ 2 的大小是．14．如图，将长方形 ABCD沿 AE折叠，使点 D落在 BC边上的点 F，若∠ BFA=34°，则∠ DAE=度．15．如图，m∥ n，直角三角板 ABC的直角极点 C在两直线之间，两直角边与两直线订交所形成的锐角分别为α、β，则α +β= ．16．如图，四边形ABCD中，∠ BAD=∠ADC=90°， AB=AD=，CD=，点 P 是四边形ABCD四条边上的一个动点，若P 到 BD的距离为，则知足条件的点P 有个．17．如图，将一副三角板和一张对边平行的纸条按以下方式摆放，两个三角板的向来角边重合，含 30°角的直角三角板的斜边与纸条一边重合，含 45°角的三角板的一个极点在纸条的另一边上，则∠ 1 的度数是．18．如图，直线 AB∥CD，BC均分∠ ABD，若∠ 1=54°，则∠ 2=．19．如图，直线 AB∥CD，CA均分∠ BCD，若∠ 1=50°，则∠ 2=．20．如图，已知 AB∥CD，BC∥DE．若∠ A=20°，∠C=120°，则∠ AED的度数是．21．如图，直线 a∥ b，直线 c 与直线 a、 b 分别订交于 A、 B 两点，若∠ 1=60°，则∠2=．22．如图， AB∥CD，直线 EF分别交 AB、CD于 M， N 两点，将一个含有45°角的直角三角尺按以下图的方式摆放，若∠EMB=75°，则∠ PNM等于度．23．如图，△ ABC中， BC=5cm，将△ ABC沿 BC方向平移至△ A′B′C′的对应位置时， A′B′恰巧经过 AC的中点 O，则△ ABC平移的距离为cm．24．如图，是赛车跑道的一段表示图，此中 AB∥DE，测得∠ B=140°，∠D=120°，则∠ C的度数为度．三．解答题（共16 小题）25．如图，一个由 4 条线段组成的“鱼”形图案，此中∠ 1=50°，∠ 2=50°，∠3=130°，找出图中的平行线，并说明原因．26．如图，已知 AC∥ED，AB∥ FD，∠ A=65°，求：∠ EDF的度数．27．如图，已知 AB∥CD，若∠ C=40°，∠ E=20°，求∠ A 的度数．28．如图，在△ ABC中，∠ B+∠C=110°， AD均分∠ BAC，交 BC于点 D，DE∥ AB，交 AC于点 E，求∠ ADE的度数．29．如图，直线 a∥ b， BC均分∠ ABD， DE⊥BC，若∠ 1=70°，求∠ 2 的度数．30．如图， E 为 AC上一点， EF∥ AB交 AF 于点 F，且 AE=EF．求证：∠ BAC=2∠1．31．如图，直线 AB、CD订交于点 O， OE均分∠ BOD，∠ AOC=76°，∠ DOF=90°，求∠ EOF的度数．32．如图，直线 AB，CD订交于 O点， OM⊥ AB于 O．（1）若∠ 1=∠2，求∠ NOD；（2）若∠ BOC=4∠1，求∠ AOC与∠ MOD．33．如图，两直线 AB、 CD订交于点 O，OE均分∠ BOD，∠ AOC：∠ AOD=7：11．（1）求∠ COE的度数．（2）若射线 OF⊥OE，请在图中画出 OF，并求∠ COF的度数．34．如图，四边形ABCD中，∠ A=∠C=90°， BE 均分∠ ABC，DF 均分∠ ADC，则BE与 DF有何地点关系？试说明原因．35．将一副三角板中的两块直角三角尺的直角极点C按如图方式叠放在一同（其中，∠ A=60°，∠ D=30°；∠ E=∠B=45°）：（ 1）①若∠ DCE=45°，则∠ ACB的度数为；②若∠ ACB=140°，求∠ DCE的度数；（2）由（ 1）猜想∠ ACB与∠ DCE的数目关系，并说明原因．（3）当∠ ACE＜180°且点 E 在直线 AC的上方时，这两块三角尺能否存在一组边相互平行？若存在，请直接写出∠ ACE 角度全部可能的值（不用说明原因）；若不存在，请说明原因．36．已知：如图，∠ C=∠ 1，∠ 2 和∠ D 互余， BE⊥FD于点 G．求证： AB∥CD．37．已知：以下图，∠ ABD和∠ BDC的均分线交于 E，BE交 CD于点 F，∠ 1+∠2=90°．（1）求证： AB∥CD；（2）尝试究∠ 2 与∠ 3 的数目关系．38．如图，∠ 1+∠2=180°，∠ A=∠ C， DA均分∠ BDF．（1） AE与 FC会平行吗？说明原因；（2） AD与 BC的地点关系怎样？为何？（3） BC均分∠ DBE吗？为何．39．如图，一条直线分别与直线BE、直线 CE、直线 BF、直线 CF订交于点 A，G，H，D且∠ 1=∠2，∠ B=∠C（1）找出图中相互平行的线，谈谈它们之间为何是平行的；（2）证明：∠ A=∠D．40．将△ ABC纸片沿 DE折叠，此中∠ B=∠C．（1）如图 1，点 C落在 BC边上的点 F 处， AB与 DF能否平行？请说明原因；（2）如图 2，点 C 落在四边形 ABCD内部的点 G处，研究∠ B 与∠ 1+∠ 2 之间的数目关系，并说明原因．订交线与平行线提升题与常考题和培优题(含分析)参照答案与试题分析一．选择题（共12 小题）1．（2017? 新城区校级模拟）如图，AB∥ CD，CD⊥EF，若∠ 1=124°，则∠ 2=（）A．56°B．66°C．24°D．34°【剖析】先依据平行线的性质，得出∠CEH=124°，再依据 CD⊥ EF，即可得出∠2的度数．【解答】解：∵ AB∥CD，∠ 1=124°，∴∠ CEH=124°，∴∠ CEG=56°，又∵ CD⊥ EF，∴∠ 2=90°﹣∠ CEG=34°．应选： D．【评论】本题主要考察了平行线的性质与垂线的定义，解题时注意：两直线平行，同位角相等．2．（ 2017? 禹州市一模）如图是婴儿车的平面表示图，此中AB∥ CD，∠1=120°，∠3=40°，那么∠ 2 的度数为（）A．80°B．90°C．100°D．102°【剖析】依据平行线性质求出∠ A，依据三角形外角性质得出∠2=∠1﹣∠ A，代入求出即可．【解答】解：∵ AB∥CD，∴∠ A=∠ 3=40°，∵∠ 1=120°，∴∠ 2=∠ 1﹣∠ A=80°，应选 A．【评论】本题考察了平行线性质和三角形外角性质的应用，重点是求出∠ A 的度数和得出∠ 2=∠ 1﹣∠ A．3．（2017? 莒县模拟）如图，直线a∥b，若∠ 2=55°，∠ 3=100°，则∠ 1 的度数为（）A．35°B．45°C．50°D．55°【剖析】依据两直线平行，同位角相等可得∠ 4=∠2，再依据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【解答】解：如图，∵直线a∥b，∴∠ 4=∠2=55°，∴∠ 1=∠ 3﹣∠ 4=100°﹣ 55°=45°．应选 B．【评论】本题考察了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并正确识图是解题的重点．4．（ 2017? 莒县模拟）如图，△ ABC的面积为 2，将△ ABC沿 AC方向平移至△ DFE，且 AC=CD，则四边形 AEFB的面积为（）A．6B．8C．10D．12【剖析】直接利用平移的性质联合三角形面积求法得出答案．【解答】解：∵将△ ABC沿 AC方向平移至△ DFE，且 AC=CD，∴A 点挪动的距离是2AC，则BF=AD，连结 FC，则 S△BFC=2S△ABC，S△ABC=S△FDC=S△FDE=2，∴四边形 AEFB的面积为： 10．【评论】本题主要考察了平移的性质以及三角形面积求法，正确得出三角形之间面积关系是解题重点．EF∥ AB，5．（2017 春?杭州月考）如图，点D、 E、 F 分别在AB，BC，AC上，且要使DF∥BC，只要再有条件（）A．∠ 1=∠2 B．∠ 1=∠DFE C．∠ 1=∠AFD D．∠ 2=∠AFD【剖析】由平行线的性质得出∠ 1=∠2，再由∠ 1=∠DFE，得出∠ 2=∠ DFE，由内错角相等，两直线平行即可得出 DF∥ BC．【解答】解：要使 DF∥ BC，只要再有条件∠ 1=∠DFE；原因以下：∵EF∥AB，∴∠ 1=∠ 2，∵∠ 1=∠ DFE，∴∠ 2=∠ DFE，∴ DF∥BC；应选： B．【评论】本题考察了平行线的判断与性质；娴熟掌握平行线的判断与性质，并能进行推理论证是解决问题的重点．6．（2016? 柳州）如图，与∠ 1 是同旁内角的是（）A．∠ 2 B．∠3 C．∠ 4 D．∠5【剖析】依据同位角、内错角、同旁内角、对顶角的定义逐一判断即可．【解答】解： A、∠ 1 和∠ 2 是对顶角，不是同旁内角，故本选项错误；B、∠ 1 和∠ 3 是同位角，不是同旁内角，故本选项错误；C、∠ 1 和∠ 4 是内错角，不是同旁内角，故本选项错误；D、∠ 1 和∠ 5 是同旁内角，故本选项正确；【评论】本题考察了同位角、内错角、同旁内角、对顶角的定义的应用，能熟记同位角、内错角、同旁内角、对顶角的定义是解本题的重点，注意：数形联合思想的应用．7．（2016? 贵宾）如图，在以下条件中，不可以判断直线a 与 b 平行的是（）A．∠ 1=∠2 B．∠ 2=∠3 C．∠ 3=∠5 D．∠ 3+∠4=180°【剖析】直接用平行线的判断直接判断．【解答】解： A、∵∠ 1 与∠ 2 是直线 a， b 被 c 所截的一组同位角，∴∠1=∠2，能够获得 a∥b，∴不切合题意，B、∵∠ 2 与∠ 3 是直线 a，b 被 c 所截的一组内错角，∴∠2=∠3，能够获得 a∥b，∴不切合题意，C、∵∠ 3 与∠ 5 既不是直线 a，b 被任何一条直线所截的一组同位角，内错角，∴∠ 3=∠ 5，不可以获得 a∥b，∴切合题意，D、∵∠ 3 与∠ 4 是直线 a，b 被 c 所截的一组同旁内角，∴∠3+∠4=180°，能够获得 a∥b，∴不切合题意，应选 C【评论】本题是平行线的判断，解本题的重点是娴熟掌握平行线的判断定理．8．（ 2016? 百色）如图，直线 a、b 被直线 c 所截，以下条件能使 a∥b 的是（）A．∠ 1=∠6 B．∠ 2=∠6 C．∠ 1=∠3 D．∠ 5=∠7【剖析】利用平行线的判断方法判断即可．【解答】解：∵∠ 2=∠6（已知），∴a∥b（同位角相等，两直线平行），则能使 a∥ b 的条件是∠ 2=∠ 6，应选 B【评论】本题考察了平行线的判断，娴熟掌握平行线的判断方法是解本题的重点．9．（2016?营口）如图，将一副三角板叠放在一同，使直角的极点重合于点O，AB∥OC， DC 与OB交于点E，则∠ DEO的度数为（）A．85°B．70°C．75°D．60°【剖析】由平行线的性质求出∠ AOC=120°，再求出∠ BOC=30°，而后依据三角形的外角性质即可得出结论．【解答】解：∵ AB∥OC，∠ A=60°，∴∠ A+∠AOC=180°，∴∠ AOC=120°，∴∠ BOC=120°﹣ 90°=30°，∴∠ DEO=∠C+∠BOC=45° +30°=75°；应选： C．【评论】本题主要考察了平行线的性质、三角形的外角性质；娴熟掌握平行线的性质和三角形的外角性质是解决问题的重点．10．（ 2016? 陕西）如图， AB∥CD，AE均分∠ CAB交 CD于点 E，若∠ C=50°，则∠ AED=（）A．65°B．115°C．125°D．130°【剖析】依据平行线性质求出∠ CAB的度数，依据角均分线求出∠ EAB的度数，依据平行线性质求出∠ AED的度数即可．【解答】解：∵ AB∥CD，∴∠ C+∠CAB=180°，∵∠ C=50°，∴∠ CAB=180°﹣ 50°=130°，∵AE均分∠CAB，∴∠ EAB=65°，∵AB∥CD，∴∠ EAB+∠AED=180°，∴∠ AED=180°﹣ 65°=115°，应选 B．【评论】本题考察了角均分线定义和平行线性质的应用，注意：平行线的性质有：①两条平行线被第三条直线所截，同位角相等，②两条平行线被第三条直线所截，内错角相等，③两条平行线被第三条直线所截，同旁内角互补．11．（ 2016? 威海）如图， AB∥CD， DA⊥ AC，垂足为A，若∠ ADC=35°，则∠ 1的度数为（）A．65°B．55°C．45°D．35°【剖析】利用已知条件易求∠ ACD的度数，再依据两线平行同位角相等即可求出∠1 的度数．【解答】解：∵ DA⊥AC，垂足为 A，∴∠ CAD=90°，∵∠ ADC=35°，∴∠ ACD=55°，∵ AB∥CD，∴∠ 1=∠ACD=55°，应选 B．【评论】本题主要考察了平行线的性质，垂直的定义等知识点，熟记平行线的性质定理是解题重点．12．（ 2016? 毕节市）如图，直线 a∥ b，∠ 1=85°，∠ 2=35°，则∠ 3=（）A．85°B．60°C．50°D．35°【剖析】先利用三角形的外角定理求出∠ 4 的度数，再利用平行线的性质得∠3=∠4=50°．【解答】解：在△ ABC中，∵∠ 1=85°，∠ 2=35°，∴∠ 4=85°﹣ 35°=50°，∵a∥ b，∴∠ 3=∠4=50°，应选 C．【评论】本题考察了平行线的性质和三角形的外角定理，比较简单；运用了三角形的一个外角等于与它不相邻的两个内角的和，及两直线平行，内错角相等；本题的解法有多种，也能够利用直线 b 下方的三角形和对顶角相等来求解．二．填空题（共12 小题）13．（ 2017? 辽宁模拟）如图，已知BD∥ AC，∠ 1=65°，∠ A=40°，则∠ 2 的大小是75°．【剖析】由 BD与 AC平行，利用两直线平行同位角相等求出∠C的度数，再利用三角形内角和定理求出所求角度数即可．【解答】解：∵ BD∥AC，∠ 1=65°，∴∠ C=∠1=65°，在△ ABC中，∠ A=40°，∠ C=65°，∴∠ 2=75°，故答案为： 75°【评论】本题考察了平行线的性质，以及三角形内角和定理，娴熟掌握平行线的性质是解本题的重点．14．（ 2017 春? 萧山区月考）如图，将长方形ABCD沿 AE 折叠，使点 D 落在 BC 边上的点 F，若∠ BFA=34°，则∠ DAE= 17度．【剖析】第一依据平行线的性质获得∠DAF的度数，再依据对折的知识即可求出∠ DAE的度数．【解答】解：∵四边形 ABCD是矩形，∴AD∥BC．∴∠ BFA=∠DAF，∵∠ BFA=34°，∴∠ DAF=34°，∵△ AFE是△ ADE沿直线 AE对折获得，∴∠ DAE=∠FAE，∴∠ DAE=∠DAF=17°，故答案为 17．【评论】本题主要考察了平行线的性质，解题的重点是依据平行线的性质求出∠ DAF的度数，本题难度不大．15．（ 2017? 河北一模）如图， m∥n，直角三角板 ABC的直角极点 C 在两直线之间，两直角边与两直线订交所形成的锐角分别为α、β，则α+β= 90°．【剖析】依据平行线的性质即可获得结论．【解答】解：过 C 作 CE∥m，∵m∥ n，∴ CE∥n，∴∠ 1=∠α，∠ 2=∠β，∵∠ 1+∠2=90°，∴∠α +∠β =90°，故答案为： 90°．【评论】本题考察了平行线的性质，娴熟掌握平行线的性质即可获得结论．16．（2016? 凉山州）如图，四边形 ABCD中，∠ BAD=∠ADC=90°， AB=AD=，CD=，点 P 是四边形 ABCD四条边上的一个动点，若 P 到 BD的距离为，则知足条件的点P有2个．【剖析】第一作出 AB、 AD边上的点 P（点 A）到 BD的垂线段 AE，即点 P 到 BD 的最长距离，作出 BC、 CD的点 P（点 C）到 BD的垂线段 CF，即点 P 到 BD的最长距离，由已知计算出 AE、CF的长为，比较得出答案．【解答】解：过点 A 作 AE⊥BD于 E，过点 C作 CF⊥BD于 F，∵∠ BAD=∠ADC=90°， AB=AD=， CD=2，∴∠ ABD=∠ADB=45°，∴∠ CDF=90°﹣∠ ADB=45°，∵sin ∠ABD=，∴AE=AB? sin ∠ ABD=3? sin45 °=3＞，CF=2＜，因此在 AB和 AD边上有切合 P 到 BD的距离为的点 2 个，故答案为： 2．【评论】本题考察认识直角三角形和点到直线的距离，解题的重点是先求出各边上点到 BD的最大距离比较得出答案．17．（2016? 菏泽）如图，将一副三角板和一张对边平行的纸条按以下方式摆放，两个三角板的向来角边重合，含 30°角的直角三角板的斜边与纸条一边重合，含 45°角的三角板的一个极点在纸条的另一边上，则∠ 1 的度数是15°．AB∥b，因此∠ 1=∠ 2，∠ 3=∠【剖析】过 A 点作 AB∥a，利用平行线的性质得4=30°，加上∠ 2+∠3=45°，易得∠ 1=15°．【解答】解：如图，过 A 点作 AB∥a，∴∠ 1=∠ 2，∵ a∥ b，∴ AB∥b，∴∠ 3=∠4=30°，而∠ 2+∠3=45°，∴∠ 2=15°，∴∠ 1=15°．故答案为 15°．【评论】本题考察了平行线的性质：两直线平行，内错角相等．18．（ 2016? 连云港）如图，直线AB∥CD，BC均分∠ ABD，若∠ 1=54°，则∠ 2= 72°．【剖析】由 AB∥ CD，依据平行线的性质找出∠ ABC=∠ 1，由 BC均分∠ ABD，依据角均分线的定义即可得出∠CBD=∠ABC，再联合三角形的内角和为180°以及对顶角相等即可得出结论．【解答】解：∵ AB∥CD，∠ 1=54°，∴∠ ABC=∠1=54°，又∵ BC均分∠ ABD，∴∠ CBD=∠ABC=54°．∵∠ CBD+∠BDC+∠DCB=180°，∠ 1=∠DCB，∠ 2=∠BDC，∴∠ 2=180°﹣∠ 1﹣∠ CBD=180°﹣ 54°﹣ 54°=72°．故答案为： 72°．【评论】本题考察了平行线的性质、角均分线的定义以及三角形内角和定理，解题的重点是找出各角的关系．本题属于基础题，难度不大，解决该题型题目时，依据平行线的性质找出相等（或互补）的角是重点．19．（ 2016? 青海）如图，直线AB∥ CD， CA 均分∠ BCD，若∠ 1=50°，则∠ 2= 65°．【剖析】先依据平行线的性质得∠ABC+∠BCD=180°，依据对顶角相等得∠ABC=∠1=50°，则∠ BCD=130°，再利用角均分线定义获得∠ACD=∠BCD=65°，而后依据平行线的性质获得∠ 2 的度数．【解答】解：∵ AB∥CD，∴∠ ABC+∠BCD=180°，而∠ ABC=∠1=50°，∴∠ BCD=130°，∵CA均分∠ BCD，∴∠ACD=∠BCD=65°，∵AB∥CD，∴∠ 2=∠ACD=65°．故答案为 65°．【评论】本题考察了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．20．（ 2016? 金华）如图，已知AB∥CD，BC∥ DE．若∠ A=20°，∠ C=120°，则∠ AED的度数是80°．【剖析】延伸 DE交 AB于 F，依据平行线的性质获得∠AFE=∠B，∠B+∠C=180°，依据三角形的外角的性质即可获得结论．【解答】解：延伸 DE交 AB于 F，∵AB∥CD，BC∥ DE，∴∠ AFE=∠B，∠ B+∠C=180°，∴∠ AFE=∠B=60°，∴∠ AED=∠A+∠AFE=80°，故答案为： 80°．【评论】本题考察了平行线的性质，三角形的外角的性质，娴熟掌握平行线的性质是解题的重点．21．（2016? 云南）如图，直线 a∥b，直线 c 与直线 a、b 分别订交于 A、B 两点，若∠ 1=60°，则∠ 2= 60°．【剖析】先依据平行线的性质求出∠ 3 的度数，再由对顶角的定义即可得出结论．【解答】解：∵直线 a∥b，∠ 1=60°，∴∠ 1=∠3=60°．∵∠ 2 与∠ 3 是对顶角，∴∠ 2=∠3=60°．故答案为： 60°．【评论】本题考察的是平行线的性质，用到的知识点为：两直线平行，同位角相等．22．（2016? 吉林）如图， AB∥ CD，直线 EF 分别交 AB、CD于 M，N 两点，将一个含有 45°角的直角三角尺按以下图的方式摆放，若∠ EMB=75°，则∠ PNM等于30度．【剖析】依据平行线的性质获得∠DNM=∠BME=75°，由等腰直角三角形的性质得到∠ PND=45°，即可获得结论．【解答】解：∵ AB∥CD，∴∠ DNM=∠BME=75°，∵∠ PND=45°，∴∠ PNM=∠DNM﹣∠ DNP=30°，故答案为： 30．【评论】本题考察了平行线的性质，等腰直角三角形的性质，娴熟掌握平行线的性质是解题的重点．23（．2016? 泰州）如图，△ABC中，BC=5cm，将△ ABC沿 BC方向平移至△ A′B′C′的对应地点时， A′B′恰巧经过 AC的中点 O，则△ ABC平移的距离为cm．【剖析】依据平移的性质：对应线段平行，以及三角形中位线定理可得 B′是 BC 的中点，求出 BB′即为所求．【解答】解：∵将△ ABC沿 BC方向平移至△ A′B′C′的对应地点，∴A′B′∥ AB，∵O是AC的中点，∴B′是 BC的中点，∴BB′=5÷ 2=（ cm）．故△ ABC平移的距离为．故答案为：．【评论】考察了平移的性质，平移的基天性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．24．（ 2016? 都匀市一模）如图，是赛车跑道的一段表示图，此中 AB∥DE，测得∠B=140°，∠ D=120°，则∠ C的度数为 100 度．【剖析】过点 C作 CF∥ AB，由平行线性质可得∠ B，∠D，∠BCF，∠ DCF的关系，从而求得∠ C．【解答】解：以下图：过点 C 作 CF∥AB．∵AB∥DE，∴ DE∥CF；∴∠ BCF=180°﹣∠ B=40°，∠ DCF=180°﹣∠D=60°；∴∠ C=∠ BCF+∠DCF=100°．故答案为： 100．【评论】本题运用了两直线平行，同旁内角互补的性质，需要作协助线求解，难度中等．三．解答题（共16 小题）25．（2016? 淄博）如图，一个由 4 条线段组成的“鱼”形图案，此中∠1=50°，∠2=50°，∠ 3=130°，找出图中的平行线，并说明原因．【剖析】依据同位角相等，两直线平行证明 OB∥ AC，依据同旁内角互补，两直线平行证明 OA∥ BC．【解答】解： OA∥BC，OB∥AC．∵∠ 1=50°，∠ 2=50°，∴∠ 1=∠ 2，∴OB∥AC，∵∠ 2=50°，∠ 3=130°，∴∠ 2+∠3=180°，∴OA∥BC．【评论】本题考察的是平行线的判断，掌握平行线的判断定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解题的重点．26．（ 2016? 槐荫区二模）如图，已知 AC∥ ED，AB∥ FD，∠ A=65°，求：∠EDF 的度数．【剖析】依据平行线的性质，即可解答．【解答】解：∵ AC∥ED，∴∠ BED=∠A=65°，∵AB∥FD，∴∠ EDF=∠BED=65°．【评论】本题考察了平行线的性质，解决本题的重点是熟记平行线的性质．27．（ 2016? 厦门校级一模）如图，已知AB∥CD，若∠ C=40°，∠ E=20°，求∠A的度数．【剖析】依据两直线平行，同位角相等可得∠ 1=∠C，再依据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【解答】解：如图，∵AB∥CD，∴∠ 1=∠C=40°，∴∠ A=∠ 1﹣∠ E=40°﹣ 20°=20°．【评论】本题考察了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质是解题的重点．28．（ 2016? 江西模拟）如图，在△ ABC中，∠ B+∠C=110°， AD均分∠ BAC，交BC于点 D，DE∥ AB，交 AC于点 E，求∠ ADE的度数．【剖析】依据三角形内角和定理求出∠ BAC，依据角均分线定义求出∠ BAD，依据平行线的性质得出∠ ADE=∠BAD即可．【解答】解：∵在△ ABC中，∠ B+∠C=110°，∴∠ BAC=180°﹣∠ B﹣∠ C=70°，∵AD是△ABC的角均分线，∴∠ BAD=∠BAC=35°，∵DE∥AB，∴∠ ADE=∠BAD=35°．【评论】本题考察了平行线的性质，三角形内角和定理，角均分线定义的应用，注意：两直线平行，内错角相等．29．（2016? 江西模拟）如图，直线a∥ b，BC均分∠ ABD，DE⊥BC，若∠ 1=70°，求∠ 2 的度数．【剖析】依据平行线的性质获得∠ 1=∠ABD=70°，由角均分线的定义获得∠EBD=ABD=35°，依据三角形的内角和即可获得结论．【解答】解：∵直线 a∥b，∴∠ 1=∠ABD=70°，∵BC均分∠ ABD，∴∠ EBD=ABD=35°，∵DE⊥BC，∴∠ 2=90°﹣∠ EBD=55°．【评论】本题考察了平行线的性质，角均分线的定义，三角形的内角和，娴熟掌握平行线的性质是解题的重点．30．（2016? 旭日区一模）如图，E 为 AC上一点，EF∥AB交 AF于点 F，且 AE=EF．求证：∠ BAC=2∠1．【剖析】依据平行线的性质获得∠ 1=∠ FAB，由等腰三角形的性质获得∠ EAF=∠EFA，依据邻补角和对顶角的定义即可获得结论．【解答】证明：∵ EF∥AB，∴∠ 1=∠ FAB，∵AE=EF，∴∠ EAF=∠EFA，∵∠ 1=∠ EFA，∴∠ EAF=∠1，∴∠ BAC=2∠ 1．【评论】本题考察了平行线的性质，邻补角的定义，娴熟掌握平行线的性质是解题的重点．31．（ 2016 秋? 宜兴市期末）如图，直线 AB、CD订交于点 O， OE均分∠ BOD，∠ AOC=76°，∠ DOF=90°，求∠ EOF的度数．【剖析】依据对顶角相等可得∠ BOD=∠ AOC，再依据角均分线的定义求出∠ DOE，而后依据∠ EOF=∠DOF﹣∠ DOE代入数据计算即可得解．【解答】解：由对顶角相等得，∠ BOD=∠AOC=76°，∵OE均分∠ BOD，∴∠DOE=∠BOD=38°，∵∠ DOF=90°，∴∠ EOF=∠DOF﹣∠ DOE=90°﹣ 38°=52°．【评论】本题考察了对顶角相等，角均分线的定义，熟记性质与观点并正确识图是解题的重点．32．（ 2016 春? 西华县期末）如图，直线AB， CD订交于 O点， OM⊥ AB于 O．（1）若∠ 1=∠2，求∠ NOD；（2）若∠ BOC=4∠1，求∠ AOC与∠ MOD．【剖析】（1）由已知条件和察看图形可知∠ 1 与∠ AOC互余，再依据平角的定义求解；（2）利用已知的∠ BOC=4∠1，联合图形以及对顶角的性质求∠ AOC与∠MOD．【解答】解：（1）由于 OM⊥AB，因此∠1+∠AOC=90°．又∠1=∠ 2，因此∠ 2+∠AOC=90°，因此∠ NOD=180°﹣（∠ 2+∠ AOC）=180°﹣ 90°=90°．（2）由已知∠ BOC=4∠1，即 90° +∠ 1=4∠1，可得∠ 1=30°，因此∠ AOC=90°﹣ 30°=60°，因此由对顶角相等得∠ BOD=60°，故∠ MOD=90° +∠BOD=150°．【评论】本题利用垂直的定义，对顶角的性质和平角的定义计算，要注意领悟由垂直得直角这一重点．33．（ 2016 春? 双城市期末）如图，两直线AB、CD订交于点 O，OE均分∠ BOD，∠AOC：∠ AOD=7：11．（1）求∠ COE的度数．（2）若射线 OF⊥OE，请在图中画出 OF，并求∠ COF的度数．【剖析】（1）依据∠AOC+∠AOD=180°可得∠AOC和∠AOD的度数，依据对顶角相等可得∠BOD=70°，再利用角均分线定义可得∠DOE=35°，再依据邻补角定义可得∠ COE的度数；（ 2）分两种状况绘图，从而求出∠COF的度数．【解答】解：（1）∠ AOC：∠ AOD=7：11，∠ AOC+∠AOD=180°，∴∠ AOC=70°，∠ AOD=110°，∵∠ BOD=∠AOC，∴∠ BOD=70°，∵OE均分∠BOD，∴∠ DOE=35°，∴∠ COE=180°﹣∠DOE=145°；（ 2）分两种状况，如图 1，∵ OF⊥OE，∴∠ EOF=90°，∴∠ COF=∠COE﹣∠ EOF=145°﹣ 90°=55°，如图 2，∠ COF=∠360°﹣∠ COE﹣∠ EOF=125°．【评论】本题主要考察了垂线、邻补角、对顶角，重点是掌握对顶角相等，邻补角互补．34．（ 2016 春? 太仓市期末）如图，四边形 ABCD中，∠ A=∠C=90°， BE均分∠ ABC， DF均分∠ ADC，则 BE与 DF有何地点关系？试说明原因．【剖析】依据四边形的内角和定理和∠ A=∠C=90°，得∠ ABC+∠ADC=180°；依据角均分线定义、等角的余角相等易证明和 BE与 DF两条直线相关的一对同位角相等，从而证明两条直线平行．【解答】解： BE∥DF．原因以下：∵∠ A=∠C=90°（已知），∴∠ ABC+∠ADC=180°（四边形的内角和等于360°）．∵BE均分∠ ABC，DF均分∠ ADC，∴∠ 1=∠ 2=∠ABC，∠ 3=∠4=∠ADC（角均分线的定义）．∴∠ 1+∠ 3=（∠ ABC+∠ADC） =×180°=90°（等式的性质）．又∠ 1+∠AEB=90°（三角形的内角和等于180°），∴∠ 3=∠ AEB（同角的余角相等）．∴ BE∥DF（同位角相等，两直线平行）．【评论】本题运用了四边形的内角和定理、角均分线定义、等角的余角相等和平行线的判断，难度中等．35．（2016 春 ? 周口期末）将一副三角板中的两块直角三角尺的直角极点 C 按如图方式叠放在一同（此中，∠A=60°，∠ D=30°；∠ E=∠B=45°）：（ 1）①若∠ DCE=45°，则∠ ACB的度数为135°；②若∠ ACB=140°，求∠ DCE的度数；（2）由（ 1）猜想∠ ACB与∠ DCE的数目关系，并说明原因．（3）当∠ ACE＜180°且点 E 在直线 AC的上方时，这两块三角尺能否存在一组边相互平行？若存在，请直接写出∠ ACE 角度全部可能的值（不用说明原因）；若不存在，请说明原因．【剖析】（1）①第一计算出∠ DCB的度数，再用∠ ACD+∠ DCB即可；②第一计算出∠ DCB的度数，再计算出∠ DCE即可；（2）依据（ 1）中的计算结果可得∠ ACB+∠DCE=180°，再依据图中的角的和差关系进行推理即可；（3）依据平行线的判断方法可得．【解答】解：（1）①∵∠ ECB=90°，∠ DCE=45°，∴∠ DCB=90°﹣ 45°=45°，∴∠ ACB=∠ACD+∠DCB=90° +45°=135°，故答案为： 135°；②∵∠ ACB=140°，∠ ACD=90°，∴∠ DCB=140°﹣ 90°=50°，∴∠ DCE=90°﹣ 50°=40°；（2）∠ ACB+∠DCE=180°，∵∠ ACB=∠ACD+∠DCB=90° +∠DCB，∴∠ ACB+∠DCE=90° +∠DCB+∠DCE=90° +90°=180°；（ 3）存在，当∠ ACE=30°时， AD∥BC，当∠ ACE=∠E=45°时， AC∥BE，当∠ ACE=120°时， AD∥CE，当∠ ACE=135°时， BE∥CD，当∠ ACE=165°时， BE∥AD．【评论】本题主要考察了角的计算，以及平行线的判断，重点是理清图中角的和差关系．36．（ 2016 秋? 郓城县期末）已知：如图，∠ C=∠1，∠ 2 和∠ D 互余， BE⊥FD 于点 G．求证： AB∥ CD．【剖析】第一由 BE⊥ FD，得∠ 1 和∠ D 互余，再由已知，∠ C=∠ 1，∠ 2 和∠D互余，因此得∠ C=∠2，从而证得 AB∥CD．【解答】证明：∵ BE⊥FD，∴∠ EGD=90°，∴∠ 1+∠D=90°，又∠ 2 和∠ D 互余，即∠ 2+∠D=90°，∴∠ 1=∠ 2，又已知∠ C=∠1，∴∠ C=∠ 2，∴AB∥CD．BE⊥ FD及三角形内角和【评论】本题考察的知识点是平行线的判断，重点是由定理得出∠ 1 和∠ D 互余．37．（2016 春 ? 广州校级期末）已知：以下图，∠ABD和∠ BDC的均分线交于 E，BE交 CD于点 F，∠ 1+∠2=90°．（1）求证： AB∥CD；（2）尝试究∠ 2 与∠ 3 的数目关系．【剖析】（1）已知 BE、 DE均分∠ ABD、∠ BDC，且∠ 1+∠2=90°，可得∠ABD+∠ BDC=180°，依据同旁内角互补，可得两直线平行．（2）已知∠ 1+∠2=90°，即∠ BED=90°；那么∠ 3+∠FDE=90°，将等角代换，即可得出∠ 3 与∠ 2 的数目关系．【解答】证明：（1）∵ BE、DE均分∠ ABD、∠ BDC，∴∠ 1=∠ ABD，∠ 2=∠BDC；∵∠ 1+∠2=90°，∴∠ ABD+∠BDC=180°；∴ AB∥CD；（同旁内角互补，两直线平行）解：（ 2）∵ DE均分∠ BDC，∴∠ 2=∠ FDE；∵∠ 1+∠2=90°，∴∠ BED=∠DEF=90°；∴∠ 3+∠FDE=90°；∴∠ 2+∠3=90°．【评论】本题主要考察了角均分线的性质以及平行线的判断，难度不大．38．（ 2016 秋? 内江期末）如图，∠ 1+∠2=180°，∠ A=∠C，DA均分∠ BDF．（1） AE与 FC会平行吗？说明原因；（2） AD与 BC的地点关系怎样？为何？（ 3） BC均分∠ DBE吗？为何．【剖析】（1）证明∠ 1=∠ CDB，利用同位角相等，两直线平行即可证得；（2）平行，依据平行线的性质能够证得∠ A=∠CBE，而后利用平行线的判断方法即可证得；（3）∠ EBC=∠CBD，依据平行线的性质即可证得．【解答】解：（1）平行．原因以下：∵∠ 1+∠2=180°，∠ 2+∠CDB=180°（邻补角定义），∴∠ 1=∠ CDB，∴ AE∥FC（同位角相等两直线平行）；（2）平行．原因以下：∵ AE∥CF，∴∠ C=∠ CBE（两直线平行，内错角相等），又∵∠ A=∠C，∴∠ A=∠ CBE，∴ AD∥BC（同位角相等，两直线平行）；（3）均分．原因以下：∵DA均分∠BDF，∴∠ FDA=∠ADB，∵AE∥CF，AD∥ BC，∴∠ FDA=∠A=∠ CBE，∠ ADB=∠CBD，∴∠ EBC=∠CBD，∴BC均分∠ DBE．【评论】本题考察了平行线的判断与性质，解答本题的重点是注意平行线的性质和判断定理的综合运用．39．（2016 秋 ? 双柏县期末）如图，一条直线分别与直线BE、直线 CE、直线 BF、直线 CF订交于点 A，G，H，D 且∠ 1=∠ 2，∠ B=∠ C（1）找出图中相互平行的线，谈谈它们之间为何是平行的；（2）证明：∠ A=∠D．【剖析】（1）依据同位角相等，两直线平行可得CE∥FB，从而可得∠C=∠BFD，再由条件∠ B=∠ C 可得∠ B=∠BFD，从而可依据内错角相等，两直线平行得 AB∥CD；（2）依据（ 1）可得 AB∥CD，再依据两直线平行，内错角相等可得∠ A=∠D．【解答】（1）解：∵∠ 1=∠2，∴ CE∥FB，∴∠ C=∠ BFD，∵∠ B=∠ C，∴∠ B=∠ BFD，∴ AB∥CD；（2）证明：由（ 1）可得 AB∥ CD，∴∠ A=∠ D．【评论】本题主要考察了平行线的判断和性质，重点是掌握平行线的判断定理和性质定理．40．（ 2016 春? 邳州市期末）将△ ABC纸片沿 DE折叠，此中∠ B=∠C．（1）如图 1，点 C落在 BC边上的点 F 处， AB与 DF能否平行？请说明原因；（2）如图 2，点 C 落在四边形 ABCD内部的点 G处，研究∠ B 与∠ 1+∠ 2 之间的数目关系，并说明原因．【剖析】（1）AB与 DF平行．依据翻折可得出∠ DFC=∠C，联合∠ B=∠C即可得出∠ B=∠DFC，从而证出 AB∥ DF；（2）连结 GC，由翻折可得出∠ DGE=∠ ACB，再依据三角形外角的性质得出∠ 1=∠ DGC+∠ DCG，∠ 2=∠ EGC+∠ ECG，经过角的运算即可得出∠1+∠2=2∠B．【解答】解：（1）AB与 DF平行．原因以下：由翻折，得∠ DFC=∠C．又∵∠ B=∠C，∴∠ B=∠ DFC，∴AB∥DF．（2）连结GC，以下图．由翻折，得∠ DGE=∠ACB．∵∠ 1=∠ DGC+∠ DCG，∠ 2=∠ EGC+∠ ECG，∴∠ 1+∠ 2=∠DGC+∠DCG+∠EGC+∠ECG=（∠ DGC+∠ EGC）+（∠ DCG+∠ECG）=∠DGE+∠DCE=2∠ACB．∵∠ B=∠ ACB，∴∠ 1+∠ 2=2∠B．【评论】本题考察了平行线的判断以及翻折得性质，解题的重点是：（1）找出∠B=∠DFC；（2）依据三角形外角的性质利用角的计算求出∠ 1+∠2=2∠ B．本题属于基础题，难度不大，解决该题型题目时，找出相等（或互补）的角是重点．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相交线与平行线一、选择题1.（2011山东德州4,3分）如图，直线l1∥l2，∠1=40°，∠2=75°，则∠3等于（A）55°（B）60°（C）65°（D）70°1l123l2【答案】C2.（2011山东日照，3，3分）如图，已知直线AB∥CD，C125°，A45°，那么E的大小为（）（A）70°（B）80°（C）90°（D）100°【答案】B3.（2011山东泰安，8，3分）如图，l∥m，等腰直角三角形ABC的直角顶点C在直线m上，若∠β=200，则∠α的度数为（）0000A.25B.30C.20D.35【答案】A4.（2011四川南充市，3，3分）如图，直线DE经过点A,DE∥BC,,∠B=60°,下列结论成立的是（）（A）∠C=60°（B）∠DAB=60°（C）∠EAC=60°（D）∠BAC=60°D AEB C【答案】B5.（2011山东枣庄，2，3分）如图，直线AB∥CD，∠A＝70，∠C＝40，则∠E等于（）ED CB AA．30°Ｂ．40°C．60°Ｄ．70°【答案】A6.（2010湖北孝感，3，3分）如图，直线AB、CD相交于点O，OT⊥AB于O，CE∥AB交CD 于点C，若∠ECO=30°，则∠DOT=（）A.30°B.45°C.60°D.120°【答案】C7.（2011河北，2，2分）如图1∠1+∠2=（）12图1A．60°B．90°C．110°D．180°【答案】B8.（2011宁波市，8，3分）如图所示，AB∥CD，∠E＝37°，∠C＝20°，∠EAB的度数为A．57°B．60°C．63°D．123°【答案】A9.（2011浙江衢州，器的一条刻度线OF12,4分）如图，直尺一边AB与量角器的零刻度线的读书为70°，OF与AB交于点E,那么AEFCD平行，若量角度.F60o 70o80o 90o 100o110oo 100o 90o 120oA50o 120110 80o 130oB40 oo1401 30 130o5650o9 1112oooo14040o30 oo150o20160o20o 16010o170oC170o 10oD0o180oO0o 180o（第12题）【答案】7010．（2011浙江绍兴，3，4分）如图，已知AB//CD,BC 平分ABE, C34，则BED的度数是()A.17B. 34C.56D. 68ABCDE（第3题图）【答案】D11. （2011浙江义乌，8，3分）如图，已知AB ∥CD ，∠A=60°，∠C=25°，则∠E 等于BD60°AECA.60°B.25°C.35°D.45°【答案】C12. （2011四川重庆，4，4分）如图，AB ∥CD ，∠C ＝80°，∠CAD ＝60°，则∠BAD 的度数等于() A ．60°【答案】DB ．50°C ．45°D ．40°13.（2011浙江丽水，5，3分）如图，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1＝20°，那么∠2的度数是（）21A．30° B.25° C.20° D.15°【答案】B14.（2011台湾台北，8）图(二)中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角。

关于这七个角的度数关系，下列何者正确？A．2＝4＋7B。

C．1＋4＋6＝180D。

【答案】C 3＝1＋62＋3＋5＝36015.（2011台湾全区，7）若△ABC中，2（∠A＋∠C）＝3∠B，则∠B的外角度数为何？A．36B．72C．108D．144【答案】Ｃ16.（2011湖南邵阳，8，3分）如图（三）所示，已知O是直线AB上一点，∠1=40°，OD平分角BOD，则∠2的度数是（）A.20°B.25°C.30°D.70°CDA12B O【答案】D.提示：∠1+2∠2=180°，∠1=40°，故∠2=70°。

17.（2011广东株洲，5，3分）某商品的商标可以抽象为如图所示的三条线段，其中AB∥CD，∠EAB=45°，则∠FDC的度数是()A．30B．45C．60D．75【答案】B18.（2011山东济宁，6，3分）如图，AE∥BD，∠1=120°，∠2=40°，则∠C的度数是A．10°B．20°C．30°D．40°A E1B2DC第6题【答案】B19.（2011山东聊城，4，3分）如图，已知a∥b，∠1＝50°，则∠2的度数是（）A．40°B．50°C．120°D．130°【答案】D20．（2011四川宜宾,4,3分）如图，直线AB、CD相交与点E，DF∥AB．若∠D=70°，则∠CEB 等于（）A．70°B．80°C．90°D．110°（第4题图）【答案】D21.（2011重庆江津，5，4分）下列说法不正确是()．．．A.两直线平行,同位角相等;B两点之间直线最短C.对顶角相等;D.半圆所对的圆周角是直角·【答案】B·22.(2011重庆綦江，5，4分)如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1＝65°，则∠2的度数是（）A.65°B.50°C.35°D.25°【答案】：D23.（2011湖南怀化，4，3分）如图2，已知直线a∥b,∠1=40°,∠2=60°,则∠3等于A.100°B.60°C．40° D.20°【答案】A24.（2011江苏南通，5，3分）已知：如图AB∥CD，∠DCE＝80°，则∠BEF的度数为A. 120°B.110°C.100°D.80°【答案】C25.（2011山东临沂，3，3分）如图，已知AB∥CD，∠1＝70°，则∠3的度数是（）A．60°B．70°C．80°D．110°【答案】D3 26.（2011湖北黄石，8，3分）平面上不重合的两点确定一条直线，不同三点最多可确定条直线，若平面上不同的n个点最多可确定21条直线，则n的值为A. 5B.6C.7D.8【答案】B27.（2011湖南邵阳，8，3分）如图（三）所示，已知O是直线AB上一点，∠1=40°，OD 平分角BOD ，则∠2的度数是（）A.20°B.25°C.30°D.70°C D12ABO【答案】D.28.（2011广东茂名，3，3分）如图，已知AB ∥CD,则图中与∠1互补的角有A ．2个B ．3个C ．4个D ．5个【答案】A29. （2011湖北襄阳，4，3分）如图1，CD ∥AB ，∠1＝120°，∠2＝80°，则∠E 的度数是EC2D1 AB图1A.40 °B.60°C.80°D.120°【答案】A30.（2011广东湛江10,3分）如图，直线AB 、CD 相交于点E ，DF//AB ,若AEC 100，则D 等于A 70B 80C 90D 100【答案】B31. （2011贵州安顺，3，3分）如图，己知AB ∥CD ，BE 平分∠ABC ，∠CDE=150°，则∠C 的度数是（）A ．100°B ．110°C ．120°D ．150°第3题图【答案】C二、填空题1.（2011广东湛江14,4分）已知 1 30，则1的补角的度数为度．【答案】1502.（2011湖南湘潭市，11，3分）如图，a∥b，若∠2＝130°，则∠1＝_______度.a12bl【答案】50°3.（2011广东广州市，15，3分）已知三条不同的直线a，b，c在同一平面内，下列四个命题：①如果a∥b，a⊥c，那么③如果b⊥a，c⊥a，那么其中真命题的是b⊥c;②如果b∥a，c∥a，那么b⊥c；④如果b⊥a，c⊥a，那么．（填写所有真命题的序号）b∥c；b∥c．【答案】①②④4.(2011浙江湖州，12，4).如图，已知CD平分∠ACD，DE∥AC，∠1＝30°，则∠2＝度．【答案】605.（2011浙江省，11，3分）已知∠A=40°,则∠A的补角等于．【答案】140o6.（2011浙江温州，13，5分）如图，a∥b，∠1＝40°，∠2=80°，则∠3=度．【答案】1207.（2011湖南邵阳，15，3分）如图（五）所示，AB∥CD，MN分别交AB，CD于点E，F。

已知∠1=35°，则∠2=________。

【答案】35°。

提示：同位角相等。

8.（2011江苏泰州，15，3分）如图，直线a、b被直线l所截，a∥b，∠1=70°，则∠2=°．l1ab2【答案】1109.（2011四川广安，12，3分）如图2所示，直线a∥b．直线c与直线a，b分别相交于点A、点B，AM b，垂足为点M，若158，则2=_________cA1a2B Mb图2【答案】32°10（．、°，则∠2=. 2011江苏淮安，12，3分）如图，直线ab被直线c所截，a∥b，∠1=70【答案】110°11.（2011江苏南通，11，3分）已知∠α＝20°，则∠α的余角等于▲度.【答案】70°.12.（2011上海，15，4分）如图，AM是△ABC的中线，设向量AB a，BC b，那么向量AM____________（结果用a、b表示）．CMA B【答案】a1b213.（2011四川绵阳14，4）如图，AB∥CP，交AB于O，AO=PO,若∠C=50，°则∠A=____度PA BO50°DC【答案】25°14.（2011安徽芜湖，11,5分）一个角的补角是3635，这个角是．【答案】1432515.（2011贵州贵阳，11，4分）如图，ED∥AB，AF交ED于点C，∠ECF=138°，则∠A=______度．（第11题图）【答案】42平行线与相交线1余角与补角1.了解互余、互补、临补的概念2.了解对顶角的概念，掌握对顶角相等的性质3.掌握同角或等角的余（补）角相等的性质1.若一个角的补角是这个角的余角的三倍，则这个角是________2.如图，已知AO⊥CO，BO⊥DO，且∠BOC=50°，则∠AOD=_________3.如果∠1和∠2互为补角，且∠1＞∠2，那么∠2的余角是________4.如图，直线CD和∠1和∠AOB两边相交于点M、N，已知∠CMO+∠CNO=180°。