第七章 玻耳兹曼统计 sect;71热力学量的统计表达式内能是粒子
热力学与统计物理:第七章 玻耳兹曼统计

双原子能量:
1 2m
(
px2
p
2 y
pz2 )
1 2I
( p2
p2
sin2
)
1
2
pr2
1 2
k
(r
r0
)2
上式中: m
m1
m2 ,
m1m2 m1 m2
,I
r2
r02
其中: t
1 2m
( px2
p
2 y
pz2 )
v
1 2I
( p2
p2
sin2
)
1
2
pr2
1 2
k(r
r0 )2
配分函数的计算
00
ex2 dx
1
ex2 dx
0
2
2
由此求
e x2
xdx
1
0
2
I n ex2 xndx
0
I 0 e x2 dx
0
2 1/2
I 1 ex2 xdx
1
0
2
I n I n 2
§7.3 麦克斯韦速度分布率
系统:V,N
al
e l l
as e s
体积V内,在dpxdpydpz的动量范围内,分子质心 平动的状态数为:
CVt
U t (
T
)V
3 Nk 2
平动配分函数的量子计算与经典计算的不同点 只在于用h取代h0,因此对热容的贡献与经典 计算结果相同。
振动配分函数的经典计算:
zv 1
h
e dp pr2 / 2
v
e d (r k (rr0 )2 / 2
r0 )
2 h
热统2012-6关于Boltzmann统计的一些解释

S k ln
eS k
热力学涨落是围绕平衡 态的涨落,令S0和Ω0代表 平衡态的熵和宏观概率
0eSS0 k
平衡态附近的展开
• 设熵依赖于一个宏观量X,其平均值 x
Nkln pi Nk pi ln pi Nk ln Z Nk
i
Nk ln Z kU S
S Nkln pi Nk pi ln pi
体系的熵与粒子出现在μ空间i单位体积的概率的
对数lnp的统计平均值成正比,熵只与概率有关
单原子分子理想气体的Z
• 容器内的质点运动,无外场
1 2m
N l l e l
k N ln N
Nl ln l
Nl ln Nl
l ln l ln Nl
l
l
lnW ln N! ln Nl! Nl lnl
W
N! N j! j
j N j
l
l
j
N ln N 1 Nl ln Nl 1 Nl lnl N ln N Nl ln Nl Nl lnl
1 T
dU
Ydy
dQ T
dS
Nk
d ln
Z
ln Z
熵
S
Nk ln
Z
ln Z
另一表达式
S Nk ln Z kU
U N ln Z
熵的统计意义
S
Nk
ln
Z
ln Z
S
k
N
ln
N
N
N
ln Z
kN ln N N U
k
N
第七章 玻尔兹曼统计

7.8
固体热容量的爱因斯坦理论
由能量均分定理可得固体的定容摩尔热容量:
CV ,m 3R
(1818年得到实验验证)
存在的问题:固体的热容量在绝对零度下趋向于0. Einstein首先采用量子理论研究了固体的热容量问题,并成功解决了上述问题 假定固体中的原子的热运动为3维简谐振动,且每个振子具有相同的频率 则振子的能级: 假设原子的振动可以分辨,遵循玻尔兹曼分布,对应的配分函数为
平均速率 方均根速率
因此
讨论:碰壁数(单位时间内碰到单位面积器壁上的分子数)
在dt时间内,碰到器壁的dA面积上,速 度在dvxdvydvz范围内的分子数
分子数
体积
练习:289/7.13-14
7.4
能量均分定理
能量均分定理:对于处在温度为T的平衡状态的经典系统,粒子能量中每 一个平方项均等于1/(2kT) 经典物理中的粒子动能:
固体的内能 其中第二项为温度为T时3N个振子的热激发能量
定容热容量 定义 Einstein 特征温度: 定容热容量可写为:
金刚石的热容量实验结果与 Einstein理论得出的曲线
其中的Einstein 温度取1320K
定容热容量可写为:
在高温区: 所以
所以
能级间隔远小于kT,所以能量的量子化效应可以忽略,经典统计理论是有效的
4. 对于封闭的空窖 空窖内的辐射场可以视为无穷多的单色平面波的叠加 单色平面波的电矢量 波矢的三个分量
考虑到辐射场的波矢和能量的对应关系
(考虑了偏振)
(瑞利-金斯 公式) 可得有限温度下平衡辐射的总能量
实验结果(也可从热力学理论推导出)
原因:由经典电动力学可得辐射场具有无穷多个振动自由度,经典统计 的能量均分定理可得每个振动自由度的平均能量为kT,故而一定 会出现紫外发散的结论。
《第七章玻耳兹曼统计》小结

《第七章 玻耳兹曼统计》小结一、基本概念: 1、1>>αe 的非定域系及定域系遵守玻耳兹曼统计。
2、经典极限条件的几种表示:1>>αe ;12232>>⎪⎭⎫ ⎝⎛⋅h m kT NVπ;m kTh N V π231>>⋅⎪⎭⎫⎝⎛;()λ>>⋅31n3、热力学第一定律的统计解释:Q d W d dU +=l ll l ll da d a dU ∑∑+=εεl ll d a W d ε∑=l ll da Q d ∑=ε即:从统计热力学观点看,做功:通过改变粒子能量引起内能变化;传热:通过改变粒子分布引起内能变化。
二、相关公式1、非定域系及定域系的最概然分布l e a l l βεαω--=2、配分函数:量子体系:∑-=ll leβεω1Z∑---==ll l l l ll le e e a βεβεβεωωωNZ N 1半经典体系:()r rr p q r hdp dp dp dq dq dq e h d e l2121,1Z ⎰⎰⎰==-βεβεω 经典体系:()r rr p q r hdp dp dp dq dq dq e h d e l2121,01Z ⎰⎰⎰==-βεβεω 3、热力学公式(热力学函数的统计表达式) 内能:β∂∂=1lnZ -NU物态方程:VlnZ N 1∂∂=βp定域系:自由能:1-NkTlnZ F = 熵:B M k .ln S Ω=或⎪⎪⎭⎫ ⎝⎛∂∂-=ββ11lnZ ln Nk S Z1>>αe 的非定域系(经典极限条件的玻色(费米)系统): 自由能:!ln -NkTlnZ F 1N kT += 熵:!ln kln S .N k BM Ω=Ω=或!ln lnZ ln Nk S 11N k Z -⎪⎪⎭⎫⎝⎛∂∂-=ββ三、应用: 1、求能量均分定理①求平均的方法要掌握:()dx x xp ⎰=x②能量均分定理的内容---能量均分定理的应用:理想气体、固体、辐射场。
第七章节-玻尔兹曼统计

在准静态过程中,系统从外界所吸收的热量等于 粒子在各能级重新分布所增加的内能. 根据热力学第二定律
dQ不是全微分,与过程有关,有一积分因子, 除以T后得全微分dS,dS是全微分
BEIJING NORMAL UNIVERSITY
BEIJING NORMAL UNIVERSITY
积分因子
熵的统计表达式
3 U = NkT 2
BEIJING NORMAL UNIVERSITY
麦克斯韦速度分布律
讨论气体分子作无规热运动时,气体分子质心的平移 运动速度所表现出来的统计分布规律。 一、麦克斯韦速度分布律 1859年,麦克斯韦在研究分子相互碰撞作无规则运 动时,得到了气体分子按其质心速度分布的统计规律 麦克斯韦速度分布律
物态方程
∂ ln Z 注:也可直接利用公式 p = NkT 计算 ∂V
⎛ ∂F ⎞ S = −⎜ ⎟ ⎝ ∂T ⎠V
2πmk 3 3 3 = Nk ln V + Nk ln 2 + Nk ln T + Nk 2 h 2 2
3 = Nk ln V + Nk ln T + S 0 2
BEIJING NORMAL UNIVERSITY
熵的统计表达式,Boltzmann 关系
BEIJING NORMAL UNIVERSITY
由于
特性函数,自由能
量子情况下,粒子不可分辨性带来的差别
BEIJING NORMAL UNIVERSITY
计算单原子分子理想气体的熵:
3 3 2πmkT S = Nk + Nk ln V + Nk ln( ) 2 2 2 h
(ⅰ)系统在热力学过程中的规律 (ⅱ)系统的基本热力学函数
热力学量的统计表达式热力学统计物理汪志诚
kT
(8.1.9)
S k ln Ξ ln Ξ ln Ξ k ln Ξ N U (8.1.10)
新课: §8.1热力学量的统计表达式
S k ln Ξ N U
ln Ξ l ln 1 e l
* 本节讨论玻色系统和费米系统热力学量的统计表达式.
新课: §8.1热力学量的统计表达式
Chap.8 玻色统计和费米统计
§8.1 热力学量的统计表达式
抛弃粒子轨道的概念 (1)微观粒子的能量和动量是不连续的 (2)微观全同粒子不可分辨 (3)微观粒子的行为要满足不确定关系 (4)费米子受泡利不相容原理的限制
2、求巨配分函数 Ξ 或 ln Ξ
3、根据统计表达式,求热力学量
§8.1 小结:
Chap.8 玻色统计和费米统计
§8.1 热力学量的统计表达式 引入巨配分函数
Ξ Ξl 1 e
l l
l l
ln Ξ l ln 1 e l
l
是以 , , y 为自然变量的特性函数
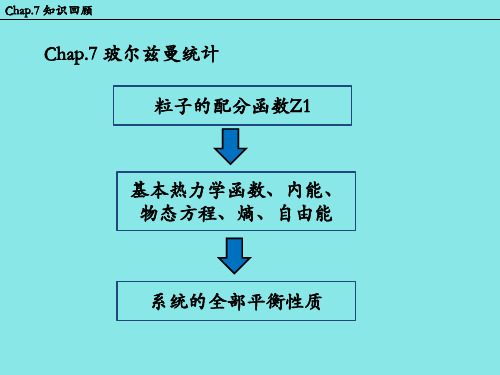
Chap.7 知识回顾
Chap.7 玻尔兹曼统计 粒子的配分函数Z1
基本热力学函数、内能、 物态方程、熵、自由能
系统的全部平衡性质
Chap.7 知识回顾
N e l e l e Z1
l
U e
e
l l l
l
N ln Z1
Z1 l e l
e 1 (e 1)
l
al 1
Chap.7 知识回顾
应用到理想气体,经典极限条件又表示为
统计物理学第7章

(dU Ydy )
ln Z1 ln Z1 ln Z1 N d d (N ) N dy y
17
ln Z1 ln Z1 ln Z1 (dU Ydy) N d d (N ) N dy y
dQ 1 (dU Ydy ) dS T T
热力学基本方程
说明1/T是积分因子,根据积分因子的理论,1/T
与β应同为积分因子,两者相差一个常数 k,称为玻耳
兹曼常数:
1 kT ,
k R N0
16
dQ (dU Ydy )
ln Z1 N d ( ln Z1 ) N dy y
V 3 e h
2m
2 2 ( px p2 p y z)
dpx dp y dpz
2m
2 px
dpx e
2 px
2m
p2 y
dp y e
0
2m
2 pz
dpz
V 3 ( e h
2m
dpx )
3
I (0)
e
x 2
l
l
受到外界 的作用力
N 1 ( ) Z1 N e Z1 Z1 y
N ln Z 1 y
8
N Y ln Z1 y
当
Y p y V ,
时,
这时广义力的统计表达式简化为:
N p ln Z 1 V
07 玻耳兹曼统计

(即定义广义力延广义位移方向)
ε l=
v v 1 mv 2 , δ w = F d x 2
(取广义位移为沿x轴平动)
∴
dε l = dx
d(
1 mv 2 ) 2 dx
= m
dv v dx
2)当转动时,
在系统的无穷小准静态过程中,系统的广义力为
ε l=
dv dt dt dx dv = m dt = ma = mv
ln z1 ) + Nd ln z1 β ln z1 = Nd (ln z1 β ) β Q dN = 0 ln z1 ∴ βδ Q = d [ N (ln z1 β )] β ∴ βδ Q = Nd ( β
∴β 和
由积分因子的理论,微分方程有一个积分因子 时,它就有无穷多个积分因子,且任意两个因子之比 是全微分函数的函数,即:
= V h3
β
dω h3
(
V 2πm 3 / 2 ( ) h3 β
(h:本质还是玻尔兹曼理论)
p2 + y
2 pz )
---即得到单原子分子理想气体的的配分函数
2m
p2 + x
dxdydzdp x dp y dpz h3
β
2
∴ 根据压强的统计表达,得
p=
+ ∞ 2 m pz ∞
+∞ 2m px ∞
1),若将分子热运动的平均能量理解为 ---- ε 热平均 = π kT 则: 2πmkT = 2m ε 热平均 = p 2
d 分子平均 >> λ热平均
或
1 1 ∴h( )2 = h = λ热平均 2πmkT p热平均
1
nλ3热平均 << 1
第七章_玻尔兹曼统计

曼分布一样,但系统的微观状态数为 ΩB(F )
=
ΩM ⋅B N!
,所以直接由分布函数导出的内能和广义
力的表达式与玻尔兹曼系统一样。(∵ 它由分布函数直接导出)
而由系统的微观状态数决定的熵
SB( F )
=
k
ln
ΩB(F )
=
k
ln
⎛ ⎜⎝
ΩM ⋅B N!
⎞ ⎟⎠
=
k
ln
ΩM ⋅B
−k
ln
N!=
SM ⋅B
玻尔兹曼系统的一样。
不同的 h0 的值对经典统计结果的影响。
经典玻尔兹曼分布
al
= e−α −βεl
Δωl h0r
由 e−α = N 得: Z1
al
=
N e−βεl Z1
Δωl h0r
式中的 h0r 与配分函数 Z1 所含的 h0r 相互抵消,与 h0 无关。
一个粒子的运动状态处于 Δωl 的概率:
n
n
n
∴ S = k ln Ω = k ln ∏ Ωi = ∑ k ln Ωi = ∑ Si 。
i =1
i =1
i =1
(2)非平衡态的熵: S = k ln Ω 可推广到非平衡态只不过在平衡态时, Ω 是系统最多的微观 状态数,而在非平衡态时, Ω 也是系统的微观状态数,但不是最多的,所以系统在由非平衡
k = 1.381×10−23 J ⋅ K −1 玻尔兹曼常数
玻尔兹曼常数 k 在统计物理学中所起的作用相当于普朗克常数 在量子力学中所起的作用。
dS
=
dQ T
= kβ dQ
=
Nkd
⎛ ⎜ ⎝
ln
Z1
热力学玻尔兹曼公式

热力学玻尔兹曼公式热力学玻尔兹曼公式,这可真是个相当厉害的东西呢!咱先来说说啥是热力学。
想象一下,大热天里,你吃着冰淇淋,可还没一会儿,它就开始融化,变得软趴趴的。
这就是热力学在生活中的一个小表现。
热力学研究的就是热和能量之间的关系,以及它们怎么影响物质的状态和变化。
而玻尔兹曼公式,那可是热力学中的一颗璀璨明珠。
这个公式就像是一把神奇的钥匙,能帮我们打开理解热力学世界的大门。
玻尔兹曼公式表示为 S = k ln W ,这里的 S 代表熵,k 是玻尔兹曼常数,W 则是微观状态数。
那啥是熵呢?咱打个比方。
假如你的房间乱得像个杂货铺,衣服扔得到处都是,书本也七零八落的,这时候房间的熵就很大。
相反,如果你的房间整理得井井有条,东西都摆放得规规矩矩,熵就比较小。
还记得我有一次去朋友家,他那房间简直了!衣服堆在床上,鞋子横在门口,书和杂志散落在地上。
我当时就跟他说:“你这房间熵太大啦,得好好收拾收拾!”朋友还一脸懵,不明白我在说啥。
我就给他解释,熵越大,就代表混乱程度越高。
后来他花了好长时间才把房间整理好,整理完后他自己都感叹,房间熵小了,感觉都清爽多了。
再来说说玻尔兹曼常数。
这个常数就像是一个稳定的基石,不管在什么情况下,它都保持不变。
它的值虽然很小很小,但在热力学的计算中却起着至关重要的作用。
微观状态数 W 呢,就有点复杂啦。
比如说一堆气体分子,它们在容器里到处乱跑,有各种各样的速度和位置组合。
每一种可能的组合就是一种微观状态。
咱们在实际生活中,也能看到玻尔兹曼公式的影子。
比如冬天的时候,热气总是往冷的地方跑,这就是为了让整个系统的熵增加,达到更稳定的状态。
在学习热力学玻尔兹曼公式的时候,很多同学一开始都觉得头疼,觉得这东西太抽象,不好理解。
但其实只要多联系实际,多想想生活中的例子,就能慢慢搞明白。
总之,热力学玻尔兹曼公式虽然看起来有点复杂,但只要我们用心去琢磨,多思考,多观察生活中的现象,就能发现它其实就在我们身边,默默地发挥着作用,影响着我们生活的方方面面。
热力学与统计物理 第七章 玻尔兹曼统计

e Z1 r dq1 dqr dp1 dpr h0
粒子自由度为3
e Z1 3 dxdydzdpx dp y dpz h0
15
Z1
V Z1 3 h0
方法一:
e
2 2 px p2 y pz
2m
h
3 0
dxdydzdp x dp y dp z
ln Z1 S Nk ln Z1
7
ln Z1 S Nk ln Z1 ln Z1 Nk ln Z1 T Nk ln Z1 自由能 F U TS N kT F NkT ln Z1
l l Z1 r e h0
体积元 l 取得足够小时,
l d dq1 dqr dp1 dpr
l l Z1 r e h0
Z1
e
h
r 0
dq1 dqr dp1 dpr
14
§7.2
理想气体的物态方程
N ln Z1 p V
Z1 l e l
Z1 l ln Z1 U N
l e l
l l e l l
2
三、广义力
Y 广义力
dW pdV
y
外参量
dW Ydy
Y l作用在该粒子上 当某个粒子处在 l 能级上,若有一“外力”
e
2 2 px p2 y pz
2m
dp x dp y dp z
V Z1 3 h0
4V Z1 3 h0
则
1 e t t 2 dt
第七章 玻耳兹曼统计 201110

说明绝对熵的概念是量子力学的结果。
小结Ⅰ :求玻耳兹曼量子体系热力学函数的一般步骤: (1)写出 l 及相应简并度 l (2)求粒子的配分函数 量子效应显著时
Z1 l e l
l
①量子力学的理论计算获得 ②分析光谱数据获得
量子效应不显著时(半经典方法)
Z1 1 e q , p dq1dq 2 dq r dp1dp 2 dp r r h
即:PV NKT nN 0 KT
与热力学中根据实验定律推导出的理想气体物态方程:
PV nRT
比较可得玻耳兹曼常量的数值: R N 0 K 讨论:
①、单原子分子理想气体内能:
2m lnV h 2 lnZ1 U -N -N
3 2
U N
ln Z1
原子光谱随原子所处的外 部环境的变化而变化现象, 证明了广义力统计意义的 正确性。
2、广义力或物态方程统计表达式: 热力学第一定律: dU dW dQ 对于准静态过程:
dW Ydy
Y是与外参量y相应的外界对系统的广义作用力。 由于外参量的改变,外界施于处于能级εl的一个粒子的力为:
N Y ln Z1 y
特例:
dW PdV Y P; y V
N P ln Z1 V
二、热力学第一定律的统计解释: 在无穷小的准静态过程中,外界对系统所作的功是:
将内能U εl al求全微分,有:
l
ε l dW Ydy dy a l a l dεl l y
与
dS
dS
1 dQ T
ln Z1 ln Z1 ln Z1 d Nd Nd ln Z 1
热力学统计物理第七章 玻耳兹曼统计

第七章 玻耳兹曼统计7.1 试根据公式lllp a Vε∂=-∂∑证明,对于非相对论粒子 ()222221222x y z p n n n m m L πε⎛⎫==++ ⎪⎝⎭, (),,0,1,2,,x y z n n n =±±有2.3U p V=上述结论对于玻耳兹曼分布、玻色分布和费米分布都成立. 解: 处在边长为L 的立方体中,非相对论粒子的能量本征值为()2222122x y zn n n x y z n n n m L πε⎛⎫=++ ⎪⎝⎭, (),,0,1,2,,x y z n n n =±± (1)为书写简便起见,我们将上式简记为23,l aV ε-= (2)其中3V L =是系统的体积,常量()()222222xy z a nn n mπ=++,并以单一指标l 代表,,x y z n n n 三个量子数.由式(2)可得511322.33aV V Vεε-∂=-=-∂ (3) 代入压强公式,有22,33l ll l llUp a a V VVεε∂=-==∂∑∑ (4) 式中l l lU a ε=∑是系统的内能.上述证明示涉及分布{}l a 的具体表达式,因此式(4)对玻耳兹曼分布、玻色分布和费米分布都成立.前面我们利用粒子能量本征值对体积V 的依赖关系直接求得了系统的压强与内能的关系. 式(4)也可以用其他方法证明. 例如,按照统计物理的一般程序,在求得玻耳兹曼系统的配分函数或玻色(费米)系统的巨配分函数后,根据热力学量的统计表达式可以求得系统的压强和内能,比较二者也可证明式(4).见式(7.2.5)和式(7.5.5)及王竹溪《统计物理学导论》§6.2式(8)和§6.5式(8). 将位力定理用于理想气体也可直接证明式(4),见第九章补充题2式(6).需要强调,式(4)只适用于粒子仅有平衡运动的情形. 如果粒子还有其他的自由度,式(4)中的U 仅指平动内能.7.2 试根据公式lllp a Vε∂=-∂∑证明,对于相对论粒子 ()122222xyzcp cnn nLπε==++, (),,0,1,2,,x y z n n n =±±有1.3Up V=上述结论对于玻耳兹曼分布、玻色分布和费米分布都成立.解: 处在边长为L 的立方体中,极端相对论粒子的能量本征值为()122222x y zn n nxyzcnn nLπε=++ (),,0,1,2,,x y z n n n =±± (1)用指标l 表示量子数,,,x y z n n n V 表示系统的体积,3V L =,可将上式简记为13,l aV ε-= (2)其中()122222.xyza c n n nπ=++由此可得4311.33l l aV V Vεε-∂=-=-∂ (3) 代入压强公式,得1.33l ll l llUp a a V V V εε∂=-==∂∑∑ (4) 本题与7.1题结果的差异来自能量本征值与体积V 函数关系的不同. 式(4)对玻耳兹曼分布、玻色分布和费米分布都适用.7.3 当选择不同的能量零点时,粒子第l 个能级的能量可以取为l ε或*.l ε以∆表示二者之差,*.l l εε∆=-试证明相应配分函数存在以下关系*11Z e Z β-∆=,并讨论由配分函数1Z 和*1Z 求得的热力学函数有何差别.解: 当选择不同的能量零点时,粒子能级的能量可以取为l ε或*.l l εε=+∆显然能级的简并度不受能量零点选择的影响. 相应的配分函数分别为1,ll lZ e βεω-=∑ (1) **1l ll ll lZ eeeβεβεβωω---∆==∑∑1,e Z β-∆= (2) 故*11ln ln .Z Z β=-∆ (3)根据内能、压强和熵的统计表达式(7.1.4),(7.1.7)和(7.1.13),容易证明*,U U N =+∆ (4)*,p p = (5)*,S S = (6)式中N 是系统的粒子数. 能量零点相差为∆时,内能相差N ∆是显然的. 式(5)和式(6)表明,压强和熵不因能量零点的选择而异. 其他热力学函数请读者自行考虑.值得注意的是,由式(7.1.3)知*,ααβ=-∆所以l l l a e αβεω--=与***l l l a e αβεω--=是相同的. 粒子数的最概然分布不因能量零点的选择而异. 在分析实际问题时可以视方便选择能量的零点.7.4 试证明,对于遵从玻耳兹曼分布的定域系统,熵函数可以表示为ln ,s s sS Nk P P =-∑式中s P 是粒子处在量子态s 的概率,1,s ss e e P N Z αβεβε---==s∑是对粒子的所有量子态求和.对于满足经典极限条件的非定域系统,熵的表达式有何不同? 解: 根据式(6.6.9),处在能量为s ε的量子态s 上的平均粒子数为.s s f e αβε--= (1)以N 表示系统的粒子数,粒子处在量子态s 上的概率为1.s ss e e P N Z αβεβε---== (2)显然,s P 满足归一化条件1,s sP =∑ (3)式中s∑是对粒子的所有可能的量子态求和. 粒子的平均能量可以表示为.s s sE P ε=∑ (4)根据式(7.1.13),定域系统的熵为()()1111ln ln ln ln s s sS Nk Z Z Nk Z Nk P Z βββεβε⎛⎫∂=- ⎪∂⎝⎭=+=+∑ln .s s sNk P P =-∑ (5)最后一步用了式(2),即1ln ln .s s P Z βε=-- (6)式(5)的熵表达式是颇具启发性的. 熵是广延量,具有相加性. 式(5)意味着一个粒子的熵等于ln .s s sk P P -∑ 它取决于粒子处在各个可能状态的概率s P . 如果粒子肯定处在某个状态r ,即s sr P δ=,粒子的熵等于零. 反之,当粒子可能处在多个微观状态时,粒子的熵大于零. 这与熵是无序度的量度的理解自然是一致的. 如果换一个角度考虑,粒子的状态完全确定意味着我们对它有完全的信息,粒子以一定的概率处在各个可能的微观状态意味着我们对它缺乏完全的信息. 所以,也可以将熵理解为信息缺乏的量度. 第九章补充题5还将证明,在正则系综理论中熵也有类似的表达式. 沙农(Shannon )在更普遍的意义上引进了信息熵的概念,成为通信理论的出发点. 甄尼斯(Jaynes )提出将熵当作统计力学的基本假设,请参看第九章补充题5. 对于满足经典极限条件的非定域系统,式(7.1.13′)给出11ln ln ln !,S Nk Z Z k N ββ⎛⎫∂=-- ⎪∂⎝⎭上式可表为0ln ,s s sS Nk P P S =-+∑ (7)其中()0ln !ln 1.S k N Nk N =-=--因为,s s f NP =将式(7)用s f 表出,并注意,ssfN =∑可得ln .s s sS k f f Nk =-+∑ (8)这是满足玻耳兹曼分布的非定域系统的熵的一个表达式. 请与习题8.2的结果比较.7.5 因体含有A ,B 两种原子. 试证明由于原子在晶体格点的随机分布引起的混合熵为()()()()!ln!1!ln 1ln 1,N S k Nx N x Nk x x x x =-⎡⎤⎣⎦=-+--⎡⎤⎣⎦其中N 是总原子数,x 是A 原子的百分比,1x -是B 原子的百分比. 注意1x <,上式给出的熵为正值.解: 玻耳兹曼关系给出物质系统某个宏观状态的熵与相应微观状态数Ω的关系:ln .S k Ω= (1)对于单一化学成分的固体(含某种元素或严格配比的化合物),Ω来自晶格振动导致的各种微观状态. 对于含有A ,B 两种原子的固体,则还存在由于两种原子在晶体格点上的随机分布所导致的Ω。
热力学统计物理第七章

三,最可几速率,平均速率,方均根速率 1,最概然速率 m 。 使速率分布函数取极大值的速率称为最概然速率, 用 表示
v
v
m
由: 得:
d e v 0 dv
mv 2 2 kT 2
2kT v m
m
2, 分子的平均速率
m v 4 2kT
x y z
x
v fdv dv dv
x x y
z
v
v dt
x
dA
1 kT nv n 2m 4
小结 麦克斯韦速度分布律
m f (v , v , v )dv dv dv n e 2kT
x y z x y z
3/ 2
1
U e e e e N Z N ln Z Z
l l l l l 1 1
1
二,广义力的统计表达式: 在热力学中有:dU dQ dW 准静态过程: dW Ydy Y 对于p,V,T系统,外参量为:V
( X ) ( Y ) 满足完整微分条件: y x
dz 是一个完整微分,
称为 dz 的积分因子
dz ds
如果 是 dz 的积分因子,则 ( s) 也必是 其中 是s的任意函数。因为: (s)dz (s)ds d
dz 的积分因子
当微分式有一个积分因子时,它就有无穷多个积分因子。 任意两积分因子的比是s 的函数。 例: 验证 ( x, y) x y 是方程 (3 y 4 xy )dx (2 x 3x y)dy
第七章 玻耳兹曼(Boltzmann)统计

ε l * ,以 Δ 表示二者差 Δ = ε l * - ε l , 试证明相应的配分函数存在以下的
并且讨论由配分函数 Z 和 Z * 所得热力学函数有何差异 关系 Z * = Ze − βΔ , 解,由配分函数的定义,及由配分函数求热力学量的关系可以求 得所有的问题。
经典统计理论中的简并度可以表达为 经典统计理论中的配分函数可以写为
Z 1 = ∑ e − β El
l
Δω l h0
r
,所以
Δω l h0
r
,
如果 Δωl 足够小,则配分函数可以写成积分。
dq1 dq 2 ...dq r dp1 dp 2 ...dp r h0
r
Z1 = ∫
… ∫ e − βE ( q , p )
U = 3 NkT , C v = 3Nk .
的平均能量为 E = 3kT , 固体的内能为
在室温和高温范围内, 理论结果与实验结果符合的很好. 低温下 固体的热容量与金属中自由电子对热容量的贡献需要用量子统 计来解释 目的 3: 用能量均分定理讨论平衡辐射(黑体辐射)问题. 具有一定波矢 k 和一定偏振的平面单色波可以看作辐射场的
l
,
系数 α 与 β 由 ∑ al
l
=N
定域系统 (由定域粒子组成的系统) 与满足经典极限条件的玻色
(费米)系统( eα >> 1 , 或者对于所有的 l ,
简并条件)都遵从玻耳兹曼分布
al
ωl
<< 1 ,
又叫做非
7.1 热力学量的统计表达式
目的 1: 由系统的微观量求得系统的配分函数 Z 1 = ∑ ω l e − βE
《第七章玻耳兹曼统计》(期末复习)

《第七章 玻耳兹曼统计》(期末复习)、热力学第一定律的统计解释:比较可知: 即:从统计热力学观点看, 做功:通过改变粒子能级引起内能变化;传热:通过改变粒子分布引起内能变化、相关公式 1、非定域系及定域系的最概然分布ai2、配分函数:3、热力学公式(热力学函数的统计表达式)内能:U 曲竽 物态方程:定域系:自由能:—熵®k"B 或s = Nk (inZ 」詈]dU =6W dQU 八 a i ;i 二 dUdQ - ';i da iI 量子体系:乙八代八I半经典体系:Z-'td-... e 1;q,pdq i dq 2 dq 「dp i dp 2 dp r1-厂h r应用:a i乙二 NI-—i^J经典体系: 乙二e_打 土 = ... e 1;q,P dqgdq r dpg dp「 齐h1、用玻耳兹曼分布推导单原子分子的理想气体物态方程并 说明所推导的物态方程对多原子分子的理想气体也适用。
2、能量均分定理 ① 能量均分定理的内容 ② 能量均分定理的应用:A 、 熟练掌握用能量均分定理求理想气体(单原子分子,多 原子分子)内能、热容量。
知道与实验结果的一致性及存在 的问题。
B 、 知道经典的固体模型,熟练掌握用能量均分定理求经典 固体的内能及定容热容量。
知道与实验结果的一致性及存在 的问题。
3、定域系的量子统计理论:①、爱因斯坦固体模型;②、熟练掌握用量子统计理论求爱因斯坦固体的内能及其热容 量;③、知道爱因斯坦固体模型成功之处及其不足和原因。
四、应熟练掌握的有关计算 1、求配分函数Z i 进而求系统的热力学性质 2、用S 二kln"的证明及相关应用 四、解题指导例1 :根据公式p = - | a*电=cp =(n XX +n : +n ;)1/2 , n * =n 厂 n z =0,±1,二2,…1、求广义力的基本公式丫八a i 」的应用;i:yT ,证明:对于极端相对论粒子,s sIi AiA I一V _ 3V 4/3 _ 3V V 1/3 _ 3V论对玻尔兹曼、玻色、费米分布均存立。
第七章 玻耳兹曼统计 sect;71热力学量的统计表达式内能是粒子

第七章
玻耳兹曼统计
所得结果对双原子分子和多原子分子同样适用。
(7.2.5)
将(7.2.4)的 Z 1 代入(7.1.3),可将经典极限条件表为:
3 V2 mkT e ( 2 ) 2 1 N h
(7.2.6)
从上式也可得经典极限条件的另一种表述:
V1 1 1 3 ( ) h ( )2 N 2 mkT
Z 1 是 、y的函数, ln Z 1 的全微分为:
ln Z ln Z 1 1 d ln Z d dy 1 y
( dU Ydy ) Nd (ln Z ln Z ) (7.1.11) 1 1 1 也是 d Q 的积分因子,既然 与 都是 d Q 的积分因子,
m v v 4 ( ) v e 2 kT0
2 s 2
m2 v 3 kT 2 2 2 2
3 kT v dv m
故:
vs
3 kT m
3 2 v v : v : : 1 1 . 225 : 1 . 128 : 1 (7.3.14) s: m 2
§7.4
能量均分定理
§7.1热力学量的统计表达式
内能是粒子无规则运动总能量的平均值:
U a e l l l l
l l
l
(7.1.1)
引入粒子配分函数 Z 1 :
第七章-玻尔兹曼统计

(ⅱ)理论: 热力学基本方程。 TdS=dU+pdV
(ⅰ)系统在热力学过程中的规律 (ⅱ)系统的基本热力学函数
BEIJING NORMAL UNIVERSITY
研究问题
{
从统计物理角度讨论理想气体 粒子服从经典力学规律 分子之间无相互作用 经典系统 近独立子系统
理想气体:经典的近独立子系统 遵从经典的M-B分布 思路: 能谱 配分函数 特性函数
物态方程
∂ ln Z 注:也可直接利用公式 p = NkT 计算 ∂V
⎛ ∂F ⎞ S = −⎜ ⎟ ⎝ ∂T ⎠V
2πmk 3 3 3 = Nk ln V + Nk ln 2 + Nk ln T + Nk 2 h 2 2
3 = Nk ln V + Nk ln T + S 0 2
BEIJING NORMAL UNIVERSITY
3 U = NkT 2
BEIJING NORMAL UNIVERSITY
麦克斯韦速度分布律
讨论气体分子作无规热运动时,气体分子质心的平移 运动速度所表现出来的统计分布规律。 一、麦克斯韦速度分布律 1859年,麦克斯韦在研究分子相互碰撞作无规则运 动时,得到了气体分子按其质心速度分布的统计规律 麦克斯韦速度分布律
热力学函数(包括物态方程)
BEIJING NORMAL UNIVERSITY
以无外场情况下的单原子分子理想气体为例 能量表达式:
第一步:求配分函数
p p z2 ε= + + 2m 2m 2m
2 x
2 py
在宏观大小容器内 是准连续的
单原子理想气体r=3,μ空间是6维的。 相体积元: 微观状态数 1 −βε Z = r ∫ e dω h +∞ +∞ +∞ β ( p x2 + p 2y + p z2 ) − 1 = 3 ∫∫∫ dxdydz ∫ ∫ ∫ e 2 m dp x dp y dp z h V − ∞− ∞− ∞
热力学量的统计表达式

热力学量的统计表达式在§6.8说过,定域系统和满足经典极限条件的玻色系统都遵从玻耳兹曼分布.本章根据玻耳兹曼分布讨论这两类系统的热力学性质.本节首先推导热力学量的统计表达式.内能是系统中粒子无规则运动总能量的统计平均值.所以∑∑--==l l a le l ll l e a U βεωεε引入函数Z 1, ∑--=ll a le l l e Z βεωε名为粒子配分函数.由式(6.6.7)得 1Z e e e N a el ll a ---==∑βω上式给出参量α与N 和Z 1的关系,可以利用它消去式(7.1.1)中的α.经过简单的运算,可得1ln Z n u β∂∂-= 式(7.1.4)是内能的统计表达式.在热力学中讲过,系统在程中可以通过功和热量两种方法与外界交换能量.在无穷小过程中.系统在过程前后内能的变化dU 等于在过程中外界对系统所作的功dW 及系统从外界吸收的热量dQ 之和如果过程是准静态的,dW 可以表达为Ydy 的形式,其中dy 是外参加的改变量,Y 是外参量y 相应的外界对系统的广义作用力.粒子的能量是外参量的函数.一个常见的例子是(6.2.8)其中自由粒子的能量是体积V 的函数.由于外参量的改变,外界施与处于能级l ε的一个粒子的力为.因此.外界对系统的广义作用力Y 为 1ln Z yN Y ∂∂-=β 式(7.1.6)是广义作用力的统计表达式.它的一个重要例子是1ln Z V N p ∂∂=β 在无穷小的准静态过程中,当外参量dy 有的改变时,外界对系统所作的功是 ∑=ll l d a Ydy ε将内能l l l αεμ∑=求全微分,有∑∑+=ll l l l l da a d a dU ε式(7.1.9)指出,内能的改变可以分成两项。
在热力学中讲过,系统在过程中从外界吸收的热量与过程有关.因此dQ 不是全微分而只是一个无穷小量.根据热力学第二定律可以证明,dQ 有积分因子T 1,用T1乘dQ 后得到完整微分dS dS Ydy dU TdQ T =-=)(11 由(7.1.4)和(7.1.6)二式可得Ydy dU dQ -=式(7.1.11)指出β也是dQ 的积分因子,既然β与T 1都是dQ 的积分因子,可以令kT1=β 根据微分方程关于积分因子的理论,当微分方程有一个积分因子时,它就有无穷多个积分因子,任意两个积分因子之比是S 的函数.S=kln Ω称为玻尔兹曼关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的 N!
S Nk (ln Z1 ln Z1 ) k ln N! (7.1.13’) M .B S k ln (7.1.15’) N! 综上所述,Z 是以 、y为变量的特性函数。以T、V为变量的 1
特性函数是自由能F,可得:
F N ln Z1 NkT (ln Z1 ln Z1 ) NkT ln Z1
一个普通的外参量,与之相对应的广义力记为Y:
(7.1.5)
广义力体现了粒子的能级随外参量的变化,我们用y代表
l l l Y al l e y y l l 1 N 1 e ( ) l e ( ) Z1 y l Z1 y
(7.1.16)
F NkT ln Z1 kT ln N!
(费米)系统。
配分函数的经典表达式为 :
(7.1.16’)
两式分别适用于定域系统和满足经典极限条件的玻色
Z1 e
l
l
l h0
r
(7.1.17)
取 l 足够小,上式的求和可化为积分:
Z1 e
l
l
1 2 2 2 ( px p y pz ) 2m
dxdydzdpx dp y dp z h0
3
(7.2.1)
在 dxdydzdpx dp y dp z 范围内,分子可能的微观状态数为: (7.2.2)
所以:
1 2m ( p x 2 p y 2 p z 2 ) Z1 3 ... e dxdydzdpx dp y dp z h
l
广义力的统计表达式:
N Y ln Z1 y
一个重要的例子:
(7.1.6)
N p ln Z1 V
(7.1.7)
准静态过程中,外参量有dy改变时,外界对系统所作的功是 :
l Ydy dy al al d l l y l
对内能求全微分有:
(7.1.8)
dU al d l l dal
l l
(7.1.9)
第一项是粒子分布不变时能级改变引起的内能的变化,对应于
外界对系统所作的功;
第二项是粒子能级不变时粒子分布改变引起的内能的改变,对 应于系统吸收的热量。
1 1 根据热力学第二定律可证明,d Q 有积分因子 , 乘后得 T T 完整积分 dS :
1 1 dQ (dU Ydy ) dS T T
由(7.1.4)式和(7.1.5)式可得:
(7.1.10)
ln Z1 N ln Z1 dQ dU Ydy Nd ( ) dy y
乘上式得:
ln Z1 ln Z1 (dU Ydy ) Nd ( ) N dy y
第七章
玻耳兹曼统计
§7.1热力学量的统计表达式
内能是粒子无规则运动总能量的平均值:
U al l l l e
l l
l
(7.1.1)
引入粒子配分函数 Z : 1
Z1 l e
可以得:
l
l
(7.1.2)
N e
e
l l
l
dl h0
r
... e
( p , q )
dq1 dq 2 ...dq r dp1 dp 2 ...dp r h0
r
(7.1.18)
将 Z 1 代入前面的式子就可以得到经典统计理论中的热力学 表达式。
§7.2
理想气体的物态方程
考虑单原子分子理想气体。可以将单原子分子理想气体中分 子的运动看作在容器内的自由运动。其能量表达式为:
代入(7.1.13)有:
S k[ N ln N N U ] k[ N ln N l ( l )]
由玻耳兹曼分布可得 : l ln
l
al
所以S可表为:
S k[ N ln N al ln l al ln al ]
l l
(7.1.14)
可以令:
所以:
T
1 kT
(7.1.12)
所以:
dS Nkd(ln Z1 ln Z1 )
积分得熵的统计表达式 :
S Nk (ln Z1 ln Z1 )
现在讨论熵的统计意义。将式(7.1.3)取对数,得:
(7.1.13)
ln Z1 ln N
1 Z1 3 h
(7.2.3)
2m
上式化为:
dxdydz e
2m
px 2
dp x e
2m
py2
dp y e
pz 2
dp z
积分可得:
2m 3 2 Z1 V ( 2 ) h
(7.2.4)
其中 V
dxdydz 是气体的体积。由(7.1.7)可得理想气体
Z 1 是 、y的函数, ln Z1 的全微分为:
ln Z1 ln Z1 d ln Z1 d dy y
(dU Ydy ) Nd (ln Z1 ln Z1 ) (7.1.11) 1 也是 d Q 的积分因子,既然 与 都是 d Q 的积分因子,
与式(6.6.4)比较,可得玻耳兹曼关系:
S k ln
(7.1.15)
玻耳兹曼关系给出熵函数明确的统计意义。热力学中曾 说过,熵是混乱度的量度,从上式可看出,某个宏观状态对应 的微观状态数愈多,它的混乱度就愈大,熵也愈大。
对于满足经典极限条件的玻色和费米系统,因为 B. E
F .D 所以它们相应的熵的统计表达式应是:
e Z1
(7.1.3)
内能统计表达式 :
U e
e
l l l
l
e ( ) l e l l
N ( ) Z1 N ln Z1 Z1
(7.1.4)
系统过程前后内能的变化等于外界作功与系统吸热之和:
dU d W d Q Ydy d Q
