2005年数学建模A题——长江水污染
2005年A题全国数学建模优秀论文3

问题假设
1. 2. 3. 假设干流的自然净化能力是均匀的; 假设两个观测站之间河段的平均流速是等于两个观测站流速的平均值; 假设废水的处理对各类污染程度的河流的影响是均匀的。
符号说明
X1 X2 X3 X4 溶解氧的浓度(DO) 高锰酸盐指数(CODMn) 氨氮浓度(NH3-N) PH 值 污染物的浓度 水流的流量 污染物的降解系数 水流的流速 污染物流过的距离 第 n 个观测站(地区)水流所含污染物的质量 第 n 个观测站(地区)排放污染物的质量 第 i 类污染程度的河流总长度比例 第 t 年排污量
再根据排污量预测值,利用 BP 神经网络对未来十年的不同水质的河长比例进行了 预测。 为了得到排污量与各类水质的河长比例,本文再次利用 BP 神经网络的高精度逼近 能力对排污量与六类水质的河长比例的关系进行拟合。 从而可以得到每年控制污染所应 当处理的废水量:单位(亿吨) 年份 废水处理量 2005 58.2 2006 123.6 2007 133.3 2008 174.3 2009 163.0 2010 189.9 2011 245.4 2012 272.1 2013 300.5 2014 300.7
华南理工大学:李宁、董泽彦、林泽彬,指导教师:陶志穗
有很多传统的系统评估方法比如加权评估法、专家评估法、综合评分法以及层次分 析法都不免受到主观因素不同程度的影响。 而本文使用的基于主成分分析所构造的评估 机制则可以避免主观因素对评估的影响,使得评估结果客观的反映系统状况。 主成分分析方法是一种将多维因子纳入同一系统进行定量化研究、 理论成熟的多元 统计分析方法。通过分析变量之间的相关性,使得所反映信息重叠的变量 被某一主成分替代,减少了变量数目,从而降低了系统评价的复杂性。再以方差贡献率 作为每个主成分的权重,由每个主成分的得分加权即可完成对水质的综合评价。 为了确定主要污染物高锰酸盐指数(CODMn)和氨氮(NH3-N)的主要污染源,我 们需要知道各个地区主要污染物的排放质量。 而本地区污染物的排放质量可以通过当前 观测站的污染物质量与上游对本地区影响部分质量的差值来确定。 通过污染物的降解公 式分析出上游对本地区影响部分质量变化关系, 进而得出本地区污染物排放的质量关系 式。根据长江干流近一年多的基本数据计算出各地区污染物的平均排放速度,进而确定 主要污染源。 长江水质被分为六个级别,代表了不同程度的污染,不同水质河长的比例可以表征 一定时期内的水污染状况。所以说预测长江未来十年的水污染趋势,就是要预测未来不 同水质的河长的比例。对每年的排污量与不同水质河长的比例做一个相关性分析: 第I类 第 II 类 第 III 类 第 IV 类 第V类 劣V类 -0.8058 0.3164 -0.3371 0.3183 0.6624 0.9570 相关系数 可见排污量与不同水质河长的比例有很高的相关性, 与劣 V 类的相关系数更是达到 了 0.9570 的水平, 因此在作对不同水质河长的比例之前, 必须先对未来的排污量有比较 精确的预测。 由于附件中数据样本少,需要预测的时间长,直接应用神经网络很难取得理想的效 果,因此本文采用 GM(1,1)模型与神经网络模型联合预测长江未来十年的水污染趋势, 尝试着首先较精确预测出部分重要的数据, 为建立神经网络预测未来不同水质的河长的 比例提供更多的数据,从而完成对不同水质河长的比例的预测。GM(1,1)模型就可以用 来较好的预测出未来的排污量。
05A

摘要问题一主要是对长江水质的综合评价和对各地水质的分析,在对长江水质的综合评价中,我们运用了标准值法,分别算出各类污染物的标准值,然后加权求和,以此判断水质类别,通过对长江水质近两年各地水质类别和个污染物浓度的处理,我们得到,长江水质处于II 类水质类别,但是特别接近III 类水质类别。
在对各地分析中,我们做出了近两年每月各地水质类别变化的折线图,图见正文,并算出各地水质平均值,得出结论湖北丹江口胡家岭属于I 水质类别,四川攀枝花,重庆朱沱,等地属于II 类水质,四川宜宾凉姜沟,四川泸州沱江二桥,等地属于III 类水质类别,四川乐山岷江大桥属于IV 水质类别,江西南昌滁槎属于V 水质类别。
问题二中主要统计了高锰酸盐和氨氮化物引起重大污染的次数以及发生的地区,并计算出各地区发生次数占总次数的比重,图见正文,得到氨氮化物污染源在江西南昌,湖南长沙,和四川攀枝花。
高锰酸盐污染源在湖南岳阳,江西九江。
问题三中主要解决的是未来十年长江水质的预测,我们用了回归模型,利用过去十年数据,分别利用Matlab 拟合了废水量--时间,废水浓度--Ⅰ类水百分比,Ⅱ类水百分比,Ⅲ类水百分比,Ⅳ类水百分比,Ⅴ类水百分比,劣Ⅴ类水百分比的曲线,预测了未来十年各类别水所占百分比,结果见正文表(3-3)问题四中主要解决要使Ⅳ类和Ⅴ类水控制在20%之内,消除劣Ⅴ类水,即使非可饮用水控制在20%之内,我们利用第三问的回归模型得到非可饮用水在20%时,各年的废水浓度从而得到每年需处理的废水量 问题五中我们根据前四问的模型对提高长江水质提出了相关建议。
关键词:标准值法 回归模型 长江水质年份2005 2006 2007 2008 2009 2010 2011 2012 2013 2014需处理废水单位(亿吨)143.39 166.29 190.79 216.99 244.89 274.49 305.69 338.69 373.19 409.49问题重述水是人类赖以生存的资源,保护水资源就是保护我们自己,对于我国大江大河水资源的保护和治理应是重中之重。
2005-2015高教社杯全国大学生数学建模竞赛A、B题评阅要点

水质排序最差的地区不一定是污染源最严重的地区。 用长江干流上的 7 个观测站点将长江分 为 6 个江段,逐段计算各江段的排污量,找出主要污染源所在的区域。 首先研究每个江段中污染物浓度 C (mg/L) 的变化规律。由于题目中给出了污染物的降 解系数,附件 3 给出了每个月的污染物浓度、流量、流速等数据,若忽略污染物的局部扩散 (研究的是总体污染) ,在考虑固定时段(月)的污染物浓度时,可利用一般一维水质模型 的近似解 C = C 0 e
2008 A 题评阅要点 ............................................................................................................. 28 2008B 题 高等教育学费标准探讨 .................................................................................... 29
2009 B 题评阅要点 ............................................................................................................. 40
CUMCM-2009, A 题:第 1 页 / 共 42 页
2005A 题: 长江水质的评价和预测
水是人类赖以生存的资源,保护水资源就是保护我们自己,对于我国大江大河水资源 的保护和治理应是重中之重。专家们呼吁: “以人为本,建设文明和谐社会,改善人与自然 的环境,减少污染。 ” 长江是我国第一、世界第三大河流,长江水质的污染程度日趋严重,已引起了相关政府 部门和专家们的高度重视。2004 年 10 月,由全国政协与中国发展研究院联合组成“保护长 江万里行”考察团,从长江上游宜宾到下游上海,对沿线 21 个重点城市做了实地考察,揭 示了一幅长江污染的真实画面,其污染程度让人触目惊心。为此,专家们提出“若不及时拯 救,长江生态 10 年内将濒临崩溃” (附件1) ,并发出了“拿什么拯救癌变长江”的呼唤(附 件 2) 。 附件 3 给出了长江沿线 17 个观测站(地区)近两年多主要水质指标的检测数据,以及 干流上7个观测站近一年多的基本数据(站点距离、水流量和水流速) 。通常认为一个观测 站(地区)的水质污染主要来自于本地区的排污和上游的污水。一般说来,江河自身对污染 物都有一定的自然净化能力, 即污染物在水环境中通过物理降解、 化学降解和生物降解等使 水中污染物的浓度降低。反映江河自然净化能力的指标称为降解系数。事实上,长江干流的 自然净化能力可以认为是近似均匀的, 根据检测可知, 主要污染物高锰酸盐指数和氨氮的降 解系数通常介于 0.1~0.5 之间,比如可以考虑取 0.2 (单位:1/天)。附件 4 是“1995~2004 年 长江流域水质报告”给出的主要统计数据。下面的附表是国标(GB3838-2002) 给出的《地表 水环境质量标准》中 4 个主要项目标准限值,其中Ⅰ、Ⅱ、Ⅲ类为可饮用水。 请你们研究下列问题: (1)对长江近两年多的水质情况做出定量的综合评价,并分析各地区水质的污染 状况。 (2)研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪 些地区? (3)假如不采取更有效的治理措施,依照过去 10 年的主要统计数据,对长江未来水 质污染的发展趋势做出预测分析,比如研究未来 10 年的情况。 (4)根据你的预测分析,如果未来 10 年内每年都要求长江干流的Ⅳ类和Ⅴ类水的比 例控制在 20%以内,且没有劣Ⅴ类水,那么每年需要处理多少污水? (5)你对解决长江水质污染问题有什么切实可行的建议和意见。
2005高教社杯全国大学生数学建模竞赛题目

2005高教社杯全国大学生数学建模竞赛题目A题: 长江水质的评价和预测水是人类赖以生存的资源,保护水资源就是保护我们自己,对于我国大江大河水资源的保护和治理应是重中之重。
专家们呼吁:“以人为本,建设文明和谐社会,改善人与自然的环境,减少污染。
”长江是我国第一、世界第三大河流,长江水质的污染程度日趋严重,已引起了相关政府部门和专家们的高度重视。
2004年10月,由全国政协与中国发展研究院联合组成“保护长江万里行”考察团,从长江上游宜宾到下游上海,对沿线21个重点城市做了实地考察,揭示了一幅长江污染的真实画面,其污染程度让人触目惊心。
为此,专家们提出“若不及时拯救,长江生态10年内将濒临崩溃”(附件1),并发出了“拿什么拯救癌变长江”的呼唤(附件2)。
附件3给出了长江沿线17个观测站(地区)近两年多主要水质指标的检测数据,以及干流上7个观测站近一年多的基本数据(站点距离、水流量和水流速)。
通常认为一个观测站(地区)的水质污染主要来自于本地区的排污和上游的污水。
一般说来,江河自身对污染物都有一定的自然净化能力,即污染物在水环境中通过物理降解、化学降解和生物降解等使水中污染物的浓度降低。
反映江河自然净化能力的指标称为降解系数。
事实上,长江干流的自然净化能力可以认为是近似均匀的,根据检测可知,主要污染物高锰酸盐指数和氨氮的降解系数通常介于0.1~0.5之间,比如可以考虑取0.2(单位:1/天)。
附件4是“1995~2004年长江流域水质报告”给出的主要统计数据。
下面的附表是国标(GB3838-2002)给出的《地表水环境质量标准》中4个主要项目标准限值,其中Ⅰ、Ⅱ、Ⅲ类为可饮用水。
请你们研究下列问题:(1)对长江近两年多的水质情况做出定量的综合评价,并分析各地区水质的污染状况。
(2)研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪些地区?(3)假如不采取更有效的治理措施,依照过去10年的主要统计数据,对长江未来水质污染的发展趋势做出预测分析,比如研究未来10年的情况。
【全国大学生数学建模竞赛获奖优秀论文作品学习借鉴】长江水质的评价和预测

长江水质的评价和预测李云锋王勇...本文利用长江流域近两年多主要城市水质检测数据,通过对原始数据进行归一化综合处理,确定了水质新的综合评判指标函数ψ。
在对整个长江流域所有观测站的位置关系作一定的简化假设后,得到长江综合评定函数值ψ=0.4331,水质为良好。
主要污染物为氨氮。
通过建立污染浓度的反应扩散方程,本文用三种方法反演出未知的污染源强迫函数f(x,t),并对,(x,t)的三种数据加以综合分析,分别给出了高锰酸钾盐和氨氮污染源的主要分布地区。
为了对长江未来水质污染发展趋势进行预测,本文建立了回归分析模型并对回归系数进行了F检验,结果是如果不采取有效的治理措施。
长江可饮用水将逐年下降,且10年后可饮用水所占长江水总量的比例将不到50%。
根据这一预测结果,我们进而使用二元线性回归模型。
通过对各种不可饮用水进行综合考虑,得到如下结果:要在未来10年内使长江干流的不可饮用水(IV类和V类水)的比例控制在20%以内,且没有劣V 类水,那么每年污水处理量至少为75.195亿吨长江水质的评价和预测.pdf (370.52 KB)水质的评价和预测模型张震张超...本文首先考虑到水质类别的差异和相同类别水质在数量上的差异对综合评价的影响。
构造“S”形的变权函数,对属于不同水质类别的同种污染指标进行“动态加权”,建立基于逼近理想点排序法的评价模型和利用灰色关联度的分析方法。
对长江水质状况做出了综合评价:其次,根据7个观测站的位置将干流分成8段,把每段河道内所有污染源都等效为一个段中央的连续稳定源,分别利用稳态条件下的一维水质模型及质量守恒定律。
得出中间6段每个月的排污量,综合比较各河段一年多来的总排污量得到主要污染源的分布区域:然后,用每年不可饮用类水的百分比之和刻画水质状况。
综合利用灰色GM(1,1)模型和时间序列分析方法,对变化趋势进行了预测:最后,建立不可饮用类水的百分比与长江水总流量和废水排放量的线性回归模型,计算在满足约束条件下排污量的极限值,用排污量的预测值减去极限值,得到未来10年的污水处理量水质的评价和预测模型.pdf (283.07 KB)长江水质的评价预测模型谯程骏张东辉...本问题是一个对长江的水质进行综合评价、预测和控制的问题。
2005年A题全国数学建模优秀论文3

华南理工大学:李宁、董泽彦、林泽彬,指导教师:陶志穗
长江水质的评价和预测
摘 要
本文首先运用主成分分析法对长江流域主要城市水质检测报告进行分析, 选取主成 分,并把主成分得分按方差贡献率加权求和,得出每个地区的污染综合评价指数,进而 可以计算每个月长江流域的污染综合评价指数。 通过一维河流的稳态水质模型,确定干流上污染物的变化,计算出各地区主要污染 物的排放质量,确定高锰酸盐指数(CODMn)的主要污染源在湖南岳阳、湖北宜昌、江 苏南京、江西九江等地区;氨氮(NH3-N)的主要污染源在湖南岳阳、江西九江、湖北 宜昌等地区。 然后利用 GM(1,1)模型与 BP 神经网络模型联合完成对未来十年不同水质的河长比 例的预测,考虑到数据少,预测期长。如果使用神经网络模型进行预测效果很差,考虑 GM(1,1)模型在很少的数据下可得到较高的预测精度,因此首先使用 GM(1,1)模型对未 来十年的排污量进行预测,结果如下:单位 (亿吨) 年份 排污量 2005 289.9 2006 306.3 2007 323.6 2008 341.9 2009 361.2 2010 381.7 2011 403.2 2012 426.0 2013 450.1 2014 475.5
2005
年全国大学生数学建模竞赛全国一等奖
华南理工大学:李宁、董泽彦、林泽彬,指导教师:陶志穗
由表可看出,前三个主成分的累积贡献率已达到 96.67%,取控制参数 α =0.06(因为 28 个月中前三个成分贡献率最低为 94%),因此取前三个主成分对各地区水质进行综合评 价。 根据 R 的特征值的相应的正则化单位特征向量, 前三个主成分关于指标的线性组合 为 y1 = -0.0660x1 + 0.6715x2 + 0.5181x3 + 0.5257x4
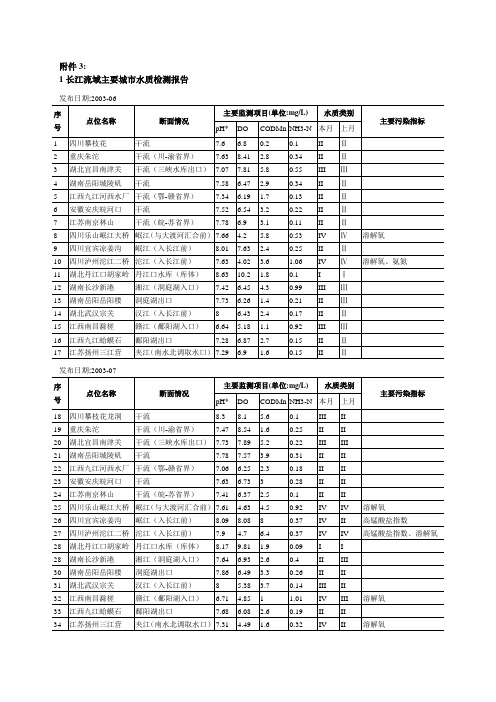
2005年数模竞赛A题长江水污染--附件3
7.55
10.6
3.6
0.36
II
II
55
湖南岳阳城陵矶
干流
7.93
8.36
3.1
0.3
II
III
56
江西九江河西水厂
干流(鄂-赣省界)
7.6
7.43
2.3
0.14
II
II
57
安徽安庆皖河口
干流
7.67
6.9
5
0.39
III
II
58
江苏南京林山
干流(皖-苏省界)
7.83
6.61
1.5
II
74
安徽安庆皖河口
干流
7.75
7.65
2.9
0.28
Ⅱ
III
75
江苏南京林山
干流(皖-苏省界)
7.73
6.89
1.9
0.16
Ⅱ
II
76
四川乐山岷江大桥
岷江(与大渡河汇合前)
7.97
5.82
5.7
0.76
Ⅲ
IV
77
四川宜宾凉姜沟
岷江(入长江前)
7.99
10.1
2.6
0.32
Ⅱ
II
78
四川泸州沱江二桥
6.41
8.7
1.33
Ⅳ
Ⅳ
高锰酸盐指数、氨氮
111
四川宜宾凉姜沟
岷江(入长江前)
7.46
10.6
3.2
1.66
Ⅴ
Ⅲ
氨氮
112
四川泸州沱江二桥
沱江(入长江前)
7.3
3.8
05竞赛题

水流速
3.7
1.9
0.8
0.9
1.1
1.1
1.2
04.06水流量 4010
14200 20300
22600 29500 32100 33100
水流速
3.9
2.1
1.2
1.3
1.5
1.5
1.6
04.07水流量 4660
16400 22700
24100 27000 31900 32100
水流速
0.6
0.7
0.7
0.8
05.02水流量 612
3603
4510
7980 10300 13700
15100
水流速
2.0
1.0
0.4
Байду номын сангаас
0.6
0.7
0.7
0.8
05.03水流量 623
4740
5180
7040 14300 21400
21500
水流速
1.9
0.9
0.4
0.6
0.8
0.8
0.9
05.04水流量 642
10四川泸州 沱江 7.63 4.02 3.6 1.06 IV Ⅳ 溶解氧、氨氮
11湖北丹江口 水库 8.63 10.2 1.8 0.1 I Ⅰ
12湖南长沙 湘江 7.42 6.45 4.3 0.99 III Ⅲ
13湖南岳阳 岳阳楼 7.73 6.26 1.4 0.21 II Ⅲ
14湖北武汉 汉江 8 6.43 2.4 0.17 II Ⅱ
通常认为一个观测站(地区)的水质污染主要来自于 本地区的排污和上游的污水。
一般说来,江河自身对污染物都有一定的自然净化能 力,即污染物在水环境中通过物理降解、化学降解和 生物降解等使水中污染物的浓度降低。
长江水质的评价和预测(2005年数学建模) 精品

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):长江水质的评价和预测摘要针对第一问首先对本题所给的数据进行分析,发现长江水质中各个污染物指标较多为了简化解题过程,比较简明地分析长江流域各个监测站水质情况,对长江流域整体水质作分析我们运用主成分分析法来减少变量,提取主成分,使其更容易得出这十七个观测站的总排名得出了江西、四川的一些地区污染比较严重。
对于第二问我们得出长江干流主要污染物CODMn和NH3-N的平均排放量第三问先运用灰色预测GM(1,1)来预测未来十年水污染的趋势,这是因为水质问题是一个复杂的非线性系统,但是由于数据样本少,需要预测的时间长。
由此我们得出未来十年长江的排污量。
第四问我们根据第三问得出的数据结合BP神经网络可以进一步算出每年需要处理的排污量。
关键词:主成分分析GM(1,1)BP神经网络问题重述作为中华民族最具象征性的的河流,长江哺育了灿烂悠久的中华文明,她是我国赖以生存的生命线,北方的干旱需要他的乳汁哺育因此有了南水北调,经济的发展所需的电力由她提供、因此有了三峡工程,可是就是这样一条对我们生存和发展都有重大影响的母亲河正在一步步走向没落---长江的污染程度日益加重,我们要积极对长江进行调查研究,通过科学的研究分析来拯救我们的生命线。
05A长江水质的评价和预测 真题分析

长江水质的评价和预测
分类
标准值
序
项目
号
Ⅰ类
Ⅱ类
Ⅲ类
Ⅳ类பைடு நூலகம்
Ⅴ类 劣Ⅴ类
7.5
1 溶解氧(DO) ≥
(或饱和率 6
他因此被评为首届“中国十大民间环保杰出人 物”、“2005中国最具影响力100人”之一,并被 联合国有关机构授予“全球生态和环保杰出成就 奖”,被中央主流媒体誉为“长江之子”。
2020/8/19
7
三、长江水质的评价与预测问题--
1.问题的背景与提出
章琦给中央有关部门撰写了长篇研究报告,发 表多篇保护长江的文章和做多场报告,促使成为 2005年两会关注的主题。
先后联系走访了单位和专家:
•中国研究院院长:章琦及其秘书;
•华东师大终身教授、博导、全国政协委员:
•中国环保局信息中心;
•水利部中国水环境研究院信息中心; •科学院水质研究所;
陆健健
•长江水利管理委员会信息中心;
•《长江年鉴》编辑部。
主要数据来源:
国家环保局网站:长江流域水质检测数据、
《长江年鉴》、长江流域相关网站等。
数学建模培训讲座 ----
长江水质的评价和预测
• 水是人类赖以生存的资源,保护水资源就是保护我们自己,对 于我国大江大河水资源的保护和治理应是重中之重。专家们呼 吁:“以人为本,建设文明和谐社会,改善人与自然的环境, 减少污染。”
• 长江是我国第一、世界第三大河流,长江水质的污染程度日趋 严重,已引起了相关政府部门和专家们的高度重视。2004年10 月,由全国政协与中国发展研究院联合组成“保护长江万里行” 考察团,从长江上游宜宾到下游上海,对沿线21个重点城市做 了实地考察,揭示了一幅长江污染的真实画面,其污染程度让 人触目惊心。为此,专家们提出“若不及时拯救,长江生态10 年内将濒临崩溃”(附件1),并发出了“拿什么拯救癌变长 江”的呼唤(附件2)。
2005A

关于2005年A题的感想一、做2005年A题的主要思路2005年全国数学建模竞赛A题是关于长江水质的评价和预测。
题目的4个附件给出了长江沿线17个观测站28个月的主要水质指标的检测数据(主要包括四个指标:PH值、氨氮含量、高锰酸盐含量以及含氧量),以及干流上7个观测站近一年多的基本数据(包括站点距离、水流量和水流速),此外还给出了“1995~2004年长江流域水质报告”给出的主要统计数据(主要是十年间不同类型水质的河长和百分比)。
要求解决的主要问题是对长江水质做出定量的评价;确定主要污染物的污染源;预测未来水质污染趋势;预测分析排污量。
那么分析题目可以确定主要问题是要做评价和预测两项工作。
首先,对于问题一附件4中给出了国家标准地表水的评价指标,先要明确水质有Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、劣Ⅴ共 6个类别,每一类对每一项指标都有相应的标准值(区间),只要有一项指标达到高类别标准就算是高类别的水质。
这是一个评价标准。
而Ⅰ、Ⅱ、Ⅲ类为可饮用水,Ⅳ、Ⅴ、劣Ⅴ类为不可饮用水,因此应该想到用归一法将两类水区分开。
另外,由于各项指标在各类别中的标准值(区间)差别很大,量纲也不同,评价时要先对各项指标的数据做标准化处理。
依据现有的四个水质指标的数据要评价水质我们有两种思考方向:一、主成分分析法提取主成分,并把主成分得分按方差贡献率加权求和,得出每个地区的污染综合评价指数,进而可以计算每个月长江流域的污染综合评价指数。
这种思想的好处是能够消除指标之间可能存在的相关性,以避免数据对结果的影响叠加造成误差,另外还可以确定不同的指标对水质影响的权重,避免了直接加权法和层次分析法过程中主观因素造成的误差;二、建立评价指标函数。
评价指标函数应当能够全面准确的描述水质。
首先可以查找资料,看有没有现成的水质评测函数。
其次就是要根据附件所给的四个指标(PH值、氨氮含量、高锰酸盐含量以及含氧量)分析权重建立合理的指标函数。
建立指标函数的过程应该系统科学。
高教社杯全国大学生数学建模竞赛长江水质的评价与预测

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛的题目是:长江水质的评价与预测我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):成都信息工程学院参赛队员(打印并签名) :1. 蒲存伟2. 严波3. 李玉辉指导教师或指导教师组负责人(打印并签名):方国敏日期: 2005 年 9 月 19 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):长江水质的评价与预测摘要本文是水质的评价、预测和污水处理的问题。
问题一,我们根据地表水环境质量标准,给出了以第III类水为基准的长江水质情况的综合评价指标,利用此指标对各个结点各年的观测数据进行了分析;问题二,利用微分方程,建立了在自然降解下的浓度关系式。
利用理论值与预测值之间的关系,确定了两个污染指标的重要污染源:(1)氨氮:湖南岳阳城陵矶、湖北宜昌南津关、重庆朱沱;(2)高锰酸盐:湖南岳阳城陵矶湖北宜昌南津关、江苏南京林山。
问题三,运用灰色预测理论中GM(1,1)模型,结合“新陈代谢”方法,预测出长江未来10年较精确的水质情况。
问题四,利用未来十年干流上各类水的百分比预测值,假设排出的废水为纯污染物,则可直接将废水按其要求的比例直接处理掉,其每年处理污水总量为:24.32,35.59,41.2,45.52,42.44,43.63,63.48,62.57,54.11,52.52亿吨。
2005年中国大学生数学建模竞赛论文(长江水质的评价和趋势分析模型)II.pdf

再根据排污量预测值,利用 BP 神经网络对未来十年的不同水质的河长比例进行了 预测。 为了得到排污量与各类水质的河长比例,本文再次利用 BP 神经网络的高精度逼近 能力对排污量与六类水质的河长比例的关系进行拟合。 从而可以得到每年控制污染所应 当处理的废水量:单位(亿吨) 年份 废水处理量 2005 58.2 2006 123.6 2007 133.3 2008 174.3 2009 163.0 2010 189.9 2011 245.4 2012 272.1 2013 300.5 2014 300.7
华南理工大学:李宁、董泽彦、林泽彬,指导教师:陶志穗
长江水质的评价和预测
摘 要
本文首先运用主成分分析法对长江流域主要城市水质检测报告进行分析, 选取主成 分,并把主成分得分按方差贡献率加权求和,得出每个地区的污染综合评价指数,进而 可以计算每个月长江流域的污染综合评价指数。 通过一维河流的稳态水质模型,确定干流上污染物的变化,计算出各地区主要污染 物的排放质量,确定高锰酸盐指数(CODMn)的主要污染源在湖南岳阳、湖北宜昌、江 苏南京、江西九江等地区;氨氮(NH3-N)的主要污染源在湖南岳阳、江西九江、湖北 宜昌等地区。 然后利用 GM(1,1)模型与 BP 神经网络模型联合完成对未来十年不同水质的河长比 例的预测,考虑到数据少,预测期长。如果使用神经网络模型进行预测效果很差,考虑 GM(1,1)模型在很少的数据下可得到较高的预测精度,因此首先使用 GM(1,1)模型对未 来十年的排污量进行预测,结果如下:单位 (亿吨) 年份 排污量 2005 289.9 2006 306.3 2007 323.6 2008 341.9 2009 361.2 2010 381.7 2011 403.2 2012 426.0 2013 450.1 2014 475.5
2005高教社杯全国大学生数学建模竞赛题目A题

单位:mg/L Ⅴ类 劣Ⅴ类
2
0
15
∞
2.0
∞
(注:附件1~4 位于压缩文件 A2005Data.rar 中, 可从 /mcm05/problems2005c.asp 下载)
附件 1: 专家称若不及时拯救,长江生态 10 年内将濒临崩溃 2004-11-13 00:36:55 来源: 南方网新闻中心
《新民周刊》:在“万里行”中,有没有让您特别感动的事情? 章琦:我们时间安排得特别紧,12 天行程万里,乘船坐车、跋山涉水,走了 21 个城市,这些城市不 是路过,每个都要看污水处理厂、听汇报。有时候晚上 12 点钟才能睡觉,清早 6 点钟就要起来了,连续 作战。但带队的全国政协人口资源环境委员会主任陈邦柱,70 岁高龄了还带头跑在前面,走到哪里都一定 要闻闻水的气味怎么样。 考察团走到南京时,有位 90 岁的老同志坐着轮椅来签名,他说:我此生的愿望就是保护长江。我没 有别的能力了,我只能签上我的名字。 10 月 22 日,“保护长江万里行”在终点站上海召开研讨会,全国政协副主席李贵鲜说:“你们一路辛 苦了,你们做了一件功在千秋的好事,我要向你们三鞠躬 。”这位老同志站起来向全体考察团成员深深地 鞠了三个躬,在场的人惊讶得鸦雀无声,继而爆发出热烈的掌声,当时感动得我几乎快要流泪了。 《新民周刊》:整个活动策划中您感到困难的事情是什么? 章琦:筹钱。活动开始之前,我们专门成立了一个筹资处,工作人员当时决心很大:保证筹到 50 万 启动资金,结果一分钱没筹到。我后来亲自出马花了两个月时间才解决这个大难题。仅谈谈保护长江大家 都觉得重要,真要拿钱都没人出声了。我到了江苏江阴一家很大的企业,它是靠着长江发财的,去年产值 100 亿,今年的产值要达到 200 亿,平时掏大笔的钱打高尔夫都是毛毛雨,但拿出几十万救长江都不干。 这是拔一毛以利天下而不为之!后来还是宝钢、武钢、鞍钢三家支持了我们 45 万。还有私营企业和平汽 车的老板周和平,他个人拿了 10 万。 《新民周刊》:“保护长江万里行”活动已经结束,您认为达到了预期构想吗? 章琦:我看到了希望,保护长江万里行的阶段性目标已经实现。我们第一步就是唤醒民众、领导干部 的环保意识。 下一步我们要求对保护长江立法,促成全国人大在明年全国两会期间进行讨论。一方面制定促进循环经济 发展的政策和法律法规;另一方面,还将建议加大对违法排污行为的处罚力度,要罚就应该罚到不法企业 破产,把对长江的生态环境的合理开发纳入沿江城市政府官员的政绩考核体系,对严重破坏生态环境并造 成生态恶果的地区,应执行官员任用的一票否决制。(新民周刊 记者张静)
2005全国大学生数学建模竞赛A题长江水质一等奖附程序

5.2.2 模型的求解 代入数据可以得到六个区段某一时刻污染物的排放量(单位:106mg/s)
区段 排污量 排名
站点 1~2 3.2215 6
站点 2~3 站点 3~4 站点 4~5
3.7932 7.6285 6.2992
5
1
2
表四:区段某一时刻 CODMn 的排放量
站点 5~6 4.0532 4
站点 6~7 4.8701 3
三、符号说明
x*(i, j, k)
x(i, j, k)
x综(i, j) h
di vi
si
ci
wi
fijk ,
f' ijk
aij , bij , cij ai'j , bi'j , ci'j
mk nk mk'
某地点某时间某一指标的原始数据 某地点某时间某一指标的标准化数据 某地点某时间的综合指标数据 主要污染物的降解系数 某一站点间区段的距离 某一站点的水流速 某一站点的水流量 某一站点的污染物浓度 某一站点间区段的排污量 某一类型某一年的ⅠⅡⅢ类水,ⅣⅤ类水的所占比例 ⅠⅡⅢ类水比例满足的回归方程的回归系数 ⅣⅤ类水比例满足的回归方程的回归系数 某年的废水总排放量 某年的长江总流量 在采取处理后保证水质比例的情况下某年的废水总排放量
4
(k)x(i, j, k)
x(i, j) k1 4
(k)
, (i 1 ~ 17, j 1 ~ 28)
k 1
5.1.2 模型的求解 1) 带入原始数据 x*(i, j, k) 可以得到 x综 (i, j) 的 17*28 矩阵: 2) 从时间上进行评价:
对数据按地点进行平均,得到污染物综合指标按时间的变化趋势如下:
2005年数学建模A题(长江污水治理)

i1
GB3838—2002 中的水质类别相对应)
YpHj „„„„„„„„„„„„„ pH 这种评价因子对 j 类水质标准的隶属度值
四、建立模型
问题一 对长江近两年多的水质情况做出定量的综合评价建立模型; 利用水质模糊综合评价方法得出函数,引入水质评价因子,隶属度函数 1.1 评价标准及水质评价因子 根据国家地表水环境质量标准( GB3838—2002) ,将水环境质量分为Ⅰ、Ⅱ、Ⅲ、
我们利用此次考察的长江沿线17个观测站(地区)近两年多主要水质指标的 检测数据,以及干流上7个观测站近一年多的基本数据(站点距离、水流量和水 流速)建立长江水质综合指标评估模型。根据国家《地表水环境质量标准》中的 规定得出各类水质的标准。
问题一:参考《基于GIS的水质模糊综合评价方法研究》[1]与《基于GIS的模 糊综合水质评价模型》[2]利用模糊变换原理和最大隶属度原则,考虑与被评价事 物相关的各个因素或主要因素,对其运用水质模糊综合评价方法,参照国《家地 表水环境质量标准(GB3838-2002)》,精确量化评价标准,建立每个测量值的 隶属度函数,进而建立起模糊综合评价的数学模型。该模型能够结合多个水质指 标,给出一个综合的评价结果,直接和中国地表水环境质量标准相对应,最后在电 子地图中我们还用不同的颜色表示水质级别,达到可视化效果。
Ⅳ、Ⅴ和劣Ⅴ类,其评价因子标准值见附表1。模型中用 Ai 、 Bi 、 Ci 、 Di 、 Ei 分
别为地表水环境质量标准中5类水质级别的第 i 种评价因子的标准值。 1.2 定义隶属度函数Yij
我们定义一个隶属度函数,用来表示评价因子对不同水质级别的隶属度值。水样
的第 i 项评价因子对第 j 项评价标准的隶属度函数可表示为下表
长江水质综合指标评估模型
全国数学建模 2005A 优秀论文

(溶解氧、高锰酸盐、氨氮和 PH 值)的实测值。为了较为贴切地反映出各地区水质的 污染状况,对四项监测项目分类统计,找出每个监测项目的最大值、最小值、平均值。 在此基础上,还应该确定出该地区的关键污染因子。所谓的关键污染因子就是指对 该地区的水质级别起着决定性作用的污染物。 如果四个监测项目中存在一个处于最高级 别的项目,那么该项目就是该地区的关键污染因子。但是,对于至少两个项目都处在较 高级别上的情况,就不好判断了。 并且,从《地表水环境质量标准》 (GB3838-2002 )可 以 看 出 ,水 质 的 类 别 是 根 据 4 个主要项目标准限值来判定的,并且哪个项目的类别最高,就将水质归为那一类。 因为水质从一个类别到下一个类别,中间经历了一个量变到质变的连续过渡过程,使得 这样的评价结果过于明确。 为了克服评价标准的边界过于明确和监测误差对评价结果的 影响,我们采用模糊数学法,找出各个监测项目在六个类别上的隶属度,由此确定每个 地区的关键污染因子。 2.1.2 长江水质的定量综合评价 由于 17 个观测站的数据在时间和空间上都是离散的,不能清晰地反映出长江水质 的整体情况。为了消除时间和地理的因素,我们通过对距离加权、在 28 个月上取算术 平均,得到长江全河段四项监测项目的均值,对照《地表水环境质量标准》 ,确定出主 要的污染物。 接下来,我们采用模糊判别法对长江近两年的水质做出科学合理的综合评价,反映 出长江水质在六个水质类别上的隶属关系和偏倚程度。 2.2 确定高锰酸盐和氨氮的污染源 一个观测站的水质污染主要来源于本地排污和上游的污水。 上游污水在流向下游的 过程中,由于河流自身的净化能力(污染物在水环境中通过物理降解、化学降解和生物 降解) ,污水中的高锰酸盐和氨氮的浓度不断降低,到下一个观测站时,是已经降解的 污水。反映江河自然净化能力的指标称为降解系数。根据降解系数的定义,可以建立高 锰酸盐和氨氮的降解函数来描述它们在流动过程中随时间的浓度变化。 在此基础上,为了找到污染源,就要确定长江干流上相邻两个观测站之间排放的污 染物浓度,进而确定污染带。第 i+1 个观测站处的溶质由第 i 个观测站处经过降解后的 溶质残留量、沿途注入的溶质和此观测站注入的溶质三部分组成。据此,可以建立降解 微分方程,进而分别得到相邻两个观测站之间注入的高锰酸盐和氨氮的质量,其中最大 者所对应的区段即为主要污染源。
2005年数学建模A题——长江水污染

长江水质的评价和预测摘 要:河流污染物浓度一维稳态衰减规律:uKxeC C -⋅=0对于点源,河水和污水的稀释混合方程为:Ep EE p p Q Q Q C Q C C +⋅+⋅=排污口允许纳污量(水环境容量)计算公式为:pp Ei ni p C C Q Q Q S W ⋅-+⋅=∑=)(1四川攀枝花、湖南岳阳和江苏扬州,这三个地区高锰酸盐的浓度常年比较高,是污染物高锰酸盐的主要排放地。
重庆朱沱、岳阳城陵矶、江苏扬州,这3个地区氨氮(NH3-N )的浓度常年比较高,是污染物氨氮(NH3-N )的主要排放地。
近几年来,长江流域水质的组成为Ⅰ类占总流域长度的2%、Ⅱ类水占总流域长度的27%、Ⅲ类水占总流域长度的39%、Ⅳ类水占总流域长度的15%、Ⅴ类水占总流域长度的7%、劣Ⅴ类水占总流域长度的10%。
其中Ⅰ类水由十年前的15%变化为目前的2%,呈减小趋势。
劣V 类水由3%变化为10%,呈增大趋势。
可饮用水在长江中的比例在逐年的变小,而Ⅳ类水以后的水在逐年的变大。
全干流域IV 类水、V 类水和劣V 类水所占百分比的预测模型分别为:IVF= 4.3-2.18* t + 0.06*t 2 +10.5* Ln(t) , VIF= 2.3 +0.5* t + 0.005* t 2 -1.14*Ln(t) , VIF= 2.3 +0.5* t + 0.005* t 2 -1.14*Ln(t) ,式中t 为时间(年)。
从1995年到2004年这10年间废水排放总量用最小二乘法数据模拟,可得变化规律为:QF =167.375+3.68* t +0.835* t 2 ,式中为t 时间(年)。
可预测今后10废水排放总量为:308.9,331.8,356.3,382.5,410.4,440.0,471.3,504.2,538.7,575.0亿吨。
如果未来10年内每年都要求长江干流的Ⅳ类和Ⅴ类水的比例控制在20%以内,且没有劣Ⅴ类水,每年需要在现有处理的基础增加污水处理数量:24,47,71,98,125,155,186,219,254,295亿吨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长江水质的评价和预测摘 要:河流污染物浓度一维稳态衰减规律:uKxeC C -⋅=0对于点源,河水和污水的稀释混合方程为:Ep EE p p Q Q Q C Q C C +⋅+⋅=排污口允许纳污量(水环境容量)计算公式为:pp Ei ni p C C Q Q Q S W ⋅-+⋅=∑=)(1四川攀枝花、湖南岳阳和江苏扬州,这三个地区高锰酸盐的浓度常年比较高,是污染物高锰酸盐的主要排放地。
重庆朱沱、岳阳城陵矶、江苏扬州,这3个地区氨氮(NH3-N )的浓度常年比较高,是污染物氨氮(NH3-N )的主要排放地。
近几年来,长江流域水质的组成为Ⅰ类占总流域长度的2%、Ⅱ类水占总流域长度的27%、Ⅲ类水占总流域长度的39%、Ⅳ类水占总流域长度的15%、Ⅴ类水占总流域长度的7%、劣Ⅴ类水占总流域长度的10%。
其中Ⅰ类水由十年前的15%变化为目前的2%,呈减小趋势。
劣V 类水由3%变化为10%,呈增大趋势。
可饮用水在长江中的比例在逐年的变小,而Ⅳ类水以后的水在逐年的变大。
全干流域IV 类水、V 类水和劣V 类水所占百分比的预测模型分别为:IVF= 4.3-2.18* t + 0.06*t 2 +10.5* Ln(t) , VIF= 2.3 +0.5* t + 0.005* t 2 -1.14*Ln(t) , VIF= 2.3 +0.5* t + 0.005* t 2 -1.14*Ln(t) ,式中t 为时间(年)。
从1995年到2004年这10年间废水排放总量用最小二乘法数据模拟,可得变化规律为:QF =167.375+3.68* t +0.835* t 2 ,式中为t 时间(年)。
可预测今后10废水排放总量为:308.9,331.8,356.3,382.5,410.4,440.0,471.3,504.2,538.7,575.0亿吨。
如果未来10年内每年都要求长江干流的Ⅳ类和Ⅴ类水的比例控制在20%以内,且没有劣Ⅴ类水,每年需要在现有处理的基础增加污水处理数量:24,47,71,98,125,155,186,219,254,295亿吨。
一:问题的提出A题: 长江水质的评价和预测水是人类赖以生存的资源,保护水资源就是保护我们自己,对于我国大江大河水资源的保护和治理应是重中之重。
专家们呼吁:“以人为本,建设文明和谐社会,改善人与自然的环境,减少污染。
”长江是我国第一、世界第三大河流,长江水质的污染程度日趋严重,已引起了相关政府部门和专家们的高度重视。
2004年10月,由全国政协与中国发展研究院联合组成“保护长江万里行”考察团,从长江上游宜宾到下游上海,对沿线21个重点城市做了实地考察,揭示了一幅长江污染的真实画面,其污染程度让人触目惊心。
为此,专家们提出“若不及时拯救,长江生态10年内将濒临崩溃”(附件1),并发出了“拿什么拯救癌变长江”的呼唤(附件2)。
附件3给出了长江沿线17个观测站(地区)近两年多主要水质指标的检测数据,以及干流上7个观测站近一年多的基本数据(站点距离、水流量和水流速)。
通常认为一个观测站(地区)的水质污染主要来自于本地区的排污和上游的污水。
一般说来,江河自身对污染物都有一定的自然净化能力,即污染物在水环境中通过物理降解、化学降解和生物降解等使水中污染物的浓度降低。
反映江河自然净化能力的指标称为降解系数。
事实上,长江干流的自然净化能力可以认为是近似均匀的,根据检测可知,主要污染物高锰酸盐指数和氨氮的降解系数通常介于0.1~0.5之间,比如可以考虑取0.2(单位:1/天)。
附件4是“1995~2004年长江流域水质报告”给出的主要统计数据。
下面的附表是国标(GB3838-2002)给出的《地表水环境质量标准》中4个主要项目标准限值,其中Ⅰ、Ⅱ、Ⅲ类为可饮用水。
请你们研究下列问题:(1)对长江近两年多的水质情况做出定量的综合评价,并分析各地区水质的污染状况。
(2)研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪些地区?(3)假如不采取更有效的治理措施,依照过去10年的主要统计数据,对长江未来水质污染的发展趋势做出预测分析,比如研究未来10年的情况。
(4)根据你的预测分析,如果未来10年内每年都要求长江干流的Ⅳ类和Ⅴ类水的比例控制在20%以内,且没有劣Ⅴ类水,那么每年需要处理多少污水? (5)你对解决长江水质污染问题有什么切实可行的建议和意见。
二、模型假设1.主要污染物高锰酸盐指数和氨氮的降解系数通常介于0.1~0.5之间,不考虑时期、温度等影响,取0.2 (单位:1/天); 2. 水流量和水流速以恒定值流动;3. 污染物在较短的时间内基本能混合均匀,即在排污口断面瞬时完成均匀混合; 4. 假定污染物浓度仅在河流纵向上发生变化,在横向和竖向的浓度梯度为零 5.增加和减少的水量只在河流上排污口、取水口、干支流汇合口等节点处发生;三、一维水质数学模型对于河流而言,一维模型假定污染物浓度仅在河流纵向上发生变化,主要适用于同时满足以下条件的河段:1)宽浅河段;2)污染物在较短的时间内基本能混合均匀;3)污染物浓度在断面横向方向变化不大,横向和垂向的污染物浓度梯度可以忽略。
如果污染物进入水域后,在一定范围内经过平流输移、纵向离散和横向混合后达到充分混合,或者根据水质管理的精度要求允许不考虑混合过程而假定在排污口断面瞬时完成均匀混合,即假定水体内在某一断面处或某一区域之外实现均匀混合,则不论水体属于江、河、湖、库的任一类,均可按一维问题概化计算条件。
在忽略离散作用时,描述河流污染物浓度一维稳态衰减规律的微分方程为:Kc dx dcu-=将dt dxu =代入,得到 Kcdt dc -=积分解得 uKxeC C -⋅=0式中:u 是河流断面平均流速,单位为m/s ; x 是沿程距离,单位为km ;K 是综合降解系数,单位为1/d ;C 是沿程污染物浓度,单位为mg/L ;C 0是前一个节点后污染物浓度,单位为mg/L 。
四、定常设计条件下河流稀释混合模型对于点源,河水和污水的稀释混合方程为:Ep EE p p Q Q Q C Q C C +⋅+⋅=式中:C ——完全混合的水质浓度(mg/L );Q p 、 C p ——上游来水设计水量(m 3/s )与设计水质浓度(mg/L );Q E 、 C E ——污水设计流量(m 3/s )与设计排放浓度(mg/L ); 由于污染源作用可线性迭加,多个污染源排放对控制点或控制断面的影响,等于各个污染源单个影响作用之和,符合线性迭加关系。
单点源计算可迭加使用,计算多点源条件。
单断面或单点约束条件,可根据节点平衡,递推多断面或多点约束条件。
对于可概化为完全均匀混合类的排污情况,排污口与控制断面之间水域的允许纳污量计算公式为:单点源排放:pp E p C C Q Q Q S W ⋅-+⋅=)(式中:W C ——水域允许纳污量(g/L);S ——控制断面水质标准(mg/L)多点源排放: pp Ei ni p C C Q Q Q S W ⋅-+⋅=∑=)(1式中:Q Ei ——第i 个排污口污水设计排放流量(m 3/s); n ——排污口个数。
五、水环境容量(1)河流概化污染物进入河流后,在一定范围内经过平流输移、纵向离散和横向混合后达到充分混合,或者根据水质管理的精度要求允许不考虑混合过程而假定在排污口断面瞬时完成均匀混合,可按一维问题概化计算条件,建立水质模型。
河流一维水质模型由河段和节点两部分组成,节点指河流上排污口、取水口、干支流汇合口等造成河道流量发生突变的点,水量与污染物在节点前后满足物质平衡规律(忽略混合过程中物质变化的化学和生物影响)。
河段指河流被节点分成的若干段,每个河段内污染物的自净规律符合一阶反应规律。
图 河流一维模型概化示意图上界j#k#如图4所示,假定功能区内有i 个节点,则将河流分成i +1个河段。
在节点处,要利用节点均匀混合模型进行节点前后的物质守恒分析,确定节点后的河段流量和污染物浓度。
节点后的河段要以节点平衡后的流量和污染物浓度为初始条件,按照一维降解规律计算到下一个节点前的污染物浓度。
(2)节点平衡方程。
考虑干流、支流、取水口、排污口均在同一节点的最复杂情况,水量平衡方程为:Q 干流混合后=Q 干流混合前+Q 支流+Q 排污口-Q 取水口污染物平衡方程为(忽略混合过程的不均匀性):取水口排污口支流干流混和前取水口取水口排污口排污口支流支流干流混和前干流混和前干流混合后=Q Q Q Q Q *C Q *C Q *C Q *C C ++++++(3)环境容量计算将 ji i Q Q Wi C C +=54.31/+代入模型,得到一维模型水环境容量的计算公式为:)(*)*(*54.31*4.86j i i uKx Q Q C eC Wi +-=式中:Wi ——第i 个排污口允许排放量,t/a ;C i ——河段第i 个节点处的水质本底浓度,mg/l ;C ——沿程浓度,mg/l ;Q i ——河道节点后流量,m 3/s ;Q j ——第i 节点处废水入河量,m 3/s ;u ——第i 个河段的设计流速,m/s ;x ——计算点到第i 节点的距离,m 。
若以下界处作为功能区考核的断面,按照上述方法沿程计算整个功能区的沿程污染物浓度变化规律,如图5所示。
若功能区要求是Ⅲ类,COD Ⅲ类标准是20mg/l ,则计算结果模拟结果显然超过Ⅲ类水质标准要求,就要通过削减每一个排污口的排污量来重新计算,直到计算结果满足水质标准要求为止。
这时各个排污口的排污量之和,即∑=ni WiW 就是此环境功能区内的一个水环境容量值。
六、模型计算6.1、对长江近两年多的水质情况做出定量的综合评价,并分析各地区水质的污染状况 主要污染物指标变化特征注:1、各地区各值的折线图形变化情况分为以下五种情况:①平稳,②上升,③下降,④波动(振幅较平缓),⑤振荡(振幅较剧烈);2、表中所列数为最小值和最大值;3、水质类别为本地区28个月汇总数据,数值越小水质越好;其中将Ⅰ类变为数字1,将Ⅱ类变为数字2,将Ⅲ类变为数字3,将Ⅳ类变为数字4,将Ⅴ类变为数字5,将劣Ⅴ类变为数字6,然后逐个相加而得。
由上述分析可得,长江水所受的污染在随时间而加剧,水值随时间而变坏。
所以,治理长江迫在眉捷!6.2 长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要地区 (1)、长江流域高锰酸盐(CODMn )浓度变化情况对长江沿线的十一个城市进行研究和分析,得到如上高锰酸盐(CODMn )浓度的变化情况图,它们分别表示在枯水期、平水期和丰水期高锰酸盐(CODMn )浓度随地域的不同而发生变化的情况。
由图可见,四川攀枝花、湖南岳阳和江苏扬州,这三个地区高锰酸盐的浓度常年比较高,是污染物高锰酸盐的主要排放地。
