前四章习题课
化工原理配套习题-4章部分答案

化工原理前四章的习题(概念题部分)答案发给你们,后面二章的题目同前几章一样,先自己做!期中考试总体考得不错,希望拿到这个后,同学们能认真比对,思考;以获得知识的强化,进而提升自己的知识面,及分析问题,解决问题的超强能力!因学校网络断网,又考虑恰逢五一小长假,故4日回校将电脑上存贮的这个文档发给你们研究一下,至上课时有疑问再讨论。
诚祝大家青年节快乐!第一章 流体流动一、选择题1. 连续操作时,物料衡算通式中的过程积累量G A 为( )。
BA.零B.正数C.负数D.任意值2. 热量衡算中,物料的焓为相对值,通常规定( )的焓为零。
AA.0℃液体B.0℃气体C.100℃液体D.100℃气体3. 流体阻力的表现,下列阐述错误的是( )。
DA.阻力越大,静压强下降就越大B.流体的粘度越大,阻力越大流体的流动状况是产生流体阻力的根本原因 D.流体的内摩擦力在流体激烈流动时不存在4. 压强的具有专门名称的国际单位是Pa ,用基本单位表示是( )。
AA.atmB.mmHgC.Kg/m.s2D.N/m25. 水在直管中流动,现保持流量不变,增大管径,则流速( )。
BA.增大B.减小C.不变D.无法判断6. 对可压缩流体,满足( ) 条件时,才能应用柏努力方程求解。
C A.)%(20p p p 121式中压强采用表压表示<- B. )%(01p p p 121式中压强采用表压表示<- C.)%(20p p p 121式中压强采用绝压表示<- D. )%(01p p p 121式中压强采用绝压表示<- 7. 判断流体的流动类型用( )准数。
CA.欧拉B.施伍德C.雷诺D.努塞尔特8. 流体在圆形直管中层流流动时的速度分布曲线为( )。
BA.直线B.抛物线C.双曲线D.椭圆线9. 增大流体的流量,则在孔板流量计的孔板前后形成的压强差( )。
AA.增大B.减小C.不变D.无法判断10. 流体在管内流动时的摩擦系数与( )有关。
自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3:KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7,. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数,(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数,试用解析法绘制出系
统的根轨迹,并判断点(-2+j0),(0+j1),
国际经济学课堂练习(前四章)

多选
五.根据H-O-S定理,国际贸易将会 ( ) 六.提高劳动力丰裕国家的劳动力价格
降低资本丰裕国的劳动力价格 提高劳动力丰裕国家的资本价格 降低资本丰裕国的资本价格 以上说法都对
多选
单击此处添加小标题
下列说法可以在一定程度上解释里昂惕夫之
谜的有 (
添加标题
古典国际贸易理论的政策主 张是
添加标题
保护贸易政策
添加标题
保护幼稚产业政策
添加标题
自由贸易政策
添加标题
战略性贸易政策
绝对技术差异论的提出者是
A、斯密
B、李嘉图
C、俄林
D、魁奈
01
单击此处添加小标题
亚当·斯密关于国际分工与国际贸易 学说的观点是
02
单击此处添加小标题
绝对优势论
03
单击此处添加小标题
)
单击此处添加小标题
美国实施的关税政策改变了贸易格局
单击此处添加小标题
资本包括有形的物质资本和无形的人力资本
单击此处添加小标题
自然资源的属性
单击此处添加小标题
现实中存在要素密集度逆转的情况
单击此处添加小标题
还应该考虑消费者的不同偏好
第四章练习题
单选
一.特定要素模型研究的是( ) 二.国际贸易的交换比例
单选
八.根据S-S定理,如果劳动密集型产品的 相对价格上升,劳动力的实际报酬将 ()
九.上升 不变 下降 上述说法都不准确
单选
九.根据H-O-S定理,国际贸易对相对要素 价格和绝对要素价格的影响是 ( )
一○.都无影响 都均衡化 绝对价格均等,相对价格不确定 相对要素价格均等,绝对价格不确定 上述说法都不正确
小学教育心理学第4章学习动机课后习题及答案

第四章学习动机1.什么是学习动机?学习动机构成因素有哪些?参考答案:学习动机是一种内部启动机制,它激发个体进行学习活动,维持已引起的学习活动,并使个体的学习活动朝向一定的学习目标前进。
动机可以分为两部分:内在动机和外在动机,二者结合起来才能产生行为动力。
内在动机是需要,外在动机是诱因。
2.强化动机理论的主要观点是什么?参考答案:强化动机理论是由联结主义心理学家提出来的,他们认为人的学习行为倾向完全取决于某种行为与刺激因强化而建立的稳固关系,受到强化的行为比没强化的行为更倾向于再次出现,因此,不断强化可以使这种联结得到加强和巩固。
任何能够提高一个特定反应出现概率的事物都是强化。
强化动机理论强调外部动机的作用,认为表扬、奖励、批评、惩罚等教育手段对激发学生的学习动机有关键作用。
3.什么是自我效能感?影响自我效能感的因素有哪些?参考答案:自我效能感是美国社会心理学家班杜拉提出的一个概念,是指个体对自己的能力是否胜任一项任务的主观感受。
影响个体自我效能感的因素主要有四种:(1)个体的成败经验;(2)替代性经验;(3)言语劝说;(4)情绪唤醒。
4.举例说明如何激发小学生的学习动机?参考答案:利用多种手段,激发学生的内部学习动机;(1)创设问题情境,实施启发式教学;(2)根据作业难度,恰当控制动机水平;(3)适当进行归因训练,培养自我效能感。
巧妙设计教学,激发学生的求知欲。
利用评定、奖惩、竞赛等手段激发学生的外部学习动机。
5.考试过后,面对考试成绩单上的分数,小学生议论纷纷。
A:“这次考试题太难了,所以我没有考好。
”B:“考题倒是不难,但我的运气太差,我复习好的部分没有考。
”C:“根本用不着复习,我只要稍稍用心就会考得很好。
”D:“教室里太乱,复习不下去。
”E:“我有些考试焦虑,一到考场就紧张。
”F:“我是天生的‘榆木脑袋’,再怎么努力也无济于事。
”根据维纳的归因理论分析学生A、B、C、D、E、F的归因特点,并说明他们的归因方式对未来学习产生的影响。
数学人教版(2024)七年级上册 第四章 整式的加减 习题课件 4.2 整式的加法与减法(1)

分层检测
A基础
7. 下列各组式子为同类项的是( D
)
A. abc 与 ab
B. 3 x 与3 x2
C. 3 xy2与4 x2 y
D. x2 y 与- yx2
8. 下面各组式子中,不是同类项的是( B )
A. -2与12
B. 2 m 与2 n
C. - a2 b 与 a2 b
D. - x2 y2与5 x2 y2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4.2
整式的加法与减法(1)
分层检测
9. 若- x3 ym 与3 xny 是同类项,则 m + n 的值为( D
A. 1
B. 2
C. 3
)
D. 4
10. 下列计算正确的是( C )
A. 8 x +4=12 x
B. 4 y -4= y
C. 4 y -3 y = y
A. a2 b 与 ab2
B. 3 xy2与-5 y2 x
C. - a2与3 a
D. 0.5 a 与0.5 b
2. 下列各组式子中,不是同类项的是( B )
A. 3 x2 y 与-2 yx2
B. 2 ab2与- ba2
C. 与5 xy
3
D. 100与-20
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. 合并同类项:
(1) a2-2 a +4 a2-7 a ;
5 a2-9 a
(2)4 ab -3 ab2+5+8 ab2-7-4 ab ;
第4章_习题课-电子衍射花样标定 (1)

放大倍数K,K=Lλ
Rd L 电子衍射基本公式
晶带定律描述了晶带轴指数[uvw]与该晶带内所 有晶面指数(hkl)之间的关系。
晶带定律 hu kv lw 0
零层倒易面:通过倒易原点且垂直于某一晶带轴的二 维倒易平面。用(uvw)0* 表示。
111
//
110
例2. Mg2SiO4 a=4.67, b=10.2, c=5.99
k = 2.15mm.nm
Ri di
4.3 5 8.8 2.44 8.8 2.44 10.5 2.05
80o 25o
di hkl
0.5 020 0.244 112 0.244 112 0.205 132
[011]γ
022γ 111γ
-111γ 000
1 1 1 1 11
0 2 20 2 2 0 -2 2
复合斑点
[011]γ
[001- ]α
022γ
1- 11γ 011 // 001
111γ
110α
000
020α
1-10α
011 // 001
五. 结构消光规律
衍射束的强度I(hkl) 和结构因素F(hkl)有关,
即 I (hkl) ∝∣F (hkl)∣2
F (hkl)表示晶体中单位晶胞内所有原子的 散射波在(hkl)晶面衍射束方向上的振幅之
和。
F (hkl)=0 叫结构消光
N
F(hkl) f j exp[ 2i(hx j kyj lz j )] j 1
2d sin n
d 为衍射晶面间距。 λ为入射电子束的波长。 θ为入射束与衍射晶面之间的夹角。 n为衍射级数(n = 0, 1, 2, 3 ……), 当 n=0就是透射束,与入射束平行。
第2~4章 习题课

解:反应活性为 C > D > A > B ② 将下列烯烃与浓H2SO4反应活性大小排列成序是: 将下列烯烃与浓H 反应活性大小排列成序是: A. CH3CH2-CH=CH2 C. CH2=CH2 B. CH3-CH=CH-CH3 CH=CHD. (CH3)2C=CH2
解:反应活性为 D > B > A > C
六、鉴别题
要求: 要求:
① 方法简单 ② 反应速度快 ③ 现象明显 ④ 简明扼要
P105P105-9- ① 2-甲基丁烷 3-甲基-1-丁烯 甲基3-甲基-1-丁炔 甲基(-) (-) ( + ) 白↓
Br2 / CCl4
Ag(NH3)2NO2
(-) ( + ) 褪色
命名步骤 1. 根据化合物中所含官能团的情况,确定好母体。 根据化合物中所含官能团的情况,确定好母体。 官能团的情况 2. 选取含母体官能团的最长的碳链作为主链。 选取含母体官能团 最长的碳链作为主链。 母体官能团的 的碳链作为主链 当具有相同长度的碳链可作为主链时, (当具有相同长度的碳链可作为主链时,应选择具 有支链最多的碳链作为主链; 有支链最多的碳链作为主链;当主链的长度和支链 数目相同时,应遵循最低系列原则。) 数目相同时,应遵循最低系列原则。) 3. 编号从离母体官能团最近的一端开始,如果母体 编号从离母体官能团最近的一端开始, 支链的一端开始 官能团位于中间, 从靠近支链的一端开始, 官能团位于中间,就从靠近支链的一端开始,尽可 能使取代基具有最低编号 最低编号。 能使取代基具有最低编号。 4. “先小后大,同基合并” 先小后大,同基合并” 烃基大小的次序(大取代基为“较优”基团) 烃基大小的次序(大取代基为“较优”基团): 甲基<乙基<丙基<丁基<戊基<己基<异戊基< 甲基<乙基<丙基<丁基<戊基<己基<异戊基< 异丁基< 异丁基<异丙基
完整版一到四章《环境化学》(戴树桂_第二版)课后习题解答..

《环境化学》(戴树桂第二版)课后部分习题解答第一章绪论4、根据环境化学的任务、内容和特点以及发展动向,你认为怎样才能学好环境化学这门课?环境化学是一门研究有害化学物质在环境介质中的存在、化学特征、行为和效应及其控制的化学原理和方法的科学。
环境化学以化学物质在环境中出现而引起环境问题为研究对象,以解决环境问题为目标的一门新型科学。
其内容主要涉及:有害物质在环境介质中存在的浓度水平和形态,潜在有害物质的来源,他们在个别环境介质中和不同介质间的环境化学行为;有害物质对环境和生态系统以及人体健康产生效用的机制和风险性;有害物质已造成影响的缓解和消除以及防止产生危害的方法和途径。
环境化学的特点是要从微观的原子、分子水平上来研究宏观的环境现象与变化的化学机制及其防治途径,其核心是研究化学污染物在环境中的化学转化和效应。
目前,国界上较为重视元素(尤其是碳、氮、硫和磷)的生物地球化学循环及其相互偶合的研究;重视化学品安全评价、臭氧层破坏、气候变暖等全球变化问题。
当前我国优先考虑的环境问题中与环境化学密切相关的是:以有机物污染为主的水质污染、以大气颗粒物和二氧化硫为主的城市空气污染;工业有毒有害废物和城市垃圾对水题和土壤的污染。
5、环境污染物有哪些类别?主要的化学污染物有哪些?按环境要素可分为:大气污染物、水体污染物和工业污染物。
按污染物的形态可分为:气态污染物、液态污染物和固体污染物;按污染物的性质可分为:化学污染物、物理污染物和生物污染物。
主要化学污染物有:1.元素:如铅、镉、准金属等。
2.无机物:氧化物、一氧化碳、卤化氢、卤素化合物等3.有机化合物及烃类:烷烃、不饱和脂肪烃、芳香烃、PAH等;4.金属有机和准金属有机化合物:如,四乙基铅、二苯基铬、二甲基胂酸等;5.含氧有机化合物:如环氧乙烷、醚、醛、有机酸、酐、酚等;6.含氮有机化合物:胺、睛、硝基苯、三硝基甲苯、亚硝胺等;7.有机卤化物:四氯化碳、多氯联苯、氯代二噁瑛;8.有机硫化物:硫醇、二甲砜、硫酸二甲酯等;9.有机磷化合物:磷酸酯化合物、有机磷农药、有机磷军用毒气等。
第四章 分子轨道理论习题课

一、判断题
1、通过变分法计算得到的微观体系的能量总是大于真实基态能量。 通过变分法计算得到的微观体系的能量总是大于真实基态能量。
×
2、对于“分子轨道”的定义,正确的叙述是分子中单电子完全 对于“分子轨道”的定义, × 态函数(包括空间运动和自旋运动) 态函数(包括空间运动和自旋运动)。 3、 在 LCAO-MO 中,所谓对称性匹配就是指两个原子轨道同 × 号重叠。 号重叠。 两个能量不同的原子轨道线性组合成两个分子轨道。 4、两个能量不同的原子轨道线性组合成两个分子轨道。在能量 较低的分子轨道中,能量较低的原子轨道贡献较大;在能量较 较低的分子轨道中,能量较低的原子轨道贡献较大; 高的分子轨道中,能量较高的原子轨道贡献较大。 高的分子轨道中,能量较高的原子轨道贡献较大。 √ × 凡是成键轨道都具有中心对称性。 5、凡是成键轨道都具有中心对称性。 用紫外光照射某双原子分子, 使该分子电离出一个电子。 6、用紫外光照射某双原子分子, 使该分子电离出一个电子。 如果电子电离后该分子的核间距变短了, 如果电子电离后该分子的核间距变短了, 则表明该电子是从 × 上电离出的。 成键 MO 上电离出的。
3、基态C2为反磁性分子。试写出其电子组态并说明原因。 、基态 为反磁性分子。试写出其电子组态并说明原因。
4、CF和CF+的键能分别为 、 和 的键能分别为548kJ/mol和753kJ/mol。试用 解释。 和 。试用MOT解释。 解释 5、构成大π键的条件是什么?下列分子生成什么大 键? 、构成大 键的条件是什么 下列分子生成什么大π键 键的条件是什么? 醌、苯胺、尿素、丁二烯、苯乙烯、臭氧、三氟化硼、二氧化氮。 苯胺、尿素、丁二烯、苯乙烯、臭氧、三氟化硼、二氧化氮。 6、说明N3-的几何构型及成键情况;用HMO法求离域 键的离域能, 、说明 的几何构型及成键情况; 法求离域π键的离域能 法求离域 键的离域能, 并画出电子的能级分布图。 并画出电子的能级分布图。 7、分析H3C-CH2-Cl、CH2=CH-Cl、CH≡C-Cl分子中 、分析 分子中C-Cl键的键长 、 、 分子中 键的键长 次序,并说明原因。 次序,并说明原因。
苏教版选择性必修1——第4章 习题课 等差数列前n项和性质的综合问题

习题课 等差数列前n 项和性质的综合问题学习目标 1.掌握总项数为奇数项或偶数项时前n 项和的特点.2.掌握含绝对值的等差数列的前n 项和的求法.一、等差数列中奇、偶项的和问题1 我们知道等差数列前n 项和公式中的n 表示等差数列的项数,你能利用公式表示S 2n ,S 2n -1吗?提示 S 2n =2n (a 1+a 2n )2=n (a 1+a 2n ),S 2n -1=(2n -1)(a 1+a 2n -1)2,由等差数列的性质m +n =p+q ⇒a m +a n =a p +a q 可知,a 1+a 2n =a n +a n +1,a 1+a 2n -1=2a n ,即S 2n =n (a n +a n +1),S 2n -1=(2n -1)a n ,发现总项数为偶数项时,其和可用中间两项表示,总项数为奇数项时,其和可用中间一项表示.问题2 当总项数为2n 项时,其奇数项和S 奇与偶数项和S 偶有何特点? 提示 S 奇=a 1+a 3+…+a 2n -1=n (a 1+a 2n -1)2=na n , S 偶=a 2+a 4+…+a 2n =n (a 2+a 2n )2=na n +1,则有S 偶-S 奇=na n +1-na n =n (a n +1-a n )=nd , S 偶S 奇=na n +1na n=a n +1a n .问题3 当总项数为2n -1项时,其奇数项和S 奇与偶数项和S 偶有何特点? 提示 S 奇=a 1+a 3+…+a 2n -1=n (a 1+a 2n -1)2=na n , S 偶=a 2+a 4+…+a 2n -2=(n -1)(a 2+a 2n -2)2=(n -1)a n ,则有S 奇-S 偶=a n ,S 奇S 偶=nn -1.知识梳理1.若等差数列{a n }的项数为2n ,则S 2n =n (a n +a n +1),S 偶-S 奇=nd ,S 偶S 奇=a n +1a n .2.若等差数列{a n }的项数为2n +1,则S 2n +1=(2n +1)·a n +1,S 偶-S 奇=-a n +1,S 偶S 奇=n n +1. 3.设两个等差数列{a n },{b n }的前n 项和分别为S n ,T n ,则a n b n =S 2n -1T 2n -1.注意点:(1)总项数为奇数时,其中间项的下标是1和总项数的平均数;(2)总项数为偶数时,其中间有两项,中间第一项的下标为总项数的一半.例1 (1)在等差数列{a n }中,S 10=120,且在这10项中,S 奇S 偶=1113,则公差d =________.答案 2 解析 由⎩⎪⎨⎪⎧S 奇+S 偶=120,S奇S偶=1113,得⎩⎪⎨⎪⎧S 奇=55,S 偶=65, 所以S 偶-S 奇=5d =10,所以d =2.(2)有两个等差数列{a n },{b n }满足a 1+a 2+a 3+…+a n b 1+b 2+b 3+…+b n =7n +2n +3,求a 5b 5.解 方法一 设等差数列{a n },{b n }的公差分别为d 1,d 2, 则a 1+a 2+a 3+…+a n b 1+b 2+b 3+…+b n =na 1+n (n -1)2d 1nb 1+n (n -1)2d 2=a 1+n -12d1b 1+n -12d2,则有a 1+n -12d1b 1+n -12d2=7n +2n +3,①又由于a 5b 5=a 1+4d 1b 1+4d 2,②观察①②,可在①中取n =9,得a 1+4d 1b 1+4d 2=7×9+29+3=6512.故a 5b 5=6512.方法二 设{a n },{b n }的前n 项和分别为A n ,B n , 则有A n B n =7n +2n +3,其中A n =(a 1+a n )n 2,由于a 1+a 9=2a 5.即a 1+a 92=a 5,故A 9=(a 1+a 9)·92=a 5×9.同理B 9=b 5×9. 故A 9B 9=a 5×9b 5×9. 故a 5b 5=A 9B 9=7×9+29+3=6512. 方法三 设{a n },{b n }的前n 项和分别为A n ,B n , 因为等差数列的前n 项和为S n =an 2+bn =an ⎝⎛⎭⎫n +b a , 根据已知,可令A n =(7n +2)kn ,B n =(n +3)kn (k ≠0). 所以a 5=A 5-A 4=(7×5+2)k ×5-(7×4+2)k ×4=65k , b 5=B 5-B 4=(5+3)k ×5-(4+3)k ×4=12k . 所以a 5b 5=65k 12k =6512.方法四 设{a n },{b n }的前n 项和分别为A n ,B n ,由A 2n -1B 2n -1=a n b n ,有a 5b 5=A 9B 9=7×9+29+3=6512.反思感悟 一般地,求等差数列奇、偶项的和需注意:如果已知和,能判断它的中间项是哪一项或哪两项;如果已知某一项或某两项,能判断它是多少项和的中间项.跟踪训练1 (1)等差数列共有2n +1项,所有奇数项之和为132,所有偶数项之和为120,则n 等于( )A .6B .8C .10D .12 答案 C解析 ∵S 奇=a 1+a 3+…+a 2n +1=132,S 偶=a 2+a 4+…+a 2n =120, ∴S 奇-S 偶=a 2n +1-nd =a n +1=12, ∴S 2n +1=S 奇+S 偶=252=()2n +1()a 1+a 2n +12=()2n +1an +1=12()2n +1,解得n =10.(2)已知数列{a n }是项数为偶数的等差数列,它的奇数项的和是50,偶数项的和为34,若它的末项比首项小28,则该数列的公差是________. 答案 -4解析 设等差数列{a n }的项数为2m , ∵末项与首项的差为-28, ∴a 2m -a 1=(2m -1)d =-28,① ∵S 奇=50,S 偶=34,∴S 偶-S 奇=34-50=-16=md ,② 由①②得d =-4.(3)若等差数列{}a n ,{}b n 的前n 项和分别为S n ,T n ,a n b n =n +1n ,则S 9T 9=________.答案 65解析 由等差数列前奇数项和性质,得S 9T 9=9a 59b 5=a 5b 5=5+15=65.二、含绝对值的等差数列的前n 项和问题4 已知等差数列a n =2n -9,求{|a n |}的前n 项和. 提示 设{a n }的前n 项和为S n ,{|a n |}的前n 项和为T n . 则当n ≤4时,T n =-S n =-n 2+8n ,当n ≥5时,T n =(-a 1)+(-a 2)+(-a 3)+(-a 4)+a 5+a 6+…+a n =-S 4+(S n -S 4)=S n -2S 4=n 2-8n +32.∴T n =⎩⎪⎨⎪⎧-n 2+8n ,n ≤4,n 2-8n +32,n ≥5.知识梳理1.若一个等差数列a 1<0,d >0,且a k ≤0,a k +1>0,则其绝对值的前n 项和为T n =⎩⎪⎨⎪⎧-S n ,1≤n ≤k ,S n -2S k ,n >k ,n ∈N *. 2.若一个等差数列a 1>0,d <0,且a k ≥0,a k +1<0,则其绝对值的前n 项和为T n =⎩⎪⎨⎪⎧S n ,1≤n ≤k ,-S n +2S k ,n >k ,n ∈N *. 注意点:(1)要先去掉绝对值才能求和;(2)找准分界点是解决此类问题的关键.例2 数列{a n }的前n 项和S n =100n -n 2(n ∈N *). (1)判断{a n }是不是等差数列,若是,求其首项、公差; (2)设b n =|a n |,求数列{b n }的前n 项和T n . 解 (1)当n ≥2时,a n =S n -S n -1=(100n -n 2)-[100(n -1)-(n -1)2]=101-2n . ∵a 1=S 1=100×1-12=99,满足上式, ∴a n =101-2n (n ∈N *). 又a n +1-a n =-2为常数,∴数列{a n }是首项为99,公差为-2的等差数列. (2)令a n =101-2n ≥0,得n ≤50.5, ∵n ∈N *,∴n ≤50(n ∈N *).①当1≤n ≤50时,a n >0,此时b n =|a n |=a n , ∴数列{b n }的前n 项和T n =100n -n 2. ②当n ≥51时,a n <0,此时b n =|a n |=-a n , 由b 51+b 52+…+b n =-(a 51+a 52+…+a n ) =-(S n -S 50)=S 50-S n ,得数列{b n }的前n 项和T n =S 50+(S 50-S n )=2S 50-S n =2×2 500-(100n -n 2)=5 000-100n +n 2.由①②得数列{b n }的前n 项和为T n =⎩⎪⎨⎪⎧100n -n 2,1≤n ≤50,5 000-100n +n 2,n ≥51,n ∈N *.延伸探究 本例中若a n =2n -101,求数列{b n }的前n 项和. 解 由本例可知,当1≤n ≤50时,a n <0,此时b n =-a n , 数列{}b n 的前n 项和T n =-n 2+100n ,当n ≥51时,a n >0,b 51+b 52+…+b n =a 51+a 52+…+a n . 数列{}b n 的前n 项和T n =-S 50+S n -S 50=n 2-100n +5 000,综上,T n =⎩⎪⎨⎪⎧-n 2+100n ,1≤n ≤50,n 2-100n +5 000,n ≥51,n ∈N *.反思感悟 已知等差数列{a n },求绝对值数列{|a n |}的有关问题是一种常见的题型,解决此类问题的核心便是去掉绝对值,此时应从其通项公式入手,分析哪些项是正的,哪些项是负的,即找出正、负项的“分界点”.跟踪训练2 在等差数列{a n }中,a 10=23,a 25=-22. (1)数列{a n }前多少项和最大? (2)求{|a n |}的前n 项和S n .解 (1)由⎩⎪⎨⎪⎧ a 1+9d =23,a 1+24d =-22,得⎩⎪⎨⎪⎧a 1=50,d =-3,∴a n =a 1+(n -1)d =-3n +53.令a n >0,得n <533,∴当n ≤17时,a n >0;当n ≥18时,a n <0,∴数列{a n }的前17项和最大. (2)当n ≤17时,|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a n =na 1+n (n -1)2d =-32n 2+1032n .当n ≥18,n ∈N *时,|a 1|+|a 2|+…+|a n | =a 1+a 2+…+a 17-a 18-a 19-…-a n =2(a 1+a 2+…+a 17)-(a 1+a 2+…+a n ) =2⎝⎛⎭⎫-32×172+1032×17-⎝⎛⎭⎫-32n 2+1032n =32n 2-1032n +884. ∴S n=⎩⎨⎧-32n 2+1032n ,n ≤17,n ∈N *,32n 2-1032n +884,n ≥18,n ∈N *.1.知识清单:(1)等差数列中奇、偶项的和. (2)含绝对值的等差数列的前n 项和.2.方法归纳:公式法、整体代换法、分类讨论法.3.常见误区:求数列{|a n |}的前n 项和时不讨论,最后不用分段函数表示.1.一个等差数列共有10项,其偶数项之和是15,奇数项之和是12.5,则它的首项与公差分别是( ) A .0.5,0.5 B .0.5,1 C .0.5,2 D .1,0.5答案 A解析 由于项数为10,故S 偶-S 奇=15-12.5=5d , ∴d =0.5,由15+12.5=10a 1+10×92×0.5,得a 1=0.5.2.设S n 是等差数列{a n }的前n 项和,若a 5a 3=59,则S 9S 5等于( )A .1B .-1C .2 D.12答案 A解析 由于S 2n -1=(2n -1)a n , 则S 9S 5=9a 55a 3=95×59=1. 3.设等差数列{a n }的前n 项和为S n ,n ∈N *.若S 12>0,S 13<0,则数列{|a n |}的最小项是( ) A .第6项 B .第7项 C .第12项 D .第13项 答案 B解析 由题意得,S 12>0,S 13<0及S 12=6(a 1+a 12)=6(a 6+a 7),S 13=13a 7,得a 6+a 7>0,a 7<0,所以a 6>0,a 6>|a 7|,且公差d <0,所以|a 7|最小.4.记S n 为等差数列{}a n 的前n 项和,已知a 1=-9,S 5=-25,b n =||a n ,{}b n 的前n 项和为T n ,则T 10=________. 答案 50解析 设等差数列{}a n 的公差为d ,∵a 1=-9,S 5=-25.∴-9×5+5×42×d =-25,解得d =2.∴a n =-9+2(n -1)=2n -11. ∵b n =||a n ,所以b n =||2n -11,∴T 10=||-9+||-7+||-5+||-3+||-1+1+3+5+7+9=2()1+3+5+7+9=50.课时对点练1.在等差数列{}a n 中,a 2+a 4+a 6=-3,a 3+a 5+a 7=6,则{}a n 的前8项的和为( ) A .3 B .4 C .5 D .6 答案 B解析 由等差中项的性质可知a 2+a 4+a 6=3a 4=-3,所以a 4=-1,同理a 5=2,所以a 4+a 5=1,S 8=4(a 4+a 5)=4.2.已知等差数列{}a n 的前n 项和为S n ,2()a 1+a 3+a 5+3()a 8+a 10=60,则S 11的值为( ) A .33 B .44 C .55 D .66 答案 C解析 ∵S n 是等差数列{}a n 的前n 项和, 2()a 1+a 3+a 5+3()a 8+a 10=60,∴2()a 1+a 1+2d +a 1+4d +3()a 1+7d +a 1+9d =60,解得a 1+5d =5,∴a 6=5,∴S 11=112()a 1+a 11=112×2a 6=11a 6=55. 3.等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若a n b n =2n 3n +1,则S 21T 21的值为( )A.1315B.2335C.1117D.49 答案 C解析 S 21T 21=21(a 1+a 21)2÷21(b 1+b 21)2=a 1+a 21b 1+b 21=a 11b 11=2×113×11+1=1117.4.已知等差数列{}a n 的通项公式为a n =5-n ,则||a 1+||a 2+…+||a 10等于( )A .24B .25C .26D .27 答案 B解析 因为a n =5-n ,所以当n ≤5时,a n ≥0,当n ≥6时,a n <0; 因此||a 1+||a 2+…+||a 10=()a 1+a 2+a 3+a 4+a 5-()a 6+a 7+a 8+a 9+a 10 =()4+3+2+1+0+()1+2+3+4+5=10+15=25.5.设等差数列{}a n 和{}b n 的前n 项和分别为S n 和T n ,且S n T n =3n -t 5n +3,若a 7b 3+b 11=14,则t 等于( )A .5B .6C .22 D.512答案 A解析 由题意可得a 7=S 1313,b 3+b 11=2b 7=2T 1313,则a 7b 3+b 11=S 132T 13=3×13-t 2×()5×13+3=14,解得t =5.6.(多选)设等差数列{a n }的前n 项和为S n (n ∈N *),当首项a 1和公差d 变化时,若a 1+a 8+a 15是定值,则下列各项中为定值的是( ) A .a 7 B .a 8 C .S 15 D .S 16 答案 BC解析 由于a 1+a 15=2a 8,故a 1+a 8+a 15是定值可得a 8是定值,S 15=12×15×(a 1+a 15)=15a 8,故S 15为定值.7.设项数为奇数的等差数列,奇数项之和为44,偶数项之和为33,则这个数列的中间项是________,项数是________. 答案 11 7解析 设等差数列{a n }的项数为2n +1(n ∈N *), S 奇=a 1+a 3+…+a 2n +1 =(n +1)(a 1+a 2n +1)2=(n +1)a n +1,S 偶=a 2+a 4+a 6+…+a 2n =n (a 2+a 2n )2=na n +1,所以S 奇S 偶=n +1n =4433,解得n =3,所以项数2n +1=7,S 奇-S 偶=a n +1, 即a 4=44-33=11,为所求的中间项.8.已知在等差数列{a n }中,公差d =1,且前100项和为148,则前100项中的所有偶数项的和为________. 答案 99解析 由题意,得S 奇+S 偶=148, S 偶-S 奇=50d =50, 解得S 偶=99.9.设等差数列{a n }的前n 项和为S n ,已知a 3=12,且S 12>0,S 13<0. (1)求公差d 的取值范围;(2)问前几项的和最大,并说明理由. 解 (1)∵a 3=12,∴a 1=12-2d . ∵S 12>0,S 13<0,∴⎩⎪⎨⎪⎧ 12a 1+66d >0,13a 1+78d <0,即⎩⎪⎨⎪⎧24+7d >0,3+d <0,∴-247<d <-3.即d 的取值范围为⎝⎛⎭⎫-247,-3. (2)∵S 12>0,S 13<0,∴⎩⎪⎨⎪⎧ a 1+a 12>0,a 1+a 13<0,∴⎩⎪⎨⎪⎧a 6+a 7>0,a 7<0,∴a 6>0, 又由(1)知d <0.∴数列前6项为正,从第7项起为负. ∴数列前6项和最大.10.在数列{a n }中,a 1=8,a 4=2,且满足a n +2-2a n +1+a n =0(n ∈N *).(1)求数列{a n }的通项公式;(2)设T n =|a 1|+|a 2|+…+|a n |,求T n .解 (1)∵a n +2-2a n +1+a n =0,∴a n +2-a n +1=a n +1-a n ,∴{a n }是等差数列,又∵a 1=8,a 4=2,∴d =-2,a n =a 1+(n -1)d =10-2n ,n ∈N *.(2)设数列{a n }的前n 项和为S n ,则S n =8n +n (n -1)2×(-2)=9n -n 2.∵a n =10-2n ,令a n =0,得n =5.当n >5时,a n <0;当n =5时,a n =0;当n <5时,a n >0.∴当n ≤5时,T n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a n =9n -n 2.当n >5时,T n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a 5-(a 6+a 7+…+a n )=S 5-(S n -S 5)=2S 5-S n=2×(9×5-25)-9n +n 2=n 2-9n +40,∴T n =⎩⎪⎨⎪⎧ 9n -n 2,n ≤5,n ∈N *,n 2-9n +40,n ≥6,n ∈N *.11.若数列{a n }的前n 项和是S n =n 2-4n +2,则|a 1|+|a 2|+…+|a 10|等于() A .15 B .35 C .66 D .100答案 C解析 易得a n =⎩⎪⎨⎪⎧-1,n =1,2n -5,n ≥2.|a 1|=1,|a 2|=1,|a 3|=1,令a n >0,则2n -5>0,∴n ≥3.∴|a 1|+|a 2|+…+|a 10|=1+1+a 3+…+a 10=2+(S 10-S 2)=2+[(102-4×10+2)-(22-4×2+2)]=66.12.已知等差数列{}a n 和{}b n 的前n 项和分别为S n 和T n ,且满足S n T n =2n +13n +2,则a 6b 4等于( ) A.32 B.23 C.1314D .1 答案 D解析 由题意,令S n =kn (2n +1),T n =kn (3n +2),∴a 6b 4=S 6-S 5T 4-T 3=78k -55k 56k -33k=1. 13.已知S n ,T n 分别是等差数列{a n },{b n }的前n 项和,且S n T n =2n +14n -2(n ∈N *),则a 10b 3+b 18+a 11b 6+b 15=________.答案 4178 解析 因为b 3+b 18=b 6+b 15=b 10+b 11,所以a 10b 3+b 18+a 11b 6+b 15=a 10+a 11b 10+b 11=10(a 10+a 11)10(b 10+b 11)=S 20T 20=2×20+14×20-2=4178. 14.已知一个有11项且各项都不为零的等差数列,那么其奇数项的和与偶数项的和之比为________.答案 65解析 由题意,得等差数列共有11项,所以奇数项的和为S 奇=6(a 1+a 11)2=6a 6,其偶数项的和为S 偶=5(a 2+a 10)2=5a 6, 所以其奇数项的和与偶数项的和之比为65.15.《九章算术》是人类科学史上应用数学的最早巅峰,书中有如下问题:“今有女子善织,日益功疾,初日织六尺,今一月织十一匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织6尺,一月织了十一匹三丈,问每天增加多少尺布?”若一个月按30天算,记该女子一个月中的第n 天所织布的尺数为a n ,则a 1+a 3+…+a 29a 2+a 4+…+a 30的值为( ) A.1415 B.1617 C.2324 D.23答案 C解析 由题意,得数列{}a n 为等差数列,a 1=6,S 30=11×40+3×10=470,设数列{}a n 的公差为d ,由等差数列前n 项和公式,得S 30=30×6+30×()30-12d =470,解得d =23, 所以a n =6+()n -1×23=23n +163, a 1+a 3+…+a 29=()a 1+a 29×152=15a 15,a 2+a 4+…+a 30=()a 2+a 30×152=15a 16,所以a 1+a 3+…+a 29a 2+a 4+…+a 30=a 15a 16=23×15+16323×16+163=2324. 16.已知数列{}a n 的首项a 1=1,前n 项和为S n ,且数列⎩⎨⎧⎭⎬⎫S n n 是公差为2的等差数列. (1)求数列{}a n 的通项公式;(2)若b n =(-1)n a n ,求数列{}b n 的前n 项和T n .解 (1)因为数列⎩⎨⎧⎭⎬⎫S n n 是公差为2的等差数列,且S 11=a 1=1,所以S n n =1+()n -1×2=2n -1,所以S n =2n 2-n ,又因为a n =S n -S n -1()n ≥2,所以当n ≥2时,a n =S n -S n -1=4n -3, 又因为a 1=1符合n ≥2的情况,所以a n =4n -3.(2)因为b n =()-1n a n =()-1n()4n -3, 当n 为偶数时,T n =()-1+5+()-9+13+…+[-()4n -7]+()4n -3,所以T n =[()-1+5]+[()-9+13]+…+{[-(4n -7)]+(4n -3)}=4×n 2=2n , 当n 为奇数时,T n =T n -1+b n =2()n -1+[-(4n -3)]=1-2n , 综上可知,T n =⎩⎪⎨⎪⎧ 2n ,n 为偶数,1-2n ,n 为奇数.。
高等数学第四章不定积分习题课

xdx
de x
或 exdx d(ex 1) ,然后进行计算。 另外,由于
f
(x)
1 1 ex
中含有
1
e x,不能直接计算,可以考虑
换元 t ex 或 t 1 ex,然后再进行计算。
解法1:因为
1
ex
1 e x e x (1 e x )
所以
1
ex
二、基本计算方法
1.直接积分法 首先要对被积函数进行恒等变形,然后利用不定
积分的基本性质和基本积分表求出不定积分。
2.第一类换元法(凑微分法): 设 F(u) f (u) ,则
f ((x))(x)dx f ((x))d(x) F((x)) C
3.第二类换元法(变量置换法):
2
2
注意 运算中综合使用不同方法往往更有效.]。
【例12】 求不定积分
I
arcsin
x dx
x
分析:由于被积函数中含有根式 x ,所以首先要令
t x 把根式去掉,然后选择合适的方法计算。
另外,观察被积表达式的特点,由于
arcsin xdx arcsin x( dx ) 2arcsin xd( x )
2 dx 1 u2 du
2u sin x 1 u2
1 u2 cos x 1 u2
从而
2u 1 u2 2
R(sin x,cos x)dx
R( 1
u2
,
1
u2
)
1
u2
du
☆ 在具体计算不定积分的过程中,不是一种方法就可
以解决,要熟练掌握几种积分法并融会贯通,综合应用。
高等数学 同济六版 第四章 习题课(A).

I1,
从而,原式 sin x ex . C. 1 cos x
7/18
例3 求
ln( x 1 x2 ) 5 dx.
1 x2
解 d [ln( x 1 x2 ) 5]
1
(1 2x )dx
x 1 x2
2 1 x2
原式
dx , 1 x2
ln( x 1 x2 ) 5 d[ln( x 1 x2 ) 5]
2
2
1 [(1 x2 ) ln(1 x2 ) x2 ]arctan x
2
1
2
[ln(1
x2)
x2 1 x2
]dx
.
12/18
例6
dx x(2 x10)
x9dx x10(2 x10 )
1
10
d ( x10 ) 1 x10 (2 x10 ) 20
(2 x10
x10 ) (2
1)没有万能的积分法;
2)有的初等函数的积分不是初等函数,从而 “积不出来”,如
积分对数
ex x
dx
和
ln1xdx,
积 分 正 弦
sin x
x
dx 、积 分 余 弦
cos x
x
dx,
及更一般形式
ex xn
dx 、
1 lnn
x
dx 、
sin x xn
dx
、
cos x xn
dx,
还有 e x2dx、 sin(x2 )dx、 cos(x2 )dx、 .
C3
1 C2
,
C3
C2
1 2
.
17/18
记 C2 C,得
max{1,| x |}dx
1 2
习题课-静力学

习题课-静力学
3.图示力偶中等效的是(B)
NEFU- Junkai Lu
(A) a和c (B) a和b (C) b和c (D) b和d
36Fd顺
36Fd顺
36Fd逆
48Fd顺
4.关于力对点之矩的说法,下列哪个是错误的(B)
(A) 互相平衡的两个力,对同一点之矩的代数和等于零。
(B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。
4.关于力对点之矩的说法,下列哪个是错误的( ) (A) 互相平衡的两个力,对同一点之矩的代数和等于零。 (B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。 (C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。 (D) 力对点之矩不会因为力矢沿其作用线移动而改变。
10
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
10. 力系的平衡
平面任意力系
Fx 0
Fy 0
M o 0
Fx 0
M A 0
M B 0
A、B两点 连线不得 与投影轴 x轴垂直
空间任意力系
Fix 0 Fiy 0 Fiz 0
(C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。
(D) 力对点之矩不会因为力矢沿其作用线移动而改变。
力有关,力偶无关
11
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
5.图示正方体顶角上作用着六个大小相等的力,此力系向任一点简化的结 果是( )
D
F3
电工与电子技术课后答案习题4(上篇第四章)

习题44-1 在题4-1图所示的电路中,电容元件原未储能。
① 求开关S 闭合后瞬间各元件上的电压、电流的初始值;② 求开关S 闭合后电路达到稳定状态各元件上的电压、电流的值。
解:①由于开关闭合前,电容元件未储能,故由换路定律可知,0)0()0(==-+C C u u 。
开关闭合后,电容元件相当短路,其等效电路如题4-1图(a )所示,则在+=0t 时各电压、电流为A 66//312//)0(21===+R R E i A 46636)0()0(2121=⨯+=+=++i R R R iA 26633)0()0(2112=⨯+=+=++i R R R iV 12)0()0(21===++Eu u② 开关S 闭合后电路达到稳定状态时,电容元件相当于断路,其等效电路如题4-1图(b )所示。
则当S 闭合后∞=t 时各电压、电流为 A 4312)()(11===∞=∞R E i i 0)(2=∞i V 12)(1==∞E u 0)(2=∞uE 题4-1图(a)+)0(2+题4-1图(b))(2∞)(∞CV 12)(==∞E u C4-2 求题4-2图所示电路中标明的各电流、电压的初始值及稳态值。
解: ① 求初始值:在开关S 断开之前电路处于稳定状态,电容相当于断路,电感相当于短路,其等效电路如题4-2图(a )所示。
则-=0t 时电容两端的电压及电感中的电流为V 410406040)0(=⨯+=-C uA 101406010)0(=+=-L i由换路定律可知:V 4)0()0(==-+C C u u,A 101)0()0(==-+L L i i 那么开关S 断开的瞬间即+=0t 时,电容元件相当于恒压源,电感元件相当于恒流源,其等效电路如题4-2(b)所示。
根据节点电压法,A 和B 两点之间的电压为201601)0(20)0(6010+-+=++i u u C ABV 42016011012056010=+-+=则 0204420)0()0(=-=-=++C AB C u u i 题4-2图题4-2图(a)-=0题4-2图(b)+0+BV 2601014)2040()0()0(-=⨯-=+⨯-=++L AB L i u u ② 求稳态值:在开关S 断开后电路达到稳定状态时,电容相当于断路,电感相当于短路,等效电路如题4-2图(c)所示。
第四章 习题课 数列中的构造问题

2.下列说法错误的是 A.任意等差数列{an}和{bn},数列{an+bn}是等差数列 B.存在等差数列{an}和{bn},数列{anbn}是等差数列
√C.任意等比数列{an}和{bn},数列{an+bn}是等比数列
D.存在等比数列{an}ຫໍສະໝຸດ {bn},数列{anbn}是等比数列
1234
解析 A项,若{an}和{bn}都是等差数列,不妨设an=k1n+b1,bn=k2n+b2, 故可得an+bn=(k1+k2)n+b1+b2,则an+1+bn+1=(k1+k2)(n+1)+b1+b2, 则an+1+bn+1-(an+bn)=k1+k2,故数列{an+bn}是等差数列,则A正确; B项,设数列{an}是数列1,1,1;数列{bn}是数列2,2,2,故可得数列{anbn} 是数列2,2,2,是等差数列,故B正确. C 项,若{an}和{bn}是等比数列,设 an=a1qn1,bn=b1qn2,故可得 an+bn= a1qn1+b1qn2,an+1+bn+1=a1qn1+1+b1qn2+1, 则ana+n1++bbnn+1=a1aqn11+ q1n1+ +bb11qq2n2n+1,不是常数,故{an+bn}不是等比数列,故 C 错误;
延伸探究 1.本例中“an=2an-1+2n”变为“an=2an-1+2n+1”,其余不变,求 数列{an}的通项公式.
解 等式两边同时除以 2n,得a2nn=a2nn--11+2,即a2nn-a2nn--11=2, 所以a2nn是以12为首项,以 2 为公差的等差数列, 所以a2nn=12+(n-1)×2,即 an=2n-23×2n.
第四章 §4.3 等比数列
学习目标
1.掌握利用构造法求数列通项公式的方法. 2.会用构造法公式解决一些简单的问题.
数学人教版(2024)七年级上册 第四章 整式的加减 习题课件 微专题2 整式加减运算
.
2
解:原式=2 xy -3 xy +12 y2+2 xy -4 y2
=8 y2+ xy .
当 x =4, y =- 时,
原式=8× +4×(- )=2-2=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
微专题2
整式加减运算
分层检测
A基础
9. 长方形的长是3 a ,宽是2 a - b ,则长方形的周长是( A )
-2 xy2
1
2
3
4
;
.
5
6
7
8
9
10
11
12
13
14
15
16
微专题2
整式加减运算
课堂学练
去括号
3. 【例】去括号:
(1)2(a- b )=
2 a -2 b
(2) a -(b- c )=
;
a-b+c
;
a +2 b -2 c
(3) a -2(- b + c )=
.
4. 去括号:
(1)-2(x-3 y )=
16
微专题2
整式加减运算
分层检测
16. 已知 a , b , c 在数轴上的位置如图所示.
(1)化简: − 1 - + + − 1 ;
解:由条件得,
a -1>0, b + c <0, b -1<0,
所以原式= a -1+ c + b - b +1
=a+c;
1
数学分析 第四章 习题课
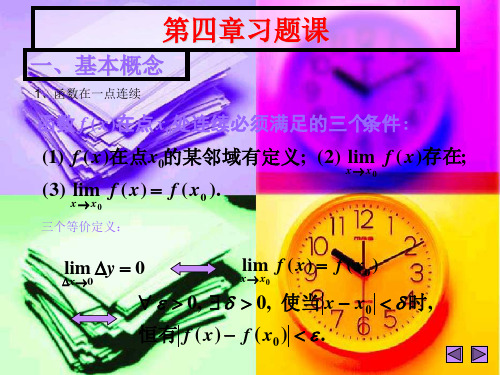
f ( x0 0); f ( x0 0).
第二类:f ( x0 0)不全存在(无穷大间断、振动间断、)
四、连续函数的性质
1、局部性质
有界性,保号性,复合运算性,四则运算性,反函数连续性。
2、整体性质(闭区间上连续函数的性质)
(1)最大最小值定理, (3)介值性定理, (5)一致连续性定理。
(2)有界性定理, (4)根的存在性定理,
第四章习题课
一、基本概念
1、函数在一点连续
函数 f ( x)在点 x0处连续必须满足的三个条件 :
(1)
f ( x)在点x0的某邻域有定义;
(2) lim x x0
f ( x)存在;
(3) lim x x0
f (x)
f ( x0 ).
三个等价定义:
lim y 0
x0
lim
x x0
f (x)
f ( x0 )
证
0,取 ,x, x I ,| x x | ,
L
有 | f ( x) f ( x) |
故f(x)在I上一致连续。
P81. 6, 16
f在[a,)上连续,lim f ( x) A, x
证明f在[a,)上有界且一致连续, 且f在[a,)上必有最大值或最小值。
证
lim f ( x) A,
五、初等函数的连续性
1、基本初等函数在其定义域内连续, 2、初等函数在其定义区间内连续。
五、连续函数作极限运算
连续函数的函数符号可与极限号交换次序。
lim f ( x) f ( lim x),
x x0
x x0
lim f ( g( x)) f ( lim g( x)), 只要f连续,g有极限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.在惯性系 S 和对 S 作等速直线运动的 S’中讨论一个质点系的运动时, 下列的各种论述 (1) 质点系在S 系中若动量守恒,则在S’系中动量也一定守恒. (2) 质点系在S 系中若机械能守恒,则在S’系中机械能也一定守恒. (3) 质点系在S 系中若动量守恒,在S’系中动量不一定守恒. (4) 质点系在S 系中若机械能守恒,在S’系中机械能不一定守恒. (5) 质点系在 S 系中若动量守恒,机械能也守恒,则在 S’系中动量一 定守恒,机械能也一定守恒. (6) 质点系在 S 系中若动量守恒,机械能也守恒,则在 S’系中动量不 一定守恒,机械能也不一定守恒. 中,只有 (A) (B) (C) (D) (E) (1)、(2)、(5)正确,其他都不正确. (1)、(4)、(5)正确,其他都不正确. (2)、(3)正确,其他都不正确. (2)、(3)、(6)正确,其他都不正确. (3)、(4)、(6)正确,其他都不正确.
10.一列火车以速度u做匀速直线运动,车上一人以速 度v(相对火车)抛出一质量为m的小球,问: (1)地面上的人认为在刚抛出小球瞬时,小球的动 1 1 Ek mu 2 mv 2 ,对否,为什么? 能
2 2
(2)当车上的人沿车前进的方向抛出小球时,车上
的人看抛出小球过程所做的功是多少?地上的人看是 多少? (3) 当车上的人竖直向上抛球时,地上的人看抛出 小球过程做的功是多少?
1.某质点作直线运动的运动学方程为x=3t-5t3 + 6 (SI),则该质点作 (A) 匀加速直线运动,加速度沿x轴正方向. (B) 匀加速直线运动,加速度沿x轴负方向. (C) 变加速直线运动,加速度沿x轴正方向. (D) 变加速直线运动,加速度沿x轴负方向. 2.一质点沿 x轴作直线运动, 其 v−t 曲线如图所示 ,如 t=0 时,质点位于坐标原 点,则 t=4.5s时,质点在 x 轴上的位置为 (A) 5m . (B) 2m . (C) 0. (D) −2 m.(E) −5 m.
dx v 而 = 0 dt 影子长度增长速率为:
l v db = h l 0 dt
l b x
h
h b = l (x + b )
l v db = h l 0 dt
所以人影头顶移动速度为: h d ( x + b ) h db = l dt = h l v0 dt
. ..
例:
9.有一小物体放在光滑的水平桌面上,有 一绳其一端连接此物体,另一端穿过桌面上 的小孔,该物体原以一定的角速度在桌面上 以小孔为圆心运动。问从小孔向下缓慢地拉 绳的过程中,物体的动能、动量、对小孔的 角动量是否变化?
A
O
解:由动量守恒
M V m ( u V) = 0 m u V= M +m
300
600
x 2 = l ( sin60 0 sin30 0 )= 2.93m x2 t= u mx2 m u x2 x 1 =V t = =M m + M +m u 2 ×2.93 0.267m = 20 + 2 =
x2
4.作为相互作用的一对静摩擦力,它们作功之和?作为相互作 用的一对滑动摩擦力,当分别作用在有相对滑动的两物体上时, 它们作功之和?
5.如图所示,劲度系数为k 的弹簧一端固定在墙上,另一端系 着质量为m 的物体,在光滑水平面上作谐振动.分别选与墙相 对静止的参考系S 和相对S 以v ( v << c,c为真空中的光速) 作直线运动的参考系 S ',以弹簧和物体为系统,指出下述说 法哪个是正确的 (A) 在两个参考系中,系统的机械能都守恒. (B) 对于两个参考系,功能原理不成立. (C) 弹性势能与参考系选取无关. (D) 弹性力作功与参考系选取无关.
7. 路灯高度为 h,人高度为 l,步行速度为 v0。 试 求:(1)人影中头顶的移动速度; (2)影子长度增长的速率。
l b x
h
解:
h l h b = l (x + b ) = b x +b 上式两边微分得到:
db d ( x + b ) l dx l db h = + =l dt dt dt dt
3.如图所示,一光滑细杆上端由光滑绞链固定,杆可绕其上端 在任意角度的锥面上绕竖直轴 OO′作匀角速转动.有一小环套 在杆的上端处.开始使杆在一个锥面上运动起来,而后小环由 静止开始沿杆下滑.在小环下滑过程中,小环、杆和地球系统 的机械能以及小环加杆对轴OO'的角动量这两个量中 (A) 机械能、角动量都守恒. (B) 机械能守恒,角动量不守恒. (C) 机械能不守恒,角动量守恒. (D) 机械能、角动量都不守恒.
11.
12.
设抛出后人的速度为v1,取人和物体为系统,则该系统水 平方向的动量守恒,即:
13.
1 =20t,由岸上吊起 m =2t的重物后,再将吊杆0A与竖直方向间的夹角 θ 由600 转到300 。设杆长l=OA=8m,水的阻力与 杆重忽略不汁,求浮吊在水平方向移动的距离, 并指明朝那边移动。
