构造哈夫曼树的过程
哈夫曼树怎么画

哈夫曼树怎么画哈夫曼树是一种用于编码和压缩数据的树型数据结构。
它由行程长度编码的概念发展而来,常用于文件压缩和通信传输中。
哈夫曼树的画法主要涉及两个步骤:构建哈夫曼树和绘制哈夫曼树。
在构建哈夫曼树之前,我们需要了解一些关于哈夫曼树的基本概念。
一、哈夫曼树的基本概念1. 频率:在构建哈夫曼树时,每个字符(或数据)的频率是非常重要的。
频率表示了字符在原始数据中出现的次数或者权重。
2. 编码:在哈夫曼树中,每个字符都有一个唯一的编码。
编码是根据字符在哈夫曼树中的位置来确定的,可以用0和1组成的字符串表示。
3. 哈夫曼树可视化:绘制哈夫曼树的目的是为了更直观地看到字符的编码和哈夫曼树的结构。
可视化可以帮助我们更好地理解和应用哈夫曼树。
二、构建哈夫曼树构建哈夫曼树的过程可以简单地分为以下几个步骤:1. 创建叶节点:根据原始数据中每个字符的频率,创建相应数量的叶节点。
每个叶节点都有对应的字符和频率。
2. 构建节点集合:将所有的叶节点集合起来,形成一个节点集合。
初始时,节点集合中只包含叶节点。
3. 合并节点:从节点集合中选择两个频率最低的节点,将它们合并为一个新的节点。
新节点的频率是两个被合并节点的频率之和,并且新节点的左子树为频率较低的节点,右子树为频率较高的节点。
4. 更新节点集合:将新合并的节点加入节点集合中,并将两个被合并的节点从节点集合中删除。
重复该步骤,直到节点集合中只剩下一个节点,即为哈夫曼树的根节点。
三、绘制哈夫曼树在绘制哈夫曼树时,我们可以遵循以下步骤:1. 绘制根节点:根节点位于哈夫曼树的顶部,可以用一个大圆圈表示。
2. 绘制子节点:根据哈夫曼树的定义,除了根节点外,每个节点都有左子节点和右子节点。
可以用箭头将父节点与子节点连接起来,表示节点之间的关系。
3. 标记叶节点:叶节点是哈夫曼树的最底层节点,可以用一个小圆圈表示,并在圈内标注对应的字符或数据。
4. 标记编码:根据哈夫曼树的路径规则,根节点到叶节点的路径上的每个箭头都有一个相应的编码(0或1)。
数据结构第六章 哈夫曼树
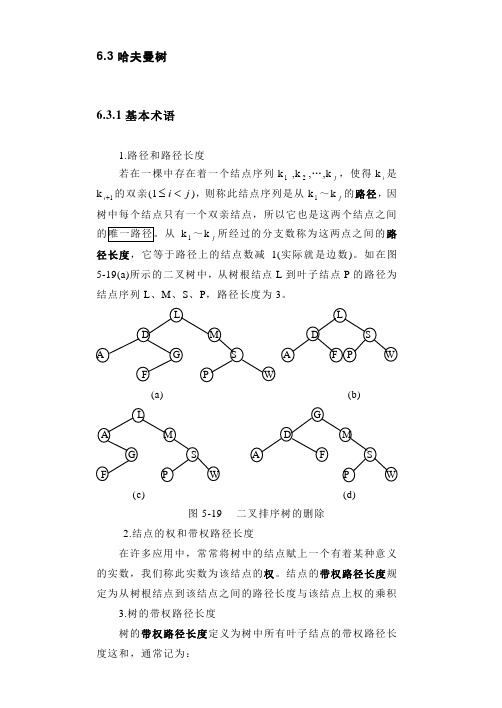
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj,使得ki是k1+i 的双亲(1ji<≤),则称此结点序列是从k1~kj的路径,因树中每个结点只有一个双亲结点,所以它也是这两个结点之间k 1~kj所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中,从树根结点L到叶子结点P的路径为结点序列L、M、S、P,路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中,常常将树中的结点赋上一个有着某种意义的实数,我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和,通常记为:2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目,i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的,所以被称之为哈夫曼树。
例如,有四个叶子结点a 、b 、c 、d ,分别带权为9、4、5、2,由它们构成的三棵不同的二叉树(当然还有其它许多种)分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为:(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小,稍后便知,此树就是哈夫曼树。
最优二叉树(哈夫曼树)的构建及编码

最优⼆叉树(哈夫曼树)的构建及编码参考:数据结构教程(第五版)李春葆主编⼀,概述1,概念 结点的带权路径长度: 从根节点到该结点之间的路径长度与该结点上权的乘积。
树的带权路径长度: 树中所有叶结点的带权路径长度之和。
2,哈夫曼树(Huffman Tree) 给定 n 个权值作为 n 个叶⼦结点,构造⼀棵⼆叉树,若该树的带权路径长度达到最⼩,则称这样的⼆叉树为最优⼆叉树,也称为哈夫曼树。
哈夫曼树是带权路径长度最短的树,权值较⼤的结点离根较近。
⼆,哈夫曼树的构建1,思考 要实现哈夫曼树⾸先有个问题摆在眼前,那就是哈夫曼树⽤什么数据结构表⽰? ⾸先,我们想到的肯定数组了,因为数组是最简单和⽅便的。
⽤数组表⽰⼆叉树有两种⽅法: 第⼀种适⽤于所有的树。
即利⽤树的每个结点最多只有⼀个⽗节点这种特性,⽤ p[ i ] 表⽰ i 结点的根节点,进⽽表⽰树的⽅法。
但这种⽅法是有缺陷的,权重的值需要另设⼀个数组表⽰;每次找⼦节点都要遍历⼀遍数组,⼗分浪费时间。
第⼆种只适⽤于⼆叉树。
即利⽤⼆叉树每个结点最多只有两个⼦节点的特点。
从下标 0 开始表⽰根节点,编号为 i 结点即为 2 * i + 1 和 2 * i + 2,⽗节点为 ( i - 1) / 2,没有⽤到的空间⽤ -1 表⽰。
但这种⽅法也有问题,即哈夫曼树是从叶结点⾃下往上构建的,⼀开始树叶的位置会因为⽆法确定⾃⾝的深度⽽⽆法确定,从⽽⽆法构造。
既然如此,只能⽤⽐较⿇烦的结构体数组表⽰⼆叉树了。
typedef struct HTNode // 哈夫曼树结点{double w; // 权重int p, lc, rc;}htn;2,算法思想 感觉⽐较偏向于贪⼼,权重最⼩的叶⼦节点要离根节点越远,⼜因为我们是从叶⼦结点开始构造最优树的,所以肯定是从最远的结点开始构造,即权重最⼩的结点开始构造。
所以先选择权重最⼩的两个结点,构造⼀棵⼩⼆叉树。
然后那两个最⼩权值的结点因为已经构造完了,不会在⽤了,就不去考虑它了,将新⽣成的根节点作为新的叶⼦节加⼊剩下的叶⼦节点,⼜因为该根节点要能代表整个以它为根节点的⼆叉树的权重,所以其权值要为其所有⼦节点的权重之和。
c语言哈夫曼树的构造及编码

c语言哈夫曼树的构造及编码一、哈夫曼树概述哈夫曼树是一种特殊的二叉树,它的构建基于贪心算法。
它的主要应用是在数据压缩和编码中,可以将频率高的字符用较短的编码表示,从而减小数据存储和传输时所需的空间和时间。
二、哈夫曼树的构造1. 哈夫曼树的定义哈夫曼树是一棵带权路径长度最短的二叉树。
带权路径长度是指所有叶子节点到根节点之间路径长度与其权值乘积之和。
2. 构造步骤(1) 将待编码字符按照出现频率从小到大排序。
(2) 取出两个权值最小的节点作为左右子节点,构建一棵新的二叉树。
(3) 将新构建的二叉树加入到原来排序后队列中。
(4) 重复上述步骤,直到队列只剩下一个节点,该节点即为哈夫曼树的根节点。
3. C语言代码实现以下代码实现了一个简单版哈夫曼树构造函数:```ctypedef struct TreeNode {int weight; // 权重值struct TreeNode *leftChild; // 左子节点指针struct TreeNode *rightChild; // 右子节点指针} TreeNode;// 构造哈夫曼树函数TreeNode* createHuffmanTree(int* weights, int n) {// 根据权值数组构建节点队列,每个节点都是一棵单独的二叉树TreeNode** nodes = (TreeNode**)malloc(sizeof(TreeNode*) * n);for (int i = 0; i < n; i++) {nodes[i] = (TreeNode*)malloc(sizeof(TreeNode));nodes[i]->weight = weights[i];nodes[i]->leftChild = NULL;nodes[i]->rightChild = NULL;}// 构建哈夫曼树while (n > 1) {int minIndex1 = -1, minIndex2 = -1;for (int i = 0; i < n; i++) {if (nodes[i] != NULL) {if (minIndex1 == -1 || nodes[i]->weight < nodes[minIndex1]->weight) {minIndex2 = minIndex1;minIndex1 = i;} else if (minIndex2 == -1 || nodes[i]->weight < nodes[minIndex2]->weight) {minIndex2 = i;}}}TreeNode* newNode =(TreeNode*)malloc(sizeof(TreeNode));newNode->weight = nodes[minIndex1]->weight + nodes[minIndex2]->weight;newNode->leftChild = nodes[minIndex1];newNode->rightChild = nodes[minIndex2];// 将新构建的二叉树加入到原来排序后队列中nodes[minIndex1] = newNode;nodes[minIndex2] = NULL;n--;}return nodes[minIndex1];}```三、哈夫曼编码1. 哈夫曼编码的定义哈夫曼编码是一种前缀编码方式,它将每个字符的编码表示为二进制串。
哈夫曼树_实验报告

一、实验目的1. 理解哈夫曼树的概念及其在数据结构中的应用。
2. 掌握哈夫曼树的构建方法。
3. 学习哈夫曼编码的原理及其在数据压缩中的应用。
4. 提高编程能力,实现哈夫曼树和哈夫曼编码的相关功能。
二、实验原理哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,又称为最优二叉树。
其构建方法如下:1. 将所有待编码的字符按照其出现的频率排序,频率低的排在前面。
2. 选择两个频率最低的字符,构造一棵新的二叉树,这两个字符分别作为左右子节点。
3. 计算新二叉树的频率,将新二叉树插入到排序后的字符列表中。
4. 重复步骤2和3,直到只剩下一个节点,这个节点即为哈夫曼树的根节点。
哈夫曼编码是一种基于哈夫曼树的编码方法,其原理如下:1. 从哈夫曼树的根节点开始,向左子树走表示0,向右子树走表示1。
2. 每个叶子节点对应一个字符,记录从根节点到叶子节点的路径,即为该字符的哈夫曼编码。
三、实验内容1. 实现哈夫曼树的构建。
2. 实现哈夫曼编码和译码功能。
3. 测试实验结果。
四、实验步骤1. 创建一个字符数组,包含待编码的字符。
2. 创建一个数组,用于存储每个字符的频率。
3. 对字符和频率进行排序。
4. 构建哈夫曼树,根据排序后的字符和频率,按照哈夫曼树的构建方法,将字符和频率插入到哈夫曼树中。
5. 实现哈夫曼编码功能,遍历哈夫曼树,记录从根节点到叶子节点的路径,即为每个字符的哈夫曼编码。
6. 实现哈夫曼译码功能,根据哈夫曼编码,从根节点开始,按照0和1的路径,找到对应的叶子节点,即为解码后的字符。
7. 测试实验结果,验证哈夫曼编码和译码的正确性。
五、实验结果与分析1. 构建哈夫曼树根据实验数据,构建的哈夫曼树如下:```A/ \B C/ \ / \D E F G```其中,A、B、C、D、E、F、G分别代表待编码的字符。
2. 哈夫曼编码根据哈夫曼树,得到以下字符的哈夫曼编码:- A: 00- B: 01- C: 10- D: 11- E: 100- F: 101- G: 1103. 哈夫曼译码根据哈夫曼编码,对以下编码进行译码:- 00101110111译码结果为:BACGACG4. 实验结果分析通过实验,验证了哈夫曼树和哈夫曼编码的正确性。
哈夫曼树的构造

哈夫曼树的构造关键思想: 依据哈弗曼树的定义,⼀棵⼆叉树要使其WPL值最⼩,必须使权值越⼤的叶⼦结点越靠近根结点,⽽权值越⼩的叶⼦结点越远离根结点。
哈弗曼根据这⼀特点提出了⼀种构造最优⼆叉树的⽅法,其基本思想如下:1。
根据给定的n个权值{w1, w2, w3 ... w n },构造n棵只有根节点的⼆叉树,令起权值为w j2。
在森林中选取两棵根节点权值最⼩的树作为左右⼦树,构造⼀颗新的⼆叉树,置新⼆叉树根节点权值为其左右⼦树根节点权值之和。
注意,左⼦树的权值应⼩于右⼦树的权值。
3。
从森林中删除这两棵树,同时将新得到的⼆叉树加⼊森林中。
(换句话说,之前的2棵最⼩的根节点已经被合并成⼀个新的结点了)4。
重复上述两步,直到只含⼀棵树为⽌,这棵树即是哈弗曼树以下演⽰了⽤Huffman算法构造⼀棵Huffman树的过程:考研题⽬:三、哈夫曼树的在编码中的应⽤在电⽂传输中,须要将电⽂中出现的每⼀个字符进⾏⼆进制编码。
在设计编码时须要遵守两个原则:(1)发送⽅传输的⼆进制编码,到接收⽅解码后必须具有唯⼀性,即解码结果与发送⽅发送的电⽂全然⼀样;(2)发送的⼆进制编码尽可能地短。
以下我们介绍两种编码的⽅式。
1. 等长编码这样的编码⽅式的特点是每⼀个字符的编码长度同样(编码长度就是每⼀个编码所含的⼆进制位数)。
如果字符集仅仅含有4个字符A,B,C,D,⽤⼆进制两位表⽰的编码分别为00,01,10,11。
若如今有⼀段电⽂为:ABACCDA,则应发送⼆进制序列:00010010101100,总长度为14位。
当接收⽅接收到这段电⽂后,将按两位⼀段进⾏译码。
这样的编码的特点是译码简单且具有唯⼀性,但编码长度并⾮最短的。
2. 不等长编码在传送电⽂时,为了使其⼆进制位数尽可能地少,能够将每⼀个字符的编码设计为不等长的,使⽤频度较⾼的字符分配⼀个相对照较短的编码,使⽤频度较低的字符分配⼀个⽐較长的编码。
⽐如,能够为A,B,C,D四个字符分别分配0,00,1,01,并可将上述电⽂⽤⼆进制序列:000011010发送,其长度仅仅有9个⼆进制位,但随之带来了⼀个问题,接收⽅接到这段电⽂后⽆法进⾏译码,由于⽆法断定前⾯4个0是4个A,1个B、2个A,还是2个B,即译码不唯⼀,因此这样的编码⽅法不可使⽤。
字符合集和出现概率构造哈夫曼树

《字符合集和出现概率构造哈夫曼树》一、引言在信息技术领域,字符合集和出现概率构造哈夫曼树是一项重要且基础的概念。
本文将深入探讨字符合集和哈夫曼树的构造过程,并分析字符出现概率对哈夫曼树构造的影响,旨在让读者对此理解更加深入、全面。
二、字符合集和出现概率字符合集是指在某种编码方式下所能使用的字符的总体。
在计算机领域中,字符合集通常指的是能够表示文本、图像、声音等信息的全部字符。
而字符的出现概率则是指在一个文本或数据集中某个字符出现的频率,通常使用概率分布来表示。
在构造哈夫曼树的过程中,首先需要了解字符合集中各个字符的出现概率,因为出现概率越高的字符,在哈夫曼编码中对应的编码长度应该越短,以提高编码效率。
对字符合集中字符出现概率的准确评估对于哈夫曼树的构造至关重要。
三、哈夫曼树的构造步骤1. 根据字符出现概率构造叶子节点:首先根据给定的字符合集以及各字符的出现概率,构造对应的叶子节点。
出现概率较高的字符对应的叶子节点应该在哈夫曼树中拥有较短的路径长度。
2. 构造哈夫曼树的内部节点:在构造叶子节点之后,根据哈夫曼树的构造规则,通过不断合并概率最小的两个节点来构造内部节点,并更新概率信息。
这一过程直到所有节点合并成为一个根节点为止。
3. 确定字符的编码:通过遍历哈夫曼树的路径,确定每个字符对应的编码,从而完成哈夫曼编码的构造。
四、字符出现概率对哈夫曼树的影响字符出现概率对哈夫曼树的构造有着重要的影响。
在实际应用中,如果字符出现概率相差较大,那么对应的编码长度也会存在较大的差异。
合理评估字符出现概率,能够在一定程度上提高哈夫曼编码的效率。
当字符出现概率相近的时候,构造的哈夫曼树将会比较平衡,对应的编码长度也会较为接近,这样能够保证在编码和解码的过程中效率的平衡。
而当字符出现概率差异较大时,哈夫曼树将会不平衡,对应的编码长度也会存在较大的差异,这样就需要根据实际情况来平衡编码的效率和解码的效率。
五、我的观点和理解在我看来,字符合集和出现概率构造哈夫曼树是一项非常重要的基础概念。
构造霍夫曼树的方法

构造霍夫曼树的方法嘿,咱今儿就来聊聊构造霍夫曼树的那些事儿!你说这霍夫曼树啊,就像是一个奇妙的拼图游戏。
想象一下,你有一堆乱七八糟的小木块,每个木块上都标着不同的数字,这就好比是各种字符和它们出现的频率。
咱的任务呢,就是要把这些小木块巧妙地组合起来,搭建成一棵漂亮又实用的树。
首先呢,咱得把这些带着数字的小木块按照数字大小排个序。
这就像是给它们排排队,让它们整整齐齐的。
然后呢,从最小的两个木块开始,把它们组合成一个新的“大块头”,这个“大块头”的数字就是那两个小木块数字的和。
接下来,再把这个新的“大块头”放回队伍里,重新排序。
就这么不断地重复这个过程,把小的组合成大的,再组合成更大的。
你看啊,这多像我们搭积木呀!一块一块往上堆,最后堆出一个神奇的形状。
在构造霍夫曼树的过程中,可不能马虎哟!每一步都得小心翼翼,就跟走钢丝似的,稍有偏差,这棵树可能就长得不那么完美啦。
而且哦,你还得有耐心。
这可不是一下子就能完成的事儿,得慢慢来,就像绣花一样,一针一线都得精细。
等咱终于把这棵霍夫曼树构造好啦,哇塞,那可真是满满的成就感呀!就好像自己创造了一个小世界一样。
这时候再回头看看那些原本杂乱无章的小木块,现在都乖乖地在树上找到自己的位置啦,多有意思!构造霍夫曼树,不仅是一个技术活儿,更是一种乐趣呀!它让我们看到数字和算法的奇妙之处,让我们感受到知识的力量。
所以呀,别小瞧了这构造霍夫曼树的方法,它能在很多地方发挥大作用呢!比如在数据压缩里,它就能帮我们节省好多空间,让信息传递得更快更高效。
怎么样,是不是对构造霍夫曼树有了更深刻的认识啦?赶紧去试试吧,说不定你就能搭出一棵超级棒的霍夫曼树呢!。
哈夫曼树构造过程

哈夫曼树构造过程哈夫曼树是一种用于数据压缩和编码的树状数据结构。
它的构造过程可以分为以下几个步骤。
1. 统计字符频率在构造哈夫曼树之前,需要先统计待编码的字符在文本中出现的频率。
这可以通过遍历文本并记录每个字符出现的次数来实现。
2. 构建叶子节点根据统计得到的字符频率,可以将每个字符作为一个叶子节点,并将其频率作为节点权值。
这样就可以得到一组初始的叶子节点。
3. 构建哈夫曼树从初始的叶子节点开始,不断合并权值最小的两个节点,直到只剩下一个节点。
合并的过程是将两个节点作为子节点创建一个新的父节点,并将父节点的权值设为两个子节点权值之和。
这个过程可以使用优先队列来实现,保证每次合并的都是权值最小的两个节点。
4. 生成哈夫曼编码通过遍历哈夫曼树的路径,可以得到每个字符对应的哈夫曼编码。
具体来说,从根节点开始,向左走表示编码0,向右走表示编码1,直到到达叶子节点。
这样,每个字符都可以用一串二进制数表示,且保证不会有编码重复的情况出现。
5. 压缩数据利用生成的哈夫曼编码,可以将原始数据进行压缩。
将每个字符替换为对应的哈夫曼编码,然后将所有的二进制数连接起来,就得到了压缩后的数据。
由于哈夫曼编码是前缀码,所以可以通过编码的分割符来解码,而不会出现歧义。
6. 解码数据解码过程与压缩过程相反。
根据哈夫曼树和压缩后的数据,可以逐个读取二进制位,并根据读取的位数沿着哈夫曼树往下走。
当到达叶子节点时,就可以确定解码出的字符,并将其输出。
重复这个过程,直到解码完所有的数据。
哈夫曼树的构造过程非常灵活和高效。
通过合并权值最小的节点,可以保证树的结构不会过深,从而实现了对数据的高效压缩。
而生成的哈夫曼编码也具有唯一性和无歧义性,可以准确地还原原始数据。
总结起来,哈夫曼树的构造过程包括统计字符频率、构建叶子节点、合并节点构建树、生成哈夫曼编码、压缩数据和解码数据等步骤。
通过这个过程,可以实现对数据的高效压缩和解压缩。
哈夫曼树在数据传输和存储中有着广泛的应用,是一种非常重要的数据结构。
哈夫曼树及其构造

第9讲 哈夫曼树及其构造——教学讲义哈夫曼树可用来构造最优编码,用于信息传输、数据压缩等方面,哈夫曼树是一种应用广泛的二叉树。
一、 哈夫曼树1.哈夫曼树的基本概念在介绍哈夫曼树之前,先给出几个基本概念。
● 结点间的路径和路径长度路径是指从一个结点到另一个结点之间的分支序列,路径长度是指从一个结点到另一个结点所经过的分支数目。
● 结点的权和带权路径长度在实际的应用中,人们常常给树的每个结点赋予一个具有某种实际意义的实数,称该实数为这个结点的权。
在树型结构中,把从树根到某一结点的路径长度与该结点的权的乘积,叫做该结点的带权路径长度。
● 树的带权路径长度树的带权路径长度为树中从根到所有叶子结点的各个带权路径长度之和,通常记为:∑=⨯=n1i ii l w WPL其中n 为叶子结点的个数,w i 为第i 个叶子结点的权值,l i 为第i 个叶子结点的路径长度。
例6-5 计算下图中三棵二叉树的带权路径长度。
WPL(a)=7×2+5×2+2×2+4×2=36 WPL(b)=4×2+7×3+5×3+2×1=46 WPL(c)=7×1+5×2+2×3+4×3=35研究树的路径长度PL 和带权路径长度WPL,目的在于寻找最优分析。
问题1: 什么样的二叉树的路径长度PL 最小?一棵树的路径长度为0结点至多只有1个 (根) 路径长度为1结点至多只有2个 (两个孩子) 路径长度为2结点至多只有4个依此类推: 路径长度为K 结点至多只有 2k个所以n 个结点二叉树其路径长度至少等于如下图所示序列的前n 项之和。
0 ,1 , 1 ,2, 2, 2, 2,3, 3,3,3,3,3,3,3,4,4,....... n=1 n=2 n=3 n=4 n=5 n=6 n=7 n=8 ... n=15结点序列及结点的路径长度A B C D 7 5 2 4 (a)权为36 C B D A 7 5 24 (b)权为46A B C D 7 5 2 4 (c)权为35 具有不同带权路径长度的二叉树由上图可知,结点n 对应的路径长度为⎣⎦n log 2,所以前n 项之和为21lognk k =⎢⎥⎣⎦∑。
哈夫曼树构造例题

哈夫曼树构造例题
摘要:
1.哈夫曼树的基本概念
2.哈夫曼树的构造方法
3.哈夫曼编码的生成
4.哈夫曼编码的应用
正文:
哈夫曼树构造例题
哈夫曼树是一种用于数据压缩的树形结构,它能将原始数据转换成对应的哈夫曼编码,从而实现压缩。
哈夫曼树构造例题将详细介绍哈夫曼树的基本概念、构造方法、哈夫曼编码的生成以及哈夫曼编码的应用。
1.哈夫曼树的基本概念
哈夫曼树是一种满二叉树,它的每个节点都包含一个字符,叶子节点对应原始数据的字符。
哈夫曼树的构造过程是通过反复合并出现频率最小的节点来完成的。
2.哈夫曼树的构造方法
哈夫曼树的构造方法分为以下几个步骤:
(1) 将原始数据的字符按照出现频率构建一个哈夫曼树。
(2) 从哈夫曼树中选出出现频率最小的两个节点进行合并,得到一个新的节点,新节点的出现频率为两个节点出现频率之和。
(3) 将新节点插入到哈夫曼树中,更新哈夫曼树的结构。
(4) 重复步骤(2) 和(3),直到哈夫曼树中只剩下一个节点,这个节点就是哈夫曼树的根节点。
3.哈夫曼编码的生成
哈夫曼编码是根据哈夫曼树生成的,它的每个字符都对应一个唯一的编码。
从根节点到达每个叶子节点的路径代表该字符的编码,其中左子节点的边表示“0”,右子节点的边表示“1”。
4.哈夫曼编码的应用
哈夫曼编码在数据压缩领域有着广泛的应用,它能有效地将原始数据转换成较短的二进制编码,从而减少存储空间和传输时间。
除了数据压缩,哈夫曼编码还可以用于其他领域,如信息论、计算机科学等。
总之,哈夫曼树构造例题详细介绍了哈夫曼树的基本概念、构造方法、哈夫曼编码的生成以及哈夫曼编码的应用。
哈夫曼树构造规则

哈夫曼树构造规则哈夫曼树是一种用于数据压缩和编码的重要数据结构。
它是由一组字符和它们对应的频率构成的,根据频率构造出来的一种特殊的二叉树。
哈夫曼树的构造规则如下:1. 频率越高的字符越靠近根节点在哈夫曼树中,频率越高的字符被赋予越短的编码,这样可以减少编码的长度,从而达到压缩数据的目的。
因此,在构造哈夫曼树时,我们需要根据字符的频率来确定它们在树中的位置,频率越高的字符越靠近根节点。
2. 构造过程中采用贪心算法构造哈夫曼树的过程中,我们需要根据字符的频率来选择合适的节点进行合并。
在每一步中,我们选择频率最小的两个节点进行合并,然后将合并后的节点作为一个新节点插入到原来的节点集合中。
这种选择最小频率的节点的策略就是贪心算法。
3. 合并节点的频率为两个节点频率之和当我们选择两个频率最小的节点进行合并时,合并后的节点的频率就是这两个节点的频率之和。
这是因为合并后的节点代表了这两个节点的集合,所以它的频率就是这两个节点频率之和。
4. 构造过程中节点数目逐渐减少在构造哈夫曼树的过程中,每次合并两个节点,树的节点数目就减少一个。
最终,当只剩下一个节点时,这个节点就是哈夫曼树的根节点。
5. 构造过程中节点的位置不变在哈夫曼树的构造过程中,每个节点的位置是固定的,只是节点之间的连接关系发生了变化。
频率越高的节点越靠近根节点,频率越低的节点越远离根节点。
6. 哈夫曼树的带权路径长度最小哈夫曼树的带权路径长度是指树中每个叶子节点的权值乘以它到根节点的路径长度之和。
在所有可能的二叉树中,哈夫曼树的带权路径长度是最小的,这也是它被广泛应用于数据压缩和编码的原因之一。
通过以上的构造规则,我们可以得到一个符合要求的哈夫曼树。
这棵树可以用于对字符进行编码和解码,实现数据的压缩和解压缩。
在哈夫曼树中,频率高的字符对应的编码较短,频率低的字符对应的编码较长,从而实现了数据的有效压缩。
同时,由于哈夫曼树的构造过程中采用了贪心算法,所以构造出来的哈夫曼树的带权路径长度是最小的,这也保证了数据压缩的效果。
哈夫曼树

比如,发送一段编码:0000011011010010, 接收方可以准确地通过译码得到:⑥⑥⑦⑤②⑧。
<
<80
<90 good
very good
图 5-
首先,将各分数段的比例数值作为权值构造一 棵哈夫曼树。 70≤...≤79
general
good
80≤...≤89
60≤...≤69 pass
...<59
图 5-30
bad
very good
<80 <70 <60 general good <90
4 8
图5-27 叶子结点带权值的二叉树
5
下面我们讨论一下权值、树形与带权的路径长 度之间的关系。假设有6个权值分别为{3,6,9,10, 7,11},以这6个权值作为叶子结点的权值可以构造 出下面三棵二叉树。
10
11
3
(a)
6
7
9
3 6 7
9
7
9
11 10
(b)
6
3
11
图 528
10
(c)
到这段电文后无法进行译码,因为无法断定前面4个0
是4个A,1个B、2个A,还是2个B,即译码不唯一, 因此这种编码方法不可使用。
(1)利用字符集中每个字符的使用频率作为权 值构造一个哈夫曼树; (2)从根结点开始,为到每个叶子结点路径上 的左分支赋予0,右分支赋予1,并从根到叶子方向形 成该叶子结点的编码。 假设有一个电文字符集中有8个字符,每个字 符的使用频率分别为 {0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11},现 以此为例设计哈夫曼编码。 哈夫曼编码设计过程为: (1)为方便计算,将所有字符的频度乘以 100,使其转换成整型数值集合,得到 {5,29,7,8,14,23,3,11}; (2)以此集合中的数值作为叶子结点的权值 构造一棵哈夫曼树,如图5-27所示;
c语言实现构造哈夫曼树代码

c语言实现构造哈夫曼树代码一、哈夫曼树简介哈夫曼树是一种特殊的二叉树,其每个叶子节点都对应一个权值,而非叶子节点则没有权值。
哈夫曼树的构造过程中,将权值较小的节点放在左子树,权值较大的节点放在右子树,这使得哈夫曼树的带权路径最短。
哈夫曼编码就是利用这种特性实现对数据进行压缩。
二、C语言实现构造哈夫曼树1. 定义结构体首先需要定义一个结构体来表示哈夫曼树中的节点。
结构体中包含了该节点的权值以及指向左右子节点的指针。
```typedef struct TreeNode {int weight;struct TreeNode *left;struct TreeNode *right;} TreeNode;2. 构造哈夫曼树接下来需要实现构造哈夫曼树的函数。
该函数接收一个数组作为输入,数组中存储了每个叶子节点的权值。
首先需要将数组中所有元素转化为TreeNode类型,并将它们存储在一个链表中。
```TreeNode *createTreeNodes(int weights[], int size) {TreeNode *nodes[size];for (int i = 0; i < size; i++) {nodes[i] = (TreeNode *)malloc(sizeof(TreeNode));nodes[i]->weight = weights[i];nodes[i]->left = NULL;nodes[i]->right = NULL;}return nodes;}```接下来,需要实现一个函数来找到权值最小的两个节点。
该函数接收一个链表作为输入,并返回该链表中权值最小的两个节点。
```void findMinNodes(TreeNode **nodes, int size, TreeNode**minNode1, TreeNode **minNode2) {*minNode1 = *minNode2 = NULL;for (int i = 0; i < size; i++) {if (*minNode1 == NULL || (*nodes)[i].weight <(*minNode1)->weight) {*minNode2 = *minNode1;*minNode1 = &(*nodes)[i];} else if (*minNode2 == NULL || (*nodes)[i].weight < (*minNode2)->weight) {*minNode2 = &(*nodes)[i];}}}```接下来,需要实现一个函数来构造哈夫曼树。
哈夫曼树的建立及操作

实验六哈夫曼树的建立与操作一、实验要求和实验内容1、输入哈夫曼树叶子结点〔信息和权值〕2、由叶子结点生成哈夫曼树内部结点3、生成叶子结点的哈夫曼编码4、显示哈夫曼树结点顺序表二、实验要点:根据哈夫曼算法,建立哈夫曼树时,可以将哈夫曼树定义为一个构造型的一维数组HuffTree,保存哈夫曼树中各结点的信息,每个结点包括:权值、左孩子、右孩子、双亲,如图5-4所示。
由于哈夫曼树中共有2n-1个结点,并且进展n-1次合并操作,所以该数组的长度为2n-1。
构造哈夫曼树的伪代码如下:在哈夫曼树中,设左分支为0,右分支为1,从根结点出发,遍历整棵哈夫曼树,求得各个叶子结点所表示字符的哈夫曼编码。
三、.函数的功能说明及算法思路BTreeNode* CreateHuffman(ElemType a[],int n)//构造哈夫曼树1.对给定n个权值{a1,a2,…,an}的叶子结点,构成具有n棵二叉树的森林F={T1,T2,…,Tn}, 其中每棵二叉树Ti只有一个权值为ai的根结点,其左右子树为空。
2.在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
3.从F中删除构成新树的两棵树,并把新树参加到F中。
4.重复 2、3两步,直到F只有一棵树为止。
则F中的树就是哈夫曼树。
void PrintBTree(BTreeNode *BT)//以广义表形式输出哈夫曼树主要用到了递归的思想。
void HuffManCoding(BTreeNode *BT, int len)//求哈夫曼编码构造一棵二叉树,左分支标识为0,右分支标识为1,把 n 个字符看成是一棵树的 n个叶子结点,把从根结点到每个叶子结点路径上的分支标识序列作为字符的编码,则得到哈夫曼编码。
四、实验步骤和提示1、编写有关哈夫曼树操作的函数:①构造哈夫曼树 BTreeNode * CreateHuffman(ElemType a[],int n);②以广义表形式输出哈夫曼树 void PrintBTree(BTreeNode *BT);③求哈夫曼编码 void HuffManCoding(BTreeNode *BT, int len)。
哈夫曼Huffman树及应用

8 11 11 0 0
9 8 11 1 7
10 15 12 3 4
哈夫曼树
11 19 13 8 9 12 29 14 5 10
哈夫曼树对应的静态三叉链表13 58 15 6 11
14 100 0 13 14
w,p,lch,rch 是 weight,parent, lchild,rchild
的缩写
哈夫曼算法
如何得到使二进制 串总长最短编码
应用中每个字符的使用频率是不一样的。显然,为使传输 的二进制串尽可能的短,使用频率高的字符用较短编码,使用 频率低的字符用较长编码,电文总长= 原文中字符总数(字符x 使用频率 字符x编码长度)
为设计电文总长最短编码,可通过构造以字符使用频率作 为权值的哈夫曼树实现。
例 某通讯系统只使用8种字符a、b、c、d、e、f、g、h,其使用频率分别为 0.05,0.29,0.07,0.08, 0.14,0.23, 0.03,0.11。构造以字符使用频率作为权值的哈夫曼 树。,将权值取为整数w=(5,29,7,8,14,23,3,11),按哈夫曼算法构造的一棵哈夫曼 树如下:
Y
a<70 N C
a<80
N a<90 Y
N
B
A
4 哈夫曼编码
哈夫曼树除了能求解最优判定问题解,还用于其他一些最优问题的
求解。这里介绍用哈夫曼树求解数据的二进制编码。
在进行数据通讯时,涉及数据编码问题。所谓数据编码就是数据与
二进制字符串的转换。例如:邮局发电报,发送方将原文转换成二进制
字符串,接收方将二进制字符串还原成原文。
1)构造以 a、b、c、d、e、f、g、h为叶子结点的二叉树; 2)将该二叉树所有左分枝标记 0,所有右分枝标记1;
利用哈夫曼树构造哈夫曼编码

利用哈夫曼树构造哈夫曼编码摘要:1.哈夫曼树的概念及构建方法2.哈夫曼编码的概念及编码步骤3.哈夫曼编码的应用实例正文:一、哈夫曼树的概念及构建方法哈夫曼树(Huffman Tree)是一种用于数据压缩的树形结构,它可以将原始数据转换为对应的编码,从而实现压缩。
哈夫曼树的构建方法如下:1.根据输入数据(字符)的出现概率,将所有字符按照出现概率从大到小的顺序进行排序。
2.取出概率最小的两个字符,将它们作为一棵新树的左右子节点,且概率较小的字符在左侧,概率较大的字符在右侧。
3.递归地重复步骤2,直到只剩下一个字符,这个字符将成为哈夫曼树的根节点。
4.从根节点到每个叶子节点的路径代表一个字符的编码,其中左子节点的边表示0,右子节点的边表示1。
二、哈夫曼编码的概念及编码步骤哈夫曼编码(Huffman Coding)是一种基于哈夫曼树的数据编码方法。
哈夫曼编码的特点是每个字符的编码长度与该字符出现的概率成反比,即出现概率较高的字符对应较短的编码,出现概率较低的字符对应较长的编码。
哈夫曼编码的编码步骤如下:1.根据输入数据(字符)的出现概率,构建一棵哈夫曼树。
2.从哈夫曼树的根节点到每个叶子节点的路径代表一个字符的编码,其中左子节点的边表示0,右子节点的边表示1。
3.将每个字符的编码转换为对应的二进制代码,从而实现数据压缩。
三、哈夫曼编码的应用实例哈夫曼编码广泛应用于数据压缩和传输领域,例如:1.在计算机文件压缩中,利用哈夫曼编码可以将原始数据转换为较短的编码,从而减少存储空间和传输时间。
2.在图像和视频压缩中,哈夫曼编码可以有效地去除冗余信息,降低数据量,从而实现更高的压缩率和更快的传输速度。
哈夫曼树的存储结构

哈夫曼树的存储结构1. 哈夫曼树简介哈夫曼树是一种特殊的二叉树,它被广泛应用于数据压缩和编码算法中。
哈夫曼树的主要特点是,频率越高的字符或数据在树中越靠近根节点,频率越低的字符或数据在树中越靠近叶子节点。
哈夫曼树是通过构建最优前缀编码来实现数据压缩的。
最优前缀编码指的是每个字符或数据都有唯一对应的编码,且任何一个字符或数据的编码都不是其他字符或数据编码的前缀。
2. 哈夫曼树的构建算法哈夫曼树的构建算法可以分为以下几个步骤:步骤1:统计字符或数据出现频率首先需要统计待编码的字符或数据出现的频率。
可以通过扫描待编码的文本或文件,记录每个字符或数据出现的次数。
步骤2:创建叶子节点列表将每个字符或数据及其对应的频率作为一个叶子节点,并将它们放入一个列表中。
步骤3:构建哈夫曼树重复以下步骤,直到列表中只剩下一个节点:1.从列表中选择两个频率最低的叶子节点作为左右子节点。
2.将这两个叶子节点的频率之和作为新节点的频率,并将新节点插入到列表中。
3.从列表中删除这两个被选中的叶子节点。
步骤4:生成哈夫曼编码通过遍历哈夫曼树,可以生成每个字符或数据对应的哈夫曼编码。
从根节点开始,遍历左子树时添加0,遍历右子树时添加1,直到达到叶子节点。
3. 哈夫曼树的存储结构哈夫曼树的存储结构可以使用数组或链表来实现。
以下是两种常见的存储结构:数组表示法在数组表示法中,将哈夫曼树的每个节点都保存在一个数组元素中。
假设有n个字符或数据,则需要2n-1个元素来保存所有的节点。
具体存储方式如下:1.使用一个二维数组tree来保存所有的节点信息。
tree[i][0]表示第i个节点的权值(频率),tree[i][1]表示第i个节点的父亲节点索引,tree[i][2]表示第i个节点的左孩子索引,tree[i][3]表示第i个节点的右孩子索引。
2.哈夫曼树的根节点存储在tree[n-1][0]中,叶子节点存储在tree[0]到tree[n-2]中。
