24.2 相似三角形的判定 课件 (沪科版九年上册)4
合集下载
2相似三角形的判定PPT课件(沪科版)

B
两个三角形应具有哪些条件 才是类似的呢?你能给类似 三角形下个定义吗?
三个角对应相等,三条边对应 成比例的两个三角形, 叫做类似 三角形
D
A
B
CE
F
△ ABC与△ DEF类似,就记作: △ ABC∽ △DEF
注意:要把表示对应顶点的
字母写在对应的位置上!
A A'
B
C
B'
C'
A A,B B,C C
类似三角形的判定
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世 界古代七大奇迹之一”。据考证,为建成大金字塔,共动 用了10万人花了20年时间.原高146.59米,但 由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有 所降低 。
埃及著名的考古专家穆罕穆德, 在一个烈日高照的上午.和儿子小穆罕 穆德来到了金字塔脚下,他要他14岁的 儿子用一根1米高的木杆,一把皮尺测 出胡夫金字塔的高度.
类似三角形对应边的比,叫做两个三
角形的类似比。(或类似系数)
A
D
2cm
3cm
B
C E
F
已知△ABC∽△DEF,AC=2cm,DF=3cm
那么△ABC与△DEF对应边的比k1
△DEF与△ABC对应边的比k2=
3 2
=
2 3
三角形的前后次序不同,所得类似比不同。
K1与k2之间是什么关系?
A A'
B'
先证明两个三角形的对应角相等. 在△ADE与△ABC中,∠A=∠A
பைடு நூலகம்
∵DE∥BC
A
∴∠ADE=∠B,∠AED=∠C 再证明两个三角形的对应边的比相等.
过点E作EF∥AB,EF交BC于点F.
相似三角形的判定 第4课时 相似三角形的判定定理3 课件 (共24张PPT) 沪科版数学九年级上册

证明 在线段A'B'(或它的延长线)上截取A'D=AB,过点D作
DE∥B'C',交A'C'于点E,则
△A'DE∽△A'B'C' .
∴
AD AB
DE BC
AE AC
.
又∵ AB BC AC ,A'D=AB, AB BC AC
∴
DE BC
BC ,AE BC AC
AC . AC
∴DE=BC,A'E=AC.
情境引入 新知探索 例例题辨析析 练习巩固 总结归纳 作业布置
典例 1 在△ABC和△A'B'C'中,已知下列条件成立,判断这两
个三角形是否相似,并说明理由. (1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°; (3)AB=2,BC= 2 ,AC= 10 ,A'B' = 2 ,B'C' =1,A' C' = 5 .
22.2 相似三角形的判定
第 4 课时 相似三角形的判定定理3
●我们每个人手里都有一把自学成才的钥匙: 理想、勤奋、毅力、虚心和科学方法。 ——华罗庚
1 理解相似三角形判定定理3的推导过程
学习 目标
2 掌握相似三角形的判定定理3.(重点) 3 能熟练运用相似三角形的判定定理3.(难点)
4
课堂学习总结感悟与知识提升
△ABC∽△A'B'C'
导情入境引新入课 新知探索 例题辨析 练习巩固 总结归纳
数学:24.2《相似三角形的判定》课件(沪科版九年级上)

练一练:
写出图中的相似三角形:
(1)条件: DE∥BC EF∥AB A (2)条件 (3)条件 ∠ACB=90° CD⊥AB于D
∠A=36°
AB=AC BD平分∠ABC A
36°
C
D
B
E F C
B
D C
△ABC∽△BDC
A
D
B
△ADE∽△ABC∽△EFC
△ACB∽△ADC∽△CDB
例题欣赏:
如图C是线段BD上的一点, AB⊥BD.ED⊥BD.AC⊥EC 求证:△ABC∽△CDE 证明: ∵AB⊥BD、ED⊥BD ∴∠ABC=∠CDE=90° ∴∠1+∠A=90°
一、知识回顾
1、根据相似多边形的定义,你知道什么样的 两个三角形相似吗?
满足 (1)对应角相等 (2)对应边成比例 两个条件的两个三角形是相似三角形.
C′ A′ B′ A
C
B
2、请同学们画图表示相似三角形
判定定理的预备定理
A E A D E
D
B
C
B
C
DE∥BC
△ADE∽△ ABC
二、课堂活动:
已知在△ABC和△A′B′C′中.∠A=∠A′ ∠ B=∠B′ ∠ C=∠C′ A 求证:△ABC∽△A′B′C′
证明: 在△ABC的边AB(或延长线)
上截取AD=A′B′.过点D作DE∥BC.交 AC于点E.则有 △ADE∽△ABC ∵∠ADE=∠B ∠B=∠B′
A′
D B
E C B′ C′
∴∠ADE=∠B′
又∵∠A=∠A′ AD=A′B′ ∴△ADE≌△A′B′C′(ASA)
∴△A′B′C′∽△ABC
由上面的数学活动我们可以得到判定三 角形相似的定理
沪科版九年级数学上册相似三角形的判定课件

随堂练习
6. 如图,△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °, ∠F=60 ° .求证:△ABC ∽△DEF.
证明:∵ 在△ ABC中,∠A=40 ° ,∠B=80 ° , A
∴ ∠C=180 °-∠A-∠B=60 °. ∵ 在△DEF中,∠E=80 °,∠F=60 °. ∴ ∠B=∠E,∠C=∠F.
【分析】欲证AB·DE=BC·CD, 可证 = ,则证明 △ABC∽△CDE即可,由题意可
知∠1+∠2=90°,∠1+∠A=
90°,则∠2=∠A.于是 Rt△ABC∽Rt△CDE.
证明:∵AB⊥BD,ED⊥BD,AC⊥CE, ∴∠B=∠D=90°,又∠1+∠A=90°,Байду номын сангаас1+∠2=90°, ∴∠A=∠2, ∴△ABC∽△CDE,
2.如图,等边三角形ABC的边长为3,P为BC上一点,且 BP=1,D为AC上一点,当∠APD=60°时,CD的长为 __________.
随堂练习
3.如图:点G在平行四边形ABCD的边DC的延长线上,AG交 BC、BD于点E、F,则△AGD∽_△__E__G_C___∽_△__E_A__B__.
探究新知
探究 如图在△A′B′C′和△ABC中,∠A′=∠A,∠B′= ∠B.求证:△A′B′C′∽△ABC. 证明:在△ABC的AB上截BD=B′A′,
过D作DE∥AC,交BC于E.
∴△ABC∽△DBE.
∵∠BDE=∠A,∠A=∠A′, ∴∠BDE=∠A′. ∵∠B=∠B′,BD=B′A′, ∴△DBE≌△B′A′C′. ∴△ABC∽△A′B′C′.
定理:两角分别相等的两个 三角形类似
类似三角形的判定定理1的运用
∴ = ,即AB·DE=BC·CD.
上海教育版数学九上24.4《相似三角形的判定》(第4课时)ppt课件

回顾与思考
1.我们学习了几种判定三角形全等的方法?
2.什么是“勾股定理”?
1
24.4(4)相似三角形的判定
2
思考与归纳
如图,在Rt△ABC和Rt△A1B1C1中,如果∠C=∠C1、
0
AB BC 90 , A1 B1 B1C1
,那么Rt△ABC和Rt△A1B1C1 相似吗?
A
A1
C1
B1
C B 直角三角形相似的判定定理: 如果一个直角三角形的斜边和一条直角边与另一个直角三角形 的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 简述:斜边和直角边对应成比例,两个直角三角形相似.
B
D
A
E
C
7
作
业
练习册:24.4(4)
8
∵ C C1 900 ,
AB BC A1B1 B1C1
∴ Rt△ABC∽Rt△A1B1C1
3
举
例1
已知: BC b, AC ab
求证: DC BC
A D
B
C
4
举
例2
已知:梯形ABCD中,∠B=900,AB∥CD,AB=3,CD=7,
BC=10,在BC上是否存在点P,使得△ABC与△DCP相似? 如存在,请求出BP的长度。 D A B C
5
举
例3
已知:梯形ABCD中,∠C=900,AD∥BC,点E是CD中点,
且 AE DE
BE
BC
求证:AE平分∠BAD A D
E B C
6
练 一 练
已知:△ABC中,∠B=900 ,AC CE CD BC 求证:ED⊥BC
1.我们学习了几种判定三角形全等的方法?
2.什么是“勾股定理”?
1
24.4(4)相似三角形的判定
2
思考与归纳
如图,在Rt△ABC和Rt△A1B1C1中,如果∠C=∠C1、
0
AB BC 90 , A1 B1 B1C1
,那么Rt△ABC和Rt△A1B1C1 相似吗?
A
A1
C1
B1
C B 直角三角形相似的判定定理: 如果一个直角三角形的斜边和一条直角边与另一个直角三角形 的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 简述:斜边和直角边对应成比例,两个直角三角形相似.
B
D
A
E
C
7
作
业
练习册:24.4(4)
8
∵ C C1 900 ,
AB BC A1B1 B1C1
∴ Rt△ABC∽Rt△A1B1C1
3
举
例1
已知: BC b, AC ab
求证: DC BC
A D
B
C
4
举
例2
已知:梯形ABCD中,∠B=900,AB∥CD,AB=3,CD=7,
BC=10,在BC上是否存在点P,使得△ABC与△DCP相似? 如存在,请求出BP的长度。 D A B C
5
举
例3
已知:梯形ABCD中,∠C=900,AD∥BC,点E是CD中点,
且 AE DE
BE
BC
求证:AE平分∠BAD A D
E B C
6
练 一 练
已知:△ABC中,∠B=900 ,AC CE CD BC 求证:ED⊥BC
沪教版(上海)初中数学九年级第一学期2相似三角形的判定课件

课堂练习:
1、如图:E是平行四边形ABCD的边BA 延长线上的一点,CE交AD于点F.图中 有那几对类似三角形?
E
E
E
A
F
D
A
F
F
A
D
B
C
B
C
C
∵AD∥BC
∵AB∥CD
∴△AFE∽△BCE
∴△AFE∽△DFC
由类似传递性可得:△DFC∽△BCE
课堂练习:
2、如图: △ABC∽△AED,AG=3,AD=6,AF=2,EF=6, 则△AFG与△ABC类似吗? 为什么?
∵ DE∥BC
ADE ∽ ABC
布置作业:练习册24.4(1)
A1B1 A1C1 B1C1
A1B1 A1C1 B1C1
A2 B2 A2C2 B2C2
A A1, B B1, C C1
类似三角形的定义
A1 A2 , B1 B2 , C1 C2
等量代换得
AB AC BC A2 B2 A2C2 B2C2
A A2 , B B2 , C C2
×可得: △ABC∽△A B C AB A1B1 AC A1C1 BC B1C1
A1B1 A2B2 A1C1 A2C22 B21C1 2 B2C2
类似三角形具有传递性(判定方法)
如果两个三角形分别与同一个三角形类似, 那么这两个三角形也类似. 符号语言:
∵ ABC ∽ A1B1C1 , A1B1C1 ∽ A2 B2C2 ∴ ABC ∽ A2B2C2 (类似三角形的传递性)
探究3 如图,点D、E分别在直线AB和AC 上,且DE∥BC ,那么△ADE 与
课堂小结: 本节课主要学习了什么,有何收获?
1、类似三角形的定义. 2、类似三角形的性质.
初中数学沪科版九年级上册第22章相似形2相似三角形的判定 全省一等奖-完美PPT课件

由此得出,BC=2B′C′
从而
B'C BC
'
1 2
A'B' AB
A'C ' . AC
因此△ A′B′C′∽△ABC. (三边对应成比例的两个三角形相似
22.2.4 相似三角形的判定(4)
课堂小结
定理:三边对应成比例的两个三角形相似
利用三边 判定三角 形相似
相似三角形的判定定理3的运用
22.2.4 相似三角形的判定(4)
22.2.4 相似三角形的判定(4)
新知应用
例1 判断图中的两个三角形是否相似,并说明理由.
C
3
3.5
D 2.4
E
1.8
2.1 F
A
4
B
解:在△ABC 中,AB>BC>CA,在△DEF中,DE>EF>FD.
DE 2.4 0.6, EF 2.1 0.6, FD 1.8 0.6,
AB 4
BC 3.5
随堂练习 已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(1)AB=3, BC=4, AC=6. 否
DE=6, EF=8, DF=9.
(2)AB=4, BC=8, AC=10. 是 DE=20, EF=16, DF=8.
(3) AB=12, BC=15, AC=24.
否
DE=16, EF=20, DF=30.
(2)两个三角形在同一图形中. C
22.2.4 相似三角形的判定(4)
新知探究
(3)判定定理1:两角分别相等的两个三角形相似.
(4)判定定理2:两边成比例且夹角相等的两个三角形相似.
思考:类比全等三角形的判定方法,还有其他判定两个三角 形相似的方法吗?
沪科版数学九年级上册相似三角形的判定定理课件

A
5
8
D 10
B 12
C
E
F
3:如图,在6×6的正方形方格中,△ABC与△DEF的顶点都 在边长为1的小正方形的顶点上,
(1)填空: BC=____2__, AC=____1_0___ EF=__2__2__, DF=__2__1__0___.
(2)△ABC与△DEF相似吗?若 A 相似,请给出证明,若不相似, 请说明理由.
是否有△ABC∽△A'B'C'
在纸上画两个三角形△ABC 和 △A'B'C' ,使AB =4厘米, AC =6厘米,
BC =8厘米,A'B' =2厘米, A'C' =3厘米 ,B'C' =4厘米. 回答下面
的问题:
A
4 cm
6cm
(1)分别计算 A' B' , B' C,' , A' C'
AB BC AC
这三个比值相等吗? (2)剪下画出的三角形,利用叠合的方法,
检验对应内角之间具有怎样的大小关系?
B
8 cm
A'
2 cm
3cm
B' 4 cm C'
C (3)△ABC与△A'B'C' 相似吗?为什么?
如果改变 △ABC与△DEF的边长,并保持 A' B' B' C' A' C' AB BC AC 还能得到同样的结论吗?
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC , ∴ ∵ AD AB, AD AB
AB AB
又 AB AC BC
相似三角形的判定定理课件沪科版数学九年级上册

课堂小结
1.两个三角形全等的判定有哪几种方法? 2.是不是需要所有的对应边和对应角都相等?
∴ ΔABC∽ΔDEF(两角对应相等,两三角形相似)。
600 C
E 800
600 F
新知讲解
例2 △ABC 中, D、E 分别是AB、 AC上的点,且 DE∥BC,试
说明△ABC与△ADE相似。
(1)试说明: AD·AC=AE·AB; (2)若AD=4,AE=3,AB=6,求AC。
A
E
D
A
D
E
B
C
22.1 相似三角形的判定
第二课时
相似三角形的判定定理1
学习目标
1.通过探索,掌握相似三角形的判定定理1(重点) 2.能运用相似三角形的判定方法解决数学问题(难点)
复习回顾
1. __对__应__边__成__比__例__,_对__应__角__相__等_________的两个
三角形, 叫做相似三角形
2. 相似三角形的特征:对__应__边__成__比__例__,__对__应__角__相__等__。
A
如果△ ABC∽ △DEF, 那么
AB AC BC DE DF EF
B D C
∠A=∠D, ∠B=∠E, ∠C=∠F
E
F
新知讲解
观察老师的两个直角三角尺
这两个三角形的三个内角之间有什么关系? 三个内角对应相等。
思 考 ?如果两个三角形仅有一对角是对应相等的,那么它们是否一 定相似?
新知讲解
它们是相似三角形吗?为什么?
A
A′
5
82° 3
82°
B 47°
66
C
10
6
51°
沪科版数学九年级上册2相似三角形的判定课件(共66张)

A
DE B AC
B
C
D
E
ED
A
B
C
符号语言 在△ABC中, 若DE∥BC,(如图所示) 则△ADE∽△ABC。
巩固练习
如图,在平行四边形ABCD中,
DE交BC于F,交AB的延长线于点E。
D
C (1)请写出图中类似的三角形;
F
(2)请由其中的一对类似三角形写
A
出相应的比例式;
B
E (3)请说明AE·BF与AD·BE是否
线),所得对应线段成比例。即可得 到 AD AE DE 。
AB AC BC
A
E C
证明:
过点D作AC的平行线,交BC于F。
∵DE∥BC,DF∥AC,
A
AD AE , FC AD .
AB AC BC AB
D
因为四边形DFCE是平行四边形,
E
∴DE=FC,
DE BC
AD AB
.
B
C
F
AD AE DE . AB AC BC
即写成△ABC∽△A′B′C′,表明对应关系 是唯一确定的,即A与A′、B与B′、C与C′分别 对应。如果仅说“这两个三角形类似”,没有 用“∽”表示的,则没有说明对应关系。
类似三角形的对应关系
对于△ABC∽△A′B′C′,根据类似三角形的定 义,应有∠A= ∠A′,∠B= ∠B′,∠C=∠C′,
想一想:
1.△ABC和△A′B′C′中,∠A=80°、∠B=40°、 ∠A′=80°、∠C′=60°,那么这两个三角形类似吗? 2.等边三角形都类似吗? 3.一个锐角对应相等的两个直角三角形类似吗? 4.有一个内角对应相等的两个等腰三角形类似吗? 5.各有一个内角为100°的两个等腰三角形类似吗?
DE B AC
B
C
D
E
ED
A
B
C
符号语言 在△ABC中, 若DE∥BC,(如图所示) 则△ADE∽△ABC。
巩固练习
如图,在平行四边形ABCD中,
DE交BC于F,交AB的延长线于点E。
D
C (1)请写出图中类似的三角形;
F
(2)请由其中的一对类似三角形写
A
出相应的比例式;
B
E (3)请说明AE·BF与AD·BE是否
线),所得对应线段成比例。即可得 到 AD AE DE 。
AB AC BC
A
E C
证明:
过点D作AC的平行线,交BC于F。
∵DE∥BC,DF∥AC,
A
AD AE , FC AD .
AB AC BC AB
D
因为四边形DFCE是平行四边形,
E
∴DE=FC,
DE BC
AD AB
.
B
C
F
AD AE DE . AB AC BC
即写成△ABC∽△A′B′C′,表明对应关系 是唯一确定的,即A与A′、B与B′、C与C′分别 对应。如果仅说“这两个三角形类似”,没有 用“∽”表示的,则没有说明对应关系。
类似三角形的对应关系
对于△ABC∽△A′B′C′,根据类似三角形的定 义,应有∠A= ∠A′,∠B= ∠B′,∠C=∠C′,
想一想:
1.△ABC和△A′B′C′中,∠A=80°、∠B=40°、 ∠A′=80°、∠C′=60°,那么这两个三角形类似吗? 2.等边三角形都类似吗? 3.一个锐角对应相等的两个直角三角形类似吗? 4.有一个内角对应相等的两个等腰三角形类似吗? 5.各有一个内角为100°的两个等腰三角形类似吗?
沪教版(上海)九年级上册数学 24.4相似三角形的判定 课件(共29张ppt)

相似吗?
A
A1
B
C B1
C1
直角三角形相似的判定定理:如 果一个直角三角形的斜边和一条 直角边与另一个直角三角形的斜 边和一条直角边对应成比例,那 么这两个直角三角形相似.
简述为:斜边和直角边对应成比 例,两个直角三角形相似.
C
C1
90 0 ,
AB A1 B1
BC B1C1
RtABC ∽ RtA1B1C1
AB AC CA A1B1 A1C1 C1A1
ABC∽ A1B1C1
例题3:已知如图,D、E、F分别是 ABC 的边BC、
CA、AB的中点.求证: DE∽F ABC
A
F
E
B
D
C
例题4:如图,在正方形网格上有两个三角形 A1B1C1 和 A2B2C2 求证:△ A1B1C1 ∽△ A2B2C2
(1)以下各图放置的小正方形的边长都相同,分别以小正方 形的顶点为顶点画三角形,则与△ABC相似的三角形图形为
24.4相似三角形的判定 (1)
1、什么叫做全等三角形?它在形状上、大小上 有何特征?
2.两个全等三角形的对应也和对应角有什么关 系?
3、复习平行线分线段成比例定理(文字表述及 基本图形)
A
A1
B
C B1
C1
新授1: 相似三角形的定义,相似比的概念 相似三角形的概念: 我们把对应角相等、对应边成比例 的两个三角形,叫做相似三角形 相似比的概念 :相似三角形对应边的比K,叫做相似比 (或相似系数). 注:①两个相似三角形的相似比具有 顺序性. ②全等三角形的相似比为1,这也说明了全等三 角形是相似三角形的特殊情形.
A1B1 A1C1 AB AC
,证明: △ABC ∽△ A1B1C1
沪教版(上海)初中数学九年级第一学期2相似三角形的判定课件

B1C1,垂足分别为点D,D1,且
AB A1B1
AD A1D1
求证:△A B C ∽△A1B1C1
课堂小结
直角三角形类似的判定方法:
预备定理
(判定定理1)两角对应相等
有一锐角相等的两Rt△类似
(判定定理2)两边对应成比例且夹角相等 (判定定理3)三边对应成比例 (特殊)斜边和直角边对应成比例
布置作业
HL
斜边和一条直角边对应相等, 两直角三角形全等
猜想:斜边和一条直角边对应成比例, 两直角三角形类似
已 知 : 如 图 , 在Rt△ABC与Rt△A1B1C1中 ,C C1 90 AB AC A1B1 A1C1
求 证 :Rt△ABC ∽ Rt△A1B1C1
A
A1
C
B
C1
B1
直角三角形类似判定方法
如果一个直角三角形的斜边和一条直角边与 另一个直角三角形的斜边和一条直角边对应成比 例,那么这两个直角三形类似。
简单地说: 斜边和直角边对应成比例,两直角三角形类似。
看一看
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列两个直 角三角形是否类似?
(1)
D
A
45
12
15
C
B
F
E
(2)
A
5
C
( 2 ) AC=3,BC=4,A'C'=6,B'C'=8
两边对应成比例且夹角相等,两三角形类似
AC BC C C △ABC ∽△ABC AC BC
( 3 ) AC=3,AB=5,A'C'=6,A'B'=10
△ABC ∽△ABC
你的判定根据是?
沪科版数学九年级上册2相似三角形判定课件
视察你与老师的直角三角尺(30O 与60O) ,会类似吗?
这两个三角形的三个内角的 大小有什么关系?
相
三个内角对应相等。
似
三个内角对应相等的两个三角 形一定类似吗?
2. 两个人画出两个三角形 ,使三个角 分别为60°,45°, 75° .
①分别量出两个三角形三边的长度; ②这两个三角形类似吗?
视察 即: 如果一个三角形的三个角分别与另一个三角 形的三个角对应相等,那么这两个三角形_______.
△ACD∽△ABC。 (或者∠ ACB=∠ ADB) (2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 DE//BC,就可以使△ADE与原△ABC类似。
(或者∠ C=∠ ADE)
A
(或者∠ B=∠ ADE)
A
D
B
C
图3
E
●
Hale Waihona Puke BC图4A
2 1
A
C
O
B
C
A
C
D
O
D
E
B
CA
B D
A
D
E
BB
C
课堂小结
一定需三个角吗?
类似三角形的辨认方法: 如果一个三角形的两角分别与另一个三角形的两
角对应相等,那么这两个三角形类似. 思考 如果两个三角形仅有一对角是对应相等的,那么它 们是否一定类似?
类似三角形的辨认
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
A
A'
∴ ΔABC ∽ ΔA'B'C'
B
C B' C'
例3.已知D、E分别是△ABC的边AB,AC上的点, 若∠A=35°, ∠C=85°,∠AED=60 °则AD·AB= AE·AC
这两个三角形的三个内角的 大小有什么关系?
相
三个内角对应相等。
似
三个内角对应相等的两个三角 形一定类似吗?
2. 两个人画出两个三角形 ,使三个角 分别为60°,45°, 75° .
①分别量出两个三角形三边的长度; ②这两个三角形类似吗?
视察 即: 如果一个三角形的三个角分别与另一个三角 形的三个角对应相等,那么这两个三角形_______.
△ACD∽△ABC。 (或者∠ ACB=∠ ADB) (2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 DE//BC,就可以使△ADE与原△ABC类似。
(或者∠ C=∠ ADE)
A
(或者∠ B=∠ ADE)
A
D
B
C
图3
E
●
Hale Waihona Puke BC图4A
2 1
A
C
O
B
C
A
C
D
O
D
E
B
CA
B D
A
D
E
BB
C
课堂小结
一定需三个角吗?
类似三角形的辨认方法: 如果一个三角形的两角分别与另一个三角形的两
角对应相等,那么这两个三角形类似. 思考 如果两个三角形仅有一对角是对应相等的,那么它 们是否一定类似?
类似三角形的辨认
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
A
A'
∴ ΔABC ∽ ΔA'B'C'
B
C B' C'
例3.已知D、E分别是△ABC的边AB,AC上的点, 若∠A=35°, ∠C=85°,∠AED=60 °则AD·AB= AE·AC
初三上数学课件(沪科版)-相似三角形的判定定理
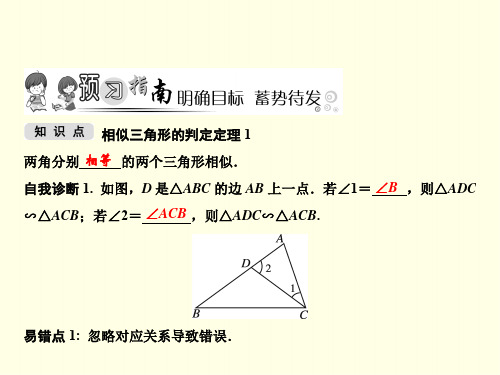
13.如图,已知∠1=∠2=∠3.求证△ABC∽△ADE.
证明:∵∠1+∠B=∠ADC=∠ADE+∠2,∠1=∠2,∴∠B=∠ADE, ∵∠1=∠3,∴∠1+∠DAC=∠3+∠DAC,即∠BAC=∠DAE,∴△ABC ∽△ADE.
14.(永州中考)如图,D 是△ABC 的边 AC 上的一点,连接 BD,已知∠ABD =∠C,AB=6,AD=4,求线段 CD 的长.
A.1
B.2
C.3
D.4
10.如图,在△ABC 中,∠C=90°,D、E 分别是 AB、AC 上的点,若 AD·AB =AC·AE,那么∠ADE 的度数为 90° .
11.如图,在矩形 ABCD 中,AB=2,BC=1,E 是 DC 上一点,∠DAE= 3
∠BAC,则 EC 的长为 2 .
12.如图,一束光线从 y 轴上的点 A(0,1)发出,经过 x 轴上点 C 反射后,经 过点 B(6,2),则点 C 的坐标是 (2,0) .
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=35°,∠B′=55°
C.∠A=∠B,∠B′=∠A′
D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
2.如图所示,在△ABC 中,∠AED=∠B,则下列等式成立的是( C )
A.DBCE=ADDB
B.ABEC=ABDC
C.DCBE=AABE
8.在△ABC 和△A′B′C′中,∠B=∠B′=90°,∠A=30°,则以下条
件,不能证明△ABC 与△A′B′C′相似的是( C )
A.∠A′=30°
B.∠C′=12∠C′
9.如图,已知△ABC 和△ADE 均为等边三角形,D 在 BC 上,DE 与 AC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
提问5:如果把提问4中的条件改为一条斜边和一条直角边对应成比例呢?
Copyright 2004-2009 版权所有 盗版必究
判定直角三角形全等,除了应用一般的SAS ,AAS,ASA,SSS以外,是否还有其他特殊的 判定方法?
直角三角形相似的判定
判定定理:如果一个直角三角形的斜边和 一条直角边与另一个直角三角形的斜边和 一条直角边对应成比例,那么这两个直角 三角形相似。
Copyright 2004-2009 版权所有 盗版必究
判定定理:如果一个直角三角形的斜边和一条直角边与另一 个直角三角形的斜边和一条直角边对应成比例,那么这两个直 角三角形相似。
(1)画图; (2)参照图形写出已知;
A
A’
已知,在△ABC与△A’B’C’中, ∠C= ∠C’=900
C
B
C’
B’
△ABC∽△A’B’C’
Copyright 2004-2009 版权所有 盗版必究
根据下列条件,判定Rt ABC和Rt A ' B ' C ' 是否相似,其中 C=C'=, 900 (1)A=63 , B ' 27 ;
o o
(2) AC 14cm, BC 6cm, A ' C ' 7cm, B ' C ' 3cm; (3) AB 6, AC 3, A ' B ' 30, A ' C ' 15.
Copyright 2004-2009 版权所有 盗版必究
已知,在Rt△ABC中,CD是斜边上的高线。求证: △CBD∽△ACD ∽ △ABC。
证明 : CDB ACB Rt
B B
}
同理可证 ∴
△CBD∽△ACD △ACD ∽ △ABC
△CBD∽△ACD ∽ △ABC
Copyright 2004-2009 版权所有 盗版必究
2、 直角三角形相似的判定 判定定理:如果一个直角三角形的斜边和一条直角边与另一个 直角三角形的斜边和一条直角边对应成比例,那么这两个直角 三角形相似。
Copyright 2004-2009 版权所有 盗版必究
能否说“如果一个三角形的两条边和另一 个三角形的两条边对应成比例,并且有一个 角对应相等,那么这两个三角形相似”? 如果这两个三角形都是直角三角形呢?
Copyright 2004-2009 版权所有 盗版必究
1、直角三角形相似判定的特殊性 (1)有一个锐角对应相等的两个三角形相似; (2)两直角边对应成比例的两直角三角形相似。
(3)参照图形写出求证; 求证: △ABC∽△A’B’C’ (4)写出证明过程。
Copyright 2004-2009 版权所有 盗版必究
已知,在△ABC与△A’B’C’中, ∠C= ∠C’= 900,
A
A’
求证: △ABC∽△A’B’C’。 C B C’ B’
证明:C C ' 90
BC B 'C '
CE⊥AB
Copyright 2004-2009 版权所有 盗版必究
练习:
1.找出例2图中的各对相似的直角三角形。
2 .如图, ∠DEB= ∠ACB=Rt ∠,DE=2,AB=5, BC=3,BD=2.5,求证:AB平分∠DBC。
Copyright 2004-2009 版权所有 盗版必究
想一想:
0
BC AB2 AC 2 B ' C ' A ' B '2 A ' C '2
AB 2 AC 2 A ' B '2 A ' C '2
Copyright 2004-2009 版权所有 盗版必究
( AB AC )( AB AC ) ( A ' B ' A ' C ')( A ' B ' A ' C ')
AB AC AB AB AC AB AC A ' B ' A ' C ' A ' B ' A ' B ' A ' C ' A ' B ' A ' C '
AB 0 A' B '
2
}
BC AB AB AC BC AB B 'C ' A' B ' A ' B ' A 'C ' B 'C ' A' B '
例二 如图,CE交△ABC的高线AD于点O,交AB于E,且 OC ·BD=AB ·OD,求证:CE⊥AB.
证明 :
OC BD AB OD
OC OD AB BD
Hale Waihona Puke ADB ODC Rt
}
∠BAD= ∠ OCD ∠AOE= ∠ COD
△ABD ∽ △COD
}
∠AEO= ∠ CDO=Rt ∠
Copyright 2004-2009 版权所有 盗版必究
学习目标
1、掌握两个直角三角形相似的 判定方法; 2、灵活应用直角三角形相似的 判定方法,解决有关计算和证 明问题。
Copyright 2004-2009 版权所有 盗版必究
提问1:目前我们判定两个三角形相似的方法有哪些? 提问2:我们已经学过几种特殊的三角形? 提问3:有一个锐角相等的两个直角三角形是否相似? 提问4:一个直角三角形的两条直角边和另一个直角三角形的两条直角边对 应成比例,这两个直角三角形是否相似?
Copyright 2004-2009 版权所有 盗版必究
例一 求证:直角三角形斜边上的高线分成的两个直角三 角形和原三角形相似。
(1)画图; (2)参照图形写出已知; 已知,在Rt△ABC中, CD是斜边上的高线 (3)参照图形写出求证; 求证: △CBD∽△ACD ∽ △ABC (4)写出证明过程。
