解绝对值不等式的方法总结(1)
绝对值不等式的解法及应用

绝对值不等式的解法及应用绝对值不等式在数学中具有重要的应用价值,在各个领域中都有广泛的运用。
本文将对绝对值不等式的解法进行简要说明,并介绍其在实际问题中的应用。
一、绝对值不等式的解法1. 求解一元绝对值不等式对于形如 |x|<a 的不等式,其中 a>0 ,我们可以将其分解为两个简单的不等式,即 x<a 和-x<a ,然后再根据这两个不等式得到解的范围。
例如,对于 |x|<3 这个不等式,我们可以拆分为 x<3 和 -x<3 ,再分别求解这两个不等式,得到解的范围为 -3<x<3 。
2. 求解含有绝对值不等式的方程对于形如 |f(x)|=g(x) 的方程,可以通过以下步骤求解:Step 1: 根据绝对值的定义,将绝对值拆解为两个条件,即 f(x)=g(x) 和 f(x)=-g(x) 。
Step 2: 分别求解这两个条件对应的方程,得到解的范围。
Step 3: 将 Step 2 中得到的解进行合并,得到最终的解集。
例如,对于 |x-2|=3 这个方程,我们可以拆解为 x-2=3 和 x-2=-3 ,然后求解这两个方程得到 x=5 和 x=-1 ,最终的解集为 {5, -1} 。
二、绝对值不等式的应用绝对值不等式在实际问题中有广泛的应用,下面将介绍其中两个常见的应用领域。
1. 绝对值不等式在不等式求解中的应用在不等式求解中,绝对值不等式是一种常见的工具。
通过合理地运用绝对值不等式,可以简化不等式的求解过程,提高解题效率。
下面通过一个例子来说明。
例题:求解不等式 |2x-1|<5 。
解:根据绝对值的定义,将不等式拆分为两个条件,即 2x-1<5 和2x-1>-5 。
然后分别求解这两个条件对应的方程,得到 x<3 和 x>-2 。
最后将这两个解的范围进行合并,得到最终的解集为 -2<x<3 。
2. 绝对值不等式在数列问题中的应用在数列问题中,绝对值不等式可以用来求解数列的范围,帮助我们找到数列的性质和规律。
含绝对值不等式的解法(1)

题型四 | f (x) | g(x) , | f (x) | g(x)
不等式两边平方法化为 | f (x) |2 g(x) 2 , | f (x) |2 g(x) 2
作业:解下列不等式。
1、|2x-3|<5x 2、|x2-3x-4|<4 3、| x-1 | > 2( x-3) 4、2x 1 x 2 5. x+|2x+3|>2.
数 都 不 是 原 不 等 式 的 解。 将 点A向 左 移 动1个 单 位 到 点A1, 这 时 有A1 A A1B 5; 同 理, 将 点B向 右 移 动 一 个 单 位 到 点B1, 这 时 也 有B1 A B1B 5, 从 数 轴 上 可 以 看 到 点A1与B1之 间 的 任 何 点 到 点A, B的 距 离 之 和 都 小 于5; 点A1的 左 边 或 点B1的 右 边 的 任 何 点 到 点A,, 的 距 离 之 和 都 大 于。 故 原 不 等
是
.
2 x 0,x 2, x ,2
【做一做】 (3)若不等式|2-x|>2-x成立,则实数x的取值范围
是
.
解析:依题意 x-2<0,解得 x<2.
答案: -∞,2
变式例题:
如果把|x|<2中的x换成“x-1”,也就是 | x-1 | <2如何解?
如果把|x|>2中的x换成“3x-1”,也就 是 | 3x-1 | >2如何解?
绝对值不等式的解法(一) 郑慧
复习绝对值的意义:
代数的意义
x X>0 |x|= 0 X=0
- x X<0 一个数的绝对值表示:
几何意义
数轴上与这个数对应的 点到原点的距离,|x|≥0
x2
绝对值不等式解法

典例讲解
例1解下列不等式
| 2 x 1 || x 1 | (3) | x 1 | | x 3 | 5 (2) (1) | 2 x 1 | 1
解:(2)原不等式两边平方得: (2x 1) ( x 1)
2
2
平 方 法
整理得: x 2 x 0
2
x 0或x 2
10 5 2 答案:(1) [ 3 , 3 ) (1, 3 ] 1 (2) ( , ) 2
(3) (,7] (2,)
不等式的解集为: (,0) (2,)
分段解不等式问题要点: 段内求交,段与段求并
典例讲解
| x 1 | | x 3 | 5 | 2 x 1 || x 1 | (3) (2) | 2 x 1 | 1 (1)
( x 1) ( x 3) 5 解:(3)当 x 1 ,原不等式可化为: 3 3 x x ,此时解为: 2 2 分 当 1 x 3 ,原不等式可化为: ( x 1) ( x 3) 5 段 4 5 ,此时解为:x无解 法 当 x 3 ,原不等式可化为: ( x 1) ( x 3) 5
典例讲解பைடு நூலகம்
例1解下列不等式
| 2 x 1 || x 1 | (3) | x 1 | | x 3 | 5 (2) (1) | 2 x 1 | 1
解:(1)原不等式可化为: 公 式 法
2 x 1 1或2 x 1 1
x 0或x 1
不等式的解集为: (,0) (1,)
7 7 x ,此时解为:x 2 2
例1解下列不等式
综上所述,不等式的解集为
3 7 ( , ) ( , ) 2 2
解绝对值不等式的方法

解绝对值不等式的方法绝对值不等式是数学中常见且重要的一种不等式类型。
解绝对值不等式可以帮助我们确定变量的取值范围,从而求解问题。
本文将介绍三种常用的方法来解绝对值不等式。
一、符号法符号法是解绝对值不等式最简单直观的方法之一。
当我们遇到简单的一元一次绝对值不等式时,可以通过考虑绝对值的取正负两种情况来解决。
例如,对于不等式|x-2|<5,我们可以先考虑取正的情况:x-2<5 --> x<7然后再考虑取负的情况:-(x-2)<5 --> x>-3综合两个不等式的解集,我们得到-3<x<7,即解为(-3,7)。
二、区间法区间法是一种更加系统和严谨的方法,适用于更复杂的绝对值不等式。
该方法基于绝对值的定义,将不等式转化为分段函数的形式。
例如,对于不等式|2x-1|≥3,我们可以先将其拆分为两个情况:1. 当2x-1≥0时,不等式变为2x-1≥3,解得x≥2。
2. 当2x-1<0时,不等式变为-(2x-1)≥3,解得x≤-1。
综合两个情况的解集,我们得到解为x≤-1或x≥2。
三、平方法平方法是解决带有二次项的绝对值不等式的常用方法。
该方法的关键是利用平方的非负性。
例如,对于不等式|x^2-4|<3,我们可以先对不等式进行拆分:1. 当x^2-4≥0时,不等式变为x^2-4<3,解得-1<x<3。
2. 当x^2-4<0时,不等式变为-(x^2-4)<3,展开后得到x^2-4>-3,解得-√7<x<√7。
综合两个情况的解集,我们得到解为-√7<x<-1或1<x<√7。
绝对值不等式的解方法还有其他变种,上述仅是其中常用的三种方法。
在解题过程中,我们需要根据不等式的形式和特点选择合适的方法。
此外,需要注意绝对值不等式的符号翻转和取等问题。
总结起来,解绝对值不等式的方法有符号法、区间法和平方法等。
解绝对值不等式的方法总结

解绝对值不等式的方法总结
1. 分类讨论法:
根据绝对值符号,将条件分为两种情况,分别对式子做处理,最后将解集联合起
来就可以求出绝对值不等式的解集。
例如:解不等式|2x+3|<5,可以写成如下形式:
2x+3<5 且 -2x-3<5,解出两个不等式的解集,解集:x<1 且 x>-2,因此解集为 x<1 U
x>-2,其中U表示并。
2. 代入法:
根据条件可以得到相应绝对值不等式,首先将相关数字代入不等式中,质疑是否
满足不等式,如果满足,表示相应数属于此绝对值不等式解集;如果不满足,表示该数不
属于此绝对值不等式解集。
例如:解不等式|x-5|≤2,x=7时,将x=7代入不等式,可得
|7-5|≤2,满足不等式,因此x=7属于此不等式的解集。
4. 化简法:
根据不等式的特殊性可以将不等式转化为熟悉的不等式,再求其解,最后再转化
回原来的绝对值不等式,以求出解集。
例如:解不等式|5x-6|>10,先将左边绝对值分离,变为 5x-6>10 且 -(5x-6)>10 ,即 5x>16 且 5x<-4,可以写为 x>16/5 且 x<-4/5,再
转化为原来的绝对值表示形式,可得解集:|5x-6|>10,x>3 且 x<-2/5。
绝对值不等式解法(1)

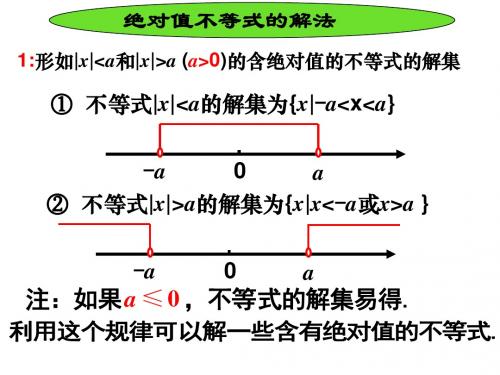
Hale Waihona Puke 绝对值不等式解法导1.含绝对值的不等式|x|<a与|x|>a的解法
不等式 a> 0 a= 0 ∅
{x∈R|x≠0}
a< 0
∅
|x|<a {x|-a<x<a} |x|>a {x|x>a或x<-a}
R
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法
(1)|ax+b|≤c⇔-c≤ax+b≤c;
(2)|ax+b|≥c⇔ ax+b≥c或ax+b≤- .c
合作学习
对议:例1与例2,并讲思路,说方法; 组议: 讨论1:分析例2的解题思路 讨论2:如何利用绝对值不等式的几何意义求最值
要求: 组长负责全员参与,分工协作。 先比对答案,然后探讨解题思路,总结解题规律方法。
展
要求:大声,规范,清晰,迅速
此类不等式的简单解法是等价命题法,即 ①|f(x)|<g(x)⇔-g(x)<f(x)<g(x),
②|f(x)|>g(x)⇔f(x)>g(x)或f(x)<-g(x)
(其中g(x)可正也可负).
若此类问题用分类讨论法来解决,就显得较复杂.
评
4、|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法
(黑板展示需在2—3分钟内书写完)
请同学们认真聆听,用红笔记录重点、疑惑点,并主动 进一步完善和补充,质疑。
板书展示:例1(2)(3)(B层)例2(A层) 口头展示:例1 (1) (C层) 了解感知 口答展示:如何利用绝对值不等式的几何意义求最 值?(C层)
评
1、m<|ax+b|<n型不等式
此类问题的简单解法是解不等式组,即
1.1.3绝对值不等式的解法
类型 3 引伸:
型如 | f(x)|<a, |f(x)|>a的不等式中 “a”用代数式替换,如何解?
例4:解不等式 | 5x-6 | < 6 – x
解不等式 | 5x-6 | < 6 – x
分析:对6-x 符号讨论, 当6-x≦0时,显然无解; 当6-x>0时,转化为-(6-x)<5x-6<(6-x) 解: 由绝对值的意义,原不等式转化为: 6-x≤0 6-x>0 -(6-x)<5x-6<(6-x)
3.不等式 x 4 x 3 a 有解的条件是( B )
1 ( A)0 a 10
( B )a 1
1 (C ) a 10
( D)a 1
4.| x-1 | > 2( x-3)
X<5 X<-1 或 x>1
5.| 2x+1 |> | x+2 |
学习小结: 解绝对值不等式的基本思路是去绝对值符号 转化为一般不等式来处理。 主要方法有: ⑴同解变形法:运用解法公式直接转化 ; ⑵定义法:分类讨论去绝对值符号 ; ①含一个绝对值符号直接分类 ;②含两个或两
3 x 解:由于y 2 是增函数,f(x) 2 2等价于 x 1 x 1 , 2
(1)当x 1时, x 1 x 1 2,上式恒成立
2当 1 x 1 时 , x 1 x 1 2 x,
3 3 上式化为2x .即 x 1 2 4 3当 x 1 时 , x 1 x 1 2 , 上 式 无 解
绝对值不等式的解法
1:形如|x|<a和|x|>a (a>0)的含绝对值的不等式的解集
绝对值不等式公式有哪些该如何解

绝对值不等式公式有哪些该如何解
绝对值不等式是数学中一个重要的知识点,同时也是考试中时常出现的考点。
下面是由编辑为大家整理的“绝对值不等式公式有哪些该如何解”,仅供参考,欢迎大家阅读本文。
绝对值不等式公式
||a|−|b||≤|a±b|≤|a|+|b|;
|ab|=|a||b|,|a/b|=|a|/|b|(b≠0);
|a|<|b| 可推出|b|>|a|;
3、∥a|−Ib∥≤la+b|≤la|+lb|当且仅当ab≤0时左边等号成立,ab≥0时右边等号成立;
4、|a−b|≤|a|+|−b|=|a|+|−1|∗|b|=|a|+|b|
怎样解绝对值不等式
解绝对值不等式的基本方法是去掉绝对值符号
1、平方,比如,|x|=3,可化为x^2=9,绝对值符号没有了;
2、讨论,即x≥0时,|x|=x;x<0时,|x|=-x,绝对值符号也没有了,令绝对值中的式子等于0,分出x的段,然后根据每段讨论得出的x值,取交集,综上所述即可。
解绝对值不等式的方法总结

解绝对值不等式的方法总结绝对值不等式是数学中常见的一类不等式,它涉及到绝对值的大小关系。
解绝对值不等式的关键是确定不等式中的变量可能取的范围,并结合绝对值的性质进行推导。
下面将从基本方法、分析方法和图像法等角度给出解绝对值不等式的方法总结。
一、基本方法1.消去绝对值:当绝对值不等式中只有一个绝对值符号时,我们可以通过将绝对值号内的条件进行分类讨论来消去绝对值。
例如,对于不等式,x-2,<3,我们可以将其分类讨论为两种情况:x-2>0时,不等式可转化为x-2<3,即x<5;x-2<0时,不等式可转化为-(x-2)<3,即-x+2<3,即x>-1、因此,原不等式的解集为-1<x<52.分离绝对值:当绝对值不等式中有两个绝对值符号时,我们可以通过分离绝对值的方法将其转化为一个带有正负号的二次不等式。
例如,对于不等式,x-2,>,x+3,由于绝对值的性质,我们有两种情况:x-2>x+3,即-5>0,这个情况显然不成立;x-2<-(x+3),即-2x-1>0,即x<-1/2、综上所述,原不等式的解集为x<-1/23.基本不等式法:针对绝对值不等式中的特殊形式,f(x),>c或,f(x),<c,其中c是正实数,通过化简找到f(x)的取值范围。
例如,对于不等式,2x-3,>5,我们可以将其转化为两个不等式:2x-3>5和2x-3<-5、从第一个不等式中解得x>4,从第二个不等式中解得x<-1、因此,原不等式的解集为x<-1或x>4二、分析方法1. 区间法:对于绝对值不等式,ax+b, < c (或 > c),我们可以通过给定 a、b 和 c 的符号情况来确定 x 的取值范围。
例如,对于不等式,4x+5, < 3,我们可以根据 4x+5 和 -4x-5 的正负号进行分类讨论。
绝对值不等式总结

1设函数f(x)中含有绝对值,则(1)绝对值三角不等式定理|a|-|b|≤|a±b|≤|a|+|b|(2)|a+b+c|≤|a|+|b|+|c|.2.f(x)>a有解⇔f(x)max>a.(2)f(x)>a恒成立⇔f(x)min>a.(3)f(x)>a恰在(c,b)上成立⇔c,b是方程f(x)=a的解.3.不等式恰成立问题(1)不等式f(x)>A在区间D上恰成立,等价于不等式f(x)>A的解集为D;(2)不等式f(x)<B在区间D上恰成立,等价于不等式f(x)<B的解集为D.定理1:如果a,b是实数,则|a+b| ≤|a|+|b|,当且仅当ab≥0时,等号成立;定理2:如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.2.绝对值不等式的解法(1)含绝对值的不等式|x|<a与|x|>a的解集(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法①|ax+b|≤c⇔-c≤ax+b≤c;②|ax+b|≥c⇔ax+b≥c或ax+b≤-c.3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法1.若关于x的不等式|a|≥|x+1|+|x-2|,存在实数解,则实数a的取值范围是________.2.不等式3≤|5-2x|<9的解集为()A.[-2,1)∪[4,7)B.(-2,1]∪(4,7]C.(-2,-1]∪[4,7)D.(-2,1]∪[4,7)3.不等式|x-5|+|x+3|≥1的解集是()A.[-5,7]B.[-4,6]C.(-∞,-5]∪[7,+∞)D.(-∞,+∞)4.已知不等式|2x-5|+|2x+1|>ax-1.(1)当a=1时,求不等式的解集;(2)若不等式的解集为R,求a的取值范围.5.已知f(x)=|x+1|-|ax-1|.(1)当a=1时,求不等式f(x)>1的解集;(2)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.6.设函数f(x)=5-|x+a|-|x-2|.①当a=1时,求不等式f(x)≥0的解集;②若f(x)≤1,求a的取值范围.7. (1)若对于实数x,y有|1-x|≤2,|y+1|≤1,求|2x+3y+1|的最大值.(2)若a≥2,x∈R,证明:|x-1+a|+|x-a|≥3.8.对于任意实数a,b,已知|a-b|≤1,|2a-1|≤1,且恒有|4a-3b+2|≤m,求实数m的取值范围.9.已知函数f(x)=|x+1|-|x-2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.10(1)已知函数f (x )=|x -a |+|x -3a |.①若f (x )的最小值为2,求a 的值;②若对∀x ∈R ,∃a ∈[-1,1],使得不等式m 2-|m |-f (x )<0成立,求实数m 的取值范围.11.已知函数f (x )=|x +1|+|x -3|-m 的定义域为R . (1)求实数m 的取值范围;(2)若m 的最大值为n ,解关于x 的不等式:|x -3|-2x ≤2n -4.12.已知函数f (x )=|x -a |.(1)若不等式f (x )≤3的解集为{x |-1≤x ≤5},求实数a 的值;(2)在(1)的条件下,若f (x )+f (x +5)≥m 对一切实数x 恒成立,求实数m 的取值范13. 已知函数f (x )=|x -a |+|2x -a |(a ∈R ).(1)若f (1)<11,求a 的取值范围;(2)若∀a ∈R ,f (x )≥x 2-x -3恒成立,求x 的取值范围.14.设函数f (x )=|2x +3|+|x -1|.(1)解不等式f (x )>4;(2)若存在x ∈⎣⎡⎦⎤-32,1使不等式a +1>f (x )成立,求实数a 的取值范围. 14.已知函数f (x )=|x -a |+12a(a ≠0).(1)若不等式f (x )-f (x +m )≤1恒成立,求实数m 的最大值; (2)当a <12时,函数g (x )=f (x )+|2x -1|有零点,求实数a 的取值范围. 15..已知函数f (x )=|x -1|+|x -a |.(1)若函数f (x )的值域为[2,+∞),求实数a 的值;(2)若f (2-a )≥f (2),求实数a 的取值范围.16.设函数f (x )=|2x -3|.(1)求不等式f (x )>5-|x +2|的解集;(2)若g (x )=f (x +m )+f (x -m )的最小值为4,求实数m 的值.17..已知函数f (x )=|2x -a |+|x -1|,a ∈R .(1)若不等式f (x )≤2-|x -1|有解,求实数a 的取值范围;(2)当a <2时,函数f (x )的最小值为3,求实数a 的值.18.设函数f (x )=|x -1|,x ∈R . (1)求不等式f (x )≤3-f (x -1)的解集;(2)已知关于x 的不等式f (x )≤f (x +1)-|x -a |的解集为M ,若⎝⎛⎭⎫1,32⊆M ,求实数a 的取值范围. 19.设函数f (x )=⎪⎪⎪⎪x +8m +|x -2m |(m >0).(1)求证:f (x )≥8恒成立; (2)求使得不等式f (1)>10成立的实数m 的取值范围.20.设a ,b 为满足ab <0的实数,那么( )A.|a +b |>|a -b |B.|a +b |<|a -b |C.|a -b |<||a |-|b || D .|a -b |<|a |+|b |21..不等式|2x -a |<b 的解集为{x |-1<x <4},则a +b 的值为( )A.-2B.2C.8D.-822.设函数f (x )=x 2-x -15,且|x -a |<1.(1)解不等式|f (x )|>5.(2)求证:|f (x )-f (a )|<2(|a |+1).23.已知函数f (x )=-x 2+ax +4,g (x )=|x +1|+|x -1|.(1)当a =1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[-1,1],求a 的取值范围24.已知函数f (x )=|x -1|+|x -a |.(1)若函数f (x )的值域为[2,+∞),求实数a 的值;(2)若f (2-a )≥f (2),求实数a 的取值范围.25.设函数f(x)=|x-3|,g(x)=|x-2|.(1)解不等式f(x)+g(x)<2;(2)对于实数x,y,若f(x)≤1,g(y)≤1,证明:|x-2y+1|≤3.。
解答绝对值不等式问题的四个“妙招”

一、分类讨论
一般地,若 x 为非负数,则 |x| = x;若 x 为负数,则
|x| = -x. 由于绝对值内部式子的符号决定去掉绝对值
符号后式子的表示形式,所以在解绝对值不等式时,
往往要采用分类讨论法,对绝对值内部式子的符号进
行讨论.可令每个绝对值内部的式子为零,然后将其零
点标在数轴上,于是这些零点把数轴分成若干个区
方法集锦
解答绝对值不等式问题的四个“妙招”
吴笋
绝对值不等式问题的常见命题形式有:(1)解绝对
值不等式;(2)求含有绝对值代数式的取值范围.其中
解绝对值不等式问题比较常见,解这类题目的关键是
去掉绝对值符号,将绝对值不等式转化为不含绝对值
的常规不等式去求解.本文介绍解绝对值不等式问题
的四个“妙招”,以供大家参考.
4
的点,只要将点向右移
1 2
个单位,那么它们的距离之
和就增加了
1
个单位,也就是把点
B(1)
移到点
B1(
3 2
)
的
位置;或者将点
A(-2)
向左移
1 2
个单位,也就是把点
A(-2)
移到点
A1(-
5 2
)
的位置,
由图可以看出,在数轴上位于
B1(
3 2
)
和
A1(-
5 2
)
之
间的点 P(x) 都满足 | x + 2 | + | x - 1| < 4 ,
解(1)得 -2 < x < -1 ,或 3 < x < 4 ,
解(2)得解集为空集, 所以原不等式的解集为{x| - 2 < x < - 1或3 < x < 4}.
绝对值不等式(绝对值三角不等式与绝对值不等式的解法)知识讲解

3.若变为|x+1|+|x-2|>k恒成立,则k的取值范围是 4.若变为不等式|x-1|+|x-3|<k的解集为空集,则k的 取值范围是
3、已知 0, x a , y b ,
求证 2x 3y 2a 3b 5
绝对值不等式的解法(一)
2x 4, x 1
例1. 解不等式|x-1|+|x+2|≥5
y
2x 6, x 2 y 2, 2 x 1
2x 4, x 1
如图,作出函数的图象,
函数的零点是-3,2.
-2 1
-3
2x
-2
由图象可知,当x 3或x 2时,y 0,
∴原不等式的解集为{x|x≤-3 或 x≥2}.
取值范围是-(------,--2-]
3.解不等式1<|2x+1|<3. 答案:(-2,-1)∪(0,1)
4.解不等式|x+3|+|x-3|>8. 答案: {x|x<-4或x>4}.
5.解不等式:|x-1|>|x-3|. 答案: {x|x>2}.
6.解不等式|5x- 6|<6-x. 答案:(0,2)
思考四:若变为不等式|x-1|+|x+2|<k的解集 为 ,则k的取值范围是 k 3
练习:解不等式│x+1│–│x–2│≥1
x | x 1
作出f (x) │x +1│–│x – 2│的图像, 并思考f (x)的最大和最小值
│x +1│–│x – 2│ k恒成立,k的取值范围是 │x +1│–│x – 2│ k恒成立,k的取值范围是
高中数学绝对值不等式的解法

-2
1 2
3
巩固练习:
解下列不等式:
1 1 (1) | x | 4 2
(3) | 5 x 4 | 6 (5)1 | 3 x 4 | 6
2 1 ( 2) | x | 3 3 (4) | 3 2 x | 7
(6) | x 3 x | 4
2
(7) | 3 2 | 1
2017/4/20
②
①
-m -n 0 n m 题型3: 形如n<| ax + b | <m (m>n>0)不等式
等价于不等式组
①
n ax b m, 或 m ax b n
推广: | f(x) | <g(x), | f(x) | >g(x)
2017/4/20 南粤名校——南海中学
3 x 4, 或 1 x 0 .
原不等式的解集是 {x | 1 x 0, 或3 x 4}.
2017/4/20 南粤名校——南海中学
解不等式 3<|3-2x|≤5 .
解法3:3 | 3 2 x | 5 3 | 2 x 3 | 5
3 2 x 3 5, 或 5 2 x 3 3
2 3 4
这是解含绝对值不等式的四种常用思路
1.探索:不等式|x|<1的解集。 方法一: 利用绝对值的几何意义观察
不等式|x|<1的解集表示到原点的距离小于1 的点的集合。
-1 0Байду номын сангаас1
所以,不等式|x|<1的解集为{x|-1<x<1}
探索:不等式|x|<1的解集。 方法二: 利用绝对值的定义去掉绝对值符号, 需要分类讨论 ①当x≥0时,原不等式可化为x<1
解绝对值不等式的方法总结

解绝对值不等式的方法总结绝对值不等式是数学中一类重要的问题,它涉及到不等式的解法和绝对值函数的性质。
下面是解绝对值不等式的方法总结:一、定义法绝对值的定义是:|a|=a(a>0),|a|=-a(a<0),|a|=0(a=0)。
利用这个定义,我们可以将绝对值不等式转化为普通不等式,然后求解。
例如,解不等式|x-3|>4,我们可以转化为解不等式x-3>4或x-3<=-4,即x>7或x<=1。
二、实数性质法利用实数的性质,我们知道对于任意实数a和b,有|a+b|<=|a|+|b|。
这个性质可以用来解一些含有绝对值的三角不等式。
例如,解不等式|x+y|<=|x|+|y|,我们可以令x=a, y=b,得到|a+b|<=|a|+|b|,即-|a+b|<=|a|-|b|<=|a+b|,从而得到-1<=cosθ<=1,其中θ为a和b的夹角。
三、平方法对于形如|ax+b|>c的不等式,我们可以利用平方法将其转化为普通不等式。
具体地,我们先将ax+b的绝对值平方,得到a^2x^2+2abx+b^2>c^2,然后解这个普通不等式。
例如,解不等式|x+3|>4,我们先将x+3的绝对值平方,得到x^2+6x+9>16,即x^2+6x-7>0。
然后解这个不等式得到x<1或x>7。
四、零点分段法对于形如|f(x)|>g(x)的不等式,我们可以先令f(x)=0,找到可能使不等式成立的x的取值范围,然后在这些范围内分别讨论g(x)的符号情况,从而得到不等式的解集。
例如,解不等式|x^2-3x+2|>x+1,我们先令x^2-3x+2=0,得到x=1或x=2。
在区间(-∞,1)内,f(x)=-x^2+3x-2<0,所以在这个区间内不等式不成立。
在区间[1,2)内,f(x)=-x^2+3x-2>0且g(x)=x+1<0,所以在这个区间内不等式成立。
绝对值不等式的解法与绝对值的三角不等式

绝对值不等式的解法与绝对值的三角不等式规律方法指导1、解绝对值不等式的基本思路解绝对值不等式的基本思路是去掉绝对值符号,因此如何去掉绝对值符号是解决这类问题的关键。
常利用绝对值的代数意义和几何意义。
2、解绝对值不等式常用的同解变形①|f(x)|>|g(x)|f2(x)>g2(x)②|f(x)|>g(x)f(x)>g(x)或f(x)<-g(x)③|f(x)|<g(x)-g(x)<f(x)<g(x)④含有两个或两个以上绝对值符号的不等式可用“按零点分区间”讨论的方法来脱去绝对值符号去求解;也可以用函数图像法来解决。
3、绝对值三角不等式等号成立的条件:①取等号②取等号③取等号④取等号经典例题透析类型一:含有一个绝对值符号的绝对值不等式的解法1、解下列不等式(1);(2);(3)解析:(1)由原不等式可得,得,∴原不等式的解集是;(2)原不等式可化为,得或整理得,或∴原不等式的解集是;(3)由原不等式可得或整理得或∴原不等式的解集是总结升华:不等式的解集为;不等式的解集为.举一反三:【变式】(2011山东,4)不等式|x-5|+|x+3|≥10的解集是(A)[-5,7] (B)[-4,6](C)(-∞,-5]∪[7,+∞) (D)(-∞,-4]∪[6,+∞)【答案】D2、解不等式|x2+4x-1|<4解析:原不等式-4<x2+4x-1<4-5<x<-3或-1<x<1.即原不等式的解集是(-5,-3)∪(-1,1).举一反三:【变式】解不等式|x2+4x-1|>4.【答案】原不等式的解集是(-∞,-5)∪(-3,-1)∪(1, +∞)3、解不等式1|2x-1|<5.解析:法一:原不等式等价于①或②解①得:1x<3 ;解②得:-2< x 0.∴原不等式的解集为{x | -2< x 0或1x<3}法二:原不等式等价于12x-1<5或–5<2x-1-1即22x<6或–4<2x0.解得1x<3或–2<x0.∴原不等式的解集为{x|-2<x0或1x<3}总结升华:比较两种解法,第二种解法比较简单,在解法二中,去掉绝对值符号的依据是a|x|b a x b或-b x-a(a0).举一反三:【变式1】解不等式:【答案】原不等式的解集是【变式2】解不等式4<|x2-5x|≤6.【答案】原不等式等价于不等式组不等式(1)等价于x2-5x<-4或x2-5x>4不等式(2)等价于-6≤x2-5x≤6利用数轴取不等式(1),(2)的解的交集:∴原不等式的解集为:4、解不等式:|4x-3|>2x+1.思路点拨:关键是去掉绝对值符号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解绝对值不等式题根探讨 题根四 解不等式2|55|1x x -+<.[题根4]解不等式2|55|1x x -+<.[思路]利用|f(x)|<a(a>0) ⇔-a<f(x)<a 去掉绝对值后转化为我们熟悉的一元二次不等式组21551x x -<-+<即22551(1)551(2)x x x x ⎧-+<⎪⎨-+>-⎪⎩求解。
[解题]原不等式等价于21551x x -<-+<,即22551(1)551(2)x x x x ⎧-+<⎪⎨-+>-⎪⎩由(1)得:14x <<;由(2)得:2x <或3x >,所以,原不等式的解集为{|12x x <<或34}x <<. [收获]1)一元一次不等式、一元二次不等式的解法是我们解不等式的基础,无论是解高次不等式、绝对值不等式还是解无理根式不等式,最终是通过代数变形后,转化为一元一次不等式、一元二次不等式组来求解。
2)本题也可用数形结合法来求解。
在同一坐标系中画出函数2551y x x y =-+=与的的图象,解方程2551x x -+=,再对照图形写出此不等式的解集。
第1变 右边的常数变代数式[变题1]解下列不等式:(1)|x +1|>2-x ;(2)|2x -2x -6|<3x[思路]利用|f(x)|<g(x) ⇔-g(x)<f(x)<g(x)和|f(x)|>g(x) ⇔f(x)>g(x)或f(x)<-g(x)去掉绝对值后转化为我们熟悉的一元一次、一元二次不等式组来处理。
解:(1)原不等式等价于x +1>2-x 或x +1<-(2-x )解得x >12或无解,所以原不等式的解集是{x |x >12} (2)原不等式等价于-3x <2x -2x -6<3x即222226360(3)(2)032(1)(6)016263560x x x x x x x x x x x x x x x x x ⎧⎧-->-+->+-><->⎧⎧⎪⎪⇒⇒⇒⎨⎨⎨⎨+-<-<<--<--<⎪⎪⎩⎩⎩⎩或 2<x <6所以原不等式的解集是{x |2<x <6}[收获]形如|()f x |<()g x ,|()f x |>()g x 型不等式这类不等式的简捷解法是等价命题法,即: ①|()f x |<()g x ⇔-()g x <()f x <()g x ②|()f x |>()g x ⇔()f x >()g x 或()f x <-()g x1.解不等式(1)|x-x 2-2|>x 2-3x-4;(2)234xx -≤1解:(1)分析一 可按解不等式的方法来解. 原不等式等价于:x-x 2-2>x 2-3x-4 ①或x-x 2-2<-(x 2-3x-4) ② 解①得:1-2<x<1+2 解②得:x>-3故原不等式解集为{x |x>-3}分析二 ∵|x-x 2-2|=|x 2-x+2| 而x 2-x+2=(x-14)2+74>0 所以|x-x 2-2|中的绝对值符号可直接去掉.故原不等式等价于x 2-x+2>x 2-3x-4 解得:x>-3∴ 原不等式解集为{x>-3} (2)分析 不等式可转化为-1≤234xx -≤1求解,但过程较繁,由于不等式234x x -≤1两边均为正,所以可平方后求解.原不等式等价于2234xx -≤1⇒9x 2≤(x 2-4)2 (x ≠±2) ⇒x 4-17x 2+16≥0 ⇒x 2≤1或x 2≥16⇒-1≤x ≤1或x ≥4或x ≤-4注意:在解绝对值不等式时,若|f(x)|中的f(x)的值的范围可确定(包括恒正或恒非负,恒负或恒非正),就可直接去掉绝对值符号,从而简化解题过程.第2变 含两个绝对值的不等式[变题2]解不等式(1)|x -1|<|x +a |;(2)|x-2|+|x+3|>5. [思路](1)题由于两边均为非负数,因此可以利用|f(x)|〈|g(x)|⇒f 2(x)〈g 2(x)两边平方去掉绝对值符号。
(2)题可采用零点分段法去绝对值求解。
[解题](1)由于|x -1|≥0,|x +a |≥0,所以两边平方后有:|x -1|2<|x +a |2即有2x -2x +1<2x +2ax +2a ,整理得(2a +2)x >1-2a 当2a +2>0即a >-1时,不等式的解为x >12(1-a ); 当2a +2=0即a =-1时,不等式无解; 当2a +2<0即a <-1时,不等式的解为x <1(1)2a - (2)解不等式|x-2|+|x+3|>5.解:当x ≤-3时,原不等式化为(2-x)-(x+3)>5⇒-2x>6⇒x<-3. 当-3<x<2时,原不等式为(2-x)+(x+3)>5⇒5>5无解. 当x ≥2时,原不等式为(x-2)+(x+3)>5⇒2x>4⇒x>2. 综合得:原不等式解集为{x |x>2或x<-3}. [收获]1)形如|()f x |<|()g x |型不等式此类不等式的简捷解法是利用平方法,即:|()f x |<|()g x |⇔22()()f x g x <⇔[()()][()()]f x g x f x g x +-<02)所谓零点分段法,是指:若数1x ,2x ,……,n x 分别使含有|x -1x |,|x -2x |,……,|x -n x |的代数式中相应绝对值为零,称1x ,2x ,……,n x 为相应绝对值的零点,零点1x ,2x ,……,n x 将数轴分为m +1段,利用绝对值的意义化去绝对值符号,得到代数式在各段上的简化式,从而化为不含绝对值符号的一般不等式来解,即令每项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集。
零点分段法是解含绝对值符号的不等式的常用解法,这种方法主要体现了化归、分类讨论等数学思想方法,它可以把求解条理化、思路直观化1 解关于x 的不等式|log (1)||log (1)|a a x x ->+(a >0且a ≠1) 解析:易知-1<x <1,换成常用对数得:lg(1)lg(1)||||lg lg x x a a-+> ∴22|lg(1)||lg(1)|x x ->+ 于是22lg (1)lg (1)0x x --+>∴[lg(1)lg(1)][lg(1)lg(1)]0x x x x -++--+> ∴21lg(1)lg 01xx x-->+ ∵-1<x <1 ∴0<1-2x <1 ∴lg (1-2x )<0∴1lg1xx -+<0 ∴1011x x -<<+解得0<x <12.不等式|x+3|-|2x-1|<2x+1的解集为 。
解:|x+3|-|2x-1|=⎪⎪⎪⎩⎪⎪⎪⎨⎧-≤-<<-+≥-)3(4)213(24)21(4x x x x x x∴当21≥x 时124+<-xx ∴x>2 当-3<x<21时4x+2<2x +1 ∴723-<<-x当3-≤x 时124+<-xx ∴3-≤x综上72-<x 或x>2故填),2()72,(+∞⋃--∞。
3.求不等式1331log log 13x x+≥-的解集. 解:因为对数必须有意义,即解不等式组0103x x>⎧⎪⎨>⎪-⎩,解得03x << 又原不等式可化为()33log log 31x x +-≥(1)当01x <≤时,不等式化为()33log log 31x x -+-≥即()33log 3log 3x x -≥∴ 33x x -≥ ∴ 34x ≤综合前提得:304x <≤。
(2)当1<x ≤2时,即()333log log 3log 3x x +-≥.∴ 2330x x -+≤ x ∴∈∅。
(1) 当23x <<时,()333log log 3log 3x x --≥(2) ∴()33x x ≥- ∴94x ≥,结合前提得:934x ≤<。
综合得原不等式的解集为390,,344⎛⎤⎡⎫⎪⎥⎢⎝⎦⎣⎭U第3变 解含参绝对值不等式[变题3]解关于x 的不等式34422+>+-m m mx x[思路]本题若从表面现象看当含一个根号的无理根式不等式来解,运算理较大。
若化简成3|2|+>-m m x ,则解题过程更简单。
在解题过程中需根据绝对值定义对3m +的正负进行讨论。
[解题]原不等式等价于 3|2|+>-m m x当03>+m 即3->m 时, )3(232+-<-+>-m m x m m x 或 ∴333-<+>m x m x 或当03=+m 即3-=m 时, 0|6|>+x ∴x ??6 当03<+m 即3-<m 时, x ?R[收获]1)一题有多解,方法的选择更重要。
2)形如|()f x |<a ,|()f x |>a (a R ∈)型不等式此类不等式的简捷解法是等价命题法,即:① 当a >0时,|()f x |<a ⇔-a <()f x <a ;|()f x |>a ⇔()f x >a 或()f x <-a ; ② 当a =0时,|()f x |<a 无解,|()f x |>a ⇔()f x ≠0 ③ 当a <0时,|()f x |<a 无解,|()f x |>a ⇔()f x 有意义。
第4变 含参绝对值不等式有解、解集为空与恒成立问题[变题4]若不等式|x -4|+|3-x |<a 的解集为空集,求a 的取值范围。
[思路]此不等式左边含有两个绝对值符号,可考虑采用零点分段法,即令每一项都等于0,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集,这是按常规去掉绝对值符号的方法求解,运算量较大。
