线性代数(本)习题册行列式-习题详解(修改)(加批注)
线性代数课后习题答案全)习题详解

线性代数课后习题答案全)习题详解第一章 行列式1.利用对角线法则计算下列三阶行列式:(1)381141102---; (2)b a c a c b c b a ; (3)222111c b a c b a ; (4)y x y x x y x yyx y x +++. 解 (1)=---381141102811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯-=416824-++-=4-(2)=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=(3)=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=(4)yx y x x y x y yx y x +++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序,求下列各排列的逆序数: (1)1 2 3 4; (2)4 1 3 2; (3)3 4 2 1; (4)2 4 1 3; (5)1 3 … )12(-n 2 4 … )2(n ; (6)1 3 … )12(-n )2(n )22(-n … 2. 解(1)逆序数为0(2)逆序数为4:4 1,4 3,4 2,3 2 (3)逆序数为5:3 2,3 1,4 2,4 1,2 1 (4)逆序数为3:2 1,4 1,4 3 (5)逆序数为2)1(-n n : 3 2 1个 5 2,5 4 2个 7 2,7 4,7 6 3个 ……………… …)12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n )1(-n 个(6)逆序数为)1(-n n3 2 1个 5 2,54 2个 ……………… …)12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n )1(-n 个4 2 1个 6 2,6 4 2个 ……………… …)2(n 2,)2(n 4,)2(n 6,…,)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解 由定义知,四阶行列式的一般项为43214321)1(p p p p t a a a a -,其中t 为4321p p p p 的逆序数.由于3,121==p p 已固定,4321p p p p 只能形如13□□,即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式:(1)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢7110025*********4; (2)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-265232112131412; (3)⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ; (4)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001解(1)7110025102021421434327c c c c --1002310021214---34)1(142101+-⨯--=143102211014-- 321132c c c c ++141717001099-(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=e c b e c b e c b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--= 右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bz ay y x by ax x z bx az z y b +++zy x y x z xz y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a (4)4444442222220001ad a c a b a ad a c a b a ad a c a b a ---------=左边)()()222222222222a d d a c c a a d a c ad a c ------ =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转,依次得n nn n a a a a D 11111 =, 11112n nn n a a a a D = ,11113a a a a D n nnn =,证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnnn nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-= 同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n Tn n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)aaD n 11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xa a ax aa a x D n =; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn n n ------=---+; 提示:利用范德蒙德行列式的结果. (4) nnn nn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(1000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n na a a (再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上,得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行交换,得 nnn n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nn nnn d c d c b a b a D 011112=n n n nd c d c b a b a a 0000111111--展开按第一行0000)11111111112c d c d c b a b a b nn n n n nn ----+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式:222)(--=n n n n n n D c b d a D即 ∏=-=ni i i iin D c b da D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=0432********0122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121n n n n a a a a a a a a +------10001001000100100010000114332展开(由下往上)按最后一列1(+n a nn n a a a a a a a ------00000000000000000000000224332 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x 解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=000100210151---= 112035122412111512-----=D 11503120270151------=313911230231115-2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 5100165100065100650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507= 5101065100065000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-= 1145108065-=--= 51100650000601000051001653=D 展开按第三列0000105165610050066100510656510650061+= 703114619=⨯+= 51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 11051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x . 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 μλμμμλ-==12111113D , 齐次线性方程组有非零解,则03=D即 0=-μλμ 得 10==λμ或不难验证,当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解?解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ齐次线性方程组有非零解,则0=D 得 32,0===λλλ或不难验证,当32,0===λλλ或时,该齐次线性方程组确有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换.解 由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T .4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635.(2)⎪⎪⎭⎫ ⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B)2=A 2+2AB +B 2吗? 解 (A +B)2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A ,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610,所以(A +B)2≠A 2+2AB +B 2.(3)(A +B)(A -B)=A 2-B 2吗? 解 (A +B)(A -B)≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B)(A -B)≠A 2-B 2.6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k.解⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k .8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k.解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB)T =B T (B T A)T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB)T =(BA)T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB)T =AB , 所以 AB =(AB)T =B T A T =BA . 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解⎪⎭⎫ ⎝⎛=5221A . |A|=1, 故A -1存在. 因为⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225.(2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A|=1≠0, 故A -1存在. 因为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos .(3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A|=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; 解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232.(2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122.(3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 因为A k =O , 所以E -A k =E . 又因为E -A k =(E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E ,由定理2推论知(E -A)可逆, 且(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A)-1(E -A).另一方面, 由A k =O , 有E =(E -A)+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),故 (E -A)-1(E -A)=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),两端同时右乘(E -A)-1, 就有(E -A)-1(E -A)=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E)-1. 证明 由A 2-A -2E =O 得A 2-A =2E , 即A(A -E)=2E ,或 E E A A =-⋅)(21, 由定理2推论知A 可逆, 且)(211E A A -=-. 由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E)(A -3E)=-4E ,或 E A E E A =-⋅+)3(41)2( 由定理2推论知(A +2E)可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得|A 2-A|=2,即 |A||A -E|=2,故 |A|≠0,所以A 可逆, 而A +2E =A 2, |A +2E|=|A 2|=|A|2≠0, 故A +2E 也可逆.由 A 2-A -2E =O ⇒A(A -E)=2E⇒A -1A(A -E)=2A -1E ⇒)(211E A A -=-, 又由 A 2-A -2E =O ⇒(A +2E)A -3(A +2E)=-4E⇒ (A +2E)(A -3E)=-4 E ,所以 (A +2E)-1(A +2E)(A -3E)=-4(A +2 E)-1,)3(41)2(1A E E A -=+-. 16. 设A 为3阶矩阵,21||=A , 求|(2A)-1-5A*|. 解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |1-A =|-2A -1|=(-2)3|A -1|=-8|A|-1=-8⨯2=-16.17. 设矩阵A 可逆, 证明其伴随阵A*也可逆, 且(A*)-1=(A -1)*.证明 由*||11A A A =-, 得A*=|A|A -1, 所以当A 可逆时, 有 |A*|=|A|n |A -1|=|A|n -1≠0,从而A*也可逆.因为A*=|A|A -1, 所以(A*)-1=|A|-1A . 又*)(||)*(||1111---==A A A A A , 所以 (A*)-1=|A|-1A =|A|-1|A|(A -1)*=(A -1)*.18. 设n 阶矩阵A 的伴随矩阵为A*, 证明:(1)若|A|=0, 则|A*|=0;(2)|A*|=|A|n -1.证明(1)用反证法证明. 假设|A*|≠0, 则有A*(A*)-1=E , 由此得A =A A*(A*)-1=|A|E(A*)-1=O ,所以A*=O , 这与|A*|≠0矛盾,故当|A|=0时, 有|A*|=0.(2)由于*||11A A A =-, 则AA*=|A|E , 取行列式得到 |A||A*|=|A|n .若|A|≠0, 则|A*|=|A|n -1;若|A|=0, 由(1)知|A*|=0, 此时命题也成立.因此|A*|=|A|n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B . 解 由AB =A +2E 可得(A -2E)B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330. 20. 设⎪⎪⎭⎫ ⎝⎛=101020101A , 且AB +E =A 2+B , 求B . 解 由AB +E =A 2+B 得(A -E)B =A 2-E ,即 (A -E)B =(A -E)(A +E).因为01001010100||≠-==-E A , 所以(A -E)可逆, 从而⎪⎪⎭⎫ ⎝⎛=+=201030102E A B . 21. 设A =diag(1, -2, 1), A*BA =2BA -8E , 求B .解 由A*BA =2BA -8E 得(A*-2E)BA =-8E ,B =-8(A*-2E)-1A -1=-8[A(A*-2E)]-1=-8(AA*-2A)-1=-8(|A|E -2A)-1=-8(-2E -2A)-1=4(E +A)-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-= =2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫ ⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A*|=|A|3=8, 得|A|=2.由ABA -1=BA -1+3E 得AB =B +3A ,B =3(A -E)-1A =3[A(E -A -1)]-1A 11*)2(6*)21(3---=-=A E A E ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--=-1030060600600006603001010010000161.23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A=P Λ11P -1.|P|=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P , 而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001, 故 ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫ ⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A)=A 8(5E -6A +A 2).解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0).ϕ(A)=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112 ⎪⎪⎭⎫⎝⎛=1111111114. 25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B)B -1=B -1+A -1=A -1+B -1,而A -1(A +B)B -1是三个可逆矩阵的乘积, 所以A -1(A +B)B -1可逆, 即A -1+B -1可逆. (A -1+B -1)-1=[A -1(A +B)B -1]-1=B(A +B)-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B , 则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A , 而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解 41001200210100101002000021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A ,故 |||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A , 故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A . ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nE BD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001.解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A BC O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2)⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4)⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020*********)2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫ ⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311141312323~r r r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---000000000022********(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r r r --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ,求A 。
线性代数(本)习题册行列式-习题详解(修改)(加批注)

线性代数(本)习题册行列式-习题详解(修改)(加批注)||班级:姓名:学号:成绩:批改日期: ||第 1 页共 18 页行列式的概念一、选择题1.下列选项中错误的是( ) (A)b a dcd c b a -= ; (B)ac bd d c b a =; (C)d c b a d c d b c a =++33; (D)dc b ad c b a -----=. 答案:D2.行列式n D 不为零,利用行列式的性质对n D 进行变换后,行列式的值().(A)保持不变;(B)可以变成任何值;(C)保持不为零;(D)保持相同的正负号.答案:C二、填空题1.ab ba log 11log = . 解析:0111log log log 11log =-=-=ab abb a ba . 2.6cos3sin6sin3cosππππ= . 解析:02cos 6sin 3sin 6cos 3cos 6 cos 3sin6sin3cos==-=πππππππππ3.函数x x xxx f 121312)(-=中,3x 的系数为; x x xx xx g 21112)(---=中,3x 的系数为 . 答案:-2;-2.||班级:姓名:学号:成绩:批改日期: ||第 2 页共 18 页4.n 阶行列式n D 中的n 最小值是 . 答案:1.5. 三阶行列式113420321-中第2行第1列元素的代数余子式等于 . 答案:5.6.若02182=x,则x = . 答案:2.7.在n 阶行列式ij a D =中,当i<="" =="" a="" i="" ij="" j="" l=",则D" p="" 时,),,2,1,(0n="" 答案:nn="">8.设a ,b 为实数,则当a = ,b = 时,010100=---a b b a . 解析:0)()1(1010022=+-=--=---b a ab ba a bba故0,0==b a .三、解答题1.用行列式的定义计算.(1)1100001001011010;解:原式=100010101)1(1010000011)1(14121++-?+-?||班级:姓名:学号:成绩:批改日期: || 第 3 页共 18 页110010100-=--=(2)000000h g f e d c b a . 原式=000000gf e d b hf e dc a - =00000g f bd hf df e c a +-=bdfg adfh -2. 设行列式λλλ01010101-=D , 3512321132=D ,若21D D =,求λ的值.解:由对角线法则,得()()0,11221=-+=D D λλ若21D D =,则()()0112=-+λλ于是1-=λ或1.四、证明题1.(略)行列式的性质一、选择题1.设行列式x x xD 0101011-=, 1133512322=D ,若21D D =,则x 的取值为 ( ).(A)2,-1; (B)1,-1; (C)0,2; (D)0,1.答案:B2.若3333231232221131211==a a a a a a a a a D ,||班级:姓名:学号:成绩:批改日期: ||第 4 页共 18 页则3332333123222321131213111525252a a a a a a a a a a a a D +++==(). (A)30; (B) -30; (C)6; (D)-6.答案:C二、填空题1.若三阶行列式D 的第一行元素分别是1,2,0,第三行元素的余子式分别是8,x ,19,则x = . 解析:1820190,4x x ?-+?==. 2.2016201420182016 = .解析:4202220162014222016201420182016===.3.行列式cb dc a bcb aD =,则312111A A A ++= . 解析:312111A A A ++0111==cb c acb .4.行列式xx x x x D 31213231232154-=的展开式中,4 x 的系数为;3x 的系数为 .解析:xx x xx x x x x x D 312131232321531213231232154--=-=xx x x 3121312512585103215---= 含4x ,3x 的项仅有主对角线上元素之积项,故4x ,3 x 的||班级:姓名:学号:成绩:批改日期: || 第 5 页共 18 页系数分别为15,-3.三、解答题1.计算下列行列式 .(1)3214214314324321;解:各行加到第一行,得原式=32142143143211111032142143143210101010= =160400004001210111110123012101210111110=---=------.(2)4444333322225432154321543215432111111;解:原式=(5-4)(5-3)(5-2)(5-1)(4-3)(4-2)(4-1)(3-2)(3-1) =288.(3)49362516362516925169416941;原式=02222222297531694113119711975975316941==.||班级:姓名:学号:成绩:批改日期: || 第 6 页共 18 页(4)000000xy y x y x x y ;原式=xy x yx x xyy y xy 0000000-- =22222)(y x xyyx x x y y x y --=-. (5)xy z zx y yz x111;原式=)(0)(01x z y x z x y z x y yzx------ =))()((11))((x z z y y x yzx z x y ---=---.(6)200012000000130012000101--;原式=31012010140131201014200001301201012---=--=-- =2031124=---.(7)43211111111111111111x x x x ++++;||班级:姓名:学号:成绩:批改日期: || 第 7 页共 18 页解:原式=432111110010011x x x x x x x ---+ =43121100000001x x x x x x x x x x x x x ---++++ =3214214314324321x x x x x x x x x x x x x x x x ++++.2.设4322321143113151-=D ,计算44434241A A A A +++的值. 其中)4,3,2,1(4=j A j 是D 的代数余子式.解:44434241A A A A +++61111321143113151=-=. 3. 已知1142113110111253------=D ,求41312111M M M M +++.解:41312111M M M M +++=41312111)1(1)1(1M M M M --?+--?=1141113*********-------=0.4.计算下列n 阶行列式.||班级:姓名:学号:成绩:批改日期: ||第 8 页共 18 页(1)2111解:原式=211121111 +++n n n =2 11121111)1( +n=110010111)1(+=+n n .(2)xy yyy x y yy y x yy y y x;解:原式=[]xy y yy x y yy y x yy n x1111)1(-+ =[]yx y x y x y n x ----+ 00000001111)1(=[]1)()1(---+n y x y n x .(3)),,2,1,0(0100101111021n i x x x x i n=≠.||班级:姓名:学号:成绩:批改日期: || 第 9 页共 18 页解:原式=nni ix x x x00000011101211∑=- =)1(121∑=-ni in x x x x .四、证明题1.设a ,b ,c 是互异的实数,证明0111333=c b a c b a的充分必要条件是a+b+c=0.证明:33333333001111a c ab a ac a b a c b ac ba----= =3333a c ab ac ab ----=222211))((a ac c a ab b a c a b ++++--=))()((22ab ac b c a c a b -+--- =))()()((c b a b c a c a b ++---=0,由于a ,b ,c 是互异的实数,故要上式成立,当且仅当a+b+c=0.2.证明4+2324323631063a b c d a a b a b c a b c da a ab a bc a b cd a a b a b c a b c d +++++=++++++++++++ 证明:左边43322102320363a b c d r r a a b a b cr r a a b a b c r r a a b a b c-+++-+++-+++433210002003a b c d r r a a b a b ca ab r r a a b-++++-+4430002000a b c d a a b a b cr r a a a b a+++-=+||班级:姓名:学号:成绩:批改日期: ||第 10 页共 18 页=右边克莱姆法则一、选择题1.方程组=++=++=++1,1,1321321321x x x x x x x x x λλλ, 有唯一解,则( ).(A)1-≠λ且2-≠λ;(B) 1≠λ且2-≠λ;(C) 1≠λ且2≠λ; (D) 1-≠λ且2≠λ.解析:由克莱姆法则,当0)1)(2(1111112≠-+=λλλλλ,即1≠λ且2-≠λ,选B .2.当≠a ()时,方程组??=+-=++=+02,02,0z y ax z ax x z ax 只有零解. (A) -1 ;(B) 0 ;(C) -2 ;(D) 2. 解析:由克莱姆法则,当0)2(212012100121210≠-=--=-a a a a a a 即2≠a ,选D .三、解答题1.用克莱姆法则下列解方程组.(1)??=+-=+-=-+;32,322,22z y x z y x z y x解: 03112221121≠=---=D ,由克莱姆法则知,此方程组有唯一解,132231221=---=D ,||班级:姓名:学号:成绩:批改日期: ||第 11 页共 18 页61322311212=-=D ,93323312213==D ,因此方程组的解为11==D D x ,22==D Dy ,33==DD z .(2)..23342,223,3232,124321432143214321=-++=+++=+-+=-++x x x x x x x x x x x x x x x x 解:043 342123121321121≠=---=D由克莱姆法则知,此方程组有唯一解,833421232213311211=---=D , 233221221213211112-=---=D ,23241231233211213=--=D ,223422231313211214=-=D . 因此方程组的解为211==D D x ,2122-==D D x ,2133==D D x ,2 144==D D x . 2.判断线性方程组=-+=+-=-+0285,042,022321321321x x x x x x x x x 是否有非零解?解:因为系数行列式285122421285421122----=---=D||班级:姓名:学号:成绩:批改日期: || 第 12 页共 18 页=030596042122180960421≠-=--=----, 所以,方程组只有零解.3.已知齐次线性方程组=+-=++=-+02,0,0321321321x x x x x kx x kx x 有非零解,求k 的值.解:因为齐次线性方程组有非零解,所以该方程组的系数行列式必为零,即32101101111211112k k k kk k --+--=-- =)21)(1()1(32k k k +++- =0)4)(1(=-+k k 解得,k =-1或k =4.4.当μ取何值时,齐次线性方程组=--+-=-+-=-++0)1(02)3(0)1(42321321321x x x x x x x x x μμμ有非零解?解:由齐次线性方程组有非零解的条件可知,0111213142=------μμμ,解得3,2,0=μ.第一章综合练习一、判断题1. n 阶行列式n D 中的n 最小为2.( ╳ )2. 在n 阶行列式ij a D =中元素),2,1,(L =j i a ij 均为整数,则D 必为整数.( √ )||班级:姓名:学号:成绩:批改日期: ||第 13 页共 18 页3.413223144433221144413332232214110000000a a a a a a a a a a a a a a a a -=.( ╳ ) 二、选择题1.若11131--+=x x x D ,211122-+=x x D ,则1D 与2D 的大小关系是( ).(A)21D D <; (B)21D D >;(C)21D D =;(D)随x 值变化而变化. 答案:C2.行列式{})2,1,1,,,(-∈d c b a dc ba 的所有可能值中,最大的是( ).(A) 0; (B)2; (C)4; (D)6. 答案:D三、填空题1.?40cos 20sin 40sin 20cos = .解析:-??=?40sin 20sin 40cos 20cos 40cos 20sin 40sin 20cos2160cos ==. 2.若y y x x y x -=-1122,则x+y = . 解析:由y y x x y x -=-1122,得xy y x 222-=+ 即0)(2=+y x ,从而x+y =0. 3.已知111,0112==yx x ,则y = . 解析:由111,0112==yx x ,得x =2,x -y =1,从而y =1||班级:姓名:学号:成绩:批改日期: ||第 14 页共 18 页4. 若222222222642531C c B b A a c b a ++=,则2C 化简后的结果等于 . 解析:242312=-=C . 5.设xx x x x x f 111123111212)(-=,则4x 的系数为;3系数为 .解析:当f (x )的主对角线的4个元素相乘才能得出4x ,系数为2;含3x 的项只能是44332112,,,a a a a 的乘积,系数为-1. 答案:2,-1.6.设0123411222641232211154321=D ,则(1)333231A A A ++= ;(2)3534A A + ;(3)5554535251A A A A A ++++ . 解析:0)(23534333231=++++A A A A A 0)()(23534333231=++++A A A A A 于是0333231=++A A A ,03534=+A A .5554535251A A A A A ++++1111111222641232211154321=||班级:姓名:学号:成绩:批改日期: ||第 15 页共 18 页01111133333641232211154321==. 即0555*******=++++A A A A A .四、解答题1.计算下列行列式.(1)4434433323134232221241312111y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x ++++++++++++++++;解:原式=14131214141312131413121214131211y y y y y y y x y y y y y y y x y y y y y y y x y y y y y y y x ---+---+---+---+=000000000014131214131211=------+x x x x x x y y y y y y y x .(2)43211111111111111111x x x x ++++;解:原式=432111110010011x x x x x x x ---+=432111413121100000001x x x x x x x x x x x x x ---++++ =3214214314324321x x x x x x x x x x x x x x x x ++++. ||班级:姓名:学号:成绩:批改日期: ||第 16 页共 18 页(3)2007000002006000200500020001000.解:原式=!2006)1(2007220052006?-?=!2007-2.已知123452221127312451112243150D ==, 求(1)434241A A A ++;(2)4544A A +. 解:27)(21114544434241=++?+?+?A A A A A0)()(24544434241=++++A A A A A得9434241-=++A A A ,184544=+A A . 3.计算下列n 阶行列式.(1)nn n n n n n D222333222111=;解:(利用范德蒙行列式计算)1122133321111!--==n n n Tn n n n n D D[])1()2()24)(23)(1()13)(12(!--------=n n n n n !2)!2()!1(! --=n n n .||班级:姓名:学号:成绩:批改日期: ||第 17 页共 18 页(2)211121112 ;解:原式=211121111 +++n n n =2121111)1( +n=110010111)1(+=+n n .(3)mx x x x m x x x x mx D n n n n ---=212121解:将第2列,L ,第n 列分别加到第一列,并提取第一列的公因子,得mx x mx x x x m x m x x x x x m x x x D n n n n n n n --+++--+++-+++=221221221mx x x m x x x m x x x n n n n ---+++=22221111(mm m x x x n ---+++= 0101001)(21121))((---+++=n n m m x x x||班级:姓名:学号:成绩:批改日期: || 第 18 页共 18 页(4)nn n n n a a a a a a b b b b b D 1322113210000000-----=(其中n i a i ,,2,1,0 =≠)解: 122110000000)1(-+----=n nnn a a a a b D122211221000000------+n n n n n a a a a a b b b b a 121-+?=n n nnn D a a b a a a==∑=n i i in a b a a a 121 . 三、证明题1.试证:如果n 次多项式n n x a x a a x f +++= 10)(对n+1个不同的x 值都是零,则此多项式恒等于零.(提示:用范德蒙行列式证明)。
《线性代数》同济大学版 课后习题答案详解

|2A1|(2)3|A1|8|A|18216
17设矩阵A可逆证明其伴随阵A*也可逆且(A*)1(A1)*
证明由 得A*|A|A1所以当A可逆时有
|A*||A|n|A1||A|n10
从而A*也可逆
因为A*|A|A1所以
(A*)1|A|1A
又 所以
(A*)1|A|1A|A|1|A|(A1)*(A1)*
5设 问
(1)ABBA吗?
解ABBA
因为 所以ABBA
(2)(AB)2A22ABB2吗?
解(AB)2A22ABB2
因为
但
所以(AB)2A22ABB2
(3)(AB)(AB)A2B2吗?
解(AB)(AB)A2B2
因为
而
故(AB)(AB)A2B2
6举反列说明下列命题是错误的
(1)若A20则A0
解取 则A20但A0
解 令
则
故
29设n阶矩阵A及s阶矩阵B都可逆求
(1)
解设 则
由此得
所以
(2)
解设 则
由此得
所以
30求下列矩阵的逆阵
(1)
解设 则
于是
(2)
解设 则
第三章 矩阵的初等变换与线性方程组
1把下列矩阵化为行最简形矩阵
(1)
解 (下一步r2(2)r1r3(3)r1)
~ (下一步r2(1)r3(2))
~ (下一步r3r2)
(3)
解 (下一步r12r4r22r4r33r4)
~ (下一步r23r1r32r1)
~ (下一步r216r4r316r2)
~
~
矩阵的秩为3 是一个最高阶非零子式
10设A、B都是mn矩阵证明A~B的充分必要条件是R(A)R(B)
线性代数课后习题答案全解.pdf

第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102−−−;解 381141102−−−=2×(−4)×3+0×(−1)×(−1)+1×1×8 −0×1×3−2×(−1)×8−1×(−4)×(−1) =−24+8+16−4=−4. (2)b a c a c b cb a ;解 ba c a cb cb a=acb +bac +cba −bbb −aaa −ccc =3abc −a 3−b 3−c 3. (3)222111c b a c b a ;解 222111c b a c b a=bc 2+ca 2+ab 2−ac 2−ba 2−cb =(a −b )(b −c )(c −a ). 2(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y )y +yx (x +y )+(x +y )yx −y 3−(x +y )3−x =3xy (x +y )−y 3 3−3x 2 y −x 3−y 3−x =−2(x 3 3+y 3 2. 按自然数从小到大为标准次序, 求下列各排列的逆序数:).(1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n −1) 2 4 ⋅ ⋅ ⋅ (2n );解 逆序数为2)1(−n n : 3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个)⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n −1)2, (2n −1)4, (2n −1)6, ⋅ ⋅ ⋅, (2n −1)(2n −2) (n −1个)(6)1 3 ⋅ ⋅ ⋅ (2n −1) (2n ) (2n −2) ⋅ ⋅ ⋅ 2. 解 逆序数为n (n −1) : 3 2(1个) 5 2, 5 4 (2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n −1)2, (2n −1)4, (2n −1)6, ⋅ ⋅ ⋅, (2n −1)(2n −2) (n −1个) 4 2(1个) 6 2, 6 4(2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n )2, (2n )4, (2n )6, ⋅ ⋅ ⋅, (2n )(2n −2) (n −1个) 3. 写出四阶行列式中含有因子a 11a 23 解 含因子a 的项. 11a 23(−1)的项的一般形式为t a 11a 23a 3r a 4s 其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42. ,所以含因子a 11a 23 (−1)的项分别是t a 11a 23a 32a 44=(−1)1a 11a 23a 32a 44=−a 11a 23a 32a 44 (−1), t a 11a 23a 34a 42=(−1)2a 11a 23a 34a 42=a 11a 23a 34a 42 4. 计算下列各行列式:.(1)71100251020214214; 解 71100251020214214010014231020211021473234−−−−−======c c c c 34)1(143102211014+−×−−−= 143102211014−−=01417172001099323211=−++======c c c c .(2)2605232112131412−; 解 2605232112131412−26053212213041224−−=====c c 041203212213041224−−=====r r 0000003212213041214=−−=====r r . (3)efcf bf de cd bd aeac ab −−−;解 ef cf bf de cd bd ae ac ab −−−ec b e c b ec b adf −−−=abcdef adfbce 4111111111=−−−=.(4)dc b a 100110011001−−−. 解d c b a 100110011001−−−dc b aab ar r 10011001101021−−−++===== d c a ab 101101)1)(1(12−−+−−=+01011123−+−++=====cd c ada ab dc ccdad ab +−+−−=+111)1)(1(23=abcd +ab +cd +ad +1. 5. 证明:(1)1112222b b a a b ab a +=(a −b )3 证明;1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c −−−−−−=====ab a b a b a ab 22)1(22213−−−−−=+21))((a b a a b a b +−−==(a −b )3 (2) . y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=y x z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ; 证明 2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4−c 3, c 3−c 2, c 2−c 1 得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4−c 3, c 3−c 2得)022122212221222122222=++++=d d c c b b a a . (4)444422221111d c b a d c b a d c b a =(a −b )(a −c )(a −d )(b −c )(b −d )(c −d )(a +b +c +d ); 证明 444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b −−−−−−−−−=)()()(111))()((222a d d a c c a b b dc b ad a c a b +++−−−= ))(())((00111))()((a b d b d d a b c b c c bd b c a d a c a b ++−++−−−−−−= )()(11))()()()((a b d d a b c c b d b c a d a c a b ++++−−−−−= =(a −b )(a −c )(a −d )(b −c )(b −d )(c −d )(a +b +c +d ). (5)12211 000 00 1000 01a x a a a a x x xn n n+⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−−− =x n +a 1x n −1+ ⋅ ⋅ ⋅ +a n −1x +a n .证明 用数学归纳法证明.当n =2时, 2121221a x a x a x a x D ++=+−=, 命题成立. 假设对于(n −1)阶行列式命题成立, 即 D n −1=x n −1+a 1 x n −2+ ⋅ ⋅ ⋅ +a n −2x +a n −1则D , n 按第一列展开, 有 11100 100 01)1(11−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−−+=+−x x a xD D n n n n =xD n −1+a n =x n +a 1x n −1+ ⋅ ⋅ ⋅ +a n −1x +a n 因此, 对于n 阶行列式命题成立. .6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90°、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nnn a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n n nn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(−−==, D 3 证明 因为D =det(a =D .ij ), 所以 nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=−⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−=−− )1()1(331122111121nnn n nn n n a a a a a a a a D D n n n n 2)1()1()2( 21)1()1(−−+−+⋅⋅⋅++−=−=.同理可证 nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−=− )1(11112)1(2D D n n T n n 2)1(2)1()1()1(−−−=−=. D D D D D n n n n n n n n =−=−−=−=−−−−)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k (1)为k 阶行列式): aa D n 1 1⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解 aa a a a D n 010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(−×−+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−=n n n aa a )1()1(2 )1(−×−⋅⋅⋅⋅−+n n n a a an n n n n a a a+⋅⋅⋅−⋅−=−−+)2)(2(1)1()1(=a n −a n −2=a n −2(a 2−1).(2)xa aa x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(−1)分别加到其余各行, 得 ax x a ax x a a x x a aa a x D n −−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−⋅⋅⋅−−⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n −⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−+=0000 0 000 00 )1(=[x +(n −1)a ](x −a )n −1 (3). 111 1 )( )1()( )1(1111⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅⋅⋅⋅−⋅⋅⋅−−⋅⋅⋅−=−−−+n a a a n a a a n a a a D n n n n nn n ; 解 根据第6题结果, 有 nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1−⋅⋅⋅−−⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−=−−−++此行列式为范德蒙德行列式.∏≥>≥++++−−+−−=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++−−−=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+−++−⋅−⋅−=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+−=11)(j i n j i .(4)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn −−−−+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−+. 再按最后一行展开得递推公式D 2n =a n d n D 2n −2−b n c n D 2n −2, 即D 2n =(a n d n −b n c n )D 2n −2于是 . ∏=−=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D −==,所以 ∏=−=ni i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij 解 a =|i −j |; ij =|i −j |, 043214 01233 10122 21011 3210)det(⋅⋅⋅−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−⋅⋅⋅==n n n n n n n n a D ij n 04321 1 11111 11111 11111 1111 2132⋅⋅⋅−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−−−⋅⋅⋅−−−⋅⋅⋅−−⋅⋅⋅−−⋅⋅⋅−=====n n n n r r r r15242321 0 22210 02210 00210 0001 1213−⋅⋅⋅−−−−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−−−−⋅⋅⋅−−−⋅⋅⋅−−⋅⋅⋅−+⋅⋅⋅+=====n n n n n c c c c =(−1)n −1(n −1)2n −2 (6).nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121 nn n n a a a a a a a a a c c c c +−⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−⋅⋅⋅−=====−−100001 000 100 0100 0100 0011332212132 1111312112111000011 000 00 11000 01100 001 −−−−−−+−⋅⋅⋅−⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅−⋅⋅⋅−⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=−−−−−−+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni i n a a a a .8. 用克莱姆法则解下列方程组: (1) =+++−=−−−−=+−+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为 14211213513241211111−=−−−−=D , 142112105132412211151−=−−−−−−=D , 284112035122412111512−=−−−−−=D , 426110135232422115113−=−−−−=D , 14202132132212151114=−−−−−=D , 所以 111==D D x , 222==D Dx , 333==DD x , 144−==D D x .(2)=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为 665510006510006510065100065==D , 15075100165100065100065000611==D , 114551010651000650000601000152−==D , 703511650000601000051001653==D , 39551601000051000651010654−==D , 2121100005100065100651100655==D , 所以66515071=x , 66511452−=x , 6657033=x , 6653954−=x , 6652124=x .9. 问λ, µ取何值时, 齐次线性方程组 =++=++=++0200321321321x x x x x x x x x µµλ有非零解?解 系数行列式为µλµµµλ−==1211111D .令D =0, 得 µ=0或λ=1.于是, 当µ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组 =−++=+−+=+−−0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解?解 系数行列式为λλλλλλλ−−+−−=−−−−=101112431111132421D=(1−λ)3 =(1−λ)+(λ−3)−4(1−λ)−2(1−λ)(−3−λ) 3+2(1−λ)2 令D =0, 得+λ−3. λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3 解 由已知:的线性变换.= 221321323513122y y y x x x ,故= −3211221323513122x x x y y y−−−−=321423736947y y y ,−+=−+=+−−=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换++=++−=+=32133212311542322y y y x y y y x y y x ,+−=+=+−=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3 解 由已知的线性变换.−= 221321514232102y y y x x x−− −=321310102013514232102z z z−−−−=321161109412316z z z ,所以有 +−−=+−=++−=3213321232111610941236z z z x z z z x z z z x .3. 设 −−=111111111A ,−−=150421321B , 求3AB −2A 及A T 解 B .−−− −− −−=−1111111112150421321111111111323A AB−−−−= −−− −=2294201722213211111111120926508503,−= −− −−=092650850150421321111111111B A T.4. 计算下列乘积: (1)−127075321134;解 −127075321134 ×+×+××+×−+××+×+×=102775132)2(71112374=49635.(2)123)321(;解123)321(=(1×3+2×2+3×1)=(10).(3))21(312−;解 )21(312−×−××−××−×=23)1(321)1(122)1(2−−−=632142. (4)−−−−20413121013143110412 ; 解−−− −20413121013143110412 −−−=6520876. (5)321332313232212131211321)(x x x a a a a a a a a a x x x ;解321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3a 13x 1+a 23x 2+a 33x 3321x x x )322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设 =3121A ,=2101B , 问: (1)AB =BA 吗? 解 AB ≠BA . 因为=6443AB ,=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2 解 (A +B )吗? 2≠A 2+2AB +B 2 因为.=+5222B A ,=+52225222)(2B A=2914148,但 + +=++43011288611483222B AB A=27151610,所以(A +B )2≠A 2+2AB +B 2 (3)(A +B )(A −B )=A . 2−B 2 解 (A +B )(A −B )≠A 吗? 2−B 2 因为.=+5222B A ,=−1020B A ,==−+906010205222))((B A B A ,而= −=−718243011148322B A ,故(A +B )(A −B )≠A 2−B 2 6. 举反列说明下列命题是错误的:.(1)若A 2 解 取=0, 则A =0;=0010A , 则A 2 (2)若A =0, 但A ≠0. 2 解 取=A , 则A =0或A =E ;=0011A , 则A 2 (3)若AX =AY , 且A ≠0, 则X =Y .=A , 但A ≠0且A ≠E . 解 取=0001A , −=1111X ,=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k 解 . ==12011011012λλλA , ===1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,=101λk A k . 8. 设=λλλ001001A , 求A k 解 首先观察. =λλλλλλ0010010010012A=222002012λλλλλ,=⋅=3232323003033λλλλλλA A A ,=⋅=43423434004064λλλλλλA A A ,=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,=k A k k k k k k k k k k λλλλλλ0002)1(121−−−−. 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立,则k +1时,−=⋅=−−−+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A+++=+−+−−+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:−=−−−k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T 证明 因为A AB 也是对称矩阵.T (B =A , 所以T AB )T =B T (B T A )T =B T A T B =B T 从而B AB ,T 10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA .AB 是对称矩阵.证明 充分性: 因为A T =A , B T (AB )=B , 且AB =BA , 所以 T =(BA )T =A T B T 即AB 是对称矩阵.=AB ,必要性: 因为A T =A , B T =B , 且(AB )T AB =(AB )=AB , 所以T =B T A T 11. 求下列矩阵的逆矩阵:=BA .(1)5221; 解=5221A . |A |=1, 故A −1 存在. 因为−−= =1225*22122111A A A A A ,故 *||11A A A =−−−=1225. (2)−θθθθcos sin sin cos ; 解−=θθθθcos sin sin cos A . |A |=1≠0, 故A −1 存在. 因为−= =θθθθcos sin sin cos *22122111A A A A A , 所以 *||11A A A =−−=θθθθcos sin sin cos . (3)−−−145243121; 解−−−=145243121A . |A |=2≠0, 故A −1 存在. 因为−−−−−= =214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =−−−−−−=1716213213012. (4)n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解=n a a a A 0021, 由对角矩阵的性质知=−n a a a A 10011211 . 12. 解下列矩阵方程:(1) −=12643152X ; 解 −=−126431521X − −−=12642153 −=80232. (2) −=−−234311*********X ; 解 1111012112234311−−− −=X−−− −=03323210123431131 −−−=32538122. (3) −= − −101311022141X ;解 11110210132141−− − − −=X− −=210110131142121 =21010366121=04111. (4)−−−= 021102341010100001100001010X . 解 11010100001021102341100001010−−−−− =X −−− =010100001021102341100001010 −−−=201431012. 13. 利用逆矩阵解下列线性方程组:(1) =++=++=++3532522132321321321x x x x x x x x x ; 解 方程组可表示为= 321153522321321x x x , 故 = = −0013211535223211321x x x ,从而有 ===001321x x x . (2) =−+=−−=−−05231322321321321x x x x x x x x x . 解 方程组可表示为=−−−−−012523312111321x x x , 故 =−−−−−= −3050125233121111321x x x , 故有 ===305321x x x . 14. 设A k =O (k 为正整数), 证明(E −A )−1=E +A +A 2+⋅ ⋅ ⋅+A k −1 证明 因为A . k =O , 所以E −A k E −A =E . 又因为k =(E −A )(E +A +A 2+⋅ ⋅ ⋅+A k −1所以 (E −A )(E +A +A ),2+⋅ ⋅ ⋅+A k −1由定理2推论知(E −A )可逆, 且)=E ,(E −A )−1=E +A +A 2+⋅ ⋅ ⋅+A k −1.证明 一方面, 有E =(E −A )−1 另一方面, 由A (E −A ).k E =(E −A )+(A −A =O , 有2)+A 2−⋅ ⋅ ⋅−A k −1+(A k −1−A k )=(E +A +A 2+⋅ ⋅ ⋅+A k −1故 (E −A ))(E −A ),−1(E −A )=(E +A +A 2+⋅ ⋅ ⋅+A k −1两端同时右乘(E −A ))(E −A ),−1 (E −A ), 就有−1(E −A )=E +A +A 2+⋅ ⋅ ⋅+A k −1.15. 设方阵A 满足A 2−A −2E =O , 证明A 及A +2E 都可逆, 并求A −1及(A +2E )−1 证明 由A .2 A −A −2E =O 得2或 −A =2E , 即A (A −E )=2E ,E E A A =−⋅)(21, 由定理2推论知A 可逆, 且)(211E A A −=−. 由A 2 A −A −2E =O 得2或 −A −6E =−4E , 即(A +2E )(A −3E )=−4E ,E A E E A =−⋅+)3(41)2( 由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A −=+−.证明 由A 2−A −2E =O 得A 2 |A −A =2E , 两端同时取行列式得 2即 |A ||A −E |=2,−A |=2,故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2由 A ≠0, 故A +2E 也可逆. 2 ⇒A −A −2E =O ⇒A (A −E )=2E−1A (A −E )=2A −1)(211E A A −=−E ⇒,又由 A 2 ⇒ (A +2E )(A −3E )=−4 E ,−A −2E =O ⇒(A +2E )A −3(A +2E )=−4E所以 (A +2E )−1(A +2E )(A −3E )=−4(A +2 E )−1 ,)3(41)2(1A E E A −=+−.16. 设A 为3阶矩阵, 21||=A , 求|(2A )−1 解 因为−5A *|.*||11A A A =−, 所以 |||521||*5)2(|111−−−−=−A A A A A |2521|11−−−=A A=|−2A −1|=(−2)3|A −1|=−8|A |−1 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)=−8×2=−16.−1=(A −1 证明 由)*.*||11A A A =−, 得A *=|A |A −1 |A *|=|A |, 所以当A 可逆时, 有n |A −1|=|A |n −1从而A *也可逆.≠0,因为A *=|A |A −1 (A *), 所以−1=|A |−1又A .*)(||)*(||1111−−−==A A A A A , 所以(A *)−1=|A |−1A =|A |−1|A |(A −1)*=(A −1 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明:)*.(1)若|A |=0, 则|A *|=0;(2)|A *|=|A |n −1 证明.(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)−1 A =A A *(A *)=E , 由此得 −1=|A |E (A *)−1所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0.=O ,(2)由于*||11A A A =−, 则AA *=|A |E , 取行列式得到 |A ||A *|=|A |n 若|A |≠0, 则|A *|=|A |.n −1 若|A |=0, 由(1)知|A *|=0, 此时命题也成立.;因此|A *|=|A |n −1.19. 设−=321011330A , AB =A +2B , 求B . 解 由AB =A +2E 可得(A −2E )B =A , 故− −−−=−=−−321011330121011332)2(11A E A B −=011321330. 20. 设 =101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2 (A −E )B =A +B 得 2即 (A −E )B =(A −E )(A +E ).−E , 因为01001010100||≠−==−E A , 所以(A −E )可逆, 从而=+=201030102E A B .21. 设A =diag(1, −2, 1), A *BA =2BA −8E , 求B . 解 由A *BA =2BA −8E 得 (A *−2E )BA =−8E , B =−8(A *−2E )−1A =−8[A (A *−2E )]−1 =−8(AA *−2A )−1 =−8(|A |E −2A )−1 =−8(−2E −2A )−1 =4(E +A )−1 =4[diag(2, −1, 2)]−1−1)21 ,1 ,21(diag 4−==2diag(1, −2, 1).22. 已知矩阵A 的伴随阵−=8030010100100001*A , 且ABA −1=BA −1+3E , 求B .解 由|A *|=|A |3 由ABA =8, 得|A |=2. −1=BA −1 AB =B +3A ,+3E 得 B =3(A −E )−1A =3[A (E −A −1)]−1 A 11*)2(6*)21(3−−−=−=A E A E−=−−=−1030060600600006603001010010000161. 23. 设P −1 −−=1141P AP =Λ, 其中,−=Λ2001, 求A 11 解 由P . −1AP =Λ, 得A =P ΛP −1, 所以A 11= A =P Λ11P −1 |P |=3, .−=1141*P ,−−=−1141311P ,而−= −=Λ11111120 012001,故−− −−−=31313431200111411111A −−=68468327322731. 24. 设AP =P Λ, 其中−−=111201111P ,−=Λ511,求ϕ(A )=A 8(5E −6A +A 2 解 ϕ(Λ)=Λ). 8(5E −6Λ+Λ2 =diag(1,1,5)8)[diag(5,5,5)−diag(−6,6,30)+diag(1,1,25)]=diag(1,1,58 ϕ(A )=P ϕ(Λ)P )diag(12,0,0)=12diag(1,0,0).−1 *)(||1P P P Λ=ϕ−−−−−− −−−=1213032220000000011112011112=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A −1+B −1 证明 因为也可逆, 并求其逆阵.A −1(A +B )B −1=B −1+A −1=A −1+B −1而A ,−1(A +B )B −1是三个可逆矩阵的乘积, 所以A −1(A +B )B −1可逆, 即A −1+B −1 (A 可逆.−1+B −1)−1=[A −1(A +B )B −1]−1=B (A +B )−1 26. 计算A .−−−30003200121013013000120010100121. 解 设 =10211A , =30122A , −=12131B ,−−=30322B ,则 2121B O B E A O E A+=222111B A O B B A A ,而 −= −−+−=+4225303212131021211B B A ,−−= −− =90343032301222B A , 所以 2121B O B E A O E A +=222111B A O B B A A−−−=9000340042102521, 即−−−30003200121013013000120010100121−−−=9000340042102521. 27. 取==−==1001D C B A , 验证|||||||| D C B A D C B A ≠.解 4100120021010*********0021010010110100101==−−=−−=D C B A , 而 01111|||||||| ==D C B A ,故 ||||||||D C B A D C B A ≠. 28. 设 −=22023443O O A , 求|A 8|及A 4解 令. −=34431A ,=22022A , 则=21A O O A A ,故 8218=A O O A A=8281A O O A ,1682818281810||||||||||===A A A A A .= =464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求 (1)1−O B A O ; 解 设 =−43211C C C C O B A O , 则O B A O 4321C C C C = =s n E O O E BC BC AC AC 2143. 由此得====s n EBC OBC O AC E AC 2143⇒ ====−−121413B C O C O C A C ,所以= −−−O A B O O B A O 111. (2)1−B C O A . 解 设 =−43211D D D D B C O A , 则 = ++= s nE O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得=+=+==s nEBD CD O BD CD O AD E AD 423121⇒ =−===−−−−14113211B D CA B D O D A D ,所以−= −−−−−11111B CA B O A BC O A . 30. 求下列矩阵的逆阵: (1)2500380000120025; 解 设 =1225A , =2538B , 则−−= =−−5221122511A ,−−==−−8532253811B .于是 −−−−= = =−−−−850032000052002125003800001200251111B A B A .(2)4121031200210001. 解 设 =2101A ,=4103B ,=2112C , 则−= =−−−−−−1111114121031200210001B CA B O A BC O A−−−−−=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵: (1)−−340313021201;解−−340313021201(下一步: r 2+(−2)r 1, r 3+(−3)r 1 ~. )−−−020*********(下一步: r 2÷(−1), r 3 ~÷(−2). )−−010*********(下一步: r 3−r 2 ~. )−−300031001201(下一步: r 3 ~÷3. )−−100031001201(下一步: r 2+3r 3 ~. )−100001001201(下一步: r 1+(−2)r 2, r 1+r 3 ~. )100001000001.(2)−−−−174034301320;解−−−−174034301320(下一步: r 2×2+(−3)r 1, r 3+(−2)r 1 ~. )−−−310031001320(下一步: r 3+r 2, r 1+3r 2 ~. )0000310010020(下一步: r 1 ~÷2. )000031005010.(3)−−−−−−−−−12433023221453334311;解−−−−−−−−−12433023221453334311(下一步: r 2−3r 1, r 3−2r 1, r 4−3r 1~. )−−−−−−−−1010500663008840034311(下一步: r 2÷(−4), r 3÷(−3) , r 4~÷(−5). )−−−−−22100221002210034311(下一步: r 1−3r 2, r 3−r 2, r 4−r 2~. )−−−00000000002210032011.(4)−−−−−−34732038234202173132. 解−−−−−−34732038234202173132(下一步: r 1−2r 2, r 3−3r 2, r 4−2r 2~. )−−−−−1187701298804202111110(下一步: r 2+2r 1, r 3−8r 1, r 4−7r 1 ~. )−−41000410002020111110(下一步: r 1↔r 2, r 2×(−1), r 4−r 3~. )−−−−00000410001111020201(下一步: r 2+r 3~. )−−00000410003011020201. 2. 设= 987654321100010101100001010A , 求A .解100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(−1))−=100010101.− =100010101987654321100001010A= − =287221254100010101987321654.3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵: (1)323513123;解 100010001323513123~−−−101011001200410123~ −−−−1012002110102/102/3023~−−−−2/102/11002110102/922/7003~−−−−2/102/11002110102/33/26/7001故逆矩阵为−−−−21021211233267.(2)−−−−−1210232112201023.解−−−−−10000100001000011210232112201023~−−−−00100301100001001220594012102321~−−−−−−−−20104301100001001200110012102321~ −−−−−−−106124301100001001000110012102321 ~−−−−−−−−−−10612631110`1022111000010000100021 ~−−−−−−−106126311101042111000010000100001故逆矩阵为−−−−−−−10612631110104211. 4. (1)设 −−=113122214A ,−−=132231B , 求X 使AX =B ;解 因为−−−−=132231 113122214) ,(B A−−412315210 100010001 ~r ,所以−−==−4123152101B A X .(2)设−−−=433312120A , −=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为−−−−=134313*********) ,(T T B A−−−411007101042001 ~r ,所以−−−==−417142)(1T T T B A X ,从而−−−==−4741121BA X . 5. 设−−−=101110011A , AX =2X +A , 求X .解 原方程化为(A −2E )X =A . 因为−−−−−−−−−=−101101110110011011) ,2(A E A−−−011100101010110001~,所以−−−=−=−011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r −1阶子式? 有没有等于0的r 阶子式?解 在秩是r 的矩阵中, 可能存在等于0的r −1阶子式, 也可能存在等于0的r 阶子式. 例如,=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, −1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:−0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式: (1)−−−443112112013;解−−−443112112013(下一步: r 1↔r 2 ~. )−−−443120131211(下一步: r 2−3r 1, r 3−r 1 ~. )−−−−564056401211(下一步: r 3−r 2 ~. )−−−000056401211, 矩阵的2秩为, 41113−=−是一个最高阶非零子式.(2)−−−−−−−815073*********;解−−−−−−−815073*********(下一步: r 1−r 2, r 2−2r 1, r 3−7r 1 ~. )−−−−−−15273321059117014431(下一步: r 3−3r 2~. )−−−−0000059117014431, 矩阵的秩是2, 71223−=−是一个最高阶非零子式.(3)−−−02301085235703273812. 解−−−02301085235703273812(下一步: r 1−2r 4, r 2−2r 4, r 3−3r 4~. )−−−−−−023*********63071210(下一步: r 2+3r 1, r 3+2r 1~. )−0230114000016000071210(下一步: r 2÷16r 4, r 3−16r 2. )~−02301000001000071210 ~−00000100007121002301, 矩阵的秩为3, 070023085570≠=−是一个最高阶非零子式.10. 设A 、B 都是m ×n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设−−−−=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 −−−−=32321321k k k A+−−−−−)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =−2且k ≠1时, R (A )=2;(3)当k ≠1且k ≠−2时, R (A )=3.12. 求解下列齐次线性方程组: (1) =+++=−++=−++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有 A = −−212211121211~ −−−3/410013100101,于是 ==−==4443424134334x x x x x x x x ,故方程组的解为−= 1343344321k x x x x (k 为任意常数).(2) =−++=−−+=−++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有 A = −−−−5110531631121~−000001001021,于是 ===+−=4432242102x x x xx x x x ,故方程组的解为+−= 10010*********k k x x x x (k 1, k 2 (3)为任意常数).=−+−=+−+=−++=+−+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有 A =−−−−−7421631472135132~1000010000100001,于是 ====0004321x x x x ,故方程组的解为 ====00004321x x x x .(4) =++−=+−+=−+−=+−+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x .解 对系数矩阵A 进行初等行变换, 有 A =−−−−−3127161311423327543~−−000000001720171910171317301,于是 ==−=−=4433432431172017191713173x x x x x x x xx x ,故方程组的解为−−+= 1017201713011719173214321k k x x x x (k 1, k 2为任意常数).13. 求解下列非齐次线性方程组: (1) =+=+−=−+83111021322421321321x x x x x x x x ;解 对增广矩阵B 进行初等行变换, 有。
《线性代数》第一章行列式精选习题及解答

(C)0, 2
(D)0,1
解 按 三 阶 行 列 式 的 对 角 线 法 则 得 D1 = (λ + 1)(λ − 1)2 , D2 = 0 . 若 D1 = D2 , 则
(λ + 1)(λ −1)2 = 0 ,于是 λ = 1,−1,故正确答案为(B).
例 1.5
方程组 ⎪⎨⎧λx1x1++λxx22
故逆序数为 1;于是这个排列的逆序数为 t=0+0+2+4+1=7,故正确答案为(B).
例 1.2 下列排列中( )是偶排列.
(A)54312 (B)51432
(C) 45312
(D) 654321
解 按照例 1 的方法计算知:排列 54312 的逆序数为 9;排列 51432 的逆序数为 7;排列
例17分析如果行列式的各行列数的和相同时一般首先采用的是将各列行加到第一列行提取第一列行的公因子简称列行加法这个行列式的特点是各列4个数的和为10于是各行加到第一行得10101010分析此类确定系数的题目首先是利用行列式的定义进行计算
第一章 行列式
1.1 目的要求
1.会求 n 元排列的逆序数; 2.会用对角线法则计算 2 阶和 3 阶行列式; 3.深入领会行列式的定义; 4.掌握行列式的性质,并且会正确使用行列式的有关性质化简、计算行列式; 5.灵活掌握行列式按(列)展开; 6.理解代数余字式的定义及性质; 7.会用克拉默法则判定线性方程组解的存在性、唯一性及求出方程组的解.
(2) A34 + A35 = ( ), (3) A51 + A52 + A53 + A54 + A55 = ( ).
分析 此类题目一般不宜算出表达式里每一项的值,而是注意观察要求的表达式的结构,
(完整版)线性代数课后习题答案第1——5章习题详解

第一章 行列式4.计算下列各行列式:(1)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢7110025*********4; (2)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-265232112131412; (3)⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ; (4)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯---=143102211014-- 321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=ec b e c b ec b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--=右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bzay y x by ax x z bxaz z y b +++z y x y x z x z y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a 949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a (4) 444444422222220001ad a c a b a ad a c a b a ad a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即 ,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转,依次得n nn n a a a a D 11111 =, 11112n nn n a a a a D = ,11113a a a a D n nnn =,证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnn n nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-=同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)a aD n 11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xaaax aa a x D n=; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n n n n n ------=---+; 提示:利用范德蒙德行列式的结果. (4) nnnnn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(100000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n na aa(再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上,得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行交换,得 nn n n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nn nnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式:222)(--=n n n n n n D c b d a D即 ∏=-=ni i i iin D c b da D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=432140123310122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121,,433221c c c c c c ---n n n n a a a a a a a a a a +-------10000100010000100010001000011433221 展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------00000000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=14200038100112109151----=142-=112035122412111512-----=D 811507312032701151-------=3139011230023101151-=2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510006510065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 51001651000651000650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507=51010651000650000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-= 1145108065-=--=51100650000601000051001653=D 展开按第三列51006500061000516500061000510065+6100510656510650061+= 703114619=⨯+=51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 110051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x . 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 μλμμμλ-==12111113D , 齐次线性方程组有非零解,则03=D即 0=-μλμ 得 10==λμ或不难验证,当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解?解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ 齐次线性方程组有非零解,则0=D得 32,0===λλλ或不难验证,当32,0===λλλ或时,该齐次线性方程组确有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x ,求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换.解 由已知:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x , 故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z , 所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B . 解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB ⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134; 解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635. (2)⎪⎪⎭⎫⎝⎛123)321(; 解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛; 解 )21(312-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876. (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ; 解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x =(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗?解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B)2=A 2+2AB +B 2吗?解 (A +B)2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148, 但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B)2≠A 2+2AB +B 2.(3)(A +B)(A -B)=A 2-B 2吗?解 (A +B)(A -B)≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A , 故(A +B)(A -B)≠A 2-B 2.6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k . 解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ, ⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=k A k k k k k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫ . 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB)T =B T (B T A)T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以(AB)T =(BA)T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB)T =AB , 所以AB =(AB)T =B T A T =BA .11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A|=1, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A , 故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A|=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A , 所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A|=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; 解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ;解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A)可逆, 且(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A)-1(E -A). 另一方面, 由A k =O , 有E =(E -A)+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),故 (E -A)-1(E -A)=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A), 两端同时右乘(E -A)-1, 就有(E -A)-1(E -A)=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E)-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A(A -E)=2E ,或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E)(A -3E)=-4E ,或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E)可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A|=2,即 |A||A -E|=2, 故 |A|≠0,所以A 可逆, 而A +2E =A 2, |A +2E|=|A 2|=|A|2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A(A -E)=2E⇒A -1A(A -E)=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E)A -3(A +2E)=-4E⇒ (A +2E)(A -3E)=-4 E ,所以 (A +2E)-1(A +2E)(A -3E)=-4(A +2 E)-1,)3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵,21||=A , 求|(2A)-1-5A*|.解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A|-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A*也可逆, 且(A*)-1=(A -1)*.证明 由*||11A A A =-, 得A*=|A|A -1, 所以当A 可逆时, 有|A*|=|A|n |A -1|=|A|n -1≠0,从而A*也可逆.因为A*=|A|A -1, 所以 (A*)-1=|A|-1A .又*)(||)*(||1111---==A A A A A , 所以(A*)-1=|A|-1A =|A|-1|A|(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A*, 证明: (1)若|A|=0, 则|A*|=0; (2)|A*|=|A|n -1. 证明(1)用反证法证明. 假设|A*|≠0, 则有A*(A*)-1=E , 由此得 A =A A*(A*)-1=|A|E(A*)-1=O ,所以A*=O , 这与|A*|≠0矛盾,故当|A|=0时, 有|A*|=0.(2)由于*||11A A A =-, 则AA*=|A|E , 取行列式得到|A||A*|=|A|n . 若|A|≠0, 则|A*|=|A|n -1;若|A|=0, 由(1)知|A*|=0, 此时命题也成立. 因此|A*|=|A|n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E)B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E)B =A 2-E ,即 (A -E)B =(A -E)(A +E).因为01001010100||≠-==-E A , 所以(A -E)可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A*BA =2BA -8E , 求B . 解 由A*BA =2BA -8E 得 (A*-2E)BA =-8E , B =-8(A*-2E)-1A -1 =-8[A(A*-2E)]-1 =-8(AA*-2A)-1 =-8(|A|E -2A)-1 =-8(-2E -2A)-1 =4(E +A)-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A*|=|A|3=8, 得|A|=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E)-1A =3[A(E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11.解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A=P Λ11P -1.|P|=3,⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001,故⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731.24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A)=A 8(5E -6A +A 2).解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A)=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B)B -1=B -1+A -1=A -1+B -1,而A -1(A +B)B -1是三个可逆矩阵的乘积, 所以A -1(A +B)B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B)B -1]-1=B(A +B)-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A ,所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解4100120021100101002000021010010110100101==--=--=D C B A , 而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A ,则⎪⎭⎫⎝⎛=21A O O A A ,故8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321. 由此得 ⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD O AD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A BC O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2)⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4)⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020*********)2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫ ⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫ ⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311 141312323~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r r r --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫ ⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ,求A 。
《线性代数》同济大学版 课后习题答案详解

4计算下列各行列式
(1)
解
(2)
解
(3)
解
(4)
解
abcdabcdad1
5证明:
(1) (ab)3;
证明
(ab)3
(2) ;
证明
(3) ;
证明
(c4c3c3c2c2c1得)
(c4c3c3c2得)
(4)
(ab)(ac)(ad)(bc)(bd)(cd)(abcd);
若|A|0则|A*||A|n1
若|A|0由(1)知|A*|0此时命题也成立
因此|A*||A|n1
19设 ABA2B求B
解由ABA2E可得(A2E)BA故
20设 且ABEA2B求B
解由ABEA2B得
(AE)BA2E
即(AE)B(AE)(AE)
因为 所以(AE)可逆从而
21设Adiag(121)A*BA2BA8E求B
|A2A|2
即|A||AE|2
故|A|0
所以A可逆而A2EA2|A2E||A2||A|20故A2E也可逆
由A2A2EOA(AE)2E
A1A(AE)2A1E
又由A2A2EO(A2E)A3(A2E)4E
(A2E)(A3E)4E
所以(A2E)1(A2E)(A3E)4(A2E)1
16设A为3阶矩阵 求|(2A)15A*|
(1)
解因为
所以
(2)
解因为
所以
9问取何值时齐次线性方程组 有非零解?
解系数行列式为
令D0得
0或1
于是当0或1时该齐次线性方程组有非零解
10问取何值时齐次线性方程组 有非零解?
(完整版)行列式习题答案

线性代数练习题 第一章 行 列 式系 专业 班 姓名 学号第一节 n 阶 行 列 式一.选择题1.若行列式 = 0,则[ C ]x52231521-=x (A )2 (B )(C )3(D )2-3-2.线性方程组,则方程组的解=[ C ]⎩⎨⎧=+=+473322121x x x x ),(21x x (A )(13,5)(B )(,5)(C )(13,)(D )()13-5-5,13--3.方程根的个数是[ C ]093142112=x x (A )0 (B )1 (C )2 (D )34.下列构成六阶行列式展开式的各项中,取“+”的有 [ A ](A ) (B ) 665144322315a a a a a a 655344322611a a a a a a (C ) (D )346542165321a a a a a a 266544133251a a a a a a 5.若是五阶行列式的一项,则的值及该项的符号为[ B ]55443211)541()1(a a a a a l k l k N -ij a l k ,(A ),符号为正; (B ),符号为负;3,2==l k 3,2==l k (C ),符号为正;(D ),符号为负2,3==l k 2,3==l k 6.下列n (n >2)阶行列式的值必为零的是 [ BD ](A) 行列式主对角线上的元素全为零 (B) 三角形行列式主对角线上有一个元素为零 (C) 行列式零的元素的个数多于n 个 (D) 行列式非零元素的个数小于n 个二、填空题1.行列式的充分必要条件是1221--k k 0≠3,1k k ≠≠-2.排列36715284的逆序数是133.已知排列为奇排列,则r =2,8,5s = 5,2,8,t = 8,5,2397461t s r4.在六阶行列式中,应取的符号为 负 。
ij a 623551461423a a a a a a 三、计算下列行列式:1.=181322133212.=55984131113.yxyx x y x yyx y x +++332()x y =-+4.=100011000001001005.000100002000010n n -1(1)!n n -=-6.0011,22111,111 n n nn a a a a a a --(1)212,11(1)n n n n n a a a --=-线性代数练习题 第一章 行 列 式系专业 班 姓名 学号第二节 行列式的性质一、选择题:1.如果, ,则 [ C ]1333231232221131211==a a a a a a a a a D 3332313123222121131211111232423242324a a a a a a a a a a a a D ---==1D (A )8(B )(C )(D )2412-24-2.如果,,则 [ B ]3333231232221131211==a a a a a a a a a D 2323331322223212212131111352352352a a a a a a a a a a a a D ---==1D (A )18(B ) (C )(D )18-9-27-3. = [ C ]2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (A )8 (B )2(C )0(D )6-二、选择题:1.行列式 12246000 2. 行列式-3=30092280923621534215=11101101101101112.多项式的所有根是0211111)(321321321321=+++++=x a a a a x a a a a x a a a a x f 0,1,2--3.若方程= 0 ,则225143214343314321x x --1,x x =±=4.行列式 5==2100121001210012D 三、计算下列行列式:1.2605232112131412-21214150620.12325062r r +=2.xa a a x a a a x 1[(1)]().n x n a x a -=+--线性代数练习题 第一章 行 列 式系专业 班 姓名 学号第三节 行列式按行(列)展开一、选择题:1.若,则中x 的一次项系数是[D]111111111111101-------=x A A (A )1(B )(C )(D )1-44-2.4阶行列式的值等于 [D ]443322110000000a b a b b a b a (A ) (B )43214321b b b b a a a a -))((43432121b b a a b b a a --(C )(D )43214321b b b b a a a a +))((41413232b b a a b b a a --3.如果,则方程组 的解是 [B]122211211=a a a a ⎩⎨⎧=+-=+-0022221211212111b x a x a b x a x a (A ), (B ),2221211a b a b x =2211112b a b a x =2221211a b a b x -=2211112b a b a x =(C ), (D ),2221211a b a b x ----=2211112b a b a x ----=2221211a b a b x ----=2211112b a b a x -----=二、填空题:1.行列式 中元素3的代数余子式是 -6122305403--2.设行列式,设分布是元素的余子式和代数余子式,4321630211118751=D j j A M 44,j a 4则 =,=-6644434241A A A A +++44434241M M M M +++3.已知四阶行列D 中第三列元素依次为,2,0,1,它们的余子式依次分布为1-5,3,4,则D = -15,7-三、计算行列式:1.321421431432432112341234134101131010141201311123031111310131160.311-==---=-=-2.12111111111na a a +++ ==121111011101110111n a a a+++121111100100100na a a---211112111110010010n c c a a a a a+--+111223211111100001000na a cc a a a a++-+11121101111000000ni ni iia a a c a c a=+++∑1211()(1)nn i i a a a a =+∑或121123113111111000000nn a r r a r r a r r a a a a+------211211212311111000000na a aa a a c c a a a a+++--11122313311111100000ni in nnaa a c c a a a c c a a a a=++++∑1122()(1)nn i ia a a a a =++∑或11221121121110111110111111111(1).n n n n nn i ia a a a a a D a a a a a a a --=++++=+=+=+∑线性代数练习题 第一章 行 列 式系专业 班 姓名学号综 合 练 习一、选择题:1.如果,则 = [ C ]0333231232221131211≠==M a a a a a a a a a D 3332312322211312111222222222a a a a a a a a a D =(A )2 M(B )-2 M(C )8 M(D )-8 M2.若,则项的系数是[ A ]xxx x x x f 171341073221)(----=2x (A )34 (B )25 (C )74 (D )6二、选择题:1.若为五阶行列式带正号的一项,则 i = 2 j = 154435231a a a a a j i 2. 设行列式,则第三行各元素余子式之和的值为 8。
线性代数习题册参考解答.docx

第一章行列式1、 求下列排列的逆序数,并确定它们的奇偶性。
(1) 1347265; (2) 〃(〃 —1)・・・321。
【解(1) r(1347265)=0 + 0 + 0 + 0 + 3 + l + 2 = 6,偶排列;(2) "〃(〃_1)...321] = 0 + ] + 2 + ... + (〃_1) = 〃(;1)。
当〃=4奴4女+ 1时,〃(〃;1)=2机4*—1),2机4* + 1)为偶数,即为偶排列;当〃 = 412,413时,丝* = (2*+1)(4*+ 1),(2*+1)(4*+ 3)为奇数,即为奇 排列。
■2、 用行列式定义计算2x x 1 21x1-1 f (X )=-- [3 2x1111%中『和r 的系数,并说明理由。
【解】由行列式定义可知:含b 有的项只能是主对角线元素乘积,故的系数为2; 含有尸的项只能是(1, 2), (2, 1), (3, 3), (4, 4)的元素乘积项,而7(2134) = 0 + 1 + 0 + 0 = 1,故/的系数为一1. ■2-512 --37-14 3、 求 =o45 -9 2 7 4-612【解】三角化法:2-5121-522 1-522 尸2+八1-12 0 6C[0 2-160 113D 4 =- _八3-211 1 0 3 0 113 0 2-16 r 4+r 211 0 60 1160 1161 -52 2 r3~2r 2 0 11 3r4~r 2 00 -3 00 0 31111 rk~r l0 10 0=120= 120o )l=2,3,40 0 100 0 0 1【解】箭形行列式(爪形行列式):利用对角线上元素将第一行(或列)中元素1化为零。
1 x 2q+C2 +•••+&n D"=(,-就1 x 2-mi=l1x21 0 0C k -X L C I 凡 q (»i) k=2,3,---,n1 —m ••- 01 0…-m【解】观察特点: 行和相等。
线性代数课后习题答案解析

线性代数课后题详解第一章 行列式1.利用对角线法则计算下列三阶行列式:相信自己加油(1)381141102---; (2)b a c a c b cb a(3)222111c b a c b a ; (4)yxy x x y x y y x y x +++.解 注意看过程解答(1)=---38114112811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯- =416824-++- =4-(2)=ba ca cb cb a ccc aaa bbb cba bac acb ---++ 3333c b a abc ---=(3)=222111c b a c b a 222222cb ba ac ab ca bc ---++ ))()((a c c b b a ---=(4)yxyx x y x y y x y x+++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序,求下列各排列的逆序数:耐心成就大业(1)1 2 3 4; (2)4 1 3 2; (3)3 4 2 1; (4)2 4 1 3; (5)1 3 … )12(-n2 4 … )2(n ;(6)1 3 … )12(-n)2(n )22(-n … 2.解(1)逆序数为0(2)逆序数为4:4 1,4 3,4 2,3 2(3)逆序数为5:3 2,3 1,4 2,4 1,2 1 (4)逆序数为3:2 1,4 1,4 3 (5)逆序数为2)1(-n n :3 2 1个 5 2,54 2个 7 2,7 4,7 6 3个 ……………… …)12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n)1(-n 个(6)逆序数为)1(-n n3 2 1个 5 2,54 2个 ……………… …)12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n)1(-n 个4 2 1个 6 2,6 4 2个 ……………… …)2(n 2,)2(n 4,)2(n 6,…,)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解 由定义知,四阶行列式的一般项为43214321)1(p p p p t a a a a -,其中t 为4321p p p p 的逆序数.由于3,121==p p已固定,4321p p p p 只能形如13□□,即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式:多练习方能成大财(1)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢71100251020214214; (2)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-260523********12; (3)⎥⎥⎥⎦⎥⎢⎢⎢⎣⎢---ef cf bfde cd bd ae ac ab ; (4)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001 解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯--- =143102211014--321132c c c c ++141717201099-=0(2)265232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)efcfbfde cd bd ae ac ab---=ecbe c b e c badf ---=111111111---adfbce=abcdef 4(4)dc b a 100110011001---21ar r +d cb a ab 100110011010---+=12)1)(1(+--dca ab 101101--+23dc c +010111-+-+cd c ad a ab=23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明:(1)1112222b b a a b ab a +=3)(b a -;(2)bzay by ax bxaz by ax bxaz bz ay bx az bz ay byax +++++++++=yxz x z yz y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅; (5)1221100000100001a x a a a a x x x n n n +----- n n n n a x a x a x ++++=--111 . 证明(1)122222221312a b a b a a b a ab a c c c c ------=左边ab a b ab a ab 22)1(22213-----=+ 21))((ab a a b a b +--=右边=-=3)(b a (2)bzay by ax z by ax bx az y bxaz bz ay x a ++++++分开按第一列左边bz ay by ax x by ax bx az z bx az bz ay y b +++++++++++++002y by ax zx bxaz y z bz ay x a 分别再分bzay yx byax x zbxaz z y b +++zyxy x zx z y b yxzx z y z y x a 33+分别再分右边=-+=233)1(yxzx z yzy x b yxzx z yz y x a (3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c964496449644964422222++++++++d d dd c c c cb b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423dd c cb b a ac c c c c c c c ----第二项第一项06416416416412222=+d dd c c cb b b a a a(4) 444444422222220001a d a c a b a a d a c a b a ad a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b a d a c a b --------- =)()()(111))()((222a d d a c c a b b ad ac ab a d ac a b++++++---=⨯---))()((a d a c a b)()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b)()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x x a xD D n n n n 右边=+=-n n a xD 1所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转,依次得nnnn a a a a D 11111=, 11112n nnn a a a a D = ,11113a a a a D n nnn=,证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnn n nn nnnn a a a a a a a a a a D 2211111111111)1(--==∴=--=--nnn n nn n n a a a a a a a a 331122111121)1()1( nn n nn n a a a a111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-=同理可证nnnn n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-=D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)aaD n11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xaaa x a a a xD n=;(3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn nn ------=---+;提示:利用范德蒙德行列式的结果.(4)nnnnn d c d c b a b a D00011112=;(5)ji a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1)aa a a a D n 00010000000000001000=按最后一行展开)1()1(100000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n n a aa(再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得a x x a a x xa a x x a a a a x D n ------=0000000 再将各列都加到第一列上,得ax a x a x a a a an x D n ----+=000000000)1( )(])1([1a x a n x n --+=-(3)从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行交换,得nn nn n n n n n n a a a n a a a n a a a D )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-∙-∙-=---=1121)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4)nnnnn d c d c b a b a D 011112=n n n n n nd d c d c b a b a a 00000011111111----展开按第一行0)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222---n n n n n n D c b D d a 都按最后一行展开由此得递推公式:222)(--=n n n n n n D c b d a D即 ∏=-=ni i i i i nD c b d a D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)ji a ij -=432140123310122210113210)det( --------==n n n n n n n n a D ij n,3221r r r r --0432111111111111111111111--------------n n n n ,,141312c c c c c c +++1524232102221002210002100001---------------n n n n n=212)1()1(----n n n(6)nn a a a D +++=11111111121,,433221c c c c c c ---nnn n a a a a a a a a a a +-------10000100010000100010001000011433221 展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------00000000000000000000000022433221nn n a a a a a a a a ----+--000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑+==n i in a a a a8.用克莱姆法则解下列方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x解 (1)11213513241211111----=D812073503211111------=145008130032101111---=1421420005410032101111-=---=112105132412211151------=D 11210513290501115----= 1121023313090509151------=23313095112109151------=12023461000112109151-----=14238100112109151----=142-=11235122412111512-----=D 81150731203271151-------=31390011230023101151-=2842840001910023101151-=----=426110135232422115113-=----=D14202132132212151114=-----=D1,3,2,144332211-========∴DD x DD x D D x DD x(2)510006510006510065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',)5100165100065100650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507=5101065100065000601000152=D 展开按第二列5100651006500061-6510065*********-365510651065⨯-=1145108065-=--=5110065000060100051001653=D 展开按第三列51006500061000516500061*********+6100510656510650061+=703114619=⨯+=5100060100005100651010654=D 展开按第四列61000510065100655000610005100651-- 51065106565--=395-=110005100065100651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x . 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 μλμμμλ-==12111113D ,齐次线性方程组有非零解,则03=D即 0=-μλμ得10==λμ或不难验证,当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解? 解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-= 3)1(2)1(23-+-+-=λλλ齐次线性方程组有非零解,则0=D得 32,0===λλλ或不难验证,当32,0===λλλ或时,该齐次线性方程组确有非零解.第二章 矩阵及其运算1.已知线性变换:⎪⎩⎪⎨⎧++=++=++=,323,53,22321332123211y y y x y y y x y y y x 求从变量321,,x x x 到变量321,,y y y 的线性变换.解由已知:⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x故 ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫⎝⎛----=321423736947y y y ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947xx x y x x x y x x x y2.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=,54,232,232133212311y y y x y y y x y y x ⎪⎩⎪⎨⎧+-=+=+-=,3,2,3323312211z z y z z y z z y 求从321,,z z z 到321,,x x x 的线性变换.解 由已知⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛-=321310102013514232102z z z ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛----=321161109412316z z z所以有 ⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236zz z x z z z x z z z x3.设⎪⎪⎪⎭⎫ ⎝⎛--=111111111A , ,150421321⎪⎪⎪⎭⎫ ⎝⎛--=B 求.23B A A AB T及-解A AB 23-⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫⎝⎛--=1504213211111111113⎪⎪⎪⎭⎫ ⎝⎛---1111111112⎪⎪⎪⎭⎫⎝⎛-=0926508503⎪⎪⎪⎭⎫⎝⎛---1111111112⎪⎪⎪⎭⎫ ⎝⎛----=22942017222132⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=150421321111111111B A T⎪⎪⎪⎭⎫ ⎝⎛-=0926508504.计算下列乘积:(1)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-127075321134; (2)()⎪⎪⎪⎭⎫ ⎝⎛1233,2,1; (3)()2,1312-⎪⎪⎪⎭⎫ ⎝⎛;(4)⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-20413121013143110412;(5)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321332313232212131211321),,(x x x a a a a a a a a a x x x ; (6)⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121. 解(1)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎪⎭⎫⎝⎛=49635 (2)()⎪⎪⎪⎭⎫ ⎝⎛123321)10()132231(=⨯+⨯+⨯=(3)()21312-⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎪⎭⎫ ⎝⎛---=632142 (4)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎪⎭⎫⎝⎛---=6520876 (5)()⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321332313232212131211321x x x a a a a a a a a a x x x ()333223113323222112313212111x a x a x a x a x a x a x a x a x a ++++++=⎪⎪⎪⎭⎫ ⎝⎛⨯321x x x 322331132112233322222111222x x a x x a x x a x a x a x a +++++= (6)⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛3000320012101313000120010100121⎪⎪⎪⎪⎪⎭⎫⎝⎛---=90003400421025215.设⎪⎪⎭⎫ ⎝⎛=3121A , ⎪⎪⎭⎫⎝⎛=2101B ,问:(1)BA AB =吗?(2)2222)(B AB A B A ++=+吗?(3)22))((B A B A B A -=-+吗?解(1)⎪⎪⎭⎫ ⎝⎛=3121A , ⎪⎪⎭⎫ ⎝⎛=2101B 则⎪⎪⎭⎫ ⎝⎛=6443AB ⎪⎪⎭⎫ ⎝⎛=8321BA BA AB ≠∴ (2) ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎪⎭⎫⎝⎛=2914148 但=++222B AB A ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛43011288611483⎪⎪⎭⎫⎝⎛=27151610 故2222)(B AB A B A ++≠+(3) =-+))((B A B A =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛10205222⎪⎪⎭⎫⎝⎛9060而 =-22B A =⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛430111483⎪⎪⎭⎫⎝⎛7182 故22))((B A B A B A -≠-+6.举反列说明下列命题是错误的:(1)若02=A ,则0=A ; (2)若A A =2,则0=A 或E A =;(3)若AY AX =,且0≠A ,则Y X =.解 (1) 取⎪⎪⎭⎫ ⎝⎛=0010A 02=A ,但0≠A(2) 取⎪⎪⎭⎫ ⎝⎛=0011A A A =2,但0≠A 且E A ≠(3) 取⎪⎪⎭⎫ ⎝⎛=0001A ⎪⎪⎭⎫ ⎝⎛-=1111X ⎪⎪⎭⎫⎝⎛=1011YAY AX =且0≠A 但Y X ≠7.设⎪⎪⎭⎫ ⎝⎛=101λA ,求kA A A ,,,32 . 解 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=12011011012λλλA⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==1301101120123λλλA A A 利用数学归纳法证明: ⎪⎪⎭⎫⎝⎛=101λk A k当1=k 时,显然成立,假设k 时成立,则1+k 时⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==1)1(01101101λλλk k A A A kk 由数学归纳法原理知:⎪⎪⎭⎫⎝⎛=101λk A k8.设⎪⎪⎪⎭⎫⎝⎛=λλλ001001A ,求k A . 解 首先观察⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎪⎭⎫⎝⎛=222002012λλλλλ⎪⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A由此推测 ⎪⎪⎪⎪⎪⎭⎫⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121)2(≥k用数学归纳法证明: 当2=k时,显然成立.假设k 时成立,则1+k 时,⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ由数学归纳法原理知: ⎪⎪⎪⎪⎪⎭⎫⎝⎛-=---kk kk k k kk k k k A λλλλλλ0002)1(1219.设B A ,为n 阶矩阵,且A 为对称矩阵,证明AB B T 也是对称矩阵.证明 已知:A A T=则AB B B A B A B B AB B T T T T TT TT ===)()(从而 AB B T也是对称矩阵.10.设B A ,都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是BA AB =.证明 由已知:A A T = B B T=充分性:BA AB =⇒A B AB TT =⇒)(AB AB T = 即AB 是对称矩阵.必要性:AB AB T =)(⇒AB A B TT =⇒AB BA =.11.求下列矩阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛5221; (2)⎪⎪⎭⎫⎝⎛-θθθθcos sin sin cos ; (3)⎪⎪⎪⎭⎫ ⎝⎛---145243121; (4)⎪⎪⎪⎪⎪⎭⎫⎝⎛4121031200210001; (5)⎪⎪⎪⎪⎪⎭⎫⎝⎛2500380000120025; (6)⎪⎪⎪⎪⎭⎫⎝⎛n a a a 0021)0(21≠a a a n解(1)⎪⎪⎭⎫ ⎝⎛=5221A 1=A1),1(2),1(2,522122111=-⨯=-⨯==A A A A⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛=*122522122111A A A A A *-=A A A 11故 ⎪⎪⎭⎫⎝⎛--=-12251A(2)01≠=A 故1-A 存在θθθθcos sin sin cos 22122111=-===A A A A从而 ⎪⎪⎭⎫ ⎝⎛-=-θθθθcos sin sin cos 1A (3) 2=A , 故1-A 存在024312111==-=A A A 而 1613322212-==-=A A A 21432332313-==-=A A A 故 *-=A A A 11⎪⎪⎪⎭⎫⎝⎛-----=1716213213012(4)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=4121031200210001A24=A 0434232413121======A A A A A A 68122444332211====A A A A12411032001)1(312-=-=A 12421012021)1(413-=-=A3121312021)1(514=-=A 4421012001)1(523-=-=A5121312001)1(624-=-=A 2121021001)1(734-=-=A*-=A A A 11故⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=-4112124581031612100212100011A(5)01≠=A 故1-A 存在而002141312111==-==A A A A005242322212===-=A A A A320043332313-====A A A A 850044342414=-===A A A A从而⎪⎪⎪⎪⎪⎭⎫⎝⎛----=-85003200005200211A (6)⎪⎪⎪⎪⎭⎫⎝⎛=n a a a A 0021 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-n a a a A 1001121112.解下列矩阵方程:(1)⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛12643152X ; (2) ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--234311*********X ;(3)⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-101311022141X ; (4)⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解 (1)⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-126431521X ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=12642153⎪⎪⎭⎫⎝⎛-=80232 (2)1111012112234311-⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=X ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122 (3)11110210132141--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=210110131142121⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111(4)11010100001021102341100001010--⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛=X ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎪⎭⎫⎝⎛---=20143101213.利用逆矩阵解下列线性方程组:(1) ⎪⎩⎪⎨⎧=++=++=++;353,2522,132321321321x x x x x x x x x (2) ⎪⎩⎪⎨⎧=-+=--=--.0523,132,2321321321x x x x x x x x x解 (1)方程组可表示为 ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321153522321321x x x故 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x 从而有 ⎪⎩⎪⎨⎧===001321x x x (2) 方程组可表示为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x故 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x 故有 ⎪⎩⎪⎨⎧===305321x x x 14.设O A k =(k 为正整数),证明121)(--++++=-k A A A E A E .证明 一方面, )()(1A E A E E --=-另一方面,由O A k =有)()()(1122k k k A A A A A A A E E -+--+-+-=-- ))((12A E A A A E k -++++=-故 )()(1A E A E ---))((12A E A A A E k -++++=-两端同时右乘1)(--A E就有121)(--++++=-k A A A E A E15.设方阵A 满足O E A A =--22,证明A 及E A 2+都可逆,并求1-A 及 1)2(-+E A .证明 由O E A A =--22得E A A 22=-两端同时取行列式: 22=-A A即 2=-E A A ,故 0≠A所以A 可逆,而22A E A =+0222≠==+A A E A 故E A 2+也可逆.由O E A A =--22E E A A 2)(=-⇒E A E A A A 112)(--=-⇒)(211E A A -=⇒-又由O E A A =--22E E A A E A 4)2(3)2(-=+-+⇒ E E A E A 4)3)(2(-=-+⇒11)2(4)3)(2()2(--+-=-++∴E A E A E A E A)3(41)2(1A E E A -=+∴-16.设⎪⎪⎪⎭⎫ ⎝⎛-=321011330A ,B A AB 2+=,求B . 解 由B A AB 2+=可得A B E A =-)2(故A E A B 1)2(--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---=-3210113301210113321⎪⎪⎪⎭⎫⎝⎛-=01132133017.设Λ=-AP P 1,其中⎪⎪⎭⎫ ⎝⎛--=1141P ,⎪⎪⎭⎫ ⎝⎛-=Λ2001,求11A .解 Λ=-AP P 1故1-Λ=P P A 所以11111-Λ=P P A3=P ⎪⎪⎭⎫ ⎝⎛-=*1141P ⎪⎪⎭⎫ ⎝⎛--=-1141311P而 ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=Λ11111120012001故⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎪⎭⎫ ⎝⎛--=6846832732273118.设m 次多项式m m x a x a x a a x f ++++= 2210)(,记m m A a A a A a E a A f ++++= 2210)()(A f 称为方阵A 的m 次多项式.(1)设⎪⎪⎭⎫ ⎝⎛=Λ2100λλ,证明: ⎪⎪⎭⎫ ⎝⎛=Λk k k2100λλ,⎪⎪⎭⎫⎝⎛=Λ)(00)()(21λλf f f ; (2)设1-Λ=P P A ,证明: 1-Λ=P P A k k ,1)()(-Λ=P Pf A f .证明(1) i)利用数学归纳法.当2=k时⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=Λ212120000λλλλ⎪⎪⎭⎫ ⎝⎛=222100λλ命题成立,假设k 时成立,则1+k 时⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=ΛΛ=Λ+212110000λλλλk kkk ⎪⎪⎭⎫⎝⎛=++121100k k λλ 故命题成立. ii)左边m m a a a E a f Λ++Λ+Λ+=Λ= 2210)(⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=m m m a a a 21211000001001λλλλ⎪⎪⎭⎫ ⎝⎛++++++++=m m m m a a a a a a a a 2222210121211000λλλλλλ ⎪⎪⎭⎫ ⎝⎛=)(00)(21λλf f =右边 (2) i) 利用数学归纳法.当2=k 时12112---Λ=ΛΛ=P P P P P P A 成立假设k 时成立,则1+k 时11111-+--+Λ=ΛΛ=⋅=P P P P P P A A A k k k k 成立,故命题成立,即 1-Λ=P P A k kii) 证明 右边1)(-Λ=P Pf12210)(-Λ++Λ+Λ+=P a a a E a P m m11221110----Λ++Λ+Λ+=P P a P P a P P a PEP a m m m m A a A a A a E a ++++= 2210)(A f ==左边19.设n 阶矩阵A 的伴随矩阵为*A ,证明:(1) 若0=A ,则0=*A ;(2) 1-*=n AA .证明(1) 用反证法证明.假设0≠*A 则有E A A =-**1)(由此得O A E A A AA A ===-*-**11)()(O A =∴*这与0≠*A 矛盾,故当0=A 时有0=*A(2) 由于*-=A AA 11, 则E A AA =* 取行列式得到: nAA A =* 若0≠A 则1-*=n A A若0=A 由(1)知0=*A 此时命题也成立故有1-*=n AA20.取⎪⎪⎭⎫ ⎝⎛==-==1001D C B A ,验证DCB A DC B A ≠检验: =D C BA =--101001011010010111001010020002--410012002== 而01111==D C B A 故 DCB A DC B A ≠21.设⎪⎪⎪⎪⎭⎫⎝⎛-=22023443O O A ,求8A 及4A解 ⎪⎪⎪⎪⎭⎫⎝⎛-=22023443O O A ,令⎪⎪⎭⎫ ⎝⎛-=34431A ⎪⎪⎭⎫ ⎝⎛=22022A则⎪⎪⎭⎫ ⎝⎛=21A O O A A故8218⎪⎪⎭⎫ ⎝⎛=A O O A A ⎪⎪⎭⎫ ⎝⎛=8281A O O A1682818281810===A A A A A ⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=464444241422025005O O A OO A A22.设n 阶矩阵A 及s 阶矩阵B 都可逆,求1-⎪⎪⎭⎫⎝⎛O B A O .解 将1-⎪⎪⎭⎫⎝⎛O B A O 分块为⎪⎪⎭⎫ ⎝⎛4321C C C C其中 1C 为n s ⨯矩阵, 2C 为s s ⨯矩阵3C 为n n ⨯矩阵, 4C 为s n ⨯矩阵则⎪⎪⎭⎫ ⎝⎛⨯⨯O B A O s s n n ⎪⎪⎭⎫ ⎝⎛4321C C C C ==E ⎪⎪⎭⎫⎝⎛s n E O O E 由此得到⎪⎪⎩⎪⎪⎨⎧=⇒==⇒==⇒==⇒=----122111144133)()(B C E BC B O C O BC A O C O AC A C E AC s n 存在存在故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛---O A B O O B A O 111.第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1)⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2) ⎪⎪⎪⎭⎫⎝⎛----174034301320; (3)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解(1) ⎪⎪⎪⎭⎫ ⎝⎛--3403130212011312)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020********* )2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320 1312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫⎝⎛000031005010 (3)⎪⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311141312323~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----221002210022*******12423213~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛---0000000000221003211(4)⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132242321232~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~r r r r r r --+⎪⎪⎪⎪⎪⎭⎫⎝⎛--4100041000202011111034221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎪⎭⎫⎝⎛----00000410001111020201 32~r r +⎪⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.在秩是r 的矩阵中,有没有等于0的1-r 阶子式?有没有等于0的r 阶子式?解 在秩是r 的矩阵中,可能存在等于0的1-r 阶子式,也可能存在等于0的r 阶子式.例如,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000000010000100001α 3)(=αR 同时存在等于0的3阶子式和2阶子式.3.从矩阵A 中划去一行得到矩阵B ,问B A ,的秩的关系怎样?解 )(A R ≥)(B R设r B R =)(,且B 的某个r 阶子式0≠D r .矩阵B 是由矩阵A 划去一行得 到的,所以在A 中能找到与D r 相同的r 阶子式D r ,由于0≠=D D r r , 故而)()(B R A R ≥.4.求作一个秩是4的方阵,它的两个行向量是)0,0,1,0,1(,)0,0,0,1,1(- 解 设54321,,,,ααααα为五维向量,且)0,0,1,0,1(1=α,)0,0,0,1,1(2-=α,则所求方阵可为,54321⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=αααααA 秩为4,不妨设⎪⎩⎪⎨⎧===)0,0,0,0,0(),0,0,0,0()0,,0,0,0(55443αααx x 取154==x x故满足条件的一个方阵为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-00000100000100000011001015.求下列矩阵的秩,并求一个最高阶非零子式:(1)⎪⎪⎪⎭⎫ ⎝⎛---443112112013; (2) ⎪⎪⎪⎭⎫⎝⎛-------815073131213123; (3)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013r r 21~↔⎪⎪⎪⎭⎫ ⎝⎛---443120131211 ⎪⎪⎪⎭⎫⎝⎛------564056401211~12133r r r r 2000056401211~23秩为⎪⎪⎪⎭⎫ ⎝⎛----r r 二阶子式41113-=-.(2) ⎪⎪⎪⎭⎫ ⎝⎛-------815073*********⎪⎪⎪⎭⎫ ⎝⎛---------15273321059117014431~27122113r r r r r r 200000591170144313~23秩为⎪⎪⎪⎭⎫⎝⎛-----r r .二阶子式71223-=-.(3)⎪⎪⎪⎪⎪⎭⎫⎝⎛---02301085235703273812434241322~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------0230102420536307121131223~r r r r ++⎪⎪⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210344314211614~r r r r r r r r -÷÷↔↔⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-00000100007121002301秩为3 三阶子式07023855023085570≠=-=-.6.求解下列齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+++=-++=-++;0222,02,02432143214321x x x x x x x x x x x x (2) ⎪⎩⎪⎨⎧=-++=--+=-++;05105,0363,02432143214321x x x x x x x x x x x x(3) ⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+;0742,0634,0723,05324321432143214321x x x x x x x x x x x x x x x x (4)⎪⎪⎩⎪⎪⎨⎧=++-=+-+=-+-=+-+.0327,01613114,02332,075434321432143214321x x x x x x x x x x x x x x x x解 (1) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛--212211121211⎪⎪⎪⎪⎭⎫⎝⎛---3410013100101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-==4443424134334x x x x x x x x故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x(2) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛----5110531631121⎪⎪⎪⎭⎫ ⎝⎛-000001001021~ 即得⎪⎪⎩⎪⎪⎨⎧===+-=4432242102x x x x x x x x故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10010012214321k k x x x x(3) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132⎪⎪⎪⎪⎪⎭⎫⎝⎛1000010*********~即得⎪⎪⎩⎪⎪⎨⎧====00004321x x x x故方程组的解为⎪⎪⎩⎪⎪⎨⎧====00004321x x x x(4) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--0000001720171910171317301~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛1017201713011719173214321k k x x x x7.求解下列非齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+=+-=-+;8311,10213,22421321321x x x x x x x x (2) ⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++;694,13283,542,432z y x z y x z y x z y x(3) ⎪⎩⎪⎨⎧=--+=+-+=+-+;12,2224,12w z y x w z y x w z y x (4) ⎪⎩⎪⎨⎧-=+-+=-+-=+-+;2534,4323,12w z y x w z y x w z y x解 (1) 对系数的增广矩阵施行行变换,有⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--60003411100833180311102132124~2)(=A R 而3)(=B R ,故方程组无解.(2) 对系数的增广矩阵施行行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201~即得⎪⎩⎪⎨⎧=+=--=zz z y z x 212亦即⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛021112k z y x(3) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫ ⎝⎛----111122122411112⎪⎪⎪⎭⎫ ⎝⎛-000000100011112~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧===++-=0212121w z z y y z y x 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00021010210012121k k w z y x(4) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛-----00007579751025341253414312311112~ ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----000007579751076717101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=++=w w z z w z y w z x 757975767171即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00757610797101757121k k w z y x8.λ取何值时,非齐次线性方程组⎪⎩⎪⎨⎧=++=++=++2321321321,,1λλλλλx x x x x x x x x (1)有唯一解;(2)无解;(3)有无穷多个解?解 (1)0111111≠λλλ,即2,1-≠λ时方程组有唯一解.(2))()(B R A R <⎪⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011~λλλλλλλλλλ由0)1)(1(,0)2)(1(2≠+-=+-λλλλ 得2-=λ时,方程组无解.(3)3)()(<=B R A R ,由0)1)(1()2)(1(2=+-=+-λλλλ,得1=λ时,方程组有无穷多个解.9.非齐次线性方程组⎪⎩⎪⎨⎧=-+=+--=++-23213213212,2,22λλx x x x x x x x x 当λ取何值时有解?并求出它的解.解 ⎪⎪⎪⎪⎭⎫ ⎝⎛+-----⎪⎪⎪⎭⎫ ⎝⎛----=)2)(1(000)1(321101212111212112~2λλλλλλB 方程组有解,须0)2)(1(=+-λλ得2,1-==λλ当1=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛001111321k x x x当2-=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛022111321k x x x10.设⎪⎩⎪⎨⎧--=-+--=--+=-+-,1)5(42,24)5(2,122)2(321321321λλλλx x x x x x x x x问λ为何值时,此方程组有唯一解、无解或有无穷多解?并在有无穷多解时求解.解⎪⎪⎪⎭⎫ ⎝⎛---------154224521222λλλλ 初等行变换~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------2)4)(1(2)10)(1(00111012251λλλλλλλλ当0≠A ,即02)10()1(2≠--λλ 1≠∴λ且10≠λ时,有唯一解.当02)10)(1(=--λλ且02)4)(1(≠--λλ,即10=λ时,无解.当02)10)(1(=--λλ且02)4)(1(=--λλ,即1=λ时,有无穷多解.此时,增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛-000000001221 原方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛00110201221321k k x x x (R k k ∈21,)11.试利用矩阵的初等变换,求下列方阵的逆矩阵:(1)⎪⎪⎪⎭⎫⎝⎛323513123; (2) ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----1210232112201023. 解(1)⎪⎪⎪⎭⎫ ⎝⎛100010001323513123⎪⎪⎪⎭⎫⎝⎛---101011001200410123~。
线性代数课后习题答案全)习题详解

线性代数课后习题答案全)习题详解前言因能力有限,资源有限,现粗略整理了《工程数学线性代数》课后习题,希望对您的了解和学习线性代数有参考价值。
第一章行列式1.利用对角线法则计算下列三阶行列式:(1)381141102---;(2)b a c a c b c b a ; (3)222111c b a c b a ;(4)y x y x x y x yyx y x +++. 解(1)=---381141102811)1()1(03)4(2??+-?-?+?-?)1()4(18)1(2310-?-?-?-?-??-=416824-++-=4-(2)=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=(3)=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=(4)yx y x x y x y yx y x +++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序,求下列各排列的逆序数:(1)1 2 3 4;(2)4 1 3 2;(3)3 4 2 1;(4)2 4 1 3;(5)1 3 … )12(-n 2 4 … )2(n ;(6)1 3 … )12(-n )2(n )22(-n … 2.解(1)逆序数为0(2)逆序数为4:4 1,4 3,4 2,3 2 (3)逆序数为5:3 2,3 1,4 2,4 1,2 1 (4)逆序数为3:2 1,4 1,4 3 (5)逆序数为2)1(-n n : 3 2 1个 5 2,5 4 2个 7 2,7 4,7 6 3个……………… …)12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n )1(-n 个(6)逆序数为)1(-n n3 2 1个 5 2,54 2个……………… …)12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n )1(-n 个4 2 1个 6 2,6 4 2个……………… …)2(n 2,)2(n 4,)2(n 6,…,)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解由定义知,四阶行列式的一般项为43214321)1(p p p p t a a a a -,其中t 为4321p p p p 的逆序数.由于3,121==p p 已固定,4321p p p p 只能形如13□□,即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式:(1)7110025*********4;(2)-265232112131412;(3)---ef cf bf de cd bd ae ac ab ;(4)---d c b a100110011001解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-?---=143102211014-- 321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=e c b e c b e c b adf ---=1 11111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(3 3+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-?;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22) 1(22213-----=+21))((a b a a b a b +--= 右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bz ay y x by ax x z bx az z y b +++zy x y x z xz y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(+++++++++++++++ +=d d d d d c c c c c b b b b b a a a a a 左边964412964412964412964412241312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+dd d c c c bb b a a a (4) 444444422222220001ad a c a b a ad a c a b a a d a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)11))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =?---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =?-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转,依次得n nn n a a a a D 11111 =, 11112n nn n a a a a D = ,11113a a a a D n nnn =,证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnnn nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-= 同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n Tn n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)aaD n 11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xa a ax aa a x D n =; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn n n ------=---+; 提示:利用范德蒙德行列式的结果. (4) n nn nn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 000100000000 00001000 =按最后一行展开)1()1(1000000000010000)1(-?-+-n n n aa a)1)(1(2)1(--?-+n n n a a a(再按第一行展开)n n n nn a a a+-?-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上,得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行交换,得 nnn n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-?-?-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式:222)(--=n n n n n n D c b d a D即∏=-=ni i i iin D c b d22)(而 111111112c b d a d c b a D -==得∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=432140123310122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0 432111111111111111111111 --------------n n n n ,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n (6)nn a a D a +++=11111111121 ,,433221c c c c c c ---n n n n a a a a a a a a a a +-------100 00100010000100010001000011433221展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------000 00000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=--- )11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组:=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x=+=++=++=++=+.15,065,065,065,165)2(545434323212 1x x x x x x x x x x x x x上一页下一页。
行列式习题及答案

行列式习题及答案行列式是线性代数中的重要概念,它在矩阵运算和方程组求解中起着重要的作用。
本文将介绍一些行列式的习题及其答案,帮助读者更好地理解和掌握这一概念。
1. 习题一:计算行列式的值已知行列式A = |2 3||4 5|求解行列式A的值。
答案:根据行列式的定义,可以得到A的值为:2*5 - 3*4 = 10 - 12 = -2。
2. 习题二:行列式的性质已知行列式B = |a b||c d|如果行列式B的值为0,是否可以得出a、b、c、d中至少有一个为0的结论?答案:是的,如果行列式B的值为0,根据行列式的性质,可以得出至少存在一组a、b、c、d中的一个为0的情况。
这是因为行列式的值为0意味着矩阵的行向量或列向量线性相关,即存在线性关系式使得行向量或列向量之间存在依赖关系。
3. 习题三:行列式的展开已知行列式C = |1 2 3||4 5 6||7 8 9|求解行列式C的值。
答案:根据行列式的展开定理,可以选择第一行或第一列展开计算。
选择第一行展开,可以得到C的值为:1 * (-1)^(1+1) * |5 6| - 2 * (-1)^(1+2) * |4 6| + 3 * (-1)^(1+3) * |4 5||8 9| |7 9| |7 8|= 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)= 1 * (-3) - 2 * (-6) + 3 * (-3)= -3 + 12 - 9= 04. 习题四:行列式的性质已知行列式D = |a b||c d|如果行列式D的值为1,是否可以得出a、b、c、d中至少有一个为1的结论?答案:不可以。
行列式的值为1并不能直接得出a、b、c、d中至少有一个为1的结论。
因为行列式的值为1并不代表矩阵的元素本身就是1,行列式的值只是表示了矩阵的行向量和列向量之间的线性关系。
5. 习题五:行列式的性质已知行列式E = |1 2||3 4|如果行列式E的值为k,是否可以得出a、b、c、d中的元素之和等于k的结论?答案:是的。
线性代数练习册附答案

第1章 矩阵 习 题1. 写出下列从变量x , y 到变量x 1, y 1的线性变换的系数矩阵: (1)⎩⎨⎧==011y xx ; (2) ⎩⎨⎧+=-=ϕϕϕϕcos sin sin cos 11y x y y x x2.(通路矩阵)a 省两个城市a 1,a 2和b 省三个城市b 1,b 2,b 3的交通联结情况如图所示,每条线上的数字表示联结这两城市的不同通路总数.试用矩阵形式表示图中城市间的通路情况.3. 设⎪⎪⎪⎭⎫ ⎝⎛--=111111111Α,⎪⎪⎪⎭⎫ ⎝⎛--=150421321B ,求3AB -2A 和A T B .4. 计算(1) 2210013112⎪⎪⎪⎭⎫ ⎝⎛(2) ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛1)1,,(212221211211y x c b b b a a b a a y x5. 已知两个线性变换 32133212311542322y y y x y y y x y y x ++=++-=+=⎪⎩⎪⎨⎧,⎪⎩⎪⎨⎧+-=+=+-=323312211323zz y z z y z z y ,写出它们的矩阵表示式,并求从321,,z z z 到321,,x x x 的线性变换.6. 设f (x )=a 0x m + a 1x m -1+…+ a m ,A 是n 阶方阵,定义f (A )=a 0A m + a 1A m -1+…+ a m E .当f (x )=x 2-5x +3,⎪⎪⎭⎫⎝⎛--=3312A 时,求f (A ).7. 举出反例说明下列命题是错误的. (1) 若A 2= O ,则A = O .(2) 若A 2= A ,则A = O 或A = E . .7. 设方阵A 满足A 2-3A -2E =O ,证明A 及A -2E 都可逆,并用A 分别表示出它们的逆矩阵.8.用初等行变换把下列矩阵化成行最简形矩阵:(1)⎪⎪⎪⎭⎫⎝⎛------=132126421321A(2)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=03341431210110122413B .9. 对下列初等变换,写出相应的初等方阵以及B 和A 之间的关系式.⎪⎪⎪⎭⎫ ⎝⎛--=121121322101A ~122r r -⎪⎪⎪⎭⎫⎝⎛---121123302101~13c c +⎪⎪⎪⎭⎫⎝⎛--131123302001=B .10. 设ΛAP P =-1,其中⎪⎪⎭⎫ ⎝⎛--=1141P ,⎪⎪⎭⎫⎝⎛-=2001Λ,求A 9.11. 设⎪⎪⎪⎭⎫⎝⎛-=200030004A ,矩阵B 满足AB =A+2B ,求B .12. 设102212533A--⎛⎫⎪=-⎪⎪-⎝⎭, 利用初等行变换求A-1.复习题一1. 设A , B , C 均为n 阶矩阵,且ABC =E ,则必有( ). (A ) ACB =E ; (B ) CBA =E ; (C ) BAC =E ; (D ) BCA =E .2. 设⎪⎪⎪⎭⎫⎝⎛=333231232221131211a a a a a a a a a A ,⎪⎪⎪⎭⎫⎝⎛+++=133312321131131211232221a a a a a a a a a a a a B , ⎪⎪⎪⎭⎫ ⎝⎛=1000010101P ,⎪⎪⎪⎭⎫⎝⎛=1010100012P ,则必有 ( ) .(A ) AP 1P 2=B ; (B )AP 2P 1=B ; (C ) P 1P 2A =B ; (D ) P 2P 1A =B .3. 设A 为4阶可逆矩阵,将A 的第1列与第4列交换得B ,再把B 的第2列与第3列交换得C ,设⎪⎪⎪⎪⎪⎭⎫⎝⎛=00010*******10001P ,⎪⎪⎪⎪⎪⎭⎫⎝⎛=10000010010000012P ,则C -1=( ). (A) A -1P 1P 2; (B) P 1A -1P 2; (C) P 2P 1A -1; (D) P 2A -1P 1.4. 设n 阶矩阵A 满足A 2-3A +2E =O ,则下列结论中一定正确的是( ). (A) A -E 不可逆 ; (B) A -2E 不可逆 ; (C) A -3E 可逆; (D) A -E 和A -2E 都可逆.5. 设A =(1,2,3),B =(1,1/2,1/3),令C =A T B ,求C n .6. 证明:如果A k =O ,则(E -A )-1=E +A +A 2+…+A k -1,k 为正整数.7.设A ,B 为三阶矩阵,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=710004100031A ,且A -1BA =6A +BA ,求B .8. 设n 阶矩阵A 及s 阶矩阵B 都可逆,求1-⎪⎪⎭⎫⎝⎛O O B A .9. 设⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-000000000000000121n n aa a a X (021≠n a a a ),求X -1.第2章 行列式习 题1.利用三阶行列式解下列三元线性方程组⎪⎩⎪⎨⎧=-+-=-+-=+-013222321321321x x x x x x x x x2.当x 取何值时,0010413≠xx x .3.求下列排列的逆序数:(1) 315624; (2)13…(2n-1)24…(2n).4. 证明: 3232a cb a b a ac b a b a a c b a=++++++.5. 已知四阶行列式|A |中第2列元素依次为1,2,-1,3,它们的余子式的值依次为3,-4,-2,0 ,求|A |.6. 计算下列行列式: (1) 1111111111111111------ (2) y xy x x yx y y x yx +++(3) 0111101111011110(4) 1222123312111x x x x x x(5)n n a a a D +++=11111111121,其中021≠n a a a .7.设n阶矩阵A的伴随矩阵为A*,证明:|A*|=|A|n-1,(n ≥2).8. 设A,B都是三阶矩阵,A*为A的伴随矩阵,且|A|=2,|B|=1,计算|-2A*B-1|.9.设⎪⎪⎪⎭⎫ ⎝⎛--=111012112A ,利用公式求A -1.复习题二1.设A , B 都是n 阶可逆矩阵,其伴随矩阵分别为A *、B *,证明:(AB )*= B *A *.2.设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=2200020000340043A ,求A -1.3.已知A 1, A 2, B 1, B 2都是3⨯1矩阵,设A =( A 1, A 2, B 1,),B =( A 1, A 2, B 2),|A |=2,|B |=3,求|A+2B |.4.设A , B 都是n 阶方阵,试证:AB E E A B E -=.第3章向量空间习题1. 设α1=(1,-1,1)T, α2=(0,1,2)T, α3=(2,1,3)T,计算3α1-2α2+α3.2. 设α1=(2,5,1,3)T, α2=(10,1,5,10)T, α3=(4,1,-1,1)T,且3(α1- x)+2(α2+x)=5(α3+x) ,求向量x.3. 判别下列向量组的线性相关性:(1) α1=(-1,3,1)T, α2=(2,-6,-2)T, α3=(5,4,1)T;(2) β1=(2,3,0)T, β2=(-1,4,0)T,β3=(0,0,2)T .4. 设β1=α1, β2=α1+α2, β3=α1+α2+a3,且向量组α1, α2, α3线性无关,证明向量组β1, β2, β3线性无关.5. 设有两个向量组α1, α2, α3和β1=α1-α2+α3, β2=α1+α2-α3,β3= -α1+α2+α3,证明这两个向量组等价.6. 求向量组α1=(1,2,-1)T, α2=(0,1,3)T, α3=(-2,-4,2)T,α4=(0,3,9)T的一个极大无关组,并将其余向量用此极大无关组线性表示.7. 设α1, α2,…,αn是一组n维向量,已知n维单位坐标向量ε1,ε2,…,εn能由它们线性表示,证明:α1, α2,…,αn线性无关.8. 设有向量组α1, α2, α3,α4, α5,其中α1, α2, α3线性无关,α4=aα1+bα2,α5=cα2+dα3(a, b, c, d 均为不为零的实数),求向量组α1, α3,α4, α5的秩.9. 设矩阵A= (1,2,…,n), B=(n,n-1,…,1),求秩R(A T B).10. 设矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=97963422644121121112A ,求A 的秩,并写出A 的一个最高阶非零子式.11. 已知矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+---=120145124023021t t A ,若A 的秩R (A )=2,求参数t 的值.12. 设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------=5913351146204532A ,求A 的列向量组的秩,并写出它的一个极大无关组.13. 设A 为n 阶矩阵,E 为n 阶单位矩阵,证明:如果A 2=A ,则R (A )+R (A -E )=n .14. 已知向量空间3R 的两组基为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=010,01121αα,⎪⎪⎪⎭⎫ ⎝⎛=1130α和⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=111,01121ββ-,⎪⎪⎪⎭⎫ ⎝⎛-=1103β, 求由基α1, α2, α3到基β1, β2, β3的过渡矩阵.复习题三1.设矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=k k k k 111111111111A ,已知A 的秩为3,求k 的值.2.设向量组A : α1, …,αs 与B : β1,…,βr ,若A 组线性无关且B 组能由A 组线性表示为(β1,…,βr )=(α1, …,αs )K ,其中K 为r s ⨯矩阵, 试证:B 组线性无关的充分必要条件是矩阵K 的秩R (K )=r .3.设有三个n维向量组A:α1, α2, α3;B:α1, α2, α3,α4;C:α1, α2, α3,α5.若A组和C组都线性无关,而B组线性相关,证明向量组α1, α2, α3,α4-α5线性无关.4.设向量组A: α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T和B: β1=(-1,1,0)T,β2=(1,1,1)T,β3=(0,1,-1)TR的基;(1) 证明:A组和B组都是三维向量空间3(2) 求由A组基到B组基的过渡矩阵;(3) 已知向量α在B组基下的坐标为(1,2,-1)T,求α在A组基下的坐标.第4章 线性方程组习 题1. 写出方程组⎪⎩⎪⎨⎧=+++=+++=+322 3512254321432121x x x x x x x x x x 的矩阵表示形式及向量表示形式.2.用克朗姆法则解下列线性方程组⎪⎩⎪⎨⎧=+=+--=-0322az cx bc bz cy abay bx ,其中0≠abc3.问μλ,取何值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++02 00 321321321x x x x x x x x x μμλ有非零解?4. 设有线性方程组⎪⎩⎪⎨⎧-=+-=++=++42 - 43212321321x x x k x kx x x k x x ,讨论当k 为何值时,(1)有唯一解?(2)有无穷多解?(3)无解?5. 求齐次线性方程组⎪⎩⎪⎨⎧=-++=-++=++-0 26 83054202108432143214321x x x x x x x x x x x x 的一个基础解系.6.设四元非齐次线性方程组的系数矩阵的秩为3,已知η1, η2, η3是它的三个解向量,且η1=(2,3,4,5)T , η2+η3=(1,2,3,4)T ,求此方程组的的通解.7 .求下列非齐次线性方程组的通解:⎪⎩⎪⎨⎧=+++=+++=+322 3512254321432121x x x x x x x x x x8. 设有向量组A :12122,131-==-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭αα,3110-=⎛⎫ ⎪ ⎪ ⎪⎝⎭α及向量131β=-⎛⎫ ⎪ ⎪ ⎪⎝⎭, 问向量β能否由向量组A 线性表示?9. 设η*是非齐次线性方程组AX=b的一个解,ξ1, ξ2,…, ξn-r是它的导出组的一个基础解系,证明:(1)η*, ξ1, ξ2,…, ξn-r线性无关;(2)η*, η*+ξ1, η*+ξ2,…, η*+ξn-r线性无关.复习题四1.设⎪⎪⎪⎭⎫ ⎝⎛=101102121a a a A ,且方程组AX =θ的解空间的维数为2,则a = .2.设齐次线性方程组a 1x 1+a 2x 2+…+a n x n =0,且a 1,a 2,…,a n 不全为零,则它的基础解系所含向量个数为 .3.设有向量组π:α1=(a ,2,10)T , α2=(-2,1,5)T , α3=(-1,1,4)T 及向量β=(1,b ,-1)T ,问a , b 为何值时,(1)向量β不能由向量组π线性表示;(2)向量β能由向量组π线性表示,且表示式唯一;(3)向量β能由向量组π线性表示,且表示式不唯一,并求一般表示式.4.设四元齐次线性方程组(Ⅰ)⎩⎨⎧=-=+004221x x x x (Ⅱ)⎩⎨⎧=+-=+-00432321x x x x x x 求: (1) 方程组(Ⅰ)与(Ⅱ)的基础解系;(2) 方程组(Ⅰ)与(Ⅱ)的公共解.5.设矩阵A =(α1, α2, α3, α4),其中α2, α3, α4线性无关,α1=2α2-α3,向量β=α1+α2+α3+α4,求非齐次线性方程组Ax= β的通解.6. 设⎪⎪⎪⎭⎫ ⎝⎛=321a a a α,⎪⎪⎪⎭⎫ ⎝⎛=321b b b β,⎪⎪⎪⎭⎫ ⎝⎛=321c c c γ,证明三直线⎪⎩⎪⎨⎧=++=++=++0:0:0:333322221111c y b x a l c y b x a l c y b x a l 3,2,1,022=≠+i b a i i相交于一点的充分必要条件是向量组βα,线性无关,且向量组γβα,,线性相关.第5章矩阵的特征值和特征向量习题1.已知向量α1=(1,-1,1)T,试求两个向量α2, α3,使α1, α2, α3为R 3的一组正交基.2.设A, B都是n阶正交矩阵,证明AB也是正交矩阵.3.设A是n阶正交矩阵,且|A|=-1,证明:-1是A的一个特征值.4.求矩阵⎪⎪⎪⎭⎫ ⎝⎛----201335212的特征值和特征向量.5. 已知三阶矩阵A 的特征值为1,2,3,计算行列式|A 3-5A 2+7E |.6.设矩阵⎪⎪⎪⎭⎫ ⎝⎛------=12422421x A 与⎪⎪⎪⎭⎫ ⎝⎛-=40000005y Λ相似,求y x ,;并求一个正交矩阵P ,使P -1AP =Λ.7.将下列对称矩阵相似对角化:(1)⎪⎪⎪⎭⎫ ⎝⎛----020212022(2)⎪⎪⎪⎭⎫ ⎝⎛310130004.8. 设λ是可逆矩阵A 的特征值,证明:(1)A 是A *的特征值.(2)当1,-2,3是3阶矩阵A的特征值时,求A *的特征值.9.设三阶实对称矩阵A的特征值为λ1=6, λ2=λ3=3,属于特征值λ1=6的特征向量为p1=(1,1,1)T,求矩阵A.复习题五1.设n 阶矩阵A 的元素全为1,则A 的n 个特征值是 .2.已知3阶矩阵A , A -E , E +2A 都不可逆,则行列式|A +E |= .3.设⎪⎪⎪⎭⎫ ⎝⎛=11111b b a a A ,⎪⎪⎪⎭⎫ ⎝⎛=200010000B ,已知A 与B 相似,则a , b 满足 .4.设A 为2阶矩阵, α1, α2为线性无关的2维列向量,A α1=0, A α2=2α1+, α2,则A 的非零特征值为 .5.已知矩阵⎪⎪⎪⎭⎫ ⎝⎛=50413102x A 可相似对角化,求x .6.设矩阵A 满足A 2-3A +2E =O ,证明A 的特征值只能是1或2.7.已知p 1=(1,1,-1)T 是对应矩阵⎪⎪⎪⎭⎫ ⎝⎛---=2135212b a A 的特征值λ的一个特征向量.(1) 求参数a , b 及特征值λ; (2) 问A 能否相似对角化?说明理由.8. 设⎪⎪⎭⎫ ⎝⎛--=3223A ,求φ(A )=A 10-5A 9.第6章 二次型习 题1.写出下列二次型的矩阵表示形式:42324131212423222146242x x x x x x x x x x x x x x f -+-+-+++=2.写出对称矩阵⎪⎪⎪⎭⎫⎝⎛----=32201112121A 所对应的二次型.3. 已知二次型322123222132164),,(x x x x ax x x x x x f ++++=的秩为2,求a 的值.4.求一个正交变换将322322213214332),,(x x x x x x x x f +++=化成标准形.5.用配方法将二次型31212322214253x x x x x x x f -+++=化成标准形,并写出所用的可逆线性变换.6. 设二次型)0(233232232221>+++=a x ax x x x f ,若通过正交变换Py x =化成标准形23222152y y y f ++=,求a 的值.7. 判别下列二次型的正定性:(1)312123222122462x x x x x x x f ++---=(2)4342312124232221126421993x x x x x x x x x x x x f --+-+++=8. 设3231212322214225x x x x x ax x x x f +-+++=为正定二次型,求a 的取值范围.复习题六1. 设A 为n m ⨯矩阵,B =λE +A T A ,试证:λ>0时,矩阵B 为正定矩阵.2.设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2100120000010010A ,写出以A , A -1为矩阵的二次型,并将所得两个二次型化成标准形.3. 已知二次曲面方程5223121232221=-+++x x x bx ax x x ,通过正交变换X=PY 化为椭圆柱面方程522221=+y y ,求b a ,的值.4. 设矩阵⎪⎪⎪⎭⎫ ⎝⎛=101020101A ,2)(A E B +=k ,其中k 为实数,求对角矩阵Λ,使B与Λ相似,并讨论k 为何值时,B 为正定矩阵.测试题一一、计算题:1.计算行列式111131112+=n D n. 2.设⎪⎪⎪⎭⎫ ⎝⎛-=201A ,⎪⎪⎪⎭⎫ ⎝⎛---=210530001B ,计算T B A 3.3.设A 、B 都是四阶正交矩阵,且0<B ,*A 为A 的伴随矩阵,计算行列式 *2BAA -.4.设三阶矩阵A 与B 相似,且⎪⎪⎪⎭⎫ ⎝⎛=321A ,计算行列式 E B 22-. 5.设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=2411120201b a A ,且A 的秩为2,求常数b a ,的值. 二、解答题: 6.设4,3,2,1),,,1(32==i t t t T i i i i α,其中4321,,,t t t t 是各不相同的数,问4维非零向量β能否由4321,,,αααα线性表示?说明理由.7.求齐次线性方程组 ⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x 的一个基础解系.8.问k 取何值时,线性方程组⎪⎩⎪⎨⎧=++=++=++23213213211k x x kx k x kx x kx x x(1)有唯一解;(2)有无穷多解;(3)无解.9.已知四阶方阵A =(4321,,,αααα),其中321,,ααα线性无关,3243ααα-=,求方程组4321αααα+++=Ax 的通解.10.三阶实对称矩阵A 的特征值是1,2,3.矩阵A 的属于特征值1,2的特征向量分别是T )1,1,1(1--=α,T )1,2,1(2--=α,求A 的属于特征值3的所有特征向量,并求A 的一个相似变换矩阵P 和对角矩阵Λ,使得Λ=-AP P 1.三、证明题:11.设2112ααβ+=,32223ααβ+=,13334ααβ+=,且321,,ααα线性无关,证明:321,,βββ也线性无关.12.设A 为实对称矩阵,且满足O E A A =--22,证明E A 2+为正定矩阵.。
线性代数(本)习题册行列式 - 习题详解(修改)(加批注)
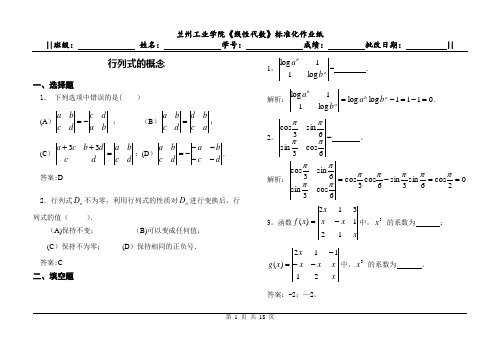
||班级: 姓名: 学号: 成绩: 批改日期: ||第 1 页 共 18 页行列式的概念一、选择题1. 下列选项中错误的是( ) (A )ba d c dc b a -= ; (B )ac bd dc b a =;(C )dc b a dcd b c a =++33; (D )dc b adc b a -----=.答案:D2.行列式n D 不为零,利用行列式的性质对n D 进行变换后,行列式的值( ). (A)保持不变;(B)可以变成任何值;(C )保持不为零; (D )保持相同的正负号. 答案:C二、填空题1。
ab b a log 11log = .解析:0111log log log 11log =-=-=ab abb a ba . 2。
6cos3sin6sin3cosππππ= 。
解析:02cos 6sin 3sin 6cos 3cos 6cos 3sin6sin3cos==-=πππππππππ3。
函数x x xxx f 121312)(-=中,3x 的系数为 ; xx xx x x g 21112)(---=中,3x 的系数为 。
答案:-2;—2。
||班级: 姓名: 学号: 成绩: 批改日期: ||第 2 页 共 18 页4。
n 阶行列式n D 中的n 最小值是 . 答案:1.5. 三阶行列式11342321-中第2行第1列元素的代数余子式等于 . 答案:5。
6。
若02182=x,则x = . 答案:2。
7。
在n 阶行列式ij a D =中,当i<j 时,),,2,1,(0n j i a ij L ==,则D = 。
答案:nn a a a 2211。
8。
设a ,b为实数,则当a = ,b =时,010100=---abb a。
解析:0)()1(1010022=+-=--=---b a ab ba abb a故0,0==b a 。
三、解答题1.用行列式的定义计算.(1)1100001001011010;解:原式=100010101)1(1010000011)1(14121++-⨯+-⨯||班级: 姓名: 学号: 成绩: 批改日期: ||第 3 页 共 18 页110010100-=--=(2)000000hgf e d c b a。
(完整版)线性代数课后习题答案第1——5章习题详解

第一章 行列式4.计算下列各行列式:(1)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢7110025*********4; (2)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-265232112131412; (3)⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ; (4)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯---=143102211014-- 321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=ec b e c b ec b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--=右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bzay y x by ax x z bxaz z y b +++z y x y x z x z y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a 949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a (4) 444444422222220001ad a c a b a ad a c a b a ad a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即 ,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转,依次得n nn n a a a a D 11111 =, 11112n nn n a a a a D = ,11113a a a a D n nnn =,证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnn n nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-=同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)a aD n 11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xaaax aa a x D n=; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n n n n n ------=---+; 提示:利用范德蒙德行列式的结果. (4) nnnnn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(100000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n na aa(再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上,得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行交换,得 nn n n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nn nnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式:222)(--=n n n n n n D c b d a D即 ∏=-=ni i i iin D c b da D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=432140123310122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121,,433221c c c c c c ---n n n n a a a a a a a a a a +-------10000100010000100010001000011433221 展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------00000000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=14200038100112109151----=142-=112035122412111512-----=D 811507312032701151-------=3139011230023101151-=2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510006510065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 51001651000651000650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507=51010651000650000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-= 1145108065-=--=51100650000601000051001653=D 展开按第三列51006500061000516500061000510065+6100510656510650061+= 703114619=⨯+=51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 110051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x . 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 μλμμμλ-==12111113D , 齐次线性方程组有非零解,则03=D即 0=-μλμ 得 10==λμ或不难验证,当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解?解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ 齐次线性方程组有非零解,则0=D得 32,0===λλλ或不难验证,当32,0===λλλ或时,该齐次线性方程组确有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x ,求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换.解 由已知:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x , 故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z , 所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B . 解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB ⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134; 解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635. (2)⎪⎪⎭⎫⎝⎛123)321(; 解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛; 解 )21(312-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876. (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ; 解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x =(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗?解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B)2=A 2+2AB +B 2吗?解 (A +B)2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148, 但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B)2≠A 2+2AB +B 2.(3)(A +B)(A -B)=A 2-B 2吗?解 (A +B)(A -B)≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A , 故(A +B)(A -B)≠A 2-B 2.6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k . 解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ, ⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=k A k k k k k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫ . 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB)T =B T (B T A)T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以(AB)T =(BA)T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB)T =AB , 所以AB =(AB)T =B T A T =BA .11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A|=1, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A , 故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A|=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A , 所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A|=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; 解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ;解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A)可逆, 且(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A)-1(E -A). 另一方面, 由A k =O , 有E =(E -A)+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),故 (E -A)-1(E -A)=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A), 两端同时右乘(E -A)-1, 就有(E -A)-1(E -A)=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E)-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A(A -E)=2E ,或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E)(A -3E)=-4E ,或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E)可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A|=2,即 |A||A -E|=2, 故 |A|≠0,所以A 可逆, 而A +2E =A 2, |A +2E|=|A 2|=|A|2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A(A -E)=2E⇒A -1A(A -E)=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E)A -3(A +2E)=-4E⇒ (A +2E)(A -3E)=-4 E ,所以 (A +2E)-1(A +2E)(A -3E)=-4(A +2 E)-1,)3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵,21||=A , 求|(2A)-1-5A*|.解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A|-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A*也可逆, 且(A*)-1=(A -1)*.证明 由*||11A A A =-, 得A*=|A|A -1, 所以当A 可逆时, 有|A*|=|A|n |A -1|=|A|n -1≠0,从而A*也可逆.因为A*=|A|A -1, 所以 (A*)-1=|A|-1A .又*)(||)*(||1111---==A A A A A , 所以(A*)-1=|A|-1A =|A|-1|A|(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A*, 证明: (1)若|A|=0, 则|A*|=0; (2)|A*|=|A|n -1. 证明(1)用反证法证明. 假设|A*|≠0, 则有A*(A*)-1=E , 由此得 A =A A*(A*)-1=|A|E(A*)-1=O ,所以A*=O , 这与|A*|≠0矛盾,故当|A|=0时, 有|A*|=0.(2)由于*||11A A A =-, 则AA*=|A|E , 取行列式得到|A||A*|=|A|n . 若|A|≠0, 则|A*|=|A|n -1;若|A|=0, 由(1)知|A*|=0, 此时命题也成立. 因此|A*|=|A|n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E)B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E)B =A 2-E ,即 (A -E)B =(A -E)(A +E).因为01001010100||≠-==-E A , 所以(A -E)可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A*BA =2BA -8E , 求B . 解 由A*BA =2BA -8E 得 (A*-2E)BA =-8E , B =-8(A*-2E)-1A -1 =-8[A(A*-2E)]-1 =-8(AA*-2A)-1 =-8(|A|E -2A)-1 =-8(-2E -2A)-1 =4(E +A)-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A*|=|A|3=8, 得|A|=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E)-1A =3[A(E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11.解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A=P Λ11P -1.|P|=3,⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001,故⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731.24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A)=A 8(5E -6A +A 2).解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A)=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B)B -1=B -1+A -1=A -1+B -1,而A -1(A +B)B -1是三个可逆矩阵的乘积, 所以A -1(A +B)B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B)B -1]-1=B(A +B)-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A ,所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解4100120021100101002000021010010110100101==--=--=D C B A , 而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A ,则⎪⎭⎫⎝⎛=21A O O A A ,故8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321. 由此得 ⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD O AD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A BC O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2)⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4)⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020*********)2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫ ⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫ ⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311 141312323~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r r r --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫ ⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ,求A 。
线性代数习题及答案解析

1. 三阶行列式()100420563= 。
A. 6B. 1C. 2 答:A 。
2. n 阶行列式()00100200n=。
A.!nB. 2!- C. 1(1)!--n nn答:C 。
二、讨论题1. n 阶行列式怎样定义的?答:n 阶行列式是这样定义的:(1)位于不同行,不同列n 个元素的乘积;(2)共有!n 项,每一项确定:行标为自然数排列,列标为1,,n m m ,当列标为偶数排列时取正号,为奇数排列时取负号;(3)一般项为11(1),-n N m nm a a 即11(1)=-∑n N m nm D a a 。
2.从左上角到右下角,对角线称为什么? 答:主对角线。
一、选择题1、将行列式转置,行列式值( )。
A. 变B. 不变C. 不确定 答:B 。
2、把行列式某一行的倍数加到另一行,行列式( )。
A. 不变B. 变C. 不确定 答:A 。
二、填空题1. 行列式123456789D =中12a 的代数余子式为 。
答 : 12(1)(6)+--。
三、讨论题1、按第一列展开行列式的定理指的是什么? 答:111111n n a A a A D ++=。
2.、按第一列展开行列式与第二列代数余子式乘积之和的定理指的是什么?答:1121120n n a A a A ++=。
一、选择题1、行列式100302540=( )。
A. 6B.(-8)C. 8答:B 。
2、行列式1000520067389104=( )。
A. 2!B. 3!C. 4!答:C 。
二、填空题1、行列式12345006D == 。
答:用上三角行列式24。
2、行列式127158169D =-=- 。
答:-8(其解题过程为:2131127715071588160816+==-+r r D r r )。
三、讨论题1、用化零降阶法计算行列式111111a D a a=等于什么?答:213222301111011(1)(1)(2)1111---+--=-=-+--a a r ar a Da a a a a r r a。
线性代数习题解答(一)行列式

线性代数习题解答习题一1.计算以下行列式 2223333223(1)(2)53(1)7.15cos sin (2)cos sin 1.sin cos log 1(3)log log 1110.1log 11(4)(1)(1)(1) 1.1113(5)2111123212.120273(6)5415670451201037a a b b b b a a a a a a a a a a a a αααααα-=-⨯-⨯-=---=+==-=-=+=+-+-=+-=-+--=-++-=---=-++-2222456178.0(7)00.01(8)112.1a ba c abc abcbc c b ca abc abc b a +-=--=-+=----=-+++2.解方程(1) 111121.16x x =解 221212281,230,(1)(3)0,1, 3.x x x x x x x x +--=--=+-==-= (2)221220110.12220,20,(2)(1)0.1, 2.x x xx x x x x x x x x -=-++-=+-=+-===- 3.解下面的线性方程组21221222222112123123123131133132(2)()()()(),.().,.235(3)35549521036, 2.424,0,22452x ax a x bx b a b a b x a b a b a b x a b x a a a b ab x ab x a b x x x x x x x x x x x x x x x x x x ⎧+=⎪⎨+=≠⎪⎩-=-=-+=+=-+=-=-⎧⎨=+⎩-+=⎧⎪+-=⎨⎪-+=⎩-=⎧==-==⎨-=⎩=-+解解13123354 1.210x x x x x -=-+=-=⎧⎪=-⎨⎪=⎩12312312320(4)3251324x x x x x x x x x -+=⎧⎪+-=⎨⎪+-=⎩ 解1231231231231233121220 (1) 325 1 (2)32 4 (3)(1)(3)32 4 (4)(4)(2)3219/4 (5)43,3/4.322/4 (6)19/4222/4313/413.327281322/413/28473x x x x x x x x x x x x x x x x x x x x -+=⎧⎪+-=⎨⎪+-=⎩++-=-+=⎧==⎨+=⎩===-==123.281328472834x x x ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩4.求下列个排列的逆序数,并且说明它们的奇偶性: (1)4213 (2)542163(3)134782695 (4)(-1)(-2)21(1)(4213)1+2+1=4,(2)(542163)123039,(3)(134782695)42410,(4)((-1)(-2)21)12(1)(1)/2.4,4142,4n n n n n n n n n n k k n k k ττττ==++++==++==+++-=-=+=+ 解偶排列,3+5.确定i 和j 的值,使得9级排列(1) 1274i 56j 9成偶排列; (2)3972i 15j 4成奇排列.解(1) τ (127435689)=1+2+1+1=5,奇排列, 127485639为偶排列. (2) τ (397261584)=1+3+2+5+3+1+5=20, 397281564为奇排列.6.下列各项,哪些是五阶行列式||ij a 中的一项.若是,试决定该项的符号.132532415431124352244321351254(1)(2);(3)a a a a a a a a a a a a a a a解(1) 1325324154.a a a a a 行号按自然顺序排列,列号排列35214. τ (35214)=2+3+1=6,取正号.(2) 3112435224.a a a a a 列号2重复,不是行列式的项.(3) 43213512541221354354.a a a a a a a a a a =行号按自然序列,列号排列是21534. τ (21534)=1+1+1=3,取符号.7.根据行列式的定义计算下面的行列式:(2(1)1)112(1)2(1)2(1)(1)(1)121(1)/212(1)1010000002000(1)00000100000(1)!(1)!.00000(2)0(1).n n n n n n n n n n n n nn nnn n n n n n n n n a a a a a a a a a a a a a τ-----------=-=-=-((1)(2)1)(1)(2)/2000010000200(3)1000000000(1)!(1)!.n n n n n n nn n τ-----=-=-1111122222331542544455(4)000000.000000a b c d e a b c d e a b a b b a a b a b εε=+= 8.用行列式性质计算下列行列式32153320533205310032053(1)72284721847218410072184320533205310032053132053100721847218410072184172184100(7218432053)4013100.1(2)2()1112()02()0x y x y y x y y x y x x y x yx x yx y x y y x yx x y xy x y x yx+=+=+==-=+++=++++=+-=+--22332()()2().y x yxx y x xy y x y ---=+-+-=-+32222(3)2212()121212()00002().111100111100(4)11110011111111000011011101111()10a b c a b c b c ab ca c a ba b a b c b c ab ac a b a b a b c b c ac a b a b c x x y x x y y yyyyx y y xy y x yy x yxy xy xy xy y xy x y ++++++=++++++=++++++=+++--=+---=----=+=-+=-2.y9。
线性代数练习题及答案解析(一)

线性代数练习题及答案解析(一)一、行列式1、排列25341的逆序数为 7 ;2、排列643125的逆序数是 9 ;3、方程211123049x x =的根为 2,3 ;(范德蒙行列式) 4、行列式D=162021304---中,元素-3的代数余子式是( A )(A )10 (B )2 (C )-10 (D )-2 考点:代数余子式定义5、(1)三阶行列式det()ij D a =中含有因子1322a a 的项为 132231-a a a ,含有因子1223a a 的项为 122331a a a . 考点:行列式展开式的定义规则(2)四阶行列式det()ij D a =中含有因子1123a a 的项为 12233144a a a a 或12233441-a a a a .6、设n 阶行列式60D =,且D 中的每列的元素之和为6,则D 中的第三行的代数余子式之和为 10 .考点:行列式的性质6,行列式按行(列)展开7、(1)设n 阶行列式det()ij D a =,j i A 是D 中元素j i a 的代数余子式,则下列各式中正确的是( C ). 考点:行列式按自己的行(列)展开等于行列式,如行(列)与代数余子式的行(列)不一致则等于零。
A 、10nijij i aA ==∑;B 、10nijij j aA ==∑; C 、1nijij j aA D ==∑; D 、121ni i i aA D==∑(2)若4阶行列式D 中第2行的元素212223242,1,3,0,a a a a ====余子式212M =,2223241,3,0M M M ===则D= -12 .注意:代数余子式与余子式的区别。
行列式的展开只与代数余子式有关。
(3)若3阶行列式D 中第1行的元素1112133,2,5,a a a ===代数余子式114A =,12131,2,A A =-=则D= 20 .8、行列式112233440000000a b a b b a b a =( B )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
||班级: 姓名: 学号: 成绩: 批改日期: ||第 1 页 共 18 页行列式的概念一、选择题1. 下列选项中错误的是( ) (A)ba d c dc b a -= ; (B)acb d dc b a =;(C)dc b a dcd b c a =++33; (D)dc b a dc b a -----=.答案:D2.行列式n D 不为零,利用行列式的性质对n D 进行变换后,行列式的值( ).(A)保持不变; (B)可以变成任何值; (C)保持不为零; (D)保持相同的正负号. 答案:C二、填空题1.ab b a log 11log = .解析:0111log log log 11log =-=-=ab abb a ba . 2.6cos3sin6sin3cosππππ= . 解析:02cos 6sin 3sin 6cos 3cos 6cos 3sin6sin3cos==-=πππππππππ3.函数x x xxx f 121312)(-=中,3x 的系数为 ; xx xx x x g 21112)(---=中,3x 的系数为 . 答案:-2;-2.||班级: 姓名: 学号: 成绩: 批改日期: ||第 2 页 共 18 页阶行列式n D 中的n 最小值是 . 答案:1.5. 三阶行列式11342321-中第2行第1列元素的代数余子式等于 . 答案:5.6.若02182=x,则x = . 答案:2. 7.在n阶行列式ija D =中,当i<j 时,),,2,1,(0n j i a ij L ==,则D = .答案:nn a a a Λ2211.8.设a ,b 为实数,则当a = ,b = 时,010100=---ab b a .解析:0)()1(1010022=+-=--=---b a ab ba abb a故0,0==b a .三、解答题1.用行列式的定义计算.(1)1100001001011010;解:原式=100010101)1(1010000011)1(14121++-⨯+-⨯||班级: 姓名: 学号: 成绩: 批改日期: ||第 3 页 共 18 页110010100-=--=(2)000000hgf e d c b a.原式=00000gf e d b hf e dc a - =00000g f bd hf df e c a +⎪⎪⎭⎫ ⎝⎛-=bdfg adfh -2. 设行列式λλλ01010101-=D , 3512321132=D ,若21D D =,求λ的值.解:由对角线法则,得()()0,11221=-+=D D λλ若21D D =,则()()0112=-+λλ于是1-=λ或1.四、证明题1.(略)行列式的性质一、选择题1.设行列式x x xD 0101011-=, 1133512322=D ,若21D D =,则x 的取值为 ( ).(A)2,-1; (B)1,-1; (C)0,2; (D)0,1.答案:B2.若3333231232221131211==a a a a a a a a a D ,||班级: 姓名: 学号: 成绩: 批改日期: ||第 4 页 共 18 页则3332333123222321131213111525252a a a a a a a a a a a a D +++==( ). (A)30; (B) -30; (C)6; (D)-6. 答案:C二、填空题1.若三阶行列式D 的第一行元素分别是1,2,0,第三行元素的余子式分别是8,x ,19,则x = . 解析:1820190,4x x ⨯-+⨯==. 2.2016201420182016 = .解析:4202220162014222016201420182016===.3.行列式cb dc a bcb aD =,则312111A A A ++= . 解析:312111A A A ++0111==cb c acb .4.行列式xx x xx D 31213231232154-=的展开式中,4x 的系数为 ;3x 的系数为 .解析:xxx x x x x x xx D 312131232321531213231232154--=-=xx x x 3121312512585103215---= 含4x ,3x 的项仅有主对角线上元素之积项,故4x ,3x 的||班级: 姓名: 学号: 成绩: 批改日期: ||第 5 页 共 18 页系数分别为15,-3.三、解答题1.计算下列行列式 .(1)3214214314324321;解:各行加到第一行,得原式=32142143143211111032142143143210101010==160400400121011111012301211210111110=---=------.(2)4444333322225432154321543215432111111;解:原式=(5-4)(5-3)(5-2)(5-1)(4-3)(4-2)(4-1)(3-2)(3-1) =288.(3)49362516362516925169416941;原式=02222222297531694113119711975975316941==.||班级: 姓名: 学号: 成绩: 批改日期: ||第 6 页 共 18 页(4)000000xyy x y x x y ;原式=xy x yx x xyy y xy 00000000-- =22222)(y x xyy x xxyy x y--=-.(5)xy z zx yyzx111; 原式=)(0)(01x z y x z x y z x y yzx------ =))()((11))((x z z y y x yz x z x y ---=---.(6)200012000000130012000101--;原式=31012010140131201014200013012001012---=--=--=2031124=---. (7)43211111111111111111x x x x ++++;||班级: 姓名: 学号: 成绩: 批改日期: ||第 7 页 共 18 页解:原式=432111110010011x x x x x x x ---+=432111413121100000001x x x x x x x x x x x x x ---++++ =3214214314324321x x x x x x x x x x x x x x x x ++++.2.设4322321143113151-=D ,计算44434241A A A A +++的值.其中)4,3,2,1(4=j A j 是D 的代数余子式.解:44434241A A A A +++61111321143113151=-=.3. 已知1142113110111253------=D ,求41312111M M M M +++.解:41312111M M M M +++=41312111)1(1)1(1M M M M --⋅+--⋅=1141113110111251-------=0.4.计算下列n 阶行列式.||班级: 姓名: 学号: 成绩: 批改日期: ||第 8 页 共 18 页(1)211121112ΛMM M ΛΛ; 解:原式=211121111ΛM M MΛΛ+++n n n =211121111)1(ΛMMM ΛΛ+n =1100010111)1(+=+n n ΛMM M ΛΛ. (2)xy yyy x y yy y x yy y y x ΛM M M M ΛΛΛ ; 解:原式=[]x y y y y x y yy y x yy n x ΛM M M M ΛΛΛ1111)1(-+ =[]yx y x y x y n x ----+ΛM M M MΛΛΛ0000001111)1(=[]1)()1(---+n y x y n x .(3)),,2,1,0(010011111021n i x x x x i nΛΛM M M M ΛΛΛ=≠.||班级: 姓名: 学号: 成绩: 批改日期: ||第 9 页 共 18 页解:原式=nni ix x x x ΛM M M M ΛΛΛ0000000011101211∑=- =)1(121∑=-ni in x x x x Λ.四、证明题1.设a ,b ,c 是互异的实数,证明0111333=c b a c b a的充分必要条件是a+b+c=0.证明:33333333001111a c ab aa c ab acbac b a----==3333a c a b a c a b ----=222211))((a ac c a ab b a c a b ++++--=))()((22ab ac b c a c a b -+--- =))()()((c b a b c a c a b ++---=0,由于a ,b ,c 是互异的实数,故要上式成立,当且仅当a+b+c=0.2.证明4+2324323631063a b c d a a b a b c a b c da a ab a bc a b cd a a b a b c a b c d +++++=++++++++++++证明:左边43322102320363a b c d r r a a b a b cr r a a b a b c r r a a b a b c-+++-+++-+++433210002003a b c d r r a a b a b ca ab r r a a b-++++-+4430002000a b c d a a b a b cr r a a a b a+++-=+||班级: 姓名: 学号: 成绩: 批改日期: ||第 10 页 共 18 页=右边克莱姆法则一、选择题1.方程组⎪⎩⎪⎨⎧=++=++=++1,1,1321321321x x x x x x x x x λλλ, 有唯一解,则( ).(A)1-≠λ且2-≠λ; (B) 1≠λ且2-≠λ;(C) 1≠λ且2≠λ; (D) 1-≠λ且2≠λ.解析:由克莱姆法则,当0)1)(2(1111112≠-+=λλλλλ,即1≠λ且2-≠λ,选B.2.当≠a ( )时,方程组⎪⎩⎪⎨⎧=+-=++=+02,02,0z y ax z ax x z ax 只有零解.(A) -1 ;(B) 0 ;(C) -2 ;(D) 2. 解析:由克莱姆法则,当0)2(212012100121210≠-=--=-a aaa aa即2≠a ,选D.三、解答题1.用克莱姆法则下列解方程组.(1)⎪⎩⎪⎨⎧=+-=+-=-+;32,322,22z y x z y x z y x解: 03112221121≠=---=D , 由克莱姆法则知,此方程组有唯一解,31132231221=---=D ,||班级: 姓名: 学号: 成绩: 批改日期: ||第 11 页 共 18 页61322311212=-=D ,93323312213==D ,因此方程组的解为11==D D x ,22==D Dy ,33==DD z .(2)..23342,223,3232,124321432143214321⎪⎪⎩⎪⎪⎨⎧=-++=+++=+-+=-++x x x x x x x x x x x x x x x x解:043342123121321121≠=---=D由克莱姆法则知,此方程组有唯一解,833421232213311211=---=D , 233221221213211112-=---=D ,232421231233211213=--=D ,223422231313211214=-=D . 因此方程组的解为211==D D x ,2122-==D D x ,2133==D D x ,2144==D D x . 2.判断线性方程组⎪⎩⎪⎨⎧=-+=+-=-+0285,042,022321321321x x x x x x x x x 是否有非零解解:因为系数行列式285122421285421122----=---=D||班级: 姓名: 学号: 成绩: 批改日期: ||第 12 页 共 18 页=0305009604212218960421≠-=--=----, 所以,方程组只有零解.3.已知齐次线性方程组⎪⎩⎪⎨⎧=+-=++=-+02,0,0321321321x x x x x kx x kx x 有非零解,求k 的值.解:因为齐次线性方程组有非零解,所以该方程组的系数行列式必为零,即32101101111211112k k kk kk --+--=--=)21)(1()1(32k k k +++- =0)4)(1(=-+k k 解得,k =-1或k =4.4.当μ取何值时,齐次线性方程组⎪⎩⎪⎨⎧=--+-=-+-=-++0)1(02)3(0)1(42321321321x x x x x x x x x μμμ有非零解解:由齐次线性方程组有非零解的条件可知,0111213142=------μμμ,解得3,2,0=μ.第一章综合练习一、判断题1. n 阶行列式n D 中的n 最小为2.( ╳ )2. 在n 阶行列式ij a D =中元素),2,1,(L =j i a ij 均为整数,则D 必为整数.( √ )||班级: 姓名: 学号: 成绩: 批改日期: ||第 13 页 共 18 页3.413223144433221144413332232214110000000a a a a a a a a a a a a a a a a -=.( ╳)二、选择题1.若11131--+=x x x D ,211122-+=x x D ,则1D 与2D 的大小关系是( ).(A)21D D <; (B)21D D >;(C)21D D =;(D)随x 值变化而变化.答案:C 2.行列式{})2,1,1,,,(-∈d c b a dc b a 的所有可能值中,最大的是( ).(A) 0; (B)2; (C)4; (D)6.答案:D三、填空题1.︒︒︒︒40cos 20sin 40sin 20cos = .解析:︒︒-︒︒=︒︒︒︒40sin 20sin 40cos 20cos 40cos 20sin 40sin 20cos2160cos =︒=. 2.若y y x x y x -=-1122,则x+y = . 解析:由y y x x y x -=-1122,得xy y x 222-=+ 即0)(2=+y x ,从而x+y =0.3.已知111,0112==yx x ,则y = . 解析:由111,0112==yxx ,得x =2,x-y =1,从而y =1||班级: 姓名: 学号: 成绩: 批改日期: ||第 14 页 共 18 页4. 若222222222642531C c B b A a c b a ++=,则2C 化简后的结果等于 . 解析:242312=-=C .5.设xxx x xx f 111123111212)(-=,则4x 的系数为 ;3x 的系数为 .解析:当f (x )的主对角线的4个元素相乘才能得出4x ,系数为2;含3x 的项只能是44332112,,,a a a a 的乘积,系数为-1. 答案:2,-1.6.设0123411222641232211154321=D ,则(1)333231A A A ++= ; (2)3534A A + ; (3)5554535251A A A A A ++++ . 解析:0)(23534333231=++++A A A A A 0)()(23534333231=++++A A A A A于是0333231=++A A A ,03534=+A A .5554535251A A A A A ++++1111111222641232211154321=||班级: 姓名: 学号: 成绩: 批改日期: ||第 15 页 共 18 页01111133333641232211154321==. 即0555*******=++++A A A A A .四、解答题1.计算下列行列式.(1)44342414433323134232221241312111y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x ++++++++++++++++;解:原式=14131214141312131413121214131211y y y y y y y x y y y y y y y x y y y y y y y x y y y y y y y x ---+---+---+---+=000000000014131214131211=------+x x x x x x y y y y y y y x .(2)43211111111111111111x x x x ++++;解:原式=432111110010011x x x x x x x ---+=432111413121100000001x x x x x x x x x x x x x ---++++ =3214214314324321x x x x x x x x x x x x x x x x ++++.||班级: 姓名: 学号: 成绩: 批改日期: ||第 16 页 共 18 页(3)2007000002006000200500020001000ΛΛΛMM M M M ΛΛ. 解:原式=!2006)1(2007220052006⨯-⋅=!2007-2.已知123452221127312451112243150D ==, 求(1)434241A A A ++;(2)4544A A +. 解:27)(21114544434241=++⋅+⋅+⋅A A A A A0)()(24544434241=++++A A A A A得9434241-=++A A A ,184544=+A A . 3.计算下列n 阶行列式.(1)nn n n n n n D ΛM M M ΛΛΛ222333222111=; 解:(利用范德蒙行列式计算)1122133321111!--==n n n Tn n n n n D D ΛM MMΛΛΛ [])1()2()24)(23)(1()13)(12(!--------=n n n n n ΛΛΛ!2)!2()!1(!Λ--=n n n .||班级: 姓名: 学号: 成绩: 批改日期: ||第 17 页 共 18 页(2)211121112ΛMM M ΛΛ; 解:原式=211121111ΛM M MΛΛ+++n n n =211121111)1(ΛMMM ΛΛ+n =1100010111)1(+=+n n ΛMM M ΛΛ.(3)mx x x x m x x x x mx D n n n n ---=ΛM M M ΛΛ212121解:将第2列,L ,第n 列分别加到第一列,并提取第一列的公因子,得m x x mx x x x m x m x x x x x m x x x D n n n n n n n --+++--+++-+++=ΛΛM M MΛΛΛΛ221221221mx x x m x x x m x x x n n n n ---+++=ΛMM M ΛΛΛ22221111)(mm m x x x n ---+++=ΛM M M ΛΛΛ0101001)(21121))((---+++=n n m m x x x Λ||班级: 姓名: 学号: 成绩: 批改日期: ||第 18 页 共 18 页(4)nn n n n a a a a a a b b b b b D 1322113210000000-----=ΛM M M M M ΛΛΛ (其中n i a i ,,2,1,0Λ=≠)解: 1221100000000)1(-+----=n nn n a a a a b D ΛM M M M ΛΛ1222112210000000------+n n n n n a a a a a b b b b a ΛM M M M ΛΛΛ 121-+⋅=n n nnn D a a b a a a Λ ⎪⎪⎭⎫⎝⎛==∑=n i i in a b a a a 121ΛΛ. 三、证明题1.试证:如果n 次多项式n n x a x a a x f +++=Λ10)(对n+1个不同的x 值都是零,则此多项式恒等于零.(提示:用范德蒙行列式证明)。
