了解偏角法的概念
偏角法
第9讲教学目标:了解偏角法的概念,理解正拨、反拨的含义,掌握曲线偏角计算公式和方法。
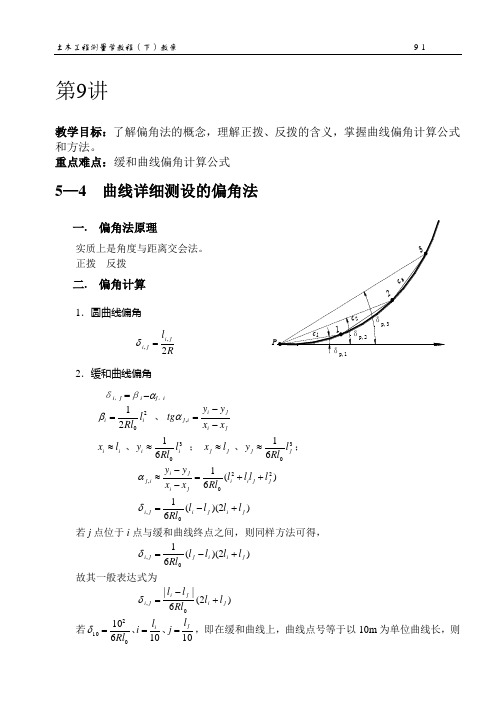
重点难点:5—4 一. 偏角法原理正拨 反拨二. 偏角计算1.圆曲线偏角Rl j i j i 2,,=δ 2.缓和曲线偏角δi ,j =βi -αj ,i ji j i i tg l Rl =,20 21αβ、;、;、 61 61 330j j j j i i i i l Rl y l x l Rl y l x ≈≈≈≈ )(61220,j j i i j i j i ij l l l l Rl x x y y ++=--≈α )2)((61,j i j i j i l l l l Rl +-=δ 若j 点位于i 点与缓和曲线终点之间,则同样方法可得,)2)((610,j i i j j i l l l l Rl +-=δ故其一般表达式为)2(6||0,j i j i j i l l Rl l l +-=δ若1010 6100210j i l j l i Rl ===、、δ,即在缓和曲线上,曲线点号等于以10m 为单位曲线长,则102,0δδj j =式中,R 为圆曲线半径,l 0为缓和曲线长,δ10为缓和曲线基本角。
当i 点位于缓和曲线起点时,则上式可化简为三. 弦线长度计算向,2至i f Z )2(||10,j i j i j i +-=δδ5—5 曲线详细测设的直角坐标法一. 直角坐标法测设曲线原理X 轴上丈量x P ,得P'点;自P'点,沿与X 轴垂直且指向曲线内侧的方向丈量y P ,即得P 点。
直角坐标法中,坐标系X 轴均选主点的切线,故曲线点的y 坐标为相对于切线的支距。
因此,直角坐标法也称为切线支距法。
二. 曲线点坐标计算直角坐标法所选定的坐标系通常为缓和曲线坐标系,则在该坐标系下,缓和曲线段曲线点坐标的计算公式为缓和曲线方程,圆曲线段曲线点的坐标:⎭⎬⎫+-=+=p R y mR x t t t t )cos 1(sin αα式中0βα+-=RK K HYt t ,K t 为t 点的里程,K HY 为HY 里程。
缓和曲线的切线支距法和偏角法的计算公式和测设方法

缓和曲线的切线支距法和偏角法的计算公式和测设方法[教程]第九章道路工程测量(圆曲线缓和曲线计算公式)第九章道路工程测量(road engineering survey)重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法§9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为:路线勘测设计测量(route reconnaissance and design survey) 和道路施工测量(road construction survey) 。
(一)勘测设计测量(route reconnaissance and design survey)分为:初测(preliminary survey) 和定测(location survey)1、初测内容:控制测量(control survey) 、测带状地形图(topographical map of a zone) 和纵断面图(profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:在选定设计方案的路线上进行路线中线测量(center line survey) 、测纵断面图(profile) 、横断面图(cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
(二)道路施工测量(road construction survey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
本章主要论述中线测量和纵、横断面测量。
二、中线测量(center line survey)1、平面线型:由直线和曲线(基本形式有:圆曲线、缓和曲线)组成。
2、概念:通过直线和曲线的测设,将道路中心线的平面位置测设到地面上,并测出其里程。
即测设直线上、圆曲线上或缓和曲线上中桩。
线路工程测量(1)

§10-4 缓和曲线
一、缓和曲线的概念与性质 1、概念:直线与圆曲线之间的一段过渡曲线
2、性质: RP∝1/ lP 或 RP = C / lP C — 缓和曲线半径的
变更率 在HY(YH)处, RP = R,则C=R l0
线路工程测量(1)
二、缓和曲线的方程
外矢距E0 (m)
切曲差q (m)
20.49
7.68
12.65
3.75
线路工程测量(1)
里程推算:
ZD
DK125+032.58
+(D1-T1)
14
ZY1
DK125+920.72
+L1/2
140.77
QZ1
DKI26+061.49
+L1/2
140.77
YZ1
DK126+202.26
+(D2-T1-T2)
线路工程测量(1)
(3)穿线
经过调整,使同一条直线的控制点处在同一直 线上。
方法:将仪器安置在一个转点上,照准该直线 上最远的一个转点,检查中间各转点的偏差,偏 差若不大,将各点调整到视线方向上。若偏差很 大,检查原因予以纠正。
线路工程测量(1)
(4)交点 将相邻两直线延长,在地面上测设出交
点(JD)的位置。
467.09
ZY2
DK126+669.35
+L2/2
111.28
QZ2
DK126+780.63
+L2/2
111.29
YZ2
DK126+891.92
检核计算:
ZY1
DK125+920.72
偏角法计算缓和曲线
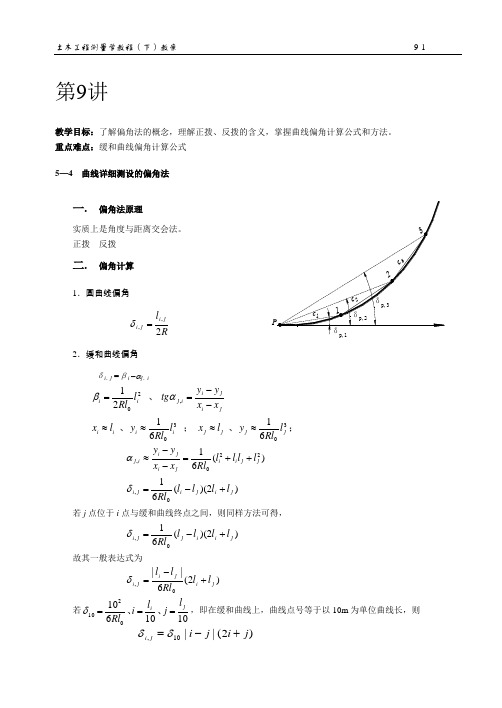
第9讲教学目标:重点难点:缓和曲线偏角计算公式5—4 曲线详细测设的偏角法一.偏角法原理实质上是角度与距离交会法。
正拨 反拨二.偏角计算1.圆曲线偏角Rl j i j i 2,,=δ 2.缓和曲线偏角δi ,j =βi -αj ,iji i j i i tg l Rl =,20 21αβ、;、;、 61 61 3030j j j j i i i i l Rl y l x l Rl y l x ≈≈≈≈ )(61220,j j i i j i j i ij l l l l Rl x x y y ++=--≈α )2)((61,j i j i j i l l l l Rl +-=δ 若j 点位于i 点与缓和曲线终点之间,则同样方法可得,)2)((610,j i i j j i l l l l Rl +-=δ 故其一般表达式为)2(6||0,j i j i j i l l Rl l l +-=δ若1010 6100210j i l j l i Rl ===、、δ,即在缓和曲线上,曲线点号等于以10m 为单位曲线长,则)2(||10,j i j i j i +-=δδ102,0δδj j =式中,R 为圆曲线半径,l 0为缓和曲线长,δ10为缓和曲线基本角。
当i 点位于缓和曲线起点时,则上式可化简为三.弦线长度计算表定向。
数。
例至i +1式中,5—5 曲线详细测设的直角坐标法一.直角坐标法测设曲线原理P ,得P'点;自P'点,沿与X 轴垂直且指向曲线内侧的方向丈量y P ,即得P 点。
直角坐标法中,坐标系X 轴均选主点的切线,故曲线点的y 坐标为相对于切线的支距。
因此,直角坐标法也称为切线支距法。
二.曲线点坐标计算直角坐标法所选定的坐标系通常为缓和曲线坐标系,则在该坐标系下,缓和曲线段曲线点坐标的计算公式为缓和曲线方程,圆曲线段曲线点的坐标:⎭⎬⎫+-=+=p R y mR x t t t t )cos 1(sin αα式中0βα+-=RK K HYt t ,K t 为t 点的里程,K HY 为HY 里程。
《测量学》课程标准

《测量学》课程标准一、课程性质本课程是工程测量专业必修的一门专业基础平台课程,是在测量技术基础、控制测量、测量平差、工程概论与识图等课程基础上,开设的理论和实践相结合的核心课程。
其任务是培养学生具备在工程建设的不同阶段完成各项工程测量的能力,为后续从事工程测量员工作奠定基础。
二、学时与学分94学时,6学分。
三、课程设计思路本课程应体现以服务发展为宗旨、以促进就业为导向,按照立德树人的要求,注重核心素养的培养,突出必备品格和关键能力,兼顾中高职衔接,高度融合职业技能的学习和职业精神的培养。
1.依据“江苏省中等职业教育工程测量专业指导性人才培养方案”中确定的培养目标、综合素质和职业能力,按照知识与技能、过程与方法、情感态度与价值观三个维度,突出工程施工测量工作岗位所必须的能力,结合学生职业生涯发展、中高职分段培养,确定本课程目标。
2.根据“江苏省中等职业教育工程测量专业岗位职业能力分析表”,依据课程目标、岗位需求,对接职业标准和行业企业技术标准,着眼于学生的职业发展与能力提升,确定本课程内容。
3.对工程测量课程所必需习得的知识和技能进行整体梳理,依照典型工程施工测量任务,兼顾不同工程的特殊性,结合学生的学习特点和技能成长规律,建构教学模块和教学单元,设计若干学习任务,将相应的专业知识和技能有机融合到学习任务中。
四、课程目标学生通过本课程的学习,掌握工程测量的基本理论和方法,能够独立从事建筑工程测量、地下工程施工测量、线路测量等常见工程测量项目,并能在一定的指导下从事其他工程测量项目。
1.理解工程测量中的基本原理、基本概念和基本知识;掌握工程测量中专门仪器的特性和使用方法;掌握施工放样的方法。
2.能正确完成建筑、线路、桥梁、地下、水下工程的测量工作。
3.具有根据工程项目的特点,布设施工控制网的能力。
4.能正确处理工程测量数据,对出现的问题进行快速的分析、改正,并且能进行资料整理。
5.培养学生踏实肯干,吃苦耐劳、实事求是、一丝不苟、爱岗敬业,团结协作的职业精神。
施工放样作业流程及方法

施工放样作业流程及方法一、施工放样的作业流程1、准备工作:熟悉施工图纸,掌握设计要求和规范规定,确定施工放样的方法和精度要求。
准备好测量仪器和工具,包括全站仪、水准仪、GPS、激光指向仪等。
2、测量定位:根据设计要求,确定施工放样的基点和基线,建立施工控制网。
对于大型工程,需要建立多个控制网,并进行相互校核。
3、测量放样:根据施工控制网,进行测量放样。
对于建筑物的轴线、标高、位置等参数,需要进行精确测量和记录。
对于桥梁、隧道等工程,需要进行地形测量和地质勘探。
4、现场校核:在施工放样后,需要对放样结果进行现场校核,以确保施工符合设计要求。
对于不符合设计要求的地方,需要进行调整和修正。
5、质量检测:在施工完成后,需要对施工成果进行质量检测。
对于不符合质量要求的部位,需要进行返工或修补。
6、资料整理:在施工完成后,需要对测量数据进行整理和分析,并编制测量报告和成果资料。
二、施工放样的方法1、直角坐标法:利用直角坐标系进行施工放样。
将已知点作为原点,建立直角坐标系,将设计图纸中的点位坐标转换为实际坐标,并进行测量放样。
2、极坐标法:利用极坐标系进行施工放样。
将已知点作为极点,建立极坐标系,将设计图纸中的点位坐标转换为极坐标,并进行测量放样。
3、方向交会法:利用两个已知方向进行交会,确定待测点的位置。
根据设计图纸中的点位坐标和已知方向,计算出待测点的方向距离和角度,并进行交会测量。
4、距离交会法:利用两个已知距离进行交会,确定待测点的位置。
根据设计图纸中的点位坐标和已知距离,计算出待测点的距离和角度,并进行交会测量。
5、高程交会法:利用两个已知高程进行交会,确定待测点的高程。
根据设计图纸中的点位坐标和高程,计算出待测点的高程差和方向角,并进行交会测量。
6、偏角法:利用偏角和距离进行施工放样。
根据设计图纸中的点位坐标和偏角大小,计算出待测点的方向距离和角度,并进行交会测量。
7、全站仪放样法:利用全站仪进行施工放样。
初学罗盘的使用方法

初学罗盘的使用方法罗盘是一种测量方向的工具,它可以帮助我们确定方向,是探险、旅行、航海等活动中必不可少的工具。
在现代生活中,由于GPS等技术的出现,罗盘的使用已经逐渐减少,但是对于喜欢户外活动的人来说,罗盘仍然是一项重要的工具。
本文将介绍初学者如何使用罗盘。
一、罗盘的基本结构罗盘由两部分组成:指南针和底盘。
指南针是罗盘的核心部件,指示方向,一般由磁针、磁针轴、指针、指针轴等组成。
底盘是指南针的支架,一般由底板、透明盖、度盘等组成。
底板上有一个透明盖,可以用来盖住度盘,方便读数。
二、罗盘的使用方法1. 确定方向罗盘最基本的功能就是确定方向。
在使用罗盘之前,我们需要先了解一些基本概念。
首先是磁北和真北的概念。
磁北是指磁针所指向的方向,也就是罗盘的指针指向的方向。
真北是指地球极点所在的方向,也就是地球的地理北极方向。
其次是偏角的概念。
由于地球的磁场并不是完全垂直于地球的轴线,所以磁北和真北之间存在一定的偏差,称为偏角。
偏角的大小和地理位置有关,一般在罗盘上都有标注。
在使用罗盘时,我们需要先确定磁北的方向。
将罗盘平放在手掌上,让指针自由旋转,直到指针稳定指向一个方向,这个方向就是磁北方向。
如果罗盘的底盘上有度盘,可以通过读数确定磁北的角度。
确定磁北方向后,我们需要根据偏角来确定真北的方向。
偏角一般在罗盘上有标注,我们可以通过减去偏角来得到真北的方向。
2. 行进导航在户外活动中,罗盘可以用来进行行进导航。
行进导航分为两种方式:直线行进和曲线行进。
直线行进是指在平坦的地形上,直接朝着目的地方向行进。
在使用罗盘进行直线行进时,我们需要先确定起点和终点的方向,然后沿着这个方向行进。
在行进过程中,我们需要不断使用罗盘来确定方向,以免偏离目标方向。
曲线行进是指在复杂的地形上,通过多次转向来到达目的地。
在使用罗盘进行曲线行进时,我们需要先确定转向点的方向,然后沿着这个方向行进。
到达转向点后,我们需要使用罗盘来确定下一个转向点的方向,然后再行进。
公路测量资料

9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为:路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。
(一)勘测设计测量 (route reconnaissance and design survey)分为:初测 (preliminary survey) 和定测 (location survey)1、初测内容:控制测量 (control survey) 、测带状地形图 (topographical map of a zone) 和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
(二)道路施工测量 (road construction survey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
本章主要论述中线测量和纵、横断面测量。
二、中线测量 (center line survey)1、平面线型:由直线和曲线(基本形式有:圆曲线、缓和曲线)组成。
2、概念:通过直线和曲线的测设,将道路中心线的平面位置测设到地面上,并测出其里程。
即测设直线上、圆曲线上或缓和曲线上中桩。
三、交点 JD(intersecting point) 的测设(一)定义:路线的转折点,即两个方向直线的交点,用 JD 来表示。
(二)方法:1、等级较低公路:现场标定2、高等级公路:图上定线;实地放线。
(三)实地放线的方法分类1、放点穿线法放直线点;穿线;定交点(1)放点可用支距法(垂直于导线边的距离)、导线相交法及极坐标法进行。
工程测量重点全部知识点(中国矿业大学)

⼯程测量重点全部知识点(中国矿业⼤学)第⼀章1、⼯程测量定义:⼯程测量学是研究各种⼯程在规划设计、施⼯建设和运营管理阶段所进⾏的各种测量⼯作的学科。
2、⼯程测量学科地位:学科交叉、学科综合、学科细分。
测绘学的⼆级学科:⼤地测量学:⼏何⼤地测量、物理⼤地测量、空间⼤地测量、海洋⼤地测量、⼯程测量学(矿⼭测量);摄影测量学与遥感;地图制图学;地理信息系统;不动产测绘(房地产测绘、地籍测绘)。
3、按服务对象分⼯程测量主要内容包括哪些?建筑⼯程测量、⽔利⼯程测量、线路⼯程测量、桥隧⼯程测量、地下⼯程的测量海洋⼯程测量、军事⼯程测量、三维⼯业测量,以及矿⼭测量、城市测量等。
4、陆⾏乘车,⽔⾏乘船。
,这段描述的含义。
这⾥所记录的就是当时的⼯程勘测情景,准绳和规矩就是当时所⽤的测量⼯具,准是可揆(kui)平的⽔准器,绳是丈量距离的⼯具,规是画圆的器具,矩则是⼀种可定平,可测长度、⾼度、深度和画圆、画矩形的通⽤测量仪器。
5、“⼴义⼯程测量学”的概念:“⼀切不属于地球测量,不属于国家地图集范畴的地形测量和不属于官⽅的测量,都属于⼯程测量”。
第⼆章1、⼯程测量各阶段的任务是什么。
规划设计阶段的测量⼯作:测绘地形图和纵、横断⾯图施⼯建设阶段的测量⼯作:按设计要求将设计的建构筑物位置、形状、⼤⼩及⾼程在实地标定出来,以便进⾏施⼯;⼯程质量监理运营管理阶段的测量⼯作:竣⼯测量以及变形监测与维修养护。
2、测量监理的⼯作任务是什么在正式施⼯开始时,对控制⽹进⾏全⾯复测、检查验收承包⼈的施⼯定线验收承包⼈测定的原始地⾯⾼程对桥梁施⼯还需进⾏桥梁下、上部结构的施⼯放样的检测对每层路基的厚度、平整度、宽度、纵横坡度进⾏抽查,检查施⼯单位的内业资料是否真实审批承包⼈提交的施⼯图第三章1、按范围和⽤途,测量控制⽹分哪⼏类,作⽤分为全球控制⽹、国家控制⽹、⼯程控制⽹全球控制⽹⽤于确定、研究地球的形状、⼤⼩及其运动变化,确定和研究地球的板块运动等。
缓和曲线的切线支距法和偏角法的计算公式和测设方法

[教程]第九章道路工程测量(圆曲线缓和曲线计算公式)第九章道路工程测量 (road engineering survey)内容:理解线路勘测设计阶段的主要测量工作(初测控制测量、带状地形图测绘、中线测设和纵横断面测量);掌握路线交点、转点、转角、里程桩的概念和测设方法;掌握圆曲线的要素计算和主点测设方法;掌握圆曲线的切线支距法和偏角法的计算公式和测设方法;了解虚交的概念和处理方法;掌握缓和曲线的要素计算和主点测设方法;理解缓和曲线的切线支距法和偏角法的计算公式和测设方法;掌握路线纵断面的基平、中平测量和横断面测量方;了解全站仪中线测设和断面测量方法。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§ 9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为:路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。
(一)勘测设计测量 (route reconnaissance and design survey)分为:初测 (preliminary survey) 和定测 (location survey)1、初测内容:控制测量 (control survey) 、测带状地形图 (topographical map of a zone) 和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
测量坐标转施工坐标的偏角怎么算

测量坐标转施工坐标的偏角怎么算在建筑施工中,测量坐标转施工坐标的偏角是一种常见的计算需求。
它用于确定基准坐标系和实际施工坐标系之间的差异,以确保施工过程的准确性和精度。
本文将介绍测量坐标转施工坐标的偏角的计算方法和步骤。
1. 了解坐标系在进行测量坐标转施工坐标的偏角之前,首先需要了解基准坐标系和施工坐标系的概念。
基准坐标系是由相关测量标志物所确定的全局坐标系,相对稳定且不易改变。
施工坐标系是在基准坐标系上建立的、针对具体施工现场的局部坐标系。
2. 准备测量数据为了计算偏角,需要准备以下测量数据:•基准坐标系下的测量数据:–X1, Y1: 基准坐标系下某一点的坐标。
•施工坐标系下的测量数据:–X2, Y2: 施工坐标系下同一点的坐标。
这些数据可以通过使用全站仪等测量设备进行测量获得。
3. 计算偏角有了准备好的测量数据,我们可以开始计算偏角。
偏角的计算方法如下:1.计算两个坐标系下的∆X和∆Y:–∆X = X2 - X1–∆Y = Y2 - Y12.计算∆Y与∆X之间的夹角θ:–θ = atan(∆Y/∆X)最终得到的θ即为坐标系的偏角,它表示的是基准坐标系与施工坐标系之间的旋转角度。
4. 验证测量结果为了验证测量结果的准确性,可以进行以下步骤:1.使用计算得到的偏角θ将基准坐标系下的测量数据旋转到施工坐标系下。
2.检查旋转后的施工坐标系下的坐标与实际测量得到的施工坐标系下的坐标是否吻合。
如果吻合,表明偏角计算准确。
5. 注意事项在进行测量坐标转施工坐标的偏角计算时,有一些注意事项需要考虑:1.测量数据的准确性和精度对计算结果的影响较大,因此在进行测量时应尽量避免误差。
2.在进行偏角计算时,要确保基准坐标系和施工坐标系的原点位置对应准确。
3.如果测量数据较多,可以使用数学软件或程序来进行自动计算,以提高效率和准确性。
结论测量坐标转施工坐标的偏角的计算方法简单且易于实施。
通过准备测量数据、计算偏角和验证测量结果,可以实现基准坐标系和实际施工坐标系之间的准确转换。
偏角法的分析原理及应用

偏角法的分析原理及应用1. 引言偏角法是一种常用于数学和物理领域的分析方法。
它基于向量的概念,通过计算向量之间的夹角来解决各种问题。
本文将介绍偏角法的分析原理以及其在不同领域中的应用。
2. 偏角法的原理偏角法的核心原理是通过计算向量的夹角来解决问题。
在二维平面上,每个向量可以用其起点和终点的坐标表示。
对于向量A(a1, a2)和向量B(b1, b2),它们之间的夹角θ可以通过以下公式计算得出:θ = arctan((b2 - a2) / (b1 - a1))其中,arctan为反正切函数。
通过计算两个向量的夹角,我们可以得到它们之间的相对位置关系。
3. 偏角法的应用3.1 几何学中的应用在几何学中,偏角法可以应用于解决直线之间的夹角、判断点在多边形内部或外部等问题。
这些问题可以通过计算向量的夹角来得到准确的答案。
3.2 物理学中的应用在物理学中,偏角法可以用于解决物体之间的相对运动问题。
通过计算物体的速度向量之间的夹角,我们可以确定它们的相对运动方向和速度大小。
这对于研究物体的碰撞、运动路径等问题非常重要。
3.3 工程学中的应用在工程学中,偏角法可以应用于解决电路中的电流和电压分析问题。
通过计算电流和电压向量之间的夹角,我们可以确定电路中的功率传输和能量消耗情况。
这对于设计和优化电路系统非常有帮助。
3.4 统计学中的应用在统计学中,偏角法可以用于解决数据集的聚类问题。
通过计算数据点的向量夹角,我们可以确定它们的相似性和相对位置关系。
这对于数据挖掘和模式识别非常有用。
4. 总结偏角法是一种基于向量夹角的分析方法,通过计算向量夹角可以解决各种问题。
它在几何学、物理学、工程学和统计学等多个领域都有广泛的应用。
通过应用偏角法,我们可以得到准确的问题答案并且更好地理解问题的本质。
希望本文能够为读者介绍偏角法的原理和应用,进一步提高对偏角法的理解和应用能力。
以上就是关于偏角法的分析原理及应用的文档,希望对您有所帮助。
圆曲线测设

JD
P2
α
P3 P4
P1 P2
41624 1 20812 2 2
1
ZY
1
YZ
41624 C1 2 R sin 2 120 sin 8.95( m) 2 2
2 1
2 41624 9 32 57 65441 2
(m) xi 0 5.95 45.77 48.92 29.09 9.14 0
y(m) i
0 0.06 1.12 3.51 4.02 1.41 0.14 0
§2-4 圆曲线测设
• 三、圆曲线的详细测设
2.圆曲线详细测设的方法 (2)切线支距法 测设步骤 ①从ZY(或YZ)点开始用钢尺或皮尺沿切线方向量 取 Pi的 横坐标xi ,得垂足Ni 。 ②在各垂足Ni上用方向架定出垂直方向,量取纵坐 标yi,即 可定出Pi点。
※分弦的偏角:
图2-5
K4=039.52-020.00=19.52m,相应的偏角值
K 4 180 4 = · 2 2R
(2)弦长计算 (如图2-4)
严密计算公式: C 2R sin 近似计算: Ck
c sin 2 , 2 R
c 2 R sin
(2-3)
图2-8 切线支距原理
图2-9 切线支距法测设圆曲线
2.测设方法:
以图2-9为例,设在圆曲线上每10m测设一点。
(1)先沿切线上每1Om量一点,将半个曲线长度测 设完毕; (2)于每10m处回量Li-xi,可得各曲线点在X轴上 的投影,即各曲线点的X值;
(3)过各曲线点在X轴上的投影点做切线的垂直方 向,并在垂直方向上量取yi ,即测设出圆曲线的各点。
测量中偏角的概念

测量中偏角的概念测量中偏角是指人们在进行方向测量时所使用的一种测量方法,它是通过测量某个目标物体或者地理点与参考方向之间的角度差来确定目标物体或地理点的方向。
在测量中,我们通常会使用方向角来表示某个物体或者地理点相对于一个参考方向的方向。
方向角是指水平面上某直线与一个基准方向之间的夹角,它是从基准方向逆时针转动到目标方向所经过的角度。
而中偏角是指从北方逆时针旋转到目标方向所经过的角度。
中偏角的测量方法主要有两种,分别是正算和反算。
正算是指根据已知的方向角和某个目标物体或地理点与参考方向之间的夹角来计算目标物体或地理点的中偏角。
反算则是根据已知的方向角和目标物体或地理点的中偏角来计算目标物体或地理点与参考方向之间的夹角。
在进行角度的测量时,人们通常会使用各种测量仪器来进行辅助。
常见的测量仪器有经纬仪、方位仪、测角仪等。
这些仪器通常会采用精确的刻度和指针来帮助我们准确地测量角度。
测量中偏角主要应用于地理测量、航海、航空等领域。
在地理测量中,我们常常需要确定地理点的方向,例如测量山脉、河流、湖泊等地理要素的方向。
在航海和航空领域中,测量中偏角可以帮助航海员或飞行员确定自身位置的方向,从而准确导航。
尽管测量中偏角在实践中非常有用,但是在测量过程中也存在一些误差和限制。
由于测量仪器的精度限制、人为因素以及目标物体的不规则形状等原因,测量结果往往会有一定的误差。
此外,测量中偏角也受到地球曲率和磁场偏角等地理现象的影响,因此在实际应用中需要进行一些修正。
总的来说,测量中偏角是一种通过测量目标物体或地理点与参考方向之间的角度差来确定方向的方法。
它在地理测量、航海、航空等领域中具有广泛的应用价值。
通过科学精确的测量和修正,我们可以准确地确定目标物体或地理点的方向,为实际应用提供可靠的数据支持。
主偏角的概念作用及选用

主偏角的概念作用及选用主偏角也被称为方位角,是指一个向量与X轴正方向之间的角度。
在数学和物理学中,主偏角的概念有着广泛的应用。
它可以帮助我们描述和分析向量的方向和位置,同时也可以在解析几何和三角函数中发挥重要作用。
在这篇文章中,我们将探讨主偏角的概念、作用及选用。
首先,我们来看一下主偏角的定义。
假设有一个向量v,那么它与X轴正方向的夹角θ就是它的主偏角。
主偏角的取值范围通常是0到360度或者-180度到180度,具体取决于所使用的坐标系。
在直角坐标系中,主偏角的定义是最为常见的,它是描述一个向量在平面内的方向的重要参数。
主偏角在几何学中有着重要的作用。
通过主偏角,我们可以描述和分析向量的方向。
当我们需要计算两个向量的夹角时,可以首先计算它们的主偏角,然后再进行进一步的分析。
另外,在解析几何中,主偏角也经常被用来描述平面内的各种图形,比如直线、圆等等。
这些都表明了主偏角在几何学中的重要性。
除了在几何学中的应用,主偏角也在三角函数中起着关键作用。
在三角函数中,我们经常要用到正弦、余弦、正切等函数,而这些函数的取值都是由主偏角来确定的。
因此,主偏角可以帮助我们计算三角函数的值,从而解决各种三角函数相关的问题。
在工程学和物理学中,三角函数的应用也是非常广泛的,因此主偏角在这些领域也有着重要的作用。
选用主偏角的时候,需要考虑一些因素。
首先,我们要明确使用的坐标系是哪一种,因为不同的坐标系对主偏角的定义和取值范围都有所不同。
其次,需要考虑需要描述的向量或图形的特点和所处的环境。
有时候,我们可能需要使用负值的主偏角,有时候则需要使用0到360度的取值范围。
最后,要根据具体问题和计算方法来选择合适的主偏角,以确保计算的准确性和可靠性。
总之,主偏角是一个重要的数学概念,它在几何学、三角函数以及工程学和物理学中都有着广泛的应用。
它可以帮助我们描述和分析向量的方向,解决各种几何学和三角函数相关的问题。
在选用主偏角的时候,需要考虑坐标系、问题的特点和计算方法等因素。
偏角 倾角 旋角

偏角倾角旋角
偏角、倾角和旋角在不同的领域中具有不同的含义。
下面是对这三个概念的介绍:- 偏角:在物理学中,偏角是指粒子在电(磁)场中速度的偏转角度。
- 倾角:在机械加工中,倾角是指刀具的主切削刃与基面的夹角。
- 旋角:在图形旋转中,旋角是指一个点与旋转中心的连线,与这个点在旋转后的对应点与旋转中心的连线,这两条线的夹角。
这些概念在不同的领域中具有不同的含义和应用,如果你想了解某个特定领域中的某个角的具体含义和应用,请提供更多的相关信息,以便我更好地为你解答。
坐标加偏角法在公路施工放样中的应用

坐标加偏角法在公路施工放样中的应用
坐标加偏角法是公路施工放样中常用的一种方法。
这种方法可以更精确地确定公路的位置和方向,以确保施工的准确性和安全性。
本文将介绍坐标加偏角法的基本概念、应用场景及其优势。
一、基本概念
坐标加偏角法是指以某个基准点为起点,在地图上用坐标表示距该基准点的距离和方向角的方法。
这种方法主要是为了定位和描述某个点或线段在一个特定的平面上的位置和方向。
在公路施工中,基准点一般是设计路线的起点或终点。
施工人员可以通过这种方法来定位公路中的各个要素,如路基、桥梁、隧道等。
二、应用场景
坐标加偏角法适用于各种地形条件下的公路施工,包括平原、山区、丘陵等。
在施工过程中,施工人员需要对道路进行较精确的放样,包括曲线的半径、切线、超高等要素。
通过坐标加偏角法,施工人员可以更加准确地测量这些要素,从而确保施工质量和安全性。
三、优势
相比于传统的放样方法,坐标加偏角法具有以下优势:
1. 提高精度:通过坐标加偏角法,施工人员可以更加准确地测量公路要素,从而提高施工的精度和准确性。
2. 提升效率:与其它放样方法相比,坐标加偏角法可以更快、更方便地完成放样工作,从而提升施工效率。
3. 降低成本:通过使用坐标加偏角法,公路施工过程中的误差可以被最大限度地减少,从而减少了额外的花费。
总之,坐标加偏角法是公路施工放样中应用广泛的一种方法。
它可以提高施工效率和精度,降低成本,为公路施工提供更加精确和安全的保障。
光学中偏角的定义

光学中偏角的定义光学中的偏角是一个重要概念,用于描述光线相对于某一参考方向的偏离程度。
在光学中,偏角可以分为入射角和出射角两种情况。
入射角是指光线与界面法线的夹角,而出射角则是光线在界面上的折射后与法线的夹角。
光学中的偏角概念是基于光的直线传播性质而建立的。
当光线从一种介质进入另一种介质时,由于介质的光密度不同,光线会发生偏折现象,即光线的传播方向发生改变。
偏角的大小和方向取决于入射光线的角度和介质的光密度。
入射角是指入射光线与界面法线之间的夹角。
根据光的反射定律,入射角和反射角相等,且位于同一平面上。
当光线从光密度较高的介质射向光密度较低的介质时,入射角大于零;而当光线从光密度较低的介质射向光密度较高的介质时,入射角小于零。
出射角是指光线在界面上折射后与法线之间的夹角。
根据斯涅尔定律,出射角和入射角之间满足折射定律的关系。
当光线从光密度较高的介质射向光密度较低的介质时,出射角大于入射角;而当光线从光密度较低的介质射向光密度较高的介质时,出射角小于入射角。
偏角的大小和方向对于光在介质之间的传播和折射过程起着重要的作用。
当光线从一种介质射向另一种介质时,入射角的改变会导致光线的传播方向发生改变,这种现象被广泛应用于透镜、棱镜、光纤等光学器件中。
通过控制入射角和出射角,可以实现对光线的聚焦、偏折和分光等功能。
除了在介质之间的传播过程中,偏角的概念也适用于光的反射现象。
当光线从光密度较高的介质射向光密度较低的介质时,入射角和反射角之间满足反射定律,光线会发生反射现象。
反射角的大小和方向取决于入射角和光密度的关系。
光学中的偏角是描述光线相对于某一参考方向的偏离程度的重要概念。
入射角和出射角分别用于描述光线在介质之间的传播和折射过程中的偏离情况。
通过控制入射角和出射角,可以实现对光线的聚焦、偏折和分光等功能,这对于光学器件和光学应用具有重要意义。
光学中的偏角概念为我们理解光的传播和反射提供了重要的工具和理论基础。
110kv铁塔允许偏角

110kv铁塔允许偏角摘要:1.110kv 铁塔的定义和作用2.铁塔的偏角概念3.110kv 铁塔允许偏角的原因4.110kv 铁塔允许偏角的标准和限制5.110kv 铁塔偏角对电力系统的影响6.结论:110kv 铁塔允许偏角的重要性和必要性正文:1.110kv 铁塔的定义和作用110kv 铁塔,全称为110 千伏高压输电铁塔,是我国高压输电系统中的一种重要设施。
其主要作用是承载高压输电线路,将发电厂产生的电能远距离传输到各个用电地区,对于保证我国电力供应的稳定和可靠具有至关重要的作用。
2.铁塔的偏角概念铁塔偏角,是指铁塔在竖直方向上的倾斜角度。
在实际建设中,由于地形、地貌、土质等多种因素的影响,铁塔很难完全垂直于地面,因此产生了偏角。
3.110kv 铁塔允许偏角的原因110kv 铁塔在设计和建设过程中,会考虑到各种自然和人为因素的影响,允许一定的偏角存在。
这是由于:首先,地形地貌的影响。
在山地、丘陵等地区,由于地形起伏大,铁塔的建设需要适应地形,允许一定的偏角可以提高铁塔的稳定性。
其次,土质的影响。
不同地区的土质差异很大,有些地区的土壤松软,有些地区的土壤坚硬,允许一定的偏角可以补偿土壤对铁塔的支持力,提高铁塔的稳定性。
最后,风力的影响。
在风力较大的地区,铁塔需要承受较大的风压力,允许一定的偏角可以提高铁塔的抗风能力。
4.110kv 铁塔允许偏角的标准和限制我国对于110kv 铁塔的偏角有一定的标准和限制。
根据《高压输电塔设计规范》的规定,110kv 铁塔的偏角应不大于5 度。
超过这个角度的偏角需要进行特殊设计和审批。
5.110kv 铁塔偏角对电力系统的影响110kv 铁塔的偏角对电力系统有一定的影响。
首先,偏角过大会影响输电线路的安全性,可能会导致输电线路断裂、短路等事故。
其次,偏角过大会影响输电线路的运行效率,可能会导致电能损耗增大。
6.结论:110kv 铁塔允许偏角的重要性和必要性综上所述,110kv 铁塔允许偏角是必要的,也是重要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9讲
教学目标:了解偏角法的概念,理解正拨、反拨的含义,掌握曲线偏角计算公式和方法。
重点难点:
5—4 一. 偏角法原理正拨 反拨
二. 偏角计算
1.圆曲线偏角
j i ,=
δ2.缓和曲线偏角
δi ,j =βi -αj i i l Rl =2
0 21β、 i i i y l x ≈)(6220
,j j i i j
i j i i j l l l l Rl x x ++=
-≈
α )2)((61
,j i j i j i l l l l Rl +-=
δ 若j 点位于i 点与缓和曲线终点之间,则同样方法可得,
)2)((61
,j i i j j i l l l l Rl +-=
δ 故其一般表达式为
)2(6||0
,j i j i j i l l Rl l l +-=
δ
若10
10 61002
10
j i l j l i Rl ===、、δ,即在缓和曲线上,曲线点号等于以10m 为单位曲线长,则 )2(||10,j i j i
j i +-=δδ
102,0δδj j =式中,R 为圆曲线半径,l 0为缓和曲线长,δ10为缓和曲线基本角。
当i 点位于缓和曲线起点时,则上式可化简为
三. 弦线长度计算
向,2至i f Z
5—5 曲线详细测设的直角坐标法
一. 直角坐标法测设曲线原理
X
轴上丈量x P ,得P'点;自P'点,沿与X 轴垂直且指向曲线内侧的方向丈量y P ,即得P 点。
直角坐标法中,坐标系X 轴均选主点的切线,故曲线点的y 坐标为相对于切线的支距。
因此,直角坐标法也称为切线支距法。
二. 曲线点坐标计算
直角坐标法所选定的坐标系通常为缓和曲线坐标系,则在该坐标系下,缓和曲线段曲线点坐标的计算公式为缓和曲线方程,圆曲线段曲线点的坐标:
⎭
⎬⎫
+-=+=p R y m
R x t t t t )cos 1(sin αα
式中0βα+-=
R
K K HY
t t ,K t 为t 点的里程,K HY 为HY 里程。
第三节 5—6 任意点极坐标法测设曲线
一. 任意点极坐标法测设曲线的原理
任意点极坐标法测设曲线的关键问题是:统一坐标系下的坐标计算;测设数据计算。
一、坐标计算
坐标系的建立主要取决于控制点的情况。
如果控制点是为测设曲线而布设的,则坐标系一般采用ZH —XY 坐标系统;如果控制点是既有控制点,则控制点所在的坐标系就是统一坐标系,即既有坐标系统。
1.ZH —X Y 测量坐标系下曲线点坐标计算
ZH~HY 段曲线点的坐标:
当曲线右偏时y A 坐标为正,左偏时y A 坐标为负。
HY ~YH 段曲线点的坐标为:
⎭
⎬⎫
+-±=+=])cos 1([sin p R y m
R x B B B B αα
式中0βα+-=
R
K K HY
B B ,曲线右偏时y B 坐标为正,左偏时y B 坐标为负。
YH~HZ 段曲线点在以HZ 点为原点,以HZ 点切线为X 轴,交点至HZ 方向为正向的测量坐标系(HZ —X'Y' )下的坐标为
式中,l C 为C 点到缓和曲线起点的曲线长;按里程增加方向,当曲线右偏时y'C 坐标为正,左偏时y'C 坐标为负。
根据坐标平移、旋转公式,将YH~HZ 段曲线点的坐标换算到ZH —XY 坐标系下,为
⎥⎦
⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡''⎥⎦⎤⎢
⎣⎡-=⎥⎦⎤⎢⎣⎡HZ HZ C C
C C y x y x y x γγ
γγcos sin sin cos 式中,γ为两坐标系X 轴间的夹角,其与线路转向角的关系是:γ=αZ 或γ= -αY ;x HZ 、y HZ
为HZ 点在ZH —XY 下的坐标,且为
3366403037
032025
⎪
⎪⎭⎪
⎪⎬⎫⎪⎪⎭⎫ ⎝⎛-±=-=l R l Rl l y l R l l x A
A A A
A A 3366403037032025
⎪
⎪⎭⎪
⎪⎬⎫⎪⎪⎭⎫ ⎝⎛-±='⎪
⎪⎭⎫ ⎝⎛--='l R l Rl l y l R l l x C
C C C C C
⎭
⎬⎫
±=+=γγsin )cos 1(T y T x HZ HZ
2.既有坐标系下曲线点坐标计算
既有坐标系下曲线点坐标计算分两步:第一步是按前述方法计算出整条曲线在ZH —XY 坐标系下的坐标;第二步是根据ZH —XY 坐标系与既有坐标系之间的关系,应用坐标平移、旋转公式,将坐标转换到既有坐标系O —XY 下。
3.控制点的坐标计算
若控制点为既有控制点,则其坐标为既有坐标;若控制点是专为测设曲线而建立的,则应测算其坐标。
如果置镜点是主点,则称为长弦偏角法。
二、测设数据计算
测设数据,即置镜点至后视点、曲线点间的坐标方位角和水平距离。
根据坐标反算的基本公式计算测设数据,
⎪⎪
⎭
⎪⎪⎬⎫-+-=--=22,,)()(i j i j j
i i
j i
j j i y y x x D x x y y tg α。
