公理、定理、推论区别与联系
高中数学八大定理和四大公理三大推论

高中数学八大定理和四大公理三大推论高中数学八大公理有:1、过两点有且只有一条直线。
2、两点之间线段最短。
3、同角或等角的补角相等。
4、同角或等角的余角相等。
5、过一点有且只有一条直线和已知直线垂直。
6、直线外一点与直线上各点连接的所有线段中,垂线段最短。
7、平行公理经过直线外一点,有且只有一条直线与这条直线平行。
8、如果两条直线都和第三条直线平行,这两条直线也互相平行。
公理是一个基本命题,它不需要根据人类理性的基本事实,经过人类长期反复实践的检验而加以证明。
在数学中,公理一词有两个相关但不同的含义,即逻辑公理和非逻辑公理。
在这两种意义上,公理都是推导其他命题的起点。
与定理不同,公理本身不是起点,而是从起点可以得到的结果,它可以简单地归类为定理,除非它是多余的,不能由其他公理推导。
补足内容:高中数学存有很多八大定理,比如立体几何八大定理、不等式八大定理、线面边线八大定理等。
直线与平面平行的认定定理:平面外的的一条直线与平面内的一条直线平行,则这条直线就与这个平面平行。
如果两个平面平行,那么其中一个平面内的任一一条直线都平行于另一个平面。
直线与平面横向的认定定理:一条直线旋转轴一个平面内的两条平行直线,则这条直线与这个平面横向。
两条平行直线中的一条旋转轴一个平面,则另一条也旋转轴这个平面。
如果两个平行平面都与第三个平面横向,则它们的交线旋转轴第三个平面。
两个平面横向,在其中一个平面内旋转轴交线的直线旋转轴另一个平面一条直线旋转轴两平行平面中的一个,一定旋转轴另一个。
平面与平面平行的认定定理:一个平面内的两条平行直线都平行于另一个平面,这两个平面平行。
旋转轴同一条直线的两个平面平行。
平行于同一个平面的两个平面平行:一个平面内的两条平行直线分别平行于另一个平面内的两条平行直线,那么这两个平面平行。
平面与平面横向的认定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面横向。
数学中 公理 定理 定义 命题的区别

数学中公理定理定义命题的区别摘要:一、引言二、数学中公理的概念与作用三、定理的概念与证明方法四、定义的用途与特点五、命题的定义与分类六、总结正文:数学是一门建立在严密逻辑基础上的学科,其中公理、定理、定义和命题是构成数学体系的重要概念。
它们在数学研究中有不同的作用,相互补充,共同推动数学的发展。
下面,我们来逐一探讨这些概念。
一、引言在数学领域,公理、定理、定义和命题等概念是紧密相连的。
了解它们之间的区别和联系有助于我们更好地理解数学的本质,从而更好地应用数学知识。
二、数学中公理的概念与作用公理是数学中一个基本的概念,它是经过长期实践检验,不需要证明的基本原理。
公理通常是对现实世界中某些现象的抽象和归纳,它们是构建数学体系的基础。
例如,欧几里得几何中的第五公设(任意两点可以作一条直线)就是一条著名的公理。
三、定理的概念与证明方法定理是数学中一个重要的概念,它是通过严密的逻辑推理,从公理或其他已知的定理中推导出来的新结论。
定理通常是数学中某个领域的基本原则或规律,它们可以用作进一步推理和证明的依据。
在证明定理时,数学家们通常会利用逻辑演绎、归纳法、反证法等方法。
四、定义的用途与特点定义是数学中对某个概念或对象赋予特定意义的表述。
定义在数学中有重要作用,它可以明确数学概念的内涵和外延,为研究和交流提供便利。
定义通常具有以下特点:简洁明了、准确描述、易于理解。
例如,直角的定义是“90 度的角”。
五、命题的定义与分类命题是数学中一个基本的概念,它是可以判断真假的陈述句。
命题在数学中有多种分类方法,可以根据命题所涉及的对象、性质、关系等进行分类。
命题在数学研究中的应用非常广泛,它可以用作证明的依据,也可以用于描述数学对象的特点。
六、总结总之,公理、定理、定义和命题在数学中具有重要的地位,它们各自承担着不同的角色,共同推动数学的发展。
定义定理公理定律的区别

定义定理公理定律的区别第一篇:定义定理公理定律的区别/ 2定义、定理、定律和定则表面上看定义、定理和定律都是由一些文字性的叙述加上数学表达式所组成,形式上确实差别不大,而老师上课往往会注重了它们在应用方面的讲授,忽略了其内在的区别和联系,造成很多学生从初中到高中甚至大学,尽管会用其去解决问题,但对三者之间的区别依然一知半解;甚至有部分教师在课堂教学中对此也存在着模糊的认识,滥用定义;误把定律当定理或者定理当定律的事情都常有发生。
下面笔者结合自己的体会,谈谈在高中物理教学中应如何讲清它们的一些特点和联系。
对于每一个概念,我们不妨先从词典里对它的解释入手来看问题,然后再辨析一下与它相近的概念,便于对比和理解。
1.定义:定义是对于一种事物的本质特征或一个概念的内涵和外延的确切而简要的说明。
如果用通俗的说法,对某个概念的“定义”告诉我们的是:“什么是”这个量,而我们常见的“物理意义”告诉我们的是:这个量“是什么”。
举个最常见的例子,如速度,定义:速度表示单位时间内通过的位移,物理意义:速度表示物体运动的快慢。
在物理学中,定义是有实际用处的,定义一个量,表面上似乎有一些任意性,但如果是为了解决生产实际的问题,那就要求定义出来的量有意义,有实际用处。
所以没有人随便找几个物理量来乘乘除除,起个名字,创造个新的物理量出来。
假设我们定义一个质点的动能和动量分别为Ek =mv3和P =,如果撇开动能定理和动量定理来说它是否正确,就没因为离开了用到它的场合,就等于失去了检验它的标准,而成为没有实际意有什么意义了,义的游戏。
而动能和动量为什么是我们熟知的Ek =mv2和P =mv呢?原因在于我们可以通过这样的定义,寻找到某种等量关系,即动能定理和动量定理,并可以运用它来帮助我们解决实际问题。
其次定义的另一个特点在于简化公式或定理,使定理的文字叙述和公式表达更易于理解和便于记忆,也使定理的物理意义更加明确。
例如:定义冲量等于力乘以力所作用时间的乘积,即I = f·t,又定义动量是物体的质量与物体速度的乘积,即P = mv,而动量定理正是I = P2 –P1,这样动量定理的表述就更加简洁明了。
初中数学-教材上的定义、公理、定理及推论

教材上的定义、公理(基本事实)、定理及推论1、直线、射线、线段定义;点动成线,线动成面,面动成体2、两点确定一条直线,两点之间线段最短3、两条直线有3种关系:重合、平行、相交4、过直线外一点,有且只有一条直线与已知直线平行5、同一平面,过一点有且只有一条直线与已知直线垂直6、垂线段最短7、两直线平行的判定定理1同一平面内,不想交的两直线平行2同位角相等,两直线平行3内错角相等,两直线平行4同旁内角互补,两直线平行5两直线与第三条直线平行,则这两直线平行6两直线与第三条直线垂直,则这两直线平行8、同角、等角、余角、补角、互补、互余定义9、邻补角定义和性质10、外角定义和性质11、对顶角相等12、角平分线定义、性质、判定1定义:从一个角的顶点引一条射线,把这个角分成两个相同的角,这条射线叫做角平分线2性质:角平分线上的点到角两边的距离相等3判定:角内部到角两边距离相等的点在这个角的平分线上13、垂直平分线(中垂线)定义、性质、判定1定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线2性质:垂直平分线上的点到线段两端点的距离相等3判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上14、三角形任意两边之和大于第三边,即最短的两条边之后大于第三边;如果三角形三条边a、b、c,则有|a-b|<c<a+b15、N边形内角和:(n-2)180,N边形外角和:360°,N边形对角线总数:n(n--3)/216、直角三角形中,30°所对的直角边是斜边的一半;直角三角形中,如果直角边是斜边的一半,那么其所对的角为30°17、三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半18、勾股定理:直角三角形中,两条直角边的平方和等于斜边平方19、勾股定理逆定理:三角形中如果两条边的平方和等于另一边的平方则该三角形为直角三角形20、三角形“四心”1三条中线的交点是重心2三边垂直平分线的交点是外心3三条内角平分线的交点为内心4三角形三条高线的交点为垂心。
定律定理和公理的区别

定律、定理和公理的区别在数学和逻辑学中,我们经常会遇到一些被称为定律、定理和公理的命题。
虽然这三个词在表达上有些类似,但它们在数学和逻辑推理中扮演着不同的角色和含义。
在本文中,我们将探讨定律、定理和公理之间的区别。
定律(Law)定律是对自然界或某一特定领域中广泛存在的简洁描述。
也可以说定律是经过实验证实和确认的自然或社会现象的总结。
定律是一种普遍适用的规律,可以被视为一种不依赖特定假设、公理或证明的自然规律或原则。
通常情况下,定律是以数学方程或公式的形式出现,用于描述已被广泛接受的事实和关系。
以牛顿运动定律为例,可以描述为:F = m \\cdot a其中,F代表物体所受的力,m代表物体的质量,a代表物体的加速度。
这个方程就是牛顿第二定律,它描述了力、质量和加速度之间的关系。
定律通常是基于大量的实验观察和验证,具有普遍的适用性,并能够描述自然界和物理现象中的普遍规律。
定理(Theorem)定理是基于一组已知条件和逻辑推理得出的结论。
定理是需要通过证明来获得的,它是由公理或已经证明的定理推导出来的命题。
定理通常是数学或逻辑上的命题,其结论可以通过逻辑推理或证明方法来推导出来。
定理一般不是直接从实际观察和实验中获得的,而是通过推理和证明逐步推导出来的。
一般情况下,定理的证明需要依赖于一些已经被证明为真的公理、定理或其他已知条件。
以费马大定理为例,这是一个著名的数论定理,经过了漫长而艰苦的证明过程,而且这个证明一直到1994年才被完成。
费马大定理是由费马提出的,经过了几个世纪的猜想和证明,最终由安德鲁·怀尔斯在1994年完成了证明。
定理是通过逻辑推理和证明方法获得的数学或逻辑命题,它们的证明过程是很重要的,因为证明过程可以让我们理解为什么定理成立。
公理(Axiom)公理是没有证明或推导的基本假设或前提条件。
公理是被视为真实的,被认为是不需要证明的基本原理。
它是逻辑推理和数学推理的起点。
公理是建立在严密的逻辑和推理基础上的,无需证明。
1.立体几何中基本概念、公理、定理、推论

立体几何中基本概念、公理、定理、推论1. 三个公理和三条推论:(1)公理1:一条直线的两点在一个平面内,那么这条直线上的所有的点都在这个平面内.这是判断直线在平面内的常用方法.(2)公理2:如果两个平面有一个公共点,它们有无数个公共点,而且这无数个公共点都在同一条直线上.这是判断几点共线(证这几点是两个平面的公共点)和三条直线共点(证其中两条直线的交点在第三条直线上)的方法之一.(3)公理3:经过不在同一直线上的三点有且只有一个平面.推论1:经过直线和直线外一点有且只有一个平面.推论2:经过两条相交直线有且只有一个平面.推论3:经过两条平行直线有且只有一个平面.公理3和三个推论是确定平面的依据.2. 直观图的画法(斜二侧画法规则):在画直观图时,要注意:(1)使045x o y '''∠=(或0135),x o y '''所确定的平面表示水平平面.(2)已知图形中平行于x 轴和z 轴的线段,在直观图中保持长度和平行性不变,平行于y 轴的线段平行性不变,但在直观图中其长度为原来的一半.3. 公理4:平行于同一直线的两直线互相平行.(即平行直线的传递性)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. (此定理说明角平移后大小不变) 若无“方向相同”,则这两个角相等或互补.4. 空间直线的位置关系:(1)相交直线――有且只有一个公共点.(2)平行直线――在同一平面内,没有公共点.(3)异面直线――不在同一平面内,也没有公共点.5. 异面直线⑴异面直线定义:不同在任何一个平面内的两条直线叫做异面直线.⑵异面直线的判定:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.⑶异面直线所成的角:已知两条异面直线a 、b ,经过空间任一点O 作直线a '、b ',使//a a '、//b b ',把a '与b '所成的锐角(或直角)叫做异面直线a 、b 所成的角(或夹角).⑷异面直线所成的角的求法:首先要判断两条异面直线是否垂直,若垂直,则它们所成的角为900;若不垂直,则利用平移法求角,一般的步骤是“作(找)—证—算”.注意,异面直线所成角的范围是π0,2⎛⎤⎥⎝⎦;求异面直线所成角的方法:计算异面直线所成角的关键是平移(中点平移,顶点平移以及补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,以便易于发现两条异面直线间的关系)转化为相交两直线的夹角. ⑸两条异面直线的公垂线:①定义:和两条异面直线都垂直且相交的直线,叫做异面直线的公垂线;两条异面直线的公垂线有且只有一条.而和两条异面直线都垂直的直线有无数条,因为空间中,垂直不一定相交.②证明:异面直线公垂线的证明常转化为证明公垂线与两条异面直线分别垂直.⑹两条异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段的长度.6. 直线与平面的位置关系:(1)直线在平面内;(2)直线与平面相交.其中,如果一条直线和平面内任何一条直线都垂直,那么这条直线和这个平面垂直.注意:任一条直线并不等同于无数条直线;(3)直线与平面平行.其中直线与平面相交、直线与平面平行都叫作直线在平面外.平面与平面的位置关系:(1)平行――没有公共点;(2)相交――有一条公共直线.7.线面平行、面面平行⑴直线与平面平行的判定定理: 如果不在一个平面(α)内的一条直线(l )和平面(α)内的一条直线(m )平行,那么这条直线(l )和这个平面(α)平行.,,////l m l m l ααα⊄⊂⇒ (作用:线线平行⇒线面平行)⑵直线与平面平行的性质定理:如果一条直线(l )和一个平面(α)平行,经过这条直线(l )的平面(β)和这个平面(α)相交(设交线是m ),那么这条直线(l )和交线(m )平行.//,,//l l m l m αβαβ⊂⋂=⇒ (作用: 线面平行⇒线线平行)⑶平面与平面平行的判定定理:如果一个平面(β)内有两条相交直线(,a b )分别平行于另一个平面(α),那么这两个平面(,βα)平行.,,,//,////a b a b P a b ββααβα⊂⊂⋂=⇒ (作用:线面平行⇒面面平行)推论:如果一个平面(β)内有两条相交直线(,a b )分别平行于另一个平面(α)内的两条直线(,a b ''), 那么这两个平面(,βα)平行.,,,,,//,////a b a b P a b a a b b ββααβα''''⊂⊂⋂=⊂⊂⇒(作用: 线线平行⇒面面平行) ⑷平面与平面平行的性质定理:如果两个平行平面(,αβ)同时与第三个平面(γ)相交(设交线分别是,a b ),那么它们的交线(,a b )平行.//,,//a b a b αβαγβγ⋂=⋂=⇒ (作用: 面面平行⇒线线平行)推论:如果两个平面(,αβ)平行,则一个平面(α)内的一条直线(a )平行于另一个平面(β). //,//a a αβαβ⊂⇒ (作用: 面面平行⇒线面平行)8.线线垂直、线面垂直、面面垂直⑴直线与平面垂直的判定定理:如果一条直线(l )和一个平面(α)内的两条相交直线(,m n )都垂直,那么这条直线(l )垂直于这个平面(α).,,,,l m l n m n m n P l ααα⊥⊥⊂⊂⋂=⇒⊥ (作用: 线线垂直⇒线面垂直)⑵直线与平面垂直的性质定理:如果一条直线(l )和一个平面(α)垂直,那么这条直线(l )和这个平面(α)内的任意一条直线(m )垂直.,l m l m αα⊥⊂⇒⊥ .⑶三垂线定理: 其作用是证两直线异面垂直和作二面角的平面角①定理: 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.②逆定理:在平面内的一条直线,如果它和这个平面的一条斜线,那么它也和这条斜线在平面内的射影垂直.(作用: 线线垂直⇒线线垂直)⑷平面与平面垂直的判定定理: 如果一个平面(α)经过另一个平面(β)的一条垂线(l ),那么这两个平面(,αβ)互相垂直.,l l βααβ⊥⊂⇒⊥ (作用: 线面垂直⇒面面垂直)⑸平面与平面垂直的性质定理:如果两个平面(,αβ)垂直,那么在一个平面(α)内垂直于它们交线(m )的直线(l )垂直于另一个平面(β).,,,m l l m l αβαβαβ⊥⋂=⊂⊥⇒⊥ (作用: 面面垂直⇒线面垂直)9. 直线和平面所成的角⑴最小角定理:平面的斜线和它在平面内的射影所成的角,是这条斜线和这个平面内任意一条直线所成的角中最小的角.满足关系式:12cos cos cos θθθ=⋅θ是平面的斜线与平面内的一条直线所成的角;1θ是平面的斜线与斜线在平面内的射影所成的角;2θ是斜线在平面内的射影与平面内的直线所成的角.⑵直线和平面所成的角: 平面的一条斜线和它在平面内的射影所成的锐角,叫这条直线和这个平面所成的角. 范围:[0,90]10.二面角⑴二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,每个半平面叫做二面角的面.棱为l ,两个面分别是α、β的二面角记为l αβ--.二面角的范围:[0,]π⑵二面角的平面角:在二面角的棱上取一点,在二面角的面内分别作两条垂直于棱的射线,这两条射线所成的角叫做二面角的平面角.11.空间距离⑴点到平面的距离:一点到它在一个平面内的正射影的距离.⑵直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离.⑶两个平行平面的距离:两个平行平面的公垂线段的长度.⑷异面直线的距离12. 多面体有关概念:(1)多面体:由若干个平面多边形围成的空间图形叫做多面体.围成多面体的各个多边形叫做多面体的面.多面体的相邻两个面的公共边叫做多面体的棱.(2)多面体的对角线:多面体中连结不在同一面上的两个顶点的线段叫做多面体的对角线.(3)凸多面体:把一个多面体的任一个面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体.13.棱柱⑴棱柱的定义: 有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫棱柱.两个互相平行的面叫棱柱的底面(简称底);其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高).⑵棱柱的分类:侧棱不垂直于底面的棱柱叫斜棱柱.侧棱垂直于底面的棱柱叫直棱柱.底面是正多边形的直棱柱叫正棱柱.棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……⑶棱柱的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等,直棱柱的各个侧面都是矩形,正棱柱的各个侧面都是全等的矩形.②与底面平行的截面是与底面对应边互相平行的全等多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.⑷平行六面体、长方体、正方体:底面是平行四边形的四棱柱是平行六面体.侧棱与底面垂直的平行六面体叫直平行六面体,底面是矩形的直平行六面体叫长方体,棱长都相等的长方体叫正方体.⑸①平行六面体的任何一个面都可以作为底面;②平行六面体的对角线交于一点,并且在交点处互相平分;③平行六面体的四条对角线的平方和等于各棱的平方和;④长方体的一条对角线的平方等于一个顶点上三条棱长的平方和.14.棱锥⑴棱锥的定义: 有一个面是多边形,其余各面是有一个公共顶点的三角形,这样的多面体叫棱锥其中有公共顶点的三角形叫棱锥的侧面;多边形叫棱锥的底面或底;各侧面的公共顶点()S ,叫棱锥的顶点,顶点到底面所在平面的垂线段()SO ,叫棱锥的高(垂线段的长也简称高).⑵棱锥的分类:(按底面多边形的边数)分别称底面是三角形,四边形,五边形……的棱锥为三棱锥,四棱锥,五棱锥…… ⑶棱锥的性质:定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积比等于顶点到截面的距离与棱锥高的平方比. 中截面:经过棱锥高的中点且平行于底面的截面,叫棱锥的中截面⑷正棱锥:底面是正多边形,顶点在底面上的射影是底面的中心的棱锥叫正棱锥. ⑸正棱锥的性质:①正棱锥的各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高(叫斜高)也相等。
公理、定理和定律的概念

公理、定理和定律的概念1、公理公理是经过人类长期反复实践的考验,是不证自明的基本事实。
公理是不需要再加证明的基本命题,是用来推导其他命题的起点。
欧几里德《几何原本》中就规定了五条公理和五条公设(以现代观点来看,公设也是公理),平面几何中的一切定理都可由这些公理和公设推导而得。
比如过相异两点,能作且只能作一直线。
2、定理定理是建立在公理和假设基础上,经过严格的推理和证明得到的,它能描述事物之间内在关系。
定理具有内在的严密性,不能存在逻辑矛盾。
比如勾股定理。
一般来说,在数学中,只有重要或有趣的陈述才叫定理。
证明定理是数学的中心活动。
相信为真但未被证明的数学叙述为猜想,当它被证明为真后便是定理。
它是定理的来源,但并非唯一来源。
一个从其他定理引伸出来的数学叙述,可以不经过证明成为猜想的过程,成为定理。
公理和定理的区别主要在于:公理的正确性不需要用逻辑推理来证明,而定理的正确性需要逻辑推理来证明。
3、定律定律是对客观事实的一种表达形式,通过大量具体的客观事实归纳而成的结论。
比如牛顿三大运动定律。
牛顿三大定律的内容和含义定律是一种理论模型,它用以描述特定情况、特定尺度下的现实世界,但在其它尺度下可能会失效或者不准确。
现在没有任何一种理论可以描述宇宙当中的所有情况。
简而言之,定律是人们通过猜想验证、通过无数次实践证明的,以特殊推导一般,以局部推导全局论断。
很多科学与哲学的发展即基于此。
简而言之,•公理:不需证明的基本命题。
•定理:用逻辑推理的方法判断为真的命题。
•定律:为实践和事实所证明,反映事物在一定条件下发展变化的客观规律。
3.区分公理和定理的不同点。

区分公理和定理的不同点。
定理和公理的区别:公理是不需要认证,大家公认的,可以直接拿来用。
而定理需要证明它是对的,才可以拿来用。
定理是经过受逻辑限制的证明为真的叙述。
一般来说,在数学中,只有重要或有趣的陈述才叫定理。
证明定理是数学的中心活动。
相信为真但未被证明的数学叙述为猜想,当它经过证明後便是定理。
它是定理的来源,但并非唯一来源。
一个从其他定理引伸出来的数学叙述可以不经过成为猜想的过程,成为定理。
公理是一个汉语词汇,读音为gōng lǐ,是指依据人类理性的不证自明的基本事实,经过人类长期反复实践的考验,不需要再加证明的基本命题。
在数学中,公理这一词被用于两种相关但相异的意思之下——逻辑公理和非逻辑公理。
在这两种意义之下,公理都是用来推导其他命题的起点。
和定理不同,一个公理(除非有冗余的)不能被其他公理推导出来,否则它就不是起点本身,而是能够从起点得出的某种结果—可以干脆被归为定理了。
(完整word)立体几何公理、定理推论汇总,推荐文档
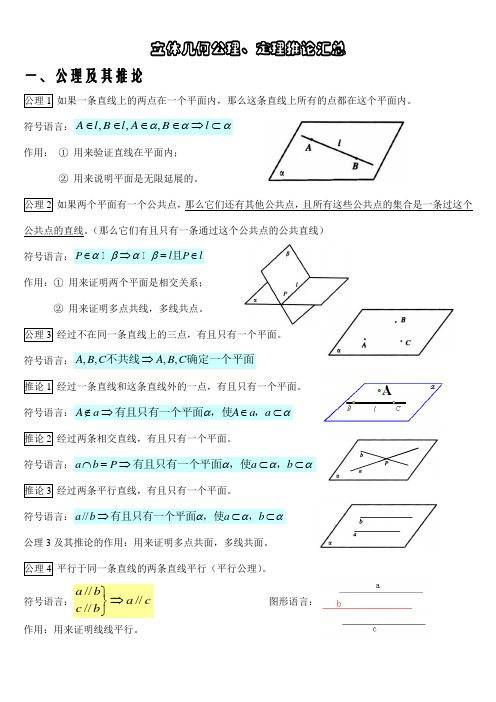
立体几何公理、定理推论汇总一、公理及其推论 公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
符号语言:,,,A l B l A B l ααα∈∈∈∈⇒⊂作用: ① 用来验证直线在平面内;② 用来说明平面是无限延展的。
公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)符号语言:P l P l αβαβ∈⇒=∈I I 且作用:① 用来证明两个平面是相交关系;② 用来证明多点共线,多线共点。
公理3 经过不在同一条直线上的三点,有且只有一个平面。
符号语言:,,,,A B C A B C ⇒不共线确定一个平面推论1 经过一条直线和这条直线外的一点,有且只有一个平面。
符号语言:A a A a a αα∉⇒∈⊂有且只有一个平面,使,推论2 经过两条相交直线,有且只有一个平面。
符号语言:a b P a b ααα⋂=⇒⊂⊂有且只有一个平面,使,推论3 经过两条平行直线,有且只有一个平面。
符号语言://a b a b ααα⇒⊂⊂有且只有一个平面,使,公理3及其推论的作用:用来证明多点共面,多线共面。
公理4 平行于同一条直线的两条直线平行(平行公理)。
符号语言://////a b a c c b ⎫⇒⎬⎭图形语言:作用:用来证明线线平行。
二、平行关系 公理4 平行于同一条直线的两条直线平行(平行公理)。
(1) 符号语言://////a b a c c b ⎫⇒⎬⎭ 图形语言:线面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(2)符号语言:////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭ 图形语言:线面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(3)符号语言:////a b a a b βαβα⎫⎪⊂⇒⎬⎪=⎭I图形语言:面面平行的判定定理 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(4)符号语言://(/,///),a b b b O a a ββαααβ⊂⊂=⎫⎪⇒⎬⎪⎭I 图形语言: 面面平行的判定 如果两个平面垂直于同一条直线,那么这两个平面平行。
数学中 公理 定理 定义 命题的区别

数学中公理定理定义命题的区别
摘要:
一、引言
二、数学中公理的定义和作用
三、数学中定理的定义和作用
四、数学中定义的定义和作用
五、数学中命题的定义和作用
六、总结
正文:
一、引言
在数学领域中,公理、定理、定义和命题是四个重要的概念,它们在数学研究和证明中起着至关重要的作用。
本文将分别介绍这四个概念的定义和作用,以帮助读者更好地理解它们在数学中的角色。
二、数学中公理的定义和作用
公理是数学中一个基本的、不需要证明的命题。
它们是数学体系的基石,通常基于直观和经验进行设定。
公理为其他命题提供了基础,并用于推导出更复杂的定理。
三、数学中定理的定义和作用
定理是数学中一个经过证明的命题。
它们基于公理和已知的定理推导得出,通常具有较高的可信度和可靠性。
定理在数学研究中起着关键作用,可以用于证明其他命题,或者用于解决实际问题。
四、数学中定义的定义和作用
定义是数学中对一个概念或对象进行的明确和规定。
定义通常基于公理和已知的事实,用于阐述一个数学概念的基本属性和特征。
定义在数学中起到澄清和规范的作用,有助于避免误解和混淆。
五、数学中命题的定义和作用
命题是数学中一个可以被判定为真或假的陈述。
命题基于公理、定理和定义进行推导,可以用于证明其他命题,或者用于构建更复杂的数学体系。
命题在数学研究中起到关键作用,是数学证明和推导的基础。
六、总结
本文详细介绍了数学中公理、定理、定义和命题的定义和作用。
立体几何公理、定理推论汇总

立体几何公理、定理推论汇总一、公理及其推论如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
符号语言:,,,A l B l A B l ααα∈∈∈∈⇒⊂ 作用: ① 用来验证直线在平面内;② 用来说明平面是无限延展的。
如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)符号语言:P l P l αβαβ∈⇒=∈且作用:① 用来证明两个平面是相交关系;②用来证明多点共线,多线共点。
经过不在同一条直线上的三点,有且只有一个平面。
符号语言:,,,,A B C A B C ⇒不共线确定一个平面经过一条直线和这条直线外的一点,有且只有一个平面。
符号语言:A a A a a αα∉⇒∈⊂有且只有一个平面,使,经过两条相交直线,有且只有一个平面。
符号语言:a b P a b ααα⋂=⇒⊂⊂有且只有一个平面,使,经过两条平行直线,有且只有一个平面。
符号语言://a b a b ααα⇒⊂⊂有且只有一个平面,使,公理3及其推论的作用:用来证明多点共面,多线共面。
平行于同一条直线的两条直线平行(平行公理)。
符号语言://////a b a c c b ⎫⇒⎬⎭图形语言: 作用:用来证明线线平行。
二、平行关系平行于同一条直线的两条直线平行(平行公理)。
(1)符号语言://// //a ba c c b⎫⇒⎬⎭图形语言:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(2)符号语言:////a baabααα⊄⎫⎪⊂⇒⎬⎪⎭图形语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(3)符号语言:////abaa bβαβα⎫⎪⊂⇒⎬⎪=⎭图形语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(4)符号语言://(/,///),abb b Oaaββαααβ⊂⊂=⎫⎪⇒⎬⎪⎭图形语言:如果两个平面垂直于同一条直线,那么这两个平面平行。
数学中 公理 定理 定义 命题的区别

数学中公理定理定义命题的区别【最新版】目录一、引言二、公理、定义、命题的区别1.公理的概念及其特点2.定义的概念及其特点3.命题的概念及其特点三、定理与定律的区别1.定理的概念及其特点2.定律的概念及其特点3.定理与定律的联系与区别四、结论正文一、引言在数学的学习和研究中,我们经常遇到一些专业术语,如公理、定义、命题、定理和定律等。
对于这些概念,我们不仅需要理解它们的意义,还要区分它们之间的差别。
本文将对这些概念进行详细解析,以帮助读者更好地理解它们。
二、公理、定义、命题的区别1.公理的概念及其特点公理是数学中的一种基本原理,它是不需要证明的、显然成立的命题。
公理通常是基于实践和观察得出的结论,它们为数学体系的建立和发展提供了基础。
公理的特点是:不言自明、无需证明、具有普遍性。
2.定义的概念及其特点定义是对一个概念或事物的准确描述,它通过列举事物的基本属性和特征来规范这个词或概念的意义。
定义的特点是:准确、简洁、明确。
在数学中,定义通常用来描述一个概念的内涵和外延,以便于理解和研究。
3.命题的概念及其特点命题是能够判断真假的陈述句,它由题设和结论两部分组成。
命题的特点是:具有判断性、可以证明或证伪。
在数学中,命题通常用来描述公理和定理之间的关系,以及它们在数学体系中的地位。
三、定理与定律的区别1.定理的概念及其特点定理是经过受逻辑限制的证明为真的陈述。
在数学中,只有重要或有趣的陈述才叫定理。
定理的特点是:有一个设定(一大堆条件),然后有一个结论(在条件下成立的数学叙述)。
通常写作若条件,则结论。
用符号逻辑来写就是条件结论。
而当中的证明不视为定理的成分。
2.定律的概念及其特点定律是对客观事实的一种表达形式,通过大量具体的客观事实归纳而成的结论。
定律是一种理论模型,它用以描述特定情况、特定尺度下的现实世界,在其它尺度下可能会失效或者不准确。
定律的特点是:具有普遍性、基于客观事实、可以部分描述现实世界。
立体几何公理定理

(一)四个公理,三个推论公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1:经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4:平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
(二)空间两直线的位置关系:1.空间两条直线只有三种位置关系:平行、相交、异面(以公共点的个数分类)2.按是否共面可分为两类:(1)共面:平行、相交(2)异面若从有无公共点的角度看可分为两类:(1)有且仅有一个公共点——相交直线;(2)没有公共点——平行或异面3.异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理:过平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角范围为( 0°,90°】两条异面直线间距离:公垂线段(有且只有一条)(三)直线和平面的位置关系:1.直线和平面只有三种位置关系:线在面内、线面相交、线面平行(以公共点的个数分类)①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点③直线与平面平行-——没有公共点2.直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角(最小角定理)。
规定:①直线与平面垂直时,所成的角为直角,②直线与平面平行或在平面内,所成的角为0角,由此得直线和平面所成角的取值范围为[0°,90°]3.三垂线定理及逆定理::如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直.直线和平面垂直(常用于证明两条异面直线垂直)4.直线和平面垂直的定义:如果一条直线阿和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直直线a叫做平面的垂线,平面叫做直线a的垂面。
定义、公理、定理、推论、命题和引理的区别

定义、公理、定理、推论、命题和引理的区别定义(definition)、公理(axiom)、定理(theorem)、推论(corollary)、命题(proposition)、引理(lemma)之间的相互关系基本如下。
首先、定义和公理是任何理论的基础,定义解决了概念的范畴,公理使得理论能够被人的理性所接受。
其次、定理和命题就是在定义和公理的基础上通过理性的加工使得理论的再延伸,我认为它们的区别主要在于,定理的理论高度比命题高些,定理主要是描述各定义(范畴)间的逻辑关系,命题一般描述的是某种对应关系(非范畴性的)。
而推论就是某一定理的附属品,是该定理的简单应用。
最后、引理就是在证明某一定理时所必须用到的其它定理。
而在一般情况下,就像前面所提到的定理的证明是依赖于定义和公理的。
WHAT IS THE DIFFERENCE BETWEEN A THEOREM(定理), A LEMMA(引理),AND A COROLLARY(推论)?PROF. DAVE RICHESON(1) Definition(定义)------a precise and unambiguous description of the meaning of a mathematical term. It characterizes the meaning of a word by giving all the properties and only those properties that must be true.(2) Theorem(定理)----a mathematical statement that is proved using rigorous mathemat-ical reasoning. In a mathematical paper, the term theorem is often reserved for the most important results.(3) Lemma(引理)----a minor result whose sole purpose is to help in proving a theorem. It is a stepping stone on the path to proving a theorem. Very occasionally lemmas can take on a life of their own (Zorn's lemma, Urysohn's lemma, Burnside'slemma,Sperner's lemma).(4) Corollary(推论)-----a result in which the (usually short) proof relies heavily on a given theorem (we often say that \this isa corollary of Theorem A").(5) Proposition(命题)-----a proved and often interesting result, but generally less important than a theorem.(6) Conjecture(推测,猜想)----a statement that is unproved, but is believed to be true (Collatz conjecture, Goldbach conjecture, twin prime conjecture).(7) Claim(断言)-----an assertion that is then proved. It is often used like an informal lemma.(8) Axiom/Postulate------(公理/假定)a statement that is assumed to be true without proof. These are the basic building blocks from which all theorems are proved (Eu-clid's ve postulates, Zermelo-Frankel axioms, Peano axioms).(9) Identity(恒等式)-----a mathematical expression giving the equality of two (often variable) quantities (trigonometric identities, Euler's identity).(10) Paradox(悖论)----a statement that can be shown, using a given set of axioms and de nitions, to be both true and false. Paradoxes are often used to show the inconsistencies in a awed theory (Russell's paradox). The term paradox is often used informally to describe a surprising or counterintuitive result that follows from a given set of rules (Banach-Tarski paradox, Alabama paradox, Gabriel's horn).。
数学中 公理 定理 定义 命题的区别

数学中的公理、定理、定义和命题是数学领域中非常重要且基础的概念。
它们在数学推理、证明和理论构建中起着至关重要的作用。
在本篇文章中,我们将深入探讨这些概念的区别和联系,并就其在数学中的重要性进行全面评估。
1. 公理公理是数学体系中最基本的、不需证明的假设或命题。
它们通常是在数学体系中的起点,其他的结论和定理都是基于这些公理推导出来的。
公理是数学体系的基石,没有公理就无法建立一个完整的数学理论体系。
公理是数学体系的基本前提,它们为数学的发展提供了必要的逻辑基础。
在几何学中,欧几里德的五个公设就是著名的公理,它们被视为几何学理论的基础。
欧几里德的第一个公设是“通过两点可以作一条直线”,这一公设被视为几何学中不需要证明的基本假设。
2. 定理定理是在给定公理或已经证明的命题的基础上,通过严密的推理和证明所得到的命题。
定理通常是数学中的重要结论,它们是基于公理和已知事实推导出来的新命题。
定理在数学推理和理论构建中扮演着重要的角色,它们扩展了数学知识的边界,推动了数学领域的进步。
费马大定理是数论领域中的一个重要定理,它是由皮耶尔·德费尔玛在17世纪提出的。
这个定理在300多年来一直是数学家们苦苦追寻的目标,直到1994年由安德鲁·怀尔斯成功证明。
费马大定理的证明不仅深刻影响了数论领域,也对整个数学领域的发展产生了重要的影响。
3. 定义定义是数学中非常重要的概念,它规定了数学对象的基本性质和特征。
定义在数学中的作用是非常突出的,它们为数学领域中的各种概念和对象确立了明确的含义和范围。
没有清晰准确的定义,就无法进行深入的数学研究和推理。
在微积分中,对于导数和积分的定义是非常重要的。
导数的定义是函数在某一点的变化率,积分的定义是曲线下方的面积,这些清晰的定义为微积分的理论和应用提供了坚实的基础。
4. 命题命题是陈述形式的有关某种性质的说法,它可以是真的,也可以是假的。
命题通常是对某个问题的断言或主张,它们可以通过推理和证明来确定其真假。
定理和公理的区别

定理和公理的区别:
公理是不能被证明,是公认的客观规律,是建立整个知识系统的基础。
定理是在一定条件下,由公理推导证明出来的的结论。
例如欧几里得的五大公理:
1.过相异两点,能作且只能作一直线(直线公理)。
2.线段(有限直线)可以任意地延长。
3.以任一点为圆心、任意长为半径,可作一圆(圆公理)。
4.凡是直角都相等(角公理)。
5.两直线被第三条直线所截,如果同侧两内角和小于两个直角,则两直线则会在该侧相交。
这五大公理是当前几何知识架构的根本,是无法被证明的,如果动
摇了任何一个公理,整个几何知识架构都要进行调整。
而定理就是以公理为基础,进行层层推导得出的结论,如:
1)过一点有且只有一条直线和已知直线垂直;
2)直线外一点与直线上各点连接的所有线段中,垂线段最短。
公理、定理、推论区别与联系

;
’. 公理与定理、推断的区别
公理:是不能被证明但确实是正确的结论,是客观规律,比如两点之间线段最短。
定理:是在一定条件下,由公理推导证明出来的正确的结论。
推论:是由公理或定理推出的结论,也可以说是一个定理,但往往推论比定理限制条件多一些。
性质:数学对象某些特征。
还有定律:通过实验数据统计的方法得到的结论,叫做定律。
其中公理、定理、推论、定律都是真命题。
物理中的原理就是公理
所有的数学证明都需要定义与公理、定理、推论。
三定理三推论

公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。
(1)判定直线在平面内的依据
(2)判定点在平面内的方法
公理2:如果两个平面有一个公共点,那它还有其它公共点,这些公共点的集合是一条直线。
(1)判定两个平面相交的依据
(2)判定若干个点在两个相交平面的交线上
公理3:经过不在同一直线上的三点,有且只有一个平面。
(1)确定一个平面的依据
(2)判定若干个点共面的依据
推论1:经过一条直线和这条直线外一点,有且仅有一个平面。
(1)判定若干条直线共面的依据
(2)判断若干个平面重合的依据
(3)判断几何图形是平面图形的依据
推论2:经过两条相交直线,有且仅有一个平面。
推论3:经过两条平行线,有且仅有一个平面。
公理4 平行于同一条直线的两条直线平行。
公理与定理

公理与定理公理与定理公理与定理是数学体系中的两个核心概念,它们在定义、证明过程以及形成方式上存在着显著的区别。
公理被视为不需要证明的基本真理,而定理则是通过逻辑推理得出的结论。
公理的定义与特性公理的特性在于其不可证性。
这意味着公理本身不能被证明,也不能被反驳。
它们构成了数学理论的基础框架,为后续的推理和证明提供了出发点。
公理的不可证性并不意味着它们是随意或主观的,相反,它们是基于长期实践经验和理性认识的基本事实。
公理在数学中的作用至关重要。
它们为数学理论提供了基础框架,确定了理论的边界和可能性。
没有公理,数学体系将失去其稳定性和一致性。
公理的选择和确定往往经过深思熟虑,以确保它们能够支撑起整个数学体系。
定理的定义与证明过程与公理不同,定理是通过逻辑推理从公理或其他已证明的定理得出的结论。
定理的验证过程需要严格的逻辑推理和证明。
证明定理是数学研究的核心活动之一,它体现了数学的严谨性和逻辑性。
定理的形成方式通常是从已知真命题出发,运用演绎推理的方法逐步推导而成。
在证明过程中,数学家们会利用公理、已知定理以及逻辑推理规则来推导出新的结论。
这些结论在逻辑上是严密的,因此具有高度的可信度。
例如,勾股定理便是一个著名的定理。
它表明在直角三角形中,直角边的平方和等于斜边的平方。
这个定理的证明过程涉及到了几何图形的性质和逻辑推理,是数学史上的一个重要里程碑。
定理在数学中的应用广泛而深入。
它们在数学体系内通过逻辑推演,揭示出更多的数学真理和规律。
这些规律不仅在数学领域内具有重要意义,还对其他学科如物理、工程等产生了深远的影响。
公理与定理的关系与互动公理与定理在数学体系中相互依存、相互促进。
公理作为不证自明的真理是理论的起点,而定理则是通过严密推理得出的结论。
公理为定理的推导提供了基础框架和出发点,而定理则进一步丰富了数学体系的内容。
在数学研究中,公理与定理的互动关系体现在多个方面。
一方面,公理的选择和确定会影响到后续定理的推导和证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
. 公理与定理、推断的区别
公理:是不能被证明但确实是正确的结论,是客观规律,比如两点之间线段最短。
定理:是在一定条件下,由公理推导证明出来的正确的结论。
推论:是由公理或定理推出的结论,也可以说是一个定理,但往往推论比定理限制条件多一些。
性质:数学对象某些特征。
还有定律:通过实验数据统计的方法得到的结论,叫做定律。
其中公理、定理、推论、定律都是真命题。
物理中的原理就是公理
所有的数学证明都需要定义与公理、定理、推论。
