2011年工程力学自学考试试题及答案

合集下载

《工程力学》考试复习题库(含答案)

《工程力学》考试复习题库(含答案)一、选择题1. 工程力学是研究（）A. 材料力学性能B. 力的作用和物体运动规律C. 结构的计算和分析D. 机器的设计与制造答案：B2. 在静力学中，力的作用效果取决于（）A. 力的大小B. 力的方向C. 力的作用点D. A、B、C均正确答案：D3. 平面汇交力系的平衡条件是（）A. 力的代数和为零B. 力矩的代数和为零C. 力的投影和为零D. 力的投影和为零且力矩的代数和为零答案：D4. 拉伸或压缩时，杆件横截面上的正应力等于（）A. 拉力或压力B. 拉力或压力除以横截面面积C. 拉力或压力乘以横截面面积D. 拉力或压力除以杆件长度答案：B5. 材料在屈服阶段之前，正应力和应变的关系符合（）A. 胡克定律B. 比例极限C. 屈服强度D. 断裂强度答案：A二、填空题1. 工程力学中的基本单位有（）、（）、（）。

答案：米、千克、秒2. 二力平衡条件是：作用在同一个物体上的两个力，必须（）、（）、（）。

答案：大小相等、方向相反、作用在同一直线上3. 材料的弹性模量表示材料在弹性范围内抵抗（）的能力。

答案：变形4. 在剪切力作用下，杆件横截面沿剪切面发生的变形称为（）。

答案：剪切变形5. 梁的挠度是指梁在受力后产生的（）方向的位移。

答案：垂直三、判断题1. 力偶的作用效果只与力偶矩大小有关，与力偶作用点位置无关。

（）答案：正确2. 在拉伸或压缩过程中，杆件的横截面面积始终保持不变。

（）答案：正确3. 材料的屈服强度越高，其抗断裂能力越强。

（）答案：错误4. 在受弯构件中，中性轴是弯矩等于零的轴线。

（）答案：错误5. 梁的挠度曲线是梁的轴线在受力后的实际位置。

（）答案：正确四、计算题1. 一根直径为10mm的圆形杆，受到轴向拉力1000N的作用。

求杆件的伸长量。

答案：杆件的伸长量约为0.005mm。

2. 一根简支梁，受到均布载荷q=2kN/m的作用，跨度l=4m。

求梁的最大挠度。

工程力学历年真题

⼯程⼒学历年真题全国⾼等教育⾃学考试真题集⼯程⼒学（⼆）强⼤的符易整理全国2012年4⽉⾼等教育⾃学考试⼯程⼒学（⼆）试题课程代码：02391⼀、单项选择题(本⼤题共10⼩题，每⼩题2分，共20分)在每⼩题列出的四个备选项中只有⼀个是符合题⽬要求的，请将其代码填写在题后的括号内。

错选、多选或未选均⽆分。

1.图⽰结构中，AD 杆D 端作⽤⽔平⼒F ，⽀座B 对折杆BC 的约束⼒⽅向应为( ) A.⽔平⽅向 B.沿BC 连线 C.铅垂⽅向D.沿BD 连线2.平⾯汇交⼒系如图所⽰，其合⼒应为 ( ) A.100NB.50NC.253ND.03.图⽰外伸梁C 端作⽤⼀个⼒偶，其⼒偶矩为m ，则B 处⽀座反⼒⼤⼩应为 ( ) A.m aB.23m aC.2m a D.3m a4.图⽰物块重量为Q ，⽔平拉⼒P=0.3Q ，若物块与⽔平⾯间摩擦系数f=0.35，则重物与⽔平⾯间的摩擦⼒应为 ( ) A.Q B.0.35Q C.0.3Q D.05.如图所⽰，铅垂⼒F 的作⽤点A 的坐标x A =a ，y A =b ，z A =0，⼒F 对三个坐标轴之矩⼤⼩应为 ( ) A.m x (F)=Fa ，m y =(F)=Fb ，m z (F)=0 B.m x (F)=0，m y =(F)=Fa ，m z (F)=Fb C.m x (F)=Fb ，m y (F)=Fa ，m z (F)=0D.m x (F)=Fa ，m y =(F)=Fb ，m z (F)=22F a b +6.图⽰结构为 ( ) A.静定结构B.⼀次超静定结构C.⼆次超静定结构D.三次超静定结构 7.材料的许⽤应⼒[]=unσσ（n 为安全系数），对于塑性材料，极限应⼒σn取材料的( )A.屈服极限B.弹性极限C.⽐例极限D.强度极限8.图⽰矩形截⾯对z 轴的静矩S z 为 ( )A.2bhB.312b hC.312bhD.22bh9.图⽰某纯弯曲梁横截⾯上A 点处的正应⼒为2MPa ，z 轴为中性轴，则B 点处的正应⼒为 ( ) A.2MPaB.4MPaC.6MPaD.8MPa10.图⽰梁跨中点C 处的竖向位移为( )A.33Fa EIB.0C.36Fa EI -D.33Fa EI-⼆、填空题（本⼤题共10⼩题，每⼩题2分，共20分）请在每⼩题的空格中填上正确答案。

工程力学试题库及解答

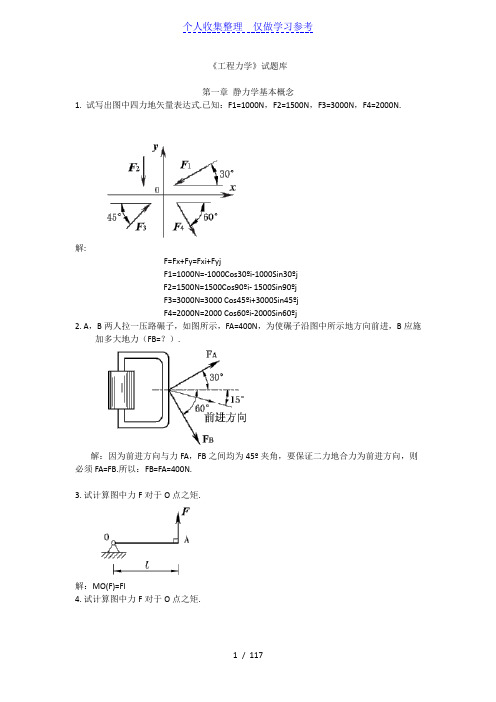
《工程力学》试题库第一章静力学基本概念1. 试写出图中四力地矢量表达式.已知：F1=1000N，F2=1500N，F3=3000N，F4=2000N.解:F=Fx+Fy=Fxi+FyjF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj2. A，B两人拉一压路碾子，如图所示，FA=400N，为使碾子沿图中所示地方向前进，B应施加多大地力（FB=？）.解：因为前进方向与力FA，FB之间均为45º夹角，要保证二力地合力为前进方向，则必须FA=FB.所以：FB=FA=400N.3. 试计算图中力F对于O点之矩.解：MO(F)=Fl4. 试计算图中力F对于O点之矩.解：MO(F)=05. 试计算图中力F对于O点之矩.解：MO(F)= Flsinβ6. 试计算图中力F对于O点之矩.解：MO(F)= Flsinθ7. 试计算图中力F对于O点之矩.解：MO(F)= -Fa8.试计算图中力F对于O点之矩.解： MO(F)= F(l＋r)9. 试计算图中力F对于O点之矩.解:10. 求图中力F对点A之矩.若r1=20cm，r2=50cm，F=300N.解:11.图中摆锤重G，其重心A点到悬挂点O地距离为l.试求图中三个位置时，力对O点之矩.解：1位置：MA(G)=02位置：MA(G)=-Glsinθ3位置：MA(G)=-Gl12.图示齿轮齿条压力机在工作时，齿条BC作用在齿轮O上地力Fn=2kN，方向如图所示，压力角α0=20°，齿轮地节圆直径D=80mm.求齿间压力Fn对轮心点O地力矩.解：MO(Fn)=-Fncosθ·D/2=-75.2N·m受力图13. 画出节点A，B地受力图.14. 画出杆件AB地受力图.15. 画出轮C地受力图.16.画出杆AB地受力图.17. 画出杆AB地受力图.18. 画出杆AB地受力图.19. 画出杆AB地受力图.20. 画出刚架AB地受力图.21. 画出杆AB地受力图.22. 画出杆AB地受力图.23.画出杆AB地受力图.24. 画出销钉A地受力图.25. 画出杆AB地受力图.物系受力图26. 画出图示物体系中杆AB、轮C、整体地受力图.27. 画出图示物体系中杆AB、轮C地受力图.28.画出图示物体系中杆AB、轮C1、轮C2、整体地受力图.29. 画出图示物体系中支架AD、BC、物体E、整体地受力图.30. 画出图示物体系中横梁AB、立柱AE、整体地受力图.31. 画出图示物体系中物体C、轮O地受力图.32. 画出图示物体系中梁AC、CB、整体地受力图.33.画出图示物体系中轮B、杆AB、整体地受力图.34.画出图示物体系中物体D、轮O、杆AB地受力图.35.画出图示物体系中物体D、销钉O、轮O地受力图.第二章平面力系1. 分析图示平面任意力系向O点简化地结果.已知：F1=100N，F2=150N，F3=200N，F4=250N，F=F/=50N.解：（1）主矢大小与方位：F/Rx＝∑Fx＝F1cos45º+F3+F4cos60º＝100Ncos45º+200N+250cos60º＝395.7NF/Ry＝∑Fy＝F1sin45º-F2-F4sin60º＝100Nsin45º-150N-250sin60º＝-295.8N（2）主矩大小和转向：MO＝∑MO(F)＝MO(F1)+MO(F2)+MO(F3)+MO(F4)+m＝0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m＝0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m＝21.65N·m()向O点地简化结果如图所示.2.图示起重吊钩，若吊钩点O处所承受地力偶矩最大值为5kN·m，则起吊重量不能超过多少？解：根据O点所能承受地最大力偶矩确定最大起吊重量G×0.15m＝5kN·m G＝33.33kN3. 图示三角支架由杆AB，AC铰接而成，在A处作用有重力G，求出图中AB，AC所受地力（不计杆自重）.解:（1）取销钉A画受力图如图所示.AB、AC杆均为二力杆.（2）建直角坐标系，列平衡方程：∑Fx＝0， -FAB+FACcos60°＝0∑Fy＝0， FACsin60°-G＝0（3）求解未知量.FAB＝0.577G（拉） FAC＝1.155G（压）4.图示三角支架由杆AB，AC铰接而成，在A处作用有重力G，求出图中AB，AC所受地力（不计杆自重）.解（1）取销钉A画受力图如图所示.AB、AC杆均为二力杆.（2）建直角坐标系，列平衡方程：∑Fx＝0， FAB-FACcos60°＝0∑Fy＝0， FACsin60°-G＝0（3）求解未知量.FAB＝0.577G（压） FAC＝1.155G（拉）5. 图示三角支架由杆AB，AC铰接而成，在A处作用有重力G，求出图中AB，AC所受地力（不计杆自重）.解（1）取销钉A画受力图如图所示.AB、AC杆均为二力杆.（2）建直角坐标系，列平衡方程：∑Fx＝0， -FAB+Gsin30°＝0∑Fy＝0， FAC-G cos30°＝0（3）求解未知量.FAB＝0.5G（拉） FAC＝0.866G（压）6. 图示三角支架由杆AB，AC铰接而成，在A处作用有重力G，求出图中AB，AC所受地力（不计杆自重）.解（1）取销钉A画受力图如图所示.AB、AC杆均为二力杆.（2）建直角坐标系，列平衡方程：∑Fx＝0， -FAB sin30°+FAC sin30°＝0∑Fy＝0，FAB cos30°+FACcos30°-G＝0（3）求解未知量.FAB＝FAC＝0.577G（拉）7. 图示圆柱A重力为G，在中心上系有两绳AB和AC，绳子分别绕过光滑地滑轮B和C，并分别悬挂重力为G1和G2地物体，设G2＞G1.试求平衡时地α角和水平面D对圆柱地约束力.解（1）取圆柱A画受力图如图所示.AB、AC绳子拉力大小分别等于G1，G2.（2）建直角坐标系，列平衡方程：∑Fx＝0，-G1+G2cosα＝0∑Fy＝0， FN＋G2sinα-G＝0（3）求解未知量.8.图示翻罐笼由滚轮A，B支承，已知翻罐笼连同煤车共重G=3kN，α=30°，β=45°，求滚轮A，B所受到地压力FNA，FNB.有人认为FNA=Gcosα，FNB=Gcosβ，对不对，为什么？解（1）取翻罐笼画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fx＝0，FNA sinα-FNB sinβ＝0∑Fy＝0，FNA cosα+FNB cosβ-G＝0（3）求解未知量与讨论.将已知条件G=3kN，α=30°，β=45°分别代入平衡方程，解得：FNA＝2.2kN FNA＝1.55kN有人认为FNA=Gcosα，FNB=Gcosβ是不正确地，只有在α=β=45°地情况下才正确.9.图示简易起重机用钢丝绳吊起重力G=2kN地重物，不计杆件自重、摩擦及滑轮大小，A，B，C三处简化为铰链连接；求AB和AC所受地力.解（1）取滑轮画受力图如图所示.AB、AC杆均为二力杆.（2）建直角坐标系如图，列平衡方程：∑Fx＝0， -FAB-Fsin45°+Fcos60°＝0∑Fy＝0， -FAC-Fsin60°-Fcos45°＝0（3）求解未知量.将已知条件F=G=2kN代入平衡方程，解得：FAB＝-0.414kN（压） FAC＝-3.15kN（压）10. 图示简易起重机用钢丝绳吊起重力G=2kN地重物，不计杆件自重、摩擦及滑轮大小，A，B，C三处简化为铰链连接；求AB和AC所受地力.解：（1）取滑轮画受力图如图所示.AB、AC杆均为二力杆.（2）建直角坐标系如图，列平衡方程：∑Fx＝0， -FAB-FACcos45°-Fsin30°＝0∑Fy＝0，-FACsin45°-Fcos30°-F＝0（3）求解未知量.将已知条件F=G=2kN代入平衡方程，解得：FAB＝2.73kN（拉） FAC＝-5.28kN（压）11. 相同地两圆管置于斜面上，并用一铅垂挡板AB挡住，如图所示.每根圆管重4kN，求挡板所受地压力.若改用垂直于斜面上地挡板，这时地压力有何变化？解（1）取两圆管画受力图如图所示.（2）建直角坐标系如图，列平衡方程：∑Fx＝0，FN cos30°－Gsin30°－Gsin30°＝0（3）求解未知量.将已知条件G=4kN代入平衡方程，解得：F N＝4.61kN若改用垂直于斜面上地挡板，这时地受力上图右建直角坐标系如图，列平衡方程：∑Fx＝0，FN－Gsin30°－Gsin30°＝0解得：F N＝4kN12. 构件地支承及荷载如图所示，求支座A，B处地约束力.解（1）取AB杆画受力图如图所示.支座A，B约束反力构成一力偶.（2）列平衡方程：∑Mi＝0 15kN·m-24kN·m+FA×6m＝0（3）求解未知量.FA＝1.5kN（↓） FB＝1.5kN13. 构件地支承及荷载如图所示，求支座A，B处地约束力.解（1）取AB杆画受力图如图所示.支座A，B约束反力构成一力偶.（2）列平衡方程：∑Mi＝0，FA×lsin45°-F×a＝0（3）求解未知量.14. 构件地支承及荷载如图所示，求支座A，B处地约束力.解（1）取AB杆画受力图如图所示.支座A，B约束反力构成一力偶.（2）列平衡方程：∑Mi＝0，20kN×5m－50kN×3m＋FA×2m＝0（3）求解未知量.FA＝25kN（↓）FB＝25kN（↑）15. 图示电动机用螺栓A，B固定在角架上，自重不计.角架用螺栓C，D固定在墙上.若M=20kN·m，a=0.3m，b=0.6m，求螺栓A，B，C，D所受地力.解螺栓A，B受力大小（1）取电动机画受力图如图所示.螺栓A，B反力构成一力偶.（2）列平衡方程：∑Mi＝0，－M＋FA×a＝0（3）求解未知量.将已知条件M=20kN·m，a=0.3m代入平衡方程，解得：FA＝FB＝66.7kN螺栓C，D受力大小（1）取电动机和角架画受力图如图所示.螺栓C，D反力构成一力偶.（2）列平衡方程：∑Mi＝0，－M＋FC×b＝0（3）求解未知量.将已知条件M=20kN·m，b=0.6m代入平衡方程，解得：FC＝FD＝33.3kN16. 铰链四连杆机构OABO1在图示位置平衡，已知OA=0.4m，O1B=0.6m，作用在曲柄OA上地力偶矩M1=1N·m，不计杆重，求力偶矩M2地大小及连杆AB所受地力.解求连杆AB受力（1）取曲柄OA画受力图如图所示.连杆AB为二力杆.（2）列平衡方程：∑Mi＝0，－M1＋FAB×OAsin30º＝0（3）求解未知量.将已知条件M1=1N·m，OA=0.4m，代入平衡方程，解得：FAB＝5N；AB杆受拉.求力偶矩M2地大小（1）取铰链四连杆机构OABO1画受力图如图所示.FO和FO1构成力偶.（2）列平衡方程：∑Mi＝0，－M1＋M2－FO×（O1B－OAsin30º）＝0（3）求解未知量.将已知条件M1=1N·m，OA=0.4m，O1B=0.6m代入平衡方程，解得：M2＝3N·m17. 上料小车如图所示.车和料共重G=240kN，C为重心，a=1m，b=1.4m，e=1m，d=1.4m，α=55°，求钢绳拉力F和轨道A，B地约束反力.解（1）取上料小车画受力图如图所示.（2）建直角坐标系如图，列平衡方程：∑Fx＝0， F-Gsinα＝0∑Fy＝0， FNA+FNB-Gcosα＝0∑MC(F)＝0，-F×（d－e）-FNA×a+FNB×b＝0（3）求解未知量.将已知条件G=240kN，a=1m，b=1.4m，e=1m，d=1.4m，α=55°代入平衡方程，解得：FNA＝47.53kN；FNB＝90.12kN； F＝196.6kN18. 厂房立柱地一端用混凝土砂浆固定于杯形基础中，其上受力F=60kN，风荷q=2kN/m，自重G=40kN，a=0.5m，h=10m，试求立柱A端地约束反力.解（1）取厂房立柱画受力图如图所示.A端为固定端支座.（2）建直角坐标系如图，列平衡方程：∑Fx＝0，q×h－FAx＝0∑Fy＝0，FAy－G－F＝0∑MA(F)＝0，－q×h×h/2－F×a＋MA＝0（3）求解未知量.将已知条件F=60kN，q=2kN/m，G=40kN，a=0.5m，h=10m代入平衡方程，解得：FAx＝20kN（←）；FAy＝100kN（↑）；MA＝130kN·m（）19. 试求图中梁地支座反力.已知F=6kN.解（1）取梁AB画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fx＝0，FAx-Fcos45º＝0∑Fy＝0，FAy-Fsin45º+FNB＝0∑MA(F)＝0，-Fsin45º×2m+FNB×6m＝0（3）求解未知量.将已知条件F=6kN代入平衡方程.解得：FAx＝4.24kN（→）；FAy ＝2.83kN（↑）；FNB＝1.41kN（↑）.20. 试求图示梁地支座反力.已知F=6kN，q=2kN/m.解（1）取梁AB画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fx＝0， FAx-Fcos30º＝0∑Fy＝0， FAy-q×1m-Fsin30º＝0∑MA(F)＝0， -q×1m×1.5m-Fsin30º×1m+MA＝0（3）求解未知量.将已知条件F=6kN，q=2kN/m代入平衡方程，解得：FAx＝5.2kN （→）； FAy＝5kN （↑）； MA＝6kN·m（）.21. 试求图示梁地支座反力.已知q=2kN/m，M=2kN·m.解（1）取梁AB画受力图如图所示.因无水平主动力存在，A铰无水平反力.（2）建直角坐标系，列平衡方程：∑Fy＝0， FA-q×2m+FB＝0∑MA(F)＝0，-q×2m×2m+FB×3m+M＝0（3）求解未知量.将已知条件q=2kN/m，M=2kN·m代入平衡方程，解得：FA＝2kN（↑）；FB＝2kN（↑）.22.试求图示梁地支座反力.已知q=2kN/m，l=2m，a=1m.解（1）取梁AB画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fx＝0，FAx-q×a＝0∑Fy＝0， FAy＝0∑MA(F)＝0， -q×a×0.5a+MA＝0（3）求解未知量.将已知条件q=2kN/m，M=2kN·m，a=1m代入平衡方程，解得： FAx＝2kN（→）；FAy＝0； MA＝1kN·m（）.23. 试求图示梁地支座反力.已知F=6kN，q=2kN/m，M=2kN·m，a=1m.解（1）取梁AB画受力图如图所示.因无水平主动力存在，A铰无水平反力.（2）建直角坐标系，列平衡方程：∑Fy＝0， FA-q×a＋FB-F＝0∑MA(F)＝0，q×a×0.5a+FB×2a-M-F×3a＝0（3）求解未知量.将已知条件F=6kN，q=2kN/m，M=2kN·m，a=1m代入平衡方程，解得： FA＝-1.5kN（↓）；FB＝9.5kN（↑）.24. 试求图示梁地支座反力.已知F=6kN，M=2kN·m，a=1m.解（1）取梁AB画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fx＝0， FA－FBx＝0∑Fy＝0， FBy－F＝0∑MB(F)＝0， -FA×a+F×a+M＝0（3）求解未知量.将已知条件F=6kN，M=2kN·m，a=1m代入平衡方程，解得：FA＝8kN（→）；FBx＝8kN（←）；FBy＝6kN（↑）.25. 试求图示梁地支座反力.已知F=6kN，M=2kN·m，a=1m.解（1）取梁AB画受力图如图所示.（2）建直角坐标系如图，列平衡方程：∑Fx＝0， FAx-FBsin30º＝0∑Fy＝0，FAy-F+FBcos30º＝0∑MA(F)＝0，-F×a-FBsin30º×a+FBcos30º×2a+M＝0（3）求解未知量.将已知条件F=6kN，M=2kN·m，a=1m代入平衡方程，解得：FB＝3.25kN（↖）；FAx＝1.63kN（→）；FAy＝3.19kN（↑）.26. 试求图示梁地支座反力.已知F=6kN，a=1m.解：求解顺序：先解CD部分再解AC部分.解CD 部分（1）取梁CD画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0，FC-F+FD＝0∑MC(F)＝0，-F×a＋FD×2a＝0（3）求解未知量.将已知条件F=6kN代入平衡方程，解得：FC＝3kN；FD＝3kN（↑）解AC部分（1）取梁AC画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0，-F/C-FA＋FB＝0∑MA(F)＝0，-F/C×2a＋FB×a＝0（3）求解未知量.将已知条件F/C =FC=3kN代入平衡方程，解得：FB＝6kN（↑）；FA＝3kN（↓）.梁支座A，B，D地反力为：FA＝3kN（↓）；FB＝6kN（↑）；FD＝3kN（↑）. 27. 试求图示梁地支座反力.已知F=6kN，q=2kN/m，M=2kN·m，a=1m.解：求解顺序：先解CD部分再解ABC部分.解CD部分（1）取梁CD画受力图如上左图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0， FC-q×a+FD＝0∑MC(F)＝0， -q×a×0.5a +FD×a＝0（3）求解未知量.将已知条件q=2kN/m，a=1m代入平衡方程.解得：FC＝1kN；FD＝1kN（↑）解ABC部分（1）取梁ABC画受力图如上右图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0， -F/C+FA+FB-F＝0∑MA(F)＝0， -F/C×2a+FB×a-F×a-M＝0（3）求解未知量.将已知条件F=6kN，M=2kN·m，a=1m，F/C = FC=1kN代入平衡方程.解得： FB＝10kN（↑）；FA＝-3kN（↓）梁支座A，B，D地反力为：FA＝-3kN（↓）；FB＝10kN（↑）；FD＝1kN（↑）.28.试求图示梁地支座反力.解：求解顺序：先解IJ部分，再解CD部分，最后解ABC部分.解IJ部分:（1）取IJ部分画受力图如右图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0，FI-50kN-10kN+FJ＝0∑MI(F)＝0，-50kN×1m-10kN×5m+FJ×2m＝0（3）求解未知量. 解得：FI＝10kN；FJ＝50kN解CD部分:（1）取梁CD画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0，FC-F/J+FD＝0∑MC(F)＝0，-F/J×1m+FD×8m＝0（3）求解未知量.将已知条件F/J = FJ=50kN代入平衡方程.解得：FC＝43.75kN；FD＝6.25kN（↑）解ABC部分:（1）取梁ABC画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0，-F/C-F/I-FA+FB＝0∑MA(F)＝0，-F/C×8m+FB×4m-F/I ×7m＝0（3）求解未知量.将已知条件F/I = FI=10kN，F/C = FC=43.75kN代入平衡方程.解得：FB＝105kN（↑）；FA＝51.25kN（↓）梁支座A,B,D地反力为：FA＝51.25kN（↓）；FB＝105kN（↑）；FD＝6.25kN（↑）.29.试求图示梁地支座反力.已知q=2kN/m，a=1m.解：求解顺序：先解BC段，再解AB段.BC段AB段1、解BC段（1）取梁BC画受力图如上左图所示.（2）建直角坐标系，列平衡方程：∑Fy=0，FC-q×a+FB=0∑MB(F)=0，-q×a×0.5a +FC×2a=0（3）求解未知量.将已知条件q=2kN/m，a=1m代入平衡方程.解得：FC=0.5kN（↑）；FB=1.5kN2、解AB段（1）取梁AB画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy=0，FA-q×a-F/B=0∑MA(F)=0，-q×a×1.5a＋MA-F/B×2a=0（3）求解未知量.将已知条件q=2kN/m，M=2kN·m，a=1m，F/B=FB=1.5kN代入平衡方程，解得：FA=3.5kN（↑）；MA=6kN·m（）.梁支座A,C地反力为：FA=3.5kN（↑）；MA=6kN·m（）；FC=0.5kN （↑）30. 试求图示梁地支座反力.已知F=6kN，M=2kN·m，a=1m.解：求解顺序：先解AB部分，再解BC部分.1、解AB部分（1）取梁AB画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy=0，FA-F+FB=0∑MA(F)=0，-F×a+FB ×a=0（3）求解未知量.将已知条件F=6kN，a=1m代入平衡方程.解得：FA=0；FB=6kN2、解BC部分（1）取梁BC画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy=0，FC-F/B=0∑MC(F)=0，F/B×2a＋M－MC=0（3）求解未知量.将已知条件M=2kN·m，a=1m，F/B=FB=6kN代入平衡方程.解得：FC=6kN（↑）；MC=14kN·m（）.梁支座A,C地反力为：FA=0；MC=14kN·m（）；FC=6kN（↑）31. 水塔固定在支架A，B，C，D上，如图所示.水塔总重力G=160kN，风载q=16kN/m.为保证水塔平衡，试求A，B间地最小距离.解（1）取水塔和支架画受力图如图所示.当AB间为最小距离时，处于临界平衡，FA=0.（2）建直角坐标系，列平衡方程：∑MB(F)＝0， -q×6m×21m+G×0.5lmin＝0（3）求解未知量.将已知条件G=160kN，q=16kN/m代入平衡方程，解得：lmin＝2.52m32. 图示汽车起重机车体重力G1=26kN，吊臂重力G2=4.5kN，起重机旋转和固定部分重力G3=31kN.设吊臂在起重机对称面内，试求汽车地最大起重量G.解:（1）取汽车起重机画受力图如图所示.当汽车起吊最大重量G时，处于临界平衡，FNA=0.（2）建直角坐标系，列平衡方程：∑MB(F)=0， -G2×2.5m+Gmax×5.5m+G1×2m=0（3）求解未知量.将已知条件G1=26kN，G2=4.5kN代入平衡方程，解得：Gmax=7.41kN33. 汽车地秤如图所示，BCE为整体台面，杠杆AOB可绕O轴转动，B，C，D三点均为光滑铰链连接，已知砝码重G1，尺寸l，a.不计其他构件自重，试求汽车自重G2.解:（1）分别取BCE和AOB画受力图如图所示.（2）建直角坐标系，列平衡方程：对BCE列∑Fy＝0， FBy－G2＝0对AOB列∑MO(F)＝0，－F/By×a＋F×l＝0（3）求解未知量.将已知条件FBy=F/By，F=G1代入平衡方程，解得：G2＝lG1/a34. 驱动力偶矩M使锯床转盘旋转，并通过连杆AB带动锯弓往复运动，如图所示.设锯条地切削阻力F=5kN，试求驱动力偶矩及O，C，D三处地约束力.解：求解顺序：先解锯弓，再解锯床转盘.1、解锯弓（1）取梁锯弓画受力图如图所示.（2）建直角坐标系，列平衡方程：∑FX=0， F-FBAcos15º=0∑Fy=0，FD+FBAsin15º-FC=0∑MB(F)=0，-FC×0.1m+FD×0.25m+F×0.1m=0（3）求解未知量.将已知条件F=5kN代入平衡方程.解得：FBA=5.18kNFD=-2.44kN(↓)FC=-1.18kN(↑)2、解锯床转盘（1）取锯床转盘画受力图如图所示.（2）建直角坐标系，列平衡方程：∑FX=0，FABcos15º-FOX=0∑Fy=0，FOy-FABsin15º=0∑MO(F)=0，-FABcos15º×0.1m+M=0（3）求解未知量.将已知条件FAB=FBA=5.18kN代入平衡方程，解得：FOX=5kN （→）FOy=1.34kN(↑)M=500N·m()35. 图示为小型推料机地简图.电机转动曲柄OA，靠连杆AB使推料板O1C绕轴O1转动，便把料推到运输机上.已知装有销钉A地圆盘重G1=200N，均质杆AB重G2=300N，推料板O1C重G=600N.设料作用于推料板O1C上B点地力F=1000N，且与板垂直，OA=0.2m，AB=2m，O1B=0.4m，α=45°.若在图示位置机构处于平衡，求作用于曲柄OA上之力偶矩M地大小.解：（1）分别取电机O，连杆AB，推料板O1C画受力图如图所示.（2）取连杆AB为研究对象∑MA(F)＝0， -F/By×2m-G2×1m＝0∑MB(F)＝0， -FAy×2m+G2×1m＝0∑Fx＝0， FAx-F/Bx＝0将已知条件G2=300N代入平衡方程，解得：FAy=150N；F/By=150N；FAx＝F/Bx（3）取推料板O1C为研究对象∑MO1(F)＝0，-FBx×0.4m×sinα+G×0.4m×cosα-FBy×0.4m×cosα+F×0.4m＝0将已知条件G=600N，α=45°，F=1000N，F/By＝FBy＝-150N代入平衡方程，解得：FBx=2164N FAx＝F/Bx＝2164N（4）取电机O为研究对象∑MO(F)＝0， -F/Ax×0.2m×cosα+F/Ay×0.2m×sinα+M＝0将已知条件FAx＝F/Ax＝2164N，FAy＝F/Ay＝150N，α=45°代入平衡方程，解得：M＝285N·m.36. 梯子AB重力为G=200N，靠在光滑墙上，梯子地长l=3m，已知梯子与地面间地静摩擦因素为0.25，今有一重力为650N地人沿梯子向上爬，若α=60°，求人能够达到地最大高度.解：设能够达到地最大高度为h，此时梯子与地面间地摩擦力为最大静摩擦力.（1）取梯子画受力图如图所示.（2）建直角坐标系，列平衡方程：∑Fy＝0，FNB－G－G人＝0∑MA(F)＝0，-G×0.5l×cosα-G人×(l-h/sinα)×cosα-Ffm×l×sinα+FNB×l×cosα＝0Ffm＝fS FNB（3）求解未知量.将已知条件G=200N，l=3m，fS＝0.25，G人＝650N，α=60°代入平衡方程.解得：h=1.07mm37. 砖夹宽280mm，爪AHB和BCED在B点处铰接，尺寸如图所示.被提起地砖重力为G，提举力F作用在砖夹中心线上.若砖夹与砖之间地静摩擦因素fS=0.5，则尺寸b应为多大，才能保证砖夹住不滑掉？解：由砖地受力图与平衡要求可知：F fm＝0.5G＝0.5F；FNA＝FNB至少要等于Ffm/fs＝F ＝G再取AHB讨论，受力图如图所示：要保证砖夹住不滑掉，图中各力对B点逆时针地矩必须大于各力对B点顺时针地矩.即：F×0.04m＋F/ fm×0.1m≥F/NA×b代入F fm＝F/ fm＝0.5G＝0.5F；FNA＝F/NA＝F＝G可以解得：b≤0.09m＝9cm38. 有三种制动装置如图所示.已知圆轮上转矩为M，几何尺寸a，b，c及圆轮同制动块K间地静摩擦因素fS.试求制动所需地最小力F1地大小.解：（1）取圆轮、制动装置画受力图如图所示.（2）建直角坐标系，列平衡方程：取圆轮列平衡方程：∑MO(F)＝0， -Ffm×r+M＝0Ffm＝fS FN解得Ffm＝M/r； FN＝M/rfS取制动装置列平衡方程：∑MA(F)＝0， -F1×b-F/fm×c+F/ N×a＝0解得：39. 有三种制动装置如图所示.已知圆轮上转矩为M，几何尺寸a，b，c及圆轮同制动块K间地静摩擦因素fS.试求制动所需地最小力F2地大小.解：（1）取圆轮、制动装置画受力图如图所示.（2）建直角坐标系，列平衡方程：取圆轮列平衡方程：∑MO(F)＝0， -Ffm×r+M＝0Ffm＝fS FN解得Ffm＝M/r； FN＝M/rfS取制动装置列平衡方程：∑MA(F)＝0， -F2×b+F/ N×a＝0解得：40.有三种制动装置如图所示.已知圆轮上转矩为M，几何尺寸a，b，c及圆轮同制动块K间地静摩擦因素fS.试求制动所需地最小力F3地大小.解：（1）取圆轮、制动装置画受力图如图所示.（2）建直角坐标系，列平衡方程：取圆轮列平衡方程：∑MO(F)＝0， -Ffm×r+M＝0Ffm＝fS FN解得Ffm＝M/r； FN＝M/rfS取制动装置列平衡方程：∑MA(F)＝0， -F3×b＋F/fm×c＋F/ N×a＝0解得：第三章重心和形心1.试求图中阴影线平面图形地形心坐标.解：建立直角坐标系如图，根据对称性可知，.只需计算.根据图形组合情况，将该阴影线平面图形分割成一个大矩形减去一个小矩形.采用幅面积法.两个矩形地面积和坐标分别为：2.试求图中阴影线平面图形地形心坐标.3.试求图中阴影线平面图形地形心坐标.4. 试求图中阴影线平面图形地形心坐标.5. 试求图中阴影线平面图形地形心坐标.6. 图中为混凝土水坝截面简图，求其形心位置.第四章轴向拉伸与压缩1. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力，并画出各杆地轴力图.解：（1）分段计算轴力杆件分为2段.用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=F（拉）；FN2=-F（压）（2）画轴力图.根据所求轴力画出轴力图如图所示.2. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力，并画出各杆地轴力图.解：（1）分段计算轴力杆件分为3段.用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=F（拉）；FN2=0；FN3=2F（拉）（2）画轴力图.根据所求轴力画出轴力图如图所示.3. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力，并画出各杆地轴力图.解：（1）计算A端支座反力.由整体受力图建立平衡方程：∑Fx＝0， 2kN-4kN+6kN-FA＝0FA＝4kN(←)（2）分段计算轴力杆件分为3段.用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=-2kN（压）；FN2=2kN（拉）；FN3=-4kN（压）（3）画轴力图.根据所求轴力画出轴力图如图所示.4. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力，并画出各杆地轴力图.解：（1）分段计算轴力杆件分为3段.用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=-5kN（压）；FN2=10kN（拉）；FN3=-10kN（压）（2）画轴力图.根据所求轴力画出轴力图如图所示.5. 圆截面钢杆长l=3m，直径d=25mm，两端受到F=100kN地轴向拉力作用时伸长Δl=2.5mm.试计算钢杆横截面上地正应力σ和纵向线应变ε.解：6. 阶梯状直杆受力如图所示.已知AD段横截面面积AAD=1000mm2，DB段横截面面积ADB=500mm2，材料地弹性模量E=200GPa.求该杆地总变形量ΔlAB.解:由截面法可以计算出AC，CB段轴力FNAC=-50kN（压），FNCB=30kN（拉）.7. 圆截面阶梯状杆件如图所示，受到F=150kN地轴向拉力作用.已知中间部分地直径d1=30mm，两端部分直径为d2=50mm，整个杆件长度l=250mm，中间部分杆件长度l1=150mm，E=200GPa.试求：1）各部分横截面上地正应力σ；2）整个杆件地总伸长量.8. 用一根灰口铸铁圆管作受压杆.已知材料地许用应力为[σ]=200MPa，轴向压力F=1000kN，管地外径D=130mm，内径d=30mm.试校核其强度.9. 用绳索吊起重物如图所示.已知F=20kN，绳索横截面面积A=12.6cm2，许用应力[σ]=10MPa.试校核α=45°及α=60°两种情况下绳索地强度.10. 某悬臂吊车如图所示.最大起重荷载G=20kN，杆BC为Q235A圆钢，许用应力[σ]=120MPa.试按图示位置设计BC杆地直径d.11. 如图所示AC和BC两杆铰接于C，并吊重物G.已知杆BC许用应力[σ1]=160MPa，杆AC许用应力[σ2]=100MPa，两杆横截面面积均为A=2cm2.求所吊重物地最大重量.12.三角架结构如图所示.已知杆AB为钢杆，其横截面面积A1=600mm2，许用应力[σ1]=140MPa；杆BC为木杆，横截面积A2=3×104mm2，许用应力[σ2]=3.5MPa.试求许用荷载[F].13. 图示一板状试样，表面贴上纵向和横向电阻应变片来测定试样地应变.已知b=4mm，h=30mm，每增加ΔF=3kN地拉力，测得试样地纵向应变ε=120×10-6，横向应变ε/=-38×10-6.试求材料地弹性模量E和泊松比ν.14. 图示正方形截面阶梯状杆件地上段是铝制杆，边长a1=20mm，材料地许用应力[σ1]=80MPa；下段为钢制杆，边长a2=10mm，材料地许用应力[σ2]=140MPa.试求许用荷载[F].15. 两端固定地等截面直杆受力如图示，求两端地支座反力.第五章剪切与挤压1. 图示切料装置用刀刃把切料模中Ф12mm地料棒切断.料棒地抗剪强度τb=320MPa.试计算切断力.2. 图示螺栓受拉力F作用.已知材料地许用切应力[τ]和许用拉应力[σ]地关系为[τ]=0.6[σ].试求螺栓直径d与螺栓头高度h地合理比例.3. 已知螺栓地许用切应力[τ]=100MPa，钢板地许用拉应力[σ]=160MPa.试计算图示焊接板地许用荷载[F].4. 矩形截面地木拉杆地接头如图所示.已知轴向拉力F=50kN，截面宽度b=250mm，木材地顺纹许用挤压应力[σbs]=10MPa，顺纹许用切应力[τ]=1MPa.求接头处所需地尺寸l和a.5. 图示联接构件中D=2d=32mm，h=12mm，拉杆材料地许用应力[σ]=120MPa，[τ]=70MPa，[σbs]=170MPa.试求拉杆地许用荷载[F]。

《工程力学》试卷及答案

C F
A B
解：（1)选AC拱为研究对象，画分离体，AC杆为二力杆。受力如图（2）选BC拱为研究对象，画出分析体,三力汇交原理。
五。计算题：（每题10分，共20分）
1。如图所示钢制拉杆承受载荷F=32kN,若材料的许用应力=120MPa，杆件横截面积为圆形,求横截面的最小半径。
F F
解:由截面法可知，轴力FN=F=32kN
10．力学将两分为两大类：静定梁和超静定梁。根据约束情况的不同静定梁可分为：__简支梁_________、__外伸梁_________、___悬臂梁_______三种常见形式.
三．判断题:（每题3分，共15分)
1.杆件两端受等值、反向、共线的一对外力作用，杆件一定发生地是轴向拉（压）变形。（错）
2。标准试件扎起常温、静载作用下测定的性能指标,作为材料测定力学性能指标.（对)
《工程力学》考试卷(A）
一、选择题（每题4分，共20分)
1.工程设计中工程力学主要包含以下内容：（ABC）
A分析作用在构件上的力，分清已知力和未知力。
B选择合适的研究对象，建立已知力和未知力的关系。
C应用平衡条件和平衡方程，确定全部未知力
D确定研究对象，取分离体
2下列说法中不正确的是：(a）
A力使物体绕矩心逆时针旋转为负
3．当挤压面为圆柱形侧面时，挤压面的计算面积按该圆柱侧面的正投影面积算.（对）
4.由于空心轴的承载能力大且节省材料，所以工程实际中的传动轴多采用空心截面。（错）
5.梁的横截面上作用有负值弯矩,其截面中性轴上侧各点受到压应力作用,下侧各点受到拉应力作用.（对）
四．作图题:（9分）
1．如图所示，三铰拱桥又左右两拱铰接而成，在BC作用一主动力。忽略各拱的自重，分别画出拱AC、BC的受力图。

自考工程力学试题及答案

自考工程力学试题及答案一、选择题（每题2分，共20分）1. 工程力学中的静力学主要研究的是（）。

A. 物体内部力的分布B. 物体在外力作用下的平衡状态C. 物体的变形D. 物体的运动答案：B2. 根据胡克定律，弹簧的形变量与作用力成正比，这个形变量是指（）。

A. 长度B. 体积C. 形心的位移D. 任意两点间的直线距离答案：C3. 在材料力学中，下列哪项不是材料的基本力学性能？（）A. 弹性B. 塑性C. 韧性D. 密度答案：D4. 力矩的国际单位是（）。

B. 牛顿米C. 帕斯卡D. 焦耳答案：B5. 一个物体在三个共点力作用下保持平衡，若撤去其中一个大小为F 的力，其余两个力的合力大小为（）。

A. FB. F/2C. 2FD. 无法确定答案：A6. 以下哪项不是梁的弯曲变形的主要原因？（）A. 材料的弹性模量B. 荷载的大小和分布C. 梁的长度D. 支撑条件答案：C7. 根据达拉姆公式，圆轴扭转时，相对扭转角θ与扭矩T和极惯性矩J之间的关系是（）。

A. θ = T/JB. θ = TJC. θ = J/TD. θ = T/(GJ)8. 在受压杆件的稳定性分析中，欧拉临界力是指（）。

A. 杆件开始弯曲的临界力B. 杆件开始失稳的临界力C. 杆件断裂的临界力D. 杆件最大承受力答案：B9. 复合梁的弯曲刚度是各单独梁弯曲刚度之（）。

A. 和B. 差C. 积D. 加权平均答案：A10. 在应力集中的分析中，应力奇异性是指（）。

A. 应力值无限增大B. 应力梯度无限增大C. 应力值突然下降D. 应力值突然上升答案：A二、简答题（每题10分，共30分）1. 简述平面力系平衡的条件是什么？答案：平面力系平衡的条件是力系中所有力在X轴和Y轴方向上的合力分别为零，即ΣFx = 0，ΣFy = 0，同时所有力矩的合力也为零，即ΣM = 0。

2. 什么是应力集中？它对结构设计有何影响？答案：应力集中是指在结构的某些局部区域，由于几何形状、载荷方式或材料不连续等原因，应力值显著高于周围区域的现象。

工程力学考试题及答案

工程力学考试题及答案第一部分：选择题（共40分，每题2分，共20小题）1.以下哪个是工程力学的基本概念？A.质量B.速度C.功率D.电流答案：A 质量2.以下哪个是工程力学的单位？A.米B.牛顿C.度D.秒答案：B 牛顿3.下列哪个是牛顿第一定律？A.质体静止B.速度恒定C.加速度不断变化D.物体受到力时才会运动答案：B 速度恒定4.物体所受的外力大小等于物体运动状态发生改变时的惯性力，这是牛顿的哪个定律？A.一定律B.二定律C.三定律D.四定律答案：B 二定律5.哪个是工程力学中动力学的研究对象？A.平衡结构B.静力学C.运动结构D.变形结构答案：C 运动结构第二部分：填空题（共30分，每空2分，共15空）1.牛顿的第一定律也叫_______定律。

答案：惯性定律2.________是测量物体运动速度的物理量。

答案：速度3.牛顿的第三定律也叫________定律。

答案：作用与反作用定律4._______是测量物体运动加速度的物理量。

答案：加速度5._______是测量物体质量大小的物理量。

答案：质量第三部分：简答题（共30分，每题10分，共3题）1.简述牛顿的三大定律。

答案：牛顿的第一定律是运动物体保持匀速直线运动或静止状态，直至受到外力的作用；牛顿的第二定律是物体所受的合力等于物体质量乘以加速度；牛顿的第三定律是每个作用力都有一个等大相反方向的反作用力。

2.什么是动力学学？答案：动力学是力及物体的相互作用，研究物体的运动状态和运动规律。

3.简述质量和重力的区别。

答案：质量是物体所拥有的物质量大小；重力是地球对物体的吸引力，是一种力的作用。

以上就是工程力学考试题及答案，希望可以帮助大家更好地理解和掌握工程力学知识。

祝大家考试顺利！。

工程力学自测及其答案.docx

全国2001年10月高等教育口学考试工程力学（一）试题课程代码：02159第一部分选择题（共20分）一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个选项中只有一个选项是符合题目要求的，请将正确选项前的字母填在题后的括号内。

1・光滑面对物体的约束反力，作用在接触点处，其方向沿接触面的公法线（） A. 指向受力物体，为压力 B.指向受力物体，为拉力 C.背离受力物体，为拉力 D.背离受力物体，为压力 2.图示三饺拱架小，若将作用于构件AC 上的力偶M 平移至构件BC±,则A 、B 、C 三处的约束反力（） A. 只有C 处的不改变 B. 只冇C 处的改变 C. 都不变 D. 都改变 3•牵连运动是指（）A. 动系相对丁•静系的运动C.静系相对于动系的运动4. 汽车以匀速率v 在不平的道路上行驶，如图所示。

当通过A 、B 、C 三个位置吋，汽车对路面的压力分别为F A 、F B 、F C ,贝lJ （）A. F A =F B =F CB. F A >F B >F CC. F A <F B <F CD. F A =F B >F C5. —・物重P,用细绳BA 、CA 悬挂如图所示，且角□ =60° CA 绳的张力为（） A. 0 B. 0.5P C. P D. 2P6. 塑性材料的伸长率6 2（）A.l%B.2%7. 两根材料和长度均相同的圆轴，第一根的直径是第二根的两倍，若受相同扭矩的作用，则两根轴的扭转角Z 比为（）8. 某轴材料为低碳钢，工作吋发生弯扭组合变形，对其进行强度计算时，宜采用（） A.笫一或笫二强度理论 B.笫二或笫三强度理论 C.第一或第四强度理论 D.笫三或笫四强度理论 9. 用钢丝绳吊重物时，在下列工况屮，钢丝绳受到静应力的工况是（） A.以匀加速度起吊重物 B.以匀速提升重物 C.以匀加速度制动 D.突然制动 10. 构件在对称循环交变应力作用下的许用应力等于（）题2图B.牵连点和对于动系的运动 D.牵连点相对于静系的运动 o 若将BA 绳突然剪断，则该瞬时 A.1 : 4 B.1 ： 8C.1 : 16D.1 : 32 题4图C.5%D.10%A.构件的持久极限B.材料的持久极限C.构件的持久极限与疲劳安全系数之比D.材料的持久极限与疲劳安全系数之比34•如图所示平面机构，半径为r 的半闘形凸轮以速度U 在固定水平面上向右滑动，长为「的直杆OA 可绕O 轴转动。

工程力学考试卷及答案

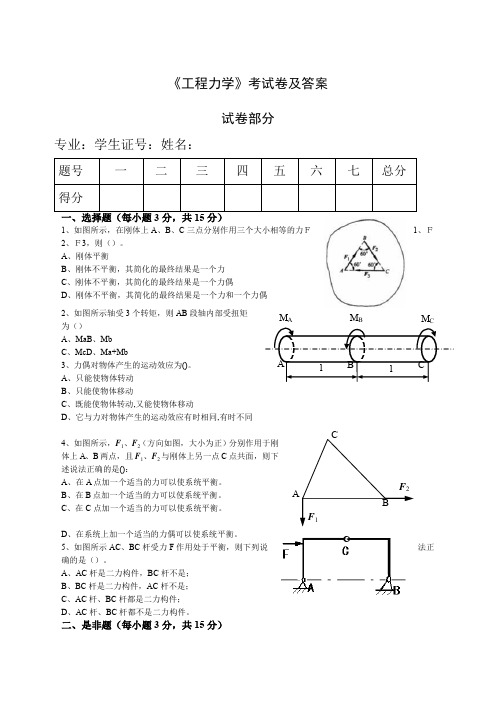
《工程力学》考试卷及答案试卷部分专业：学生证号：姓名：1、如图所示，在刚体上A 、B 、C 三点分别作用三个大小相等的力Ｆ1、Ｆ2、Ｆ3，则（）。

A 、刚体平衡B 、刚体不平衡，其简化的最终结果是一个力C 、刚体不平衡，其简化的最终结果是一个力偶D 、刚体不平衡，其简化的最终结果是一个力和一个力偶 2、如图所示轴受3个转矩，则AB 段轴内部受扭矩为（） A 、MaB 、Mb C 、McD 、Ma+Mb3、力偶对物体产生的运动效应为()。

A 、只能使物体转动 B 、只能使物体移动C 、既能使物体转动,又能使物体移动D 、它与力对物体产生的运动效应有时相同,有时不同4、如图所示，F 1、F 2（方向如图，大小为正）分别作用于刚体上A 、B 两点，且F 1、F 2与刚体上另一点C 点共面，则下述说法正确的是()：A 、在A 点加一个适当的力可以使系统平衡。

B 、在B 点加一个适当的力可以使系统平衡。

C 、在C 点加一个适当的力可以使系统平衡。

D 、在系统上加一个适当的力偶可以使系统平衡。

5、如图所示AC 、BC 杆受力F 作用处于平衡，则下列说法正确的是（）。

A 、AC 杆是二力构件，BC 杆不是；B 、BC 杆是二力构件，AC 杆不是； C 、AC 杆、BC 杆都是二力构件；D 、AC 杆、BC 杆都不是二力构件。

二、是非题（每小题3分，共15分）M A M BM C1、如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。

()2、成力偶的两个力F=-F ，所以力偶的合力等于零。

()3、静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

()4、杆件的基本变形有四种：轴向拉伸或压缩、剪切、挤压和弯曲。

()5、作用在同一物体上的两个力，使物体处于平衡的必要和充分条件是：这两个力大小相等、方向相反、沿同一条直线。

()三、填空题（每个空2分，共30分）1、力对物体的作用效果一般分为效应和效应。

高等教育自学考试《工程力学（二）》试题及参考答案

高等教育自学考试《工程力学（二）》试题及答案高等教育自学考试《工程力学（二）》试题及答案（课程代码：（课程代码：023910239102391））一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

内。

错选、多选或未选均无分。

1•如图所示的平面汇交力系中，1•如图所示的平面汇交力系中， F i =4kN =4kN，，F 2=2 2 kN ，F 3=5kN =5kN，则该力系在两个坐标轴上的，则该力系在两个坐标轴上的，则该力系在两个坐标轴上的投影为（）A.X= 1，Y= 1B. X= , Y=0 2C. X=0, Y= 4 5、. 31D. X=- — , Y= 2 2.2.如图所示，刚架在如图所示，刚架在如图所示，刚架在 C C 点受水平力P 作用，则支座作用，则支座 A A的约束反力N A 的方向应（ A. 沿水平方向沿水平方向 B. 沿铅垂方向沿铅垂方向 C. 沿AD 连线连线D. 沿BC 连线连线b=10cm 的正方形，的正方形，y y 轴是薄板对称轴轴是薄板对称轴,,3.3.如图所示，边长如图所示，边长a=20cm 的正方形匀质薄板挖去边长的正方形匀质薄板挖去边长则其重心的y 坐标等于（）2A.y c =11 — cm 3B. y c =10cmC. y c = 7 1cm 2 题d 图D.y c =5cm D. m x (F)=Fa (F)=Fa，， m y (F)=Fa (F)=Fa，， m z (F)=Fa 6.6.图示结构为图示结构为（）A. 静定结构静定结构B. 一次超静定结构一次超静定结构16.16.图示钉盖挤压面的面积为图示钉盖挤压面的面积为C.C.二次超静定结构二次超静定结构二次超静定结构D.D.三次超静定结构三次超静定结构三次超静定结构 7•工程上，通常脆性材料的延伸率为7•工程上，通常脆性材料的延伸率为（）A. <5 %B. <10 %C. <50 %D. <100 %8•如图，若截面图形的8•如图，若截面图形的 z z 轴过形心，则该图形对轴过形心，则该图形对 z z 轴的（ A. 静矩不为零，惯性矩为零静矩不为零，惯性矩为零B. 静矩和惯性矩均为零静矩和惯性矩均为零C. 静矩和惯性矩均不为零静矩和惯性矩均不为零D. 静矩为零，惯性矩不为零矩为零，惯性矩不为零)题&图二、填空题（本大题共10小题，每小题2分，共20分）分）请在每小题的空格中填上正确答案。

10月工程力学自考试题

全国20XX 年10月高等教育自学考试工程力学（一）试题课程代码：02159一、单项选择题(本大题共量10小题，每小题2分，共20分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.已知力1F 和2F 都作用于同一点，其合力合F =1F +2F ，则各力大小之间的关系为 ( )A.必有F 合=F 1+F 2B.不可能有F 合=F l +F 2C.必有F 合> F 1，F 合> F 2D.可能有F 合< F 1，F 合< F 22.在不计自重和摩擦的图示平面结构中，杆AC 上作用有一力偶矩为M 的力偶，则支座A 处的约束力A F 与水平线所夹的锐角θ为( )A.60°B.45°C.30°D.0°3.重为W 的物块在与水平线成30°角的推力P 的作用下静止于铅垂墙面上，已知力P 的大小也为W ，物块与墙面间的静摩擦因数为23，则墙面对物块的摩擦力s F 的大小为( ) A.2W B.W 23 C.W 43 D.W4.已知动点A 沿其轨迹的运动方程为s =b +ct ，式中b 、c 为常量，则( )A.点A 的轨迹必为直线B.点A 的轨迹必为曲线C.点A 必作匀速运动D.点A 的加速度必等于零5.塑性材料的极限应力是( )A.比例极限p σB.弹性极限e σC.屈服极限s σD.强度极限b σ6.轴向拉伸时，杆的伸长量( )A.与轴力和抗拉刚度均成正比B.与轴力和抗拉刚度均成反比C.与轴力成反比，与抗拉刚度成正比D.与轴力成正比，与抗拉刚度成反比7.两个材料不同的受扭转作用的轴，其载荷、约束、截面形状、尺寸及其长度均相同，则其( )A.变形相同，应力不同B.变形和应力均相同C.变形不同，应力相同D.变形和应力均不相同8.圆形截面梁剪切弯曲时，横截面上最大切应力发生在( )A.中性轴上，方向平行于剪力B.中性轴上，方向垂直于剪力C.距中性轴最远处，方向平行于剪力D.距中性轴最远处，方向垂直于剪力9.图示弯曲梁的BC 段A.有变形，无位移B.有位移，无变形C.既有变形，又有位移D.既无变形，又无位移10.材料的持久极限是指材料能经受无限次应力循环而不发生疲劳破坏的( )A.最低应力B.平均应力C.最高应力D.应力幅度二、填空题(本大题共l5小题，每小题2分，共30分)请在每小题的空格中填上正确答案。

(完整版)《工程力学》复习题及答案

《工程力学》复习题一、填空题1、工程力学包括、、和动力学的有关内容。

2、力的三要素是力的、、。

用符号表示力的单位是或。

３、力偶的三要素是力偶矩的、和。

用符号表示力偶矩的单位为或。

4、常见的约束类型有约束、约束、约束和固定端约束。

5、低碳钢拉伸时的大致可分为、、和阶段。

6、剪切变形的特点是工件受到一对大小、方向、作用线且相距很近的外力作用。

7、圆轴扭转的变形特点是：杆件的各横截面绕杆轴线发生相对，杆轴线始终保持。

8、平面弯曲变形的变形特点是杆的轴线被弯成一条。

9、静定梁可分为三种类型，即、和。

10、平面汇交力系平衡的解析条件是：力系中所有的力在投影的代数均为。

11、在工程中受拉伸的杆件，其共同的特点是：作用于杆件上的外力或外力的合力的作用线与构件轴线，杆件发生方向，伸长或压缩。

12、力矩的大小等于和的乘积。

通常规定力使物体绕矩心时力矩为正，反之为负。

13、大小，方向，作用线的两个力组成的力系，称为力偶。

力偶中二力之间的距离称为，力偶所在的平面称为。

14、力的平将作用在刚体某点的力平移到刚体上别指定一点，而不改变原力对刚体的作用效果，则必须附加一力偶，其力偶矩等于。

15、构件的强度是指的能力；构件的刚度是指的能力；构件的稳定性是指的能力。

二、判断题：（对的画“√”，错的画“×”）1、力的可传性定理，只适用于刚体。

（）2、两物体间相互作用的力总是同时存在，并且两力等值、反向共线，作用在同一个物体上。

（）3、力的大小等于零或力的作用线通过矩心时，力矩等于零。

（）4、力偶无合力，且力偶只能用力偶来等效。

（）5、柔体约束特点是限制物体沿绳索伸长方向的运动，只能给物体提供拉力。

（）6、二力杆的约束力不一沿杆件两端铰链中心的连线，指向固定。

（）7、截面法求轴力杆件受拉时轴力为负，受压时轴力为正。

（）8、常用的塑性指标有两个：伸长率和断面收缩率。

（）9、工程上通常把伸长率大于等于5%的材料称为塑性材料。

《工程力学》单选题题库(二)及答案(共3套)

《工程力学》题库单选题（二）及答案1、拉伸过程中杆件表面出现滑移线，是因为（）。

A、 45度方向切应力最大B、 30度方向切应力最大C、横截面正应力最大D、纵向截面切应力最大正确答案： A2、弯曲变形内力有剪力和弯矩，F作用处剪力图不变，弯矩图发生（）。

A、突变B、转折C、不变正确答案： B3、以上四步是轴类零件未知力的求解步骤，其中拆画平面受力图这步坚持（）原则。

A、相互平行的力放在一个平面受力图中B、矩放在一个平面受力图中C、只要是同一作用面的力和矩就放在同一个平面受力图中正确答案： C4、图中跷跷板受力发生（）变形。

A、旋转B、扭转C、弯曲D、拉伸正确答案： C5、如图所示，猎人非法猎猴，用两根轻绳将猴子悬于空中，猴子处于静止状态，以下说法正确的是（）。

A、猴子受到三个力作用B、绳拉猴子的力和猴子拉绳的力相互平衡C、地球对猴子有引力，猴子对地球没有引力D、人将绳子拉得越紧，猴子受到的合力越大正确答案： A6、下列曲柄滑块机构中，先画（）的受力图。

A、 AO杆B、 AB杆C、滑块正确答案： B7、物体作匀速运动时合力（）。

A、不一定为零B、一定为零C、一定不为零D、不确定正确答案： A8、图中哪个力对O点的力矩为正？（）A、B、正确答案： A9、梁发生平面弯曲时，其横截面绕（）旋转。

A、梁的轴线B、中性轴C、截面的对称轴D、截面的上（或下）边缘正确答案： B10、剪切变形受力特点是构件受到的两个力，大小相等，方向相反，作用线（）。

A、平行B、垂直C、平行，而且相距很近。

正确答案： C11、图中A点受到的力系是（）。

A、空间汇交力系B、空间平行力系C、空间任意力系正确答案： A12、（）弯曲变形内力有剪力和弯矩，上图简支梁中3-3截面弯矩和（）截面相同。

A、 1-1B、 2-2C、 3-3D、 4-4正确答案： B13、光滑墙角处于平衡状态的小球受到（）个光滑面约束。

A、 1B、 2正确答案： A14、车刀车削工件时车刀发生（（））。

工程力学试卷及答案完整版

工程力学试卷及答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】《工程力学》试卷及答案班级姓名得分一、填空题（每空1分，共22分）1、力的三要素是力的大小、方向、作用点。

用符号表示力的单位是（ N ）或（KN ）。

2、力偶的三要素是力偶矩的大小、转向和作用面方位。

用符号表示力偶矩的单位为（N·m）或（KN·m）。

3、常见的约束类型有柔性约束、光滑接触面约束、光滑铰链约束和固定端约束。

4、作用于一个刚体上的二力，使刚体保持平衡状态的充要条件是两个力大小相等、方向相反、作用线相同。

5、平面汇交力系平衡的充要条件是该力系的合力等于___零______。

6、平面任意力系的平衡条件为,0=∑ix F 0=∑iyF和___∑M 0（F ）=0。

7、当平面任意力系有合力时，合力对作用面内任意点的矩，等于力系中各力对同一点之矩的代数和。

8、空间力系根据力的作用线不同可分为空间汇交力系、空间平行力系和空间任意力系。

9、力在空间坐标轴上的投影有两种运算方法，即直接投影法和二次投影法。

10、工程中二力杆需满足三个条件，即自重不计、两端均用铰链连接和不受其他力的作用。

二、判断题：（对的画“√”，错的画“×”）（每题2分，共20分） 1、力的可传性定理，只适用于刚体。

（√）2、两物体间相互作用的力总是同时存在，并且两力等值、反向共线，作用在同一个物体上。

（×）3、力的大小等于零或力的作用线通过矩心时，力矩等于零（√）4、力偶无合力，且力偶只能用力偶来等效。

（√）5、共线力系是平面汇交力系的特殊情况，但汇交点不能确定。

（√）6、二力杆的约束力不沿杆件两端铰链中心的连线，指向固定。

（×）7、平面汇交力系的合力一定等于各分力的矢量和。

（√）8、力使物体运动状态发生变化的效应称力的外效应。

（√）9、力的三要素中只要有一个要素不改变，力对物体的作用效应就不变。

工程力学复习题及参考答案

2011年课程考试复习题及参考答案工程力学一、填空题：1.受力后几何形状和尺寸均保持不变的物体称为 .2.构件抵抗的能力称为强度.3.圆轴扭转时,横截面上各点的切应力与其到圆心的距离成比.4.梁上作用着均布载荷,该段梁上的弯矩图为 .5.偏心压缩为的组合变形.6.柔索的约束反力沿离开物体.7.构件保持的能力称为稳定性.8.力对轴之矩在情况下为零.9.梁的中性层与横截面的交线称为 .10.图所示点的应力状态,其最大切应力是 .11.物体在外力作用下产生两种效应分别是 .12.外力解除后可消失的变形,称为 .13.力偶对任意点之矩都 .14.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则杆中最大正应力为 .15.梁上作用集中力处,其剪力图在该位置有 .16.光滑接触面约束的约束力沿指向物体.17.外力解除后不能消失的变形,称为 .18.平面任意力系平衡方程的三矩式,只有满足三个矩心的条件时,才能成为力系平衡的充要条件.19.图所示,梁最大拉应力的位置在点处.20.图所示点的应力状态,已知材料的许用正应力σ,其第三强度理论的强度条件是 .21.物体相对于地球处于静止或匀速直线运动状态,称为 .22.在截面突变的位置存在集中现象.23.梁上作用集中力偶位置处,其弯矩图在该位置有 .24.图所示点的应力状态,已知材料的许用正应力σ,其第三强度理论的强度条件是 .25.临界应力的欧拉公式只适用于杆.26.只受两个力作用而处于平衡状态的构件,称为 .27.作用力与反作用力的关系是 .28.平面任意力系向一点简化的结果的三种情形是 .29.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则截面C的位移为 .30.若一段梁上作用着均布载荷,则这段梁上的剪力图为 .二、计算题：1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力.2.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心.已知I z=mm4,y C=,材料许用压应力σc=160MPa,许用拉应力σt=40MPa.试求：①画梁的剪力图、弯矩图.②按正应力强度条件校核梁的强度.3.传动轴如图所示.已知F r=2KN,F t=5KN,M=1KN·m,l=600mm,齿轮直径D=400mm,轴的σ=100MPa.试求：①力偶M的大小；②作AB轴各基本变形的内力图.③用第三强度理论设计轴AB的直径d.4.图示外伸梁由铸铁制成,截面形状如图示.已知I z=4500cm4,y1=,y2=,材料许用压应力σc=120MPa,许用拉应力σt=35MPa,a=1m.试求：①画梁的剪力图、弯矩图.②按正应力强度条件确定梁截荷P.5.如图6所示,钢制直角拐轴,已知铅垂力F1,水平力F2,实心轴AB的直径d,长度l,拐臂的长度a.试求：①作AB轴各基本变形的内力图.②计算AB轴危险点的第三强度理论相当应力.6.图所示结构,载荷P=50KkN,AB杆的直径d=40mm,长度l=1000mm,两端铰支.已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=,稳定安全系数n st=,σ=140MPa.试校核AB杆是否安全.7.铸铁梁如图5,单位为mm,已知I z=10180cm4,材料许用压应力σc=160MPa,许用拉应力σt=40MPa,试求：①画梁的剪力图、弯矩图.②按正应力强度条件确定梁截荷P.8.第七大题, 应力状态图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用.已知M=200GPa,μ=,σ=140MPa.试求：①作图示圆轴表面点的应力状态图.②求圆轴表面点图示方向的正应变.③按第四强度理论校核圆轴强度.9.图所示结构中,q=20kN/m,柱的截面为圆形d=80mm,材料为Q235钢.已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=,稳定安全系数n st=,σ=140MPa.试校核柱BC是否安全.10.如图所示的平面桁架,在铰链H处作用了一个20kN的水平力,在铰链D处作用了一个60kN的垂直力.求A、E处的约束力和FH杆的内力.11.图所示圆截面杆件d=80mm,长度l=1000mm,承受轴向力F1=30kN,横向力F2=,外力偶M=700N·m的作用,材料的许用应力σ=40MPa,试求：①作杆件内力图.②按第三强度理论校核杆的强度.12.图所示三角桁架由Q235钢制成,已知AB、AC、BC为1m,杆直径均为d=20mm,已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=,稳定安全系数n st=.试由BC杆的稳定性求这个三角架所能承受的外载F.13.槽形截面梁尺寸及受力图如图所示,AB=3m,BC=1m,z轴为截面形心轴,I z=×108mm4,q=15kN/m.材料许用压应力σc=160MPa,许用拉应力σt=80MPa.试求：①画梁的剪力图、弯矩图.②按正应力强度条件校核梁的强度.14.图所示平面直角刚架ABC在水平面xz内,AB段为直径d=20mm的圆截面杆.在垂直平面内F1=,在水平面内沿z轴方向F2=,材料的σ=140MPa.试求：①作AB段各基本变形的内力图.②按第三强度理论校核刚架AB段强度.15.图所示由5根圆钢组成正方形结构,载荷P=50KkN,l=1000mm,杆的直径d=40mm,联结处均为铰链.已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=,稳定安全系数n st=,σ=140MPa.试校核1杆是否安全.15分16.图所示为一连续梁,已知q、a及θ,不计梁的自重,求A、B、C三处的约束力.17.图所示直径为d的实心圆轴,受力如图示,试求：①作轴各基本变形的内力图.②用第三强度理论导出此轴危险点相当应力的表达式.18.如图所示,AB=800mm,AC=600mm,BC=1000mm,杆件均为等直圆杆,直径d=20mm,材料为Q235钢.已知材料的弹性模量E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=.压杆的稳定安全系数n st=3,试由CB杆的稳定性求这个三角架所能承受的外载F.参考答案一、填空题：1.刚体2.破坏3.正4.二次抛物线5.轴向压缩与弯曲6.柔索轴线7.原有平衡状态8.力与轴相交或平行9.中性轴 11.变形效应内效应与运动效应外效应 12.弹性变形 13.相等 2A 15.突变 16.接触面的公法线 17.塑性变形 18.不共线 τx ≤σ 22.平衡 22.应力 23.突变 24.[]σ 25.大柔度细长 26.二力构件 27.等值、反向、共线 28.力、力偶、平衡 2EA 30.斜直线二、计算题：1.解：以CB 为研究对象,建立平衡方程B()0:=∑MF C 1010.520⨯⨯-⨯=F:0=∑yFB C 1010+-⨯=F F解得： B 7.5kN =F C 2.5kN =F 以AC 为研究对象,建立平衡方程:0=∑yFA C 0-=y F FA()0:=∑MF A C 1020M F +-⨯=解得： A 2.5kN =y F A 5kN m =-⋅M 2.解：①求支座约束力,作剪力图、弯矩图B()0:=∑MF D 102120340⨯⨯-⨯+⨯=F:0=∑yFB D 102200+-⨯-=F F解得： B 30kN =F D 10kN =F②梁的强度校核1157.5mm =y 2230157.572.5mm =-=y拉应力强度校核B 截面33B 2tmaxt 12201072.51024.1MPa []6012500010--⨯⨯⨯σ===≤σ⨯z M y I C 截面33C 1tmaxt 121010157.51026.2MPa []6012500010--⨯⨯⨯σ===≤σ⨯z M y I 压应力强度校核经分析最大压应力在B 截面33B 1cmaxc 122010157.51052.4MPa []6012500010--⨯⨯⨯σ===≤σ⨯z M y I 所以梁的强度满足要求3.解：①以整个系统为为研究对象,建立平衡方程()0:=∑x M F t 02⨯-=DF M 解得：1kN m =⋅M 3分②求支座约束力,作内力图由题可得：A B 1kN ==y y F F A B 2.5kN ==z z F F③由内力图可判断危险截面在C 处22222r332()[]σσ+++==≤y z M M T M T222332() 5.1mm []πσ++∴≥=y z M M T d4.解：①求支座约束力,作剪力图、弯矩图A()0:MF =∑ D 22130y F P P ⨯-⨯-⨯=:0=∑yFA D 20y y F F P P +--=解得：A 12y F P = D 52y F P =②梁的强度校核拉应力强度校核C 截面C 22tmax t 0.5[]z zM y Pa y I I ⋅σ==≤σ 24.5kN P ∴≤D 截面D 11tmax t []z zM y Pa y I I ⋅σ==≤σ 22.1kN P ∴≤压应力强度校核经分析最大压应力在D 截面D 22cmax c []z zM y Pa y I I ⋅σ==≤σ 42.0kN P ∴≤所以梁载荷22.1kN P ≤5.解：①② 由内力图可判断危险截面在A 处,该截面危险点在横截面上的正应力、切应力为2221N 2232()()4F a Fl F F M A W d σπ+=+=13p 16F a T W d τπ== 2221222221r323332()()4164()4()F a Fl F F a d d d σστπππ+∴=+=++6.解：以CD 杆为研究对象,建立平衡方程C ()0:MF =∑ AB 0.80.6500.90F ⨯⨯-⨯=解得： AB 93.75kN F =AB 杆柔度1100010040/4li μλ⨯=== 229p 6p 2001099.320010ππλσ⨯⨯===⨯E 由于p λλ>,所以压杆AB 属于大柔度杆222926cr cr 22200104010248.1kN 41004E dF A ππππσλ-⨯⨯⨯⨯===⨯=工作安全因数 cr st AB 248.1 2.6593.75F n n F ===> 所以AB 杆安全7.解：①②梁的强度校核196.4mm y = 225096.4153.6mm y =-=拉应力强度校核A 截面A 11tmax t 0.8[]z zM y P y I I ⋅σ==≤σ 52.8kN P ∴≤C 截面C 22tmax t 0.6[]z zM y P y I I ⋅σ==≤σ 44.2kN P ∴≤压应力强度校核经分析最大压应力在A 截面A 22cmax c 0.8[]z zM y P y I I ⋅σ==≤σ132.6kN P ∴≤所以梁载荷44.2kN P ≤8.解：①点在横截面上正应力、切应力3N 247001089.1MPa 0.1F A σπ⨯⨯===⨯ 33P 1661030.6MPa 0.1T W τπ⨯⨯===⨯ 点的应力状态图如下图：②由应力状态图可知σx =,σy =0,τx =cos 2sin 222x yx yx ασσσσσατα+-=+-o 4513.95MPa σ∴= o 4575.15MPa σ-=由广义胡克定律o o o 65945454511139503751510429751020010()(...).E εσμσ--=-=⨯-⨯⨯=-⨯⨯ ③强度校核2222r4389133061037MPa []...σστσ=+=+⨯=≤所以圆轴强度满足要求 9.解：以梁AD 为研究对象,建立平衡方程A ()0:MF =∑ AB 4205 2.50F ⨯-⨯⨯=解得： BC 62.5kN F =BC 杆柔度1400020080/4li μλ⨯===p 99.3λ=== 由于p λλ>,所以压杆BC 属于大柔度杆222926cr cr 22200108010248.1kN 42004E dF A ππππσλ-⨯⨯⨯⨯===⨯= 工作安全因数cr st AB 248.1 3.9762.5F n n F ===> 所以柱BC 安全10.解：以整个系统为研究对象,建立平衡方程:=∑0x FE 200xF -= :0=∑yF A E 600y y F F +-= A ()0:M F =∑ E 82036060y F ⨯-⨯-⨯=解得：E 20kN xF = E 52.5kN y F = A 7.5kN y F =过杆FH 、FC 、BC 作截面,取左半部分为研究对象,建立平衡方程C ()0:M F =∑ A HF 12405y F F -⨯-⨯= 解得： HF 12.5kN F =-11.解：①②由内力图可判断危险截面在固定端处,该截面危险点在横截面上的正应力、切应力为33N 234301032 1.21029.84MPa 0.080.08z z F M A W σππ⨯⨯⨯⨯=+=+=⨯⨯ 3p 16700 6.96MPa 0.08T W τπ⨯===⨯ 2222r3429.844 6.9632.9MPa []σστσ∴=++⨯≤所以杆的强度满足要求12.解：以节点C 为研究对象,由平衡条件可求BC F F =BC 杆柔度1100020020/4li μλ⨯=== 229p 6p 2001099.320010ππλσ⨯⨯===⨯E 由于p λλ>,所以压杆BC 属于大柔度杆222926cr cr 2220010201015.5kN 42004E dF A ππππσλ-⨯⨯⨯⨯===⨯= cr st AB 15.5 3.0F n n F F∴==≥= 解得： 5.17kN F ≤13.解：①求支座约束力,作剪力图、弯矩图A ()0:M F =∑B 315420y F ⨯-⨯⨯=:0=∑y F A B 1540y y F F +-⨯=解得：A 20kN y F =B 40kN y F =②梁的强度校核拉应力强度校核D 截面33D 1tmax t 81240/3101831014.1MPa []1.731010z M y I --⨯⨯⨯σ===≤σ⨯⨯ B 截面33B 2tmax t 8127.5104001017.3MPa []1.731010z M y I --⨯⨯⨯σ===≤σ⨯⨯ 压应力强度校核经分析最大压应力在D 截面33D 2tmax c 81240/3104001030.8MPa []1.731010z M y I --⨯⨯⨯σ===≤σ⨯⨯ 所以梁的强度满足要求14.解：①②由内力图可判断危险截面在A 处,该截面危险点在横截面上的正应力、切应力为2232604897.8MPa M W σ⨯+=== 3p 166038.2MPa 0.02T W τπ⨯===⨯ 2222r3497.8438.2124.1MPa []σστσ∴=++⨯=≤所以刚架AB 段的强度满足要求15.解：以节点为研究对象,由平衡条件可求1235.36kN F P == 1杆柔度1100010040/4li μλ⨯=== 229p 6p 2001099.320010ππλσ⨯⨯===⨯E 由于p λλ>,所以压杆AB 属于大柔度杆222926cr cr 22200104010248.1kN 41004E dF A ππππσλ-⨯⨯⨯⨯===⨯=工作安全因数cr st 1248.1735.36F n n F ===>所以1杆安全16.解：以BC 为研究对象,建立平衡方程B ()0:=∑M FC cos 02a F a q a θ⨯-⨯⨯= 0:x F =∑ B C sin 0x F F θ-=C ()0:M F =∑ B 02y a q a F a ⨯⨯-⨯= 解得：B tan 2x qa F θ= B 2y qa F =C 2cos qa F θ= 以AB 为研究对象,建立平衡方程0:x F=∑ A B 0x x F F -= :0=∑y F A B 0y y F F -=A ()0:=∑M F AB 0y M F a -⨯=解得： A tan 2x qa F θ= A 2y qa F = 2A 2qa M = 17.解：①② 由内力图可判断危险截面在固定端处,该截面危险点在横截面上的正应力、切应力为2223N 1232(2)()4F l F l F F M A W d σπ+=+=3p 16e M T W d τπ==r3σ∴=18.解：以节点B 为研究对象,由平衡条件可求BC 53F F = BC 杆柔度1100020020/4li μλ⨯===p 99.3λ=== 由于p λλ>,所以压杆AB 属于大柔度杆222926cr cr 2220010201015.5kN 42004E d F A ππππσλ-⨯⨯⨯⨯===⨯= cr st BC 15.535/3F n n F F ∴==≥= 解得： 3.1kN F ≤。

工程力学试卷及答案7套

工程力学试卷1一、选择题（每题4分，共20分）1、材料的失效模式。

A 只与材料本身有关，而与应力状态无关；B 与材料本身、应力状态均有关；C 只与应力状态有关，而与材料本身无关；D 与材料本身、应力状态均无关。

2、图中应力圆a 、b 、c 表示的应力状态分别为A 二向应力状态、纯剪切应力状态、三向应力状态；B 单向拉应力状态、单向压应力状态、三向应力状态；C 单向压应力状态、纯剪切应力状态、单向拉应力状态；D 单向拉应力状态、单向压应力状态、纯剪切应力状态。

正确答案是3、关于压杆临界力的大小，说法正确的答案是 A 与压杆所承受的轴向压力大小有关； B 与压杆的柔度大小有关；C 与压杆所承受的轴向压力大小有关；D 与压杆的柔度大小无关。

4、图示交变应力的循环特征r 、平均应力m σ、应力幅值a σ的值分别是A 40、20、10B 20、10、20C 0、20、10D 0、20、205、如图所示重量为Q 的重物自由下落冲击梁，冲击时动荷系数A Cd V h k 211++= BB d V h k ++=11 C B d V h k 211++= DB C d V V hk +++=211 ABCABCQQ二、计算题（共80分，信息学院学生做1、2、3、4、6，非信息学院学生做1、2、3、4、5）1、（16分）简支梁受载荷如图所示，请画出梁的剪力图，弯矩图。

2、（15分）已知三向应力状态如图所示（图中应力单位：MPa ），试求：1）主应力；2）主切应力；3）形变应变能密度f u 。

3、（16分）圆截面杆，受横向外力F 和绕轴线的外力偶0m 作用。

由实验测得杆表面A 点处沿轴线方向的线应变40104-⨯= ε，杆表面B 点处沿与轴线成45︒方向的线应变4451075.3-⨯= ε。

材料的弹性模量E = 200GPa ，泊松比v = 0.25，a=0.25L ，L=800mm ，d=60mm 。

试求横向外力F 和绕轴线的外力偶0m 。

工程力学考试题及答案

工程力学考试题及答案一、单项选择题（每题2分，共20分）1. 以下哪项是工程力学中研究的主要对象？A. 材料B. 结构C. 力D. 以上都是答案：D2. 静力学中，平衡状态是指物体所受的合力为：A. 非零B. 零C. 任意值D. 不可确定答案：B3. 材料力学中，弹性模量是描述材料的哪种性质？A. 强度B. 硬度C. 弹性D. 塑性答案：C4. 根据牛顿第三定律，作用力和反作用力的大小关系是：A. 相等B. 不相等C. 相反D. 无法确定答案：A5. 在梁的弯曲问题中，梁的弯曲刚度与以下哪项无关？A. 梁的截面形状B. 梁的长度C. 梁的材料D. 梁的截面尺寸答案：B6. 应力集中是指在材料的哪些部位应力会显著增大？A. 光滑表面B. 无缺陷区域C. 几何突变处D. 均匀受力区域答案：C7. 动载荷是指：A. 静止不动的载荷B. 随时间变化的载荷C. 随空间变化的载荷D. 均匀分布的载荷答案：B8. 能量守恒定律在工程力学中的应用主要体现在：A. 热力学B. 动力学C. 静力学D. 流体力学答案：B9. 以下哪种材料可以认为是理想弹性体？A. 橡胶B. 钢铁C. 玻璃D. 木材答案：B10. 塑性变形是指材料在外力作用下发生变形后，去掉外力后：A. 不能恢复原状B. 完全恢复原状C. 部分恢复原状D. 无法确定答案：A二、填空题（每空1分，共20分）1. 物体在受到三个力的作用下，若这三个力的合力为零，则物体处于______状态。

答案：平衡2. 材料力学中，梁的挠度是指梁在受力后与______之间的最大垂直距离。

答案：原始直线3. 材料在拉伸过程中，其应力与应变的关系曲线称为______曲线。

答案：应力-应变4. 根据胡克定律，弹簧的变形量与施加在其上的力成正比，其比例系数称为______。

答案：弹簧常数5. 在材料力学中，材料的屈服强度是指材料在______状态下的最大应力。

答案：塑性变形6. 动载荷引起的振动通常需要考虑______效应。

(完整版)工程力学试题及答案

工程力学试题及答案、填空题（每空1分，共16分）1•物体的平衡是指物体相对于地面 ___________ 或作 _________ 运动的状态。

2•平面汇交力系平衡的必要与充分条件是： ________ 。

该力系中各力构成的力多边形3•—物块重600N ，放在不光滑的平面上，摩擦系数f=0.3，在左侧有一推力 150N ，物块有向右滑动的趋势。

F max = ________ ,所以此物块处于静止状态，而其F= _________ 。

4•刚体在作平动过程中，其上各点的 ______________ 相同，每一瞬时，各点具有 ___________ 的速度和加速度。

5. AB 杆质量为m ，长为L ，曲柄O i A 、O 2B 质量不计，且O i A=O 2B=R , O i O 2=L ,当 $ =60。

时，O i A 杆绕 O i 轴转动，角速度3为常量，则该瞬时AB 杆应加的惯性力大小为 ___________ ，方向为 ___________ 。

6. 使材料丧失正常工作能力的应力称为极限应力。

工程上一般把 ___________ 作为塑性材料的极限应力；对于脆性材料，则把 ________ 作为极限应力。

7. _______ 面称为主平面。

主平面上的正应力称为。

8. 当圆环匀速转动时，环内的动应力只与材料的密度p 和有关，而与__________ 无关。

二、单项选择题（在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内。

每小题 3分，共i8分）i .某简支梁AB 受载荷如图所示，现分别用的关系为（）。

A. R A <R B B. R A >R B C. R A =R B3 在无阻共振曲线中，当激振力频率等于系统的固有频率时，振幅B 趋近于（）。

A.零 B.静变形C.无穷大D.一个定值4 虎克定律应用的条件是（）。

A.只适用于塑性材料B.只适用于轴向拉伸C.应力不超过比例极限D.应力不超过屈服极限5 梁的截面为T 字型，Z 轴通过横截面的形心，弯矩图如图所示，则有（D. 无法比较R A 、R B 表示支座A 、B 处的约束反力，则它们& x3 4 5卜纠^12. 材料不同的两物块A和B叠放在水平面上，已知物块A重0.5kN，物块B重0.2kN ,物块A、B间的摩擦系数f 1=0.25，物块B与地面间的摩擦系数f2=0.2，拉动B物块所需要的最小力为（）。

工程力学自测题一及答案重点

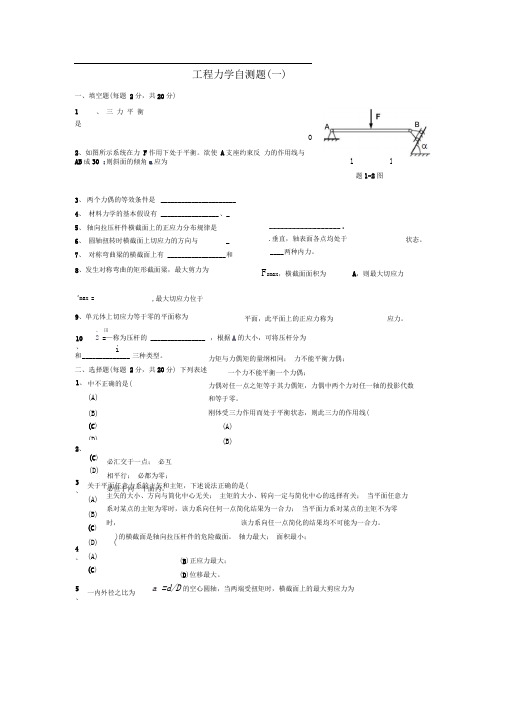
工程力学自测题(一)一、填空题(每题 2分，共20分) 1 、三力平衡是O2、如图所示系统在力 F 作用下处于平衡。

欲使 A 支座约束反力的作用线与AB 成30 :则斜面的倾角a 应为3、两个力偶的等效条件是 ______________________4、材料力学的基本假设有 _________________ 、_5、轴向拉压杆件横截面上的正应力分布规律是6、圆轴扭转时横截面上切应力的方向与_7、对称弯曲梁的横截面上有 _________________ 和8、发生对称弯曲的矩形截面梁，最大剪力为F smax ，横截面面积为A ，则最大切应力力矩与力偶矩的量纲相同；力不能平衡力偶；一个力不能平衡一个力偶；力偶对任一点之矩等于其力偶矩，力偶中两个力对任一轴的投影代数和等于零。

刚体受三力作用而处于平衡状态，则此三力的作用线((A) (B)(C )(D)题1-2图^max = ,最大切应力位于 9、单元体上切应力等于零的平面称为、田 2 =—称为压杆的 ________________ i平面，此平面上的正应力称为应力。

10、，根据A 的大小，可将压杆分为 3、4、关于平面任意力系的主矢和主矩，下述说法正确的是( (A)(B) (C ) (D) ( (A) (C )主矢的大小、方向与简化中心无关；主矩的大小、转向一定与简化中心的选择有关；当平面任意力系对某点的主矩为零时，该力系向任何一点简化结果为一合力；当平面力系对某点的主矩不为零时，该力系向任一点简化的结果均不可能为一合力。

)的横截面是轴向拉压杆件的危险截面。

轴力最大；面积最小； 5、一内外径之比为 (B )正应力最大； (D )位移最大。

a =d/D 的空心圆轴，当两端受扭矩时，横截面上的最大剪应力为______________________________________________________ O.垂直，轴表面各点均处于 ____ 两种内力。