流体力学第十一章 翼型与叶栅理论
流体动力学及叶栅理论.

流体动力学及叶栅理论课程小结《流体动力学及叶栅理论》下篇课程主要包括流体动力学和叶栅理论两部分。
其中流体动力学的主要内容是:流体力学性质及概念、流体运动的基本方程、平面有势流动、势流叠加、旋涡理论等。
叶栅理论主要内容是:机翼及翼型特性、茹科夫斯基翼型、薄翼绕流及有限机翼理论、叶栅及叶栅特性方程、平面叶栅绕流求解方法等。
一、流体动力学流体力学是研究流体平衡和运动的规律以及它与固体间的相互作用的科学。
流体力学性质及概念:包括流体的流动性和粘滞性(相互运动时的内摩擦力产生的)、迹线(流体为团运动的轨迹线)、流线(指某时刻t时,连接流场中各点流体微团运动方向的光滑曲线)、微团分析(流体微团具有平移、旋转及变形的特征)等。
流体运动的基本方程:包括连续性方程、动量方程与动量矩方程、纳维-斯托克斯方程、欧拉方程(粘度为零的方程)、能量方程等。
平面有势流动:包括均匀流(流动过程中运动要素不随坐标位置(流程)而变化)、平面源、汇(与平面源的流向相反)、点涡(环流)、偶极子等基本概念,速度势函数和流函数,简单平面势流、偶极流、有环量绕流和无环量绕流(两者相差一个点窝)等。
势流叠加:包括源流和均匀流叠加、等强度源和汇流与直线流叠加、偶极流、圆柱绕流、汇流和环流的叠加、以及其他由两种或两种或以上的基本势流叠加等。
旋涡理论:包括涡线、涡管、涡束、涡通量(旋涡强度)等基本概念,开尔文-汤姆逊定理、斯托克斯定理(当封闭周线内有涡束时,则沿封闭轴线的速度环量等于该封闭周线内所有涡束的涡通量之和),亥姆兹定理(包括第一定律、第二定律和第三定律),二元旋涡内外压力分布等。
二、叶栅理论1、机翼及翼型机翼的外形以椭圆形状最为有利,但由于制造上的困难难,实际多采用与椭圆相近的形状。
翼型指的是顺着来流方向切下来的剖面。
翼型通常都具有流线型外形,头部圆滑,尾巴尖瘦,背(上弧)稍拱曲,腹(下弧)的形状则有凹的、凸的、半凹半凸的及平的。
机翼几何参数:机翼翼展b、机翼面积A、平均翼弦lm(A/b)、展翼比 (b/lm)、翼弦l、翼型厚度d(最大的叫翼型最大厚度dmax)、翼型弯度f、前、后缘圆角半径。
流体动力学及叶栅理论

1.升、阻力系数曲线
通过实验测取 Cy、Cx 与α的一系列对应值,并在以 Cy、Cx 为纵轴,α为横轴的平面直角坐标系 里绘制 Cy、Cx~α关系曲线(图 5-4a),则得升、阻力系数与冲角关系曲线。 图 5-4a 给出了一种翼型的 Cy、Cx~α曲线(Cx 值巳被放大五倍)。从图上可以看出: (1)当冲角α在-6~8°之间时,升力系数曲线接近一条直线而阻力系数曲线则类似一条二次曲 线,随着α的增大 Cy 值成比例的上升,而 Cx 值则增加较缓慢,翼型通常就在这一范围工作,称为该 翼型的工作区间。 (2)当冲角取α=-6°时,升力系数为零、阻力系数为最小。这时的冲角 (各翼型不一样)叫做无 升力冲角或零冲角 0 。过后缘沿此方向作一直线(不计长度),叫做该翼型的气动力翼弦(参看图 5-3)。 由此弦起算的冲角,称为动力冲角。从动力学角度看,动力冲角比几何冲角更合理。 (3)当冲角超过α=-12°后,Cy 开始徒降,而 Cx 则大幅度增加,这是由于边界层与翼型表面分 离所致。这个冲角叫临界冲角 c ,各翼型不一样,一般为十几度。超过临界冲角以后的分离绕流,叫 做失速流动(图 5-5) 。
上式中 Cy, 、Cx 分别称为升力系数和阻力系数,其数值取决于冲角及机翼形状,通常由实验确定。 工程应用上除升、阻力(总动力特性)外,有时对机翼上的压力分布(局部动力特性)也很关心,压力 也取决于来流、冲角和机翼的形状。
α 0 α
∞
图 5-3
5.1.3 机翼绕流
根据所给的条件及要解决的问题的不同,工程上提出的机翼绕流问题大体可分为两大类:
xd 。这些相对值,习惯上常用百分数表示: l d d max d 100% l d max 100% l
3
xd
流体动力学及叶栅理论课程作业—河海大学

流体动力学及叶栅理论(下篇)一、课程内容小结1.机翼及翼型特性机翼的几何特性:翼型几何参数(翼弦、翼型厚度、翼型弯度、前、后缘圆角半径和后缘角),机翼几何参数(机翼翼展、机翼面积、平均翼弦、展弦比)。
机翼的气动力特性:机翼与绕流流体相互作用的力学特性,叫做机翼的气动力特性。
机翼绕流:正问题和反问题。
机翼分类:无限翼展机翼和有限翼展机翼。
翼型绕流的实验结果:介绍翼型气动方性能,随冲角及翼型几何形状变化的实验结果。
冲角对翼型气动力性能的影响翼型的升力和助力:升、阻力系数曲线,升、阻力极曲线。
压力沿翼型表面的分布:工程上不仅很重视翼型上的总作用力,而且对压力沿翼型表面如何分布也很关心,特别是在水利机械中,压力沿叶片的分布情况,关系到叶轮汽蚀性能的好坏。
翼型几何形状对动力性能的影响:弯度的影响,厚度的影响,前缘抬高度的影响,表面粗糙度的影响,雷诺数的影响。
常见翼型:NACA四位数字翼型,NACA五位数字翼族,以及其他翼型。
2.茹可夫斯基翼型对于翼型绕流的理论分析,分别介绍翼型绕流的保角变换与点奇点分布两种解法。
茹可夫斯基变换变换图解。
变换图形:圆心在原点的圆,圆心在坐标轴上的圆,圆心在第二象限的圆。
圆柱绕流。
圆柱绕流的来流速度。
圆柱绕流的来流环量。
绕流翼型流动的复势绕翼型流动的速度场。
翼型气动力特性。
翼型上的作用力:在理想流体的条件下,翼型将不受阻力,翼型上只作用者升力。
升力的大小,可以类似于圆柱绕流那样求出,结果也和圆柱绕流时一样。
升力系数。
3.薄翼绕流及有限翼展机翼理论当流体绕流翼型时,由于翼型的存在产生对来流的扰动,改变了来流的性态。
它一方面使流动顺翼型表面偏折,并形成一条流线;另一方面使流速值在翼型两侧产生跃变,出现了速度差和压力差,并进而产生了升力。
由于翼型对来流的扰动的作用,可以用沿翼型适当分布的涡、源(奇点)来代替,把这种计算绕翼型流场的方法,称为奇点分布法。
薄翼绕流。
薄翼绕流的特点:翼型厚度很薄,翼型中弧线微弯,在小冲角之下被绕流。
电子教案 流体力学与流体机械--赵琴

3. 阻力系数 表面摩擦阻力
翼型阻力 压差阻力
翼型阻力大小与翼型参数、冲角大小、 Re有密切关系。
D
翼型阻力系数:
CD
1 2
v2 b
CL CD
Re CD
CL=0时CD取极小值
为提高流动性能,需特别重视翼型阻力的最小 值。实验表明,t 6% 时,其翼型阻力最小。 由于冲角对翼型阻力的影响很大,因此欲设计 获得一定升力系数而阻力最小的话,应考虑使 用有弯度的翼型。用弯度来提高升力系数所引 起的阻力增加量最小。
1
2i C f (z)dz
柯西留数定理: 假定C是一条封闭曲线,除 了C内的有限个一阶奇点外,函数f(z)在C内 和C上都是解析的。如在那些奇点上的留数 等于r1,r2,…,rn,则留数定理为
C f (z)dz 2i(r1 r2 rn )
5. 柯西公式
假定f(z)在封闭曲线C内和C上都是解析函数, 如有z0是不在C上一个点,柯西公式有:
1
2i
C
f (z) z z0
dz
0, z0在C外
f
(
z
0
),
z
0
在C内
第四节 儒可夫斯基翼型 与保角变换法
一、保角变换法求解平面势流
利用解析的复变函数 z =f(ζ)将ζ平面上的圆域变换
成z平面上的实用域。
Z
y
z
Cz
ζ
η
Cζ
o
V∞z αz
x
V∞ζ
o
αζ
ξ
注意:
保角变换过程中,同一点两个线段的夹角在变换过 程中保持不变。
va 2
e i
v e i (
a2 )
儒可夫斯基变换函数的反函数为
叶栅理论 PPT

第二节 翼型受力及等价平板翼栅
一、栅中流动
oxy
讨 论 叶 栅 流 动 时 选 用 随 叶 片 一 起 流 动 的 坐 标 系 , 设 栅 前 无 穷 远 处 来 流 速 度 为 w1(w1x, w1y) ,栅 后 无 穷 远 处 的 流 速 w 2(w 2x, w 2y) 。由 于 叶 栅 对 流 场 的 作 用,通常栅前、栅后的速度大小和方向都会发生变化,使二者不相等。
2. 空 间 叶 栅 流 经 叶 栅 流 道 的 流 动 是 空 间 流 动 。如 :混 流 式 水 轮 机 、水 泵 、风 机 的 叶 轮 。
3. 直 列 叶 栅 流面上列线成一无限长直线,为直列叶栅,如:轴流式叶轮叶栅。 4. 环 列 叶 栅 流面上列线为圆周线,为环列叶栅。如:离心式叶轮叶栅为环列叶栅。 5. 不 动 叶 栅 叶栅本身不运动为不动叶栅。如:导叶。 6. 运 动 叶 栅 叶栅本身运动,为运动叶栅。又可以分为移动和转动叶栅。
( 3)
z1
p1 g
w
2 1
2g
z2
p2 g
w
2 2
2g
( 4)
z1
z2,
w
2 1
w
2 1x
w
2 1y
,
w
2 2
w
2 2
x
w
2 2
y
,
又
w1x
w 2x ,
代
入
伯
努
利
方
程
,
得:
p1
p2
1 2
(
w
2 2y
w
2 1y
)
( 5)
Rx,Ry可 表 示 为 :
R
x
《流体力学与叶栅理论》课程思政优秀案例

《流体力学与叶栅理论》课程思政优秀案例一、课程介绍《流体力学与叶栅理论》课程40学时,2.5学分,秋季学期开课,面向我校能源与动力工程专业大三学生,是能源与动力工程专业基础课与核心课程。
课程主要涵盖3个单元的内容:理想流体动力学、粘性流体动力学基础和机翼理论与叶栅理论基础,其中理想流体动力学和粘性流体动力学基础是基础理论部分,机翼理论与叶栅理论基础是前两个部分在机翼和叶栅中的应用。
从课程知识结构可以看出本课程是一门面向工程实际应用的课程,在课程学习过程中需要与工程实际紧密结合,是一门从理论学习到实际应用全覆盖的课程。
二、课程思政育人目标课程以知识掌握、创新能力培养和价值观树立为育人目标。
(1)在知识掌握层面,不仅使学生掌握流体力学知识,还应掌握课程所涉及的数学、物理和流动测量等方面的综合知识。
(2)在创新能力培养方面,利用流体力学课程面向工程实际应用的特点,训练学生综合运用所学知识识别、表达、并通过文献研究等分析问题和解决问题的能力,在此过程中激发学生的创新意识,培养学生的创新能力。
(3)在价值观树立方面,利用流体力学课程前沿属性和在卡脖子领域中的应用,激发学生爱国和服务建设祖国的热情,形成社会主义核心价值观,并坚定成为社会主义建设者和接班人的理想信念。
三、经典课程思政案例设计和展示在育人大纲制定方面,秉承以学生为中心和以学为核心的教育理念,将立德树人教育和创新能力培养融入教育教学全过程。
在以学生为中心方面,将课程内容知识点化,让学生选择自己感兴趣的知识点进行准备和课堂讲解,采用这种知识点学生讲的翻转课堂形式,激发学生学习兴趣和主动性,配合学生互评、过程评价的课程成绩评价体系,融合教与学,达到以学生为中心、以学为核心的教学效果。
在立德树人教育方面,结合流体力学在国防和航空航天领域的应用案例讲解,分享国家在科技封锁的严峻条件下自主研发所取得的成就,激发学生的爱国和服务建设祖国的社会主义价值观。
在创新能力培养方面,结合流体力学课程面向工程实际应用的特点,结合教师自身的科研工作,在教学过程中融入相关课程领域的前沿知识和应用,通过已有的一些前沿应用实例讲解,激发学生的创新意识,培养学生的创新能力。
机翼和叶栅工作原理

第十章机翼和叶栅工作原理本章将分别讨论机翼和叶栅最基本的工作原理,讨论机翼工作原理是为叶栅理论奠定基础的。
二者均为叶轮机械(汽轮机,泵与风机及燃气轮机等)流体动力学的基础,同时也是力学理论在解决流体与被绕流物体间相互作用问题的一个重要应用。
§10-1 机翼的几何特性机翼一词常用于航空工程,也可泛指相对于流体运动的各种升力装置。
因此,叶轮机械中的工作轮叶片(汽轮机叶片、轴流泵与风机叶片等)就是一个机翼。
工程上引用机翼主要是为了获取升力。
由于在流体中运动的物体,必然会受到粘性阻力的作用。
因此对机翼提出的技术要求首先就是尽可能大的升力和尽量小的阻力,这就要求机翼采用适当的几何形状。
图10-1是机翼的外形图。
将机翼顺着来流方向切开的剖面形状称为翼型,翼型的周线称为型线,翼型的形状直接决定了翼(或者叶片)的空气动力特性。
通常翼型具有:圆滑的头部、尖瘦的尾巴、拱曲的背(上弧),至于腹(下弧)形状则有凹的、也有凸的,也有半凹半凸及平的。
表征机翼的几何特性基本参数如下(参照图10-2):(1) 翼型中线翼型型线内切圆心的连线称为翼型中线,或者称翼型骨线。
(2) 翼弦b翼型中线与型线的两个交点分别称为前缘点和后缘点,前缘点与后缘点的边线长度b称为翼弦或者弦长。
与(3) 翼型厚度d翼型型线内切圆的直径d称为翼型厚度,最大厚度dmax翼弦之比d/b称为最大相对厚度。
max与翼(4) 翼型弯度f翼型中线至翼弦的距离f称为翼型弯度,最大弯度fmax弦之比f/b称为最大相对弯度。
若相对弯度等于零,则中线与翼弦重合,称为max对称翼型。
(5) 翼展h机翼(或者叶片)在垂直于流动方向的最大长度h称为翼展(或者叶片高度)。
翼展与翼弦之比h/b称为展弦比。
根据展弦比的大小,可把机翼分为两种:一为无限翼展机翼(大展弦比),一为有限翼展机翼,如图10-1所示。
实际机翼翼展都是有限的,且翼弦b沿翼展是变化的。
§10-2 翼型升力原理翼型是具有一定的空气动力特性的几何型线。
2010年度《流体与叶栅》课程考题参考答案(上B)

《流体力学与叶栅理论》课程考试参考答案及评分标准(09-10学年春学期)(上B )一.回答下列各题(1—4题每题5分,5题10分,共30分) 1.什么是流体的连续介质模型?它在流体力学中有何作用?答:连续介质模型:流体连续地无空隙地充满它所占据的空间,在那里到处都具有流体的一切属性。
采用了这一假定之后,可用连续充满流动空间的流体质点代替大量的离散的分子,这样就可借助场的方法加以研究,也就可用数学分析这一有力工具来研究流体运动。
2.用工程单位制表示流体的速度、管径、运动粘性系数时,管流的雷诺数4Re 10=,问采用国际单位制时,该条件下的雷诺数是多少?为什么?答:该条件下的雷诺数仍是4Re 10=,因为雷诺数是无量纲准数,与单位制无关。
3.沿程阻力系数值λ与雷诺数Re 和相对粗糙度Δ/d 有什么关系?答:管流的沿程阻力系数λ与流体的流动状态Re 、流体特性(),,v ρυ以及管道材质(),d ∆有关。
具体来说,对于层流区、层流与紊流的过渡区、紊流水力光滑区:()Re f λ=;对于紊流水力过渡区:Re f d λ∆⎛⎫= ⎪⎝⎭,对于紊流水力粗糙区:f d λ∆⎛⎫= ⎪⎝⎭4.什么是迹线?什么是流线?在什么情况下流线与迹线重合?答:迹线是流体质点在运动过程中在流场中所描绘的曲线,是质点运动规律的几何表示,是时间过程形成的曲线。
流线是某固定时刻流场中的瞬时曲线,是流场的几何表示,是同一瞬时形成的曲线。
当流场定常时,迹线与流线重合。
5.常见的流速的测量方法有哪些?各有何特点? 答:常见的流速的测量方法有: (1) 皮托管。
原理:由皮托管分别测出总压0p 和静压p ,由能量方程求出速度V 。
201,2p p v v ρ=+∴= 特点:结构简单,使用方便,价格便宜;但对流场有干扰,且标定困难。
(2) 热线(膜)风速仪。
原理:利用高温物体在流场中放热与流速有关这一物理现象。
特点:动态响应高,测量精确;但对流场有干扰,探头极脆弱,稳定性差,且标定困难。
3 翼型和叶栅的空气动力特性解析

B、实际流体 由于实际流体存在粘性,流体绕流时, 在柱体表面要产生附面层。 绕流前:均匀平行流线 绕流中: a——前驻点,速度为零; b——速度不为零; 流场上下对称,在垂直于流动方向上, 无外力产生,即FL =0 。 流场左右不对称,在平行于流动方向 上,前半部流场中压力大于后半部流场, 产生一个沿流动方向的外力,称之为形状阻 力;此外由于流体的粘性会产生摩擦阻力。 故平行于流体运动方向,有阻力产生,即 FD ≠ 0 。 绕流后:均匀平行流线 a
a
b c
三、儒柯夫斯基升力定理
1、气流对孤立翼型的作用力 已知无穷远处来流速度为w∞ , 其方向与叶弦的夹角为α(称之为 来流攻角)。来流密度为ρ∞,流动 为不可压缩流动。 则在垂直于来流速度方向, 会产生一个升力Py,
P Py Px
α
w∞
Py w
其中, Γ为绕翼型的环量。 定义升力系数
3-1 翼型和叶栅参数
一、翼型几何参数
弦线
前缘点
c
θ
后缘点
x1
e a b
f
x2
型面 —— 叶型型线所包围的切面 中线 —— 叶型型线内切圆圆心的连线 b —— 弦长
θ
c
x1
e a b
f
x2
符号 c e f a x1 最大厚度
意义
符号
c c/b e e/b
f f/b
意义 最大相对厚度 最大厚度处的相对距离 中线最大相对挠度 最大挠度处的相对距离
叶栅进、出口速度图
w
1
β1
β
wm
w1 w2 ,平均气流速度 2
βm —— 平均气流角 wz —— 轴向分速度,此处令w1z= w2z = wz
02 第二节 机翼与叶栅的升力理论
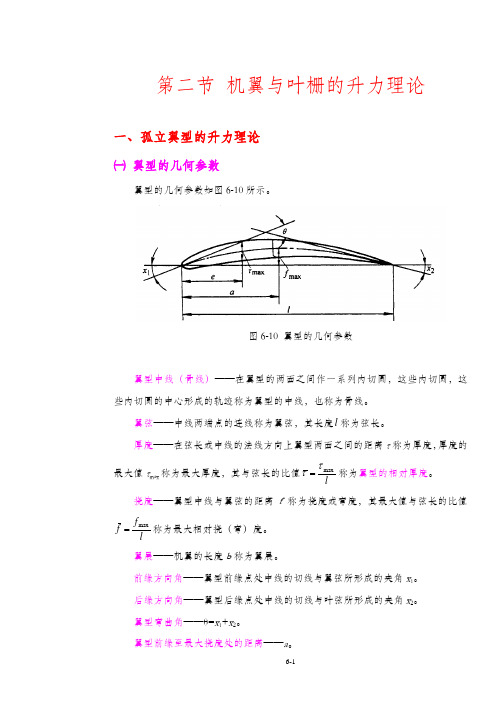
w∞ ——翼型前后无穷远处未受翼型影响的来流速度。 ▲说明
△如果介质是实际流体,则 F 力的大小与式(6-37)所计算的值有所偏差。
3、升力和阻力 ▲F 力可以看作是垂直于 w∞ 的升力 Fy 和平行于 w∞ 的阻力 Fx 的合力,如图 6-11 所示。
6-2
▲攻角 △来流 w∞ 与翼弦的夹角 α 称为攻角,如图 6-11 所示。
Fy
=
ρ mtw∞z ∆wu cos λ sin(b ∞ + λ)
b
(6 − 47)
由式(6-43)和式(6-47)可得
cy
l t
=
2 cos l sin 2 β ∞ ∆wu sin(β ∞ + l)w∞z
(6 − 48)
根据三角恒等式,上式还可以写成
cy
λ t
=
2∆wu w∞z
sin β ∞ 1 + tan λ / tan β ∞
参数。 ◇其倒数 t/l 称相对栅距。
翼型安放角——翼弦与列线方向之夹角 βb。 进口安放角——翼型前缘点中线的切线与圆周方向之夹角 βb1。 出口安放角——翼型后缘点中线的切线与圆周方向之夹角 βb2。 翼型弯曲角——θ=βb2-βb1。
⑵ 叶栅的动力特性 ▲叶栅绕流如图 6-17 所示。
▲说明 △叶栅绕流与孤立翼型绕流不同,由于栅中翼型有无穷多,因此对流场的扰 动可以传播到无穷远的地方,这样流场中就不再有未受扰动的流动速度 w∞,栅前 栅后足够远处的速度 w1 和 w2 的大小和方向都是不同的。
⑵ 平面直列叶栅 ▲ 圆柱面沿母线割开后,可以展开在平面上。 ▲圆柱面和各叶片相交,其截面(翼型剖面或翼型)在平面上构成一组叶栅。如 图:
流体动力学及叶栅理论

CR
R 1 2 v l 2
式中 R 为合力,而且此直线与横轴夹角就等于合力与来流的夹角; (3)上述直线斜率为
Cy Cx FY FX
即为在该点冲角下工作时的翼型升阻比;
(4)通过极曲线很容易确定翼型的最佳冲角——与ε最大值对应的冲角。过原点作极曲线的切线,其 切点所对应的冲角,就是最佳冲角。
5
5.2 翼型绕流的实验结果
在这一节里,介绍翼型气动方性能,随冲角及翼型几何形状变化的实验结果。
5.2.1 冲角对翼型气动力性能的影响
5.2.1.1 翼型的升力与阻力 在单翼型绕流情况下,由于沿翼展取为单位长,从而机翼面积:
A l 1 l
升、阻力公式(5-1)对翼型可写成:
2 v
FY C y FX C x
2
录
第5章
5.1 概 述
机翼及翼型特性
机翼一词,最早出现于航空工程,指的是飞机翅膀。如今它可用以泛指相对于流体运动的各种升 力装置。因此,流体机械中的工作轮叶片也可视为一个机翼。
5.1.1 机翼的几何特性
工程上引用机翼主要是为了获取升力,但由于在流体中运动的物体,不可避免地会遭受到流体阻 力的作用,因此对机翼性能的要求,首先就是尽可能大的升力 Fy 和尽量小的阻力 Fx,也就是希望具有 这就要求机翼采取适当的几何形状, 图 5-1 是一个低速机翼的一般外形图。 最佳的、 阻力比值ε=Fy/Fx。
f max
xf f max , xf l l
像厚度一样,这些相对值习惯上常用百分数表示:
f max xf
f max 100% l xf l 100%
(4)前、后缘圆角半径和后缘角 翼型前,后缘的曲率半径,叫做翼型的圆角半径,分别以 RL、RT 记之。它们的相对值 RL=RL/l、
《流体力学与流体机械》教学课件—10机翼与叶栅理论

中弧线的y坐标
局部厚度的一半
NACA翼型
NACA翼型是美国国家航空资讯委员会(National Advisory Committee for Aeronautics)所发表的 翼型系列,有以下常用的系列翼型:
(1)NACA四位数字翼型
厚度方程为: 最大厚度
1
2i
C
f (z) z z0
dz
0, z0在C外
f
(
z
0
),
z
0
在C内
第四节 儒可夫斯基翼型 与保角变换法
一、保角变换法求解平面势流
利用解析的复变函数 z =f(ζ)将ζ平面上的圆域变换
成z平面上的实用域。
Z
y
z
Cz
ζ
η
Cζ
o
V∞z αz
x
V∞ζ
o
αζ
ξ
注意:
保角变换过程中,同一点两个线段的夹角在变换过 程中保持不变。
机翼一部分是由流过上表面的空气把它吸 起来的,且上表面产生的负压对全部升力的 贡献大于下表面的贡献。
吸力
压力系数分布曲线
压力
较大攻角翼型绕流
翼型表面压强的分布
大攻角翼型绕流
流体绕过翼型时要产生升力,是由于翼型 上下表面速度不同造成压强分布的不同。 将上下翼面速度分布的差异视为均匀的无 穷远来流与由翼型形成的有一定环量的环 流两者叠加而成。 升力的大小与流体绕流翼型的环量Γ成正比, 即
f (z)
f
(z0
)
(z
z0
)
f
'(z0
)
(z
z0 n!
)n
第10章(机翼与叶栅理论6-7)

将式(1)、式(2)改写成标量形式:
v x av1 x bv2 x v y ' av1 y ' bv2 y ' v y ' ' av1 y ' ' bv2 y ' '
a
v x v2 y 'v2 x v y ' v1 x v2 y 'v2 x v2 y '
b
1 ' ' 2 ' ' ' ' K 1 ' 2 ' '
表示单位栅前速度环量变化所造成的栅后 速度环量的变化。
系数K、i0的物理意义 t→0,栅后速度方向不受栅前流动影响而保 持恒定,因此K=0; t→∞,视为孤立翼型,栅前、后足够远处 速度相同,因此K=1。 当t→0,b/t →∞时,流体无法穿过叶栅, 当t→∞,b/t →0时,流体完全穿过叶栅, 故特征系数K称为叶栅的穿透系数,0≤K≤1。
第六节 叶栅及叶栅特征方程
叶片式水力机械的转轮、导叶轮都由若干 个相同的叶片或翼型按相互等距离排列组 成,叶片或翼型之间将彼此相互影响。 按 照一定规律排列起来而又相互影响的叶片 或翼型的组合,叫做翼栅或叶栅。 叶栅理论的目的在于寻找叶栅与流体之间
相互作用的运动学和动力学规律,以及影
响这些规律的各种因素,是叶片式水力机
式(5)即为静止直列叶栅前、后流动的特 征方程。 上式中,Γ’’是圆柱流面出口处的速度环量, Γ’是进口处的速度环量,Q是两径向距离为 1的圆柱流面间的流量。
系数K、i0的物理意义 两个流量相同、绕流同一叶栅的不同流动, 它们的特征方程为:
1 ' ' K1 '(1 K )i0Q
流体动力学及叶栅理论.

流体动力学及叶栅理论课程小结《流体动力学及叶栅理论》下篇课程主要包括流体动力学和叶栅理论两部分。
其中流体动力学的主要内容是:流体力学性质及概念、流体运动的基本方程、平面有势流动、势流叠加、旋涡理论等。
叶栅理论主要内容是:机翼及翼型特性、茹科夫斯基翼型、薄翼绕流及有限机翼理论、叶栅及叶栅特性方程、平面叶栅绕流求解方法等。
一、流体动力学流体力学是研究流体平衡和运动的规律以及它与固体间的相互作用的科学。
流体力学性质及概念:包括流体的流动性和粘滞性(相互运动时的内摩擦力产生的)、迹线(流体为团运动的轨迹线)、流线(指某时刻t时,连接流场中各点流体微团运动方向的光滑曲线)、微团分析(流体微团具有平移、旋转及变形的特征)等。
流体运动的基本方程:包括连续性方程、动量方程与动量矩方程、纳维-斯托克斯方程、欧拉方程(粘度为零的方程)、能量方程等。
平面有势流动:包括均匀流(流动过程中运动要素不随坐标位置(流程)而变化)、平面源、汇(与平面源的流向相反)、点涡(环流)、偶极子等基本概念,速度势函数和流函数,简单平面势流、偶极流、有环量绕流和无环量绕流(两者相差一个点窝)等。
势流叠加:包括源流和均匀流叠加、等强度源和汇流与直线流叠加、偶极流、圆柱绕流、汇流和环流的叠加、以及其他由两种或两种或以上的基本势流叠加等。
旋涡理论:包括涡线、涡管、涡束、涡通量(旋涡强度)等基本概念,开尔文-汤姆逊定理、斯托克斯定理(当封闭周线内有涡束时,则沿封闭轴线的速度环量等于该封闭周线内所有涡束的涡通量之和),亥姆兹定理(包括第一定律、第二定律和第三定律),二元旋涡内外压力分布等。
二、叶栅理论1、机翼及翼型机翼的外形以椭圆形状最为有利,但由于制造上的困难难,实际多采用与椭圆相近的形状。
翼型指的是顺着来流方向切下来的剖面。
翼型通常都具有流线型外形,头部圆滑,尾巴尖瘦,背(上弧)稍拱曲,腹(下弧)的形状则有凹的、凸的、半凹半凸的及平的。
机翼几何参数:机翼翼展b、机翼面积A、平均翼弦lm(A/b)、展翼比 (b/lm)、翼弦l、翼型厚度d(最大的叫翼型最大厚度dmax)、翼型弯度f、前、后缘圆角半径。
流体力学与流体机械——第10章(机翼与叶栅理论4b)

2
x2
b2
8f
0.385t
1
2x b
1
2x b
2
1.4.P18
平面上的复位势为
W
mei
ei
a2 mei
ei
i 2
ln
mei a
由此式可得W(z)。
其环量为
b
1
0.77
t b
sin
2f b
升力系数为
Cl
2
1
0.77
t b
sin
2f b
可见,增大翼型厚度和弯度与增大攻角一样,可
曲线方程为
y
2c
1
x 2c
1
x 2c
2
翼型表面方程也可记为
y
0.385t
1
2
x b
1
2
x b
2
式中t 2 ymax
式中b —— 弦长
1.4.P13
对于 平面绕圆流动有复位势
W
m ei
a2 ei m
i 2
ln
m a
可由此求得 W z。
环量为 4
c
1
sin
变换到 z 平面上环量为
b sin
dቤተ መጻሕፍቲ ባይዱ f b
1.4.P16
圆弧翼型升力为
L
v
2
b
sin(
2f b
)
升力系数
Cl
2 sin
2f b
(六)儒可夫斯基翼型绕流
图示 平面上圆心在二象限的圆,变换后得 z 平面上的儒可夫斯基翼型。
1.4.P17
此变换可看成是前述变换的叠加。其曲线方程为
叶栅理论

Rx , Ry 用 wmx , wmy 表示为: Rx = ρwmy ( w2 y w1 y ) t Ry = ρ wmx ( w2 y w1 y ) t
(7)
下面求绕翼型的环量(设法将式(7)表示成 R = ρ wmΓ 的形式)
Γ = ∫ABCDA wS ds = ∫AB wS ds + ∫BC wS ds + ∫CD wS ds + ∫DA wS ds
1 2 p1 p2 = ρ ( w2 y w12y ) 2
(5)
Rx , Ry 可表示为:
1 2 Rx = ρ ( w2 y w12y ) t 2 Ry = ρ wx ( w2 y w1 y ) t
(6)
现定义一个平均流速
1 wm = ( w1 + w2 ) 2
分量形式为:
1 wmx = ( w1x + w2 x ) = wx 2 1 wmy = ( wy1 + w2 y ) 2
t 叶栅中两相邻翼型上相应点的的距离叫栅距,常用 表示。对环列叶栅不引用 2π 这一参数,而用角距 ( n 表示叶片数)替代。
n
5.安放角 。 叶型的弦和列线的夹角 β S ,称为安放角(叶型的安放角) 叶型的中线在前后缘的切线与列线的夹角 β S 1 、 β S 2 称为进出口安放角。 对环列叶栅,只定义进出口安放角。 6.稠密度 弦长 b 与栅距 t 之比 叫做叶栅的稠密度,把它的倒数称为相对叶栅,对环列 叶栅不引用这一参数。 二、叶栅分类 根据水力机械常用分类方法,介绍如下: 1.平面叶栅 流经叶栅流道的流动是平面流动,如:水轮机导叶叶栅、低比转数水泵、 水轮机转轮叶栅。 对轴流式水泵、水轮机、风机等转轮叶栅可展成平面,即将圆柱面展成平 面,则也可称为平面叶栅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
儒可夫斯基假设最简单的敘述是:在实际流动中无限大的 速度是不允许的。
库塔---儒可夫斯基定理描述了升力与环量的关系,没有环 量,就没有升力。而且升力方向垂直于来流速度;如果绕物体 的流动为势流并且不发生分离,平行于来流方向上没有力(阻力), 阻力仅由边界层内表面摩擦产生。
第十一章 翼型与叶栅理论
翼型的几何参数 翼型的气动参数 儒可夫斯基变换 库塔—儒可夫斯基原理 叶栅理论 二维叶栅流动理论 离心泵及内流图例
翼型的几何参数
翼型的气动参数
升力 阻力 俯仰力矩
儒可夫斯基变换
z
1 2
b2
儒可夫斯基变换在平板绕流问题中的应用
叶栅理论
按照一定规律排列起来的相同机翼,叫做翼栅。 翼栅理论是研究翼栅绕流规律的,是单个翼型绕流的推广。 在叶片式流体机械方面应用极广泛,故翼栅也称叶栅,组成它 的机翼也因此称为叶片。
叶栅的几何参数: 列线:叶栅中叶片上对应点连线(直线和圆周线)。 栅轴:与列线垂直的直线。 叶型:叶片与过列线之流面相交所得截面。 栅距:同一列线上,两相邻的对应点间线段长度。 安放角:弦与列线的夹角。 疏密度:弦长与栅距之比,倒数为相对栅距。
(b)
Ry wx (w'y' w'y )t
在上下游断面AD与BC处列出伯努利方程:
p' 1 2
wx2 w'y2
p''
1 2
(wx2
w'y' 2 )
从而:
p' p'' 1 2
w'' 2 y
w'y 2
代入方程(b):
Rx
1 2
(w'y' 2
对控制线内流体列出沿坐标方向动量方程
( p' p'' )t Rx q(wx'' wx' )
Ry q(w'y' w'y )
(a)
由连续性方程得:
q wx' t wx''t
从而: wx' wx'' wx
代入方程(a): Rx ( p' p'' )t
有时称 ( ) 为绝对攻角
二元机翼中:
CL
FL
b v02
2
对于儒可夫斯基翼型:
b 4R
故升力系数为:
CL
v0 2 Rv0 sin( 4Rv02 / 2
)
(
)
对于小的绝对攻角,升力系数随绝对攻角线性增加,迫近 失 速角时,升力会急剧下降。
库塔—儒可夫斯基原理
w'y2 )t
(c)
Ry wx (w'y' w'y )t
令:
w
1 2
w' w''
写成分量式:
wx wx
1
wy 2
w'y w'y'
代入方程组 (c):
Rx wy (w'y' w'y )t
(d)
Ry wx (w'y' w'y )t
静止流场中有一翼型,翼型起动前,整个流场无旋; 翼型起动并达到图示速度,此时后缘点处速度达到很大的值,压力 很低,机翼下侧面流体绕过后缘点流向驻点,流体同低压流向高压,流 动产生分离,产生逆时针旋涡随流体向尾部移动,在尾部脱落; 总环量为零,在翼型上同时产生一个脱落涡强度相同而方向相反的 涡,这个涡的作用使驻点向后缘点移动,在沿未达到后缘点时,不断有 逆时针旋涡产生并脱落,而在翼型上涡的强度也将继续加强。 不断脱落流向下游的涡称为起动涡,附在翼型上的涡称为附着涡; 驻点移至后缘点后,上下两股流动在后缘汇合,不再有涡脱落,附着涡 的强度也不再变化,机翼环量值对应均匀直线来流情况下翼型绕流的环 量值。
取”+”,取板外区 域
得:
W (z) 2iv z2 a2
由条件:
dW dz
z
i
v0
dW dz
z
2iv
z z2 a2
z
2iv
速度关系: v0 2v W i v0 z2 a2
儒可夫斯基翼型绕流
无环量时:
W(
)
计算绕叶型的环量:
ABCDA wsds AB wsds w'y'
dy
BC
代入方程组(d)得:
DC wsds w'y
dy
AD
(w'y' w'y )t
lei
2
2
i
1
lei
由图示得:
lei b Rei( )
故在 b 处:
dW
d
1 2
v0
1 e2i( )2i
ei( )i 0
2 Ri
解得:
2 Rv0 sin( )
己知: 旋转变换:
W ( ) v (
a2 )
i
1 e 2 i i1
W
( 1 )
v
(i 1
a2i
1
)
iv
(
1
a2
1
)
儒可夫斯基变换:
z
1 2
( 1
a2
1
)
1
2
z
a2
1
2 1
2z1
a2
0
1 z z2 a2
lei
b 映射为: z b
后缘点复速度为: 后缘点处:
dW dW d
dz A d dz A
dz
d
1 2
1
b2
2
b
0
故若使后缘点复速度为有限值,必须满足:
dW 0
d
则:
dW
d
1 2
v0
类
平面叶栅与空间叶栅 直列叶栅与环列叶栅 不动叶栅与运动叶栅
叶栅绕流的正反问题
正问题:给定叶栅和栅前无穷远处的来流,要求 确定叶片表面及其周围空间的流速分布及栅后无 穷远处的流动情况。
反问题:给定叶栅前、后无穷远处的速度及某些 叶栅几何参数,要求作出叶栅。
二维叶栅流动理论
理想流体绕流时叶栅受力
1 2 v0
lei
ei
R2ei
lei
z
1 2
b2
同样会得出后缘点处速度无穷大的结论。
有环量时:
W(
)
1 2
v0
lei
ei
R2ei
lei
ln
2i
