平行线辅助线的作法
平行线中常见作辅助线的技巧的九种类型

( 2 ) 如 图 ① , 在 AB ∥ DE 的 条 件 下 , 你 能 得 出 ∠ B , ∠BCD,∠D之间的数量关系吗?请说明理由. 解:∠B+∠BCD+∠D=360°.理由如下: 因为CF∥AB,所以∠B+∠BCF=180°. 因为AB∥DE,所以CF∥DE. 所以∠FCD+∠D=180°. 所以∠B+∠BCF+∠FCD+∠D=180°+ 180°,即∠B+∠BCD+∠D=360°.
6.如图,AB∥DE,则∠BCD,∠B,∠D有何关系?为什么?
解:∠BCD=∠B-∠D.理由如下: 如图,过点C作CF∥AB,所以∠B=∠BCF. 因为AB∥DE,CF∥AB,所以CF∥DE. 所以∠DCF=∠D.所以∠B-∠D=∠BCF-∠DCF. 因为∠BCD=∠BCF-∠DCF, 所以∠BCD=∠B-∠D.
解:AB∥CD.理由如下: 如图,连接 BD. 在三角形 BDE 中,∠1+∠2+∠E=180°. 因为∠E=∠3+∠4, 所以∠1+∠2+∠3+∠4=180°, 即∠ABD+∠CDB=180°. 所以 AB∥CD.
2.【2020·攀枝花】如图,平行线AB,CD被直线EF所截, 过点B作BG⊥EF于点G,已知∠1=50°,则∠B= ( C) A.20° B.30° C.40° D.50°
BS版平行线中常见作辅助线的技巧的九种
类型
提示:点击 进入习题
1 见习题 2C 3 见习题 4 见习题
5 见习题 6 见习题 7 见习题 8 见习题 9 见习题
答案显示
1.如图,∠E=∠B+∠D,猜想AB与CD有怎样的位 置关系,并说明理由.
【点拨】本题可通过连接 B,D 两点构造截线,进而利用平行线 的判定说明 AB∥CD.
4 . ( 1 ) 如 图 ① , 若 AB ∥ DE , ∠ B = 135° , ∠ D = 145°,求∠BCD的度数.
平行线中添辅助线的方法

平行线中添辅助线的方法在几何学中,平行线是指在同一个平面内,永远不会相交的线。
平行线可以用于解决许多几何问题。
有时,为了更好地理解和解决问题,我们可能需要在已知的平行线中添加辅助线。
这篇文章将介绍一些经常在平行线中添加辅助线的方法,以及如何利用这些辅助线解决几何问题。
方法一:创建平行线之间的等距线段这是最常见的方法之一,可以通过创建平行线之间的等距线段来添加辅助线。
这个方法可以在几何证明中使用,以创建所需的形状或角度。
下面是一个例子:假设有两个平行线AB和CD,在这两条平行线上选择两个等距点E和F。
然后,通过连接EF,你就创建了一个辅助线,使得EF平行于AB和CD。
这样,你就可以利用这个平行四边形来证明或解决其他几何问题。
方法二:使用交叉线段这个方法涉及到在平行线上选择一个点,并通过它绘制一条与其他平行线相交的线段。
这种方法通常用于证明几何性质。
例如,假设有两个平行线AB和CD,我们可以在AB上选择一个点E,并通过它绘制一条线段EF与CD相交。
然后,通过观察EF与AB的关系,可以证明一些三角形的性质或者其他几何关系。
方法三:利用平行线之间的相似三角形利用平行线之间的相似三角形是另一种常用的方法。
通过观察平行线和与它们相交的第三条线,可以找到相似的三角形。
然后,利用这些相似三角形的性质来解决几何问题。
例如,假设有两个平行线AB和CD,以及一条与它们相交的第三条线EF。
通过观察,可以发现三角形ADE与三角形BCF相似。
这意味着可以使用相似三角形的性质来计算未知角度或线段的长度。
方法四:利用中位线和对角线这个方法通常涉及到在平行线形成的平行四边形中绘制中位线或对角线。
中位线是连接平行四边形两对相对顶点的线段,对角线是连接两对非相邻顶点的线段。
这些辅助线可以帮助我们找到形状的性质,或计算线段的长度。
例如,假设有一个平行四边形ABCD,你可以通过绘制对角线AC来创建两个互相重叠的三角形ABC和ADC。
通过观察这些三角形的性质,可以得出许多结论,例如它们的面积相等或角度相等。
几何证明题辅助线基本方法

几何证明题辅助线基本方法几何证明题是数学中的一种重要题型,需要通过逻辑推理和几何知识来证明给定的几何关系。
在解决几何证明题时,辅助线是一种常用的策略,可以帮助我们简化问题、构建更简洁的证明过程。
本文将介绍几何证明题中常用的辅助线基本方法。
1. 平行辅助线法当我们需要证明两条线段平行时,可以在图形中引入一条辅助线来构建平行关系。
具体步骤如下:1. 观察图形,找到可能存在平行关系的线段。
2. 在相应的位置引入一条辅助线。
3. 利用平行线的性质进行推理,证明所需的平行关系。
2. 相等辅助线法当我们需要证明两个线段相等时,可以通过引入一条相等的辅助线来简化证明过程。
具体步骤如下:1. 观察图形,找到可能具有相等关系的线段。
2. 在相应的位置引入一条相等的辅助线。
3. 利用等边、等角等性质进行推理,证明所需的相等关系。
3. 垂直辅助线法当我们需要证明两条线段垂直时,可以通过引入一条垂直的辅助线来简化证明过程。
具体步骤如下:1. 观察图形,找到可能具有垂直关系的线段。
2. 在相应的位置引入一条垂直的辅助线。
3. 利用垂直线的性质进行推理,证明所需的垂直关系。
4. 同位角辅助线法当我们需要证明两条直线的同位角相等时,可以通过引入同位角的辅助线来简化证明过程。
具体步骤如下:1. 观察图形,找到可能存在同位角的直线。
2. 在相应的位置引入同位角的辅助线。
3. 利用同位角的性质进行推理,证明所需的同位角相等关系。
5. 其他辅助线方法除了上述介绍的常用辅助线方法外,还可以根据具体的几何证明题目选择其他辅助线的方法。
例如,可以利用中位线、角平分线、内切圆、外接圆等辅助线,根据题目要求灵活运用。
综上所述,几何证明题辅助线基本方法包括平行辅助线法、相等辅助线法、垂直辅助线法、同位角辅助线法等。
通过合理引入辅助线,可以帮助我们简化问题、构建更简洁的证明过程,提高解题效率。
在实际解题中,我们需要综合运用不同的辅助线方法,根据题目要求灵活选择适合的策略。
数学作辅助线的方法

作辅助线的方法一:中点、中位线,延线,平行线.如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的.二:垂线、分角线,翻转全等连.如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生.其对称轴往往是垂线或角的平分线.三:边边若相等,旋转做实验.如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生.其对称中心,因题而异,有时没有中心.故可分“有心”和“无心”旋转两种.四:造角、平、相似,和、差、积、商见.如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关.在制造两个三角形相似时,一般地,有两种方法:第一,造一个辅助角等于已知角;第二,是把三角形中的某一线段进行平移.故作歌诀:“造角、平、相似,和差积商见.”(托列米定理和梅叶劳定理的证明辅助线分别是造角和平移的代表)五:两圆若相交,连心公共弦.如果条件中出现两圆相交,那么辅助线往往是连心线或公共弦.六:两圆相切、离,连心,公切线.如条件中出现两圆相切(外切,内切),或相离(内含、外离),那么,辅助线往往是连心线或内外公切线.七:切线连直径,直角与半圆.如果条件中出现圆的切线,那么辅助线是过切点的直径或半径使出现直角;相反,条件中是圆的直径,半径,那么辅助线是过直径(或半径)端点的切线.即切线与直径互为辅助线.如果条件中有直角三角形,那么作辅助线往往是斜边为直径作辅助圆,或半圆;相反,条件中有半圆,那么在直径上找圆周角——直角为辅助线.即直角与半圆互为辅助线.八:弧、弦、弦心距;平行、等距、弦.如遇弧,则弧上的弦是辅助线;如遇弦,则弦心距为辅助线.如遇平行线,则平行线间的距离相等,距离为辅助线;反之,亦成立.如遇平行弦,则平行线间的距离相等,所夹的弦亦相等,距离和所夹的弦都可视为辅助线,反之,亦成立.有时,圆周角,弦切角,圆心角,圆内角和圆外角也存在因果关系互相联想作辅助线.九:面积找底高,多边变三边.如遇求面积,(在条件和结论中出现线段的平方、乘积,仍可视为求面积),往往作底或高为辅助线,而两三角形的等底或等高是思考的关键.如遇多边形,想法割补成三角形;反之,亦成立.另外,我国明清数学家用面积证明勾股定理,其辅助线的做法,即“割补”有二百多种,大多数为“面积找底高,多边变三边”。
做数学怎么懂得做辅助线方法

做数学怎么懂得做辅助线方法几何最难的地方就是辅助线的添加了,但是对于添加辅助线,还是有规律可循的,下面给大家分享一些关于做数学怎么懂得做辅助线方法,希望对大家有所帮助。
一.三角形中常见辅助线的添加1. 与角平分线有关的(1) 可向两边作垂线。
(2)可作平行线,构造等腰三角形(3)在角的两边截取相等的线段,构造全等三角形2. 与线段长度相关的(1) 截长:证明某两条线段的和或差等于第三条线段时,经常在较长的线段上截取一段,使得它和其中的一条相等,再利用全等或相似证明余下的等于另一条线段即可(2) 补短:证明某两条线段的和或差等于第三条线段时,也可以在较短的线段上延长一段,使得延长的部分等于另外一条较短的线段,再利用全等或相似证明延长后的线段等于那一条长线段即可(3)倍长中线:题目中如果出现了三角形的中线,方法是将中线延长一倍,再将端点连结,便可得到全等三角形。
(4)遇到中点,考虑中位线或等腰等边中的三线合一。
3. 与等腰等边三角形相关的(1)考虑三线合一(2)旋转一定的度数,构造全都三角形,等腰一般旋转顶角的度数,等边旋转60 °二.四边形中常见辅助线的添加特殊四边形主要包括平行四边形、矩形、菱形、正方形和梯形.在解决一些和四边形有关的问题时往往需要添加辅助线。
下面介绍一些辅助线的添加方法。
1. 和平行四边形有关的辅助线作法平行四边形是最常见的特殊四边形之一,它有许多可以利用性质,为了利用这些性质往往需要添加辅助线构造平行四边形。
(1) 利用一组对边平行且相等构造平行四边形(2)利用两组对边平行构造平行四边形(3)利用对角线互相平分构造平行四边形2. 与矩形有辅助线作法(1)计算型题,一般通过作辅助线构造直角三角形借助勾股定理解决问题(2)证明或探索题,一般连结矩形的对角线借助对角线相等这一性质解决问题.和矩形有关的试题的辅助线的作法较少.3. 和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线,借助菱形的判定定理或性质定定理解决问题.(1)作菱形的高(2)连结菱形的对角线4. 与正方形有关辅助线的作法正方形是一种完美的几何图形,它既是轴对称图形,又是中心对称图形,有关正方形的试题较多.解决正方形的问题有时需要作辅助线,作正方形对角线是解决正方形问题的常用辅助线三.圆中常见辅助线的添加1. 遇到弦时(解决有关弦的问题时)常常添加弦心距,或者作垂直于弦的半径(或直径)或再连结过弦的端点的半径。
第3讲 平行线辅助线(学生版)

第3讲平行线辅助线一、知识回顾:在解决平行线的问题时,当无法直接得到角的关系或两条线之间的位置关系时,通常借助辅助线来帮助解答,如何作辅助线需根据已知条件确定,辅助线的添加既可以产生新的条件,又能将题目中原有的条件联系在一起.一、加截线(连接两点或延长线段)1.如图,已知AB∥CD,∠ABF=∠DCE.∠BFE与∠FEC有何关系?并说明理由.(第1题)【解析】:∠BFE=∠FEC.理由一:连接BC,如图①.∵AB∥CD,∴∠ABC=∠BCD(两直线平行,内错角相等).又∵∠ABF=∠DCE,∴∠ABC-∠ABF=∠BCD-∠DCE,即∠FBC=∠ECB.∴BF∥CE(内错角相等,两直线平行).∴∠BFE=∠FEC(两直线平行,内错角相等).(第1题)理由二:延长AB,CE相交于点G,如图②.∵AB∥CD,∴AG∥CD.∴∠DCE=∠G(两直线平行,内错角相等).又∵∠ABF=∠DCE,∴∠ABF=∠G.∴BF∥CG(同位角相等,两直线平行).∴∠BFE=∠FEC(两直线平行,内错角相等).二、过“拐点”作平行线a.“”形图2.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.(第2题)【解析】:方法一:过点P作射线PN∥AB,如图①.∵AB∥CD,∴PN∥CD.∴∠4=∠2=25°.∵PN∥AB,∴∠3=∠1=32°.∴∠BPC=∠3+∠4=57°.(第2题)方法二:过点P作射线PM∥AB,如图②.∵AB∥CD,∴PM∥CD.∴∠4=180°-∠2=180°-25°=155°.∵AB∥PM,∴∠3=180°-∠1=180°-32°=148°.∴∠BPC=360°-∠3-∠4=360°-148°-155°=57°. 方法三:连接BC,略。
初二做辅助线的技巧

初二做辅助线的技巧初二时学习数学,辅助线是一个非常重要的技巧。
辅助线可以帮助我们更好地理解和解决各种数学问题。
下面我将介绍一些初二做辅助线的技巧。
我们来看一下如何在几何图形中使用辅助线。
在求解几何问题时,辅助线可以帮助我们找到一些隐藏的几何关系,从而简化问题。
比如,在求解平行线问题时,我们可以通过画一条与已知直线平行的辅助线,来找到与所求直线平行的线段。
通过这样的辅助线,我们可以很容易地得到所求的答案。
在代数中,辅助线同样可以发挥重要的作用。
比如,在解方程的过程中,我们可以通过引入一个新的变量来构造一个辅助方程,从而简化问题。
通过这个辅助方程,我们可以得到原方程的解。
在解决分数运算问题时,辅助线也是一个非常有用的工具。
当我们需要对两个分数进行比较或运算时,可以通过引入一个相同的分母来简化计算。
这个相同的分母就是我们引入的辅助线,通过它,我们可以将分数转化为整数,从而更方便地进行计算。
在解决几何问题时,辅助线还可以帮助我们证明定理。
通过引入一些辅助线,我们可以得到一些额外的几何关系,从而证明所要证明的定理。
这种方法在解决几何证明问题时非常常用。
除了上述的几种情况,辅助线还可以用于解决其他类型的数学问题。
无论是代数、几何还是其他数学领域,辅助线都是一个非常有用的工具。
通过合理地使用辅助线,我们可以将原来复杂的问题简化为易于理解和解决的问题。
初二做辅助线是一个非常重要的技巧。
通过合理地使用辅助线,我们可以更好地理解和解决各种数学问题。
在几何中,辅助线可以帮助我们找到隐藏的几何关系;在代数中,辅助线可以简化方程的解法;在分数运算中,辅助线可以简化计算;在几何证明中,辅助线可以帮助我们证明定理。
在解决其他类型的数学问题时,辅助线同样是一个非常有用的工具。
通过合理地使用辅助线,我们可以更好地理解和解决各种数学问题。
希望以上的介绍能够帮助到大家,提高大家的数学水平。
中考数学-全等三角形问题中常见的8种辅助线的作法

全等三角形问题中常见的辅助线的作法(有答案)总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变D C BAED F CB A换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
初中数学几何做辅助线方法技巧

初中数学几何做辅助线方法技巧初中数学里面,几何这个部分是比较重要的,因为对我们日后的学习和生活有一定的帮助。
在学习几何的过程中,我们常常需要用到做辅助线的方法来帮助我们更好的理解和解决问题。
下面是关于初中数学几何做辅助线方法技巧的介绍。
1. 画出平行线在处理一些证明题或求几何中的相关数据时,使用画一条平行线的方法,这条线起到辅助线的作用。
具体来说,我们可以根据题目已知的条件,画出一条平行于两条线的直接过这两条线的平行线。
这样做可以帮助我们更好的理解题目所需要求解的问题。
2. 画出垂线在几何中,垂线是非常重要的一种线。
垂线可以将一条线分成两段,并且在某些时候可以帮助我们求解一些困难的问题。
具体的做法是在需要求解的点上,画出一条线段与目标线段垂直相交。
3. 构造相似三角形有时候在处理一些题目时,不好直接得出一个结论或者一些数据,使用相似三角形来帮助我们更好的理解和求解问题。
相似三角形有一个共同的特点就是它们的对应角度相等,边长成比。
具体的做法是在画图的时候,根据题目条件构造一个相似三角形,利用等比例关系求解相关数据或者结论。
4. 利用勾股定理在解析几何中,勾股定理是一个非常重要的公式,它在很多问题中都有很大的帮助。
利用勾股定理可以求出直角三角形的三个边长。
同时在画图的时候,也可以利用勾股定理来帮助画出直角三角形。
5. 使用比例关系在某些问题中,我们可能需要根据已知条件来求出一些距离或长度之类的数据。
在这种情况下,我们可以通过比例关系来帮助我们快速求解。
具体的做法是在画图的时候,根据已知条件构造出一定的比例关系,在求出需要的数据。
6. 构造平行四边形和等边三角形利用平行四边形和等边三角形来帮助我们求解问题也是一个非常不错的方法。
具体的做法是在求解相关问题时,根据已知条件或者所求的条件,在画出平行四边形或者等边三角形,利用它们的性质来求解所需要求解的问题。
几何学是一个非常重要的数学分支,它在我们的生活中起着非常重要的作用。
初中数学常见辅助线做法

初中数学常用辅助线一.添辅助线有二种情况:1按定义添辅助线:如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。
2按基本图形添辅助线:每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往就是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”!这样可防止乱添线,添辅助线也有规律可循。
举例如下:(1)平行线就是个基本图形:当几何中出现平行线时添辅助线的关键就是添与二条平行线都相交的等第三条直线(2)等腰三角形就是个简单的基本图形:当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
(3)等腰三角形中的重要线段就是个重要的基本图形:出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段就是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点就是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
(6)全等三角形:全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形:或添对称轴,或将三角形沿对称轴翻转。
高中立体几何辅助线技巧简述

高中立体几何辅助线技巧简述高中立体几何是数学中的一门重要分支,它主要研究空间中各种几何体的性质和相互关系。
在解决立体几何问题时,辅助线技巧是非常实用的工具。
通过巧妙地引入辅助线,可以简化问题的解决过程,提高解题效率。
本文将简要介绍一些常用的高中立体几何辅助线技巧,帮助读者更好地理解和应用这些方法。
一、平行线辅助线技巧在解决与平行线相关的立体几何问题时,可以尝试通过引入平行线辅助线来简化问题。
具体而言,可以考虑以下两种情况:1. 使用平行线比例关系当需要求解立体几何体的长度比或面积比时,可以尝试通过引入平行线辅助线来构造相应的比例关系。
在求解平行四边形的面积比时,可以通过连接对角线,将平行四边形分割成两个三角形,从而利用三角形面积公式求解面积比。
2. 使用平行线截线关系当需要求解立体几何体内部的长度或角度关系时,可以考虑通过引入平行线截线关系来简化问题。
在求解空间中两条直线的夹角时,可以通过引入一条与之平行的辅助线,从而将问题转化为求解两条平行线与辅助线的夹角,利用平行线夹角定理求解出所需的夹角值。
二、相似三角形辅助线技巧在解决与相似三角形相关的立体几何问题时,可以尝试通过引入相似三角形辅助线来简化问题。
具体而言,可以考虑以下两种情况:1. 使用相似三角形比例关系当需要求解立体几何体的长度比或面积比时,可以尝试通过引入相似三角形辅助线来构造相应的比例关系。
在求解棱锥的体积或表面积比时,可以通过在棱锥中引入一条高线,构造出两个相似三角形,从而利用相似三角形的边比关系求解出所需的比例值。
2. 使用相似三角形角度关系当需要求解立体几何体内部的角度关系时,可以尝试通过引入相似三角形辅助线来简化问题。
在求解棱锥的顶角时,可以通过在棱锥中引入一条高线,构造出一个与之相似的三角形,从而将该问题转化为求解相似三角形的对应角度关系,进而得到所需的顶角值。
三、垂线辅助线技巧在解决与垂线相关的立体几何问题时,可以尝试通过引入垂线辅助线来简化问题。
人教版数学第5章平行线的性质与判定及辅助线模型

平行线判定和性质以及四大模型汇总第一部分平行线的判定判定方法l:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知∠1=∠2,则AB∥CD(同位角相等,两直线平行);若已知∠1=∠3,则AB∥CD(内错角相等,两直线平行);若已知∠1+ ∠4= 180°,则AB∥CD(同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.第二部分平行线的性质性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补第三部分平行线的四大模型模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°;结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.模型二“猪蹄”模型(M模型)点P在EF左侧,在AB、CD内部“猪蹄”模型结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.模型三“臭脚”模型点P在EF右侧,在AB、CD外部“臭脚”模型结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.模型四“骨折”模型点P在EF左侧,在AB、CD外部“骨折”模型结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.第四部分平行线的四大模型证明(1)已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°.(2)已知∠P=∠AEP+∠CFP,求证AE∥CF.(3)已知AE∥CF,求证∠P=∠AEP-∠CFP.(4)已知∠P= ∠CFP -∠AEP,求证AE //CF.第五部分平行线的四大模型的应用案例1如图,a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠l+∠2+∠3= .2如图,AB∥CD,且∠A=25°,∠C=45°,则∠E的度数是.3如图,已知AB∥DE,∠ABC=80°,∠CDE =140°,则∠BCD= .4如图,射线AC∥BD,∠A= 70°,∠B= 40°,则∠P= .5如图所示,AB ∥CD ,∠E =37°,∠C = 20°,则∠EAB 的度数为 .6 如图,AB ∥CD ,∠B =30°,∠O =∠C .则∠C = .7如图,已知AB ∥DE ,BF 、 DF 分别平分∠ABC 、∠CDE ,求∠C 、 ∠F 的关系.8如图,已知AB ∥DE ,∠FBC =n 1∠ABF ,∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ; (2)若n =3,试探宄∠C 、∠F 的关系;(3)直接写出∠C 、∠F 的关系 (用含n 的等式表示).9如图,已知AB ∥CD ,BE 平分∠ABC ,DE 平分∠ADC .求证:∠E = 2 (∠A +∠C ) .10如图,己知AB∥DE,BF、DF分别平分∠ABC、∠CDE,求∠C、∠F的关系.11如图,∠3==∠1+∠2,求证:∠A+∠B+∠C+∠D= 180°.12如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠l+∠2= 90°,M、N分别是BA、CD的延长线上的点,∠EAM和∠EDN的平分线相交于点F则∠F的度数为().A. 120°B. 135°C. 145°D. 150°133如图,直线AB∥CD,∠EF A= 30°,∠FGH= 90°,∠HMN=30°,∠CNP= 50°,则∠GHM= .14如图,直线AB∥CD,∠EFG =100°,∠FGH =140°,则∠AEF+ ∠CHG= .15 已知∠B =25°,∠BCD=45°,∠CDE =30°,∠E=l0°,求证:AB∥EF.16已知AB∥EF,求∠l-∠2+∠3+∠4的度数.17如图(l ),已知MA 1∥NA n ,探索∠A 1、∠A 2、…、∠A n ,∠B 1、∠B 2…∠B n -1之间的 关系.(2)如图(2),己知MA 1∥NA 4,探索∠A 1、∠A 2、∠A 3、∠A 4,∠B 1、∠B 2之间的关系. (3)如图(3),已知MA 1∥NA n ,探索∠A 1、∠A 2、…、∠A n 之间的关系.如图所示,两直线AB ∥CD 平行,求∠1+∠2+∠3+∠4+∠5+∠6.18如图1,直线AB ∥CD ,P 是截线MN 上的一点,MN 与CD 、AB 分别交于E 、F . (1) 若∠EFB =55°,∠EDP = 30°,求∠MPD 的度数;(2) 当点P 在线段EF 上运动时,∠CPD 与∠ABP 的平分线交于Q ,问:DPBQ∠∠是否为定值?若是定值,请求出定值;若不是,说明其范围;(3) 当点P 在线段EF 的延长线上运动时,∠CDP 与∠ABP 的平分线交于Q ,问DPBQ∠∠的值足否定值,请在图2中将图形补充完整并说明理由.第六部分 平行线的四大模型实战演练1.如图,AB // CD // EF , EH ⊥CD 于H ,则∠BAC +∠ACE +∠CEH 等于( ).A . 180°B . 270°C . 360°D . 450° 2 若AB ∥CD ,∠CDF =32∠CDE ,∠ABF =32∠ABE ,则∠E :∠F =( ).A .2:1B .3:1C .4:3D .3:23.如图3,己知AE ∥BD ,∠1=130°,∠2=30°,则∠C = .4.如图,已知直线AB ∥CD ,∠C =115°,∠A = 25°,则∠E = .5. 6. 7.8.如阁所示,AB∥CD,∠l=l l0°,∠2=120°,则∠α= .9.如图所示,AB∥DF,∠D =116°,∠DCB=93°,则∠B= .10.如图,将三角尺的直角顶点放在直线a上,a∥b.∠1=50°,∠2 =60°,则∠3的度数为 .11.如图,AB∥CD,EP⊥FP, 已知∠1=30°,∠2=20°.则∠F的度数为.9.如图,若AB∥CD,∠BEF=70°,求∠B+∠F+∠C的度数.10.已知,直线AB∥CD.(1)如图l,∠A、∠C、∠AEC之间有什么关系?请说明理由;(2)如图2,∠AEF、∠EFC、∠FCD之间有什么关系?请说明理由;(3)如图3,∠A、∠E、∠F、∠G、∠H、∠O、∠C之间的关是.第七部分平行线的性质和判定综合应用1.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD =95°,∠CDE=25°,则∠DEF的度数是()A.110°B.115°C.120°D.125°2.如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1=()A.30°B.25°C.20°D.15°3.如图,AE∥BF,∠1=110°,∠2=130°,求∠3的度数为()4.如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=.5.如图,如果∠C=70°,∠B=135°,∠D=110°,那么∠1+∠2=6.如图,AB∥CD,求∠1+∠2+∠3+∠4=7.如图,AB∥CD,试找出∠B、∠C、∠BEC三者之间的数量关系.8.如图,三角形ABC中,点E为BC上一点(1)作图:过点E作EM∥AC交AB于M,过点E作EN∥AB交AC于N;(2)求∠A+∠B+∠C的度数,写出推理过程.9.如图,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED.10.如图,AC∥BD.(1)作图,过点B作BM∥AP交AC于M;(2)求证:∠PBD﹣∠P AC=∠P.11.如图,AB∥CD,∠B=∠C,求证:BE∥CF.12.如图①,木杆EB与FC平行,木杆的两端B,C用一橡皮筋连接,现将图①中的橡皮筋拉成下列各图②③的形状,请问∠A、∠B、∠C之间的数量关系?。
初中数学做辅助线的方法总结

初中数学做辅助线的方法总结初中数学中,辅助线是解题的一种重要方法,可以帮助我们清晰地理解题意和问题,并找到解题的思路。
下面是关于初中数学做辅助线的方法总结。
一、直线法1.作垂线:当题目中出现垂直关系时,我们可以通过作垂线来解决问题。
例如,求两个直线的垂直平分线、两个线段的中垂线等。
2.作平行线:当需要证明两条直线平行时,可以通过作一条与已知直线平行的辅助线,再应用平行线的性质进行证明。
二、角度法1.作角平分线:当需要求一个角平分线时,可以通过作一个角的辅助线将该角分成两个相等的角,进而求出角平分线。
2.作等角:当题目中需要证明两个角相等时,可以通过作一条等角的辅助线,将两个角变成等角,然后再应用等角的性质进行证明。
三、三角形法1.作高:当需要求一个三角形的高时,可以通过作条辅助线,形成一个矩形或直角三角形,从而利用高的性质求解。
2.作中线:当需要求一个三角形的中线时,可以通过作条辅助线,形成一个平行四边形或直角三角形,从而利用中线的性质求解。
3.作角平分线:当需要求一个三角形的角平分线时,可以通过作条辅助线,将该角分成两个相等的角,进而求出角平分线。
四、平行四边形法1.作对角线:当题目中出现平行四边形时,可以通过作对角线来将该平行四边形分成两个相等的三角形,进而利用三角形的性质进行求解。
五、轴对称法1.关于对称轴作对称点:当题目中出现轴对称图形时,可以通过作关于对称轴的对称点,将原图形和对称点所成的线段连结起来,形成对称图形,从而利用对称性进行求解。
六、相似三角形法1.作比例:当需要求解两个三角形相似的比例时,可以通过作条辅助线,形成相似三角形,并利用相似三角形的性质求解。
七、图形拓展法1.分割图形:当需要对一个复杂的图形进行分析时,可以通过作一些辅助线,将复杂图形分割成若干个简单的图形,进而分别求解。
总之,在初中数学中,辅助线是解题的有力工具,可以帮助我们合理分析题目,找到解题的思路,解决数学问题。
初中数学常见辅助线做法

初中数学常用辅助线一.添辅助线有二种情况:1按定义添辅助线:如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线;2按基本图形添辅助线:每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”这样可防止乱添线,添辅助线也有规律可循;举例如下:1平行线是个基本图形:当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线2等腰三角形是个简单的基本图形:当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形;出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形;3等腰三角形中的重要线段是个重要的基本图形:出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形;4直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线;出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形;5三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形;6全等三角形:全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形:或添对称轴,或将三角形沿对称轴翻转;当几何问题中出现一组或两组相等线段位于一组对顶角两边且成一直线时可添加中心对称形全等三角形加以证明,添加方法是将四个端点两两连结或过二端点添平行线7相似三角形:相似三角形有平行线型带平行线的相似三角形,相交线型,旋转型;当出现相比线段重叠在一直线上时中点可看成比为1可添加平行线得平行线型相似三角形;若平行线过端点添则可以分点或另一端点的线段为平行方向,这类题目中往往有多种浅线方法;8特殊角直角三角形当出现30,45,60,135,150度特殊角时可添加特殊角直角三角形,利用45角直角三角形三边比为1:1:√2;30度角直角三角形三边比为1:2:√3进行证明9半圆上的圆周角出现直径与半圆上的点,添90度的圆周角;出现90度的圆周角则添它所对弦---直径;平面几何中总共只有二十多个基本图形就像房子不外有一砧,瓦,水泥,石灰,木等组成一样;二.基本图形的辅助线的画法1.三角形问题添加辅助线方法方法1:有关三角形中线的题目,常将中线加倍;含有中点的题目,常常利用三角形的中位线,通过这种方法,把要证的结论恰当的转移,很容易地解决了问题;方法2:含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题;方法3:结论是两线段相等的题目常画辅助线构成全等三角形,或利用关于平分线段的一些定理;方法4:结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法,所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段;2.平行四边形中常用辅助线的添法平行四边形包括矩形、正方形、菱形的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下:1连对角线或平移对角线:2过顶点作对边的垂线构造直角三角形3连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线4连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形;5过顶点作对角线的垂线,构成线段平行或三角形全等.3.梯形中常用辅助线的添法梯形是一种特殊的四边形;它是平行四边形、三角形知识的综合,通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决;辅助线的添加成为问题解决的桥梁,梯形中常用到的辅助线有:1在梯形内部平移一腰;2梯形外平移一腰3梯形内平移两腰4延长两腰5过梯形上底的两端点向下底作高6平移对角线7连接梯形一顶点及一腰的中点;8过一腰的中点作另一腰的平行线;9作中位线当然在梯形的有关证明和计算中,添加的辅助线并不一定是固定不变的、单一的;通过辅助线这座桥梁,将梯形问题化归为平行四边形问题或三角形问题来解决,这是解决问题的关键;4.圆中常用辅助线的添法在平面几何中,解决与圆有关的问题时,常常需要添加适当的辅助线,架起题设和结论间的桥梁,从而使问题化难为易,顺其自然地得到解决,因此,灵活掌握作辅助线的一般规律和常见方法,对提高学生分析问题和解决问题的能力是大有帮助的;1见弦作弦心距有关弦的问题,常作其弦心距有时还须作出相应的半径,通过垂径平分定理,来沟通题设与结论间的联系;2见直径作圆周角在题目中若已知圆的直径,一般是作直径所对的圆周角,利用"直径所对的圆周角是直角"这一特征来证明问题;3见切线作半径命题的条件中含有圆的切线,往往是连结过切点的半径,利用"切线与半径垂直"这一性质来证明问题;4两圆相切作公切线对两圆相切的问题,一般是经过切点作两圆的公切线或作它们的连心线,通过公切线可以找到与圆有关的角的关系;5两圆相交作公共弦对两圆相交的问题,通常是作出公共弦,通过公共弦既可把两圆的弦联系起来,又可以把两圆中的圆周角或圆心角联系起来;。
相似三角形中几种常见的辅助线作法(有辅助线)
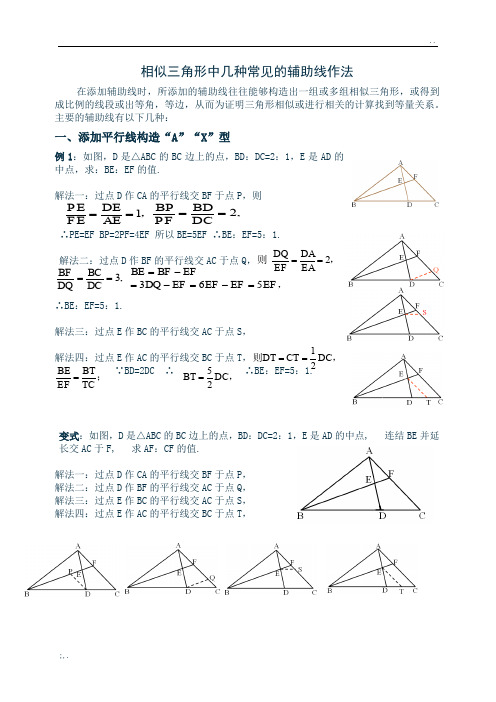
相似三角形中几种常见的辅助线作法在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。
主要的辅助线有以下几种:一、添加平行线构造“A”“X”型例1:如图,D是△ABC的BC边上的点,BD:DC=2:1,E是AD的中点,求:BE:EF的值.解法一:过点D作CA的平行线交BF于点P,则∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE:EF=5:1.解法二:过点D作BF的平行线交AC于点Q,∴BE:EF=5:1.解法三:过点E作BC的平行线交AC于点S,解法四:过点E作AC的平行线交BC于点T,∵BD=2DC ∴∴BE:EF=5:1.变式:如图,D是△ABC的BC边上的点,BD:DC=2:1,E是AD的中点,连结BE并延长交AC于F,求AF:CF的值.解法一:过点D作CA的平行线交BF于点P,解法二:过点D作BF的平行线交AC于点Q,解法三:过点E作BC的平行线交AC于点S,解法四:过点E作AC的平行线交BC于点T,,1==AEDEFEPE,2==DCBDPFBP,则2==EADAEFDQ,3==DCBCDQBF,EFEFEFEFDQEFBFBE563=-=-=-=,则DCCTDT21==;TCBTEFBE=,DCBT25=例2:如图,在△ABC 的AB 边和AC 边上各取一点D 和E ,且使AD =AE ,DE 延长线与BC 延长线相交于F ,求证:(证明:过点C 作CG//FD 交AB 于G )例3:如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB ·DF=AC ·EF.分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。
不相似,因而要通过两组三角形相似,运用中间比代换得到,为构造相似三角形,需添加平行线。
初中几何辅助线作法大全

线,角,相交线,平行线规律1.假如平面上有n (n ≥2)个点,其中任何三点都不在同一直线上,那么每两点画一款直线,一共可以画出12n (n -1)款.规律2.平面上地n 款直线最多可把平面分成〔12n (n +1)+1〕个部分.规律3.假如一款直线上有n 个点,那么在这个图形中共有线段地款数为12n (n -1)款.规律4.线段(或延长线)上任一点分线段为两段,这两款线段地中点地距离等于线段长地一半.例:如图,B 在线段AC 上,M 是AB 地中点,N 是BC 地中点.求证:MN =12AC 证明:∵M 是AB 地中点,N 是BC 地中点∴AM = BM =12AB ,BN = CN = 12BC ∴MN = MB +BN = 12AB + 12BC = 12(AB + BC )∴MN =12AC练习:1.如图,点C 是线段AB 上地一点,M 是线段BC 地中点.求证:AM =12(AB + BC ) 2.如图,点B 在线段AC 上,M 是AB 地中点,N 是AC 地中点.求证:MN =12BC 3.如图,点B 在线段AC 上,N 是AC 地中点,M 是BC 地中点.求证:MN =12AB 规律5.有公共端点地n 款射线所构成地交点地个数一共有12n (n -1)个.规律6.假如平面内有n 款直线都经过同一点,则可构成小于平角地角共有2n (n -1)个.规律7. 假如平面内有n 款直线都经过同一点,则可构成n (n -1)对对顶角.规律8.平面上若有n (n ≥3)个点,任意三个点不在同一直线上,过任意三点作三角形一共可作出16n (n -1)(n -2)个.规律9.互为邻补角地两个角平分线所成地角地度数为90o .规律10.平面上有n 款直线相交,最多交点地个数为12n (n -1)个.规律11.互为补角中较小角地余角等于这两个互为补角地角地差地一半.N M CB A MC BA N M CB A N MCB A规律12.当两直线平行时,同位角地角平分线互相平行,内错角地角平分线互相平行,同旁内角地角平分线互相垂直.例:如图,以下三种情况请同学们自己证明.规律13.已知AB ∥DE ,如图⑴~⑹,规律如下:规律14.成“8”字形地两个三角形地一对内角平分线相交所成地角等于另两个内角和地一半.例:已知,BE ,DE 分别平分∠ABC 和∠ADC ,若∠A = 45o ,∠C = 55o ,求∠E 地度数.解:∠A +∠ABE =∠E +∠ADE ①∠C +∠CDE =∠E +∠CBE ②①+②得∠A +∠ABE +∠C +∠CDE =∠E +∠ADE +∠E +∠CBE ∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠ABE =∠CBE ,∠CDE =∠ADE ∴2∠E =∠A +∠C∴∠E =12(∠A +∠C )1()∠ABC+∠BCD+∠CDE=360︒E D C BA +=∠CDE∠ABC ∠BCD 2()E DCBA-=∠CDE ∠ABC∠BCD 3()E DC BA-=∠CDE∠ABC ∠BCD 4()E D CBA +=∠CDE ∠ABC∠BCD 5()EDCB A +=∠CDE∠ABC ∠BCD 6()EDCBANME DBCAH GFE D BCAHGFED BCAH GFEDBCA∵∠A =45o,∠C =55o,∴∠E =50o三角形部分规律15.在利用三角形三边关系证明线段不等关系时,假如直接证不出来,可连结两点或延长某边构造三角形,使结论中出现地线段在一个或几个三角形中,再利用三边关系定理及不等式性质证题.例:如图,已知D,E为△ABC内两点,求证:AB+AC>BD+DE+CE.证法(一):将DE向两边延长,分别交AB,AC于M,N在△AMN中, AM+AN>MD+DE+NE①在△BDM中,MB+MD>BD②在△CEN中,CN+NE>CE③①+②+③得AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE∴AB+AC>BD+DE+CE证法(二)延长BD交AC于F,延长CE交BF于G,在△ABF和△GFC和△GDE中有,①AB+AF>BD+DG+GF②GF+FC>GE+CE③DG+GE>DE∴①+②+③有AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE∴AB+AC>BD+DE+CE注意:利用三角形三边关系定理及推论证题时,常通过引辅助线,把求证地量(或与求证相关地量)移到同一个或几个三角形中去然后再证题.练习:已知:如图P为△ABC内任一点,求证:12(AB+BC+AC)<PA+PB+PC<AB+BC+AC规律16.三角形地一个内角平分线与一个外角平分线相交所成地锐角,等于第三个内角地一半.例:如图,已知BD为△ABC地角平分线,CD为△ABC地外角∠ACE地平分线,它与BD地延长线交于D.求证:∠A = 2∠D证明:∵BD,CD分别是∠ABC,∠ACE地平分线∴∠ACE =2∠1, ∠ABC =2∠2∵∠A = ∠ACE-∠ABC∴∠A = 2∠1-2∠2又∵∠D =∠1-∠2∴∠A =2∠D规律17. 三角形地两个内角平分线相交所成地钝角等于90o加上第三个内角地一半.例:如图,BD,CD分别平分∠ABC,∠ACB, 求证:∠BDC = 90o+12∠A证明:∵BD,CD分别平分∠ABC,∠ACBFGNMEDBA21C EDBA∴∠A+2∠1+2∠2 = 180o∴2(∠1+∠2)= 180o-∠A①∵∠BDC = 180o-(∠1+∠2)∴(∠1+∠2) = 180o-∠BDC②把②式代入①式得2(180o-∠BDC)= 180o-∠A 即:360o-2∠BDC =180o-∠A ∴2∠BDC = 180o+∠A∴∠BDC = 90o+12∠A规律18. 三角形地两个外角平分线相交所成地锐角等于90o减去第三个内角地一半.例:如图,BD,CD分别平分∠EBC,∠FCB, 求证:∠BDC = 90o-12∠A证明:∵BD,CD分别平分∠EBC,∠FCB∴∠EBC = 2∠1,∠FCB = 2∠2∴2∠1 =∠A+∠ACB①2∠2 =∠A+∠ABC②①+②得2(∠1+∠2)= ∠A+∠ABC+∠ACB+∠A2(∠1+∠2)= 180o+∠A∴(∠1+∠2)= 90o+12∠A∵∠BDC = 180o-(∠1+∠2)∴∠BDC = 180o-(90o+12∠A)∴∠BDC = 90o-12∠A规律19. 从三角形地一个顶点作高线和角平分线,它们所夹地角等于三角形另外两个角差(地绝对值)地一半.例:已知,如图,在△ABC中,∠C>∠B, AD⊥BC于D, AE平分∠BAC.求证:∠EAD = 12(∠C-∠B)证明:∵AE平分∠BAC∴∠BAE =∠CAE =12∠BAC∵∠BAC =180o-(∠B+∠C)∴∠EAC = 12〔180o-(∠B+∠C)〕∵AD⊥BC∴∠DAC = 90o-∠C∵∠EAD = ∠EAC-∠DACDCBA2121FEDCBAE D CBA∴∠EAD = 12〔180o -(∠B +∠C )〕-(90o -∠C ) = 90o -12(∠B +∠C )-90o +∠C= 12(∠C -∠B )假如把AD 平移可以得到如下两图,FD ⊥BC 其它款件不变,结论为∠EFD =12(∠C -∠B ).注意:同学们在学习几何时,可以把自己证完地题进行适当变换,从而使自己通过解一道题掌握一类题,提高自己举一反三,灵活应变地能力.规律20.在利用三角形地外角大于任何和它不相邻地内角证明角地不等关系时,假如直接证不出来,可连结两点或延长某边,构造三角形,使求证地大角在某个三角形外角地位置上,小角处在内角地位置上,再利用外角定理证题.例:已知D 为△ABC 内任一点,求证:∠BDC >∠BAC证法(一):延长BD 交AC 于E ,∵∠BDC 是△EDC 地外角,∴∠BDC >∠DEC同理:∠DEC >∠BAC ∴∠BDC >∠BAC 证法(二):连结AD ,并延长交BC 于F∵∠BDF 是△ABD 地外角,∴∠BDF >∠BAD 同理∠CDF >∠CAD∴∠BDF +∠CDF >∠BAD +∠CAD 即:∠BDC >∠BAC规律21.有角平分线时常在角两边截取相等地线段,构造全等三角形. 例:已知,如图,AD 为△ABC 地中线且∠1 = ∠2,∠3 = ∠4,求证:BE +CF >EF证明:在DA 上截取DN = DB ,连结NE ,NF ,则DN = DC 在△BDE 和△NDE 中,DN = DB∠1 = ∠2ED = ED∴△BDE ≌△NDE ∴BE = NE同理可证:CF = NF在△EFN 中,EN +FN >EF ∴BE +CF >EF规律22. 有以线段中点为端点地线段时,常加倍延长此线段构造全等三角形.例:已知,如图,AD 为△ABC 地中线,且∠1 = ∠2,∠3 = ∠4,求证:BE +CF >EF证明:延长ED 到M ,使DM = DE ,连结CM ,FMABCDEF FE DCBA FABC DE D C B A 4321NFEDCBABD = CD ∠1 = ∠5ED = MD∴△BDE ≌△CDM ∴CM = BE又∵∠1 = ∠2,∠3 = ∠4∠1+∠2+∠3 + ∠4 = 180o ∴∠3 +∠2 = 90o 即∠EDF = 90o∴∠FDM = ∠EDF = 90o △EDF 和△MDF 中ED = MD ∠FDM = ∠EDF DF = DF∴△EDF ≌△MDF ∴EF = MF∵在△CMF 中,CF +CM >MF BE +CF >EF(此题也可加倍FD ,证法同上)规律23. 在三角形中有中线时,常加倍延长中线构造全等三角形.例:已知,如图,AD 为△ABC 地中线,求证:AB +AC >2AD证明:延长AD 至E ,使DE = AD ,连结BE∵AD 为△ABC 地中线∴BD = CD在△ACD 和△EBD 中BD = CD ∠1 = ∠2AD = ED∴△ACD ≌△EBD∵△ABE 中有AB +BE >AE ∴AB +AC >2AD规律24.截长补短作辅助线地方式截长法:在较长地线段上截取一款线段等于较短线段。
