专题:平行线中作辅助线的方法(含答案)
专题02 相交线与平行线【易错题型专项训练】解析版

专题02 相交线与平行线【易错题型专项训练】易错点一:两条直线的位置关系1.若∠α=54°,∠β的两边与∠α两边互相垂直,则∠β=____________.【难度】★★【答案】54︒或126︒.【解析】∠α和∠β是相等或者互补的关系.【总结】考察垂线的意义以及两解问题,注意分类讨论.2.平面上三条直线两两相交,最多有m 个交点,最少有n 个交点,则m n +=____________.【难度】★★【答案】4.【解析】最多有3个交点,最少有1个交点.3m =,1n =,4m n +=.【总结】考察学生的作图分析能力.3.作图:已知线段AB 上一点Q 及线段外一点P .(1) 过点Q 作线段AB 的垂线;(2) 过点P 作线段AB 的垂线.【难度】★★【答案】如右图.【解析】注意标注垂直符号,以及字母的标注.【总结】画图一定要写结论.4.下列说法中正确的是( )A .有公共顶点、公共边且和为180°的两个角是邻补角B .有公共顶点且相等的是对顶角C .对顶角的补角一定相等D .互为邻补角的两个角不可能相等【难度】★【答案】C【解析】有一条公共边,并且另一条边互为反向延长线的两个角互为邻补角,故选项A 错误;有公共顶点且相等的两个角不一定是对顶角,故选项B 错误;C 正确;互为邻补角的两个角可能都为90︒,故选型D 错误.【总结】本题主要考查了对顶角和邻补角的概念.5.下列说法正确的是( )A .如果两个角相等,那么这两个角是对顶角B .经过一点有且只有一条直线与已知直线平行C .如果两条直线被第三条直线所截,那么内错角相等D.联结直线外一点与直线上各点的所有线段中,垂线段最短【难度】★【答案】D【解析】对顶角相等,但相等的角不一定是对顶角,故选项A错误;过直线外一点有且只有一条直线与已知直线平行,故选项B错误;只有两直线平行时,它们的内错角才相等,故选项C错误;联结直线外一点与直线上各点的所有线段中,垂线段最短,故选项D正确.【总结】本题主要考查了对顶角、内错角、平行线、点到直线的距离的概念.易错点二:同位角、内错角、同旁内角1.在直线AB、CD被直线EF所截的八个角中∠1和∠5是一对________角,∠3和∠5是一对________角,∠4和∠5是一对________角.【难度】★【答案】同位角;内错角;同旁内角.【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U.【总结】本题考查同位角、内错角、同旁内角的概念及特征.2.(1)如图∠1和∠2是直线________与________被直线_______所截,所形成的______角;(2)∠3和∠4是直线_____与_______被直线______所截,所形成的_______角;(3)∠C的同旁内角是_________.【难度】★【答案】(1)DC、AB、DB、内错角;(2)AD、CB、DB、内错角;(3)14、、、.∠∠∠∠CBA CDA【解析】两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角叫做内错角,内错角像字母Z,同旁内角像字母U.【总结】本题考查内错角、同旁内角的概念及特征.3.如图,下列说法错误的是()A.∠5和∠3是同位角B.∠1和∠4是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角【难度】★【答案】B【解析】两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角,故∠1和∠4不是同位角.【总结】本题考查同位角、内错角、同旁内角的概念及特征.4,如图,与∠C是同旁内角的有()A.5个 B.4个C.3个D.2个【难度】★【答案】B【解析】∠C的同旁内角有:∠CED、∠B、∠EDC、∠ADC共四个.【总结】本题考查同旁内角的概念及特征.5.如图,同旁内角的对数是()A.5对B.4对C.3对D.2对【难度】★★【答案】B【解析】两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.【总结】本题考查同旁内角的概念及特征.6.如图,∠1和∠2是同位角的是( )A .(1)(2)B .(2)(3)(4)C .(1)(2)(4)D .(3)(4)(4)(3)(2)(1)21212121【难度】★★【答案】C【解析】(1)(2)(4)中∠1与∠2都在截线的同旁,并且都在被截直线的同侧,是同位角;(3)中∠1与∠2两边不在同一直线上,不是同位角,故选C .【总结】本题考查同位角的概念及特征,注意很多学生会容易误以为(2)中的两个角不是同位角,老师们要注意纠错哦.7.指出下图中:(1)∠C 与∠D 的关系;(2)∠B 与∠GEF 的关系;(3)∠A 与∠D 的关系;(4)∠AGE 与∠BGE 的关系;(5)∠CFD 与∠AFB 的关系.【难度】★★【答案】(1)同旁内角;(2)同位角;(3)内错角;(4)邻补角;(5)对顶角.【解析】 两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角叫做内错角.两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.【总结】本题考查同位角、内错角、同旁内角、邻补角、对顶角的概念及特征.8.找出图中∠1的所有的同位角.【难度】★★【答案】∠GEF 、∠CBM 、∠ADF 、∠BCN .【解析】两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.【总结】本题考查同位角的概念及特征.易错点三:平行线的判定与性质1.如果两个角的一边在同一条直线上,另一边互相平行,那么这两个角() A .相等或互补B .互补C .相等D .相等且互余【难度】★★【答案】A【解析】分为同侧相等和异侧互补两种情况,故选A .【总结】本题考查平行线的基本应用,注意分类讨论.2.已若∠A 的两边与∠B 的两边分别平行,且∠A 是∠B 的2倍少30°,求∠A 与∠B 的度数.【难度】★★【答案】3030B A ∠=︒∠=︒,或70110B A ∠=︒∠=︒,.【解析】由题意可知,180A B A B ∠=∠∠+∠=︒或,又因为∠A 是∠B 的2倍少30°,所以230A B ∠=∠-︒,即3030B A ∠=︒∠=︒,或70110B A ∠=︒∠=︒,【总结】本题考查平行线的性质及两个角的两边平行时的两种情况的讨论.3.如果两个角的两边分别平行,其中一个角比另一个角的3倍多12°,则这两个角是( ).A .42°和138°B .都是10°C .42°和138°或都是10°D .以上都不对【难度】★★【答案】A 【解析】由题意假设这两个角分别为A 、B ,则有:180A B A B ∠=∠∠+∠=︒或,又因为∠A 是∠B 的3倍多12°,则有:312A B ∠=∠+︒,即180********B B B A ︒-∠=∠+︒∠=︒∠=︒,解得:,.【总结】本题考查两角位置关系的可能性,注意两种情况的讨论.5.已知:如图,E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,试说明:∠B =∠C .【难度】★★【解析】因为121AHB ∠=∠∠=∠(已知),(对顶角相等)所以2AHB ∠=∠(等量代换), 所以//AF ED (同位角相等,两直线平行)所以D AFC ∠=∠(两直线平行,同位角相等)因为A D ∠=∠(已知), 所以A AFC ∠=∠(等量代换) 所以//AB CD (内错角相等,两直线平行)所以B C ∠=∠(两直线平行,内错角相等)【总结】本题主要考察平行线的性质定理和判定定理的综合运用.6.如图,直线GC 截两条直线AB 、CD ,AE 是GAB ∠的平分线,CF 是ACD ∠的平分线,且//AE CF ,那么AB CD ∥吗?为什么?【难度】★★【解析】因为AE 是GAB ∠的平分线,CF 是ACD ∠的平分线(已知)所以GAE EAB ACF FCD ∠=∠∠=∠,(角平分线的性质)因为//AE CF (已知),所以GAE ACF ∠=∠(两直线平行,同位角相等)所以EAB FCD ∠=∠(等量代换)所以//(AB CD 同位角相等,两直线平行)【总结】本题主要考查平行线的判定定理及性质定理的综合运用.7.已知,正方形ABCD 的边长为4cm ,求三角形EBC 的面积.【难度】★★【答案】8平方厘米.【解析】由题意可知:三角形EBC 与正方形同底BC ,且其高即是正方形的边DC ,故三角形面积为正方形面积的一半:24428cm ⨯÷=【总结】本题考查三角形的面积的计算,注意三角形与正方形同底等高.8.如图,AD //BC ,52BC AD =,求三角形ABC 与三角形ACD 的面积之比.【难度】★★★【答案】5:2.【解析】因为//AD BC (已知)所以三角形ABC 与三角形ACD 的高相等(平行线间的距离处处相等)所以::52ABC ACD S S BC AD ∆∆==:(两三角形高相等,面积比等于底之比)【总结】本题考查平行线距离处处相等及三角形的面积比问题.9.如图,a ∥b ,.若△ABC 的面积是5,△ABE 的面积是2,则BEC S △=________;DEC S =__________;DBC S =__________;ADE S =___________.【难度】★★★【答案】3;2;5;43.【解析】因为△ABC的面积是5,△ABE的面积是2,所以△BEC的面积为5-2=3,因为△ABC和△DBC为同底等高的三角形,所以△DBC的面积为5,所以△DEC的面积为5-3=2,因为△ABE和△BEC为等高三角形,所以面积之比为底之比,即AE:EC=2:3,因为△ADE和△DEC为等高三角形,所以底之比为面积之比,所以△ADE的面积为4 232=3÷⨯.【总结】本题主要考查了平行线的性质和三角形面积的求法.10.如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求三角形CAD的面积.【难度】★★【答案】6【解析】因为∠1=∠2(已知)所以AD∥BC(内错角相等,两直线平行),所以AD到BC的距离相等,设为a,所以三角形ABC面积=12a BC⨯ =3,所以三角形ACD面积= 12a AD a BC⨯=⨯=6.【总结】本题主要考查了等高三角形的面积之比为底之比的应用.11.如图△ABC中,∠ABC=∠ACB,AE是△ABC的外角的平分线,F是AE上的一点,试说明△ABC与△FBC的面积相等.【难度】★★【解析】因为AE 是△ABC 的外角的平分线(已知)所以∠DAF =12∠DAC (角平分线的意义)因为180DAC BAC ∠+∠=(邻补角的意义),180BAC ABC ACB ∠+∠+∠=(三角形内角和等于180°)所以∠DAC =∠ABC +∠ACB (等式性质)因为DAC DAF CAF ∠=∠+∠(角的和差),∠ABC=∠ACB (已知)所以∠DAF =∠ABC (等式性质)所以AF//BC (同位角相等,两直线平行),所以点A 到直线BC 的距离等于点F 到直线BC 的距离(夹在平行线间的距离处处相等)所以△ABC 与△FBC 为同底等高三角形,所以△ABC 与△FBC 的面积相等.【总结】本题主要考查了平行线的判定和同底等高三角形面积相等的应用.12.如图,已知AB ∥ED ,试说明:∠B +∠D =∠C .【难度】★★【解析】过点C 作AB 的平行线CF ,因为AB ∥ED (已知)所以////AB CF ED (平行的传递性)所以B BCF D DCF ∠=∠∠=∠,(两直线平行,内错角相等)所以B D BCF DCF BCD ∠+∠=∠+∠=∠(等式性质)【总结】本题考查平行线的性质及辅助线的添加.13.如图所示,已知,++360A B C ︒∠∠∠=,试说明AE ∥CD .【难度】★★【解析】过点B向右作BF//AE,所以180A ABF∠+∠=︒(两直线平行,同旁内角互补)因为++360∠∠∠=(已知)A B C︒所以180∠+∠=︒(等式性质)FBC C所以//BF CD(同旁内角互补,两直线平行)所以//AE CD(平行的传递性)【总结】本题考查平行线的判定及性质的综合运用,注意简单的辅助线的添加方法.14.如图,已知:AB//CD,试说明:∠B+∠D+∠BED=360︒(至少用三种方法).【难度】★★【解析】方法一:连接BD则∠EBD+∠EDB+∠E=180°(三角形内角和等于180°)因为AB//CD(已知),所以∠ABD+∠BDC=180°(两直线平行,同旁内角互补)所以∠ABD+∠EBD+∠EDB+∠BDC+∠E=360°,即∠B+∠D+∠BED=360°方法二:过点E作EF//CD,因为//EF AB(平行的传递性)AB CD(已知),所以//所以∠B+∠BEF=180°,∠D+∠DEF=180°(两直线平行,同旁内角互补)所以∠B+∠BEF+∠D+∠DEF=360°(等式性质)即∠B+∠D+∠BED=360°;方法三:过点E作//EF BA因为//EF AB(平行的传递性)AB CD(已知),所以//所以180180,(两直线平行,同旁内角互补)ABE BEF FED EDC∠+∠=︒∠+∠=︒所以∠B+∠D+∠BED=360︒(等式性质);方法四:过点E作EF⊥CD的延长线与F,EG垂直于AB的延长线于G,则有:∠B=∠BGE+∠GEB,∠D=∠EDF+∠DFE,所以∠B+∠D+∠BED=∠BGE+∠DFE+∠GED=180+180=360°.【总结】本题考查平行线的判定及性质的综合运用,注意多种方法的归纳总结.11。
平行线中添辅助线的方法

平行线中添辅助线的方法在几何学中,平行线是指在同一个平面内,永远不会相交的线。
平行线可以用于解决许多几何问题。
有时,为了更好地理解和解决问题,我们可能需要在已知的平行线中添加辅助线。
这篇文章将介绍一些经常在平行线中添加辅助线的方法,以及如何利用这些辅助线解决几何问题。
方法一:创建平行线之间的等距线段这是最常见的方法之一,可以通过创建平行线之间的等距线段来添加辅助线。
这个方法可以在几何证明中使用,以创建所需的形状或角度。
下面是一个例子:假设有两个平行线AB和CD,在这两条平行线上选择两个等距点E和F。
然后,通过连接EF,你就创建了一个辅助线,使得EF平行于AB和CD。
这样,你就可以利用这个平行四边形来证明或解决其他几何问题。
方法二:使用交叉线段这个方法涉及到在平行线上选择一个点,并通过它绘制一条与其他平行线相交的线段。
这种方法通常用于证明几何性质。
例如,假设有两个平行线AB和CD,我们可以在AB上选择一个点E,并通过它绘制一条线段EF与CD相交。
然后,通过观察EF与AB的关系,可以证明一些三角形的性质或者其他几何关系。
方法三:利用平行线之间的相似三角形利用平行线之间的相似三角形是另一种常用的方法。
通过观察平行线和与它们相交的第三条线,可以找到相似的三角形。
然后,利用这些相似三角形的性质来解决几何问题。
例如,假设有两个平行线AB和CD,以及一条与它们相交的第三条线EF。
通过观察,可以发现三角形ADE与三角形BCF相似。
这意味着可以使用相似三角形的性质来计算未知角度或线段的长度。
方法四:利用中位线和对角线这个方法通常涉及到在平行线形成的平行四边形中绘制中位线或对角线。
中位线是连接平行四边形两对相对顶点的线段,对角线是连接两对非相邻顶点的线段。
这些辅助线可以帮助我们找到形状的性质,或计算线段的长度。
例如,假设有一个平行四边形ABCD,你可以通过绘制对角线AC来创建两个互相重叠的三角形ABC和ADC。
通过观察这些三角形的性质,可以得出许多结论,例如它们的面积相等或角度相等。
初中数学特殊四边形的辅助线做法及口决

特殊四边形主要包括平行四边形、矩形、菱形、正方形和梯形.在解决一些和四边形有关的问题时往往需要添加辅助线.下面介绍一些辅助线的添加方法.一、和平行四边形有关的辅助线作法平行四边形是最常见的特殊四边形之一,它有许多可以利用性质,为了利用这些性质往往需要添加辅助线构造平行四边形.1.利用一组对边平行且相等构造平行四边形例1 、如图1,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形.求证:OE与AD互相平分.分析:因为四边形OCDE是平行四边形,所以OC//ED,OC=DE,又由O是AC的中点,得出AO//ED,AO=ED,则四边形AODE是平行四边形,问题得证.证明:连结AE、OD,因为是四边形OCDE是平行四边形,所以OC//DE,OC=DE,因为0是AC的中点,所以A0//ED,AO=ED,所以四边形AODE是平行四边形,所以AD与OE互相平分.说明:当已知条件中涉及到平行,且要求证的结论中和平行四边形的性质有关,可试通过添加辅助线构造平行四边形.2.利用两组对边平行构造平行四边形例2、如图2,在△ABC中,E、F为AB上两点,AE=BF,ED//AC,FG//AC交BC分别为D,G.求证:ED+FG=AC.分析:要证明ED+FG=AC,因为DE//AC,可以经过点E作EH//CD交AC于H得平行四边形,得ED=HC,然后根据三角形全等,证明FG=AH.证明:过点E作EH//BC,交AC于H,因为ED//AC,所以四边形CDEH是平行四边形,所以ED=HC,又FG//AC,EH//BC,所以∠AEH=∠B,∠A=∠BFG,又AE=BF,所以△AEH≌△FBG,所以AH=FG,所以FG+DE=AH+HC=AC.说明:当图形中涉及到一组对边平行时,可通过作平行线构造另一组对边平行,得到平行四边形解决问题.3.利用对角线互相平分构造平行四边形例3 、如图3,已知AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证BF=AC.分析:要证明BF=AC,一种方法是将BF和AC变换到同一个三角形中,利用等边对等角;另一种方法是通过等量代换,寻找和BF、AC相等的相段代换.寻找相等的线段的方法一般是构造平行四边形.证明:延长AD到G,使DG=AD,连结BG,CG,因为BD=CD,所以四边形ABGC是平行四边形,所以AC=BG,AC//BG,所以∠1=∠4,因为AE=EF,所以∠1=∠2,又∠2=∠3,所以∠1=∠4,所以BF=BG=AC.图3 图4说明:本题通过利用对角线互相平分构造平行四边形,实际上是采用了平移法构造平行四边形.当已知中点或中线应思考这种方法.二、和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线,借助菱形的判定定理或性质定定理解决问题.例4 、如图5,在△ABC中,∠ACB=90°,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF//BC交AD于点F,求证:四边形CDEF 是菱形.分析:要证明四边形CDEF是菱形,根据已知条件,本题有量种判定方法,一是证明四边相等的四边形是菱形,二是证明对角线互相垂直平分的四边形是菱形.根据AD是∠BAC的平分线,AE=AC,可通过连接CE,构造等腰三角形,借助三线合一证明AD垂直CE.求AD平分CE.证明:连结CE交AD于点O,由AC=AE,得△ACE是等腰三角形,因为AO平分∠CAE,所以AO⊥CE,且OC=OE,因为EF//CD,所以∠1=∠2,又因为∠EOF=∠COD,所以△DOC可以看成由△FOE绕点O旋转而成,所以OF=OD,所以CE、DF互相垂直平分.所以四边形CDEF是菱形.例5、如图6,四边形ABCD是菱形,E为边AB上一个定点,F是AC 上一个动点,求证EF+BF的最小值等于DE长.分析:要证明EF+BF的最小值是DE的长,可以通过连结菱形的对角线BD,借助菱形的对角线互相垂直平分得到DF=BF,然后结合三角形两边之和大于第三边解决问题.证明:连结BD、DF.因为AC、BD是菱形的对角线,所以AC垂直BD且平分BD,所以BF=DF,所以EF+BF=EF+DF≥DE,当且仅当F运动到DE与AC的交点G处时,上式等号成立,所以EF+BF的最小值恰好等于DE的长.说明:菱形是一种特殊的平行四边形,和菱形的有关证明题或计算题作辅助线的不是很多,常见的几种辅助线的方法有:(1)作菱形的高;(2)连结菱形的对角线.三、与矩形有辅助线作法和矩形有关的题型一般有两种:(1)计算型题,一般通过作辅助线构造直角三角形借助勾股定理解决问题;(2)证明或探索题,一般连结矩形的对角线借助对角线相等这一性质解决问题.和矩形有关的试题的辅助线的作法较少.例6、如图7,已知矩形ABCD内一点,PA=3,PB=4,PC=5.求 PD的长.分析:要利用已知条件,因为矩形ABCD,可过P分别作两组对边的平行线,构造直角三角形借助勾股定理解决问题.解:过点P分别作两组对边的平行线EF、GH交AB于E,交CD于F,交BC于点H,交AD于G.因为四边形ABCD是矩形,所以PF2=CH2=PC2-PH2,DF2=AE2=AP2-EP2,PH2+PE2=BP2,所以 PD2=PC2-PH2+AP2-EP2=PC2+AP2-PB2=52+32-42=18,所以 PD=3.说明:本题主要是借助矩形的四个角都是直角,通过作平行线构造四个小矩形,然后根据对角线得到直角三角形,利用勾股定理找到PD与PA、PB、PC之间的关系,进而求到PD的长.四、与正方形有关辅助线的作法正方形是一种完美的几何图形,它既是轴对称图形,又是中心对称图形,有关正方形的试题较多.解决正方形的问题有时需要作辅助线,作正方形对角线是解决正方形问题的常用辅助线.例7、如图8,过正方形ABCD的顶点B作BE//AC,且AE=AC,又CF//AE.求证:∠BCF=∠AEB.分析:由BE//AC,CF//AE,AE=AC,可知四边形AEFC是菱形,作AH ⊥BE于H,根据正方形的性质可知四边形AHBO是正方形,从AH=OB= AC,可算出∠E=∠ACF=30°,∠BCF=15°.证明:连接BD交AC于O,作AH⊥BE交BE于H.在正方形ABCD中,AC⊥BD,AO=BO,又BE//AC,AH⊥BE,所以BO⊥AC,所以四边形AOBH为正方形,所以AH=AO=AC,因为AE=AC,所以∠AEH=30°,因为BE//AC,AE//CF,所以ACFE是菱形,所以∠AEF=∠ACF=30°,因为AC是正方形的对角线,所以∠ACB=45°,所以∠BCF=15°,所以∠BCF=∠AEB.说明:本题是一道综合题,既涉及正方形的性质,又涉及到菱形的性质.通过连接正方形的对角线构造正方形AHBO,进一步得到菱形,借助菱形的性质解决问题.三角形中两中点,连结则成中位线。
初二数学辅助线常用做法及例题(含答案)

DCB A常见的辅助线的作法总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”: 遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转” 法构造全等三角形.3) 遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
第3讲 平行线辅助线(学生版)

第3讲平行线辅助线一、知识回顾:在解决平行线的问题时,当无法直接得到角的关系或两条线之间的位置关系时,通常借助辅助线来帮助解答,如何作辅助线需根据已知条件确定,辅助线的添加既可以产生新的条件,又能将题目中原有的条件联系在一起.一、加截线(连接两点或延长线段)1.如图,已知AB∥CD,∠ABF=∠DCE.∠BFE与∠FEC有何关系?并说明理由.(第1题)【解析】:∠BFE=∠FEC.理由一:连接BC,如图①.∵AB∥CD,∴∠ABC=∠BCD(两直线平行,内错角相等).又∵∠ABF=∠DCE,∴∠ABC-∠ABF=∠BCD-∠DCE,即∠FBC=∠ECB.∴BF∥CE(内错角相等,两直线平行).∴∠BFE=∠FEC(两直线平行,内错角相等).(第1题)理由二:延长AB,CE相交于点G,如图②.∵AB∥CD,∴AG∥CD.∴∠DCE=∠G(两直线平行,内错角相等).又∵∠ABF=∠DCE,∴∠ABF=∠G.∴BF∥CG(同位角相等,两直线平行).∴∠BFE=∠FEC(两直线平行,内错角相等).二、过“拐点”作平行线a.“”形图2.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.(第2题)【解析】:方法一:过点P作射线PN∥AB,如图①.∵AB∥CD,∴PN∥CD.∴∠4=∠2=25°.∵PN∥AB,∴∠3=∠1=32°.∴∠BPC=∠3+∠4=57°.(第2题)方法二:过点P作射线PM∥AB,如图②.∵AB∥CD,∴PM∥CD.∴∠4=180°-∠2=180°-25°=155°.∵AB∥PM,∴∠3=180°-∠1=180°-32°=148°.∴∠BPC=360°-∠3-∠4=360°-148°-155°=57°. 方法三:连接BC,略。
平行四边形几何辅助线专题详解
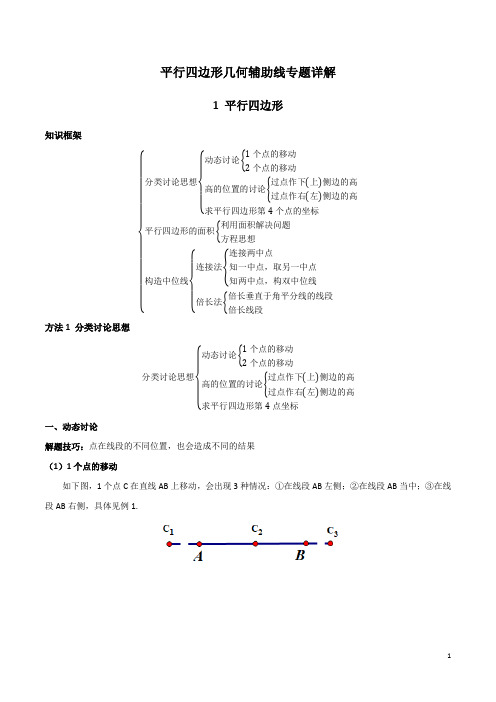
平行四边形几何辅助线专题详解1 平行四边形知识框架{分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4个点的坐标平行四边形的面积{利用面积解决问题方程思想构造中位线{连接法{连接两中点知一中点,取另一中点知两中点,构双中位线倍长法{倍长垂直于角平分线的线段倍长线段 方法1 分类讨论思想分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4点坐标一、动态讨论解题技巧:点在线段的不同位置,也会造成不同的结果 (1)1个点的移动如下图,1个点C 在直线AB 上移动,会出现3种情况:①在线段AB 左侧;②在线段AB 当中;③在线段AB 右侧,具体见例1.(2)2个点的移动如下图,2个点C、D在线段AB上移动(C、D两点在AB中),会出现2种情况:①点C在点D的左侧;②点C在点D的右侧,具体见例2.例1.▱ABCD的内角∠BCD的平分线CE交射线DA于点E,若AE=3,DE=4,求▱ABCD的周长。
例2.在▱ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,求AB的长。
二、高的位置的讨论解题技巧:在平行四边形中作高,会出现2种情况:①在图形内;②在图形外。
(1)过点作下(上)侧边的高如下图,过点A作▱ABCD下侧的边CD上的高AE。
因▱ABCD倾斜方向的变化,高会存在两种情况,具体见例1(2)过点右(左)侧边的高如下图,过点B作▱ABCD的右侧边AD上的高AE。
因▱ABCD倾斜大小的变化,高会存在两种情况,具体见例2上述两种情况实质是同一种情况经过翻折后得到的,为同一种情况。
例1.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,若AB=5,BC=6,求CE的值。
例2.在▱ABCD中,AD=BD=4,BE是AD边上的高,∠EBD=30°,求△ABD的面积。
平行线中添辅助线的方法
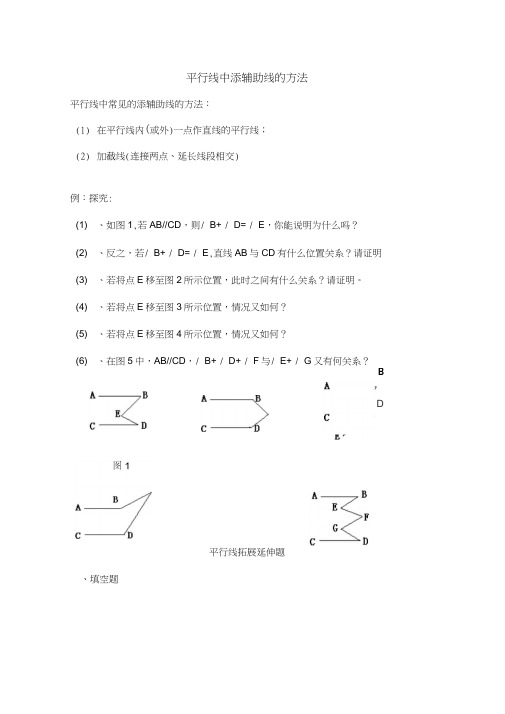
平行线中添辅助线的方法平行线中常见的添辅助线的方法:(1) 在平行线内(或外)一点作直线的平行线;(2) 加截线(连接两点、延长线段相交)例:探究:(1) 、如图1,若AB//CD ,则/ B+ / D= / E ,你能说明为什么吗?(2) 、反之,若/ B+ / D= / E ,直线AB 与CD 有什么位置关系?请证明(3) 、若将点E 移至图2所示位置,此时之间有什么关系?请证明。
(4) 、若将点E 移至图3所示位置,情况又如何?(5) 、若将点E 移至图4所示位置,情况又如何?(6) 、在图5中,AB//CD ,/ B+ / D+ / F 与/ E+ / G 又有何关系?平行线拓展延伸题、填空题BDA 、10° B 、15° C 、20° A L ________ ~B A —-------------------- B \E ZP C z f --------------------— — C D CD图1图2 1 如图,已知 AB // CD ,若/ A=20。
,/ E=35°,则/ C 等于____________2、如图,I 1//I 2,/ 1=120°,/ 2=100°,则/ 3= ________________ 。
4、如图,AB // CD , 1 50°, 2 110°,则 3 ______________ 。
6、如图,已知 AB // EF ,/ BAC=p ,/ ACD=x ,/ CDE=y ,/ DEF=q,用 p 、q 、 y 来表示x 得 ___________________________ 。
、选择题如图1, AB / CD ,且/BAP=60° —a ,Z APC=45° + a ,2、 如图2, AB//CD ,且 A 25 , C 45,贝U E 的度数是(A. 60B. 70C. 110D. 80 3、如图3,已知AB // CD ,则角a 、B 、丫之间的关系为( )BD/ PCD=30°—a ,贝U a (),证明:BC丄CD。
七年级下册数学期中好题必刷 专题04解答题压轴题(人教版)(解析版)

专题04解答题压轴题一、解答题1.已知AM CN ∥,点B 为平面内一点,AB BC ⊥于B . (1)如图,直接写出A ∠和C ∠之间的数量关系.(2)如图,过点B 作BD AM ⊥于点D ,求证:ABD C ∠=∠.(3)如图,在(2)问的条件下,点E ,F 在DM 上,连接BE ,BF ,CF ,BF 那平分DBC ∠,BE 平分ABD ∠,若180FCB NCF ∠+∠=︒,3BFC DBE ∠=∠,求EBC ∠的度数.【答案】(1)90A C ∠+∠=︒ (2)证明见解析 (3)105︒ 【提示】(1)根据平行线的性质及直角三角形的性质证明即可;(2)过点B 作//BG DM ,根据同角的余角相等得出ABD CBG ∠=∠,再根据平行线的性质得到C CBG ∠=∠,即可得到ABD C ∠=∠;(3)过点B 作//BG DM ,根据角平分线的定义得出ABF GBF ∠=∠,设DBE α∠=,ABF β∠=,可得3=75αβ+︒,再根据AB BC ⊥,得到290ββα++=︒,解方程得到=15ABE ∠︒,继而得出,1590105EBC ABE ABC ∠=∠+∠=︒+︒=︒. (1) 如图1,∵//AM CN , ∴C AOB ∠=∠, ∵AB BC ⊥, ∴90ABC ∠=︒,∴90A AOB ∠+∠=︒,90A C ∠+∠=︒, 故答案为:90A C ∠+∠=︒; (2)如图2,过点B 作//BG DM ,∵BD AM ⊥, ∴DB BG ⊥, ∴90∠=︒DBG , ∴90ABD ABG ∠+∠=︒, ∵AB BC ⊥,∴90CBG ABG ∠+∠=︒, ∴ABD CBG ∠=∠, ∵//AM BG ,∴C CBG ∠=∠,ABD C ∠=∠. (3)如图3,过点B 作//BG DM ,∵BF 平分DBC ∠,BE 平分ABD ∠, ∴DBF CBF ∠=∠,DBE ABE ∠=∠, 由(2)知ABD CBG ∠=∠,∴ABF GBF ∠=∠,设DBE α∠=,ABF β∠=,则ABE α∠=,2ABD CBG α∠==∠,GBF AFB β∠=∠=,33BFC DBE α∠=∠=,∴3AFC αβ∠=+∵180AFC NCF ∠+∠=︒,180FCB NCF ∠+∠=︒, ∴3FCB AFC αβ∠=∠=+,BCF △中,由180CBF BFC BCF ∠+∠+∠=︒得 233180αβααβ++++=︒,∵AB BC ⊥, ∴290ββα++=︒, ∴15α=︒, ∴15ABE ∠=︒,∴1590105EBC ABE ABC ∠=∠+∠=︒+︒=︒. 【点睛】本题考查平行线的性质与应用、角平分线的性质、方程思想等知识,学会添加辅助线,掌握相关知识是解题关键.2.如图1,已知直线m ∥n ,AB 是一个平面镜,光线从直线m 上的点O 射出,在平面镜AB 上经点P 反射后,到达直线n 上的点Q .我们称OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OP A=∠QPB .(1)如图1,若∠OPQ=82°,求∠OP A的度数;(2)如图2,若∠AOP=43°,∠BQP=49°,求∠OP A的度数;(3)如图3,再放置3块平面镜,其中两块平面镜在直线m和n上,另一块在两直线之间,四块平面镜构成四边形ABCD,光线从点O以适当的角度射出后,其传播路径为O→P→Q→R→O→P→…试判断∠OPQ和∠ORQ的数量关系,并说明理由.【答案】(1)49°,(2)44°,(3)∠OPQ=∠ORQ【提示】(1)根据∠OP A=∠QP B.可求出∠OP A的度数;(2)由∠AOP=43°,∠BQP=49°可求出∠OPQ的度数,转化为(1)来解决问题;(3)由(2)推理可知:∠OPQ=∠AOP+∠BQP,∠ORQ=∠DOR+∠RQC,从而∠OPQ=∠ORQ.【解答】解:(1)∵∠OP A=∠QPB,∠OPQ=82°,∴∠OP A=(180°-∠OPQ)×12=(180°-82°)×12=49°,(2)作PC∥m,∵m∥n,∴m∥PC∥n,∴∠AOP=∠OPC=43°,∠BQP=∠QPC=49°,∴∠OPQ=∠OPC+∠QPC=43°+49°=92°,∴∠OP A=(180°-∠OPQ)×12=(180°-92°)×1244°,(3)∠OPQ=∠ORQ.理由如下:由(2)可知:∠OPQ=∠AOP+∠BQP,∠ORQ=∠DOR+∠RQC,∵入射光线与平面镜的夹角等于反射光线与平面镜的夹角,∴∠AOP=∠DOR,∠BQP=∠RQC,∴∠OPQ=∠ORQ.【点睛】本题主要考查了平行线的性质和入射角等于反射角的规定,解决本题的关键是注意问题的设置环环相扣、前为后用的设置目的.3.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.(1)求证:∠ABF+∠DCF=∠BFC;(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.【答案】(1)证明见解析;(2)证明见解析;(3)∠FBE=35°.【提示】(1)根据平行线的性质得出∠ABF=∠BFE,∠DCF=∠EFC,进而解答即可;(2)由(1)的结论和垂直的定义解答即可;(3)由(1)的结论和三角形的角的关系解答即可.【解答】证明:(1)∵AB∥CD,EF∥CD,∴AB∥EF,∴∠ABF=∠BFE,∵EF∥CD,∴∠DCF=∠EFC,∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;(2)∵BE⊥EC,∴∠BEC=90°,∴∠EBC+∠BCE=90°,由(1)可得:∠BFC=∠ABE+∠ECD=90°,∴∠ABE+∠ECD=∠EBC+∠BCE,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ECD=∠BCE,∴CE平分∠BCD;(3)设∠BCE=β,∠ECF=γ,∵CE平分∠BCD,∴∠DCE=∠BCE=β,∴∠DCF=∠DCE﹣∠ECF=β﹣γ,∴∠EFC=β﹣γ,∵∠BFC=∠BCF,∴∠BFC=∠BCE+∠ECF=γ+β,∴∠ABF=∠BFE=2γ,∵∠FBG=2∠ECF,∴∠FBG=2γ,∴∠ABE+∠DCE=∠BEC=90°,∴∠ABE=90°﹣β,∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ, ∵BE平分∠ABC,∴∠CBE=∠ABE=90°﹣β,∴∠CBG=∠CBE+∠GBE,∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,整理得:2γ+β=55°, ∴∠FBE =∠FBG +∠GBE =2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°. 【点睛】本题主要考查平行线的性质,解决本题的关键是根据平行线的性质解答. 4.已知AB //CD .(1)如图1,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED .求证:∠BED =∠B +∠D ; (2)如图,连接AD ,BC ,BF 平分∠ABC ,DF 平分∠ADC ,且BF ,DF 所在的直线交于点F . ①如图2,当点B 在点A 的左侧时,若∠ABC =50°,∠ADC =60°,求∠BFD 的度数.②如图3,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BFD 的度数.(用含有α,β的式子表示)【答案】(1)见解析;(2)55°;(3)1118022αβ︒-+【提示】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数;②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数. 【解答】解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠, BF 平分ABC ∠,DF 平分ADC ∠,1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒,55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒; ②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠, BF 平分ABC ∠,DF 平分ADC ∠,1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=,1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+.答:BFD ∠的度数为1118022αβ︒-+.【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质.5.(1)如图①,若∠B +∠D =∠E ,则直线AB 与CD 有什么位置关系?请证明(不需要注明理由). (2)如图②中,AB //CD ,又能得出什么结论?请直接写出结论 . (3)如图③,已知AB //CD ,则∠1+∠2+…+∠n -1+∠n 的度数为 .【答案】(1)AB //CD ,证明见解析;(2)∠E 1+∠E 2+…∠En =∠B +∠F 1+∠F 2+…∠Fn -1+∠D ;(3)(n -1)•180° 【提示】(1)过点E 作EF //AB ,利用平行线的性质则可得出∠B =∠BEF ,再由已知及平行线的判定即可得出AB ∥CD ;(2)如图,过点E 作EM ∥AB ,过点F 作FN ∥AB ,过点G 作GH ∥AB ,根据探究(1)的证明过程及方法,可推出∠E +∠G =∠B +∠F +∠D ,则可由此得出规律,并得出∠E 1+∠E 2+…∠En =∠B +∠F 1+∠F 2+…∠Fn -1+∠D ;(3)如图,过点M 作EF ∥AB ,过点N 作GH ∥AB,则可由平行线的性质得出∠1+∠2+∠MNG =180°×2,依此即可得出此题结论. 【解答】解:(1)过点E 作EF //AB ,∴∠B =∠BEF . ∵∠BEF +∠FED =∠BED ,∴∠B +∠FED =∠BED .∵∠B+∠D=∠E(已知),∴∠FED=∠D.∴CD//EF(内错角相等,两直线平行).∴AB//CD.(2)过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥AB,∵AB∥CD,∴AB∥EM∥FN∥GH∥CD,∴∠B=∠BEM,∠MEF=∠EFN,∠NFG=∠FGH,∠HGD=∠D,∴∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D, 即∠E+∠G=∠B+∠F+∠D.由此可得:开口朝左的所有角度之和与开口朝右的所有角度之和相等,∴∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠Fn-1+∠D.故答案为:∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠Fn-1+∠D.(3)如图,过点M作EF∥AB,过点N作GH∥AB,∴∠APM+∠PME=180°,∵EF∥AB,GH∥AB,∴EF∥GH,∴∠EMN+∠MNG=180°,∴∠1+∠2+∠MNG =180°×2,依次类推:∠1+∠2+…+∠n-1+∠n=(n-1)•180°.故答案为:(n-1)•180°.【点睛】本题考查了平行线的性质与判定,属于基础题,关键是过E 点作AB (或CD )的平行线,把复杂的图形化归为基本图形.6.已知,AB ∥CD ,点E 为射线FG 上一点.(1)如图1,若∠EAF =25°,∠EDG =45°,则∠AED = . (2)如图2,当点E 在FG 延长线上时,此时CD 与AE 交于点H ,则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系,请说明你的结论;(3)如图3,当点E 在FG 延长线上时,DP 平分∠EDC ,且∠EAP :∠BAP =l : 2,∠AED =32°,∠P =30°,求∠EKD 的度数.【答案】(1)70°;(2)EAF AED EDG ∠=∠+∠,证明见解析;(3)122° 【提示】(1)过E 作//EF AB ,根据平行线的性质得到25EAF AEH ∠=∠=︒,45EAG DEH ∠=∠=︒,即可求得AED ∠;(2)过过E 作//EM AB ,根据平行线的性质得到180EAF MEH ∠=︒-∠,180EDG AED MEH ∠+∠=︒-,即EAF AED EDG ∠=∠+∠;(3)设EAI x ∠=,则3BAE x ∠=,通过三角形内角和得到2EDK x ∠=-︒,由角平分线定义及//AB CD 得到33224x x =︒+-︒,求出x 的值再通过三角形内角和求EKD ∠.【解答】解:(1)过E 作//EF AB ,//AB CD ,//EF CD ∴,25EAF AEH ∴∠=∠=︒,45EAG DEH ∠=∠=︒, 70AED AEH DEH ∴∠=∠+∠=︒,故答案为:70︒;(2)EAF AED EDG ∠=∠+∠. 理由如下: 过E 作//EM AB ,//AB CD ,//EM CD ∴,180EAF MEH ∴∠+∠=︒,180EDG AED MEH ∠+∠+=︒, 180EAF MEH ∴∠=︒-∠,180EDG AED MEH ∠+∠=︒-,EAF AED EDG ∴∠=∠+∠;(3):1:2EAP BAP ∠∠=, 设EAP x ∠=,则3BAE x ∠=,32302AED P ∠-∠=︒-︒=︒,DKE AKP ∠=∠,又180EDK DKE DEK ∠+∠+∠=︒,180KAP KPA AKP ∠+∠+∠=︒,22EDK EAP x ∴∠=∠-︒=-︒,DP 平分EDC ∠,224CDE EDK x ∴∠=∠=-︒,//AB CD ,EHC EAF AED EDG ∴∠=∠=∠+∠,即33224x x =︒+-︒,解得28x =︒,28226EDK ∴∠=︒-︒=︒, 1802632122EKD ∴∠=︒-︒-︒=︒.【点睛】本题主要考查了平行线的性质和判定,正确做出辅助线是解决问题的关键.7.(1)(问题)如图1,若//AB CD ,40AEP ∠=︒,130PFD ∠=︒.求EPF ∠的度数;(2)(问题迁移)如图2,//AB CD ,点P 在AB 的上方,问PEA ∠,PFC ∠,EPF ∠之间有何数量关系?请说明理由;(3)(联想拓展)如图3所示,在(2)的条件下,已知EPF α∠=,PEA ∠的平分线和PFC ∠的平分线交于点G ,用含有α的式子表示G ∠的度数.【答案】(1)90°;(2)∠PFC =∠PEA +∠P ;(3)∠G =12α 【提示】(1)根据平行线的性质与判定可求解;(2)过P 点作PN ∥AB ,则PN ∥CD ,可得∠FPN =∠PEA +∠FPE ,进而可得∠PFC =∠PEA +∠FPE ,即可求解;(3)令AB 与PF 交点为O ,连接EF ,根据三角形的内角和定理可得∠GEF +∠GFE =12∠PEA +12∠PFC +∠OEF +∠OFE ,由(2)得∠PEA =∠PFC -α,由∠OFE +∠OEF =180°-∠FOE =180°-∠PFC 可求解. 【解答】解:(1)如图1,过点P 作PM ∥AB , ∴∠1=∠AEP . 又∠AEP =40°, ∴∠1=40°. ∵AB ∥CD , ∴PM ∥CD , ∴∠2+∠PFD =180°. ∵∠PFD =130°, ∴∠2=180°-130°=50°. ∴∠1+∠2=40°+50°=90°. 即∠EPF =90°.(2)∠PFC=∠PEA+∠P.理由:过P点作PN∥AB,则PN∥CD,∴∠PEA=∠NPE,∵∠FPN=∠NPE+∠FPE,∴∠FPN=∠PEA+∠FPE,∵PN∥CD,∴∠FPN=∠PFC,∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;(3)令AB与PF交点为O,连接EF,如图3.在△GFE中,∠G=180°-(∠GFE+∠GEF),∵∠GEF=12∠PEA+∠OEF,∠GFE=12∠PFC+∠OFE,∴∠GEF+∠GFE=12∠PEA+12∠PFC+∠OEF+∠OFE,∵由(2)知∠PFC=∠PEA+∠P,∴∠PEA=∠PFC-α,∵∠OFE+∠OEF=180°-∠FOE=180°-∠PFC,∴∠GEF+∠GFE=12(∠PFC−α)+12∠PFC+180°−∠PFC=180°−12α,∴∠G=180°−(∠GEF+∠GFE)=180°−180°+12α=12α.【点睛】本题主要考查平行线的性质与判定,灵活运用平行线的性质与判定是解题的关键.8.已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.(1)求证:AB//CD;(2)如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)如图(3),在(2)的条件下,过P点作PH//EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.【答案】(1)见解析;(2)∠PEQ+2∠PFQ=360°;(3)30°【提示】(1)首先证明∠1=∠3,易证得AB//CD;(2)如图2中,∠PEQ+2∠PFQ=360°.作EH//AB.理由平行线的性质即可证明;(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,想办法构建方程即可解决问题;【解答】(1)如图1中,∵∠2=∠3,∠1=∠2,∴∠1=∠3,∴AB//CD.(2)结论:如图2中,∠PEQ+2∠PFQ=360°.理由:作EH//AB.∵AB//CD,EH//AB,∴EH//CD,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠1+∠4,∴∠PEQ=∠1+∠4,同法可证:∠PFQ=∠BPF+∠FQD,∵∠BPE=2∠BPF,∠EQD=2∠FQD,∠1+∠BPE=180°,∠4+∠EQD=180°, ∴∠1+∠4+∠EQD+∠BPE=2×180°,即∠PEQ+2(∠FQD+∠BPF)=360°,∴∠PEQ+2∠PFQ=360°.(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,∵EQ//PH,∴∠EQC=∠PHQ=x,∴x+10y=180°,∵AB//CD,∴∠BPH=∠PHQ=x,∵PF平分∠BPE,∴∠EPQ+∠FPQ=∠FPH+∠BPH,∴∠FPH=y+z﹣x,∵PQ平分∠EPH,∴Z=y+y+z﹣x,∴x=2y,∴12y =180°, ∴y =15°, ∴x =30°, ∴∠PHQ =30°. 【点睛】本题考查了平行线的判定与性质,角平分线的定义等知识.(2)中能正确作出辅助线是解题的关键;(3)中能熟练掌握相关性质,找到角度之间的关系是解题的关键.9.如图,以直角三角形AOC 的直角顶点О为原点,以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点()0,A a ,(),0C b 满足220a b b -+-=.(1)C 点的坐标为______;A 点的坐标为______.(2)如图1,已知坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.AC 的中点D 的坐标是()1,2,设运动时间为()0t t >.问:是否存在这样的t ,使ODPODQSS=?若存在,请求出t 的值:若不存在,请说明理由.(3)如图2,过O 作//OG AC ,作AOF AOG ∠=∠交AC 于点F ,点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACEOEC∠+∠∠的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.【答案】(1)()2,0C ,()0,4A ;(2)1;(3)不变,值为2 【提示】(1)根据绝对值和算术平方根的非负性,求得a ,b 的值,再利用中点坐标公式即可得出答案; (2)先得出CP =t ,OP =2-t ,OQ =2t ,AQ =4-2t ,再根据S △ODP =S △ODQ ,列出关于t 的方程,求得t 的值即可; (3)过H 点作AC 的平行线,交x 轴于P ,先判定OG ∥AC ,再根据角的和差关系以及平行线的性质,得出∠PHO =∠GOF =∠1+∠2,∠OHC =∠OHP +∠PHC =∠GOF +∠4=∠1+∠2+∠4,最后代入OHC ACEOEC∠+∠∠进行计算即可.【解答】解:(1)∵2a b -+|b -2|=0, ∴a -2b =0,b -2=0, 解得a =4,b =2, ∴A (0,4),C (2,0).(2)存在, 理由:如图1中,D (1,2),由条件可知:P 点从C 点运动到O 点时间为2秒,Q 点从O 点运动到A 点时间为2秒, ∴0<t ≤2时,点Q 在线段AO 上, 即 CP =t ,OP =2-t ,OQ =2t ,AQ =4-2t , ∴S △DOP =12•OP •yD =12(2-t )×2=2-t ,S △DOQ =12•OQ •xD =12×2t ×1=t ,∵S △ODP =S △ODQ , ∴2-t =t , ∴t =1. (3)结论:OHC ACEOEC∠+∠∠的值不变,其值为2.理由如下:如图2中,∵∠2+∠3=90°, 又∵∠1=∠2,∠3=∠FCO , ∴∠GOC +∠ACO =180°, ∴OG ∥AC , ∴∠1=∠CAO ,∴∠OEC =∠CAO +∠4=∠1+∠4,如图,过H 点作AC 的平行线,交x 轴于P ,则∠4=∠PHC ,PH ∥OG , ∴∠PHO =∠GOF =∠1+∠2,∴∠OHC =∠OHP +∠PHC =∠GOF +∠4=∠1+∠2+∠4, ∴124414OHC ACE OEC ∠+∠∠+∠+∠+∠=∠∠+∠=2.【点睛】本题主要考查三角形综合题、非负数的性质、三角形的面积、平行线的性质等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题.10.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由;(2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AENCDG∠∠的值;(3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.【答案】(1)见解析;(2)12;(3)75° 【提示】(1)根据平行线的性质、余角和补角的性质即可求解. (2)根据平行线的性质、对顶角的性质和平角的定义解答即可. (3)根据平行线的性质和角平分线的定义以及三角形内角和解答即可. 【解答】解:(1)∠C =∠1+∠2,证明:过C 作l ∥MN ,如下图所示,∵l∥MN,∴∠4=∠2(两直线平行,内错角相等), ∵l∥MN,PQ∥MN,∴l∥PQ,∴∠3=∠1(两直线平行,内错角相等), ∴∠3+∠4=∠1+∠2,∴∠C=∠1+∠2;(2)∵∠BDF=∠GDF,∵∠BDF=∠PDC,∴∠GDF=∠PDC,∵∠PDC+∠CDG+∠GDF=180°,∴∠CDG+2∠PDC=180°,∴∠PDC=90°-12∠CDG,由(1)可得,∠PDC+∠CEM=∠C=90°, ∴∠AEN=∠CEM,∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠,(3)设BD交MN于J.∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°, ∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,∵PQ∥MN,∴∠BJA=∠PBD=50°,∴∠ADB =∠AJB -∠JAD =50°-∠JAD =50°-∠CAM , 由(1)可得,∠ACB =∠PBC +∠CAM ,∴∠ACB +∠ADB =∠PBC +∠CAM +50°-∠CAM =25°+50°=75°. 【点睛】本题考查了平行线的性质、余角和补角的性质,解题的关键是根据平行找出角度之间的关系. 11.阅读理解:一个多位数,如果根据它的位数,可以从左到右分成左、中、右三个数位相同的整数,其中a 代表这个整数分出来的左边数,b 代表的这个整数分出来的中间数,c 代表这个整数分出来的右边数,其中a ,b ,c 数位相同,若b ﹣a =c ﹣b ,我们称这个多位数为等差数. 例如:357分成了三个数3,5,7,并且满足:5﹣3=7﹣5; 413223分成三个数41,32,23,并且满足:32﹣41=23﹣32; 所以:357和413223都是等差数.(1)判断:148 等差数,514335 等差数;(用“是”或“不是”填空) (2)若一个三位数是等差数,试说明它一定能被3整除; (3)若一个三位数T 是等差数,且T 是24的倍数,求该等差数T .【答案】(1)不是,是;(2)见解析;(3)432或456或840或864或888 【提示】(1)根据等差数的定义判定即可;(2)设这个三位数是M ,10010M a b c =++,根据等差数的定义可知2a cb +=,进而得出()3352M ac =+即可.(3)根据等差数的定义以及24的倍数的数的特征可先求出a 的值,再根据是8的倍数可确定c 的值,又因为2a cb +=,所以可确定a 、c 为偶数时b 才可取整数有意义,排除不符合条件的a 、c 值,再将符合条件的a 、c 代入2a cb +=求出b 的值,即可求解. 【解答】解:(1)∵4184-≠- , ∴148不是等差数, ∵435135438-=-=- , ∴514335是等差数;(2)设这个三位数是M ,10010M a b c =++, ∵b a c b -=- ,∴2a cb +=, ∵()10010105633522a cM a c a c a c +=+⨯+=+=+ , ∴这个等差数是3的倍数; (3)由(2)知()3352,2a cT a c b +=+= , ∵T 是24的倍数, ∴352a c + 是8的倍数, ∵2c 是偶数,∴只有当35a 也是偶数时352a c +才有可能是8的倍数, ∴2a =或4或6或8,当2a =时,3570a = ,此时若1c =,则35272a c += ,若5c = ,则35+280a c = ,若9c = ,则35+288a c =,大于70又是8的倍数的最小数是72,之后是80,88当35+296a c =时10c > 不符合题意;当4a =时,35140a =,此时若2c =,则352144a c +=,若6c =,则352152a c +=,(144、152是8的倍数), 当6a =时,35210a =,此时若3c =,则352216a c +=,若7c =,则352224a c +=, (216、244是8的倍数),当8a =时,35280a =,此时若0c ,则352280a c +=,若4c =,则352288a c +=, 若8c =,则352296a c +=,(280,288,296是8的倍数), ∵2a cb +=, ∴若a 是偶数,则c 也是偶数时b 才有意义, ∴2a =和6a =是c 是奇数均不符合题意, 当4,2a c ==时,423,4322b T +=== , 当4,6ac ==时,465,4562b T +===, 当8,0ac ==时,804,8402b T +===, 当8,4ac ==时,846,8642b T +===, 当8,8ac ==时,888,8882b T +===, 综上,T 为432或456或840或864或888. 【点睛】本题考查新定义下的实数运算、有理数混合运算,整式的加减运算,能够结合倍数的特点及熟练掌握整数的奇偶性是解题关键.12.阅读下面的文字,解答问题.对于实数a ,我们规定:用符号[a ]表示不大于a 的最大整数;用{a }表示a 减去[a ]所得的差. 例如:=1,[2.2]=1,{2.2}=2.2﹣2=0.2.(1)仿照以上方法计算:]= {5= ;(2)若=1,写出所有满足题意的整数x 的值: .(3)已知y 0是一个不大于280的非负数,且满足}=0.我们规定:y 1=],y 2=y 3=],…,以此类推,直到yn 第一次等于1时停止计算.当y 0是符合条件的所有数中的最大数时,此时y 0= ,n = .【答案】(1)2;32)1、2、3;(3)256,4 【提示】(1)依照定义进行计算即可;(2)由题可知,04x <<,则可得满足题意的整数的x 的值为1、2、3;(3)由0=,可知,0y 是某个整数的平方,又0y 是符合条件的所有数中最大的数,则0256y =,再依次进行计算. 【解答】解:(1)由定义可得,2=,[52=,{53∴=故答案为:2;3. (2)[]1x =,2∴<,即04x <<,∴整数x 的值为1、2、3. 故答案为:1、2、3.(3)0{}0y =,即0==,∴2t =,且t 是自然数,0y 是符合条件的所有数中的最大数, 0256y ∴=,1[16]16y ∴===,2[4]4y ===,3[2]2y ===,41y ===,即4n =. 故答案为:256,4. 【点睛】本题属于新定义类问题,主要考查估算无理数大小,无理数的整数部分和小数部分,理解定义内容是解题关键.13.对任意一个三位数n ,如果n 满足各数位上的数字互不相同,且都不为零,那么称这个数为“梦幻数”,将一个“梦幻数”任意两个数位上的数字对调后可以得到三个不同的新三数,把这三个新三位数的和与111的商记为K (n ),例如123n =,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213321132666++=,6661116÷=,所以()1236K =.(1)计算:()342K 和()658K ;(2)若x 是“梦幻数”,说明:()K x 等于x 的各数位上的数字之和;(3)若x ,y 都是“梦幻数”,且1000x y +=,猜想:()()K x K y +=________,并说明你猜想的正确性. 【答案】(1)(342)9,(658)19K K ==;(2)见解析;(3)28 【提示】(1)根据K 的定义,可以直接计算得出;(2)设x abc =,得到新的三个数分别是:acb cba bac ,,,这三个新三位数的和为100()10()()111()a b c a b c a b c a b c ++++++++=++,可以得到:()K x a b c =++;(3)根据(2)中的结论,猜想:()()28K x K y +=. 【解答】解:(1)已知342n =,所以新的三个数分别是:324,243,432, 这三个新三位数的和为324243342999++=, (342)9K ∴=;同样658n =,所以新的三个数分别是:685,568,856, 这三个新三位数的和为6855688562109++=, (658)19K ∴=.(2)设x abc =,得到新的三个数分别是:acb cba bac ,,,这三个新三位数的和为100()10()()111()a b c a b c a b c a b c ++++++++=++, 可得到:()K x a b c =++,即()K x 等于x 的各数位上的数字之和. (3)设,x abc y mnp ==,由(2)的结论可以得到: ()()()()K x K y a b c m n P +=+++++, 1000x y +=,100()10()()1000a m b n c p ∴+++++=,根据三位数的特点,可知必然有: 10,9,9c p b n a m +=+=+=,()()()()28K x K y a b c m n p ∴+=+++++=,故答案是:28. 【点睛】此题考查了多位数的数字特征,每个数字是10以内的自然数且不为0,解题的关键是:结合新定义,可以计算出问题的解,注意把握每个数字都会出现一次的特点,区别数字与多为数的不同.14.数学中有很多的可逆的推理.如果10b n =,那么利用可逆推理,已知n 可求b 的运算,记为()b f n =,如210100=,则42(100);1010000f ==,则4(10000)f =.①根据定义,填空:(10)f =_________,()310f =__________.②若有如下运算性质:()()(),()()n f mn f m f n f f n f m m⎛⎫=+=- ⎪⎝⎭.根据运算性质填空,填空:若(2)0.3010f =,则(4)f =__________;(5)f =___________; ③下表中与数x 对应的()f x 有且只有两个是错误的,请直接找出错误并改正.错误的式子是__________,_____________;分别改为__________,_____________.【答案】①1,3;②0.6020;0.6990;③f (1.5),f (12);f (1.5)=3a -b +c -1,f (12)=2-b -2c . 【提示】①根据定义可得:f (10b )=b ,即可求得结论; ②根据运算性质:f (mn )=f (m )+f (n ),f (nm)=f (n )-f (m )进行计算;③通过9=32,27=33,可以判断f (3)是否正确,同样依据5=102,假设f (5)正确,可以求得f (2)的值,即可通过f (8),f (12)作出判断. 【解答】解:①根据定义知:f (10b )=b , ∴f (10)=1, f (103)=3. 故答案为:1,3.②根据运算性质,得:f (4)=f (2×2)=f (2)+f (2)=2f (2)=0.3010×2=0.6020, f (5)=f (102)=f (10)-f (2)=1-0.3010=0.6990. 故答案为:0.6020;0.6990.③若f (3)≠2a -b ,则f (9)=2f (3)≠4a -2b , f (27)=3f (3)≠6a -3b ,从而表中有三个对应的f (x )是错误的,与题设矛盾, ∴f (3)=2a -b ;若f (5)≠a +c ,则f (2)=1-f (5)≠1-a -c , ∴f (8)=3f (2)≠3-3a -3c , f (6)=f (3)+f (2)≠1+a -b -c ,表中也有三个对应的f (x )是错误的,与题设矛盾, ∴f (5)=a +c ,∴表中只有f (1.5)和f (12)的对应值是错误的,应改正为: f (1.5)=f (32)=f (3)-f (2)=(2a -b )-(1-a -c )=3a -b +c -1,f (12)=f (663⨯)=2f (6)-f (3)=2(1+a -b -c )-(2a -b )=2-b -2c . ∵9=32,27=33,∴f (9)=2f (3)=2(2a -b )=4a -2b ,f (27)=3f (3)=3(2a -b )=6a -3b . 【点睛】本题考查了幂的应用,新定义运算等,解题的关键是深刻理解所给出的定义或规则,将它们转化为我们所熟悉的运算.15.阅读理解题:定义:如果一个数的平方等于-1,记为2i 1=-①,这个数i 叫做虚数单位,那么和我们所学的实数对应起来就叫做复数,复数一般表示为i a b +(a ,b 为实数),a 叫做这个复数的实部,b 叫做这个复数的虚部,它与整式的加法,减法,乘法运算类似.例如:解方程21x =-,解得:1i x =,2i x =-.同2i ==.读完这段文字,请你解答以下问题: (1)填空:3i =______,4i =______,2342021i i i i +++⋅⋅⋅+=______. (2)已知()()i i 13i a b ++=-,写出一个以a ,b 的值为解的一元二次方程. (3)在复数范围内解方程:2480x x -+=.【答案】(1)-i ,1,0;(2)2320x x ++=;(3)122i x =+,222i x =-. 【提示】(1)根据题意21i =-,则32i i i =⋅,422()i i =,然后计算即可;(2)利用()()i i 13i a b ++=-,得到11ab -=,2ab =,3a b +=-,即可求解 (3)利用配方法求解即可. 【解答】 (1)32i i ii ,4222()(1)1i i ==-=,∵2345110i i i i i i +++=--++=,∴6789423452345()1()100i i i i i i i i i i i i i +++=+++=⨯+++=⨯=, 同理:101112130i i i i +++=, 每四个为一组,和为0, 共有(20211)4505-÷=组, ∴23452021...0i i i i i +++++=, (2)∵()()i i 13i a b ++=-,∴2i i i 13i ab a b +++=-,()1i 13i ab a b -++=-, ∴11ab -=,2ab =,3a b +=-,∴以a ,b 的值为解的一元二次方程可以为:2320x x ++=. (3)2480x x -+=, 2444x x -+=-, 22(2)4x i -=,22x i -=±,∴122i x =+,222i x =-. 【点睛】本题考查了实数的运算,解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.16.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.(1)图2中A、B两点表示的数分别为___________,____________;(2)请你参照上面的方法:①把图3中51⨯的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网a___________.(注:小正方形边长都为1,拼接不重叠格中画出拼成的大正方形,该正方形的边长=也无空隙)a-.(图中标出必要线段②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及3的长)【答案】(1)222)①图见解析5②见解析【提示】(1)根据图1得到小正方形的对角线长,即可得出数轴上点A和点B表示的数(2)根据长方形的面积得正方形的面积,即可得到正方形的边长,再画出图象即可;(3)从原点开始画一个长是2,高是1的长方形,对角线长即是a,再用圆规以这个长度画弧,交数轴于点M,再把这个长方形向左平移3个单位,用同样的方法得到点N.【解答】(1)由图1知,2∴图2中点A表示的数是2-点B2故答案是:2-2(2)①长方形的面积是5,拼成的正方形的面积也应该是5, ∴正方形的边长是5, 如图所示:故答案是:5; ②如图所示:【点睛】本题考查无理数的表示方法,解题的关键是理解题意,模仿题目中给出的解题方法进行求解. 17.先阅读材料,再解答问题:我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口而出,给出了答案,众人十分惊讶,忙问计算的奥妙,你知道华罗庚怎样迅速而准确地计算出结果吗?请你按下面的步骤也试一试:(1310001031000000100,那么,请你猜想:59319的立方根是_______位数 (2)在自然数1到9这九个数字中,33311,327,5===________,37=________,39=________. 猜想:59319的个位数字是9,则59319的立方根的个位数字是________.(3)如果划去59319后面的三位“319”得到数59,而3327=,3464=,由此可确定59319的立方根的十位数字是________,因此59319的立方根是________.(4)现在换一个数103823,你能按这种方法得出它的立方根吗? 【答案】(1)两;(2)125,343,729,9;(3)3,39;(4)47 【提示】(1)根据夹逼法和立方根的定义进行解答;(2)先分别求得1至9中奇数的立方,然后根据末位数字是几进行判断即可; (3)先利用(2)中的方法判断出个数数字,然后再利用夹逼法判断出十位数字即可;(4)利用(3)中的方法确定出个位数字和十位数字即可. 【解答】(1)∵1000<59319<1000000, ∴59319的立方根是两位数;(2)∵3311,327,==35=125,37=343,39=729,∴59319的个位数字是9,则59319的立方根的个位数字是9; (3)∵3327=59<<3464=,且59319的立方根是两位数, ∴59319的立方根的十位数字是3, 又∵59319的立方根的个位数字是9, ∴59319的立方根是39; (4)∵1000<103823<1000000, ∴103823的立方根是两位数;∵3311,327,==35=125,37=343,39=729,∴103823的个位数字是3,则103823的立方根的个位数字是7; ∵3464=3195552<<=,且103823的立方根是两位数, ∴103823的立方根的十位数字是4, 又∵103823的立方根的个位数字是7, ∴103823的立方根是47. 【点睛】考查了立方根的概念和求法,解题关键是理解一个数的立方的个位数就是这个数的个位数的立方的个位数.18.阅读材料:求2320192020122222++++++的值.解:设2320192020122222S =++++++①,将等式①的两边同乘以2, 得234202020212222222S =++++++②,用②-①得,2021221S S -=- 即202121S =-. 即2320192020202112222221++++++=-.请仿照此法计算:(1)请直接填写231222+++的值为______; (2)求231015555+++++值;(3)请直接写出20212345201920201011010101010101011-+-+-+-+-的值. 【答案】(1)15;(2)11514-;(3)111.【提示】(1)先计算乘方,即可求出答案;(2)根据题目中的运算法则进行计算,即可求出答案; (3)根据题目中的运算法则进行计算,即可求出答案; 【解答】解:(1)231248125122=++++=++; 故答案为:15; (2)设231015555T =+++++①,把等式①两边同时乘以5,得112310555555T =+++++②,由②-①,得:11451T =-, ∴11514T -=,∴31121015551455++=+++-;(3)设234520192020110101010101010M =-+-+-+-+①,把等式①乘以10,得:3456222019020202110101010101010101010M =-+-+-+-++②,把①+②,得:202111110M =+, ∴202110111M +=,∴23245201920002211101010101011001111-+-+-+-++=, ∴20212345201920201011010101010101011-+-+-+-+- 20212021101101111+=-111=. 【点睛】本题考查了数字的变化规律,熟练掌握运算法则,熟练运用有理数乘法,以及运用消项的思想是解题的关键.19.观察下列各式,并用所得出的规律解决问题:(11.414≈14.14141.4≈,……0.1732 1.732≈17.32,……由此可见,被开方数的小数点每向右移动______位,其算术平方根的小数点向______移动______位.(2 3.873≈ 1.225≈,≈_____≈______.(31=10=100=,…… 小数点的变化规律是_______________________.(4 2.154≈0.2154≈-,则y =______.【答案】(1)两;右;一;(2)12.25;0.3873;(3)被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;(4)-0.01 【提示】(1)观察已知等式,得到一般性规律,写出即可; (2)利用得出的规律计算即可得到结果; (3)归纳总结得到规律,写出即可; (4)利用得出的规律计算即可得到结果. 【解答】解:(11.414≈14.14≈141.4,……0.1732 1.732≈17.32,……由此可见,被开方数的小数点每向右移动两位,其算术平方根的小数点向右移动一位. 故答案为:两;右;一;(2 3.873≈ 1.225≈,12.250.3873≈; 故答案为:12.25;0.3873;(31=10=100=,……小数点的变化规律是:被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;(4) 2.154≈0.2154≈-,0.2154≈,0.2154-, ∴y=-0.01. 【点睛】此题考查了立方根,以及算术平方根,弄清题中的规律是解本题的关键.20.思考与探究:(1)在如图所示的计算程序中,若开始输入的数值是4,则最后输出的结果是___________.(2)在如图所示的计算程序中,若最后输出的结果是58,则开始输入的数值是___________.(3)按下面的程序计算,若开始输入的值x为正数,最后输出的结果为1621,则满足条件的x的不同值最多有多少个?【答案】(1)17;(2)6或-10;(3)6个【提示】(1)根据程序运算图可得算式4×3+5,按运算顺序进行求解即可;(2)设输入的数字为m,根据题意可得关于x的方程,解方程即可求得答案;(3)根据最后输出的结果,可计算出它前面的那个数,依此类推,可将符合题意的正数求出.【解答】(1)由题意得:4×3+5=17,故答案为:17;(2)设输入的数字为m,则有(m+2)2-6=58,解得:m=6或m=-10,故答案为:6或--10;(3)∵最后输出的数为1621,∴4[(x+5)-(-2)2]-3=1621,解得:x=405>0,又∵4[(x+5)-(-2)2]-3=405,解得:x=101>0,又∵4[(x+5)-(-2)2]-3=101,解得:x=25>0,又∵4[(x+5)-(-2)2]-3=25,解得:x=6>0,又∵4[(x+5)-(-2)2]-3=6,解得:x=54>0,又∵4[(x+5)-(-2)2]-3=5 4 ,解得:x=116>0,又∵4[(x+5)-(-2)2]-3=1 16,解得:x=1564-<0,(不符合题意)∴符合题意的正数最多有6个.【点睛】本题考查了程序运算,涉及了一元一次方程,利用平方根的解方程等知识,正确审题,弄清程序运算中的运算顺序,熟练掌握相关和运算法则和解题方法是解此类问题的关键.21.读一读,式子“1+2+3+4+5+…+100”表示从1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为1001n n=∑,这里“∑”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为501(21)nn =-∑,又知13+23+33+43+53+63+73+83+93+103可表示为1031nn=∑.通过对以上材料的阅读,请解答下列问题.(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为_________.(2)1+12+13+…+110用求和符号可表示为_________.(3)计算6211nn=-∑()=_________.(填写最后的计算结果)【答案】(1)5012nn =∑;(2)1011nn =∑;(3)50【提示】(1)根据题中的新定义得出结果即可;(2)根据题中的新定义得出结果即可;(3)利用题中的新定义将原式变形,计算即可得到结果.【解答】解:解:(1)根据题意得:2+4+6+8+10+ (100)5012nn =∑;(2)1+12+13+…+110=1011n n=∑; (3)原式=1-1+4-1+9-1+16-1+25-1+36-1=85. 故答案为:(1)5012n n =∑;(2)1011n n=∑;(3)85.【点睛】此题考查了有理数的加法和减法运算,弄清题中的新定义是解本题的关键. 22.如图,已知点()0,0O ,()2,0A ,()1,2B -.(1)求OAB 的面积;(2)点C 是在坐标轴上异于点A 的一点,且OBC 的面积等于OAB 的面积,求满足条件的点C 的坐标;(3)若点D 的坐标为()m,2,且1m <-,连接AD 交OB 于点E ,在x 轴上有一点F ,使BDE 的面积等于BEF 的面积,请直接写出点F 的坐标__________(用含m 的式子表示).【答案】(1)2;(2)(0,4),(0,4),(2,0)--;(3)1(1,0)F m +或2(1,0)F m -- 【提示】(1)直接利用以OA 为底,进行求面积;(2)OBC 的面积等于OAB 的面积,需要分三种情况进行分类讨论; (3)根据BDEBEFSS=推导出OBDOBFSS=,然后分两种情况进行讨论,即当F 位于x 轴负半轴上时与F 位于x 轴正半轴上时.【解答】 解:(1)1122222OABB SOA y =⋅⋅=⨯⨯=. (2)作如下图形,进行分类讨论:。
做辅助线的方法

做辅助线的⽅法前⾔[摘录于⽹络,已经加以修订,感谢原作者]有⼈说,解⼏何题“得辅助线者得天下”。
这句话虽然有些夸张,但是学好添加辅助线是我们快速解题的重要途径,那么辅助线应该如何添加呢?使⽤原因解证⼏何问题的基本思路就是要利⽤已知⼏何条件求得所求⼏何关系。
这往往需要将已知条件与所求条件集中到⼀个或两个⼏何关系⼗分明确的简单的⼏何图形之中。
如⼀个三⾓形(特别是直⾓三⾓形、等腰三⾓形),⼀个平⾏四边形(特别是矩形、菱形、正⽅形),⼀个圆,或两个全等三⾓形,两个相似三⾓形之中。
这种思路可称为条件集中法。
为了达到条件集中的⽬标,我们需要将远离的、分散的已知条件和所求条件,通过连线、作线、平移、翻转、旋转等⽅法来补全或构造⼀个三⾓形、⼀个平⾏四边形、⼀个圆、或两个全等三⾓形、两个相似三⾓形,便于运⽤这些图形的⼏何关系(性质定理)解题,这就需要添加辅助线。
考量原则添加什么样的辅助线,总的来说,由以下三⽅⾯决定:⑴.由所求决定:问什么,先要作什么。
⑵.由已知决定:已知什么,作出什么,并为充分运⽤已知条件提供的性质定理添加辅助线。
⑶.由条件集中的需要决定:为补全或构造⼏何关系⼗分明确的⼀个三⾓形、⼀个平⾏四边形、⼀个圆,或两个全等三⾓形、两个相似三⾓形⽽添加辅助线。
分类细述添加辅助线的⽬的,就是将题⽬中的已知条件之间建⽴联系。
做辅助线的⽅法多种多样,具体题⽬要具体分析,但是也有其相对固定的套路。
以下的总结的很全⾯,希望细细品味。
(Ⅰ).在三⾓形中如何添加①等腰Δ:常连底边上的中线或⾼或顶⾓的平分线(构造两个全等的直⾓Δ,或便于运⽤等腰Δ三线合⼀的性质.)②直⾓Δ斜边上有中点:连中线(构造两个等腰Δ,或便于运⽤直⾓Δ斜边上的中线的特殊性质.)或做斜边的中垂线,构造等腰三⾓形。
③斜Δ[锐⾓和钝⾓三⾓形的统称]有中点或中线:连中线(构造两个等底同⾼的等积Δ);或⾃左右两顶点分别作中线的垂线(构造两个全等直⾓三⾓形);或连中位线、或过⼀中点作另⼀边的平⾏线(构造两个相似⽐为1:2的相似Δ,或便于运⽤Δ中位线定理);或延长中位线以补全为⼀个平⾏四边形;或延长中线的⼀倍以构造两个全等Δ;或延长中线的13,以构造两个全等Δ或补全为⼀个平⾏四边形。
专题02 平行线及其判定 (题型归纳)【2022春人教七下数学核心考点题型归纳+变式集训】(解析版)

专题02 平行线及其判定(一题三变)【思维导图】◎考点题型1 平面内两直线的位置关系例.(2022·全国·七年级)下列说法正确的是()A.不相交的两条直线是平行线.B.如果线段AB与线段CD不相交,那么直线AB与直线CD平行.C.同一平面内,不相交的两条射线叫做平行线.D.同一平面内,没有公共点的两条直线是平行线.【答案】D【解析】【分析】根据平行线的定义逐项分析即可.【详解】A、同一平面内不相交的两条直线是平行线,故此说法错误;B、两条线段不相交也可以不平行,故此说法错误;C、同一平面内,不相交的两条射线可以平行,也可以既不平行也不相交,故此说法错误;D、同一平面内,没有公共点的两条直线是平行线,此说法正确,故选D.【点睛】本题考查了平行线的定义,理解此定义是关键,属于概念基础题.变式1.(2022·江苏·南京市第二十九中学七年级期末)下列说法正确的是()A.不相交的两条直线叫做平行线B.过一点有且仅有一条直线与已知直线垂直C.平角是一条直线D.过同一平面内三点中任意两点,只能画出3条直线【答案】B【解析】【分析】根据平行线的定义,垂直的性质,平角的定义,两点确定一条直线的性质依次判断.【详解】解:同一平面内,不相交的两条直线叫做平行线,故选项A错误;过一点有且仅有一条直线与已知直线垂直,故选项B正确;平角是角的两边在同一直线上的角,故选项C错误;过同一平面内三点中任意两点,能画出1条或3条直线故选项D错误;故选:B.【点睛】此题考查语句的正确性,正确掌握平行线的定义,垂直的性质,平角的定义,两点确定一条直线的性质是解题的关键.变式2.(2022·江苏江阴·七年级期末)有下列说法:①两条不相交的直线叫平行线;①同一平面内,过一点有且只有一条直线与已知直线垂直;①两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线互相垂直;①有公共顶点的两个角是对顶角.其中说法正确的个数是()A.1B.2C.3D.4【答案】A【解析】【分析】根据平行线的定义、垂直的定义及垂线的唯一性、对顶角的含义即可判断.【详解】同一平面内不相交的两条直线叫做平行线,故说法①错误;说法①正确;两条直线相交所成的四个角中,如果有一个角是直角,那么这两条直线互相垂直,当这两个相等的角是对顶角时则不垂直,故说法①错误;根据对顶角的定义知,说法①错误;故正确的说法有1个;故选:A【点睛】本题考查了两条直线的位置关系中的相关概念及性质,掌握这些概念是关键.变式3.(2021·湖北汉阳·七年级期中)下列命题不正确的是()A.直线外一点与直线上各点连接的所有线段中,垂线段最短B.在同一平面内,两条不重合的直线位置关系不平行必相交C.两点确定一条直线D.两点之间直线最短.【答案】D【解析】【分析】根据垂线段最短、两直线的位置关系、两点确定一条直线、两点之间线段最短判断.【详解】解:A、直线外一点与直线上各点连接的所有线段中,垂线段最短,本选项说法正确,不符合题意;B、在同一平面内,两条不重合的直线位置关系不平行必相交,本选项说法正确,不符合题意;C、两点确定一条直线,本选项说法正确,不符合题意;D、两点之间线段最短,故本选项说法错误,符合题意;故选:D.【点睛】本题考查的是命题的真假判断,掌握垂线段最短、两直线的位置关系、两点确定一条直线、两点之间线段最短是解题的关键.◎考点题型2立体图形中平面的棱例.(2021·上海市实验学校二模)如图,在长方体ABCD-EFGH中,与棱AD平行的平面共有()A .1个B .2个C .3个D .4个【答案】B【解析】【分析】 先找出不过棱AD 的平面,确定平面内有与AD 平行的直线即可.【详解】解:①在长方体ABCD-EFGH 中,AD //EH ①BC ,①AD ①平面EFGH ,AD ①平面BCGF ,①与棱AD 平行的平面共有2个.故选择:B .【点睛】本题主要考查立体图形与平行线,利用平行线的定义找出与棱AD 平行的平面并准确观察图形是解题的关键.变式1.(2019·全国·七年级单元测试)如图所示,在长方体1111ABCD A B C D 中,与棱AD 异面的棱有( )A .2条B .3条C .4条D .5条【答案】C【解析】【分析】 根据判断异面直线的方法判断即可.【详解】由题意得:与棱AD 异面的棱有:BB 1,CC 1,A 1B 1,C 1D 1故选C.【点睛】本题考查异面直线的概念:过平面外一点和平面内一点与平面内不经过该点的直线是异面直线,熟记概念是本题关键.变式2.(2012·上海奉贤·一模)已知长方体如图所示,那么下列直线中与直线不平行也不垂直的直线是A.B.GH C.HC D.【答案】C【解析】【详解】解:A、EA是长方体的棱,与AB互相垂直,故本选项错误;B、GH是长方体的棱,与AB互相平行,故本选项错误;C、HC不是长方体的棱,与AB不平行也不垂直,故本选项正确;D、EF是长方体的棱,与AB互相平行,故本选项错误.故选C.变式3.(2020·上海浦东新·三模)已知长方体ABCD-EFGH如图所示,那么下列各条棱中与棱GC平行的是()A.棱EA;B.棱AB;C.棱GH;D.棱GF.【答案】A【解析】【分析】首先确定与GC平行的棱,再确定选项即可求解.【详解】解:观察图象可知,与棱GC平行的棱有AE、BF、DH.故选:A.【点睛】本题考查认识立体图形,平行线的判定等知识,解题的关键是理解题意,属于基础题.◎考点题型3用直尺、三角板画平行线例.(2021·吉林九台·八年级期中)在下列各题中,属于尺规作图的是()A.用直尺画一工件边缘的垂线B.用直尺和三角板画平行线C.利用三角板画45 的角D.用圆规在已知直线上截取一条线段等于已知线段【答案】D【解析】【分析】根据尺规作图的定义:用没有刻度的直尺和圆规作图,只使用圆规和直尺来解决平面几何作图,进行逐一判断即可.【详解】解:A、用直尺画一工件边缘的垂线,这里没有用到圆规,故此选项不符合题意;B、用直尺和三角板画平行线,这里没有用到圆规,故此选项不符合题意;C、利用三角板画45°的角,这里没有用到圆规,故此选项不符合题意;D、用圆规在已知直线上截取一条线段等于已知线段,是尺规作图,故此选项符合题意;故选D.【点睛】本题主要考查了尺规作图的定义,解题的关键在于熟知定义.变式1.(2014·山东滨州·中考真题)如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等【答案】A【解析】【分析】由已知可知①DPF=①BAF,从而得出同位角相等,两直线平行.【详解】①①DPF=①BAF,①AB①PD(同位角相等,两直线平行).故选A.【点睛】此题主要考查了基本作图与平行线的判定,正确理解题目的含义是解决本题的关键.变式2.(2011·北京石景山·中考模拟)已知:如图,l①m,等边①ABC的顶点B在直线m 上,边BC与直线m所夹锐角为20°,则①α的度数为A.60°B.45°C.55°D.40°【答案】D【解析】【详解】过C作CE①直线m①l①m,①l①m①CE,①①ACE=①α,①BCE=①CBF=20°,①等边①ABC,①①ACB=60°,①①α+①CBF=①ACB=60°,①①α=40°.故选D.变式3.(2021·辽宁和平·八年级期末)如图,是我们学过的用直尺和三角板画平行线的方法示意图,画图的原理是()A.两直线平行,同位角相等B.同位角相等,两直线平行C.内错角相等,两直线平行D.同旁内角互补,两直线平行【答案】B【解析】【分析】由已知可知①DPF=①BAF,从而得出同位角相等,两直线平行.【详解】解:如图:①①DPF=①BAF,①a①b(同位角相等,两直线平行).故选:B.【点睛】本题考查了平行线的判定方法,熟练掌握平行线的判定方法,根据题意得出同位角相等是解决问题的关键.◎考点题型4平行公理的应用例.(2022·江苏玄武·七年级期末)下列说法错误的是()A.经过两点,有且仅有一条直线B.平面内过一点有且只有一条直线与已知直线垂直C.两点之间的所有连线中,线段最短D.平面内过一点有且只有一条直线与已知直线平行【答案】D【解析】【分析】根据垂线的性质、线段的性质、直线的性质、平行公理判断下列选项.【详解】解:由垂线的性质、线段的性质、直线的性质可知A、B、C正确;A、根据直线的性质可知选项正确,不符合题意;B、根据垂线的性质可知选项正确,不符合题意;C、根据线段的性质可知选项正确,不符合题意;D、由平行公理可知选项不正确,需要保证该点不在已知直线上,符合题意;故选:D.【点睛】本题主要考查了垂线的性质、线段的性质、直线的性质、平行公理,解题的关键是掌握相关的概念.变式1.(2022·江苏·无锡市东林中学七年级期末)下列说法正确的有()①两点之间的所有连线中,线段最短;①相等的角叫对顶角;①过一点有且只有一条直线与已知直线平行;①若AC=BC,则点C是线段AB的中点;①在同一平面内,经过一点有且只有一条直线与已知直线垂直.A.1个B.2个C.3个D.4个【答案】B【解析】【分析】根据线段的性质,对顶角相等的性质,平行公理,对各小题分析判断即可得解.【详解】解:①两点之间的所有连线中,线段最短,正确;①相等的角不一定是对顶角,但对顶角相等,故本小题错误;①过直线外一点有且仅有一条直线与已知直线平行,故本小题错误;①若AC=BC,且A、B、C三点共线,则点C是线段AB的中点,否则不是,故本小题错误,①在同一平面内,过一点有且只有一条直线与已知直线垂直,正确;所以,正确的结论有①①共2个.故选:B.【点睛】本题考查了平行公理,线段的性质,对顶角的判断,是基础题,熟记概念与性质是解题的关键.变式2.(2021·全国·七年级课时练习)下列说法:(1)两条不相交的直线是平行线;(2)过一点有且只有一条直线与已知直线平行;(3)在同一平面内两条不相交的线段一定平行;(4)过一点有且只有一条直线与已知直线垂直;(5)两点之间,直线最短;其中正确个数是()A.0个B.1个C.2个D.3个【答案】B【解析】【分析】根据平面内相交线和平行线的基本性质逐项分析即可.【详解】解:(1)在同一平面内,两条不相交的直线是平行线,故原说法错误;(2)过直线外一点有且只有一条直线与已知直线平行,故原说法错误;(3)在同一平面内两条不相交的线段不一定平行,故原说法错误;(4)过一点有且只有一条直线与已知直线垂直,故原说法正确;(5)两点之间,线段最短,故原说法错误;故选:B.【点睛】本题考查平面内两直线的关系,及其推论等,掌握基本概念和推论是解题关键.变式3.(2021·黑龙江·哈尔滨市第四十七中学七年级期中)下列说法中正确的有()个①两条直线被第三条直线所截,同位角相等;①同一平面内,不相交的两条线段一定平行;①过一点有且只有一条直线垂直于已知直线;①经过直线外一点有且只有一条直线与这条直线平行;①从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.A .1B .2C .3D .4【答案】A【解析】【分析】 根据平行线的性质,垂线的性质,平行公理,点到直线的距离的定义逐项分析判断即可.【详解】①互相平行的两条直线被第三条直线所截,同位角相等,故①不正确;①同一平面内,不相交的两条直线一定平行,故①不正确;①同一平面内,过一点有且只有一条直线垂直于已知直线,故①不正确;①经过直线外一点有且只有一条直线与这条直线平行,故①正确①从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故①不正确. 故正确的有①,共1个,故选A .【点睛】本题考查了平行线的性质,平行公理,垂线的性质,点到直线的距离,掌握相关定理性质是解题的关键.◎考点题型5平行公理推论的应用例.(2021·山东·济宁学院附属中学二模)如图,直线//a b ,将含有45°角的三角板ABC 的直角顶点C 放在直线b 上,若120∠=︒,则2∠的度数是( )A .25°B .20C .35D .30【答案】A【解析】【分析】 过B 作//BE 直线a ,推出////a b BE ,根据平行线性质得出120ABE ∠=∠=︒,2CBE ∠=∠,根据45ABC ∠=︒求出CBE ∠,即可得出答案.【详解】解:过B 作//BE 直线a ,a b,直线//①////a b BE,∴∠=∠=︒,2CBE∠=∠,ABE120∠=︒,45ABC∴∠=∠2CBEABC ABE=∠-∠=︒-︒4520=︒,25故选:A.【点睛】本题考查了平行线性质的应用,解此题的关键是正确作出辅助线.变式1.(2021·河北石家庄·一模)经过直线l 外一点O的四条直线中,与直线l相交的直线至少有()A.1条B.2条C.3条D.4条【答案】C【解析】【分析】根据经过直线外一点有且只有一条直线和已知直线平行得出即可.【详解】解:根据经过直线外一点有且只有一条直线和已知直线平行,得出如果有和直线l平行的,只能是一条,即与直线l相交的直线至少有3条,故选:C.【点睛】本题考查了平行公理及推论,注意:经过直线外一点有且只有一条直线和已知直线平行.变式2.(2021·河南邓州·七年级期末)如图,一块直角三角尺的一个顶点落在直尺的一边上,若①2=25°,则①1的度数为()A.45°B.55°C.65°D.75°【答案】C【解析】【分析】如图,过直角顶点O作EF①AB,根据平行公理的推论可得EF①AB①CD,进而可得①2=①3,①1=①4,再结合①3+①4=90°即可求出答案.【详解】解:如图,过直角顶点O作EF①AB,由于AB①CD,则EF①AB①CD,①①2=①3,①1=①4,①①2=25°,①①3=25°,①①3+①4=90°,①①4=65°,①①1=65°.故选:C.【点睛】本题主要考查了平行公理的推论和平行线的性质,属于基本题型,熟练掌握平行线的性质是解题关键.变式3.(2020·湖南望城·七年级期末)直角三角板和直尺如图放置,若①1=70°,则①2的度数为()A.70°B.30°C.20°D.15°【答案】C【解析】【分析】过点F做FH①AD,先求出①3,再根据题意求出①4,最后根据平行线的性质即可求解.【详解】解:如图,过点F做FH①AD,①①1=①3=70°,由题意得①EFG=90°,AD①BC①FH①BC,①4=90°-①3=20°,①①2=①4=20°.故选:C【点睛】本题考查了平行公理推论,平行线的性质.解题关键是熟记相关定理,并能根据题意添加辅助线FH①AD.◎考点题型6同位角相等,两直线平行例.(2021·北京房山·七年级期末)下列图形中,由①1=①2能得到AB∥CD的图形有()个A.4B.3C.2D.1【答案】C【解析】【分析】在三线八角的前提下,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此判断即可.【详解】解:第一个图形,①①1=①2,①AC ①BD ;故不符合题意;第二个图形,①①1=①2,①AB ①CD ,故符合题意;第三个图形,①①1=①2,①2=①3,①①1=①3,①AB ①CD ;第四个图形,①①1=①2不能得到AB ①CD ,故不符合题意;故选:C .【点睛】本题考查了平行线的判定,解题的关键是注意平行线判定的前提条件必须是三线八角. 变式1.(2022·广东阳山·八年级期末)如图,不能推出a ①b 的条件是( )A .①4=①2B .①3+①4=180°C .①1=①3D .①2+①3=180°【答案】B【解析】【分析】 根据平行线的判定方法,逐项判断即可.【详解】解:A 、2∠和4∠是一对内错角,当42∠=∠时,可判断//a b ,故A 不符合题意;B 、3∠和4∠是邻补角,当34180∠+∠=︒时,不能判定//a b ,故B 符合题意;C 、1∠和3∠是一对同位角,当13∠=∠时,可判断//a b ,故C 不合题意;D 、2∠和3∠是一对同旁内角,当23180∠+∠=︒时,可判断//a b ,故D 不合题意; 故选B .【点睛】本题考查了平行线的判定.解题的关键是:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.变式2.(2021·重庆实验外国语学校七年级期中)如图,能判断a //b 的条件是( )A .①1=①2B .①2+①4=180°C .①4+①5=180°D .①2=①3【答案】B【解析】【分析】 同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,两直线平行,再逐一判断各选项即可得到答案.【详解】解:1=2,//,c d ∠∠∴ 故A 不符合题意;2+4=180,//,a b ∠∠︒∴ 故B 符合题意;4+5=180//,c d ∠∠︒∴, 故C 不符合题意;2=3,//,c d ∠∠∴ 故D 不符合题意;故选:.B【点睛】本题考查的是平行线的判定,掌握平行线的判定方法是解题的关键.变式3.(2021·广东·江南外国语学校七年级期中)如图,以下四个条件:①①1=①3,①①2=①4,①①BAD +①D =180°,①①EAD =①B .其中能够判断AB ①DC 的条件有( )A .①①B .①①C .①①D .①①【答案】D【解析】【分析】 根据平行线的判定定理分别进行分析即可.【详解】解:若①1=①3,则AB ①DC ;若①2=①4,则AD ①BC ;若①BAD +①D =180°,则AB ①DC ;若①EAD =①B ,则AD ①BC ;故选:D .【点睛】此题主要考查了平行线的判定,关键是掌握判定定理:同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.◎考点题型7内错角相等,两直线平行例.(2021·重庆·七年级期中)如图,点E 在CD 延长线上,下列条件中不能判定//AB CD 的是( )A .12∠=∠B .34∠=∠C .5B ∠=∠D .180B BDC ∠+∠=︒【答案】A【解析】【分析】 根据平行线的判定方法直接判定即可.【详解】解:选项B 中,34∠∠=,//AB CD ∴(内错角相等,两直线平行),所以正确; 选项C 中,5B ∠=∠,//AB CD ∴(内错角相等,两直线平行),所以正确;选项D 中,180B BDC ∠+∠=︒,//AB CD ∴(同旁内角互补,两直线平行),所以正确; 而选项A 中,1∠与2∠是直线AC 、BD 被AD 所截形成的内错角,因为12∠=∠,所以应是//AC BD ,故A 错误.故选:A .【点睛】本题主要考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.变式1.(2022·辽宁丹东·八年级期末)如图,①13∠=∠,①23∠∠=,①14∠=∠,①25180+=︒∠∠可以判定b c ∥的条件有( ).A .①①①B .①①①C .①①①D .①①①①【答案】A【解析】【分析】 根据平行线的判定定理逐个排查即可.【详解】解:①由于①1和①3是同位角,则①可判定b c ∥;①由于①2和①3是内错角,则①可判定b c ∥;①①由于①1和①4既不是同位角、也不是内错角,则①不能判定b c ∥;①①由于①2和①5是同旁内角,则①可判定b c ∥;即①①①可判定b c ∥.故选A .【点睛】本题主要考查了平行线的判定定理,平行线的判定定理主要有:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;如果内错角相等,那么这两条直线平行;如果同旁内角互补,那么这两条直线平行.变式2.(2021·上海·七年级期末)如图,一定能推出AB CD ∥的条件是( )A .DAC ACB ∠=∠ B .ADC DCE ∠=∠ C .ABC ACD ∠=∠ D .ABC DCE ∠=∠【解析】【分析】平行线的判定方法有:同位角相等,两直线平行;内错角相等,两直线平行,同旁内角互补,两直线平行;根据平行线的判定方法逐一判定即可.【详解】解:A .DAC ∠和ACB ∠是直线AD 和BC 被直线AC 所截所成的内错角,DAC ACB ∴∠=∠不能推出AB CD ∥,故本选项不符合题意;B .ADC ∠和DCE ∠是直线AD 和BC 被直线DC 所截所成的内错角,ADC DCE ∴∠=∠不能推出AB CD ∥,故本选项不符合题意;C .ACD ∠和BAC ∠是直线AB 和CD 被直线AC 所截所成的内错角,但不能判定ABC BAC ∠=∠,∴不能判定ACD BAC ∠=∠,ABC ∠和DCE ∠是直线AB 和CD 被直线BC 所截所成的同位角,但不能判定ACD DCE ∠=∠,∴不能判定ABC DCE ∠=∠,ABC ACD ∴∠=∠不能推出AB CD ∥,故本选项不符合题意;D .ABC ∠和DCE ∠是直线AB 和DC 被直线BC 所截所成的同位角,ABC DCE ∴∠=∠能推出AB CD ∥,故本选项符合题意;故选:D .【点睛】本题主要考查了平行线的判定,熟记同位角相等,两直线平行是解决问题的关键. 变式3.(2021·山东郯城·七年级期末)下列图形中,由①1=①2,能得到AB ①CD 的是( )A .B .C .D .【答案】C【分析】根据平行线的判定定理逐项分析即可.【详解】解:A 、①1=①2,不能判断//AB CD ,故该选项不正确,不符合题意;B 、12∠=∠,//AC BD ∴,故该选项不正确,不符合题意;C 、①12∠=∠,∴//AB CD ,故该选项正确,符合题意;D 、①1=①2,不能判断//AB CD ,故该选项不正确,不符合题意.故选C .【点睛】本题考查了内错角相等,两直线平行,掌握平行线的判定定理是解题的关键.◎考点题型8同旁内角互补,两直线平行例.(2021·安徽长丰·七年级期末)如图,点D ,E 分别是AB ,AC 上的点,连接DE ,CD ,则下列条件不能判定DE ①BC 的是( )A .①AED =①ACDB .①ADE =①BC .①EDC =①DCBD .①DEC +①ACB =180°【答案】A【解析】【分析】 同位角相等,则两直线平行;内错角相等,则两直线平行 ;同旁内角互补,则两直线平行;根据这三点对四个选项逐一判断.【详解】A 、∠AED =∠ACD ,不能判定DE ∥BC ,不符合题意;B 、∠ADE =∠B ,同位角相等,则两直线平行,能判定DE ∥BC ,符合题意; C 、∠EDC =∠DCB ,内错角相等,则两直线平行,能判定DE ∥BC ,符合题意;D 、∠DEC +∠ACB =180°,同旁内角互补,则两直线平行,能判定DE ∥BC ,符合题意. 故选:A .【点睛】本题考查两直线平行的判定,掌握相关角度之间的关系推断平行时本题解题关键. 变式1.(2021·全国·七年级课时练习)如图所示,下列条件( )成立时,//AD BC .A .23∠∠=B .14∠=∠C .1234∠+∠=∠+∠D .180A C ∠+∠=︒ 【答案】A【解析】【分析】根据平行线的判定定理逐一判断,排除错误答案.【详解】解:A 、正确,根据内错角相等,两直线平行;B 、错误,由内错角相等,两直线平行,得出AB //CD ,而不是//AD BC ;C 、错误,①1+①2=①3+①4,即①ABC =①ADC ,无法说明//AD BC ;D 、错误,①A +①C =180°,但这两个角不是同旁内角,所以无法说明//AD BC . 故选:A .【点睛】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.变式2.(2020·贵州·铜仁一中实验学校八年级阶段练习)下列图形中,由①1=①2,能得到AB ①CD 的是( ).A .B .C.D.【答案】C【解析】【分析】在三线八角的前提下,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.据此判断即可.【详解】解:A、①1、①2是同旁内角,由①1=①2不一定能判定AB①CD,故本选项错误;B、①1、①2是内错角,由①1=①2能判定AC①BD,故本选项错误;C、①1、①2是内错角,由①1=①2能判定AB①CD,故本选项正确;D、①1、①2是四边形中的对角,由①1=①2不能判定AB①CD,故本选项错误;故选:C.【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.变式3.(2021·广东·佛山市华英学校七年级阶段练习)如图,在下列给出的条件中,不能判定AB∥EF的是()A.∠B+∠2=180°B.∠1=∠4C.∠B=∠3D.∠1=∠B【答案】D【解析】【分析】根据平行线的判定逐项进行判断即可.【详解】解:A、①①B+①2=180,①AB ①EF (同旁内角互补,两直线平行),不符合题意;B 、①①1=①4,①AB ①EF (内错角相等,两直线平行),不符合题意;C 、①①B =①3,①AB ①EF (同位角相等,两直线平行),不符合题意;D 、①①1=①B ,①BC ①DF (同位角相等,两直线平行),不能证出AB ①EF ,符合题意.故选:D .【点睛】本题主要考查平行线的判定方法,掌握平行线的判定方法是解题的关键,即①同位角相等⇔两直线平行,①内错角相等⇔两直线平行,①同旁内角互补⇔两直线平行.◎考点题型9垂直于同一直线的两直线平行例.(2021·河北·石家庄外国语学校七年级期末)如图所示,AC BC ⊥,DE BC ⊥,CD AB ⊥,40ACD ∠=︒,则BDE ∠等于( )A .40︒B .50︒C .60︒D .不能确定【答案】B【解析】【分析】 利用AC BC ⊥,DE BC ⊥推出DE ①AC ,求出①EDC 的度数,再根据CD AB ⊥求出答案.【详解】AC BC ⊥,DE BC ⊥,//DE AC ∴,40EDC ACD ∴∠=∠=︒又CD AB ⊥,90BDE EDC ∴∠=︒-∠904050=︒-︒=︒,故选:B .【点睛】此题考查两直线平行内错角相等,垂直于同一条直线的两直线平行,互余角的求法,正确理解平行线的性质是解题的关键.变式1.(2019·上海虹口·七年级阶段练习)下列推理判断正确的是( )A .a①b ,b①c ,c①d ,∴a①dB .1l ①2l ,2l 3l ⊥,1l ∴①3l (123l l l 在同一平面内)C .如图,AB①CD,12∠∠∴=D .如图,AD①BC,34∴∠=∠【答案】A【解析】【分析】根据平行线的判定与性质进行判断即可.【详解】 A.a①b ,b①c ,c①d ,∴a①d ,正确; B. 1l ①2l ,2l 3l ⊥,1l ∴①3l (123l l l 在同一平面内),故此选项错误;C. 如图,AB①CD,34∴∠=∠,故此选项错误;D. 如图,AD①BC,12∠∠∴=,故此选项错误.故选A.【点睛】本题主要考查了平行线的判定与性质,熟练掌握判定与性质是解决问题的关键.变式2.(2021·辽宁营口·七年级期末)如图,①ABC 中,AH①BC ,BF 平分①ABC ,BE①BF ,EF①BC ,以下四个结论:①AH①EF ,①①ABF=①EFB ,①AC①BE ,①①E=①ABE ,正确的是( )A .①①①①B .①①C .①①①D .①①①【答案】D【解析】【详解】 解:①AH①BC ,EF①BC ,①①AH①EF正确;①BF平分①ABC,①①ABF=①CBF,①EF①BC,①①EFB=①CBF,①①①ABF=①EFB正确;①BE①BF,而AC与BF不一定垂直,①BE①AC不一定成立,故①错误;①BE①BF,①①E和①EFB互余,①ABE和①ABF互余,而①EFB=①ABF,①①①E=①ABE正确.故选D.变式3.(2020·辽宁黑山·七年级期中)如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是()①同位角相等,两直线平行;①内错角相等,两直线平行;①同旁内角互补,两直线平行;①平面内垂直于同一直线的两条直线平行.A.①①①B.①①①C.①①①D.①①【答案】C【解析】【详解】解:如图①①1=①2=90°①①1+①2=180°,①a//b;①①1=①3=90°①a//b;①a①c,b①c,①a//b故①①①正确;故选C考点:平行线的判定。
2023年中考数学专题《平行线四大模型》含答案解析

专题03 平行线四大模型(知识解读)【专题说明】历年中考考试中,有不少题目都考查了平行线的性质及应用,现汲取四大模型,供同学们赏析,希望能到达指导学习之目的。
【方法技巧】模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.模型二“猪蹄”模型(M模型)点P在EF左侧,在AB、CD内部“猪蹄”模型结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.模型三“臭脚”模型点P在EF右侧,在AB、CD外部“臭脚”模型结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD模型四“骨折”模型点P在EF左侧,在AB、CD外部·“骨折”模型结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.【典例分析】【模型1 “铅笔”模型】【典例1】如图,直线a∥b,点M、N分别在直线a、b上,P为两平行线间一点,那么∠1+∠2+∠3等于( )A.360°B.300°C.270°D.180°【答案】A【解答】解:如图,过点P作PA∥a,则a∥b∥PA,∴∠3+∠NPA=180°,∠1+∠MPA=180°,∴∠1+∠2+∠3=180°+180°=360°.故选:A.【变式1-1】把一块等腰直角三角尺和直尺按如图所示的方式放置,若∠1=32°,则∠2的度数为( )A.20°B.18°C.15°D.13°【答案】D【解答】解:如图,过点O作OP∥AB,则OP∥AB∥CD,∴∠1=∠3,∠2=∠4,∵∠3+∠4=45°,∴∠1+∠2=45°,∴∠2=45°﹣∠1=45°﹣32°=13°.故选:D.【典例2】问题情境:(1)如图1,AB∥CD,∠BAP=120°,∠PCD=130°,求∠APC的度数.(提示:如图2,过P作PE∥AB)问题迁移:(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP =α,∠PCB=β,α、β、∠DPC之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出α、β、∠DPC之间的数量关系.(提示:三角形内角和为180°)【解答】解:(1)∵AB∥CD,∠PAB=120°,∠PCD=130°,∴∠PAB+∠APE=180°,∠EPC+∠C=180°,∴∠APE=180°﹣120°=60°,∠EPC=180°﹣130°=50°,∴∠APC=∠APE+∠EPC=60°+50°=110°;(2)∠CPD=∠α+∠β,理由如下:如图3,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(3)①当P在OA延长线时,∠CPD=∠β﹣∠α;②当P在AB延长线时,∠CPD=∠α﹣∠β,①当P在OA延长线时,∠CPD=∠β﹣∠α;理由:如图4,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;②当P在AB延长线时,∠CPD=∠α﹣∠β,理由:如图5,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.【变式2-1】已知,AB∥CD,试解决下列问题:(1)如图1,∠1+∠2= ;(2)如图2,∠1+∠2+∠3= ;(3)如图3,∠1+∠2+∠3+∠4= ;(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n= .【解答】解:(1)∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补);(2)过点E作一条直线EF∥AB,∵AB∥CD,∴CD∥EF,∴∠1+∠AEF=180°,∠FEC+∠3=180°,∴∠1+∠2+∠3=360°;(3)过点E、F作EG、FH平行于AB,∵AB∥CD,∴AB∥EG∥FH∥CD,∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°;∴∠1+∠2+∠3+∠4=540°;(4)根据上述规律,显然作(n﹣2)条辅助线,运用(n﹣1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n﹣1).【变式2-2】如图,已知BQ∥GE,AF∥DE,∠1=50°.(1)求∠AFG的度数;(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.【解答】解:(1)∵BQ∥GE,∠1=50°,∴∠E=∠1=50°,∵AF∥DE,∴∠AFG=∠E=50°;(2)过点A作AM∥BQ,由(1)得∠AFG=∠E=50°,∵BQ∥GE,∴AM∥BQ∥GE,∴∠FAM=∠AFG=50°,∠MAQ=∠Q=15°,∴∠FAQ=∠FAM+∠MAQ=65°,∵AQ平分∠FAC,∴∠QAC=∠FAQ=65°,∴∠MAC=∠QAC+∠MAQ=80°,∵AM∥BQ,∴∠ACB=∠MAC=80°.【模型2 “猪蹄”模型(M模型)】【典例3】【问题背景】同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.【问题解决】(1)如图1,AB∥CD,E为AB、CD之间一点,连接AE、CE.若∠A=42°,∠C=28°.则∠AEC= .【问题探究】(2)如图2,AB∥CD,线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.【问题拓展】(3)如图3.AB∥CD,线段AD与线段BC相交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数.【解答】解:(1)延长CE交AB于点F,∵AB∥CD,∴∠AFC=∠C=28°,∵∠AEC是△AEF的一个外角,∴∠AEC=∠A+∠AFC=∠A+∠C=70°,故答案为:70°;(2)利用(1)的结论可得:∠AEC=∠A+∠C=36°+54°=90°,∴∠AEC=∠BED=90°,∵EF平分∠BED,∴∠BEF=∠BED=45°,∴∠BEF的度数为45°;(3)∵BC∥DF,∴∠CDF=180°﹣∠BCD=124°,∵DG平分∠CDF,∴∠CDG=∠CDF=62°,∵AB∥CD,∴∠BAG=∠CDG=62°,∵AE平分∠BAD,∴∠BAE=∠BAD=31°,∵∠GDE=20°,∴∠EDH=180°﹣∠CDG﹣∠GDE=98°,利用(1)的结论可得:∠AED=∠BAE+∠EDH=31°+98°=129°,∴∠AED的度数为129°.。
人教版数学第5章平行线的性质与判定及辅助线模型

平行线判定和性质以及四大模型汇总第一部分平行线的判定判定方法l:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知∠1=∠2,则AB∥CD(同位角相等,两直线平行);若已知∠1=∠3,则AB∥CD(内错角相等,两直线平行);若已知∠1+ ∠4= 180°,则AB∥CD(同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.第二部分平行线的性质性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补第三部分平行线的四大模型模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°;结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.模型二“猪蹄”模型(M模型)点P在EF左侧,在AB、CD内部“猪蹄”模型结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.模型三“臭脚”模型点P在EF右侧,在AB、CD外部“臭脚”模型结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.模型四“骨折”模型点P在EF左侧,在AB、CD外部“骨折”模型结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.第四部分平行线的四大模型证明(1)已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°.(2)已知∠P=∠AEP+∠CFP,求证AE∥CF.(3)已知AE∥CF,求证∠P=∠AEP-∠CFP.(4)已知∠P= ∠CFP -∠AEP,求证AE //CF.第五部分平行线的四大模型的应用案例1如图,a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠l+∠2+∠3= .2如图,AB∥CD,且∠A=25°,∠C=45°,则∠E的度数是.3如图,已知AB∥DE,∠ABC=80°,∠CDE =140°,则∠BCD= .4如图,射线AC∥BD,∠A= 70°,∠B= 40°,则∠P= .5如图所示,AB ∥CD ,∠E =37°,∠C = 20°,则∠EAB 的度数为 .6 如图,AB ∥CD ,∠B =30°,∠O =∠C .则∠C = .7如图,已知AB ∥DE ,BF 、 DF 分别平分∠ABC 、∠CDE ,求∠C 、 ∠F 的关系.8如图,已知AB ∥DE ,∠FBC =n 1∠ABF ,∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ; (2)若n =3,试探宄∠C 、∠F 的关系;(3)直接写出∠C 、∠F 的关系 (用含n 的等式表示).9如图,已知AB ∥CD ,BE 平分∠ABC ,DE 平分∠ADC .求证:∠E = 2 (∠A +∠C ) .10如图,己知AB∥DE,BF、DF分别平分∠ABC、∠CDE,求∠C、∠F的关系.11如图,∠3==∠1+∠2,求证:∠A+∠B+∠C+∠D= 180°.12如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠l+∠2= 90°,M、N分别是BA、CD的延长线上的点,∠EAM和∠EDN的平分线相交于点F则∠F的度数为().A. 120°B. 135°C. 145°D. 150°133如图,直线AB∥CD,∠EF A= 30°,∠FGH= 90°,∠HMN=30°,∠CNP= 50°,则∠GHM= .14如图,直线AB∥CD,∠EFG =100°,∠FGH =140°,则∠AEF+ ∠CHG= .15 已知∠B =25°,∠BCD=45°,∠CDE =30°,∠E=l0°,求证:AB∥EF.16已知AB∥EF,求∠l-∠2+∠3+∠4的度数.17如图(l ),已知MA 1∥NA n ,探索∠A 1、∠A 2、…、∠A n ,∠B 1、∠B 2…∠B n -1之间的 关系.(2)如图(2),己知MA 1∥NA 4,探索∠A 1、∠A 2、∠A 3、∠A 4,∠B 1、∠B 2之间的关系. (3)如图(3),已知MA 1∥NA n ,探索∠A 1、∠A 2、…、∠A n 之间的关系.如图所示,两直线AB ∥CD 平行,求∠1+∠2+∠3+∠4+∠5+∠6.18如图1,直线AB ∥CD ,P 是截线MN 上的一点,MN 与CD 、AB 分别交于E 、F . (1) 若∠EFB =55°,∠EDP = 30°,求∠MPD 的度数;(2) 当点P 在线段EF 上运动时,∠CPD 与∠ABP 的平分线交于Q ,问:DPBQ∠∠是否为定值?若是定值,请求出定值;若不是,说明其范围;(3) 当点P 在线段EF 的延长线上运动时,∠CDP 与∠ABP 的平分线交于Q ,问DPBQ∠∠的值足否定值,请在图2中将图形补充完整并说明理由.第六部分 平行线的四大模型实战演练1.如图,AB // CD // EF , EH ⊥CD 于H ,则∠BAC +∠ACE +∠CEH 等于( ).A . 180°B . 270°C . 360°D . 450° 2 若AB ∥CD ,∠CDF =32∠CDE ,∠ABF =32∠ABE ,则∠E :∠F =( ).A .2:1B .3:1C .4:3D .3:23.如图3,己知AE ∥BD ,∠1=130°,∠2=30°,则∠C = .4.如图,已知直线AB ∥CD ,∠C =115°,∠A = 25°,则∠E = .5. 6. 7.8.如阁所示,AB∥CD,∠l=l l0°,∠2=120°,则∠α= .9.如图所示,AB∥DF,∠D =116°,∠DCB=93°,则∠B= .10.如图,将三角尺的直角顶点放在直线a上,a∥b.∠1=50°,∠2 =60°,则∠3的度数为 .11.如图,AB∥CD,EP⊥FP, 已知∠1=30°,∠2=20°.则∠F的度数为.9.如图,若AB∥CD,∠BEF=70°,求∠B+∠F+∠C的度数.10.已知,直线AB∥CD.(1)如图l,∠A、∠C、∠AEC之间有什么关系?请说明理由;(2)如图2,∠AEF、∠EFC、∠FCD之间有什么关系?请说明理由;(3)如图3,∠A、∠E、∠F、∠G、∠H、∠O、∠C之间的关是.第七部分平行线的性质和判定综合应用1.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD =95°,∠CDE=25°,则∠DEF的度数是()A.110°B.115°C.120°D.125°2.如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1=()A.30°B.25°C.20°D.15°3.如图,AE∥BF,∠1=110°,∠2=130°,求∠3的度数为()4.如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=.5.如图,如果∠C=70°,∠B=135°,∠D=110°,那么∠1+∠2=6.如图,AB∥CD,求∠1+∠2+∠3+∠4=7.如图,AB∥CD,试找出∠B、∠C、∠BEC三者之间的数量关系.8.如图,三角形ABC中,点E为BC上一点(1)作图:过点E作EM∥AC交AB于M,过点E作EN∥AB交AC于N;(2)求∠A+∠B+∠C的度数,写出推理过程.9.如图,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED.10.如图,AC∥BD.(1)作图,过点B作BM∥AP交AC于M;(2)求证:∠PBD﹣∠P AC=∠P.11.如图,AB∥CD,∠B=∠C,求证:BE∥CF.12.如图①,木杆EB与FC平行,木杆的两端B,C用一橡皮筋连接,现将图①中的橡皮筋拉成下列各图②③的形状,请问∠A、∠B、∠C之间的数量关系?。
2023年九年级数学中考压轴复习专题几何综合——添加辅助线

1
(2)若弦MN垂直于AB,垂足为G, = ,MN= 3,求⊙O的半径;
4
(3)在(2)的条件下,当∠BAC=36°时,求线段CE的长
【详解】
(3) 作∠ABC的平分线BF交AC于F,连接AD
∵∠BNC=36°,AB=AC
∴∠ABC=∠ACB=72°
∵BF平分∠ABC
∴∠ABF=∠CBP=36°
∴∠BFC=72°即∠BAF=∠ABF、
∠BFC=∠ACB
∴BC=BF=AF
∵∠CBF=∠BAC,∠C=∠C
∴△CBF∽△CAB
∴BC²=CF·AC
设BC=x则AF=x
∴CF=2-x
∴x²=2(2-x)解得:x=± 5 − 1
∴BC= 5 − 1
∴AB是⊙O的直径
∴∠ADB=90°
∵AB=AC
1
∴CD=BD= BC
【分析】①由旋转性质证明△ABD∽△ACE即可判断;
②由①的结论可得,∠ABD=∠ACE,进而得到∠BOC=∠CAB=45°,即可判断∠COD;
③证明△ABD为等腰三角形即可判断;
④由题意直线BD、CE相交于点O,当AD⊥AC时,△AOC的面积最大,通过勾股定理计
算求出最大值,进而进行判断
试炼场:
从而得出∠ODE=90°,即可得证DE是CO的切线;
3
1
(2)连接OM,先求出MG= ,得出OG= OM,最后用勾股定理求解,即可得
2
2
出结论;
(3)作∠ABC的平分线交AC于F,判断出△BCF∽△ACB,得出比例式求成
BC= 5 − 1,连接AD,再求出CD=
例式求解,即可得出结论
5−1
,再判断出△DEC∽△ADC,得出比
冀教版2018-2019年七年级数学下册3.微专题:教材P65T1拓展——平行线中作辅助线的方法(含答案)
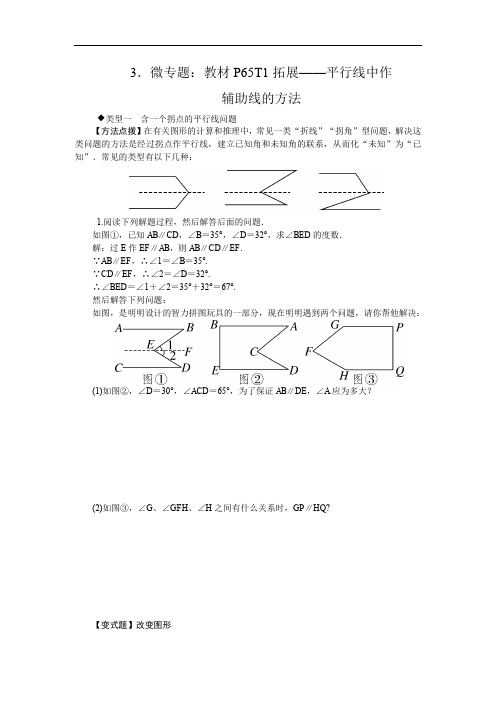
3.微专题:教材P65T1拓展——平行线中作辅助线的方法◆类型一含一个拐点的平行线问题【方法点拨】在有关图形的计算和推理中,常见一类“折线”“拐角”型问题,解决这类问题的方法是经过拐点作平行线,建立已知角和未知角的联系,从而化“未知”为“已知”.常见的类型有以下几种:1.阅读下列解题过程,然后解答后面的问题.如图①,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.解:过E作EF∥AB,则AB∥CD∥EF.∵AB∥EF,∴∠1=∠B=35°.∵CD∥EF,∴∠2=∠D=32°.∴∠BED=∠1+∠2=35°+32°=67°.然后解答下列问题:如图,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决:(1)如图②,∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A应为多大?(2)如图③,∠G、∠GFH、∠H之间有什么关系时,GP∥HQ?【变式题】改变图形(2017·邢台期末)如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图①位置时,试说明:∠3=∠1+∠2;(2)若点P在图②位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图③位置时,写出∠1、∠2、∠3之间的关系并说明理由.◆类型二含多个拐点的平行线问题【方法点拨】遇到含多个拐点的平行线问题时,通常过每个拐点作已知直线的平行线,然后根据平行线的性质解决.2.如图①,已知AB∥CD,E,F分别为AB,CD上的点.(1)在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系.请补全图形,并在图形下面写出相应的数量关系,选其中一个进行说明;(2)如图②,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形直接写出∠AEM,∠EMN,∠MNF,∠NFC之间存在的数量关系.【变式题】改变图形如图,已知AB∥CD,试解决下列问题:(1)如图①,∠1+∠2=________°;(2)如图②,∠1+∠2+∠3=________°;(3)如图③,求∠1+∠2+∠3+∠4的度数;(4)如图④,试探究∠1+∠2+∠3+∠4+…+∠n的度数.参考答案与解析1.解:(1)∠A=35°.理由如下:如图②,过C作CM∥DE,则∠1=∠D=30°,∴∠2=∠ACD-∠1=35°,∴∠2=∠A,∴CM∥AB.又∵CM∥DE,∴AB∥DE.即∠A=35°时,AB∥DE.(2)当∠G+∠GFH+∠H=360°时,GP∥HQ.理由如下:如图③,过F作FN∥GP,则∠G+∠4=180°.又∵∠G+∠GFH+∠H=360°,∴∠3+∠H=180°,∴FN∥HQ,∴GP∥HQ.即∠G+∠GFH+∠H=360°时,GP∥HQ.【变式题】解:(1)如图①,过P作PQ∥l1.∵l1∥l2,∴PQ∥l1∥l2,∴∠1=∠QPE,∠2=∠QPF.∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)∠3=∠2-∠1.解析:如图②,过P作PQ∥l1.∵l1∥l2,∴PQ∥l2.∴∠1=∠QPE,∠2=∠QPF.∵∠3=∠QPF-∠QPE,∴∠3=∠2-∠1.(3)∠3=360°-∠1-∠2.理由如下:如图③,过P作PQ∥l1,∵l1∥l2,∴PQ∥l2.同(1)可证得:∠3=∠CEP+∠DFP.∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP +∠1+∠2=360°,即∠3=360°-∠1-∠2.2.解:(1)在图①中,∠EMF=∠AEM+∠MFC.理由如下:过点M作MP∥AB.∵AB∥CD,∴MP∥CD∥AB,∴∠4=∠3,∠1=∠2.∵∠EMF=∠2+∠3,∴∠EMF=∠1+∠4=∠AEM+∠MFC.在图②中,∠AEM+∠EMF+∠MFC=360°.理由如下:过点M作MQ∥AB.∵AB∥CD,∴MQ∥CD∥AB,∴∠CFM+∠1=180°,∠AEM+∠2=180°,∴∠CFM+∠1+∠AEM+∠2=360°.∵∠EMF=∠1+∠2,∴∠AEM+∠EMF+∠MFC=360°.(2)在图③中,∠EMN+∠MNF-∠AEM-∠NFC=180°;在图④中,∠EMN-∠MNF +∠AEM+∠NFC=180°.【变式题】解:(1)180(2)360(3)如图③,分别过点E,F作EG∥AB,FH∥AB.∵AB∥CD,∴AB∥EG∥FH∥CD,∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°.∴∠1+∠2+∠3+∠4=540°.(4)如图④,根据上述规律,作(n-2)条辅助线,运用(n-1)次两条直线平行,同旁内角互补,即可得到n个角的和是180°(n-1).∴∠1+∠2+∠3+∠4+…+∠n=180°(n-1).。
专题5 平行线中常见模型专项训练(30道)(举一反三)(学生版)

专题平行线中常见模型专项训练(30道)1.如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为()A.70°B.65°C.35°D.5°2.如图,AB∥CD,那么∠A,∠P,∠C的数量关系是()A.∠A+∠P+∠C=90°B.∠A+∠P+∠C=180°C.∠A+∠P+∠C=360°D.∠P+∠C=∠A3.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是()A.75°B.65°C.55°D.50°4.如图,AB∥CD,∠ABF=23∠ABE,∠CDF=23∠CDE,则∠E:∠F=()A.2:1B.3:1C.3:2D.4:35.如图,已知AB∥DE,∠B=20°,∠D=130°,那么∠BCD等于()A.60°B.70°C.80°D.90°6.如图,已知AB∥CD,EF∥CD,则下列结论中一定正确的是()A.∠BCD=∠DCE B.∠ABC+∠BCE+∠CEF=360°C.∠BCE+∠DCE=∠ABC+∠BCD D.∠ABC+∠BCE﹣∠CEF=180°7.如图,AB∥EF,∠C=90°,则α、β和γ的关系是()A.β=α+γB.α+β+γ=180°C.α+β﹣γ=90°D.β+γ﹣α=180°8.一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=()A.62°B.58°C.52°D.48°9.如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=.11.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=110°,则∠2=.12.如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=.13.如图,AB∥CD,∠1=30°,∠2=50°,∠3=60°,则∠4=.14.如图,若直线a∥b,那么∠x=度.15.如图,AB∥CD,AD与BC相交于点F,BE平分∠ABC,DE平分∠ADC,∠AFB=96°,则∠BED的度数为度.16.如图,已知直线l1∥l2,∠A=125°,∠B=85°,且∠1比∠2大4°,那么∠1=.17.如图,AB∥ED,α=∠A+∠E,β=∠B+∠C+∠D.证明:β=2α18.如图,AB∥CD,CP∥FG,点E,G分别在CP,PQ上,连接EF,若∠FGQ+∠ACP=∠CAB,判断AB与PQ 存在什么位置关系?请详细说明理由.19.已知,AB∥CD,分别探讨四个图形中∠APC,∠P AB,∠PCD的关系.(1)请说明图1、图2中三个角的关系,并任选一个加以证明.(2)猜想图3、图4中三个角的关系,不必说明理由.(提示:注意适当添加辅助线吆!)20.探究:(1)如图a,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗?(2)如图a,反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请证明;(3)若将点E移至图b所示位置,AB∥CD,此时∠B,∠D,∠E之间有什么关系?请证明;(4)若将点E移至图c所示位置,AB∥CD,情况又如何?(5)在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?(6)在图e中,若AB∥CD,又得到什么结论?21.已知,AB∥CD,试解决下列问题:(1)如图1,∠1+∠2=;(2)如图2,∠1+∠2+∠3=;(3)如图3,∠1+∠2+∠3+∠4=;(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n=.22.如图所示,AB∥CD,在AB与CD之间有P1、P2、P3三点,顺次连接B、P1、P2、P3、D.(1)分别写出图甲、图乙中的∠B、P1、P2、P3、∠D之间的关系,这个关系与B、D之间的点的个数有关吗?如果有,写出这个规律;(2)如果在图甲、图乙中,B、D之间的点变为P1、P2、P3、…、P n,根据在(1)中的结论,直接写出图甲、图乙中的∠B、P1、P2、P3、∠D之间的关系.23.已知,直线AB∥CD(1)如图(1),点G为AB、CD间的一点,联结AG、CG.若∠A=140°,∠C=150°,则∠AGC的度数是多少?(2)如图(2),点G为AB、CD间的一点,联结AG、CG.∠A=x°,∠C=y°,则∠AGC的度数是多少?(3)如图(3),写出∠BAE、∠AEF、∠EFG、∠FGC、∠GCD之间有何关系?直接写出结论.24.问题情境:如图1,已知AB∥CD,∠APC=108°.求∠P AB+∠PCD的度数.经过思考,小敏的思路是:如图2,过P作PE∥AB,根据平行线有关性质,可得∠P AB+∠PCD=.问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.问题拓展:如图4,MA1∥NA n,A1﹣B1﹣A2﹣…﹣B n﹣1﹣A n是一条折线段.依据此图信息,把你所发现的结论,用简洁的数学式子表达为.25.如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于点O.(1)若∠AMF=52°,∠CNE=38°,求∠MEN、∠MFN的度数;(2)若2∠MFN﹣∠MEN=45°,求出∠AMF的度数;(3)探究∠MEN、∠MFN与∠MON之间存在怎样的数量关系.(直接写出结果)26.课堂上老师呈现一个问题:已知:如图,AB∥CD,EF⊥AB与点O,FG交CD与点P,当∠1=30°时,求∠EFG的度数.下面提供三种思路:思路一:过点F作MN∥CD(如图(1));思路二:过点P作PN∥EF,交AB于点N;思路三:过点O作ON∥FG,交CD于点N.解答下列问题:(1)根据思路一(图(1)),可求得∠EFG的度数为;(2)根据思路二、思路三分别在图(2)和图(3)中作出符合要求的辅助线;(3)请你从思路二、思路三中任选其中一种,试写出求∠EFG的度数的解答过程.27.已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC 的度数;(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC 的度数;(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.28.如图1,已知AB∥CD,点E和点H分别在直线AB和CD上,点F在直线AB和CD之间,连接EF和HF.(1)求∠AEF+∠CHF+∠EFH的度数;(2)如图2,若∠AEF+∠CHF=2∠EFH,HM平分∠CHF交FE的延长线于点M,∠DHF=80°,求∠FMH 的度数.29.(1)(问题)如图1,若AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数;(2)(问题迁移)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;(3)(联想拓展)如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.30.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.(1)如图①,当∠A=20°,∠APC=70°时,求∠C的度数;(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量?试证明你的结论;(3)如图③,当点P在直线EF上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立,直接写出它们之间的数量关系.。
(完整版)初二数学辅助线常用做法及例题(含答案)

DCB A常见的辅助线的作法总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”: 遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转” 法构造全等三角形.3) 遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
湘教版七年级数学下册解题技巧专题:平行线中作辅助线的方法

解题技巧专题:平行线中作辅助线的方法◆类型一含一个拐点的平行线问题【方法17】1.(天门中考)如图,将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a,b上,如果∠2=50°,那么∠1的度数为()A.10°B.20°C.30°D.40°第1题图第2题图2.如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的度数为()A.20°B.30°C.40°D.70°3.(金华中考)如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是________.第3题图第4题图4.如图,AB∥CD,∠A=120°,∠1=70°,则∠D的度数为________.5.小柯同学平时学习善于自己动手操作,以加深对知识的理解和掌握.学习了相交线与平行线的知识后,他又探索起来:如图,按虚线剪去长方形纸片的相邻两角,并使∠1=115°,AB⊥CB于B,那么∠2的度数是多少呢?请你帮他计算出来.◆类型二含多个拐点的平行线问题【方法17】6.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=()A.30°B.35°C.36°D.40°第6题图第7题图7.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.8.如图,如果AB∥CD,则∠α,∠β,∠γ之间的关系为______________.第8题图9.★如图①,AB∥CD,EOF是直线AB,CD间的一条折线.(1)试说明:∠EOF=∠BEO+∠DFO;(2)如果将平行线间的1个拐点改为2个拐点,如图②,则∠BEO,∠EOP,∠OPF,∠PFC 之间会满足怎样的数量关系,请说明理由.参考答案与解析1.A2.B解析:如图,过C作CF∥DE,∴∠CDE+∠DCF=180°.∵∠CDE=140°,∴∠DCF =40°.∵AB∥DE,∴CF∥AB,∴∠FCB=∠ABC=70°,∴∠BCD=70°-40°=30°.3.80° 4.50°5.解:过点B向左作BE∥AD.∵AD∥CF,∴AD∥BE∥CF,∴∠1+∠ABE=180°,∠2+∠CBE=180°,∴∠1+∠2+∠ABC=360°.∵∠1=115°,∠ABC=90°,∴∠2=360°-∠1-∠ABC=155°.6.A解析:如图,作AC∥l1,BD∥l2,∴∠1=∠3,∠2=∠4.∵l1∥l2,∴AC∥BD,∴∠CAB+∠ABD=180°,∴∠3+∠4=125°+85°-180°=30°,∴∠1+∠2=30°.7.140°解析:如图,延长AE交l2于点B.∵l1∥l2,∴∠3=∠1=40°.∵∠α=∠β,∴AB∥CD,∴∠2+∠3=180°,∴∠2=180°-∠3=180°-40°=140°.8.∠α+∠β-∠γ=180°解析:如图,过点E作EF∥AB,∴∠α+∠AEF=180°.∵AB∥CD,∴EF∥CD,∴∠FED=∠γ,∴∠AEF=∠β-∠FED=∠β-∠γ,∴∠α+∠β-∠γ=180°.9.解:(1)过点O作OM∥AB,如图①,∴∠1=∠BEO.∵AB∥CD,∴OM∥CD,∴∠2=∠DFO,∴∠1+∠2=∠BEO+∠DFO,即∠EOF=∠BEO+∠DFO.(2)∠EOP+∠PFC=∠BEO+∠OPF.理由如下:分别过点O,P作OM∥AB,PN∥CD,如图②.∵AB∥CD,∴OM∥PN∥AB∥CD,∴∠1=∠BEO,∠2=∠3,∠4=∠PFC,∴∠1+∠2+∠PFC=∠BEO+∠3+∠4,即∠EOP+∠PFC=∠BEO+∠OPF.。
2023学年八年级数学上册高分突破必练专题(人教版) 等边三角形常考作辅助线(原卷版)

等边三角形常考作辅助线法技巧1:作平行线法技巧2:截长补短法【典例1】(烟台)如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.【问题解决】如图1,若点D在边BC上,求证:CE+CF=CD;【类比探究】如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.【变式1-1】(2020秋•句容市期中)如图,在等边三角形ABC中,点E是边AC上一定点,点D是射线BC上一动点,以DE为一边作等边三角形DEF,连接CF.【问题解决】如图1,点D与点B重合,求证:AE=FC;【类比探究】(1)如图2,点D在边BC上,求证:CE+CF=CD;(2)如图3,点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?直接写出你的结论.【变式1-2】(天心区期中)如图,在等边△ABC中,点D是边AC上一定点,点E是直线BC上一动点,以DE为一边作等边△DEF,连接CF.(1)如图1,若点E在边BC上,且DE⊥BC,垂足为E,求证:CD=2CE;(2)如图1,若点E在边BC上,且DE⊥BC,垂足为E,求证:CE+CF=CD;(3)如图2,若点E在射线CB上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.【典例2】(2020秋•湖南期末)如图,△ABC是等边三角形,点D、E分别是射线AB、射线CB上的动点,点D从点A出发沿射线AB移动,点E从点B出发沿BG移动,点D、点E同时出发并且运动速度相同.连接CD、DE.(1)如图①,当点D移动到线段AB的中点时,求证:DE=DC.(2)如图②,当点D在线段AB上移动但不是中点时,试探索DE与DC之间的数量关系,并说明理由.(3)如图③,当点D移动到线段AB的延长线上,并且ED⊥DC时,求∠DEC度数.【变式2-1】(道外区期末)如图,△ABC中,AB=AC,点D在AB边上,点E在AC的延长线上,且CE=BD,连接DE交BC于点F.(1)求证:EF=DF;(2)过点D作DG⊥BC,垂足为G,求证:BC=2FG.【变式2-2】(东城区期末)(1)老师在课上给出了这样一道题目:如图1,等边△ABC边长为2,过AB边上一点P作PE⊥AC于E,Q为BC延长线上一点,且AP=CQ,连接PQ交AC于D,求DE的长.小明同学经过认真思考后认为,可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.(2)【类比探究】老师引导同学继续研究:1.等边△ABC边长为2,当P为BA的延长线上一点时,作PE⊥CA的延长线于点E,Q为边BC上一点,且AP=CQ,连接PQ交AC于D.请你在图2中补全图形并求DE 的长.2.已知等边△ABC,当P为AB的延长线上一点时,作PE⊥射线AC于点E,Q为②(①BC边上;②BC的延长线上;③CB的延长线上)一点,且AP=CQ,连接PQ交直线AC于点D,能使得DE的长度保持不变.(将答案的编号填在横线上)1.(2021秋•咸丰县期末)如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于点P,点P为DE中点(1)求证:CD=BE;(2)若DE⊥AC,求BP的长.2.(2021秋•绵竹市期末)在等边△ABC中,点E是AB上的动点,点E与点A、B不重合,点D在CB的延长线上,且EC=ED.(1)如图1,若点E是AB的中点,求证:BD=AE;(2)如图2,若点E不是AB的中点时,(1)中的结论“BD=AE”能否成立?若不成立,请直接写出BD与AE数量关系,若成立,请给予证明.3.(2020秋•旅顺口区期中)如图,在等边三角形ABC中,点E是边CA延长线上一点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.(1)如图1,若点D在边BC上,求证:CE=CF+CD;(2)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系,并说明理由.4.(2020•安徽)如图,D是等边△ABC的边AB上一点,E是BC延长线上一点,CE=DA,连接DE交AC于F,过D点作DG⊥AC于G点.证明下列结论:(1)AG=AD;(2)DF=EF;(3)S△DGF=S△ADG+S△ECF.5.(2020秋•花雨区校级月考)我们在前面曾遇到过这样一道题目:小明与同桌小聪讨论后,进行了如下解答:(1)特殊情况,探索结论当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“>”、“<”或“=”)(2)一般情况,证明结论:如图2,过点E作EF∥BC,交AC于点F.请你继续完成对以上问题(1)中所填写结论的证明.(3)变式探究:如图3,△ABC是等边三角形,D是边BC上一点,点E在BA的延长线上,且BD=AE,此时,CE和DE有何数量关系?请画出图形,作出判断,并说明理6.(2020秋•河西区期末)如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)证明:在运动过程中,点D是线段PQ的中点;(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.7.(2020秋•裕华区校级期末)知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.如图,等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.(1)请直接写出AD长.(用x的代数式表示)(2)当△ADE为直角三角形时,运动时间为几秒?(3)求证:在运动过程中,点P始终为线段DE的中点.8.(2021秋•营口期末)已知A(﹣10,0),以OA为边在第二象限作等边△AOB.(1)求点B的横坐标;(2)如下图,点M、N分别为OA、OB边上的动点,以MN为边在x轴上方作等边△MNE,连结OE,当∠EMO=45°时,求∠MEO的度数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:平行线中作辅助线的方法
——形成思维定式,快速解题
◆类型一含一个拐点的平行线问题
1.(2017·南充中考)如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放.若∠1=58°,则∠2的度数为()
A.30°B.32°C.42°D.58°
第1题图第2题图
2.(2017·潍坊中考)如图,∠BCD=90°,AB∥DE,则∠α与∠β满足()
A.∠α+∠β=180°B.∠β-∠α=90°
C.∠β=3∠αD.∠α+∠β=90°
3.阅读下列解题过程,然后解答后面的问题.
如图①,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:过E作EF∥AB.∵AB∥CD,∴CD∥EF.∵AB∥EF,∴∠1=∠B=35°.又∵CD∥EF,∴∠2=∠D=32°,∴∠BED=∠1+∠2=35°+32°=67°.
如图②、图③,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决.
(1)如图②,已知∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A应多大?
(2)如图③,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?【方法4】
◆类型二含多个拐点的平行线问题
4.如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的大小为【方法4】() A.20°B.30°C.40°D.70°
第4题图第5题图
5.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2的度数为________.
6.如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以剩余一个论断作为结论,填入“结论”栏中,使之成为一道由已知可得到结论的题目,并解答该题.
已知:______________,结论:______________.
解:
7.如图①,AB∥CD,EOF 是直线AB,CD间的一条折线.【方法4】
(1)试说明:∠EOF=∠BEO+∠DFO;
(2)如果将折一次改为折两次,如图②,则∠BEO,∠EOP,∠OPF,∠PFC之间会满足怎样的数量关系?并说明理由.
参考答案与解析
1.B 2.B
3.解:(1)∠A=∠ACD-∠D=35°.
(2)过点F向右作FM∥PG.∵GP∥HQ,∴FM∥HQ,∴∠G+∠MFG=180°,∠H+∠MFH=180°,∴∠G+∠GFH+∠H=360°.
4.B解析:如图,过C向右作CM∥AB.∵AB∥DE,∴DE∥CM.∵∠ABC=70°,∠CDE =140°,∴∠BCM=70°,∠DCM=180°-140°=40°,∴∠BCD=∠BCM-∠DCM=70°-40°=30°.
5.140°解析:如图,延长AE交l2于点B.∵l1∥l2,∴∠3=∠1=40°.∵∠α=∠β,∴AB∥CD,∴∠2+∠3=180°,∴∠2=180°-∠3=180°-40°=140°.
6.解:①②③∵AB∥CD,∴∠B=∠C.又∵∠B+∠D=180°,∴∠C+∠D=180°,∴BC∥DE(答案不唯一).
7.解:(1)如图①,过O向左作OM∥AB,∴∠1=∠BEO.∵AB∥CD,∴OM∥CD,∴∠2=∠DFO,∴∠1+∠2=∠BEO+∠DFO,即∠EOF=∠BEO+∠DFO.
(2)∠EOP+∠PFC=∠BEO+∠OPF.理由如下:如图②,过O向左作OQ∥AB,过P 向右作PN∥CD.∵AB∥CD,∴OQ∥PN∥AB∥CD,∴∠1=∠BEO,∠2=∠3,∠4=∠PFC,∴∠1+∠2+∠PFC=∠BEO+∠3+∠4,∴∠EOP+∠PFC=∠BEO+∠OPF.。
