4 机械振动习题详解
高中物理寒假作业4机械振动含解析

机械振动1.如图所示,弹簧振子在BC 间振动,O 为平衡位置,BO =OC =5 cm 。
若振子从B 到C 的运动时间是1 s ,则下列说法中正确的是( )A .振子从B 经O 到C 完成一次全振动 B .振动周期是1 s ,振幅是10 cmC .经过两次全振动,振子通过的路程是20 cmD .从B 开始经过3 s ,振子通过的路程是30 cm 【答案】D【解析】振子从B 经O 到C 仅完成了半次全振动,所以其振动周期T =2×1 s=2 s ,振幅A =BO =5 cm 。
振子在一次全振动中通过的路程为4A =20 cm ,所以两次全振动中通过的路程为40 cm ,3 s 的时间为1.5T ,所以振子通过的路程为30 cm 。
综上可知,只有D 正确。
2.如图所示为两个单摆的受迫振动的共振曲线,则下列说法正确的是( )A .若两个受迫振动分别在月球上和地球上进行,且摆长相同,则图线Ⅰ表示月球上单摆的共振曲线B .若两个受迫振动是在地球上同一地点进行,则两个摆长之比L Ⅰ∶L Ⅱ=25∶4C .图线Ⅱ若是在地面上完成的,则该单摆摆长约为1 mD .若摆长均为1 m ,则图线Ⅰ是在地面上完成的 【答案】ABC【解析】图线中振幅最大处对应的频率应与做受迫振动的单摆的固有频率相等,从图线上可以看出,两摆的固有频率f Ⅰ=0.2 Hz ,f Ⅱ=0.5 Hz 。
当两摆在月球和地球上分别做受迫振动且摆长相等时,根据f =12πgL可知,g 越大,f 越大,所以g Ⅱ>g Ⅰ,又因为g 地>g 月,因此可推知图线Ⅰ表示月球上单摆的共振曲线,A 正确;若在地球上同一地点进行两次受迫振动,g 相同,摆长长的f 小,且有f Ⅰf Ⅱ=0.20.5,所以L ⅠL Ⅱ=254,B 正确;f Ⅱ=0.5 Hz ,若图线Ⅱ是在地面上完成的,根据g =9.8 m/s 2,可计算出L Ⅱ约为1 m ,C 正确,D 错误。
机械振动习题详解

习题四一、选择题1.两个质点各自作简谐振动,它们的振幅相同、周期相同,第一个质点的振动方程为1cos()x A t ωα=+。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处,则第二个质点的振动方程为 [ ] (A ))π21cos(2++=αωt A x ; (B ))π21cos(2-+=αωt A x ; (C ))π23cos(2-+=αωt A x ; (D ))cos(2π++=αωt A x 。
答案:B解:由题意,第二个质点相位落后第一个质点相位π/2,因此,第二个质点的初相位为π21-α,所以答案应选取B 。
2.劲度系数分别为k 1和k 2的两个轻弹簧串联在一起,下面挂着质量为m 的物体,构成一个竖挂的弹簧振子,则该系统的振动周期为[](A )21212)(2k k k k m T +π=;(B ))(221k k mT +π=;(C )2121)(2k k k k m T +=π;(D )2122k k mT +π=。
答案:C解:两根弹簧串联,其总劲度系数2121k k k k k +=,根椐弹簧振子周期公式,k mT π2=,代入2121k k k k k +=可得答案为C 。
3.一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为[] (A )g l π2;(B )g l 22π;(C )g l 322π;(D )gl 3π。
答案:C解:由于是复摆,其振动的周期公式为glmgl J T 322222πππ===ω,所以答案为C 。
4.一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[] 答案:B解:根椐题意,此简谐振动的初相位为3π-,或35π,所以答案为B 。
5.一物体作简谐振动,振动方程为)21cos(π+=t A x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为[](A )1:4;(B )1:2;(C )1:1;(D )2:1。
清华大学《大学物理》习题库试题及答案 04 机械振动习题

清华大学《大学物理》习题库试题及答案 04 机械振动习题清华大学《大学物理》习题库试题及答案--04-机械振动习题清华大学《大学物理》习题库试题及答案机械振动习题一、选择题:1.3001:把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度?,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为(a)?(b)?/2(c)0(d)??[]2.3002:两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x1=acos(?t+?)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动方程为:11x2?acos(?tπ)x2?acos(?tπ)2(b)2(a)3x2?acos(?tπ)2(d)x2?acos(?t?)(c)[]3.3007:一质量为m的物体挂在劲度系数为k的轻弹簧下面,振动角频率为?。
若把此弹簧分割成二等份,将物体m挂在分割后的一根弹簧上,则振动角频率是(a)2??(b)2?(c)?/2(d)?/2[]4.3396:一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律v(m/s)用余弦函数叙述,则其初适当为vm(a)?/6(b)5?/612vm(c)-5?/6(d)-?/6o(e)-2?/3[]5.3552:一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为t1和t2。
将它们拿到月球上去,相应的周期分别为t1?和t2?。
则有(a)t1??t1且t2??t2(b)t1??t1且t2??t2(c)t1??t1且t2??t2(d)t1??t1且t2??t2[]t(s)1x?4?10?2cos(2?t??)3(si)。
6.5178:一质点沿x轴作四极振动,振动方程为从t=0时刻起,到质点位置在x=-2cm处,且向x轴正方向运动的最短时间间隔为11111sssss86432(a)(b)(c)(d)(e)[]7.5179:一弹簧振子,重物的质量为m,弹簧的劲度系数为k,该振子并作振幅为a 的四极振动。
机械振动课后习题答案

机械振动课后习题答案机械振动是力学中的一个重要分支,研究物体在受到外力作用后的振动特性。
在学习机械振动的过程中,课后习题是巩固知识、提高能力的重要途径。
本文将为大家提供一些机械振动课后习题的答案,希望能够帮助大家更好地理解和掌握这一知识。
1. 一个质量为m的弹簧振子在无阻尼情况下振动,其振动方程为mx'' + kx = 0,其中x为振子的位移,k为弹簧的劲度系数。
试求振动的周期。
解答:根据振动方程可知,振子的振动是简谐振动,其周期T与振子的质量m和弹簧的劲度系数k有关。
根据简谐振动的周期公式T = 2π√(m/k),可得振动的周期为T = 2π√(m/k)。
2. 一个质量为m的弹簧振子在受到外力F(t)的作用下振动,其振动方程为mx''+ kx = F(t),其中F(t) = F0cos(ωt)。
试求振动的解析解。
解答:根据振动方程可知,振子的振动是受迫振动,其解析解可以通过求解齐次方程和非齐次方程得到。
首先求解齐次方程mx'' + kx = 0的解xh(t),得到振子在无外力作用下的自由振动解。
然后根据外力F(t)的形式,假设其特解为xp(t) = Acos(ωt + φ),其中A为振幅,φ为相位差。
将特解xp(t)代入非齐次方程,求解得到A和φ的值。
最后,振动的解析解为x(t) = xh(t) + xp(t)。
3. 一个质量为m的弹簧振子在受到阻尼力和外力的作用下振动,其振动方程为mx'' + bx' + kx = F(t),其中b为阻尼系数。
试求振动的稳定解。
解答:根据振动方程可知,振子的振动是受到阻尼力和外力的作用,其稳定解可以通过求解齐次方程和非齐次方程得到。
首先求解齐次方程mx'' + bx' + kx = 0的解xh(t),得到振子在无外力和阻尼作用下的自由振动解。
然后根据外力F(t)的形式,假设其特解为xp(t) = Acos(ωt + φ),其中A为振幅,φ为相位差。
机械振动 习题解答

©物理系_2015_09《大学物理AII 》作业 No.01 机械振动班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、 判断题:(用“T ”表示正确和“F ”表示错误)1/3/5 2 4[ F ] 1.只有受弹性力作用的物体才能做简谐振动。
解:如单摆在作小角度摆动的时候也是简谐振动,其回复力为重力的分力。
[ F ] 2.简谐振动系统的角频率由振动系统的初始条件决定。
解:P5. 根据简谐振子角频率公式mk=ω,可知角频率是一个完全由振动系统本身性质决定的常量,与初始条件无关。
我们也将角频率称为固有角频率。
[ F ] 3.单摆的运动就是简谐振动。
解:P14-15 单摆小角度的摆动才可看做是简谐振动。
[ T ] 4.孤立简谐振动系统的动能与势能反相变化。
解:P9 孤立的谐振系统 机械能守恒,动能势能反相变化。
[ F ] 5.两个简谐振动的合成振动一定是简谐振动。
解: 同向不同频率的简谐振动的合成结果就不一定是简谐振动。
总结:1、3、5小题均为简谐振动的定义性判断.简谐运动是最基本也是最简单的一种机械振动。
当某物体进行简谐运动时,物体所受的力跟位移成正比,并且力总是指向平衡位置。
二、选择题:1. 把单摆从平衡位置拉开,使摆线与竖直方向成一微小角度θ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相位为[ C ] (A) θ; (B) π23; (C) 0; (D) π21。
解:对于小角度摆动的单摆,可以视为简谐振动,其运动方程为:()()0cos ϕωθθ+=t t m ,根据题意,t = 0时,摆角处于正最大处,θθ=m,即:01cos cos 0000=⇒=⇒==ϕϕθϕθθ。
类似公式: ()()0cos ϕω+=t A t x2.一个简谐振动系统,如果振子质量和振幅都加倍,振动周期将是原来的 [D] (A) 4倍(B) 8倍(C) 2倍(D)2倍解: P5 公式(12.1.8) m T k m T m k T ∝⇒=⇒⎪⎭⎪⎬⎫==/2/2πωωπ,所以选D 。
大学物理(第四版)课后习题及答案-机械振动
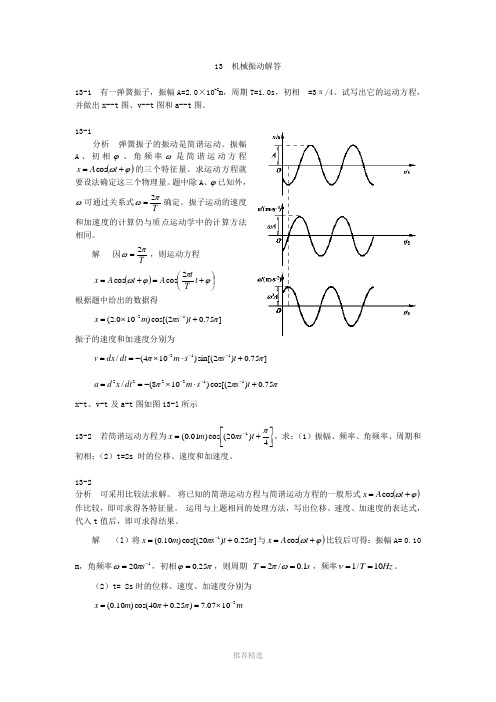
13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m ,周期T=1.0s ,初相=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为mm x 21007.7)25.040cos()10.0(-⨯=+=ππ)25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ5.5×103kg •m -3。
机械振动总结复习习题及解答

1、某测量低频振动用的测振仪(倒置摆)如下图所示。
试根据能量原理推导系统静平衡稳定条件。
若已知整个系统的转动惯量23010725.1m kg I ⋅⨯=-,弹簧刚度m N k /5.24=,小球质量kg m 0856.0=,直角折杆的一边cm l 4=。
另一边cm b 5=。
试求固有频率。
解:弹性势能 2)(21θb k U k =, 重力势能 )cos (θl l mg U g --=总势能 mgl mgl kb U U U g k -+=+=θθcos 2122 代入0==i x x dxdU可得 可求得0=θ满足上式。
再根据公式022>=i x x dx U d 判别0=θ位置是否稳定及其条件:即满足mgl kb >2条件时,振动系统方可在0=θ位置附近作微幅振动。
系统的动能为 2210θ•=I T代入0)(=+dtU T d 可得 由0=θ为稳定位置,则在微振动时0sin ≈θ,可得线性振动方程为: 固有频率代入已知数据,可得2、用能量法解此题:一个质量为均匀半圆柱体在水平面上做无滑动的往复滚动,如上图所示,设圆柱体半径为R ,重心在c 点,oc=r,,物体对重心的回转体半径为L ,试导出运动微分方程。
解:如图所示,在任意角度θ(t )时,重心c 的升高量为∆=r (1-cos θ)=2rsin 22θ取重心c 的最低位置为势能零点,并进行线性化处理,则柱体势能为 V=mg ∆=2mg r sin 22θ≈ 21mgr 2θ (a )I b =I c +m bc 2=m(L 2+bc 2) (b )bc 2=r 2+R 2-2rRcos θ(t) (c )而柱体的动能为 T=21I b •θ2 把(b )式,(c )式两式代入,并线性化有 T=21m[L 2+(R -r )2]•θ2 (d ) 根据能量守恒定理,有21m[L 2+(R -r )2]•θ2+21mgr 2θ=E=const 对上式求导并化简,得运动微分方程为 [L 2+(R -r )2]••θ+gr θ=0 (e ) 3、一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。
机械振动试题(含答案)(4)

机械振动试题(含答案)(4)一、机械振动 选择题1.如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M 点,与竖直墙相切于A 点,竖直墙上另一点B 与M 的连线和水平面的夹角为60°,C 是圆环轨道的圆心,D 是圆环上与M 靠得很近的一点(DM 远小于CM ).已知在同一时刻,a 、b 两球分别由A 、B 两点从静止开始沿光滑倾斜直轨道运动到M 点;c 球由C 点自由下落到M 点;d 球从D 点静止出发沿圆环运动到M 点.则:A .c 球最先到达M 点B .b 球最先到达M 点C .a 球最先到达M 点D .d 球比a 球先到达M 点2.如图所示,在一条张紧的绳子上悬挂A 、B 、C 三个单摆,摆长分别为L 1、L 2、L 3,且L 1<L 2<L 3,现将A 拉起一较小角度后释放,已知当地重力加速度为g ,对释放A 之后较短时间内的运动,以下说法正确的是( )A .C 的振幅比B 的大B .B 和C 的振幅相等 C .B 的周期为2L gD .C 的周期为1L g3.如图所示的单摆,摆球a 向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b 发生碰撞,并粘在一起,且摆动平面不便.已知碰撞前a 球摆动的最高点与最低点的高度差为h ,摆动的周期为T ,a 球质量是b 球质量的5倍,碰撞前a 球在最低点的速度是b 球速度的一半.则碰撞后A .摆动的周期为56T B .摆动的周期为65T C .摆球最高点与最低点的高度差为0.3hD .摆球最高点与最低点的高度差为0.25h4.如图所示,水平方向的弹簧振子振动过程中,振子先后经过a 、b 两点时的速度相同,且从a 到b 历时0.2s ,从b 再回到a 的最短时间为0.4s ,aO bO =,c 、d 为振子最大位移处,则该振子的振动频率为( )A .1HzB .1.25HzC .2HzD .2.5Hz5.一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动.可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm ,周期为3.0 s .当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10 cm 时,游客能舒服地登船.在一个周期内,游客能舒服登船的时间是( )A .0.5 sB .0.75 sC .1.0 sD .1.5 s6.如图甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x 随时间t 变化的图象如图乙所示.不计空气阻力,g 取10m/s 2.对于这个单摆的振动过程,下列说法中不正确的是( )A .单摆的位移x 随时间t 变化的关系式为8sin(π)cm x t =B .单摆的摆长约为1.0mC .从 2.5s t =到 3.0s t =的过程中,摆球的重力势能逐渐增大D .从 2.5s t =到 3.0s t =的过程中,摆球所受回复力逐渐减小7.如右图甲所示,水平的光滑杆上有一弹簧振子,振子以O 点为平衡位置,在a 、b 两点之间做简谐运动,其振动图象如图乙所示.由振动图象可以得知( )A .振子的振动周期等于t 1B .在t =0时刻,振子的位置在a 点C .在t =t 1时刻,振子的速度为零D .从t 1到t 2,振子正从O 点向b 点运动8.图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子,图(乙)为这个弹簧振子的振动图象,由图可知下列说法中正确的是( )A .在t =0.2s 时,弹簧振子可能运动到B 位置B .在t =0.1s 与t =0.3s 两个时刻,弹簧振子的速度相同C .从t =0到t =0.2s 的时间内,弹簧振子的动能持续地增加D .在t =0.2s 与t =0.6s 两个时刻,弹簧振子的加速度相同9.如图所示,质量为A m 的物块A 用不可伸长的细绳吊着,在A 的下方用弹簧连着质量为B m 的物块B ,开始时静止不动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题四一、选择题1.两个质点各自作简谐振动,它们的振幅相同、周期相同,第一个质点的振动方程为1cos()x A t ωα=+。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处,则第二个质点的振动方程为 [ ](A ))π21cos(2++=αωt A x ; (B ))π21cos(2-+=αωt A x ;(C ))π23cos(2-+=αωt A x ; (D ))cos(2π++=αωt A x 。
答案:B解:由题意,第二个质点相位落后第一个质点相位π/2,因此,第二个质点的初相位为π21-α,所以答案应选取B 。
2.劲度系数分别为k 1和k 2的两个轻弹簧串联在一起,下面挂着质量为m 的物体,构成一个竖挂的弹簧振子,则该系统的振动周期为 [ ](A )21212)(2k k k k m T +π=; (B ))(221k k mT +π= ;(C ) 2121)(2k k k k m T +=π; (D )2122k k mT +π=。
答案:C解:两根弹簧串联,其总劲度系数2121k k k k k +=,根椐弹簧振子周期公式,k mT π2=,代入2121k k k k k +=可得答案为C 。
3.一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为 [ ] (A )g l π2; (B )g l 22π; (C )g l 322π; (D )gl 3π。
答案:C解:由于是复摆,其振动的周期公式为glmgl J T 322222πππ===ω,所以答案为C 。
4.一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[ ] 答案:B解:根椐题意,此简谐振动的初相位为3π-,或35π,所以答案为B 。
5.一物体作简谐振动,振动方程为)21cos(π+=t A x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为[ ](A )1:4; (B )1:2; (C )1:1; (D )2:1。
答案:D解:物体的速度为)21sin(π+-=t A v ωω,动能为)21(sin 21222π+t mA ωω。
所以在t = 0时刻的动能为2221ωmA ,t = T /8时的动能为2241ωmA ,因此,两时刻的动能之比为2:1,答案应选D 。
二、填空题1.一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为A = _______cm ;ω =__________rad/s ;ϕ =________。
答案:10;(π/6);π/3。
解:由图可直接看出,A =10cm ,周期T =12s ,所以2rad/s 6T ππω==;再由图看出,t = 0时刻质点在位移5cm处,下一时刻向着平衡位置方向移动,所以其初相为 ϕ = π/3。
2.一水平弹簧简谐振子的振动曲线如图所示。
当振子处在位移为零、速度为A ω-、加速度为零和弹性力为零的状态时,应对应于曲线上的________点;当振子处在位移的绝对值为A 、速度为零、加速度为2A ω-和弹性力为kA -的状态时,应对应于曲线上的____________点。
ω-答案:(b ,f );( a ,e )。
解:因b 和f 点对应着位移为零、速度为A ω-、加速度为零和弹性力为零的状态,a ,e .点对应着位移的绝对值为A 、速度为零、加速度为2A ω-和弹性力为kA -的状态。
3.两个同方向的简谐振动曲线如图所示。
其合振动的振 幅为__________________________;合振动的振动方程为_____________________________。
)212cos(12π+π-=t T A A x 。
解:由图可知,两振动其初相位差为π11221122sin sin tan cos cos A A A A ϕϕϕϕϕ+=+,而123, 22ππϕϕ==,由此得2πϕ=。
所以合振动的振动方程为)212cos(12π+π-=t T A A x4.在一竖直轻弹簧下端悬挂质量 = 5g m 的小球,弹簧伸长=1cm l 而平衡。
经推动后,该小球在竖直方向作振幅为 = 4cm A 的振动,则小球的振动周期为__________;振动能量为_________________。
答案:0.201s ;-3 3.9210J ⨯。
解:平衡时,有k l mg ∆=,所以/k mg l =∆。
(1)2220.201s T ω===π;(2) 22-311= 3.9210J 22mg E kA A l==⨯∆。
5.为测定某音叉C 的频率,选取频率已知且与C 接近的另两个音叉A 和B ,已知A 的频率为800 Hz ,B 的频率是797 Hz ,进行下面试验:第一步,使音叉A 和C 同时振动,测得拍频为每秒2次。
第二步,使音叉B 和C 同时振动,测得拍频为每秒5次。
由此可确定音叉C 的频率为______________。
答案:802 Hz解:设音叉C 的频率为ν,由2800=-ν和5797=-ν,联立求得802Hz ν=。
三、计算题·--1.在一竖直轻弹簧的下端悬挂一小球,弹簧被拉长0=1.2cm l 而平衡.再经拉动后,该小球在竖直方向作振幅为 = 2cm A 的振动,试证此振动为简谐振动;选小球在正最大位移处开始计时,写出此振动的数值表达式。
答案:)1.9cos(1022t x π⨯=-。
解:设小球的质量为m ,则弹簧的劲度系数0/l mg k =选平衡位置为原点,向下为正方向。
小球在x 处时,根据牛顿第二定律得202d ()d xmg k l x m t -+= 将 0/l mg k = 代入整理后得 220d 0d x gx t l +=所以此振动为简谐振动,其角频率为 28.589.1ω===π 设振动表达式为 cos()x A t ωϕ=+由题意: 0t =时,20210m x A -==⨯,00v =,由此解得 0ϕ=。
所以 )1.9cos(1022t x π⨯=-2.一质量0.25kg m =的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点. 弹簧的劲度系数25N/m k =。
(1)求振动的周期T 和角频率ω;(2)如果振幅15cm A =,0t =时物体位于7.5cm x =处,且物体沿x 轴反向运动,求初速0v 及初相ϕ;(3)写出振动方程表达式。
答案:(1)0.63s T =,10rad/s ω=;(2)0 1.3m/s v =-,13ϕ=π;(3))3110cos(10152π+⨯=-t x 。
解: (1) 10rad/s ω=,20.63s T ω==π; (2) 15cm A =;当0t =时,07.5cm x =,00v <,+x )由A =得0 1.3m/s v =-=-由 100tg v x ϕω--=,得13ϕ=π,或43π 因00x >,所以应取 13ϕ=π(3)振动方程)3110cos(10152π+⨯=-t x (SI)3.一质点作简谐振动,其振动方程为)4131cos(100.62π-π⨯=-t x (SI)(1)当x 值为多大时,系统的势能为总能量的一半?(2)质点从平衡位置移动到上述位置所需最短时间为多少? 答案:(1)24.2410m x -=±⨯;(2)0.75 s 。
解:(1)势能 221kx W P =; 总能量 221kA E = 由题意 4/2122kA kx =,24.2410m x -==±⨯。
(2)周期 26s T ω==π从平衡位置运动到2A x ±=的最短时间t ∆为T /8,所以0.75 s t t =∆=4.一质量 = 3.96 kg M 的物体,悬挂在劲度系数 = 400 N/m k 的轻弹簧下端.一质量= 40g m 的子弹以 = 152 m/s v 的速度从下方竖直朝上射入物体之中 ,然后子弹与物体一起作谐振动 .若取平衡位置为原点。
x 轴指向下方,如图,求:(1)振动方程(因 m M <<,m 射入M 后对原来平衡位置的影响可以忽略);(2)弹簧振子的总能量。
答案:(1))2110cos(152.0π+=t x ;(2) 4.62J E =。
解:(1)由动量守恒定律 ()mv M m V =+,得 mvV M m=+;又010rad/s ω= 0t =时,00cos x A ϕ== 00sin v A V ωϕ=-=- 由上二式解得 =0.152 m A ,12ϕ=π,所以,振动方程 )2110cos(152.0π+=t x (SI)(2)振子中的总能量 21() 4.62J 2E M m V =+=5.一质点同时参与两个同方向的简谐振动,其振动方程分别为-21 =510cos(4 +)3x t π⨯(SI) ,-22 =310sin(4 -)6x t π⨯画出两振动的旋转矢量图,并求合振动的振动方程。
答案:(1)旋转矢量如图;(2)合振动方程-2=210cos(4 +)3x t π⨯。
解: -2-2-222 =310sin(4 -)=310cos(4 --)=310cos(4 -)6623x t t t ππππ⨯⨯⨯ 作两振动的旋转矢量图,如图所示。
由图得,合振动的振幅和初相分别为 = (5-3)cm = 2cm A , =3πϕ,所以 合振动方程为 -2=210cos(4 +)3x t π⨯ (SI)x O ω ω π/3 -2π/3 A1A 2A。
