杭州电子科技大学_高等数学_期末试题

数学实验_杭州电子科技大学中国大学mooc课后章节答案期末考试题库2023年

数学实验_杭州电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.MATLAB中的函数log2(x)表示求自变量x的答案:以2为底数的对数2.请在高于2006a的版本中，通过帮助系统，查阅函数polyder(p)的功能是：答案:k = polyder(p) 返回 p 中的系数表示的多项式的导数，即3.假设A是一个矩阵，语句M=norm(A,1)表示求矩阵A的：答案:矩阵A的1范数4.在MATLAB中, 变量的命名须遵循如下的规则：答案:字符间不可留空格;_可以使用下划线当作字母使用但不能用作首字符；_第一个字符必须是英文字母;5.下面选项中，哪些属于MATLAB的特点？答案:语言简洁紧凑，使用方便灵活，库函数极其丰富；_具有结构化的控制语句(如for循环，while循环，switch语句和if语句)；6.要做好数学实验，需要做到：答案:清楚MATLAB（或Octave）函数中参数的含义_熟知实验内容的数学背景；_了解MATLAB软件（或Octave软件）的相关函数_能熟练使用MATLAB软件（或Octave软件）；7.已知两个同阶矩阵A和B，求矩阵A和矩阵B的对应元素的乘积的MATLAB语句是:答案:B.*A8.下列语句中哪个语句可以求出矩阵A的逆矩阵:答案:A^(-1)9.MATLAB中表示“虚单位”，“无穷大”，“圆周率”，“非数值”的依次是：答案:i, inf, pi, NaN_j, inf, pi, NaN_i, inf, pi, nan10.关于MATLAB文件名，下列哪个表述不正确：（可多选）答案:可以用任何字母作为函数文件或脚本文件的扩展名；_仅函数文件的扩展名为m；_仅脚本文件的扩展名为m；11.设X=[1,2,5,3,7,-1]，则下列选项中，哪个是norm(X,inf)的计算结果。

712.在新版本的MATLAB中，求解非线性方程的函数solve的用法有所改变，如求解方程x+1=2的语句为syms xsolve(x+1 == 2, x)那么，用下面哪段代码，可以求解方程【图片】？答案:clearsyms xX=solve(x^3-x^2+x-1 == 0,x)13.在利用fsolve求解非线性方程组的解时，方程的自变量：答案:可以是多个，但一定要定义成向量；14.当使用函数solve求解方程时，下列哪个表述是正确答案:表达式S = solve(eqn,var,Name,Value)中的Name取值为'Real'时，Value 的可取值是 false (default) 或 true15.在新版本的MATLAB中，求解非线性方程的函数solve的用法有所改变，如求解方程【图片】的语句为syms xsolve(x^2+2*x == 2, x)，那么，用下面哪段代码，可以求解方程【图片】？答案:clearsyms xX=solve(x^3+3*x+4 == 0,x)16.使用fsolve函数求解某个非线性方程在区间[a,b]上的全部解时，描述正确的是：将此非线性方程转化为函数并在[a,b]区间上作图，根据图形选择合适的初始值（可能有多个），就可计算出相应的全部解17.设非线性方程组为：【图片】我们要求将该函数定义为【图片】的形式，则下面哪组语句正确的定义了函数F(x)：答案:function z=F(x)z(1)=x(1)+x(1)*sin(x(2))-2.2378z(2)=x(1)^3-x(2) -cos(x(2))18.MATLAB语句eqn = x^3 == 125的含义是：答案:将方程 x^3 == 125 存储到变量 eqn 中19.函数 solve 参数中的可选参数 'Real'答案:不出现时，表示其值为 false，即函数solve会求出包含复数在内的所有解20.函数fsolve的输出变量[x,fval,exitflag,output] = fsolve(___)中的exitflag表示方程的求解状态，其中当exitflag大于0时，表示答案:方程已解，结果可靠21.把拟合多项式和原始数据绘制在同一个图形窗口里答案:是为了形象的显示拟合曲线和原始数据的具体位置22.MATLAB/Octave函数polyval(p,x)的功能是答案:求以向量p的分量为系数的多项式在x处的值23.已知数据xdata = [0.9 1.5 13.8 19.8 24.1 28.2 35.2 60.3 74.6 81.3];ydata =[455.2 428.6 124.1 67.3 43.2 28.1 13.1 -0.4 -1.3 -1.5];且xdata和ydata间满足关系：ydata=x(1)*exp(x(2)*xdata)则，我们可以用下面哪个表示方式来定义拟合函数答案:fun = @(x,xdata) x(1)*exp(x(2)*xdata);24.要做好数学实验，答案:需要清楚MATLAB函数中参数的含义；_需要熟知实验内容的数学背景；_需要熟练使用MATLAB软件；25.MATLAB/Octave函数interp1中有一个描述插值方法的参数，其中spline表示答案:三次样条插值26.MATLAB/Octave函数 Zi=interp2(X,Y,Z,Xi,Yi) 返回的数据Zi的数据类型是答案:和meshgrid(Xi,Yi)同类型27.在新版本的MATLAB中，用于插值的函数interp1有较大的变化，增加了一些参数，请问，下列哪个参数不是可以使用的参数答案:'gauss'28.今假设有四分之一个圆周上的四个点，例如(0,1),(0.5,0.866),(0.866,0.5),(1,0)，显然，这四个点的y值是单调减少的，请问，用函数interp1插值时，下列哪种方法得到的插值函数不一定单调？答案:'spline'29.根据定义，[X,Y] = meshgrid(x,y) 基于向量 x 和 y 中包含的坐标返回二维网格坐标。

电子科技大学级微积分(下)期末复习

证明题常考内容：
主要是关于常数项级数的收敛性证明；（仅2003,2008年没有考）
多元函数连续、可导、可微的关系
函数连续
函数可偏导
函数可微偏导数连续
例选择题
1、若 f (x, y) 在点 (x0, y0 ) 处不连续，则（Ｃ）
(A) lim f (x, y)必不存在； xx0 y y0
(B) f (x0 , y0 )必不存在； (C) f (x, y)在(x0, y0 )必不可微； (D) fx (x0 , y0 ), f y (x0 , y0 )必不存在；
2、 z f (x, y) 在点 (x0, y0 ) 处可微是 f 在该点的两个偏
导数 fx , f y 都存的（ B ）
S2
Dxy
1 4x2 4 y2 dxdy
Dz
三重积分在柱坐标下的计算：
若 (1)被积函数为f(x2+y2) ；
(2)区域V的边界面的方程含x2+y2 ；
（如边界面为球面、圆柱面、圆锥面、旋转抛物面等）
则可选用柱坐标系.
方法： (1) “先一后二法”(投影
rdrd 法z2(r), ) f (r cos , r sin , z)dz.
Dr
方法二、格林公式: Pdx Qdy ( Q P )dxdy.
L
x y
D
(注意:(1)积分曲线 L 要封闭;
(2)P,Q函数要在区域D内有连续偏导.)
方法三、(直接法) 化为定积分。
第二类曲面积分的计算
方法一：高斯公式法;
Pdydz Qdzdx Rdxdy
S
V
(P Q R )dV x y z
x2n2
2n

高等数学——电子科技大学2021秋

试卷1一、选择题（本题共20小题，每题5分，共计100分，错选、漏选均不得分）1. 若()F x 在[,]a b 上有'()()F x f x =，则()F x 为()f x 在[,]a b 上的（ A ）A. 原函数B. 导函数C. 指数函数D. 幂函数2. 若()2x f x dx x C =++⎰，则()f x =（ A ）A. 2ln 21x +B. 221ln 22x x +C. 121x ++D. 21x +3. 设()cos3f x xdx =⎰，则'()3f π=（ D ） A. 0 B. 13 C. 1 D. 1-4. 由分项积分法，不定积分(1)(2)ln |(2)|(2)2dx dx dx x x C x x x x+-+--⎰⎰⎰,则上述运算中（ D ） A. 第（1）步正确，第（2）步不正确B. 第（1）步正确，第（2）步也正确C. 第（1）步不正确，第（2）步正确D. 第（1）步不正确，第（2）步也不正确5. 不定积分(sin 1)x dx +=⎰（ C ）A. cos x x C --+B. cos x x C -+C. cos x x C -++D. cos x x C ++6. 设4t x =，则不定积分22(1)(2)(3)arctan arctan 41611dx dt t C x C x t ++++⎰⎰上述解法中（ A ） A. 第（1）步开始出错 B. 第（2）步开始出错C. 第（3）步开始出错D. 全部正确 7. 不定积分sin(ln )x dx x=⎰（ C ） A. sin (ln )x x C -+B. sin(ln )x C +C. cos(ln )x C -+D. cos(ln )x C + 8. 不定积分cos sin x xe dx =⎰（ C ）A. sin x e C -+B. sin x e C +C. cos x e C -+D. cos x e C +9. 不定积分2sin x d x ⎰对应的分部积分公式可表为（ C ）A. 2cos 2sin x x x xdx -⎰B. 2sin 2cos x x x xdx -⎰C. 2sin 2sin x x x xdx -⎰D. 2cos 2cos x x x xdx =⎰10. 设(),()f x g x 为连续函数，且()()f x g x ≥且()(),f x g x a b ≠<，12(),()b ba a I f x dx I g x dx ==⎰⎰，则有（ B ）A. 12I I <B. 12I I >C. 12I I =D. 12,I I 大小不能确定11. 设0a >，定积分2(a ax dx -+=⎰（ C ） A. 0B. 3aC. 32aD. 34a 12. 极限2300sin lim t x x e t dt x →=⎰（D ） A. 3B. 2C. 12D. 13 13. 定积分31dx =⎰（ D ） A. 0B. 12C. 1D. 214. 定积分220sin 2ππ=⎰a xdx ，则常数a =（ D ） A. 12B. 1C. 32D. 2 15. 定积分09912(21)x dx -+=⎰（ C ） A. 1200- B. 1100- C. 1200 D. 1100 16. 若0(23)2ax x dx -=⎰，则常数a =（D ）A. 1B.12C. 0D. 1- 17. 曲线cos y x =，直线x π=及x 轴，y 轴围成的平面图形的面积，可表为（ D ） A. 0cos xdx π⎰ B. 202cos cos xdx xdx πππ-+⎰⎰ C. 0cos xdx π-⎰ D. 202cos cos xdx xdx πππ-⎰⎰18. 设()f x 为连续函数，则由曲线()y f x =，直线,()x a x b a b ==<及x 轴所围成的曲边梯形的面积为（ D ）A. ()b a f x dx -⎰B. ()b a f x dx ⎰C. |()|b a f x dx -⎰D. |()|b a f x dx ⎰19. 下列微分方程中属于变量可分离的是（ D ）A. sin()0xy dx ydy +=B. sin()0x y dx ydy ++=C. sin cos ln()0x ydx xy dy +=D. sin cos 0x y x ydx e dy ++=20. 微分方程2'32xy y x x +=++的通解是（A ） A. 213232C y x x x =+++ B. 3213232y x x x C =+++C. 2132ln 2y x x x C =+++D. 2132ln 32y x x x C =+++试卷1参考答案01-05AADDC06-10ACCCB 11-15CDDDC16-20DDDA。

现代数字电子技术基础_杭州电子科技大学中国大学mooc课后章节答案期末考试题库2023年

现代数字电子技术基础_杭州电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.从大到小依次排列下列数据 (120)10, (10011010)2 , (117)8 , (B4)16。

正确的顺序为答案:(B4)16 > (10011010)2 > (120)10 > (117)82.二进制数111001的余3码是答案:100010103.8421BCD码的1000相当于十进制的数值答案:84.求[X]原=1.1101的真值和补码，求[x]反=0.1111的补码答案:-0.1101; 1.0011; 0.11115.已知十进制数为92，其对应的余3码为：答案:(11000101)余3码6.要表达一个逻辑函数常见的方法有答案:其余都是7.试选择下图门电路的输出状态答案:高阻态8.集成电路74LS245的内部结构如图所示，试说明该电路的逻辑功能。

答案:双向传输，当C=0，X的信号传送到Y；当C=1，Y的信号传送到X9.试写出图中NMOS门电路的输出逻辑表达式。

答案:10.标准或-与式是由（）构成的逻辑表达式。

答案:最大项相与11.卡诺图上变量的取值顺序是采用（）的形式，以便能够用几何上相邻的关系表示逻辑上的相邻。

答案:循环码12.已知逻辑电路如图所示，分析该电路的逻辑功能：答案:13.引起组合逻辑电路中竟争与冒险的原因是答案:电路延时14.已知某电路的真值表如下，该电路的逻辑表达式为答案:Y=AB+C15.八选一数据选择器74151组成的电路如图所示，则输出函数为答案:16. 7４153是四选一数据选择器，电路如下。

则Ｙ的表达式是答案:17.以下电路中常用于总线应用的有答案:三态门18.若F（A，B，C）=∑m（1，3，4，7），以下叙述正确的是：答案:F的反函数是∑m（0，2，5，6）19.可以直接实现线与的器件答案:集电极开路门20.三变量逻辑函数F(A,B,C)= A+BC，以ABC为顺序组成最小项表示中不含下列哪项答案:m1m2m0。

电子科技大学微积分试题及答案

电子科技大学期末微积分一、选择题(每题2分)1、设x ƒ()定义域为（1,2），则lg x ƒ()的定义域为（） A 、（0,lg2）B 、（0，lg2]C 、（10,100）D 、（1,2）2、x=-1是函数x ƒ()=()221x x x x --的（） A 、跳跃间断点 B 、可去间断点 C 、无穷间断点 D 、不是间断点3、试求02lim x x→A 、-14B 、0C 、1D 、∞ 4、若1y xx y+=，求y '等于（） A 、22x y y x -- B 、22y x y x -- C 、22y x x y-- D 、22x yx y +-5、曲线221xy x =-的渐近线条数为（） A 、0 B 、1 C 、2 D 、36、下列函数中，那个不是映射（）A 、2y x = (,)x R y R +-∈∈B 、221y x =-+C 、2y x =D 、ln y x = (0)x > 二、填空题（每题2分） 1、__________2、、2(1))lim ()1x n xf x f x nx →∞-=+设（，则的间断点为__________3、21lim51x x bx ax→++=-已知常数 a 、b,，则此函数的最大值为__________ 4、263y x k y x k =-==已知直线是的切线，则 __________ 5、ln 2111x y y x +-=求曲线，在点（，）的法线方程是__________ 三、判断题（每题2分）1、221x y x =+函数是有界函数 ( ) 2、有界函数是收敛数列的充分不必要条件 ( ) 3、limββαα=∞若，就说是比低阶的无穷小 ( ) 4、可导函数的极值点未必是它的驻点 ( ) 5、曲线上凹弧与凸弧的分界点称为拐点 ( ) 四、计算题（每题6分） 1、1sin xy x=求函数的导数2、21()arctan ln(12f x x x x dy =-+已知），求3、2326x xy y y x y -+="已知，确定是的函数，求4、20tan sin limsin x x xx x→-求5、计算 6、21lim (cos )x x x +→计算五、应用题1、设某企业在生产一种商品x 件时的总收益为2)100R x x x =-（，总成本函数为2()20050C x x x =++，问政府对每件商品征收货物税为多少时，在企业获得利润最大的情况下，总税额最大？（8分）2、描绘函数21y x x=+的图形（12分）六、证明题（每题6分）1、用极限的定义证明：设01lim (),lim()x x f x A f A x+→+∞→==则 2、证明方程10,1x xe =在区间（）内有且仅有一个实数一、选择题1、C2、C3、A4、B5、D6、B 二、填空题1、0x =2、6,7a b ==-3、184、35、20x y +-= 三、判断题1、√2、×3、√4、×5、× 四、计算题 1、1sin1sin1sin ln 1sin ln 22))1111cos ()ln sin 1111(cos ln sin )xxx xx xy x ee x x x x x x x x x x x'='='⎡⎤=-+⎢⎥⎣⎦=-+（（2、22()112(arctan )121arctan dy f x dxxx x dx x xxdx='=+-++= 3、解：2222)2)222302323(23)(23(22)(26)(23x y xy y y x yy x y y x y x y yy y x y--'+'=-∴'=--'----'∴''=-4、解：2223000tan sin ,1cos 21tan (1cos )12lim lim sin 2x x x xx x x xx x x x xx x →→→--∴==当时，原式=5、解：65232222261)61116116(1)166arctan 6arctanx t dx t tt t t t t tt t C C===+=++-=+=-+=-+=-+⎰⎰⎰⎰令原式（6、解：2201ln cos 01limln cos 20200012lim 1lim ln cos ln cos lim 1(sin )cos lim 2tan 1lim 22x xx x xx x x x x e exx xx x x xx x e++→++++→→→→→-===-=-==-∴= 原式其中：原式五、应用题1、解：设每件商品征收的货物税为a ，利润为()L x222()()()100(20050)2(50)200()45050()0,,()4(50)41(502)410250225L x R x C x axx x x x ax x a x L x x aaL x x L x a a ax T a T a T a =--=--++-=-+--'=-+--'==-='=-'==''=-<∴=令得此时取得最大值税收T=令得当时，T 取得最大值2、解：()()2300,01202201D x y x x y x y x y x =-∞⋃+∞='=-'==''=+''==-，间断点为令则令则渐进线：32lim lim 001lim x x x y y y x y y x y x x→∞→→∞=∞∴=∴=+==∞∴无水平渐近线是的铅直渐近线无斜渐近线图象六、证明题1、证明：lim ()0,0()11101()1lim ()x x f x AM x M f x A x MM M x f A x f A xεεξε→∞→∞=∴∀>∃>>-<><<>∴-<=当时，有取=，则当0时，有即2、证明：[]()1()0,1(0)10,(1)100,1()0,1()(1)0,(0,1)()0,110,1x x x f x xe f x f f e f e f x x e x f x xe ξξξξ=-=-<=->∈=='=+>∈∴-令在（）上连续由零点定理：至少存在一个（），使得即又则在上单调递增方程在（）内有且仅有一个实根Chapter 33.2 Solution:for, 10=a , 4/2πj ea --= , 4/2πj ea = , 3/42πj ea --=, 3/42πj ea =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=n j j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++= )358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n n3.3 Solution: for the period of )32cos(t πis 3=T , the period of )35sin(t πis 6=T so the period of )(t x is 6 , i.e. 3/6/20ππ==w )35sin(4)32cos(2)(t t t x ππ++=)5sin(4)2cos(21200t w t w ++=)(2)(21200005522t w j t w j t w j t w j e e j e e ----++=then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x ,that is 12T T =, 12w w =(2). dt e t x t x dt e t x b t jkw t jkw k 12))1()1(()(112-∞∞--∞∞--+-==⎰⎰dt e t x dt et x t jkw tjkw 11)1()1(11-∞∞--∞∞--+-=⎰⎰111)(jkw k k jkw k jkw k e a a e a ea -----+=+=3.8 Solution:kt jw k k e a t x 0)(∑∞-∞==while:)(t x is real and odd, then 00=a , k k a a --=2=T , then ππ==2/20wand0=k a for 1>kso kt jw k k e a t x 0)(∑∞-∞==t jw t jw e a e a a 00110++=--)sin(2)(11t a e ea t j tj πππ=-=-for12)(2121212120220==++=-⎰a a a a dt t x∴ 2/21±=a∴)sin(2)(t t x π±=3.15 Solution:kt jw k k e a t x 0)(∑∞-∞==∴ t jkw k k e jkw H a t y 0)()(0∑∞-∞==∴dt e jkw H t y Ta t jkw Tk 0)()(10-⎰=for⎪⎩⎪⎨⎧>≤=100, (0100),.......1)(w w jw H∴if 0=k a , it needs 1000>kwthat is 12100,........1006/2>>k kππand k is integer, so 8>K3.22 Solution:021)(1110===⎰⎰-tdt dt t x Ta Tdt te dt te dt e t x T a t jk t jk tjkw T k ππ-----⎰⎰⎰===1122112121)(10t jk tde jk ππ--⎰-=1121⎥⎥⎦⎤⎢⎢⎣⎡---=----111121ππππjk e te jk t jk tjk⎥⎦⎤⎢⎣⎡---+-=--ππππππjk e e e e jk jk jk jk jk )()(21⎥⎦⎤⎢⎣⎡-+-=ππππjk k k jk )sin(2)cos(221[]πππππk jk k j k jk k)1()cos()cos(221-==-=0............≠k 3.35 Solution:kt jw k k e a t x 0)(∑∞-∞==∴ t jkw k k e jkw H a t y 0)()(0∑∞-∞==∴dt e jkw H t y Ta t jkw Tk 0)()(10-⎰=for⎩⎨⎧≥=otherwise w jw H ,.......0250,.......1)(∴if 0=k a , it needs 2500<kwthat is 14250,........2507/2<<k kππand k is integer, so 17....18≤<k k 或3.40 Solution:According to the property of fourier series: (a). )2cos(2)cos(20000000t Tka t kw a e a ea a k k t jkw k t jkw k k π==+='- (b). Because 2)()()}({t x t x t x E v -+=}{2k v k k k a E a a a =+='-(c). Because 2)(*)()}({t x t x t x R e +=2*kk k a a a -+='(d). k k k a Tjka jkw a 220)2()(π=='(e). first, the period of )13(-t x is 3T T ='then 3)(1)13(131213120dmem x T dt e t x T a m T jk T t T jk T k +'--'-'-'⎰⎰'=-'='ππTjkk m Tjk T T jk T jk m T jk T ea dm em x T e dm e e m x T πππππ221122211)(1)(1---------=⎥⎦⎤⎢⎣⎡==⎰⎰ Extra problems:∑∞-∞=-=k kT t t x )()(δ, π=T (1). Consider )(t y , when )(jw H is(2). Consider )(t y , when )(jw H isSolution:∑∞-∞=-=k kT t t x )()(δ ↔ π11=T , 220==T w π (1). kt j k k t jkw k k e k j H a e jkw H a t y 20)2(1)()(0∑∑∞-∞=∞-∞===π π2= (for k can only has value 0)(2). kt j k k t jkw k k e k j H a e jkw H a t y 20)2(1)()(0∑∑∞-∞=∞-∞===πππt e e t j t j 2cos 2)(122=+=- (for k can only has value –1 and 1)。

XXXX杭州电子科技大学概率论期末试卷(b)-8页精选文档

杭州电子科技大学学生考试卷期末（ B ）卷一、选择题，将正确答案填在括号内（每小题3分，共18分）1．对于任意两事件B A ,，)(B A P ⋃等于（ A ）A ．)()()(AB P B P A P -+ B ．)()()()(B P A P B P A P -+C ．)()(B P A P +D ．)()(1B P A P - 2．设随机变量X ～)2.0,5(b ，则下列结论中正确的是（C ）A ．328.02.0}2{⨯==X PB ．322.08.0}2{⨯==X PC ． 32258.02.0}2{⨯==C X PD ．32252.08.0}2{⨯==C X P 3．随机变量X 的概率密度为),(,21)(4)3(2+∞-∞∈=+-x ex f x π，则=Y （ B ）)1,0(~NA ．23+X B ．23+X C ．23-X D ．23-X 4．设随机变量X 和Y 相互独立，),(~211σμN X ，),(~222σμN Y ，则随机变量132+-=Y X Z 的方差)(Z D 等于（ D ）A ．222132σσ- B ． 222194σσ- C ．1942221++σσ D ．222194σσ+5．设),(Y X 的联合分布律如下表所示：则(s,t)= ( C )时，X 与Y 相互独立．（A ）(1/5,1/15)； (B) (1/15,1/5)；（C ）(1/10,2/15)；（D ）(2/15,1/10).6．设),(~2σμN X ，其中2σ已知，n X X X ,,,21Λ为来自总体X 的一个样本，则μ的置信度为95%的置信区间为（ A ）． A ．),(025.0025.0Z nX Z nX σσ+-； B ．),(025.0025.0t nX t nX σσ+-C ．),(05.005.0Z nX Z nX σσ+-D ． ),(05.005.0t nX t nX σσ+-二、填空题（每空格2分，共12分）1．设事件B A ,相互独立，6.0)(,4.0)(==B P A P ，则概率)(B A P ⋃= 0.76 .2．袋内装有6个白球，4个黑球.从中任取三个，取出的三个球都是白球的概率 1/6 .3．设3.0}2010{),,10(~2=<<X P N X σ，则}100{<<X P 的值为 0.3 .4．设随机变量X 服从（0，2）上的均匀分布，则随机变量2X Y =在（0，4）上概率密度)(y f Y5．设随机变量X 服从二项分布)3.0,10(b ，随机变量Y 服从正态分布)4,2(N ，且Y X ,相互独立，则)2(Y X E -=1- ，)2(Y X D -= 18.1 .三、（本题6分）将两信息分别编码为A 和B 传递出去，接收站收到时，A被误作B 的概率为04.0，而B 被误作A 的概率为03.0，信息A 与信息B 传递的频繁程度为1:2，若接收站收到的信息是A ，求原发信息是A 的概率.解：设事件1A 为发出信息A ，事件2A 为收到信息A 所求概率为)()()()()()()(12112112121A A P A P A A P A P A A P A P A A P +=—————————— 3分656403.031)04.01(32)04.01(32=⨯+-⨯-⨯= —————————— 6分四．本题10分）设随机变量X 的密度函数为⎩⎨⎧<<=elsex ax x f ,010,)(，（1）(3分) 求常数a ；(2) (3分) 求X 的分布函数)(x F ；（3） (4分) 方差)(X D . 解：（1）因为⎰+∞∞-=1)(dx x f___________________1分所以 110=⎰axdx得12=a ，即2=a___________________ 3分（2）X的分布函数()F x =⎰∞-xdt t f )(___________________ 1分⎪⎩⎪⎨⎧≥<<≤=1,110,0,0)(2x x x x x F ___________________ 3分（3）⎰+∞∞-==32)()(dx x xf X E ___________________ 1分⎰+∞∞-==21)()(22dx x f x X E___________________ 3分181)]([)()(22=-=X E X E X D ___________________ 4分五．（本题18分）设随机变量),(Y X 的概率分布律为：求：（1）(8分) X 的边缘分布律和Y 的边缘分布律, 并问X 与Y 是否相互独立？（2）(6分) 相关系数XY ρ，并问X 与Y 是否相关？（3）(4分)条件概率}11{=≥Y X P解：（1）关于X 的边缘分布律为_______ 3分关于Y 的边缘分布律为_________ 3分因}1{}0{}1,0({-=⋅=≠-==Y P X P Y X P所以X与Y 不相互独立._________ 2分（2）2.03.014.001.0)1(2.02)(-=⨯+⨯+⨯-+⨯-=XY E 得04.0)()()(),(-=-=Y E X E XY E Y X Cov____________ 4分又2.12.024.014.00)(2222=⨯+⨯+⨯=X E 得56.0)]([)()(22=-=X E X E X D 所以X与Y 相关___________ 6分（3）条件概率}11{=≥Y X P }1{}1,1{==≥=Y P Y X P___________ 2分=434.03.0}0{}1,2{}1,1{=====+==X P Y X P Y X P______ 4分六．（本题8分）某单位有150架电话机,每架分机有4%的时间要使用外线,假设每架分机是否使用外线是相互独立的,求该单位有10条外线时,至少有一架分机使用外线时需要等待的概率？解：设X 表示使用外线的电话分机台数，由于)04.0,150(~b X ，_________ 3分则6)(=X E ，76.5)(=X D ，由中心极限定理可知：)5.2()083.2(2Φ+Φ-=______________ 8分七．（每小题5分,共10分）设总体X 的概率密度为⎩⎨⎧≤≤+=else x x x f ,010,)1()(θθ，其中1->θ是未知参数，n x x x ,,,21Λ是X 的一个样本n X X X ,,,21Λ的观察值，试求参数θ的矩估计量和最大似然估计值. 解：（1）21)1()()(1++=+==⎰⎰+∞∞-θθθθdx x x dx x xf X E ___________ 3分所以令 X X E =)(，即X =++21θθ ___________________ 4分解得参数θ的矩估计量为：XX --=112ˆθ _________________ 5分（2）似然函数)()(1i n i x f L =∏=θ=θθθθ)()1()1(211n n i ni x x x x Λ+=+∏=_______ 2分取对数)ln()1ln()(ln 21n x x x n L Λθθθ++= 令0ln 1)(ln 1=++=∑=ni i x nd L d θθθ ____________ 4分解得参数θ的最大似然估计值1ln ˆ1--=∑=ni ixnθ_______________ 5分八．（8分）设某批电子元件的寿命Ｘ服从正态分布),(2σμN ，2,σμ均为未知，随机抽取１６只，测得32,1509==s x （单位为小时）。

杭州电子科技大学高等数学期末试卷及答案

3．曲面在点处的切平面方程是：( C )
(A) ；(B) ；
(C) ；(D) ．
4．设曲面 ,则对面积的曲面积分等于（D）
(A) (B) (C) (D)
5．级数（A）
（A）收敛；（B）发散；（C）敛散性不能确定；（D）不是正项级数
三、试解下列各题（每小题6分，共计12分）
1．一平面过点且平行于向量和 ,试求这平面的方程.
解得驻点是唯一的驻点,..............................................................................7分
根据问题的性质可知,到三直线的距离平方之和最小的点一定存在,故即为所求...............8分.
六、二题中选一题做（本题9分）
七、证明题（本题5分）
证明级数发散.
证明:反证.设收敛于 ,设级数的部分和数列为 ..........1分
那么, ,从而................2分
........................3分
但 ,...............4分
故 ........................5分
与假设收敛矛盾,这说明级数发散
第 3 页共 3 页
...............4分
..............5分
............................6分
6.计算对坐标的曲线积分，其中是在圆周
上由点到点的一段弧.
解:令 ,.............................1分
..................................................2分

杭州电子科技大学信息工程学院学生考试卷(A)卷

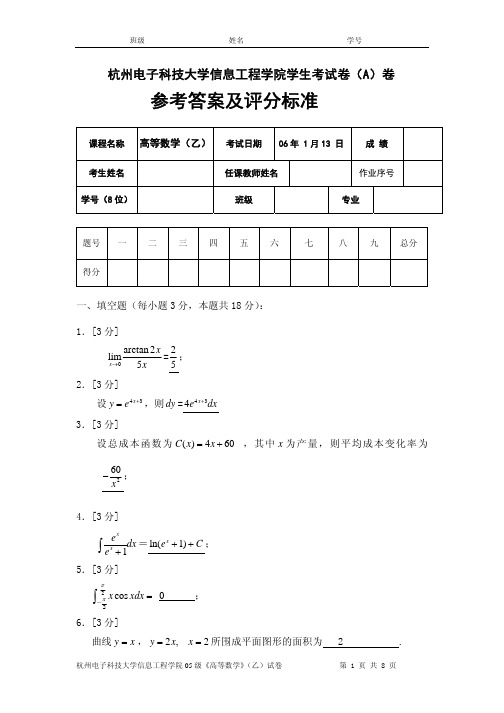
π
1．[5 分] 求 f ( x) = x 2 e− x 的单调区间. 解 f ( x ) 的定义域为 ( −∞, +∞) 。令 f ′( x ) = 2 xe − x − x 2 e − x = xe − x (2 − x ) = 0
………………………………2
分
得驻点 x = 0, x = 2 ，它们将定义域分成以下三个区间：
证明设 F ( x ) = e x f ( x ) ，
2
…………………………………………2
分
已知 f ( x ) 在[0,1]上连续，在（0， 1）内可导且 f (0) = f (1) = 0 ，所以 F ( x ) 在[0,1] 上连续，在（0，1）内可导。 F (0) = f (0) = 0
y
解如图，所求面积
杭州电子科技大学信息工程学院 05 级《高等数学》（乙）试卷第 4 页共 8 页
班级
姓名
学号
S = ∫ ln xdx
2
4
y = ln x
……………………3 ……………………4 …………………………5
4 4 ＝ x ln x − ∫ dx 2 2
＝ 4 ln 4 − 2 ln 2 − 2 ＝ 2(3ln 2 − 1)
x →0
1 + sin x − 1 − sin x x
解一 lim
x →0
1 + sin x − 1 − sin x ( 1 + sin x − 1 − sin x )( 1 + sin x + 1 − sin x ) = lim x → 0 x x ( 1 + sin x + 1 − sin x )

电子科技大学微积分试题

电子科技大学期末微积分一、选择题(每题2分)1、设x ƒ()定义域为（1,2），则lg x ƒ()的定义域为（） A 、（0,lg2）B 、（0，lg2]C 、（10,100）D 、（1,2）2、x=-1是函数x ƒ()=()221x x x x --的（） A 、跳跃间断点 B 、可去间断点 C 、无穷间断点 D 、不是间断点3、试求02lim x x→等于（）A 、-14B 、0C 、1D 、∞ 4、若1y xx y+=，求y '等于（） A 、22x y y x -- B 、22y x y x -- C 、22y x x y-- D 、22x yx y +-5、曲线221xy x =-的渐近线条数为（） A 、0 B 、1 C 、2 D 、36、下列函数中，那个不是映射（） A 、2y x = (,)x R y R +-∈∈ B 、221y x =-+ C 、2y x = D 、ln y x = (0)x > 二、填空题（每题2分） 1、__________2、、2(1))lim()1x n xf x f x nx →∞-=+设（，则的间断点为__________3、21lim51x x bx ax→++=-已知常数 a 、b,，则此函数的最大值为__________ 4、263y x k y x k =-==已知直线是的切线，则 __________5、ln 2111x y y x +-=求曲线，在点（，）的法线方程是__________ 三、判断题（每题2分）1、221x y x =+函数是有界函数 ( ) 2、有界函数是收敛数列的充分不必要条件 ( ) 3、limββαα=∞若，就说是比低阶的无穷小 ( ) 4、可导函数的极值点未必是它的驻点 ( ) 5、曲线上凹弧与凸弧的分界点称为拐点 ( ) 四、计算题（每题6分） 1、1sin xy x=求函数的导数2、21()arctan ln(12f x x x x dy =-+已知），求3、2326x xy y y x y -+="已知，确定是的函数，求4、20tan sin limsin x x xx x→-求 5、计算 6、21lim(cos )x x x +→计算五、应用题1、设某企业在生产一种商品x 件时的总收益为2)100Rx x x =-（，总成本函数为2()20050C x x x =++，问政府对每件商品征收货物税为多少时，在企业获得利润最大的情况下，总税额最大？（8分）2、描绘函数21y x x=+的图形（12分）六、证明题（每题6分）1、用极限的定义证明：设01lim (),lim()x x f x A f A x +→+∞→==则 2、证明方程10,1x xe =在区间（）内有且仅有一个实数一、选择题1、C2、C3、A4、B5、D6、B 二、填空题1、0x =2、6,7a b ==-3、184、35、20x y +-= 三、判断题1、√2、×3、√4、×5、× 四、计算题 1、1sin1sin1sin ln 1sin ln 22))1111cos ()ln sin 1111(cos ln sin )xxx xx xy x ee x x x x x x x x x x x'='='⎡⎤=-+⎢⎥⎣⎦=-+（（2、22()112(arctan )121arctan dy f x dxxx x dx x x xdx='=+-++=3、解：2222)2)222302323(23)(23(22)(26)(23x y xy y y x yy x y y x y x y yy y x y--'+'=-∴'=--'----'∴''=-4、解：2223000tan sin ,1cos 21tan (1cos )12lim lim sin 2x x x x x x x x x x x x x x x →→→--∴==Q :::当时，原式=5、解：65232222261)61116116(1)166arctan 6arctanx t dx t tt t t t t tt t C C===+=++-=+=-+=-+=-+⎰⎰⎰⎰令原式（6、解：2201ln cos 01limln cos 20200012lim 1lim ln cos ln cos lim 1(sin )cos lim 2tan 1lim 22x xx x xx x x x x e ex xxx x x xx x e++→++++→→→→→-===-=-==-∴= 原式其中：原式五、应用题1、解：设每件商品征收的货物税为a ，利润为()L x222()()()100(20050)2(50)200()45050()0,,()4(50)41(502)410250225L x R x C x axx x x x ax x a x L x x aaL x x L x a a ax T a T a T a =--=--++-=-+--'=-+--'==-='=-'==''=-<∴=令得此时取得最大值税收T=令得当时，T 取得最大值2、解：()()2300,01202201D x y x x y x y x y x =-∞⋃+∞='=-'==''=+''==-，间断点为令则令则渐进线：32lim lim 001lim x x x y y y x y y x y x x→∞→→∞=∞∴=∴=+==∞∴无水平渐近线是的铅直渐近线无斜渐近线图象六、证明题1、证明：lim ()0,0()11101()1lim ()x x f x AM x M f x A x MM M xf A x f A xεεξε→∞→∞=∴∀>∃>>-<><<>∴-<=Q 当时，有取=，则当0时，有即2、证明：[]()1()0,1(0)10,(1)100,1()0,1()(1)0,(0,1)()0,110,1x xx f x xe f x f f e f e f x x e x f x xe ξξξξ=-=-<=->∈=='=+>∈∴-Q Q 令在（）上连续由零点定理：至少存在一个（），使得即又则在上单调递增方程在（）内有且仅有一个实根。

杭州电子科技大学信息工程学院高数考试题目

2010年杭州电子科技大学信息工程学院学生考试卷（期末）A 卷课程名称高等数学（上）考试日期时间共120分钟考生姓名任课教师姓名学号班级专业题号一、二、三四五、六、七总分得分一、填空题(每小题3分，共计15分)1．21lim (2)nn n→+∞-= . 2．方程0y y ''+=的通解为 .3．⎰-=2/2/sin ππdx x .4．设2()1f x x =+,则()f x '= .5．设x x f 22cos )(sin =',则)(x f = .二、单项选择题（每小题3分，共计15分）1．设sin ,0()0,01cos ,0x x x x f x x x x x ⎧+<⎪⎪==⎨⎪⎪>⎩，则x =0是)(x f 的 ( ) （A ）连续点（B ）可去间断点（C ）跳跃间断点（D ）振荡间断点2．下列各式中正确的是 ( )（A ）1211021<<⎰dx x （B ）12112<<⎰dx x（C ）⎰⎰<---11222dx dx xx（D ）⎰⎰<-2/02/cos cos ππxdx xdx 3．下列命题不正确的是 ( )(A)非零常数与无穷大之积是无穷大 (B)常数0与无穷大之积是无穷小(C)无界函数是无穷大 (D)无穷大的倒数是无穷小 4．设)(x f 在0x x =处连续且)(0x f '不存在，则)(x f y =在))(,(00x f x 处 ( )（A ）没有切线（B ）有一条不垂直x 轴的切线（C ）有一条垂直x 轴的切线（D ）或者不存在切线或者有一条垂直于x 轴的切线。

5．设微分方程22cos xy y y ex -'''++=,则可设方程的一个特解形式为 ( )(a b 、为待定系数）（A ）(cos sin )xxe a x b x -+ （B ）cos x axe x -（C ）(cos sin )xea xb x -+ (D) cos x ae x -三、试求下导数或微分（每小题6分，共计18分）(要有解题过程)1．设sin 21x t y dt t=+⎰，求dy2．设tan x yx =，求y '3．设(())y f u x =,函数()()f u u x 、二阶可导，求22dx yd四、试求下列积分（每小题6分，共24分）(要有解题过程) 1．⎰dx x sin2．⎰+21ln 1e xx dx3．2122dx x x +∞-∞++⎰ 4．201sin xdx π-⎰五、求曲线32535y xx x =-++的凹凸区间及拐点。

电子科技大学《高等数学理科(本科)》20春期末考试

15.6. 设图，则不定积分图上述解法中() A.1)步开始出错 B.第(2)步开始出错 C.第(3)步开始出错 D.全部正确
正确答案：D
16.6. 不定积分图() A. B.图 C.图 D.图正确答案：B
17.9. 不定积分图() A. B.图 C.图 D.图正确答案：C
ห้องสมุดไป่ตู้18.9. 不定积分图() A. B.图 C.图 D.图正确答案：A
19.15. 定积分图() A.图2 B.3 正确答案：B
20.6.设图，则不定积分图上述解法中() A.1)步开始出错 B.第(2)步开始出错 C.第(3)步开始出错 D.全部正确正确答案：B
3.10. 定积分图，则有() A.图图 B.I的大小不确定正确答案：B
4.16. 定积分图() A.图图 B.图正确答案：A
5.11. 下列积分等于零的是() A. B.图 C.图 D.图正确答案：D
6.18. 由曲线图及直线图所围成图形面积可表示为() A. B.图 C.图 D.图正确答案：D
电子科技大学《高等数学理科(本科)》20春期末考试
一、单选题 1.图( B ) A.图图 B.图正确答案：B
2.4. 由分项积分法，不定积分图,则上述运算中() A.1)步正确，第(2)步不正确 B.第(1)步正确，第(2)步也正确 C.第(1)步不不正确，第(2)步正确 D.第(1)不正确，第(2)步也不正确正确答案：B
7.4. 由分项积分法，不定积分图,则上述运算中() A.1)步正确，第(2)步不正确 B.第(1)步正确，第(2)步也正确 C.第(1)步不正确，第(2)步正确 D.第(1)步不正确，第(2)步也不正确正确答案：D
8.7. 不定积分图() A. B.图

大学杭州电子科技信息工程学院学生考试卷(A)卷

x→0
x
解一 lim 1 + sin x − 1 − sin x = lim ( 1 + sin x − 1 − sin x )( 1 + sin x + 1 − sin x )
x→0
x
x→0
x( 1 + sin x + 1 − sin x )
＝
lim
x→0
x(
2sin x 1 + sin x + 1 − sin x )
1 1
)n
n +1
………………………………………………………………3 分
1+ 1
＝ lim n→∞ (1 +
n +1 1 )n+1
n +1
…………………………………………………………………4 分
杭州电子科技大学信息工程学院 05 级《高等数学》（乙）试卷
第2页共8页
班级
姓名
学号
＝1
………………………………………………………………5 分
；
5．[3 分]
π
∫2 －π
x
cos
xdx
=
0
；
2
6．[3 分]
曲线 y = x ， y = 2x, x = 2 所围成平面图形的面积为 2
.
杭州电子科技大学信息工程学院 05 级《高等数学》（乙）试卷
第1页共8页
班级
姓名
学号
二、试解下列各题（每小题 5 分，本题共 20 分）：
1．[5 分] 求极限 lim 1 + sin x − 1 − sin x
…………………………………4 分

杭州电子科技大学高等数学期末试题.doc

杭州电子科技大学高数期末下学期考试卷一、填空题（每小题3分，本题共18分）：1．[3分]设二元函数)sin(xy ez =，dz = ； 2．[3分]将二次积分⎰⎰-ππππ2),(y dx y x f dy 交换积分次序为；3．[3分] 设L 是抛物线x y =2从)0,0(O 到)1,1(A 的弧段，则⎰L xydx = ；4．[3分]函数xx f +=21)(展开成x 的幂级数为； 5．[3分] 微分方程0)(3)(2)(=-'-''x y x y x y 的通解为；6．[3分]幂级数n n n x n )1(21+∑∞=的收敛半径为；二、试解下列各题（每小题5分，本题共15分）：1．[5分] 设)sin(xy xez xy +=-，求y x z z '',； 2．[5分] 计算dxdy y x D ⎰⎰+)23( ，其中D 是由两坐标轴及直线2=+y x 所围成的区域；3．[5分] 判别级数 )1()1(1n n n n -+-∑∞=的敛散性，收敛的话，是条件收敛还是绝对收敛；试解下列各题（每小题5分，本题共15分）：1．[5分] 设y x e z 2-= ，其中3,sin t y t x ==，求全导数dtdz ； 2．[5分] 计算三重积分yzdxdydz x I ⎰⎰⎰Ω=2，这里Ω是由,402x y -≤≤02≤≤-x ，10≤≤z 所确定；3．[5分] 求微分方程xdx y ydy x sin cos sin cos =满足初始条件40π==x y的特解。

四、试解下列各题（每小题6分，本题共12分）：1．[6分] 求椭球面623222=++z y x 在点)1,1,1(处的切平面方程和法线方程；2．[6分] 求圆锥面22y x z +=被圆柱面x y x 222=+所割下部分的面积。

五、试解下列各题（每小题6分，本题共12分）：1．[6分] 设⎩⎨⎧<<≤≤-=ππx x x x x f 0,0,2)(，试写出)(x f 的以π2为周期的傅立叶级数的和函数)(x s 在],[ππ-上的表达式。