2012年天津中考数学试题答案
2012中考数学真题及答案解析-圆

2012中考数学试题及答案分类汇编:圆一、选择题1. (天津3分)已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ,若12O O =7 cm ,则⊙1O 与⊙2O 的位置关系是(A) 相交 (B) 相离 (C) 内切 (D) 外切2、(内蒙古包头3分)已知AB 是⊙O 的直径,点P 是AB延长线上的一个动点,过P 作⊙O 的切线,切点为C ,∠APC的平分线交AC 于点D ,则∠CDP 等于A 、30°B 、60°C 、45°D 、50°3.(内蒙古呼和浩特3分)如图所示,四边形ABCD 中,DC ∥AB ,BC=1,AB=AC=AD=2.则BD 的长为A.B. C. D.二:填空题:1.(天津3分)如图,AD ,AC 分别是⊙O 的直径和弦.且∠CAD=30°.OB ⊥AD ,交AC 于点B .若OB=5,则BC 的长等于 。
2、(河北省3分)如图,点0为优弧ACB 所在圆的圆心,∠AOC=108°,点D 在AB 延长线上,BD=BC ,则∠D= .3.(内蒙古巴彦淖尔、赤峰3分)如图,直线PA 过半圆的圆心O ,交半圆于A ,B 两点,PC 切半圆与点C ,已知PC=3,PB=1,则该半圆的半径为 .4.(内蒙古呼伦贝尔3分)已知扇形的面积为12π,半径是6,则它的圆心角是 。
三:解答题1、(内蒙古呼和浩特8分)如图所示,AC 为⊙O 的直径且PA ⊥AC ,BC 是⊙O 的一条弦,直线PB 交直线AC 于点D ,DB DC 2DP DO 3==. (1)求证:直线PB 是⊙O 的切线;(2)求cos ∠BCA 的值.2、(内蒙古包头12分)如图,已知∠ABC=90°,AB=BC .直线l 与以BC 为直径的圆O 相切于点C .点F 是圆O 上异于B 、C 的动点,直线BF 与l 相交于点E ,过点F 作AF 的垂线交直线BC 与点D .(1)如果BE=15,CE=9,求EF 的长;(2)证明:①△CDF ∽△BAF ;②CD=CE ;(3)探求动点F 在什么位置时,相应的点D 位于线段BC 的延长线上,且使,请说明你的理由.3、(内蒙古乌兰察布10分)如图,在 Rt △ABC 中,∠ACB =900D 是AB 边上的一点,以BD 为直径的 ⊙0与边 AC 相切于点E ,连结DE 并延长,与BC 的延长线交于点 F . ( 1 )求证: BD = BF ;( 2 )若 BC = 12 , AD = 8 ,求 BF 的长.。
全国各地2012年中考数学分类解析 专题54 图形的旋转变换

2012年全国中考数学试题分类解析汇编专题54:图形的旋转变换一、选择题1. (2012天津市3分)将下列图形绕其对角线的交点逆时针旋转900,所得图形一定与原图形重合的是【 】(A )平行四边形 (B )矩形 (C )菱形 (D )正方形 【答案】D 。
【考点】旋转对称图形【分析】根据旋转对称图形的性质,可得出四边形需要满足的条件:此四边形的对角线互相垂直、平分且相等,则这个四边形是正方形。
故选D 。
2. (2012广东佛山3分)如图,把一个斜边长为2且含有300角的直角三角板ABC 绕直角顶点C 顺时针旋转900到△A 1B 1C ,则在旋转过程中这个三角板扫过的图形的面积是【 】A .πB .34π D .1112π 【答案】D 。
【考点】旋转的性质,勾股定理,等边三角形的性质,扇形面积。
【分析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA 1、 BCD 和△ACD 计算即可:在△ABC 中,∠ACB=90°,∠BAC=30°,AB=2,∴BC=12AB=1,∠B=90°-∠BAC=60°。
∴AC∴ABC 1S BC AC 2∆=⨯⨯=设点B 扫过的路线与AB 的交点为D ,连接CD , ∵BC=DC,∴△BCD 是等边三角形。
∴BD=CD=1。
∴点D 是AB 的中点。
∴ACD ABC 11S S 22∆∆===S 。
∴1ACD ACA BCD ABC S S S ∆∆=++扇形扇形的面扫过积26013113604612ππππ⨯⨯=++=++=+故选D 。
3. (2012广东汕头4分)如图,将△ABC 绕着点C 顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是【 】A .110° B.80° C.40° D.30° 【答案】B 。
天津市历年中考数学真题及答案

2014年天津市初中毕业生学业考试试卷数学本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。
第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第8页。
试卷满分120分。
考试时间100分钟。
答卷前,考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。
答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。
考试结束后,将本试卷和“答题卡”一并交回。
祝各你考试顺利!第Ⅰ卷注意事项:1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共12题,共36分。
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)(1)计算(-6)×(-1)的结果等于(A)6 (B)-6 (C)1 (D)-1(2)cos60o的值等于(A)(B)(C)(D)(3)下列标志中,可以看作是轴对称图形的是(A)(B)(C)(D)(4)为让市民出行更加方便,天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608 000000人次.将1608 000 000用科学记数法表示应为(A)×107(B)×108(C)×109(D)×1010(5)如图,从左面观察这个立体图形,能得到的平面图形是(A)(B)(C)(D)(6)正六边形的边心距为,则该正六边形的边长是(A)(B)2(C)3 (D)(7)如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25o,则∠C的大小等于(A)20o(B)25o(C)40o(D)50o(8)如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC 等于(A)3:2 (B)3:1(C)1:1 (D)1:2(9)已知反比例函数,当1<x<2时,y的取值范围是(A)0<y<5 (B)1<y<2(C)5<y<10(D)y>10(10)要组织一次排球邀请赛,参赛的每两个队都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为(A)(B)(C)(D)(11)某公司招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表所示:如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.公司将录取(A)甲(B)乙(C)丙(D)丁(12)已知二次函数y=ax2+b x+c(a≠0)的图象如下图所示,且关于x的一元二次方程ax2+bx+c-m=9没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中,正确结论的个数是(A)0 (B)1 (C)2 (D)32014年天津市初中毕业生学业考试试卷数学第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。
【中考12年】天津市2001-2012年中考数学试题分类解析 专题9 三角形

2001-2012年某某市中考数学试题分类解析汇编(12专题)专题9:三角形一、选择题1.(某某市2002年3分)sin450的值等于【】(A)12(B)22(C)32(D)1【答案】B。
【考点】特殊角的三角函数值。
【分析】根据特殊角度的三角函数值解答即可:sin45°=22。
故选B。
2.(某某市2002年3分)如图,在ΔABC中,AB=AC,∠A=360,BD、CE分别为∠ABC与∠ACB的角平分线,且相交于点F,则图中的等腰三角形有【】(A)6个(B)7个(C)8个(D)9个【答案】D。
【考点】等腰三角形的判定和性质,三角形内角和定理,角平分线的性质。
【分析】由已知条件,根据等腰三角形的性质和判定,角的平分线的性质,三角形内角和等于180°得到各个角的度数,应用度数进行判断即可:∵AB=AC,∠A=36°,∴△ABC是等腰三角形,且∠ABC=∠ACB=00180362=72°。
∵BD是∠ABC的角的平分线,∴∠ABD=∠DBC=12∠ABC=36°=∠A。
∴AD=BD。
∴△ADB是等腰三角形。
同理,△AEC是等腰三角形。
∵∠DBC=36°,∠ACB=72°,∴∠BDC=180°-72°-36°=72°=∠ACB。
∴BD=BC。
∴△BDC是等腰三角形。
同理,△BCE是等腰三角形。
∵∠FBC=∠FCB=36°,∴BF=CF。
∴△BCF是等腰三角形。
∵∠BEF=∠BFE=∠CDF=∠CFD=72°,∴BE=BF,CD=CF。
∴△BEF,△CDF是等腰三角形。
∴共8个等腰三角形。
故选D。
3.(某某市2003年3分)sin30°的值等于【】(A)12(B)22(C)32(D)1【答案】D。
【考点】特殊角的三角函数值。
【分析】根据特殊角的三角函数值直接作答:sin30°=12。
2012年全国中考数学试题分类解析汇编专题44:矩形、菱形、正方形

2012年全国中考数学试题分类解析汇编(159套63专题)专题44:矩形、菱形、正方形一、选择题1. (2012天津市3分)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD 至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为【】(A1(B)3(C(D1【答案】D。
【考点】正方形的性质,勾股定理。
【分析】利用勾股定理求出CM的长,即ME的长,有DM=DE,所以可以求出DE,从而得到DG的长:∵四边形ABCD是正方形,M为边AD的中点,∴DM=12DC=1。
∴CM=1。
∵四边形EDGF1。
故选D。
2. (2012安徽省4分)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为【】A.22a B. 32a C. 42a D.52a【答案】A 。
【考点】正多边形和圆,等腰直角三角形的性质,正方形的性质。
【分析】图案中间的阴影部分是正方形,面积是2a ,由于原来地砖更换成正八边形,四周一个阴影部分是对角线为a 的正方形的一半,它的面积用对角线积的一半来计算:222114222a a a +⨯⨯=。
故选A 。
3. (2012山西省2分)如图,已知菱形ABCD 的对角线AC .BD 的长分别为6cm 、8cm ,AE⊥BC 于点E ,则AE 的长是【 】A .B .C .48cm 5D .24cm 5 【答案】D 。
【考点】菱形的性质,勾股定理。
【分析】∵四边形ABCD 是菱形,∴CO=12AC=3,BO=12BD=,AO⊥BO,∴5=。
∴ABCD 11S BD AC 682422=⋅=⨯⨯=菱形。
又∵ABCD S BC AE =⋅菱形,∴BC·AE=24,即()24AE cm 5=。
故选D 。
4. (2012陕西省3分)如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,OE⊥AB,垂足为E ,若∠ADC=1300,则∠AOE 的大小为【 】A .75°B .65°C .55°D .50°【答案】B 。
2012年中考数学分类解析(159套63专题)专题44_矩形、菱形、正方形

2012年全国中考数学试题分类解析汇编(159套63专题)专题44:矩形、菱形、正方形一、选择题1. (2012天津市3分)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD 至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为【】(A1--(B)3-(C(D1【答案】D。
【考点】正方形的性质,勾股定理。
【分析】利用勾股定理求出CM的长,即ME的长,有DM=DE,所以可以求出DE,从而得到DC=1。
DG的长:∵四边形ABCD是正方形,M为边AD的中点,∴DM=12∴CM=1。
∵四边形EDGF1。
故选D。
2. (2012安徽省4分)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为【】A.22aB. 32aC. 42aD.52a【答案】A。
【考点】正多边形和圆,等腰直角三角形的性质,正方形的性质。
【分析】图案中间的阴影部分是正方形,面积是2a ,由于原来地砖更换成正八边形,四周一个阴影部分是对角线为a 的正方形的一半,它的面积用对角线积的一半来计算:222114222a a a +⨯⨯=。
故选A 。
3. (2012山西省2分)如图,已知菱形ABCD 的对角线AC .BD 的长分别为6cm 、8cm ,AE⊥BC 于点E ,则AE 的长是【 】A .B .C .48cm 5D .24cm 5【答案】D 。
【考点】菱形的性质,勾股定理。
【分析】∵四边形ABCD 是菱形,∴CO=12AC=3,BO=12BD=,AO⊥BO,∴5==。
∴ABC D 11S BD AC 682422=⋅=⨯⨯=菱形。
又∵ABC D S BC AE =⋅菱形,∴BC·AE=24,即()24AE cm 5=。
故选D 。
4. (2012陕西省3分)如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,OE⊥AB,垂足为E ,若∠ADC=1300,则∠AOE 的大小为【 】A .75°B .65°C .55°D .50°【答案】B 。
天津市2012-中考数学试题分类解析汇编专题3:几何问题

天津市2012-2014年中考数学试题分类解析汇编专题3:几何问题一、选择题1.(3分)(2014•天津)cos60°的值等于()A.B.C.D.考点:特殊角的三角函数值.分析:根据特殊角的三角函数值解题即可.解答:解:cos60°=.故选A.点评:本题考查特殊角的三角函数值,准确掌握特殊角的函数值是解题关键.2.(3分)(2014•天津)下列标志中,可以看作是轴对称图形的是()A.B.C.D.考点:轴对称图形.分析:根据轴对称图形与中心对称图形的概念求解.解答:解:A、不是轴对称图形,是中心对称图形,不符合题意;B、不是轴对称图形,是中心对称图形,不符合题意;C、不是轴对称图形,是中心对称图形,不符合题意;D、是轴对称图形,符合题意.故选:D.点评:此题主要考查了中心对称图形和轴对称图形的定义,掌握中心对称图形与轴对称图形的概念,解答时要注意:判断轴对称图形的关键是寻找对称轴,图形两部沿对称轴叠后可重合;判断中心对称图形是要寻找对称中心,图形旋转180度后与原图重合.3.(3分)(2014•天津)如图,从左面观察这个立体图形,能得到的平面图形是()A.B.C.D.考点:简单组合体的三视图.分析:根据从左面看得到的图形是左视图,可得答案.解答:解;从左面看下面一个正方形,上面一个正方形,故选:A.点评:本题考查了简单组合体的三视图,从左面看得到的图形是左视图.4.(3分)(2014•天津)正六边形的边心距为,则该正六边形的边长是()A.B.2C.3D.2考点:正多边形和圆.分析:运用正六边形的性质,正六边形边长等于外接圆的半径,再利用勾股定理解决.解答:解:∵正六边形的边心距为,∴OB=,AB=OA,∵OA2=AB2+OB2,∴OA2=(OA)2+()2,解得OA=2.故选B.点评:本题主要考查了正六边形和圆,注意:外接圆的半径等于正六边形的边长.5.(3分)(2014•天津)如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于()A.20°B.25°C.40°D.50°考点:切线的性质.分析:连接OA,根据切线的性质,即可求得∠C的度数.解答:解:如图,连接OA,∵AC是⊙O的切线,∴∠OAC=90°,∵OA=OB,∴∠B=∠OAB=25°,∴∠AOC=50°,∴∠C=40°.点评:本题考查了圆的切线性质,以及等腰三角形的性质,已知切线时常用的辅助线是连接圆心与切点.6.(3分)(2014•天津)如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于()A.3:2 B.3:1 C.1:1 D.1:2考点:平行四边形的性质;相似三角形的判定与性质.分析:根据题意得出△DEF∽△BCF,进而得出=,利用点E是边AD的中点得出答案即可.解答:解:∵▱ABCD,故AD∥BC,∴△DEF∽△BCF,∴=,∵点E是边AD的中点,∴AE=DE=AD,∴=.故选:D.点评:此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△DEF∽△BCF 是解题关键.7.(3分)(2013•天津)tan60°的值等于()A.1B .C.D.2考点:特殊角的三角函数值.分析:根据记忆的特殊角的三角函数值即可得出答案.解答:解:tan60°=.故选C.点评:本题考查了特殊角的三角函数值,一些特殊角的三角函数值是需要我们熟练记忆的内容.8.(3分)(2013•天津)下列标志中,可以看作是中心对称图形的是()A.B.C.D.考点:中心对称图形分析:根据中心对称图形的定义,结合选项所给图形进行判断即可.解答:解:A、不是中心对称图形,故本选项错误;B、不是中心对称图形,故本选项错误;C、不是中心对称图形,故本选项错误;D、是中心对称图形,故本选项正确;故选D.点评:本题考查了中心对称图形的知识,判断中心对称图形是要寻找对称中心,图形旋转180度后与原图形重合.9.(3分)(2013•天津)如图是由3个相同的正方体组成的一个立体图形,它的三视图是()A.B.C.D.考点:简单组合体的三视图.分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.解答:解:所给图形的三视图是A选项所给的三个图形.故选A.点评:本题考查了几何体的三种视图,掌握定义是关键.10.(3分)(2012•天津)2cos60°的值等于()A.1B.C.D.2考点:特殊角的三角函数值.分析:根据60°角的余弦值等于进行计算即可得解.解答:解:2cos60°=2×=1.故选A.点评:本题考查了特殊角的三角函数值,熟记30°、45°、60°角的三角函数值是解题的关键.11.(3分)(2012•天津)下列标志中,可以看作是中心对称图形的是()A.B.C.D.考点:中心对称图形.分析:根据中心对称图形的概念:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,由此结合各图形的特点求解.解答:解:根据中心对称的定义可得:A、C、D都不符合中心对称的定义.故选B.点评:本题考查中心对称的定义,属于基础题,注意掌握基本概念.12.(3分)(2012•天津)将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是()A.平行四边形B.矩形C.菱形D.正方形考点:旋转对称图形.分析:根据旋转对称图形的性质,可得出四边形需要满足的条件,结合选项即可得出答案.解答:解:由题意可得,此四边形的对角线互相垂直、平分且相等,则这个四边形是正方形.故选D.点评:本题主要考查了旋转对称图形旋转的最小的度数的计算方法,把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.13.(3分)(2012•天津)如图是一个由4个相同的正方体组成的立体图形,它的三视图是()A.B.C.D.考点:简单组合体的三视图.分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.解答:解:从正面看可得从左往右2列正方形的个数依次为1,2;从左面看可得到从左往右2列正方形的个数依次为2,1;从上面看可得从上到下2行正方形的个数依次为1,2,故选A.点评:本题考查了三视图的知识,左视图是从物体的左面看得到的视图.14.(3分)(2012•天津)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为()A.B.C.D.考点:正方形的性质;勾股定理.专题:压轴题.分析:利用勾股定理求出CM的长,即ME的长,有DE=DG,所以可以求出DE,进而得到DG的长.解答:解:∵四边形ABCD是正方形,M为边DA的中点,∴DM=AD=DC=1,∴CM==,∴ME=MC=,∵ED=EM﹣DM=﹣1,∵四边形EDGF是正方形,∴DG=DE=﹣1.故选D.点评:本题考查了正方形的性质和勾股定理的运用,属于基础题目.二、填空题1.(3分)(2013•天津)如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段AC=BD(答案不唯一).考点:全等三角形的判定与性质.专题:开放型.分析:利用“角角边”证明△ABC和△BAD全等,再根据全等三角形对应边相等解答即可.解答:解:∵在△ABC和△BAD中,,∴△ABC≌△BAD(AAS),∴AC=BD,AD=BC.故答案为:AC=BD(答案不唯一).点评:本题考查了全等三角形的判定与性质,是基础题,关键在于公共边AB的应用,开放型题目,答案不唯一.2.(3分)(2013•天津)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为55 (度).考点:切线的性质.分析:首先连接OA,OB,由PA、PB分别切⊙O于点A、B,根据切线的性质可得:OA⊥PA,OB⊥PB,然后由四边形的内角和等于360°,求得∠AOB的度数,又由圆周角定理,即可求得答案.解答:解:连接OA,OB,∵PA、PB分别切⊙O于点A、B,∴OA⊥PA,OB⊥PB,即∠PAO=∠PBO=90°,∴∠AOB=360°﹣∠PAO﹣∠P﹣∠PBO=360°﹣90°﹣70°﹣90°=110°,∴∠C=∠AOB=55°.故答案为:55.点评:此题考查了切线的性质以及圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.3.(3分)(2013•天津)如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为7 .考点:相似三角形的判定与性质;等边三角形的性质.分析:先根据边长为9,BD=3,求出CD的长度,然后根据∠ADE=60°和等边三角形的性质,证明△ABD∽△DCE,进而根据相似三角形的对应边成比例,求得CE的长度,即可求出AE的长度.解答:解:∵△ABC是等边三角形,∴∠B=∠C=60°,AB=BC;∴CD=BC﹣BD=9﹣3=6;∴∠BAD+∠ADB=120°∵∠ADE=60°,∴∠ADB+∠EDC=120°,∴∠DAB=∠EDC,又∵∠B=∠C=60°,∴△ABD∽△DCE,则=,即=,解得:CE=2,故AE=AC﹣CE=9﹣2=7.故答案为:7.点评:此题主要考查了相似三角形的判定和性质以及等边三角形的性质,根据等边三角形的性质证得△ABD∽△DCE是解答此题的关键.4.(3分)(2012•天津)如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D为⊙O上一点,若∠CAB=55°,则∠ADC的大小为35 (度).考点:圆周角定理.分析:由AB为⊙O的直径,根据直径所对的圆周角是直角,∠ACB=90°,又由直角三角形的两锐角互余,即可求得∠B的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得答案.解答:解:∵AB为⊙O的直径,∴∠ACB=90°,∵∠CAB=55°,∴∠B=90°﹣∠CAB=35°,∴∠ADC=∠B=35°.故答案为:35°.点评:此题考查了圆周角定理与直角三角形的性质.此题难度不大,注意直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用,注意数形结合思想的应用.三、解答题1.(10分)(2014•天津)解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A′C′的位置时,A′C′的长为23.5 m;(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).考点:解直角三角形的应用.专题:应用题.分析:(1)根据中点的性质即可得出A′C′的长;(2)设PQ=x,在Rt△PMQ中表示出MQ,在Rt△PNQ中表示出NQ,再由MN=40m,可得关于x的方程,解出即可.解答:解:(I)∵点C是AB的中点,∴A'C'=AB=23.5m.(II)设PQ=x,在Rt△PMQ中,tan∠PMQ==1.4,∴MQ=,在Rt△PNQ中,tan∠PNQ==3.3,∴NQ=,∵MN=MQ﹣NQ=40,即﹣=40,解得:x≈97.答:解放桥的全长约为97m.点评:本题考查了解直角三角形的应用,解答本题的关键是熟练锐角三角函数的定义,难度一般.2.(8分)(2012•天津)如图,甲楼AB的高度为123m,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到0.1m,取1.73).考点:解直角三角形的应用-仰角俯角问题.分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.解答:解:如图,过点A作AE⊥CD于点E,根据题意,∠CAE=45°,∠DAE=30°.∵AB⊥BD,CD⊥BD,∴四边形ABDE为矩形.∴DE=AB=123.在Rt△ADE中,tan∠DAE=,∴AE====.在Rt△ACE中,由∠CAE=45°,得CE=AE=.∴CD=CE+DE=≈335.8.答:乙楼CD的高度约为335.8m.点评:考查了解直角三角形的应用﹣仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.。
【中考12年】天津市2001-2012年中考数学试题分类解析专题3方程(组)和不等式(组)

结论:
①x1=2, x 2=3;
② m>
1 ;
4
③二次函数 y=( x -x1)( x - x 2)+ m的图象与 x 轴交点的坐标 为( 2, 0)和( 3, 0).
其中,正确结论的个数是【
】
( A) 0 ( B) 1 ( C) 2
( D)3
【答案】 C。
【考点】抛物线与 x 轴的交点,一元二次方程的解,一元二次方程根的判别式和根与系数的关系。
a- b> 0。
故选 D。
2. ( 2001 天津市 3 分) 甲、乙两人骑自行车同时从相距 65km的两地相向而行, 2h 相遇,若甲比乙每小时
多骑 2.5km,则乙的速度是每小时【
】
A. 12.5km
B
. 15km
C . 17.5km
D
.20km
【答案】 B。
【考点】二元一次方程组的应用。
【分析】设甲的速度是每小时 x 千米,乙的速度是每小时 y 千米,
当 a=- 1, b=-2 时,满足 a> b,但 b < 1 不成立; a
当 a=2 , b=1 时,满足 a> b,但 b > 1 不成立; a
当 0>a> b 时,满足 a>b,但- a>- b 不成立;
由 a>b 根据不等式两边加 (或减) 同一个数 (或式子),不等号的方向不变. 两边同时减去 b 得到:
=7.42 (D)
x
y
1326 1326
=7.42
y
x
【答案】 C。
【考点】由实际问题抽象出方程。 【分析】由实际问题抽象出方程解题关键是找出关键描述语和等量关系,列出方程。本题关键描述语是: “由天津到上海的时间缩短了 7.42 小时”,等量关系为:
2012年天津市中考数学试卷-答案

【解析】解;袋中球的总数为: ,取到红球的概率为:
【提示】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【考点】概率公式.
14.【答案】
【解析】“上加下减”的原则可知该函数的解析式可以是: (答案不唯一).
【提示】根据“上加下减”的原则在函数解析式后加一个大于0的数即可.
B.乡村公路总长为 (km),故本选项错误;
C.汽车在乡村公路上的行驶速度为 (km/h),故本选项正确;
D. (h),故该记者在出发后5(h)到达采访地,故本选项错误.
【提示】根据函数的图象和已知条件对每一项分别进行分析,即可得出正确答案.
【考点】函数的图象.
10.【答案】C
【解析】一元二次方程 化为一般形式得: ,∵方程有两个不相等的实数根 、 ,∴ ,解得: ,故选项②正确;
【考点】正方形的性质,全等三角形的判定与性质,勾股定理.
18.【答案】(Ⅰ)
(Ⅱ)见解析
【解析】(Ⅰ)
(Ⅱ)如图,让直尺有刻度一边过点A,设该边与过点B的竖直方向的网格线交于点C,与过点B水平方向的网格线交于点D,保持直尺有刻度的一边过点A,调整点C.D的位置,使 cm,画射线AD,此时 即为所求的 .
【考点】中心对称图形.
3.【答案】C
【解析】 .
【提示】科学记数法的表示形式为 的形式,其中 , 为整数.确定 的值是易错点,由于560000有6位,所以可以确定 .
【考点】科学记数法—表示较大的数.
4.【答案】B
【解析】∵ ,∴ .
【提示】利用“夹逼法”得出 的范围,继而也可得出 的范围.
【考点】估算无理数的大小.
【考点】一次函数图象上点的坐标特征.
华北地区2012年中考数学试题分类解析专题5:综合问题

华北地区2012年中考数学试题(8套)分类解析汇编(6专题)专题5:综合问题锦元数学工作室编辑一、选择题1. (2012天津市3分)若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1≠x2,有下列结论:①x1=2,x2=3;②1m4 >-;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是【】(A)0 (B)1 (C)2 (D)3【答案】C。
【考点】抛物线与x轴的交点,一元二次方程的解,一元二次方程根的判别式和根与系数的关系。
【分析】①∵一元二次方程实数根分别为x1、x2,∴x1=2,x2=3,只有在m=0时才能成立,故结论①错误。
②一元二次方程(x-2)(x-3)=m化为一般形式得:x2-5x+6-m=0,∵方程有两个不相等的实数根x1、x2,∴△=b2-4ac=(-5)2-4(6-m)=4m+1>0,解得:1m4>-。
故结论②正确。
③∵一元二次方程x2-5x+6-m=0实数根分别为x1、x2,∴x1+x2=5,x1x2=6-m。
∴二次函数y=(x-x1)(x-x2)+m=x2-(x1+x2)x+x1x2+m=x2-5x+(6-m)+m=x2-5x+6=(x-2)(x-3)。
令y=0,即(x-2)(x-3)=0,解得:x=2或3。
∴抛物线与x轴的交点为(2,0)或(3,0),故结论③正确。
综上所述,正确的结论有2个:②③。
故选C。
2. (2012河北省3分)如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a-b)等于【】A.7 B.6 C.5 D.4【答案】A。
【考点】整式的加减。
【分析】设重叠部分面积为c,(a-b)可理解为(a+c)-(b+c),即两个正方形面积的差,所以。
A-b=(a+c)-(b+c)=16-9=7。
故选A。
3. (2012内蒙古包头3分)已知下列命题:① 若a≤0 ,则lal =一a ;② 若ma2 > na2,则m > n ;③ 两组对角分别相等的四边形是平行四边形;④ 垂直于弦的直径平分弦.其中原命题与逆命题均为真命题的个数是【】A.1 个 B .2 个 C.3 个 D .4 个【答案】B。
2012年天津中考数学试题及答案

2012年天津市中考数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)(2012•天津)2cos60°的值等于()A. 1 B.C.D. 22.(3分)(2012•天津)下列标志中,可以看作是中心对称图形的是()A.B. C.D.3.(3分)(2012•天津)据某域名统计机构公布的数据显示,截至2012年5月21日,我国“.NET”域名注册量约为560000个,居全球第三位,将560000用科学记数法表示应为()A.560×103B.56×104C. 5.6×105D. 0.56×1064.(3分)(2012•天津)估计的值在()A.2到3之间B.3到4之间C. 4到5之间D. 5到6之间5.(3分)(2012•天津)为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有()A.300名B.400名C. 500名D. 600名6.(3分)(2012•天津)将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是()A.平行四边形B.矩形C.菱形D.正方形7.(3分)(2012•天津)如图是一个由4个相同的正方体组成的立体图形,它的三视图是()A.B.C.D.8.(3分)(2012•天津)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为()A.B.C.D.9.(3分)(2012•天津)某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是()A.汽车在高速公路上的行驶速度为100km/hB.乡村公路总长为90kmC.汽车在乡村公路上的行驶速度为60km/hD.该记者在出发后4.5h到达采访地10.(3分)(2012•天津)若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>﹣;③二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0 B. 1 C. 2 D. 3二、填空题(共8小题,每小题3分,满分24分)11.(3分)(2011•铜仁地区)|﹣3|=_________.12.(3分)(2012•天津)化简的结果是_________.13.(3分)(2012•天津)袋子中装有5个红球和3个黑球,这些球除了颜色外都相同.从袋子中随机的摸出一个球,则它是红球的概率是_________.14.(3分)(2012•天津)将正比例函数y=﹣6x的图象向上平移,则平移后所得图象对应的函数解析式可以是_________(写出一个即可).15.(3分)(2012•天津)如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D为⊙O上一点,若∠CAB=55°,则∠ADC的大小为_________(度).16.(3分)(2012•天津)若一个正六边形的周长为24,则该六边形的面积为_________.17.(3分)(2012•天津)如图,已知正方形ABCD的边长为1,以顶点A、B为圆心,1为半径的两弧交于点E,以顶点C、D为圆心,1为半径的两弧交于点F,则EF的长为_________.18.(3分)(2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=∠MAN.(Ⅰ)当∠MAN=69°时,∠α的大小为_________(度);(Ⅱ)如图,将∠MAN放置在每个小正方形的边长为1cm的网格中,角的一边AM与水平方向的网格线平行,另一边AN经过格点B,且AB=2.5cm.现要求只能使用带刻度的直尺,请你在图中作出∠α,并简要说明做法(不要求证明)_________.三、解答题(共8小题,满分66分)19.(6分)(2012•天津)解不等式组.20.(8分)(2012•天津)已知反比例函数y=(k为常数,k≠1).(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;(Ⅲ)若其图象的一直位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.21.(8分)(2012•天津)在开展“学雷锋社会实践”活动中,某校为了解全校1200名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如图.(Ⅰ)求这50个样本数据的平均数、众数和中位数;(Ⅱ)根据样本数据,估算该校1200名学生共参加了多少次活动?22.(8分)(2012•天津)已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.(Ⅰ)如图①,若∠BAC=25°,求∠AMB的大小;(Ⅱ)如图②,过点B作BD⊥AC于E,交⊙O于点D,若BD=MA,求∠AMB的大小.23.(8分)(2012•天津)如图,甲楼AB的高度为123m,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到0.1m,取1.73).24.(8分)(2012•天津)某通讯公司推出了移动电话的两种计费方式(详情见下表).月使用费/元主叫限定时间/分主叫超时费/(元/分)被叫方式一58 150 0.25 免费方式二88 350 0.19 免费设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:(Ⅰ)用含有t的式子填写下表:t≤150 150<t<350 t=350 t>350方式一计费/元58 _________108 _________方式二计费/元88 88 88 _________(Ⅱ)当t为何值时,两种计费方式的费用相等?(Ⅲ)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可).25.(10分)(2012•天津)已知一个矩形纸片OACB,将该纸片放置在平面直角坐标洗中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).26.(10分)(2012•天津)已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,y A)、B(0,y B)、C(﹣1,y C)在该抛物线上.(Ⅰ)当a=1,b=4,c=10时,①求顶点P的坐标;②求的值;(Ⅱ)当y0≥0恒成立时,求的最小值.2012年天津市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.3分)(2012•天津)2cos60°的值等于()A.( 1 B.C.D. 2故选A.点评:本题考查了特殊角的三角函数值,熟记30°、45°、60°角的三角函数值是解题的关键.2.(3分)(2012•天津)下列标志中,可以看作是中心对称图形的是()A.B.C.D.考点:中心对称图形。
2012年天津中考数学真题卷含答案解析

2012年天津市初中毕业生学业考试试卷数学2A(满分:120分 时间:100分钟)第Ⅰ卷(选择题,共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.2cos 60°的值等于( )A.1B.√2 C .√3 D .22.下列标志中,可以看作是中心对称图形的是( )3.据某域名统计机构公布的数据显示,截至2012年5月21日,我国“.NET ”域名注册量约为560 000个,居全球第三位.将560 000用科学记数法表示应为( ) A.560×103B.56×104C.5.6×105D.0.56×1064.估计√6+1的值在( )A.2到3之间B.3到4之间C.4到5之间D.5到6之间5.为调查某校2 000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( )A.300名B.400名C.500名D.600名6.将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是()A.平行四边形B.矩形C.菱形D.正方形7.如图是一个由4个相同的正方体组成的立体图形,它的三视图是()8.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE 为边作正方形DEFG,点G在边CD上,则DG的长为()A.√3-1B.3-√5C.√5+1D.√5-19.某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是()A.汽车在高速公路上的行驶速度为100km/hB.乡村公路总长为90kmC.汽车在乡村公路上的行驶速度为60km/hD.该记者在出发后4.5h到达采访地10.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>-14;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0B.1 C.2 D.3第Ⅱ卷(非选择题,共90分)二、填空题(本大题共8小题,每小题3分,共24分)11.|-3|=.12.化简x(x-1)2-1(x-1)2的结果是.13.袋子中装有5个红球和3个黑球,这些球除了颜色外都相同.从袋子中随机地摸出1个球,则它是红球的概率是.14.将正比例函数y=-6x的图象向上平移,则平移后所得图象对应的函数解析式可以是(写出一个即可).15.如图,△ABC是☉O的内接三角形,AB为☉O的直径,点D为☉O上一点,若∠CAB=55°,则∠ADC的大小为(度).16.若一个正六边形的周长为24,则该正六边形的面积为.17.如图,已知正方形ABCD的边长为1,以顶点A、B为圆心,1为半径的两弧交于点E,以顶点C、D为圆心,1为半径的两弧交于点F,则EF的长为.∠MAN.18.“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=13(Ⅰ)当∠MAN=69°时,∠α的大小为(度);(Ⅱ)如图,将∠MAN放置在每个小正方形的边长为1cm的网格中,角的一边AM与水平方向的网格线平行,另一边AN经过格点B,且AB=2.5cm.现要求只能使用带刻度...的直尺,请你在图中作出∠α,并简要说明作法(不要求证明).三、解答题(本大题共8小题,共66分.解答应写出文字说明、演算步骤或推理过程)19.(本小题6分)解不等式组{3x+1>x+3,2x-1<x+1.20.(本小题8分)(k为常数,k≠1).已知反比例函数y=k-1x(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.2B21.(本小题8分)在开展“学雷锋社会实践”活动中,某校为了解全校1200名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如下:(Ⅰ)求这50个样本数据的平均数、众数和中位数;(Ⅱ)根据样本数据,估算该校1200名学生共参加了多少次活动.22.(本小题8分)已知☉O中,AC为直径,MA、MB分别切☉O于点A、B.(Ⅰ)如图①,若∠BAC=25°,求∠AMB的大小;(Ⅱ)如图②,过点B作BD⊥AC于点E,交☉O于点D,若BD=MA,求∠AMB的大小.23.(本小题8分)如图,甲楼AB的高度为123m,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到0.1m,√3取1.73).24.(本小题8分)某通讯公司推出了移动电话的两种计费方式(详情见下表).月使用主叫限主叫超时被叫费/元定费/(元/分)时间/分方式一581500.25免费方式二883500.19免费设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:(Ⅰ)用含有t的式子填写下表:t≤150150<t<350t=350t>350方式一计费/元58108方式二计费/元888888(Ⅱ)当t为何值时,两种计费方式的费用相等;(Ⅲ)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可).25.(本小题10分)已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B'和折痕OP.设BP=t.(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB'上,得点C'和折痕PQ,若AQ=m,试用含有t的式子表示m;(Ⅲ)在(Ⅱ)的条件下,当点C'恰好落在边OA上时,求点P的坐标(直接写出结果即可).2012年天津市初中毕业生学业考试试卷一、选择题,所以2cos60°=1,故选A.1.A因为cos60°=12评析考查学生特殊角的三角函数值的掌握情况,熟记特殊角的三角函数值是解答关键. 2.B因为只有选项B中的图形绕着某一点旋转180°后可以与它本身重合,所以按照中心对称图形的定义,知选B.3.C对于绝对值大于等于1的实数,科学记数法a×10n中,1≤|a|<10,n比原数的整数位数少1,故选C.4.B√4<√6<√9,故2<√6<3.故3<√6+1<4,故选B.评析本题考查学生对根式形式的无理数取值范围的估算能力.5.B由扇形统计图中其他四项所占的百分比可以求出喜欢体育类节目的人数所占的百分比为100%-30%-10%-5%-35%=20%,2000×20%=400,故选B.评析本题考查学生从扇形统计图中获取信息的能力和用样本估计总体的数学思想.6.D平行四边形、矩形、菱形、正方形四种图形中,只有正方形的对角线互相平分、相等且垂直,故只有正方形绕其对角线交点逆时针旋转90°能与自身重合,故选D.7.A根据三视图的定义以及画三视图时对三种视图的位置要求,只有A选项正确,故选A.8.D正方形ABCD的边长为2,M为AD的中点,故MD=1,在Rt△MDC中,根据勾股定理可得MC=√5,因为ME=MC,故ME=√5,DE=√5-1,因为四边形DEFG是正方形,所以DG=DE=√5-1,故选D.9.C在函数图象中,直线的倾斜度越大,说明汽车的速度越大.由图象可得:高速公路为前180 km,汽车在高速公路上行驶了2小时,故汽车在高速公路上的速度应为90km/h,故A错.高速公路长180km,总长为360km,所以乡村公路应该也为180km,故B错.从图象中可以明显地看出,汽车在乡村公路上行驶90km用了1.5小时,故汽车在乡村公路上的速度为60km/h,故C正确.行驶了270km,后边还剩90km,以60km/h的速度行驶还需要1.5小时,故记者从出发到达采访地共需要5小时,所以D选项也是错误的.故选C.评析本题考查的是学生从函数图象中获取信息的能力以及速度、时间、路程的有关计算.10.C很明显,①只有在m=0的时候才成立.根据题意可得,方程(x-2)(x-3)=m的判别式大于零,解得m>-14,故②正确.整理y=(x-x1)(x-x2)+m可得,y=x2-(x1+x2)x+x1x2+m,整理(x-2)(x-3)=m 得,x2-5x+6-m=0,根据根与系数的关系可得,x1+x2=5,x1x2=6-m,把这两个式子代入函数式y=x2-(x1+x2)x+x1x2+m得y=x2-5x+6,令y=0,得方程x2-5x+6=0,解方程可得,x1=2,x2=3.即得二次函数y=(x-x1)(x-x2)+m与x轴的交点坐标为(2,0),(3,0),故③正确.两个结论正确,故应该选C.评析本题综合考查了一元二次方程判别式、一元二次方程根与系数的关系、二次函数图象和x轴交点坐标等多个知识点.属较难题.二、填空题11.答案3解析因为负数的绝对值是它的相反数,故填3.12.答案1x-1解析x(x-1)2-1(x-1)2=x-1(x-1)2=1x-1.13.答案58解析根据概率的定义可得,摸出的球是红球的概率为58.14.答案y=-6x+1(答案不唯一,可以是形如y=-6x+b,b>0的一次函数)解析y=kx+b的图象的位置由k、b的正负决定,k表示直线的倾斜方向,k值相同的直线互相平行,因为是平移,故k值还是-6,b表示直线与y轴交点的纵坐标,因为是向上平移,故直线与y轴交点在y轴的正半轴上,所以b值取任意的一个正数都可以.评析本题重点考查一次函数的图象中k、b的几何意义.15.答案35解析因为AB是圆的直径,故∠ACB=90°,因为∠CAB=55°,所以∠CBA=35°,又因为∠ADC 和∠CBA是同一条弧所对的圆周角,故∠ADC=∠CBA=35°.16.答案24√3解析连结正六边形中心与六个顶点,把正六边形分成六个全等的三角形,每一个三角形都×42=4√3,故正六边形的面积为是边长为4的正三角形,每一个正三角形的面积S=√344√3×6=24√3.评析本题重点考查“把求正六边形的面积转化为求正三角形的面积”这一做题技巧,多边形的问题经常会转化成三角形的问题来解决,此技巧是数学中转化思想的具体体现.17.答案√3-1解析连结EA、EB,则△EAB是边长为1的正三角形,延长EF交AB于点G,根据圆及正三,连结FC、FD,延长FE交CD 角形的对称性,EG为正三角形EAB的边AB上的高,得EG=√32,故EF=EG+FH-1=√3-1.于H,同理可得FH=√32评析本题重点考查圆、正三角形的对称性,另外用EF=EG+FH-GH来求EF的长度也是一种常用的数学解题技巧.18.答案(Ⅰ)23;(Ⅱ)如图,让直尺有刻度的一边过点A,设该边与过点B的竖直方向的网格线交于点C,与过点B的水平方向的网格纸交于点D;保持直尺有刻度的一边过点A,调整点C、D的位置,使CD=5cm,画射线AD,此时∠MAD即为所求的∠α解析(Ⅰ)∠α=1×69°=23°.3(Ⅱ)设点E是CD的中点,根据已知可得BE=DE=AB=2.5cm,∴∠1=∠2=2∠D,又∵BD∥AM,∴∠1=2∠3,即∠α=13∠MAN.三、解答题19.解析{3x+1>x+3,①2x-1<x+1,②解不等式①,得x>1.解不等式②,得x<2.∴原不等式组的解集为1<x<2.20.解析(Ⅰ)由题意,设点P的坐标为(m,2),∵点P在正比例函数y=x的图象上,∴2=m,即m=2.∴点P的坐标为(2,2).∵点P在反比例函数y=k-1x的图象上,∴2=k-12,解得k=5.(Ⅱ)∵在反比例函数y=k-1x图象的每一支上,y随x的增大而减小,∴k-1>0,解得k>1.(Ⅲ)∵反比例函数y=k-1x图象的一支位于第二象限,∴在该函数图象的每一支上,y随x的增大而增大.∵点A(x1,y1)与点B(x2,y2)在该函数的第二象限的图象上,且y1>y2,∴x1>x2.21.解析(Ⅰ)观察条形统计图,可知这组样本数据的平均数是x=1×3+2×7+3×17+4×18+5×550=3.3,∴这组样本数据的平均数是3.3.∵在这组样本数据中,4出现了18次,出现的次数最多,∴这组数据的众数是4.∵将这组样本数据按从小到大的顺序排列,其中处在中间的两个数都是3,有3+32=3,∴这组数据的中位数是3.(Ⅱ)∵这组样本数据的平均数是3.3,∴估计全校1200人参加活动次数的总体平均数是3.3,有3.3×1200=3960.∴该校学生共参加活动约3960次.评析本题重点考查平均数、众数、中位数的意义,从条形统计图中获取信息的能力以及用样本估计总体的数学思想.学生在解答本题的时候,一部分同学由于理解不清平均数的概念或者是看不明白条形图,容易把平均数错算成(3+7+17+18+5)÷50.22.解析(Ⅰ)∵MA切☉O于点A,有∠MAC=90°.又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°.∵MA、MB分别切☉O于点A、B,∴MA=MB,有∠MAB=∠MBA.∴∠AMB=180°-(∠MAB+∠MBA)=50°.(Ⅱ)如图,连结AD、AB.∵MA⊥AC,又BD⊥AC,∴BD∥MA.又BD=MA,∴四边形MADB是平行四边形.∵MA=MB,∴四边形MADB是菱形,有AD=BD.又AC为直径,AC⊥BD,得AB⏜=AD⏜,有AB=AD.∴△ABD是等边三角形,有∠D=60°.∴在菱形MADB中,∠AMB=∠D=60°.评析本题综合考查了切线长定理、垂径定理、切线的性质定理等圆的有关性质和定理,平行四边形、菱形性质和判定的熟练运用以及综合所学知识解决数学问题的能力也是本题考查的一个重点.23.解析如图,过点A作AE⊥CD于点E,根据题意,∠CAE=45°,∠DAE=30°.∵AB⊥BD,CD⊥BD,∴四边形ABDE为矩形.∴DE=AB=123.在Rt△ADE中,tan∠DAE=DEAE,∴AE=DEtan∠DAE =123tan30°=√33=123√3.在Rt △ACE 中,由∠CAE=45°,得CE=AE=123√3.∴CD=CE+DE=123(√3+1)≈335.8.答:乙楼CD 的高度约为335.8 m. 评析 本题重点考查利用三角函数解直角三角形的能力,巧作辅助线、巧妙架起条件和结论之间的桥梁也是本题考查的一个重点.24.解析 (Ⅰ)当150<t<350时,方式一:0.25t+20.5;当t>350时,方式一:0.25t+20.5;方式二:0.19t+21.5.(Ⅱ)∵当t>350时,(0.25t+20.5)-(0.19t+21.5)=0.06t-1>0,∴当两种计费方式的费用相等时,t 的值在150<t<350取得.∴列方程0.25t+20.5=88,解得t=270.答:当主叫时间为270分时,两种计费方式的费用相等.(Ⅲ)方式二.25.解析 (Ⅰ)根据题意,∠OBP=90°,OB=6,在Rt △OBP 中,由∠BOP=30°,BP=t,得OP=2t. 根据勾股定理,OP 2=OB 2+BP 2,即(2t)2=62+t 2,解得t=2√3(t=-2√3舍去).∴点P 的坐标为(2√3,6).(Ⅱ)∵△OB'P 、△QC'P 分别是由△OBP 、△QCP 折叠得到的,有△OB'P ≌△OBP,△QC'P ≌△QCP.∴∠OPB'=∠OPB,∠QPC'=∠QPC.∵∠OPB'+∠OPB+∠QPC'+∠QPC=180°,∴∠OPB+∠QPC=90°.∵∠BOP+∠OPB=90°,∴∠BOP=∠CPQ.又∠OBP=∠C=90°,∴△OBP ∽△PCQ,有OB PC =BP CQ. 由题设BP=t,AQ=m,BC=11,AC=6,则PC=11-t,CQ=6-m.∴611-t =t 6-m.∴m=16t2-116t+6(0<t<11)即为所求.(Ⅲ)点P的坐标为(11-√133,6)或(11+√133,6).评析本题重点考查图形的折叠、较复杂图形中相似三角形的判定及性质的综合应用能力.26.解析(Ⅰ)a=1,b=4,c=10,此时抛物线的解析式为y=x2+4x+10.①∵y=x2+4x+10=(x+2)2+6,∴抛物线的顶点坐标为P(-2,6);②∵点A(1,y A)、B(0,y B)、C(-1,y C)在抛物线y=x2+4x+10上,∴y A=15,y B=10,y C=7.∴y Ay B-y C =1510-7=5.(Ⅱ)由0<2a<b,得x0=-b2a<-1.由题意,如图,过点A作AA1⊥x轴于点A1,则AA1=y A,OA1=1.连结BC,过点C作CD⊥y轴于点D,则BD=y B-y C,CD=1.过点A作AF∥BC,交抛物线于点E(x1,y E),交x轴于点F(x2,0),则∠FAA1=∠CBD.于是Rt△AFA1∽Rt△BCD.有AA1BD =FA1CD,即y Ay B-y C=1-x21=1-x2.过点E作EG⊥AA1于点G,易得△AEG∽△BCD.有AGBD =EGCD,即y A-y Ey B-y C=1-x1.∵点A(1,y A)、B(0,y B)、C(-1,y C)、E(x1,y E)在抛物线y=ax2+bx+c上,得y A=a+b+c,y B=c,y C=a-b+c,y E=a x12+bx1+c,∴(a+b+c)-(ax12+bx1+c)c-(a-b+c)=1-x1.化简,得x12+x1-2=0,解得x1=-2(x1=1舍去).∵y0≥0恒成立,根据题意,有x2≤x1<-1,则1-x2≥1-x1,即1-x2≥3.∴y Ay B-y C的最小值为3.评析本题重点考查综合运用二次函数、三角形相似的知识解决较复杂的数学问题的能力,二次函数的顶点坐标和增减性也是本题考查的一个内容,题目综合性较强,难度较大.26.(本小题10分)已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,y A)、B(0,y B)、C(-1,y C)在该抛物线上.的值;(Ⅰ)当a=1,b=4,c=10时,①求顶点P的坐标;②求y Ay B-y C的最小值.(Ⅱ)当y0≥0恒成立时,求y Ay B-y C。
全国各地2012年中考数学分类解析(159套)专题9:一元二次方程

2012年全国中考数学试题分类解析汇编(159套63专题)专题9:一元二次方程一、选择题1. (2012天津市3分)若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1≠x2,有下列结论:①x1=2,x2=3;②1m4>-;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是【】(A)0 (B)1 (C)2 (D)3【答案】C。
【考点】抛物线与x轴的交点,一元二次方程的解,一元二次方程根的判别式和根与系数的关系。
【分析】①∵一元二次方程实数根分别为x1、x2,∴x1=2,x2=3,只有在m=0时才能成立,故结论①错误。
②一元二次方程(x-2)(x-3)=m化为一般形式得:x2-5x+6-m=0,∵方程有两个不相等的实数根x1、x2,∴△=b2-4ac=(-5)2-4(6-m)=4m+1>0,解得:1m4>-。
故结论②正确。
③∵一元二次方程x2-5x+6-m=0实数根分别为x1、x2,∴x1+x2=5,x1x2=6-m。
∴二次函数y=(x-x1)(x-x2)+m=x2-(x1+x2)x+x1x2+m=x2-5x+(6-m)+m =x2-5x+6=(x-2)(x-3)。
令y=0,即(x-2)(x-3)=0,解得:x=2或3。
∴抛物线与x轴的交点为(2,0)或(3,0),故结论③正确。
综上所述,正确的结论有2个:②③。
故选C。
2. (2012广东佛山3分)用配方法解一元二次方程x2-2x-3=0时,方程变形正确的是【】 A.(x-1)2=2 B.(x-1)2=4 C.(x-1)2=1 D.(x-1)2=7【答案】B。
【考点】用配方法解一元二次方程。
【分析】由x2-2x-3=0移项得:x2-2x=3,两边都加上1得:x2-2x+1=3+1,即(x-1)2=4。
则用配方法解一元二次方程x 2-2x -3=0时,方程变形正确的是(x -1)2=4。
2012年中考数学分类解析(159套63专题)专题26_数据的分析与整理

2012年全国中考数学试题分类解析汇编(159套63专题)专题26:数据的分析与整理祝您中考顺利!一、选择题1. (2012北京市4分)某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:用电量(度)120 140 160 180 200 户数 2 3 6 7 2 则这20户家庭该月用电量的众数和中位数分别是【】A.180,160 B.160,180 C.160,160 D.180,180【答案】A。
【考点】众数,中位数。
【分析】众数是在一组数据中,出现次数最多的数据,这组数据中,出现次数最多的是180,故这组数据的众数为180。
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)。
由此将这组数据重新排序为120,120,140,140,140,160,160,160,160,160,160,180,180,180,180,180,180,180,200,200,∴中位数是第10和11个平均数,它们都是160,故这组数据的中位数为160。
故选A。
2. (2012天津市3分)为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有【】(A)300名(B)400名(C)500名(D)600名【答案】B。
【考点】扇形统计图,用样本估计总体。
【分析】根据扇形图可以得出该校喜爱体育节目的学生所占比例:1-5%-35%-30%-10%=20%,从而根据用样本估计总体得出该校喜爱体育节目的学生数目:2000×20%=400。
故选B。
3. (2012上海市4分)数据5,7,5,8,6,13,5的中位数是【】A. 5 B. 6 C. 7 D. 8【答案】B。
【考点】中位数。
【分析】中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)。
全国各地2012年中考数学分类解析(159套)专题29:投影与视图
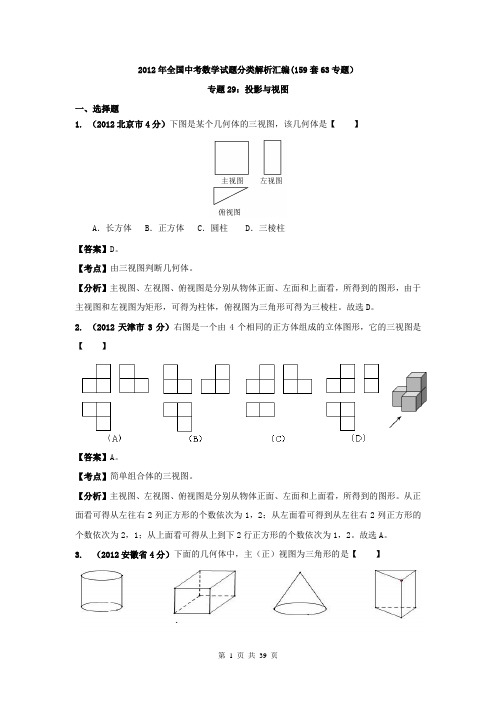
2012年全国中考数学试题分类解析汇编(159套63专题)专题29:投影与视图一、选择题1. (2012北京市4分)下图是某个几何体的三视图,该几何体是【】A.长方体 B.正方体 C.圆柱 D.三棱柱【答案】D。
【考点】由三视图判断几何体。
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,由于主视图和左视图为矩形,可得为柱体,俯视图为三角形可得为三棱柱。
故选D。
2. (2012天津市3分)右图是一个由4个相同的正方体组成的立体图形,它的三视图是【】【答案】A。
【考点】简单组合体的三视图。
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形。
从正面看可得从左往右2列正方形的个数依次为1,2;从左面看可得到从左往右2列正方形的个数依次为2,1;从上面看可得从上到下2行正方形的个数依次为1,2。
故选A。
3. (2012安徽省4分)下面的几何体中,主(正)视图为三角形的是【】A. B. C.D.【答案】C。
【考点】判断立体图形的三视图。
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形。
因此,根据这几个常见几何题的视图可知:圆柱的主视图是矩形,正方体的主视图是正方形,圆锥的主视图是三角形,三棱柱的主视图是宽相等两个相连的矩形。
故选C。
4. (2012山西省2分)如图所示的工件的主视图是【】A. B. C. D.【答案】B。
【考点】简单组合体的三视图。
【分析】从物体正面看,看到的是一个横放的矩形,且一条斜线将其分成一个直角梯形和一个直角三角形。
故选B。
5. (2012海南省3分)如图竖直放置的圆柱体的俯视图是【】A.长方体 B.正方体 C.圆 D.等腰梯形【答案】C。
【考点】简单组合体的三视图。
【分析】找到从上面看所得到的图形即可:从上面看易得是圆。
故选C。
6. (2012陕西省3分)如图,是由三个相同的小正方体组成的几何体,该几何体的左视图是【】A. B. C. D.【答案】C。
