图的最小生成树

合集下载

图以及最小生成树和最短路径

图的连通在无向图G中，若两个顶点vi和vj之间有
路径存在，则称vi 和vj 是连通的。若G中任意两个顶点都是连通的，则称G为连通图。非连通图的极大连通子图叫做连通分量。

强连通图与强连通分量在有向图中, 若对于每一对顶点vi和vj, 都存在一条从vi到vj和从vj到vi的路径, 则称此图是强连通图。非强连通图的极大强连通子图叫做强连通分量。
顶点结点 Data firstin firstout 弧结点 tailvex headvex info hlink tlink
图9-12 十字链表结点结构
◆ data域：存储和顶点相关的信息；
◆ 指针域firstin：指向以该顶点为弧头的第一条弧所对应的弧结点；
◆ 指针域firstout：指向以该顶点为弧尾的第一条弧所对应的弧结点； ◆ 尾域tailvex：指示弧尾顶点在图中的位置；
a
2 6 3 1

b 3
4 5
e
c
d
(a) 带权无向图
vexs a b c d e
∞ 6 2 ∞ ∞
6 2 ∞ ∞ 3 4 3 ∞ 1 4 3 ∞ 3 ∞ 5
∞ 3 ∞ 5 ∞
(b) 顶点矩阵 (c) 邻接矩阵图9-6 无向带权图的数组存储
(3) 无向图邻接矩阵的特性
◆ 邻接矩阵是对称方阵； ◆ 对于顶点vi，其度数是第i行的非0元素的个数；
(b) 顶点矩阵
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0
(a) 无向图
(c) 邻接矩阵
图9-5 无向无权图的数组存储
(2) 带权图的邻接矩阵
无向带权图G=(V，E) 的邻接矩阵如图9-6所示。其元素的定义如下： Wij 若(vi , vj)E，即vi , vj邻接，权值为wij A[i][j]= ∞ 若(vi , vj)E，即vi , vj不邻接时

最小生成树例子

最小生成树例子
最小生成树是一个在图论中常见的问题，通常在计算机网络和电路设计中出现。

它是指一个连通无环图，它的一棵生成树，如果再添加任何一条边都会产生环。

以下是一个简单的最小生成树的例子：
假设我们有一个由五个节点（A、B、C、D、E）和七条边组成的网络，每条边的权重表示连接两个节点所需的成本或距离。

节点 A - B: 3
节点 A - C: 5
节点 A - D: 6
节点 B - C: 4
节点 B - D: 7
节点 C - D: 8
节点 C - E: 2
节点 D - E: 9
节点 E - A: 10
我们可以使用Kruskal算法或Prim算法找到这个图的最小生成树。

在这个例子中，最小生成树可能是：A - B - C - D - E，总权重为18。

这是所有可能的生成树中权重最小的。

需要注意的是，这个结果可能会因图的结构和使用的算法而变化。

在实际应用中，可能还需要考虑其他因素，如网络的拓扑结构、流量需求等。

数据结构15--最小生成树PPT课件

proc Union(i,j,c:longint); /*合并i和j所在集合 */
Var x,y:longint;
{ x←top(i); y←top(j); 点j所在子树的根*/
/*分别取出顶点i和顶
if x<>y Then { inc(ans,c);f[y]←x;}; /*若i 和j分属于两棵子树，则该边权计入最小生成树的权和，两棵子树合并*/
Writeln(ans);
显然, Kruskal算法的效率取决于边数m,因此适用与
稀疏图。
.
②、Prim算法
集合A中的边总是只形成单棵树，每次添加到树中的边都是使树的权尽可能小的边。
.
设 d[i]—顶点i与生成树相连的最短边长； ba[i]—顶点i在生成树的标志； w[i,j]—（i,j）的边长。若图中不存在边（i,j），则w[i,j]=∞ min—所有未在生成树的顶点的最小距离值
top←f[i]; /*返回顶点i所在并查集的代表顶点*/ };/*top*/
.
通过过程Union(i,j,c)合并顶点i和顶点j所在的两棵树
现有边权为c的边（i，j）。若该边的两个端点分属于两棵树，顶点i和顶点j所在子树的根分别为x和v，则(i,j) 加入最小生成树，合并两棵树（即顶点i和顶点j所在的并查集）。
for j←1 to n do
if not ba[j]and(d[j]<min) then { k←j；min←d[j] }； /*then*/
if min= maxint then { ans←-1；break；}；/*若这样的顶点不存在，则无解退出*/
ans←ans+min；ba[k]←true；/*最小距离值min计入生成树的权和, 顶点k进入生成树*/

最小生成树和最短路径 -回复

最小生成树和最短路径-回复什么是最小生成树和最短路径？如何确定它们？这两个概念通常在计算机科学中被广泛应用于解决图论中的相关问题。

在这篇文章中，我们将一步一步地回答这些问题。

首先，让我们来了解最小生成树是什么。

在图论中，最小生成树是一个连通无向图的生成树，其所有边的权重之和最小，并且包含该图的所有顶点。

生成树是一种树状结构，它是由图中所有的顶点以及它们之间的一些边组成，并且这些边必须满足以下条件：它们连接图中的不同顶点，并且不形成环。

为了更好地理解这个定义，让我们通过一个简单的例子来说明最小生成树的概念。

假设我们有一个城市网络，城市之间的路径可以用边来表示，边上的权重表示两个城市之间的距离。

现在我们的目标是建设一条最小的路径，连接这些城市，使得整个网络的总距离最小。

这条路径就是最小生成树。

那么如何确定最小生成树呢？在解决这个问题时，我们可以使用一些经典的算法，其中最著名的是普里姆算法和克鲁斯卡尔算法。

普里姆算法是一种贪心算法，在每一步中选择一个顶点并将其加入最小生成树中，然后选择一个连通该顶点的边权重最小的顶点，将其也加入最小生成树中。

这个过程会一直重复，直到所有的顶点都被添加到最小生成树中。

克鲁斯卡尔算法也是一种贪心算法，它首先将所有的边按权重进行排序，然后从最小权重的边开始，依次将边添加到最小生成树中，直到所有的顶点都被连接起来。

在添加每一条边时，需要判断是否会形成环，如果会形成环，则不选择该边。

当然，最小生成树不止有普里姆算法和克鲁斯卡尔算法这两种求解方法，还有其他一些算法，例如克鲁斯卡尔算法的变体Prim-Dijkstra算法和Boruvka算法等等。

每种算法都有其自身的特点和适用场景，根据具体的问题需求选择合适的算法进行求解。

接下来，让我们来了解最短路径是什么。

在一个加权有向图中，最短路径是指两个顶点之间的路径，其边的权重之和最小。

最短路径问题在计算机科学中有许多应用，例如导航系统、网络路由以及大规模数据处理等领域。

图的常用算法——最小生成树

TE= {（V1，V4）5，（V4，V2）3 ，（V4，V6）7，
（V6，V3）2 ，（V3，V5）6 } LW= {（V4，V7）15
9
第六次 U={ V1，V4，V2 ，V6，V3 ，V5，V7 } TE= {（V1，V4）5，（V4，V2）3 ，（V4，V6）7，（V6，V3）2 ，（V3，V5）6}，（V4，V7）15 } LW= { }
3
5
7
20
所以最小生成树由GE数组中的1，2，3，5，7 边组成。 2012-1-10
2012-1-10
10
2012-1-10
11
（4）算法如下： Procedure Prim(GA,CT); begin for I:=1 to n-1 do { 给CT赋初值，对应第0次的LW值 } [ CT[I].from :=1 ; ct[I].end: =I+1 ; ct[I].w:=GA[1, i+1 ]; for k:=1 to n-1 do { 进行n-1次循环，求出最小生成树的第K条边 } ①[ min:=maxint ; m:=k ; for j:=k to n-1 do if ct[j].w < min then min:=ct[j].w ; m:=j; ] ② if m<> k then ct[k] 与ct[m] 的交换 { 将最短边调到第K单元 }
1. 从图“G”的选取一个顶点放到“G’” 中，因只有一个顶点，因此该图是连通的； 2. 以后每加入一个顶点，都要加入以该点为顶点与已连通的顶点之中的一个顶点为端点的一条边，使其既连通而不产生回路，进行n-1次后，就产生G’，在G’ 中有n个顶点，n-1条边且不产生回路。
二、图的最小生成树

最小生成树唯一的充要条件

最小生成树唯一的充要条件最小生成树是一种在图论中常见的概念，它是一个连通无向图中的一棵生成树，其所有边的权值之和最小。

在实际应用中，最小生成树有着广泛的应用，比如在通信网络、电力网络和交通运输等领域。

要确定一个图的最小生成树是否唯一，需要满足以下充要条件：图中的每条边的权值互不相同。

这个条件是非常重要的，因为只有当图中的每条边的权值都不相同时，才能确保最小生成树的唯一性。

如果图中存在两条或多条边的权值相同，那么可能会有多个最小生成树。

为了更好地理解最小生成树唯一的充要条件，我们可以通过一个简单的例子来说明。

假设有一个无向图，其中包含4个顶点A、B、C、D，以及4条边AB、AC、BC、BD。

如果这些边的权值分别为1、2、3、4，那么根据最小生成树的算法，我们可以得到唯一的最小生成树，即连接顶点A、B、C的边AB、AC。

因为在这种情况下，每条边的权值都不相同，所以最小生成树是唯一的。

相反，如果图中存在两条或多条边的权值相同，那么就会出现多个最小生成树的情况。

比如，如果在上面的例子中，边AC的权值改为1，那么就会有两个最小生成树，一个是连接顶点A、B、C的边AB、AC，另一个是连接顶点A、C、D的边AC、CD。

这是因为存在两条权值相同的边AB和AC，所以会有多个最小生成树。

因此，最小生成树的唯一性与图中每条边的权值是否相同密切相关。

只有当图中的每条边的权值都不相同时，最小生成树才是唯一的。

这个充要条件在实际应用中非常重要，因为只有满足这个条件，我们才能准确地求解出最小生成树，从而优化网络结构，提高效率。

最小生成树唯一的充要条件是图中的每条边的权值互不相同。

只有当图中的每条边的权值都不相同时，最小生成树才是唯一的。

这个条件在实际应用中非常重要，因为只有满足这个条件，我们才能准确地求解出最小生成树，从而优化网络结构，提高效率。

希望通过本文的介绍，读者能够更好地理解最小生成树的唯一性条件，为实际应用提供参考。

图论-最小生成树

图论算法二、最小生成树算法.什么是图的最小生成树（MST）？不知道大家还记不记得关于树的一个定理：N个点用N-1条边连接起来，形成的图形只可能是树，没有别的可能。

一个有N个点的图，边一定是大于等于N-1条的。

图的最小生成树，就是在这些边中选择N-1条出来，连接所有的N个点。

这N-1条边的边权之和是所有方案中最小的。

.最小生成树用来解决什么问题？就是用来解决如何用最小的“代价”用N-1条边连接N个点的问题。

例如：城市公交网建设问题[问题描述]有一张城市地图，图中的顶点为城市，无向边代表两个城市间的连通关系，边上的权为在这两个城市之间修建高速公路的造价，研究后发现，这个地图有一个特点，即任一对城市都是连通的。

现在的问题是，要修建若干高速公路把所有城市联系起来，问如何设计可使得工程的总造价最少？.1.Prim算法根据图的基本定义，一个有n个点的图，它的最小生成树必定含有n个点，（n-1）条边。

prime算法所采取的是每条向树中添加的边，都采取贪心算法选取权值最小的进行。

2).算法时间复杂度：O (N算法描述：假设从s点开始生成最小生成树（一般s都设为1），dis[v]表示从v点到已生成的树的最短路径,w[I,j]表示i到j的距离，如果i，j不相连就设为无穷大。

pre[v]为v的前驱节点，用来输出进入最小生成树的边。

a)初始化：dis[v]=maxint(v≠s); dis[s]=0; pre[s]=s; 起点s标记为未进入最小生成树; tot=0;b)For i:=1 to n1.在没有进入最小生成树的点中找一个到树的距离（dis[u]）最小的点u。

2.u标记为已经进入最小生成树3.tot = tot + dis[u];4.For 与u相连的每个未进入最小生成树的顶点v doif w[u,v]<dis[v] thenbegindis[v]:=w[u,v];pre[v]:=u;end；c)算法结束：tot为最小生成树的总权值；pre[v]为v的前驱节点，用来输出进入最小生成树的边。

最小生成树算法详解

Kruskal算法的核心是使用并查集来维护连通性，当一条边的两个顶点属于不同的连通分量时，将这条边加入到生成树中，同时将两个连通分量合并为一个连通分量，直到所有的连通分量都被合并为一个连通分量，生成树构建完毕。
算法步骤
初始化
将所有的边按照权值从小到大排序，初始化并查集和生成树。
选择边
从最小的边开始，依次选择每一条边，如果这条边的两个顶点属于不同的连通分量，将这条边加入到生成树中，并将两个连通分量合并为一个连通分量。
最小生成树算法详解
xx年xx月xx日
目录
• 最小生成树概述 • 普里姆算法（Prim算法） • 克鲁斯卡尔算法（Kruskal算法） • 最小生成树算法比较 • 最小生成树算法实践
01
最小生成树概述
定义与性质
定义
最小生成树是一个图的所有顶点连接起来形成的树，其所有边的权重之和最小。
性质
最小生成树是一种最优树，它代表了从图中所有顶点中选择一些顶点，使得这些顶点之间连接的边的权重之和最小。
重复选择
重复以上步骤，直到所有的边都被考虑过，生成树构建完毕。
Kruskal算法的拓展与优化
拓展
Kruskal算法适用于任何连通的带权图，不仅限于树和森林。
优化
在实现Kruskal算法时，可以通过优化查找和排序算法来提高效率。例如，使用并查集的路径压缩和按秩合并优化来减少查找和合并操作的时间复杂度。
01
图论
最小生成树算法是图论中的一个经典问题，需要使用图的数据结构来
表示和解决问题。
02
并查集
并查集是一种用于处理不相交集合的数据结构，可以高效地解决最小
生成树算法中的连通性问题。
03

图的最短路径与最小生成树

图的最短路径与最小生成树在图论中，最短路径和最小生成树是两个重要的概念，它们在解决实际问题中具有广泛的应用。

最短路径指的是在图中找到连接两个节点的路径中权重之和最小的路径；最小生成树则是指在一个连通图中找到一个生成树，所有边的权重之和最小。

一、最短路径在图中，每个节点可以看作一个点，边可以看作连接这些点的路径。

而这些边上的权重则表示了路径的长度或者消耗。

最短路径算法可以帮助我们找到连接两个节点之间最短的路径。

最短路径算法有很多种，其中最著名的是迪杰斯特拉算法和弗洛伊德算法。

迪杰斯特拉算法适用于解决单源最短路径问题，也就是从一个节点出发到其他所有节点的最短路径。

它通过不断更新起点到其他节点的距离，并选择距离最短的节点作为下一个起点，直到找到所有节点的最短路径。

弗洛伊德算法则适用于解决任意两个节点之间的最短路径问题。

它通过动态规划的思想，逐步计算出从任意节点到其他节点的最短路径。

具体来说，它会用一个矩阵表示任意两个节点之间的距离，然后逐步更新矩阵，直到找到最短路径。

二、最小生成树最小生成树是一个连通图的生成树中边的权重之和最小的树。

生成树是指由图中的节点和边组成的一个树，它包含了图中的所有节点，并且不存在环。

最小生成树算法常用的有普里姆算法和克鲁斯卡尔算法。

普里姆算法以一个顶点作为起点开始，然后逐步找到与已经生成的树连接的权重最小的边，直到生成一棵包含图中所有节点的最小生成树。

克鲁斯卡尔算法则以边作为中心，首先将图中的边按照权重从小到大排序，然后逐步选择权重最小的边，当选择的边不构成环时，将其加入生成树，直到生成一棵包含图中所有节点的最小生成树。

总结：最短路径和最小生成树是图论中的两个重要概念，它们在许多实际问题中具有重要意义。

最短路径算法可以帮助我们找到两个节点之间最短的路径，而最小生成树算法则可以帮助我们找到一个连通图中边的权重之和最小的树。

在求解最短路径和最小生成树的过程中，我们可以使用迪杰斯特拉算法、弗洛伊德算法、普里姆算法或者克鲁斯卡尔算法等不同的算法。

图的最小生成树（java实现）

图的最⼩⽣成树（java实现）1.图的最⼩⽣成树（贪⼼算法）我两个算法的输出都是数组表⽰的，当前的索引值和当前索引对应的数据就是通路，⽐如parent[2] = 5;即2和5之间有⼀个通路，第⼆个可能⽐较好理解，第⼀个有点混乱是什么？将⼀个有权图中的所有顶点都连接起来，并保证连接的边的总权重最⼩，即最⼩⽣成树，最⼩⽣成树不唯⼀为什么？传⼊邻接矩阵，返回可以⽣成最⼩⽣成树的数据我们有两种⽅式⽣成图的最⼩⽣成树1.普⾥姆（Prim）算法2.克鲁斯卡尔（Kruskal）算法怎样做？图⽚参考博客：下⾯是普⾥姆算法的最⼩⽣成树下⾯是克鲁斯卡尔算法的最⼩⽣成树：图的邻接矩阵表⽰法（⽆向图，上三⾓矩阵）int[][] arr = new int[][]{{-1, 4, 0, 0, 0, 0, 0, 8, 0},{0, -1, 8, 0, 0, 0, 0, 11, 0},{0, 0, -1, 7, 0, 4, 0, 0, 2},{0, 0, 0, -1, 9, 14, 0, 0, 0},{0, 0, 0, 0, -1, 10, 0, 0, 0},{0, 0, 0, 0, 0, -1, 2, 0, 0},{0, 0, 0, 0, 0, 0, -1, 1, 6},{0, 0, 0, 0, 0, 0, 0, -1, 7},{0, 0, 0, 0, 0, 0, 0, 0, -1}};1.普⾥姆算法（加点法）需求：求出最⼩⽣成树的权值输⼊参数：⼆维数组arr（邻接矩阵），列表list（存放已经被加⼊的点），整型sum（存放权值）输出参数：整型数组parent1）先找⼀个起点，这个起点为任意⼀点，放⼊list中2）如果list中不包含全部节点，进⼊循环 1>遍历list中节点，查找不存在list中的邻接节点的最⼩值，记录下begin和end 2>将begin和end放⼊数组中，较⼩值节点赋值给较⼤值所在数组位置3）返回parent实现：import java.util.ArrayList;import java.util.Arrays;import java.util.List;/*** 普⾥姆（Prim）算法** @author Xiong YuSong* 2019/3/22 16:02*/public class Prim {public static void main(String[] args) {int[][] arr = new int[][]{{-1, 4, 0, 0, 0, 0, 0, 8, 0},{0, -1, 8, 0, 0, 0, 0, 11, 0},{0, 0, -1, 7, 0, 4, 0, 0, 2},{0, 0, 0, -1, 9, 14, 0, 0, 0},{0, 0, 0, 0, -1, 10, 0, 0, 0},{0, 0, 0, 0, 0, -1, 2, 0, 0},{0, 0, 0, 0, 0, 0, -1, 1, 6},{0, 0, 0, 0, 0, 0, 0, -1, 7},{0, 0, 0, 0, 0, 0, 0, 0, -1}};List<Integer> list = new ArrayList<>();//先将0放置在list中list.add(0);int begin = 0, end = 0, weight;int[] parent = new int[arr.length];for (int i = 0; i < arr.length; i++) {parent[i] = -1;}while (list.size() < arr.length) {weight = Integer.MAX_VALUE;for (Integer row : list) {for (int i = 0; i < arr.length; i++) {if (!list.contains(i)) {if (i >= row + 1) {if (arr[row][i] > 0 && arr[row][i] < weight) {begin = row;end = i;weight = arr[row][i];}} else if (i <= row - 1) {//我这⾥只⽤了上三⾓矩阵，所以这⾥需要画蛇添⾜写这⼀部分if (arr[i][row] > 0 && arr[i][row] < weight) {begin = row;end = i;weight = arr[i][row];}}}}}list.add(end);parent[end] = begin;}System.out.println(Arrays.toString(parent));}}2.克鲁斯卡尔算法（加边法）需求：求出最⼩⽣成树的权值构建类：Edge<begin,end,weight>三元组，根据weight（权值）排序输⼊参数：存放有Edge的列表list，并查集parent输出参数：并查集parent（最⼩⽣成树的数组表现形式）原理：贪⼼算法的实现，程序中使⽤了并查集（判断两个集合中是否存在相同的数据）这种特殊的数据结构，使⽤数组实现1）创建⼀个三元组<起始点，终⽌点，权值>，将邻接矩阵中数据放⼊三元组中，再放⼊list中，根据权值进⾏排序2）创建变量count=0，整型数组parent3）如果list中还存在值，则进⾏循环 1>判断begin和end是否存在于不同的集合中（判断是否在同⼀棵树中，即判断当前节点在并查集parent中的根节点是否为同⼀个） 2>如果存在不同的集合中，则将较⼩值节点赋值给较⼤值所在数组位置，较⼩值节点为较⼤值节点的⽗节点4）返回parent实现：import java.util.ArrayList;import java.util.Arrays;import java.util.Collections;import java.util.List;/*** @author Xiong YuSong* 2019/3/22 17:04*/class Edge implements Comparable<Edge> {//起始点private int begin;//终⽌点private int end;//权值private int weight;public Edge(int begin, int end, int weight) {this.begin = begin;this.end = end;this.weight = weight;}public int getBegin() {return begin;}public void setBegin(int begin) {this.begin = begin;}public int getEnd() {return end;}public void setEnd(int end) {this.end = end;}public int getWeight() {return weight;}public void setWeight(int weight) {this.weight = weight;}@Overridepublic int compareTo(Edge o) {if (o.weight > this.weight) {return -1;} else {return 1;}}}public class Kruskal {public static void main(String[] args) {//默认以a为根节点的最⼩⽣成树List<Edge> list = new ArrayList<>();int[][] arr = new int[][]{{-1, 4, 0, 0, 0, 0, 0, 8, 0},{0, -1, 8, 0, 0, 0, 0, 11, 0},{0, 0, -1, 7, 0, 4, 0, 0, 2},{0, 0, 0, -1, 9, 14, 0, 0, 0},{0, 0, 0, 0, -1, 10, 0, 0, 0},{0, 0, 0, 0, 0, -1, 2, 0, 0},{0, 0, 0, 0, 0, 0, -1, 1, 6},{0, 0, 0, 0, 0, 0, 0, -1, 7},{0, 0, 0, 0, 0, 0, 0, 0, -1}};for (int i = 0; i < arr.length; i++) {for (int j = i + 1; j < arr.length; j++) {if (arr[i][j] > 0) {list.add(new Edge(i, j, arr[i][j]));}}}Collections.sort(list);//数组中每⼀个节点都只知道他的⽗节点是什么，-1表⽰不存在⽗节点，0位置是根节点int[] parent = new int[arr.length];for (int i = 1; i < arr.length; i++) {parent[i] = -1;}int m = 0, n = 0;for (Edge edge : list) {//寻找这两个点有没有相同的⽗节点m = find(parent, edge.getBegin());n = find(parent, edge.getEnd());if (m != n && parent[edge.getEnd()]>0) {parent[edge.getEnd()] = edge.getBegin();}}System.out.println(Arrays.toString(parent));}private static int find(int[] parent, int ch) {while (parent[ch] > 0) {ch = parent[ch];}return ch;}}。

详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)

详解图的应用（最小生成树、拓扑排序、关键路径、最短路径）1.最小生成树：无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景：假设要在n个城市之间建立通信联络网，则连通n个城市只需要n—1条线路。

这时，自然会考虑这样一个问题，如何在最节省经费的前提下建立这个通信网。

在每两个城市之间都可以设置一条线路，相应地都要付出一定的经济代价。

n个城市之间，最多可能设置n(n-1)/2条线路，那么，如何在这些可能的线路中选择n-1条，以使总的耗费最少呢?1.2 分析问题（建立模型）：可以用连通网来表示n个城市以及n个城市间可能设置的通信线路，其中网的顶点表示城市，边表示两城市之间的线路，赋于边的权值表示相应的代价。

对于n个顶点的连通网可以建立许多不同的生成树，每一棵生成树都可以是一个通信网。

即无向连通图的生成树不是唯一的。

连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树，对连通图的不同遍历，就可能得到不同的生成树。

图G5无向连通图的生成树为(a)、(b)和(c)图所示：G5G5的三棵生成树：可以证明，对于有n 个顶点的无向连通图，无论其生成树的形态如何，所有生成树中都有且仅有n－1 条边。

1.3最小生成树的定义：如果无向连通图是一个网，那么，它的所有生成树中必有一棵边的权值总和最小的生成树，我们称这棵生成树为最小生成树，简称为最小生成树。

最小生成树的性质：假设N=(V,{ E}) 是个连通网，U是顶点集合V的一个非空子集，若（u,v）是个一条具有最小权值(代价)的边，其中，则必存在一棵包含边（u,v）的最小生成树。

1.4 解决方案：两种常用的构造最小生成树的算法：普里姆（Prim）和克鲁斯卡尔（Kruskal）。

他们都利用了最小生成树的性质1.普里姆（Prim）算法：有线到点，适合边稠密。

时间复杂度O(N^2)假设G＝（V，E）为连通图，其中V 为网图中所有顶点的集合，E 为网图中所有带权边的集合。

最小生成树01型算法

最小生成树01型算法最小生成树算法是一种用于解决图论中最小生成树问题的算法，其中最常见的是最小生成树01型算法。

本文将介绍最小生成树01型算法的原理、实现步骤以及应用场景。

一、最小生成树01型算法的原理最小生成树是指一个连通图的最小权重生成树，其中权重是边的属性。

最小生成树01型算法是基于贪心策略的算法，它通过选择权重最小的边来构建最小生成树。

算法的基本思想是从图中选择一条权重最小的边，并保证该边的两个顶点在生成树中没有形成环路。

然后再从剩余的边中选择下一条权重最小的边，直到所有顶点都被包含在生成树中为止。

最小生成树01型算法的步骤如下：1. 初始化一个空的生成树，将第一个顶点加入生成树中；2. 从剩余的边中选择一条权重最小的边，并检查该边的两个顶点是否已经在生成树中；3. 若两个顶点都已经在生成树中，则该边不符合条件，舍弃；4. 若两个顶点中有一个已经在生成树中，则将该边加入生成树，并将另一个顶点加入生成树中；5. 重复步骤2~4，直到所有顶点都被包含在生成树中。

三、最小生成树01型算法的应用场景最小生成树01型算法在实际应用中有着广泛的应用场景，以下为几个常见的应用场景：1. 网络规划：在网络规划中，最小生成树算法可以用于确定网络中最优的传输路径，以降低网络开销；2. 电力传输：在电力传输中，最小生成树算法可以用于确定电力线路的最优布局，以降低能源损耗；3. 道路规划：在道路规划中，最小生成树算法可以用于确定最短路径，以提高交通效率；4. 电路布局：在电路布局中，最小生成树算法可以用于确定电路板上各个元件之间的连接方式，以降低电路布局的复杂度。

最小生成树01型算法是一种经典的图论算法，它通过选择权重最小的边来构建最小生成树。

通过对算法的理解和实践，我们能够更好地应用它解决实际问题。

同时，最小生成树01型算法也为我们提供了一种思路，即通过贪心策略来解决问题。

在实际应用中，我们可以根据具体需求选择合适的算法，以达到最优解。

最小生成树算法详解

closedge[5].adjvex=3 .lowcost=6
closedge[6].adjvex=3 .lowcost=4
adjvex lowcost
v1 6
v1 1
v1 5
{v1}
{v2,v3,v4,v5,v6}
V4
V1
V3
V2
V6
V5
V4
V1
V3
1
｛V1 ｝
｛ V2 ,V3 ,V4 , V5 ,V6 ｝
步骤
(0)
｛V1 ,V3 ｝
｛ V2 ,V4 , V5 ,V6 ｝
(1)
V2
V6
V5
｛V1 ,V3 ,V6 ｝
｛ V2 ,V4 , V5 ｝
(2)
4
｛V1 ,V3 ,V6 ,V4 ｝
｛ V2, V5 ｝
adjvex lowcost
v1 6
v1 1
v1 5
{v1}
{v2,v3,v4,v5,v6}
3
adjvex lowcost
v3 5
0
v1 5
v3 6
v3 4
{v1,v3}
{v2,v4,v5,v6}
6
adjvex lowcost
v3 5
0
v6 2
v3 6
0
{v1,v3,v6}
{v2,v4,v5 }
(3)
2
｛V1 ,V3 ,V6 ,V4 ,V2 ｝
｛ V5 ｝
(4)
5
｛V1 ,V3 ,V6 ,V4 ,V2 ,V5 ｝
｛｝
(5)
3
V-U
普里姆(Prim)算法
生成树中只放置一个顶点

最小生成树唯一的充要条件

最小生成树唯一的充要条件最小生成树是图论中的一个重要概念，它是一棵生成树，包含所有图中的节点，并且具有最小的总权值。

在实际应用中，最小生成树被广泛运用于网络设计、城市规划等领域，因此，了解最小生成树的充要条件对于深入理解这些应用至关重要。

接下来，我们将介绍最小生成树唯一的充要条件。

一、什么是最小生成树最小生成树指的是一个无向图的生成树，它的所有边的权值之和最小。

一个无向图的生成树是指一棵树，包含所有图中的节点，并且只有图中的边。

因此，最小生成树是一个无向图的一种特殊情况。

二、最小生成树的唯一充要条件最小生成树有一个重要的性质，即它是唯一的当且仅当该无向图中不存在权值相同的边。

具体来说，设有一个无向图G=(V,E)，其中V是节点的集合，E是边的集合。

假设生成树T是G的一个生成树，我们需要证明最小生成树T是唯一的当且仅当G中不存在权值相同的边。

充分性证明：首先，假设最小生成树T是唯一的，我们需要证明G中不存在权值相同的边。

假设存在权值相同的边e1和e2，它们的权值都为w。

根据前提条件，T是最小生成树，因此T必须包含一条边e1或e2，假设T包含边e1，那么将边e1替换成e2，得到一棵新的生成树T'。

此时，T'中还有n-2条边需要加入。

因为T是最小生成树，所以T'的总权值必须大于等于T的总权值。

但是，由于e1和e2都是权值为w的边，所以将其替换不会改变T的总权值，即T'的总权值等于T的总权值。

因此，T'不能是最小生成树，与前提条件不符。

综上所述，最小生成树T是唯一的，则G中不存在权值相同的边。

必要性证明：然后，我们需要证明G中不存在权值相同的边，则最小生成树T是唯一的。

假设存在两棵生成树T1和T2，它们的权值之和相等，但是它们不相同。

由于T1和T2都是生成树，因此它们都包含n-1条边。

我们假设T1中有一条边e不在T2中，而T2中有一条边f不在T1中。

由于e不在T2中，因此e和f可以构成一个环。

图的最小生成树算法

图的最小生成树算法图的最小生成树算法是指找到一个图中的一棵生成树，使得该生成树的所有边的权值之和最小。

最小生成树算法在网络设计、电力传输、交通规划等领域有着广泛的应用。

本篇文章将详细介绍两种常用的最小生成树算法：Prim算法和Kruskal算法。

一、Prim算法Prim算法是一种贪心算法，它从一个顶点开始，逐步扩展生成树，直到包含所有顶点为止。

算法具体步骤如下：1. 初始化生成树为空集，选择任意一个顶点作为起始顶点。

2. 从与生成树中的顶点相连的所有边中选择一条权值最小的边，并将该边的另一个顶点加入生成树。

3. 重复步骤2，直到生成树包含所有顶点为止。

Prim算法的时间复杂度为O(V^2)，其中V是图的顶点数。

算法的优化版本可以使用优先队列来选择最小权值的边，时间复杂度可以优化到O(ElogV)，其中E是图的边数。

二、Kruskal算法Kruskal算法是一种基于并查集的贪心算法，它将图中的所有边按照权值从小到大进行排序，然后依次选取权值最小的边，如果该边的两个顶点不在同一个连通分量中，则将该边加入生成树中。

算法具体步骤如下：1. 初始化生成树为空集，将图中的所有边按照权值从小到大进行排序。

2. 依次选取权值最小的边，如果该边的两个顶点不在同一个连通分量中，则将该边加入生成树。

3. 重复步骤2，直到生成树的边数等于顶点数减一为止。

Kruskal算法的时间复杂度为O(ElogE)，其中E是图的边数。

并查集的操作时间复杂度为O(logV)，所以整体的时间复杂度为O(ElogE)。

三、比较与应用Prim算法适用于稠密图，即边的数量接近于顶点数量的平方。

而Kruskal算法适用于稀疏图，即边的数量相对较少。

另外，Prim算法的实现相对简单，而Kruskal算法需要使用并查集来判断两个顶点是否在同一个连通分量中。

最小生成树算法在实际应用中有着广泛的作用。

例如，在网络设计中，最小生成树算法可以用来确定网络中的主干链路，以最小的代价满足网络的连通要求；在电力传输中，最小生成树算法可以用来确定输电线路的布置，以保证电力传输的稳定性和可靠性。

图的最小生成树_prim算法

11
4 最小生成树
①初始化候选边数组edges[]； ② U={v0}； ③for (i=1; i<=n-1; i++) { k=最小候选边的未选的一端； U=U+{k}；以k修改edges[]； } 注：edges的元素可以设置为{v} 思考：权值最小的边一定在最小生成树中么？分析 : prim算法的时间复杂度？
1
12 15
9
9 5 4
2
17
6 9 10 3 4
(1,2)/12 (1,3)/∞
3
{1,6} {1,6,5}
(1,2)/12 (6,3)/17 (6,4)/20 (6,2)/15 (6,4)/20 (1,2)/12 (6,3)/17 (5,4)/4 (6,2)/15 (1,2)/12 (6,3)/17 (6,2)/15 (4,3)/3
2
6 15 17 3 3 6 9 10 4
7
5 4
4 最小生成树
1 12 2 6 15 17 3 3 9 6 9 10 4 9 5 4 2 6 12 15 17 3
1 9
6 9 12 5 4 4 2 6 15 17 3
1 9
6 9
9
10
9
10
5 4 4
3
1
3
1
1 12 9 15 17 3 3 6 9 10 4 9 5 4 2 6
6
4 最小生成树
问题：修建一个连接各个小区与供应站点之间的管道使得造价成本最低，即构造一颗最小生成树。但是如何求解？ 4.1 prim算法 1. 基本思想在满足如下条件的过程中选出一条最小的边：一端已选，另一端未选。因此，该算法需要给出起点，以作为已选顶点。 2. 实例 1 对右图所示图， 12 9 9 用Prim算法求最小生成树。

图论算法--最小生成树

最小生成树。在此例中，最小
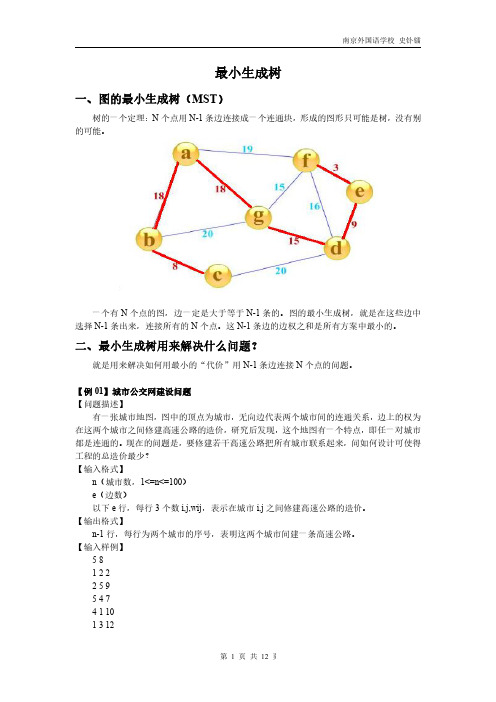
生成树的权值之和为 39。
A, D, F, 无 B, E, C,
G
算法时间复杂度：O (N2)。【例 02】最优布线问题(wire) 【问题描述】
学校有 n 台计算机，为了方便数据传输，现要将它们用数据线连接起来。两台计算机被连接是指它们间有数据线连接。由于计算机所处的位置不同，因此不同的两台计算机的连接费用往往是不同的。
率先选择了边 AD。这样我们的图就变成了左图
第 6 页共 12 页
南京外国语学校史钋镭
在剩下的变中寻找。我们找到了 CE。这里边的权重也是5
依次类推我们找到了 6,7,7，即 DF，AB，BE。
下面继续选择，BC 或者 EF 尽管现在长度为 8 的边是最小的未选择的边。但是现在他们已经连通了（对于 BC 可以通过 CE,EB 来连接，类似的 EF 可以通过 EB,BA,AD,DF 来接连）。所以不需要选择他们。类似的 BD 也已经连通了（这里上图的连通线用红色表示了）。最后就剩下 EG 和 FG 了。当然我们选择了 EG。
二、最小生成树用来解决什么问题？
就是用来解决如何用最小的“代价”用 N-1 条边连接 N 个点的问题。
【例 01】城市公交网建设问题【问题描述】
有一张城市地图，图中的顶点为城市，无向边代表两个城市间的连通关系，边上的权为在这两个城市之间修建高速公路的造价，研究后发现，这个地图有一个特点，即任一对城市都是连通的。现在的问题是，要修建若干高速公路把所有城市联系起来，问如何设计可使得工程的总造价最少？【输入格式】
}
int cmp(const point &a,const point &b){
//sort()自定义的比较函数

图的最小生成树算法

图的最小生成树算法图论是计算机科学中一门非常重要的学科，在各种领域得到了广泛的应用。

其中，最小生成树算法是图论中比较重要的一种算法。

同时，最小生成树问题也是最好的优化问题之一。

本文将会深入探讨图的最小生成树算法及其应用。

一、最小生成树问题的定义最小生成树问题就是为一个具有权重的连通无向图找到一棵生成树，使得所有权值之和最小。

需要注意的是，如果该图不连通，则最小生成树并不存在。

二、最小生成树算法1. Kruskal算法Kruskal算法是一种贪心算法，能够解决最小生成树问题。

在该算法中，将图中所有边按照权重从小到大排序，并依次加入生成树中（前提是加入该边不产生环）。

当所有边都被加入生成树中时，生成树就构造完成了。

2. Prim算法Prim算法也是一种贪心算法用于解决最小生成树问题。

与Kruskal算法不同的是，需要从一个初始点开始，每次加入到该点的边中权值最小的那条边。

这个过程可以看作是将所有点分为两个集合，一个是已经被访问过的集合，一个是还没有访问过的集合，然后每次找到两个集合相连的一条权值最小的边，并把这个边所连接的点加入已经被访问过的集合中去。

三、最小生成树算法的应用最小生成树算法在实际中的应用很多，其中一个经典的应用是设计网络。

在网络中，节点之间可以用边来表示，而边的权重可以表示节点之间的通讯成本。

所以，在设计网络时，希望选择尽可能低廉的边连接节点，从而节省通讯成本。

在这种情况下，最小生成树算法可以帮助我们确定哪些边应该被使用，进而构建出网络拓扑结构。

四、总结最小生成树算法在计算机科学中是非常重要的一个算法。

本文对最小生成树问题及其两种算法进行了深入的讨论。

同时，介绍了最小生成树算法在网络拓扑结构设计中的应用。

希望本文能够帮助读者深入理解最小生成树问题及其应用。

最小生成树算法

最小生成树算法及应用
[举例] 举例] 下面的图（A）表示一个5个城市的地图，图（B）、（C）是对图（A）分别进下面的图（表示一个5个城市的地图，）、（C 是对图（行深度优先遍历和广度优先遍历得到的一棵生成树，其权和分别为20 33， 20和行深度优先遍历和广度优先遍历得到的一棵生成树，其权和分别为20和33，前者比后者好一些，但并不是最小生成树，最小生成树的权和为19 19。后者好一些，但并不是最小生成树，最小生成树的权和为19。
最小生成树算法及应用
2、用Kruskal算法求最小生成树的思想如下： Kruskal算法求最小生成树的思想如下：算法求最小生成树的思想如下设最小生成树为T= T=（ TE），设置边的集合TE的初始状态为空集。将图G ），设置边的集合TE的初始状态为空集设最小生成树为T=（V，TE），设置边的集合TE的初始状态为空集。将图G中的边按权值从小到大排好序，然后从小的开始依次选取，若选取的边使生成树T 边按权值从小到大排好序，然后从小的开始依次选取，若选取的边使生成树T不形成回路，则把它并入TE TE中保留作为T的一条边；若选取的边使生成树形成回路，成回路，则把它并入TE中，保留作为T的一条边；若选取的边使生成树形成回路，则将其舍弃；如此进行下去，直到TE中包含n 条边为止。最后的T即为最小生成树。 TE中包含则将其舍弃；如此进行下去，直到TE中包含n-1条边为止。最后的T即为最小生成树。
最小生成树算法及应用
1、用Prim算法求最小生成树的思想如下： Prim算法求最小生成树的思想如下：算法求最小生成树的思想如下设置一个顶点的集合S和一个边的集合TE TE， TE的初始状态均为空集的初始状态均为空集； ①设置一个顶点的集合S和一个边的集合TE，S和TE的初始状态均为空集；选定图中的一个顶点K 开始生成最小生成树，加入到集合S ②选定图中的一个顶点K，从K开始生成最小生成树，将K加入到集合S；重复下列操作，直到选取了n 条边： ③重复下列操作，直到选取了n-1条边：选取一条权值最小的边（X，Y），其中X∈S，not (Y∈S)；选取一条权值最小的边（），其中X∈S， (Y∈S)；其中X∈S 将顶点Y加入集合S 加入集合TE TE；将顶点Y加入集合S，边（X，Y）加入集合TE； ④得到最小生成树T =（S，TE）。得到最小生成树T =（ TE）