复化梯形公式和复化辛卜生公式
复化梯形公式,复化辛普森公式,复化柯特斯公式
复化梯形公式,复化辛普森公式,复化柯特斯公式
复化梯形公式、复化辛普森公式和复化柯特斯公式都是用来计算定积分的近似值的方法。
1. 复化梯形公式：将积分区间分成若干个小区间，在每个小区间上用梯形面积近似代替该小区间的曲边梯形面积，然后将这些梯形面积相加，得到积分的近似值。
2. 复化辛普森公式：将积分区间分成若干个等分小区间，在每个小区间上用矩形面积近似代替该小区间的曲边梯形面积，然后将这些矩形面积相加，得到积分的近似值。
3. 复化柯特斯公式：将积分区间分成若干个等分小区间，在每个小区间上用切线段长度近似代替该小区间的曲边梯形面积，然后将这些切线段长度相加，得到积分的近似值。
这三种方法都是通过将积分区间分成若干个小区间，然后在每个小区间上用近似方法计算该小区间的曲边梯形面积，最后将这些近似值相加得到积分的近似值。
它们的精度和误差都与分区间的大小有关。
复化梯形公式和复化辛普生公式
}
void simpson::integration()//实现积分
{
cout<<"输入上限和下限";
cin>>b>>a;
cout<<"输入你要使用simposn法则的数目(即等分数)";
cin>>n;
h=(b-a)/n;
sum_even_terms=0.0;
sum_odd_terms=0.0;
for(k=1;k<n;k++)
{
sum_even_terms+=sine(k*h);
}
for(k=0;k<n;k++)
{
sum_odd_terms+=sine((2*k+1)*h/2);
}
integral=(2.0*sum_even_terms+4.0*sum_odd_terms+sine(b)+1)*h/6.0;
《数值分析》实验报告
姓名
学号
日期
2012．11.20
实验室
设备编号
实验题目
用复化梯形公式和复化辛普生公式求I=∫01sinx/xdx
一实验目的
1．了解复化梯形公式和复化辛普生公式。
2.用复化梯形公式和复化辛普生公式求I=∫01sinx/xdx。
二实验内容
算法：复化梯形公式是Tn=∑h/2[f(xi)+ f(xi+1)]=(b-a)/2n[f(a)+2∑f(xi)+f(b)]记子段[xi,xi+1]的中点为xi+1/2,则复化Simpson公式为Sn=∑h/6[f(xi)+4f(xi+1/2)+ f(xi+1)]=b-a/6n[f(a)+4∑f(xi+1/2)+2f(xi)+f(b)]
龙贝格积分算法实验[1]
![龙贝格积分算法实验[1]](https://img.taocdn.com/s3/m/1c3c3ec18bd63186bcebbcf8.png)
且 （ 为等份次数）
2．按梯形公式的递推关系，计算
3．按龙贝格公式计算加速值
4．精度控制。对给定的精度 ，若
则终止计算，并取 作为所求结果；否则 ，重复2~4步，直到满足精度为止。
问题
（1）程序运行如下：
I = Romberginterg(inline('x.^2.*exp(x)'),0,1,25,1e-6)
function I = GaussInterg(fun, type, a, b, tol)
% GaussInterg用Gauss型求积公式求积分,具体形式由使用者选取
%
% Synopsis: I = GaussInterg(fun, type, a, b)
% I = GaussInterg(fun, type, a, b, tol)
if nargin < 4
npanel = 25;
end
if nargin < 5
tol = 5e-9;
end
if nargin < 6
flag = 0;
end
T(1,1) = TrapezoidInteg(fun, a, b, npanel); %T0(h) = T(h)
err = 1; %初始化误差值
if nargin < 4
npanel = 25;
end
nnode = npanel + 1; %节点数=段数+ 1
h = (b-a)/(nnode-1); %步长
x = a:h:b; %将积分区间分段
f = feval(fun,x);%求节点处被积函数的值
I = h * ( 0.5*f(1) + sum(f(2:nnode-1)) + 0.5*f(nnode) );
复化梯形公式、复化辛卜生公式
复化梯形公式、复化辛卜生公式
一、复化梯形公式及其余项
在区间不大时,用梯形公式、辛卜生公式计算定积分是简单实用的,但当区间较大时, 用梯形公式、辛卜生公式计算定积分达不到精确度要求. 为了提高计算的精确度，我们将 [a,b] 区间n等分，在每个小区间上应用梯形公式、辛卜生公式计算定积分, 然后将其结果相加，这样就得到了复化梯形公式和复化辛卜生公式。
1. 复化梯形公式
将积分区间等分,设, 则节点为
对每个小区间上应用梯形公式, 然后将其结果相加，则得
(3.14)
称(3.14)式为复化梯形公式.
当在[a,b]上有连续的二阶导数时，则复化梯形公式(3.14)的余项推导如下：
因为
所以在区间[a,b]上公式(3.14)的误差为
又因为在区间[a,b]上连续，由连续函数的性质知，在区间[a,b]上存在一点，
于是
（3.15）
称(3.15)式为复化梯形公式的余项。
例1用复化梯形公式计算得
使误差小于
解和公式(3.15), 解不等式
得
即时，用复化梯形公式计算可达到精度要求，则取,用公式（3.14）计算得
而积分的准确值。
复合梯形公式与复合辛普森公式对比
下面利用余项公式来估计两种算法的误差。首先需要求
f (x) sin x 1cos(xt)dt ,
x
0
所以有
的高阶导数。由于
于是
f k (x)
1 0
dk dxk
(cos
xt)dt
1tk cos(xt k )dt ,
0
2
max f k (x) 1 cos(xt k )tk dt 1tk dt 1 .
输出积分值 结束
图 4-1 复合梯形公式算法流程图 4.2 复合辛普森公式算法流程图
开始 输入区间断点 a, b
及等分数 n 求出步长各h节，各点节函点数值，相邻节求点和中su点m1, 及
各相相邻应节的点函中数心值输点出函结积数束,分值值
k=1求,2,和..n-s1um2
k=1,2,..n-1
图 4-2 复合辛普5.森M公A式TL算AB法源流程程序
1. 对多个算例进行分析，保证计算量基本相同的情况下去比较计算精度，验证复合辛普森
公式具有更高精度的结论。
2. 对多个算例进行 MATLAB 编程分析，在要求相同计算精度的前提下去比较计算量的大小，
从而分析复合梯形公式与复合辛普森公式的优劣。
参考文献
[1]穆耶赛尔·艾合买提,阿布都热西提·阿布都外力. 改进复合梯形求积公式[J]. 首都师范大学学报(自然科学 版),2016,06:1-4. [2] 刘 智 颖 , 王 向 公 , 任 威龙 , 龙 耀 萍 . 辛 普 森 公 式的 推 广 形 式 及 应 用 [J]. 山 东 理 工 大 学 学 报 ( 自 然科 学 版),2014,01:29-31. [3]陈凤忠. 辛普森公式的统一美[J]. 长春理工大学学报(综合版),2005,03:59-60+80. [4]李庆扬, 王能超, 易大义. 数值分析.第 5 版[M]. 清华大学出版社, 2008,12:106-109.
复合梯形公式和复合辛普森公式
复合梯形公式和复合辛普森公式1.复合梯形公式步骤1：将积分区间[a,b]均匀地分成n个小区间，每个小区间的长度为h=(b-a)/n，其中n为正整数。
步骤2：定义一个函数f(x)，并在每个小区间上求出函数在小区间两个端点的函数值，记作f(x0), f(x1), f(x2), ..., f(xn)。
步骤3：根据梯形公式，每个小区间上的定积分近似值为(h/2) * (f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn))。
步骤4：将所有小区间上的定积分近似值相加，得到最终的近似值。
复合辛普森公式是通过将积分区间划分成若干个小区间，然后在每个小区间上应用辛普森公式来逼近定积分的值。
具体的步骤如下：步骤1：将积分区间[a,b]均匀地分成n个小区间，每个小区间的长度为h=(b-a)/n，其中n为正偶数。
步骤2：定义一个函数f(x)，并在每个小区间上求出函数在小区间三个点的函数值，记作f(x0),f(x1),f(x2)。
步骤3：根据辛普森公式，每个小区间上的定积分近似值为(h/3)*(f(x0)+4f(x1)+f(x2))。
步骤4：将所有小区间上的定积分近似值相加，得到最终的近似值。
复合辛普森公式的误差主要取决于小区间的数量和函数在每个小区间上的变化情况。
与复合梯形公式相比，复合辛普森公式的精度更高，但计算复杂度也更高。
综上所述，复合梯形公式和复合辛普森公式是数值积分中常用的近似计算方法。
它们通过将积分区间划分成小区间，并在每个小区间上应用相应的公式来逼近定积分的值。
这两种方法都可以通过增加小区间的数量来提高近似的精度，但相应地也会增加计算的复杂度。
根据实际情况，我们可以选择合适的方法来计算需要求解的定积分。
复化梯形公式和复化辛普森公式的精度比较(共7页)
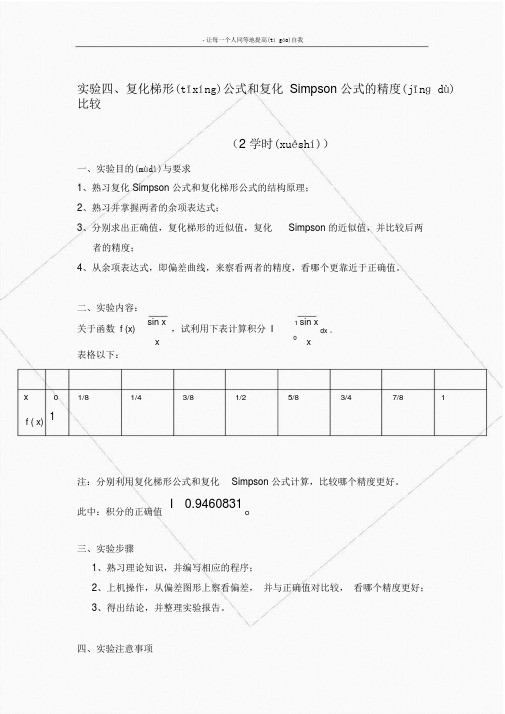
- 让每一个人同等地提高(tí gāo)自我实验四、复化梯形(tīxíng)公式和复化Simpson 公式的精度(jīnɡ dù)比较（2 学时(xuéshí)）一、实验目的(mùdì)与要求1、熟习复化 Simpson 公式和复化梯形公式的结构原理；2、熟习并掌握两者的余项表达式；3、分别求出正确值，复化梯形的近似值，复化Simpson 的近似值，并比较后两者的精度；4、从余项表达式，即偏差曲线，来察看两者的精度，看哪个更靠近于正确值。
二、实验内容：关于函数 f (x) sin x，试利用下表计算积分 I 1sin xdx 。
x x表格以下：x 0 1/8 1/4 3/8 1/2 5/8 3/4 7/8 1 f ( x)1注：分别利用复化梯形公式和复化Simpson 公式计算，比较哪个精度更好。
此中：积分的正确值I0.9460831。
三、实验步骤1、熟习理论知识，并编写相应的程序；2、上机操作，从偏差图形上察看偏差，并与正确值对比较，看哪个精度更好；3、得出结论，并整理实验报告。
四、实验注意事项11- 让每一个人同等地提高(tí gāo)自我1、复化梯形公式，程序主体(zhǔtǐ)部分：for n=2:10T(n)=*T(n-1)for i=1:2^(n-2)；endend2、复化 Simpson 公式(gōngshì)，程序主体部分：for i=1:10n=2.^ix=0:1/n:1f=sin(x)./xf(1)=1s=0for j=1:n/2s=s+f(2*j)endt=0for j=1:(n/2-1)t=t+f(2*j-1)endS(i)=1/3/n*(f(1)+4*s+2*t+f(n+1))end五．实验(shíyàn)内容复化梯形(tīxíng)公式和复化辛普森公式的引入22- 让每一个(yī ɡè)人同等地提高自我复化梯形(tīxíng)公式：T n n 1 h [ f (x k f ( x k 1 )] ；k 0 2复化辛普森公式：S n n 1 h4 f ( x 1 ) f (x k 1 )] ；[ f (x kk 0 6k2依据题意(tí yì)和复化梯形公式、复化辛普森公式的原理编写程序求解代码以下：Matlab 代码(dài mǎ)clcs=quad( 'sin(x)./x',0,1)p1=zeros(10,1);p2=zeros(10,1);for k=6:15s1=0;s2=0;x=linspace(0,1,k);y=sin(x)./x;z=(1/(2*(k-1))):(1/(k-1)):1;sz=sin(z)./z;y(1)=1;for i=1:(k-1)s1=s1+*(x(i+1)-x(i))*(y(i)+y(i+1));endfor j=1:(k-1)s2=s2+(1/6)*(x(j+1)-x(j))*(y(j)+y(j+1)+4*sz(j));endp1(k-5)=s1-s;p2(k-5)=s2-s;endp1;33- 让每一个人同等地提高(tí gāo)自我p2;s1=s+p1(4)s2=s+p2(4)format longfor k=1:length(p1)p1(k)=abs(p1(k));p2(k)=abs(p2(k));endp1p2plot(6:1:15,p1,'-r' )hold onplot(6:1:15,10000*(p2),'-c' )hold off部分(bù fen)程序结果输出：s=s1 =s2 =结果剖析1 sin( x)；依据结果输出可知：积分 I dx 的正确值为： I=x44- 让每一个人同等(tóngděng)地提高自我经过复化梯形公式(gōngshì)和复化辛普森公式获得的积分值为：s1 =:s2 =;相对偏差为：S 1 I 100 4.15 10 4 ； 1I 100S 2 I 100 1.62 10 8 ； 2 I 100明显，从相对偏差可知经过辛普森公式获得(huòdé)的结果偏差小精度高。
09-1复化辛甫生公式
2013-2014（1）专业课程实践论文题目：复化辛甫生公式牛顿-柯特斯公式是插值型求积公式，而多节点的高次插值有很大的误差，即有龙格现象，因而高阶牛顿-柯特斯公式误差会很大。
其次当8≥n 时，柯特斯系数会有正有负，从而也不能保证求积公式的稳定性。
此外，当区间],[b a 较大时，由误差表达式可以看出精确度较差。
一种实用的做法是将积分区间],[b a 等分成n 个小区间，对每个小区间采用低阶的牛顿-柯特斯公式，再将结果加起来作为积分的近似值，这就是复化牛顿-柯特斯公式。
（1）复化梯形公式将],[b a 区间n 等分，子区间长度na b h -=，于是有复化梯形公式 )],()(2)([2)]()([211110b f x f a f h x f x f h T n k k k k n k n ++=+=∑∑-=+-= 其余项公式为)()(12)](12[2103ηηf a b h f h R k n k T ''--=''-=∑-= 这是因为如果)(x f ''在区间],[b a 上连续，由介值定理存在],[b a ∈η使得)()(10ηηf f n nk k ''=''∑=。
复化辛甫生公式是在复化梯形公式的基础上演变而来的，设子区间1[,]k k x x +的中点为12k x +，复化辛甫生公式为： ))()(2)(4)((6))()(4)((611102112110b f x f x f a f h x f x f x f h S n k k n k k k k k n k n +++=++=∑∑∑-=-=+++-=类似于复化梯形公式余项的推导，可得其余项公式为：],[),()2(180)()4(4b a f h a b R n s ∈--=ηη复化辛甫生公式的算法如下：（1）输入区间端点a ，b 及等分数n/2（n 为偶数），半步长h=（b-a ）/n ，（2）置),....,2,1)((n i ih a f f i =+=（3）置.0,1==Q f P ，（4）对2,...3,2-=n j ，置.,1Q f Q P f P j j ⇒+⇒++（5）输出S=6h )](24)([b f Q P a f +++。
matlab实现复化梯形公式,复化simpson公式以及romberg积分
（一）实验目的熟悉并掌握数值积分的方法，重要训练复化梯形公式，复化simpson 公式以及romberg 积分。
（二）问题描述问题三数值积分椭圆周长的计算。
考虑椭圆,为计算其周22221x y a b+=长,只要计算其第一象限的长度即可.用参数方程可以表示为,cos (0/2)sin x a t t y b t π=⎧≤≤⎨=⎩计算公式为/0π⎰为计算方便,我们可以令,即计算下面的积分1a =/0π⎰/0π=⎰(可以归结为上面的/0π⎰/0a π=⎰形式)采用复化梯形公式，复化Simpson 公式以及Romberg 积分的方法计算积分/0()I b π=⎰给出通用程序，该通用程序可以计算任何一个函数在任意一个区间在给定的精度下的数值积分。
程序输出为计算出的数值积分值以及计算函数值的次数。
（三）算法介绍首先利用给出的各迭代公式，设计程序。
在matlab 对话框中输入要计算的函数，给出区间和精度。
复化梯形的迭代公式为：;∫b a f(x)dx =ℎ/2[f (a )+2∑n ‒1j =1f (x j )+f(b)]复化simpson 迭代公式为：;∫b a f(x)dx =ℎ/3[f (a )+2∑(n 2)‒1j =1f (x 2j )+4∑(n 2)j =1f (x 2j ‒1)+f(b)]Romberg 迭代公式为：。
R k,j =R k,j ‒1+R k,j ‒1—R k ‒1,j ‒14j ‒1-1（四）程序对于复化梯形公式和复化simpson 公式，我们放在jifenn.m 中。
（%标记后的程序可用来把b 看为变量时的算法实现）%复化梯形公式function y=jifenn(f,n,a,b) （说明：f 表示任一函数，n 精度，a ，b 为区间）fi=f(a)+f(b);h=(b-a)/n;d=1;%function f=jifen(n,a,b,c)%syms t%y=sqrt(1+(c^2-1)*cos(t)^2);%ya=subs(y,t,a);%yb=subs(y,t,b);%fi=ya+yb;for i=1:n-1x=a+i*h;fi=fi+2*f(x);d=d+1;%yx=subs(y,t,x);%fi=fi+2*yx;endf4=h/2*fi,d%复化simposon 公式f1=0;f2=0;dd=1;for i=1:n-1dd=dd+1;if rem(i,2)~=0;x1=a+i*h;f1=f1+f(x1);else rem(i,2)==0;x2=a+i*h;f2=f2+f(x2) ;endendf3=(h/3)*(f(a)+4*f1+2*f2+f(b)),dd对于romberg积分，建立romberg.m文件。
复化梯形公式和复化辛普森公式
复化梯形公式和复化辛普森公式1. 引言嘿，大家好！今天我们来聊聊数学里那些看似高深莫测的公式，尤其是复化梯形公式和复化辛普森公式。
这些名字听起来就像是从某部科幻片里蹦出来的角色，但其实它们是我们在数值积分中不可或缺的好帮手。
你知道吗？它们就像是数学世界里的“超能英雄”，让我们轻松搞定积分，简直是妙不可言。
2. 复化梯形公式2.1 你知道什么是梯形吗？首先，咱们得聊聊复化梯形公式。
说白了，就是把一个复杂的积分任务，分解成几个小的梯形来求解。
想象一下，你在河边钓鱼，河水流得可欢了。
为了找一个合适的钓鱼点，你可能得把河分成几段，然后每一段的宽度就是你的小梯形。
你看，这就是复化梯形的魅力所在！2.2 如何运用复化梯形公式？用这个公式的时候，你只需把整个区间分成N个小区间，每个区间的宽度都是一样的。
然后，把每个小区间的函数值拿来加一加，再乘上宽度的一半，最后再把头尾的函数值加上。
这听起来是不是很简单？比如，你想算从0到1的某个函数的积分，只要把这个区间分成若干段，像切蛋糕一样，每一片都求个函数值，然后把结果合起来就行了。
简单得就像吃个冰淇淋，大家都喜欢。
3. 复化辛普森公式3.1 辛普森是谁？接下来，让我们来看看复化辛普森公式。
辛普森这个名字，大家可能都听过，或者说过“这是辛普森家的事儿”。
其实，他是一位牛逼的数学家，专门研究如何让积分变得更加简单。
辛普森公式就像是对梯形公式的一次升级，像换了个新款手机，功能更强大，效果更好。
3.2 如何运用复化辛普森公式？用复化辛普森公式的时候，我们也是把整个区间分成N个小区间，不过这里的N必须是偶数哦！每个小区间的宽度仍然是一样的。
然后，用函数值的加权平均法来计算。
换句话说，你把每个小区间的头尾和中间的函数值都考虑进来，像是为你的冰淇淋加上各种口味的配料。
最后，你的结果就会比单纯用梯形公式得来的要精准多了，仿佛一口下去，味蕾都在舞蹈。
4. 比较与应用4.1 谁更强？说到这儿，很多人就会问，复化梯形公式和复化辛普森公式，谁更厉害呢？其实，这就像问“苹果和橘子，哪个更好吃”。
matlab实现复化梯形公式,复化simpson公式以及romberg积分
（一） 实验目的熟悉并掌握数值积分的方法，重要训练复化梯形公式，复化simpson 公式以及romberg 积分。
（二） 问题描述问题三数值积分椭圆周长的计算。
考虑椭圆22221x y a b+=,为计算其周长,只要计算其第一象限的长度即可.用参数方程可以表示为cos (0/2)sin x a t t y b t π=⎧≤≤⎨=⎩,计算公式为/0π⎰为计算方便,我们可以令1a =,即计算下面的积分/0π⎰/0π=⎰(/0π⎰/0a π=⎰可以归结为上面的形式)采用复化梯形公式，复化Simpson 公式以及Romberg 积分的方法计算积分/0()I b π=⎰给出通用程序，该通用程序可以计算任何一个函数在任意一个区间在给定的精度下的数值积分。
程序输出为计算出的数值积分值以及计算函数值的次数。
（三） 算法介绍首先利用给出的各迭代公式，设计程序。
在matlab 对话框中输入要计算的函数，给出区间和精度。
复化梯形的迭代公式为：;复化simpson迭代公式为：;Romberg迭代公式为：。
（四）程序对于复化梯形公式和复化simpson公式，我们放在中。
（%标记后的程序可用来把b看为变量时的算法实现）%复化梯形公式function y=jifenn(f,n,a,b) （说明：f表示任一函数，n精度，a，b为区间）fi=f(a)+f(b);h=(b-a)/n;d=1;%function f=jifen(n,a,b,c)%syms t%y=sqrt(1+(c^2-1)*cos(t)^2);%ya=subs(y,t,a);%yb=subs(y,t,b);%fi=ya+yb;for i=1:n-1x=a+i*h;fi=fi+2*f(x);d=d+1;%yx=subs(y,t,x);%fi=fi+2*yx;endf4=h/2*fi,d%复化simposon公式f1=0;f2=0;dd=1;for i=1:n-1dd=dd+1;if rem(i,2)~=0;x1=a+i*h;f1=f1+f(x1);else rem(i,2)==0;x2=a+i*h;f2=f2+f(x2) ;endendf3=(h/3)*(f(a)+4*f1+2*f2+f(b)),dd对于romberg积分，建立文件。
复化梯形公式和复化Simpson公式
数值计算方法上机题目3一、计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。
1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。
复化梯形公式和复化Simpson公式
数值计算方法上机题目3一、计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。
1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果 Tn= 7.3891等分数 n=7019已知值与计算值的误差 R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果 Sn= 7.3891等分数 n=24已知值与计算值的误差 R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。
复化梯形公式和复化Simpson公式
数值计算方法上机题目3一、计算定积分的近似值：要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。
1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数 结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x %定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可 f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))' %因fminbnd （）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。
数值分析作业复化求积公式
数值计算方法上机题目3计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。
解：（1) x xe x f =)(,所以x x k xe ke x f +=)()(，x x xe e x f +=2)(''，x x xe e x f +=4)()4(x x xe e x f +=6)()6(对于复化梯形公式： )(12)(''2ηf h a b f R n --=，2max ''4)(e f =η，n h 1= 代入数据可知 7221021124-⨯≤n e ，57.7018≥n 取7019=n对于复化Simpson 公式 )()2(180)()4(4ηf h a b f R n --=，2max )4(6)(e f =η，n h 1= 代入数据可知 742102128806-⨯≤n e ，56.23≥n 取24=n（2）复化梯形公式：函数function y=fun(x)y=x*exp(x);程序：clcClear% 复化梯形计算format longa=1;b=2;n=7019;% 区间划分为m等份h=(b-a)/n;% 步长，根据误差限由该算法的余项作事前估计得到ty1=fun(a)+fun(b);ty2=0;for i=1:n-1x=a+i*h1;ty2=ty2+fun(x);endT=h*(ty1+2*ty2)/2;T对于复化Simpson公式clcClear% 复化Simpon计算format longa=1;b=2;n=24;% 区间划分为n等份h=(b-a)/(2*n);% 步长，根据误差限由该算法的余项作事前估计得到sy1=fun(a)+fun(b);sy2=0;sy3=0;for j=1:2*n-1x=a+j*h2;if rem(j,2)==0sy3=sy3+fun(x);elsesy2=sy2+fun(x);endendS=h*(sy1+4*sy2+2*sy3)/3;S% 精确值Exactanswer=exp(2)运算结果：T =7.389056127230221S =7.389056126214707Exactanswer =7.389056098930650（3）比较可知复化梯形公式的计算量较大1．用共轭梯度法和G-S迭代法分别求解下面的方程组：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-14514103131021310321x x x 迭代20次或满足()(1)1110k k x x --∞-<时停止计算。
复化梯形公式和复化Simpson公式
数值计算方法上机题目3一、计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。
1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。
复化梯形公式,辛普森公式的matlab程序
复化梯形公式与辛普森公式的matlab程序【程序代码】cclc;disp('1.复化梯形公式求解');disp('2.simpson公式求解');disp('请进行选择：');c=input(' ');if c==1clc;disp('复化梯形公式');disp('请输入积分下限 ');a=input('a=');disp('请输入积分上限 ');b=input('b=');disp('请输入等分的数目 ');n=input('n=');h=(b-a)/n;s1=0;for i=1:n-1s1=s1+fun1(i*h);enddisp('复化梯形公式的结果：');T=h/2*(fun1(a)+2*s1+fun1(b))else if c==2clc;disp('simpson公式');disp('请输入积分下限 ');a=input('a=');disp('请输入积分上限 ');b=input('b=');disp('请输入等分的数目 ');n=input('n=');h=(b-a)/n;s2=0;for i=0:n-1s2=s2+fun1((i+0.5)*h);enddisp('辛普森公式的结果： ');S=h/6*(fun1(a)+4*s2+2*s1+fun1(b))endenddisp('菜单选项');disp('1.继续运算');disp('2.退出程序！');p=input(' ');if p==1(fuhua);else if p==2disp('正在退出，请稍候。
复化梯形公式和复化Simpson公式
数值计算方法上机题目3一、计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。
1.复化梯形公式程序：程序1（求f （x ）的n 阶导数：syms xf=x*exp(x) %定义函数f （x ）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点，也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序：程序1：（求f（x）的n阶导数）：syms xf=x*exp(x) %定义函数f（x）n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2：clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x)，换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数，输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd（）函数求的是表达式的最小值，且要求表达式带引号，故取负号，一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点，也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值，故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示：用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为：7.3891，与精确解的误差为：2.8300e-008。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验三：分别用复化梯形公式和复化辛卜生公式计算f(x)=sin(x)/x的积分，并与准确值比较判断精度。
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
double Trapezoid(float,float,float,int);
double Simpson(float,float,float,int);
double Integral(float,float);
int SigDigT(double,double,int);
void Euler(float a[50],float b);
float f(float);
float Bisection(float,float);
main()
{char q;
double d1,d2;
float a,b,h1,h2;
int i,m,n;
printf("\t\t\t实验三：数值积分\n");
printf("实验题目：分别用复化梯形公式和复化辛卜生公式计算f(x)=sin(x)/x的积分，并与准确值比较判断精度。
\n\n");
printf("请输入定积分的上下限：\n");
printf("定积分下限：a=");
scanf("%f",&a);
printf("定积分上限：b=");
scanf("%f",&b);
if(a==b)
{printf("积分上下限相等，定积分的值为0。
\n");
goto sign1;}
else
printf("请输入复化梯形公式划分的份数：");
scanf("%d",&n);
printf("请输入复化辛卜生公式划分的份数：");
scanf("%d",&m);
h1=(b-a)/n;
h2=(b-a)/m;
printf("复化梯形公式的步长为：h=%f\n",h1);
printf("复化辛朴生公式的步长为：h=%f\n",h2);
printf("复化梯形公式的结果是：\nT=%f\n",Trapezoid(a,b,h1,n));
printf("复化辛卜生公式的结果是：\nS=%f\n",Simpson(a,b,h2,m));
printf("定义计算该公式的结果是：\nI=%f\n",Integral(a,b));
d1=fabs(Integral(a,b)-Trapezoid(a,b,h1,n));
d2=fabs(Integral(a,b)-Simpson(a,b,h2,m));
printf("复化梯形公式的误差是：\nd=%f\n",d1);
printf("复化辛卜生公式的误差是：\nd=%f\n",d2);
if(d1>d2) printf("复化梯形公式的精度高于复化辛卜生公式的精度\n");
else if(d1==d2) printf("复化辛卜生公式和复化梯形公式的精度相等\n");
else printf("复化辛卜生公式的精度高于复化梯形公式的精度\n");
for(i=0;i<2;i++)
{if(i==0) printf("划分%d份的复化梯形公式的有效位数是小数点后的第%d位\n",n,SigDigT(d1,d2,i));
else printf("划分%d份的复化辛卜生公式的有效位数是小数点后的第%d位\n",m,SigDigT(d1,d2,i));}
sign1:
printf("\n是否继续?(y/n)\n");
printf("注：选y重新输入，选n返回主界面\n");
getchar();
q=getchar();
if(q=='y')
system("cls");
else if(q=='n')
{system("cls");
main();}
else {printf("您输入的字符不可识别，请重新输入!\n");
goto sign1;}}
double Trapezoid(float a,float b,float h1,int n)
{double x,y,t=0;
int i;
for(i=1;i<n;i++)
{x=a+i*h1;
if(x==0) y=2;
else y=2*(sin(x)/x);
t=t+y;}
if(a==0) t=t+1+sin(b)/b;
else if(b==0) t=t+1+sin(a)/a;
else t=t+sin(a)/a+sin(b)/b;
t=(h1/2)*t;
return t;}
double Simpson(float a,float b,float h2,int m)
{double x,y,s=0;
int i;
for(i=1;i<m;i++)
{x=a+i*h2;
if(x==0) y=2;
else y=2*(sin(x)/x);
s=s+y;}
for(i=0;i<m;i++)
{x=a+((1+2*i)*h2)/2;
if(x==0) y=4;
else y=4*(sin(x)/x);
s=s+y;}
if(a==0) s=s+1+sin(b)/b;
else if(b==0) s=s+1+sin(a)/a; else s=s+sin(a)/a+sin(b)/b;
s=(h2/6)*s;
return s;}
double Integral(float a,float b) {double h,x,y,I=0;
int n=500000;
h=(b-a)/500000;
for(n=0;n<500000;n++)
{x=a+n*h;
if(x==0) y=1;
else y=sin(x)/x;
I=I+y*h;}
return I;}
SigDigT(double d1,double d2,int i) {int j=0,k=0;
double r=1,t;
if(i==0)
{do{r=r*(0.1);
t=d1/r;
j++;}while(t<0.1);
return j;}
else
{do{r=r*(0.1);
t=d2/r;
j++;}while(t<0.1);
return j;}}。