研究生数学建模竞赛优秀论文设计(最终版)C
数学建模C题论文

191])()([),(20200y y x x r z y x z -+--=c y b x a y x y x z +⋅+⋅++=22),(4753⨯41i D i D 20.000160.001162021421339915152112032534791410.1 6660.1 2.5 2.666.11212.12525.16060.1/mcm05/probX 53⨯47Y 53⨯47k n m Z ⨯53⨯47 k n m Z ⨯~53⨯47i n m k H ⨯m m n k n 21n +120i n m k S ⨯i D126 18319719141164512X Y⎪⎪⎪⎭⎫ ⎝⎛=⨯⨯⨯⨯⨯⨯47532531534712111..................x x x x x x X ⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111..................y y y y y y),(y x Z =mnk ⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯),(...),,(),,(............),(...),,(),,(4753475325325315315347147121211111y x f y x f y x f y x f y x f y x f ⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111..................Z Z Z Z Z Z 1=imnk Z ~⎪⎪⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111~...~~............~...~~Z Z Z Z Z Z i imnkH ∆mnk Z i mnk Z ~⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯ii i i i i h h h h h h 47532531534712111............... (2)i mnkS∆∑∑=⨯=⨯4712531)(47531j i ji i hi D ∆∑=16411641i mnk S 4i i imnk H 5347imnk S mnk H i D 41 2),(y x Z = ),(y x Z =i D nk m ⨯ i mnk H mnk Z i mnk Z ~1~mnk Z 2~mnk Z 1mnk H 2mnk H imnkS∆∑∑=⨯=⨯4712531)(47531j ij i i h1mnk S 2mnk S⑤ 用i D ∆∑=16411641i mnk S 计算出1D 与2D ,则1D 和2D 的值较小者为最优方案.3 主要程序及结论通过数据处理与分析我们认为预测方法一比预测方法二好.所得计算结果值分别为:(1)不同时段的两种方法的实测与预测值的均方差:1mnkS =[0.9247218269e-1, .165797962696, 0.9247218269e-1,0.9247218269e-1, .2586806182, .2586806182, .2586806182, 2.791713932, .2474029514, .2539943168, .2715902174, .2715902174182, .2586806182, 2.791713932, .2474029514, .2539943168, .2715902174]2mnkS := [0.921412432e-1, .1098068392, 0.2234955063e-1,0.1592933205e-1, .2851304286, .2851304286, .2851304286, 2.792910527, .2612701098, .2381007694, .2613774987, 0.5183032655e-1,.2851304286,2.792810527, .2612701098, .2381007694, .2613774987] (2) 方法一的均方差为:1D := .8311398371方案二的均方差: 2D = .8417760978得1D <2D .主要程序与运行结果为: (1) 局域曲面拟合程序> solve({0.3=0.6-r*(0.045^2+0.042^2)},{r});> z1:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> z2:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> z3:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> z4:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> solve({0.15=0.3-r*(0.045^2+0.042^2)},{r});> z4:=0.3-39.58828187*[(x-118.1833)^2+(y-31.0833)^2];> solve({5.1=10.2-r*(0.045^2+0.042^2)},{r});> z1:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> z2:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> z3:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> z4:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> solve({0.1=0.2-r*(0.045^2+0.042^2)},{r});> z4:=0.2-26.39218791*[(x-118.4000)^2+(y-30.6833)^2];>z4:=solve({118.9833^2+30.6167^2+a*118.9833+b*30.6167+c=0.7000,118.5833^ 2+30.0833^2+a*118.5833+b*30.0833+c=1.8000,119.4167^2+30.8833^2+a*119.41 67+b*30.8833+c=0.5});> solve({0.05=0.1-r*(0.045^2+0.042^2)},{r});> z1:=0.1-13.19609396*[(x-119.4167)^2+(y-30.8833)^2];>> solve({2.9=5.8-r*(0.045^2+0.042^2)},{r});> z4:=0.1-765.3734495*[(x-118.2833)^2+(y-29.7167)^2];(2)均方差求值程序:>sq1:=[0.09247218269,0.165797962696,0.09247218269,0.09247218269,0.258680 6182,0.2586806182,0.2586806182,2.791713932,0.2474029514,0.2539943168,0. 2715902174,0.2715902174182,0.2586806182,2.791713932,0.2474029514,0.2539 943168,0.2715902174];> sum1:=add(i,i=sq1);> ave1:=sum1/17;>ve1:=[.5222900020,.5222900020,.5222900020,.5222900020,.5222900020,.5222 900020,.5222900020,.5222900020,.5222900020,.5222900020,.5222900020,.522 2900020,.5222900020,.5222900020,.5222900020,.5222900020,.5222900020,.52 22900020];>sq2:=[0.0921412432,0.1098068392,0.022********,0.01592933205,0.285130428 6,0.2851304286,0.2851304286,2.792910527,0.2612701098,0.2381007694,0.261 3774987,0.0518*******,0.2851304286,2.792810527,0.2612701098,0.238100769 4,0.2613774987];(2)数据模拟图程序:> with(linalg):> l:=matrix(91,7,[58138,32.9833,118.5167, 0.0000, 5.0000, 0.2000, 0.0000, 58139, 33.3000,118.8500, 0.0000, 3.9000, 0.0000, 0.0000,58141, 33.6667,119.2667, 0.0000, 0.0000, 0.0000, 0.0000,58143, 33.8000,119.8000, 0.0000, 0.0000, 0.0000, 0.0000,58146, 33.4833,119.8167, 0.0000, 0.0000, 0.0000, 0.0000,58147, 33.0333,119.0333, 0.0000, 6.0000, 1.4000, 0.0000,58148, 33.2333,119.3000, 0.0000, 1.1000, 0.3000, 0.0000,58150, 33.7667,120.2500, 0.0000, 0.0000, 0.0000, 0.1000,58154, 33.3833,120.1500, 0.0000, 0.0000, 0.0000, 0.0000,58158, 33.2000,120.4833, 0.0000, 0.0000, 0.0000, 0.0000,58230, 32.1000,118.2667, 3.3000,20.7000, 6.6000, 0.0000,58236, 32.3000,118.3000, 0.0000, 8.2000, 3.6000, 1.4000,58238, 32.0000,118.8000, 0.0000, 0.0000, 0.0000, 0.0000,58240, 32.6833,119.0167, 0.0000, 3.0000, 1.4000, 0.0000,58241, 32.8000,119.4500, 0.1000, 1.4000, 1.5000, 0.1000,58243, 32.9333,119.8333, 0.0000, 0.7000, 0.4000, 0.0000,58245, 32.4167,119.4167, 0.3000, 2.7000, 3.8000, 0.0000,58246, 32.3333,119.9333, 7.9000, 2.7000, 0.1000, 0.0000,58249, 32.2000,120.0000,12.3000, 2.4000, 5.6000, 0.0000,58251, 32.8667,120.3167, 5.2000, 0.1000, 0.0000, 0.0000, 58252, 32.1833,119.4667, 0.4000, 3.2000, 4.8000, 0.0000, 58254, 32.5333,120.4500, 0.0000, 0.0000, 0.0000, 0.0000, 58255, 32.3833,120.5667, 1.1000,18.5000, 0.5000, 0.0000, 58264, 32.3333,121.1833,35.4000, 0.1000, 0.2000, 0.0000, 58265, 32.0667,121.6000, 0.0000, 0.0000, 0.0000, 0.0000, 58269, 31.8000,121.6667,31.3000, 0.7000, 2.8000, 0.1000, 58333, 31.9500,118.8500, 8.2000, 8.5000,16.9000, 0.1000, 58334, 31.3333,118.3833, 4.9000,58.1000, 9.0000, 0.1000, 58335, 31.5667,118.5000, 5.4000,26.0000,11.0000, 0.8000, 58336, 31.7000,118.5167, 3.6000,27.8000,15.3000, 0.6000, 58337, 31.0833,118.1833, 7.0000, 6.4000,15.3000, 0.2000, 58341, 31.9833,119.5833,11.5000, 5.4000,16.1000, 0.0000, 58342, 31.7500,119.5500,32.6000,37.9000, 5.8000, 0.0000, 58343, 31.7667,119.9333,20.7000,24.3000, 5.3000, 0.0000, 58344, 31.9500,119.1667,12.4000, 5.9000,16.3000, 0.0000, 58345, 31.4333,119.4833,21.8000,18.1000, 9.8000, 0.1000, 58346, 31.3667,119.8167, 0.1000,12.7000, 5.1000, 0.2000, 58349, 31.2667,120.6333, 1.1000, 5.1000, 0.0000, 0.0000, 58351, 31.8833,120.2667,22.9000,15.5000, 6.2000, 0.0000, 58352, 31.6500,120.7333,15.1000, 5.4000, 2.4000, 0.0000, 58354, 31.5833,120.3167, 0.1000,12.5000, 2.4000, 0.0000, 58356, 31.4167,120.9500, 5.1000, 4.9000, 0.4000, 0.0000, 58358, 31.0667,120.4333, 2.4000, 3.4000, 0.0000, 0.8000, 58359, 31.1500,120.6333, 1.5000, 3.8000, 0.5000, 0.1000, 58360, 31.9000,121.2000, 5.6000, 3.2000, 2.9000, 0.1000, 58361, 31.1000,121.3667, 3.5000, 0.6000, 0.2000, 0.7000, 58362, 31.4000,121.4833,33.0000, 4.1000, 0.9000, 0.0000, 58365, 31.3667,121.2500,17.7000, 2.2000, 0.1000, 0.0000, 58366, 31.6167,121.4500,75.2000, 0.4000, 1.5000, 0.0000, 58367, 31.2000,121.4333, 7.2000, 2.8000, 0.2000, 0.2000, 58369, 31.0500,121.7833, 3.2000, 0.3000, 0.0000, 0.3000, 58370, 31.2333,121.5333, 7.0000, 3.4000, 0.2000, 0.2000, 58377, 31.4667,121.1000, 7.8000, 7.2000, 0.3000, 0.0000, 58426, 30.3000,118.1333, 0.0000, 0.0000,17.6000, 6.2000, 58431, 30.8500,118.3167, 5.1000, 2.3000,16.5000, 0.1000, 58432, 30.6833,118.4000, 3.6000, 1.4000,20.5000, 0.2000, 58433, 30.9333,118.7500, 2.1000, 3.4000, 8.5000, 0.2000, 58435, 30.3000,118.5333, 0.0000, 0.0000,13.6000, 8.5000, 58436, 30.6167,118.9833, 0.0000, 0.0000, 5.3000, 0.5000, 58438, 30.0833,118.5833, 0.0000, 0.0000,27.6000,21.8000, 58441, 30.8833,119.4167, 0.1000, 1.6000, 1.6000, 1.0000, 58442, 31.1333,119.1833, 3.0000, 8.8000, 5.4000, 0.2000, 58443, 30.9833,119.8833, 0.1000, 2.7000, 0.1000, 0.9000,58446, 30.9667,119.6833, 0.0000, 0.1000, 5.1000, 2.5000, 58448, 30.2333,119.7000, 0.0000, 0.0000,15.1000, 6.9000, 58449, 30.0500,119.9500, 0.0000, 0.0000,23.5000, 8.2000, 58450, 30.8500,120.0833, 0.0000, 0.7000, 0.0000, 4.1000, 58451, 30.8500,120.9000, 0.5000, 0.1000, 0.0000, 3.8000, 58452, 30.7833,120.7333, 0.3000, 0.0000, 0.0000, 3.0000, 58453, 30.0000,120.6333, 0.0000, 0.0000, 0.0000,18.2000, 58454, 30.5333,120.0667, 0.0000, 0.0000, 0.5000, 4.9000, 58455, 30.5167,120.6833, 0.0000, 0.0000, 0.0000, 4.6000, 58456, 30.6333,120.5333, 0.0000, 0.0000, 0.0000, 4.2000, 58457, 30.2333,120.1667, 0.0000, 0.0000, 2.0000,12.6000, 58459, 30.2000,120.3167, 0.0000, 0.0000, 0.0000,15.0000, 58460, 30.8833,121.1667, 1.2000, 0.1000, 0.0000, 2.3000, 58461, 31.1333,121.1167, 4.0000, 1.4000, 0.4000, 0.2000, 58462, 31.0000,121.2500, 2.7000, 0.3000, 0.4000, 1.7000, 58463, 30.9333,121.4833, 1.7000, 0.1000, 0.0000, 0.8000, 58464, 30.6167,121.0833, 0.0000, 0.0000, 0.0000, 3.6000, 58467, 30.2667,121.2167, 0.0000, 0.0000, 0.0000, 1.8000, 58468, 30.0667,121.1500, 0.0000, 0.1000, 5.1000, 2.5000, 58472, 30.7333,122.4500, 0.3000, 0.6000, 0.0000, 4.9000, 58477, 30.0333,122.1000, 0.0000, 0.0000, 0.0000, 0.0000, 58484, 30.2500,122.1833, 0.0000, 0.0000, 0.0000, 0.0000, 58530, 29.8667,118.4333, 0.0000, 0.0000,27.5000,23.6000, 58531, 29.7167,118.2833, 0.0000, 0.0000, 3.7000,11.5000, 58534, 29.7833,118.1833, 0.0000, 0.0000, 9.3000, 6.5000, 58542, 29.8167,119.6833, 0.0000, 0.0000, 0.0000,27.6000, 58550, 29.7000,120.2500, 0.0000, 0.0000, 0.0000, 4.9000, 58562, 29.9667,121.7500, 0.0000, 0.0000, 0.0000, 0.9000]);> lat:=col(l,2);> lon:=col(l,3); > sd1:=col(l,4);> sd2:=col(l,5); > sd3:=col(l,6); > sd4:=col(l,7);> abc1:=seq([lat[i],lon[i],sd1[i]],i=1..91);> abc2:=seq([lat[i],lon[i],sd2[i]],i=1..91);> abc3:=seq([lat[i],lon[i],sd3[i]],i=1..91);> abc4:=seq([lat[i],lon[i],sd4[i]],i=1..91);> with(plots):> pointplot3d([abc1],color=green,axes=boxed);> surfdata([abc1],labels=["x","y","z"],axes=boxed);> with(stats):> with(fit):> with(plots):fx1:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc1]);> plot3d(fx1,x=25..35,y=119..135);> pointplot3d([abc2],color=blue,axes=boxed);> surfdata([abc2],labels=["x","y","z"],axes=boxed);>fx2:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc2]);> plot3d(fx2,x=25..35,y=119..135);> pointplot3d([abc3],color=red,axes=boxed)> surfdata([abc3],labels=["x","y","z"],axes=boxed);>fx3:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc3]);> surfdata([abc4],labels=["x","y","z"],axes=boxed);>fx4:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc4]);五.如何在评价方法中考虑公众感受的数学模型建立.1660.1 2.5 2.666.11212.12525.16060.1z } 1.00 {0≤≤=z z R } 5.21.0 {1≤≤=z z R } 66.2 {2≤≤=z z R } 121.6 {3≤≤=z z R } 251.12 {4≤≤=z z R } 601.25 {5≤≤=z z R } 1.60 {6≥=z z R 0ˆR 1ˆR 2ˆR 3ˆR 4ˆR 5ˆR 6ˆR } 1)( {ˆ000R z z z R ∈≤=,μ} 1)( {ˆ111R z z z R ∈≤=,μ} 1)( {ˆ222R z z z R ∈≤=,μ } 1)( {ˆ333R z z z R ∈≤=,μ} 1)( {ˆ444R z z z R ∈≤=,μ} 1)( {ˆ555R z z z R ∈≤=,μ } 1)( {ˆ666R z z z R ∈≤=,μ)(z i μ i 1z ∈i R i R )(z i μ i 16i R ˆ i 1 2)(z i μ i 1⎩⎨⎧≤<+-≤≤=1.006.0 , 5.22506.00, 1)(0z z z z μ)(1z μ] 2369277587.0e [2369277587.0112)3.1(----z 5.21.0≤≤z )(2z μ] 20555762126.0e [20555762126.0112)3.4(----z 66.2≤≤z)(3z μ] 2287787270.0e [2287787270.0119.5)05.9(2----z 121.6≤≤z )(4z μ] 70397557815.0e[70397557815.0119.12)55.18(2----z 251.12≤≤z)(5z μ] 00475951221.0e[00475951221.011100)55.42(2----z 601.25≤≤z)(6z μ2)]5.60(5 [11--+z 1.60≥z 74)(z i μ及iR ˆ i =0,1,…,6合并可得} 0 {≥=z z R 上的模糊集合} , 1)( {ˆR z z z R∈≤=μ.其中R 是论域,)(z μ是模糊集合R ˆ的隶属函数,由)(z i μ分段合)(z μ小雨的隶属函数图特大暴雨隶属函数图大暴雨隶属函数图暴雨隶属函数图⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧>≤<≤<≤<≤<≤<≤≤=60)(6025)(2512)(126)(65.2)(5.21.0)(1.00)()(6543210z z z z z z z z z z z z z z t μμμμμμμμ 5 353⨯47imnkZ ~)(z μ53⨯47=M mnk⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111..................μμμμμμ=M imnk~⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111~...~~............~...~~μμμμμμi ),(y x Z =i mnk ∏∆mnk M =M i mnk~⎪⎪⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯⨯i i i i i i 47532531534712111..................λλλλλλ 6imnkΓ∆∑∑=⨯=⨯4712531)(47531j i j i i λ i Ω∆∑=16411641i imnkΓ 8 i 2i i i mnk ∏5347imnk Γi mnk ∏i Ω411Ω2Ω 1Ω2Ω1D 2D19811999。
优秀的数学建模论文范文(通用8篇)

优秀的数学建模论文范文第1篇摘要:将数学建模思想融入高等数学的教学中来,是目前大学数学教育的重要教学方式。
建模思想的有效应用,不仅显著提高了学生应用数学模式解决实际问题的能力,还在培养大学生发散思维能力和综合素质方面起到重要作用。
本文试从当前高等数学教学现状着手,分析在高等数学中融入建模思想的重要性,并从教学实践中给出相应的教学方法,以期能给同行教师们一些帮助。
关键词:数学建模;高等数学;教学研究一、引言建模思想使高等数学教育的基础与本质。
从目前情况来看,将数学建模思想融入高等教学中的趋势越来越明显。
但是在实际的教学过程中,大部分高校的数学教育仍处在传统的理论知识简单传授阶段。
其教学成果与社会实践还是有脱节的现象存在,难以让学生学以致用,感受到应用数学在现实生活中的魅力,这种教学方式需要亟待改善。
二、高等数学教学现状高等数学是现在大学数学教育中的基础课程,也是一门必修的课程。
他能为其他理工科专业的学生提供很多种解题方式与解题思路,是很多专业,如自动化工程、机械工程、计算机、电气化等必不可少的基础课程。
同时,现实生活中也有很多方面都涉及高数的运算,如,银行理财基金的使用问题、彩票的概率计算问题等,从这些方面都可以看出人们不能仅仅把高数看成是一门学科而已,它还与日常生活各个方面有重要的联系。
但现在很多学校仍以应试教育为主,采取填鸭式教学方式,加上高数的教材并没有与时俱进,将其与生活的关系融入教材内,使学生无法意识到高数的重要性以及高数在日常生活中的魅力,因此产生排斥甚至对抗的心理,只是在临考前突击而已。
因此,对高数进行教学改革是十分有必要的,而且怎么改,怎么让学生发现高数的魅力,并积极主动学习高数也是作为教师所面临的一个重大问题。
三、将数学建模思想融入高等数学的重要性第一,能够激发学生学习高数的兴趣。
建模思想实际上是使用数学语言来对生活中的实际现象进行描述的过程。
把建模思想应用到高等数学的学习中,能够让学生们在日常生活中理解数学的实际应用状况与解决日常生活问题的方便性,让学生们了解到高数并不只是一门课程,而是整个日常生活的基础。
研究生数学建模竞赛优秀论文(最终版)C

研究生数学建模竞赛优秀论文(最终版)C全国第三届研究生数学建模竞赛题目维修线性流量阀时的内筒设计问题(C 题)针对问题1,首先考察了内孔为四种特殊形状的情况下,“过流面积”随曲线下降距离的变化情况,得到凸凹圆曲线与严格线性面积特性曲线偏差的平方和最小,线性关系保持得比较良好。
此后利用微元法证明了“过流面积”呈严格线性变化时曲线和外孔圆交点横坐标的差为定值这一性质,得出了在此种情况下曲线在两交点处的斜率应为无穷大。
基于以上分析,利用最小二乘原理建立了无约束泛函极值模型,采用了变分法将其转化为微分方程,再转化为等效的变分原理,采用Ritz 算法近似求解。
最后通过对内筒孔曲线的合理假设,得到了满足线性关系较好的内孔曲线形状(见图11),其样本点的偏差平方和为0.064412。
针对问题2,利用最小二乘原理建立了有约束泛函极值模型。
根据文中第四节中的引理,给出理想状态下的内孔形状。
之后对其进行了微调,通过牺牲严格的线性关系来使其逐渐满足两个约束75%h Q ≥和85%S Q ≥,并最终找到了合适的内孔设计方案(见图13(b ))。
最后针对外孔磨损情况提出了基于自动控制理论和逆向工程技术等的解决办法。
本文提出的模型是从考察内孔的特殊形状中得到启发的,从而具有实际应用价值和准确性。
关键词:线性阀体最小二乘法泛函极值模型变分原理非线性规划一、问题的提出阀体是我们日常工作和生活中一种十分常见的工具。
它种类繁多,其中线性阀体可使阀体的旋转角度和流量成正比。
因而它可使人们方便地对流量进行控制。
而如何设计线性阀体成为当今控制领域中研究的热点问题之一。
现在我们需要设计出一种阀体,它由两个同心圆柱筒组成。
外筒固定,其侧面上有一个孔,形状为两个直径不等的圆柱体的交线。
内筒和外筒轴向之间没有相对运动,内筒可以自由转动。
内筒的侧面上也有一个孔,但它原来的形状未知。
要求设计出内筒孔的形状,使得“过流面积”与内筒旋转角成近似线性关系;在线性区间至少达“最大范围”区间长度的75%以上,而且主要工作区的最大“过流面积”至少要达到外筒孔面积的85%以上,并且使“过流面积”和内筒的旋转角度之间的“线性关系”尽量好的约束限制下,重新设计内筒孔的形状。
数学建模优秀论文(精选范文10篇) 2021

根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题,这就是数学建模,本篇文章主要是向大家介绍几篇数学建模优秀论文得范文,希望对有这方面参考得学者有所帮助。
数学建模优秀论文精选范文10篇之第一篇:培养低年段学生数学建模意识得微课教学---------------------------------------------------------------------------------------------------------------------感谢使用本套资料,希望本套资料能带给您一些思维上的灵感和帮助,个人建议您可根据实际情况对内容做适当修改和调整,以符合您自己的风格,不太建议完全照抄照搬哦。
---------------------------------------------------------------------------------------------------------------------摘要:本文阐述了录制微课对培养学生建模意识得必要性和可行性,认为在小学数学教学中,鼓励低年段学生录制微课有积极意义,主张提高小学生建模语言表达能力,通过任务驱动和学生自主录制微课,逐步深入学习建模内容,培养并增强学生得建模意识。
关键词:低年段数学; 微课; 建模意识;当今社会,信息技术高速发展使教学资源高度丰富。
广大教师纷纷探讨如何利用信息技术更好地为教学服务,有效地改进教与学得方式,提高学生学习兴趣。
一、录制微课对培养学生建模意识得必要性和可行性“三年级现象”备受关注,很多人认为小学三年级是道坎,有得学生一、二年级数学成绩很好,到了三年级就断崖式下降。
如果真得出现这种现象,那么学生一、二年级数学成绩好只是表象。
一、二年级是学生初步感知数学得重要时期。
低年段数学知识是基础,对于低年段数学教学包括建模教学必须引起广大教育工作者得重视,让学生从小接受正确得教学模式,真正掌握学习数学得思想方法,避免出现短暂成绩好得现象。
2023全国研究生数学建模竞赛c题

2023全国研究生数学建模竞赛c题数学建模竞赛是促进数学教育和科研创新的重要平台,对于培养学生的综合素质和创新能力起到了积极的推动作用。
2023年全国研究生数学建模竞赛C题是一道涉及到车辆行驶路径规划的问题。
本文将从问题背景、模型建立、解决方案和实施效果等方面进行论述。
1. 问题背景题目所描述的背景为某城市的道路网格以及道路上的车流量数据。
我们需要使用给定的数据进行最佳路径规划,即通过合理的算法找到两个道路网格之间的最短路径,并在此基础上进行路径优化。
这样可以实现减少行驶距离、提高交通效率的目标。
2. 模型建立在建立数学模型之前,我们首先需要对问题进行分析和抽象。
通过对题目的仔细阅读和理解,我们可以将其抽象为一个图论中的最短路径问题。
在这个问题中,每一个网格可以看作是图的一个节点,道路可以看作是节点之间的边,车流量则可以看作是边的权重。
基于上述分析,我们可以使用迪杰斯特拉算法来解决最短路径问题。
该算法可以在有向图中找到从一个节点到其他节点的最短路径,并且可以通过添加权重来优化路径。
3. 解决方案(1)数据预处理:首先,我们需要对车流量数据进行预处理,将车流量转化为边的权重。
可以根据车流量数据的大小来设定不同的权重,例如车流量越小,权重越大。
(2)最短路径规划:我们使用迪杰斯特拉算法来计算两个节点之间的最短路径。
算法的具体步骤如下:a. 创建一个距离数组dist[],用于存储每个节点到起始节点的最短距离,初始化为无穷大。
b. 创建一个visited[]数组,用于标记节点是否已经被访问过,初始化为False。
c. 设置起始节点的最短距离为0,将其加入到已访问节点集合中。
d. 遍历与起始节点相连的节点,更新节点的最短距离,即若通过当前节点到达其他节点的距离小于已知最短距离,则更新最短距离。
e. 选择一个未被访问的节点中最小距离的节点,将其标记为已访问,并重复上述步骤。
(3)路径优化:基于最短路径规划的结果,我们可以通过添加权重来进一步优化路径。
数学建模竞赛2005年C题论文

雨量预报方法评价的数学模型摘要:降雨是日常生活中最常见的天气现象,及时准确地对降雨量作出预报是一个十分困难的问题。
题目给出了用两种降雨量预测方法预测得出的41天各时段网格结点的预报数据,我们对预报方法进行评价。
先使用二元三次样条插值法,对91个站点位置进行插值,从而求出各站点预报数据,然后用方差分析计算两种预测方法每一天的拟合优度2R ,从而评价两种预报方法的准确性。
第一种方法拟合优度2R 的平均值为0.9087,第二种方法为0.9054,可见这两种方法的预测准确性都比较高,但第一种比第二种的精确度更高。
在评价方法中考虑公众的感受,即考虑公众对预报结果的满意率和满意度。
本文建立了两个模型,即满意率模型和满意度模型。
满意率指满意数与总数的比率;满意度指达到公众满意的程度。
两个模型分别运用算术平均数和加权平均数的方法以及概率的知识进行求解,第一种方法的9953.0=ε,9447.5=f ,第二种方法的9950.0=ε,9397.5=f ,可见公众对这两种方法的预测值都比较满意,但第一种方法给公众的感受优于第二种。
关键词:二元三次样条插值法 拟合优度 满意率 满意度1、问题的重述本题是一道由气象部门提出,期望建立一种科学评价雨量预报方法好坏的数学模型与方法。
在本题中,气象部门所采用了两种方案研究6小时雨量预报方法。
所谓6小时雨量预报方法是指每天晚上20点预报从21点开始的4个时段(21点至次日3点,次日3点至9点,9点至15点,15点至21点)在某些位置的雨量,这些位置位于东经120度、北纬32度附近的53×47的等距网格点上。
同时设立91个观测站点实测这些时段的实际雨量,由于各种条件的限制,站点的设置是不均匀的。
气象部门提供了41天的用两种不同方法的预报数据和相应的实测数据。
预报数据在文件夹FORECAST中,实测数据在文件夹MEASURING中。
FORECAST中的文件lon.dat 和lat.dat分别包含网格点的经纬度,其余文件名为<f日期i>_dis1和<f日期i>_dis2,例如f6181_dis1中包含2002年6月18日晚上20点采用第一种方法预报的第一时段数据(其2491个数据为该时段各网格点的雨量),而f6183_dis2中包含2002年6月18日晚上20点采用第二种方法预报的第三时段数据。
仅供参考第十二届五一数学建模联赛C题优秀论文

仅供参考第十二届五一数学建模联赛C题优秀论文本文是一篇关于第十二届五一数学建模联赛C题的优秀论文,旨在为读者提供一个参考。
第十二届五一数学建模联赛C题是一个涉及网络传输的问题。
具体而言,该题目要求考察在网络传输的场景下,如何通过合理安排传输路径来实现数据的快速传输。
这是一个非常实际的问题,因为在现实生活中,网络传输一直是我们所依赖的重要工具之一。
为了解决该问题,我们可以从以下几个方面进行论述。
首先,我们可以从理论角度出发,探讨网络传输的原理和相关概念。
例如,我们可以介绍数据传输的基本原理,如分组交换和电路交换等。
此外,我们还可以介绍网络拓扑结构和路由算法等概念,以及它们在实际网络中的应用。
通过对这些基本概念的深入理解,我们可以更好地理解网络传输问题的本质。
其次,我们可以从实际问题出发,讨论网络传输中常见的挑战和解决方案。
例如,网络中常常会遇到拥塞的问题,即当数据流量过大时,网络的带宽无法满足需求,从而导致数据传输的延迟和丢包现象。
为了解决这一问题,可以采取一些调度算法,如流量控制和拥塞避免等。
此外,我们还可以讨论其他可能的问题,如安全性和可靠性等方面。
在研究网络传输问题时,我们还可以结合数学建模的方法,将问题抽象为数学模型,并通过数学工具对问题进行分析和求解。
例如,我们可以采用图论的方法来描述网络拓扑结构,并通过最短路径算法来确定合适的传输路径。
此外,我们还可以使用排队论的方法来分析网络传输的延迟和丢包概率等问题。
最后,我们可以通过实例分析来验证我们所提出的解决方案的有效性。
通过选择一些实际案例或仿真结果,我们可以对我们的方案进行评估,并与其他现有的方法进行比较。
这将有助于读者更好地理解我们的解决方案,并对其可行性和适用性进行评估。
综上所述,本文围绕第十二届五一数学建模联赛C题,从理论角度和实际问题出发,探讨了网络传输问题的解决方法。
通过深入研究相关概念和数学建模的方法,我们提出了一种可行的解决方案,并通过实例验证了其有效性。
2023 数学建模 c题

2023 数学建模 c题
2023年数学建模竞赛C题:
题目:在工业生产中,原料的纯度是一个重要的质量指标。
例如,在半导体行业中,高纯度硅是制造集成电路的重要原料。
为了获得高纯度的硅,需要从含有多种杂质的硅原料中去除杂质。
本题将探讨如何通过数学建模和优化方法来提高硅原料的纯度。
具体问题:假设你是一家半导体公司的工程师,需要从含有多种杂质的硅原料中去除杂质。
给定原料中各杂质的含量,以及可用的净化设备和操作参数,你的任务是制定一个有效的净化方案,以最大限度地提高最终产品的纯度。
要求:
1. 分析影响硅原料纯度的主要因素;
2. 建立一个数学模型,描述杂质去除的过程,并使用该模型进行优化;
3. 根据给定的数据和约束条件,提出一个可行的净化方案;
4. 使用适当的软件或编程语言实现该方案,并模拟净化过程;
5. 根据模拟结果,评估所提出方案的性能,并给出改进建议。
注意事项:
1. 硅原料的纯度可以通过测量杂质含量来评估;
2. 净化设备的操作参数可能受到物理和化学限制;
3. 净化过程可能需要多个步骤,每个步骤都可能影响最终产品的纯度。
提示:为了解决这个问题,你可能需要考虑杂质去除的机制、操作参数的选择、多步骤净化的策略、数学建模和优化方法的应用等多个方面。
第二届研究生数学建模竞赛C题优秀论文(1)

城市出租车交通规划综合模型一、问题重述城市中出租车的需求随着经济发展、城市规模扩大及居民生活方式改变而不断变化。
目前某城市中出租车行业管理存在一定的问题,城市居民普遍反映出租车价格偏高,另一方面,出租车司机却抱怨劳动强度大,收入相对来说偏低,整个出租车行业不景气,长此以往将影响社会稳定。
现为了配合该城市发展的战略目标,最大限度地满足城市中各类人口的出行需要,并协调市民、出租车司机和社会三者的关系,实现该城市交通规划可持续发展,需解决以下的问题:(1)从该城市当前经济发展、城市规模及总体人口规划情况出发,类比国内城市情况,预测该城市居民的出行强度和出行总量,这里的居民指的是该城市的常住人口。
同时结合人口出行特征,进一步给出该城市当前与今后若干年乘坐出租车人口的预测模型。
(2)根据该城市的公共出行情况与出租车主要状况,建立出租车最佳数量预测模型。
(3)油价调整(3.87元/升与4.30元/升)会影响城市居民与出租车司机的双方的利益关系,给出能够使双方都满意的价格调节最优方案。
(4)针对当前的数据采集情况,提出更合理且实际可行的数据采集方案。
(5)从公用事业管理部门的角度考虑出租车规划的问题,写一篇短文介绍自己的方案。
二、模型假设1.常住人口和暂住人口的出行特征相近,划分为第一类人,在所有分析过程中假设其出行特征完全一样。
而短期及当日进出人口为第二类。
2.由于短期及当日进出人口情况复杂,假设第二类人口在于乘坐出租车方面相关出行特征(如乘车出行强度等)在未来几年内保持不变。
3.由于城市地理状况和居民的生活习惯在短时期内不易改变,所以在各交通小4.假设居民中出行人口占总人口数的比例不变。
5.假设对于出行人口而言,在出行方式选择方面的比例与出行人次的比例一样。
6.假设在未来几年内,出租车固定营运成本不变。
7.由于每次一起打车的人数,与居民的生活习惯相关,所以假设出租车每趟载客人次不变,即不受出租车数目和收费方案的不同而改变。
全国大学生数学建模竞赛C题国家奖一等奖优秀论文

脑卒中发病环境因素分析及干预摘要本文主要讨论脑卒中发病环境因素分析及干预问题。
根据题中所给出的数据,利用SPSS20 软件进行相关性统计分析,分别对各气象因素进行单因素分析,进而建立后退法线性回归分析模型,得到脑卒中与气压、气温、相对湿度之间的关系。
同时在广泛收集各种资料并综合考虑环境因素,对脑卒中高危人群提出预警和干预的建议方案。
首先,利用SPSS20软件,从患病人群的性别、年龄、职业进行统计分析,得到2007-2010年男性患病人数高于女性,且男性所占比例有逐年下降趋势,女性则有上升趋势,因此,性别比例呈减小趋势。
分析不同年龄段患病人数,得到患病高峰期为75-77岁之间,且青少年比例逐年呈增长趋势,可见患病比例趋于年轻化。
同时在不同的职业中,农民发病人数最多,教师,渔民,医务人员,职工,离退人员的发病人数较少。
其次,由题中所给数据先进行单因素分析,剔除对脑卒中影响不显著的因素,得出气温、气压、相对湿度对脑卒中的影响程度大小,进而采用后退法线性回归分析建立模型,利用SPSS20对数据进行分析,求得脑卒中发病率与气温、气压、相对湿度之间的关系。
即发病率与平均温度成正相关,与最高温度成负相关,发病率与平均气压成正相关,与最低气压成负相关,与平均相对湿度成负相关,与最小相对湿度成正相关。
最后,通过查找资料发现,影响脑卒中的因素有两类,一类是不可干预因素,如年龄、性别、家族史,另一类是可干预因素,如高血压、高血脂、糖尿病、肥胖、抽烟、酗酒等因素。
分析这些因素,建立双变量因素分析模型,并结合问题1和问题2,对高危人群提出预警和干预的建议方案。
关键词脑卒中单因素分析后退法线性回归分析双变量因素分析一问题的重述脑卒中(俗称脑中风)是目前威胁人类生命的严重疾病之一,它的发生是一个漫长的过程,一旦得病就很难逆转。
这种疾病的诱发已经被证实与环境因素,包括气温、湿度之间存在密切的关系。
对脑卒中的发病环境因素进行分析,其目的是为了进行疾病的风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病的健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护。
数学建模论文(精选4篇)

数学建模论文(精选4篇)数学建模论文模板篇一1数学建模竞赛培训过程中存在的问题1.1学生数学、计算机基础薄弱,参赛学生人数少以我校理学院为例,数学专业是本校开设最早的专业,面向全国28个省、市、自治区招生,包括内地较发达地区的学生、贫困地区(包括民族地区)的学生,招收的学生数学基础水平参差不齐.内地较发达地区的学生由于所处地区的经济文化条件较好,教育水平较高,高考数学成绩普遍高于民族地区的学生.民族地区由于所处地区经济文化较落后,中小学师资力量严重不足,使得少数民族学生数学基础薄弱,对数学学习普遍抱有畏难情绪,从每年理学院新生入学申请转系的同学较多可以窥见一斑.虽然学校每年都组织学生参加全国大学生数学建模竞赛,但人数都不算多.从专业来看,参赛学生主要以数学系和计算机系的学生为主,间有化学、生科、医学等理工科学生,文科学生则相对更少.理工科类的学生基本功比较扎实,他们在参赛过程中起到了重要作用.文科学生数学和计算机功底大多薄弱,更多的只是一种参与.从年级来看,参赛学生以大二的学生居多;大一的学生已学的数学和计算机课程有限,基本功还有些欠缺;大三、大四的学生忙着考研和找工作,对数学建模竞赛兴趣不大.从参赛的目的来看,有20%左右的学生是非常希望通过数学建模提高自己的综合能力,他们一般能坚持到最后;还有50%的学生抱着试试看的态度参加培训,想锻炼但又怕学不懂,觉得可以坚持就坚持,不能则中途放弃;剩下的30%的学生则抱着好奇好玩的态度,他们大多早早就出局了.学生的参赛积极性不高,是制约数学建模教学及竞赛有效开展的不利因素.1.2无专职数学建模培训教师,培训教师水平有限,培训方法落后数学建模的培训教师主要由理学院选派数学老师临时组成,没有专职从事数学建模的教师.由于学校扩招,学生人数多,教师人数少,数学教师所承担的专业课和公共课课程多,授课任务重;备课、授课、批改作业占用了教师的大部分工作时间,并且还要完成相应的科研任务.而参加数学建模教学及竞赛培训等工作需要花费很多时间和精力,很多老师都没有时间和精力去认真从事数学建模的教学工作.培训教师队伍整体素质不够强、能力欠缺,指导起学生来也不是那么得心应手,且从事数学建模教学的老师每年都在调整,不利于经验的积累.另外,学校对参与数学建模教学及竞赛培训的教师的鼓励措施还不是十分到位和吸引人,培训教师对数学建模相关的工作热情不够,缺乏奉献精神.在2011年以前,数学建模培训主要采用教师授课的方式进行,但各位老师授课的内容互不联系.比如说上概率论的老师就讲概率论的内容,上常微分方程的老师就讲常微分的内容.学生学习了这些知识,不知道有什么用,怎么用,不能将这些知识联系起来转化为数学建模的能力.这中间缺少了很重要的一个环节,就是没有进行真题实训.结果就是学生既没有运用这些知识构建数学模型的能力,也谈不上数学建模论文写作的技巧.虽然学校年年都组织学生参加全国大学生数学建模竞赛,但结果却不尽如人意,获奖等次不高,获奖数量不多.1.3学校重视程度不够,相关配套措施还有待完善任何一项工作离开了学校的支持,都是不可能开展得好的,数学建模也不例外.在前些年,数学建模并没有引起足够的重视,学校盼望出成绩但是结果并不理想,对老师和学生的信心不足.由于经费紧张,并未专门对数学建模安排实验室,图书资料很少,学生用电脑和查资料不方便,没有学习氛围.每年数学建模竞赛主要由分管教学的副院长兼任组长,没有相应专职的负责人,培训教师去参加数学建模相关交流会议和学习的机会很少.学校和二级学院对参加数学建模教学、培训的老师奖励很少,学生则几乎没有.在课程的开设上也未引起重视,虽然理学院早在1997年就将数学实验和数学建模课列为专业必修课,但非数学专业只是近几年才开始列为公选课开设,且选修率低.2针对存在问题所采取的相应措施2.1扩大宣传,重视数学和计算机公选课开设,举办数学建模学习讨论班最近两年,学院组建了数学建模协会,负责数学建模的宣传和参赛队员的海选,通过各种方式扩大了对数学建模的宣传和影响,安排数学任课教师鼓励数学基础不错的学生参赛.同时邀请重点大学具有丰富培训经验的老师来做数学建模专题讲座,交流经验.学院重视数学专业的基础课程、核心课程的教学,选派经验丰富的老教师、青年骨干教师担任主讲,随时抽查教学质量,教学效果.严抓考风学风,对考试作弊学生绝不姑息;学生上课迟到、早退、旷课一律严肃处理.通过这些举措,学生学习态度明显好转,数学能力慢慢得到提高.学校有意识在大一新生中开设数学实验、数学建模和相关计算机公选课,让对数学有兴趣的学生能多接触这方面的知识,减少距离感.选用的教材内容浅显而有趣味,主要目的是让同学们感受到数学建模并非高不可攀,数学是有用的,增加学生学习数学的热情和参加数学建模竞赛的可能性.为了解决学生学习数学建模过程中的遇到的困难,学院组织老师、学生参加数学建模周末讨论班,老师就学生学习过程中遇到的普遍问题进行讲解,学生分小组相互讨论,尽量不让问题堆积,影响后续学习积极性.通过这些措施,参赛学生的人数比以往有了大的改观,参赛过程中退赛的学生越来越少,参赛过程中的主动性也越来越明显.2.2成立数学建模指导教师组,分批培养培训教师,改进培训方法近年来,学院开始重视对数学建模培训教师的梯队建设,成立了数学建模指导教师组.把培训教师分批送出去进修,参加交流会议,学习其它高校的经验,并安排老教师带新教师,培训教师队伍越来越稳定、壮大.从去年开始,理学院组织学生进行了为期一个月的暑期数学建模真题实训,从8月初到8月底,培训共分为7轮.学生首先进行三天封闭式真题训练———其次答辩———最后交流讨论.效果明显,学生的数学建模能力普遍得到了提高,学习积极性普遍高涨.9月份顺利参加了全国大学生数学建模竞赛.从竞赛结果来看,比以前有了比较大的进步,不管是获奖的等次还是获奖的人数上都取得了历史性突破.有了这些可喜的变化,教师和学生的积极性都得到了提高,对以后的数学建模教学和培训工作将起着极大的促进作用.除了这种集训,今后,数学建模还需要加强平时的教学和培训工作.2.3学校逐渐重视,加大了相关投入,完善了激励措施最近几年,学校加大了对数学建模教学和培训工作的相关投入和鼓励措施.安排了专门的数学建模实验室,配备了学院最先进的电脑、打印机等设备,购买了数学建模相关的书籍.划拨了数学建模教学和培训专项经费.虽然数学建模教学还没有计入教学工作量,但已经考虑计入职称评定的相关工作量中,对参加数学建模教学和培训的老师减少了基本的教学工作量,使他们有更多的时间和精力投入到数学建模的相关工作中去.对参加全国大学生数学建模竞赛获奖的老师和学生的奖励额度也比以前有了很大的提高,老师和学生的积极性得到了极大的提高.3结束语对我们这类院校而言,最重要的数学建模赛事就是一年一度的全国大学生数学建模竞赛了.竞赛结果大体可以衡量老师和学生的付出与收获,但不是绝对的,教育部组织这项赛事的初衷主要是为了促进各个院校数学建模教学的有效开展.如果过分的看重获奖等次和数量,对学校的数学建模教学和组织工作都是一种伤害.参赛的过程对学生而言,肯定是有益的,绝大多数参加过数学建模竞赛的学生都认为这个过程很重要.这个过程可能是四年的大学学习过程中体会最深的,它用枯燥的理论知识解决了活生生的现实中存在的问题,虽然这种解决还有部分的理想化.由于我校地处偏远山区,教育经费相对紧张,投入不可能跟重点院校的水平比,只能按照自身实际来.只要学校、老师、学生三方都重视并积极参与这一赛事,数学建模活动就能开展的更好.数学建模论文模板篇二培养应用型人才是我国高等教育从精英教育向大众教育发展的必然产物,也是知识经济飞速发展和市场对人才多元化需求的必然要求。
研究生数学建模竞赛优秀论文

题 目
基于临床与基因图谱的结肠癌基因标签提取
摘
要
由于基因间的调控和相互作用表现为“功能基因组合”形式,基因的功能与 作用是集体作用的结果,而非单个基因单独作用的结果,表现在分类特征对样本 的分类能力方面就是以特征集合的形式整体体现出来的。根据这个生物学知识, 本文考察由多个基因构成的基因簇作为区分正常人和癌症患者的分类因素, 利用 独立成分分析(ICA)技术对已给出的基因表达采样数据进行分析,最大程度地降 低基因之间强烈的相互影响, 从而获得对判断是否患有肿瘤或者癌症的最有直接 关系但数目较少的潜在因素, 即基因簇信息。 随后, 我们采用了支持向量机(SVM) 依据提取出的潜在因素 (基因簇) 进行分类, 筛选出致病的癌症基因15个。 另外, 我们还运用基于灵敏度的支持向量机对基因本身进行分类,而不是基于基因簇。 利用得到的结果与基于独立成分分析的方法所提取的基因提供比较。 发现所筛选 的基因簇中有三个基因与灵敏度支持向量机方法筛选的基因相同。 对预处理过后的1908个基因,通过独立成分分析提取出61个基因簇,这些基 因簇中含有与分类无关的基因簇,即噪声,以及与分类相关的分类因素5个。事 实上,为了能够得到最好的分类因素,我们将问题转化为一类信号稀疏表示的优 化问题。此外,为了进一步进行基因分类,我们利用含噪声的ICA和带松弛因子 的非光滑优化模型研究带有噪声的基因图谱信息。 通过含噪声模型与不含噪声模 型进行对比,说明含噪模型的优势。 最后,借助于条件概率模型,对病人数据进行了筛选,将临床结论与基因图 谱相结合,通过已有文献以及生物信息网站所获取资料发现,所筛选的大部分基 因标签与当今临床医学所得到的直肠癌研究结论相吻合。
2
强度值均为 1000,而在另外一种实验条件下的强度值分别为 100 和 10000。如果 从对照与实验的绝对值来看,一个基因表达的变化远远大于另一基因,即 但是, 从生物学的角度出发, 两个基因变化的是相等的, 10000-1000>>1000-100 。 都是 10 倍的变化。用对数转换可以消除这种由两个相对变化间的不成比例所引 起的误导。例如,对数据进行以 10 为底的对数变换,则 lg100 2 lg1000 3 lg10000 4 可以看出,基因的变化是相等的,只是方向不同,一个增大,另一个减小。对数 变换减弱了数据的平均值和方差,使得表达的变化独立于其产生的强度位置,从 而使得低强度值与高强度值发生的倍数变化具有可比性。 另外,对数变换使得数据的分布具有对称性和接近正态分布性质,而一些常 用的统计方法,如 t 检验、F 检验等方法都要求数据满足正态分布或近似正态分 布。由于本问题中所提供的数据已经是对数形式的,所以可以忽略这一步。 (二) 重复数据的合并 重复的测量可以用于估计实验中的噪声,比较不同处理组间和处理组内的 变异。然而,在特定的条件下把所有的重复值合并成一个数值可能更为方便,而 这一个值就是给定基因(条件)的代表。根据不同的情况,这些重复测量可能是 同一芯片上的重复点,或是同一基因在不同芯片上的测量值。通常的合并是指计 算这些重复值的集中趋势指标,如均数、中位数或众数。 (三)数据归一化 系统误差使得采集到的数据可能含有奇异样本数据, 所谓奇异样本数据指的 是相对于其他输入样本特别大或特别小的样本矢量。 奇异样本数据的存在会影响 特征基因的提取。所以,在数据预处理部分,需要对原始数据进行归一化。归一 化的具体作用就是归纳统一样本的统计分布性。 归一化在 0~1 之间是统计的概率 分布,归一化在-1~+1 之间是统计的坐标分布。例如规整原数据到 0,1 内,这样 可以降低奇异样本数据对整体的误差影响, 从而更加有效地提取特征基因。 另外, 数据归一化对于独立分量分析(ICA) 、支持向量机(SVM)数据处理也是有帮 助的。 首先,根据附件的文件说明,我们需要对 project_data.txt 里的数据进行以下 预处理: 1. 在project_data.txt数据文件中,第二列为UMGAP,HSAC07 或者i的数据 是和RNA控制相关的,对下面所做的工作没有关系,为冗余数据,所以需要把 这些数据去除。 2. 基因芯片探针探测到的序列表明了基因的表达水平,有些数据可能是同 一基因探针的重复点,也有可能是同一基因在不同基因探针上的探测值。因而, 对于project_data.txt中基因相同的序列,需消除重复表示,采用了类均值算法, 对其进行取平均或取中值处理,给出特定基因的唯一表达数据。 以上两步的数据预处理可以保证: 处理后的数据较真实地反映了不同基因的 不同表达水平。 通过以上的预处理,原基因数据从2000个基因减少到了1908个。实验表明, 1908个基因数据为可靠性较高的数据。 其次,进行数据归一化处理。采用的归一化映射为:
2015年全国研究生数学建模大赛优秀论文C题5

问题 4:基于无线信道“指纹”特征的区域高精度定位算法研究 该部分针对无线信道“指纹”特征,对问题 3 的区域分别进行 了粗划分与精划分,进一步细化了了“指纹”特征,最终对问题 4 的测量数据实现了高精度定位:测量结果 1 位于 121.67m,误差为 0.83m;测量结果 2 位于 75m,误差为 0.83m。 关键词: 无线信道;指纹提取;K 均值聚类。
-3-
的样本加以分析,给出无线信道 “指纹 ”的模型。在此基础上,给出简洁而明确的 “评 价指标 ”,用于分析验证所建模 “指纹 ”合理有效。所谓有效是指,该模型应能从数学 上对已知的三种场景进行合理区分。要求详细说明建模的思路、使用的方法以及得出 结论的过程。另外,所提取的特征或所建立的模型最好有一定的物理意义。最后,提 供获取“指纹”的程序代码,要求代码可运行,但代码形式不限。 问题 2: “数据包 2”提供了与 “问题 1”中某些场景相对应的二个真实信道测量结果。 基于“问题 1”中所提供的三个场景,以及所建立的 “指纹 ”模型和 “评价指标 ”,采用数 学的方法,识别出此处提供的二个样本分别属于哪个场景。需要保证“场景识别 ”的结 果正确,且对识别的结果进行合理的分析。请明确给出 “场景识别 ”的结果,并详细描 述分析的过程。 问题 3:“数据包 3”提供了一条连续路段的真实信道测量结果。该结果对应于以 3km/h 的速度步行近 150m 的测试距离。该路段可能包含不同的场景或环境,对应不 同的“指纹 ”特征。基于上述测量结果,先自行分段,采用 “问题 1”中的建模方法,给 出分段的“指纹 ”分析。在分段分析的基础上,对所提取的 “指纹 ”进行合理分类。通过 对比不同段的分析结果,最终决定该路段可以依“指纹 ”划分为多少个区域。理论上, “区域划分 ”越细, 后续做 “区域识别 ”的精确程度越高, 但过细的 “区域划分 ”会在 “指纹 ” 特征中引入更多的错误, 导致误判概率增大。 要求详细说明“区域划分 ”的思路及过程, 并对划分结果进行合理的分析。 问题 4:“数据包 4”提供了二个真实信道测量结果。基于 “问题 3”中的 “区域划分 ” 和“问题 1”中的 “评价指标 ”, 首先判断此处提供的二个样本是否采集自 “问题 3”中所提 供的路段。对于已判断出的采自上述路段的样本,请识别其对应于“问题 3”中的哪一 块区域。需要保证“样本判断 ”的结果正确,以及 “区域识别 ”的误判距离尽可能小,同 时对所识别的结果进行合理的分析。要求详细说明样本判别的思路和方法,以及得出 结论的过程。
2020数模竞赛c题范文

2020数模竞赛c题范文在2020年的数学建模竞赛C题中,参赛者需要解决一个与公路交通流量预测相关的问题。
本文将从问题的背景介绍、分析方法、模型建立以及结果分析等几个方面进行论述,以期全面准确地解决该问题。
1. 问题背景介绍公路交通流量预测是城市交通规划和交通管理的重要组成部分。
在现实生活中,交通流量的准确预测能够帮助交通部门合理规划交通网络、减少交通拥堵,并且对于交通事故的防范也具有重要意义。
因此,对于公路交通流量预测进行研究具有重要的现实意义。
2. 分析方法为了准确地预测公路交通流量,我们首先需要对问题进行全面的分析。
我们可以通过收集历史交通流量数据,分析交通流量的周期性、趋势性以及季节性变化等。
同时,对于影响交通流量的外部因素,如天气、道路状况等,也需要进行充分的考虑。
在此基础上,我们可以选择合适的数学模型来进行预测,如时间序列分析、回归分析等。
3. 模型建立在本次竞赛中,我们选择了基于时间序列的ARIMA模型来进行公路交通流量预测。
ARIMA模型是一种常用的时间序列分析方法,它可以用来描述时间序列数据的特征,并且能够预测未来的数值。
我们首先对历史交通流量数据进行平稳性检验,确保数据的平稳性,然后通过自相关图和偏自相关图来确定ARIMA模型的参数。
最后,我们使用ARIMA模型进行交通流量的预测,并通过均方根误差(RMSE)来评估模型的拟合效果。
4. 结果分析在实际应用中,我们使用了2019年的交通流量数据作为训练集来建立ARIMA模型,并使用该模型对2020年的交通流量进行预测。
通过与实际观测值进行比较,我们发现ARIMA模型在交通流量预测方面表现出较好的准确性和稳定性,其RMSE值为X。
同时,我们还发现交通流量的季节性变化对预测结果有一定的影响,因此在建立模型时需要充分考虑季节因素的调整。
综上所述,通过对2020数学建模竞赛C题的分析与建模,我们选取了ARIMA模型来预测公路交通流量。
该模型能够准确预测交通流量的变化趋势,并对实际交通管理提供重要参考依据。
数学建模C题优秀论文

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C 我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员 (打印并签名) :1.2.3.指导教师或指导教师组负责人 (打印并签名):日期: 2010 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):输油管的布置摘要“输油管的布置”数学建模的目的是设计最优化的路线,建立一条费用最省的输油管线路,但是不同于普遍的最短路径问题,该题需要考虑多种情况,例如,城区和郊区费用的不同,采用共用管线和非公用管线价格的不同等等。
我们基于最短路径模型,对于题目实际情况进行研究和分析,对三个问题都设计了合适的数学模型做出了相应的解答和处理。
问题一:此问只需考虑两个加油站和铁路之间位置的关系,根据位置的不同设计相应的模型,我们基于光的传播原理,设计了一种改进的最短路径模型,在不考虑共用管线价格差异的情况下,只考虑如何设计最短的路线,因此只需一个未知变量便可以列出最短路径函数;在考虑到共用管线价格差异的情况下,则需要建立2个未知变量,如果带入已知常量,可以解出变量的值。
问题二:此问给出了两个加油站的具体位置,并且增加了城区和郊区的特殊情况,我们进一步改进数学模型,将输油管路线横跨两个不同的区域考虑为光在两种不同介质中传播的情况,输油管在城区和郊区的铺设将不会是直线方式,我们将其考虑为光在不同介质中传播发生了折射。
C题数学建模论文终结版

承诺书我们仔细阅读了五一数学建模联赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与本队以外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其它公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们愿意承担由此引起的一切后果。
我们授权五一数学建模联赛赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号为(从A/B/C中选择一项填写): C我们的参赛报名号为:1950参赛组别(研究生或本科或专科):本科生所属学校(请填写完整的全名)山东科技大学参赛队员(打印并签名) :1. 宫晨2. 李帅3. 徐温博日期:2014 年 5 月 3 日获奖证书邮寄地址:山东省青岛市黄岛区前湾港路579号山东科技大学信息科学与工程学院物联网工程2013级1班宫晨(收)邮政编码266510编号专用页竞赛评阅编号(由竞赛评委会评阅前进行编号):裁剪线裁剪线裁剪线竞赛评阅编号(由竞赛评委会评阅前进行编号):参赛队伍的参赛号码:(请各参赛队提前填写好):题 目 “延迟退休”问题摘 要目前我国已经进入人口老龄化快速发展期,“延迟退休”已成为人们关注的热点话题,如何尽快作出“延迟退休”科学可行的制度设计,是人们关心的问题。
对问题一,我们查阅文献资料,获得四个指标的计算公式,分别为:出生时的平均预期寿命:∑-===1101ωi i x x x L l l T e ;人口老龄化程度指标计算公式:%10%100≥⨯=Z X S 或%7%100≥⨯=ZYS ;劳动力供求状况指标计算公式: )1(r Sq W S N Q +==;国民受教育情况指标计算公式:e ×I +d ×L +c ×M +b ×H +a ×U =C然后分别研究这四个指标对延迟退休的影响,得出了我国确实有必要延迟退休年龄的结论。
数学建模优秀论文(精选范文10篇)2021

数学建模优秀论文(精选范文10篇)2021一、基于数学建模的空气质量预测研究本文以某城市为研究对象,通过数学建模方法对空气质量进行预测。
通过收集历史空气质量数据,构建空气质量预测模型。
运用机器学习算法对模型进行训练和优化,提高预测精度。
通过对预测结果的分析,为城市环境管理部门提供决策支持,有助于改善城市空气质量。
二、数学建模在物流优化中的应用本文针对某物流公司配送路线优化问题,运用数学建模方法进行求解。
建立物流配送模型,考虑配送成本、时间、距离等因素。
运用线性规划、遗传算法等优化算法对模型进行求解。
通过对求解结果的分析,为物流公司提供优化配送路线的建议,降低物流成本,提高配送效率。
三、基于数学建模的金融风险管理研究本文以某银行为研究对象,通过数学建模方法对金融风险进行管理。
构建金融风险预测模型,考虑市场风险、信用风险、操作风险等因素。
运用风险度量方法对模型进行评估。
通过对预测结果的分析,为银行提供风险控制策略,降低金融风险,提高银行稳健性。
四、数学建模在能源消耗优化中的应用本文针对某工厂能源消耗优化问题,运用数学建模方法进行求解。
建立能源消耗模型,考虑设备运行、生产计划等因素。
运用优化算法对模型进行求解。
通过对求解结果的分析,为工厂提供能源消耗优化策略,降低能源消耗,提高生产效益。
五、基于数学建模的交通流量预测研究本文以某城市交通流量为研究对象,通过数学建模方法进行预测。
收集历史交通流量数据,构建交通流量预测模型。
运用时间序列分析方法对模型进行训练和优化。
通过对预测结果的分析,为城市交通管理部门提供决策支持,有助于缓解城市交通拥堵。
数学建模优秀论文(精选范文10篇)2021六、数学建模在医疗资源优化配置中的应用本文以某地区医疗资源优化配置问题为研究对象,通过数学建模方法进行求解。
建立医疗资源需求模型,考虑人口分布、疾病类型等因素。
运用线性规划、遗传算法等优化算法对模型进行求解。
通过对求解结果的分析,为政府部门提供医疗资源优化配置策略,提高医疗服务质量。
数学建模C题论文资料(工件加工排序)
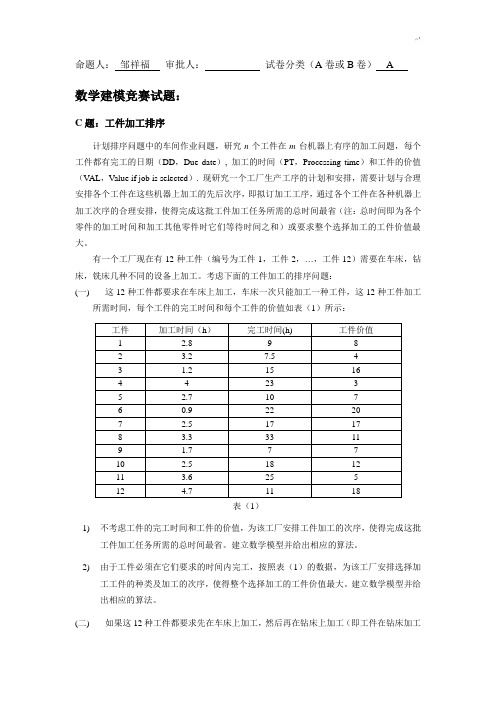
enddata
end
模型结果:
导出列表:
工件顺序
车床加工时间
规定的完工时间
各工件价值
0
0
0
0
0
0
1
2.8
9
8
5
1.7
7
7
12
4.7
11
18
10
2.5
18
12
3
1.2
15
16
6
0.9
22
20
7
2.5
17
17
2
4
23
3
11
3.6
问题(一)题目要求:12种工件都要求在车床上加工,车床一次只能加工一种工件。设i工件车床加工时间为A ,规定完工时间为B ,工件价值为C
1)不考虑工件的完工时间和工件的价值,安排工件加工的次序,使得完成这批工件加工任务所需的总时间最省。
分析:引入0/1变量,利用目标函数最优化工件排序。
设 为i工件实际完工时间,所以完成这批工件的总时间为T= ,而 =A +A =A +A +A =A +A +………+ =
@for(shunxu(I):
@sum(gongjian(J): note(I,J))=1;
);
!每个工件只能排在一个顺序位上;
@for(gongjian(J):
@sum(shunxu(I): note(I,J))=1;
);
!定义0/1变量;
@for(links:@bin(note));
data:
!输出数据到Excel文档;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国第三届研究生数学建模竞赛题 目 维修线性流量阀时的筒设计问题(C 题)针对问题1,首先考察了孔为四种特殊形状的情况下,“过流面积”随曲线下降距离的变化情况,得到凸凹圆曲线与严格线性面积特性曲线偏差的平方和最小,线性关系保持得比较良好。
此后利用微元法证明了“过流面积”呈严格线性变化时曲线和外孔圆交点横坐标的差为定值这一性质,得出了在此种情况下曲线在两交点处的斜率应为无穷大。
基于以上分析,利用最小二乘原理建立了无约束泛函极值模型,采用了变分法将其转化为微分方程,再转化为等效的变分原理,采用Ritz 算法近似求解。
最后通过对筒孔曲线的合理假设,得到了满足线性关系较好的孔曲线形状(见图11),其样本点的偏差平方和为0.064412。
针对问题2,利用最小二乘原理建立了有约束泛函极值模型。
根据文中第四节中的引理,给出理想状态下的孔形状。
之后对其进行了微调,通过牺牲严格的线性关系来使其逐渐满足两个约束75%h Q ≥和85%S Q ≥,并最终找到了合适的孔设计方案(见图13(b ))。
最后针对外孔磨损情况提出了基于自动控制理论和逆向工程技术等的解决办法。
本文提出的模型是从考察孔的特殊形状中得到启发的,从而具有实际应用价值和准确性。
关键词:线性阀体 最小二乘法 泛函极值模型 变分原理 非线性规划一、问题的提出阀体是我们日常工作和生活中一种十分常见的工具。
它种类繁多,其中线性阀体可使阀体的旋转角度和流量成正比。
因而它可使人们方便地对流量进行控制。
而如何设计线性阀体成为当今控制领域中研究的热点问题之一。
现在我们需要设计出一种阀体,它由两个同心圆柱筒组成。
外筒固定,其侧面上有一个孔,形状为两个直径不等的圆柱体的交线。
筒和外筒轴向之间没有相对运动,筒可以自由转动。
筒的侧面上也有一个孔,但它原来的形状未知。
要求设计出筒孔的形状,使得“过流面积”与筒旋转角成近似线性关系;在线性区间至少达“最大围”区间长度的75%以上,而且主要工作区的最大“过流面积”至少要达到外筒孔面积的85%以上,并且使“过流面积”和筒的旋转角度之间的“线性关系”尽量好的约束限制下,重新设计筒孔的形状。
并且还要考虑当外筒孔发生磨损时要采取的应对措施。
二、模型假设1、阀体的旋转角度与圆筒相对移动距离成正比,圆筒移动距离与“过流面积”成正比。
2.线性阀体外筒为薄壁筒,不考虑其壁厚给设计带来的影响。
3、外圆筒直径与外圆孔直径相差很大,展开后外圆孔面积变化足够小,可近似视为圆形。
4、筒在转动过程中,只存在周向水平运动,不存在垂直方向的运动。
5、假设圆孔设计曲线与外圆孔曲线最多只有两个交点,可以有一段相切,且曲线连续。
6、为简化计算,假设外圆孔半径为一个单位长度。
三、变量设定R :圆的半径,在本文中R 为一个单位长度1;()F x :待求孔的曲线方程;()f x :孔下边沿曲线方程;()G x:外圆孔上半圆方程,y 221x y +=;h ∆:曲线下降的距离微元;h :曲线()F x 下降到某一位置时其与初始位置的距离;max h :曲线()F x 从初始位置下降至“过流面积”达到最大值时的距离; A 、B 、C 、D :分别表示曲线F(x)在移动过程中与曲线G(x)的交点;()11,x y ,()22,x y ,()33,x y ,()44,x y :分别表示点A 、B 、C 、D 的坐标值; k :曲线()F x 下降的距离与“过流面积”之间的线性比例;()S h ∆∆:曲线下降h 时“过流面积”的增加量;()h ϕ:“过流面积”的理想值,()h kh ϕ=。
四、问题的分析本文将外两个圆柱筒展开为平面,得到两个长方形,于是将三维空间中物体的转动问题化简为二维平面上孔与外孔相对移动的问题来求解,此外根据问题假设可将外筒孔近似视为圆孔。
建立如图1外圆孔,X 表示成封闭图形,但是未画出的部分与圆不相交,如图1(a )所示。
(a )(b )引理:若要使孔旋转角度(称为开度)与“过流面积”满足线性关系(这种关系称为面积特性曲线),则孔曲线必满足其与外孔圆的交点横坐标之差衡为常数k ,即12x x k -=,其中12,x x 分别为孔曲线与外孔圆的交点横坐标。
或者可以说12x x k -=即为面积特性曲线保持线性的必要条件。
证明:假设某一时刻孔曲线向下移动h 与圆相交,其方程为()()f x f x h =-),当曲线向下移动微元h ∆时,“过流面积”的增加量S ∆由三部分组成,两边近似三角形面积和中间矩形面积(如图1(b )所示),并可用以下积分表示: ()()()()231412()()()()x x x x x x S G x f x h h dx G x f x h h dx hdx ∆=---∆+---∆+∆⎰⎰⎰ (1)若要使孔旋转角度(称为开度)与“过流面积”满足线性关系(这种关系式称为面积特性曲线),则只须使曲线的向下移动距离与“过流面积”满足线性关系即可,即微元面积S ∆也与h ∆有线性关系:S k h ∆=∆ (2)曲线与圆的交点坐标x 由方程()()G x f x =)(表示()f x 下降时的曲线)求得:()()()i i i G x f x f x h ===-),1,2i = (3)()()()i i i G x f x f x h h ===--∆),3,4i = (4) 整理方程(1)至(4)得:()()234112()()()()()()()()()()g h g h g h g h g h g h G x f x h h dx G x f x h h dx hdx k h -++∆+-++∆+∆=∆⎰⎰⎰ (5)其中()i g h 表示利用(3)、(4)式算出的i x 关于自变量h 的表达式,1,2,3,4i =,将(5)式整理可得:()()()2341()()()()243134()()()()()()()()()g h g h g h g h G x f x dx G x f x dx h g h g h g h g h h x x k h -+-+-+-+∆-=∆⎰⎰ (6)两边同时取微分,并用i x 代替()i g h ,整理可得:()()()()21221134443334()()()()()()()()()()()()()dg h dg h G x f x h G x f x h dh dh dg h dg h G x f x h G x f x h x x k dh dh-+--+--++-++-= 在满足0h ∆→条件下,根据方程(3)、(4)得:34x x k -= (7)即:12x x k -=(7)式的含义为:如果“过流面积”线性增加,则孔曲线必满足其与外孔圆的交点横坐标之差为常数k 。
即在()f x 向下移动过程中,其与圆的交点横坐标之差为常数k 。
到此引理证明完毕。
以下在面积特性曲线呈严格线性关系时,对曲线()f x 的形状进行讨论。
()f x沿坐标系y轴的负方向移动,根据()f x在与外孔圆交点处的斜率分两种情况讨论:1.如果斜率的符号相反,则下一时刻新产生交点的横坐标必然一个增大一个减小,那么它们的差值改变,因而不满严格足线性关系;2.如果斜率的符号相同,在曲线下移过程中两交点横坐标在某一时间段的增减情况是一致的,但是当()f x的某一交点先和外孔圆与X轴的交点重合后,该分支与外孔圆交点的横坐标的增减情况将改变,而另一交点横坐标的增减情况保持不变,此时差值改变,同样也不满足严格线性关系。
由以上分析我们得出结论:只有在曲线()f x在同外孔圆两交点处的斜率都是无穷大的情况下,两交点的横坐标的差才是恒定的,此时,曲线下移距离与“过流面积”呈严格线性关系,见图2。
由上图可见该曲线从开始下降到A点时,完全满足面积特性曲线呈线性关系,但是在A点以下就出现了非线性,且不满足题目中“最大围”为外筒孔面积的要求,因此不可能存在严格线性关系的面积特性曲线,即不能通过选择筒孔形状实现“过流面积”与筒旋转角度呈严格的线性关系。
但此曲线证明了只要曲线与圆相交两点的横坐标之差为常数,那么面积特性曲线一定是线性的。
当曲线与圆相交面积最大时即为外圆的面积2R ππ⨯=,又因为面积与下降距离成线性比例,故max k h π=五、基于问题1的模型建立1.模型探索在二维坐标系,假设孔曲线沿Y 轴负方向移动。
为了探索最佳孔曲线形状,本文首先考虑四种特殊的孔:矩形孔,凸圆孔,凹圆孔和凸凹圆孔,分别见图3,图4,图5及图6。
以下利用方差分析评价四种不同形状孔的控制效果。
根据最小二乘原则可得:面积特性曲线与严格面积特性曲线偏差的平方和越小,则其控制效果越好。
(1)矩形孔:矩形是最为简单的情况,它在移动过程中与外圆孔所围面积可表示为:()arccos(1)(S h h h =-+-在曲线()S h 上均匀选取200个样本点,利用最小二乘法求得其与理想面积曲线偏差的平方和为3.4190。
(2)凸圆孔:凸圆与外圆孔所围面积可表示为:21(2)]x x y h dx =⎰。
由两圆方程可得方程组2y h y ⎧=-⎪⎨=⎪⎩,求解得到上式的积分区间为22-⎢⎥⎣⎦。
选取样本点后利用最小二乘法求得其与理想面积曲线偏差的平方和为13.6761。
(3)凹圆孔:我们设开始时凹圆和外圆孔是相切的,其方程为y =h后凹圆与外圆孔相交的边界曲线方程为1y h =,而外筒孔下半圆曲线方程为2y =2112()x x y y y dx π=--⎰。
由y h y ⎧=⎪⎨=⎪⎩可得到上式的积分区间为⎢⎥⎣⎦。
选取样本点后利用最小二乘法求得其与理想面积特性曲线偏差的平方和为13.6761。
(4)凹凸圆孔:凹凸圆与外圆孔所围面积分为Y 轴左边凸圆与外圆孔所围面积和Y 轴右边凹圆与外圆孔所围面积之和。
我们分别计算两部分面积,左边凸圆与外圆孔所围面积为:1(2)]x y h dx =⎰,我们由2y h y ⎧=⎪⎨=⎪⎩得出上式中的1x = 右边凹圆与外圆孔所围面积为:20(2x y h dx π=--⎰,由y h y ⎧=⎪⎨=⎪⎩得出上式中22x =。
选取样本点后利用最小二乘法求得2100(2)](2x x y h dx h dx π=+--⎰⎰所对应的曲线与理想面积特性曲线偏差的平方和为0.4750。
以上四种孔形状控制的面积特性曲线于严格的线性面积特性曲线如图7所示。
通过对上述几种特殊形状孔面积特性曲线的分析可知,凸凹圆作为孔的形状对砂浆流量的控制效果比较理想,然而与实际精度要求还相差甚远。
2.建立泛函极值模型结合以上对问题的分析和模型的初探,发现选取极特殊的孔形状无法得到较理想的面积特性曲线,为了更精确地逼近线性面积特性曲线,本文引入了最小二乘法的思想,通过残差的平方和是否达到最小,来判断面积特性曲线是否最优。
