标量衍射理论习题
合集下载
第二章标量衍射理论
2、 基尔霍夫衍射理论
基尔霍夫利用数学工具格林定理，通过 假定衍射屏的边界条件，求解波动方程， 导出了更严格的衍射公式 ，从而把惠更 斯—菲涅耳原理置于更为可靠的波动理论 基础上 。
第十七页，编辑于星期五：十七点 五十三分。
基尔霍夫衍射理论—基尔霍夫衍射公式
P0点的单色点光源
P为孔径平面上任一点，Q为孔径 后方
涅尔原理无法解释。 3 K(θ)的具体函数形式难以确定。
第十五页，编辑于星期五：十七点 五十三分。
衍射理论所要解决的问题
光场中任一点Q的复振幅能 否用光场中其它各点的复振 幅表示出来？
例如能否由如图孔径平面
上的场分布计算孔径后面任
一点Q处的复振幅？这是一个 入射光
Q
根据边界值求解波动方程的
问题。
第十六页，编辑于星期五：十七点 五十三分。
射理论，完善了惠更斯-菲涅耳理论。
可定性、定量分析衍射现象。 h.索末菲利用格林函数理论修正了基尔霍夫衍
射理论，成为瑞利-索末菲理论
第七页，编辑于星期五：十七点 五十三分。
§2.2 从矢量理论到标量理论
光的电磁理论
介质中无自由电荷
麦
E 0
克 斯
H 0
韦 方 程
E H
t
组
H E
2，标量的方法（基尔霍夫标量衍射理论），一定条件下， 可以不考虑电磁场矢量各个分量之间的联系，电磁波矢量方 程可以写为分量方程（标量方程），把光作为标量来处理， 只考虑电磁场一个分量的复振幅。
标量衍射理论条件： （1）衍射孔径比光波长大得多;
（2）观察点距离衍射孔足够的远。
第三页，编辑于星期五：十七点 五十三分。
与脉冲响应 hx x0 , y
11-标量衍射理论3-衍射的角谱理论、菲涅耳衍射
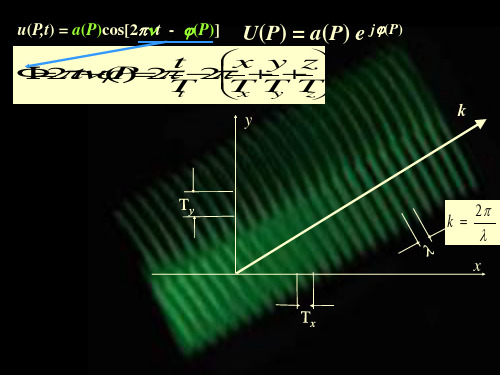
即为普遍的衍射公式。
使用时需要化简。 在不同的近似条件下，可 以得到菲涅耳衍射公式和夫琅禾费衍射公式
§2-3 标量衍射的角谱理论
3、菲涅耳衍射公式
x0
x
y0
y
近似条件：
z
孔径和观察平面
z
x02maxy02max
之间的距离远远 大于孔径的线度
z
xm 2 axym 2 ax
只对轴附 近的一个
U 0 ( x 0 ,y 0 )ex j2 k z ( p x 0 2 [ y 0 2 ) ] fx x z ,fy y z
§2-3 标量衍射的角谱理论
3、菲涅耳衍射公式：频域形式
或写成卷积式: U (x ,y) U 0(x ,y) h (x ,y)
其中, 脉冲响应函数为:
h(x,y)j1 zexjp k)e z (x jp 2 kz(x2y2)
§2-3 标量衍射的角谱理论
3、菲涅耳衍射公式：F.T.形式
由菲涅耳衍射的空域表达式：
p U ( x ,y ,z ) ejx j z) k p U z ( x ( ,y , ) ex jz [ p x (x { ) ( y y ) ]d } d x
§2-3 标量衍射的角谱理论
2、基于平面波角谱的衍射理论
从频域的角度即用平面波角谱方法来讨论衍射问题
xyz平面的光场分布与x0y00平面光场分布的关系：
U(x,y,z) U(x0,y0,0)exjp2p(z 12fx22fy2)
exjp 2p{ [fx(xx0)fy(yy0)]d}0xd0ydxfdyf
xyz平面上复振幅分布U(x,y,z)的空间频谱, 其 空间频率宗量用传播矢量的方向余弦表示
第三章 标量衍射理论(二)
空间频率的正负，仅表示平面波不同的传播方向 复振幅分布的空间频谱：
dxdy A f x , f y U x, y exp j 2 f x f y x y
复振幅分布的角谱：
cos cos cos cos A , x U x, y exp j 2
x y x y x
y
A0 f x , f y U x0 , y0 exp j 2 f x x0 f y y0 dx0dy0
A0 f x , f y e
jkz 1 f x f y
2
2
e
j 2 f x x f y y
传播距离z后
利用两者的关系， 确定整个光场的传播特性
cos cos cos cos A , , z exp j 2 x
观察平面
U x, y, z
cos cos y d d
A A0 exp jkz 1 cos2 cos2
传播效应为相移 倏逝波
A A0 exp kz cos2 cos2 1 A0e z
A A0
不沿z轴传播
思考：利用角谱理论证明光线传播的线性关系
3、衍射的角谱理论
cos cos cos cos 2 2 A , A , 0 exp jkz 1 cos cos
u P, t Re U P e j 2 t
光波的标量衍射理论
～
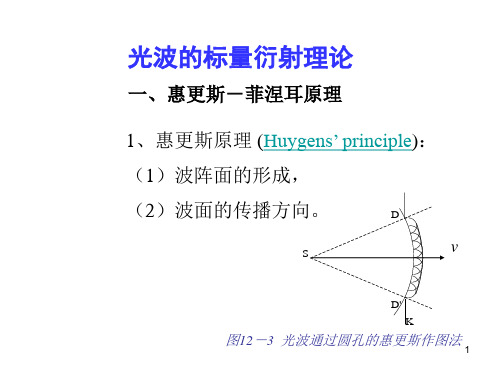
E
P＝
A i
e
xpik
l
l
e
xpik
r
r
cosn,
r
2
cosn,
l
d
子波的复振幅与
K() cosn, r cosn,l
2 成正比，与波长成反比。
i 1 exp[i p]
i
2
表示子波的振动位相超前于入射波90。
6
当光线接近于正入射时 exp(ikl) exp(ikR)
l
R
cos(n, l) 1,
1 x x1 2 y y1 2
z12
z1
x
x1 2 y
2z1
y1 2
[x
x1 2 y
8z13
y1 2 ]2 ....
级数展开
r
z1
x
x1
2 y
2z1
y1 2
近似条件：
[x x1 2 y y1 2 ]2 p
z13
4
y1
Q C
K
x1 r
z1
y x
P
P0 E
11
r
z1
x
x1 2 y
2
光源S在波面ZZ '上
波阵面外任一点光振动应该是波面
上所有子波相干叠加的结果。
任意Q点产生的复振幅：
E~Q
A
exp ikR
R
Z
Q
R
Q点处d 大小的面元
r P
对P点的贡献为： S
dE~P
CK
E~Q
expik
r
r
d
Z'
子波向P点的球面波公式 子波法线方向的振幅 子波振幅随角的变化
第三章-标量衍射理论2-角谱及其传播
l
l
l
l
cos cos A( , , z)
l
l
称为xyz平面上复振幅分布的角谱, 表示不 同传播方向()的单色平面波的振幅(|A|) 和初位相(arg{A})
角谱是xyz平面上复振幅分布U(x,y,z)的空间频谱, 其空 间频率宗量用传播矢量的方向余弦表示
复振幅分布的角谱： 例
在x-y平面上, 光场复 振幅分布为余弦型: 可以分解为:
Angular Spectrum of Complex Amplitude Distribution
对在 z 处的x-y平面上单色光场的复振幅分布U(x,y,z)作傅里叶变换: 称为x-y平面 A( f x , f y , z) U ( x, y, z) exp[ j 2 ( f x x f y y)]dxdy 上复振幅分 布的频谱 其逆变换为：
2、平面波角谱的传播
角谱是传播距离 z 的函数
在孔径平面(x,y, 0)的光场U0(x, y , 0) :
U 0 ( x, y,0) A(
cos cos cos cos cos cos , ,0) exp[ j 2 ( x y)]d ( )d ( )
l
l
l
普遍的光振动的复振幅表达式： U(P) = a(P) e jj(P)
光强分布: I = UU*
a0 jkr e 球面波的复振幅表示（三维空间）：U ( P ) r
(P(x,y,z)) 球面波的复振幅表示（x-y 平面）： y a0 k 2 (r 2 U ( P) U ( x, y) exp( jkz) exp j ( x x0 ) ( y y0 ) k z 2z
chap2标量衍射的角谱理论
U ( x, y, z) U0 ( x0 , y0 ,0)e
(4)式：
jkz
x d f y dx0 dy0
e U ( x, y, z ) U 0 ( x0 , y0 ,0)e jz
(5)式：
j
[( x x0 ) 2 ( y y0 ) 2 ] z dx
U ( x, y, z ) U 0 ( x0 , y0 ,0)e
当： 1
2
j
2 z 12 f x2 2 f y2 j 2 [ f ( x x ) f ( y y )] x 0 y 0 e df
x d f y dx0 dy0
f x2 2 f y2
df x df y
, A( f x , f y , z) A( cos
2012
cos
, z)
角谱的传播
• z=0平面上
U ( x, y,0) A( f x , f y ,0)e
j 2 ( xf x yf y )
df x df y
• z=z平面上
U ( x, y, z ) A( f x , f y , z )e
j [( x x0 ) 2 ( y y0 ) 2 ] e z ]dx0 dy0
j [( x x0 ) 2 ( y y0 ) 2 ] U 0 ( x0 , y0 ,0)e z dx0 dy0 2012
平面波角谱衍射理论
• 由平面波角谱衍射理论得到的精确表达式：
j 2 z 12 f x2 2 f y2 j 2 [ f ( x x ) f ( y y )] e x 0 y 0 df
a0 jkr e r •平面波的复振幅表示 U (P) ae jk r
光学原理 第三章 标量衍射理论基础
+
ak 2
= a1 + ak (P点相长, 亮点) 22
当k为偶数时 :
Ak
=
a1 2
+ ⎜⎛ ⎝
a1 2
− a2
+
a3 2
⎟⎞ + ⎜⎛ ⎠⎝
a3 2
− a4
+
a5 2
⎟⎞ + L + ⎜⎛
⎠
⎝
ak −3 2
− ak−2
+
ak −1 2
⎟⎞ + ⎠
ak −1 2
−
ak
=
a1 2
+
ak −1 2
−
ak
4.若λ/a趋于零Æ衍射现象消失—几何光学是λ/a趋于零 的极限情况
• 格里马耳迪(F.M.Grimaldi)1665 年首先报道 和描述了衍射现象。他当时用来观察光衍射的 装置由光源发出的光照射到一个不透明的屏所 开的孔径上，在孔径后方用一个平面屏来观察 经孔径透射的光在它上面分布的情况。
• 按照几何光学的观点，在观察平面上影子与亮 区的交界处应该是轮廓分明的，然而实际的观 察表明有一部分光线进入了几何阴影的暗区， 同时在亮区中却出现了暗纹。索未菲将这种 “不能用反射或折射来解释的光线对直线光路 的任何偏离”的现象定义为衍射。
r0
+
3⋅
λ
2
L
Bk
P
=
r0
+
k
⋅
λ
2
B0
r0
C‘ 极点
P
对称轴， S的法线
相邻波面到观察点距离 均相差λ/2的环形带波 面称为半波带。
二、半波带性质
标量衍射理论-2
U0 (x0 , y0 ,0)
cosα cos β A0 , ,0 λ λ
xy
Uz ( x, y, z)
cosα cos β Az , , z λ λ
z
z=0
U 0 ( x0 , y0 ;0) = U z ( x, y; z ) =
∞ ∞
z=z
cos β cosα cos β cosα cos β cosα A0 , ;0 exp j 2π x0 + y0 d d ∫∞−∫∞ λ λ λ λ λ λ −
3.3 标量衍射的角谱理论
3.3-1单色平面波与线性平移不变系统的本征函数 单色平面波与线性平移不变系统的本征函数 在 z=0 平面上的复振幅分布为：
exp j 2π ( f x ⋅ x + f y ⋅ y ) = exp[ j 2π (ux + vy )]
[
]
cos β cosα = exp j 2π x+ y λ λ
3.2 基尔霍夫衍射理论
光波的传播过程就是光波衍射 衍射过程 衍射 矢 量 波 衍 射 理 论 假设与近似
(1)整个光波场内光矢量振动方向不 变，或只考虑光矢量的一个分量 (2)衍射屏的最小尺度远大于波长. (3)观测距离远大于波长． (4)折射率与光强无关.
标 量 波 衍 射 理 论
波动光学
信息光学 （基础)
∞ ∞
cos β cosα cos β cosα cos β cosα Az , ; z exp j 2π x+ y d d ∫∞−∫∞ λ λ λ λ λ λ −
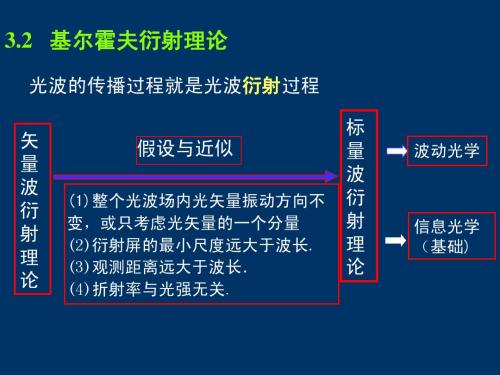
cosα cos β A0 , ,0 λ λ
xy
Uz ( x, y, z)
cosα cos β Az , , z λ λ
z
z=0
U 0 ( x0 , y0 ;0) = U z ( x, y; z ) =
∞ ∞
z=z
cos β cosα cos β cosα cos β cosα A0 , ;0 exp j 2π x0 + y0 d d ∫∞−∫∞ λ λ λ λ λ λ −
3.3 标量衍射的角谱理论
3.3-1单色平面波与线性平移不变系统的本征函数 单色平面波与线性平移不变系统的本征函数 在 z=0 平面上的复振幅分布为：
exp j 2π ( f x ⋅ x + f y ⋅ y ) = exp[ j 2π (ux + vy )]
[
]
cos β cosα = exp j 2π x+ y λ λ
3.2 基尔霍夫衍射理论
光波的传播过程就是光波衍射 衍射过程 衍射 矢 量 波 衍 射 理 论 假设与近似
(1)整个光波场内光矢量振动方向不 变，或只考虑光矢量的一个分量 (2)衍射屏的最小尺度远大于波长. (3)观测距离远大于波长． (4)折射率与光强无关.
标 量 波 衍 射 理 论
波动光学
信息光学 （基础)
∞ ∞
cos β cosα cos β cosα cos β cosα Az , ; z exp j 2π x+ y d d ∫∞−∫∞ λ λ λ λ λ λ −
3.2标量衍射理论
2015/3/27
第三章 标量衍射理论
15
三、衍射理论五：简化为傅里叶变换
– 3. 6、二次位相因子的消除1：远场与富里叶变换
1 k U ( x, y ) exp( jkz) U ( x0 , y0 ) exp j ( x x0 ) 2 ( y y0 ) 2 jz 2z
U ( x, y ) U ( x0 , y0 )h( x x0 , y y0 )dx0 dy0 h( x x0 , y y0 )
1 j r
e jkr
1 x x0 2 1 y y0 2 r z 2 ( x x0 ) 2 ( y y0 ) 2 z 1 ( ) ( ) 2 z 2 z h( x x0 , y y0 ) 1 k exp( jkz) exp j ( x x0 ) 2 ( y y0 ) 2 jz 2z
– 3.4、菲涅耳衍射公式二次曲面近似的三种表示
（卷积、脉冲响应，FT）及其Matlab两种实现
– 3.5、菲涅耳变换：衍射可看做是输入受二次位相因子调制的FT – 3.6、二次位相因子的消除1：远场衍射或衍射的富里叶变换 及其Matlab实现 – 3.7、二次位相因子的消除2：光源作用的结果 – 3.8、二次位相因子的消除3：物体的自我调制成像
dx dy
0
0
1 k U ( x, y ) exp( jkz) exp j ( x 2 y 2 ) U ( x0 , y0 ) jz 2z k 2 exp j x0 y0 2z
2 exp j ( xx yy ) dx dy z
10-标量衍射理论2-角谱及传播
2、平面波角谱的传播
角谱沿 z 传播遵循的规律
l l l l l l l A c, o c, s o z 4 s 2 2 c2o c2 s o d d 2 s 2 A z c, o c, s o z k s 2 A c, o c, s o z 0 s
方向余弦 cos2 cos2 的平面波, /, k 在xy 平面,不
沿 z 轴传播.
cos2 cos2 > : 代表倏逝波
2、平面波角谱的传播
传播现象作为线性空不变系统
A co ,cs o ,z sA co ,cs o ,0 e sx jk 1 p c z( 2 o c s2 o )s
l l l l
Afx, fy
系统的输出
A0 fx, fy
系统的输入
fx
coαs, λ
fy
coβs λ
表征系统频谱特性的传递函数 ：
l l H fx,fyA A ((ffx x ,,ffy y )) ex jk p zfxfy
系统的
传递函数:Hfx,fy
ex jk p1 z λ fx2λ fy2
0
fx 2fy 2<λ 1 2 其他
2、平面波角谱的传播
传播现象作为线性空不变系统
系统的
传递函数:Hfx,fy
ex jk p1 z λ fx2λ fy2
g (x ,y ) G (fx ,fy )ex j2( p fx x [fy y )d ] x d f y f
3.1 标量衍射理论
1 cos Y l
fy 0
fx
1 cos X l
1
平面波的空间频率
fy
1 cos Y l 1 cos fz Z l
f x f y fz
2 2 2
l2Hale Waihona Puke 平面波的波矢 k 2
l
k x k y kz
2 2
2
这里的 k x k cos
第三章
标量衍射理论
傅立叶光学主要研究内容：光波作为载波，实现 信息的传递、变换、记录和再现问题。 标量衍射理论是研究上述问题的物理基础，我们 用它来研究光波传播规律。 光波是矢量波。当满足下列条件时，标量衍射理 论得到的结果与实际情况十分相符。 条件： 1）衍射孔径比波长大得多； 2）观察屏离衍射孔径相当远。
fx
cos
l
, fy
cos
l
通过上面几个图像，可以看出：
高空间频率信息决定图像的细节
时间频率与空间频率的比较：
时间 周期 频率 圆频率
T (s )
1 1 (s ) T
2 2 T
1
空间 单色光波
l (cm)
l
(cm 1 ) / f x cos
• 传播矢量 k 位于 x ,z 平面的平面波在 x, y 平面上的空间频率 。
（3）平面波的空间频率
平面波前相位图
两相邻等相位线在x方向的间距为 X
l
cos
x方向的空间频率用
y方向的空间频率用
1 cos f x 表示，f x X l
单位是周/mm。
标量衍射理论
x0
基尔霍夫衍射公式
n
光源 P0
θ
θ
1
2
P r0 r z
Q(x,y)
1 a0 exp( jkr0 ) cos(n, r ) cos(n, r0 ) exp( jkr) U (Q) [ ] ds j r0 2 2 r 1 exp( jkr) U 0 P K r ds U 0 PhP, Qds j
平面x y的任一光波可分解成向空间各方向传播的平面波 每一平面波成份与一组空间频率值（ξ, η）对应： 传播方向为cosα =λ ξ, cosβ =λ η ，振幅为G(ξ, η)
G( , ) g ( x, y) exp[ j 2 (x y)]dxdy
亦可写成：
cos cos cos cos G( , ) g ( x, y) exp[ j 2 ( x y)]dxdy
传播方向余弦为（ cosα ,cosβ ）的一般情形
u u0 exp[ jk ( x cos y cos )]
(x,y)平面等相位线
x cos y cos 常数
空间周期 d x cos cos 空间频率
dy cos
cos
Cl xl y sin c(lx ) sin c(l y )
ly y lx x sin( ) sin( ) z z Cl l sin cl , l Cl xl y x y x x lx x ly y z z
x z
y z
光强
I I 0 sin c (lx , l y)
y y0 2 1 x x0 2 z{1 [( ) ( ) ]} 2 z z
第二章习题解答及参考答案
2 I λz Is = 0 π d
∫
∞
0
J1 (ψ ) ψ ψdψ
2 2 2 2
∞J ( ∞J ( ψ J ( I (r ) ψ J (ψ ) ψ ) ψ ) 1 ψ ) 故： F (r0 ) = i 0 = ∫ 1 ψdψ / ∫ 1 ψ dψ = ∫ 1 dψ dψ / ∫0 0 0 0 Is ψ ψ ψ ψ
第二章 标量衍射理论
部分习题解答及参考答案
[2-1] 在基尔霍夫衍射公式（2-2-16）或（2-2-20）中，同时对光场及其法向导数施加了边 界条件，从而导致了理论本身的不自恰性。为了消除这种不自恰性，索末菲选择了换用格林 函数的办法，使新的格林函数或其法向导数在表面 S1 上为 0,这时就不必同时对光场及其法 向导数施加边界条件。例如，可以选择 G 同时由观察点 P0 及其对衍射屏的镜对称点 P0 各
1 ikz i 2 z (x0 2 + y 0 2 ) U ( x0 , y0 ) = e e F {t (x1 , y1 )} iλ z k 1 ikz i 2 z (x0 2 + y 0 2 ) 2 = [a sinc (af x , af y ) − b 2sinc (bf x ,bf y )] e e iλ z
解：方形环带的透过率函数为：
当用单位振幅的单色平面波垂直照明时，其透过此环带的光场 U t ( x1 , y1 ) = t ( x1 , y1 ) ，故观察 面上的光场分布为：
x y x y t ( x1 , y1 ) = rect 1 , 1 − rect 1 , 1 a a b b
按极值条件，令 x J 0 (x ) − 2 J1 (x ) x = 0 = 0, εx J 0 (εx ) − 2 J1 (εx ) x = 0 = 0 求得：
标量衍射理论
第二章 标量衍射理论
本章主要研究内容
• 基尔霍夫衍射理论 • 衍射的角谱理论 • 菲涅尔衍射和夫琅禾费衍射 • 透镜的傅里叶变换性质
2.1 基尔霍夫衍射理论
• 惠更斯－菲涅尔原理与基尔霍夫衍射公式 • 惠更斯－菲涅尔原理与叠加积分 • 相干光场在自由空间传播的平移不变性 • 相干光场在自由空间传播的脉冲响应
二 惠更斯－菲涅耳原理 目的：以子波相干叠加的方法对衍射结果进行定量描述。
菲涅耳子波干涉说 (1818): 子波间应当互相干涉,并且应当 考虑不同方向子波的差异. — 惠更斯-菲涅耳原理
研究方法：单色点光源S发出的球面波波面为，波面半径为R， 光波传播空间内任意一点P的振动应是波面上发出的所有子波 在该点振动的相干叠加。
ds
3 基尔霍夫衍射公式（续）
在单色点光源照明平面孔径的情况下: 惠-菲原理
U (Q)
c
U0 (P)K ( )
e jkr r
ds
n
r0 P0
P
∑
r
基尔霍夫 边界条件
Q
U (Q)
1
j
U
0
(
P)
cos(n,
r
)
cos(n, 2
r0 )
e jkr r
ds
基尔霍夫衍射公式
主要研究问题：
研究光源P0发出的球面波照明无限大的不透明屏上的孔， 计算孔径右边空间衍射场中某点Q的场值－－小孔衍射问题
三、基尔霍夫衍射公式
1. 格林定理
令U(P)和G(P)为位置坐标的两个任意的复值函数，并令S 为包围体积V的封闭曲面。若U(P)和G(P)的一阶和二阶偏导数
都是单值的，并在S内和S上连续，则有
本章主要研究内容
• 基尔霍夫衍射理论 • 衍射的角谱理论 • 菲涅尔衍射和夫琅禾费衍射 • 透镜的傅里叶变换性质
2.1 基尔霍夫衍射理论
• 惠更斯－菲涅尔原理与基尔霍夫衍射公式 • 惠更斯－菲涅尔原理与叠加积分 • 相干光场在自由空间传播的平移不变性 • 相干光场在自由空间传播的脉冲响应
二 惠更斯－菲涅耳原理 目的：以子波相干叠加的方法对衍射结果进行定量描述。
菲涅耳子波干涉说 (1818): 子波间应当互相干涉,并且应当 考虑不同方向子波的差异. — 惠更斯-菲涅耳原理
研究方法：单色点光源S发出的球面波波面为，波面半径为R， 光波传播空间内任意一点P的振动应是波面上发出的所有子波 在该点振动的相干叠加。
ds
3 基尔霍夫衍射公式（续）
在单色点光源照明平面孔径的情况下: 惠-菲原理
U (Q)
c
U0 (P)K ( )
e jkr r
ds
n
r0 P0
P
∑
r
基尔霍夫 边界条件
Q
U (Q)
1
j
U
0
(
P)
cos(n,
r
)
cos(n, 2
r0 )
e jkr r
ds
基尔霍夫衍射公式
主要研究问题：
研究光源P0发出的球面波照明无限大的不透明屏上的孔， 计算孔径右边空间衍射场中某点Q的场值－－小孔衍射问题
三、基尔霍夫衍射公式
1. 格林定理
令U(P)和G(P)为位置坐标的两个任意的复值函数，并令S 为包围体积V的封闭曲面。若U(P)和G(P)的一阶和二阶偏导数
都是单值的，并在S内和S上连续，则有
13-标量衍射理论5-夫琅和费衍射、衍射光
2 2
用平面波照明的光栅后方光能量 重新分布，其能量只集中在三个 衍射级上。0级与+1级衍射间的距 离为f0z 。
l
傅里叶分析方法比传统的光程差分析方法要简捷得多
§2.4 夫琅禾费衍射与傅里叶变换
光栅的分辨本领
光栅的有限的分辨本领是由实际光栅的有限尺寸引起的
有限尺寸Lx谱线的线形为sinc函数，其半宽度
x z
fx
, fy
y z
exp( jkz) exp jz ( f x f y )
2 2
菲涅耳衍射的传 递函数（频域）
菲涅耳衍射的脉冲 响应函数（空域）
线性不 ) exp j k ( x 2 y 2 ) U ( x0 , y0 0 2z 0 变系统
§2.4 夫琅禾费衍射与傅里叶变换
夫琅和费衍射公式:讨论 • 夫琅和费衍射区的条件苛刻
例: P48, 2.10题 =632.8nm, Rmax = 31mm 菲涅耳衍射区 z >> 1.2m 夫琅和费衍射区要求 z >> 6.3m =532nm,夫琅和费衍射区要求 z >> 7.5m
• 与菲涅耳衍射的关系
强度分布是|T(x)|2, 并附加传播引起的振幅衰减因子
aLx I ( f x ) dz
2
n 2 an 2 sin c d sinc Lx ( f x d ) fx =x/z, fy =y/z n
#
§2.4 夫琅禾费衍射与傅里叶变换
§2.4 夫琅禾费衍射与傅里叶变换
简单孔径的夫琅和费衍射：矩孔
x0 y0 t ( x0 , y0 ) rect rect a b x y t ( x0 , y0 ) absinc(afx )sinc(bf y ), f x , f y z z ab 2 ax 2 by I ( x, y ) sinc sinc z z z
用平面波照明的光栅后方光能量 重新分布，其能量只集中在三个 衍射级上。0级与+1级衍射间的距 离为f0z 。
l
傅里叶分析方法比传统的光程差分析方法要简捷得多
§2.4 夫琅禾费衍射与傅里叶变换
光栅的分辨本领
光栅的有限的分辨本领是由实际光栅的有限尺寸引起的
有限尺寸Lx谱线的线形为sinc函数，其半宽度
x z
fx
, fy
y z
exp( jkz) exp jz ( f x f y )
2 2
菲涅耳衍射的传 递函数（频域）
菲涅耳衍射的脉冲 响应函数（空域）
线性不 ) exp j k ( x 2 y 2 ) U ( x0 , y0 0 2z 0 变系统
§2.4 夫琅禾费衍射与傅里叶变换
夫琅和费衍射公式:讨论 • 夫琅和费衍射区的条件苛刻
例: P48, 2.10题 =632.8nm, Rmax = 31mm 菲涅耳衍射区 z >> 1.2m 夫琅和费衍射区要求 z >> 6.3m =532nm,夫琅和费衍射区要求 z >> 7.5m
• 与菲涅耳衍射的关系
强度分布是|T(x)|2, 并附加传播引起的振幅衰减因子
aLx I ( f x ) dz
2
n 2 an 2 sin c d sinc Lx ( f x d ) fx =x/z, fy =y/z n
#
§2.4 夫琅禾费衍射与傅里叶变换
§2.4 夫琅禾费衍射与傅里叶变换
简单孔径的夫琅和费衍射：矩孔
x0 y0 t ( x0 , y0 ) rect rect a b x y t ( x0 , y0 ) absinc(afx )sinc(bf y ), f x , f y z z ab 2 ax 2 by I ( x, y ) sinc sinc z z z
傅里叶光学第2版教学作者吕乃光第3章标量衍射理论
U ( x, y, z) = a exp ( jkz cosγ ) exp ⎡⎣ jk ( x cosα + y cos β )⎤⎦
=
a
exp
⎡ ⎣
jkz
1−
cos2
α
−
cos2
β
⎤ ⎦
exp
⎡⎣
jk
(
x
cosα
+
y
cos
β
)⎤⎦
= Aexp ⎡⎣ jk ( x cosα + y cos β )⎤⎦
其中， exp ⎡⎣ jk ( x cosα + y cos β )⎤⎦
称为平面波的位相因子。
9 思考题：等相位线是什么形式？ Answer: 等位线方程为
x cosα + y cos β = C
不同C值所对应的等位相线是一些平行斜线，如右图所示。
1、光波的数学描述
1.4 平面波的空间频率 9 平面波的空间频率是傅里叶光学中常用的基本物理量，透彻理解这个 概念的物理意义是非常重要的。 9 如下图，首先研究传播矢量位于x0z平面的简单情况，此时cos β=0, （1）xy平面上复振幅分布为
fx
=
1 X
= cosα λ
fy
=
1 Y
=
cos β λ
则xy平面上的复振幅分布可表示为
和初相位。根据欧拉公式，可将该波函数表示为复指数函数取实部的形式：
{ } ( ) ( ) u x, y, z, t = Re a x, y,⎦
{ } ( ) = Re a x, y, z e e jϕ(x,y,z) − j2πνt
式中，Re{ }表示对括号内复函数取实部。为简单，去掉“Re”而直接用 复指数函数表示简谐波的波函数，并定义一个新的物理量：
高等光学教程-第4章参考答案
第四章 标量衍射理论基础4.1证明（4-21）式所示的索末菲辐射条件成立。
证明：球面2S 是中心位于1S 面上的发散球面波的波面，假定2S 面 上的光场分布表示为 rjkr )exp(=U 式中r 表示产生发散球面波的点光源到球面2S 上任意一点的距离。
1exp()cos()cos(,)r jkr jk n r n r r r ∂∂∂∂⎛⎫===- ⎪∂∂∂∂⎝⎭U U U n,r n r 当∞→R 时，有∞→r ，所以这时有1),cos(≈r n2)exp()exp(1rjkr jk r jkr r jk jk n -≅-⎪⎭⎫ ⎝⎛-=-∂∂U U U 当∞→R 时，上式分母中的r 可用R 来代替，于是 2exp()1lim lim lim (cos sin )R R R jkr R jk R kr j kr n R R →∞→∞→∞∂⎛⎫⎡⎤⎛⎫-=-=-+⎪ ⎪⎢⎥∂⎝⎭⎣⎦⎝⎭U U lim 0jkrR e R →∞⎛⎫=-= ⎪⎝⎭4.2 参考图4-8，考虑在瑞利—索末菲理论中采用下式所表示的格林函数，即010110101exp()exp()()jkr jkr P r r +=+G %%(1) 证明+G 的法线方向的导数在孔径平面上为零。
(2) 利用这个格林函数，求出用孔径上的任意扰动来表示0()p U 的表达式，要得到这个结果必须用什么样的边界条件。
(3) 利用(2)的结果，求出当孔径被从2P 点发散的球面波照明时0()p U 的表达式 证明: 下面是教材中图4-8（1）)(1P +G 由两项迭加而成，它们分别表示从互为镜像的点0P 和0~P 发出的两个初相位相同的单位振幅的球面波。
孔径平面1S 上任一点1P 的+G 值为010101011~)~exp()exp()(r r jk r jkr P +=+G （P4.2-1） 1()P +G 的法向导数为0101010101010101~)~exp(~1)~,cos()exp(1),cos(r r r r n r n G jk jk r jkr r jk n ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=∂∂+ （P4.2-2） 对于互为镜像点的0P 和0~P 来说，有)~,cos(),cos(0101r n r n -= 0101~r r = （P4.2-3）将以上关系式代入（P4.2-2）式，得到0n+∂=∂G （P4.2-4） （2）根据（4-22）式，观察点0P 的光扰动可以用整个平面1S 上的光扰动U 和它的法向导数来表示⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=1d 41)(0S s n n P G U G U U π（P4.2-5） 由0101~r r =，得01011)exp(2)(r jkr P =+G （P4.2-6）将上式和（P4.2-4）式一同代入（P4.2-5）式，得到⎰⎰⎰⎰∂∂=∂∂=+11d )exp(21d 41)(01010S S s r jkr n s G n P U U U ππ（P4.2-7）为了将上式所表示的结果进一步简化，根据孔径∑上的场去计算0P 点的复振幅分布)(0P U ，只需要规定如下两个边界条件：（a ）在孔径∑上，场分布的法向导数n U ∂与不存在衍射屏时的值完全相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 a ≤ x12 + y12 ≤ 1,0 < a < 1 其他 0
今采用单位振幅的单色平面波垂直照明上述孔径，求菲涅耳衍射图样在孔径轴上的强度分 布。 一衍射屏的透过率函数为： t ( x1 , y1 ) =
[2-13]
1 (1 + m cos 2πf 0 x1 ) 2
今用单位振幅的单色平面波垂直照明该衍射屏，求观察平面上的菲涅耳衍射光场复振幅分 布； 并讨论观察屏与衍射屏之间的距离满足什么条件时， 屏上光振动的相位不随空间位置而 变，即在空间是纯调幅的。又当观察屏与衍射屏之间的距离满足什么条件时，才是近似空间 调相的。
图 X2-3
方形环带
[2-8] 如图 X2-4 所示， 边长为 2a 的正方形孔径内再放置一个边长为 a 的正方形掩模， 其中 心落在 (ξ ,η ) 点。采用单位振幅的单色平面波垂直照明，求出与它相距为 z 的观察平面上夫 琅和费衍射图样的光强度分布。
图 X2-4பைடு நூலகம்
[2-8]题图示
[2-9]
波长为 λ 的单位振幅平面波垂直入射到一孔径平面上， 在孔径平面上有一足够大的模
布的光能流等于 I i (r0 ) ，它占总光能流的百分比为 F (r0 ) .试求出 F (r0 ) 的表达式，并与教材 中表 2-5-1 进行比较。 [2-4] [2-5] [2-6] 试证明关系式（2-5-15） 。 试证明关系式（2-5-28） 。 设用单位振幅的单色平面波垂直照明如图 X2-2 所示的双矩孔，求其夫琅和费衍射图
将它们按条纹方向垂直地密着叠放在一起（见图 X2-5） 。当用单位振幅的单色平面波垂直照 明时，求其夫琅和费衍射斑的方向角。
图 X2-5
两正弦光栅正交密着叠放
[2-11]
两个正弦光栅 G1 和 G2 的透射率函数分别为：
′ cos(2πf1 x ) G1 ： t1 ( x ) = t10 + t10 ′ cos(2πf 2 x ) G2 ： t2 ( x ) = t20 + t20
板，其透过率函数为： t ( x )1 =
1 2π x1 ，求透射场的角谱。 1 + cos 2 3λ
[2-10]
两个正弦振幅光栅 G1 和 G2 的透过率函数分别为：
′ cos(2πf x x ) G1 ： t1 ( x ) = t10 + t10 ′ cos(2πf y y ) G2 ： t2 ( y ) = t20 + t20
第二章 标量衍射理论
习题
[2-1] 在基尔霍夫衍射公式（2-2-16）或（2-2-20）中，同时对光场及其法向导数施加了边 界条件，从而导致了理论本身的不自恰性。为了消除这种不自恰性，索末菲选择了换用格林 函数的办法，使新的格林函数或其法向导数在表面 S1 上为 0,这时就不必同时对光场及其法 向导数施加边界条件。例如，可以选择 G 同时由观察点 P0 及其对衍射屏的镜对称点 P0 各
~
eikr01 eikr01 ~ 自出发的同相位的单位振幅的球面波给定（图 X2-1）,即 G+ = r01 是 P0 + ~ 式中， ~ r01 r01 点与 P 1 点间的距离。 (1) 试求： G+ (P ) 在衍射屏上的法向导数； (2) 欲将观察点的复振幅用衍射孔 Σ 上的光扰动来表示，需要什么样的边界条件？ (3) 利用(2)的结果，求出孔径被从 P2 点发出的单色球面波照明时， U (P0 ) 的表达式。
~
图 X2-1
习题[2-1]图示
~
e ikr01 eikr01 [2-2] 如果选择格林函数为： G− = − ~ r01 r01 ~ 其中“－”号表示由 P0 点和 P0 点发出的球面波的位相正好相反。在此条件下，完成上题中
的(1)、(2)和(3)。 [2-3] 在圆孔的夫琅和费衍射花样中， 设观察平面上的总光能流为 I,半径为 r0 的圆面内所分
样的强度分布，并画出衍射强度沿 x 轴和 y 轴的截面图。设
∆ 3 −1 = m ，z 是观察距离， λ 是照明光波长。 λz 2
X Y = 10m −1 ， = 1m −1 ， λz λz
图 X2-2
双矩孔
[2-7] 若用一单位振幅的单色平面波垂直照明如图 X2-3 所示的方形环带，试导出该方形环 带的夫琅和费衍射的表达式。
将它们按条纹方向平行地密着叠放在一起（见图 X2-6） 。当用单位振幅的单色平面波垂直照 明时，求夫琅和费衍射斑的方向角。
图 X2-6
两正弦光栅平行密着叠放
[2-12]
若衍射孔径的透射率函数分别为
2 2 （1） t ( x1 , y1 ) = circ x1 + y1
（2） t ( x1 , y1 ) =