第二章标量衍射理论
合集下载
标量衍射理论习题
1 a ≤ x12 + y12 ≤ 1,0 < a < 1 其他 0
今采用单位振幅的单色平面波垂直照明上述孔径，求菲涅耳衍射图样在孔径轴上的强度分 布。 一衍射屏的透过率函数为： t ( x1 , y1 ) =
[2-13]
1 (1 + m cos 2πf 0 x1 ) 2
今用单位振幅的单色平面波垂直照明该衍射屏，求观察平面上的菲涅耳衍射光场复振幅分 布； 并讨论观察屏与衍射屏之间的距离满足什么条件时， 屏上光振动的相位不随空间位置而 变，即在空间是纯调幅的。又当观察屏与衍射屏之间的距离满足什么条件时，才是近似空间 调相的。
图 X2-3
方形环带
[2-8] 如图 X2-4 所示， 边长为 2a 的正方形孔径内再放置一个边长为 a 的正方形掩模， 其中 心落在 (ξ ,η ) 点。采用单位振幅的单色平面波垂直照明，求出与它相距为 z 的观察平面上夫 琅和费衍射图样的光强度分布。
图 X2-4பைடு நூலகம்
[2-8]题图示
[2-9]
波长为 λ 的单位振幅平面波垂直入射到一孔径平面上， 在孔径平面上有一足够大的模
布的光能流等于 I i (r0 ) ，它占总光能流的百分比为 F (r0 ) .试求出 F (r0 ) 的表达式，并与教材 中表 2-5-1 进行比较。 [2-4] [2-5] [2-6] 试证明关系式（2-5-15） 。 试证明关系式（2-5-28） 。 设用单位振幅的单色平面波垂直照明如图 X2-2 所示的双矩孔，求其夫琅和费衍射图
将它们按条纹方向垂直地密着叠放在一起（见图 X2-5） 。当用单位振幅的单色平面波垂直照 明时，求其夫琅和费衍射斑的方向角。
图 X2-5
两正弦光栅正交密着叠放
第二章 光的标量衍射理论
（2-1-15）
（2-1-15）式称为菲涅尔衍射积分公式 式称为菲涅尔衍射积分公式 满足菲涅耳近似条件的衍射称为菲涅耳衍射 满足菲涅耳近似条件的观察区域称为“菲涅尔衍射区” 满足菲涅耳近似条件的观察区域称为“菲涅尔衍射区” 在菲涅耳衍射区中放置一个二维观察屏， 在菲涅耳衍射区中放置一个二维观察屏，屏上显示的图 形即物体的菲涅耳衍射图形。 形即物体的菲涅耳衍射图形。 辐照度L(x,y) 为： 辐照度
• 2.1.1 惠更斯 菲涅耳原理 惠更斯-菲涅耳原理 • 假设：波前上的每一个面元都可以看做是一个次级扰 假设： 动中心，它们能产生球面子波． 动中心，它们能产生球面子波．后一时刻的波前位置 是所有这些子波波前的包络面。 是所有这些子波波前的包络面。 波前”即是某一时刻光波的波面(等相面 等相面)， “波前”即是某一时刻光波的波面 等相面 ， 次级扰动中心” 是一个点光源或称为子波源。 “次级扰动中心” 是一个点光源或称为子波源。
该近似称为夫琅和费近似 该近似下 基尔霍夫衍射积分公式化简为： 在该近似下，基尔霍夫衍射积分公式化简为：
x2 + y2 E ( x, y ) = exp j k d + jλ d 2d 1 ∞ k ∫ ∫ A(ξ ,η ) exp − j ( xξ + yη ) d ξ d η d −∞ （2-1-19） ）
（2-1-16） ）
L(x,y)等于菲涅耳衍射复振幅分布 等于菲涅耳衍射复振幅分布E(x,y)的模的平方 等于菲涅耳衍射复振幅分布 的模的平方
二、夫琅和费近似和天琅和费衍射
进一步增大观察平面∏到衍射孔径 的距离 进一步增大观察平面 到衍射孔径∑的距离 ，则衍射 到衍射孔径 的距离d， 图形将随之放大。 图形将随之放大。
第2章 标量衍射理论
一级近似 二级近似
对振幅中r 的可作一级近似. 但因为 k 很大, 对位相中的 r 须作二级近似
§2.1 光波的数学描述
球面波 : 近轴近似
a0 k 2 2 U ( P) U ( x, y) exp( jkz) exp j ( x x0 ) ( y y0 ) z 2z
本章将从基尔霍夫衍射理论和角谱出发，讨论衍射问题。前者
与经典物理光学的陈述一致，但利用线性系统理论赋予了新的 解释。我们将把衍射这一物理现象看做线性不变系统，分别讨 论其脉冲响应和传递函数。重点放在角谱理论上。
第2章 标量衍射理论（Theory of Scalar Diffraction）
§2.1 光波的数学描述 2.1.1 单色光波场的复振幅表示
p
l
l
z l fx l f y )
在任一距离z的平面上的复振幅分布，由在 z =0平面上的复 振幅和与传播距离及方向有关的一个复指数函数的乘积给出。 这说明了传播过程对复振幅分布的影响，已经在实质上解决 了最基础的平面波衍射问题
普遍的光振动的复振幅表达式： U(P) = a(P) e jj(P) 光强分布: I = UU*
U ( x, y) A exp[jk ( x cosa y cos b )]
§2-2 基尔霍夫衍射理论
2.2.1 从惠更斯-菲涅耳原理到基尔霍夫衍射公式
衍射理论要解决的问题是：光场中任意一点为P 的复 振幅 U(P) 能否用光场中其它各点的复振幅表示出来。
1. 惠更斯包络作图法 (1678): 从某一时刻的波阵面求下一 时刻波阵面的方法。把波阵面上每一面元作为次级子波 的中心,后一时刻的波阵面是所有这些子波的包络面。
对振幅中r 的可作一级近似. 但因为 k 很大, 对位相中的 r 须作二级近似
§2.1 光波的数学描述
球面波 : 近轴近似
a0 k 2 2 U ( P) U ( x, y) exp( jkz) exp j ( x x0 ) ( y y0 ) z 2z
本章将从基尔霍夫衍射理论和角谱出发，讨论衍射问题。前者
与经典物理光学的陈述一致，但利用线性系统理论赋予了新的 解释。我们将把衍射这一物理现象看做线性不变系统，分别讨 论其脉冲响应和传递函数。重点放在角谱理论上。
第2章 标量衍射理论（Theory of Scalar Diffraction）
§2.1 光波的数学描述 2.1.1 单色光波场的复振幅表示
p
l
l
z l fx l f y )
在任一距离z的平面上的复振幅分布，由在 z =0平面上的复 振幅和与传播距离及方向有关的一个复指数函数的乘积给出。 这说明了传播过程对复振幅分布的影响，已经在实质上解决 了最基础的平面波衍射问题
普遍的光振动的复振幅表达式： U(P) = a(P) e jj(P) 光强分布: I = UU*
U ( x, y) A exp[jk ( x cosa y cos b )]
§2-2 基尔霍夫衍射理论
2.2.1 从惠更斯-菲涅耳原理到基尔霍夫衍射公式
衍射理论要解决的问题是：光场中任意一点为P 的复 振幅 U(P) 能否用光场中其它各点的复振幅表示出来。
1. 惠更斯包络作图法 (1678): 从某一时刻的波阵面求下一 时刻波阵面的方法。把波阵面上每一面元作为次级子波 的中心,后一时刻的波阵面是所有这些子波的包络面。
第二章 光的标量衍射理论
4.若/a趋于零衍射现象消失—几何光学是/a趋于零 的极限情况
2.1.1.2.衍射屏和衍射系统 障碍物—衍射屏
照明 空间
x0 , y0
衍射 空间
x, y
U 0 U0
U0是衍射屏前表面的复振幅
是衍射屏后表面的复振幅 U0
照明 空间
U0 U0
衍射屏
t
U x, y
(2.2.1)
．
y
．
0
复振幅分布U(x,y可分解为频率不同的复指数分 量的线性组合，各频率分量的权重因子为A(fx,fy)
z
A( f x , f y )
exp[ j 2 ( f x x f y y)] 代表一个沿 cos f x ,cos f y 所确定方向传播的单色振幅平面波。
复振幅透射函数—屏函数 图2.1.1 衍射系统及其三个重要的分析平面 ( x0 , y0 ) U0 t ( x0 , y0 ) U 0 ( x0 , y0 ) --瞳函数 振幅型—只改变振幅 位相型—只改变位相 ( x0 , y0 ) t ( x0 , y0 )U 0 ( x0 , y0 ) 或 U0
exp( jkr ) dU ( P) CU ( P0 )dSK ( ) r
dS
U ( P0 )
n
P0
r
Σ
图2.1.2
U (P)
波面Σ 在P点的复振幅 (2.1.3)
P
Σ 上所有子波源在P点产生的总振动为
U ( P) C U ( P0 ) K ( )
exp( jkr ) dS r
y
3D
k与x轴夹角为 , 与y轴夹角为，与z轴夹角为
x
2.1.1.2.衍射屏和衍射系统 障碍物—衍射屏
照明 空间
x0 , y0
衍射 空间
x, y
U 0 U0
U0是衍射屏前表面的复振幅
是衍射屏后表面的复振幅 U0
照明 空间
U0 U0
衍射屏
t
U x, y
(2.2.1)
．
y
．
0
复振幅分布U(x,y可分解为频率不同的复指数分 量的线性组合，各频率分量的权重因子为A(fx,fy)
z
A( f x , f y )
exp[ j 2 ( f x x f y y)] 代表一个沿 cos f x ,cos f y 所确定方向传播的单色振幅平面波。
复振幅透射函数—屏函数 图2.1.1 衍射系统及其三个重要的分析平面 ( x0 , y0 ) U0 t ( x0 , y0 ) U 0 ( x0 , y0 ) --瞳函数 振幅型—只改变振幅 位相型—只改变位相 ( x0 , y0 ) t ( x0 , y0 )U 0 ( x0 , y0 ) 或 U0
exp( jkr ) dU ( P) CU ( P0 )dSK ( ) r
dS
U ( P0 )
n
P0
r
Σ
图2.1.2
U (P)
波面Σ 在P点的复振幅 (2.1.3)
P
Σ 上所有子波源在P点产生的总振动为
U ( P) C U ( P0 ) K ( )
exp( jkr ) dS r
y
3D
k与x轴夹角为 , 与y轴夹角为，与z轴夹角为
x
标量的衍射理论
基尔霍夫的贡献：1.给出了倾斜因子2.给出了常数C的具体形式
方法：将光场当作标量处理，只考虑电场的一个横向分量的标量振幅，而假定其它分量也可以用同样的方法处理，忽略电磁场矢量间的耦合特性，称之为标量衍射理论。
基尔霍夫从ห้องสมุดไป่ตู้量波动方程剥离时间变量得到亥姆赫兹方程，利用格林定理和通过假定衍射屏的边界条件，求解了波动方程，导出了严格的衍射公式。
光的衍射是指光波在传播过程中遇到障碍物时，所发生的偏离直线传播的现象。光的衍射，也可以叫光的绕射，即光可绕过障碍物，传播到障碍物的几何阴影区域中，并在障碍物后的观察屏上呈现出光强的不均匀分布。通常将观察屏上的不均匀光强分布称为衍射图样。
现在一般认为，光波在传播的过程中，不论任何原因导致波前的复振幅分布（包括振幅分布和相位分布）的改变，使自由传播光场变为衍射光场的现象都称为衍射。
惠更斯原理能够很好地解释光的直线传播，光的反射和折射方向，也可以说明衍射的存在；但不能确定光波通过衍射屏后沿不同方向传播的振幅，因而也就无法确定衍射图样中的光强分布。
1818年，在巴黎科学院举行的以解释衍射现象为内容的有奖竞赛会上，年青的菲涅耳出人意料地取得了优胜，他吸收了惠更斯提出的次波概念，用“次波相干迭加”的思想将所有衍射情况引到统一的原理中来,这个原理就是惠更斯－菲涅耳原理。
惠更斯－菲涅耳原理：光场中任一给定曲面上的诸面元可以看做是子波源，如果子波源是相干的，则在波继续传播的空间上任一点处的光振动，都可看作是这些子波源各自发出的子波在该点相干叠加的结果。
设Σ是某光波的波阵面，在其上任一面元ds都可看作是次波的光源，各子波在空间某点的相干叠加，就决定了该点处光波的强度。
惠更斯—菲涅耳原理是对光的衍射现象物理规律的认识。但其数学表达式则不够精确，表达式中的一些参数也不够严格。基尔霍夫根据惠更斯—菲涅耳原理，利用电磁场理论推导出了严格的衍射公式---基尔霍夫衍射公式。
方法：将光场当作标量处理，只考虑电场的一个横向分量的标量振幅，而假定其它分量也可以用同样的方法处理，忽略电磁场矢量间的耦合特性，称之为标量衍射理论。
基尔霍夫从ห้องสมุดไป่ตู้量波动方程剥离时间变量得到亥姆赫兹方程，利用格林定理和通过假定衍射屏的边界条件，求解了波动方程，导出了严格的衍射公式。
光的衍射是指光波在传播过程中遇到障碍物时，所发生的偏离直线传播的现象。光的衍射，也可以叫光的绕射，即光可绕过障碍物，传播到障碍物的几何阴影区域中，并在障碍物后的观察屏上呈现出光强的不均匀分布。通常将观察屏上的不均匀光强分布称为衍射图样。
现在一般认为，光波在传播的过程中，不论任何原因导致波前的复振幅分布（包括振幅分布和相位分布）的改变，使自由传播光场变为衍射光场的现象都称为衍射。
惠更斯原理能够很好地解释光的直线传播，光的反射和折射方向，也可以说明衍射的存在；但不能确定光波通过衍射屏后沿不同方向传播的振幅，因而也就无法确定衍射图样中的光强分布。
1818年，在巴黎科学院举行的以解释衍射现象为内容的有奖竞赛会上，年青的菲涅耳出人意料地取得了优胜，他吸收了惠更斯提出的次波概念，用“次波相干迭加”的思想将所有衍射情况引到统一的原理中来,这个原理就是惠更斯－菲涅耳原理。
惠更斯－菲涅耳原理：光场中任一给定曲面上的诸面元可以看做是子波源，如果子波源是相干的，则在波继续传播的空间上任一点处的光振动，都可看作是这些子波源各自发出的子波在该点相干叠加的结果。
设Σ是某光波的波阵面，在其上任一面元ds都可看作是次波的光源，各子波在空间某点的相干叠加，就决定了该点处光波的强度。
惠更斯—菲涅耳原理是对光的衍射现象物理规律的认识。但其数学表达式则不够精确，表达式中的一些参数也不够严格。基尔霍夫根据惠更斯—菲涅耳原理，利用电磁场理论推导出了严格的衍射公式---基尔霍夫衍射公式。
2 标量衍射理论
第二章 标量衍射理论 （Scalar diffraction theory）
衍射
l Sommerfeld定义
标量衍射理论（ scalar diffraction theory）的适用范围
电场的偏振性可以忽略，（ 傍轴近似paraxial aproximation）.
以Kirchhoff衍射公式讨论衍射问题，并 利用线性系统理论赋予新的解释。
r = z x- x y - y
x- x y- y 忽略倾斜因子的变化后，就可以 z z z \把光波过一个线性不变系统。
U ( x, y ) = U ( x0 , y0 )h( x - x0 , y - y0 )dx0 dy0
近似条件 当
j =
2p x - x0 y - y 0 8z 3
2
2 2
x - x0 2 y - y0 2
即
取最大值时，Δj<<2pz3来自1 8x - x
0
2
y - y0
2 2 max
充分但非必要条件 在一般问题中，菲涅尔衍射很容易实现
2 f 2
其
1 λ2 他
等价于低通滤波器，截止频率1/
基尔霍夫理论 空域 角谱理论 频域 平面波 球面子波 系统的脉冲响应：球面子波在观 察平面上的复振幅分布
系统的传递函数：脉冲响应的傅 立叶变换
三、孔径对角谱的影响
入射到孔径平面的光场
U i ( x0 , y0 )
衍射屏的复振幅透过率 t ( x0 , y0 ) 衍射屏后表面光场
衍射
l Sommerfeld定义
标量衍射理论（ scalar diffraction theory）的适用范围
电场的偏振性可以忽略，（ 傍轴近似paraxial aproximation）.
以Kirchhoff衍射公式讨论衍射问题，并 利用线性系统理论赋予新的解释。
r = z x- x y - y
x- x y- y 忽略倾斜因子的变化后，就可以 z z z \把光波过一个线性不变系统。
U ( x, y ) = U ( x0 , y0 )h( x - x0 , y - y0 )dx0 dy0
近似条件 当
j =
2p x - x0 y - y 0 8z 3
2
2 2
x - x0 2 y - y0 2
即
取最大值时，Δj<<2pz3来自1 8x - x
0
2
y - y0
2 2 max
充分但非必要条件 在一般问题中，菲涅尔衍射很容易实现
2 f 2
其
1 λ2 他
等价于低通滤波器，截止频率1/
基尔霍夫理论 空域 角谱理论 频域 平面波 球面子波 系统的脉冲响应：球面子波在观 察平面上的复振幅分布
系统的传递函数：脉冲响应的傅 立叶变换
三、孔径对角谱的影响
入射到孔径平面的光场
U i ( x0 , y0 )
衍射屏的复振幅透过率 t ( x0 , y0 ) 衍射屏后表面光场
第2章 光的标量衍射理论
a0 ±jkr U(P) = e 球面波的复振幅表示（三维空间）： 球面波的复振幅表示（三维空间）： r
光强分布: 光强分布
I = UU*
[
]
对给定平面是常 量
z
源点S 源点 z 随x, y变化的二次位相因子 变化的二次位相因子 0 球面波特征位相 x
（续）
U ( x, y, z ) = a exp( jk ⋅ r ) = a exp[ jk ( x cos α + y cos β + z cos γ )]
20
2、菲涅耳—基尔霍夫积分公式 、菲涅耳 基尔霍夫积分公式
通过小孔衍射问题
→ 导出菲涅耳—基尔霍夫积分公式
I） 设点光源S 发出的球面单色波，照射到一个开有小孔A 的 光屏上，求光屏右边某点P 的光场，为了应用亥一基积分公式， 围绕P点作一闭合曲面 Σ ，由图可知 Σ 由三部分组成：
A、开孔A B、不透明部分B C、大球面C A
4
2. 1 基尔霍夫衍射理论
2.1. 1 衍射的概念 2.1. 1.1 衍射概念认识的深化
5
惠更斯-菲涅耳定义：光波在传播过程中波面产 惠更斯-菲涅耳定义： 生破缺的现象，称为衍射 现在一般认为： 现在一般认为：光波在传播的过程中，不论任何原因 导致波前的复振幅分布（包括振幅分布和相位分布） 的改变，使自由传播光场变为衍射光场的现象都称为 衍射。
而（已设辅助函数G由 P点向外发散的光照明）
G (Q ) = 1 jkr e r r r e jkr r r ∂G(Q) e jkr 1 jk cos (n ⋅ r ) = jk − cos(n ⋅ r ′) ≈ r r ∂n r
24
将上述关系代入 U ( p ) 式得：
标量衍射理论-2
U0 (x0 , y0 ,0)
cosα cos β A0 , ,0 λ λ
xy
Uz ( x, y, z)
cosα cos β Az , , z λ λ
z
z=0
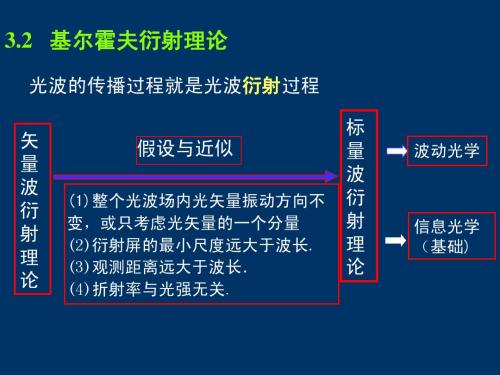
U 0 ( x0 , y0 ;0) = U z ( x, y; z ) =
∞ ∞
z=z
cos β cosα cos β cosα cos β cosα A0 , ;0 exp j 2π x0 + y0 d d ∫∞−∫∞ λ λ λ λ λ λ −
3.3 标量衍射的角谱理论
3.3-1单色平面波与线性平移不变系统的本征函数 单色平面波与线性平移不变系统的本征函数 在 z=0 平面上的复振幅分布为：
exp j 2π ( f x ⋅ x + f y ⋅ y ) = exp[ j 2π (ux + vy )]
[
]
cos β cosα = exp j 2π x+ y λ λ
3.2 基尔霍夫衍射理论
光波的传播过程就是光波衍射 衍射过程 衍射 矢 量 波 衍 射 理 论 假设与近似
(1)整个光波场内光矢量振动方向不 变，或只考虑光矢量的一个分量 (2)衍射屏的最小尺度远大于波长. (3)观测距离远大于波长． (4)折射率与光强无关.
标 量 波 衍 射 理 论
波动光学
信息光学 （基础)
∞ ∞
cos β cosα cos β cosα cos β cosα Az , ; z exp j 2π x+ y d d ∫∞−∫∞ λ λ λ λ λ λ −
cosα cos β A0 , ,0 λ λ
xy
Uz ( x, y, z)
cosα cos β Az , , z λ λ
z
z=0
U 0 ( x0 , y0 ;0) = U z ( x, y; z ) =
∞ ∞
z=z
cos β cosα cos β cosα cos β cosα A0 , ;0 exp j 2π x0 + y0 d d ∫∞−∫∞ λ λ λ λ λ λ −
3.3 标量衍射的角谱理论
3.3-1单色平面波与线性平移不变系统的本征函数 单色平面波与线性平移不变系统的本征函数 在 z=0 平面上的复振幅分布为：
exp j 2π ( f x ⋅ x + f y ⋅ y ) = exp[ j 2π (ux + vy )]
[
]
cos β cosα = exp j 2π x+ y λ λ
3.2 基尔霍夫衍射理论
光波的传播过程就是光波衍射 衍射过程 衍射 矢 量 波 衍 射 理 论 假设与近似
(1)整个光波场内光矢量振动方向不 变，或只考虑光矢量的一个分量 (2)衍射屏的最小尺度远大于波长. (3)观测距离远大于波长． (4)折射率与光强无关.
标 量 波 衍 射 理 论
波动光学
信息光学 （基础)
∞ ∞
cos β cosα cos β cosα cos β cosα Az , ; z exp j 2π x+ y d d ∫∞−∫∞ λ λ λ λ λ λ −
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
21
U (P ) A 1
U
r21
e 21 jk cos( n , r21 ) A n r21
图2.2.2 单色点光 源照明孔径 jk ( r01 r21 ) cos(n , r01 ) cos(n , r21 ) e dS (2.2.20） r01r21 2
§ 2. 基尔霍夫衍射理论
a.惠更斯-菲涅耳原理 波传到的任何一点都是子波的波源， 各子波在空间某点的相干叠加，就 决定了该点波的强度。
dU ( p ) U ( p1 ) K ( θ ) r
S *
p
dS
dS
p1 S(波前) 设初相为零
·
n
r
dU(p)
p
·
§ 2. 基尔霍夫衍射理论 a.惠更斯-菲涅耳原理
§ 2. 基尔霍夫衍射理论
c.衍射公式与叠加积分
将(2.2.20)式写成：
U (P ) 0
U ( P )h( P , P )dxdy
1 1 0
其中
h( P , P ) 1 0
1 e j
jkr01
K ( )
r01
(2.2.25)
则(2.2.24)式具有叠加积分的意义。光波由 P 点传播到 P 点 1 0 的过程实际上是一个衍射过程,该过程将U ( P )变换成 U ( P ) ,这 1 0 等效于一个“系统”的作用，由于满足叠加积分，故此系统还是 线性系统。对于这个系统， h( P , P ) 表征了它的全部特性。 1 0
0
2
2
1
§3.衍射规律的频域表达式
b.传播现象作为一种线性空间滤波器
图2.3.2 传递函数相当于一个低通滤波圆孔 该滤波器的作用是阻止高频信息进入衍射光场。例如在分 析一幅图像结构时，比波长还小的精细结构或者空间频率 大于 1/ 的信息，在单色光照明下不能沿z方向传播。
§3.衍射规律的频域表达式
d d
§3.衍射规律的频域表达式
a.衍射规律的频域描述
利用亥姆霍兹方程得：
即
( k )[GZ ( , )e
2 2
j 2 ( x y )
]0
d
2
dz
GZ ( , ) ( 2
2
) [1 ( ) ( ) ]GZ ( , ) 0
2 2 2
上式为二阶线性齐次常微分方程，其特征根
§4.菲涅耳衍射与夫琅和费衍射
用普遍形式下的标量衍射理论来计算具体衍射问 题时，在数学上是非常困难的。因此有必要讨论某些 近似。按照近似条件的不同，分为菲涅耳近似和夫琅 和费近似两种，从而有菲涅耳衍射和夫琅和费衍射。
由此可见孔径限制入射光场,导致其频谱展宽了。 例如对矩孔
t ( x, y ) rect(
则
x
,
y
)
a b
cos cos acos bcos Gt ( , ) T ( , ) absinc( , )
故当用一定大小的孔径限制入射光场时，其效果是使入射光场 的频谱展宽。孔径越小，频谱展宽越显著。
第二章
Scalar Quantity Diffraction Theory
标量衍射理论
衍射（索末菲）：不能用反射或折射来解释的光线对直线 光路的任何偏离。衍射是光传播的普遍属性，是光的波 动性的表现。 衍射问题的解决方式：
1，考虑光波的矢量性，用矢量波方法求解。（数学 上很复杂，但是在某些问题 （如研究高分辨率光栅时） 必须要用这个方法。 2，标量的方法（基尔霍夫标量衍射理论），把光作 为标量来处理，只考虑电磁场一个分量的复振幅。适用 范围：衍射孔径比波长大的多，观测点离衍射孔径比较 远。
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
3.基尔霍夫积分定理
r01 r0 1 的长度，则必有： ( 2 k 2 )G 0 的矢量 据此首先将格林定理表达式作适当简化，再通过 微分运算，最后可得
选择
G( P ) 1
exp( jkr01 )
r01 1 ， 表示从观察点P0 指向P 点
2 2
u(P,t)满足标量波动方程 由此得
2 2
1 u c
2
t
0
( k )U ( p ) 0
（亥姆霍兹方程)
U n G n
2.格林定理 ：设函数U、G单值连续可导，则有
(G U U G)dV (G
2 2
U
)dS
S
其中G是一个辅助函数,称为格林函数。必须慎重选择格林函 数和封闭面S。
U (P ) 0 1 4 U n G n
S1 S2
(G
U)Βιβλιοθήκη S在S2面上，G e jkR R G 1 jkR ( jk )e R jkG R n
S2
(G
U n
U
G n
)dS G (
U n
图2.2.1
§3.衍射规律的频域表达式
a.衍射规律的频域描述
图2.3.1 计算角谱用的坐标系 令 则由
G0 ( , ) F{U ( x, y,0)}, GZ ( , ) F{U ( x, y, z)}
U ( x, y , z )
G
Z
( , )e
j 2 ( x y )
这对应于沿某一确定方向传播的平面波。
⑵. ( )2 ( ) 2 1 按指数 e z 急速衰减，称为 隐失波。 ⑶. ( ) 2 ( ) 2 1 cos 0, 900
表示在 z 轴的方向上净能流为零。
§3.衍射规律的频域表达式
b.传播现象作为一种线性空间滤波器
K( ):倾斜因子
0 , K K max K ( ) 2 , K 0
dU ( p )
U ( p1 ) K ( θ )
U( p)
r U ( p1 ) K ( θ )
s
exp( jkr )dS
分析：1.从定性到定量，但仍然基于子波假设。 2.倾斜因子实际上是未知量。
c.衍射孔径对角谱的效应
首先引入衍射屏的屏函数 或透过率函数(图2.3.3)：
x, y t x, y U i x, y
Ut
则有 图2.3.3 衍射屏的屏函数
cos cos Gi ( , ) ( , ) ( , )
Ut ( x, y) U i ( x, y)t ( x, y) Gt ( , ) Gi ( , )* T ( , )
2
jkU ) R d
显然有
| RG || e
jkR
| 1
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
再由索莫菲辐射条件
R
lim R(
U n
jkU ) 0
(2.2.14)
故S 2 面上的整个积分随 R 趋于无穷大而消失。 在 S1 面上的积分,应用基尔霍夫边界条件: ⑴在孔径上,光场分布U及其导数 U 与没有屏幕时 n 完全相同。 ⑵在孔径阴影区内的那部分,光场分布及其导数恒 等于零。
e
jkr 01
其中
则可把(2.2.21)式解释为惠更斯-菲涅耳原理。其中
K ( ) cos( n , r01 ) cos( n , r21 ) 2
称为倾斜因子。若 P0 点在与入射方向相同一侧 ，则在近轴条件 下 cos(n, r01 ) cos(n, r21 ) 1 K ( ) 0 ,无倒退波。
本章将以基尔霍夫衍射公式讨论衍射问题，并利用线 性系统理论赋新的解释，我们把衍射过程看做是一个线 性不变系统，讨论其脉冲响应和传递函数。
§ 1. 衍射现象概述
a.”衍射”现象 最早研究衍射现象的是格里马第 (F.H.Grimaldi) ——1655年发表论文 b.”衍射”的最初定义（索莫菲A.Sommerfeld)
jkr
最后得
U (P ) 0 A j
上式称为菲涅耳-基尔霍夫衍射公式。
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
讨论:1).光源位置与观察点位置是对称的。(亥姆霍兹互易定理) 2).说明倒退波是不可能的。 如果把菲涅耳衍射公式改写成
U (P ) 0
' 1 U ( P )( r )dS (2.2.21) 01 jkr21 cos(n , r01 ) cos( n , r21 ) (2.2.22) A e ' U (P ) ( ) 1 j r21 2
由 得
GZ ( , ) G0 ( , ) H ( , )
2 2 2 exp j z 1( ) ( ) H , 0
其 他
2
2
1
2
能求出传递函数这个事实表明，与自由传播等效的系统是 一个线性空间不变系统，并且该系统的传递函数相当于一 个低通滤波器。其截止空间频率为
最后得:
U (P ) 0
1 4
(G
U n
U
G n
)dS
(2.2.16)
说明：基尔霍夫边界条件具有不自洽性,可通过选择别的 格林函数予以改善。
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
5.菲涅耳—基尔霍夫衍射公式 对孔径采取具体的照明方式后, 基尔霍夫衍射公式会有 更具体的形式。 设孔径由 P 点处的单色点光源照明 2 jkr 则有 e
2 2
或 讨论: ⑴.
cos cos cos cos 2 2 2 Gz , G0 , exp j z 1 cos cos
U (P ) A 1
U
r21
e 21 jk cos( n , r21 ) A n r21
图2.2.2 单色点光 源照明孔径 jk ( r01 r21 ) cos(n , r01 ) cos(n , r21 ) e dS (2.2.20） r01r21 2
§ 2. 基尔霍夫衍射理论
a.惠更斯-菲涅耳原理 波传到的任何一点都是子波的波源， 各子波在空间某点的相干叠加，就 决定了该点波的强度。
dU ( p ) U ( p1 ) K ( θ ) r
S *
p
dS
dS
p1 S(波前) 设初相为零
·
n
r
dU(p)
p
·
§ 2. 基尔霍夫衍射理论 a.惠更斯-菲涅耳原理
§ 2. 基尔霍夫衍射理论
c.衍射公式与叠加积分
将(2.2.20)式写成：
U (P ) 0
U ( P )h( P , P )dxdy
1 1 0
其中
h( P , P ) 1 0
1 e j
jkr01
K ( )
r01
(2.2.25)
则(2.2.24)式具有叠加积分的意义。光波由 P 点传播到 P 点 1 0 的过程实际上是一个衍射过程,该过程将U ( P )变换成 U ( P ) ,这 1 0 等效于一个“系统”的作用，由于满足叠加积分，故此系统还是 线性系统。对于这个系统， h( P , P ) 表征了它的全部特性。 1 0
0
2
2
1
§3.衍射规律的频域表达式
b.传播现象作为一种线性空间滤波器
图2.3.2 传递函数相当于一个低通滤波圆孔 该滤波器的作用是阻止高频信息进入衍射光场。例如在分 析一幅图像结构时，比波长还小的精细结构或者空间频率 大于 1/ 的信息，在单色光照明下不能沿z方向传播。
§3.衍射规律的频域表达式
d d
§3.衍射规律的频域表达式
a.衍射规律的频域描述
利用亥姆霍兹方程得：
即
( k )[GZ ( , )e
2 2
j 2 ( x y )
]0
d
2
dz
GZ ( , ) ( 2
2
) [1 ( ) ( ) ]GZ ( , ) 0
2 2 2
上式为二阶线性齐次常微分方程，其特征根
§4.菲涅耳衍射与夫琅和费衍射
用普遍形式下的标量衍射理论来计算具体衍射问 题时，在数学上是非常困难的。因此有必要讨论某些 近似。按照近似条件的不同，分为菲涅耳近似和夫琅 和费近似两种，从而有菲涅耳衍射和夫琅和费衍射。
由此可见孔径限制入射光场,导致其频谱展宽了。 例如对矩孔
t ( x, y ) rect(
则
x
,
y
)
a b
cos cos acos bcos Gt ( , ) T ( , ) absinc( , )
故当用一定大小的孔径限制入射光场时，其效果是使入射光场 的频谱展宽。孔径越小，频谱展宽越显著。
第二章
Scalar Quantity Diffraction Theory
标量衍射理论
衍射（索末菲）：不能用反射或折射来解释的光线对直线 光路的任何偏离。衍射是光传播的普遍属性，是光的波 动性的表现。 衍射问题的解决方式：
1，考虑光波的矢量性，用矢量波方法求解。（数学 上很复杂，但是在某些问题 （如研究高分辨率光栅时） 必须要用这个方法。 2，标量的方法（基尔霍夫标量衍射理论），把光作 为标量来处理，只考虑电磁场一个分量的复振幅。适用 范围：衍射孔径比波长大的多，观测点离衍射孔径比较 远。
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
3.基尔霍夫积分定理
r01 r0 1 的长度，则必有： ( 2 k 2 )G 0 的矢量 据此首先将格林定理表达式作适当简化，再通过 微分运算，最后可得
选择
G( P ) 1
exp( jkr01 )
r01 1 ， 表示从观察点P0 指向P 点
2 2
u(P,t)满足标量波动方程 由此得
2 2
1 u c
2
t
0
( k )U ( p ) 0
（亥姆霍兹方程)
U n G n
2.格林定理 ：设函数U、G单值连续可导，则有
(G U U G)dV (G
2 2
U
)dS
S
其中G是一个辅助函数,称为格林函数。必须慎重选择格林函 数和封闭面S。
U (P ) 0 1 4 U n G n
S1 S2
(G
U)Βιβλιοθήκη S在S2面上，G e jkR R G 1 jkR ( jk )e R jkG R n
S2
(G
U n
U
G n
)dS G (
U n
图2.2.1
§3.衍射规律的频域表达式
a.衍射规律的频域描述
图2.3.1 计算角谱用的坐标系 令 则由
G0 ( , ) F{U ( x, y,0)}, GZ ( , ) F{U ( x, y, z)}
U ( x, y , z )
G
Z
( , )e
j 2 ( x y )
这对应于沿某一确定方向传播的平面波。
⑵. ( )2 ( ) 2 1 按指数 e z 急速衰减，称为 隐失波。 ⑶. ( ) 2 ( ) 2 1 cos 0, 900
表示在 z 轴的方向上净能流为零。
§3.衍射规律的频域表达式
b.传播现象作为一种线性空间滤波器
K( ):倾斜因子
0 , K K max K ( ) 2 , K 0
dU ( p )
U ( p1 ) K ( θ )
U( p)
r U ( p1 ) K ( θ )
s
exp( jkr )dS
分析：1.从定性到定量，但仍然基于子波假设。 2.倾斜因子实际上是未知量。
c.衍射孔径对角谱的效应
首先引入衍射屏的屏函数 或透过率函数(图2.3.3)：
x, y t x, y U i x, y
Ut
则有 图2.3.3 衍射屏的屏函数
cos cos Gi ( , ) ( , ) ( , )
Ut ( x, y) U i ( x, y)t ( x, y) Gt ( , ) Gi ( , )* T ( , )
2
jkU ) R d
显然有
| RG || e
jkR
| 1
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
再由索莫菲辐射条件
R
lim R(
U n
jkU ) 0
(2.2.14)
故S 2 面上的整个积分随 R 趋于无穷大而消失。 在 S1 面上的积分,应用基尔霍夫边界条件: ⑴在孔径上,光场分布U及其导数 U 与没有屏幕时 n 完全相同。 ⑵在孔径阴影区内的那部分,光场分布及其导数恒 等于零。
e
jkr 01
其中
则可把(2.2.21)式解释为惠更斯-菲涅耳原理。其中
K ( ) cos( n , r01 ) cos( n , r21 ) 2
称为倾斜因子。若 P0 点在与入射方向相同一侧 ，则在近轴条件 下 cos(n, r01 ) cos(n, r21 ) 1 K ( ) 0 ,无倒退波。
本章将以基尔霍夫衍射公式讨论衍射问题，并利用线 性系统理论赋新的解释，我们把衍射过程看做是一个线 性不变系统，讨论其脉冲响应和传递函数。
§ 1. 衍射现象概述
a.”衍射”现象 最早研究衍射现象的是格里马第 (F.H.Grimaldi) ——1655年发表论文 b.”衍射”的最初定义（索莫菲A.Sommerfeld)
jkr
最后得
U (P ) 0 A j
上式称为菲涅耳-基尔霍夫衍射公式。
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
讨论:1).光源位置与观察点位置是对称的。(亥姆霍兹互易定理) 2).说明倒退波是不可能的。 如果把菲涅耳衍射公式改写成
U (P ) 0
' 1 U ( P )( r )dS (2.2.21) 01 jkr21 cos(n , r01 ) cos( n , r21 ) (2.2.22) A e ' U (P ) ( ) 1 j r21 2
由 得
GZ ( , ) G0 ( , ) H ( , )
2 2 2 exp j z 1( ) ( ) H , 0
其 他
2
2
1
2
能求出传递函数这个事实表明，与自由传播等效的系统是 一个线性空间不变系统，并且该系统的传递函数相当于一 个低通滤波器。其截止空间频率为
最后得:
U (P ) 0
1 4
(G
U n
U
G n
)dS
(2.2.16)
说明：基尔霍夫边界条件具有不自洽性,可通过选择别的 格林函数予以改善。
§ 2. 基尔霍夫衍射理论 b.基尔霍夫衍射公式
5.菲涅耳—基尔霍夫衍射公式 对孔径采取具体的照明方式后, 基尔霍夫衍射公式会有 更具体的形式。 设孔径由 P 点处的单色点光源照明 2 jkr 则有 e
2 2
或 讨论: ⑴.
cos cos cos cos 2 2 2 Gz , G0 , exp j z 1 cos cos