实验四核衰变的统计规律与放射性测定的实验数据处理资料
核衰变统计规律

实验二 核衰变的统计规律实验人:*** 合作者:*** 实验时间:2011/06/03一、引言对核衰变产生的射线可用计数方式测量。
然而多次测量相同时间间隔内的计数,即使保持相同的实验条件,每次测量的结果并不相同,而是围绕某一平均值上下涨落,反映出核衰变的随机性二、实验目的1、了解并验证原子核衰变及放射性计数的统计性2、了解统计误差的意义,掌握计算统计误差的方法3、学习检验测量数据的分布类型的方法三.原理1.放射性测量的随机性和统计性在做重复的放射性测量中,即使保持完全相同的实验条件(例如放射性的半衰期足够长,因此在实验时间内可以认为其强度基本上没有变化;源与计数器的相对位置始终保持不变;每次测量时间不变;测量仪器足够精确,不会产生其它的附加误差等等),每次的测量结果并不完全相同,而是围绕其平均值上下涨落,有时甚至有很大的差别,也就是说物理实验的测量结果具有偶然性,或者说随机性。
物理测量的随机性产生原因不仅在于测量时的偶然误差,而且更是物理现象(当然包括放射性核衰变)本身的随机性质,即——物理量的实际数值时刻围绕着平均值发生微小起伏。
在微观现象领域,特别是在高能物理实验中,物理现象本身的统计性更为突出。
按照量子力学的原理,对处于同一个态的微观粒子,测量同一个可观测的物理量时,即使不存在任何测量误差,各次测量结果也会不同,除非粒子处于这个可观测量的本征态;比如同一种粒子的寿命,其实测值分布在从相当短到相当长的范围内。
另一方面,所谓偶然的东西,是一种有必然性隐藏在里面的形式;我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。
2.核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。
放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,与其他原子核是否衰变无关;因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。
在N 0个原子核的体系中,单位时间内对于每个原子核来说只有两种可能:A 类是原子核发生衰变,B 类是没有发生核衰变。
探索核物质的衰变实验步骤

探索核物质的衰变实验步骤核物质的衰变是核能学中的重要研究内容之一。
为了探索核物质的衰变规律,科学家们进行了一系列的实验研究。
本文将介绍探索核物质的衰变实验步骤。
为了使文章易于阅读,我们将按照以下顺序展开叙述:实验目的、实验所需材料、实验步骤及数据处理。
一、实验目的通过实验,探索核物质的衰变规律,了解不同衰变类型的特点及其在实验中的表现,进一步理解核物质的性质。
二、实验所需材料1. 放射性样品:选择具有放射性衰变性质的核物质样品,如放射性同位素。
2. 探测器:可选用放射线探测器、Geiger-Muller管或闪烁体探测器等,以便测量放射性衰变的放射线。
3. 计数器:用于记录和计算衰变事件的次数。
4. 实验设备:包括支架、样品夹持器、闪烁体探测器固定装置等。
5. 安全防护措施:实验室应配备必要的辐射防护设备和个人防护用品。
三、实验步骤1. 样品准备:选取一定数量的放射性样品,并将其放置于样品夹持器中进行固定。
2. 设备安装:将放射线探测器(如闪烁体探测器)固定在样品旁边的支架上,确保其与样品保持一定距离。
3. 数据记录与采集:开启计数器,并将其连接到探测器上,对放射线进行连续计数,记录衰变事件的次数。
4. 实验观测:通过连续观测一定时间段内的衰变事件次数,绘制出衰变事件与时间的关系曲线(即衰变曲线)。
5. 数据处理:根据实验数据,计算出核物质的衰变常数和半衰期等相关参数,并进行分析与讨论。
四、数据处理1. 计算衰变常数:根据衰变曲线的指数衰减形式,采用半对数坐标纸绘制衰变曲线,通过回归分析得到衰变常数。
2. 计算半衰期:利用衰变常数可计算出核物质的半衰期,半衰期是指在衰变曲线上一半原子核衰变所需的时间。
3. 分析与讨论:根据实验得到的衰变常数和半衰期,进行数据分析与讨论,比较不同样品或不同衰变模式下的衰变特点。
通过以上实验步骤和数据处理,我们可以探索核物质的衰变规律,进一步了解核物质的性质,为核能学和相关领域的研究提供实验依据和理论支持。
原子核的衰变与放射性的实验研究

放射性是指某些原子核自发地放出射 线并转变为另一种原子核的现象。
放射性来源
放射性主要来源于原子核内部的不稳 定性,这种不稳定性可能由质子数和 中子数的不平衡引起。
放射性强度和单位
放射性强度定义
放射性强度是指单位时间内发生放射 性衰变的原子核数目。
放射性强度单位
放射性强度的国际单位是贝克勒(Bq ),表示每秒有一个原子核衰变。其 他常用单位包括居里(Ci)等。
2023
REPORTING
THANKS
感谢观看
XX
实验精度有待提高
在本研究中,由于受到实验条件和技术的限制,部分实验结果的精度不够高。未来可以通过改进实验设备和技术手段 ,提高实验的精度和可靠性。
理论模型需要进一步完善
虽然本研究取得了一定的成果,但理论模型在某些方面仍需要进一步完善。未来可以深入研究原子核衰变的微观机制 ,建立更精确的理论模型,以更好地解释实验结果。
对未来研究的建议
根据实验结果和讨论,提出对未来研究的建议和 展望。
2023
PART 06
结论与展望
REPORTING
研究结论和意义
01
揭示了原子核衰变的内在机制
通过实验研究,我们更深入地理解了原子核衰变的本质,揭示了其内在
的物理机制,为核物理理论的发展提供了重要的实验依据。
02 03
丰富了放射性同位素的应用领域
2023
PART 04
实验方法和步骤
REPORTING
实验器材和准备
放射源
选择适当的放射性同位 素作为放射源,如铀、
钍等。
探测器
用于检测放射性衰变产 生的粒子,如盖革-米勒 计数器、闪烁计数器等
核衰变与放射性计数的统计规律
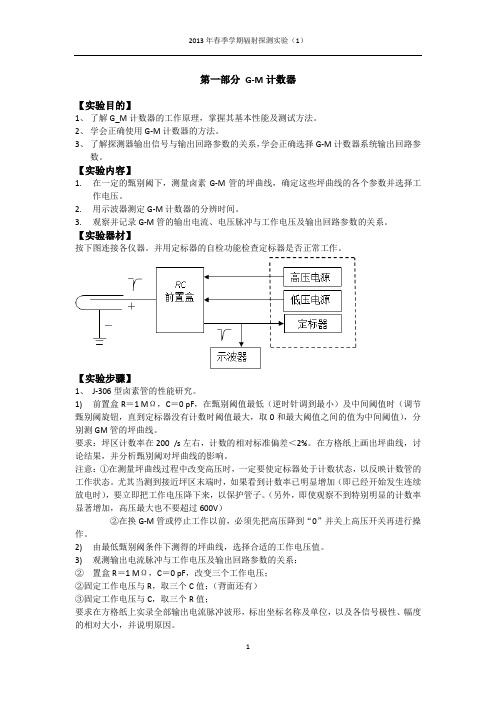
第一部分G-M计数器【实验目的】1、了解G_M计数器的工作原理,掌握其基本性能及测试方法。
2、学会正确使用G-M计数器的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M计数器系统输出回路参数。
【实验内容】1.在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参数并选择工作电压。
2.用示波器测定G-M计数器的分辨时间。
3.观察并记录G-M管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
【实验器材】按下图连接各仪器。
并用定标器的自检功能检查定标器是否正常工作。
【实验步骤】1、J-306型卤素管的性能研究。
1) 前置盒R=1 MΩ,C=0 pF,在甄别阈值最低(逆时针调到最小)及中间阈值时(调节甄别阈旋钮,直到定标器没有计数时阈值最大,取0和最大阈值之间的值为中间阈值),分别测GM管的坪曲线。
要求:坪区计数率在200 /s左右,计数的相对标准偏差<2%。
在方格纸上画出坪曲线,讨论结果,并分析甄别阈对坪曲线的影响。
注意:①在测量坪曲线过程中改变高压时,一定要使定标器处于计数状态,以反映计数管的工作状态。
尤其当测到接近坪区末端时,如果看到计数率已明显增加(即已经开始发生连续放电时),要立即把工作电压降下来,以保护管子。
(另外,即使观察不到特别明显的计数率显著增加,高压最大也不要超过600V)②在换G-M管或停止工作以前,必须先把高压降到“0”并关上高压开关再进行操作。
2) 由最低甄别阈条件下测得的坪曲线,选择合适的工作电压值。
3) 观测输出电流脉冲与工作电压及输出回路参数的关系:②置盒R=1 MΩ,C=0 pF,改变三个工作电压;②固定工作电压与R,取三个C值;(背面还有)③固定工作电压与C,取三个R值;要求在方格纸上实录全部输出电流脉冲波形,标出坐标名称及单位,以及各信号极性、幅度的相对大小,并说明原因。
注意:①中的三个电压值必须在坪区范围内;为观察到形状较好的电流和电压波形,②、③及以下各步骤中的工作电压可比步骤(2)中选择的工作电压低,具体数值可以取R =1 M Ω,C =0 pF 时,示波器观察电流或电压波形不出现饱和的最大工作电压值。
衰变实验报告

衰变实验报告实验目的:本实验的目的是通过观察和记录放射性同位素的衰变过程,了解和研究放射性衰变的基本规律及其应用。
实验原理:放射性衰变是指放射性同位素在一段时间内自发地转变为其他核素的过程,这一过程伴随着放射性射线的放出。
衰变过程中核素的不稳定性逐渐减弱,最终转化为稳定的核素。
实验步骤:1. 将一个含有放射性同位素的样本置于探测器旁,确保样本与探测器之间的距离适当。
2. 打开探测器并记录初始读数,作为实验开始的时间点。
3. 按照设定的时间间隔,记录探测器上显示的衰变事件数,并计算衰变速率。
4. 持续观察和记录衰变事件数,直至一定时间后或衰变事件数过小,实验结束。
实验结果与数据分析:通过实验记录的数据,我们可以得到衰变事件数随时间变化的曲线图。
根据曲线的特点,我们可以推断衰变的过程和规律。
通常情况下,衰变曲线呈指数衰减的形式,即随时间的增加,衰变事件数逐渐减少。
通过对曲线的拟合,可以得到衰变的半衰期,即衰变事件数减少一半所需的时间。
根据实验数据,我们可以计算得到放射性同位素的衰变常数和半衰期等相关参数。
这些参数的计算可以通过数学方法进行,也可以利用相应的软件进行计算。
实验结论:本实验通过观察和记录放射性同位素的衰变过程,研究了放射性衰变的规律。
实验结果表明,放射性同位素的衰变服从指数衰减定律,衰变事件数随时间呈现递减趋势。
通过计算衰变常数和半衰期,我们可以更准确地描述放射性衰变的特点和性质。
实验的局限性与改进:1. 实验过程中可能存在测量误差,例如仪器的误差或操作上的误差,这会对实验结果产生一定的影响。
2. 在实验过程中,需要尽量减少环境因素对实验结果的干扰,比如背景辐射的影响。
3. 实验中使用的放射性同位素应遵守相关的安全规定,并在实验后进行正确的处理和处置。
总结:通过本次实验,我们深入了解了放射性衰变的基本原理和规律。
放射性衰变在许多领域都有重要的应用,例如核能的利用、放射性同位素的医学应用等。
实验四核衰变的统计规律与放射性测定的实验数据处理

实验四核衰变的统计规律与放射性测定的实验数据处理学生:学号:同组:一、实验目的1.验证核衰变所服从的统计规律2.熟悉放射性测量误差的表示方法3.了解测量时间对准确度的影响4.学会根据准确度的要求选择测量时间二、实验原理实验证明 ,在对长寿命放射性物质活度进行多次重复测量时,即使周围条件相同,每次测量的结果仍不相同。
然而,每次结果都围绕某一平均值上下涨落,并且,这种涨落是服从一定的统计规律的。
假如在时间间隔t 内核衰变的平均数为 n ,则在某一特定的时间间隔t 内,核衰变为 n 的出现机率 P(n)服从统计规律的泊松分布:P(n)(n)n e n(2-4-1)n!图一表示 n =3.5的泊松分布曲线。
泊松分布在平均数 n 较小的情况下比较适用;如果值相当大,计算起来十分复杂,实际应用对泊松分布利用斯蒂令近似公式:n!2 n n n e n( 2-4-2)化为高斯分布,得:1(n n)2e 2 n( 2-4-3)P(n)2n图 1 泊松分布曲线高斯分布说明,与平均值的偏差 ( n n) 对于 n 而言具有对称性,而绝对值大的偏差出现的几率小。
放射性衰变并不是均匀地进行,所以在相同的时间间隔内作重复的测量时测量的放射性粒子数并不严格保持一致,而是在某平均值附近起伏。
通常把平均值 n 看作是测量结果的几率值,并用它来表示放射性活度,而把起伏带来的误差叫做测量的统计误差,习惯用标准误差n 来表描述。
实验室都将一次测量的结果当作平均值,图 2高斯分布曲线并作类似的处理而计为N N 。
计数的相对标准误差为:N1(2-4-4)N N它能说明测量的准确度。
当N 大时,相对标准误差小,而准确度高。
反之,则相对标准误差大,而准确度低。
为了得到足够计数N 来保证准确度,就需要延长测量时间t 或增加相同测量的次数m。
根据计算可知,从时间t 内测的结果中算出的计数率的标准误差为:N N n(2-4-5)t t2t计数率的相对标准误差 E 用下式表示:n1E t(2-4-6)ntn若实验重复进行 m 次,则平均计数率的标准误差等于:n( 2-4-7)mt考虑本底后,标准误差为:N c N b n c n b(2-4-8)t c2t b2t c t bN c为 t c时间内源加本底的计数,n b为 t b时间内本底的计数, n c为源加本底的计数率, n b为本底的计数率。
核物理学小实验放射性衰变和半衰期

根据放出的射线和衰变产物的不同, 放射性衰变可分为α衰变、β衰变和γ 衰变三种类型。
半衰期计算公式
半衰期定义
放射性元素的原子核有半数发生衰变所需的时间,具有统计规律。少量氡原子不满足半数衰变规律。
半衰期计算公式
放射性元素的原子核有半数发生衰变后,剩余原子核的数量将按照指数方式减少,其数学表达式为 N = N0 * (1/2)^(t/T),其中 N0 是初始原子核数量,N 是经过时间 t 后的原子核数量,T 是半衰期。
根据实验数据记录表中 的数据,绘制计数率随 时间变化的曲线图。通 过观察曲线图的变化趋 势,分析放射性源的半 衰期特点。
根据实验结果和半衰期 计算公式,计算放射性 源的半衰期并与已知值 进行比较。讨论实验结 果与理论值之间的差异 及可能原因。
03
实验器材与材料
放射源选择及特性
放射源类型
通常选用α、β或γ放射源 ,如镅-241、锶-90或钴-
数值展示
在图表中标注关键数值,如半衰 期、衰变率等,方便读者快速了 解实验结论。
文字描述
对实验结果进行简要的文字描述 ,阐述实验现象、规律和结论, 帮助读者深入理解实验内容。
05
实验现象观察与分析
放射性衰变现象观察
放射性物质自发地放出射线
在实验中,可以观察到放射性物质在没有外界干预的情况 下,自发地放出射线,这些射线包括α射线、β射线和γ射 线等。
、环保等领域的创新应用。
谢谢您的聆听
THANKS
半衰期是放射性元素原子 核有半数发生衰变所需的 时间,是放射性元素的特 征参数之一。
通过实验测量放射性元素 的衰变产物和半衰期,可 以验证放射性衰变的规律 性和半衰期的概念。
对半衰期概念的理解和应用
核衰变实验数据分析与处理.

实验数据分析与处理:工作电压的选择:根据坪曲线规律,选择较为平坦时工作电压为880V。
测放射源计数率实验数据分析:实验分析:1. 探测器与放射源的几何位置应保持合理(两者不宜离开太远2.实验中要保证不触碰探测仪,因为本实验是一种强度测量,所以一切有可能影响探测器探测效率的因素都必须严格保持不变,如工作点要保持稳定探测器和源的几何位置也不可以改变。
3.实验数据分析时,软件曾出现提示框显示:“已超出正态分布范围,无法分析”的字样。
打开实验数据后发现实验的第一个数据与之后的数据相去甚远(后面数据均维持在3300~3500范围内,第一个数据为20000+的值,在去除第一个数据后分析实验,软件得以成功分析。
可能由于电压值发生一定变化导致第一个数据出现一定问题,须删除无效数据后进行数据处理。
思考题1.什么是坪曲线?谈谈坪曲线的测量在研究核衰变统计规律实验中的意义? 答:坪曲线是入射粒子的强度不变时,计数器的计数率随工作电压变化的曲线。
测定坪曲线是为了选择一个合适的工作电压,以减少电压漂移对实验的影响.工作点若选在坪区,即使仪器和探头的性能都有变化,也可使总计数率保持稳定。
所以应在曲线较平的部分以及源计数率高本底计数率相对较低处选择工作电压。
2.什么是放射性核衰变的统计性?它服从什么规律?答:放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,与其他原子核是否衰变无关;因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。
其统计分布满足一定的规律性,称此规律性为核衰变的统计性,它服从正态分布。
3.σ的物理意义是什么?以单次测量值N 来表示测量值时,为什么是N N ±?其物理意义又是什么?答:σ的物理意义是在相同条件下作重复测量时,每次测量结果围绕着平均计数值的一个涨落大小。
在实际运算中由于出现概率较大的计数值与平均值N 的偏差不大,我们可以用N 来代N ;因此对于单次测量值N ,可以近似地说在N N ±范围内包含真值的概率是68.3%,这样一来用单次测量值就大体上确定了真值的范围。
4-1.核衰变的统计规律95-103

实验10-2 核衰变的统计规律【实验目的】1.测量NaI(Tl)闪烁探测器的坪曲线,确定合适的工作电压;指导:用闪烁探测器测量强度不变的放射源时,改变光电倍增管的高压,计数率也会随之改变;原因在于任何一种射线在闪烁探测器中产生的脉冲幅度都不会完全一样,输出脉冲的幅度也分布在一定范围内。
尽管如此,只要射线的能量不是特别低而探测器的工作状态又选择得当,绝大部分信号脉冲都会比光电倍增管的噪声脉冲大。
当电压足够高,信号脉冲幅度基本上都超过了仪器的甄别阈而绝大部分噪声的幅度又还比甄别阈小很多时,随着高压的增加计数率的增加就很缓慢了,这时就出现了“坪区”。
在实验中,重要的是向学生说明在许多核物理实验中测量坪曲线的意义何在。
在本实验中,由于高压相对比较稳定,因此我们在实践中发现选取坪曲线较为平坦(计数率随高压漂移变化较小)的工作点和坪曲线较为陡峭的工作点两者的差异不大。
2.了解并验证原子核衰变及放射性计数的统计性;指导:本实验通过反复测量放射源(137Cs 或60Co )在一段时间内强度并作为一个随机事件,取一个样本容量为A 的样本来观察其结果是否符合正态分布。
当然,源的强度本身随时间衰减,但137Cs 的半衰期长达30年,可以近似认为在实验时间内(大约1——2小时)源强不变。
3.了解统计误差的意义,掌握计算统计误差的方法;指导:这一实验需要一定的概率论和数理统计方面的基础,比如二项式分布、泊松分布、正态分布以及样本均值、样本方差、样本方差的无偏估计;学生应该已经学习过相关课程,若没有接受过类似训练,实验讲义的原理部分已经列出了所需知识。
需要说明的是: 鉴于A x x Ai i /)(12∑=-不是方差2S 的无偏估计,)1/()(12--∑=A x x Ai i 才是,因此取)1/()(12--=∑=A x x S Ai ix 作为样本标准差的无偏估计。
(参见任一概率论数理统计教材) 4.学习检验测量数据的分布类型的方法。
放射性衰变的实验观察与分析

放射性衰变的实验观察与分析实验观察与分析:放射性衰变放射性衰变是指一种原子核自发地发射出射线,从而转变成另一种元素或同位素的现象。
在这个实验中,我们对一种放射性物质的衰变进行了观察与分析。
实验设备与材料:1. 放射性样品(已知是铀)2. 探测器3. 电子计数器4. 实验记录表格实验步骤:1. 将放射性样品放置在探测器旁边,并将探测器连接到电子计数器上。
2. 开始记录计数器每隔一段时间(比如5分钟)所测得的粒子数目,并将其填写在实验记录表格中。
观察与结果:在实验过程中,我们观察到计数器每隔一段时间就会记录到一定数量的粒子。
最初的数目较多,随着时间的推移,记录到的粒子数目逐渐减少,但并未完全消失。
这是因为放射性衰变是一个随机的过程,每个原子核发生衰变的概率是相同的,但时间上的分布是不确定的。
根据粒子数目的变化曲线,我们可以看到一些规律。
一开始,衰变速率很快,数目下降得很快。
但随着时间的推移,衰变速率逐渐减慢,说明衰变速率是逐渐减小的。
这是因为随着原子核数量的减少,相互碰撞的概率也减小,从而导致衰变速率的减缓。
然而,即使在很长时间之后,仍然会记录到一些粒子,这说明放射性衰变是一个持久的过程,不会完全停止。
分析与讨论:根据实验结果,我们可以通过衰变速率的变化来推断放射性物质的半衰期。
半衰期是指在一半的放射性原子核衰变所需的时间。
通过观察衰变速率逐渐减慢的趋势,我们可以估算出半衰期的大致大小。
此外,还可以通过观察放射性衰变产生的射线类型来进一步确认放射性物质的性质。
射线的类型包括阿尔法粒子(α粒子)、贝塔粒子(β粒子)和伽马射线(γ射线)。
通过分析这些射线的能量和穿透能力,可以确定放射性物质的具体类型和原子核的结构。
需要注意的是,放射性衰变是一个存在一定风险的实验。
对于放射性物质的处理和测量需要符合安全操作规程,并使用适当的防护设备。
总结:通过对放射性衰变的实验观察与分析,我们可以了解放射性物质的特性,并且可以通过衰变速率的变化推断出物质的半衰期。
盖革弥勒计数器及核衰变的统计规律实验报告

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是气体探测器的一种,用来测定射线强度,既单位时间的粒子个数。
近年来,随着闪烁探测器及半导体探测器的发展,其重要性有所下降,但由于它的设备简单,使用方便,在有关的放射性测量中仍在广泛使用。
一、实验目的掌握G-M计数器的工作基础,测定其有关特性,学会使用;以G-M计数器未测试设备,验证核衰变的统计规律;学会使用放射性测量结果的误差表示法,学会多次测量结果的误差计算及测试时间的选择。
二、实验原理1、G-M计数器原理:G-M计数器是利用射线使计数管内的工作气体电离,然后收集产生的电荷来记录射线的探测器。
玻璃管内有圆筒状阴极,在阴极对称轴上装有丝状阳极。
先将管内抽成真空,再充入一定量的惰性气体和少量猝灭气体(卤素或有机物)在G-M计数管两级加上电压,设其阳极半径为a,阴极半径为b,阳极与阴极间的电压为U,则沿着管径向位置为r处的电场强度为,可见随着r减小,电场强度增大,且阳极附近急剧增大。
2、脉冲原理(1)当射线进入G-M管中使得管中气体电离后,正离子和负离子在管内电场的作用下分别向阴极和阳极移动。
在阳极附近强大的电场作用下,电子获得强大的动能以至于将阳极附近的气体电离。
经过多次碰撞,殃及附近的电子急剧增多,形成了“雪崩电子”;在这些碰撞中会产生大量的紫外线光子,这些光子能进一步的产生第二波的“雪崩”效应,增加电子。
这个电子不断增加的过程称为气体放大。
(2)雪崩过程发生在殃及附近,加上电子的质量远远小于阳离子的质量,速度比阳离子快,因此电子很快被阳极吸收,在管内留下一个被大量阳离子构成的阳离子鞘包围着的阳极。
正离子鞘将随着电离的发生逐渐增厚,由于正离子鞘的作用,阳极附近的电场将随之减小,以致新电子无法增殖,即电场强度不足以引发雪崩效应,雪崩效应停止,正离子鞘停止生成,放电便终止了,伺候,正离子鞘在电场的作用下慢慢移向阴极,最后到达阴极被中和,阳极附近的电场也随之恢复,使得与G-M串联的电阻记录下一个电压脉冲。
原子核的衰变与核辐射的实验探究

核辐射的来源和性质
核辐射的来源:放 射性物质、核反应 堆、核武器等
核辐射的种类:α 射线、β射线、γ射 线、中子辐射等
核辐射的性质: 电离辐射、穿透 力强、致癌性等
核辐射的危害:对 人体造成辐射损伤 、对环境造成污染 等
实验方法和测量技术
• 实验目的:探究核辐射的性质和影响因素
• 实验材料:放射性物质、探测器、测量仪器等
• 实验步骤: a. 准备放射性物质和探测器 b. 设置实验条件,如温度、压力等 c. 启动探测器,记录数据 d. 分析数据,得出结论 • a. 准备放射性物质和探测器 • b. 设置实验条件,如温度、压力等 • c. 启动探测器,记录数据 • d. 分析数据,得出结论
• 测量技术: a. 辐射剂量测量:使用剂量仪测量辐射剂量 b. 辐射类型鉴别:使用光谱仪鉴别辐射类型 c. 辐射强度测量:使用辐射强度计测 量辐射强度 d. 辐射时间测量:使用计时器测量辐射时间 • a. 辐射剂量测量:使用剂量仪测量辐射剂量 • b. 辐射类型鉴别:使用光谱仪鉴别辐射类型 • c. 辐射强度测量:使用辐射强度计测量辐射强度 • d. 辐射时间测量:使用计时器测量辐射时间
实验结果和数据分析
实验目的:探究核辐射对生物体的影响
实验材料:放射性同位素、生物样本、辐射探测器等
实验方法:放射性同位素标记、辐射剂量测定、生物样本观察等
实验结果:不同辐射剂量对生物体的影响不同,低剂量辐射对生物体影响较小,高剂 量辐射对生物体影响较大。
03
实验结果和结论
实验结果总结
实验目的:探究 原子核的衰变与 核辐射的关系
α衰变:释放一个α粒子, 变为新的原子核
电子捕获:原子核捕获一 个电子,变为新的原子核
实验四 核衰变的统计规律与放射性测定的实验数据处理
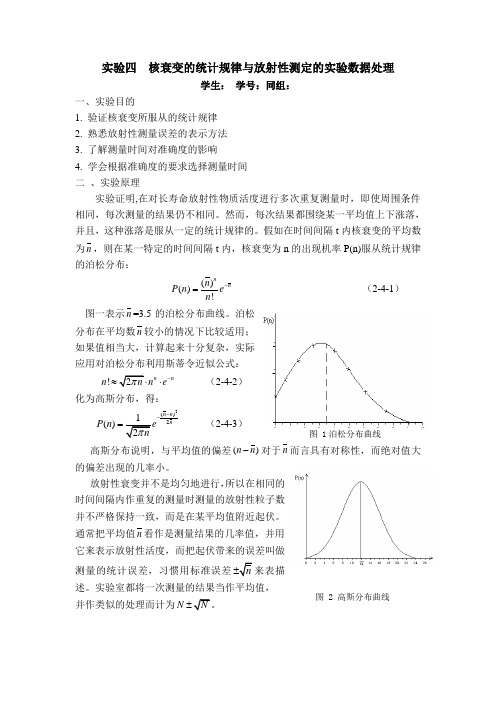
实验四 核衰变的统计规律与放射性测定的实验数据处理学生: 学号:同组:一、实验目的1. 验证核衰变所服从的统计规律2. 熟悉放射性测量误差的表示方法3. 了解测量时间对准确度的影响4. 学会根据准确度的要求选择测量时间 二 、实验原理实验证明,在对长寿命放射性物质活度进行多次重复测量时,即使周围条件相同,每次测量的结果仍不相同。
然而,每次结果都围绕某一平均值上下涨落,并且,这种涨落是服从一定的统计规律的。
假如在时间间隔t 内核衰变的平均数为n ,则在某一特定的时间间隔t 内,核衰变为n 的出现机率P(n)服从统计规律的泊松分布:()()!n nn P n e n -= (2-4-1) 图一表示n =3.5的泊松分布曲线。
泊松分布在平均数n 较小的情况下比较适用;如果值相当大,计算起来十分复杂,实际应用对泊松分布利用斯蒂令近似公式: !2n n n n n e π-≈⋅⋅ (2-4-2) 化为高斯分布,得:2()21()2n n nP n enπ--= (2-4-3)高斯分布说明,与平均值的偏差()n n -对于n 而言具有对称性,而绝对值大的偏差出现的几率小。
放射性衰变并不是均匀地进行,所以在相同的时间间隔内作重复的测量时测量的放射性粒子数并不严格保持一致,而是在某平均值附近起伏。
通常把平均值n 看作是测量结果的几率值,并用它来表示放射性活度,而把起伏带来的误差叫做测量的统计误差,习惯用标准误差n ±来表描述。
实验室都将一次测量的结果当作平均值,并作类似的处理而计为N N ±。
图 1泊松分布曲线图 2 高斯分布曲线计数的相对标准误差为:= (2-4-4)它能说明测量的准确度。
当N 大时,相对标准误差小,而准确度高。
反之,则相对标准误差大,而准确度低。
为了得到足够计数N 来保证准确度,就需要延长测量时间t 或增加相同测量的次数m 。
根据计算可知,从时间t 内测的结果中算出的计数率的标准误差为:t ±== (2-4-5) 计数率的相对标准误差E 用下式表示:E == (2-4-6)若实验重复进行m 次,则平均计数率的标准误差等于:(2-4-7) 考虑本底后,标准误差为:σ== (2-4-8) N c 为t c 时间内源加本底的计数,n b 为t b 时间内本底的计数,n c 为源加本底的计数率,n b 为本底的计数率。
实验一、核衰变与放射性计数的统计规律实验报告

实验一核衰变与放射性计数的统计规律实验报告第一部分G-M计数器一.实验目的1、了解G-M管的工作原理,掌握其基本性能及其测试方法。
2、学会正确使用G-M管计数装置的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M管计数系统输出回路参量。
二.实验内容1、在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参量并选择工作电压。
2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。
3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
三.实验原理1、G-M管是一种气体探测器。
当带电粒子射入其灵敏体积时,引起气体原子电离。
电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离,即触发“自持放电”。
这一过程产生的电子和正离子向两极漂移时,在外回路产生脉冲信号。
2、从G-M管的工作机制可以看出,入射带电粒子仅仅起一个触发放电的作用,G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关,只和计数管的几何参量、工作电压以及输出回路参量有关。
在G-M管的使用中,坪特性是其最重要的性能之一。
坪特性是判断管子好坏的主要依据,也是选择管子工作电压的依据。
坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时,计数管的计数率随工作电压变化的曲线,见图1-1。
图1-1 G-M计数管的坪曲线表征坪特性的参量主要有:起始电压(Vs):即计数管开始计数时的电压。
坪长: B A =V -V 坪长(单位:百伏)(1-1) 这是管子的工作区域,工作电压一般可选在坪区的21~31的范围内。
坪斜:()100% ()2B A B A B A n n n n V V -=⨯+-坪斜(单位:%/百伏) (1-2)坪斜主要是由假计数引起的,当然它的值越小越好。
当工作电压高于B V 时,曲线急剧上升,表明管子内发生了持续放电,这会大大缩短管子的寿命,因此在使用中必须注意避免这种情况。
放射性测量中的统计学

= m
在m数值较大时:
= (m n)+n n
即σ可以用任意一次观测到的衰变核数代替其平均值
来进行计算
11
§7.1.
核衰变数和计数的统计分布
2.
泊松分布
若N0很大,且λt« 1 ,p=1-e-λt« 1 , m=N0p« N0,意味着n和m与N0相比足够 小,在平均值m附近的n值,可得到:
对称的;若m较大时,分布逐渐趋于对称,泊松分布的均方根差为:
= m
13
§7.1
核衰变数和计数的统计分布
【例题】设测量样品的真平均计数率是5s-1,使用泊松分布确定
在任1秒内计数小于或等于2个的概率。
m 解:泊松分布公式:P(n) = mn e n!
,
则
5 5 5 P(n 2) = P(0)+ P(1)+ P(2) = 50 e + 51 e + 52 e 0! 0! 0! 5 = (1+5+ 25 )e =12.47% 2
4
§7.1
核衰变数和计数的统计分布
核衰变的统计分布
假定在t=0时刻有N0个不稳定的原子核,在某一时间t内将有一部分核发 生衰变。先考虑一个原子核的情形。假如在某一短时间间隔Δt内放射性 原子核衰变概率pΔt与此原子核过去的历史和现在的环境无关,则pΔt正 比于Δt,因此:
p t = t
比例常数λ是该种放射性核素的特征值,该原子核经过Δt未发生率变的
放射性测量中的统计学
1. 核衰变数和计数的统计分布
2. 放射性测量的统计误差
1
放射性测量中的统计学
放射性事件与核事件,例如核衰变、带电粒子在介 质中消耗能量产生电子-离子对、γ射线或中子与 物质相互作用产生带电粒子等,在一定时间间隔内
盖革-弥勒计数器及核衰变的统计规律

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是一种用于测量放射性核素活度的仪器。
它基于核反应速率与放射性核素的活度之间的关系,通过测量辐射计数来估算样品的放射性活度。
本文将探讨盖革-弥勒计数器的工作原理以及核衰变的统计规律。
一、盖革-弥勒计数器的工作原理盖革-弥勒计数器主要由两个部分组成:探头和电子学装置。
探头是由放射性样品和闪烁体组成,通过放射线和闪烁效应将辐射计数转化成可感测的光脉冲。
电子学装置负责对探头输出的信号进行放大、滤波和数字化处理。
当探头接受放射性样品的辐射时,闪烁体被激发并发出光子。
这些光子与光导管中的正电子发生相遇,产生光电效应并产生电子-空穴对。
这些电子会经过倍增器的放大器,产生更多的电子-空穴对,最终形成一个能够被电子学装置记录和分析的电脉冲。
通过校准和标准曲线法,可以将盖革-弥勒计数器的输出辐射计数转化成样品的放射性活度。
在核废料储存和放射性医学诊断等领域中,盖革-弥勒计数器被广泛使用。
二、核衰变的统计规律核衰变是一种随机性过程,每个放射性核素的衰变和放射发生率并不是恒定值。
相反,这些过程遵循一些统计规律,包括:1.指数规律指数规律是最普遍的核衰变统计规律之一。
在这一规律下,放射性核素的活度随时间呈指数下降。
每个放射性核素的半衰期是指其放射性活度减半所需的时间。
每次单个核衰变的发生是一个独立的随机过程,发生的概率在时间上是均匀分布的。
2.泊松分布泊松分布是描述随机事件发生的分布。
在核衰变中,每次放射性衰变是一个随机过程,一个时间点上出现较多的衰变事件比出现较少的衰变事件的概率要小。
这种规律被称为泊松分布。
3.高斯分布高斯分布是另一种随机分布,常常用于描述实验测量误差。
在放射性核素活度的测量中,测量误差会引入高斯分布的误差,并将造成测量值与理论值之间存在一定差异。
结论盖革-弥勒计数器在核科学、医疗和环境监测等领域中起着重要作用。
这种仪器通过电子学装置对辐射计数进行放大和数字化处理,以确定放射性样品的含量和活度。
验证原子核衰变的统计规律

1. 实验目的
验证原子核衰变的统计规律
1.1. 学会测量原子核衰变数量的概率分布; 1.2. 学会通过作图法和 χ2 检验法验证原子核衰变数量的分布类型。
2. 实验方法的原理
原子核衰变数量的泊松近似 原子核总数 N0(每组试验次数 n)通常很大,而原子核衰变概率 1-e-λt (事件 A 的发生概率 p)通常很小。例如 1 克 60Co 的原子核总数为 1× 1022 个,60Co 原子核的衰变概率为 4.2× 10-9。此时 t 时间内原子核衰变数量 k 的 分布可用泊松分布 P(N0(1-e-λt))来近似。设 N0(1-e-λt)=M,根据公式(11)易 得, M 恰好为 t 时间内发生衰变的原子核数的统计平均值, 即 k 的期望值。 由公式(8)可得:
2
( f j f j) 2 f j j 1
h
(20)
(20)式中 h 为计数值的分组数量(未分组时即为 xi 的样本数) ,fj 为 每组的实际观测次数,fj'为根据理论分布计算的每组的理论观测次数。每组 理论观测次数的计算方法为:利用(18)式和(19)式计算出每组对应的泊 松分布或正态分布的 f(xi),再乘以总次数。 b)确定自由度 h-l-1,h 为分组数,l 为 fj 的参数数量,泊松分布 l=1, 正态分布 l=2。
5
计数平均值 xi =∑xi /500=96.7
由图知,计数结果满足泊松分布
6
计数值 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121
核衰变的统计规律实验

核衰变的统计规律实验薛佳柳083822一、实验目的1.了解并验证原子核衰变及放射性计数的统计性。
2.了解统计误差的意义,掌握计算统计误差的方法。
3.学习检验测量数据的分布类型的方法。
二、实验原理1. 测量NaI(Tl)闪烁晶体探测器的计数率随工作变化的坪曲线,选定合适的工作电压。
2. 在相同条件下,对某放射源进行重复测量,画出放射性计数的频率直方图并与理论分布曲线作比较。
3. 在相同条件下对本底进行重复测量,画出本底计数的频率分布图,并与理论分布曲线作比较。
4. 用2检验法检验放射性计数的统计分布类型。
三、实验仪器①NaI(Tl)闪烁探测器;②γ放射源(137Cs或60Co);③高压电源、放大器和多道脉冲幅度分析器。
二、实验内容1.放射性测量的随机性和统计性在做重复的放射性测量中,即使保持完全相同的实验条件(例如放射性的半衰期足够长,因此在实验时间内可以认为其强度基本上没有变化;源与计数器的相对位置始终保持不变;每次测量时间不变;测量仪器足够精确,不会产生其它的附加误差等等),每次的测量结果并不完全相同,而是围绕其平均值上下涨落,有时甚至有很大的差别,也就是说物理实验的测量结果具有偶然性,或者说随机性。
物理测量的随机性产生原因不仅在于测量时的偶然误差,而且更是物理现象(当然包括放射性核衰变)本身的随机性质,即——物理量的实际数值时刻围绕着平均值发生微小起伏。
在微观现象领域,特别是在高能物理实验中,物理现象本身的统计性更为突出。
按照量子力学的原理,对处于同一个态的微观粒子,测量同一个可观测的物理量时,即使不存在任何测量误差,各次测量结果也会不同,除非粒子处于这个可观测量的本征态;比如同一种粒子的寿命,其实测值分布在从相当短到相当长的范围内。
另一方面,所谓偶然的东西,是一种有必然性隐藏在里面的形式;我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。
2.核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。
核物理实验讲义

实验1 核衰变的统计规律实验目的1. 了解并验证原子核衰变及放射性计数的统计性。
2. 了解统计误差的意义,掌握计算统计误差的方法。
3. 学习检验测量数据的分布类型的方法。
内容1. 在相同条件下,对某放射源进行重复测量,画出放射性计数的频率直方图,并与理论分布曲线作比较。
2. 在相同条件下,对本底进行重复测量,画出本底计数的频率分布图,并与理论分布图作比较。
3. 用2χ检验法检验放射性计数的统计分布类型。
原理在重复的放射性测量中,即使保持完全相同的实验条件(例如放射源的半衰期足够长,在实验时间内可以认为其活度基本上没有变化,源与计数管的相对位置始终保持不变;每次测量时间不变,测量仪器足够精确,不会产生其它的附加误差等等),每次的测量结果并不完全相同,而是围绕着其平均值上下涨落,有时甚至有很大的差别。
这种现象就叫做放射性计数的统计性。
放射性计数的这种统计性反映了放射性原子核衰变本身固有的特性,与使用的测量仪器及技术无关。
1. 核衰变的统计规律放射性原子核衰变的统计分布可以根据数理统计分布的理论来推导。
放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,和别的原子核是否衰变没有关系,而且哪一个原子核先衰变,哪一个原子核后衰变也纯属偶然的,并无一定的次序,因此放射性原子核的衰变可以看成是一种伯努里试验问题。
设在t=0时,放射性原子核的总数是0N ,在t 时间内将有一部分核发生了衰变。
已知任何一个核在t 时间内衰变的概率为)1(te p λ--=,不衰变的概率为q=1-p=e t λ-,λ是该放射性原子核的衰变常数。
利用二项式分布可以得到在t 时间内有n 个核发生衰变的概率P(n)为nN t n t e e n n N N n p -----=0)()1(!)!(!)(00λλ (1)在t 时间内,衰变掉的粒子平均数为)1(00t e N p N m λ--== (2) 其相应的均方根差为210)()1(t me p m pq N λσ-=-== (3) 假如1<<t λ,即时间t 远比半衰期小,这时σ可简化为m =σ (4)0N 总是一个很大的数目,而且如果满足1<<t λ,则二项式分布可以简化为泊松分布,因为在二项式分布中,0N 不小于100,而且p 不大于0.01的情况下,泊松分布能很好的近似于二项式分布,此时mn e n m n p -=!)( (5) 在泊松分布中,n 的取值范围为所有的正整数(0,1,2,3,…),并且在n=m 附近时,)(n p 有一极大值,当m 较小时,分布是不对称的,m 较大时,分布渐趋近于对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
次的测量结果之间稍有偏差,是因为核衰变过程是一种随机过程,并不是
每一个核的衰变是完全独立的,每次测量之间毫无相互依赖关系,
而是在某平均值附近起伏。因此,我们应该增加测量次数或采用较长时间测
根据放射源的活度选择测量时间(要求E=2% )
取平均值为67.3脉冲/秒,nb/na=0.0037<2%,可见本底计数相对于放射源
4 0.0045 0.0053 116 17 0.0190 0.0185
4 0.0045 0.0064 117 19 0.0212 0.0164
9 0.0101 0.0076 118 6 0.0067 0.0143
5 0.0056 0.0091 119 4 0.0045 0.0124
28 0.0313 0.0387 135 2 0.0022 0.0003
36 0.0402 0.0391 139 1 0.0011 0.0001
38 0.0425 0.0391 142 1 0.0011 0.0000
193 1 0.0011 0.0000
做出高斯分布的实验曲线,然后用实验所得平均值根据公式
每次测量之间毫无相互依赖关系,也是造成一定波动的
问题讨论
试说明为什么测量时间增长时标准误差会减小?
2-4-9)可知,本底计数率越大,对放射性测量的准
t
和tb越大,准确度就越高。而且,由时间t 内
NNn
tt,因此,在实际测量
增长测量时间则结果的标准误差就相对减小。但是,测量时间过长也并
比如外界因素产生影响的几率就增大,另外重复测量也比较困难,
N来保证准确度,就需要
t或增加相同测量的次数m。根据计算可知,从时间t 内测的结果
NNn
tt (2-4-5)
E用下式表示:
1nt
(2-4-6)
m次,则平均计数率的标准误差等于:
n
(2-4-7)
考虑本底后,标准误差为:
2cbcb
bcbNNnntttt (2-4-8)
N
为tc时间内源加本底的计数,nb为tb时间内本底的计数,nc为源加本底
n
为本底的计数率。
12()cbcb
23 0.0257 0.0254 127 3 0.0034 0.0028
22 0.0246 0.0277 128 1 0.0011 0.0022
26 0.0291 0.0299 129 2 0.0022 0.0017
29 0.0324 0.0320 130 2 0.0022 0.0014
3)将放射源放在计数管下面的适当位置上,然后分别以1min,5min,10min
4)将实验结果填入表内,算出每次测量的标准误差,从中得出必要的结论。
重复测量次数对计数率标准误差的影响
1)将放射源放在计数管下面的适当位置上,保持几何条件不变,重复测量5
100s;
2)将数据列入适当的表格,算出每次测得的计数率的标准误差及5次平均值
()()
nnnPnen (2-4-1)
图一表示n=3.5的泊松分布曲线。泊松
n较小的情况下比较适用;
!2nnnnne (2-4-2)
2()
1()
nnnPnen (2-4-3)
11 0.0123 0.0107 120 8 0.0089 0.0106
次数a 实际几率 P’ 理论几率P 计数 n 次数a 实际几率P’ 理论几率P
15 0.0168 0.0124 121 11 0.0123 0.0090
11 0.0123 0.0143 122 9 0.0101 0.0076
18 0.0201 0.0164 123 5 0.0056 0.0063
20 0.0223 0.0186 124 12 0.0134 0.0052
14 0.0156 0.0208 125 9 0.0101 0.0043
18 0.0201 0.0231 126 9 0.0101 0.0035
4051 67.52 67.27 1.06 67.27±1.06
20320 67.73 67.48 0.48 67.48±0.48
40438 67.4 67.15 0.34 67.15±0.34
脉冲计数的标准误差随着时间的不断增加而相对
因此,要想在测量时得到比较小的标准误差,有必要延长每次的测量时间。
2-4-3)做出理论曲线:
由高斯分布的试验曲线与理论曲线可以看出:实验曲线的整体趋势与理论曲
都呈正态分布,只是在实验曲线上相邻的两个计数出现的几率波动
2s20次
另外核衰变过程是一种随机过程,并不是均匀地进行的,每一个7080901001101201301400.000.010.020.030.040.05P(n)n实际曲线理论曲线104
24 0.0268 0.0339 131 2 0.0022 0.0010
38 0.0425 0.0356 132 1 0.0011 0.0008
30 0.0335 0.0369 133 2 0.0022 0.0006
44 0.0492 0.0380 134 0 0.0000 0.0005
重复测量次数对计数率标准误差的影响
1 2 3 4 5 平均值
/s 100
(脉冲) 6995 6717 6819 6738 6780 6995
(脉冲/秒) 69.95 67.17 68.19 67.38 67.8 69.95
±0.83 ±0.82 ±0.83 ±0.82 ±0.82 ±0.82
高斯分布说明,与平均值的偏差()nn对于n而言具有对称性,而绝对值大
放射性衰变并不是均匀地进行,所以在相同的
n看作是测量结果的几率值,并用
n来表描
NN。
图 1泊松分布曲线 图 2 高斯分布曲线
N
(2-4-4)
它能说明测量的准确度。当N大时,相对标准误差小,而准确度高。反之,
5次结果多不相同。
根据放射源活度和测量准确度的要求选择测量时间(相对标准误差为2% )
1)根据放射源和计数管间的距离,使其计数率为4000脉冲/分~5000脉冲/分。
确定选用公式算出测量时间,
2)根据实验数据算出相对标准误差,并与所要求值(2%)相比较。
验证核衰变所服从的统计规律
1)用放射源计数验证高斯分布,时间间隔以2s计,使其计数在每2s20次左
2-4-12中,得t≈37.16s,近似于40s 。
t=40s,测量得N
=2754脉冲,因而nc=68.85脉冲/秒;
=nc-nb=68.85-0.25=68.60;将数据代入公式2-4-6中,得到E=1.96%(<2%),在
验证核衰变所服从的统计规律
t=2s,共测895次,平均计数为52脉冲/秒)
800次以上;
2)根据实验数据,绘出高斯分布曲线;
3)用时间所得平均值根据公式作出高斯分布的理论曲线,比较实验曲线与理
时间数据处理
测量时间对计数率标准误差的影响
n
=Nb/tb=74/300=0.25脉冲/秒
Nc nc=Nc/tc na=nc-nb σ Na±σ
min) (脉冲) (脉冲/秒) (脉冲/秒) (脉冲/分)
核衰变的统计规律与放射性测定的实验数据处理
学号:同组:
验证核衰变所服从的统计规律
熟悉放射性测量误差的表示方法
了解测量时间对准确度的影响
学会根据准确度的要求选择测量时间
、实验原理
实验证明,在对长寿命放射性物质活度进行多次重复测量时,即使周围条件
t内核衰变的平均数
n,则在某一特定的时间间隔t内,核衰变为n的出现机率P(n)服从统计规律
并且,在高斯分布曲线中可以看出,与平均值的偏
3 0.0034 0.0022 1பைடு நூலகம்2 28 0.0313 0.0277
1 0.0011 0.0028 113 27 0.0302 0.0254
2 0.0022 0.0035 114 20 0.0223 0.0231
5 0.0056 0.0043 115 13 0.0145 0.0208
泊松分布和高斯分布说明了核衰变的什么问题?
如果平均值相当大时,计算起
实际应用中很不方便,这时就可以对其利用斯蒂令近似,化
很显然,泊松分布和高斯分布均说明:放射性物质的衰变并不是均
在相同的时间间隔内重复测量所测得的放射性计数并不是严格的保
而是在某个平均值上下波动,其整体波动趋势符合正态分布,也即核衰
次数a 实际几率 P’ 理论几率P 计数 n 次数a 实际几率P’ 理论几率P
1 0.0011 0.0001 105 30 0.0335 0.0387
3 0.0034 0.0005 106 28 0.0313 0.0380
1 0.0011 0.0006 107 25 0.0279 0.0369
1 0.0011 0.0008 108 37 0.0413 0.0355
2 0.0022 0.0011 109 23 0.0257 0.0339
0 0.0000 0.0014 110 20 0.0223 0.0320
4 0.0045 0.0018 111 27 0.0302 0.0299
bnnttEnn (2-4-9)
c
btntn (2-4-10)
究竟需要选择多长的测量时间,要根据对测量准确度的要求而定,即:
2ccbc
nnntnE (2-4-11)
式中
cbnnn为放射源的计数率
(b
nEn)的情况下,上式
1
tnE (2-4-12)
