土压力理论与挡土墙设计.ppt
合集下载
朗肯土压力理论课件

被动土压力
挡土墙向填土相反方向移动或转 动时,作用在墙上的土压力。
朗肯土压力研究历史
早期研究
1857年,英国科学家W.J.M.朗肯首 次提出古典土压力理论,奠定了土压 力研究的基础。
改进与发展
后续研究者针对朗肯理论的不足,提 出了库仑土压力理论等改进和发展方 案。
朗肯土压力理论应用领域
挡土墙设计
素对支护结构的影响。
朗肯土压力计算
运用朗肯土压力理论,计算支 护结构所受的土压力,为结构 设计提供依据。
支护结构选型
对比多种支护结构类型,如地 下连续墙、钢支撑、混凝土支 撑等,选择最适合本工程的支 护结构形式。
设计优化建议
根据计算结果和工程实际情况 ,提出支护结构设计的优化建 议,如调整支护结构尺寸、增
通过实际工程案例,掌握朗肯土压力计算步骤和实际应用。
未来发展趋势预测
数值模拟方法在土压力研 究中的应用
随着计算机技术的发展,数值 模拟方法在土压力研究中将发 挥越来越重要的作用,如有限 元法、离散元法等。
考虑复杂环境因素的土压 力研究
未来土压力研究将更加注重考 虑复杂环境因素的影响,如地 震、地下水、降雨等。
的土体变形和破坏模式。
朗肯土压力公式推导
假设条件
朗肯土压力理论基于一系列假设条件,包括土体为均质、各向同 性、无粘性等。
公式推导
根据土体平衡条件和极限平衡状态,可以推导出朗肯土压力公式。 该公式可以用来计算挡土墙背后的主动和被动土压力。
参数影响
朗肯土压力公式中的参数包括内摩擦角、粘聚力、挡土墙倾角等, 这些参数的变化会对计算结果产生影响。
03
朗肯土压力计算方法及 实例分析
计算方法介绍
基本假设
挡土墙向填土相反方向移动或转 动时,作用在墙上的土压力。
朗肯土压力研究历史
早期研究
1857年,英国科学家W.J.M.朗肯首 次提出古典土压力理论,奠定了土压 力研究的基础。
改进与发展
后续研究者针对朗肯理论的不足,提 出了库仑土压力理论等改进和发展方 案。
朗肯土压力理论应用领域
挡土墙设计
素对支护结构的影响。
朗肯土压力计算
运用朗肯土压力理论,计算支 护结构所受的土压力,为结构 设计提供依据。
支护结构选型
对比多种支护结构类型,如地 下连续墙、钢支撑、混凝土支 撑等,选择最适合本工程的支 护结构形式。
设计优化建议
根据计算结果和工程实际情况 ,提出支护结构设计的优化建 议,如调整支护结构尺寸、增
通过实际工程案例,掌握朗肯土压力计算步骤和实际应用。
未来发展趋势预测
数值模拟方法在土压力研 究中的应用
随着计算机技术的发展,数值 模拟方法在土压力研究中将发 挥越来越重要的作用,如有限 元法、离散元法等。
考虑复杂环境因素的土压 力研究
未来土压力研究将更加注重考 虑复杂环境因素的影响,如地 震、地下水、降雨等。
的土体变形和破坏模式。
朗肯土压力公式推导
假设条件
朗肯土压力理论基于一系列假设条件,包括土体为均质、各向同 性、无粘性等。
公式推导
根据土体平衡条件和极限平衡状态,可以推导出朗肯土压力公式。 该公式可以用来计算挡土墙背后的主动和被动土压力。
参数影响
朗肯土压力公式中的参数包括内摩擦角、粘聚力、挡土墙倾角等, 这些参数的变化会对计算结果产生影响。
03
朗肯土压力计算方法及 实例分析
计算方法介绍
基本假设
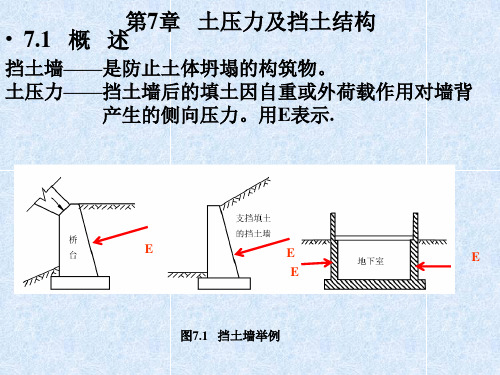
第六章 土压力与挡土墙

粘性土的抗剪强度: f c tg
等值抗剪强度: f tgD
D —等值内摩擦角
D
tg 1 (tg
c
)
2H
3
2.土压力相等方法
Ea1
1 2
H
2tg 2 (45o
)
2
2c
H
tg (45o
2
)
2c2
Ea2
1 2
H
2tg 2 (45
D
2
)
tg(45 D ) tg(45 ) 2c
2
2 H
四、稳定性验算
1、抗滑稳定性
1)验算公式
Ks
抗滑力=(G 滑动力
Eaz )
Eax
1.3
G
Ea
2)弥补措施 ①修改挡土墙的断面尺寸,通常加大底宽增加墙自重G以增大抗滑力; ②在挡土墙基底铺砂、碎石垫层,提高摩擦系数值增大抗滑力; ③加大逆坡角度; ④墙后面加钢筋混凝土拖板。利用拖板上的填土重增大抗滑力。拖 板和挡土墙之间用钢筋连接。
衡状态
性平衡状态
衡状态
主动朗 肯状态
处于主动朗肯状态,σ1方向竖直,剪切破坏面 被动朗肯
与竖直面夹角为45o-/2
状态
处于被动朗肯状态,σ3方向竖直,剪切破坏面与竖直 面夹角为45o+/2
二、主动土压力 1、主动土压力集度
3
1tg 2 (45o
) 2c tg(45o
2
)
2
粘性土 无粘性土
A
A’ E F
A
B
h q
h' Ka
(h'H )Ka
讨论:土压力计算的几个应用问题
1.朗金理论与库仑理论的比较
《库仑土压力理论》课件

理论意义
库仑土压力理论是土力学中的重要理论之一,它为土压力的计算和挡土墙设计提供了基础。该理论通 过分析土的应力和应变关系,推导出土压力的分布规律,为解决实际工程问题提供了重要的理论支持 。
实践价值
在实际工程中,挡土墙的设计和建造是必不可少的。库仑土压力理论的应用可以帮助工程师更准确地 预测和控制土压力,从而设计出更加安全、经济、可靠的挡土墙。此外,该理论在岩土工程、地质工 程等领域也有广泛的应用。
主动土压力的计算公式
• 主动土压力的计算公式为:P = c + (σtan(θ) + kd) * H
主动土压力的计算公式
P为主动土压力; c为土壤粘聚力; σ为土壤内摩擦角;
主动土压力的计算公式
θ为剪切面与水平面的夹角; d为土壤压缩厚度;
k为土壤压缩系数; H为挡土墙高度。
被动土压力的计算公式
04
应用
挡土墙设计
挡土墙是利用土压力来平衡外力的结构物,库仑土压力理论在挡土墙设计 中具有重要应用。
根据库仑土压力理论,可以通过合理设计挡土墙的尺寸、倾斜角、埋深等 因素,使其能够承受来自土体的压力,保持稳定。
挡土墙设计时需要考虑土的性质、环境条件、荷载情况等因素,结合库仑 土压力理论进行计算和分析,以确保其安全性和经济性。
主动土压力
当墙后土体处于侧向极限平衡状态时 ,墙后土体对墙背产生的侧向压力, 称为主动土压力。
被动土压力
当墙后土体处于被动极限平衡状态时 ,墙后土体对墙背产生的侧向压力, 称为被动土压力。
静止土压力
• 静止土压力:当挡土墙静止不动 ,不产生任何位移和变形时,墙 后填土对墙背产生的侧向压力, 称为静止土压力。
• 被动土压力的计算公式为:P = c + (σtan(φ) - kd) * H
库仑土压力理论是土力学中的重要理论之一,它为土压力的计算和挡土墙设计提供了基础。该理论通 过分析土的应力和应变关系,推导出土压力的分布规律,为解决实际工程问题提供了重要的理论支持 。
实践价值
在实际工程中,挡土墙的设计和建造是必不可少的。库仑土压力理论的应用可以帮助工程师更准确地 预测和控制土压力,从而设计出更加安全、经济、可靠的挡土墙。此外,该理论在岩土工程、地质工 程等领域也有广泛的应用。
主动土压力的计算公式
• 主动土压力的计算公式为:P = c + (σtan(θ) + kd) * H
主动土压力的计算公式
P为主动土压力; c为土壤粘聚力; σ为土壤内摩擦角;
主动土压力的计算公式
θ为剪切面与水平面的夹角; d为土壤压缩厚度;
k为土壤压缩系数; H为挡土墙高度。
被动土压力的计算公式
04
应用
挡土墙设计
挡土墙是利用土压力来平衡外力的结构物,库仑土压力理论在挡土墙设计 中具有重要应用。
根据库仑土压力理论,可以通过合理设计挡土墙的尺寸、倾斜角、埋深等 因素,使其能够承受来自土体的压力,保持稳定。
挡土墙设计时需要考虑土的性质、环境条件、荷载情况等因素,结合库仑 土压力理论进行计算和分析,以确保其安全性和经济性。
主动土压力
当墙后土体处于侧向极限平衡状态时 ,墙后土体对墙背产生的侧向压力, 称为主动土压力。
被动土压力
当墙后土体处于被动极限平衡状态时 ,墙后土体对墙背产生的侧向压力, 称为被动土压力。
静止土压力
• 静止土压力:当挡土墙静止不动 ,不产生任何位移和变形时,墙 后填土对墙背产生的侧向压力, 称为静止土压力。
• 被动土压力的计算公式为:P = c + (σtan(φ) - kd) * H
土压力计算及挡土墙设计最终版

③朗肯主动土压力系数
Ka
tan2(45 φ) 2
④单位墙长度上的土压力合
力Ea
Ea
1 2
γh2Ka
无粘性土主动土压力
2.朗肯主动土压力计算——粘性土
①②沿粘深性度土方的向极主限动平土衡压条力件的:分σ3 布σ 1ta 2(4 n 5φ 2)2cta4n 5φ 2 ()
p a γ z ta 2 (4 n 5 φ 2 ) 2 c ta 4 n 5 φ 2 ) ( γ za K 2 cK a
③土压力分布特点:墙背受到的土压力一般呈三角形分布,最大
压力强度发生在底部,类似于静水压力的分布。
刚性挡土墙背上的图压力分布
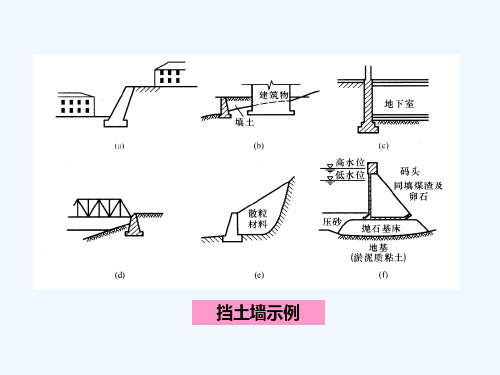
二、挡土墙类型
(按刚度及位移方式分为刚性挡土墙和柔性挡土墙)
2.柔性挡土墙
①定义:一般指用钢筋混凝土桩或地下连续墙所筑成的断面较小而长
度较大的挡土结构
锚杆
板桩 基坑
基坑
板桩变形
②根据土的极限平衡条件:
粘性土: pa (qγz)Ka2c Ka
砂土: pa (qγz)Ka
2c q
③填土为粘性土时,临界深度:
z0 γ
Ka γ
④若超载q较大,计算的z0为负值,
墙顶处土压力
paqK a2c Ka
2.分层填土:按各层的土质情况,分
别确定每层土作用于墙背的土压力。 ①第一层土按指标γ1、φ1和c1计算土压
在相同的墙高和填土条件下:Ea<E0<Ep
3.静止土压力计算
①按半空间弹性变形体在土的自重作用 下无侧向变形时的水平侧压力:
p =K0γz ②若土体为均质土,则K0与γ均为常数
K0=μ/(1-μ) 由计于算土。的μ很难确定,K0常用经验公式
Ka
tan2(45 φ) 2
④单位墙长度上的土压力合
力Ea
Ea
1 2
γh2Ka
无粘性土主动土压力
2.朗肯主动土压力计算——粘性土
①②沿粘深性度土方的向极主限动平土衡压条力件的:分σ3 布σ 1ta 2(4 n 5φ 2)2cta4n 5φ 2 ()
p a γ z ta 2 (4 n 5 φ 2 ) 2 c ta 4 n 5 φ 2 ) ( γ za K 2 cK a
③土压力分布特点:墙背受到的土压力一般呈三角形分布,最大
压力强度发生在底部,类似于静水压力的分布。
刚性挡土墙背上的图压力分布
二、挡土墙类型
(按刚度及位移方式分为刚性挡土墙和柔性挡土墙)
2.柔性挡土墙
①定义:一般指用钢筋混凝土桩或地下连续墙所筑成的断面较小而长
度较大的挡土结构
锚杆
板桩 基坑
基坑
板桩变形
②根据土的极限平衡条件:
粘性土: pa (qγz)Ka2c Ka
砂土: pa (qγz)Ka
2c q
③填土为粘性土时,临界深度:
z0 γ
Ka γ
④若超载q较大,计算的z0为负值,
墙顶处土压力
paqK a2c Ka
2.分层填土:按各层的土质情况,分
别确定每层土作用于墙背的土压力。 ①第一层土按指标γ1、φ1和c1计算土压
在相同的墙高和填土条件下:Ea<E0<Ep
3.静止土压力计算
①按半空间弹性变形体在土的自重作用 下无侧向变形时的水平侧压力:
p =K0γz ②若土体为均质土,则K0与γ均为常数
K0=μ/(1-μ) 由计于算土。的μ很难确定,K0常用经验公式
《库仑土压力理论》课件

实际工程中的静止土压力应用
总结词
静止土压力是库仑土压力理论中的一种特殊情况,是指土体处于静止状态时所受的压力,主要应用于 地下工程和隧道工程等领域。
详细描述
在地下工程和隧道工程中,静止土压力的大小直接关系到结构的稳定性和安全性。通过应用库仑土压 力理论,可以计算出静止土压力,从而设计出符合要求的支护结构。在施工中,合理利用静止土压力 ,可以有效控制土体的位移和变形,保证施工安全。
擦角。
静止土压力的计算
1
静止土压力是指挡土墙在静止状态下作用在墙背 上的土压力。
2
公式推导基于静止土压力的定义,通过分析墙后 土体的应力状态进行计算。
3
计算中需考虑墙后土体的内摩擦角和粘聚力,以 及墙背与土之间的摩擦角。
03
CATALOGUE
库仑土压力理论的应用实例
实际工程中的主动土压力应用
总结词
库仑土压力理论的局限性
假设限制
库仑土压力理论基于一系列假设,如土体为刚性、不可压缩等,与 实际情况可能存在差异。
精度有限
由于理论简化,库仑土压力理论的计算精度可能受到限制,无法准 确模拟复杂工况下的土压力分布。
对土性依赖较大
库仑土压力理论对土的物理性质依赖较大,对于不同土性,可能需要 调整参数或采用其他方法。
计算中需考虑墙后土体的内摩擦角和粘聚力,以 及墙背与土之间的摩擦角。
被动土压力的计算
01
02
03
被动土压力是指挡土墙 在外力作用下向后移动 ,作用在墙背上的土压
力。
公式推导同样基于库仑 理论,通过分析墙后土 体的应力状态,结合土 的抗剪强度指标进行计
算。
计算中需考虑墙后土体 的内摩擦角和粘聚力, 以及墙背与土之间的摩
土压力理论

8-14b
20 k a tg (45 ) tg (45 ) 0.49 2 2
2
【例题8-1】
-14 Z0=1.59 H=5m C=10kpa φ=20° γ=18kN/m3
+
44.13
-
3.41
Ea
30.13
H z0 1.14 m 3
a zk a 2C k a a 18 5 0.49 2 10 0.49
锚定板
墙趾
墙踵
锚杆
墙板
基岩
挡土墙各部名称:
填土面 墙顶 墙前 墙后 填土 墙面 挡 土 墙 墙背 墙 高
墙趾
墙底
墙踵
第8章 土压力
§8.2 挡土墙侧的土压力
8.2.1 土压力种类
太沙基等人通过挡土墙的模型试验,研究了墙的位 移与土压力的关系,发现作用在墙背上的土压力随 墙的移动方向和大小变化。
第8章 土压力
§8.1 概述
特指挡土
结构物
土压力—土对结构物的压力。 挡土结构物—防止土体塌滑的支撑结构物。
挡土墙、地下洞室衬砌等
本章所讲的土压力特指作用在挡土墙上的土压力。 挡土墙—侧向支撑土体的结构物。 研究方法:按平面问题进行研究,即取一延向米。 挡土墙的用途:阻挡土体下滑或截断土坡延伸。
§8.3 郎肯土压力理论
2.粘性土的郎肯主动土压力 土压力分布:
a zk a 2C k a
8-14b
第8章 土压力
8.3.2 主动土压力
§8.3 郎肯土压力理论
2.粘性土的郎肯主动土压力
Z0及总土压力:
kpa
1 E a ( zk a 2c k a )( H z 0 ) 2
第六章挡土墙上的土压力
总被动土压力
Ep
1 2
gH
2K
p
2cH
Kp
§2 朗肯土压力理论
小结
问题:
1 朗肯土压力理论的基本条件和假定
2 请画出刚性墙后粘性土的主动和被动破坏面形状
3 给出粘性土主动和被动土压力分布及计算公式
复习上节内容
(一) 填土为砂土-主动土压力 1. 土压力分布和墙后破裂面形状
pa=Kagz
H
H/3
g H Ka
EAp
1 gH
2
2Kp
W
C E库仑
Kp
Ecos2
cos(
cos2(f ) )[1 sin(f
) sin(f
)
]2
R
W
cos(
)
cos(
R
)
B
§3 库仑土压力理论
(二) 被动土压力
土压力分布
H
-
Ep
Ep H/3
gHKp
pp
dE p dz
d
1 2
g
z
2
K
p
dz
g
zK p
§3 库仑土压力理论
(二) 应用条件
朗肯
库仑
1
墙背光滑垂直 墙背、填土无限制
填土水平
粘性土一般用图解法
2
坦墙
3
墙背垂直
填土倾斜
坦墙
§6.4 朗肯和库仑土压力理论的比较
(三) 计算误差--朗肯土压力理论
E朗肯
E库仑 W R
墙背垂直 填土水平 实际 > 0
E库仑
郎肯主动土压力偏大 郎肯被动土压力偏小
E朗肯
W R
土力学第八章挡土墙土压力

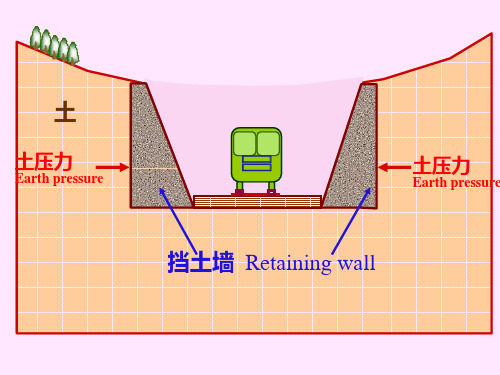
土压力是作用于这类建筑物上的重要荷载,它是由 于土体自重、土上荷载或结构物的侧向挤压作用,挡土 结构物所承受的来自墙后填土的侧向压力。
挡土墙的种类 作用在挡土墙上的土压力
第一节 概述
一、挡土墙的几种类型
E
地下室
地下室侧墙
填土E 重力式挡土墙
桥面支撑土坡的 挡土墙 填土 EE
堤岸挡土墙
填土
E
拱桥桥台
pa z Ka
其中:Ka为朗肯主动土压力系数
Ka tg 2 (45 / 2)
总主动土压力
Ea
1 2
KaH 2
s1
z
pa=s3
45+/2
Ea Ka H 2 / 2
1 H
3
pa KaH
2)粘性土
主动土压力强度
pa z Ka 2c Ka
库仑和朗肯土压力的比较
1、朗肯土压力理论
1)依据:半空间的应力状态和土的极限平衡条件; 2)概念明确、计算简单、使用方便; 3)理论假设条件; 4)理论公式直接适用于粘性土和无粘性土; 5)由于忽略了墙背与填土之间的摩擦,主动土压力偏 大,被动土压力偏小。
2、库仑土压力理论:
1)依据:墙后土体极限平衡状态、楔体的静力平衡条件; 2)理论假设条件; 3)理论公式仅直接适用于无粘性土; 4)考虑了墙背与土之间的摩擦力,并可用于墙背倾斜,填 土面倾斜的情况。但库伦理论假设破裂面是一平面,与按 滑动面为曲面的计算结果有出入。
4、填土表面倾斜
滑裂面1
A
B
cr
Ea´
B
= 时
cr
45
2
挡土墙的种类 作用在挡土墙上的土压力
第一节 概述
一、挡土墙的几种类型
E
地下室
地下室侧墙
填土E 重力式挡土墙
桥面支撑土坡的 挡土墙 填土 EE
堤岸挡土墙
填土
E
拱桥桥台
pa z Ka
其中:Ka为朗肯主动土压力系数
Ka tg 2 (45 / 2)
总主动土压力
Ea
1 2
KaH 2
s1
z
pa=s3
45+/2
Ea Ka H 2 / 2
1 H
3
pa KaH
2)粘性土
主动土压力强度
pa z Ka 2c Ka
库仑和朗肯土压力的比较
1、朗肯土压力理论
1)依据:半空间的应力状态和土的极限平衡条件; 2)概念明确、计算简单、使用方便; 3)理论假设条件; 4)理论公式直接适用于粘性土和无粘性土; 5)由于忽略了墙背与填土之间的摩擦,主动土压力偏 大,被动土压力偏小。
2、库仑土压力理论:
1)依据:墙后土体极限平衡状态、楔体的静力平衡条件; 2)理论假设条件; 3)理论公式仅直接适用于无粘性土; 4)考虑了墙背与土之间的摩擦力,并可用于墙背倾斜,填 土面倾斜的情况。但库伦理论假设破裂面是一平面,与按 滑动面为曲面的计算结果有出入。
4、填土表面倾斜
滑裂面1
A
B
cr
Ea´
B
= 时
cr
45
2
土力学-土压力及挡土结构
①墙背倾斜 ;②填土倾斜 ;③墙背粗糙(墙背与填土之
间有摩擦力),④填土为无粘性土的土压力计算。
•3.库仑公式推导
对土楔ABC作受力分析,受到三 个力W、R、E作用,由平衡 条件及正弦定律得库仑主动土压
力Ea和被动土压力EP的算式
——滑裂面与水平面的夹角 ——墙背与土之间的摩擦角,外摩擦角。 ——土与土之间的摩擦角,内摩擦角。
HK p
Ep作用在距离墙底H/3处
Ep
1
2
H2
kp
朗肯主动土压力 pa z ka 2c ka
Ka=tan2(45o — /2 )
•7.3.3 常见情况下朗肯主动土压力计算
(1)填土面有连续均布荷载q 土压力的计算方法是将均布荷载换算成当量的土重。
hq
pa qka 2c ka q
计算步骤
3.挡土墙验算
A.稳定性验算:抗倾覆验算和抗滑移验算 B.地基承载力验算
C .墙身强度验算、变形验算
4.如不满足条件,重新改变尺寸,再验算
• 7.5.5 防水排水设计
孔直径不小于100mm 坡度5%间距2~3米
砂土、卵石,500mm宽
图7.21 挡土墙排水防水设计
1
3tg2
45
2
2c
tg
45
2
将σ1=pp 、σ3=γz代入上式,得
令kp=tan2(45o + /2 )可得 pp z kp 2c kp
无粘性土 c=0
pp z kp
kp——被动土压力系数
间有摩擦力),④填土为无粘性土的土压力计算。
•3.库仑公式推导
对土楔ABC作受力分析,受到三 个力W、R、E作用,由平衡 条件及正弦定律得库仑主动土压
力Ea和被动土压力EP的算式
——滑裂面与水平面的夹角 ——墙背与土之间的摩擦角,外摩擦角。 ——土与土之间的摩擦角,内摩擦角。
HK p
Ep作用在距离墙底H/3处
Ep
1
2
H2
kp
朗肯主动土压力 pa z ka 2c ka
Ka=tan2(45o — /2 )
•7.3.3 常见情况下朗肯主动土压力计算
(1)填土面有连续均布荷载q 土压力的计算方法是将均布荷载换算成当量的土重。
hq
pa qka 2c ka q
计算步骤
3.挡土墙验算
A.稳定性验算:抗倾覆验算和抗滑移验算 B.地基承载力验算
C .墙身强度验算、变形验算
4.如不满足条件,重新改变尺寸,再验算
• 7.5.5 防水排水设计
孔直径不小于100mm 坡度5%间距2~3米
砂土、卵石,500mm宽
图7.21 挡土墙排水防水设计
1
3tg2
45
2
2c
tg
45
2
将σ1=pp 、σ3=γz代入上式,得
令kp=tan2(45o + /2 )可得 pp z kp 2c kp
无粘性土 c=0
pp z kp
kp——被动土压力系数
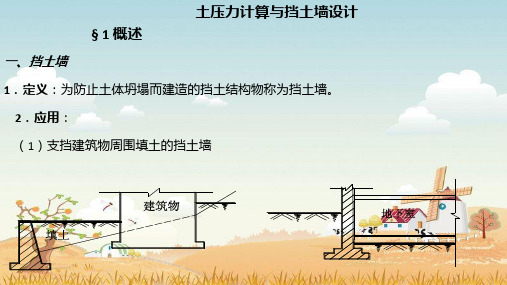
土力学与地基基础任务11 土压力及挡土墙设计

任务11 土压力及挡土墙设计
一、 概述 二、 土压力的分类 三、 郎肯土压力理论 四、 库仑土压力理论
学习目标:
1. 理解三种土压力的概念。 2. 掌握朗肯土压力理论; 3. 理解库伦土压力理论及其与朗肯土压力理论的比较; 4. 掌握常见情况下土压力的计算。
一、 概述
(一)挡土墙的应用
挡土墙——防止土体坍 塌的构筑物。
2,2
1H1K 1H1
(1H1 2H
下层应为 ', ' ,可近
似认为
h1Ka 'h2Ka wh2
三、朗肯土压力理论(Rankine,1857)
【例题7.1】某挡土墙,高度为5m,墙背垂直光滑,填土面水 平。填土为粘性土,其物理力学性质指标如下:c 8kPa , 18 , 18kN / m3。试计算该挡土墙主动土压力及其作用点位 置,并绘出主动土压力强度分布图。
(4)主动土压力 主动土压力强度分布如图7.7
所示。
总主动土压力
Ea
35.89 5 1.223 1
2
67.78kN / m
主动土压力作用点距墙底的距离为
(h z0 ) 5 1.223 1.26m
3
3
作业
1、某挡土墙,高度为5m,墙背垂直光滑,填 土面水平。填土为粘性土,其物理力学性质指 标如下:c 8kPa ,
2
三、朗肯土压力理论(Rankine,1857)
假定条件:墙背光滑(满足剪应力为零的边界条件)、直
立、填土面水平。当挡墙偏离土体时, x逐渐减小到 a时达到
朗肯主动极限平衡状态,主动土压力强度 a为:
粘性土:
a
z
tan
2
45
2
2c
一、 概述 二、 土压力的分类 三、 郎肯土压力理论 四、 库仑土压力理论
学习目标:
1. 理解三种土压力的概念。 2. 掌握朗肯土压力理论; 3. 理解库伦土压力理论及其与朗肯土压力理论的比较; 4. 掌握常见情况下土压力的计算。
一、 概述
(一)挡土墙的应用
挡土墙——防止土体坍 塌的构筑物。
2,2
1H1K 1H1
(1H1 2H
下层应为 ', ' ,可近
似认为
h1Ka 'h2Ka wh2
三、朗肯土压力理论(Rankine,1857)
【例题7.1】某挡土墙,高度为5m,墙背垂直光滑,填土面水 平。填土为粘性土,其物理力学性质指标如下:c 8kPa , 18 , 18kN / m3。试计算该挡土墙主动土压力及其作用点位 置,并绘出主动土压力强度分布图。
(4)主动土压力 主动土压力强度分布如图7.7
所示。
总主动土压力
Ea
35.89 5 1.223 1
2
67.78kN / m
主动土压力作用点距墙底的距离为
(h z0 ) 5 1.223 1.26m
3
3
作业
1、某挡土墙,高度为5m,墙背垂直光滑,填 土面水平。填土为粘性土,其物理力学性质指 标如下:c 8kPa ,
2
三、朗肯土压力理论(Rankine,1857)
假定条件:墙背光滑(满足剪应力为零的边界条件)、直
立、填土面水平。当挡墙偏离土体时, x逐渐减小到 a时达到
朗肯主动极限平衡状态,主动土压力强度 a为:
粘性土:
a
z
tan
2
45
2
2c
精品课件- 土压力计算与挡土墙设计
能滑动,二者之间的相互作用力即为主动土压力。所以,主动土压力的大小可由土 楔体的静力平衡条件来确定。
1. 作用在土楔体ABC上的力 • 假设滑动面AC与水平面夹角为α,取滑动土楔体ABC为脱离体,则作用在土楔体ABC上
的力有:
(1)土楔体自重 • 在三角形ABC中,利用正弦定理可得:
(2)滑动面 上B的C反力R
应力分别为:
• (因为已假设墙背是光滑的、直立的,所以在单元上不存在剪应力。) • 该应力状态仅由填土的自重产生,故此时土体处于弹性状态,其相应的莫尔园如下
图所示的园Ⅰ,一定处于填土抗剪强度曲线之下。
• 当挡土墙离开填土向前发生微小的转动或位移时, σ1 =σz =yz不变, σ3 =σx而却不断减 少,相应的莫尔园也在逐步扩大。当位移量达到一定值时, σ3减少到σ3f ,由σ3f与 σ1 =yz构成的应力园与抗剪强度曲线相切,如图Ⅱ所示,称为主动极限应力园。此时, 土中各点均处于极限平衡状态,达到最低什的小主应力σ3f称为朗肯主动土压力pa(即 pa = σ3f )。与此同时,土体中存在过墙踵的滑动面(剪切破坏面),滑动面与大主 应力作用平面(水平面)的夹角为450+φ/2。
•
q——填土面上的均布荷载,kPa。
四、墙后有地下水时
• 若墙后有地下水时,水下应取浮重度,同时应考虑静水压力,如下图所示。
• 五、墙背倾斜时 • 式中:W0——楔体ABB‘的自重。
§3 朗肯土压力理论
一、基本概念
1.假设 (1)墙背直立、光滑; (2)墙后填土面水平; (3)土体为均质各向
同性体。 2.主动朗肯状态 • 如上图所示,在墙后土体中深度Z处任取一单元体,当挡土墙静止不动时,则两个主
•
h=q/r
1. 作用在土楔体ABC上的力 • 假设滑动面AC与水平面夹角为α,取滑动土楔体ABC为脱离体,则作用在土楔体ABC上
的力有:
(1)土楔体自重 • 在三角形ABC中,利用正弦定理可得:
(2)滑动面 上B的C反力R
应力分别为:
• (因为已假设墙背是光滑的、直立的,所以在单元上不存在剪应力。) • 该应力状态仅由填土的自重产生,故此时土体处于弹性状态,其相应的莫尔园如下
图所示的园Ⅰ,一定处于填土抗剪强度曲线之下。
• 当挡土墙离开填土向前发生微小的转动或位移时, σ1 =σz =yz不变, σ3 =σx而却不断减 少,相应的莫尔园也在逐步扩大。当位移量达到一定值时, σ3减少到σ3f ,由σ3f与 σ1 =yz构成的应力园与抗剪强度曲线相切,如图Ⅱ所示,称为主动极限应力园。此时, 土中各点均处于极限平衡状态,达到最低什的小主应力σ3f称为朗肯主动土压力pa(即 pa = σ3f )。与此同时,土体中存在过墙踵的滑动面(剪切破坏面),滑动面与大主 应力作用平面(水平面)的夹角为450+φ/2。
•
q——填土面上的均布荷载,kPa。
四、墙后有地下水时
• 若墙后有地下水时,水下应取浮重度,同时应考虑静水压力,如下图所示。
• 五、墙背倾斜时 • 式中:W0——楔体ABB‘的自重。
§3 朗肯土压力理论
一、基本概念
1.假设 (1)墙背直立、光滑; (2)墙后填土面水平; (3)土体为均质各向
同性体。 2.主动朗肯状态 • 如上图所示,在墙后土体中深度Z处任取一单元体,当挡土墙静止不动时,则两个主
•
h=q/r
挡土墙ppt课件

04
挡土墙的维护与加固
定期检查与维护措施
01
02
03
定期检查
每季度或半年对挡土墙进 行一次全面检查,包括墙 体、排水系统、植被覆盖 等方面。
日常维护
及时清理挡土墙表面的杂 草、垃圾,保持墙体整洁; 定期疏通排水系统,防止 积水对墙体造成损害。
专项检查
在遭遇极端天气、地震等 自然灾害后,应立即对挡 土墙进行专项检查,评估 其稳定性和安全性。
在加固完成后,应对挡土墙进行定期 监测和效果评估,确保加固措施的有 效性和安全性。
案例分析
结合具体案例,详细介绍加固方法的 应用和效果,如某挡土墙出现裂缝后 采用灌浆法进行加固,有效提高了墙 体的整体性和稳定性。
05
挡土墙的环境影响与生态保 护
对环境的影响分析
01
建设过程中产生的噪音、振动和尘土对周围环境 的影响;
验算挡土墙在水平荷载作用下的 抗滑稳定性,确保满足规范要求。
抗倾覆稳定性验算
验算挡土墙在垂直荷载作用下的 抗倾覆稳定性,确保满足规范要
求。
地基承载力验算
验算地基承载力是否满足挡土墙 的要求,如不满足需进行地基处
理。
结构优化
在满足稳定性和承载力的前提下, 对挡土墙结构进行优化设计,降
低造价和提高经济效益。
06
挡土墙的创新与发展趋势
新型材料与技术的应用
高性能混凝土
采用高强度、高耐久性混凝土, 提高挡土墙承载能力和使用寿命。
纤维增强混凝土
通过添加纤维材料改善混凝土的韧 性和抗裂性,提高挡土墙的整体性 能。
新型土工合成材料
利用土工格栅、土工布等合成材料, 增强土体的强度和稳定性,减少挡 土墙的变形和破坏。
土力学第8章土压力和挡土墙
• 挡土墙的位移 • 挡土墙的形状:竖直或倾斜,墙背光滑情况 • 填土的性质:填土的松密程度,含水量,土的强度指标 • 挡土墙的材料:素混凝土,钢筋混凝土,砌石
由于土压力是挡土墙的主要荷载。因此,设计挡土墙时首先要 确定土压力的性质、大小、方向和作用点。
No Image
挡土墙结构类型对土压力分布的影响
以上两式当β=0时, Ka' ,Kp' 分别变成 Ka,K 了p。
No Image
Ea作用点在距墙体底部1/3H=2.67m处,见图。
No Image
合力点计算为图示面积的形心位置。作用点在距墙体底部1/3H=2.67m处,见图。
水压力的作用点在距离底H2/3=1.33m处。
No Image
No Image
静止土压力
前面图中的O点
静止土压力:当挡土墙静止不动,土体处于弹性平衡状态时,土对墙
的压力称为静止土压力E0 。
主动土压力
主动土压力:当挡土墙在墙后土体推力作用下向离开土体方向偏移至 土体达到极限平衡状态时,作用在墙上的土压力称为主动土压力,一 般用Ea表示。
被动土压力
被动土压力:当挡土墙在外力作用下向土体方向偏移至土体达到极限
平衡状态时,作用在挡土墙上的土压力称为被动土压力,用Ep表示。
挡土墙上的三种土压力
不同土压力的大小关系
挡土墙模型实验、原型观测和理论研究表明:在相同条件下,主 动土压力小于静止土压力,而静止土压力又小于被动土压力,亦即 :
Ea < Eo < Ep
No Image
影响土压力的因素
作用在挡土墙上的土压力是个非常复杂的问题。土压力的大小 受多方面因素的影响:
1. 刚性挡土墙
由于土压力是挡土墙的主要荷载。因此,设计挡土墙时首先要 确定土压力的性质、大小、方向和作用点。
No Image
挡土墙结构类型对土压力分布的影响
以上两式当β=0时, Ka' ,Kp' 分别变成 Ka,K 了p。
No Image
Ea作用点在距墙体底部1/3H=2.67m处,见图。
No Image
合力点计算为图示面积的形心位置。作用点在距墙体底部1/3H=2.67m处,见图。
水压力的作用点在距离底H2/3=1.33m处。
No Image
No Image
静止土压力
前面图中的O点
静止土压力:当挡土墙静止不动,土体处于弹性平衡状态时,土对墙
的压力称为静止土压力E0 。
主动土压力
主动土压力:当挡土墙在墙后土体推力作用下向离开土体方向偏移至 土体达到极限平衡状态时,作用在墙上的土压力称为主动土压力,一 般用Ea表示。
被动土压力
被动土压力:当挡土墙在外力作用下向土体方向偏移至土体达到极限
平衡状态时,作用在挡土墙上的土压力称为被动土压力,用Ep表示。
挡土墙上的三种土压力
不同土压力的大小关系
挡土墙模型实验、原型观测和理论研究表明:在相同条件下,主 动土压力小于静止土压力,而静止土压力又小于被动土压力,亦即 :
Ea < Eo < Ep
No Image
影响土压力的因素
作用在挡土墙上的土压力是个非常复杂的问题。土压力的大小 受多方面因素的影响:
1. 刚性挡土墙
土压力计算获奖课件

p
1
3
tan
2
45
2
2ctan 45
2
z tan2 45 2ctan 45
2
2
p
三种状 态时旳 莫尔圆
0
0 K 0z
f c tg
a K0 z z
p
a
z tan2 45
2
2ctan 45
2
p
z tan2 45
2
2ctan 45
a
3
1tan
2
45
2
2ctan
45
2
z tan2 45 2ctan 45
2
2
2.土体在水平方向压缩
单元体在水平截面上旳法向应力z不变而竖 直截面上旳法向应力x却逐渐增大,直至满足极
限平衡条件(称为被动朗肯状态)。
被动朗肯状态 f c tg 时旳莫尔圆
0 K0 z z
2c K p
Ep
HK p 2c K p
Ep
1 H 2K
2
p
2cH
Kp
例题5-3 有一挡墙高6m,墙背竖直、光滑,
墙后填土表面水平,填土旳重度
γ=18.5kN/m3,内摩擦角φ =20° ,粘聚
力c=19kPa 。求被动土压力并绘出被动土
压力分布图。
解(1)计算被动土压力系数。
,
Kp tan2 45 20 2.04
底面 a 2 1h1 2 z K a 2 2C K a 2
17 2 19 3 0.57 2 10 0.75
第二节 静止土压力计算 水平向旳自重应力
H
E0
H 3
静止土压力旳分布
例5-1 已知某挡土墙高4.0m,墙背垂直光 滑,墙后填土面水平,填土重力密度为γ =18.0kN/m3,静止土压力系数Ko=0.65,试计 算作用在墙背旳静止土压力大小及其作用点, 并绘出土压力沿墙高旳分布图。
土力学土压力与挡土墙计算

第六章 土压力与挡土墙设计
墙体位移和土压力性质
拱桥桥台
岩石
2.主动土压力
Active earth pressure
1.静止土压力
Earth pressure at rest
3.被动土压力
Passive earth pressure
§6.3 朗肯(Rankine)土压力理论 一.半无限土体中极限平衡应力状态和朗肯土压力
半无限土体内各点的应力从弹性平 衡状态发展为极限平衡状态的条件
半无限土体
v z
h
45o+/2 90o-
主动极限平衡状态
Pa
K0v
v
朗肯土压力理论基本条件和假定 条件 墙背光滑 墙背垂直 填土表面水平
假设 墙后各点均处于极限平衡状态
(一) 填土为砂土
1.主动土压力
v
pa=h=tg2(45- /2 )gz (kN/m2) Pa K0v
土压力 pa = Kaz
水压力 pu=u (静水压力、 渗流压力、超静孔压)
土工织物反滤
砂砾石料
排水管
排水孔
墙基不透水 A
gf
H1
B
gf
H2
C 不透水层
土压力
Ka gH1
水压力
Ka (gH1+gH2) gwH2
§6.4 库仑土压力理论
假设条件:
平面滑裂面假设:滑裂面为平面 刚体滑动假设:破坏土楔为刚体 滑动楔体在两个平面上处于极限平衡状态
主动土压力系数 Ka= tg2(45-f/2 )
土压力直线分布
合力 Ea=1/2 Ka gH2 (kN/m)
H
作用点:底部以上1/3H处
H/3
墙体位移和土压力性质
拱桥桥台
岩石
2.主动土压力
Active earth pressure
1.静止土压力
Earth pressure at rest
3.被动土压力
Passive earth pressure
§6.3 朗肯(Rankine)土压力理论 一.半无限土体中极限平衡应力状态和朗肯土压力
半无限土体内各点的应力从弹性平 衡状态发展为极限平衡状态的条件
半无限土体
v z
h
45o+/2 90o-
主动极限平衡状态
Pa
K0v
v
朗肯土压力理论基本条件和假定 条件 墙背光滑 墙背垂直 填土表面水平
假设 墙后各点均处于极限平衡状态
(一) 填土为砂土
1.主动土压力
v
pa=h=tg2(45- /2 )gz (kN/m2) Pa K0v
土压力 pa = Kaz
水压力 pu=u (静水压力、 渗流压力、超静孔压)
土工织物反滤
砂砾石料
排水管
排水孔
墙基不透水 A
gf
H1
B
gf
H2
C 不透水层
土压力
Ka gH1
水压力
Ka (gH1+gH2) gwH2
§6.4 库仑土压力理论
假设条件:
平面滑裂面假设:滑裂面为平面 刚体滑动假设:破坏土楔为刚体 滑动楔体在两个平面上处于极限平衡状态
主动土压力系数 Ka= tg2(45-f/2 )
土压力直线分布
合力 Ea=1/2 Ka gH2 (kN/m)
H
作用点:底部以上1/3H处
H/3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Let, dEa 0
d
Ea
1 2
H
2
cos2
cos
cos2
1
sin cos
sin cos
i i
2
where,
cos2
cos
cos2
1
sin cos
sin i 2
cos
i
, active
pressure
coefficient
Ea
1 H 2
2
a
If i=0,α=0,δ=0, Then
3
1
tg 2 45
2
2c tg 45
2
45
2
Z0
2c
tg 45
2
, vertical
wall
depth
Ea
1 H
2
Z0 2
tg 2 45
2
1 H 2
2
tg 2 45
2cHtg 45
2
2
2c 2
E
1 H 2
2
K
2cH
K
2c 2
where
Ea
1 2
H
2
1
cos2 sin
2
1
2
H 2 1 sin 1 sin
1
2
H 2tg2 45
2
Ea
1
2
H2
a
where
a
tg2 45
2
• Complex boundary conditions/复杂边界条件
S
1 2
H
a2
tg
1 2
H
a2
tg
1 2
ab
1 2
a2
tg
• General solution
AB H cos
AD AB sin
BC
AB
sin sin
90 90
i i
then,G
1 2
H
2
sin
sin 90 cos2 cos i
i
E
1 2
H
2
sin
cos2
sin 90
cos i
i
sin 90
sin
A0
tg
B0
G A0tg B0
where,
A0
1 2
(H
a)2
B0
1 2
(H
a)2
tg
1 2
a2
tg
1 2
ab
Ea
G
sin 90
sin
A0tg
B0
cos sin
where,
Let, dEa 0
d
then,
A0tg
B0
sin
sin
sin 2
cos
1
3
tg2
45
2
3
K
p
where
Kp
tg2 45
2
,
passive
pressure
coefficient
Ep
1 H 2
2
tg 2 45
2
1 H 2
2
Kp
•In Cohesive soils (soil surface horizontal)/ /地表水平粘性土
1
3
tg2
45
2
-Assuming
-Active earth pressure
E
G
sin 90
sin
dEa 0
d
-Passive earth pressure
sin 90
Ep G sin
Ea f ( ) Ep f ( )
6.3.2 Active Case/主动情形
Ka
tg2 45
2
•For sloping soil surface(β) /地表倾斜
EaLeabharlann 12H2
cos
cos cos
cos2 cos2 cos2 cos2
6.2.3 Rankine passive earth pressure/被动土压力
•In Non-Cohesive soils (soil surface horizontal) /地表水平无粘性土
Ea
A0
tg
B0
cos sin
Ea
A0tg B0 tg tg
tg
tg
cos sin
A0tg B0 tg tg
a
a
tg
tg
cos sin
where,
-Distribution of active earth pressure /土压力的分布
-Example
3
1
tg2 45
2
where 1 H
45
2
E
1 H 2 tg2 45
2
2
Ea
1
2
H
2
Ka
where
Ka
tg2 45
2
, active
pressure
coefficient
•In Cohesive soils (soil surface horizontal)/地表水平粘性土
A retaining wall of embankment is 6m high. And the relative parameters are c=0,φ=30。,α=14 。 00’,δ=φ/3, as well as shown in Fig. below. Calculate the active earth pressure and draw the distribution.
§6 Earth Pressure and Retaining Wall
土压力理论与挡土墙设计
• Introduction/引言
• Rankine’s earth pressure theory / 朗肯土压力理论 • Coulomb’s earth pressure theory / 库仑土压力理论 • Discuss / 讨论 • Retaining wall design / 挡土墙设计
6.2.1 Limit state/极限状态 -Active limit equilibrium/主动极限平衡 -Passive limit equilibrium/被动极限平衡
x K0 z
6.2.2 Rankine active earth pressure/主动土压力
•In Non-Cohesive soils (soil surface horizontal)/地表水平无粘性土
6.1 Introduction/引言
x k0 z
k0 1
-Coefficient of earth pressure at rest 静止土压力
k0 1 sin ' Bishop, 1958
E0
1
2
H
2
K0
主动土压力
被动土压力
6.2 Rankine Earth Pressure theory /朗肯土压力理论
cos
A0 cos sin cos2
0
tg 2 2tg tg ctg tg B0 ctg tg 0
A0
tg tg
tg
ctg tg
B0 A0
where,
-Coefficient of active earth pressure /主动土压力系数λa
a
a h
2c
tg
45
2
3
K
p
2c
Kp
3 H
where
Kp
tg2 45
2
,
passive
pressure
coefficient
Ep
1 H 2 2
tg 2 45
2c H 2
tg 45
2
1 H 2 2
Kp
2cH
Kp
6.3 Coulomb’s Earth Pressure theory / 库仑土压力理论 6.3.1Basic concept
