第十一章 反常积分
数学《反常积分》讲义

第十一章 反常积分1 反常积分概念一、问题提出定积分 1) 积分区间的有穷性2) 被积函数的有界性如果函数(被积函数)的积分区间为无穷区间或被积函数在积分区间上无界,应如何讨论它们的积分,这类积分称为反常积分(或广义积分,Cauchy-Riemann 积分, C-R 积分), 而上一章的定积分称为正常积分.例 1 (第二宇宙速度) 例 2 (流水时间)二、两类反常积分的定义定义1 设函数f 定义在无穷区间[,)a +∞上, 且在任何有限区间[,]a u 上可积, 如果存在极限lim()uau f x dx J →+∞=⎰, 那么称极限J 为函数f 在[,)a +∞上的无穷限反常积分(无穷积分),记作()aJ f x dx +∞=⎰,并称()af x dx +∞⎰收敛, 有时也称f 在[,)a +∞上(Cauchy-Riemann )可积; 反之,若上述极限不存在, 则称()af x dx +∞⎰发散.注 1()af x dx +∞⎰收敛的几何意义:若f 在[,)a +∞上为非负连续函数,则介于曲线()y f x =,直线x a =及x 轴之间一块向右无限延伸的区域有面积J .注 2 类似可定义()lim()aauu f x dx f x dx -∞→-∞=⎰⎰()()()aaf x dx f x dx f x dx +∞+∞-∞-∞=+⎰⎰⎰lim()lim()uaauu u f x dx f x dx →+∞→-∞=+⎰⎰例 3 1) 讨论积分211dx x +∞+⎰,0211dx x -∞+⎰,211dx x +∞-∞+⎰的敛散性.2) 计算积分20125dx x x +∞++⎰.例4 讨论下列积分的敛散性.1) 11pdx x +∞⎰; 2) 21(ln )pdx x x +∞⎰.注3 设f 在[,)a +∞上连续,F 为f 的一个原函数,则()lim ()lim ()()()()uaau u f x dx f x dx F u F a F F a +∞→+∞→+∞==-=+∞-⎰⎰例 5 讨论sin axdx +∞⎰的敛散性注 4 ()f x dx +∞-∞⎰为两个非正常积分之和,而非lim()uuu f x dx -→+∞⎰.定义 2 设函数f 定义在区间(,]a b 上,在点a 的任一右邻域内无界, 但在任意内闭区间[,](,]b a b α⊂上有界且可积. 如果存在极限lim ()bu u af x dx J +→=⎰,那么称此极限为无界函数f 在(,]a b 上的反常积分,记作()baJ f x dx =⎰,并称反常积分()baf x dx ⎰收敛,如果上述极限不存在,则称反常积分()baf x dx ⎰发散.在上述定义中函数f 在点a 的附近无界, 我们称a 为f 的瑕点, 而无界函数的反常积分()ba f x dx ⎰也称为瑕积分.注 5 1) 类似可定义瑕点为b 的瑕积分()lim ()buaau bf x dx f x dx -→=⎰⎰其中f 在b 的任一左邻域内无界,且在任何内闭区间[,][,)a a b β⊂上可积.2) 若,a b 都为f 的瑕点,且在任一内闭子区间[,](,)u v a b ⊂上可积,此时可定义瑕积分()()()bc b aacf x dx f x dx f x dx =+⎰⎰⎰lim ()lim ()c vucu av bf x dx f x dx +-→→=+⎰⎰其中c 为(,)a b 内的任一实数,当且仅当右式两个瑕积分都收敛时,左式的瑕积分收敛.3) 若f 的瑕点(,)c a b ∈,则定义瑕积分()()()bc b aacf x dx f x dx f x dx =+⎰⎰⎰lim ()lim ()u bavu cv cf x dx f x dx +-→→=+⎰⎰其中f 在[,)(,]a c c b ⋃上有定义,在c 的任一邻域内无界, 且在任何闭子区间[,][,)a u a c ⊂, [,](,]v b c b ⊂都可积,当且仅当右边两个瑕积分收敛时, 左边的瑕积分收敛.例 6 1) 计算瑕积分1⎰2) 讨论瑕积分1pdxx ⎰的敛散性(p >0)3) 讨论瑕积分0p dxx+∞⎰的敛散性(p >0) 4) 24=⎰5) 1⎰三、两类反常积分的关系设()f x 连续,b 为瑕点,则11211()()t b xbab af x dx f b dt t t=-+∞-=-⎰⎰瑕积分可转化为无穷积分设0a >,1121()()t xaadtg x dx g t t =+∞=-⎰⎰12011()a g dt t t =⎰无穷积分可转化为瑕积分由此可见,瑕积分与无穷积分可相互转化,因而它们有平行的理论和性质. 例 7 讨论下列反常积分是否收敛 1) 2x xe dx +∞--∞⎰2) cos x e xdx +∞--∞⎰3) 2⎰4) 1(1)(ln )pdxp x x >⎰5) 1⎰例 8 举例说明瑕积分()b af x dx ⎰收敛,2()baf x dx ⎰未必收敛.例 9 1) 证明:若()af x dx +∞⎰收敛,且lim ()x f x A →+∞=,则0A =;2) 举例说明: ()af x dx +∞⎰收敛,f 在[,)a +∞上连续,未必有lim ()0x f x →+∞=成立.例 10 若f 在[,)a +∞上可导,且()af x dx +∞⎰与()af x dx +∞'⎰收敛,则lim ()0x f x →+∞=.2 无穷积分的性质与收敛判别一、 无穷积分性质由()af x dx +∞⎰收敛lim ()lim()duau u F u f x dx →+∞→+∞⇔=⎰存在, 根据函数极限收敛的Cauchy 准则,我们有定理 1 (Cauchy 准则) 无穷积分()af x dx +∞⎰收敛⇔120,,,:G a u u G ε∀>∃≥∀>1221()()()u u u aau f x dx f x dx f x dx ε-=<⎰⎰⎰.性质1 (线性性质) 若1()af x dx +∞⎰和2()af x dx +∞⎰都收敛, 12,k k 为任意常数, 则1122[()()]ak f x k f x dx +∞+⎰也收敛,且11221122[()()]()()aaak f x k f x dx k f x dx k f x dx +∞+∞+∞+=+⎰⎰⎰.性质2 (区间可加性) 若f 在任何有限区间[,]a u 上可积,b a >,则()af x dx +∞⎰与()bf x dx +∞⎰同敛散,且()()()b aabf x dx f x dx f x dx +∞+∞=+⎰⎰⎰.定理2 无穷积分()af x dx +∞⎰收敛0,,:()uG a u G f x dx εε+∞⇔∀>∃≥><⎰当.性质 3 (绝对收敛) 若f 在任何有限区间[,]a u 上可积,且()af x dx +∞⎰收敛,则()af x dx +∞⎰也收敛,且()()aaf x dx f x dx +∞+∞≤⎰⎰.定义1 若()af x dx +∞⎰收敛, 则称()af x dx +∞⎰绝对收敛.性质3 说明绝对收敛的无穷积分其本身一定收敛,而反之未必成立. 我们称收敛而不绝对收敛的无穷积分为条件收敛的无穷积分.性质4 (换元) 设:[,)[,)a ϕα+∞→+∞是光滑严格单调映射,且()a ϕα=,lim ()t t ϕ→+∞=+∞. 若()af x dx +∞⎰收敛,则(())()f t t dt αϕϕ+∞'⎰收敛,且()(())()af x dx f t t dt αϕϕ+∞+∞'=⎰⎰.性质5 (分部积分) 设,f g 为[,)a +∞上的光滑函数, 且lim ()()x f x g x →+∞⋅存在, 则()()af xg x dx +∞'⋅⎰与()()af xg x dx +∞'⎰同敛散,且它们收敛时有等式()()()()()()aaaf xg x dx f x g x f x g x dx +∞+∞+∞''⋅=⋅-⋅⎰⎰其中()()lim ()()()()ax f x g x f x g x f a g a +∞→+∞⋅=-.二、 无穷积分判别法1、比较判别法 (绝对收敛判别法)定理 3 (比较法则) 设定义在[,)a +∞上的两个函数f 和g 在任何有限区间[,]a u 上可积,且()()f x g x ≤,[,)x a ∈+∞. 则i) 当()ag x dx +∞⎰收敛时, 必有()af x dx +∞⎰收敛;ii) 当()af x dx +∞⎰发散时, 必有()ag x dx +∞⎰发散.例 1 判断积分22sin(1)5x dx x+∞++⎰的敛散性.1) Cauchy 判别法推论1 设f 定义在[,)(0)a a +∞>上,且在任何有限区间[,]a u 上可积,则有i) 当1(),[,)1p f x x a p x≤∈+∞>且时,()a f x dx +∞⎰收敛. ii) 当1(),[,)1p f x x a p x≥∈+∞≤且时,()a f x dx +∞⎰发散.2) 比较原则的极限形式推论 2 设f 和g 都在任何区间[,]a u 上可积, ()0g x >, 且()lim ()x f x c g x →+∞=. i) 当0c <<+∞时,()af x dx +∞⎰与()ag x dx +∞⎰同敛散;ii) 当0c =时,若()ag x dx +∞⎰收敛,则()af x dx +∞⎰收敛;iii) 当c =+∞时,若()ag x dx +∞⎰发散,则()af x dx +∞⎰发散.推论 3 设f 定义在[,)(0)a a +∞>上,且在任何有限区间[,]a u 上可积,且lim ()p x x f x λ→+∞=,则有i) 当1p >,0λ≤<+∞时,()af x dx +∞⎰收敛; ii) 当1p ≤,0λ<≤+∞时,()af x dx +∞⎰发散.例 2 讨论下列无穷积分的敛散性:1) 1x x e dx α-⎰2)21+∞⎰2、 Dirichlet 和Abel 判别法定理4 (Dirichlet ) 若()()ua F u f x dx =⎰在[,)a +∞上有界, ()g x 在[,)a +∞上x →+∞时单调趋于0, 则()()a f x g x dx +∞⋅⎰收敛.定理5 (Abel ) 若()af x dx +∞⎰收敛, ()g x 在[,)a +∞上单调有界, 则()()af xg x dx +∞⋅⎰收敛.定理6 (Dirichlet- Abel ) 设无穷积分()()()aaf x dx u x dv x +∞+∞=⎰⎰, 其中()u x单调, 且(),()u x v x 中一个有界, 另一个在x →+∞时趋于0, 则()af x dx +∞⎰收敛.例 3 讨论无穷积分1sin p xdx x +∞⎰与1cos (0)px dx p x +∞>⎰的敛散性.例 4 证明下列积分条件收敛.1) 21sin x dx +∞⎰,21cos x dx +∞⎰;2) 41sin x x dx +∞⋅⎰;3)1+∞⎰. 例 5 若()af x dx +∞⎰绝对收敛. 且lim ()0x f x →+∞=,则2()af x dx +∞⎰必收敛.例6 设,,f g h 为[,)a +∞上三个连续函数,且()()()h x f x g x ≤≤. 证明:如果()ah x dx +∞⎰,()ag x dx +∞⎰收敛,那么()af x dx +∞⎰亦收敛.例 7 证明: 若f 在[,)a +∞上一致连续,且()af x dx +∞⎰收敛,则lim ()0x f x →+∞=.例 8 讨论下列无穷积分的敛散性1) 1ln n xdx x+∞⎰2) 31arctan 1x xdx x +∞+⎰3)21x edx +∞-⎰4) 1ln(1)px dx x +∞+⎰5) 0ln(1)px dx p x+∞+ (>0)⎰6) 0xdx ⎰7)21cos x e xdx +∞-⎰8) 0sin arctan xxdx x+∞⎰例9 证明:若f 是[,)a +∞上的单调函数,()af x dx +∞⎰收敛,则lim ()0x f x →+∞=, 且1()()f x o x x= , →+∞.注: 由()lim 1()x f x g x →+∞=, ()ag x dx +∞⎰收敛, 推不出()af x dx +∞⎰收敛.3 瑕积分的性质与判别法一、 瑕积分的性质 (瑕点为x a =)定理1 瑕积分()ba f x dx ⎰收敛0,0,εδ⇔∀>∃>当12,(,)u u a a δ∈+时,2121()()()bbu u u u f x dx f x dx f x dx ε-=<⎰⎰⎰.性质1 设函数1f , 2f 的瑕点同为a ,1k ,2k 为常数,则当瑕积分1()baf x dx ⎰,2()baf x dx ⎰都收敛时,瑕积分1122[()()]bak f x k f x dx +⎰必收敛,且11221122[()()]()()bb baaak f x k f x dx k f x dx k f x dx +=+⎰⎰⎰.性质2 设函数f 的瑕点为x a =,(,)c a b ∈, 则瑕积分()baf x dx ⎰与()caf x dx ⎰同敛散且()()()b c b aacf x dx f x dx f x dx =+⎰⎰⎰, 其中()bcf x dx ⎰为定积分.性质3 若f 的瑕点为a , f 在(,]a b 的任一闭子区间[,]u b 上可积, 则当()baf x dx ⎰收敛时,()baf x dx ⎰必收敛且()()bbaaf x dx f x dx ≤⎰⎰.当()baf x dx ⎰收敛时,称()baf x dx ⎰为绝对收敛; 而称本身收敛但不绝对收敛的瑕积分为条件收敛的瑕积分.二、瑕积分判别法定理2 (比较原则) 定义在(,]a b 上的两个函数,f g , 瑕点同为a , 在任闭子区间[,](,]u b a b ⊂上可积,且()()(,]f x g x x a b ≤ ∈,则i) 当()bag x dx ⎰收敛时,()baf x dx ⎰必收敛 (从而()baf x dx ⎰也收敛) ;ii) 当()baf x dx ⎰发散时,()bag x dx ⎰发散.推论1 设f 定义在(,]a b 上,瑕点为a ,且在任何闭子区间[,](,]u b a b ⊂上可积,则 i) 当1()01()pf x p x a ≤, <<-时, ()baf x dx ⎰收敛;ii) 当1()1()pf x p x a ≥, ≥-时, ()baf x dx ⎰发散.推论2 若()0g x >,且()lim ()x af x cg x +→=, 则 i) 当0c <<+∞时,()b af x dx ⎰与()bag x dx ⎰同敛散;ii) 当0c =,()b ag x dx ⎰收敛时,()baf x dx ⎰收敛;iii) 当c =+∞,()b ag x dx ⎰发散时, ()b af x dx ⎰发散.推论3 在推论2的条件下,若lim()()p x ax a f x λ+→-=, 则 i) 01,0p λ<<≤<+∞时, ()baf x dx ⎰收敛;ii) 1,0p λ≥<≤+∞时, ()baf x dx ⎰发散.定理 3 (Dirichlet- Abel ) 设瑕积分()()()b baaf x dx u x dv x =⎰⎰有唯一奇点a ,其中()u x 单调, 且(),()u x v x 中一个有界, 另一个在x a +→时趋于0, 则()baf x dx ⎰收敛.例 1 讨论下列瑕积分的敛散性.1) 10⎰2) 21ln dx x⎰3) 130arctan 1xdx x -⎰4) 201cos mxdx xπ-⎰5) 1⎰6) 10⎰7) 20(,0)sin cos p q dxp q x xπ>⎰例 2 讨论反常积分1()1x x dx xα-+∞Φ=+⎰的敛散性.例 3 证明瑕积分20ln(sin )J x dx π=⎰收敛,且ln 22J π=-,同时利用上述结果证明:1) 2ln(sin )ln 22d ππθθθ=-⎰2) 0sin 2ln 21cos d πθθθπθ=-⎰三、反常积分与正常积分的区别1、 Riemann 积分 f 在[,]a b 上可积,则f 在[,]a b 上有界. 无穷积分 f 在[,)a +∞上可积(()af x dx +∞⎰收敛) f ⇒在[,)a +∞上有界.如4()sin f x x x =⋅ 或者 ,()0,n x nf x x n =⎧=⎨≠⎩.2、Riemann 积分 f 在[,]a b 上可积⇒()f x 在[,]a b 上可积,但反之未必, 故Riemann 积分是绝对型积分,而无穷积分 ()f x 在[,)a +∞上可积⇒f 在[,)a +∞上可积,但反之未必, 故Cauchy-Reimann 积分是非绝对型积分, 如sin (),[1,)xf x x x=∈+∞.3、Riemann 积分 ,f g 在[,]a b 上可积⇒f g ⋅在[,]a b 上可积, 而无穷积分 ,f g 在[,)a +∞上可积⇒f g ⋅在[,)a +∞上可积.例4 证明:1) 11111p p x x dx dx x x --+∞=++⎰⎰2) 12π<<⎰3) 设f 在[,)a +∞上连续0a b <<,若lim ()x f x k →+∞=,则()()((0))ln f ax f bx adx f k x b+∞-=-⎰例5 证明: 1) 设f 在[,)a +∞上非负连续, 若0()xf x dx +∞⎰收敛, 则0()f x dx +∞⎰也收敛.2) 设f 在[,)a +∞上连续可微且当x →+∞时,()f x 递减趋于0, 则()f x dx +∞⎰收敛⇔0()xf x dx +∞'⎰收敛.习 题 课例 1 论述题:1) 设f 在(,)-∞+∞上连续,且()f x dx +∞-∞⎰收敛,则()(),()()x x d d f t dt f x f t dt f x dx dx +∞-∞==-⎰⎰. 2) 积分0()f x dx +∞⎰收敛,则lim ()0x f x →+∞=.3) 积分()baf x dx ⎰收敛,则此积分可用和式公式01lim ()ni i T i f x ξ→=∑来计算.4) 若lim ()x f x A →+∞=存在,()af x dx +∞⎰收敛,则0A =.5) 若0()f x dx +∞⎰收敛,lim ()0x f x →+∞=,则2()af x dx +∞⎰必收敛.6) 若()af x dx A +∞=⎰,则lim()nan f x dx A →+∞=⎰,但反之不成立.7) 若()af x dx +∞⎰收敛,g 有界, 则()()af xg x dx +∞⎰收敛.8) 若lim ()AAA f x dx -→+∞⎰存在,则()f x dx +∞-∞⎰收敛.例 2 计算下列无穷积分: 1) 0()x n n I e x dx n N +∞-=∈⎰2) 21dxx x+∞++⎰3) (1)(ln )padxa x x +∞>⎰4) 24011x dx x +∞++⎰5) 31⎰6)1+∞⎰例 3 1) 设1()(2)x x x x ϕ+=-,求321()1()x dx x ϕϕ'+⎰;2) 已知01()cos x x dt tϕ=⎰,求(0)ϕ'.例 4 证明: 0cos 1xdx x+∞+⎰收敛, 且0cos 11xdx x+∞≤+⎰.例 5 讨论下列积分收敛性 1)2301dx x x x +∞+++⎰2)0cos (0)kx e xdx k +∞->⎰3)0ln(1)m x dx x +∞+⎰4)1+∞⎰5)20sin mx dx x +∞⎰6) 01m n x dx x +∞+⎰ 7) 10p x x e dx +∞--⎰ 8) 0cos (0)1n ax dx n x+∞≥+⎰。
十一章反常积分

0
1
b
x
二、两类反常积分的定义. 两类反常积分的定义
定义1: 定义 设函数 f (x)定义在区间[a, +∞)上, 且在任何 有限区间[a, u]上可积,如果存在极限
u →+∞ a
lim
∫ f ( x )dx = J
u
则称此极限为函数 f (x)在无穷区间[a, +∞)上 (x) [a, +∞) 的无穷限反常积分, 记作
u2
u 1
f (x)d <ε. x
2,比较原则
设定义在[ a,+∞)上的两个函数f和g都在任何有限区间上可积,
且满足
f (x ≤g(x x∈ a+ ) ) ), [, ∞
定理11.2(比较原则) (比较原则) 定理
设定义在[ a,+∞)上的两个函数f和g都在任何有限区间上可积,
[, ∞ 且满足 f (x) ≤g(x), x∈ a+ ) 则
若 g(x d 收 ,则 ∫ )x 敛 ∫
a
+ ∞
+ ∞
a
f (x d 收 ; ) x 敛
若 ∫
例1 : 讨论 ∫
+∞ 0
+ ∞
a
f (x d 发 ,则 g(x d 发 . ) x 散 ∫ )x 散
a
+ ∞
sin x dx的收敛性. 2 1+ x
a sin x x +b
3 2
例 2 : 讨论 ∫
+∞
a
+∞
a +∞
[k1 f1 ( x) + k 2 f 2 ( x)]dx也收敛, 且 [k1 f1 ( x) + k 2 f 2 ( x)]dx = k1 ∫
第十一章反常积分习题课教学总结

第十一章 反常积分习题课一 概念叙述 1.叙述()dx x f a⎰+∞收敛的定义.答:()dx x f a⎰+∞收敛⇔()()lim+∞→+∞=⎰⎰uaau f x dx f x dx 存在.⇔()lim0+∞→+∞=⎰uu f x dx . ⇔()()0,0,,εε+∞∀>∃>∀>-<⎰⎰u aaM u M f x dx f x dx 有⇔()0,0,,εε+∞∀>∃>∀><⎰uM u M f x dx 有2.叙述()baf x dx ⎰(a 是暇点)收敛的定义.答:()baf x dx ⎰收敛⇔()()lim +→=⎰⎰bbuau af x dx f x dx 存在.⇔0,0,εδ∀>∃>当δ<<+a u a ,有()()ε-<⎰⎰bbuaf x dx f x dx .3. 叙述()dx x f a⎰+∞收敛的柯西准则.答:无穷积分()dx x f a⎰+∞收敛的柯西准则是:任给0ε>,存在0M >,只要12,u u M >,便有()()()2121u u u aau f x dx f x dx f x dx ε-=<⎰⎰⎰.4. 叙述()b af x dx ⎰(a 是暇点)收敛的柯西准则.答:瑕积分()dx x f ba ⎰(瑕点为a )收敛的充要条件是:任给0ε>,存在0δ>,只要()12,,u u a a ∈+δ,总有()()()2121b bu u u u f x dx f x dx f x dx -=<ε⎰⎰⎰.二 疑难问题1.试问⎰+∞adx x f )(收敛与0)(lim =+∞→x f x 有无联系?答:首先,0)(lim =+∞→x f x 肯定不是⎰+∞adx x f )(收敛的充分条件,例如01lim=+∞→xx ,但⎰+∞11dx x发散.那么0)(lim =+∞→x f x 是否是⎰+∞a dx x f )(收敛的必要条件呢?也不是!例如⎰+∞12sin dx x ,⎰+∞12cos dx x ,⎰+∞14sin dx x x 都收敛,因为前两个无穷积分经换元2t x =得到⎰+∞12sin dx x 1+∞=⎰,21cos x dx +∞=⎰=dt tt ⎰+∞12cos ,则⎰+∞12sin dx x ,⎰+∞12cos dxx 是条件收敛,对于第三个无穷积分,经换元2t x =而得⎰+∞14sin dx x x =⎰+∞12sin 21dt t ,它也是条件收敛的. 从这三个无穷积分的收敛性可以看到,当x →+∞时被积函数即使不趋于零,甚至是无界的,无穷积分仍有可能收敛.注:若lim ()0x f x A →+∞=≠,则⎰+∞ax x f d )(发散.注:1)若⎰+∞ax x f d )(收敛,且lim ()x f x A →+∞=存在, 则定有0)(lim =+∞→x f x ;2)若⎰+∞a x x f d )(收敛,且f 在[)+∞,a 上为单调,则0)(lim =+∞→x f x ;3)若⎰+∞a x x f d )(收敛,且f 在[)+∞,a 上一致连续,则0)(lim =+∞→x f x ;4)若⎰+∞ax x f d )(收敛,且()d af x x +∞'⎰收敛,则0)(lim =+∞→x f x .证:1)设A x f x =+∞→)(lim .若0≠A (不妨设0A >),则由极限保号性,M a ∃>,当x M ≥时满足()0.2Af x ≥> 于是有()()()uMuaaMf x dx f x dx f x dx =+⎰⎰⎰()()2MaAf x dx u M ≥+-⎰, 于是⎰+∞=+∞→uau dx x f .)(lim而这与⎰+∞ax x f d )(收敛相矛盾,故0A =.2)不妨f 在[)+∞,a 上单调增,若f 在[)+∞,a 上无上界,则0A ∀>,M a ∃>,当x M ≥时,使A x f ≥)(.类似于1)的证明,推知⎰+∞+∞=a dx x f )(,矛盾.所以f 在[)+∞,a 上单调增而有上界,于是由单调有界定理知A x f x =+∞→)(lim 存在.依据已证得的命题1),0)(lim =+∞→x f x .3)由f 在[)+∞,a 上一致连续,则0,0εδ∀>∃>,(设)δε≤[),,x x a '''∀∈+∞x x δ'''-<只要时,就有()()2f x f x ε'''-<.又因⎰+∞adx x f )(收敛,故对上述,M a δ∃>,当12,x x M >时,有212()2x x f x dx δ<⎰.现对任何x M >,取12,x x M >,且使1221,.x x x x x δ<<-=此时由⎰⎰⎰+-=212121)()()()(x x x x x x dt t f dt t f dt x f x f δ⎰⎰+-≤2121)()()(x x x x dt t f dt t f x f2,22εδδεδ<⋅+≤便得(),.f x x M ε<>这就证得.0)(lim =+∞→x f x4)因为()d af x x +∞'⎰收敛,则()()()lim()d lim uau u f x x f u f a →+∞→+∞'=-⎰存在,于是()lim u f u →+∞存在,由1)得证.2.()af x dx +∞⎰收敛,与|()|af x dx +∞⎰收敛,2()af x dx +∞⎰收敛的关系?答:1)因为绝对收敛⇒收敛,反之不对,条件收敛的例子都是反例,则|()|af x dx +∞⎰收敛()af x dx +∞⎰收敛.2)()af x dx +∞⎰2()af x dx +∞⎰收敛,例1+∞⎰条件收敛,但 21111sin 1cos 21cos 2222xx x dx dx dx dx x x x x+∞+∞+∞+∞-==-⎰⎰⎰⎰,112dx x +∞⎰发散,1cos 22x dx x+∞⎰发散,则21sin x dx x +∞⎰发散. 例 211dx x +∞⎰收敛,但11dx x+∞⎰发散.3)()af x dx +∞⎰收敛2()af x dx +∞收敛,例 ()2441,10,1n n x n n f x n x n n ⎧≤<+⎪⎪=⎨⎪+≤<+⎪⎩,对ε∀,总存在1M >,使当n M >时,都有41221n n nn dx nε+=<⎰. 故但对于()2f x ,例302sin x dx x+∞⎰绝对收敛,即302sin x dx x+∞⎰收敛,因为133301222sin sin sin x x x dx dx dx xxx+∞+∞=+⎰⎰⎰312sin x dx x+∞⎰绝对收敛,即312sin x dx x+∞⎰收敛,而1302sin x dx x⎰,0是暇点,取12p =,则33022sin lim lim 1ppx x x x x x xx++→→==,因为112p =<收敛. 因为213333010sin 1cos 21cos 21cos 2222xx x x dx dx dx dx x x x x +∞+∞+∞---==+⎰⎰⎰⎰,311cos 22xdx x +∞-⎰收敛.1301cos 22x dx x -⎰,0是暇点,取1p = ,则23300141cos 22lim lim 122p p x x xx x x x x++→→-==, 因为1p =,则发散.例 211dx x +∞⎰收敛,但11dx x+∞⎰发散.3.()baf x dx ⎰(a 为瑕点)收敛,与|()|baf x dx ⎰收敛 ,2()baf x dx ⎰收敛的关系?答:1)|()|baf x dx ⎰收敛()baf x dx ⎰收敛.因为绝对收敛⇒收敛,反之不对,条件收敛的例子都是反例. 2)()baf x dx ⎰收敛2()baf x dx ⇒⎰收敛,()baf x dx ⎰收敛2()baf x dx ⇒⎰收敛.反例1⎰收敛,但101dx x ⎰发散.3)若2()b af x dx ⎰(a 为瑕点)收敛,则|()|baf x dx ⎰(a 为瑕点)收敛.证 因()()212f x f x +≤,则由比较原则,可得|()|b a f x dx ⎰收敛,从而()b a f x dx ⎰收敛.3.下列说法对吗?1)因为sin xx 在0没有定义,则10sin x dx x⎰是瑕积分;2)因为ln 1xx-在1x =没有定义,则1x =是10ln 1x dx x -⎰的暇点.答:若被积函数f 在点a 的近旁是无界的,这时点a 称为f 的瑕点. 1)错误,因为0sin lim 1x x x +→=,则sin xx 在0的近旁有界,因此不是瑕点,10sin x dx x⎰是定积分.若()x f 在(]b a ,上连续,()A x f ax =+→lim (常数),则()⎰badx x f 可看成正常积分,事实上,定义()()(]⎩⎨⎧∈==.,,,,b a x x f a x A x F 知()x F 在[]b a ,上连续,即()⎰b adx x F 存在,而()()()⎰⎰⎰-→-→++==ba ba badx x F dx x f dx x f εεεε0lim lim ,由于()x F 在[]b a ,上连续,知变下限函数()()⎰-=ba dx x F G εε在[]ab -,0上连续,有()()()⎰==+→badx x F G G 0lim 0εε,即()().⎰⎰=babadx x F dx x f 故()⎰badx x f 可看成正常积分。
Chapter11-反常积分

分),称 a 为瑕点。记作ab f ( x)dx .
b
b
b
f ( x)dx lim f ( x)dx lim f ( x)dx
a
ua u
0 a
当极限存在时,称反常积分收敛;当极限不存在
时,称反常积分发散.
数学分析
12
北方工业大学数学系
uc a
va v
如果 c a
f
(
x
)dx
和 b c
f
( x)dx 都收敛,就称反常积分
b
a
f
(
x
)dx
收敛;否则,就称发散.
数学分析
13
(4)如果a,b都是瑕点,则定义
北方工业大学数学系
b
a
f
( x)dx
c
a
f
( x)dx
b
c
f
( x)dx ,
c为(a,b)内任一实数。
当且仅当右端两个积分都收敛时,才称左端 瑕积分收敛。
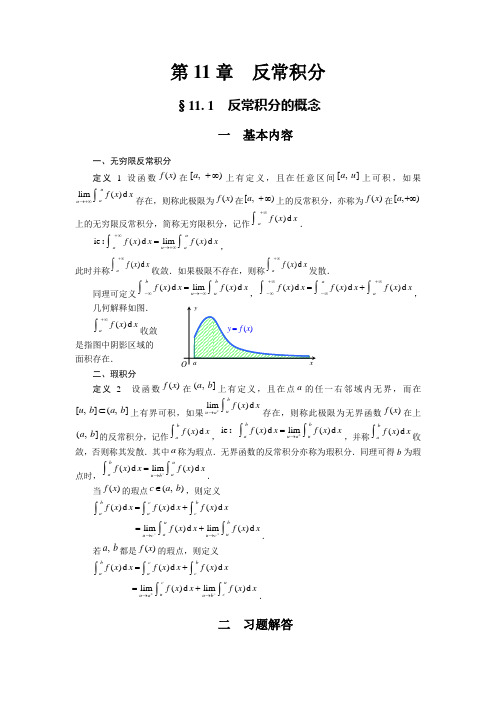
解 设地球半径为R,火箭质量为m,地面上的重力
加速度为g。 按万有引力定律,
在距地心
x(
R)
处火箭所受的引力为
F
mgR 2 x2
.
火箭从地面上升到距离地心为 r( R)
处需作的功为
r
r R
mgR x2
2
dx
mgR
2
1 R
1 r
.
x R
o
数学分析
2
北方工业大学数学系
当r
时,
r R
mgR x2
2
a b a b b
第十一章 反常积分

[
]
=
p 1 +¥ - 2 k p e + 1 - ( 2 k +1 ) p - ( 2 k + 2 ) p e + 2 e + e = . å p 2 k = 0 2 ( e - 1 )
[
]
(3)此为瑕积分,瑕点为 0。令 x = 2t ,化为
x 0
p
+ u ®0 u
亦收敛。而这与 ò f ( x ) dx 为条件收敛的假设相矛盾,所以这两个无穷积分都是发散的,且
ò [ f ( x ) + f ( x ) ]dx = +¥ = ò [ f ( x ) - f ( x ) ]dx ,
a a
+¥
+¥
意即它们都是无穷大量。 (2)这里是要证明(1)中两个正无穷大量是等价无穷大量。为此考察
p
1 n 2 . 2
设 ò f ( x ) dx 为条件收敛。证明:
a +¥ a
(1) ò 都为发散;
[ f ( x ) + f ( x ) ]dx 与 ò [ f ( x ) - f ( x ) ]dx
a
+¥
ò [ f ( t ) + f ( t ) ]dt = 1 . (2) lim ò [ f ( t ) - f ( t ) ]dt
( 2 k + 2 ) p
( 2 k +1 ) p
- x e sin xdx ö ÷ ø
( 2 k + 2 ) p 1 +¥ - x k p - x e (sin x + cos x ) 2 ) å ( 2 k +1 ) p + e (sin x + cos x ( 2 k +1 ) p 2 k = 0
第11章反常积分答案

第十一章 反常积分一、单选题(每题2分)1、广义积分dxx x ⎰∞+-1211=( )A 、0B 、2πC 、4πD 、发散2、广义积分dx x x ⎰∞+-+2221=( ) A 、4ln B 、0 C 、4ln 31 D 、发散3、广义积分⎰+-20234x x dx =( )A 、3ln 1-B 、32ln 21 C 、3ln D 、发散 4、下列广义积分收敛的是( )A 、⎰∞+edx x xln B 、⎰∞+e x x dx ln C 、⎰∞+e x x dx 2)(ln D 、⎰∞+ex x dx21)(ln~5、下列广义积分发散的是( )A 、⎰∞-0dxe xB 、⎰π2cos x dx C 、⎰-202x dx D 、⎰∞+-0dx e x6、下列积分中( )是收敛的A 、⎰∞+∞-xdx sin B 、⎰-222sin ππx dx C 、⎰∞+0dx e xD 、⎰-101x dx 7、下列广义积分发散的是( )A 、⎰-11sin x dx B 、⎰--1121x dx C 、⎰∞+-02dx xe x D 、⎰∞+22)(ln x x dx8、⎰=-10121dx e x x( )A 、e 1B 、11-eC 、e 1-D 、∞9、已知2sin 0π=⎰∞+dx x x ,则=⎰∞+dx x x x 0cos sin ( )A 、0B 、4πC 、 2πD 、π》10、广义积分=+⎰∞+∞-dx x 211( )A 、0B 、2πC 、2π-D 、π11、下列积分中绝对收敛的是( )A 、dx x x ⎰∞+12sin B 、dx x x ⎰∞+1sin C 、dx x ⎰∞+12sin D 、dx x x ⎰∞+14sin12、已知广义积分dxx ⎰∞+∞-sin ,则下列答案中正确的是( )A 、因为()x f 在()+∞∞-,上是奇函数,所以0sin =⎰∞+∞-dx x B 、dx x ⎰∞+∞-sin =()()()[]0cos cos cos =∞--∞+-=∞-∞+-xC 、dx x ⎰∞+∞-sin =()0cos cos lim sin lim =+-=⎰-+∞→+∞→b b xdx bbb bD 、dxx ⎰∞+∞-sin 发散13、设广义积分dxe kb ⎰∞+-0收敛,则k ( )^A 、0≥B 、0>C 、0<D 、0=答案:BCDCB DAABD ADB二、判断题(每题2分)1、当10<<λ时,无穷积分dx x x⎰∞+1cos λ条件收敛; ( )2、当10<<λ时,无穷积分dx x x⎰∞+1sin λ绝对收敛; ( )3、若无穷积分()⎰∞+adxx f 收敛,而函数()x ϕ在[)+∞,a 单调有界, 则无穷积分()()⎰∞+adxx x f ϕ收敛; ( )4、若()⎰∞+adxx f 收敛,则()0lim =+∞→x f x ; ( )/5、若()x f 在[)+∞,a 无界,则()⎰∞+a dx x f 发散; ( )6、若()x f x +∞→lim 不存在,则()⎰∞+adxx f 发散; ( )7、若()x f 单调,()⎰∞+adxx f 收敛,则()0lim =+∞→x f x ; ( )8、若()⎰∞+adxx f 收敛,则()⎰∞+adxx f 2收敛; ( )9、若()⎰∞+adxx f 2,()⎰∞+adxx g 2收敛,则()()⎰∞+adxx g x f 收敛; ( )10、如果()⎰∞+adxx f 收敛,()x g 在[)+∞,a 上有界,则()()⎰∞+a dx x g x f 收敛;( )11、若()⎰∞+adxx f 收敛,()0lim =+∞→x f x ,则()⎰∞+adxx f 2收敛; ( )12、如果()⎰∞+adxx f 绝对收敛,()1lim =+∞→x g x ,则()()⎰∞+adxx g x f 收敛;( )答案:××× ××× ×、三、填空题(每题2分) 1、若无穷积分()⎰∞+a dx x f 收敛,则()=⎰∞++∞→dx x f pp lim;2、若无穷积分()⎰∞+adxx f 收敛,则a b >时,无穷积分()⎰∞+bdxx f ;3、设(]b a x ,∈∀,函数()0≥x f ,a 是其瑕点,且极限())0()(lim +∞≤≤=-+→d d x f a x ax λ,若+∞≤<≥d 0,1λ,则瑕积分()⎰ba dx x f ;4、设[)+∞∈∀,a x ,函数()0≥x f ,0>a ,且极限())0(lim +∞≤≤=+→d d x f x a x λ, 若+∞<≤>d 0,1λ,则无穷积分()⎰∞+a dx x f ;5、若()⎰∞+adxx f 收敛,则无穷积分()⎰∞+adxx f ;6、当1>λ时,无穷积分dx x x⎰∞+1cos λ ;7、当1≥p 时,瑕积分⎰10px dx ;'8、若()⎰∞+adxx f 收敛,且存在极限()Ax f x =+∞→lim ,则=A ;9、=+⎰∞+12)1(x x dx ;=⎰∞+e x x dx 2ln ;10、设⎰∞-∞→=⎪⎭⎫ ⎝⎛+at axx dtte x x 1lim ,则常数=a ;11、如果广义积分dxx p ⎰∞++11收敛,则p ;12、如果广义积分dxx p ⎰-11发散,则p ;答案:1、0 2、收敛 3、发散 4、收敛 5、绝对收敛 6、绝对收敛7、发散 8、0 9、2ln 21;1 10、2 11、2-< 12、2≥四、计算题(每题5分) | 1、⎰∞+++0284x x dx解:⎰∞+++0284x x dx =)022arctan 21(lim 4)2(lim 02u x x dx u u u +=+++∞→+∞→⎰=8)42(21)422(arctan 21lim ππππ=-=-++∞→u u 2、dxx x 1sin 122⎰∞+π解:设x t 1=,则dt t dx 21-=,有dx x x 1sin 122⎰∞+π=120cos sin 02==-⎰ππt tdt 3、⎰∞+-+222x x dx解:⎰∞+-+222x x dx =221ln 31lim )2111(31lim 2u x x dx x x u u u ⎪⎭⎫ ⎝⎛+-=+--+∞→+∞→⎰ =2ln 32)2ln 221ln lim (31=-+-+∞←u u u4、⎰1ln xdx,解:⎰1ln xdx =()1)ln 1(lim 1ln lim ln lim 0100-=+--=-=+++→→→⎰εεεεεεεεx x x xdx5、⎰--1121x dx解:⎰--1121x dx=⎰⎰-→+-→-+-++εεεε10200121lim 1lim x dxx dx =)01arcsin 10(arcsin lim 0εεε-++-+→x x))1arcsin()1arcsin((lim 0εεε-++--=+→=πππ=+226、()⎰--112x x dx 解:因为()C x C t t dtt x xx dx+--=+-=+-=---⎰⎰1arctan 2arctan 2121122所以()⎰--1012x x dx=01)1arctan 2(lim 1)2(lim 010εεεε---=--++→-→⎰x xx dx=2)4arctan lim (20ππεε=--+→7、⎰∞+++04211dx x x-解:由 Cx x x x xx d dx x x x dx x x +-=+--=++=++⎰⎰⎰21arctan 212)1()1(111112222342得 ⎰∞+++04211dx x x =221arctan 21lim 11lim 20420πεεεε=-=++⎰++→+∞→→+∞→u x x dx x x u u u8、())0(ln >⎰∞+a x x dxa p解:1=p 时,+∞===+∞→∞++∞→⎰⎰a u x x x d x x dxu u a au ln ln lim ln ln lim ln1≠p 时,()()a u x p x xd x x dxpu uapu a p-+∞→+∞→∞+-==⎰⎰1)(ln 11limln ln limln=⎪⎩⎪⎨⎧<∞>--11)(ln 111p p a p p故当1>p 时,()⎰∞+a px x dx ln =()pa p --1ln 111≤p 时,()⎰∞+apx x dxln 发散;9、⎰2)ln(sin πdxx解:=I ⎰20)ln(sin πdx x =⎰+→20sin ln lim πεxdx ⎰+→=422sin ln lim 2πεεtdt t x、=⎰+++→42)cos ln sin ln 2(ln lim 2πεεdtt t=⎰⎰++⋅404cos ln 2sin ln 242ln 2πππtdttdt=⎰⎰+=++404022ln 2cos ln 2sin ln 22ln 2ππππIxdx xdx由此求得 2ln 2π-=I10、⎰∞+-∈=0)(N n dx e x I x n n解:当0=n 时,⎰∞+-==001dx e I x当1≥n 时,dx x e n ux e dx x e I un x u nx u un x u n ⎰⎰--+∞→-+∞→-+∞→+-==010lim 0)(lim lim=⎰---+∞→=u n n x u nI dx x e n 011lim则 !12)1(0n I n n I n =⋅⋅-= 五、证明题(每题5分) ~ 1、证明01ln 02=+⎰∞+dx x x证:令t x 1=,则 ⎰⎰⎰∞-∞+∞++-=⎪⎭⎫ ⎝⎛⋅+=+00222021ln 1111ln1ln dt t t dt t t t dx x x =⎰∞++-021ln dxx x则有 01ln 02=+⎰∞+dx x x2、证明dx x x⎰∞++01cos 收敛,且11cos 0≤+⎰∞+dx x x证:dx x x ⎰∞++01cos =dxx x x x ⎰∞+++∞++02)1(sin 01sin =dxx x⎰∞++02)1(sin又()22111sin x x x+≤+)(,而dxx ⎰∞++02)1(1收敛,所以dx x x ⎰∞++02)1(sin 收敛⇒dxx x ⎰∞++01cos 收敛而≤+=+⎰⎰∞+∞+02)1(sin 1cos dx x xdx xx1011)1(102=∞++-=+⎰∞+x dx x3、证明:若()x f 在()+∞∞-,上连续,且()⎰∞+∞-dx x f 收敛,则对任何()+∞∞-∈,x ,有()()⎰∞-=x x f dt t f dx d , ()()⎰∞+-=x x f dt t f dx d ,证:,a ∀由条件()1J dx x f =⎰∞-,()⎰∞+=02J dx x f 都存在;再由()x f 连续可得…()()()⎰⎰∞-=⎪⎭⎫ ⎝⎛+=x x a x f dt t f J dx d dt t f dx d ,1()()()⎰⎰∞+-=⎪⎭⎫ ⎝⎛+=x a x x f J dt t f dx d dt t f dx d ,24、 设()⎰∞+adxx f 收敛,证明:(1)若极限()x f x +∞→lim 存在,则()0lim =+∞→x f x(2)若()x f 在[)∞+a 上为单调函数,则()0lim =+∞→x f x证:(1)设()Ax f x =+∞→lim 。
第十一章 反常积分

定义中C为瑕点,以上积分称为瑕积分.
例5 计算广义积分 0 解
a
dx a2 x2
(a 0).
lim
xa 0
1 , 2 2 a x
x a 为被积函数的无穷间断点.
0
a
a dx lim 0 2 2 0 a x
a
dx a2 x2
x a . lim arcsin lim arcsin 0 0 a 0 0 a 2
(注意:不能忽略内部的瑕点)
a f ( x )dx a f ( x )dx c
b
c
b
f ( x )dx
思考题
积分 0
1
ln x dx 的瑕点是哪几点? x 1
思考题解答
积分 0
1
ln x dx 可能的瑕点是 x 0, x 1
x 1
ln x 1 lim 1, lim x 1 x x 1 x 1 0
b b
a
f ( x )dx lim a f ( x )dx
当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散.
类似地,设函数 f ( x ) 在区间( , b ] 上连续,取
a b ,如果极限 lim
b
f ( x )dx 存在,则称此极 a a
0
.
故原广义积分发散.
例8 计算广义积分 0
3
dx ( x 1)
3 1
2 3
. dx
x 1瑕点
2 3
解
0
1
3
dx ( x 1) dx
2 3 2 3
( )
数学分析(华东师大)第十一章反常积分,DOC

第十一章反常积分§1反常积分概念一问题提出在讨论定积分时有两个最基本的限制:积分区间的有穷性和被积函数的有界性.但在很多实际问题中往往需要突破这些限制,考虑无穷区间上的“积分”,或是无界函数的“积分”,这便是本章的主题.例1(第二宇宙速度问题)在地球表面垂直发射火箭(图11-1),要使火箭克服地球引力无限远离地球,试问初速度v0至少要多大?设地球半径为R,火箭质量为m,地面上的重力加速度为g.仅供个人学习参考r mgR ∫∫2∫d x= mgR21-1 .Rx2R r当r →+∞时,其极限mgR 就是火箭无限远离地球需作的功.我们很自然地会把这极限写作上限为+∞的“积分”:图11-1+∞mgR2d x= limrmgR2Rx2r →+∞Rd x= mgR.x2最后,由机械能守恒定律可求得初速度v 0至少应使122mv 0= mgR.用g =9.81(m 6s /2),R =6.371×106(m )代入,便得例211-2).2∫ ∫ ∫ §1反常积分概念265从物理学知道,在不计摩擦力的情形下,当桶内水位高度为(h -x)时,水从孔中流出的流速(单位时间内流过单位截面积的流量)为 v=2g(h- x),其中g 为重力加速度. 设在很小一段时间d t 内,桶中液面降低的微小量为d x,它们之间应满足πR 2d x=v πr 2d t, 图11-2由此则有t=Rd 2.上可积.(1)+∞J=f(x )d x,(1′)a+∞ +∞ 并称 f(x)d x 收敛.如果极限(1)不存在,为方便起见,亦称f(x)d xaa发散.类似地,可定义f 在(-∞,b]上的无穷积分:bb∫∫ ∫ ∫∫266第十一章反常积分∫f(x)d x=lim∫f(x )d x.(2)-∞u →-∞u对于f 在(-∞,+∞)上的无穷积分,它用前面两种无穷积分来定义:+∞af(x)d x=-∞-∞+∞ f(x)d x+af(x)d x, (3)其中a 为任一实数,当且仅当右边两个无穷积分都收敛时它才是收敛的.注1无穷积分(3)的收敛性与收敛时的值,都和实数a 的选取无关.注2由于无穷积分(3)是由(1)、(2)两类无穷积分来定义的,因此,f 在任何有限区间[v,u]ì(-∞,+∞)上,首先必须是可积的.+∞注3af(x)d x 收敛的几何意义是:若f 在[a,+线轴之间那一块向右无限延伸的 图11-31∫) +∞ d x 2 x(ln x)p ; 2) +∞d x-∞1+x 2.解1)由于无穷积分是通过变限定积分的极限来定义的,因此有关定积分的换元积分法和图11-4a∫∫§1反常积分概念267分部积分法一般都可引用到无穷积分中来.对于本例来说,就有∫+∞d x+∞d t2x(ln x)p =∫ln2tp.从例3知道,该无穷积分当p >1时收敛,当p ≤1时发散.2)任取实数a,讨论如下两个无穷积分:∫d x+∞d x -∞1+x2和∫a由于a1+x2.lim∫d x = lim (arctan a-arctan u)u →-∞ u1+x 2v u →-∞=arctan a+π,2注定义[u,b]ì(5)(5′)bf(x)a 而无 b界函数反常积分 f(x)d x 又称为瑕积分.a类似地,可定义瑕点为b 时的瑕积分:bu∫f(x)d x=lim∫f(x)d x.au →b-a其中f 在[a,b)有定义,在点b 的任一左邻域内无界,但在任何[a,u]ì[a,b)1 1 x 268 第十一章反常积分上可积.若f 的瑕点c ∈(a,b),则定义瑕积分b c b∫f(x )d x=∫f(x )d x+∫f(x)d xaacub=lim ∫f(x )d x+lim ∫f(x )d x.(6)u →c-av →c+v其中f 在[a,c)∪(c,b]上有定义,在点c 的任一领域内无界,但在任何[a,u]ì[a,c)和[v,b]ì(c,b]上都可积.当且仅当(6)式右边两个瑕积分都收敛时,左边的瑕积分才是收敛的.又若a 、b 两点都是f 的瑕点,而f 在任何[u,v]ì(a,b)上可积,这时定义瑕积分b c b∫f(x)d x=∫f(x)d x+∫f(x )d x(7)其中c ,上可积例6(8)故当0<q <1时,瑕积分(8)收敛,且∫d x ∫d x 1q = lim 0 u →0+u x q=1- q ;∫∫§1反常积分概念269而当q ≥1时,瑕积分(8)发散于+∞.上述结论在图11-4中同样能获得直观的反映. 如果把例3与例6联系起来,考察反常积分 +∞我们定义d xx p (p>0). (9)∫+∞d x 1d x+∞d x 0xp=∫0x p+∫1xp,它当且仅当右边的瑕积分和无穷积分都收敛时才收敛.但由例3与例6的结果可知,这两个反常积分不能同时收敛,故反常积分(9)对任何实数p 都是发散的.习题1.讨论下列无穷积分是否收敛?若收敛,则求其值:+∞2.3.4.举例说明: f(x)d x 收敛且f 在[a,+∞)上连续时,不一定有limax →+∞f(x)=0.+∞5.证明:若af(x)d x 收敛,且存在极限lim x →+∞f(x)=A,则A=0.∫ ∫∫ ∫∫ ∫ ∫ ∫ 270第十一章反常积分+∞6.证明:若f 在[a,+∞)上可导,且a+∞f(x)d x 与 af ′(x )d x 都收敛,则lim x →+∞f(x)=0.§2无穷积分的性质与收敛判别一无穷积分的性质+∞由定义知道,无穷积分auf(x)d x 收敛与否,取决于函数F(u) =f(x)d x 在u →+∞时是否存在极限.因此可由函数极限的柯西准则导出无穷 a积分收敛的柯西准则.+∞定理11.1无穷积分af(x)d x 收敛的充要条件是:任给ε>0,存在G此外,+∞ [k a(1)性质d x 与+∞ b(2)另一充要条件:任给ε>0,存在G ≥a,当u> G 时,总有 +∞f(x)d x<ε.u∫ ∫ ∫ ∫∫ ∫ ∫ §2无穷积分的性质与收敛判别271事实上,这可由+∞u +∞∫f(x)d x=∫f(x)d x+∫f(x)d xaau结合无穷积分的收敛定义而得.+∞性质3若f 在任何有限区间[a,u ]上可积,且有a+∞f(x)d x 亦必收敛,并有a|f(x)|d x 收敛,则+∞+∞f(x)d x≤aa+∞f(x) d x. (3)证由≥a,当u等式(u +∞由于 |f(x)|d x 关于上限u 是单调递增的,因此aa|f(x)|d x 收敛的u 充要条件是 a| f(x)|d x 存在上界.根据这一分析,便立即导出下述比较判别法(请读者自己写出证明):定理11.2(比较法则)设定义在[a,+∞)上的两个函数f 和g 都在任何∫ ∫ ∫ ∫∫∫∫272 第十一章反常积分有限区间[a,u]上可积,且满足f(x)≤g(x),x ∈[a,+∞),+∞+∞ 则当 g(x )d x 收敛时aa+∞ +∞|f(x)|d x 必收敛(或者,当 a|f(x)|d x 发散时,ag(x)d x 必发散).+∞例1讨论sin xd x 的收敛性. 1+x 2+∞解由于sin x1d x π1+x2≤1+x 2,x ∈[0,+∞),以及∫1+x 2=为收敛2(§1sin xd x 为绝对收敛. =c,则有:(i i .则有:.xp a推论3设f 定义于[a,+∞),在任何有限区间[a,u]上可积,且则有: lim x →+∞x pf(x) =λ.+∞(i)当p >1,0≤λ<+∞时, f(x)d x 收敛;a+∞(ii)当p ≤1,0<λ≤+∞时,af(x)d x 发散.+∞∫∫∫1§2无穷积分的性质与收敛判别273例2讨论下列无穷限积分的收敛性:1∫)+∞x αe -xd x;2)1+∞x 2d x. 0x 5+1解本例中两个被积函数都是非负的,故收敛与绝对收敛是同一回事.1)由于对任何实数α都有limx →+∞x 2·x αe -x= lim x →+∞ x α+2ex=0,因此根据上述推论3(p =2,λ=0),推知1)对任何实数α都是收敛的.2)由于12limx →+∞x 2·x x 5+1=1,, g(x)limx →+∞又因u 2>u 1 11于是有uξuf(x)g(x)d x ≤g(u 1)·uuf(x)d x+ g(u 2)·∫ f(x)d x11ξξ u=g(u 1)·∫f(x )d x ∫-f(x)d xaa22u∫∫ ∫ ∫∫∫∫ ∫274第十一章反常积分2+ g(u 2)·ξf(x)d x-∫f(x)d xε4M ·2M+ +∞ aaε4M·2M=ε.根据柯西准则,证得af(x)g(x)d x 收敛.+∞定理11.4(阿贝尔(Abel)判别法)若 af(x)d x 收敛,g(x)在[a,+∞)+∞上单调有界,则a f(x)g(x)d x 收敛.这定理同样可用积分第二中值定理来证明,但又可利用狄利克雷判别法更方便地获得证明(留作习题).:+而1 u∫1cos2x 1 其中12xd x=2 2 cos ttd t 满足狄利克雷判别条件,是收敛的,而+∞d x12x是发散的,因此当0<p ≤1时该无穷积分不是绝对收敛的.所以它是条 件收敛的.例4证明下列无穷积分都是条件收敛的:<∫∫ ∫∫ ∫ ∫∫ ∫∫+∞ §2无穷积分的性质与收敛判别275+∞sin x 2d x,1+∞cos x 2d x,1+∞x sin x 4d x.1证前两个无穷积分经换元t =x 2得到+∞+∞sin x 2d x=1 1+∞ +∞ cos x 2d x= 11sin t d t, 2 tcos t d t.2 t由例3已知它们是条件收敛的.对于第三个无穷积分,经换元t =x 2而得∫x sin x 4d x=1+∞sin t 2d t,,甚至是无界的,1.2.+∞若a收敛.3.g(x).(1(4.(5∫)ln (1+x)d x;(6)11+x +∞x md x(n 、m ≥0).1xn0 1+xn5.讨论下列无穷积分为绝对收敛还是条件收敛:(1∫)sin xd x;(2)1x+∞sgn(sin x)d x;1+x2+∞+∞∫ ∫∫∫∫∫276第十一章反常积分(3∫)x cos xd x; (4)100+xln(ln x)sin x d x.eln x6.举例说明∫:+∞+∞ +∞f(x)d x 收敛时aaf 2(x )d x 不一定收敛∫; +∞ f(x)d x 绝对收敛时,af 2(x)d x 也不一定收敛. a+∞ +∞7.证明:若af(x)d x 绝对收敛,且lim x →+∞f(x)=0,则a+∞f 2(x)d x 必定收敛.8.证明:若f 是[a,+∞)上的单调函数,且 af(x)d x 收敛,则lim x →+∞f(x)=0,且f(x)=o 1x,x →+∞.+∞9.10,存在δ>性质b∫f 1(x )a敛,(1)性质b c∫f(x)d x 与∫f(x)d x 同敛态,并有aab c b∫f(x)d x=∫f(x )d x+∫f(x)d x,(2)aacb其中 f(x)d x 为定积分.c+∞+∞∫∫∫∫(x- a)p ∫§3瑕积分的性质与收敛判别277性质3设函数f的瑕点为x=a,f在(a,b]的任一内闭区间[u,b]上可b积.则当af(x) d x收敛时∫,b bf(x)d x也必定收敛,并有ab∫f(x)d x ≤∫f(x) d x. (3)a ab b同样地,当a f(x) d x收敛时,称f(x)d x为绝对收敛.又称收敛而不绝a对收敛的瑕积分是条件收敛的.判别瑕积分绝对收敛的比较法则及其推论如下:定理11.6(比较法则)设定义在(a,b]上的两个函数f与g,瑕点同为x=a,在任何[u,b]ì(a,b]上都可积,且满足则当, bg(x)a((成为则有:(ii)当f(x) ≥1,且p≥1时,af(x) d x发散.推论3设f定义于(a,b],a为其瑕点,且在任何[u,b]ì(a,b]上可积. 如果则有: limx→a +(x- a)p f(x) =λ,∫ ∫x278第十一章反常积分b(i )当0<p <1,0≤λ<+∞时af(x)d x 收敛;b(ii)当p ≥1,0<λ≤+∞时a例1判别下列瑕积分的收敛性:f(x)d x 发散.1∫) ln x d x ;2∫)0 x2x1ln xd x.解本例两个瑕积分的被积函数在各自的积分区间上分别保持同号———ln x在(0,1]上恒为负, x 在(1,2]上恒为正———所以它们的瑕积分收敛与绝xln x2(i)x →0+x1-α· 1+x =1,根据定理11.6推论3,当0<p =1-α<1,即α>0且λ=1时,瑕积分I(α)收1∫ §3瑕积分的性质与收敛判别279敛;当p =1-α≥1,即α≤0且λ=1时,I(α)发散.(ii)再讨论J(α),它是无穷积分.由于α-1lim x →+∞ x 2-α·x1+x= lim x →+∞ x 1+x =1,根据定理11.2推论3,当p =2-α>1,即α<1且λ=1时,J(α)收敛;而当p =2-α≤1,即α≥1且λ=1时,J(α)发散.1.2.3.4.5.x)d x=π62/6.(1∫) =-πln20 2(2∫)θsin θd θ=2πln2. 01-cos θπ1∫2∫ 280 第十一章反常积分总练习题1.证明下列等式:1 p-1 +∞-p (1∫) x d x=∫x d x,p>0;0x+1 1 x+1+∞ p-1 +∞-p (2∫) x d x=∫xd x,0<p<1.0 x+1 0 x+12.证明下列不等式:(1)π<∫d x <π;22 (2)1 20 1-1 e 1-x 4 +∞ < 0 2 e -x d x<1+1. 2e3.计算下列反常积分的值:4.5.(2)若6.(也收敛.(2+∞ a●。
分析方法 第十一章 反常积分
b
c
b
当且仅当 f ( x)dx与 f ( x)dx同时收敛时, 称 f ( x)dx收敛, 且其值
a c a
c
a
b
c
b
f ( x)dx f ( x)dx f ( x)dx
若a, b都是f的瑕点, 并且f在任何u, v a, b上可积, 可任取c a, b,
u
f ( x)dx I , 则称极限值I为函数f ( x)在[a,)上的无
a
u
u
f ( x)dx lim f ( x)dx I .
a u a
也称无穷积分 f ( x)dx收敛.
a
u
反之, 若 lim
u
f ( x)dx不存在, 称无穷积分 f ( x)dx发散.
1 a
, 并且它们收敛时, 有 与 f ( x)dx 同敛态即同时收敛或发散
a, u 上可积, 则对b : a b, f ( x)dx 性质2 若函数f ( x)在任何有限区间
a
b
f ( x)dx f ( x)dx f ( x)dx.
a a b
0 0
dx dx dx ,积分收敛 . 2 2 2 1 x 1 x 1 x 0
0
定义2 设函数f ( x)定义在区间 (a, b]上, 且在点a的任意右邻域无界 ,
u, b (a, b], f ( x)在u, b上可积, 若存在极限 称a为函数f ( x)的瑕点, 并对任何
u
由例3知,当p 1时无穷积分收敛 ,当p 1时发散.
dx dx (2) lim lim arctan u , 2 2 u u 1 x 1 x 2 0 0 dx dx lim lim arctan u . 2 2 u u 1 x 1 x 2 u
反常积分

第十一章 反常积分一、内容简介本章主要介绍无穷积分与无界函数反常积分的概念、计算及其绝对收敛和条件收敛性的判别。
本章是常义积分理论的扩展,也是含参变量积分理论的基础,其中关于含参数反常积分的收敛性的判别相当繁琐,做习题的难度较大.二、学习要求 (1)了解无界函数反常积分的收敛性判别法以及绝对可积和平方可积的概念;(2)正确理解无穷积分与无界函数反常积分的收敛性; (3)掌握无穷积分收敛性的比较判别法和A-D 判别法 三、学习的重点和难点重点:反常积分收敛性的比较判别法和A-D 判别法 难点:含参数反常积分的条件收敛性的判别§1 概念及计算一 概念 例:002222200lim lim 11111B A A B dx dx dx dx dx x x x x x +∞+∞-∞-∞→-∞→+∞=+=++++++⎰⎰⎰⎰⎰ lim [arctan ]lim [arctan ]()22A B A B πππ→-∞→+∞=-+=--+=. 例:222R hR hh RRmgRmgR mghRW dr r r R h++⎡⎤==-=⎢⎥+⎣⎦⎰lim h h W W mgR ∞→∞==220212RmgR W dr mv r ∞∞=≥⎰初始动能(机械能守恒). 反常积分:()af x dx +∞⎰积分区间无限或函数无界.定义1:设()f x 在[,)a +∞有定义,且在任意区间[,][,)a A a ⊂+∞上可积,若极限lim()Aax f x dx →+∞⎰存在,则称()af x dx +∞⎰收敛,否则,称发散.称该极限为()f x 的反常积分(无穷积分).值记为()aI f x dx +∞=⎰.例:11()p dx p x+∞∈⎰解:1p ≠时,111111111111lim lim lim 11Ap A pp p A A A p p A dx dx x p x x p pp -+∞-→+∞→+∞→+∞⎧>⎪-⎪-⎪====+∞⎨--⎪+∞⎪⎪⎩⎰⎰ <1 =1. 1p =时,11ln Adx A x=⎰. ()f x dx +∞-∞⎰收敛⇔0()f x dx +∞⎰,0()f x dx -∞⎰均收敛.定义2:设()f x 在(,]a b 上无界,但在区间[,](,]a b a b ε+⊂上有界且可积,若极限0lim ()ba f x dx εε+→⎰存在,则称该极限为()f x 的反常积分(瑕积分),称反常积分()baf x dx ⎰收敛,否则称发散.例:112201111()()p p dx p dt dt x t t+∞-+∞∈→-=-⎰⎰⎰ 11111111111ln ln 1pp p xp p pdx x x p εεεεε--⎧-=≠⎪⎪--=⎨⎪==⎪⎩⎰ , 110011111lim 1p p p p dx dx x x p εε→⎧<⎪-∴==⎨⎪+∞≥⎩⎰⎰ . ()f x 的瑕点为0[,]x a b ∈,则()baf x dx ⎰收敛⇔0()x af x dx ⎰与0()bx f x dx ⎰收敛.二 Cauchy 主值 定义3:若极限lim ()AAA f x dx -→+∞⎰存在,则称该极限为的反常积分()f x dx +∞-∞⎰的Cauchy主值.记为()cpvf x dx +∞-∞⎰.例:101110111dx dx dx x x x --=+⎰⎰⎰ 发散 110011lim lim dx dx x x ηηηη'-'-→→=+⎰⎰11111100111lim()lim()0cpv dx dx dx x x x ηηηηηη---→→=+=-+=⎰⎰⎰⎰⎰.()f x dx +∞-∞⎰发散 ()lim()0AAA cpv f x dx f x dx +∞-∞-→+∞==⎰⎰.若()f x 为奇函数,则 ()0aacpv f x dx +-=⎰()0cpv f x dx +∞-∞=⎰.例:概率密度函数()f x :()1f x dx +∞-∞=⎰证:0()cxx g x ce x -⎧=⎨⎩ <0>0 为概率.例:tan 220001cos 1sec x tdt tdt t ππ=+∞===⎰⎰⎰.三 计算 注:(1)无穷积分的计算可与常义积分同法(2)瑕积分的计算:奇点为边界点时可以按常义积分法计算:奇点为内点时不可. 例:222222cos (1sin )ln 1sin ln 21sin 1sin xd x dx xx x ππππππ+==+=-++⎰⎰ (⨯)32223222cos (1sin )(1sin )1sin 1sin 1sin x d x d x dx x x x ππππππ++=++++⎰⎰⎰ 发散. 四 性质线性性,保序性,区间可加性成立;绝对可积性,乘积可积性不成立. 既为无穷积分又为瑕积分时,()af x dx +∞⎰收敛⇔()bf x dx +∞⎰及()baf x dx ⎰均收敛.例:+∞⎰+∞⎰。
《数学分析》第11章 反常积分ppt课件

f ( x)dx 收敛, 则可得
c g( x)dx
收敛,从而
a
a2
a g( x)dx 收敛.反之,若 a g( x) dx 收敛, 可得
3c g( x)dx 收敛,从而
f ( x)dx 收敛.
a2
a
(ii)由 lim f ( x) 0, 存在 G a, 使 x G, 有 x g( x) f (x) 1 , g( x)
的积分
R
m gR 2 x2
dx
lim
r
r R
mgR x2
2
dx
mgR.
由机械能守恒定律可求初速度 v0 至少应使
1 2
mv02
mgR.
用 g 9.81(m / s2) , R 6.371 106 (m) 代入,得
v0 2gR 11.2 (km / s).
例2 圆柱形桶的内壁高为 h,内半径为 R,桶底有
ln u,
,q1 q 1,
故当 0 q 1 时,
1 dx 0 xq
lim
u0
1 dx u xq
1
1
; q
当 1 q 时,
1 0
dx xq
发散.
同样, 若 f (x) 的原函数为 F (x), 瑕积分的牛顿-莱
布尼茨公式写作
b a
f
(x)
dx
F(x)
b a
F (b)
F (a
)
F (b) lim F (u). ua
a f ( x) dx 与 b f ( x) dx (b a ),
同时收敛或同时发散,且
f ( x)dx
b f ( x)dx
f ( x)dx.
《数学分析》第十一章反常积分

《数学分析》第十一章反常积分首先,我们来讨论无界函数的积分。
对于一个在区间[a,b)上定义的无界函数f(x),其积分可以表示为:∫f(x)dx = lim(ξ→b-)∫f(x)dx,其中ξ是趋于b的数列。
这种积分的定义方式是将区间[a,b)划分为有限多个子区间并对每个子区间的积分进行求和,然后再取极限。
如果极限存在且有限,则称该反常积分收敛;若极限不存在或为无穷大,则称该反常积分发散。
接下来,我们来讨论无界区间上的积分。
对于一个定义在区间(-∞,a)或(a,∞)上的无界函数f(x),其积分可以表示为:∫f(x)dx = lim(ξ→±∞)∫f(x)dx,其中ξ是趋于±∞的数列。
这种积分的定义方式与上述无界函数的积分类似,即将区间划分为有限多个子区间并对每个子区间的积分进行求和,然后取极限。
同样地,如果极限存在且有限,则该反常积分收敛;若极限不存在或为无穷大,则该反常积分发散。
在讨论反常积分时,还需考虑奇点的分类。
奇点是指函数在一些点上不满足积分条件的情况。
常见的奇点包括无界点、端点以及间断点。
对于无界点,通常情况下我们可以通过取极限的方式来处理;而对于端点,需要分别对两个方向上的积分进行讨论,并判断两个反常积分是否收敛;对于间断点,要分别对间断点左、右两侧的积分进行求和,并判断两个反常积分是否收敛。
在实际应用中,我们常常需要计算一些函数的反常积分,比如Gaussian函数的积分、Beta函数的积分等。
这些积分在数学、物理、工程等领域都有广泛的应用。
在计算这些积分时,我们可以利用换元法、分部积分法等积分技巧来简化计算过程,并帮助判断反常积分的收敛性。
总之,反常积分是对于不满足黎曼积分条件的函数取极限得到的积分。
本章介绍了无界函数的积分、无界区间上的积分以及奇点的分类等内容。
通过学习本章的内容,我们能够更好地理解和应用反常积分的概念和方法。
《数学分析》第十一章反常积分1

《数学分析》第十一章反常积分1《数学分析》第十一章反常积分1第十一章反常积分在数学分析中,我们经常研究的是定义在有界闭区间上的函数的积分,这些函数在有界闭区间上的积分被称为定积分。
但是,在实际应用中,有时会遇到一些函数在一些点上的值没有定义,或者函数在一些有界闭区间上的积分不存在,这就引出了反常积分的概念。
反常积分是对于在有界闭区间上不满足定积分条件的函数进行积分,也可以看作是对定积分的扩充。
反常积分分为无穷积分和广义积分两种类型。
一、无穷积分如果函数f(x)在区间[a,+∞)上定义,而对于任意的x∈[a,+∞),f(x)都是有定义的,那么这样的函数f(x)在[a,+∞)上的积分称为无穷积分。
记作∫[a,+∞) f(x)dx如果函数f(x)在区间(-∞,a]上定义,而对于任意的x∈(-∞,a],f(x)都是有定义的,那么这样的函数f(x)在(-∞,a]上的积分称为无穷积分。
记作∫(-∞,a] f(x)dx在计算无穷积分时,常常使用变量替换或者部分积分等方法。
二、广义积分如果函数f(x)在区间[a,b]上除了其中一点x=c外都是有定义的,而在x=c处f(x)的定义和c的极限存在,那么这样的函数f(x)在[a,b]上的积分称为广义积分。
记作∫[a,b] f(x)dx如果函数f(x)在区间[a,b)上除了其中一点x=b外都是有定义的,而在x=b处f(x)的定义和b的极限存在,那么这样的函数f(x)在[a,b)上的积分称为广义积分。
记作∫[a,b) f(x)dx如果函数f(x)在区间(a,b]上除了其中一点x=a外都是有定义的,而在x=a处f(x)的定义和a的极限存在,那么这样的函数f(x)在(a,b]上的积分称为广义积分。
记作∫(a,b] f(x)dx如果函数f(x)在区间(a,b)上除了其中一点x=a和x=b外都是有定义的,而在x=a和x=b处f(x)的定义和a、b的极限存在,那么这样的函数f(x)在(a,b)上的积分称为广义积分。
《数学分析》第十一章 反常积分

绝对收敛 收敛, ( 证 ) 但反之不确. 绝对型积分与非绝对型积
分.
3. 无穷积分判敛法:
非负函数无穷积分判敛法: 对非负函数,有 F (A) ↗. 非负函数无穷积
分敛散性记法. ⑴ 比较判敛法:
设在区间 [ a , ) 上函数 f (x) 和 g (x) 非负且
下一页
上一页
例 2 从盛满水开始打开小孔,问需多
长 时 间 才能 把 桶里 水 全部 放 完?
解 由物 理 学知 识 知道 ,( 在 不计 摩 擦情
况 下 ), 桶 里水 位 高度 为 h x 时 , 水 从小
孔 里 流 出的 速 度为
xO
O
v 2g(h x)
设在很短一段时间 t 内,桶里水面降低的
ⅰ> p 1, 0 , f < ;
a
ⅱ> p 1, 0 , f .
a
例 5 讨论以下无穷积分的敛散性 :
ⅰ> x ex dx, ( 0);
0
ⅱ>
x 2 dx.
b
a
t
1 bx
f (x)dx
1
f
b
1 t
1 t2
dt ,
ba
3. 把瑕积分化成了无穷积分;
设a
0,
有
t 1 x
g(x)dx
a
0 1
g
1 t
dt t2
1 a
0
g1 t
dt t2
,
a
把无穷积分化成了瑕积分.
可见 , 瑕积分与无穷积分可以互化 . 因此 , 它们有平行的理论和结果 .
例 11 证明
无穷限反常积分几何意义
数学分析》第十一章反常积分复习自测题[1]
![数学分析》第十一章反常积分复习自测题[1]](https://img.taocdn.com/s3/m/cfb6825c0508763231121291.png)
第十一章 反常积分复习自测题一、体会各类反常积分(无穷积分、瑕积分和混合反常积分)的特点,能准确地判定所给反常积分的类型;熟习并熟练掌握各类反常积分收敛和发散的含义,并用各类反常积分收敛和发散的含义解决下面的问题:1、正确地判断下列反常积分的敛散性:(1)1d p ax x +∞⎰(0a >);(2)01d a p x x ⎰(0a >);(3)01d px x +∞⎰(0a >)。
2、正确地判断下列反常积分的敛散性: (1)1d (ln )pax x x +∞⎰(1a >);(2)11d (ln )a p x x x ⎰(1a >);(3)11d (ln )p x x x +∞⎰。
3、探索下列反常积分的敛散性,若收敛,并求其值: (1)201d 1x x +∞+⎰;(2)21d 1x x+∞-∞+⎰;(3)10x ⎰;(4)11x -⎰。
4、用定义据理说明下面的关系:(反常积分的牛顿—莱布尼茨公式、分部积分法、换元法、奇偶函数的积分特征)(1)若函数()f x 在[,)a +∞上连续,()F x 为()f x 在[,)a +∞上的原函数,记()lim ()x F f x →+∞+∞=,则无穷积分()d af x x +∞⎰收敛⇔()lim ()x F f x →+∞+∞=存在,且()d ()af x x F x a+∞+∞=⎰。
(2)若函数()f x 在(,)-∞+∞上连续,()F x 为()f x 在(,)-∞+∞上的原函数,记()lim ()x F f x →+∞+∞=,()lim ()x F f x →-∞-∞=,则无穷积分()d f x x +∞-∞⎰收敛⇔()lim ()x F f x →+∞+∞=和()lim ()x F f x →-∞-∞=都存在,且()d ()af x x F x a+∞+∞=⎰。
(3)若函数()f x 和()g x 都在[,)a +∞上连续可微,且lim ()()x f x g x →+∞存在,则无穷积分()()d af xg x x +∞'⎰收敛⇔()()d af xg x x +∞'⎰收敛,且()()()d ()()()()d aaf xg x x f x g x f x g x x a +∞+∞+∞''=-⎰⎰,其中()()lim ()()x f g f x g x →+∞+∞+∞=。
数学分析第十一章 反常积分

b
lim f (x)dx J
ua u
(5)
则称此极限为无界函数 f 在(a, b]上的反常积分,记作
b
J f (x)dx a
(5' ) .
b
并称反常积分 a f (x)dx 收敛;当极限(5)不存
b
在时,称反常积分 a f (x)dx 发散.
W
lim
r
Wr
lim
r
r mgR 2 dx mgR R x2
自然把上面极限写作上限为的"积分"
RmgR 2 x2源自dxlimr r R
mgR 2 x2
dx
mgR
最后由机械能守恒定律得:
1 2
mv02
mgR
即 v0 2gR 11.2(km/ s)
例2:圆柱形桶的内壁高为h , 内半径为 R ,桶底 有一半径为 r 的小孔。试问从盛满水开始打开小孔直 至流完桶中的水,共需多少时间?
u u
3)对 f 在 (,) 上的无穷积分,可定义为:
a
f (x)dx f (x)dx f (x)dx (3)
a
当且仅当右边两个无穷积分都收敛时才收敛。
注 1 (3)的收敛性与 a 的选取无关。
注 2 对(3)需 f 在任何[u,u]上可积。
注 3 a f (x)dx 的几何意义:介于曲线 y f (x), 直线
b
注 2 求(判断敛散性)瑕积分 a f (x)dx (b 为瑕点)
步骤;
u
(1) 求G(u) a f (x)dx ;
(2)
设地球半径为R,火箭质量为m, 初速度为v0,地面上的 重力加速度为g.则火箭在距地心x ( R)处所受的引力为
反常积分-的审敛法
第11章 反常积分§11. 1 反常积分的概念一 基本内容一、无穷限反常积分定义 1 设函数()f x 在[, )a +∞上有定义,且在任意区间[, ]a u 上可积,如果lim()d uau f x x→+∞⎰存在,则称此极限为()f x 在[, )a +∞上的反常积分,亦称为()f x 在[,)a +∞上的无穷限反常积分,简称无穷限积分,记作 ()d af x x+∞⎰.ie ()d lim()d uaau f x x f x x+∞→+∞=⎰⎰:,此时并称 ()d af x x+∞⎰收敛.如果极限不存在,则称 ()d af x x+∞⎰发散.同理可定义 ()d lim()d bbuu f x x f x x-∞→-∞=⎰⎰, ()d ()d ()d a af x x f x x f x x+∞+∞-∞-∞=+⎰⎰⎰,几何解释如图.()d af x x+∞⎰收敛是指图中阴影区域的 面积存在.二、瑕积分定义 2 设函数()f x 在(, ]a b 上有定义,且在点a 的任一右邻域内无界,而在[, ](, ]u b a b ⊂上有界可积,如果 lim ()d buu a f x x+→⎰存在,则称此极限为无界函数()f x 在上(, ]a b 的反常积分,记作 ()d baf x x⎰,ie ()d lim ()d bbauu af x x f x x+→=⎰⎰:,并称 ()d baf x x⎰收敛,否则称其发散.其中a 称为瑕点.无界函数的反常积分亦称为瑕积分.同理可得b 为瑕点时,()d lim ()d buaau bf x x f x x-→=⎰⎰.当()f x 的瑕点(, )c a b ∈,则定义()d ()d ()d bcbaacf x x f x x f x x=+⎰⎰⎰lim ()d lim ()d u bauu cu cf x x f x x -+→→=+⎰⎰.若, a b 都是()f x 的瑕点,则定义()d ()d ()d bc baacf x x f x x f x x=+⎰⎰⎰lim ()d lim ()d c uucu au bf x x f x x+-→→=+⎰⎰.二 习题解答1 讨论下列无穷积分是否收敛?若收敛,则求其值 (1)2d x xe x+∞-⎰;解:由于2201d (1)2ux u xe x e --=--⎰,21limd 2ux u xe x -→+∞=⎰.所以该反常积分收敛,且收敛于12.(2)2d x xe x+∞--∞⎰;解:由于22 01d (1)2x u uxe x e -=--⎰21limd 2x ux xe x -→-∞=-⎰而2220d d d 0x x x xe x xe x xe x +∞+∞----∞-∞=+=⎰⎰⎰所以该反常积分收敛,且收敛于0.(3)0x +∞⎰;解:由于21ux ⎛⎫= ⎝⎰,lim 212u →+∞⎛⎫= ⎝.所以该反常积分收敛,且收敛于2.(4) 2 11d (1)x x x +∞+⎰;解:由于22 111111d d (1)1uu x x x x xx x ⎛⎫=-+ ⎪++⎝⎭⎰⎰ 11111ln 1ln ln 2ux u x x u u ++⎛⎫=-+=-+- ⎪⎝⎭.2 11limd 1ln 2(1)uu x x x →+∞=-+⎰.所以该反常积分收敛,且收敛于1ln 2-.(5) 2 1d 445x x x +∞-∞++⎰;解:由于 22 0 0111d d(21)4452(21)1u u x x x x x =+++++⎰⎰011arctan(21)arctan(21)228|u x u π=+=+-2 01lim d 445488uu x x x πππ→+∞=-=++⎰,0 022 111d d(21)4452(21)1u u x x x x x =+++++⎰⎰ 011arctan(21)arctan(21)282|u x u π=+=-+02 1lim d 44584u u x x x ππ→-∞=+++⎰所以该反常积分收敛,且收敛于2π.(6)1sin d x e x x+∞-⎰;解:由于 11sin d [1(sin cos )]2ux ue x x e u u --=-+⎰,11lim sin d 2ux u e x x -→+∞=⎰.所以该反常积分收敛,且收敛于12.(7) sin d x e x x+∞-∞⎰;解:由于 01sin d [1(sin cos )]2uxu e x x e u u =-+⎰,1limsin d ux u e x x →+∞=∞⎰.所以该反常积分发散. (8)1x +∞⎰.解:由于 1ln(u x u =+⎰,1lim u u x →+∞=+∞⎰.所以该反常积分发散.2 讨论下列瑕积分是否收敛?若收敛,则求其值(1) 1d ()b p a x x a -⎰; 解:由于x a =为瑕点,而11 ()1()11d 11()ln()ln()1p p b p u b a u a p x p px a b a u a p --⎧---≠⎪=--⎨-⎪---=⎩⎰,1 ()11lim d 1()1pb p u u a b a p x p x a p +-→⎧-<⎪=-⎨-⎪∞≥⎩⎰,所以1p <时,该瑕积分收敛,且值为1()1pb a p ---; 所以1p ≥时,该瑕积分发散.(2) 1201d 1x x -⎰;解:由于1x =为瑕点,而u2011d [ln(1)ln(1)]12x u u x =+---⎰,u2011lim d 1u x x -→=∞-⎰.所以该瑕积分发散.(3)2x⎰;解:由于1x =为瑕点,而2(1uux x ==⎰⎰,1lim 2uu x -→=⎰.同理21lim 2uu x +→=⎰,所以该瑕积分收敛,且值为4.(4)1x ⎰;解:由于1x =为瑕点,而1u x =⎰,1lim 1uu x -→=⎰所以该瑕积分收敛,且值为1. (5)1ln d x x⎰;解:由于0x =为瑕点,而1ln d 1ln ux x u u u=-+-⎰,1lim ln d 1uu x x +→=-⎰.所以该瑕积分收敛,且值为1-. (6)x ⎰;解:令2sin x t =,则cos dx t t t=⎰⎰2220 02sin d(1cos2)d2t t t tπππ==-=⎰⎰,所以该瑕积分收敛,且值为2π.(7)1x⎰;解:令2sinx t=,则12x tπ=⎰⎰22d tππ==⎰.所以该瑕积分收敛,且值为π.(8)11d(ln)pxx x⎰.解:由于0x=,1为瑕点,又11(ln)111d(ln)ln ln1ppx C ppxx xx C p-⎧+≠⎪-=⎨⎪+=⎩⎰,而1p=时,1limlnlnxx-→=∞,1p<时,11lim(ln)1pxxp+-→=∞-1p>时,111lim(ln)1pxxp--→=∞-所以p R∀∈,瑕积分11d(ln)pxx x⎰发散.3 举例说明:瑕积分()dbaf x x⎰收敛时,2()dbaf x x⎰不一定收敛.解:例如x⎰收敛于2π,但1d1xxx-⎰发散.4 举例说明:积分()daf x x+∞⎰收敛,且()f x在[,)a+∞上连续时,不一定有lim()0xf x→+∞=.解:例如+41sin dx x x∞⎰.因令x=+ +41 11sin d4x x x t∞∞=⎰⎰.所以 +4 1sin d x x x∞⎰收敛,且4()sin f x x x =在[,)a +∞上连续,但lim ()x f x →+∞不存在.5 证明:若 ()d af x x+∞⎰收敛,且lim ()x f x A→+∞=存在,则0A =. 证:假设0A ≠,不妨设0A >,因lim ()x f x A→+∞=,所以0M ∃>,()2Ax M f x ∍>⇒>“”.于是()d ()2uMAf x x u M >-⎰,从而lim()d uMu f x x →+∞=∞⎰.此与 ()d af x x+∞⎰收敛矛盾,故0A =.6 证明:若()f x 在[,)a +∞上可导,且 ()d af x x+∞⎰与()d af x x+∞'⎰都收敛,则lim ()0x f x →+∞=.证:因为()d ()()u af x x f u f a '=-⎰,所以由()d af x x+∞'⎰都收敛知lim ()x f x →+∞存在,故由上一题知lim ()0x f x →+∞=.§11. 2 无穷限积分的性质与收敛判别一 基本内容一、无穷限积分的性质 由无穷限积分的定义知()d af x x+∞⎰收敛lim()d uau f x x→+∞⇔⎰存在;由极限的柯西收敛准则知lim()d uau f x x→+∞⎰存在0,,G a ε⇔∀>∃≥2112 ,()d u u u u G f x x ε∍>⇒<⎰“”.定理1()d af x x+∞⎰收敛0,,G a ε⇔∀>∃≥2112 ,()d u u u u G f x x ε∍>⇒<⎰“”.性质1 若 1 ()d ,af x x +∞⎰ 2 ()d af x x+∞⎰都收敛,则12,k k ∀,[] 1111()()d ak f x k f x x +∞+⎰也收敛,且[] 11111122 ()()d ()d ()d aaak f x k f x x k f x x k f x x+∞+∞+∞+=+⎰⎰⎰.性质2 若,()u a f x ∀>在[, ]a u 上可积,则b a ∀>, ()d af x x+∞⎰与 ()d bf x x+∞⎰同收同发,且()d ()d ()d b aabf x x f x x f x x+∞+∞=+⎰⎰⎰.性质3 若,()u a f x ∀>在[, ]a u 上可积,则()d af x x+∞⎰收敛()d af x x+∞⇒⎰收敛,且()d ()d aaf x x f x x+∞+∞≤⎰⎰.定义1 如果 ()d af x x+∞⎰收敛,则 ()d af x x+∞⎰称绝对收敛.二、比较判别法比较判别法仅应用于绝对收敛的判别. 由于()()d uaF u f x x=⎰单调上升,所以,()d af x x+∞⎰收敛()()d ua F u f x x⇔=⎰有上界.定理2 若,(),()u a f x g x ∀>在[, ]a u 上可积,且,()()x a f x g x ∀>≤,则 ()d ag x x+∞⎰收敛()d af x x+∞⇒⎰收敛;而 ()d af x x+∞⎰发散()d ag x x+∞⇒⎰发散.推论 (比较判别法的极限形式)若,(),()u a f x g x ∀>在[, ]a u 上可积,, ()0x a g x ∀>>,且()lim()x f x cg x →+∞=, 则(1) 0c <<+∞ ()d af x x+∞⇒⎰与 ()d ag x x+∞⎰同收同发; (2) 0c =时, ()d ag x x+∞⎰收敛()d af x x+∞⇒⎰收敛; (3) c =+∞时, ()d ag x x+∞⎰发散()d af x x+∞⇒⎰发散.当选用 11d p x x +∞⎰为比较“尺子”时,则得下面的柯西判别法.定理3 (柯西判别法) 若0,()u a f x ∀>>在[, ]a u 上可积,则 1(1) ()p f x x ≤,且1p >时, ()d a f x x+∞⎰收敛;1(2) ()p f x x ≥,且1p ≤时, ()d a f x x+∞⎰发散.定理'3(柯西判别法的极限形式) 若0,()u a f x ∀>>在[, ]a u 上可积,且lim ()p x x f x λ→+∞=,则(1) 0λ≤<+∞,且1p >时, ()d af x x +∞⎰收敛; (2) 0λ<≤+∞,且1p ≤时, ()d af x x+∞⎰发散.三、狄立克雷判别法与阿贝尔判别法 此法是对一般无穷限积分的敛散性判别. 定理4 (狄立克雷判别法) 若,()()d uau a F u f x x∀>=⎰有界,()g x 在[,)a +∞上单调,且lim ()0x g x →+∞=,则()()a f x g x dx +∞⎰收敛.定理 5 (阿贝尔判别法) 若()d af x x+∞⎰收敛,()g x 在[,)a +∞上单调有界,则()()d af xg x x+∞⎰收敛.二 习题解答1 设()f x 与()g x 是定义在[,)a +∞上的函数,u a ∀>,()f x 与()g x 在[,]a u 上可积,证明:若2 ()d a f x x+∞⎰与 2 ()d ag x x+∞⎰都收敛,则 ()()d af xg x x+∞⎰与 2 [()()]d af xg x x+∞+⎰亦收敛.证:(1) 因为t R ∀∈,()2()()0tf x g x -≥,从而()2()()d 0a tf x g x x +∞+≥⎰, 即222()d 2()()d ()d 0aaatf x x t f xg x x g x x +∞+∞+∞-+≥⎰⎰⎰.故由判别式为负得()2222()()d 4()d ()d 0aaaf xg x x f x x g x x +∞+∞+∞-≤⎰⎰⎰.即()222()()d ()d ()d aaaf xg x xf x xg x x+∞+∞+∞≤⎰⎰⎰.而 2()d af x x+∞⎰,2()d ag x x+∞⎰收敛,所以 ()()d a f x g x x+∞⎰收敛.又2 [()()]d af xg x x+∞+⎰2()d af x x +∞=⎰2()()d af xg x x +∞+⎰2()d ag x x+∞+⎰,所以2 [()()]d af xg x x+∞+⎰收敛.证:(2) 因为 2 ()d a f x x+∞⎰与 2 ()d ag x x+∞⎰都收敛,所以22 ()()d 2af xg x x+∞+⎰收敛.而 22()()()()2f x g x f x g x +≤,故 ()()d a f x g x x+∞⎰绝对收敛,亦收敛.又2 [()()]d af xg x x+∞+⎰22 ()d 2()()d ()d aaaf x x f xg x x g x x+∞+∞+∞=++⎰⎰⎰.所以由四则运算知 2 [()()]d af xg x x+∞+⎰收敛.2 设()f x 、()g x 、()h x 是定义在[,)a +∞上的三个连续函数,且()()()f x g x h x ≤≤,证明(1) 若 ()d a f x x +∞⎰, ()d a h x x +∞⎰都收敛,则 ()d a g x x+∞⎰也收敛; 证:因为()()()f x g x h x ≤≤,所以u a ∀>,()d uaf x x ⎰()d u ag x x ≤⎰ ()d uah x x≤⎰.而()d af x x+∞⎰, ()d ah x x+∞⎰都收敛,所以 lim()d uau f x x →+∞⎰, lim ()d ua u h x x →+∞⎰都存在,从而 lim()d uau g x x→+∞⎰存在,故 ()d ag x x+∞⎰收敛.(2) 若 ()d af x x +∞⎰ ()d ah x x A+∞==⎰,则 ()d a g x x A+∞=⎰.证:因为 ()d a f x x +∞⎰ ()d ah x x A +∞==⎰所以lim()d uau f x x A→+∞=⎰, lim()d uau h x x A→+∞=⎰,于是由夹逼性定理得 lim()d uau g x x A→+∞=⎰,故 ()d a g x x A+∞=⎰.3 讨论下列无穷限积分的收敛性:(1) 0x +∞⎰;解:因为43lim 1x x →+∞=,而x+∞⎰收敛,故x+∞⎰收敛.(2)1d 1x xx e +∞-⎰;解:因为2lim 01x x x x e →+∞⋅=-,而 2 11d x x +∞⎰收敛,故 1d 1xxx e +∞-⎰收敛.(3)x +∞⎰;解:因为lim 1x =,而1x+∞⎰发散,故x+∞⎰发散.(4) 3 1arctan d 1x xx x +∞+⎰;解:因为23arctan lim 12x x x x x π→+∞⋅=+,而 2 01d x x +∞⎰收敛, 故 3 1arctan d 1x xx x +∞+⎰收敛.(5) 1ln(1)d n x x x +∞+⎰; 解:当1n ≤时, 1ln(1)d n x x x +∞+⎰发散,当1n >时, 1ln(1)d n x x x +∞+⎰收敛.(6)d (,0)1mn x x m n x +∞>+⎰.解:因为lim 11m n mn x x x x -→+∞⋅=+,所以当1n m -≤时,0d 1mn xx x +∞+⎰发散,当1n m ->时,0d 1mnx x x +∞+⎰收敛.4 讨论下列无穷限积分绝对收敛还是条件收敛: (1)1x ⎰;解:因为12lim 1x x →+∞=,而1x+∞⎰发散,所以1x ⎰发散.又1()2cos14F u x ==-≤⎰,()g x 在x →+∞时单调下降以零为极限,所以由狄氏判别法知1x x +∞⎰收敛.综上可知 1x ⎰条件收敛.(2) 2 0sgn(sin )d 1x x x +∞+⎰; 解:因为22sgn(sin )111x x x ≤++,而 201d 1x x +∞+⎰收敛,所以 2 0sgn(sin )d 1x x x +∞+⎰绝对收敛.(3)x⎰;解:因为0()cos d sin 1u F u x x u ==≤⎰,而()100g x x =+在x →+∞时单调下降以零为极限,所以由狄氏判别法知x⎰收敛.=+,而d 100x x +∞+⎰发散,0d 100xxx +∞+⎰收敛,所以x⎰发散,综上可知0x⎰条件收敛.(4)ln(ln )sin d ln ex x x x +∞⎰.解:因为()sin d cos cos 2u eF u x x e u ==-≤⎰,ln(ln )()ln x g x x =在x →+∞时单调下降以零为极限,所以由狄氏判别法知ln(ln)sin dlnexx xx+∞⎰收敛.又2ln(ln)ln(ln)ln(ln)ln(ln)sin sin cos2ln ln2ln2lnx x x xx x x x x x x≥=-,而ln(ln)dlnexxx+∞⎰发散,ln(ln)cos2dlnexx xx+∞⎰收敛,所以ln(ln)sin dlnexx xx+∞⎰条件收敛.5 举例说明,()daf x x+∞⎰收敛时,2()daf x x+∞⎰不一定收敛;()daf x x+∞⎰绝对收敛时,2()daf x x+∞⎰也不一定收敛.证:例如()f x1()df x x+∞⎰收敛,但221 1()df x x x+∞+∞=⎰⎰发散.又如345345333100,221,()1,11 01,(1)xn x n n x n nnf xn x n n x n nnx n nn n ⎧⎡⎤∈-⎪⎢⎥⎣⎦⎪⎪⎛⎫+-∈-⎪ ⎪⎝⎭⎪=⎨⎡⎤⎪-++∈+⎢⎥⎪⎣⎦⎪⎛⎫⎪∈-+-⎪⎪-⎝⎭⎩,如图.则23331111()d231236f x x nnπ+∞=⋅+⋅++⋅+=-⎰,所以 1()d f x x+∞⎰收敛且为绝对收敛.但21()df x x+∞⎰发散.6 证明:()daf x x+∞⎰若绝对收敛,且lim()0xf x→+∞=,则2()daf x x+∞⎰必定收敛.证:因为lim()0xf x→+∞=,所以110,,()1M a x M f x ε∀>∃>∍>⇒≤“”,于是1x M >时,2 ()()f x f x ≤, 又()d af x x+∞⎰收敛,就上述ε,2M a ∃>,21122,()d u u u u M f x x ε∍>⇒<⎰“”取12max{,}M M M =,则12,u u M >时,22112()d ()d u u u u f x x f x x ε≤<⎰⎰,故 2 ()d af x x+∞⎰收敛.7 证明:若()f x 是[,)a +∞上的单调函数,且 ()d a f x x +∞⎰收敛,则lim ()0x f x →+∞=. 证:不妨设()f x ,则[,),()0x a f x ∀∈+∞≥.实因假设00[,),()0x a f x ∃∈+∞<,则0x x >时,0()()f x f x ≤, 从而 000 ()d ()()ux f x x f x u x ≥-⎰,即 0lim()d ux u f x x →+∞=∞⎰,此与 ()d af x x+∞⎰收敛矛盾.又由 ()d af x x+∞⎰收敛得 0,M a ε∀>∃>,22()d 2xx x M f t t ε∍>⇒<⎰“”. 而221()d ()d ()02x xxx f t t f x t xf x ≥=≥⎰⎰,所以2x M >时,0()xf x ε≤<,于是0()f x ε≤<, 故lim ()0x f x →+∞=.8 证明:若()f x 在[,)a +∞上一致连续,且 ()d a f x x+∞⎰收敛,则lim ()0x f x →+∞=.证:假设lim ()0x f x →+∞≠,则00ε∃>,M a ∀>,0x M ∃>,00()f x ε∍≥“”.因为()f x 在[,)a +∞上一致连续,所以0δ∃>,000()()22x x f x f x εδδ∍<-<⇒-<“”. 从而00()()()()2f x f x f x f x ε≥--≥于是M a ∀>,0,x x M ∃>,00()d 24xx f x x x x εεδ∍≥->⎰“”.此与 ()d af x x+∞⎰收敛矛盾,故lim ()0x f x →+∞=.9 利用狄利克雷判别法证明阿贝尔判别法. 证:因为 ()d af x x+∞⎰收敛,所以0M ∃>,u a ∀>,()()d uaF u f x x M=≤⎰,即()F u 在[,)a +∞上有界.又()g x 单调有界,所以极限存在.设lim ()x g x A→+∞=,则()lim ()0x g x A →+∞-=,从而由狄氏差别法知() ()()d af xg x A x+∞-⎰收敛.而() ()()d ()()d ()d a aaf xg x x f x g x A x A f x x+∞+∞+∞=--⎰⎰⎰故 ()()d af xg x x+∞⎰收敛.§11. 3 瑕积分的性质与收敛判别一 基本内容一、瑕积分的性质设a 为瑕点,由瑕积分的定义知()d baf x x⎰收敛存在lim ()d buu af x x+→⇔⎰,由极限的柯西收敛准则知lim ()d buu af x x+→⎰存在0,0,εδ⇔∀>∃>2112 ,(,)()u u u u a a f x dx δε∍∈+⇒<⎰“”.定理1()d baf x x⎰收敛0,0εδ⇔∀>∃>,2112 ,(,)()d u u u u a a f x x δε∍∈+⇒<⎰“”.性质 1 设 a 为瑕点,若1 ()d baf x x⎰、2 ()d baf x x⎰都收敛,则12,k k ∀,[] 1122()()d bak f x kf x x+⎰也收敛,且[] 11221122 ()()d ()d ()d bbbaaak f x k f x x k f x x k f x x+=+⎰⎰⎰.性质2 设a 为瑕点,则(,)c a b ∀∈, ()d baf x x⎰与 ()d caf x x⎰同收同发,且收敛时,()d ()d ()d bcb aacf x x f x x f x x=+⎰⎰⎰.性质3 设 a 为瑕点,若,()u a f x ∀>在[, ]u b 上可积,则()d baf x x⎰收敛()d baf x x⇒⎰收敛,且()d ()d bbaaf x x f x x≤⎰⎰.定义1 如果收敛 ()d ba f x x⎰,则称 ()d ba f x x⎰绝对收敛. 二、比较判别法比较判别法仅应用于绝对收敛的判别.定理2 设a 为瑕点,若,(),()u a f x g x ∀>在[, ]u b 上可积,且,()()x a f x g x ∀>≤, 则 ()d ba g x x⎰收敛()d baf x x⇒⎰收敛,而()d baf x x⎰发散⇒()d bag x x⎰发散.推论(比较判别法的极限形式) 若,(),()u a f x g x ∀>在[, ]u b 上可积,, ()0x a g x ∀>>,且()lim ()x a f x c g x +→=,则(1) 0c <<+∞时, ()d ba f x x⎰与 ()d bag x x ⎰同收同发; (2) 0c =时, ()d bag x x⎰收敛()d b af x x⇒⎰收敛;(3) c =+∞时, ()d bag x x⎰发散 ()d ba f x x⇒⎰发散.定理3 (柯西判别法) 若0,()u a f x ∀>>在[, ]u b 上可积,则(1)1()()pf x x a ≤-且01p <<时, ()d b a f x x ⎰收敛; (2)1()()pf x x a ≥-且1p ≥时, ()d ba f x x ⎰发散. 定理 3 (柯西判别法的极限形式) 若0,()u a f x ∀>>在[, ]ub 上可积,且lim()|()|p x a x a f x λ+→-=,则(1) 0λ≤<+∞且01p <<时, ()d ba f x x⎰收敛;(2) 0λ<≤+∞且1p ≥时, ()d ba f x x⎰发散.二 习题解答1 讨论瑕积分的收敛性(1) 22 01d (1)x x -⎰;解:瑕点为1x =.改写积分为 2 1 2222 0 0 1111d d d (1)(1)(1)x x xx x x =+---⎰⎰⎰.因为 12 01d (1)x x -⎰发散,所以 22 01d (1)xx -⎰发散.(2) 32sin d xxx π⎰; 解:瑕点为0x =.因为2lim 1x x →=,而xπ⎰收敛,所以32sin d x xxπ⎰收敛.(3)1x⎰;解:瑕点为0,1x =.因为H 1111lim(1)lim 11x x x x x --→→→-==,而 1 01d 1x x -⎰发散,所以 1x ⎰发散.(4) 10ln d 1xx x -⎰;解:瑕点为1x =.而112H211112ln ln (1)lim(1)lim lim 012(1)x x x xx x x x xx ---→→→--⋅===--,又1x⎰收敛,所以 10ln d 1xx x -⎰收敛.(5) 130arctan d 1xx x -⎰; 解:瑕点为1x =.而3211arctan arctan lim(1)lim 1112x x x x x x x x π--→→-⋅==-++, 又 1 01d 1x x -⎰发散,所以 130arctan d 1xx x -⎰发散.(6)2 01cos d m xx x π-⎰;解:瑕点为0x =.而21cos 1lim 2m m x x x x +-→-⋅=,所以当21m -<,即3m <时21cos d m xx x π-⎰收敛;所以当21m -≥,即3m ≥时2 01cos d mxx x π-⎰发散.(7)1011sin d x x x α⎰; 解:瑕点为0x =.而111sin x x x αα≤, 所以当01α<<时, 1 011sin d x x x α⎰绝对收敛;又2α≥时,1111sin xx x αα-≤,而 1101d x x α-⎰发散,所以此时 1011sin d x x x α⎰发散; 当12α≤<时,1 011sin d x x x α⎰条件收敛. (8) 0ln d x e x x+∞-⎰.解:积分表为11ln d ln d ln d xxx e x x e x x e x x+∞+∞---=+⎰⎰⎰.就 1 0ln d x e x x-⎰,瑕点为0x =,而120lim ln 0xx x e x +-→⋅=,所以 1ln d x e x x-⎰收敛;就 1ln d x e x x+∞-⎰,因20lim ln 0xx x e x +-→⋅=,所以 1ln d x e x x+∞-⎰收敛.综上可知 0ln d x e x x+∞-⎰收敛.2 计算下列瑕积分的值 (1) 1(ln )d n x x⎰;解:设1 0(ln )d n n I x x=⎰,则1111 0lim(ln )lim (ln )d |n n n n eee e I x x n x x nI ++--→→=-=-⎰,而10 0d 1I x ==⎰,所以 1 0(ln )d (1)!n n x x n =-⎰.(2)1nx ⎰.解:令2sin x t =,则d 2sin cos d x t t t =,于是1212 02sin d nn n I x t t π+==⎰⎰ 22 02sin d(cos )n t t π=-⎰22122202sin cos 22sin cos d |nn t t n t t tππ-=-+⋅⎰212122 04sin d 4sin d n n n t t n t tππ-+=-⎰⎰12()n n n I I -=-,于是 1221n n n I I n -=+,而0I =2 02sin d 2t t π==⎰,所以212(2)!!2(!)2(21)!!(21)!n n n n I n n +=⋅=++.3 证明瑕积分2 0ln(sin )d J x xπ=⎰收敛,且ln 22J π=-,(提示:利用22 0ln(sin )d ln(cos )d x x x xππ=⎰⎰,并将它们相加).证:瑕点为0x =,而3H 20001sin lim ln(sin )lim lim 2cos x x x x x x x+++→→→=-⋅3201sin lim 02cos x x x x +→=-=,所以2 0ln(sin )d J x xπ=⎰收敛.令2x t π=-知22 0 0ln(sin )d ln(cos )d x x x x ππ=⎰⎰,于是22 0 02ln(sin )d ln(cos )d J x x x xππ=+⎰⎰22 0 0sin 2ln(sin cos )d lnd 2xx x x x ππ==⎰⎰2 0ln sin 2d ln 22x x ππ=-⎰.而令2x t =得201ln sin 2d ln sin d 2x x t t ππ=⎰⎰ 2 0 211ln sin d ln sin d 22t t t t πππ=+⎰⎰ 22 0 011ln sin d ln cos d 22t t t t J ππ=+=⎰⎰.所以ln 22J π=-.4 利用上题结果,证明(1)2ln(sin )d ln 22ππθθθ=-⎰;证:令t θπ=-,则ln(sin )d ()ln(sin )d t t tππθθθπ=-⎰⎰,于是ln(sin )d ln(sin )d 2πππθθθθθ=⎰⎰220ln(sin )d ln 22πππθθ==-⎰.(2) 0sin d 2ln 21cos πθθθπθ=-⎰.证:() 0 0sin d d ln(1cos )1cos ππθθθθθθ=--⎰⎰ln 2ln(1cos )d ππθθ=--⎰2 0 0ln 2ln 2d ln sin d 2ππθπθθ⎛⎫=-- ⎪⎝⎭⎰⎰ 02lnsin d 2πθθ=-⎰2 04lnsin d t tπ=-⎰2ln2π=. 所以 0sin d 2ln 21cos πθθθπθ=-⎰.总练习题111 证明下列等式(1) 110 1d d ,011p px x x x p x x --+∞=>++⎰⎰;证:令1x t =,则21d d x t t =-,于是1111 1112 0 00111d lim d lim d 1111p p p e e e e x x x x t x x t t t ++---→→⎛⎫==⋅⋅-⎪++⎝⎭+⎰⎰⎰1 1 10lim d d 11p p ee t t t t t t +--+∞→==++⎰⎰, 所以110 1d d ,011p px x x x p x x --+∞=>++⎰⎰.(2) 10 0d d ,0111p px x x x p x x --+∞+∞=<<++⎰⎰.证:因为01p <<,所以0x =为瑕点.令1x t =,则21d d x t t =-,于是1 0 12 00111d d d 1111p pp x t x t tx t t t t --+∞+∞-+∞=-⋅⋅=+++⎰⎰⎰所以 10 0d d 11p px x x x x x --+∞+∞=++⎰⎰.2 证明下列不等式(1)12π<<⎰; 证:1x =为瑕点.而12111lim(1)lim 2x x x --→→-==,所以1⎰收敛.又设sin x t =,则d cos d x t t =,于是12 0π=⎰⎰而1≤≤, 所以12π<<⎰. (2)201111d 122x e x e e +∞-⎛⎫-<<+ ⎪⎝⎭⎰. 证:因为22lim 0x x x e -→∞=,所以2d xe x+∞-⎰收敛.而2222110 1d d d d x x x xe x e x e x e x+∞+∞----=+>⎰⎰⎰⎰22 11201d d()2x x xe x e x --≥=--⎰⎰1122e =-.222211d d d 1d x x x xe x e x e x xe x+∞+∞+∞----=+<+⎰⎰⎰⎰()22111d 2x e x +∞-=--⎰112e =+. 故结论成立.3 计算下列反常积分的值. (1) 0cos d (0)ax e bx x a +∞->⎰;解:01cos d d(sin )axaxebx x e bx b +∞+∞--=⎰⎰1sin sin d ax axa e bx e bx x bb +∞+∞--=+⎰2d(cos )ax a e bx b +∞-=-⎰2 22cos cos d ax ax a a e bx e bx xb b +∞+∞--=--⎰222 0cos d ax a a e bx xb b+∞-=-⎰所以22 0cos d ax ae bx x a b +∞-=+⎰为所求.(2) 0sin d (0)ax e bx x a +∞->⎰;解:方法同上可得22 0sin d ax be bx x a b +∞-=+⎰.(3) 2 0ln d 1xx x +∞+⎰;解: 1 222 0 0 1ln ln ln d d d 111x x xx x x xx x +∞+∞=++++⎰⎰⎰,就 2 1ln d 1x x x +∞+⎰作变换1x t =,则21d d x t t =-,于是20 12222 1 1 0ln ln 1ln d d d 111x t t t x t t x t t t +∞⎛⎫=-⋅-=- ⎪+++⎝⎭⎰⎰⎰ 所以 20ln d 01xx x +∞=+⎰. (4)2ln(tan )d πθθ⎰.解:设tan x θ=,则21d d 1x x θ=+,于是2ln(tan )d πθθ⎰2 0ln d 01xx x +∞==+⎰.4 讨论反常积分sin d (0)bxx b x λ+∞≠⎰,λ取何值时绝对收敛,λ取何值时条件收敛.解: 1 0 0 1sin sin sin d d d bx bx bxx x x x x x λλλ+∞+∞=+⎰⎰⎰,就 1 0sin d bxx x λ⎰,当0λ>时,0x =为瑕点.当01λ<<时,sin 1bx x x λλ≤,而 1 01d x x λ⎰收敛, 所以当01λ<<时, 1 0sin d bxx xλ⎰绝对收敛.当12λ≤<时,因为10sin sin lim lim 0x x bx bxx b x x λλ-→→==>,而111d xx λ-⎰收敛,所以当12λ≤<时,10sin d bxx x λ⎰绝对收敛.当2λ≥时,因为10sin sin lim lim 0x x bx bxx b x x λλ-→→==>,而111d xx λ-⎰发散,所以当2λ≥时,10sin d bxx x λ⎰发散.就 1sin d bx x x λ+∞⎰,当0λ≤时, 1sin d bxx x λ+∞⎰发散.当01λ<≤时, 1()sin d uF u bx x=⎰在[1,)+∞上有界,1()g x x λ=单调以零为极限,由狄氏判别法知1sin d bxx x λ+∞⎰收敛.而 22sin sin 1cos bx bx bx x x x x λλλλ≥=-, 所以 1sin d bx x x λ+∞⎰发散,故 1sin d bxx x λ+∞⎰条件收敛. 当1λ>时,因为sin 1bx xx λλ≤, 而 1 01d x x λ⎰收敛,所以当1λ>时,1 0sin d bxx x λ⎰绝对收敛.综上可知,当0λ≤时,或2λ≥时, + 0sin d bxx xλ∞⎰发散;当01λ<≤时, + 0sin d bxx x λ∞⎰条件收敛;当12λ<<时, + 0sin d bxx x λ∞⎰绝对收敛.5 证明:设f 在[0,)+∞上连续,0a b <<. (1) 若lim ()x f x k→+∞=,则()()d ((0))ln f ax f bx bx f k x a +∞-=-⎰;证:令ax t =,则 ()()d d A aA a f ax f t x t x t δδ=⎰⎰,令bx t =,则 ()()d d A bA b f bx f t x t x t δδ=⎰⎰,于是 0()()()()d d d aA bA a b f ax f bx f t f t x t t x t t δδ+∞-=-⎰⎰⎰ ()()()()d d d d b bA aA bA a b bA b f t f t f t f t t t t t t t t t δδδδ=++-⎰⎰⎰⎰()()d d b bA a aA f t f t t t t t δδ=-⎰⎰ ()()d d b b a a f y f Ay y y y y ε=-⎰⎰1[()()]d b a f f A yyδξη=-⎰(积分中值定理,,(,)a b ξη∈)[()()]lnbf f A a δξη=-.令0,A δ+→→+∞得 0()()d ((0))lnf ax f bx bx f k x a +∞-=-⎰.(2) 若 ()d a f x x x +∞⎰收敛,则 0()()d (0)ln f ax f bx bx f x a +∞-=⎰.证:由(1)得()()d f ax f bx x x +∞-⎰()()d d b bA a aA f t f t t tt t δδ=-⎰⎰.因()d af x x x +∞⎰收敛,所以由柯西收敛准则得0,M a ε∀>∃>,2112(),d u u f x u u M x x ε∍>⇒<⎰“”.即 ()lim d 0bA aA A f t t t →∞=⎰. 故 0()()d (0)ln f ax f bx bx f x a +∞-=⎰.6 证明下述命题(1) 设0a >,()f x 为[,)a +∞上的非负连续函数.若 ()d axf x x+∞⎰收敛,则 ()d af x x+∞⎰也收敛.证:因为 ()d axf x x+∞⎰收敛,所以所以由柯西收敛准则得0,M a ε∀>∃>,2112,()d u u u u M xf x x a ε∍>⇒<⎰“”.而1()d ()d aa f x x xf x x a +∞+∞<⎰⎰,于是亦有21()d u u f x x ε<⎰.故 ()d af x x+∞⎰收敛.(2) 设0a >,()f x 为[,)a +∞上的连续可微函数,且当x →+∞时,()f x 递减地趋于0,则 ()d af x x+∞⎰收敛的充要条件为 ()d axf x x+∞'⎰收敛.证:()⇒设 ()d af x x+∞⎰收敛,因()d ()()d |aaaf x x xf x xf x x+∞+∞+∞'=-⎰⎰而lim ()0x xf x →+∞=(本章第二节第8题) 所以 ()d axf x x+∞'⎰收敛.()⇐设 ()d a xf x x +∞'⎰收敛,则0ε∀>,M a ∃>,()d AxA x M tf t t ε'∍>>⇒<⎰“”.因为()f x 递减地趋于0,所以()0f x '≤, 于是由积分中值定理得()d ()d [()()]AAxxtf t t f t t f A f x ξξ''==-⎰⎰,从而 0[()()][()()]x f A f x f A f x ξε≤-≤-<.又lim ()0A f A →+∞=,所以lim ()0x xf x →+∞=.从而()d ()()d |aaaxf x x xf x f x x+∞+∞+∞'=-⎰⎰()()d aaf a f x x+∞=-⎰,故 ()d af x x+∞⎰收敛.反常积分无限区间上的积分或的积分,这两类积分叫作,又名反常积分.1.无限区间上的积分一般地,我们有下列定义定义6.2设函数在区间上连续,如果极限()存在,就称上极限值为在上的广义积分.记作即( 6.24 )这时我们说广义积分存在或收敛;如果不存在,就说不存在、发散或不收敛.类似地,可以定义在及上的广义积分.( 6.25 )其中( 6.26 )对于广义积分,其收敛的充要条件是:与都收敛.广义积分收敛时,具有积分的那些性质与积分方法,如换元法、分部积分法以及等,但有时代数和运算要注意,不要随便拆开.在用广义的牛顿—莱布尼兹公式时,无穷远点应取极限.为方便起见,引入记号,这样,若为的一个原函数,则(其中)注意:这里与是独立变化的,不能合并成 .2.无界函数的积分先给出瑕点或奇点的概念,若(或)时,,则点(或点)称为无界函数的瑕点或奇点. 的无穷间断点就是的瑕点.定义6.3设函数在上连续,左端点为的瑕点,如果存在,就称此极限值为无界函数在上的广义积分.记作( 6.27 )这时我们说广义积分存在或收敛.如果不存在,就说广义积分不存在、不收敛或发散.注:表明从大于0的方向趋于0,已经隐含了 .类似地,设函数在上连续,右端点为的瑕点,如果存在,就称此极限值为无界函数在上的广义积分.记作( 6.28 )这时我们说广义积分存在或收敛.如果不存在,就说广义积分不存在、不收敛或发散.还有,设函数在上连续,左端点、右端点均为的瑕点,如果及均存在,其中为内的一个确定点,且与两者之间是独立变化的,就称存在或收敛,记作如果及中至少有一个不存在,则称不存在、不收敛或发散.对于区间端点、均为的瑕点的广义积分有存在和均存在. 和都存在.其中为内的一个确定点,且与两者之间是独立变化的,另外,设函数在上除一个内部点外连续,且内部点为的瑕点,如果和均存在,也即和都存在,其中与两者之间是独立变化的,就称存在或收敛,记作( 6.29 )如果及中至少有一个不存在,则称不存在、不收敛或发散.对于内部点为的瑕点的广义积分有存在和均存在.和都存在.广义积分收敛时,具有常义积分的那些性质与积分方法,如换元法、分部积分法以及广义牛顿—莱布尼兹公式等,但有时代数和运算要注意,不要随便拆开,参见例5与例6.在用广义的牛顿—莱布尼兹公式时,无界点处原函数应取极限.为方便起见,引入记号左端点为瑕点时,记,这时广义的牛顿—莱布尼兹公式为右端点为瑕点时,记,这时广义的牛顿—莱布尼兹公式为左端点、右端点均为瑕点时,广义的牛顿—莱布尼兹公式为(为内的一个确定点)()( 这里的值有时不必马上算出,可对抵掉. )仅内部点为瑕点时,广义的牛顿—莱布尼兹公式为注意:由于有限区间上的无界函数的广义积分常常会与常义积分混淆,因此求积分时,首先应判断积分区间上有无瑕点.有瑕点的,是广义积分;无瑕点的,是常义积分.若是广义积分,还要保证积分区间仅有一端是瑕点,中间没有瑕点.若不然,要将积分区间分段,使每一段区间仅有一端是瑕点,中间没有瑕点.。
第十一章反常积分

第十一章 反常积分课后习题全解§1 反常积分概念1.讨论下列无穷积分是否收敛?若收敛,则求其值: (1)2.x xe dx +∞-⎰; (2)2x xe dx +∞--∞⎰;(3)0+∞⎰dx; (4) 20(1)dx x x +∞+⎰; (5)2445dxx x +∞-∞++⎰; (6) sin ;0x e xdx -+∞⎰(7)sin ;xe xdx +∞-∞⎰ (8)0+∞⎰解:(1)由于22211(1),lim 0022x u x u u u xe dx e xe dx ---→+∞=-=⎰⎰ 因此该无穷积分收敛,且值为12(2)由于222001(1),lim 02x u x u xe dx e xe dx u u ---→-∞=--=⎰⎰则222000x x x xe dx xe dx xe dx ---+∞+∞=+=-∞-∞⎰⎰⎰因此该无穷积分收敛,且值为0(3)由于2(1lim 2u u u →+∞==⎰⎰ 因此该无穷积分收敛,且值为2(4)由于221(ln ||),lim 1ln 211(1)1(1)u u u dx xdx x x x x x x →+∞=-+=-+++⎰⎰因此该无穷积分收敛,且值为1-ln2(5)22lim 004454454u u dx dx x x x x π→+∞+∞==++++⎰⎰因此该无穷积分收敛,且值为4π(6)由于11sin [1(sin cos )],lim sin 0022x ux u u u e xdx u u e e xdx ---→+∞=-+=⎰⎰ 因此该无穷积分收敛,且积分为12(7)1sin lim sin lim [1(sin cos )]02x x u u u e xdx e adx u u e →+∞→+∞+∞===-=∞⎰则0sin sin sin 0x x xe xdx e adx e xdx +∞+∞=+=∞-∞-∞⎰⎰⎰所以该无穷不收敛(8)由于ln |limu uuu →+∞=+=+∞⎰⎰所以该无穷积分分散2.讨论下列瑕积分是否收敛?若收敛,则求其值 (1)()p b dx a x a -⎰; (2)2101dxx -⎰;(3)2⎰; (4)1⎰;(5)1ln ;0xdx ⎰ (6);⎰(7)1⎰ (8)10(ln )p dxx x ⎰解:(1) 被积函数f(x)=1()px a -在(a,b )上连续,从而在任何[u,b]⊂(a,b)上可积,x=a 为其瑕点,依定义2求得lim ()()p pu a b b dx dxa u x a x a →+=--⎰⎰而1()111lim{()Pb a p p p pu a bdxu x a --<-∞≥→+=-⎰ 当P<1时,该遐积分收敛至1()1pb a p---;当P ≥1时,该瑕积分发散(2) 该积分函数f(x)=211x-在[0,1]上连续,从而在任何[0,u]⊂[0,1]上可积,x=1为其瑕点,依定义2求得221111lim lim [ln(1)ln(1)]00112u u u dx dx u u x x --→→==+--=+∞--⎰⎰因此该瑕积分发散(3) 被积函数[0,1]∪(1,2)上连续,x=1为其瑕点,依定义2得1111lim lim lim(22u u u u u ---→→→===-=⎰⎰⎰111222lim lim lim(221u u u +++→→→===-=⎰⎰⎰则21241=+=⎰⎰⎰,瑕积分收敛(4) 被积函数[0,1]上连续,从而在任何[0,u]⊂[0,1]上可积,x=1为其瑕点,依定义2得111lim lim(11u u u--→→===⎰⎰(5) 被积函数f(x)=lnx 在(0,1)上连续,从而在任何[u ,1]⊂(0,1)上可积,x=0为其瑕点,依定义2得0011ln lim ln lim[1(ln 1)]10u u xdx xdx u u u ++→→==---=-⎰⎰ 因此该瑕积分收敛至-1(6) 令2sin ,[0,],2x t t π=∈则22sin(1cos2)2t t dtππ==-=⎰⎰(7)令2sin,[0,],2x t tπ=∈则21220002dtπππ===⎰⎰⎰(8)被积分函数f(x)=1(ln)px x在(0,1)连续,x=0,1为其瑕点,因1111220001lim lim[(ln2)(ln)](ln)(ln)1p pp puu udx dxux x x x p+--→+→==--=∞-⎰⎰因此该瑕积分分散§2 无穷积分的性质与收敛判别(教材上册P275)1.证明定理11.2及其推论1解:(1)定理11.2的证明;由()g x dxa+∞⎰收敛,根据柯西准则,任给ε>0,存在G≥a,当21u u>>G时,总有21|()|uug x dxε<⎰2211|()|()||()|||()|u uu uf xg x f x dx g x dxε≤⇒≤<⎰⎰在由柯西准则,证得|()|f x dxa+∞⎰收敛(2)推论1的证明:(ī)|()|lim,()0()xf xC g xg x→+∞=>⇒取2cε=,存在M>0,当x>M时,有30()|()|()22c Cg x f x g x<<<<+∞3|()|(),2f x Cg x<由定理11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章反常积分
教学要点
反常积分收敛和发散的概念及敛散性判别法。
教学时数 8学时
教学内容
§1 反常积分的概念(4学时)
反常积分的引入,两类反常积分的定义反常积分的计算。
§2 无穷积分的性质与收敛判别(4学时)
无穷积分的性质,非负函数反常积分的比较判别法,Cauchy判别法,反常积分的Dirichlet判别法
与Abel判别法。
§3 瑕积分的性质与收敛判别
瑕积分的性质,绝对收敛,条件收敛,比较法则。
考核要求
掌握反常积分敛散性的定义,奇点,掌握一些重要的反常积分收敛和发散的例子,理解并掌握绝对收敛
和条件收敛的概念,并能用反常积分的Cauchy收敛原理、非负函数反常积分的比较判别法、Cauchy判别
法,以及一般函数反常积分的Abel、Dirichlet判别法判别基本的反常积分。
§1 反常积分概念
一问题的提出
例1(第二宇宙速度问题)在地球表面初值发射火箭,要是火箭克服地球引力,无限远离地球,问初速度至少多大?
解设地球半径为,火箭质量为
地面重力加速度为,有万有引力定理,在距地心处火箭受到的引理为
于是火箭上升到距地心处需要做到功为
当时,其极限就是火箭无限远离地球需要作的功
在由能量守恒定律,可求得处速度至少应使
例2 从盛满水开始打开小孔,问需多长时间才能把桶里水全部放完?
解由物理学知识知道,(在不计摩擦情况下),桶里水位高度为时,水从小孔里流出的速度为
设在很短一段时间内,桶里水面降低的高度为,则有下面关系:
由此得
所以流完一桶水所需的时间应为
但是,被积函数在上是无界函数,,所一我们取
相对于以前学习的定积分(正常积分),我们把这里的积分叫做反常积分。
二反常积分的定义
1无穷限反常积分的定义,
.
无穷限反常积分几何意义
例1 ⑴讨论积分, , 的敛散性 .
⑵计算积分.
例 2 讨论以下积分的敛散性 :
⑴; ⑵.
例3讨论积分的敛散性 .
2 瑕积分的定义:以点为瑕点给出定义. 然后就点为瑕点、点
为瑕点以及有多个瑕点的情况给出说明.
例4 判断积分的敛散性 .
例6 讨论瑕积分的敛散性 , 并讨论积分的敛散性 .
瑕积分与无穷积分的关系: 设函数连续 , 为瑕点. 有
, 把瑕积分化成了无穷积分;
设, 有,把无穷积分化成了瑕积分。
