川师大学物理第十一章恒定电流的磁场习题解讲课稿
《大学物理》11磁场习题解析共141页文档

25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
《大学物理》11磁场习题解 析
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。Байду номын сангаас—培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
大学物理课件第11章稳恒磁场

p
已知:I、c
解:
0
B AO
0I 4a
(cos 1
cos 2 )
B
I cP
•
Ia
0 I [cos 0 cos( )]
A
4a
2
0I 4c sin
(1 cos )
2
所以 B p BAO BOB
2
方向
同理
BOB
0I 4c sin
(1 cos )
2
0I 2c sin
(1 cos )
r0
OR
dB dB
p•
dBx
X
方向
Idl r0
分析对称性、写出分量式
B
dB 0
Bx
dBx
0 4
Idl sin
r2
统一积分变量
Y
sin R r
Bx
dBx
0 4
Idl sin
r2
I Idl
O
0 IR 4r 3
dl
0 IR 4r 3
2R
r0
R x
2(
0 IR 2
R2 x2
)3
R
•
a LI
a
I
A a
•P
0 0I 5 105T S•
•T
4a R点
方向
BR BLA BLA
0 I (cos 0 cos 3 ) 0 I (cos 1 cos )
4a
4 4a 4
1.71 105T
方向 •
S点
BLA
0I 4a
(cos 0
cos
3
4
)
BLA
0I 4a
(cos
大学物理稳恒磁场 ppt课件

NI R
B2
0 NI R2
2(R2 x2 )32
R
O1
O2
x
(1) 电流方向相同:
B B1 B2
0 NI
2R
[1
(R2
R3
x2
3
)2
]
8.51105 T
(2) 电流方向相反:
B B1 B2
0 NI
2R
[1 pp(t课R件2
R3
x
2
)
3 2
]
4.06 105 T
R 2 Indx R2 x2 3/2
B
dB 0nI
2
x2 x1
R2dx μ0nI ( R2 x2 3/2 2
x2 R2 x22
x1 ) R2 x12
B
0nI
2
cos2
ppt课件
cos1
27
讨论
B
0nI
2
cos2
cos1
I
在弧长为 dl 的线元内 流过的电流元为:
dI
dI I dl
真空的磁导率ppt课件
13
O
r P
Idl
dB
dB
Idl
P r
dB
I
电流元的磁感应线在垂直于电流元的平面内 是圆心在电流元轴线上的一系列同心圆。
磁感应线绕向与电流流向成右手螺旋关系
磁场叠加原理: B dB
oIdl rˆ
ppt课L件
L 4r 2
dB
μ0 4π
最新第十一章-恒定电流的磁场(一)-作业及参考答案-

一.选择题:1.(基础训练1)[D ]载流的圆形线圈(半径a1)与正方形线圈(边长a2 )通有相同电流I.若两个线圈的中心O1、O2处的磁感强度大小相同,则半径a1与边长a2之比a1∶a2为(A) 1∶1 (B) π2∶1(C) π2∶4 (D) π2∶8提示()82,,22135cos45cos244,2212212121ππμπμμ===-⨯⨯⨯==aaBBaIaIBaIBoooo得由2.(基础训练3)[B ].有一无限长通电流的扁平铜片,宽度为a,厚度不计,电流I在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b处的P点(如图)的磁感强度B的大小为(A))(2baI+πμ.(B)bbaaI+πln2μ.(C)bbabI+πln2μ.(D))2(baI+πμ.提示:bbaaIrdraIrrdIdBdraIdIabb+======⎰⎰⎰+ln222dIBBB,BdB,2P,)(drrPπμπμπμπμ的大小为:,的方向也垂直纸面向内据方向垂直纸面向内;根处产生的它在,电流为导线相当于一根无限长的直的电流元处选取一个宽度为点为在距离3. .(基础训练4)[D ]如图,两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I从a端流入而从d端流出,则磁感强度B沿图中闭合路径L的积分⎰⋅LlBd(A) I0μ.(B) I031μ.(C) 4/Iμ.(D) 3/2Iμ.提示⎰∑⎰=⋅∴=-==∴===⋅LLIl dBIIslIIslIslIIIl dB32322)(RRRIRI11122112122111Lμρρρμμ得为两条支路的电阻。
,,其中,而内4. 自测提高7[C ]如图,正方形的四个角上固定有四个电荷量均为q 的点电荷.此正方形以角速度ω 绕AC 轴旋转时,在中心O 点产生的磁感应强度大小为B 1;此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为B 2,则B 1与B 2间的关系为(A) B 1 = B 2. (B) B 1 = 2B 2.(C) B 1 =21B 2. (D) B 1 = B 2 /4. 提示: 设正方形边长为a ,)22(a b b OC AO ===式中, 两种情况下正方形旋转时的角速度ω 相同,所以每个点电荷随着正方形旋转时形成的等效电流相同, 为 πω2q I =当正方形绕AC 轴旋转时,一个点电荷在O 点产生的磁感应强度的大小为bIB 20μ=,实际上有两个点电荷同时绕AC 旋转产生电流,在O 点产生的总磁感应强度的大小为b IbIB B 001222μμ=⨯==同理,当正方形绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为bIb IB B 0022244μμ=⨯== 故有122B B =5. 附录C 2[ B ]有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数为2=N 的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感应强度和磁矩分别是原来的:(A) 4倍和1/8 (B) 4倍和1/2 (C) 2倍和1/4 . (D) 2倍和1/2提示:由半径为R 的单匝线圈弯成匝数为2=N 的线圈以后,每一个线圈的半径变为R r 21=,故磁感应强度变为原来的4倍,磁矩变为原来的1/2,总的变化为4倍和1/2二. 填空题6.(基础训练11)均匀磁场的磁感强度B 与半径为r 的圆形平面的法线n的夹角为α ,今以圆周为边界,作一个半球面S ,S 与圆形平面组成封闭面如所示.则通过S 面的磁通量Φ = απcos 2B r -。
第11章 恒定电流的磁场3

I
O
B
n
P(O)
平面载流线圈在均匀磁场中受的磁力矩
l1 sin F2
M NISn B
M(N) F1
n
B
大学物理 第三次修订本
5
第11章 恒定电流的磁场
讨论
稳定平衡
× × × × × × × × × ×
(1) n 与 B 同向
M NISn B
大学物理 第三次修订本
20
第11章 恒定电流的磁场
第11章 小结
一、磁感应强度
其中dFmax为电流元 Idl 在该点受到的最大磁场力。 B 的方向 为电流元 Idl 在该点受到的磁场力为零时电流元所指方向, 且指向满足安培公式 dF Idl B 。
磁感应强度是描述磁场的基本物理量。
I
Fde
x
F合=0
另解
Fea
e
F Idl B I ( dl ) B 0
大学物理 第三次修订本
1
第11章 恒定电流的磁场
例2 求一载流导线框 CDEFC 在无限长直导线磁场中的受力。
解
B
0 I1
2x
×
FCD
0 I1 I 2l1 B1 I 2l1 2a
I1
I2 FCD l1 FEF l2
×
x C
×
E
方向向左。
D
×
0 I1 FEF I 2l2 B2 I 2l2 2 (a b)
方向向右。
大学物理 第三次修订本
b
F
x
2
大学物理下第11章稳恒磁场-dai

稳恒电场
电荷分布不随时间改变 但伴随着电荷的定向移动
导体内电场不为零,导 体内任意两点不是等势 电场有保守性,它是 保守场,或有势场 稳恒电场的存在总要 伴随着能量的转换
三
电阻率,欧姆定律
1、欧姆定律(积分形式)
U I R l l R S S
2、电阻率和电导率
电阻率
0 (1 t )
是一矢量
方向: 该点处电流的方向 大小: 通过该点单位垂直截面的电流
dI J dS
单位(SI):安每平方米 ( A m )
2
n
dS
若在导体中某点取一个与电 流方向垂直的截面元 dS
dI JdS
若面元 dS 的法线 n 与电流的方向成
角
n
dI J cos dS
写成矢量式
F q, v
大小: B Fmax q0v
方向: 小磁针在该点的N 极指向
v
磁力 Fm +
单位:
T(特斯拉)
B
1T 104 G (高斯)
11-3 毕奥---沙伐尔定律
奥斯特的实验使整个科学界大为震惊,人们长期以 来所信奉的“电和磁之间没有内在联系”的信条崩溃了。 1820年8月,法国物理学家阿拉果在瑞士听到了奥斯特 的发现,敏锐地感到其重要性。回到巴黎后,他在9月 11日法国科学院的会议上报告了奥斯特的新发现,在法 国引起巨大反响。 最先对电流磁效应进行定量分析的是法国物理学 家毕奥(1774-1862)和萨伐尔(1791-1841)。毕奥 曾任法兰西学院物理学教授,兴趣广泛,对光学尤有 研究,还写了许多数学著作。萨伐尔早年行医,1819 年他给毕奥呈送一篇论文,毕奥对这人发生了兴趣, 并给予了鼓励,1828年萨伐尔就担任了法兰西学院实 验物理教授。
大学物理下-吴百诗-ch11恒定电流的磁场ppt课件

三、磁感应强度
1、引入 电场——电场强度
需要一个既具有大小又有方向的物理量来定量描述
磁场。
完整最新ppt
10
ch11
2、实验:运动电荷在磁场中的受力情况,确定空 间一点的磁感应强度
①、类比:静电场中用试探电荷研究电场
测 F , 出 E = 用 F /q 描述电 E 表 场 示 强 电 度 场 。 ,
带电粒子在磁场中沿
其力他垂方直向于运v与动时所B ,组其成受
的平面
在磁场中的任一点,当 带电粒子在磁场中垂直于 B方向运动时受力最大, 且F max 大小是一确定值
qv
与 q,无v关
完整最新ppt
13
ch11
3、磁感应强度的定义
•磁场中任一点都存在一个特殊的方向和确定的比值
Fmax /qv •反映了磁场在该点的方向特征和强弱特征
两带电线上的电流为导体带电量线密度单位长度上的导线所受的安培力ch11两带电线单位长度上的电荷之间的库仑力导体带电量线密度在一般情况下磁场力远小于电场力ch11二磁场对平面载流线圈的作用如图所示均匀磁场中有一矩形刚性载流线圈mnop线圈中的电流为i磁感应强度b沿水平方向与线圈平面成求磁场对四条载流导线边的作用力根据方向相反不在一条直线上方向相反作用在同一直线上线圈在磁场中无平动线圈在磁场中有无转动
I Ild d B B d 完B 整最新ppt
16
ch11
2.电流元矢量 Idl
如图 ,I为回路导线中的电流, dl 为闭合回路导线中沿着电流
Idl
I
Idl
方向所取的一个长为dl的矢量线元,
大小:直线元的长度乘以I 方向:该点直线上电流的方向
第十一章 恒定电流的磁场(二) 作业及参考答案 2014

式中 B1 为长直导线 I1 产生的磁感应强度。
G
4
2014-2015(1)《大学物理 A(2)》作业参考答案
所以
Φ m1 = − ∫
a
2a
μ 0 I1a dr μ I a ln 2 =− 0 1 2π r 2π
3
Φ m2
μ 0 I1a ln μ I a dr 2 = −∫ 0 1 =− 2 π 2 π r 2a
K
K
匀磁场中,若 Pm 与 B 的方向相同,则通过线圈的磁通量 Φ 与线圈所受的磁力矩 M 的大小 为 (A) (C)
K
K
K
Φ = IBPm , M = 0 Φ = IBPm , M = BPm
G G
(B) (D)
Φ = BPm /I , M = 0 Φ = BPm /I , M = BPm
G K G pm ;磁力矩 M = pm × B = 0 I
α
a I1 a
3 2
3 a (如图),在维持它们的电流不变和保证共面的条件下,将它们的 2 3 5 距离从 a 变为 a ,求磁场对正方形线圈所做的功. 2 2
解: 其中
I2
a
A = I 2 (Φ m 2 − Φ m1 ) G G μI Φ m = ∫∫ B1 ⋅ dS = − ∫∫ 0 1 adr 2πr
G G G M = pm2 × B1 = 0
[
B
]3. (基础训练 7) 两根载流直导线相互正交放置, 如图 11-29
y x I2
I1 所示.I1 沿 y 轴的正方向,I2 沿 z 轴负方向.若载流 I1 的导线不能动, z 载流 I2 的导线可以自由运动,则载流 I2 的导线开始运动的趋势是 (A) 沿 x 方向平动. (B) 绕 x 轴转动. 图 11-29 (C) 绕 y 轴转动. (D) 无法判断.
大学物理第11章-恒定电流的磁场
根据对称性分析
B Bx dB sin
13
dB
0 Id l
4π r
2
Idl
R
r
*
dB
dB x
0 I cos dl
4π r2
o
x
P
x
cos R , r 2 R2 x2 r
0 IR cos d l B 2 l 4π r 4 π r3
//
// cosθ
sinθ
m 2π m R T qB qB
2πm 螺距 d // T cos qB
30
★ 安培力 安培力:磁场对载流导体的作用力。 安培定律:
dF Idl B
dF IdlB sin
0I
2 π r0
o
x
C
1
无限长载流长直导线的磁场
B
0I
2π r
⊙
电流与磁感强度成右螺旋关系
半无限长载流长直导线的磁场
1 / 2 2 π
BP
0I
4π r
I
o
r
*P
12
★ 圆形电流的磁场
Idl
B
r
dB
p *
o
R
B
x
0 Id l
4π r 2
I
dB
B dl 0 I
l ( L内)
电流 I 正负的规定 : I 与 B 成右螺旋时, I 为正;反之为负. 静电场 稳恒磁场
E dl 0
l
保守力场 非保守力场
大学物理课件 第11章 稳恒电流的磁场

讨论 (1) 积分回路方向与电流方向呈右螺旋关系。
满足右螺旋关系时 Ii 0 ,反之 Ii 0。 (2) 磁场是有旋场— 电流是磁场涡旋的轴心。
LB dl 不代表磁力的功,是磁场与电流的关系。
(3) 环路上各点的磁场为所有电流的贡献。
利用安培环路定理, 可以计算具有一定对 称性分布的载流导线周围的磁场分布。
7.2 毕奥-萨伐尔定律
一产、生毕电的奥流磁-元场萨IddBl伐 在的尔空大定间小律为P点:
Idl dB
dB
dB
o
4π
Idl sin r2
o
4π
Idl r
3
r
μ0 称为真空磁导率,
r
I
dB
P* r Idl
在国际单位制中:
o
1
oc2
4π 107 (N/A2 )
任意载B流 导线dB在 p点4处πo 的 I磁dlr感3应r 强度:
上式也称为磁感应
Idl dB
强度叠加原理。 毕奥-萨伐尔
r
定律不能由实验直 接证明, 然而由这
dB
I
个定律出发得到的
P*
结果都很好的和实
r Idl
验相符合。
二、毕奥-萨伐尔定律的应用
例2 求距离载流直导线为a
2
处一点P 的磁感应强度。
I
解
dB
0
4
Idl sin r2
r a a csc
sin( π )
l
0I rd
L 2r
cos 1 dl rd
设闭合回路l为圆形回路
0I
(l与I成右螺旋关系)
磁场的环流与环路中所包围的电流有关。
若回路绕向为顺时针
大学物理第十一章习题解答..

第十一章:恒定电流的磁场习题解答1.题号:40941001分值:10分如下图所示,是一段通有电流I 的圆弧形导线,它的半径为R ,对圆心的张角为θ。
求该圆弧形电流所激发的在圆心O 处的磁感强度。
解答及评分标准:在圆弧形电流中取一电流元l Id (1分),则该电流元l Id 在圆心处的磁感强度为: θπμπμd R I RIdl dB 490sin 40020==(2分) 其中θRd dl =则整段电流在圆心处的磁感强度为:θπμθπμθR I d R I dB B 44000===⎰⎰(2分)2.题号:40941002分值:10分一无限长的载流导线中部被弯成圆弧形,如图所示,圆弧形半径为cm R 3=,导线中的电流为A I 2=。
求圆弧形中心O 点的磁感应强度。
解答及评分标准:两根半无限长直电流在O 点的磁感应强度方向同为垂直图面向外,大小相等,以垂直图面向里为正向,叠加后得RI R I B πμπμ242001-=•-= (3分) 圆弧形导线在O 点产生的磁感应强度方向垂直图面向里,大小为R I R I B 83432002μμ==(3分) 二者叠加后得 T RI R I B B B 500121081.1283-⨯=-=+=πμμ (3分) 方向垂直图面向里。
(1分)3.题号:40941003分值:10分难度系数等级:1一段导线先弯成图(a )所示形状,然后将同样长的导线再弯成图(b )所示形状。
在导线通以电流I 后,求两个图形中P 点的磁感应强度之比。
(a ) (b )解答及评分标准:图中(a )可分解为5段电流。
处于同一直线的两段电流对P 点的磁感应强度为零,其他三段在P 点的磁感应强度方向相同。
长为l 的两段在P 点的磁感应强度为 lI B πμ4201= (2分) 长为2l 的一段在P 点的磁感应强度为 l I B πμ4202=(2分) 所以lI B B B πμ22012=+= (2分) 图(b )中可分解为3段电流。
大学物理 稳恒磁场教学文稿

大学物理稳恒磁场第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比。
§11-1 基本磁现象磁性,磁力,磁现象;磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
一、电流的磁效应1819年,丹麦科学家奥斯特发现电流的磁效应;1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B 的定义:(1)规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B 垂直的方向运动时,其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值,规定为磁场中某点磁感强度的大小。
即:qvF B max磁感强度B 是描写磁场性质的基本物理量。
若空间各点B 的大小和方向均相等,则该磁场为均匀磁场....;若空间各点B 的大小和方向均不随时间改变,称该磁场为稳恒磁场....。
磁感强度B 的单位:特斯拉(T )。
§11-3 毕奥-萨伐尔定律 一、毕-萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。
34rrlIdBd⨯=πμ式中μ0:真空磁导率,μ0=4π×10-7 NA2dB的大小:2sin4rIdldBθπμ=d B的方向:d B总是垂直于Id l与r组成的平面,并服从右手定则。
一段有限长电流的磁场:⎰⎰⨯==ll rrlIdBdB34πμ二、应用1。
一段载流直导线的磁场)cos(cos4210θθπμ-=rIB说明:(1)导线“无限长”:2rIBπμ=(2)半“无限长”:4221rIrIBπμπμ==2。
大学普通物理学习题答案-第十一章-恒定电流与恒定磁场

第十一章恒定电流与恒定磁场一、选择题1.如图11-1所示,有两根载有相同电流的无限长直导线,分别通过x1=1m、x2=3m的点,且平行于y轴,则磁感应强度B等于零的地方是()。
A.x=2m的直线上B.在x>2m的区域C.在x<1m的区域D.不在x、y平面上图11-11.【答案】A。
解析:根据对称性可得,两条载流导线在x=2m的直线上产生的磁感应强度大小相等;用右手螺旋定则可判断两磁感应强度的方向相反,相互抵消,合磁感应强度为零,故选A。
2.图11-2中6根无限长导线互相绝缘,通过电流均为I,区域Ⅰ、Ⅰ、Ⅰ、Ⅰ均为全等的正方形,哪一个区域指向纸内的磁通量最大()。
A. Ⅰ区域B. Ⅰ区域C. Ⅰ区域D. Ⅰ区域2.【答案】B。
解析:通过Ⅰ区域的磁通量为0,通过Ⅰ区城的磁通量最大且指向纸内,通过Ⅰ区域的磁通量最大但指向纸外,通过IV区域的磁通量为0。
故选B。
3.如图11-3所示,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知()。
A.d 0LB l ⋅=⎰,且环路上任意一点B =0 B.d 0LB l ⋅=⎰,且环路上任意一点B ≠0 C.d 0LB l ⋅≠⎰,且环路上任意一点B ≠0 D.d 0LB l ⋅≠⎰,且环路上任意一点B =常量3.【答案】B 。
解析:根据安培环路定理,闭合回路内没有电流穿过,所以环路积分等于0.但是由于圆形电流的存在,环路上任意一点的磁感应强度都不等于0。
故选B 。
4.无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(r <R )的磁感应强度为B i ,圆柱体外(r>R )的磁感应强度为B e ,则有:()。
A.B i 、B e 均与r 成正比B.B i 、B e 均与r 成反比C.B i 与r 成反比,B e 与r 成正比D.B i 与r 成正比,B e 与r 成反比4.【答案】B 。
解析:导体横截面上的电流密度2πR I J =,以圆柱体轴线为圆心,半径为r 的同心圆作为安培环路,当r <R ,20ππ2r J r B i ⋅=⋅μ,20π2R IrB i μ=;当r <R ,I r B e ⋅=⋅0π2μ,rIB e π20μ=;所以选D 。
大学物理学下册答案解析第11章

第11章 稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈,分别用图11-1中所示的两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为:[ ](A )10B =,20B =(B )10B =,02IB lπ=(C)01IB lπ=,20B =(D)01I B l π=,02IB lπ= 答案:C解析:有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-,并结合右手螺旋定则判断磁感应强度方向,按照磁场的叠加原理,可计算01IB lπ=,20B =。
故正确答案为(C )。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图11-2所示,则在圆心O 处的磁感应强度大小为多少? [ ]习题11-1图习题11-2图(A )0 (B )R I 2/0μ (C )R I 2/20μ (D )R I /0μ 答案:C解析:圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==,按照右手螺旋定则判断知1B 和2B 的方向相互垂直,依照磁场的矢量叠加原理,计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示,在均匀磁场B 中,有一个半径为R 的半球面S ,S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α,则通过该半球面的磁通量的大小为[ ](A )B R 2π (B )B R 22π (C )2cos R B πα (D )2sin R B πα 答案:C解析:通过半球面的磁感应线线必通过底面,因此2cos m B S R B παΦ=⋅=。
故正确答案为(C )。
11-4 如图11-4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ何变化?[ ](A )Φ增大,B 也增大 (B )Φ不变,B 也不变 (C )Φ增大,B 不变 (D )Φ不变,B 增大I习题11-4图习题11-3图答案:D解析:根据磁场的高斯定理0SBdS Φ==⎰,通过闭合曲面S 的磁感应强度始终为0,保持不变。
第11 章 恒定电流的磁场
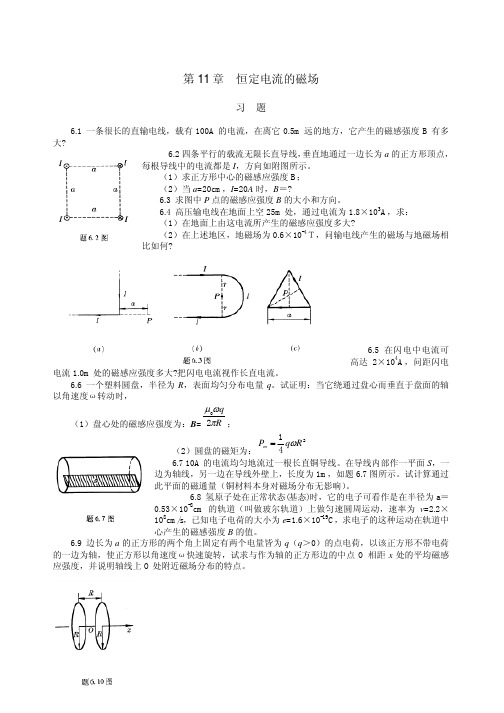
第11章 恒定电流的磁场习 题6.1 一条很长的直输电线,载有100A 的电流,在离它0.5m 远的地方,它产生的磁感强度B 有多大?6.2四条平行的载流无限长直导线,垂直地通过一边长为a 的正方形顶点,每根导线中的电流都是I ,方向如附图所示。
(1)求正方形中心的磁感应强度B ; (2)当a =20cm ,I =20A 时,B =?6.3 求图中P 点的磁感应强度B 的大小和方向。
6.4 高压输电线在地面上空25m 处,通过电流为1.8×103A ,求: (1)在地面上由这电流所产生的磁感应强度多大?(2)在上述地区,地磁场为0.6×10-4T,问输电线产生的磁场与地磁场相比如何?6.5 在闪电中电流可高达2×104A ,问距闪电电流1.0m 处的磁感应强度多大?把闪电电流视作长直电流。
6.6 一个塑料圆盘,半径为R ,表面均匀分布电量q 。
试证明:当它绕通过盘心而垂直于盘面的轴以角速度ω转动时,(1)盘心处的磁感应强度为:B =R qπωµ20;(2)圆盘的磁矩为:241R q P m ω=6.7 10A 的电流均匀地流过一根长直铜导线。
在导线内部作一平面S ,一边为轴线,另一边在导线外壁上,长度为1m ,如题6.7图所示。
试计算通过此平面的磁通量(铜材料本身对磁场分布无影响)。
6.8 氢原子处在正常状态(基态)时,它的电子可看作是在半径为a =0.53×10-8cm 的轨道(叫做玻尔轨道)上做匀速圆周运动,速率为v =2.2×108cm/s ,已知电子电荷的大小为e =1.6×10-19C ,求电子的这种运动在轨道中心产生的磁感强度B 的值。
6.9 边长为a 的正方形的两个角上固定有两个电量皆为q (q >0)的点电荷,以该正方形不带电荷的一边为轴,使正方形以角速度ω快速旋转,试求与作为轴的正方形边的中点O 相距x 处的平均磁感应强度,并说明轴线上O 处附近磁场分布的特点。
