反比例函数与二次函数
初中反比例函数与二次函数知识点详解
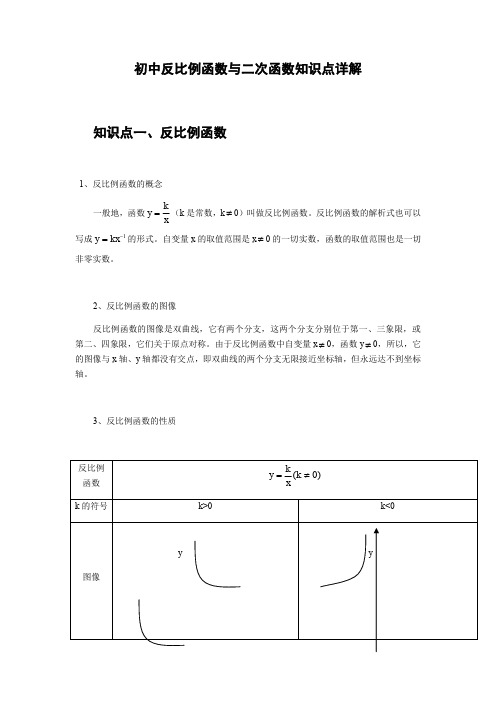
初中反比例函数与二次函数知识点详解知识点一、反比例函数1、反比例函数的概念一般地,函数xky =(k 是常数,k ≠0)叫做反比例函数。
反比例函数的解析式也可以写成1-=kx y 的形式。
自变量x 的取值范围是x ≠0的一切实数,函数的取值范围也是一切非零实数。
2、反比例函数的图像反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图像与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
3、反比例函数的性质4、反比例函数解析式的确定确定及诶是的方法仍是待定系数法。
由于在反比例函数xky =中,只有一个待定系数,因此只需要一对对应值或图像上的一个点的坐标,即可求出k 的值,从而确定其解析式。
5、反比例函数中反比例系数的几何意义如下图,过反比例函数)0(≠=k xky 图像上任一点P 作x 轴、y 轴的垂线PM ,PN ,则所得的矩形PMON 的面积S=PM ∙PN=xy x y =∙。
k S k xy xky ==∴=,, 。
知识点二、二次函数的概念和图像1、二次函数的概念一般地,如果特)0,,(2≠++=a c b a c bx ax y 是常数,,特别注意a 不为零那么y 叫做x 的二次函数。
)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向;②有对称轴;③有顶点。
3、二次函数图像的画法 五点法:(1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M ,并用虚线画出对称轴(2)求抛物线c bx ax y ++=2与坐标轴的交点:当抛物线与x 轴有两个交点时,描出这两个交点A,B 及抛物线与y 轴的交点C ,再找到点C 的对称点D 。
知识归纳:二次函数和反比例函数五点通

二次函数和反比例函数五点通二次函数和反比例函数是初中数学的重点、难点,也是中考的热点.学好二次函数和反比例函数,需要把握好如下五点.一、了解二次函数的概念一般地,形如y=ax 2+bx+c(a ,b ,c 是常数,a≠0)的函数叫做x 的二次函数. 说明: (1)a≠0是二次函数定义的组成部分,不能忽视.但b ,c 可以是任意实数,特别地,当b=c=0时,就是y=ax 2.(2)任何一个二次函数都可化为y=ax 2+bx+c 的形式,我们称之为一般式,其特征是:等号右边是关于自变量x 的二次多项式.二、理解二次函数的图象和性质1.二次函数的图象:二次函数y=ax 2+bx+c(a≠0)的图象是抛物线,它的开口方向和大小是由a 决定的,而位置则是由a ,b ,c 共同决定的.(1) a>0,抛物线开口向上; a<0, 抛物线开口向下.(2)越大,开口越小; 越小,开口越大.(3) c 是抛物线与y 轴交点的纵坐标.c=0, 抛物线经过原点; c>0, 抛物线与y 轴正半轴相交; c<0, 抛物线与y 轴负半轴相交.2.二次函数的性质:(1) 顶点:二次函数图象的顶点坐标为(ab ac a b 44,22--).当a>0时,顶点为最低点,此时函数有最小值,即当x=ab 2-时,最小值为a b ac 442-; a<0时,顶点为最高点,此时函数有最大值,即当x=ab 2-时,最大值为a b ac 442-. (2)对称性:二次函数的图象是轴对称图形,对称轴x=ab 2-是过顶点且与y 轴平行的直线(b=0时, 对称轴为y 轴).当a ,b 同号时,对称轴在y 轴左侧;当a ,b 异号时,对称轴在y 轴右侧.(3)增减性:①当a>0时,在对称轴的左侧,即x<a b 2-时, y 随x 的增大而减小,在对称轴的右侧,即x>ab 2-时, y 随x 的增大而增大;②当a<0时,在对称轴的左侧,即x<a b 2-时, y 随x 的增大而增大,在对称轴的右侧,即x>a b 2-时, y 随x 的增大而减小.三、掌握二次函数顶点坐标的求法1.公式法: 先确定出a ,b ,c 的值,再分别将其代入公式ab 2-和a b ac 442-中,计算后即可得到顶点的横、纵坐标.2.配方法:将二次函数关系式经过配方,化为y=a(x-h)2+k(a≠0)的形式,即可求得顶点坐标为(h ,k).说明:上述两种方法都是确定顶点坐标的常用方法,应根据系数a ,b ,c 的特征灵活选用.四、掌握二次函数关系式的求法求二次函数关系式的基本方法是待定系数法,根据已知条件的不同,常用如下两种形式:(1)一般式:y=ax 2+bx+c;(2)顶点式: y=a(x-h)2+k 来求函数关系式.说明: (1)求二次函数关系式的实质是确定三个系数的值,因此需要三个独立的已知条件. (2)当已知抛物线上任意三点的坐标(或函数的三对对应值)时,可选用一般式;当当已知抛物线的顶点坐标时,常用顶点式.五、反比例函数知识要点1、经历抽象反比例函数概念的过程,并能类推归纳出反比例函数的表达式2、一般地,如果两个变量x ,y 之间的关系可以表示成y=xk (k 为常数,k 不等于0)的形式,那么称y 是x 的反比例函数.从y=x k 中可知,x 作为分母,所以不能为零3、画反比例函数图像时要注意以下几点a 列表时自变量的取值应取绝对值相等而符号相反的一对数值,这样既可以简化计算,又便于标点b 列表、描点时,要尽量多取一些数值,多描一些点,这样方便连线c 在连线时要用“光滑的曲线”,不能用折线4、反比例函数的性质反比例函数()0≠=k x k y k 的取值范围 0>k 0<k图像性质 ①x 的取值范围是0≠x ,y 的取值范围是0≠y②函数图像的两个分支分别在第一、三象限,在每一个象限内y 随x 的增大而减小 ①x 的取值范围是0≠x ,y 的取值范围是0≠y ②函数图像的两个分支分别在第二、四象限,在每一个象限内y 随x 的增大而增大 注意:1)反比例函数是轴对称图形和中心对称图形;2)双曲线的两个分支都与x 轴、y 轴无限接近,但永远不能与坐标轴相交;3)在利用图像性质比较函数值的大小时,前提应是“在同一象限”内。
二次函数与反比例函数的对应关系与应用

二次函数与反比例函数的对应关系与应用在数学中,二次函数和反比例函数是常见的数学函数类型之一。
二次函数是指形式为f(x) = ax^2 + bx + c的函数,其中a、b、c为常数且a ≠ 0;而反比例函数是指形式为f(x) = k/x的函数,其中k是常数且k ≠ 0。
本文将深入探讨二次函数与反比例函数之间的对应关系以及它们在实际生活中的应用。
一、二次函数与反比例函数之间的对应关系在数学中,二次函数与反比例函数之间存在一定的对应关系。
具体来说,当二次函数的自变量和函数值互换位置时,可以得到一个对应的反比例函数。
例如,对于二次函数f(x) = ax^2 + bx + c,可以将自变量x和函数值f(x)互换位置后得到新的函数g(x) = a/f(x)。
通过这种方式,二次函数和反比例函数之间可以建立一种对应的关系。
这种对应关系在数学中是有一定意义的。
通过分析二次函数和反比例函数之间的对应关系,可以深入理解两者之间的性质和特点。
在实际应用中,这种对应关系也为求解二次函数和反比例函数提供了一种有效的方法。
二、二次函数与反比例函数的应用二次函数和反比例函数在实际生活中有着广泛的应用。
下面将介绍它们在几个不同领域的具体应用。
1. 物理学:二次函数和反比例函数在物理学中经常被用来描述物体的运动和变化规律。
例如,通过使用二次函数,可以分析抛物线轨迹下的物体运动情况;反比例函数则可以描述两个变量之间的相对关系,比如在光学中的透镜成像过程中。
2. 经济学:二次函数和反比例函数在经济学领域中有着广泛的应用。
例如,二次函数可以用来描述成本、收益和利润之间的关系,帮助经济学家制定相关政策和决策;反比例函数则可以用来描述供求关系中的价格与需求量或供给量之间的关系。
3. 工程学:在工程学中,二次函数和反比例函数被广泛应用于各种设计和分析中。
例如,通过使用二次函数可以优化车辆行驶的轨迹,降低能耗和成本;反比例函数可用于电路设计中的电阻或电容的选取。
反比例函数、二次函数知识梳理

反比例函数核心知识梳理1.反比例函数的定义:一般地,形如y=k/x(k是常数,且k≠0)的函数叫做反比例函数.其表达式还可写为y=kxˉ¹(k≠0)或xy=k(k≠0).对此概念要注意以下几点:①k是常数,且k≠0.②自变量x在分母中的指数为1,如y=3/x²就不是反比例函数.③自变量x的取值范围是x≠0的全体实数,函数y 的取值范围是y≠0的全体实数。
2.反比例函数的图像:反比例函数y=k/x(k是常数,且k≠0)的图像由两支曲线组成,称为“双曲线”.其图像具有以下特点:①图像的两个分支分别在不同的象限,不能连接起来.②由于在反比例函数中,x和y的值都不能为0,所以画出的双曲线的两个分支要分别体现出无限的接近坐标轴,但永远不能达到x轴和y轴的变化趋势。
③图像既是轴对称图形也是中心对称图形,对称轴是y=x或y=-x,对称中心为原点.④画反比例函数的图像时,可先画出一个分支,然后根据对称性画出另一分支。
3.反比例函数的性质:当k>0时,图像的两个分支在一、三象限,在每个象限内,y随x的增大而减小;当k<0时,图像的两个分支在二、四象限,在每个象限内,y随x的增大而增大。
4.反比例函数解析式的确定:由于反比例函数y=k/x只有一个比例系数k,所以只要知道一组x、y的值或图像任意一点的坐标,就可确定反比例函数的解析式,进而解决相关问题。
考点易错点解析反比例函数是中考的必考内容,题型有选择题、填空题和解答题,其考点主要体现在以下几个方面:①求反比例函数的解析式②领悟反比例函数的意义,确定函数图像的位置③已知函数图像,求参数的值或取值范围,以及函数增减性的确定④利用反比例函数解决有关实际应用问题⑤反比例函数与其他函数、方程(组)、不等式(组)的有关综合问题。
有关本部分内容再解题中应注意以下几点,以避免错误的解答:1.注意反比例函数y=k/x的表达式成立的限制条件是k≠0,不要忽视这一点2.正确区分反比例与反比例函数,避免因混淆相关概念而出错。
二次函数和反比例函数的知识点

二次函数知识点1:二次函数的概念形如y=ax2+bx+c (a≠0, a,b,c是常数)的函数叫做二次函数.知识点2:在理解二次函数的定义时,应注意下述问题:(1) 在解析式中最高项是ax2项且系数a≠0,而b,c可以不为零,也可以为零。
(2) 自变量x的取值范围是任何实数.(3) 如果a=0,则该函数一定不是二次函数,但不一定是一次函数,如果a=0,b≠0才是一次函数。
知识点3:用二次函数描述有关实际问题中的变量间的关系在实际生活中,变化规律,解决实际问题,如何建立实际问题中的二次函数关系式(1)审清题意,找出实际问题中的已知量(定量),未知量(变量)并分析它们之间的关系,将文字或图形语言转化为数学符号语言.(2)建立函数关系式,根据前面的思考和分析,得到函数关系,即用自变量解析式来表示函数,并判断它是否为二次函数.(3) 确定函数的定义域,在实际问题中,变量都有一定的实际意义,要受到一定的条件限制,所以在求出二次函数解析式时,还要指明它的定义域.知识点4:二次函数的画法:(1)先列表;(2)描点,(3)连线.2函数开口方向顶点坐标对称轴函数变化最大(小)值y=ax2 a>向上(0,0) y轴x>0时,y随x增大而增大x<0时,y随x增大而减小当x=0时,y最大=0y=ax2 a<向下(0,0) y轴x>0时,y随x增大而减小x<0时,y随x增大而增大当x=0时y最大=0知识点6:.二次函数y=ax2+k的图象二次函数y=ax2+k的图象是由函数y=ax2的图象上、下平移得到的,当k>0时,抛物线y=ax2向上平移︱k︱个单位得到y=ax2+k的图象;当k<0时,抛物丝y=ax2向下平移︱k︱个单位得到y=ax2+k的图象.注意:抛物线y=ax2+k与抛物丝y=ax2形状完全相同,开口方向相同,对称轴都是y轴,但顶点位置不同,y=ax 2的顶点是(0,0),y=ax 2+k 的顶点是(0,k ),,顶点在y 轴上. 知识点7:.二次函数y=a (x -h )2的图象二次函数y=a (x -h )2的图象可由抛物线y=ax 2向左(或向右)平移而得到,当n >0时,抛物线y=ax 2向右平称︱n ︱个单位,得到y=a (x -n )2的图象;当n <0时,抛物线y=ax 2向左平移︱n ︱个单位得到y=a (x -n )2的图象.注意:抛物线y=a (x -n )2与抛物线y=ax 2的形状完全相同,开口相同只是在坐标系中的位置不同,抛物线y=a (x -n )2的对称轴是x=n ,顶点是(n ,0),顶点在x 轴上. 知识点8:.二次函数y=a (x -n )2+k 的图象1)二次函数y=a (x -h )2+k (a ≠0)与二次函数y=ax 2(a ≠0)的图象都是抛物线,在a 相等的情况下,形状相同,只是位置不同。
二次函数及反比例函数知识点

二次函数及反比例函数知识点二次函数和反比例函数是初中和高中数学中经常涉及的函数。
它们在数学上有着重要的应用,同时也具有一定的难度。
下面我们来详细介绍二次函数和反比例函数的知识点。
一、二次函数1. 定义:二次函数是指形如y = ax^2 + bx + c的函数,其中a、b、c为实数,且a≠0。
2.二次函数的图像:二次函数的图像是一个开口朝上或开口朝下的抛物线。
当a>0时,抛物线开口朝上;当a<0时,抛物线开口朝下。
3.二次函数的性质:(1) 顶点坐标:二次函数的顶点坐标为(-b/2a, f(-b/2a)),其中f(x)=ax^2 + bx + c。
(2)对称轴:顶点坐标为(-b/2a,f(-b/2a))的直线称为二次函数的对称轴,方程为x=-b/2a。
(3)开口方向:二次函数的开口方向取决于系数a的正负。
(4) 判别式:二次函数ax^2 + bx + c的判别式为Δ = b^2 - 4ac,当Δ > 0时,二次函数有两个不相等的实根;当Δ = 0时,有两个相等的实根;当Δ < 0时,无实根。
4.二次函数的平移:二次函数的横向平移和纵向平移可以通过对函数的自变量和因变量进行平移操作实现。
5.二次函数的解析式:通过给定的定点和顶点坐标,可以确定一条与x轴相交的二次函数。
6.二次函数的应用:二次函数在数学和物理等领域有着广泛的应用,如碰撞问题、抛物线运动等。
二、反比例函数1.定义:反比例函数是指形如y=k/x的函数,其中k为非零实数。
2.变化规律:反比例函数的特点是随着x的增大,y的值会逐渐减小;反之,随着x的减小,y的值会逐渐增大。
3.反比例函数的性质:(1)零点:当x≠0时,y=0称为反比例函数的零点。
(2)渐近线:反比例函数y=k/x的图像有两个渐进线x=0和y=0。
(3)对称性:反比例函数的图象关于坐标轴对称。
(4)奇函数:反比例函数是一个奇函数,满足f(-x)=-f(x)。
二次函数及反比例函数知识点

二次函数及反比例函数知识点二次函数是高中数学中的重要内容之一,它在数学建模、物理学、经济学等领域中有广泛应用。
本文将介绍二次函数的定义、性质以及常见的应用,同时也会介绍反比例函数的定义、性质和应用。
二次函数的定义与性质二次函数是形如y = ax^2 + bx + c的方程,其中a、b、c为实数且a ≠ 0。
其中,a决定了二次函数的开口方向,当a > 0时,函数图像开口向上,当a < 0时,函数图像开口向下。
b决定了二次函数的对称轴的位置,对称轴的方程为x = -b/(2a)。
c则决定了二次函数的纵坐标平移。
二次函数的图像通常是一个抛物线,根据a、b、c的具体取值,抛物线可以与x轴相切、相交或者没有交点。
当抛物线与x轴相交时,方程的解即为交点的横坐标。
当抛物线有最小值时,最小值的纵坐标为抛物线的顶点。
二次函数还有一些特殊的形式,例如完全平方式和标准形式。
完全平方式的二次函数为y = a(x - h)^2 + k,其中(h, k)为顶点坐标。
标准形式的二次函数为y = a(x - h)(x - k),其中(h, 0)和(k, 0)为x轴上两个交点的坐标。
二次函数的应用二次函数在现实生活中有很多应用。
其中,最常见的是抛物线的运动轨迹问题。
例如,一个抛物线可以描述一个抛出的物体在经过一段时间后的运动情况。
我们可以利用二次函数来计算物体的高度、速度等信息。
二次函数在经济学中也有广泛应用。
例如,成本函数、收益函数等都可以用二次函数来表示。
这样一方面可以方便计算和优化,另一方面也可以通过分析二次函数的图像来研究经济问题的特性。
反比例函数的定义与性质反比例函数是形如y = k/x的方程,其中k为常数且k ≠ 0。
反比例函数的定义域为除了x = 0以外的所有实数,值域为除了y = 0以外的所有实数。
反比例函数的图像是一条经过原点的双曲线,其特点是随着x的增大而逐渐趋近于x轴,随着x的减小而逐渐趋近于y轴。
二次函数和反比例函数的知识点

二次函数和反比例函数的知识点一、二次函数的知识点(600字)1. 二次函数的定义:二次函数是指形如f(x) = ax² + bx + c的函数,其中a、b、c是给定的常数,且a≠0。
2.二次函数的图像:二次函数的图像是一条开口向上或向下的抛物线。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
3.抛物线的顶点:二次函数的顶点坐标可以通过公式x=-b/(2a)得到。
即在二次函数的图像中,顶点的横坐标为减去b再除以2a,纵坐标为代入这个横坐标后的函数值。
4.抛物线的对称轴:二次函数的对称轴是过顶点的直线,其方程可以表示为x=-b/(2a)。
5.抛物线的焦点和准线:二次函数的焦点和准线与二次函数的系数a有关。
当a>0时,抛物线有焦点且焦点在开口的上方,准线在抛物线下方;当a<0时,抛物线有焦点且焦点在开口的下方,准线在抛物线上方。
6. 零点和交点:二次函数的零点是使得f(x) = 0的解,可以通过求解ax²+bx+c=0的二次方程来得到。
交点是抛物线与x轴或y轴相交的点。
7. 判别式与二次函数的性质:判别式D = b²-4ac可以用来判断二次方程ax²+bx+c=0的解的性质。
当D>0时,方程有两个不相等的实数解;D=0时,方程有两个相等的实数解;D<0时,方程没有实数解。
8. 二次函数的不等式:对于二次函数f(x) = ax² + bx + c,可以通过将f(x)关于x的表达式移到一边,得到ax²+bx+c>0或ax²+bx+c<0的二次不等式。
二、反比例函数的知识点(600字)1.反比例函数的定义:反比例函数是指形如f(x)=k/x的函数,其中k是一个常数,且k≠0。
也称为倒数函数。
2.反比例函数的图像:反比例函数的图像是一条经过原点的曲线,其特点是随着自变量x的增大,函数值f(x)单调递减。
二次函数与反比例函数初步总结

二次函数与反比例函数初步总结
二次函数是指最高次项为二次项的多项式函数,通常是形如
y=ax²+bx+c的函数,其中a、b、c为常数,a不等于0。
二次
函数的图像为抛物线,有开口方向、顶点和对称轴等特征。
二次函数的图像可以是开口向上的,即a>0;也可以是开口向下的,即a<0。
二次函数的性质包括:
1. 开口方向:a>0时,抛物线开口向上;a<0时,抛物线开口
向下。
2. 顶点:当a>0时,顶点为图像的最低点;当a<0时,顶点为图像的最高点。
3. 对称轴:对称轴是与y轴垂直且通过顶点的直线,方程为x = -b/2a。
反比例函数是指函数y=k/x,其中k为常数且不等于0。
反比
例函数的图像通常为双曲线。
反比例函数的性质包括:
1. 定义域:反比例函数的定义域为x ≠ 0,即不含有x=0的点。
2. 值域:反比例函数的值域为y ≠ 0,即不含有y=0的点。
3. 变化趋势:当x增大时,y的值减小;当x减小时,y的值
增大。
可以通过构造反比例函数的表格来观察这种变化趋势。
总结:二次函数和反比例函数是两种常见的函数形式。
二次函
数是抛物线,其图像的特征包括开口方向、顶点和对称轴;反比例函数是双曲线,其图像的特征包括定义域、值域和变化趋势。
理解这些特征和性质有助于我们对二次函数和反比例函数的图像和变化趋势等方面进行分析和应用。
反比例函数与二次函数

反比例函数与二次函数在数学中,反比例函数和二次函数都是常见的函数类型,它们在不同的数学问题中具有不同的应用和特点。
本文将从定义、图像、性质、应用等方面介绍反比例函数和二次函数的相关知识。
一、反比例函数1. 定义:反比例函数是指两个变量之间的关系,其中一个变量的值与另一个变量的值成反比。
一般而言,反比例函数的形式可以表示为 y = k/x (其中k ≠ 0),x 和 y 分别表示两个变量,k 为常数。
2. 图像:反比例函数的图像呈现出一条从第一象限原点 (0, 0) 开始的曲线,并向 x 轴和 y 轴无限延伸。
其特点是随着 x 的增大,y 的值逐渐减小;反之,随着 x 的减小,y 的值逐渐增大。
这种关系如同两个变量的“倒数”关系。
3. 性质:(1)反比例函数的定义域为除了 x = 0 的所有实数,值域为除了 y= 0 的所有实数。
(2)反比例函数的图像关于 y 轴和 x 轴对称。
(3)反比例函数的渐近线分别为 x 轴和 y 轴。
当 x 趋向于正无穷大或负无穷大时,y 趋向于 0。
4. 应用:反比例函数在实际问题中具有广泛的应用,如电阻与电流的关系、速度与时间的关系等。
反比例函数的特性使得在一些情况下,两个变量之间的变化趋势可以用反比例函数来表示和计算。
二、二次函数1. 定义:二次函数是指一个变量的平方与另一个变量之间的关系。
一般而言,二次函数的形式可以表示为 y = ax^2 + bx + c,其中 a、b 和 c 为常数,且a ≠ 0。
2. 图像:二次函数的图像呈现出一个开口向上或向下的抛物线。
开口的方向由二次项系数 a 的正负决定。
当 a > 0 时,抛物线开口向上;当 a < 0 时,抛物线开口向下。
3. 性质:(1)二次函数的定义域为所有实数,值域视图像的开口方向而定。
(2)二次函数的顶点为抛物线的最高点或最低点,其 x 坐标为 -b/2a,y 坐标可以通过代入计算得出。
(3)二次函数的对称轴为通过顶点的直线。
二次函数和反比例函数的交点

二次函数和反比例函数的交点二次函数和反比例函数,是中学数学中重要的两类函数。
它们的交点有其特殊的含义和应用。
一、二次函数的基本概念二次函数是指函数的自变量为二次元的函数,通常表现为 y = ax^2 + bx + c 的形式,其中 a 为非零实数,称为二次项系数,b 和 c 分别为实数,称为一次项系数和常数项。
二次函数与抛物线的关系密不可分。
二次函数的图像是一个关于 y 轴对称的抛物线,开口方向为上或下,取决于 a 的正负。
当 a > 0 时,二次函数的图像开口向上;当 a < 0 时,图像开口向下。
二次函数有很强的求最值能力,一般应用于对关于某一自变量的抛物线物理问题的建模、求解等。
二、反比例函数的基本概念反比例函数是指函数的形式为 y = k/x 的函数,其中k 为非零实数,称为比例系数。
这种函数的图像是一个关于 x 轴和 y 轴的反比例曲线,通常呈现一条双曲线的形式。
抛物线则是它的变形。
反比例函数一般被用于描述“比例”的关系,如人数、价格、速度等,通常在物理、经济、生物中广泛应用。
反比例函数的一个重要的性质是,当 x 趋近于 0 时,函数值趋向无穷大或无穷小,具有良好的定义域和值域。
三、二次函数和反比例函数的交点对于二次函数与反比例函数,它们的图像通常不会相交,因为它们的开口方向是不同的。
但是当特殊的条件满足时,它们的图像可以交于一点,这一点也是二次函数和反比例函数的交点。
这些条件包括但不限于以下情形:1. 当二次函数与反比例函数都对于 y 轴对称时,它们的交点一定在 y 轴上,且 y 坐标相等。
2. 当二次函数与反比例函数的交点在第一象限时,其横坐标和纵坐标均为正数。
3. 当二次函数与反比例函数的交点在第三象限时,其横坐标和纵坐标均为负数。
在应用问题中,二次函数和反比例函数的交点可能有多种解释。
例如在物理问题中,它可能表示物体运动过程中的某个时刻,速度和距离相等的情况。
在经济学中,交点可能代表产量和成本的平衡点,即收益最大点。
反比例函数与二次函数的交点问题

反比例函数与二次函数的交点问题哎,今天咱们聊聊反比例函数和二次函数的交点问题。
这可是个挺有趣的数学话题,别看名字听起来复杂,其实只要抓住关键,没那么难。
反比例函数嘛,就是那种像个乖乖虎,永远不跟你对称,总是保持着一种奇特的关系。
想想看,y=1/x,这样的函数图像在坐标系里就像一个优雅的舞者,左边和右边对称,却永远不接触。
说到这里,脑海中不禁浮现出一句老话:水火不容。
这也是反比例函数的一个特点,数值一大,另一边就小,真是妙不可言。
然后咱们再说说二次函数,哎哟,那可是个调皮的家伙。
它的标准形式是y=ax²+bx+c,听起来是不是像在唱歌?二次函数的图像是一条优美的抛物线,开口向上或向下,像极了春天里的小花朵,随风摇曳。
你瞧,它跟反比例函数的碰撞,就像两位舞者在舞池中相遇,互相辉映。
想象一下,一个是灵巧的旋转,一个是稳重的步伐,组合起来,绝对是绝妙的化学反应。
交点在哪呢?要找这两者的交点,其实就是求它们的解。
很简单,咱们把反比例函数的表达式代入到二次函数中,或者反过来。
就像拼图一样,把不同的片段放到一起,看看有没有合适的地方。
可以说,解这个方程就是寻找“好兄弟”的过程,两个函数的交点就像命运的交错,可能一见如故,也可能擦肩而过。
这其中的奥妙,仿佛在告诉我们人生的哲理:不一定每次相遇都有结果,但每一次交集都值得我们去探索。
想想看,反比例和二次的交点,有可能是两个实数,也可能是两个虚数,甚至还有可能是一重根。
说实话,这就像人生的各种选择,咱们常常在岔路口犹豫不决。
碰上这种情况,难免有些抓狂,但这也让人觉得,嘿,生活真是充满了惊喜,没准儿下一个拐角就能遇到美好呢。
解完这个方程,回头看看,你会发现那些交点,就像你生命中的朋友,虽不常见,却总能给你带来新的视角。
再说了,生活中的每个交点,也都充满了挑战。
假如你遇到一个交点难解,那不妨换个角度,试试不同的方法。
就像解决问题,永远不要固步自封。
今天我们找的是函数的交点,明天可能就是找工作的面试,都是一场“博弈”。
二次函数及反比例函数知识点

二次函数及反比例函数知识点1.定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的二次函数.2.二次函数2ax y =的性质(1)抛物线2ax y =)(0≠a 的顶点是坐标原点,对称轴是y 轴.(2)函数2ax y =的图像与a 的符号关系.①当0>a 时⇔抛物线开口向上⇔顶点为其最低点;②当0<a 时⇔抛物线开口向下⇔顶点为其最高点3.二次函数 c bx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线.4.二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中ab ac k a b h 4422-=-=,.5.二次函数由特殊到一般,可分为以下几种形式: ①2axy =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2.6.抛物线的三要素:开口方向、对称轴、顶点. ①a 决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 相等,抛物线的开口大小、形状相同. ②平行于y 轴(或重合)的直线记作h x =.特别地,y 轴记作直线0=x .7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. 8.求抛物线的顶点、对称轴的方法(1)公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=,最值为纵坐标.(2)配方法:运用配方法将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是h x =.(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点. 9.抛物线c bx ax y ++=2中,c b a ,,的作用(1)a 决定开口方向及开口大小,这与2ax y =中的a 完全一样.(2)b 和a 共同决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2的对称轴是直线ab x 2-=,故:(左同右异)①0=b 时,对称轴为y 轴;②0>ab (即a 、b 同号)时,对称轴在y 轴左侧;③0<ab (即a 、b 异号)时,对称轴在y 轴右侧.(3)c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置.当0=x 时,c y =,∴抛物线c bx ax y ++=2与y 轴有且只有一个交点(0,c ):①0=c ,抛物线经过原点; ②0>c ,与y 轴交于正半轴;③0<c ,与y 轴交于负半轴. 以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在y 轴右侧,则 0<ab .10.几种特殊的二次函数的图像特征如下:函数解析式 开口方向对称轴 顶点坐标 2ax y =当0>a 时开口向上当0<a 时开口向下0=x (y 轴)(0,0) k ax y +=20=x (y 轴) (0, k ) ()2h x a y -= h x = (h ,0) ()k h x a y +-=2h x = (h ,k )c bx ax y ++=2ab x 2-=(ab ac a b 4422--,) 11.用待定系数法求二次函数的解析式(1)一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.(3)交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=.12.直线与抛物线的交点(1)y 轴与抛物线c bx ax y ++=2得交点为(c ,0)(2)与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2). (3)抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离. (4)平行于x 轴的直线与抛物线的交点同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.(5)一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组⎩⎨⎧++=+=c bx ax y nkx y 2的解的数目来确定: ①方程组有两组不同的解时⇔l 与G 有两个交点;②方程组只有一组解时⇔l 与G 只有一个交点;③方程组无解时⇔l 与G 没有交点. (6)抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故ac x x a b x x =⋅-=+2121,()()a a acb a ca b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=--=-=-=44422212212212113.二次函数与一元二次方程的关系:(1)一元二次方程c bx ax y ++=2就是二次函数c bx ax y ++=2当函数y 的值为0时的情况.(2)二次函数c bx ax y ++=2的图象与x 轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数c bx ax y ++=2的图象与x 轴有交点时,交点的横坐标就是当0=y 时自变量x 的值,即一元二次方程02=++c bx ax 的根.(3)当二次函数c bx ax y ++=2的图象与x 轴有两个交点时,则一元二次方程c bx ax y ++=2有两个不相等的实数根;当二次函数c bx ax y ++=2的图象与x 轴有一个交点时,则一元二次方程02=++c bx ax 有两个相等的实数根;当二次函数c bx ax y ++=2的图象与x 轴没有交点时,则一元二次方程02=++c bx ax 没有实数根14.二次函数的应用:(1)二次函数常用来解决最优化问题,这类问题实际上就是求函数的最大(小)值;(2)二次函数的应用包括以下方面:分析和表示不同背景下实际问题中变量之间的二次函数关系;运用二次函数的知识解决实际问题中的最大(小)值.15. 解决实际问题时的基本思路:(1)理解问题;(2)分析问题中的变量和常量;(3)用函数表达式表示出它们之间的关系;(4)利用二次函数的有关性质进行求解;(5)检验结果的合理性,对问题加以拓展等. 反比例函数1.反比例函数的图像是双曲线,xky =(k 为常数,0≠k )中自变量0≠x ,函数值0≠y ,所以双曲线是不经过原点,断开的两个分支,延伸部分逐渐靠近坐标轴,但是永远不与坐标轴相交。
初中数学 反比例函数和二次函数的图像有何区别

初中数学反比例函数和二次函数的图像有何区别反比例函数和二次函数是两种不同的函数类型,它们的图像具有一些显著的区别。
在下文中,我将详细介绍这些区别。
反比例函数的图像通常是曲线,而二次函数的图像则是一条曲线。
1. 反比例函数的图像:反比例函数的一般形式为y = k/x,其中k 是非零常数。
反比例函数的图像通常是一条曲线,曲线的形状取决于函数的参数k。
具体来说,反比例函数的图像是一个通过原点的双曲线。
当x 趋近于零时,y 的值趋近于无穷大或无穷小。
随着x 的增大,曲线逐渐趋近于x 轴。
反比例函数的图像具有原点对称性和轴对称性。
2. 二次函数的图像:二次函数的一般形式为y = ax^2 + bx + c,其中a、b、c 是常数且a 不等于零。
二次函数的图像通常是一条抛物线。
抛物线的开口方向取决于二次项的系数 a 的正负。
当a 大于零时,抛物线开口向上;当 a 小于零时,抛物线开口向下。
二次函数的图像关于一个对称轴对称,这个对称轴被称为抛物线的轴。
抛物线的轴与y 轴的交点称为顶点。
下面是一些具体的区别:1. 形状:反比例函数的图像是一条通过原点的双曲线,而二次函数的图像是一条抛物线。
2. 对称性:反比例函数的图像具有原点对称性和轴对称性,而二次函数的图像具有关于抛物线的轴对称性。
3. 开口方向:反比例函数的图像没有固定的开口方向,而二次函数的图像的开口方向由二次项的系数a 的正负决定。
4. 零点:反比例函数的图像与x 轴相交于x 不等于零的点,而二次函数的图像与x 轴相交于零点。
总的来说,反比例函数和二次函数的图像具有明显的区别。
反比例函数的图像是一条通过原点的双曲线,而二次函数的图像是一条抛物线。
它们的对称性、形状和开口方向都不相同。
这些区别是我们在学习和理解这两种函数时需要注意的重要特征。
初中数学(4)--函数(2)--反比例函数与二次函数

6.(2005 徐州) 已知正比例函数 1).求这两个函数关系式.
y k1 x 与反比例函数 y
k2 x
的图象都经过点(2,
7. (2004 贵阳)如图,一次函数
y ax b 的图象与反比例函数 y
k 的图象交于 M 、 N 两点 . x
17 已知关于x的一次函数y=(m-1)x+7,如果y随x的增大而减小,则m的取值范围是 18 某乡粮食总产值为m吨,那么该乡每人平均拥有粮食y(吨) ,与该乡人口数x的函数关系式是 19、函数y= x-5 中,自变量x的取值范围 (A)x>5 (A)第一象限 (A)0 (B)x<5
2
( (
) (D)x≥5 ) (D) 第四象限 ( ) ) (D) (3,-5)
y O
3/5
y x O x
y O x
y O x
数学复习
版权所有,翻版必究
By fangjiyong
y 4. (2005 安徽)任意写出一个图象经过二、 四象限的反比例函数的解析式:__________ M(2,m) O N(-1,-4) x
k 2 5. (2005 苏州)已知反比例函数 y ,其图象在第一、第三象限内,则 k 的值 x
28.某幢建筑物,从 10 米高的窗口 A 用水管和向外喷水,喷的水流呈抛物线(抛物线所在平 面与墙面垂直, (如图)如果抛物线的最高点 M 离墙 1 米,离地面 距离 OB 是( (A)2 米 ) (B)3 米 (C)4 米 (D)5 米 40 米,则水流下落点 B 离墙 3
29.求下列函数的最大值或最小值. (1)
x1 x2 2 y1 y2 2
2、函数平移规律(中考试题中,只占 3 分,但掌握这个知识点,对提高答题速度有很大帮 助,可以大大节省做题的时间)左加右减、上加下减 随堂练习:
九年级 反比例函数与二次函数

第一章 反比例函数一、反比例函数的定义:若两个变量x ,y 可以表示成为x k y =(k ≠0)的形式,则我们称y 是x 的反比例函数。
二、反比例函数的判定方法:1、函数解析式满足形如xk y =(k ≠0)的形式; 2、如果两个变量的积为常数,则两个变量建立的是反比例函数;3、如果函数的图像是双曲线或双曲线的某一支,则这两个变量建立的是反比例函数。
三、反比例函数的图像:反比例函数的图像是双曲线,并且位于坐标系的一三象限或二四象限;当k >0时,在一三象限;k <0,则在二四象限四、反比例函数的性质:当k >0时,在每一个象限内,y 随x 的增大而减小;当k <0时,在每一个象限内,y 随x 的增大而增大。
五、函数表达式的确定:反比例函数的解析式的确定,只需确定k 值即可,所以一般只需在图像找任意一点带进去求k 值即可。
第二章 二次函数一、二次函数的定义:形如c bx ax y ++=2(a ≠0,a 、b 、c 为常数)的函数叫做x 的二次函数。
二次函数的另一种形式:ab ac a b x a y 44)2(22-++=二、二次函数的特殊形式:1、当b =c =0时,函数解析式形如2ax y =;2、当b =0时,函数解析式形如c ax y +=23、当c =0时,函数解析式形如bx ax y +=2三、二次函数的图像:二次函数的图像是一条抛物线。
二次函数是轴对称图形。
四、二次函数的开口问题:二次函数的开口方向和开口大小只与a 值有关。
a >0时,开口向上;a <0时,开口向下。
五、二次函数的对称轴问题:二次函数的对称轴为ab x 2-= 六、二次函数的交点问题:二次函数的交点与判别式ac b 42-=∆有关。
当△>0时,有两个交点;当△=0时,有一个交点;△<0时,没有交点。
七、二次函数的最值问题:当a <0时有最大值,当a >0时有最小值。
八、顶点坐标为⎪⎪⎭⎫ ⎝⎛--a ac b a b 4422,;当x =0时的坐标为(0,c ) 九、韦达定理:044)2(0222=-++⇒=++a b ac a b x a c bx ax aac b b x a ac b b x 24242221---=-+-=, ac x x a b x x =-=+2121,十、二次函数的三种表达式:1、一般式:c bx ax y ++=22、顶点式:()k m x a y ++=23、交点式:()()21x x x x a y --=十一、二次函数与二次不等式:(难点,根据图像去理解)。
二次函数及反比例函数知识点

二次函数及反比例函数知识点二次函数是一种重要的数学函数形式,其形式为 f(x) = ax^2 + bx + c,其中 a、b、c 是实数,且a ≠ 0。
这种函数在数学和科学中有广泛的应用。
反比例函数也是常见的函数形式,其形式为 f(x) = k/x,其中 k 是非零常数。
本文将介绍二次函数和反比例函数的基本性质和应用。
一、二次函数的基本性质1. 定义域和值域:二次函数 f(x) = ax^2 + bx + c 的定义域为全体实数,值域的范围取决于二次函数的开口方向和 a 的正负性。
当 a > 0 时,二次函数的开口向上,值域为[f(c), ∞)。
当 a < 0 时,二次函数的开口向下,值域为 (-∞, f(c)]。
2. 对称轴和顶点:二次函数的对称轴为 x = -b/2a,对称轴将二次函数分成两个对称的部分。
二次函数的顶点为 (-b/2a, f(-b/2a)),是二次函数的最值点。
3. 最值点和开口方向:当二次函数的开口向上时,顶点是最小值点,当二次函数的开口向下时,顶点是最大值点。
4. 零点与判别式:二次函数的零点是函数的解,即满足 ax^2 + bx + c = 0 的 x 值。
二次函数的判别式Δ = b^2 - 4ac 可以用来判断二次函数的零点情况:a) 当Δ > 0 时,二次函数有两个不相等的实数根;b) 当Δ = 0 时,二次函数有两个相等的实数根;c) 当Δ < 0 时,二次函数没有实数根。
二、二次函数的应用1. 抛物线运动:抛物线运动是二次函数的经典应用,它可以描述抛射物体的运动轨迹。
通过控制二次函数的参数,可以调节抛射物的抛射角度和最远射程。
2. 优化问题:二次函数经常被用于解决优化问题,如寻找函数的最大值或最小值。
例如,在生产制造中,可以利用二次函数来确定产品的最佳产量和成本。
三、反比例函数的基本性质1. 定义域和值域:反比例函数 f(x) = k/x 的定义域为除了 x = 0 外的全体实数,值域也为除了 k = 0 外的全体实数。
二次函数与反比例函数初步总结

二次函数与反比例函数初步总结二次函数和反比例函数是高中数学中重要的内容,而且在实际生活中也有广泛的应用。
本文将对二次函数和反比例函数进行初步总结,主要包括定义、特点、图像、性质等方面的内容。
一、二次函数1. 定义:二次函数是形如y = ax² + bx + c(a ≠ 0)的函数,其中a、b、c是已知的实数,a表示二次项的系数,b表示一次项的系数,c 表示常数项。
2.特点:(1)曲线的形状:二次函数的图像是一条平滑的曲线,且开口方向由二次项系数a的正负决定。
-当a>0时,开口向上,形如"U"形;-当a<0时,开口向下,形如"倒U"形。
(2) 零点:二次函数的零点是函数图像与x轴的交点,即满足y = 0的x值。
二次函数的零点个数与判别式Δ(即b²-4ac)有关:-当Δ>0时,二次函数有两个不同的零点;-当Δ=0时,二次函数有两个相等的零点;-当Δ<0时,二次函数没有实数解,无零点。
(3)对称轴:二次函数的对称轴是函数图像的中心线,也是二次函数图像的对称轴。
对称轴的方程为x=-b/2a。
(4)极值点:二次函数的极值点是函数图像的最高点或最低点,也是对称轴上的点。
极值点的纵坐标为y轴上的最小值或最大值。
3.图像:通过画出对称轴、极值点、零点等关键点,可以得到二次函数的图像。
通过连接关键点,就能画出完整的二次函数曲线。
二、反比例函数1.定义:反比例函数是形如y=k/x的函数,其中k是常数,x≠0。
2.特点:(1)曲线的形状:反比例函数的图像是一条拱形曲线,且通过原点(0,0)。
当x趋近于正无穷或负无穷时,函数值趋于0。
(2)反比例关系:反比例函数表达了两个变量之间的反比关系,即一个变量的增大导致另一个变量的减小,反之亦然。
(3)单调性:反比例函数在定义域内是单调的,即x增大导致y减小,x减小导致y增大。
(4)随x趋于0的变化:当x趋近于0时,y的绝对值趋近于无穷大,即y趋于正无穷或负无穷。
二次函数与反比例函数二次函数与反比例函数的综合应用

二次函数与反比例函数二次函数与反比例函数的综合应用随着数学的发展,二次函数与反比例函数的综合应用在现实生活中扮演着重要的角色。
本文将探讨二次函数与反比例函数的基本概念,并通过实际案例来说明它们在应用中的价值。
二次函数是一种以x的平方为最高次的多项式函数。
它的一般形式为:y=ax^2+bx+c,其中a、b和c为常数,且a不等于0。
二次函数的图像通常呈现为一条抛物线,其开口的方向取决于a的正负。
反比例函数,也被称为倒数函数,是指两个变量之间的关系满足乘积为常数的特性。
反比例函数的一般形式为:y=k/x,其中k为常数。
二次函数与反比例函数的综合应用可以广泛应用于物理学、经济学和工程学等实际领域。
下面将分别介绍它们在这些领域中的应用。
一、物理学中的应用二次函数在物理学中常用于描述抛体运动的轨迹。
例如,当一个物体被抛出时,它的运动轨迹可以用一个二次函数来表示。
其中,抛物线的开口方向与抛出的物体的初速度和抛出角度有关。
反比例函数在物理学中也有着重要的应用,特别是在描述压力和容积之间的关系时。
根据波义耳定律,一个封闭系统中的气体压力与其容积成反比。
因此,我们可以使用反比例函数来表示它们之间的关系,从而帮助我们理解气体的性质和行为。
二、经济学中的应用二次函数在经济学中被广泛应用于成本函数和利润函数的建模。
在生产过程中,成本往往与生产规模和产量呈二次函数关系。
通过分析二次函数的图像和性质,经济学家可以研究如何最大化利润或最小化成本,从而为企业的经营决策提供依据。
反比例函数在经济学中的一个重要应用是供求关系的建模。
根据经济学原理,供求关系可以用反比例函数来表示。
市场上的物品价格往往与供给量和需求量成反比。
通过解析反比例函数,经济学家可以预测市场价格的变化趋势,并为政府和企业的决策提供参考。
三、工程学中的应用二次函数在工程学中常用于描述材料的应力-应变关系。
通过对材料的试验数据进行拟合,可以得到二次函数模型,从而推导出材料的力学性质和特点。
第22章:二次函数与反比例函数知识点总结

第22章:二次函数与反比例函数强化记忆知识点知识点1:二次函数的图象与系数的关系.二次函数2y ax bx c =++中图象与系数的关系:(1)二次项系数a 的正负决定开口方向,a 的大小决定开口的大小. a>0时,开口向上,a<0时,开口向下。
a 越大,开口越小。
a 越小,开口越大。
(2)一次项系数b ,在a 确定的前提下,b 决定了抛物线对称轴的位置.若0>ab ,则对称轴a b x 2-=在y 轴左边,若0<ab ,则对称轴a bx 2-=在y 轴的右侧。
若b=0,则对称轴abx 2-==0,即对称轴是y 轴.概括的说就是“左同右异,y 轴0” (3)常数项c ,c 决定了抛物线与y 轴交点的位置.当0c >时,交点在y 轴的正半轴上 ;当0c =时,抛物线经过原点,;当0c <时,交点在y 轴的负半轴上, 简记为“上正下负原点0”(4) △=b 2-4ac 决定了抛物线与x 轴交点的个数. ① 当0∆>时,抛物线与x 轴有两个交点 ② 当0∆=时,抛物线与x 轴只有一个交点; ③ 当0∆<时,抛物线与x 轴没有交点.另外当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.注:a +b +c 表示x=1时,对应的函数值。
a -b +c 表示x= -1时,对应的函数值.4a +2b +c 表示x=2时,对应的函数值。
9a -3b +c 表示x= -3时,对应的函数值.等知识2:一次函数的图象与系数的关系.一次函数:y=kx +b(k,b 是常数,k≠0) 中图象与系数的关系:(1)走向:k>0,图象经过第一、三象限;k<0,图象经过第二、四象限b>0,图象经过第一、二象限;b<0,图象经过第三、四象限⇔⎩⎨⎧>>00b k 直线经过第一、二、三象限 ⇔⎩⎨⎧<>00b k 直线经过第一、三、四象限 ⇔⎩⎨⎧><00b k 直线经过第一、二、四象限 ⇔⎩⎨⎧<<00b k 直线经过第二、三、四象限 (2)增减性: k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小.(3)截距: 当b>0时,图象交于y 轴正半轴, 当b<0时,图象交于y 轴负半轴,当b=0时,图象交于原点.(4)倾斜度:|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴.知识3:反比例函数的图象与系数的关系以及反比例函数性质. 反比例函数:y =xk(k 为常数,k ≠0)中图象与系数的关系: (1)反比例函数的增减性不连续,在讨论函数增减问题时,必须有“在每一个象限内”这一条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.3
B.9
C.15
D.-15
5.已知二次函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范
围是( )
A.k<4
B.k≤4 C.k<4且k≠3 D.k≤4且k≠3
6.在同一平面直角坐标系内,将函数y=2x2+4x+1的图象沿x轴方向向右
平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐
1.图像在第二、四象 限; 2.在每个象限内,函 数y的值随x的增大而增 大.
3.反比例函数y= (k≠0)中比例系数k的几何意义:即过双曲线y= (k≠0)上
任意一点引x轴、y轴垂线,所得矩形面积为│k│。
1.若双曲线y=与直线y=2x+1一个交点的横坐标为-1,则k的值为(
)
A.-1
B.1
C.-2
2),则当时,自变量x的取值范围是( )
A.
B.
C.
D.
11.如图3,点A,B的坐标分别为(1, 4)和(4, 4),抛物线的顶点在线 段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小 值为,则点D的横坐标最大值为( )
A.-3
B.1
C.5 D.8
12.如图,在矩形ABCD中, AB=4,BC=6,当直角三角板MPN 的直角顶
.
14.如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边
在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小 值是 . 15.已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三 点,直线l是抛物线的对称轴. (1)求抛物线的函数关系式; (2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐 标; (3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写 出所有符合条件的点M的坐标;若不存在,请说明理由.
D.2
2.已知点A(-1,y1)、B(2,y2)都在双曲线y=上,且y1>y2,则m的取
值范围是( )
A.m<0
B.m>0
C.m>-
D.m<-
3.点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=-图像上的三
点,且,则大小关系是( )
A.y1< y2< y3
B. y2<y3<y1
C. y3<y2<y1
A.y1>y2>y3
B.y1<y2<y3 C.y2>y3>y1 D.y2
<y3<y1
9.如图1是二次函数y=ax2+bx+c部分图象,由图象可知不等式ax2+bx+c
<0的解集是( )
A. B. C. D.
图3 图1 图2
10.如图2,抛物线与两坐标轴的交点分别为(-1,0),(2,0), (0,
16.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0, 1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得 到△A′B′O. (1)一抛物线经过点A′、B′、B,求该抛物线的解析式; (2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边 形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存 在,请说明理由. (3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并
为6.下面各点
也在这个反比例函数图象上的是( )
A.(2,3)
B. (-2,6)
C. (2,6)
D. (-2,3)
6.已知直线y=kx(k>0)与双曲线y=
交于点A(x1,y1),B(x2,y2)
两点,则x1y2+x2y1的值为( )
A. ﹣6
B. ﹣9
C. 0
D. 9
7.如图3,已知梯形ABCO的底边AO在轴上,BC∥AO,AB⊥AO,过点C的双
2.二次函数的图像与性质
y=a (x-h)2+k
开口方向
顶点坐标
对称轴
当x=____时,y有最 当x=____时,y有最
函数最值 值,
是______.
是______.
函数值的增
减性
3. 二次函数可化成的形式,其中= ,=
.
4.抛物线的对称性:若抛物线上有两个点的纵坐标相等,横坐标分别
为,则这两个点关于抛物线的对称轴对称,可求得对称轴为 5.二次函数与一元二次方程的关系:
标是( )
A.(-1,1)
B.(1,-2)
C.(2,-2)
D.(1,-1)
7.已知拋物线y=-x2+2,当1≤x≤5时,y的最大值是( )
A.2
B.
C.
D.
8.已知二次函数y=﹣
x2﹣7x+
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值
y1,y2,y3的大小关系正确的是( )
四、反比例函数
1.反比例函数:一般地,如果两个变量x、y之间的关系可以表示成 (k为常数,k≠0)的形式(或y=kx-1,k≠0),那么称y是x的反比例函 数. 2.反比例函数的图象和性质.
表达式
y= (k≠0)
k>0
k<0
图像
性质
1.图像在第一、三象 限; 2.在每个象限内,函数 y的值随x的增大而减 小.
上,若四边形ABCD为矩形,则它的面积为 .
图7 图6 图5 图4
11.如图5,直线(>0)与双曲线在第一象限的交点为R,与轴的交点为P, 与轴的交点为Q;作RM⊥轴于点M,若△OPQ与△PRM的面积是 9∶1,则 . 12.如图6,点A是反比例函数y=
(x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣
(1)一元二次方程ax2+bx+c=0就是二次函数y=ax2+bx+c当函数y的值为
0时的情况.
(2)二次函数y=ax2+bx+c的图象与x轴的交点有三种情况:有两个交
点、有一个交点、没有交点;当二次函数y=ax2+bx+c的图象与x轴有交
点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+
bx+c=0的根.
1.抛物线y=-(x+2)2-3的顶点坐标是( ).
A(2,-3) B(-2,3) C(2,3) D(-2,-3) .
2.下列二次函数中,图象以直线x = 2为对称轴,且经过点(0,1)的是( )
A. B. C D.
Байду номын сангаас
3.二次函数有( )
A最大值
B最小值
C最大值 D最小值
4.抛物线y=ax2+bx-3经过点(2,4),则代数式8a+4b+1的值为( )
D.
无法确定
4.如图1,反比例函数y1=和正比例函数y2=k2x的图象交于A(-1,-
3),B(1,3)两点,若>k2x,则x的取值范围是( )
A.-1<x<0 B.-1<x<1 C.x<-1或0<x<1 D.-1<x<0或x>
1
图2
图3
图1
5.如图2,P为反比例函数y=的图象上一点,PA⊥x轴于点A, △PAO的面积
曲线 交
OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值是(
)
A.等于2
B.等于
C.等于
D无法确
定
8.已知反比例函数的图象经过点(m,2)和(-2,3),则m的值为
__________.
9.已知都在反比例函数的图象上。若,则的值为
。
10.如图4,点A在双曲线上,点B在双曲线上,且AB∥x轴,C、D在x轴
点P在BC边上移动时,直角边MP始终经过点A,设直角三角板的另一直
角边PN与CD相交于点Q.BP=x,CQ=y,那么y与x之间的函数图象大致
是( )
13.如图,已知二次函数的图象经过点(-1,0),(1,-2),该图象 与x轴的另 一个交点为C,则AC长为 , 当随的增大而增大时,的取值范围是
写出四边形PB′A′B的两条性质.
的图象于点B,以AB为边作▱ABCD,其中C、D在x轴上,则S□ABCD
为__________ 13.如图7,双曲线经过直角三角形OAB的斜边OB的中点D,与直角边AB相 交于点C.当时,k= . 14.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反 比例函数y= (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C 点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点, 且sin∠AOE=. (1)求该反比例函数和一次函数; (2)求△AOC的面积.
15.如图,已知反比例函数的图象经过点(,8),直线经过该反比例函 数图象上的点Q(4,).
(1)求上述反比例函数和直线的函数表达式; (2)设该直线与轴、轴分别相交于A 、B两点,与反比例函数图象的另 一个交点为P,连结0P、OQ,求△OPQ的面积.
五、二次函数
1.定义:形如
( )的函数叫做二次函数,其图象是 .
