第二章 原子的玻尔—索末菲理论 小结
原子物理_总结

Be ,~
RBe
4
2
1 m2
1 n2
2. 原子核运动对里德堡常数的影响
2 2e4
2 2me4
1
RA (40 )2 h3c (40 )2 h3c 1 m
M
R
1 1 m
M
3、 索末菲理论
量子化通则
pdq nh n 1,2,3,
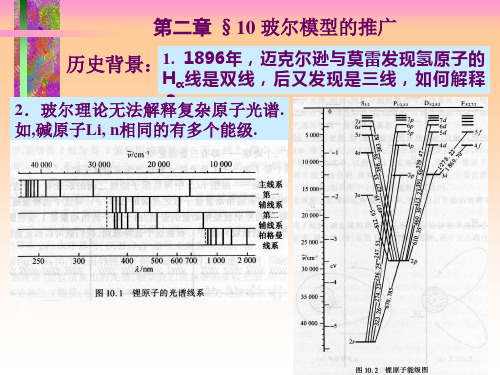
气体分子发出, 谱线分段密集, 形成一个个带。
二、氢原子光谱
巴耳末公式
=B
n
n2 2
4
n 3, 4,5,...
令 % 1 , ṽ 称为波数,巴耳末公式可改写为
%
1
1 B
n2 4 n2
4 B
1 22
1 n2
RH
1 22
1 n2
n 3, 4,5,...
原子物理学
课程总复习
第一章 原子的基本状况
一、了解汤姆逊原子模型
• 1903年英国科学家 汤姆逊提出 “葡萄干 蛋糕”式原子模型或
称为“西瓜”模型。
卢瑟福的粒子散射实验
放射源
放射源为放入一小铅盒中的少量放射性元素钋,用来产生α粒子。 轰击对象金箔为微米级薄片。荧光屏为接受屏,其后有显微镜可观 察到发生的现象。荧光屏和显微镜可以围绕金箔在一圆周上运动,
巴耳末系
氢原子光谱的其他线系
1914年 赖曼发现 赖曼系:
1908年 帕邢发现 帕邢系:
~
RH
1 (12
1 n2
),
n
《原子物理学》(褚圣麟)第二章 原子的能级和辐射要点

第2章 原子的能级和辐射
一、 黑体辐射 普朗克能量子
第2章 原子的能级和辐射 二、光电效应 爱因斯坦光量子 (1)光电效应的实验规律
早在1887年,德国物理学家赫兹第一个观察到用紫光照射的尖端放电特别容 易发生,这实际上是光电效应导致的。由于当时还没有电子的概念,所以对其机 制不是很清楚。直到1897年汤姆逊发现了电子。人们才注意到一定频率的光照 射在金属表面上时,有大量电子从表面逸出,称之为光电效应。
第2章 原子的能级和辐射
经过近二个月的努力,普朗克在同年12月14日的一次德国物理学会议上提出: 对一定频率的电磁波,物体只能以 h为单位吸收或发射它,即吸收或发射电磁 波只能以“量子”方式进行,每一份能量 叫一能量子。
电子辐射的能量
E nhv (n 1,2,3)
这一概念严重偏离了经典物理;因此,这一假设提出后的5年时间内,没有 引起人的注意,并且在这以后的十多年时间里,普朗克很后悔当时的提法,在 很多场合他还极力的掩饰这种不连续性是“假设量子论”。
难点 • 量子理论的建立
• 空间量子化
第2章 原子的能级和辐射
2.1 玻尔理论的实验基础
1. 黑体辐射 普朗克能量子 2. 光电效应 爱因斯坦光量子 3. 氢原子光谱
第2章 原子的能级和辐射
卢瑟福模型把原子看成由带正电的原子核和围绕核运动的一些电子组成, 这个模型成功地解释了α粒子散射实验中粒子的大角度散射现象,可是当我们 准备进入原子内部作进一步的考察时,却发现已经建立的物理规律无法解释原 子的稳定性,同一性和再生性。
第二章 原子的玻尔—索末菲理论 (4)
principal
diffuse
fundament al
(next in alphabet after f)
g
4
18
5th shell and higher (theoretically)
原子实极化和轨道贯穿
碱金属原子的光谱可以用类似氢原子的公式表示。这些原 子的能级,当n较大时,非常近氢原子的能级,只有当 n较小 时差别较大。如果考虑到碱金属原子化学上是一价的,它们 容易电离成为带一个单位电荷的离子等情况,可以设想上节 讨论过的那些光谱也是由于单电子的活动产生的。
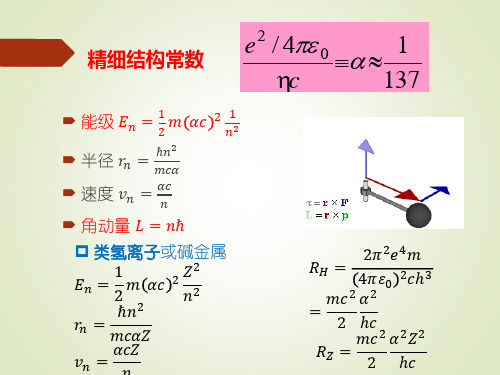
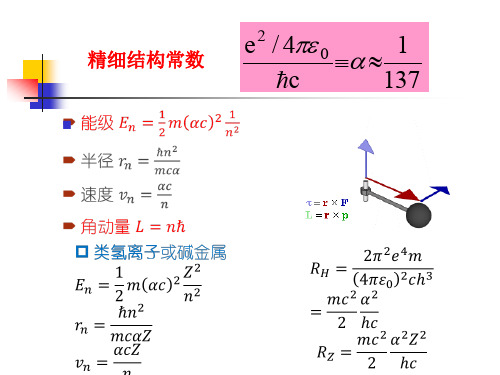
此式中第一项就是玻尔理论的结果,第二项起则是相对论效 应的修正。显然,对同一n不同nφ,第二项的数值是不同的。 由此可见,同一n而nφ不同的那些轨道运动具有不同的能量。 这样,原来的能级简并在考虑了相对论修正后就消除了。不 过,第二项代表的数值比第一项小得多,所以分裂的能级只 有微小的差别。这个差别被称为能级的精细结构,与它相联 系的常数α称为精细结构常数。索末菲的功绩之一就是引入了 这一十分重要的常数。
n nr n 1,2,3,; n 1,2,3,,n.
上式所表达的是索末菲推广到椭圆轨道后得到的结果,把 它们与玻尔的圆运动情况相比较,不难看出:能量的表达 式没变,但轨道的半径有了长、短半轴之分,且出现了两 个量子数n和nφ。这个结果所包含的物理意义是:轨道的 长半轴和体系的能量只决定于主量子数 n,而与nφ无关; 轨道角动量决定于角量子数nφ,形状取决于 之比。
①椭圆轨道推广 索末菲认为电子绕原子核在一个平面上作椭圆运动,是一 个二维的运动。描述椭圆运动中电子的位置,可用平面极坐 标中的坐标φ和r,与这两个坐标对应的广义动量就是角动量 L 和动量Pr。这体系的能量可表示为
索末菲对玻尔理论的推广(2)——相对论计算

式中, R 为里德堡常数(即 R∞ )。可见,定态能量表达式的前半部分与玻尔及索末菲所得
结果相同,却出现了后半部分的修正项。
结果与分析:
1)考虑相对论效应后,定态能量不完全由主量子数 n 而定,还会因角量子数 nϕ 的不同而分 为 n 个次能级;但能量主要还由 n 确定,由于修正项中α 值很小,故修正量很小(“α --精细结
总效果:椭圆进动,电子运动一周,ϕ 从原来的 0 → 2π ,变为 0 → 2π ω 。如图。
“总起来说,此电子的运动可以看成是两种运动的叠加:一种是电子绕核作椭圆轨道运动, 另一种是该椭圆的长轴绕原子核绥绥转动,二者转向相同.两种运动同时进行,电子轨道将不
-3-
是一根闭合曲线。上图中的两个虚线因,表近核点和远核点的轨迹.”
⋅
Rhc
,
n = 1, 2,3......
式中
R
=
R∞
=
2π 2mee4
(4πε0 )2 h3c
;
椭圆轨道:
⎧⎪⎪a ⎨ ⎪⎪⎩ b
= =
a0 Z a0 Z
n2 nnϕ
nϕ = 1, 2,3......n
式中, a0
=
4πε 0 h2 4π 2mee2
;
空间量子化: Pz = m , m = 0, ±1, ±2… ± nϕ
−
⎞ 1⎟⎟⎠
−
1 4πε
0
⋅ Ze2 r
⇒
1 1− β2
=
1+
1 me0c2
⎛ ⎜ ⎝
E
+
1 4πε 0
⋅
Ze2 r
⎞ ⎟ ⎠
又: υ 2 = r2 + r 2ϕ 2 , β = υ c «1,(将1 1− β 2 展开)
第二章 原子的玻尔—索末菲理论 (4)
之比。
这即意味着,当n相同nφ不同时,在不同轨道中运动的体系会具有相同的 能量,这种情况称为简并(或退化)。例如对同一n,由于nφ=1,2,…, n,便有n个可能的轨道,我们说它有n个状态,但这n个状态的能量是相 同的,故这种情况就被称为n度简并(或退化)。下图所示的是氢原子能 级简并(或退化)的情况。
n 4 n
在上面的简单推导过程中,我们不难看出相对论效应是如何被考虑进去的。显 而易见,上式中第一项就是玻尔理论原来给出的,第二基则是考虑了相对论效 应后增加的修正项。虽然这一简单推导只对圆轨道才成立,但是,它已包含了 相对论修正引起的主要效果。
值得指出,在作上述展开时,认为β<< 1,至少是β<1,那么当β=αZ/n>1,
T
m
m0
c
2
m0c
2
1
1
2
1
与经典公式不同,当v << c ,即β很小时,对上式右
边第一项作级数展开,且略去高阶无穷小量,就得到了动 能的经典表述形式。
下面将用相对论对圆周轨道进行修正。让我们从能量 角度看,能量可写成动能与势能之和,即
E
T
V
m
m0
c
2
精细结构常数
e2 / 4 0 1
c
137
光谱
类氢离子,毕克林系 折合质量,里德堡常数随不同类氢离子变化
Franck-Hertz实验
广义量子化条件和索末菲理论
A. 广义量子化条件
玻尔在氢原子理论中得出,只有满足角动量量子化条件
Ln,n1,2,3,
的电子轨道运动才是实际上可能存在的,将上式改写一下,即
第二章 原子的玻尔—索末菲理论 (4)

碱金属原子的光谱
玻尔理论已经成功讨论和解释了氢原子和类氢离子的结 构和光谱,这里要讨论的是另一类与氢原子类似结构的原 子——碱金属原子,包括锂Li、钠Na、钾K、铷Rb、铯Cs和 钫Fr,原子序数分别为3、11、19、37、55和87。这些元素 在周期表中属同一族,有相仿的化学性质,都是一价的。它 们的电离电势都比较小,易被电离,具有金属的一般性质。 对与氢原子类似结构的两大类原子来说,在谁更像氢原子的 问题上各有所长。从核外只有一个电子 e 这个角度看,显然类氢离子优于碱金 e 属原子,但从最外层那个电子所感受 到的那个“原子实”的作用来说,碱金 属原子中原子实的净电荷Z是1,在这 一点上又优于类氢离子。
2 Ze E T V m m0 c 2 4 0 r
根据类氢离子的玻尔理论上式可以写为
cZ 2 2 2 2 2 E m m0 c 2 m m m0 c mv m m0 c mc n m0 c mc 1 m0 c
按照玻尔 — 索末菲理论 Hα 线应为n=3到n=2的跃迁,n=3为 三条能级, n=2 为二条能级,考 虑能级跃迁的选择定则 △ =±1,就得到了三条Hα 线,与实验完全符合,但这完全 是巧合,有人称索末菲理论是物 理学中最值得纪念的失败。
图中的s,p,d,f,g,…等字母代表 4,…等值。
=0,1,2,3,
精细结构常数
e / 40 1 c 137
2
光谱
类氢离子,毕克林系 折合质量,里德堡常数随不同类氢离子变化
Franck-Hertz实验
广义量子化条件和索末菲理论
A. 广义量子化条件
玻尔在氢原子理论中得出,只有满足角动量量子化条件
第二章 原子的玻尔—索末菲理论

这表明,1m2的钠金属板上,每个原子每秒钟接受到的 能量约为0.1μeV,既使每个原子中只有一个电子接受能量, 要使这个电子获得1eV的能量,还需要107s≈1/3a!这与实验 事实发生严重的矛盾。光电效应的响应时间快(T<10-9s), 是经典物理最难理解的。 另外,依照经典理论,决定电子能量的是光强,而不 是光的频率。但实验事实却是:暗淡的蓝光照出的电子的 能量居然比强烈的红光照出的电子的能量大。这种电子能 量与光频率的关系是经典物理所无法解释的。
普朗克发表的常数
h=6.55×10-34J· S
只比现代值低1%;同时导出的玻耳兹曼常数
k=1.346×10-23J/K
比现代值低约2.5%。由此可相当精确地算出阿伏伽德 罗常数N0及电子的电荷e,而在实验上只是在近二十年 之后才独立地把N0和e测量到这样精确的水平。 普朗克常数在1986年的推荐值为:
§2.2 光谱
光谱是光的 频率(或波长) 成分和强度分 布的关系图, 它是研究原子 结构的重要途 径之一。
若要了解物质 的内部情况, 只要看其光谱 就可以了。
光谱是用光谱仪测量的。光谱仪的种类繁多,但其基 本结构原理却几乎都一样,大致由三部分组成:光源;分光 器(棱镜,或光栅);记录仪(把分出的不同成分的光强记 录下来)。 光源:研究光谱所用的光源,除自然光外,可有各种类 型,有火焰、高温炉、电弧、火花放电、气体放电、化学发 光、荧光等。
A、黑体辐射
什么叫黑体辐射?记得有时在评论某人物时(例如, 莎士比亚的喜剧《威尼斯商人》中的高利贷者夏洛克),人 们会贬称他‚黑心‛,就是说这个人对什么东西都贪得无厌。 与此相比,若一物体对什么光都吸收而无反射,我们就称这 种物体为‚绝对黑体‛,简称‚黑体‛。事实上当然不存在 ‚绝对黑体‛,不过有些物体可以近似地作为‚黑体‛来处 理,如一束光一旦从狭缝射入某一空腔后,就很难再通过狭 缝反射出来,这个空腔的开口就可以被看作是黑体。
原子物理学各章节小结(1-4)

l =1,2,3,…,(n-1)
轨道角动量大小:
L
h l ( l 1) 2
角量子数l越小,椭圆轨道的偏心率越大,轨道越扁。
上一页
下一页
目录
结束
空间量子化 轨道磁量子数(ml):表示轨道在空间的可能取向。
ml 0, 1, 2,…, ( - 1) l l ,
h 在外磁场方向的投影: L m z l 2
目录
结束
4、对应原理
玻尔认为:
理解,并能用 自己的话说出
在原子范围内微观现象和在宏观范围内的现
象,它们各自遵循本范围的规律,但微观范围内
的规律和宏观范围内的规律间存在对应关系,当 把微观范围内的规律延伸到宏观范围时,应与宏 观规律一致。
上一页
下一页
目录
结束
5、量子力学处理结果
主量子数(n):原子中的电子在核外空间运动轨 道大小和能量高低主要决定于主量子数。 n=1,2,3…… 轨道角量子数(l ):表示轨道形状和角动量大 小,同时还表示在同一主壳层中电子能量的分裂。
记住处理结论,且 能用其处理具体问 2 n题,要求会画能级 a1 图。
Z
o 4 0 h 2 10 a1 0.53 10 m 0.53 A 2 2 4 me
2 2 me 4 Z 2 Z2 能量: En hcR( 2 ) hcT ( n) 2 2 2 (4 0 ) h n n 2 2 me 4 13.6 对氢原子n=1时, E1 13.6eV En 2 eV 2 2 (4 0 ) h n
En E1 h 1 h 2 h 3 En E1 hc
1
hc
2
hc
原子物理2

轨道角动量的量子化 原子中能够实现电子轨道只是符合以下条件的
p mvr
2r mv 2 mvr nh
h p n n 2
角动量的量子化
3、玻尔的氢原子图象(能级、光谱)
光 谱 项
光 谱 项
给出了量子化的轨道(轨道半径的量子化)
氢光谱的 经验公式
1 1 RH RH 1 ~ RH 2 2 2 2 n m n m
n2 巴尔末公式 B 2 n 4
(经验常数)B 3646.6 A
0
n 3、 4、 5、
和波长更短的都可纳入 上式,公式显然和实验 的结果相符合。
H 、H 、H 、H
红 深绿 青 紫
谱线系 谱线的波长(波数)满足同一个公式的一组谱线
n 线系限波长(1/λ波数) B
线系,各谱线的波长可用一个公式表示出
来。不同的谱线系也有一些关系。如有共同
的光谱项。 m一定 n=m+1的整数,同一谱线系的不同谱线。 m不同 n=m+1的整数,不同谱线系的谱线。
任一谱线波数可表示为两光谱项之差
以上三条不仅对氢原子光谱成立,对所有的原 子光谱都适用,所不同的只是各原子的光谱项的具 体结构不同而已。
说明与能量联系的 电子轨道是分立的, 不能连续变化
hc hcR hcR ~ hc h 2 2 m n
2 ze h E2 E1 E 40 2r 2 1 ze hRc E 2 40 2r n
1
对氢原子z=1
2 ze mv 2 40 r
1
h p mvr n 2
能级上下跃迁时,将导致电磁波的吸收和发射,
电磁波频率为 h E E ( E E ) 2 1 2 1 该式称频率条件,不难看出该式与氢光谱公式相对应。 即原子从一较大能量E2的定态向另一较低能量E1的 定态跃迁时,辐射一个光子 。原子从较低能量E1 的定态向较大能量E2的定态跃迁时,吸收一个光子
§2.4 波尔模型的推广——索末菲模型(PPT-YBY)

n 1 a r1 ① n 1 b r1
n 2 a 4r1 n 1 b a / 2 ② n 2 b a
n 3 n 1 ③ n 2 n 3 a 9r1 b a/3 b 2a / 3 b a 9r1
§2.4 波尔模型的推广——索末菲模型 索末菲(A.Sommerfeld,1868-1951德国物理学家) 1916年提出 了椭圆轨道理论。 其一、提出了广义量子化条件(即量子化通则),把玻尔的圆 轨道推广为椭圆轨道。 其二、引入了相对论修正。 一、量子化通则及椭圆轨道 1、量子化通则
L mrV n
现在我们进一步了解到原子内部运动复杂性,同一n还有不同 形状的轨道,而每种轨道具有不同的能量。
第 1 、 2 章 卢 瑟 福 玻 尔 模 型 小 结
2 2 Z 2 2 E c c 1 n (n2 2 Z 2 )1/2 2 r
2 m0 z e
2
2 4
2 4
2
(8)
1 4 0 c 137
这种不同量子态具有相等能量的情况成为简并。 简并度
e2
二、相对论修正
1、相对论动能 质速关系为:
m
m0 1
2
v/c
2 2
(9)
1 1 动能表达式: EK (m m0 )c m0c 2 1 用级数展开式:
(10)
这就是经典表达式。
2、圆轨道的能量修正 (1)求电子运动的速度。利用(8)式的经典能量表达式
1 1 z En Ek U Ek U m0 c 2 2 n
第二章,氢原子光谱

Back
Next
第五节:玻尔理论的推广
玻尔—索末非模型 碱金属的光谱 Back
第五节:玻尔理论的推广
玻尔—索末非模型
碱金属的光谱
Next
第五节:玻尔理论的推广
玻尔—索末非模型
碱金属的光谱
Back
Next
第五节:玻尔理论的推广
原子实是一个球形对称的 结构,它里边的原子核带 有Ze正电荷和(Z-1)e负 电荷,在原子最外层运动 的价电子好象是处在一个 单位正电荷的库仑场中, 当价电子运动到靠近原子 实时,由于价电子的电场 作用,原子实中带正电的 原子核与带负电的电子的 中心会发生微小的偏移, 于是负电的中心不再在原 子核上,形成一个电偶极 子。这就是原子实的极化。
rnn2a 0
c vnn
n1 ,2 ,3 ,K
a0 4m πee0h22 0.53Å 玻尔半径
En
1 2n2
e2 4π0a0
e2 1 精细结构常数 4π0hc 137
1 2n2
m e
2c 2
n 1 E 1 1 3 . 6 e V r 1 a 0 基态(ground state)
n 2 激发态(excited state)
质心系
核系
En
1 2n2
Z 2e2 4π0a0
1 2n2
Z
2
2c 2
rnn Z 2a0
vnZ nc n1 ,2 ,3 ,K
r1n
me rn
n2
Z
4π0h2
mee2
e4
1
RM4π4π02h3c1m e MR
R1 0 7m 1 M 1 .0 9 73 7 3 1
1 1H 1 .0 9 67 7 58 1 2D 1 .0 9 70 7 42 1 3T 1 .0 9 7 1 7 35 4 2H e 1 .0 9 72 2 27 3 7L i2 1 .0 9 72 8 80 9 4H e3 1 .0 9 73 0 70
人教版高中物理选修3-5 2.4第二章第4节 玻尔的原子模型 能级

• [例1] 氢原子基态的能量为E1=-13.6 eV。
大量氢原子处于某一激发态。由这些氢原子
可能发出的所有的光子中,频率最大的光子
能量为-0.96E1,频率最小的光子的能量为 ________eV(保留两位有效数字),这些光子
解析
可具有________种不同的频率。
频率最大的光子能量为- 0.96E1 ,即 En - E1 =-
判天地之美,析万物之理
当我一看到巴尔末公式,整个事情就豁然 开朗了。
————玻尔
4
玻尔的原子模型
能级
活动一
玻尔对原子结构的研究
1900年普朗克提出了能量量子化的概念, 认为电磁波的能量不是连续变化的,而是 只能取一些分立的值。 1905年爱因斯坦为了解释光电效应的实验 规律提出了光量子假说,认为光子的能量 也是不连续的。 1885年巴尔末分析了可见光区的四条谱线, 说明了原子光谱波长的分立特性。
一、玻尔提出原子模型的背景:
卢瑟福的原子核式结构学说很好地解释了a粒子 的散射实验,初步建立了原子结构的正确图景,但 跟经典的电磁理论发生了矛盾。 1、原来,电子没有被库仑力吸引到核上,它 一定是以很大的速度绕核运动,就象行星绕着太阳 运动那样。按照经典理论,绕核运动的电子应该辐 射出电磁波,因此它的能量要逐渐减少。随着能量 的减少,电子绕核运行的轨道半径也要减小,于是电 子将沿着螺旋线的轨道落入原子核,就像绕地球运 动的人造卫星受到上层大气阻力不断损失能量后要 落到地面上一样。 这样看来,原子应当是不稳定的, 然而实际上并不是这样。
一、玻尔的原子模型 围绕原子核运动的电子轨道半径只 1.轨道量子化假设::
能是某些不连续(分立)的数值。 (1)如氢原子电子的可能轨道r半经: …) r = n 2r ( n = 1, 2 , 3 1 n r = 0.053nm r = 0.212nm 2 1
原子物理第2章

原子物理第2章第三节:玻尔模型从理论上导出里德伯常数:结束目录nextback 氢光谱的解释玻尔假设电子的运动第二章:原子的能级与辐射:玻尔理论第三节:玻尔模型氢原子轨道半径与谱系结束目录nextback氢光谱的解释玻尔假设电子的运动赖曼系n=1n=2n=3n=4n=5r04r09r016r025r0布喇开系巴耳末系帕邢系第二章:原子的能级与辐射:玻尔理论第三节:玻尔模型结束目录nextback氢光谱的解释玻尔假设电子的运动第二章:原子的能级与辐射:玻尔理论第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论毕克林系起初以为是星体上的一种特殊氢,后在实验室中加氦后的氢光谱中观察到,得以确认是氦离子的光谱。
氢光谱类氢光谱第四节:类氢离子光谱结束目录nextba ck第二章:原子的能级与辐射:玻尔理论如果套用玻尔理论,只需要将氢原子理论中的Z改为2,就可得到氦离子的光谱理论公式上式中n1取4,n2取5、6、7、….就与毕克林系规律相同第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论尽管上述结果与观察结果非常一致,但还有一个明显的差别:类氢离子光谱与氢光谱并不完全重合。
这一差别后来被认为是里德伯常数的变化引起的。
考虑原子核的运动,推导出修正后的里德伯常数核的质量有关。
修正后的里德伯常数与观测结果非常一致第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论里德伯常数受核的质量影响的理论曾被用来证实氢的同位素-氘-的存在。
起初有人从原子质量测定估计有原子量为2的氢存在,但如存在,含量应很低,一时难以确认。
1932年尤雷(HCUre y),观察到类氢光谱,通过质量修正,能很好得到解释。
从而确认氘-的存在。
第四节:类氢离子光谱结束目录nextback第二章:原子的能级与辐射:玻尔理论玻尔理论非常成功地解释了氢、类氢离子光谱的规律,一度被人们广泛接受。
选修3-5 第二、三、四章知识点总结_波粒二象性_原子结构_原子核

选修3-5 第二章、第三章、第四章知识点总结第二章 波粒二象性知识梳理1、光电效应①光电效应现象:在弧光灯的照射下,锌板中有一部分电子吸收了光能,挣脱了原子核的束缚,飞离金属表面,使锌板带上正电。
②光电效应定义:物体在光(包括不可见光)的照射下发射电子的现象称为光电效应。
③光电子:物体在光的照射下发射出来的电子。
④当入射光的频率大于极限频率时,光电流强度与入射光的强度成正比。
(光强即光电强度,简单来说就是电子个数多少)。
⑤锌板带正电,验电器指针带正电。
2、光电管:利用光电效应制成的一种常见的光电器件。
①用途:光电管应用在各种自动化装置及有声电影、无线电传真、光纤通信等技术装置里。
②原理:光电管的阴极表面敷有碱金属,对电子的束缚能力比较弱,在光的照射下容易发射电子,阴极发出的电子被阳极收集,在回路中形成电流,称为光电流。
注意:①光电管两极加上正向电压,可以增强光电流。
②光电流的大小跟入射光的强度和正向电压有关,与入射光的频率无关。
入射光的强度越大,光电流越大。
3、 物体在光照的条件下发射电子而发生光电效应现象时遵循如下规律:(1)对于任何一种金属,入射光的频率必须大于某一极限频率才能产生光电效应,低于这个极限频率,无论强度如何,无论照射时间多长,也不能产生光电效应;(2)在单位时间里从金属极板中发射出的光电子数跟入射光的强度成正比;(3)发射出的光电子的最大初动能与入射光强度无关,只随入射光频率的增大而增大;(4)只要入射光的频率高于金属极板的极限频率,无论其强度如何,光电子的产生都几乎是瞬时的,不超过10—9s. 4、最大初动能:光电效应中从金属出来的电子,有的从金属表面直接飞出,有的从内部出来,沿途与其它粒子碰撞,损失部分能量,因此电子速度会有差异,直接从金属表面飞出的速度最大,其动能为最大初动能。
5、最大初动能的测定:①在强度和频率一定的光的照射下,回路中的光电流随着反向电压的增加而减小,当反向电压达到某一数值时,光电流将会减小到零,这时的电压称为遏止电压U 0 ②光电子出射时的最大初始动能:02max 21eU mv ③遏止电压与入射光的强度无关,与入射光的频率有关,随着入射光频率的增大而增大。
第二章 原子的玻尔—索末菲理论 小结

Bohr模型
处理原子结构的方法:对于电子绕原子核运 动,用经典力学处理;对于电子轨道半径, 则用量子条件来处理。也就是所谓的半经典 的量子论。只对电子的径向运动采取量子理 论,而对其角向运动采取量子理论。
之所以先量子化径向运动,由于卢瑟福模型 电子塌缩就是与轨道半径有关。只要量子化 而不收缩,塌缩问题就解决了。 解释了近30年的巴尔末公式之谜。 解释了类氢离子光谱。
光谱
光谱是用光谱仪测量的。光谱仪的种类繁多,但其基 本结构原理却几乎都一样,大致由三部分组成:光源;分光 器;记录仪。 连续光谱 固体热辐射 线状光谱 带状光谱 发射光谱
样品光源 分光器 纪录仪
原子发光 分子发光
I
吸收光谱
连续光源 样品 分光器 纪录仪
I
氢原子光谱及其经验规律
巴耳末公式
2n 2 Rc Rc 4 与经典比较 n n3
2Rc e 3 2 n 1 40 mr 3
e2 2 rn 3 n 40 16 2 R 2 c 2 m 1
2 e m R 2 40 ch 3
2 4
h 2
4 0 2 2 h rn n ; 2 2 me
原子实极化和轨道贯穿
电偶极子
碱金属原子光谱的精细结构
me 4 1 En 2 2 2 4 0 2 n
玻尔模型的推广
一个线系的线系限:同一线系中最大的波数,
或波数公式中的第一个光谱项(不动的光谱项 )。
原子的共振线:该原子从基态到第一激发态吸
收的谱线。一个原子共振线只有一条。
一个线系的主线:该线系的第一条谱线或该线
系的波数最小的谱线。
2.碱原子能级与光谱的定性解释
A.碱原子结构可以看成:原子实+一个价电 子. 原子实=原子核+(Z-1)电子,带+e电 荷这。种结构与氢原子相似,从而碱原子价电子的 能量先粗略近似为与氢原子的相同,仅与n有关 : EnZn *22Rh, c H 对 , Z*= 1
附注:碱原子能级的半经验公式
EnlZn 22RhcZn 22Rhc(Z n R )2hc(nR l)h2 c
l 称为量子亏损,仅与角量子数l有关,一般由 实验给出。
如, Na, Li 的量子亏损 l见下表
原子 Δs
Δp
Δd
Δf
Na 1.35 0.86 0.01 0.00
Li 0.40 0.05 0.001 0.000
漫线系: nd(n=3,4,5,…)->2p;
基线系: nf(n=4,5,6,…)->3d.
Na能级图
Na 能 级 跃 迁 与 四 个 线系对应为:
主线系: np(n=3,4,…)->3s;
锐线系: ns(n=4,5,…)->3p;
漫线系: nd(n=3,4,5,…)->3p;
基线系: nf(n=4,5,6,…)->3d.
1 323.26 T 2 S T 3 P ;
T3S
T3P
T2S
T2P
T3S
T3P
1 670.785
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精细结构常数
e / 40 1 c 137
2
里德伯指出毕克林系 可用下列公式代表:
1 1 R 2 2 , n 2.5,3,3.5,4,4.5, 2 n
起初有人以为毕克林系就是氢的光谱线,并认为地球 上的氢不同于星球上的氢。然而,玻尔从他的理论出发, 郑重指出:毕克林系不是氢发出的,而是属于氦离子。英 国物理学家埃万斯(E.J.Evans)在听到玻尔的见解后,立 即到实验室里他细观察氦离子的光谱,结果证实玻尔的判 断完全正确。玻尔理论对类氢光谱的成功解释,促使人们 更们服了它的可靠性。当这一消息传到爱因斯坦那里时, 他也心悦诚服,并称玻尔的理论是一个“伟大的发现”。
§2.8碱金属原子的光谱
碱金属原子的光谱项可以表达为
根据表中锂的数据可以画成能级图。主要特征归结为 如下四条: A、四组谱线(每一组的初始位臵是不同的,即表明 有四套动项)。 B、有三个终端(即有三套固定项)。 是角动量量子数)。 C、两个量子数(n 和 , D、一条规则(图中画出的虚线表示在实验中不存在 这样的跃迁,因原子能级之间的跃迁有一个选择规则,即 △ =±1)。 对这个选择规则,我们可以这样解释: 的差别就是 角动量的差别,由于光子的角动量是1,要在跃迁时放出 一个光子,角动量就只能差1。根据这个选择规则,我们 就可以画成能级跃迁图。
光照到金属表面, 电流几乎同时产生
光电流与光强成正比
光电流随减速势增大而减小 对不同光强遏止电压相同 遏止电压依赖频率而非光强
光电效应的响应时间快(T<10-9s),是 经典物理最难理解的。 另外,依照经典理论,决定电子能 量的是光强,而不是光的频率。但实验事 实却是:暗淡的蓝光照出的电子的能量居 然比强烈的红光照出的电子的能量大。这 种电子能量与光频率的关系是经典物理所 无法解释的。
Subshell label s
ℓ 0
Max electrons 2
Shells containing it Every shell
Historical name sharp
p
d f
1
2 3
6
10 14
2nd shell and higher
3rd shell and higher 4th shell and higher
1
4 B
1 1 2 22 n
, n 3,4,5,
B = 3645.6 Å
1 1 1 里德伯公式 Rh 2 2 T nT n n n n 1,2,3,;n n 1, n 2, n 3,.
Rh Tn 2 n
n是整数。
Bohr模型
h En En
考虑简单的圆周运动,那么根据经典力学和经典电动 力学有 2 2
v F m 2 r 4 0 r
e
原子的内部能量由电子的动能和体系的势能构成(原子 核假设为静止,所以不计算动能)。假设r = ∞ 时的势能 定为零,那么
1 2 e2 1 e2 1 2 E T V mv mv 2 4 0 r 2 4 0 r 2
Rh=4/B=1.0967758×107m-1
以上是氢原子光谱的情况。这些情况可以总结为下列 三条:
(1)光谱是线状的,谱线有一定位臵。这就是说,有确定 的波长值,而且是彼此分立的。 (2)谱线间有一定的关系,例如谱线构成一个谱线系,它 们的波长可以用一个公式表达出来。不同系的谱线有些也 有关系,例如有共同的光谱项。 (3)每一谱线的波数都可以表达为二光谱项之 ~ T m T n v 差, 。氢的光谱项是
为什么用电子作为激发原子的手段呢?在非弹性碰撞时,只 有当两个粒子的质量相差很大时,轻粒子的动能才能全部转 移为重粒子的内能。把原子作为整体,则按上述定律,电子 可把全部动能转为原子的内能。电子作为一种激发原子的手 段,是十分有效的 。
F-H实验与原子能级的量子化
B. 玻尔-索末菲模型
在玻尔理论发表不久,索末菲便于 1916 年提出了椭圆 轨道的理论。索末菲主要做了两件事,其一是把玻尔的圆 形轨道推广为椭圆轨道,其二是引入了相对论修正。 索末菲目的是解释在实验观察到的氢光谱的精细结构 ,迈克尔逊和莫雷在1896年就发现氢的Hα线是双线,后在 高分辨率谱仪中呈现出三条线。玻尔猜测可能是由于电子 在椭圆轨道上运动时作进动所引起的。按此想法索末菲作 了计算。在考虑椭圆轨道并引入相对论修正后,原来由玻 尔模型得到的能级发生分裂,根据选择定则,定量计算出 了三条Hα线,与实验完全符合。但这一“完全符合”纯粹 是一种巧合。实际上一条Hα将呈现出七条精细结构谱线。 对此,玻尔-索末菲模型就完全无能为力了。
碱金属原子中因原子实的存在,较小的电子轨道已被原 子实的电子占据,价电子的最小轨道不能是原子中最小 的电子轨道。例如锂原子中原子实的两个电子占了n=1的 轨道,所以价电子只能处在 n≥2 的轨道上。同理,钠原 子中原子实的 10个电子占了 n=1 和n=2 的轨道,价电子的 轨道只能从n=3开始。钾原子中价电子的轨道从n =4起, 铷从n=5起,铯从n=6起,钫从n=7起。
Bohr模型
处理原子结构的方法:对于电子绕原子核运 动,用经典力学处理;对于电子轨道半径, 则用量子条件来处理。也就是所谓的半经典 的量子论。只对电子的径向运动采取量子理 论,而对其角向运动采取量子理论。
之所以先量子化径向运动,由于卢瑟福模型 电子塌缩就是与轨道半径有关。只要量子化 而不收缩,塌缩问题就解决了。 解释了近30年的巴尔末公式之谜。 解释了类氢离子光谱。
而电子作圆周运动的频率
v e f 2r 2
1 4 0 mr 3
与R公式比较 对应原理
Rhc En 2 n
e2 2 rn n 40 2Rhc 1
2 2 1 1 n n nnnn c Rc 2 2 Rc 2 2 Rc n n n2n 2 n n
me 4 1 En 2 2 2 4 0 2 n
e2 me 2 r L mvr m r ;L n,n 1,2,3, 4 0 mr 4 0
精细结构常数
e / 40 1 c 137
2
D.数值计算法
组合常数我们已经有了里德伯常数和氢原子的能量、半径 的表达式,为了进行数值计算,显然,只要把一些基本常数 (e,m,h,c) 代入即可。但是,这样做既麻烦又缺乏物理 意义,为简便计算法,引入(其物理意义将逐步清楚):
principal
diffuse
fundament al
(next in alphabet after f)
g
4
18
5th shell and higher (theoretically)
碱金属元素
Li Na K Rb Cs Fr 3=2×1+1, 11=2×(12+22)+1, 19=2×(12+22+22)+1, 37=2×(12+22+32+22)+1, 55=2×(12+22+32+32+22)+1, 87=2×(12+22+32+42+32+22)+1。
原子实极化和轨道贯穿
电偶极子
碱金属原子光谱的精细结构
B. 玻尔-索末菲模型 ①椭圆轨道推广
引入新量子数
2 1 2 Ze 2 1 Ze 2 2 r 2 E mv mr 2 40 r 2 40 r
a1 2 a1 a n ; b nn ; Z Z Z2 1 cZ 2 En Rhc 2 m( ) 2 n n n nr n 1,2,3,; n 1,2,3,, n.
B. 里德伯常数的变化
m M r1 r2 r , Mr1 mr2 ; r1 r , r2 r; m M m M MV 2 Ze 2 mv 2 V v mM 2 r ; ; ; r1 4 0 r 2 n; 4 0 2 2 rn n ; 2 e
2 4 2 4
2
在这些公式中已经用不同标记加以区别(在 R的右下角 标注了原子符号)不同原子的里德伯常数, R∞ 是里德伯常 数的理论值,相当于原子核质量为无穷大时的里德伯常数 。 里德伯常数随原子核质量变化这情况曾被用来证实氢 的同位素 ─氘 ─ 的存在。 1932 年尤雷( H.C.Urey 1893~1981 )把三升液氢蒸发到不足一立方厘米,他这样提高了剩余 液氢中重氢的含量;然后把剩下的混合物装入放电管,摄 取其光谱,当时发现摄得赖曼系的头四条谱线都是双线, 在氢的 Hα 线( 6562.79Å)的旁边还有一条谱线( 6561.00Å ),两者只差1.79Å。他假定这一谱线属于氢的同位素 —氘 ,并认为m(H)/m(D)=1/2,然后计算得到不同的里德伯常数 RH 和RD,进而算出相应的波长。结果发现,计算值与实验 值相符得很好,从而肯定了氘(D—重氢)的存在。
F-H实验与原子能级的量子化
玻尔理论的要点是:原子内部存在稳定的量子态,电子在 量子态之间跃迁时伴随着电磁波的吸收或发射。光谱实验 ,就是从电磁波发射或吸收的分立特征,证明量子态的存 在。而夫兰克 -赫兹实验则是用电子束激发原子,如果原子 只能处于某些分立的能态(量子态),那末,实验一定会 显示,只有某种能量的电子才能引起原子的激发。
2n 2 Rc Rc 4 与经典比较 n n3
2Rc e 3 2 n 1 40 mr 3
e2 2 rn 3 n 40 16 2 R 2 c 2 m 1
2 e m R 2 40 ch 3
2 4
h 2
4 0 2 2 h rn n ; 2 2 me
E.氢原子能级和光谱
F.非量子化的状态与连续光谱
2 1 1 e 2 E mv 0 mv 2 4 r 2 2 0
